Study on Self-Excited Oscillation Suppression of Supersonic Inlet Based on Parallel Cavity

Aiming at the problem of self-excited oscillation in a supersonic inlet, the oscillation suppression of parallel cavities in a shock system is studied. Based on the shock dynamic model, the theoretical calculation model of parallel cavity under dynamic shock is established, and the effects of cavity volume and oscillation frequency on shock oscillation flow field parameters are analyzed. On this basis, an integrated numerical model including cavity and inlet and outflow fields is established, and the effects of cavity on the inlet flow field parameter distribution and parameter oscillation are compared by using unsteady numerical calculation algorithm. The theoretical calculation results show that the parallel cavity can reduce the amplitude of flow field pressure oscillation, and increasing the cavity volume is beneficial to suppress parameter oscillation. The unsteady numerical calculation of three groups of working conditions shows that the cavity changes the amplitude of parameter oscillation, and the high amplitude frequency point also decreases compared to the model without cavity. Through the alternating change of pressure between the channel and cavity during the movement of the shock wave, the cavity gas filling and overflow dampen the shock wave forward and pressure change of the mainstream, so as to suppress the self-excited oscillation.

Introduction

The flow field of a supersonic inlet is very complex. For a supersonic inlet or hypersonic inlet, an isolation section with equal cross section is usually set after the compression section to stabilize the shock system (Curran et al., 1996). At higher flight speeds, the Mach number of the flow in front of the positive shock in the inlet increases, the interference between the shock and the boundary layer intensifies, and the local separation induced by the shock makes the positive shock evolve into an oblique shock train (Rybalko et al., 2012; Tan et al., 2012). As the back pressure of the inlet increases, the shock train moves forward to the isolation section gradually, and the shock wave changes from symmetrical to asymmetrical and continues its entire movement (Tian et al., 2014). The research shows that even if the back pressure of the inlet remains constant, the shock position will move forward and backward, presenting a state of “self-excitation oscillation” (Meier et al., 1990), which may change the parameters of flow field pressure and flow rate and may cause the structure flutter of the inlet or the pressure oscillation of the inlet/combustion chamber, which will affect the combustion stability (Matsuo et al., 1999; Huang et al., 2018). Therefore, the study of shock wave unsteady oscillation is of great significance for engine design.

A lot of theoretical modeling and research work has been carried out for the shock oscillation phenomenon in a supersonic inlet. Ikui et al. (1974) believed that shock oscillations were caused by the propagation of turbulence pulsation from the upstream of shock waves to the downstream, and the oscillation frequency was related to the Helmholtz resonance frequency and pipeline resonance frequency in the experimental state. Hankey and Shang (1980) deduced the formula of pipe resonance frequency, which can estimate the acoustic resonance frequency under different test conditions. Piponniau et al. (2009) proposed a shock wave separation oscillation frequency model with high reliability through theoretical analysis based on the principle of flow conservation inside and outside the boundary layer separation envelope. Li et al. (2017) established a model of front movement of shock train in a complex background wave system by a theoretical method, predicted the forward propagation process of shock train, and achieved good results. Xu et al. (2019) improved the minimum contraction ratio analysis method of the equivalent throat through the supersonic free interaction theory and predicted the conversion law between the shock train jump and slow movement with reference to the Kantrowitz limit. In addition, based on the test and simulation methods, the pressure fluctuation and energy conversion process of the shock train (Sugiyama et al., 2008; Wang and Zhang, 2010; Li et al., 2012), variation characteristics of flow field parameters of self-excited and forced oscillations (Xiong et al., 2017a; Xiong et al., 2017b; Zhang and Yan, 2021), and the shock wave forward propagation rule (Xu et al., 2015; Lu et al., 2019) have been extensively studied. In addition, there are also relevant studies on the coupling between flow and combustion oscillations (Chen and Zhao, 2018; Zhao et al., 2018). These works provide a reference for understanding the dynamic behavior of shock waves by studying the behavior of shock wave oscillations in a complex flow field.

At present, the research on shock wave oscillation of a supersonic inlet mainly focuses on mechanism analysis, prediction model establishment, flow process research, and so on. On the suppression of shock oscillation in inlets, Herrmann et al. (2013) and Huang et al. (2020) have studied the inlet with a boundary layer suction device, which shows that the suction device has an influence on the process of shock oscillations and the changes of pressure parameters and will restrict the shock position in a certain state. Li (2019) studied the control algorithm under an unstable shock train from the aspect of an engine design by studying the characteristics of shock oscillations. In addition, in order to solve the problem of the local shock wave oscillation in a compressor, Ma (2019) used local boundary layer suction to control the oscillation amplitude and achieved good results in a certain range. Most of these research works control the local flow through the boundary layer overflow, so as to weaken the shock oscillation process. In general, research work on shock wave vibration suppression methods in the supersonic state is relatively less.

In this article, the shock wave oscillation suppression of a supersonic inlet is studied by parallel passive cavities in the isolation section. A theoretical model is established to analyze the feasibility of parallel cavity to suppress the oscillation of main flow parameters. The coupled self-excited oscillation process between the inlet and cavity is calculated based on the numerical method. Then, the effects of parallel passive cavities on the suppression of parameter fluctuations and the convection field in the process of inlet self-excited oscillation are analyzed.

Calculation Model

Inlet Geometry

Based on the inlet in Reinartz et al. (2003), the cavities are closed in parallel in the isolation section and are connected to the main flow channel through slots. The calculation model is shown in Figure 1. The inlet includes a supersonic compression section, an isometric straight throat section, and an expansion section. The parameter inlet height H₁ = 29 mm, compression angle ${\delta }_1$ = 20.5 degrees, lower lip distance from the leading edge point L₁ = 35 mm, length of the isolation section L₂ = 79.4 mm, height H₂ = 15 mm, and the other main parameters are the same as in Reinartz et al. (2003).

FIGURE 1

FIGURE 1. Schematic of the calculation model.

This article studies the influence and suppression of cavity on vibration. Considering the realizability of the structure, the cavity is located in the region composed of the upper wall of the inner channel and the outer wall of the inlet. Due to the nonuniformity of pressure distribution in the isolation section and the shock surface moving back and forth in the isometric section during oscillation, the cavity is divided into five equal volume parts and connected to the isolation section through a gap with a width of 0.75 mm. Cavity height H₄ is used as a variable parameter to change the volume of the cavity. L₄ is the width of the cavity, and its value is 6.61 mm.

Numerical Method and Verification

According to the basic model of the inlet shown in Figure 1 (Reinartz et al., 2003), the numerical model is established. The boundary conditions of the model include the pressure far-field conditions at the inlet of the external flow field, the pressure outlet conditions at the outlet of the inlet, and the adiabatic wall conditions at the inner and outer walls of the inlet. The finite volume method is used to solve the inlet flow field. The diffusion and convection terms in the control equation are discretized by the second-order central difference scheme and second-order upwind scheme, respectively. The coupled implicit method is used to solve the control equation. Since the SST $k-\omega$ model can simulate separated flow with a strong adverse pressure gradient, it is widely used in simulation calculation (Ma et al., 2017; Zhang and Yan, 2021). Therefore, the SST $k-\omega$ model is adopted in this article.

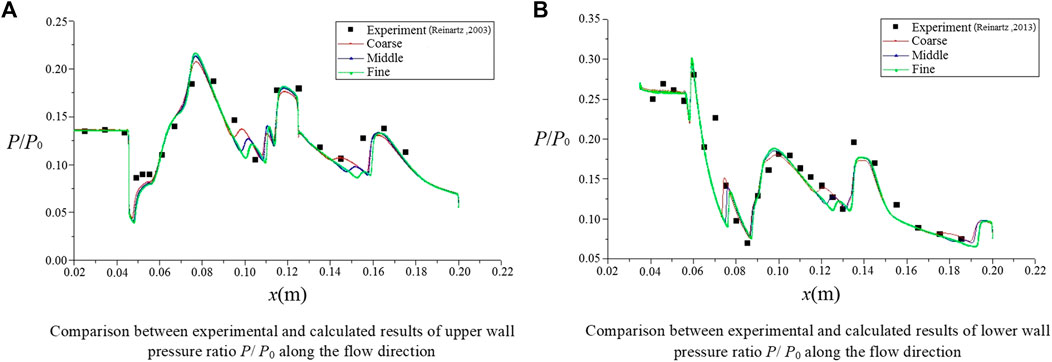
A grid scale has an important influence on shock wave resolution. In order to compare the influence of the different grid precision on the flow field calculation, three different grid number models are established, and 150,000 (Coarse), 300,000 (Middle), and 600,000 (Fine) grids are generated by local encryption and other measures.

The numerical calculation was carried out for the working condition of Ma2.41. The total inlet temperature is 305 K, the total pressure is 540 kPa, and the angle of attack of the inlet is −10⁰. The calculation conditions are in accordance with the test conditions in Reinartz et al. (2003). During the calculation, the integral value of the wall pressure of the inner channel is monitored and the flow change at the outlet ensured such that the relative amount of parameter change is within 0.2%, within 1,000 iteration steps, so as to ensure the convergence of the calculation process.

From the comparison of the pressure distribution in Figure 2, the variation trends of the upper and lower wall pressures of the three grid models with different precisions are basically the same. There is a slight difference in the local pressure jump caused by the shock wave, that is, the position resolution of the shock wave is different. The Middle model and Fine model are relatively close in the local position of the pressure jump. Compared with the test results, the calculation results are in good agreement with the pressure change process of the test points. For the three groups of models, the pressure on the inner wall is integrated respectively. The errors of the Coarse model and Middle model relative to the Fine model are 2.87 and 0.79%, respectively. In general, the different simulation models have good accuracy.

FIGURE 2

FIGURE 2. Comparison of wall pressure distribution.

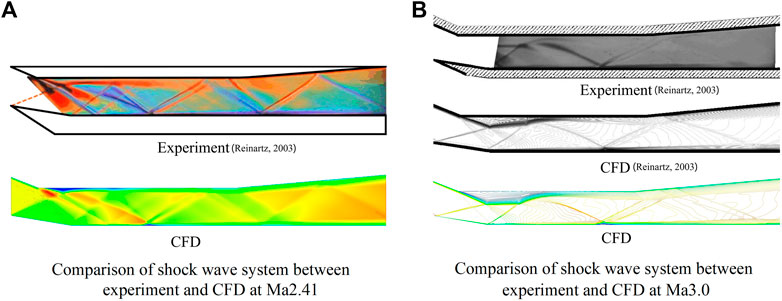
The shock train at two Mach numbers calculated by the Middle model is compared with the experimental schlieren (Reinartz et al., 2003) in Figure 3. It can be seen from Figure 3A that when $M{a}_{\infty }$ = 2.41, the shock wave reflected by the lower lip intersects with the upper wall surface after the turning point of the compression surface, resulting in a local expansion wave and the local separation of the boundary layer due to the incidence of the oblique shock wave. The interaction and reflection of the shock and expansion waves in the isolation section and the expansion section, and the changes and flow characteristics of these complex wave systems are close to the experimental schlieren. From the comparison of the results of $M{a}_{\infty }$ = 3.0, the separation zone with a large range of the upper wall turning zone reflected in the simulation results in this article is consistent with the simulation and test results in Reinartz et al. (2003), and the expansion flow and reflected wave system after the separation zone are also the same as those of the referenced study.

FIGURE 3

FIGURE 3. Comparison of the inlet flow field.

The comparison with the experimental results shows that the numerical modeling method is feasible. The results of the Middle model in this article are close to those of the Fine model, but the number of grids is reduced by half. Considering the trade-off between computational efficiency and accuracy, the Middle model with 300,000 medium number of grids is used for calculation and analysis.

Sampling Location and Calculation Strategy

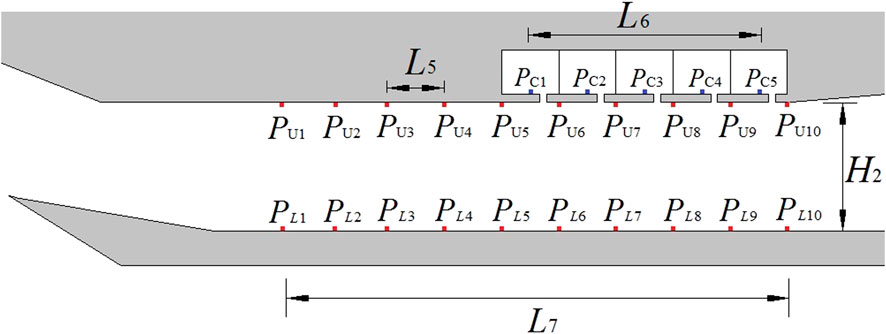
In the unsteady calculation, sampling points are set to monitor the pressure change process, including the upper and lower walls of the isolation section and the cavity area. As shown in Figure 4, there are a total of 20 sampling points in the isolation section. The sampling points P_U1–P_U10 on the upper wall are evenly distributed at an interval of L₅ = 6.61 mm from the end point of the equal–straight isolation section to the front. The sampling points, numbered P_C1–Pc₅, are located near the midpoint of the lower wall of the cavity. The length of the cavity sampling area L₆ = 26.44 mm, and the length of the isolation section sampling area L₇ = 59.49 mm.

FIGURE 4

FIGURE 4. Location of sampling points.

For the model with cavity, during the numerical calculation, the gap between the cavity and the mainstream is closed first, and the initial flow field is calculated by the steady method, then by the unsteady method. After 2–3 shock oscillation cycles, the cavity pressure is initialized with the mainstream pressure at the gap between the cavity and mainstream, the flow velocity in the cavity is set to zero, and the calculation is further iterated until the calculation process is stable.

Theoretical Modeling and Analysis

Shock Dynamics Model

Using the theoretical method, a shock dynamic model is established for the channel with equal cross section. For the two configurations, the change law of the flow field parameters when the outlet backpressure oscillates is analyzed to compare the influence of the cavity on the parameter oscillation.

1) Constant Cross-Section Channel Shock Dynamics Model

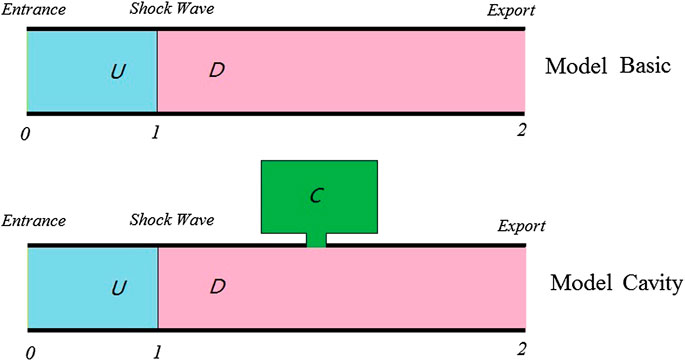
The theoretical model adopts the constant cross-section channel (Model Basic), the positive shock is located at position 1 in the channel, and the inlet and outlet of the channel are numbered 0 and 2, respectively. Taking the shock surface as the boundary, the pipeline is divided into upstream area U and downstream area D, as shown in Figure 5 (Model Basic). In Model B with cavity, cavity C is located on the upper side of the downstream area D and connected through the main flow of the gap, as shown in Figure 5 (Model Cavity).

FIGURE 5

FIGURE 5. Theoretical calculation model of shock wave motion.

According to the pressures $P_{1U}$ and $P_{1D}$ before and after the shock surface 1 and the flow velocity $M{a}_{1U}$ before the shock, the motion velocity ${\dot{x}}_1$ of the shock surface is calculated as follows (Pan and Shan, 2011):

${\dot{x}}_1=a_{1U}\left(M{a}_{1U}-\sqrt{\frac{P_{1D}}{P_{1U}}\frac{k+1}{2k}+\frac{k-1}{2k}}\right).(1)$

Set: $M{a}_M=M{a}_{1U}-{\dot{x}}_1/a_0$, where a₀ is the sound velocity in front of the shock wave.

The relationship between the flow downstream of the moving shock wave Ma_1u and the forward moving speed of the shock wave Ma_1u, the parameter Ma_M, and the moving speed ${\dot{x}}_1$ is:

${\dot{m}}_{1D}={\dot{m}}_{1U}\left(1+\frac{1}{a_{1U}M{a}_{1U}}\frac{2\left(M{a}_M^2-1\right)}{2+\left(k-1\right)M{a}_M^2}{\dot{x}}_1\right).(2)$

The volume change rate of downstream control volume V_D after the shock wave is:

${\dot{V}}_D=-A{\dot{x}}_1.(3)$

For the downstream control body D, the relationship between the inlet and outlet flow and the volume V_D, density ${\rho }_D$, and its rate of change is:

${\dot{m}}_{1D}-{\dot{m}}_2=V_D{\dot{\rho }}_D+{\rho }_D{\dot{V}}_D.(4)$

In addition, according to the ideal gas equation, the density change rate is:

${\dot{\rho }}_D=\frac{M}{R{T}_D}{\dot{P}}_D.(5)$

Combining Formulas 4 and 5, the flow formula becomes:

${\dot{m}}_{1D}-{\dot{m}}_2=V_D\frac{M}{R{T}_D}{\dot{P}}_D+\frac{M{P}_D}{R{T}_D}{\dot{V}}_D.(6)$

According to the above formula, the change rate of downstream control body D pressure is calculated as:

${\dot{P}}_D=\left(\left({\dot{m}}_{1D}-{\dot{m}}_2\right)-\frac{M{P}_D}{R{T}_D}{\dot{V}}_D\right)\frac{R{T}_D}{V_{D}M}.(7)$

For the upstream controlled body U, the upstream pressure change rate is:

${\dot{P}}_U=\left(\left({\dot{m}}_0-{\dot{m}}_{1U}\right)-\frac{M{P}_U}{R{T}_U}{\dot{V}}_U\right)\frac{R{T}_U}{V_{U}M}.(8)$

According to the volume change rate ${\dot{V}}_U$ of the upstream control body, the shock wave motion speed ${\dot{x}}_1$, and the parameters of the inlet 0 section, the inlet and outlet flow rates ${\dot{m}}_0$ and ${\dot{m}}_{1U}$ of the control body are calculated, and the upstream pressure change rate ${\dot{P}}_U$ is calculated according to Formula 8.

In addition, it also includes the relationship between aerodynamic parameters and their differential values:

$P_D={\displaystyle \int {\dot{P}}_D}dt{V}_D={\displaystyle \int {\dot{V}}_D}dt{\rho }_D={\displaystyle \int {\dot{\rho }}_D}dt.(9)$

For the equations composed of the above formulas, the change process of the upstream and downstream parameters and the change of the shock surface position x can be calculated by a simultaneous solution.

2) Computational model with cavity

In the Model Cavity with a cavity, when the pressure in the downstream D area changes, due to the pressure imbalance in the cavity C and D areas, there will be a flow into or out of cavity C under the action of the pressure difference, and the flow in C cavity is close to the stagnation, i.e., $T_C\approx T_0^{\ast }$. The cavity volume $V_C$ is a constant value, and the relationship between the flow entering the C cavity ${\dot{m}}_C$ and the pressure differential ${\dot{P}}_C$ is:

${\dot{m}}_C=V_C{\dot{\rho }}_C=V_C\frac{M}{R{T}_0^{\ast }}{\dot{P}}_C.(10)$

According to the flow balance relationship, Formula 4 is transformed into:

${\dot{m}}_{1D}-V_C\frac{M}{R{T}_0^{\ast }}{\dot{P}}_C-{\dot{m}}_2=V_D{\dot{\rho }}_D+{\rho }_D{\dot{V}}_D.(11)$

Further deformation obtains the pressure change rate ${\dot{P}}_D$ downstream of the shock wave as:

${\dot{P}}_D=\left(\left({\dot{m}}_{1D}-{\dot{m}}_2\right)-\frac{M{P}_D}{R{T}_D}{\dot{V}}_D\right)/\left(\frac{M{V}_D}{R{T}_D}+\frac{M{V}_C}{R{T}_0^{\ast }}\right).(12)$

Since the airflow velocity in the cavity is close to stagnation, the total pressure is taken as pressure $P_D$ in the mainstream area, and the static pressure is the cavity pressure $P_C$. According to the relationship between the total pressure p*, static pressure p, and Mach number, the flow Mach number in the gap $M{a}_{Fx}$ can be calculated as:

$M{a}_{Fx}=\sqrt{\left({\left(\frac{P}{P^{\ast }}\right)}^{-\frac{k-1}{k}}-1\right)/0.2}.(13)$

When $P_C$ > $P_D$, Formula 13 is transformed into:

$M{a}_{Fx}=\sqrt{\left({\left(\frac{P_D}{P_C}\right)}^{-\frac{k-1}{k}}-1\right)/0.2}.(14)$

When $P_C$ < $P_D$, Formula 13 is transformed into:

$M{a}_{Fx}=\sqrt{\left({\left(\frac{P_C}{P_D}\right)}^{-\frac{k-1}{k}}-1\right)/0.2}.(15)$

The velocity coefficient ${\lambda }_{Fx}$ and flow function $q\left({\lambda }_{Fx}\right)$ are calculated according to the gap flow $M{a}_{Fx}$ as:

${\lambda }_{Fx}=\sqrt{1.2M{a}^2/\left(1+0.2M{a}^2\right)},$

$q\left({\lambda }_{Fx}\right)={1.2}^{2.5}{\lambda }_{Fx}{\left(1-\frac{0.4}{2.4}{\lambda }_{Fx}^2\right)}^{2.5}.(16)$

The flow through the gap is:

${\dot{m}}_C=0.0404\frac{P_C}{\sqrt{T_0^{\ast }}}q\left({\lambda }_{Fx}\right)A_{Fx}$

or:

${\dot{m}}_C=0.0404\frac{P_D}{\sqrt{T_0^{\ast }}}q\left({\lambda }_{Fx}\right)A_{Fx}.(17)$

According to ${\dot{m}}_C$, the cavity pressure change rate ${\dot{P}}_C$ is calculated as:

${\dot{P}}_C={\dot{m}}_{C}KR{T}_0^{\ast }/V_C.(18)$

By combining the above parameters, the variation of the downstream parameters of the shock wave with a cavity can be solved.

Case Analysis

1) Static parameter calculation

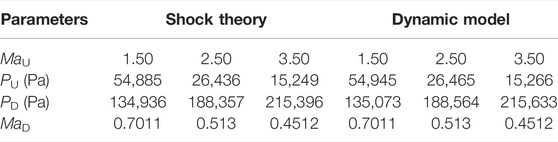
Using the established shock wave dynamic model, the theoretical parameters at different inlet velocities are calculated. The total inlet temperature is 502.088 k and the inlet flow is 3.092 kg/s. The steady-state parameters before and after the shock wave are calculated according to the above inlet conditions, which are compared with the shock wave theory in Table 1. It can be seen that the parameters calculated by the shock dynamic model in the Shock Dynamics Model section are consistent with the results calculated by the shock theory.

TABLE 1

TABLE 1. Comparison of calculation parameters of different models.

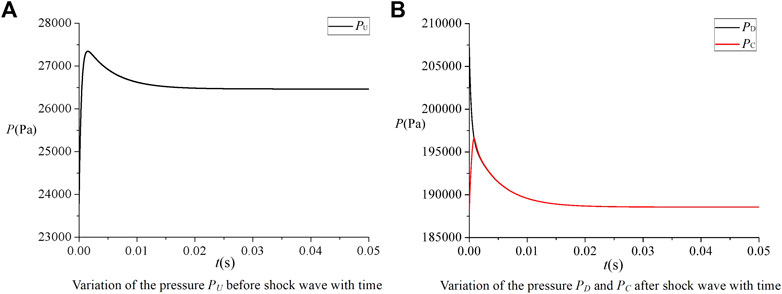
For the velocity of Ma25, the initial values of pressure P_U before shock, pressure P_D after shock and cavity pressure P_C are set to be −10%, −10% and 10% different from the theoretical steady-state value respectively. The steady-state parameters are calculated based on the dynamic model, and the time step is 0.5 × 10⁻⁶ s. Figure 6 shows the dynamic change process of the pressure before and after the shock wave. The pressure P_U before the shock wave has a certain overshoot in the rising process and can quickly stabilize to the steady-state value. The initial values of pressures P_D and P_C after the shock wave are quite different and gradually tend to be consistent with time and remain at the theoretical steady-state value, and the adjustment time from the initial value to parameter stability is about 0.01 s. The calculation results show that the dynamic model can converge to the theoretical steady-state value under large initial value deviation.

FIGURE 6

FIGURE 6. Pressure change process.

The comparison between the two theoretical methods shows the feasibility of the dynamic calculation model.

2) Theoretical analysis of cavity effect on oscillation

Based on the shock wave dynamics model, the influence of the cavity on the parametric oscillation during shock oscillation is analyzed. Since there is no self-excited oscillation in the theoretical model, in order to simulate the oscillation process of the shock wave, a certain frequency and amplitude of back pressure P₂ is applied at the outlet:

$P_2\left(t\right)=P_0+K{P}_0\sin \left(\omega t\right).(19)$

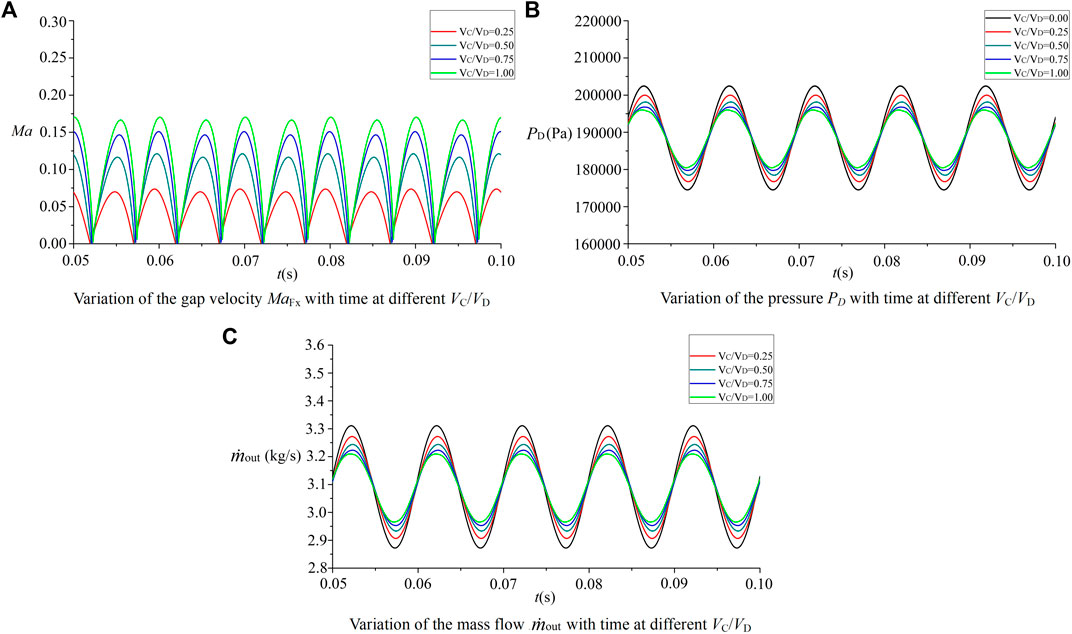
The dynamic response of flow field parameters is calculated for different cavity volume ratios V_C/V_D. In the calculation example, the analysis is carried out for the working condition of Ma₀ = 2.5, taking the amplitude K = 0.1, the frequency $\omega$ = 100, and $P_0$ = 26,465 Pa. The calculation results are compared in Figure 7.

FIGURE 7

FIGURE 7. Parameter variations under the different volume ratios V_C/V_D.

As can be seen from Figure 7, when the outlet back pressure $P_2$ fluctuates, after the stable process is established, the pressure and flow change periodically with the same frequency of the back pressure. Due to the periodic change of pressure $P_2$, the shock wave moves back and forth under the action of the back pressure. After the shock wave, the volume of the control body D area changes, resulting in the change of the pressure $P_2$ in the mainstream area, which in turn causes the flow velocity $M{a}_{Fx}$ in the gap entering the cavity to fluctuate. The value of the Mach number is a positive value. In one cycle, the airflow experiences the process of entering cavity C and entering the main channel D, and the oscillation frequency of the Mach number doubles in value.

Comparing the calculation results of different volume ratios V_C/V_D, it can be seen that under the same back pressure condition, with the increase of the cavity volume, the mainstream can continue to fill when entering the cavity, which hinders the change trend of the mainstream pressure $P_D$, and the fluctuation amplitude of pressure $P_D$ and flow ${\dot{m}}_{out}$ decreases. At the same time, after the amplitude of pressure $P_D$ decreases, the pressure difference between the main flow and cavity decreases, and the Mach number $M{a}_{Fx}$ of the gap flow also decreases. From the calculation results, compared with the scheme without cavity, the pressure P_D and outlet flow ${\dot{m}}_{out}$ at V_C/V_D = 0.5 decrease to 71.62 and 72.09%, respectively.

For the state of V_C/V_D = 0.5, two different back pressure pulsation frequencies were selected, and the changes in pressure P_D and P_C were compared to study the influence of the oscillation frequency. From the 100-Hz curve, the variation rules and amplitudes of the cavity pressure P_C and the flow channel pressure P_D are basically the same, while the cavity pressure curve slightly lags behind the pressure change of the main flow channel, which indicates that the pressure difference between the two cavities is small. Under the action of the maximum pressure difference, the maximum value of the gap flow velocity does not exceed Ma0.15.

When the oscillation frequency of back pressure $P_2$ is increased to 500 Hz, the amplitude of the mainstream pressure P_D increases compared with 100 Hz, while the amplitude of the cavity pressure P_C decreases, as shown in Figure 8. In the process of repeated filling of air flow in the mainstream and cavity, the change of flow pressure through the gap needs a certain time history. When the frequency increases, the dynamic process time of air flow entering or exiting the cavity is relatively shorter. In one cycle, the amplitude of cavity pressure P_C does not increase to the same as that of the mainstream, and the pressure of the mainstream begins to decrease again. Therefore, P_C is significantly smaller than P_D in the mainstream area, and the cavity pressure P_C has a phase difference of about half a cycle relative to the channel pressure P_D. Compared with the results of 100 Hz, there is a significant difference between the two cases. Due to the changes in the internal and external pressure difference and phase change, the Mach number of the gap is relatively higher. The calculation shows that the maximum velocity of the gap reaches Ma_Fx = 0.36.

FIGURE 8

FIGURE 8. Pressure comparisons under different back pressure variation frequencies.

Based on the above theoretical model analysis, when the shock position and pressure after the shock change, a parallel cavity is added in the downstream area of the shock, and due to the change of the relative pressure between the main stream and cavity, the air flows between the cavity and main stream, which can weaken the parameter change amplitude in the oscillation process of the shock to a certain extent and inhibit the shock oscillation. Through analysis, the volume of the cavity and frequency of parameter oscillation have an impact on the effect of oscillation suppression. Increasing the volume of the cavity can “accommodate” or “release” more air flow when the mainstream pressure increases or decreases, so as to hinder the change of parameters. At a lower frequency, the air can flow between the cavity and mainstream for more time, so as to improve the effect of parameter change suppression.

Simulation and Analysis of Shock Dynamic Process

The theoretical analysis shows that the cavity can restrain the parameter fluctuation. In practice, when the outlet pressure remains constant, it will also produce a certain range of self-excited oscillation, which will cause the fluctuation of flow, pressure, and other parameters, as well as the forward and backward movement of the shock. Moreover, due to the gas viscosity and wall boundary layer, the coupling with the compression wave system of the inlet will produce strong shock/boundary layer interference, and the unsteady motion of the shock train adds to the complexity of the flow. In the process of shock wave oscillation, when the shock wave moves forward and backward, it may also cross the gap of the cavity. The filling process of the cavity will be very complex, which is difficult to analyze by these theoretical methods. Therefore, the unsteady numerical calculation method is used for research.

Calculation Condition and Time Step

According to the calculation model shown in Figure 1, the self-excited oscillation processes under two different cavity volumes are calculated and compared with the results without cavity. The calculation conditions are listed in Table 2. The difference between the three models lies in the numerical difference of cavity height H₄ (as shown in Figure 1).

TABLE 2

TABLE 2. Computational model.

In the shock wave oscillation simulation of the inlet, the calculation is carried out for the state of incoming flow $M{a}_{\infty }$ = 3.0 and back pressure ratio $P_{out}/P_{\infty }$ = 9.0. Other parameters of the inlet are consistent with those in Reinartz et al. (2003). The selection of the time step has a very important impact on unsteady calculation and is related to the frequency of shock oscillation and grid scale. There are enough iterative steps in one cycle to ensure the convergence of calculation results. When determining the time step, on the one hand, a larger time step is started with initially and the value of the time step is then reduced until the calculated shock oscillation frequency analysis result has nothing to do with the step; on the other hand, according to the spectrum analysis, the shock wave oscillation frequency is about 400 Hz and the iteration step in one cycle is guaranteed to be 5,000 steps; through the analysis, the iterative step size of 0.5 × 10⁻⁶ s is taken in this article.

Flow Parameter Comparison and Analysis

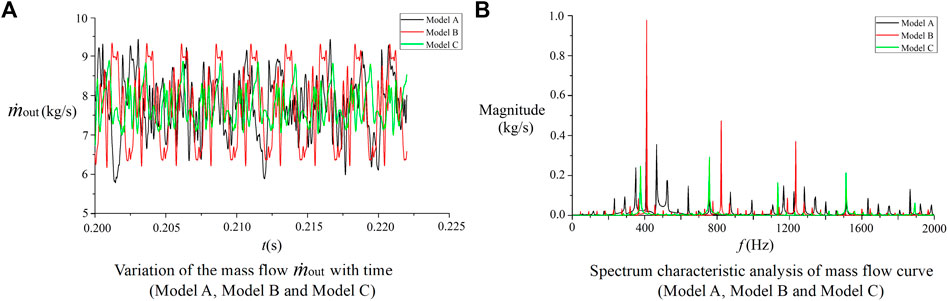
According to the working conditions in Table 2, the variation laws of outlet flow ${\dot{m}}_{out}$ and pressure at typical sampling points are compared. According to the calculation results in Figure 9, when the back pressure is fixed, the outlet flow of the inlet of the different models oscillates and the amplitude and frequency of the flow curve oscillation of the three models are different.

FIGURE 9

FIGURE 9. Variation of the mass flow of outlet.

The flow fluctuation range of Model A is 5.79–9.42 kg/s, and the maximum variation amplitude exceeds $\pm 30\%$ relative to the steady-state value, with a large fluctuation and jump. The periodicity of the flow curve change is poor, and the peak value of different cycles is also different. Model B has a smaller cavity added, and the flow curves of the different cycles are relatively consistent. In each cycle, it includes the process of rapid rise and rapid decline, and the outlet flow fluctuates in the range of 6.13–9.37 kg/s. Numerically, it is slightly smaller than the fluctuation range of Model A, but due to the differences between the different cycles of Model A, the flow fluctuation of Model B in some cycles is greater than that of Model A. The vibration amplitude of the flow curve of Model C is relatively reduced, and the consistency of the curve change is also good. The variation range of the outlet flow is 7.04–8.82 kg/s.

FFT analysis on the flow curve was performed to analyze the spectral characteristics. From the comparison in Figure 9B, it can be seen that the two frequencies with larger amplitudes of the flow curve of Model A are 408 and 466 Hz, respectively, and there are two frequency ranges with larger amplitudes, 300–550 and 1100–1400 Hz, respectively. It shows the complexity of the shock oscillation process. The frequency corresponding to the maximum amplitude of Model B is 411 Hz, and the maximum amplitude at this frequency is significantly higher than that of Model A. In addition, there are also larger amplitudes at the two frequency points of 823 and 1230 Hz. Model C is relatively high at the four frequency points of 377, 758, 1140, and 1510 Hz, but it is lower than the maximum amplitude of Model A, which indicates that the cavity has a certain influence on the amplitude and frequency of the flow. This indicates that under the action of the cavity, the flow curve changes from multiple frequency points of Model A to three and four main frequency points of Model B and Model C, respectively. The main frequency points decrease and the curve changes periodically. From the perspective of the amplitude, although it increases at some frequencies, the total oscillation energy decreases due to the decrease of frequency points. The fundamental frequencies of the three models are close, and Model C with a larger cavity volume has a better suppression effect on the flow oscillation.

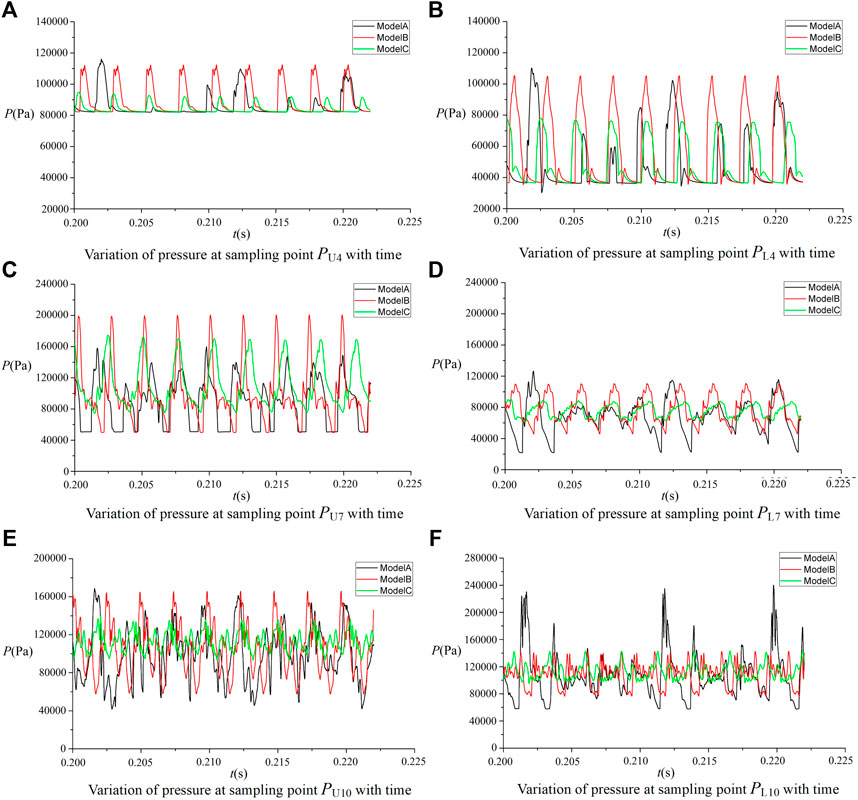
According to the simulation calculation, the shock wave oscillation in the inlet is mainly in the middle and rear of the isolation section. For sampling points 4, 7, and 10, the pressure fluctuation process is compared in Figure 10.

FIGURE 10

FIGURE 10. Variation of the pressure at different sampling points.

From the pressure changes of the sampling points P_U4 and P_L4 in Figure 10, the sampling points are close to the front of the isolating section. In Model A without a cavity, the pressure fluctuations are nonperiodic, and there are small peaks between larger peaks. This indicates that the leading edge of the separation shock only moves forward to this sampling position for part of the time during the oscillation process. The periodicity of the pressure oscillation in Model B is obvious. The frequency of the pressure oscillation on the upper and lower walls is the same. Due to the asymmetry of the shock wave in the flow field, the pressure values are different at the same sampling position. The amplitude of the sampling point P_L4 on the lower wall is higher than that of P_U4. The volume of the Model C cavity increases, the amplitude of the pressure oscillation at the sampling point P_U4 is significantly reduced, and the amplitude of the sampling point P_L4 on the upper and lower walls also drops to about half of that of Model B. The peaks and constants appear alternately in the pressure curve, indicating that the shock wave moves forward before sampling point 4 for a part of the time, and moves backward after the sampling point for a part of the time. Due to the increase in the volume of the cavity of Model C, for the system composed of the inlet and the cavity, it is equivalent to increasing the overall space volume. According to the acoustic theory, the acoustic oscillation frequency decreases. According to the spectrum analysis, the main frequencies of pressure oscillations of Model B and Model C are 411 and 372 Hz, respectively, which are close to the results of the spectrum analysis of the outlet flow.

When comparing the pressure curve at sampling point 7 in Figures 10C,D, although the pressure oscillations at sampling points P_U7 and P_L7 on the upper and lower walls of Model A also show a certain periodicity, the change process, however, between curves is different. The curve of the sampling point P_U7 contains the change process of the alternating ratio between the peak and the constant value, and the peak also shows the process of rapid rise and fall; the P_L7 curve of the sampling point on the lower wall has no constant value part and only contains alternating large and small amplitudes. The amplitudes of Model B under different cycles are basically the same. The amplitude of the sampling point P_U7 on the upper wall is larger than that in Model A, but the oscillation amplitude of P_L7 on the lower wall is smaller than that in Model A. The oscillation amplitude of Model C is significantly reduced, and the sampling point amplitude is about half that in Model B.

The sampling point 10 is located behind the parallel cavity, and the cavity in this region interacts with the airflow in the inlet. As can be seen from Figure 10E, the pressure oscillation range of P_U10 on the upper wall of Model A is large, and the large amplitude oscillation and small amplitude oscillation of P_L10 on the lower wall occur alternately. The cavity volume of Model B is small, the amplitude of P_U10 on the upper wall is slightly less than that of Model A, and the amplitude of pressure fluctuation at the sampling point P_L10 is consistent and significantly reduced in different periods. After the cavity volume further increases, the pressure curve fluctuation of Model C at sampling points P_U10 and P_L10 decreases significantly when compared with that of Model A.

Comparing the calculation results in Figure 10 with those in the Theoretical Modeling and Analysis section, it can be seen that the interference of the shock boundary layer cannot be considered in the process of theoretical analysis, and the periodicity of the parameter change is good. In the actual inlet, due to the shock boundary layer's interference, coupled with the shock oscillation process, the shape of the parameter change curve is more complex. However, the results of the theoretical model and inlet numerical calculation show that the parallel cavity can reduce the amplitude of pressure oscillation at different sampling points and inhibit the shock oscillation process.

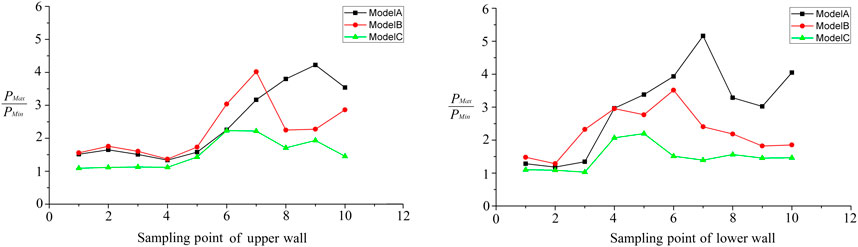
The pressure fluctuation amplitude ratio P_Max/p_Min was compared at different sampling points. From the comparison as shown in Figure 11, the amplitudes before the sampling point P_U4 on the upper wall and sampling point P_L2 on the lower wall are relatively small. In the rear part of the isolation section, the pressure of Model A oscillates greatly, with a maximum amplitude ratio exceeding 5. Compared with Model A, the maximum pressure amplitude of Model B increased at points P_U4–P_U7 on the upper wall, and decreased after P_U8; the lower wall decreased significantly from P_L4 onward. The pressure does not oscillate before P_U1–P_U5 on the wall of Model C, while the amplitude ratio is within 2 between P_U6 and P_U10. Among the sampling points on the lower wall, the amplitude ratio of P_L4 and P_L5 is about 2, and the amplitude ratio of the other sampling points does not exceed 1.5. Compared with the case that the maximum amplitude ratio of Model A without cavity exceeds 5, the Model C cavity significantly reduces the pressure amplitude ratio at the sampling point, especially the influence of the lower wall is more obvious, which shows that the cavity can significantly reduce the pressure oscillation.

FIGURE 11

FIGURE 11. Comparison of the maximum amplitude at sampling points.

Flow Field Characteristic Analysis

According to different calculation models, the variations of the flow field in the process of inlet self-excited oscillation is analyzed.

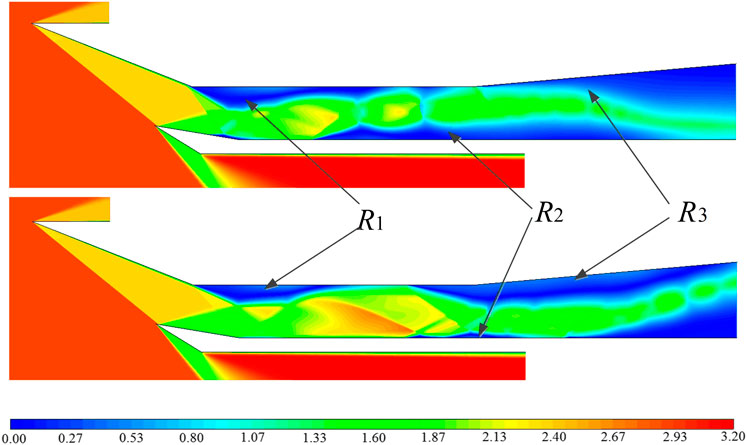
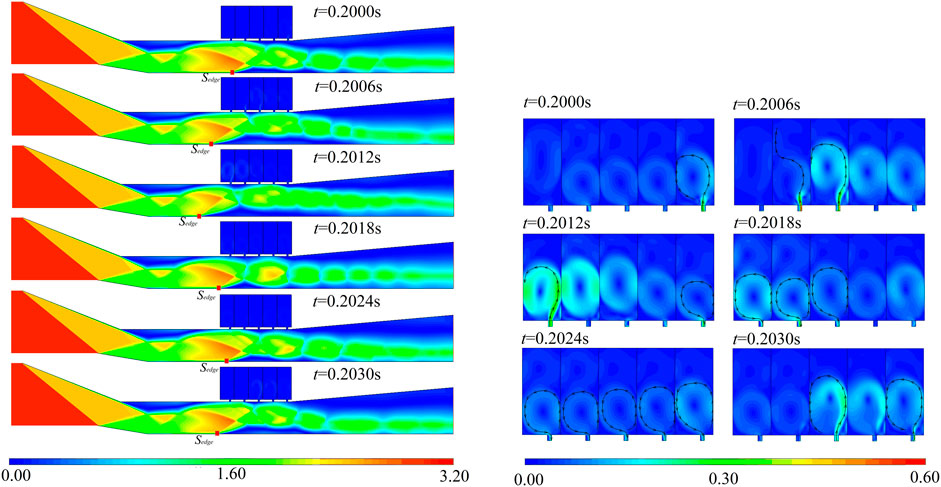
Figure 12 shows the Mach number distribution of the typical flow field in the inlet. It can be seen that under the action of back pressure, the positive shock evolves into a complex wave system which includes the expansion wave, oblique shock, local separation, and shock reflection. There is a strong shock wave/boundary layer interference in the flow field, resulting in the local separation, It includes the R₁ separation zone generated by the interference of the shock wave reflected from the lower lip after the turning point of the compression surface, the R₂ separation zone generated by the interference of the shock train and the boundary layer on the lower wall, and the R₃ separation zone developed from the inlet along the wall under the adverse pressure gradient of the expansion section. The positions and scales of these separation regions change in a large range with the self-excited oscillation in the inlet and are coupled to oscillate with the flow field parameters such as the outlet flow rate and the pressure at the sampling point.

FIGURE 12

FIGURE 12. Typical Mach number contours of Model A at different times.

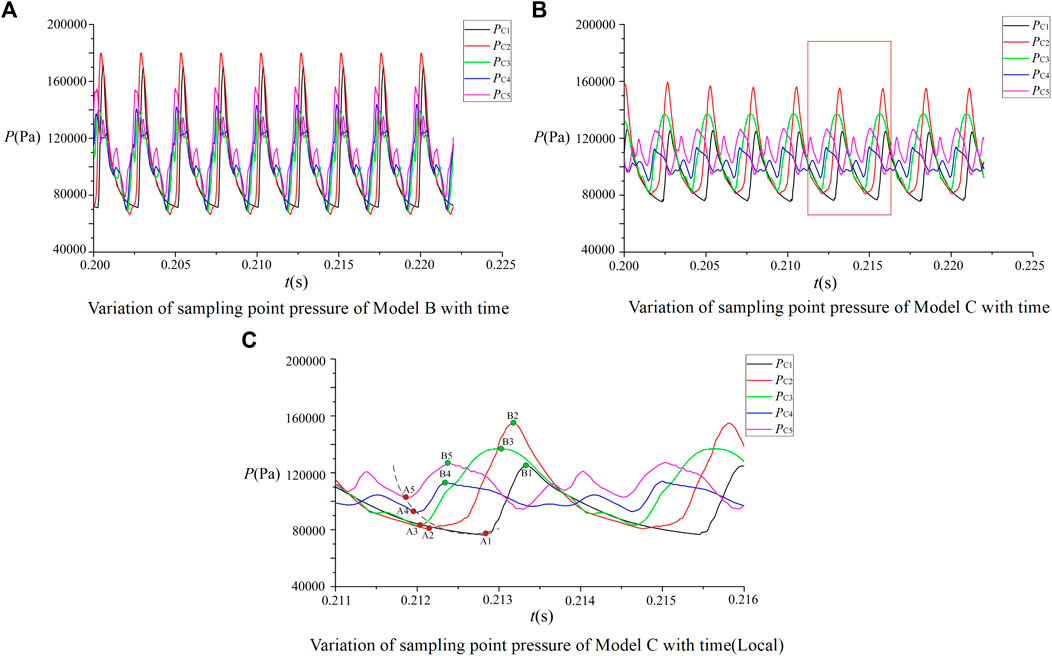
It can be seen from the results of Figure 10 that there is a clear difference in the amplitude of sampling points between Model B and Model C. Comparing the pressure of the corresponding cavity sampling point with that in Figure 13, the pressure oscillation frequency of the cavity is close to that of the mainstream sampling point. At the same sampling point, the pressure oscillation amplitude of Model C is small. From the analysis of the consistency of pressure oscillation at different sampling points, the amplitude and phase of the pressure curve oscillation of each sampling point in Model B are basically consistent. The sampling points P_C1 and P_C2 of Model C have large pressure amplitudes, but other points have relatively small amplitudes, which correspond to the small pressure amplitudes of sampling points 6–8 in the mainstream area. Moreover, there is an obvious phase difference between the different sampling points of Model C.

FIGURE 13

FIGURE 13. Variation of pressure at cavity sampling point.

The pressure change process in the cavity of Model C was further analyzed. From the local pressure curve, as shown in Figure 13C, the amplitude of the sampling point P_C2 is the largest. Combined with the Mach number analysis of the flow field in Figure 14, this sampling point is located in the leading edge of the shock system, where the shock wave swept across this position repeatedly in the process of periodic movement. The large fluctuation of pressure before and after the shock wave causes the pressure in the cavity to change under the alternating low–high–low pressure environment of the mainstream, where the pressure amplitude of the sampling point change is larger and the pressure amplitude of the P_C2 point changes more than two times. The pressure waveforms of the different sampling points also change. Among them, P_C1–P_C3 basically show a relatively regular periodic change process, while the pressure waveforms of P_C4 and P_C5 superimpose more frequencies in one cycle.

FIGURE 14

FIGURE 14. Mach number contours of Model C.

Comparing the change processes of the different curves, it can also see that there are obvious phase differences between the different sampling points. The pressure troughs of different curves develop from point A₅ to point A₁, which takes about 1 ms, indicating that the shock wave moves forward in the region of the sampling point. When the mainstream pressure increases, the pressure difference within the cavity increases, the air flow fills the cavity, and the sampling point curve rises. The relationship between the internal and external pressure differences at the different sampling points is different, and the time and value of the pressure curve reaching the peak value are also different. After this, the leading edge of the shock wave moves backward; the cavity pressure, filled by the high pressure after the shock wave, is higher than the pressure of the main stream before the shock wave; the air flow enters the main stream from the cavity; and the pressure at the sampling points P_C1–P_C5 begins to decrease. The periodic motion of the shock wave causes the periodic fluctuation of the main flow and cavity pressure.

Analyzing the Mach number change of the flow field in Figure 14, it can be seen that there are still some fluctuations in the flow field after the shock wave system in the isolator, corresponding to the separation areas of R₁ and R₂ in Figure 12. In one cycle, the leading edge S_edge of the separation zone R₂ moves back and forth within a certain range, and the range of R₂ also changes, but its range of change is significantly reduced compared to the two typical flow fields in Figure 12. At the same time, after the parallel cavity, the R₃ separation zone from the outlet to the inlet of the expansion section basically does not cross the straight section and continues to develop. Due to the movement of S_edge, the reflected shock generated by the compression of the main stream by the lower separation bubble will be reflected to the upper wall to produce a certain separation zone, but this separation zone is relatively small and does not develop greatly in scale, and the leading edge of the upper wall of the shock wave system lags behind the leading edge of the lower wall.

Combined with the local velocity and streamline of the cavity in Figure 14, at t = 0.200 s, the leading edge of the shock string is located in the middle of the isolator section, and the pressure of the inlet channel is higher than that of the fifth cavity, so air flow is injected into the cavity through the gap. As the shock wave moves forward, the inflation process of cavity 5 in space–time with t = 0.206 s is basically completed. When the leading edge of the shock wave crosses the second and third cavities, high-pressure air flow enters the two cavities. When t = 0.206 s, cavity 1 begins to be filled with mainstream gas. At the same time, due to the front movement of the shock wave, the pressure after the shock wave decreases relatively, and cavity 5 begins to exhaust to the mainstream area after the pressure is higher than the mainstream. After this, the leading edge of the shock wave begins to move backward, the mainstream pressure as the back pressure of the cavity drops sharply, and the cavity overflows into the mainstream. The periodic movement before and after the shock wave also leads to the periodic filling process of the cavity. This filling process has time differences between the different cavities, and there is a phase difference corresponding to the pressure curve, as shown in Figure 14.

Through the above analysis, the cavity is equivalent to the pressure comparison device relative to the mainstream. When the shock wave moves forward and the pressure increases, the air flow enters the cavity, which “hinders” the trend of shock wave moving forward to a certain extent; when the shock wave moves backward, the movement of the shock wave is also restrained by the deflation process. Therefore, the pressure oscillation process of the cavity in the inlet increases the aerodynamic damping, so as to reduce the shock amplitude and the change of flow field parameters, which is consistent with the analysis of the theoretical model.

Conclusion

In this article, the self-excited oscillation of a supersonic inlet is studied, and the dynamic theoretical model of shock oscillation is established. The variation laws of parameter oscillation and flow field under three different models are compared through numerical simulation. The results show that:

1) based on the shock dynamic model, the theoretical model and numerical simulation model of shock oscillation analysis are established. The comparison with the shock theory and public reference shows that the theory and numerical modeling method in this article are feasible.

2) the theoretical model analysis of different volume cavities and shock oscillation frequencies shows that increasing the volume of parallel cavities can reduce the parametric oscillation amplitude. According to the example analysis, when the cavity volume is 0.5 times the volume of the pipeline downstream of the shock wave, the oscillation amplitudes of the downstream pressure P_D and flow ${\dot{m}}_{out}$ decrease to 71.62 and 72.09% of those without the cavity, respectively.

3) in the actual viscous flow field, the shock wave system produces self-excited oscillation, the leading edge separation point moves in a large range, the flow field pressure and outlet flow produce large amplitude oscillation, and the corresponding Mach number distribution also produces asymmetric changes. The analysis of the outlet flow curve shows that the parameter oscillation has many frequency points with large amplitude.

4) the parallel cavity has an effect on the outlet flow and the pressure at the sampling point. The parameters of the two parallel cavity models in this article change periodically. The cavity volume of Model C is relatively large, the pressure oscillation amplitude at the sampling point decreases from more than 5 to less than 2 of Model A without cavity, and the amplitude of parameter oscillation decreases significantly.

5) from the comparative analysis of the flow field, when the shock wave moves back and forth, the leading edge repeatedly sweeps the parallel cavity. Under the alternating change of internal and external pressure, the air flow in the cavity is filled repeatedly, which hinders the main flow of the inlet to a certain extent, thus inhibiting the parameter oscillation process.

The research results of this article show that it is a feasible technical way to suppress the change of self-excited oscillation parameters of the inlet to a certain extent by paralleling the cavity in the isolator.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

In this article, FC established the shock dynamic model, carried out theoretical analysis, verified the numerical calculation method, and completed the calculation of unsteady shock oscillation in the inlet. XH completed the sorting and analysis of some calculation results.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, S., and Zhao, D. (2018). Numerical Study of Guide Vane Effects on Reacting Flow Characteristics in a Trapped Vortex Combustor. Combustion Sci. Techn. 190 (10-12), 2111–2133. doi:10.1080/00102202.2018.1492568

CrossRef Full Text | Google Scholar

Curran, E. T., Heiser, W. H., and Pratt, D. T. (1996). Fluid Phenomena in Scramjet Combustion Systems. Annu. Rev. Fluid Mech. 28 (1), 323∼360. doi:10.1146/annurev.fl.28.010196.001543

CrossRef Full Text | Google Scholar

Hankey, W., and Shang, J. (1980). Analysis of Self-Excited Oscillations in Fluid Flows.” in 13th Fluid and PlasmaDynamics Conference, Snowmass, CO, July 14–16. doi:10.2514/6.1980-1346

CrossRef Full Text | Google Scholar

Herrmann, D., Siebe, F., and Gülhan, A. (2013). Pressure Fluctuations (Buzzing) and Inlet Performance of an Airbreathing MissileBuzzingand Inlet Performance of an Airbreathing Missile. J. Propulsion Power 29 (4), 839–848. doi:10.2514/1.b34629

CrossRef Full Text | Google Scholar

Huang, H. X., Tan, H. J., and Zhuang, Y. (2018). Progress in Internal Flow Characteristics of Hypersonic Inlet/Isolator. J. Propulsion Techn. 39 (10), 2252–2273. doi:10.13675/j.cnki.tjjs.2018.10.010

CrossRef Full Text | Google Scholar

Huang, R., Li, Z. F., and Nie, B. P. (2020). Shock Train Oscillations in a Two-Dimensional Inlet/Isolator with Suction. J. Propulsion Techn. 41 (4), 767–777.

Google Scholar

Ikui, T., Matsuo, K., Nagai, M., and Honjo, M. (1974). Oscillation Phenomena of Pseudo-shock Waves. Bull. JSME 17 (112), 1278–1285. doi:10.1299/jsme1958.17.1278

CrossRef Full Text | Google Scholar

Li, N., Chang, J., Yu, D., Bao, W., and Song, Y. (2017). Mathematical Model of Shock-Train Path with Complex Background Waves. J. Propulsion Power 33 (2), 468–478. doi:10.2514/1.b36234

CrossRef Full Text | Google Scholar

Li, N. (2019). Investigation of the Shock Train Instability and Control Method in Scramjet. Harbin: Harbin Institute of Technology. doi:10.27061/d.cnki.ghgdu.2019.000250

CrossRef Full Text | Google Scholar

Li, Z. F., Gao, W. Z., and Li, P. (2012). Experimental Investigation on the Shock Wave Oscillation Behaviors in a Two-Dimensional Hypersonic Inlet Flow. J. Propulsion Techn. 33 (5), 676∼682.

Google Scholar

Lu, L., Wang, Y., and Fan, X. Q. (2019). Investigation of Shock-Train Forward Movement in Mixer of RBCC. J. Propulsion Techn. 40 (1), 69∼75. doi:10.13675/j.cnki.tjjs.170736

CrossRef Full Text | Google Scholar

Ma, G. F., Xie, W., and Lin, Y. (2017). Pseudo-shock Characteristics in the Two-Dimensional Supersonic Inlet Diffuser. J. Aerospace Power 32 (8), 1950∼1961.

Google Scholar

Ma, L. C. (2019). Study on the Effect of Suction Structure and Parameters on the Boundary Layer Oscillation Suction. Harbin: Harbin Institute of Technology. doi:10.27061/d.cnki.ghgdu.2019.002664

CrossRef Full Text | Google Scholar

Matsuo, K., Miyazato, Y., and Kim, H.-D. (1999). Shock Train and Pseudo-shock Phenomena in Internal Gas Flows. Prog. Aerospace Sci. 35 (1), 33–100. doi:10.1016/s0376-0421(98)00011-6

CrossRef Full Text | Google Scholar

Meier, G. E. A., Szumowski, A. P., and Selerowicz, W. C. (1990). Self-Excited Oscillations in Internal Transonic Flows. Prog. Aerospace Sci. 27 (2), 145–200. doi:10.1016/0376-0421(90)90004-4

CrossRef Full Text | Google Scholar

Pan, J. S., and Shan, P. (2011). Fundamentals of Das Dynamics. Beijing: National Defense Industry Press.

Google Scholar

Piponniau, S., Dussauge, J. P., Debiève, J. F., and Dupont, P. (2009). A Simple Model for Low-Frequency Unsteadiness in Shock-Induced Separation. J. Fluid Mech. 629, 87–108. doi:10.1017/s0022112009006417

CrossRef Full Text | Google Scholar

Reinartz, B. U., Herrmann, C. D., Ballmann, J., and Koschel, W. W. (2003). Aerodynamic Performance Analysis of a Hypersonic Inlet Isolator Using Computation and Experiment. J. Propulsion Power 19 (5), 868–875. doi:10.2514/2.617710.2514/2.6177

CrossRef Full Text | Google Scholar

Rybalko, M., Babinsky, H., and Loth, E. (2012). Vortex Generators for a Normal Shock/Boundary Layer Interaction with a Downstream Diffuser. J. Propulsion Power 28 (1), 71–82. doi:10.2514/1.5704610.2514/1.b34241

CrossRef Full Text | Google Scholar

Sugiyama, H., Tsujiguchi, Y., and Honma, T. (2008). Structure and Oscillation Phenomena of Pseudo-Shock Waves in a Straight Square Duct at Mach 2 and 4.”in 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, April 28–May 1, 2008. doi:10.2514/6.2008-2646

CrossRef Full Text | Google Scholar

Tan, H. J., Sun, S., and Huang, H. X. (2012). Behavior of Shock Trains in a Hypersonic Inlet/Isolator Model with Complex Background Waves. Exp. Fluids 53 (6), 1647–1661. doi:10.1007/s00348-012-1386-1

CrossRef Full Text | Google Scholar

Tian, X, A., Wang, C, P., and Cheng, K. M. (2014). Experimental Investigation of Dynamic Characteristics of Oblique Shock Train in Mach 5 Flow. J. Propulsion Technol. 35 (8), 1030∼1039. doi:10.13675/j.cnki.tjjs.2014.08.004

CrossRef Full Text | Google Scholar

Wang, C. P., and Zhang, K. Y. (2010). Shock Train Oscillation and Wall Pressure Fluctuation in Internal Flow. J. Experiments Fluid Mechanic 24 (5), 57–62. doi:10.3969/j.issn.1672-9897.2010.05.012

CrossRef Full Text | Google Scholar

Xiong, B., Wang, Z.-G., Fan, X.-Q., and Wang, Y. (2017a). Experimental Study on the Flow Separation and Self-Excited Oscillation Phenomenon in a Rectangular Duct. Acta Astronautica 133, 158–165. doi:10.1016/j.actaastro.2017.01.009

CrossRef Full Text | Google Scholar

Xiong, B., Wang, Z. G., and Fan, X. Q. (2017b). Characteristics of Forced Normal Shock-Train Oscillation in Isolator. J. Propulsion Techn. 38 (1), 1∼7. doi:10.13675/j.cnki.tjjs.2017.01.001

CrossRef Full Text | Google Scholar

Xu, K., Chang, J., and Li, N. (2019). Experimental Investigation of Mechanism and Limits for Shock Train Rapid Forward Movernt. Expermental Therm. Fluid Sci. 98, 336∼345. doi:10.1016/j.expthermflusci.2018.06.015

CrossRef Full Text | Google Scholar

Xu, K., Chang, J., Zhou, W., and Yu, D. (2016). Mechanism and Prediction for Occurrence of Shock-Train Sharp Forward Movement. AIAA J. 54 (4), 1403–1412. doi:10.2514/1.J054577

CrossRef Full Text | Google Scholar

Zhan, W. J., and Yan, H. (2021). Numerical Study of Effects of Steady and Oscillating Back-Pressure on Shock Train in an Isolator. J. Popul. Techn. 42 (5), 980–990. doi:10.13675/j.cnki.tjjs.190671

CrossRef Full Text | Google Scholar

Zhao, D., Gutmark, E., and de Goey, P. (2018). A Review of Cavity-Based Trapped Vortex, Ultra-compact, High-G, Inter-turbine Combustors. Prog. Energ. Combustion Sci. 66 (may), 42–82. doi:10.1016/j.pecs.2017.12.001

CrossRef Full Text | Google Scholar