IASA-Based Capacity Allocation Optimization Study for a Hydro–Pumped Storage–Photovoltaic–Wind Complementary Clean Energy Base

Photovoltaic and wind power is uncontrollable, while a hydro–pumped storage–photovoltaic–wind complementary clean energy base can ensure stable power transmission in the whole system through power quantity regulation by the hydropower station and the pumped storage station. Reasonable allocation of installed capacities of various power sources in the system can improve the reliability and economy of systematic power supply. A system model was built generalizing the hydropower station and the pumped storage station as an energy storage unit, compensating and regulating the natural output process to match the system output and the load and to establish a correlation between the installed capacity of the base and the output index. Installed capacity allocation optimization was studied through an optimization model built with an initial investment of the base as the objective function and with power supply guarantee rate, power abandonment rate, and installed capacity as restraints and solved using improved artificial sheep algorithm (IASA) based on the shepherd dog supervision mechanism. A Yellow River clean energy base was selected for a case study analyzing the influence of power supply guarantee rate and power abandonment rate on installed capacity allocation and investment. For the two most important parameters in the optimization process, that is, the power supply guarantee rate and the power abandonment rate, after qualitative and quantitative analysis, it is found that the power supply guarantee rate has a greater impact on the initial investment. In this study, a combination of the power abandonment rate of 18% and the guaranteed rate of 90% is finally selected for the optimization calculation. The case study indicates that sole increase of installed photovoltaic or wind capacity resulted in the increase of both power supply guarantee rate and power abandonment rate; an appropriate increase in the installed capacity of the pumped storage station raised the power supply guarantee rate and lowered the power abandonment rate; and the optimal installed capacity allocation of the photovoltaic, wind, pumped storage, and hydropower under a specific load condition of the case project is 4.6:1.4:1.7:1.

1 Introduction

Wind and photovoltaic energies are inconstant and fluctuant. It is uncontrollable to use such kinds of energies to generate power, which will impede the stable operation of the power grid (Liu, 2015). In order to solve grid connection issues, thus, caused, a multi-energy complementary system has been applied to make power generation controllable by using complementarity of various energies and the energy storage (Sun et al., 2015; Zhao et al., 2015; Zhong et al., 2018). From the perspective of power sources, such a system has been progressively developing from wind–photovoltaic power (Tian et al., 2017; Anoune et al., 2018; Zhang et al., 2018) and hydro–photovoltaic power (Huang et al., 2020; Jiang et al., 2020) to wind–photovoltaic–hydro power (Xia et al., 2017; Xiao and Dong, 2017), and the more diverse complementary wind–photovoltaic–hydro–pumped storage power includes geothermal and chemical energy storage (Lu, 2016). In the hydro–pumped storage–photovoltaic–wind complementary system, stable power transmission is achieved by reasonable allocation of installed capacity of the photovoltaic, wind, hydro, and pumped storage power and by regulation of the output correlation. Mamdouh and Rosen (2021) used advanced mathematical methods such as thermodynamic dynamic analysis and artificial neural networks to systematically study the performance design and optimization of various new energy sources including geothermal, hydroelectric, photovoltaic, and wind power. Khosravi et al. (2019) proposed a system combining ocean thermal energy conversion and photovoltaic and hydrogen energy storage and optimized and analyzed its working fluid, temperature conditions, and economics. In the aspect of installed capacity allocation, Zhu et al. (2018) considered the certain rate of abandoned wind and photovoltaic energy and developed an optimized capacity allocation scheme with the targets of minimum wind and photovoltaic power abandonment rate and maximum installed capacity of wind and photovoltaic power connected, producing an optimal capacity allocation of wind and photovoltaic power connected to Gangtuo Hydropower Station of 0.5:1. Yang and Ren (2015) studied the influence of the installed capacity of pumped storage stations on power abandonment rate and system economic efficiency, indicating that a properly installed capacity of pumped storage station in the system can improve the utilization rate of wind and photovoltaic energy and increase power generation benefits. Dai and Dong (2019) put forward an installed capacity optimization design of pumped storage station under the fixed installed capacity of wind and photovoltaic power targeting at the maximum overall system economic efficiency and minimum fluctuation of output power. Kefif et al. (2021) analyzed the load adaptation and economic economy of micro-off-grid water–wind systems in areas with different wind speed conditions, and their analysis showed a negative correlation between wind speed and the economic cost of the system. When studying installed capacity allocation using the optimization method, objective functions often used are minimum total system cost (Lasseter, 2011), minimum annual loss of load probability (LOLP) (Mathiesen et al., 2015), minimum operation cost (Feroldi and Zumoffen, 2014), minimum pollutant emission (Tan et al., 2014; Tan et al., 2017), maximum economic return (Khan and Iqbal, 2005; Chen et al., 2006; Belmili et al., 2014), etc. with corresponding constraints of load, loss of power supply probability (LPSP) (Guo et al., 2019), etc. The optimization algorithms used include genetic algorithm (Zhang et al., 2015), particle swarm optimization (PSO) (Peng et al., 2018), and improved PSO (Zhou and Sun, 2015; Zhang et al., 2018). In previous studies, there are abundant capacity allocation optimization models based on specific project needs, but studies based on power station operation modes and analysis of capacity and output indexes are lacking (Sun and Harrison, 2019). For a hydro–pumped storage–photovoltaic–wind complementary system, there are still many technical challenges in the capacity allocation optimization based on operation modes due to complex dispatching methods of pumped storage power and hydropower (Kamal et al., 2018).

This study built a hydro/pumped storage/photovoltaic/wind complementary system. Compared with other studies, this study uses part of hydropower as an energy storage unit to store or release electricity by changing the planned output and combines it with pumped storage to compensate for the net load of the system, constructs a model to simulate the system operation process, and establishes the relationship between installed capacity configuration and power generation index. Based on this operation method, the study of installed capacity allocation optimization is carried out. Finally, using the Black Hills Gorge water/pumped storage/photovoltaic/wind complementary renewable energy base as a specific case, an improved artificial flock algorithm is used to optimize the capacity allocation and explore the technical feasibility and the application effect of the construction of the water/pumped storage/light/wind complementary renewable energy base. The results of this study are of great significance for promoting regional economic development, improving energy structure and ecological environment, and promoting ecological protection and high-quality development of the Yellow River Basin.

2 Base System Building

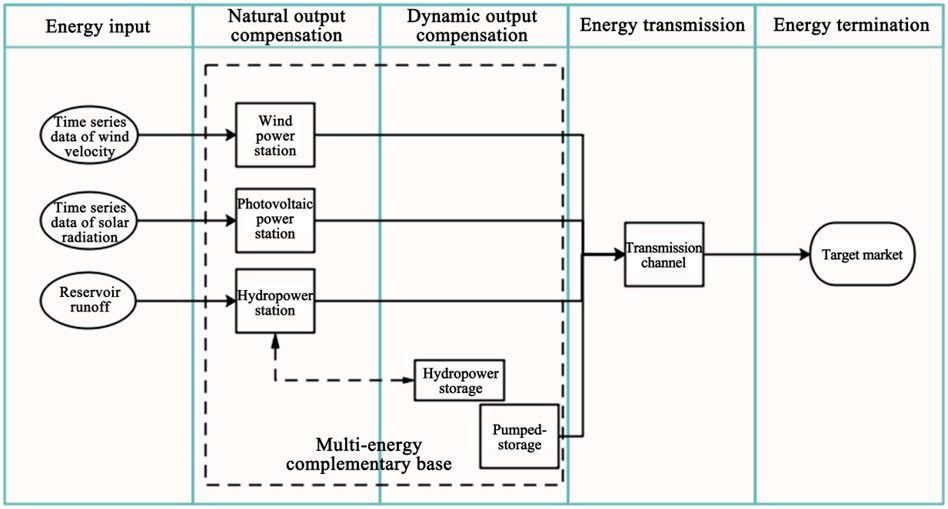
The system was composed of hydropower, pumped storage, photovoltaic, and wind stations as shown in Figure 1, in which the hydropower station with adjustable reservoir capacity and the pumped storage station together formed the energy storage unit. The load model was an output limit model of the UHV DC transmission channel. The system was operated in a compensation mode, meaning that the superposition output of photovoltaic power, wind power, and hydropower was compensated through the energy storage unit to match the total output of the system with the load.

FIGURE 1

FIGURE 1. System structure.

2.1 Output Model

The output model of the photovoltaic station (Yang et al., 2019) is as follows:

$p_s=\frac{{\eta }_{p}S{A}_p}{1000},(1)$

where p_s is the power of the photovoltaic station, kW; η_p is the comprehensive power generation efficiency, considering the power degradation of the polysilicon PV module, such as the cable, inverter, and transformer, about 75–82% (Q CPI 173-2015, 2015); S is the solar radiation intensity, W/m²; and A_p is the installation area of the photovoltaic cell array, m².

The output model of the wind station (Zhang, 2020) is given as follows:

$p_w=\{\begin{array}{l}0v\le v_{cr}\\ p_r\frac{v-v_{cr}}{v_r-v_{cr}}{v}_{cr}\le v\le v_r\\ p_r{v}_r\le v\le v_{co}\\ 0v>v_{co}\end{array},(2)$

where p_w and p_r are the actual power and the rated power of the wind turbine generator unit, kW, and V_cr, V_r, and V_co are the cut-in speed, rated speed, and cut-out speed of wind, m/s.

The output model of the hydropower station is as follows:

$p_h=9.81{\eta }_{h}QH,(3)$

where p_h is the hydropower output; η_h is the power generation efficiency of the hydraulic turbine generator unit; Q is the volumetric flow rate of the hydropower station, m³/s; and H is the head of the hydropower station, m.

2.2 Operation Model

The system is operated in a compensation mode using hydropower and pumped storage power for compensation and the energy storage thereof for electricity quantity regulation. Assuming the difference between the total output of photovoltaic, wind and hydro power, and the load as the net load, the formula for net load calculation is

$l_n^i=L^i-p_s^i-p_w^i-p_h^i,(4)$

where $l_n^i$ and $L^i$ are the net load and the target load, respectively, kW.

The net load is also the output required for energy storage. When the net load $l_n$ is greater than 0, the energy storage unit supplies power; when the net load $l_n$ is less than 0, the unit stores power. The superscript i represents the time period.

The energy storage model is

$s^{i+1}=s^i-t^i{n}^i.(5)$

When storing energy,

$\{\begin{array}{c}{n}^i={\eta }_{in}{l}_n^i\left|l_n^i\right|\le C_{in}^i\\ n^i=-{\eta }_{in}{C}_{in}^i\left|l_n^i\right|>C_{in}^i\end{array}.(6)$

When supplying energy,

$\{\begin{array}{c}{n}^i=\frac{l_n^i}{{\eta }_{out}}{l}_n^i\le C_{out}^i\\ n^i=\frac{C_{out}^i}{{\eta }_{out}}{l}_n^i>C_{out}^i\end{array},(7)$

where $s^i$ is the energy stored in the unit at the beginning of a period, kWh; $n^i$ is the virtual energy storage power, kW; $t^i$ is the time duration; ${\eta }_{in}$ and ${\eta }_{out}$ are the efficiency of energy storage and energy supply, respectively; and $C_{in}^i$ and $C_{out}^i$ are the maximum energy storage power and the maximum energy supply power of the unit in period i, kW. $C_{in}^i$ and $C_{out}^i$ are determined based on factors such as allowable minimum output and installed capacity of the hydropower and pumped storage power. The energy storage and energy supply process is first realized by changing the way of hydropower station output. Pumped storage power continues to bear the remaining net load when the output or energy storage capacity is insufficient.

Limited by installed capacity, there will be power abandoned due to insufficient energy storage power. The power of such abandonment is expressed as

$w_1^i=n^i-l_n^i,(8)$

where $w_1^i$ is the power of abandonment due to insufficient energy storage power, kW.

When the energy storage capacity is used up, power abandonment will also occur. The power of abandonment is the difference between the actual storage power and the planned storage power. The formula for calculation of the power of abandonment is as follows:

$w_2^i=\left({n^{\prime }}^i-n^i\right)/{\eta }_{in},(9)$

${n^{\prime }}^i=\left(s^i-s^{i+1}\right)/t^i,(10)$

where $w_2^i$ is the power abandoned after the energy storage capacity is fully used, kW; $n^i$ and ${n^{\prime }}^i$ are the planned energy storage power and the actual energy storage power, kW.

At the end of the period, ${n^{\prime }}^i$ will be smaller than $n^i$ when the energy storage capacity is used up.

The energy storage capacity of a pumped storage station is determined by the elevation difference between the upper and lower reservoirs and volume of the upper reservoir, while that of hydropower station is determined by the reservoir capacity and water regulation requirements.

The total output of the system is the sum of the photovoltaic, wind, and hydro output, plus the output of the energy storage unit, subtracting the abandoned power, expressed as

$P^i=p_s^i+p_w^i+p_h^i+n^i-w_1^i-w_2^i,(11)$

where $P^i$ is the total system output in period i, kW.

2.3 Output Indexes

Under fixed installed capacity of multi-energy source of the base, simulation operation can be performed according to the output process of various sources. Thus, the power generation process of the system can be obtained and the output indexes such as the power supply guarantee rate and the power abandonment rate can be calculated, thereby establishing the relationship between the installed capacity and project benefits.

The power supply guarantee rate is the rate of the number of periods during which the system meets the load to the total number of operation periods when the system matches the design load requirement, represented by γ and expressed as

$\gamma =\frac{n}{N},(12)$

where n is the number of periods during which the total output of the system matches the load, and N is the total number of periods for calculation.

The power abandonment rate is the rate of the sum of the power abandoned due to the limitation of installed capacity and energy storage capacity to the natural power output, represented as $\eta$, expressed as

$\eta =\frac{{\displaystyle \sum _i\left[\left(w_1^i+w_2^i\right)\times t^i\right]}}{{\displaystyle \sum _i\left[\left(p_s^i+p_w^i+p_h^i\right)\times t^i\right]}}.(13)$

3 Capacity Allocation Optimization of the Base

Based on the correlation between the installed capacity and the output index established by the system model, the optimization method was used to study the installed capacity allocation of the multisource complementary energy base and analyze the optimal allocation of installed capacity of various power sources.

3.1 Building the Optimization Model

Based on the base system model, an optimization model is constructed to optimize the configuration of the installed capacity of various energy sources. The model consists of optimization variables, objective function and constraints, where the objective function is calculated from the optimization variables.

3.1.1 Optimization Variables

Optimization variables were installed capacity of photovoltaic, wind, hydro, pumped storage, and other power sources. When power storage capacity and the installed capacity of the pumped storage station can be designed independently, installed capacities of photovoltaic, wind, and hydropower stations can also be used as variables of optimization.

3.1.2 Objective Function

The optimization model was built based on the most economical installed capacity required under the premise of meeting project benefits, and the minimum initial investment of the base was taken as the objective function, presented as follows:

$\min f={\displaystyle \sum _j{m}_j{c}_j},(14)$

where f is the objective function; $m_j$ is the investment of unit installed capacity of type j power source, CNY/kW; and $c_j$ is the installed capacity of type j power source, kW.

3.1.3 Constraints

1) Constraint on power supply guarantee rate:

Constraint on the optimization model was considered from the perspective of ensuring the power generation benefits. The system made output by matching the load model requirement and setting the constraint on the power supply guarantee rate, presented as follows:

$\gamma \ge {\gamma }_{\min },(15)$

where $\gamma$ is the power supply guarantee rate and ${\gamma }_{\min }$ is the allowable minimum guarantee rate.

2) Constraint on power abandonment rate:

Constraint on power abandonment rate was set based on analysis of economic efficiency of the base considering the regulation capacity of the energy storage unit of the system against natural power, presented as follows:

$\eta \le {\eta }_{\max },(16)$

where $\eta$ is the power abandonment rate of the system and ${\eta }_{\max }$ is the set maximum power abandonment rate.

3) Constraint on installed capacity:

Based on the limits of maximum installed capacities of photovoltaic, wind, and pumped storage stations due to geographical and topographical restrictions in the project area, the constraint on the installed capacity was set and presented as follows:

$c_j\le C_{\max ,j},(17)$

where $C_{\max ,j}$ is the maximum possible installed capacity of type j power source.

3.2 Optimization by Improved Artificial Sheep Algorithm

Swarm Intelligence shows outstanding performance in terms of solving problems about complex optimization of various combinations and function optimization (Vitousek et al., 1997). Particle swarm optimization (PSO) is considered an efficient and simple global optimization algorithm for its simple structure, few adjustment parameters, and easy implementation. It has achieved good results in optimization featuring multi-peak, multi-objective, and constraint. ASA, proposed in recent years (WANG et al., 2017) inspired by sheep flock behavior, simulates the behavior of the leading sheep and interaction among the remaining sheep and designs corresponding global exploration and local development operators in the swarm intelligence algorithm. ASA has brought improvement in both effect and efficiency of intelligent optimization.

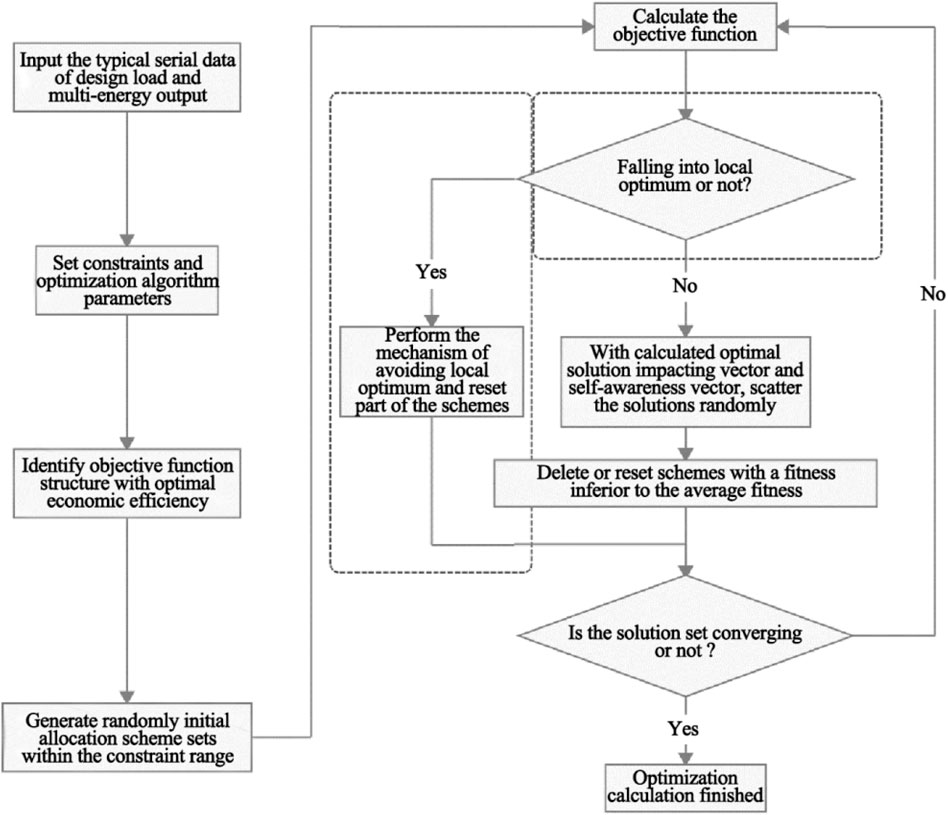
In order to further improve the optimization quality of ASA, especially to improve its defect of falling into local optimum, the ASA was improved herein. The operators escaping local optimum similar to shepherd dog supervision mechanism were introduced to improve the quality of each iteration (Qu et al., 2018). The improved artificial sheep algorithm (IASA) was thus proposed. A specific optimization process based on IASA is shown in Figure 2, where the part marked by dotted lines was determined and operators escaped local optimum.

FIGURE 2

FIGURE 2. Allocation optimization calculation process based on IASA.

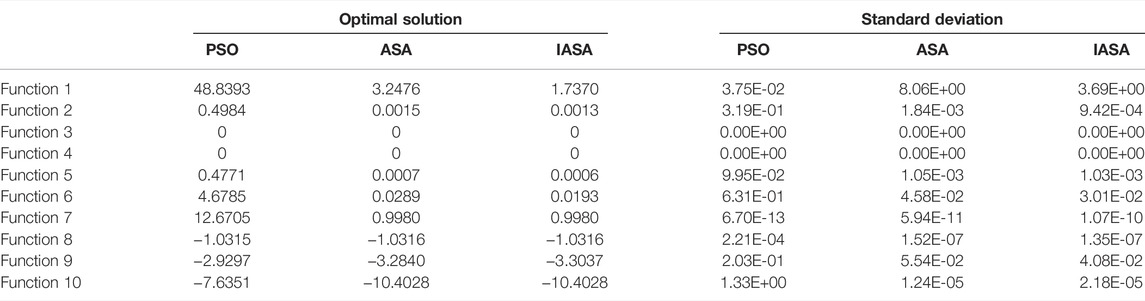
Optimization calculations by traditional PSO, original ASA, and IASA were conducted with 10 typical benchmark test functions (Wang et al., 2018) to deal with a minimum value problem, and 30 repetitions were performed. The results are compared in Table 1 with the average convergence value and the standard deviation of the convergence results. The optimization results showed that for functions 3, 4, and 8, equivalent optimal solutions have been obtained, so the performance of the three algorithms was on the same level. For functions 7 and 10, the performance of the original ASA and IASA were equivalent and much better than that of traditional PSO. For the other five functions, the IASA had outstanding performance compared with the other two algorithms.

TABLE 1

TABLE 1. Performance comparison of the three optimization algorithms.

The stability of the algorithm was also analyzed using the standard deviation of the optimization results. Compared with PSO and ASA, the standard deviation (SD) of IASA was slightly higher for functions 1 and 7, but for all other functions, the standard deviation was more favorable than the other two algorithms. Calculations with IASA show better stability during the optimization process.

Taking two test functions as examples, both Figure 3 and Tables 2, 3 show the optimization convergence process with these three algorithms. From the trend of the curve and the objective function value evolution, IASA demonstrates a better optimization efficiency and faster calculation convergence than the other two algorithms.

FIGURE 3

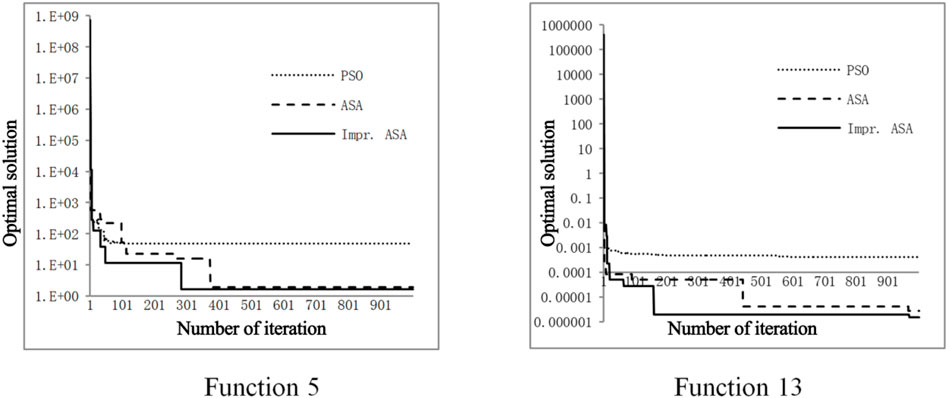
FIGURE 3. Convergence process curve of the optimal solution obtained from the optimization of two test functions by the three optimization algorithms.

TABLE 2

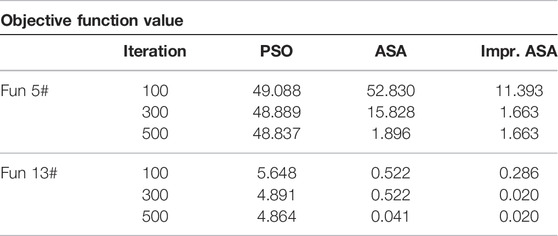
TABLE 2. Evolution of the objective function during the optimization of two test functions by three optimization algorithms.

TABLE 3

TABLE 3. Overview of power supply of the multisource complementary energy base.

From the above analysis, it can be concluded that, compared with the classic PSO and the original ASA algorithms, the main advantage of the IASA algorithm is that a faster and more stable convergence can be obtained. This innovative algorithm has been improved as per the shortcomings of PSO and ASA such as early convergence and local optimum problems.

4 Case Study on Installed Capacity Allocation Optimization

4.1 Base Overview

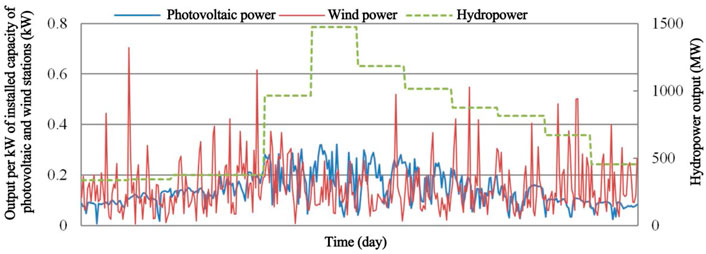
The Yellow River area was selected as a typical case to study the installed capacity allocation optimization. The base includes four types of power sources: hydro, pumped storage, photovoltaic, and wind power. The annual average unit output process of photovoltaic and wind stations was determined based on NASA meteorological data and the installed capacity and output of the hydropower station were determined based on the river basin planning. In this case, the installed capacity of the hydropower station was 2,000,000 kW and not considered an optimization variable, with its output process varying from month to month. Figure 4 shows the process for output per kW of the installed capacity of the photovoltaic and wind stations and the output of the hydropower station within a year.

FIGURE 4

FIGURE 4. Output characteristic curves of various power sources.

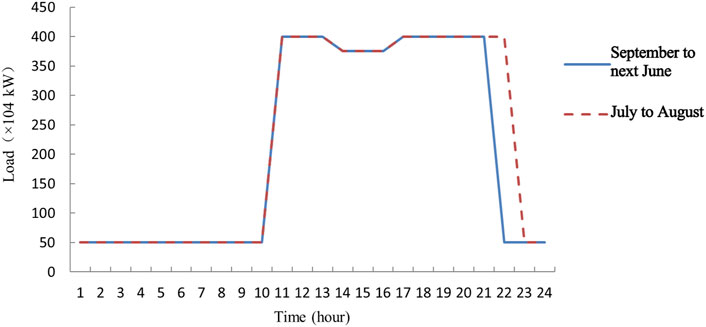
Figure 5 shows the daily load process of the DC transmission channel adopted. The process is divided into peak periods from July to August and the off-peak period from September to next June. The late peak of the peak period is 1 h longer than the off-peak period, and loads of such two periods alternate within the year, with an annual average load of 2,100,000 kW.

FIGURE 5

FIGURE 5. Load curves of the DC output channel.

Technical and economic indexes of various power sources of the base are shown in Tables 2, 3.

4.2 Analysis of Installed Capacity

The variation of output indexes under different allocations of installed capacity was analyzed for the base. as given in Figure 6when increasing the installed capacity of the photovoltaic station from 5000 to 30000 MW while maintaining that of other stations, the power abandonment rate showed a trend of increasing from 0.28 to 39.20%, and the power supply guarantee rate showed a trend of increasing from 73.21 to 97.74%. When increasing the installed capacity of the wind station from 1000 to 10000 MW while maintaining that of other stations, the power abandonment rate showed a trend of increasing from 8.52 to 17.39%, and the power supply guarantee rate showed an increase from 84.63 to 94.39%. As for the installed capacity of the pumped storage station, when increased from 1000 to 10000 MW while maintaining that of other stations, the power abandonment rate showed a trend of decreasing from 15.66% down to 11.48%, meanwhile, the power supply guarantee rate increased from 85.44% up to 93.00%. It indicates that increasing the installed capacity of photovoltaic or wind stations independently can improve the power supply guarantee rate but increase the power abandonment rate at the same time, while the energy storage unit plays a positive role in reducing power abandonment and ensuring power supply by storing electric energy at low load and compensating for power supply at high load.

FIGURE 6

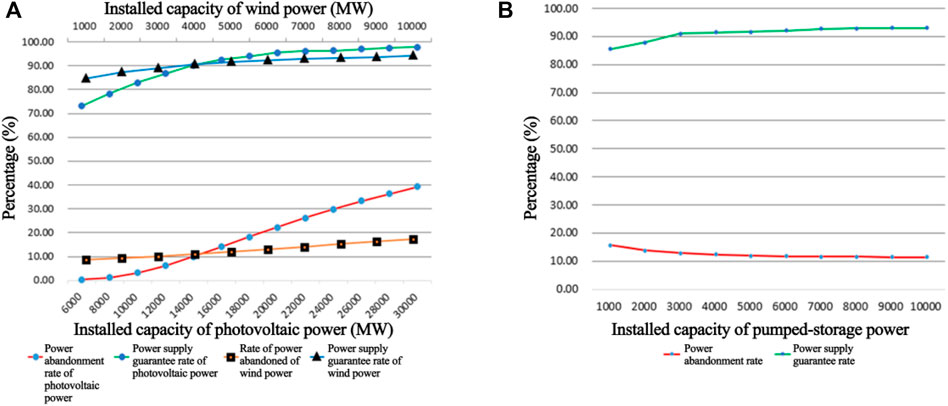
FIGURE 6. Correlation between output indexes and installed capacity of photovoltaic, wind, and pumped storage power. (A) Correlation between the installed capacity and output indexes of photovoltaic and wind power and (B) correlation between installed capacity and output indexes of pumped storage power.

4.3 Study on Capacity Allocation Optimization

The optimization model established was used to analyze the capacity allocation, in which the variables were installed capacities of photovoltaic, wind, and pumped storage power, and the objective function was a minimum total investment of the base.

The power abandonment rate was set with a constraint threshold step size of 0.5%, the rate varying between 13 and 20%, while the power supply guarantee was set with a constraint threshold step size of 0.5%, the rate varying between 90 and 94%. In such variation intervals, optimization tests were carried out repeatedly with the same optimization calculation parameters to obtain the most economical initial investment under different constraints. The initial investment was the least when the power abandonment rate was the maximum and the power supply guarantee rate was the minimum. Such minimum investment was taken as a reference value to get the ratio of the optimal investment under other constraints to the reference value, which indicated that the initial investment would gradually increase along with the gradual increase in power supply guarantee rate or gradual decrease of power abandonment rate.

Table 4 shows the calculation results of the ratio of the optimal investment under different constraints to the reference value. It indicates that when the power supply guarantee rate is fixed at 90%, the optimal power abandonment rate can be controlled at a level of 18%, and the total investment of the base is only increased by about 1% compared to the reference value; when there is a slight increase of power supply guarantee rate, the investment increase significantly. Based on this, a power abandonment rate of 18% and power supply guarantee rate of 90% were selected for the final optimization calculation.

TABLE 4

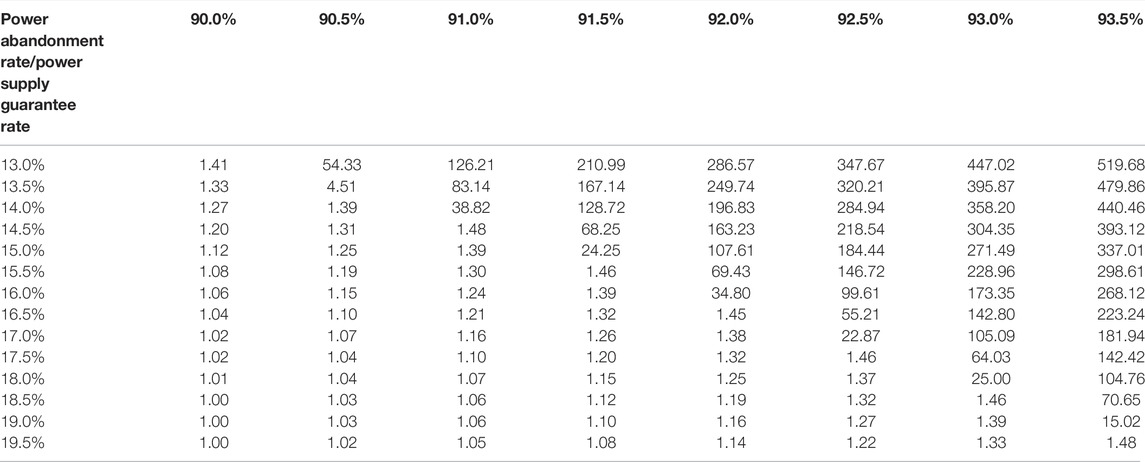
TABLE 4. Influence of power abandonment rate and power supply guarantee rate on the initial investment of the base.

When the power abandonment rate is small or the power supply guarantee rate is large, the initial investment in the base is relatively high. When the power abandonment rate is large or the power supply guarantee rate is small, the initial investment is relatively low.

To analyze the influence of these two constraints on the higher investment, a comparison was made for variation of investment correlated with power supply guarantee rate when the power abandonment rate was the minimum and that correlated with power abandonment rate when power supply guarantee rate was the maximum. Similarly, to analyze the influence of these two constraints on the lower investment, a comparison was made for variation of investment correlated with power supply guarantee rate when power abandonment rate was the maximum and that of investment correlated with power abandonment rate when power supply guarantee rate was the minimum. The comparative analysis curve is shown in Figure 7, which indicates that under the same variation rate of 0.5% for the gradual increase of power supply guarantee rate and gradual decrease of power abandonment rate, the variation of power supply guarantee rate leads to a faster increase of investment, that is, the initial investment is more sensitive to the power supply guarantee rate.

FIGURE 7

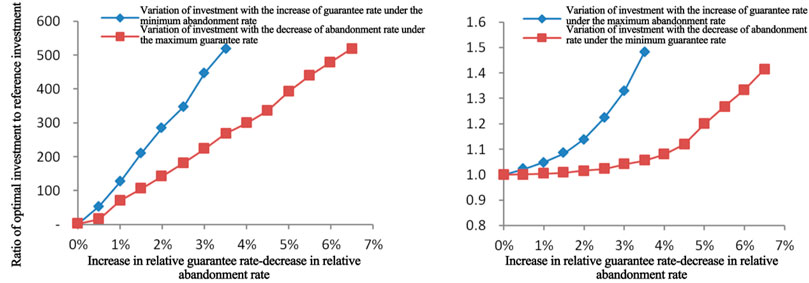
FIGURE 7. Comparison of the influence of abandonment rate and guarantee rate on investment in the case of higher investment (left) and lower investment (right).

The cumulative histogram in Figure 8 shows the correlation between the installed capacity allocation of three types of energy in the optimal capacity allocation scheme and the power abandonment rate under the case of a fixed power supply guarantee rate of 90% and varying power abandonment rate. When constraint on power abandonment rate was decreased from 20 to 13% in the optimal scheme, the proportion of installed capacity of photovoltaic power tended to decrease, while the proportion of installed capacity of both wind and pumped storage power tended to increase, and installed capacity proportion of the three power sources gradually tended to balance. However, when the power abandonment rate was fixed and the power supply guarantee rate varied, there was no obvious law in the variation of the installed capacity proportion of the three power sources. It qualitatively shows from another perspective that the power supply guarantee rate has greater influence on the initial investment than the power abandonment rate.

FIGURE 8

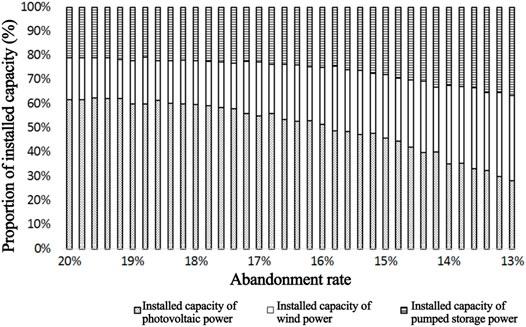
FIGURE 8. Variation of optimal installed capacity allocation scheme under various constraints of abandonment rates.

4.4 IASA Optimization Results and Analysis

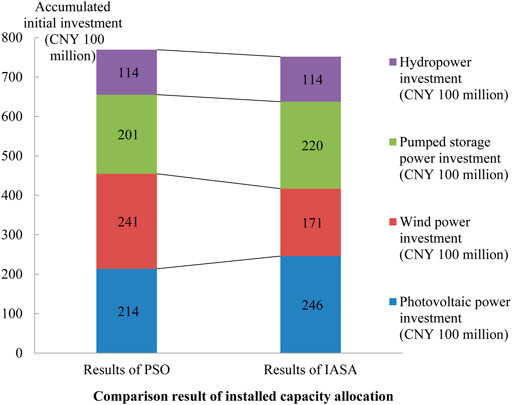
The general PSO and the IASA were used for multiple trial calculations under a power abandonment rate of 18% and power supply guarantee rate of 90%, obtaining optimization results as shown in Table 5 and Figure 9. Table 4 compares the installed capacity allocation and corresponding investment obtained by the two optimization methods, indicating that the total investment of the base obtained by the IASA is lower and the installed capacity allocation for various energy sources is more reasonable and elaborate.

TABLE 5

TABLE 5. Comparison of various installed capacity allocation schemes and investment.

FIGURE 9

FIGURE 9. Comparison of the installed capacity allocation schemes obtained by PSO and IASA.

Figure 9 gives the change of investment of various energy sources and the total investment of the base corresponding to the installed capacity allocation obtained by the two optimization methods, indicating that the IASA produces lower total investment of the base and better project economic benefits. With the installed capacity of hydropower as the benchmark, the final installed capacity proportion of photovoltaic, wind, pumped storage, and hydropower is 4.6:1.4:1.7:1.

5 Conclusion

The multisource complimentary energy base can achieve stable power generation of the system by using an energy storage unit for power regulation based on the reasonable installed capacity of photovoltaic and wind power, where the compensation function of the storage unit is crucial to ensure power generation stability and load matching. Based on the establishment of the system model of energy base and the optimization model of installed capacity allocation, as well as a case study of installed capacity allocation optimization, the following results, and conclusion are obtained.

1) The model of multisource renewable clean energy base system and the model of installed capacity allocation optimization based on hydropower and pumped storage power were established to simulate the system operation process, which provided a platform for analyzing installed capacity allocation of the system by optimization

2) Compared with the classical PSO and the original ASA algorithms, the IASA proposed in this study is faster in convergence (obtained at the 300th iteration for IASA) and better in calculation stability, by absorbing the rapid convergence of ASA and overcoming shortcomings of ASA such as early convergence and local optimum. The IASA is an effective improvement of the previous intelligent optimization algorithms.

3) For the Yellow River area case project, when increasing the installed capacity of the photovoltaic station from 5000 to 30000 MW independently, the power abandonment rate showed a trend of increasing from 0.28 to 39.20%, and an increase in power supply guarantee rate from 73.21 to 97.74%. When increasing the installed capacity of the wind station from 1000 to 10000 MW independently, the power abandonment rate showed a trend of increase from 8.52 to 17.39% and an increase in power supply guarantee rate from 84.63 to 94.39%. While the installed capacity of the pumped storage station increased from 1000 to 10000 MW, the power abandonment rate decreased from 15.66% down to 11.48%, and the power supply guarantee rate increased from 85.44% up to 93.00%. The figures indicate that increasing the installed capacity of photovoltaic or wind stations independently can improve the power supply guarantee rate and also increase the power abandonment rate at the same time, while the energy storage unit plays a positive role in reducing the power abandonment and ensuring power supply by storing electric energy at low load and compensating for power supply at high load.

4) Through optimization calculations under various constraint combinations of power supply guarantee rate and power abandonment rate, the case study on installed capacity allocation optimization for the Yellow River multisource complementary energy base shows that the initial investment is more sensitive to the change of power guarantee rate. Based on the specific conditions of the case project and the planned transmission capacity constraint, as well as a power supply guarantee rate of 90% and a target of achieving minimum investment, the calculated installed capacity allocation of photovoltaic–wind–pumped storage–hydro power is 4.6:1.4:1.7:1, which can be used as a reference for project development.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JZ and XHJ: methodology, resources, writing—original draft, supervision, project administration, and funding acquisition. YR: software model. JY and YQ: visualization and formal analysis. XJ and SY: investigation, data curation, and validation. RQ: writing—review and editing.

Conflict of Interest

Authors JZ, XHJ, JY, YQ, XJ, and SY were employed by Yellow River Engineering Consulting Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anoune, K., Bouya, M., Astito, A., and Abdellah, A. B. (2018). Sizing Methods and Optimization Techniques for PV-Wind Based Hybrid Renewable Energy System: A Review. Renew. Sustain. Energ. Rev. 93, 652–673. doi:10.1016/j.rser.2018.05.032

CrossRef Full Text | Google Scholar

Belmili, H., Haddadi, M., Bacha, S., Almi, M. F., and Bendib, B. (2014). Sizing Stand-Alone Photovoltaic-Wind Hybrid System: Techno-Economic Analysis and Optimization. Renew. Sustain. Energ. Rev. 30, 821–832. doi:10.1016/j.rser.2013.11.011

CrossRef Full Text | Google Scholar

Chen, H., Chen, J., and Duan, X. (2006). Fuzzy Modeling and Optimization Algorithm on Dynamic Economic Dispatch in Wind Power Integrated System[J]. Automation Electric Power Syst. 30 (2), 22.

Google Scholar

Dai, J., and Dong, H. (2019). Research on the Capacity Optimization of the Wind-Solar Hybrid Power Supply System Based on Pumped Storage Power Station[J]. Power Syst. Clean Energ. 35 (6), 76.

Google Scholar

Feroldi, D., and Zumoffen, D. (2014). Sizing Methodology for Hybrid Systems Based on Multiple Renewable Power Sources Integrated to the Energy Management Strategy. Int. J. Hydrogen Energ. 39 (16), 8609–8620. doi:10.1016/j.ijhydene.2014.01.003

CrossRef Full Text | Google Scholar

Guo, H., Lei, P., Zhang, Y., Jing, W., Rui, Z., and Zhongfu, T. (2019). Optimization Model for Integrated Complementary System of Wind-Pv-Pump Storage Based on Rough Set Theory[J]. J. Zhejiang University(Engineering Science) 53 (4), 801.

Google Scholar

Huang, H., Qin, L., Yang, Y. Y., and Daowan, W. (2020). Smart-Power Generation Technology of Clean Energy with Water-Light Multi-Energy Complementary[J]. Distributed Energy 5 (2), 21.

Google Scholar

Jiang, Li., Xu, M., and Zhou, Yi. (2020). Optimal Configuration of Hydro-Solar Complementary Distributed Power Systems in Cities[J]. Huadian Technol. 42 (2), 58.

Google Scholar

Kamal, A., Mohsine, B., Abdelali, A., and Abdellah, A. B. (2018). Sizing Methods and Optimization Techniques for Pv-Wind Based Hybrid Renewable Energy System: A Review[J]. Renew. Sustain. Energ. Rev. 93, 652. doi:10.1016/j.rser.2018.05.032

CrossRef Full Text | Google Scholar

Kefif, N., Melzi, B., Hashemian, M., Assad, M. E. H., and Hoseinzadeh, S. (2021). Feasibility and Optimal Operation of Micro Energy Hybrid System (Hydro/wind) in the Rural valley Region. Int. J. Low-Carbon Tech. 17, 58–68. doi:10.1093/ijlct/ctab081

CrossRef Full Text | Google Scholar

Khan, M. J., and Iqbal, M. T. (2005). Pre-feasibility Study of Stand-Alone Hybrid Energy Systems for Applications in Newfoundland. Renew. Energ. 30 (6), 835–854. doi:10.1016/j.renene.2004.09.001

CrossRef Full Text | Google Scholar

Khosravi, A., Syri, S., Assad, M. E. H., and Malekan, M. (2019). Thermodynamic and Economic Analysis of a Hybrid Ocean thermal Energy Conversion/photovoltaic System with Hydrogen-Based Energy Storage System. Energy 172 (1), 304–319. doi:10.1016/j.energy.2019.01.100

CrossRef Full Text | Google Scholar

Lasseter, R. H. (2011). Smart Distribution: Coupled Microgrids. Proc. IEEE 99 (6), 1074–1082. doi:10.1109/jproc.2011.2114630

CrossRef Full Text | Google Scholar

Liu, J. (2015). New Energy Power System Modeling and Control[M]. Beijing: Science Press.

Google Scholar

Lu, C. (2016). Research on Optimal Dispatching of Power System with Wind Solar Water Storage Power [D]. Harbin City: Harbin Institute of technology.

Google Scholar

Mamdouh, E., and Rosen, M. A. (2021). Design and Performance Optimization of Renewable Energy Systems[M]. Academic Press Publishing.

Google Scholar

Mathiesen, B. V., Lund, H., Connolly, D., Wenzel, H., Østergaard, P. A., Möller, B., et al. (2015). Smart Energy Systems For Coherent 100% Renewable Energy And Transport Solutions [J]. Appl. Energ. 145, 139.

Google Scholar

Peng, Y., Li, F., Xin, C., and Weiwei, C. (2018). Capacity Optimization of Pumped Storage Station with High Wind and Photovoltaic Penetration Based on IPSO[J]. J. Xinjiang Univ. (Natural Sci. Edition) 35 (3), 372. doi:10.13568/j.cnki.651094.2018.03.018

CrossRef Full Text | Google Scholar

Q Cpi 173-2015, (2015). Photovoltaic Power Generation Project Design Management Guidelines and Depth Requirements[S]. Beijing City: China Power Investment Corporation.

Google Scholar

Qu, D., Xu, L., Lu, Y., Xiaokun, Y., Min, H., and Xingwei, W. (2018). A New Swarm Intelligence Algorithm by Simulating Sheep Behaviors [J]. Acta Electronica Sinica 46 (6), 1300. doi:10.3969/j.issn.0372-2112.2018.06.004

CrossRef Full Text | Google Scholar

Sun, H., Guo, Q., and Pan, Z. (2015). Energy Internet:Concept, Architecture and Frontier Outlook[J]. Automation Electric Power Syst. 19, 1. doi:10.7500/AEPS20150701007

CrossRef Full Text | Google Scholar

Sun, W., and Harrison, G. P. (2019). Wind-solar Complementarity and Effective Use of Distribution Network Capacity. Appl. Energ. 247, 89–101. doi:10.1016/j.apenergy.2019.04.042

CrossRef Full Text | Google Scholar

Tan, Z., Ju, L., Chen, Z., Huanhuan, L., Changqing, X., and Baozhu, Z. (2014). An Environmental Economic Dispatch Optimization Model Based on Rough Set Theory and Chaotic Local Search Strategy Differential Evolution Algorithm. Power Syst. Technol. 38 (5), 1339.

Google Scholar

Tan, Z., Wang, G., Ju, L., Tan, Q., and Yang, W. (2017). Application of CVaR Risk Aversion Approach in the Dynamical Scheduling Optimization Model for Virtual Power Plant Connected with Wind-Photovoltaic-Energy Storage System with Uncertainties and Demand Response. Energy 124, 198–213. doi:10.1016/j.energy.2017.02.063

CrossRef Full Text | Google Scholar

Tian, C., Cai, Z., Xie, P., Auger, F., and Bourguet, S. (2017). Capacity Optimization of Wind-Solar Hybrid Power Generation System Based on Improved Differential Evolution Algorithm[J]. J. Electric Power Sci. Technol. 32 (3), 22. doi:10.3969/j.issn.1673-9140.2017.03.004

CrossRef Full Text | Google Scholar

Vitousek, P. M., Mooney, H. A., Lubchenco, J., and Melillo, J. M. (1997). Human Domination of Earth’s Ecosystems[J]. Science 277 (25), 494–499. doi:10.1126/science.277.5325.494

CrossRef Full Text | Google Scholar

Wang, W., Li, C., Liao, X., and Qin, H. (2017). Study on Unit Commitment Problem Considering Pumped Storage and Renewable Energy via a Novel Binary Artificial Sheep Algorithm. Appl. Energ. 187, 612–626. doi:10.1016/j.apenergy.2016.11.085

CrossRef Full Text | Google Scholar

Wang, Z., Li, C., Lai, X., Zhang, N., Xu, Y., and Hou, J. (2018). An Integrated Start-Up Method for Pumped Storage Units Based on a Novel Artificial Sheep Algorithm. Energies 11 (1), 151. doi:10.3390/en11010151

CrossRef Full Text | Google Scholar

Xia, X., Gao, Z., and Li, H. (2017). Combined Optimization Dispatching of Multi-Source Hybrid Power Bases Considering the Time-Space Complementary Characteristics[J]. Electric Power Eng. Technol. 36 (5), 5. doi:10.3969/j.issn.1009-0665.2017.05.010

CrossRef Full Text | Google Scholar

Xiao, L., and Dong, F. (2017). Joint Compensation Dispatching of the Hydropower, Wind Power and Solar Power Generation in Hubei Province[J]. Hydropower and New Energy (9), 74–78.

Google Scholar

Yang, D., Wang, S., Wang, Y., Chen, C., Zheng, T., Zhou, T., et al. (2019). Optimal Complementary Photovoltaic Capacity Configuration for Grid-Connected Wind Farms Expansion[J]. J. Shandong Univ. (Engineering Science) 49 (5), 44. doi:10.6040/j.issn.1672-3961.0.2019.162

CrossRef Full Text | Google Scholar

Yang, H., and Ren, Z. (2015). Research on Optimal Allocation of Pumped Storage Station in Wind and Photovoltaic Complementary Generation System[J]. Computer Simulation 32 (4), 111.

Google Scholar

Zhang, Lu. (2020). Optimization Scheduling Model and Method for Wind-PV-Pumped Joint Operation in High Proportion Renewable Energy base[D]. Lanzhou City: Lanzhou University of Technology.

Google Scholar

Zhang, S., Yao, L., Zhang, j., and Guoqing, Y. (2015). Capacity Optimization Research on Genetic Algorithms Hydro-Solar Complementary Photovoltaic Power Plant[J]. Qinghai Electric Power 34 (4), 29. doi:10.15919/j.cnki.qhep.2015.04.009

CrossRef Full Text | Google Scholar

Zhang, X., Li, S., Hu, X., Yanhao, F., Ming, C., and Yeye, F. (2018). Optimal Design of Wind and Solar Hybrid Power System Based on Particle Swarm Optimization[J]. J. Zhejiang Univ. Technol. 46 (6), 650. doi:10.3969/j.issn.1006-4303.2018.06.011

CrossRef Full Text | Google Scholar

Zhao, M., Zhou, X., and Shang, Yu. (2015). Exploring the Concept, Key Technologies and Development Model of Energy Internet[J]. Power Syst. Technol. 39 (11), 3014. doi:10.13335/j.1000-3673.pst.2015.11.002

CrossRef Full Text | Google Scholar

Zhong, D., Li, Q., and Zhou, X. (2018). Research Status and Development Trends for Key Technologies of Multi-Energy Complementary Comprehensive Utilization System[J]. Therm. Power Generation 47 (2), 1. doi:10.19666/j.rlfd.201706049

CrossRef Full Text | Google Scholar

Zhou, T., and Sun, W. (2015). Capacity Optimization of Hybrid Energy Storage Units in Wind-Solar Generation System[J]. Acta Energiae Solaris Sinica 36 (3), 756. doi:10.3969/j.issn.0254-0096.2015.03.038

CrossRef Full Text | Google Scholar

Zhu, Y., Chen, S., Huang, W., Li, W., and Guangwen, M. (2018). Optimal Capacity Configuration of Hydro-Photovoltaic-Wind Complementary Power Generation System under Wind and Photovoltaic Curtailment[J]. Water Resour. Power 36 (7), 215

Google Scholar

Nomenclature

$C_{in}^i$ maximum energy storage power of the unit in period i, kW

Abbreviations

$C_{out}^i$ maximum energy supply power of the unit in period i, kW

LOLP loss of load probability

$w_1^i$ power of abandonment due to insufficient energy storage power, kW

LPSP loss of power supply probability

$w_2^i$ power abandoned after the energy storage capacity is fully used, kW

PSO particle swarm optimization

$n^i$ planned energy storage power, kW

IASA improved artificial sheep algorithm

$n{\text{'}}^i$ actual energy storage power, kW

Parameters

$P^i$ total system output in period i, kW

$P_S$ power of photovoltaic station, kW

$n$ number of periods during which the total output of the system matches the load

${\eta }_P$ comprehensive power generation efficiency

$N$ total number of periods for calculation

$S$ solar radiation intensity, W/m²

$\eta$ power abandonment rate

$A_P$ installation area of the photovoltaic cell array, m²

$f$ objective function

$P_w$ the actual power of the wind turbine generator unit, kW

$m_j$ investment of unit installed capacity of type j power source, CNY/kW

$P_r$ rated power of the wind turbine generator unit, kW

$c_j$ installed capacity of type j power source, kW

$V_{cr}$ cut-in speed of wind, m/s

$\gamma$ power supply guarantee rate

$V_r$ rated speed of wind, m/s

${\gamma }_{\min }$ allowable minimum guarantee rate

$V_{co}$ cut-out speed of wind, m/s

${\eta }_{\max }$ set maximum power abandonment rate

$p_h$ hydropower output

$C_{\max ,j}$ maximum possible installed capacity of type j power source

${\eta }_h$ power generation efficiency of the hydraulic turbine generator unit

$n^i$ virtual energy storage power, kW

$Q$ volumetric flow rate of the hydropower station, m³/s

$t^i$ time duration

$H$ head of the hydropower station, m

${\eta }_{in}$ efficiency of energy storage

$I_n^i$ net load, kW

${\eta }_{out}$ efficiency of energy supply

$S^i$ energy stored in the unit at the beginning of a period, kWh

$L^i$ target load, kW