Improved System Frequency Regulation Capability of a Battery Energy Storage System

Introduction

With the growing issues of air pollutants and energy shortage, a large amount of renewable energy generation including wind generation has been integrated into the electric power grid (Bevrani, 2014; Huang et al., 2022). Due to the advanced control characteristics, the most used type of wind generation is the variable-speed wind turbine generators (VSWTGs) interfaced with the power electronic devices (Xiong et al., 2020). However, the VSWTGs are unable to participate in frequency regulation due to the decoupled relationship between the rotor speed of the wind turbine and the synchronous generator (Kim et al., 2019a; Xiong et al., 2022). As the penetrations of renewable energy generator grow, the system frequency excursions, maximum rate of change of the system frequency, and the frequency of the steady state become severe (Yang et al., 2022; Keung et al., 2019); the power system should deploy more generators with rapid ramping capability to maintain the system frequency stability (Tto, 2010).

When modifying the control strategy of the VSWTGs, they are able to participate in frequency regulation by storing or releasing the power into or from the rotating masses including wind turbine, gearbox, and rotor of the generator (Kheshti et al., 2019; Yang et al., 2021). As in Lee et al. (2016), Dreidy and Mokhlis (2017), and Kim et al. (2019b), the rate of change of the system frequency and the frequency excursion control loops are employed to provide frequency regulation capability. The pitch angle controller of the doubly fed induction generator (DFIG) is implemented to provide frequency response by releasing the pitch angle (Ye et al., 2019). However, the frequent activations would increase mechanical fatigue and further reduce the lifetime of the DFIG.

The energy storage systems can be regarded as a better option for frequency regulation due to the fast response and advanced control capability (Zhao et al., 2015; Kim et al., 2019c). In (Mercier et al., 2009), a control scheme of a BESS providing frequency regulation is addressed with the aim of minimizing the use of the BESS. Several control strategies for the BESS are evaluated in Oudalov et al. (2007) and Stroe et al. (2017) for investigating the primary frequency regulation service. However, the fixed control coefficient is utilized so as to restrict the benefits for regulating frequency. Obaid et al. (2020) suggest a hierarchical control strategy of the BESS to provide frequency regulation capability. Five bands are divided according to the measured SOC. However, the control coefficient in each band is fixed so as to result in over-charging of the SOC. Meng et al. (2021) suggest that the SOC is used as the feedback variable of the control coefficient of the frequency regulation scheme. However, for a severe disturbance, the frequency regulation potential of the BESS is underutilized.

This research addresses a frequency regulation scheme of the BESS to suppress the maximum frequency deviations and improve the maximum rate of change of the system frequency and the system frequency of the steady state. To this end, the droop control with the input of the frequency deviation is implemented in the controller of the BESS. To improve the frequency supporting capability and prevent the over-discharging phenomenon, the control coefficient is defined as a proportional function of the state of charge and the system frequency excursions. The contributions of the proposed frequency regulation scheme are investigated with different wind power penetration level conditions, initial SOCs, and sizes of the disturbance based on the electromagnetic transient program restructured version (EMTP-RV).

Control of the DFIG and BESS

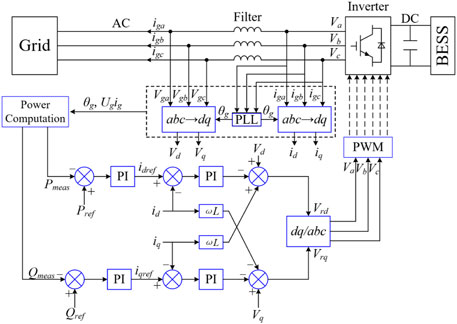
Figure 1 illustrates the vector control strategy of the rotor side converter and grid side converter. The stator flux vector oriented control strategy is applied in the rotor side converter, and the grid voltage vector oriented control strategy is applied in the grid side converter; as a result, the DFIG can achieve decoupled control of the active power and reactive power (Ye et al., 2008). As shown in Figure 1A, the rotor side converter employs dual-loop control technology (outer power controller and inner current controller). The active power and reactive power injected into the grid are controlled by regulating the rotor current components of the d-axis and q-axis, respectively (Fernandez et al., 2008). As illustrated in Figure 1B, the voltage of the dc-link is controlled by regulating the current component of the d-axis. The reference of the current component of the q-axis (i_gq) is set to a zero or non-zero value depending on the control objectives (Fernandez et al., 2008).

FIGURE 1

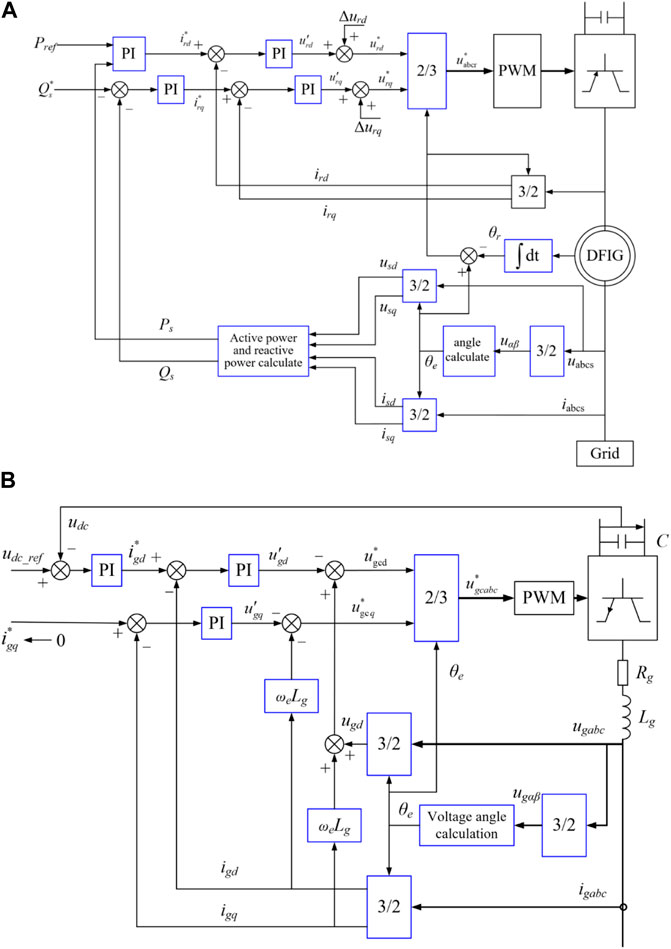
FIGURE 1. Typical vector control scheme of the rotor side and grid side converters of a DFIG. (A) Vector control strategy of the rotor side converter. (B) Vector control strategy of the grid side converter.

The maximum wind power can be extracted when the rotor speed of the wind turbine is controlled at the optimal rotor speed by regulating the tip-speed ratio. This process can be achieved in the top loop of the rotor side converter. The reference for MPPT of the DFIG is able to be expressed in (1) (Yang et al., 2018).

$P_{MPPT}=\frac{1}{2}{c}_{P,\max }\rho \pi R^2{\left(\frac{{\omega }_{r}R}{{\lambda }_{opt}}\right)}^3=k_g{\omega }_r^3,(1)$

where ρ, v_w, and c_p represent the air density, the wind speed, and the power coefficient, respectively. ω_r and R represent the rotor angular speed and the blade length, respectively. c_{P, max} and λ_opt are the maximum c_P and optimal tip-speed ratio, respectively.

As in (1), when performing the MPPT, the output power of the DFIG mainly relates to the rotor speed irrespective of the system frequency, so that the DFIGs are unable to provide frequency regulation service to the power grid.

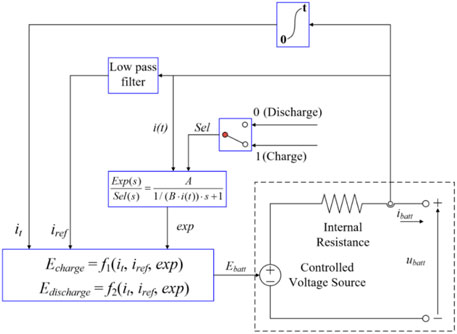
The equivalent model of the BESS used in this research is illustrated in Figure 2, where E_BESS is a nonlinear function of the following variables; E₀ is the constant voltage; exp(s) is the exponential zone dynamics; sel(s) means the battery mode (“1” for charging mode and “0” for discharging mode); α is the polarization constant or polarization resistance; i_ref and i_batt are the low frequency current dynamics and batter current, respectively; Q is the maximum battery capacity; and A and B are the exponential voltage and exponential capacity, respectively (Wu et al., 2017).

FIGURE 2

FIGURE 2. Model of the BESS.

The equations of the charge and discharge modes for the BESS are written as:

Charging mode

$f_1({\mathit{i}}_t,{\mathit{i}}_{\mathrm{ref}},\exp )=E_0-\alpha \cdot \frac{Q}{{\mathit{i}}_t+0.1\cdot Q}\cdot {\mathit{i}}_{\mathrm{ref}}-\alpha \cdot \frac{Q}{Q-{\mathit{i}}_t}\cdot {\mathit{i}}_t+Laplac{e}^{-1}\left(\frac{\exp (s)}{sel(s)}\cdot \frac{1}{\text{s}}\right),{\mathit{i}}_{\text{ref}}<0.(2)$

Discharging mode

$f_2({\mathit{i}}_t,{\mathit{i}}_{\mathrm{ref}},\exp )=E_0-\alpha \cdot \frac{Q}{Q-{\mathit{i}}_t}\cdot {\mathit{i}}_{\mathrm{ref}}-\alpha \cdot \frac{Q}{Q-{\mathit{i}}_t}\cdot {\mathit{i}}_t+Laplac{e}^{-1}\left(\frac{\exp (s)}{sel(s)}\cdot 0\right),{\mathit{i}}_{\mathrm{ref}}>0.(3)$

The grid voltage vector oriented control strategy is applied in the BESS (see in Figure 3). This implies that the d-axis of the synchronous frame aligns with the stator voltage vector. As a result, the grid voltage of the d-axis equals to the magnitude of stator voltage, and the voltage of the q-axis equals to zero (Serban and Marinescu, 2014). The current of the d-axis component (i_d) is responsible for regulation of the active power injecting into the grid and the current of the q-axis current component (i_q) focuses on regulating the reactive power.

FIGURE 3

FIGURE 3. Control structure of the BESS.

As illustrated in Figures 1, 2, a phase-locked loop is implemented to detect the angle frequency and grid voltage for passively synchronizing the DFIG and BESS with the electric power grid.

The SOC is defined as the ratio of the instantaneous charge to the total charge in a fully charged state. When the BESS performs the frequency regulation, the power command and available SOC (frequency regulation potential) should be considered.

Droop Control Strategy

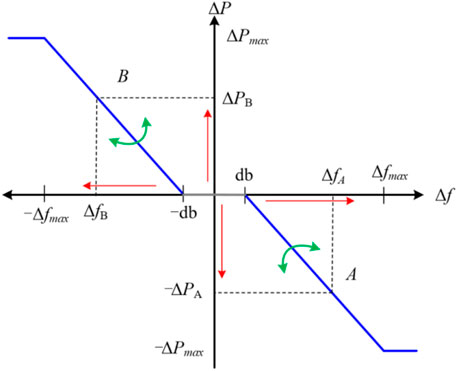
The droop control strategy for frequency regulation can be represented as:

$\mathrm{\Delta }\mathit{P=}\mathrm{Gain}\times \mathrm{\Delta }\mathit{f,}(4)$

where Gain is the coefficient of the droop control and means the slope; ΔP and Δf mean the power variation and system frequency excursion, respectively.

The characteristics of the droop control strategy are shown in Figure 4. As Δf increases, ΔP increases so as to improve the frequency regulation capability. The power variation depends upon the slope (gain). With the use of electronic devices, the regulating response becomes rapid; the dynamic control gains are suggested based on the operating conditions and system frequency regulation requirement.

FIGURE 4

FIGURE 4. Characteristics of the droop control strategy.

This droop control strategy can be utilized in synchronous generators, DFIG, PV, BESS, electric vehicles, and so on. However, some of these devices have different operating characteristics. This means that when designing the frequency regulation scheme using droop control, the considerations are different, for e.g., the mechanical component should be paid more attention, and the reserve power of PVs should be considered. In addition, due to the various response times and potential for the frequency regulation of the aforementioned devices, it should be designed in accordance with the frequency regulation strategies of the targeted research in detail.

The control coefficient of the droop control scheme can be regulated by adjusting the slope. However, difficulties raise in designing the control coefficients suitable for various SOC and disturbances.

Proposed Frequency Regulation Scheme of the BESS

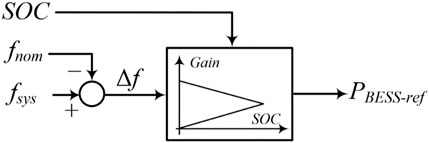
To enhance the system frequency stability, a frequency regulation strategy of the BESS is suggested. As illustrated in Figure 5, the control loop is the same as the droop control strategy, and the power reference of the BESS (P_BESS) when performing frequency regulation is expressed as:

${\mathit{P}}_{BESS}\mathit{=K}\times \mathrm{\Delta }\mathit{f,}(5)$

where K means the control coefficient of the frequency regulation.

FIGURE 5

FIGURE 5. Control concept of the proposed frequency regulation scheme of the BESS.

The power reference combined with the DFIG and BESS can be represented as follows:

$\begin{array}{l}{\mathit{P}}_{\text{ref}}\mathit{=}{\mathit{P}}_{BESS}\mathit{+}{\mathit{P}}_{\text{DFIG}},\\ =\mathit{K}\times \mathrm{\Delta }\mathit{f+}{\mathit{P}}_{\text{MPPT}}.\end{array}(6)$

In (6), it is evident that the BESS can compensate for the power deficit by decreasing the SOC. The benefit of the frequency regulation is mainly related to the control coefficient. To flexibly utilize the potential of the frequency regulation of the BESS while avoiding over-discharging of the BESS, the control coefficient is defined as in (7) and (8):

$\mathit{K=}\alpha \frac{\mathit{SO}{\mathit{C}}_{\text{meas}}\mathit{-SO}{\mathit{C}}_{\min }}{\mathit{SO}{\mathit{C}}_{\max }-\mathit{SO}{\mathit{C}}_{\min }},(7)$

$\alpha \mathit{=}\gamma \mathrm{\Delta }f+1,(8)$

where SOC_meas, SOC_max, and SOC_min are the SOC, maximum SOC, and minimum SOC of the BESS, respectively. γ represents the adjustable factor for the frequency regulation.

To improve the frequency regulation capability and avoid the over-charging phenomenon under various disturbances, K is defined as (7), which is a linear function of the SOC and the system frequency excursions. The control coefficient includes two characteristics. The first characteristic is that K is a monotonic linear function of the SOC so that it reaches a great value with the increasing SOC and becomes zero to avoid over-discharging. The second characteristic is that K varies with the frequency deviation so that it adaptively is adjusted under various disturbances.

The injected power (P_BESS) from the BESS to the frequency drop can be regarded as a negative load so that the power mismatch can be represented as:

$\mathrm{\Delta }P=\mathrm{\Delta }{P}_{\mathrm{L}}-P_{\mathrm{BESS}},(9)$

where ΔP means the equivalent power mismatch considering the injected power from the BESS.

Based on Anderson and Mirheydar (1990) and Shi et al. (2018), the system frequency excursion [Δf(t)], the maximum rate of the change of frequency (ROCOF_max), and the system frequency of the steady state (Δf_ss) could be derived from the low-order system frequency response model, as in (10), (11), and (12):

$\mathrm{\Delta }f\left(t\right)=\frac{R\mathrm{\Delta }P}{DR+1}[1+\mathit{\alpha }{e}^{-\mathit{\varsigma }{\mathit{\omega }}_{\mathrm{n}}t}\sin ({\mathit{\omega }}_{\mathrm{d}}t+\mathit{\phi }),(10)$

$\mathrm{ROCO}{\mathrm{F}}_{\max }=f_{sys}\frac{\mathrm{\Delta }P}{2{\mathit{H}}_{\mathit{sys}}},(11)$

$\mathrm{\Delta }{\mathit{f}}_{ss}=\frac{\mathrm{\Delta }P}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\mathit{+D}},(12)$

where D is load damping factor, R is the setting of the governor speed regulation, ∆P_L is the active power mismatch, ω_n means the natural oscillation frequency, ζ is the damping ratio, ω_d is the damped frequency, α is the coefficient when deriving the frequency excursion, and H_sys indicates the inertia constant of the power grid provided by the synchronous generators.

In 10, t approaches to infinity, the component including exponential and sinusoidal functions becomes zero; thus, the system frequency in (10) is the same as in (12) and becomes the setting frequency without implementing secondary frequency control.

In (10), (11), and (12), once the BESS participates in frequency regulation following a disturbance, ΔP becomes small. Thus, the BESS can compensate for the power to the electric power grid so as to reduce the active power mismatch; consequently Δf(t), Δf_ss, and ROCOF_max can be enhanced. The large use of ΔP is able to enhance the frequency regulation capability.

Model System

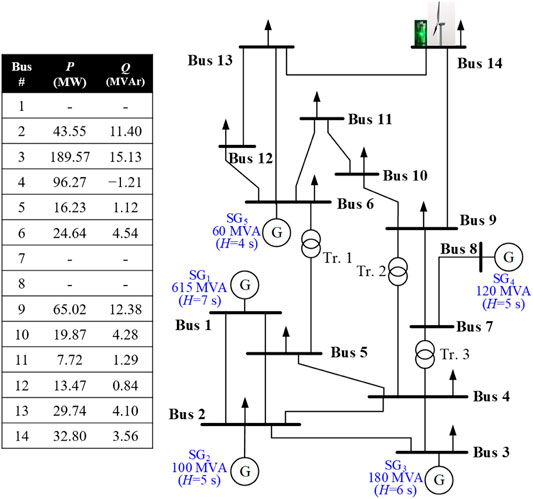
Figure 6 illustrates the modified IEEE 14-bus system, which is used to explore the performance of the proposed frequency regulation scheme of the BESS based on an EMTP-RV simulator. It includes an aggregated doubly fed induction generator (DFIG)-based wind power plant embedded with the BESS (which is connected to Bus 14), five traditional synchronous generators, and static loads.

FIGURE 6

FIGURE 6. Modified IEEE 14-bus system embedded with a DFIG-based wind power plant and BESS.

The droop gains for the primary frequency regulation of all of the traditional synchronous generators are set to 5%. All traditional synchronous generators are modeled as steam turbine generators by employing the IEEEG1 steam governor model (see in Figure 7). The total load is set to 600.0 MW and 57.4 MVAr.

FIGURE 7

FIGURE 7. Tandem-compound, single-reheat governor model.

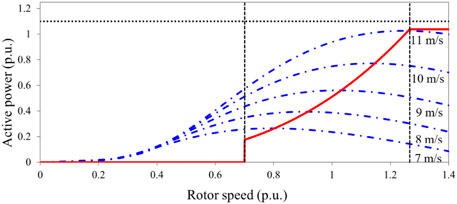
Figure 8 shows the operating characteristics of the DFIG. The operating range of ω_r of the DFIG ranges between 0.7 p.u. (ω_min) and 1.25 p.u. (ω_max). The rated, cut-in, and cut-out speeds of the DFIG are set to 11.0 m/s, 4.0 m/s, and 25.0 m/s, respectively.

FIGURE 8

FIGURE 8. Operating characteristics of the DFIG.

The capacity of the BESS is 5.0 MWh. The battery is connected to the terminal of the wind power plant by a 5-MW DC/AC inverter with the SOC of 50% and 30%. The terminal voltage is 13.8 kV. The SOC_max and SOC_min are set to 90% and 10%, respectively.

The performances of the proposed frequency regulation scheme under various wind power penetration level conditions and sizes of the disturbance are investigated. The performance of the proposed frequency regulation scheme with γ = 10 [proposed (10) represented in the simulation result] is compared to that of the no control scheme and the proposed frequency regulation scheme with γ = 5 [proposed (5) represented in the simulation result] in terms of the maximum frequency excursion, the system frequency of the steady state, and maximum rate of change of frequency.

In this section, since the system frequency indexes are related to the wind power penetrations, sizes of disturbance, and SOCs of the BESS, Case 1 and Case 2 are used to indicate the effectiveness of the proposed scheme under various disturbances. Case 1 and Case 3 are utilized to illustrate the effectiveness of the proposed scheme under various sizes of the disturbance. In addition, Case 1 and Case 4 are employed to show the effectiveness under various SOCs of the BESS.

Case 1: Wind Power Penetration Level of 15% and Disturbance of 50 MW

Figure 9 illustrates the simulation results of Case 1 with low wind power penetration level and small size of the disturbance.

FIGURE 9

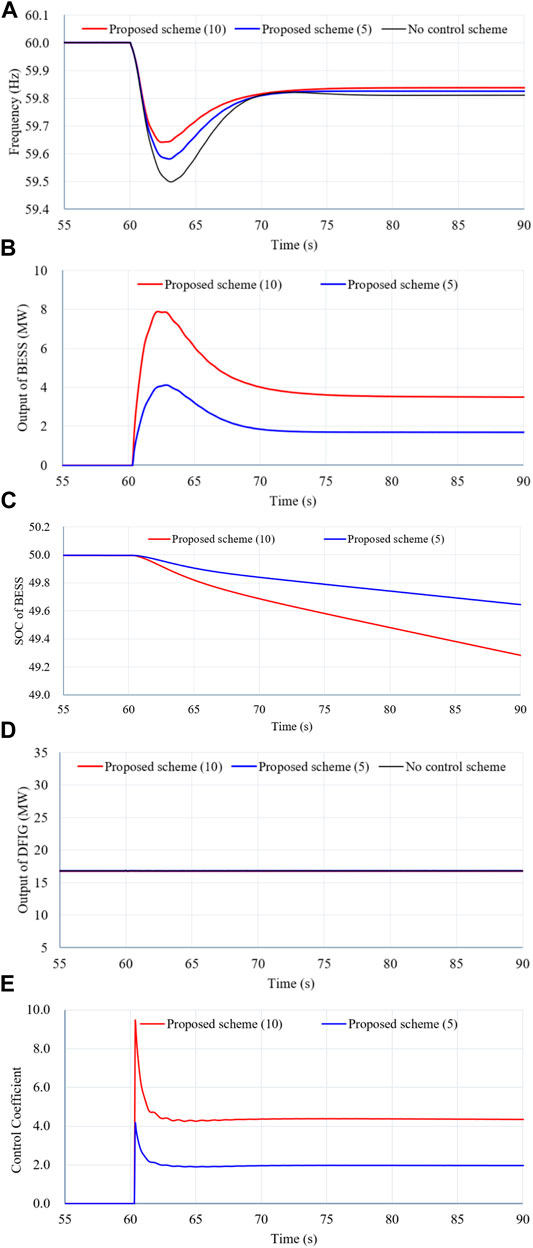
FIGURE 9. Results for Case 1. (A) System frequency. (B) Output power of the BESS. (C) SOC of the BESS. (D) Output power of the DFIG. (E) Control coefficient.

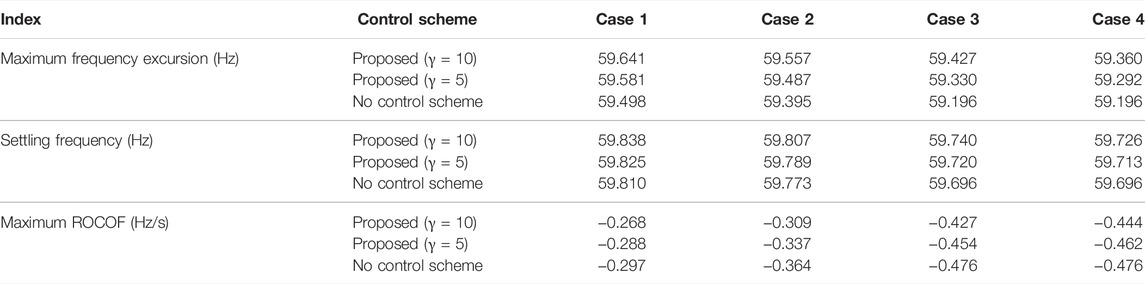
As shown in Figure 9, the maximum frequency excursion, maximum ROCOF, and the system frequency of the steady state of no control scheme are 59.498 Hz, −0.297 Hz/s, and 59.838 Hz, respectively. In the proposed scheme with γ = 5, they are improved to 59.581 Hz, −0.288 Hz/s, and 59.825 Hz, respectively (see in Table 1). This is because the BESS generates amount of active power for compensating for the active power mismatch. In the proposed scheme with γ = 10, they are improved to 59.641 Hz, −0.268 Hz/s, and 59.838 Hz, respectively. This is because the BESS generates more active power to the electric power grid to compensate for the active power mismatch (see Figure 9B).

TABLE 1

TABLE 1. Summary of all cases.

As shown in Figure 9B, the peak values of the active power for the proposed scheme with γ = 10 and the proposed scheme with γ = 5 are 7.9 and 4.0 MW, respectively. In the steady state, the power generated to the grid for both schemes are 3.5 and 1.7 MW, respectively; this is the detailed reason that the improving performances of the system frequency stability in the proposed scheme with γ = 10 are better.

As shown in Figure 9C, the SOC of the proposed scheme decreases from 50. Due to the use of large control coefficient, the SOC of the proposed scheme with γ = 10 decreases more than that of the proposed scheme with γ = 5.

The output powers the DFIG for all schemes remain fixed due to the DFIG operates in MPPT operation, which is unable to participate in frequency regulation (see Figure 9D).

As shown in Figure 9E, the control coefficient of the proposed scheme with γ = 10 so that it is output power is more than that of γ = 5.

Case 2: Wind Power Penetration Level of 30% and Disturbance of 50 MW

Figure 10 illustrates the simulation results of Case 2 with a high wind power penetration level and small size of the disturbance.

FIGURE 10

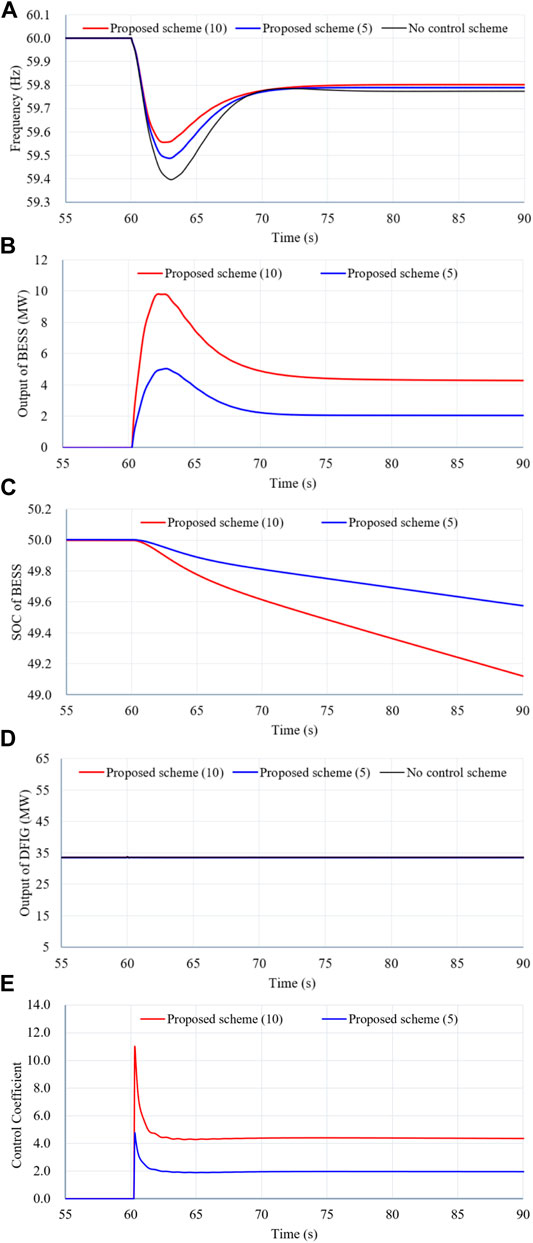
FIGURE 10. Results for Case 2. (A) System frequency. (B) Output power of the BESS. (C) SOC of the BESS. (D) Output power of the DFIG. (E) Control coefficient.

Compared with Case 1, the maximum frequency excursion, maximum ROCOF, and the system frequency of the steady state of no control scheme decrease to 59.395 Hz, −0.364 Hz/s, and 59.773 Hz, respectively; this is due to the online inertial constant and primary frequency regulation capability. In the proposed scheme with γ = 5, compared with the no control scheme, the improvements of theses indices are 0.092 Hz, 0.027 Hz/s, and 0.016 Hz, respectively (see in Table 1). In the proposed scheme with γ = 10, compared with the no control scheme, the improvements of theses indices are 0.162 Hz, 0.055 Hz/s, and 0.034 Hz, respectively. This is because the BESS generates more active power to the electric power grid to compensate for the active power mismatch (see Figures 9B,E).

The improvements of the system frequency maximum excursion, the maximum rate of change of frequency, and the settling system frequency in the proposed frequency regulation schemes are more than those in Case 1 due to the large increase of the active power injection.

In Figure 10B, the peak values of the active power for the proposed scheme with γ = 10 and the proposed scheme with γ = 5 are 9.8 and 5.1 MW, respectively. In the steady state, the power generated to the grid for both schemes are 4.3 and 2.1 MW, respectively. This is because of the large control coefficient (see Figure 10E). As a result, due to the use of large control coefficient, the SOC of the proposed scheme with γ = 10 decreases more than that of the proposed scheme with γ = 5 (see Figure 10C).

Case 3: Wind Power Penetration Level of 15% and Disturbance of 80 MW

Figure 11 illustrates the simulation results of Case 3 with a low wind power penetration level and a large size of the disturbance.

FIGURE 11

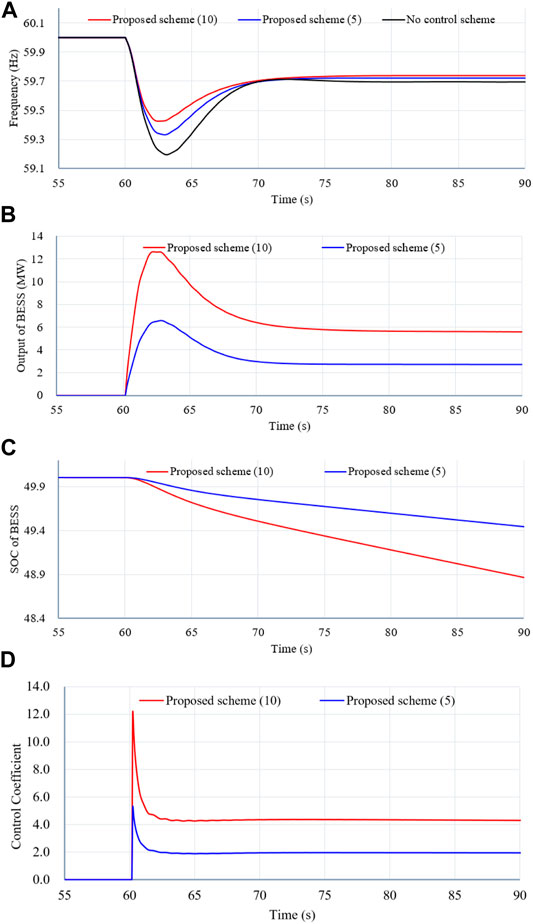
FIGURE 11. Results for Case 3. (A) System frequency. (B) Output power of the BESS. (C) SOC of the BESS. (D) Control coefficient.

Compared with Case 1, the maximum frequency excursion, maximum ROCOF, and the system frequency of the steady state of no control scheme decrease to 59.196 Hz, −0.476 Hz/s, and 59.696 Hz, respectively; this is due to the large power deficit. Compared with the no control scheme, the proposed schemes (with γ = 5 and γ = 10) are able to improve the indices in terms of the maximum frequency excursion, rate of change of the system frequency, and the settling frequency.

The improvements of the system frequency maximum excursion, maximum rate of change of frequency, and the settling system frequency in the proposed frequency regulation schemes are more than those in Case 1 due to the large increase of the active power injection calculation by (6) (see Figure 11B).

Case 4: Wind Power Penetration Level of 15%, Disturbance of 80 MW, and Inertial SOC of 30%

Figure 12 illustrates the simulation results of Case 4 with a low wind power penetration level, large size of the disturbance, and low initial SOC of the BESS.

FIGURE 12

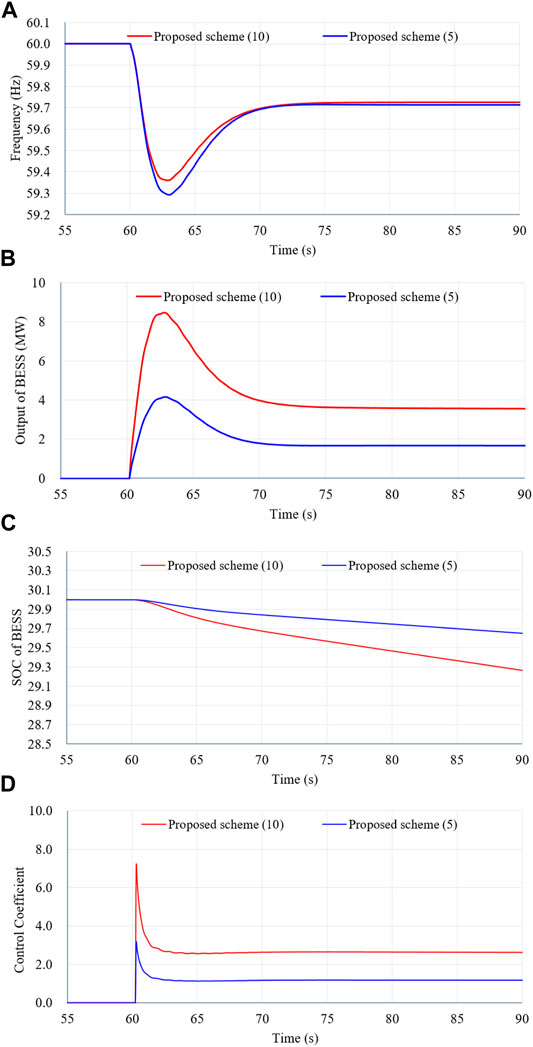
FIGURE 12. Results for Case 4. (A) System frequency. (B) Output power of the BESS. (C) SOC of the BESS. (D) Control coefficient.

Compared with Case 3, the indices of the maximum frequency excursion, maximum ROCOF, and the settling frequency of the proposed schemes with γ = 5 decrease to 59.292 Hz, −0.462 Hz/s, and 59.713 Hz, respectively; this is due to the less power injection from the BESS. The proposed scheme with γ = 10 is able to improve the indices in terms of the maximum frequency excursion, rate of change of the system frequency, the settling frequency due to the larger control coefficient (see Figure 12D).

Results of all the aforementioned cases represent that the proposed frequency regulation scheme of the BESS can enhance the maximum rate of change of the system frequency and the settling frequency, and suppress the maximum frequency excursion effectively under various disturbances and wind power penetration level. As the sizes of disturbances and wind power penetration level increase, the frequency excursion becomes severe; as a result, the benefits for improving the frequency regulation capability become better. The frequency regulation capability becomes worse in the case of a low initial SOC.

Conclusion

This research suggests a frequency regulation scheme of the BESS to improve the maximum frequency excursion, rate of change of the system frequency, and the settling frequency. To this end, the droop control with the input of the frequency deviation is implemented in the controller of the BESS. The performances of the proposed frequency regulation strategy are verified with various sizes of disturbance, various initial SOCs, and wind penetration levels based on the EMTP-RV simulator. The contributions of this proposed strategy are as follows:

1) The proposed frequency regulation coefficient is a function of the SOC. Thus, the proposed droop control scheme can adaptively adjust the frequency regulation capability while avoiding over-charging to the frequency drop based on the SOC.

2) The proposed frequency regulation coefficient is coupled with the frequency deviation which can reflect the size of the disturbance. Thus, the proposed frequency regulation strategy can adaptively adjust the frequency regulation capability under severe disturbances.

Simulations clearly indicate that the proposed frequency regulation scheme of the BESS can reduce the maximum rate of change of the system frequency and the settling frequency and suppress the maximum frequency excursion effectively under various disturbances and wind power penetration levels. With the increasing sizes of disturbance and wind power penetration levels, the frequency excursion becomes severe; consequently, the benefits for enhancing the frequency regulation capability grow better. The proposed frequency regulation strategy is conducive to integrating more wind power into the power grid.

In the future, the frequency regulation strategy would be designed to suppress the frequency excursions for a long time period under various wind speeds and load conditions in a realist power system.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JH and DY conducted the back ground research of the project. DY proposed the methodology of the project. JH and DY completed the main theory and simulation content. JH and DY completed the writing of the paper. The work was supported by the fund of JH and DY.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anderson, P. M., and Mirheydar, M. (1990). A Low-Order System Frequency Response Model. IEEE Trans. Power Syst. 5 (3), 720–729. doi:10.1109/59.65898

CrossRef Full Text | Google Scholar

Bevrani, H. (2014). Robust Power System Frequency Control. 2nd ed. New York, NY, USA: Springer.

Google Scholar

Dreidy, M., and Mokhlis, H. (2017). Inertia Response and Frequency Control Techniques for Renewable Energy Sources: A Review. Rene. Sustain. Energy Rev. 69, 144. doi:10.1016/j.rser.2016.11.170

CrossRef Full Text | Google Scholar

Fernandez, L. M., Garcia, C. A., and Jurado, F. (2008). Comparative Study on the Performance of Control Systems for Doubly Fed Induction Generator (DFIG) Wind Turbines Operating with Power Regulation. Energy 33 (9), 1438–1452. doi:10.1016/j.energy.2008.05.006

CrossRef Full Text | Google Scholar

Huang, J., Zhang, L., Sang, S., Xue, X., Zhang, X., Sun, T., et al. (2022). Optimized Series Dynamic Braking Resistor for LVRT of Doubly-Fed Induction Generator with Uncertain Fault Scenarios. IEEE Access 10, 22533–22546. doi:10.1109/ACCESS.2022.3154042

CrossRef Full Text | Google Scholar

Keung, P.-K., Li, P., Banaka, r. H., and Ooi, B. T. (2019). Kinetic Energy of Wind-Turbine Generators for System Frequency Support. IEEE Trans. Power Syst. 24, 279. doi:10.1109/TPWRS.2008.2004827

CrossRef Full Text | Google Scholar

Kheshti, M., Ding, L., Nayeripour, M., Wang, X., and Terzijia, V. (2019). Active Power Support of Wind Turbines for Grid Frequency Events Using a Reliable Power Reference Scheme. Renew. Energy 139, 1421–1454. doi:10.1016/j.renene.2019.03.016

CrossRef Full Text | Google Scholar

Kim, J., Gevorgian, V., Luo, Y., Mohanpurkar, M., Koritarov, V., Hovsapian, R., et al. (2019). Supercapacitor to Provide Ancillary Services with Control Coordination. IEEE Trans. Ind. Appl. 55, 5119–5127. doi:10.1109/tia.2019.2924859

CrossRef Full Text | Google Scholar

Kim, J., Muljadi, E., Gevorgian, V., and Hoke, A. F. (2019a). Dynamic Capabilities of an Energy Storage-Embedded DFIG System. IEEE Trans. Ind. Appl. 55 (4), 4124–4134. doi:10.1109/TIA.2019.2904932

CrossRef Full Text | Google Scholar

Kim, J., Muljadi, E., Gevorgian, V., Mohanpurkar, M., Luo, Y., Hovsapian, R., et al. (2019b). Capability‐coordinated Frequency Control Scheme of a Virtual Power Plant with Renewable Energy Sources. IET Gener. Transm. Distrib. 13, 3642–3648. doi:10.1049/iet-gtd.2018.5828

CrossRef Full Text | Google Scholar

Lee, J., Jang, G., Muljadi, E., Blaabjerg, F., Chen, Z., and Cheol Kang, Y. (2016). Stable Short-Term Frequency Support Using Adaptive Gains for a DFIG-Based Wind Power Plant. IEEE Trans. Energy Convers. 31 (3), 1068–1079. doi:10.1109/tec.2016.2532366

CrossRef Full Text | Google Scholar

Meng, Y., Li, X., and Liu, X. (2021). A Control Strategy for Battery Energy Storage Systems Participating in Primary Frequency Control Considering the Disturbance Type. IEEE Access 9, 2169–3536. doi:10.1109/access.2021.3094309

CrossRef Full Text | Google Scholar

Mercier, P., Cherkaoui, R., and Oudalov, A. (2009). Optimizing a Battery Energy Storage System for Frequency Control Application in an Isolated Power System. IEEE Trans. Power Syst. 24 (3), 1469–1477. doi:10.1109/tpwrs.2009.2022997

CrossRef Full Text | Google Scholar

Obaid, Z. A., Cipcigan, L. M., Muhssin, M. T., and Sami, S. S. (2020). Control of a Population of Battery Energy Storage Systems for Frequency Response. Int. J. Electr. Power Energy Syst. 115, 1–8. doi:10.1016/j.ijepes.2019.105463

CrossRef Full Text | Google Scholar

Oudalov, A., Chartouni, D., and Ohler, C. (2007). Optimizing a Battery Energy Storage System for Primary Frequency Control. IEEE Trans. Power Syst. 22 (3), 1259–1266. doi:10.1109/tpwrs.2007.901459

CrossRef Full Text | Google Scholar

Ye, Y., Li, Y., Chen, Z., and Gao, Q., “Comparison of Transient Behaviors of Wind Turbines with DFIG Considering the Shaft Flexible Models,” in 2008 International Conference on Electrical Machines and Systems, 2008, 2585

Google Scholar

Serban, I., and Marinescu, C. (2014). Control Strategy of Three-phase Battery Energy Storage Systems for Frequency Support in Microgrids and with Uninterrupted Supply of Local Loads. IEEE Trans. Power Electron. 29 (9), 5010–5020. doi:10.1109/tpel.2013.2283298

CrossRef Full Text | Google Scholar

Shi, Q., Li, F., and Cui, H. (2018). Analytical Method to Aggregate Multi-Machine SFR Model with Applications in Power System Dynamic Studies. IEEE Trans. Power Syst. 33 (6), 6355–6367. doi:10.1109/tpwrs.2018.2824823

CrossRef Full Text | Google Scholar

Stroe, D.-I., Knap, V., Swierczynski, M., Stroe, A.-I., and Teodorescu, R. (2017). Operation of a Grid-Connected Lithium-Ion Battery Energy Storage System for Primary Frequency Regulation: A Battery Lifetime Perspective. IEEE Trans. Ind. Appl. 53, 430–438. doi:10.1109/tia.2016.2616319

CrossRef Full Text | Google Scholar

Tto, J. H. (2010). Use of Frequency Response Metrics to Assess the Planning and Operating Requirements for Reliable Integration of Variable Renewable GenerationTech. Rep. (Berkeley, CA, USA: Ernest Orlando Lawrence Berkeley National Laboratory).

Google Scholar

Wu, Z., Gao, D. W., Zhang, H., Yan, S., and Wang, X. (2017). Coordinated Control Strategy of Battery Energy Storage System and PMSG-WTG to Enhance System Frequency Regulation Capability. IEEE Trans. Sustain. Energy 8 (3), 1330–1343. doi:10.1109/tste.2017.2679716

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, Y., and Zhuo, F. (2020). Modeling and Stability Issues of Voltage-Source Converter Dominated Power Systems: a Review. CSEE J. Power. Energy. Sys. doi:10.17775/CSEEJPES.2020.03590

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, H., and Liu, Y. (2022). Performance Comparison of Typical Frequency Response Strategies for Power Systems with High Penetration of Renewable Energy Sources. IEEE J. Emerg. Sel. Top. Circuits Syst. 12, 41–47. (Early Access). doi:10.1109/JETCAS.2022.3141691

CrossRef Full Text | Google Scholar

Yang, D., Jin, Z., and Zheng, T. (2022). An Adaptive Droop Control Strategy with Smooth Rotor Speed Recovery Capability for Type III Wind Turbine Generators. Int. J. Electr. Power. Energy Syst. 135, 2022. doi:10.1016/j.ijepes.2021.107532

CrossRef Full Text | Google Scholar

Yang, D., Kim, J., Kang, Y. C., Muljadi, E., Zhang, N., Hong, J., et al. (2018). Temporary Frequency Support of a DFIG for High Wind Power Penetration. IEEE Trans. Power Syst. 33 (3), 3428–3437. doi:10.1109/tpwrs.2018.2810841

CrossRef Full Text | Google Scholar

Yang, D., Sang, S., and Zhang, X. (2021). Two-Phase Short-Term Frequency Response Scheme of a DFIG-Based Wind Farm. Front. Energy Res. 9, 781989. doi:10.3389/fenrg.2021.781989

CrossRef Full Text | Google Scholar

Ye, Y., Qiao, Y., and Lu, Z. (2019). Revolution of Frequency Regulation in the Converter-Dominated Power System. Renew. Sustain. Energy Rev. 111, 145–156. doi:10.1016/j.rser.2019.04.066

CrossRef Full Text | Google Scholar

Zhao, H., Wu, Q., Hu, S., Xu, H., and Rasmussen, C. N. (2015). Review of Energy Storage System for Wind Power Integration Support. Appl. Energy 137, 545–553. doi:10.1016/j.apenergy.2014.04.103

CrossRef Full Text | Google Scholar