Clearance flow patterns and pressure distribution of a pump-turbine: Measurement and simulation of a rotating disk flow

1 Introduction

To achieve the goal of “carbon neutrality and emission peak,” the power system must be dominated by clean energy, such as wind power, photovoltaic power, and solar energy, which faces a new challenge to energy storage. As the main way to store energy on a large scale, a pumped-storage plant plays an important role in ensuring grid safety and enhancing performance, known as the “stabilizer” and “regulator” of the power system. In the power grid, pumped-storage power undertakes functions such as peak and valley load regulation, frequency modulation, phase modulation, spinning reserve, and black-start with the advantages of quick start-up and fast regulation. To match the time-varying demand of the power grid, pump-turbine units frequently operate in various off-design conditions and fast and frequent transitions of operating modes, which easily lead to runner dynamic instabilities (Goyal and Gandhi, 2018). One of the most concerning issues is the axial force imbalance of pump-turbine units, which has been frequently reported, such as at the Kazunogawa Pumped Storage Plant in Japan (Kurokawa et al., 2002) and Tianhuangping Pumped Storage Plant in China (Le and Kong, 2005; Mao et al., 2021). The unit axial instability can be attributed to the imbalanced axial hydraulic thrust acting on the runner (Zhang, 2017), which can be divided into the axial hydraulic thrust in the main flow channel (MFC) and that in the clearance flow channel (CFC) for the pump turbine. Many studies showed that the axial hydraulic thrust in the CFC is huge enough to affect the runner’s stability (Zhang, 2017; Fu et al., 2018). For example, a small variation in clearance leakage could cause huge fluctuations of the clearance axial hydraulic force, resulting in accidents of bearing burning and unit lifting (Wu et al., 2004; Wu et al., 2005). During the runaway transient process, the axial hydraulic thrust in the CFC fluctuates violently and is as important to runner stability as the axial hydraulic thrust in the MFC (Hou et al., 2021b). However, because the clearance flow patterns and pressure distribution and the relationship between them are not clear, the axial thrust in the CFC cannot be described quantitatively and accurately at present. Moreover, the CFC design is largely dependent on engineering experience because of a lack of relevant specifications and references. In research methods, due to the small size and complicated structure of the CFC, the model test is constrained by geometric scale, while prototype observation is difficult to perform. When taking the clearance flow as a part of the CFD model, the calculation cost of multi-scale grid coupling between the large grid in the MFC and the small grid in the CFC is extremely high, and the results are not necessarily completely accurate. All of the aforementioned limitations make the clearance flow research stagnant, despite the fact that it is critical to uncover the unit axial imbalance mechanism. Fortunately, the clearance flow channel of the Francis pump turbine is similar to a thin-layer cavity composed of two parallel disks, in which one disk is rotating and the other is stationary. Therefore, the clearance flow patterns and pressure distribution of the pump turbine can be studied using a rotating–stationary disk model, which is a simplified model of the clearance flow channel of a pump turbine.

For studies of the disk flow, Von Kármán (1921) found a boundary layer around the rotating disk by self-similarly solving a single rotating disk in infinite stationary fluid as early as 1921. Bödewadt (1940) studied the rotating flow on a stationary disk and found a boundary layer around the stationary disk in the same way as Kármán. Combining the research from Kármán and Bödewadt, Batchelor (1951) proposed the flow between a rotating and stationary disk with infinite boundary. It was found that there were two separated boundary layers around the rotating disk and the stationary disk, but the fluid between the two boundary layers rotated at a fixed circumferential speed, called the Batchelor flow. Different from Batchelor, Stewartson (1952) pointed out that the fluid between the two boundary layers was stationary, and only the boundary layer around the rotating disk was rotating, called the Stewartson flow. The two flow patterns represented different solutions to the flow equation, which were verified by many studies (Mellor et al., 1968; Kreiss and Parter, 1983; Zandbergen and Dijkstra, 1987). In recent years, van Eeten et al. (2013) found that the Stewartson flow was an intermediate flow pattern that would eventually develop into the Batchelor flow. The research on the rotating–stationary disk flow described previously was conducted with an infinite boundary condition.

Under the finite boundary, most studies focused on the qualitative flow pattern. Daily and Nece (1960) summarized four kinds of flow patterns for a rotating–stationary disk flow, which were the laminar flow and turbulence flow with combined and separated boundary layers, respectively. Brady and Durlofsky (1987) discovered that the flow patterns showed Batchelor flow characteristics, even if the flow did not quantitatively conform to the self-similarity solution for the two coaxial rotating disk models. During the transient process, axisymmetric propagating waves and helical flow were observed around the stationary disk when the rotating disk was spinning to stop (Savaş, 1983; Lopez and Weidman, 1996; Lopez, 1996). With the increase in the rotating disk speed, the flow patterns showed circular flow, spiral flow, and corrugated turbulence, successively (Gauthier et al., 2002; Poncet et al., 2009; Hendriks, 2010; Watanabe et al., 2016). Singh (2014) found that the circumferential velocity of the rotating–stationary disk increased gradually from zero on the stationary wall to the maximum on the rotating wall for laminar flow. For the turbulence with large flow leakage, Poncet et al. (2005) observed a core region of circumferential velocity, which increased with the increase of the flow coefficient. Gauthier et al. (1999) and Serre et al. (2001) claimed that the circumferential velocity of the core region was closely related to the radius. For the pressure distribution in the rotating–stationary disk cavity, Singh (2017) pointed out that the pressure drop in the cavity increased with the rotating disk speed. In summary, the possible flow patterns of disk flow systems have been widely investigated, ranging from single rotating disk flow to flow between two disks with infinite boundary, then to rotating–stationary disk flow with finite boundary. However, the quantitative descriptions of flow patterns, cavity pressure distribution, and the relationship between flow patterns and pressure are not clearly clarified at present.

To explore the clearance flow patterns and pressure distribution in the clearance region of the pump turbine, we conducted a model test with PIV measurements and CFD simulations of a rotating–stationary disk flow that was a simplified model of the pump turbine clearance flow. Based on the model test and numerical simulation, some sensitive factors that could affect the clearance flow patterns and clearance axial thrust were analyzed. Finally, the calculation formulas of clearance pressure and axial hydraulic thrust were obtained by combining the theoretical analysis and model test, providing a foundation for the axial force imbalance problems of pump turbine units.

2 Testing setup and the numerical simulation method

2.1 Testing setup for particle image velocimetry measurement

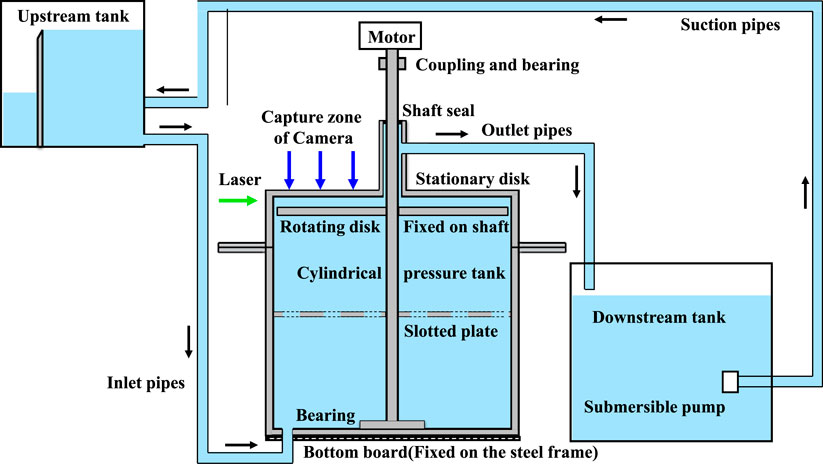
The testing setup of the rotating–stationary disk model test is shown in Figure 1. It was composed of a rotating disk, cylindrical pressure tank, shaft, motor, upstream and downstream tanks, small submersible pump, and pipes. The rotating disk was fixed on the shaft in the center of the cylindrical pressure tank and driven to rotate by the motor. In this way, a clearance cavity was formed between the rotating disk and the head cover of the stationary cylindrical pressure tank. In shape, it was similar to the clearance flow channel that was composed of the hub upper surface and the cover lower surface of the pump turbine. The rotating disk and tank were made of plexiglass. The water flows into the tank from the bottom plate and flows out of the tank at the middle of the head cover, and is then pumped from the downstream tank to the upstream tank, forming the water recirculation. The velocity distributions in different height cross-sections of the rotating–stationary disk cavity were measured by PIV. The laser light was shot horizontally, while the images were captured from the top of the cylinder pressure tank. The laser exposure plane was adjusted to be perpendicular to the camera capture plane.

FIGURE 1

FIGURE 1. Testing setup of the rotating–stationary disk model test.

The geometrical characteristics of the rotating–stationary disk cavity are shown in Figure 2A. The radii of the rotating disk and the cylindrical pressure tank were 280 and 290 mm, respectively. There was a 10 mm gap between the rotating disk and the pressure tank to fill water in the clearance cavity. The cylindrical pressure tank was divided into two parts along the height direction to adjust the clearance height and a flange was used to connect them. The adjustment range of the clearance cavity height was from 40–130 mm, which was consistent with the clearance heights of most pump turbines at present. To simulate the shape of the seal ring of the pump turbine, the shaft at the outlet was slotted with a depth and height of 10 and 8 mm, respectively. The outlet pipe was sleeved on the shaft with a 10 mm gap between them. In addition, a speed sensor was set to monitor the rotation angular velocity of the rotating disk, and seven piezometer tubes were arranged on the head cover of the cylindrical pressure tank to detect the radial pressure distribution. The photo of the model test is shown in Figure 2B.

FIGURE 2

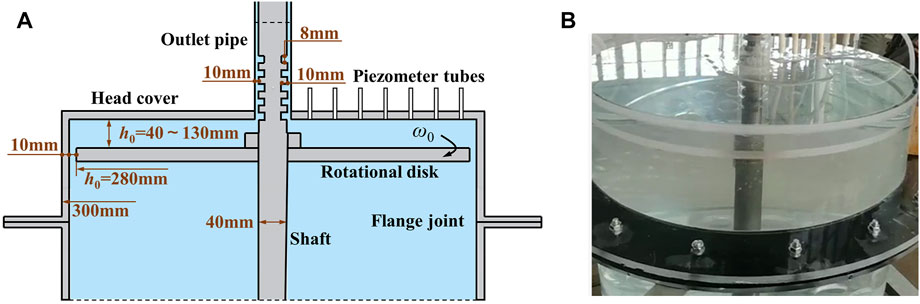
FIGURE 2. Schematic of the experimental setup with adjustable parameters. (A) Geometrical characteristics of the model. (B) Photo of the rotating–stationary disk model.

2.2 Numerical simulation method

As the main way to study the clearance flow of a pump turbine, CFD numerical simulation was also used to calculate the rotating–stationary disk model in this study for two reasons. The first is to find out the suitable numerical method for clearance flow by comparing it with the test, and the second is to offer data that are difficult to measure in the model test.

2.2.1 Simulation domain and grid discretization

As shown in Figure 3A, the numerical calculation domain was completely consistent with the model test. Structural hexahedral grids were used in the whole domain and all of the walls were treated with boundary layers (Figure 3B). The grid size for the first layer was set as 0.005 mm, and the grid growth was controlled within 1.2. Grid independence verification adopted five stepwise levels, from 2.12 to 3.10, 4.21, 5.14, and 6.00 million. According to the results, the circumferential velocity of the simulation was in good agreement with the model test when the grid number was more than 6 million and treated with boundary layers. Therefore, the 6.38 million grid level was used for the simulations. For the boundary conditions, the bottom of the cylinder pressure tank was set as the pressure inlet boundary, while the outlet of the cylinder pressure tank was set as the zero mass outlet boundary because of extremely small clearance flow leakage of the pump turbine. The rotating disk and shaft were specified as the rotating wall, while the rest surfaces were set as the stationary wall.

FIGURE 3

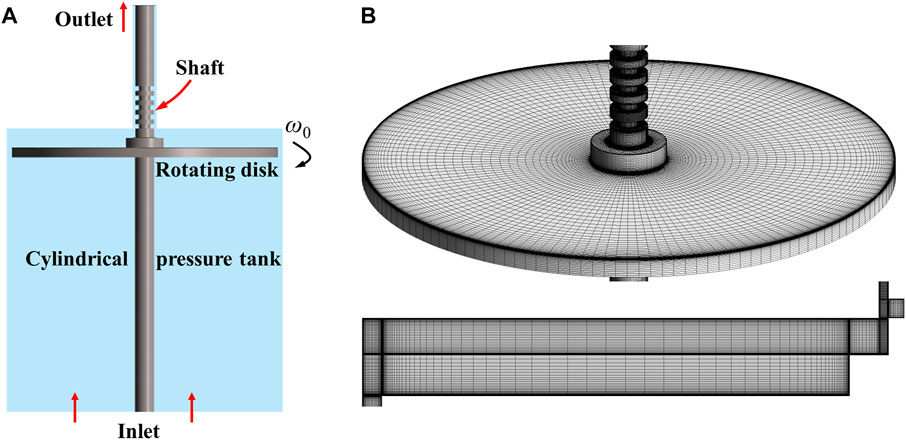
FIGURE 3. Simulation model and grid discretization. (A) Simulation model. (B) Grid discretization and boundary layer treatments.

2.2.2 Numerical simulation method

The finite volume method of commercial software Fluent was used for the simulations and the SIMPLEC pressure velocity coupling algorithm was selected. The second-order scheme was adopted both in space and time discretization. The time step size was set as 0.001 s. Due to the driving action of the rotating disk, the near-wall treatments and turbulence models are very important for accurate CFD simulations.

2.2.2.1 Near-wall treatments and the turbulence model

There are two approaches for near-wall treatments at present. One is the near-wall modeling approach, which can accurately solve the viscous boundary layer but requires extremely fine grids; the other is the wall function approach, which uses semi-empirical wall functions to bridge the viscosity-affected region between the wall and the fully-turbulence region. Even if the viscosity-affected region is not resolved, the wall function approach is ideal for calculations that do not pay much attention to walls due to lower grid requirements. For the advanced turbulence model SST and SAS–SST that are often applied to the simulation of the pump turbine, the wall treatments revert to near-wall modeling if the grid is fine enough, while reverting to the wall function approach if the grid is coarse enough. In theory, the near-wall modeling method has some deficiencies, such as the regions with very low values of turbulence kinetic energy might be treated with a near-wall formulation, even if they are far away from the wall. However, the Menter–Lechner (ML) near-wall treatment is designed to avoid these defects.

2.2.2.2 Calculation method selection

To select a suitable simulation model, we compared the wall function method and the near-wall modeling method of the SAS–SST turbulence model, and the ML method of the $k-\epsilon$ turbulence model in this model. Consistent with the analysis in Section 2.2.2.1, the velocity distribution of the clearance cavity obtained by the ML boundary treatment method matches best with the test results, as shown in Figure 4A (T and S in this study represent the results of the model test and numerical simulation, respectively). In terms of velocity value, the velocity obtained by the wall function method (the SAS–SST turbulence model with coarse grids) is 15% larger than the test results, but their distribution laws are similar (Figure 4B). In addition, the velocity difference obtained by the ML boundary treatment and near-wall modeling of SAS-SST with a fine grid is only 4.5%. Due to the advantages of the ML boundary treatment, the ML wall treatment method of the $k-\epsilon$ turbulence model was selected for the numerical simulation in this study.

FIGURE 4

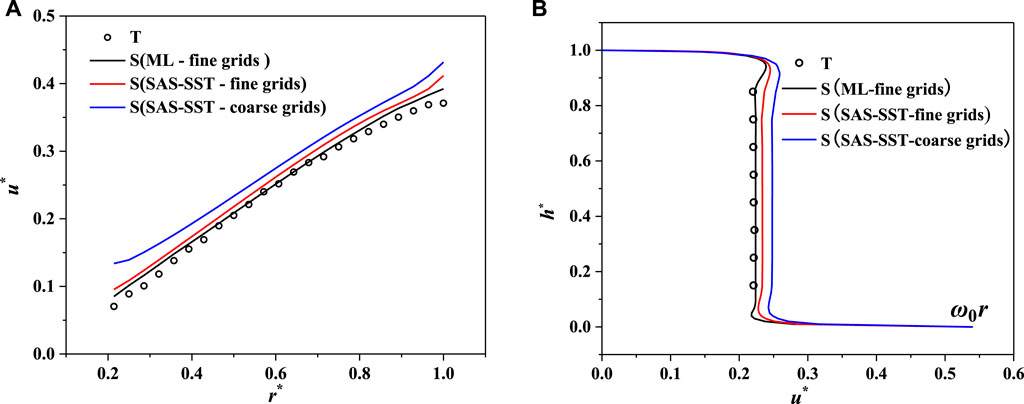
FIGURE 4. Circumferential velocity distribution with different simulation methods (${\omega }_0$=200rpm, $h_0$= 40 mm). (A) Distribution in radial direction (0.45 $h_0$). (B) Distribution in height direction ($r^{\ast }$ =0.536).

It is worth noting that it is indispensable to reconcile the contradiction between calculation accuracy and resources when applying the CFD method to simulate the clearance flow of a prototype pump turbine. Due to the large size of the prototype pump turbine, the semi-empirical wall function method is often used because it is very difficult to meet the fine grid requirements. According to the aforementioned analysis, the circumferential velocity obtained by the wall function method is 15% larger than the model test in value, but their flow patterns are similar. Therefore, the wall function approach can still be used to analyze the clearance flow of the prototype pump turbine.

3 Results and discussions

To generally describe the results, the radial size, circumferential velocity, and pressure are expressed as the following dimensionless parameters:

$r^{\ast }=\frac{r}{r_0},u^{\ast }=\frac{u}{{\omega }_0{r}_0},p^{\ast }=\frac{p}{p_0},(1)$

where $r$, $u$, and $p$ and $r^{\ast }$, $u^{\ast }$, and $p^{\ast }$ are the radius, circumferential velocity, and pressure before and after the normalization, respectively; $r_0$ is the radius of the rotating disk, with a value of 280 mm; and ${\omega }_0$ and $p_0$ are the rotating disk speed and the inlet pressure of the model, respectively. They were set as 200 rpm and 2.12 m because most calculation conditions in this study were analyzed in this condition.

3.1 Clearance axial hydraulic thrust of the pump turbine

For the pump turbine, the clearance flow channels are the small gaps between the rotating and stationary parts. It can be divided into the clearance region between the hub upper surface (rotating surface) and the head cover lower surface (stationary surface), and the clearance region between the shroud lower surface (rotating surface) and the bottom ring upper surface (stationary surface). The schematic of the runner axial forces is shown in Figure 5A, where $F_1$ is the axial hydraulic force in the main flow channel in the upward or downward direction; $F_2$ is that in the hub clearance in the downward direction; $F_3$ is that in the shroud clearance in the upward direction; $F_4$ is the self-weight of the runner in the downward direction; $F_5$ is the buoyancy force in the upward direction; and $F_6$ is the axial force acting on the shaft end in the downward direction. The total axial force on the runner is the summation of these six forces. Compared with other axial forces, the summation of $F_4$ and $F_5$ is small enough to be neglected. Since the value of $F_6$ is fixed, it will not be discussed in this study. The sum of $F_1$, $F_2$, and $F_3$ is the total axial hydraulic thrust of the runner.

FIGURE 5

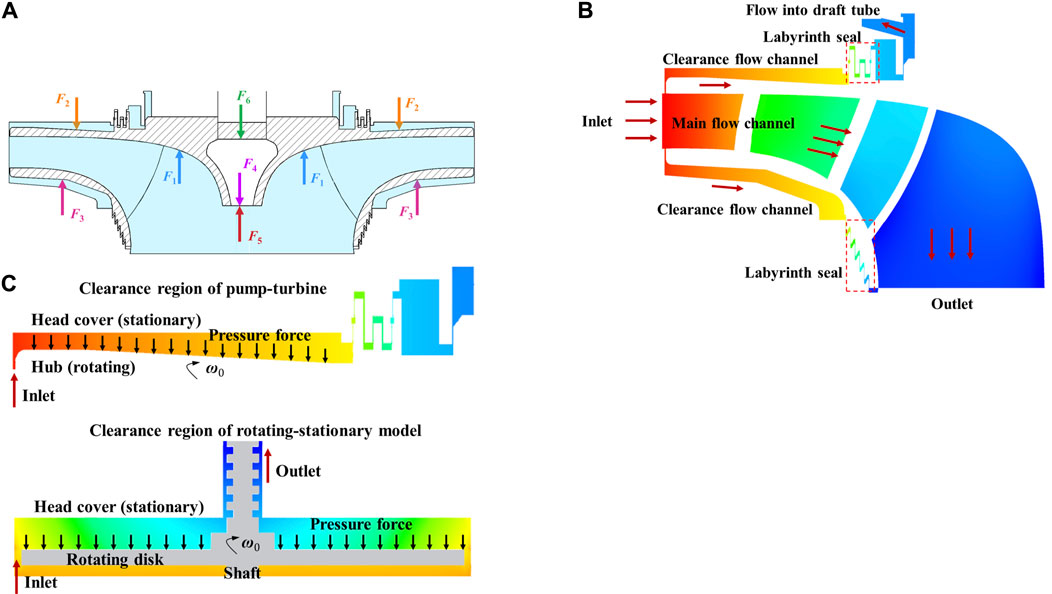
FIGURE 5. Pressure and axial hydraulic thrust in the clearance cavity. (A) Schematic of axial forces of the pump turbine. (B) Clearance pressure distributions of the pump turbine. (C) Axial hydraulic thrust in the clearance cavity of the pumpturbine and rotating–stationary model.

Because the clearance regions are directly connected with the vaneless space of the main flow channel, the inlet pressure of the clearance flow channel is equal to the pressure in the vaneless space and is extremely high (Figure 5B) (Hou et al., 2021b). After entering the clearance flow channel, the pressure in the clearance flow channel drops inward along the radial direction due to the pressure consumption caused by a strong rotating shear flow. Different from the main flow channel, the hydraulic pressure in the clearance flow channel cannot be converted into kinetic energy; therefore, the pressure drop is relatively low. Radially inward, the pressure in the clearance channel decreases slower than that in the main flow channel; therefore, the axial thrust of the clearance flow channel is greater than that of the main flow channel on the hub or shroud of the runner. The enormous pressure in the clearance region generates a huge axial hydraulic thrust on the runner, which can be calculated by integrating the pressure acting on the hub and shroud (Figure 5C). Similarly, for the rotating–stationary disk model, the pressure in the clearance cavity acts on the rotating disk and produces an axial hydraulic thrust. To calculate the clearance axial hydraulic thrust, it is essential to clarify the flow pattern and clearance pressure distribution laws and the relationship between them.

3.2 Clearance flow patterns and pressure distribution

The clearance basic flow patterns and pressure distribution were investigated with a disk rotating speed ${\omega }_0$ of 200 rpm and a clearance height $h_0$ of 40 mm. PIV was used to measure the velocity distributions in eight horizontal cross-sections of the clearance cavity (0.15 $h_0$ to 0.85 $h_0$ with an interval of 0.1 $h_0$).

3.2.1 Clearance flow patterns

The velocity contours in the $0.45h_0$ section of the rotating–stationary disk cavity obtained by the model test and numerical simulation are shown in Figure 6A. Qualitatively, the main flow patterns show a strong rotating shear flow under the driving action of the rotating disk. The circumferential velocity is circumferentially uniform but increases outward along the radial direction. Driven by the centrifugal force, the water flows outward around the rotating disk in the meridian section, then flows inward around the stationary wall because of the boundary effect (Figure 6B), forming secondary flow vortices. To maintain continuity, the water body near the stationary wall continues to supply water to the rotating wall. In terms of velocity magnitude, the circumferential rotating shear flow dominates the flow patterns in the clearance cavity, and the radial and axial velocities are very small.

FIGURE 6

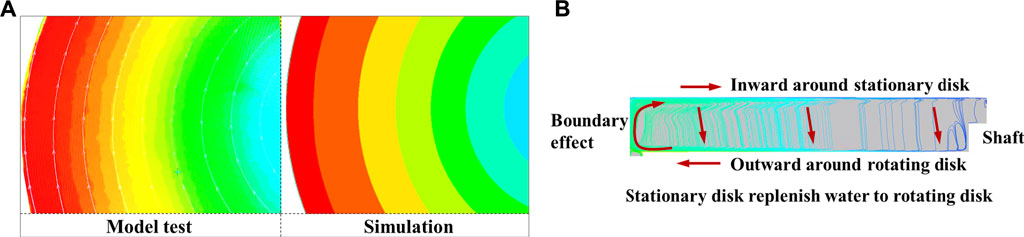
FIGURE 6. Qualitative velocity distributions (${\omega }_0$=200 rpm, $h_0$= 40 mm). (A) Circumferential velocity contours ($0.45h_0$). (B) Velocity distribution in the meridian section.

Quantitatively, the circumferential velocity follows linear distribution laws along the radial direction (Figure 7A), except for the outer edge position of the rotating disk, which is impacted by boundary effects. Along the height direction, a “core region + double boundary layers” distribution is presented for the circumferential velocity (Figure 7B). The circumferential velocity in the core region is constant along the height direction, suggesting that the water body in the clearance cavity rotates like a rigid body. The circumferential velocity is the largest on the rotating disk surface, while it is zero on the stationary wall due to the non-slipping wall, and the core region velocity is between them. Around the rotating wall and the stationary wall, two boundary layers are formed with thicknesses of ${\delta }_d$ and ${\delta }_s$, respectively. In terms of the value, ${\delta }_s$ is larger than ${\delta }_d$, and both of them increase with the radius, which is consistent with the conclusion of Singh (2014).

FIGURE 7

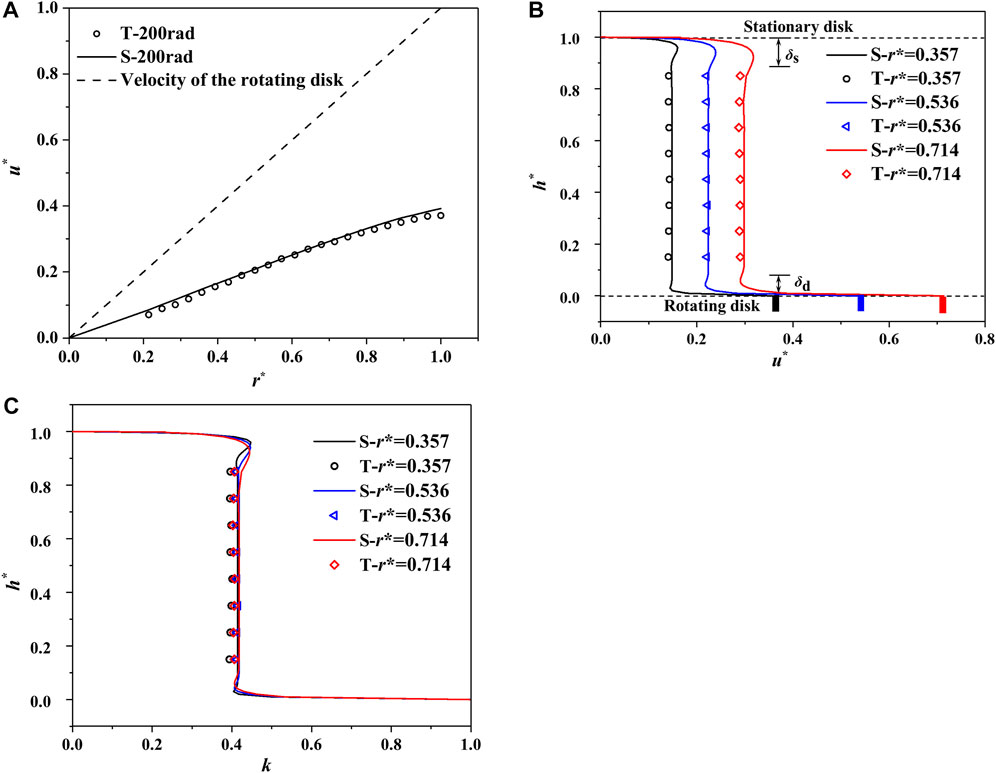
FIGURE 7. Quantitative circumferential velocity distributions (${\omega }_0$=200 rpm, $h_0$= 40 mm). (A) Velocity along the radial direction ($0.45h_0$). (B) Velocity along the height direction. (C) Rotating coefficient k along the height direction.

In the laminar flow condition, Singh and Zosimovych (2016) found that the circumferential velocity continuously decreased from the maximum on the rotating disk to zero on the stationary disk, and no velocity core region exists by linearizing the N-S equation. According to the flow pattern classification from Daily and Nece (1960), the flow patterns in the rotating–stationary disk cavity belong to the turbulent flow. Moreover, because the distance between the two disks is substantially greater than the thickness sum of the two boundary layers, the boundary layers around the rotating and stationary walls are separated, called Kármán and Bödewadt boundary layers, respectively. In short, the flow patterns in this model test show a “core region + double boundary layers” distribution and belong to typical Batchelor flow. The flow in the clearance cavity is dominated by the circumferential velocity of the core region, in which the inertial force is considerably larger than the viscous force, and there is no velocity gradient along the height direction.

Despite the fact that the circumferential velocity in the core region increases as the radius grows, the rotating coefficient k (rotating velocity radio of the core region to the rotating disk) remains constant and does not change with the radius (Figure 7C). When ${\omega }_0$ and $h_0$ are set as 200 rpm and 40 mm, respectively, k is about 0.413 for the model test, while it is around 0.42 for numerical simulation. Elena and Roland (1996) and Cheah et al. (1994) investigated the rotating coefficient k at a fixed radius and found that k is also around 0.41. Therefore, the model test and numerical simulation results in this study are reliable.

For the turbulent plane Couette flow, it is composed of two plates, in which one plate translates with constant velocity in a direction and the other is stationary. Similar to the rotating–stationary disk flow, the velocity core region was also formed for Couette flow, and it flowed at 0.5 times the moving plate velocity (Bech et al., 2006; Pirozzoli et al., 2014). However, the rotating coefficient of the core region for the rotating–stationary disk is less than 0.5 for two reasons. The first is that the circular shear deformation rate in the core region is not equal to zero due to the rotating effect; therefore, the driving action of the rotating disk needs to provide more energy consumption to keep up with the shear deformation rate. In addition, the radial secondary flow in the radial direction weakens the circumferential velocity in the core region due to the centrifugal force and the boundary effect.

3.2.2 Pressure distributions and the axial hydraulic thrust

In the model test and numerical simulation, the cavity pressure shows a circumferentially symmetric distribution. Due to the energy consumption caused by the strong rotating shear flow, the pressure gradually drops inward in the radial direction (Figures 8A,C). For the water body in the clearance cavity, the core region circumferential velocity of the strong rotating shear flow dominates the major flow patterns in the clearance cavity due to the driving action of the rotating disk, while the radial velocity is extremely small. Therefore, Eq. 2 can be obtained by applying the liquid equilibrium differential equation in the radial direction. Due to the extremely small radial velocity, the surface forces are equal to the mass forces on any fluid mass in the radial direction (Figure 8B), and Eq. 2 can be simplified as Eq. 3:

$\left(p-\frac{\partial p}{\partial x}\right)\mathrm{d}y\mathrm{d}z-\left(p+\frac{\partial p}{\partial x}\right)\mathrm{d}y\mathrm{d}z+\rho f_x\mathrm{d}x\mathrm{d}y\mathrm{d}z=0,(2)$

$\frac{\partial p}{\partial x}=\rho f_x,(3)$

where $\rho$ is the density; $p$ is the pressure; and$f_x$ is the mass force, which is the centrifugal force for the flow in the cavity. Assuming that the core region rotational velocity is $k{\omega }_0$, we can modify Eq. 3 to

$\mathrm{d}p=\rho {\left(k{\omega }_0\right)}^{2}r.(4)$

By integrating Eq. 4 from the outer edge of the rotating disk, we can obtain the radial pressure drop $\mathrm{\Delta }p$ and the pressure distribution $p$ in the clearance cavity as Eq. 5 and Eq. 6:

$\mathrm{\Delta }p=\frac{\rho {\left(k{\omega }_0\right)}^2}{2}\left(R_1^2-r^2\right),(5)$

$p=p_1-\frac{\rho {\left(k{\omega }_0\right)}^2}{2}\left(R_1^2-r^2\right),(6)$

where $R_1$ and $p_1$ are the radius and pressure, respectively, at the outer edge of the rotating disk. According to Eq. 6, the pressure distribution along the radial direction can be expressed as a function of the clearance inlet pressure $p_1$ and the circumferential velocity of core region $k{\omega }_0.$

FIGURE 8

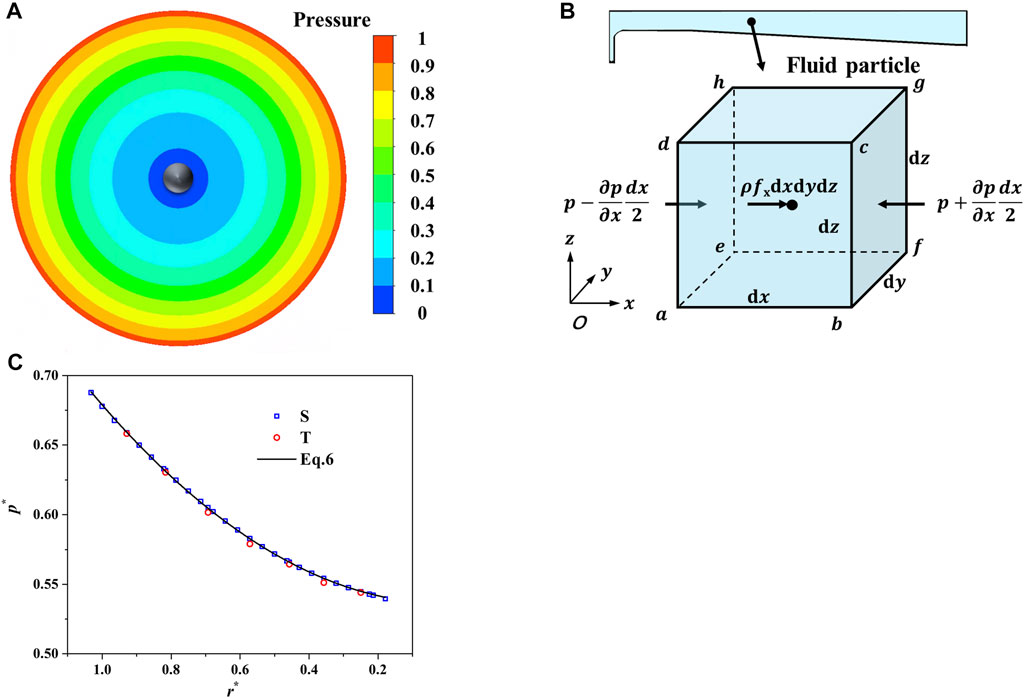
FIGURE 8. Pressure distributions (${\omega }_0$=200 rpm and $h_0$ = 40 mm). (A) Pressure contours in the $0.45h_0$ cross-section. (B) Fluid force diagram (Hou et al., 2021b). (C) Pressure distribution along the radial direction.

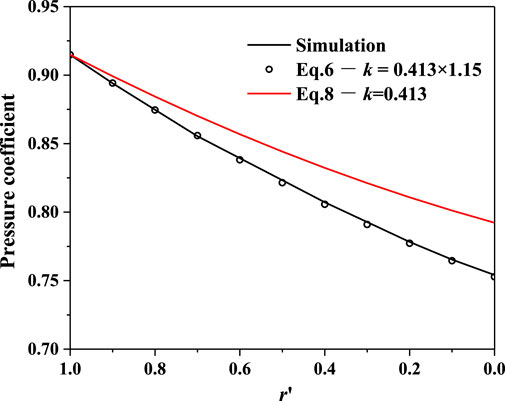
As shown in Figure 8C, the pressure distribution estimated by Eq. 6 matches well with the model test and numerical simulation when the rotating coefficient k is set as 0.413 according to Section 3.2.1, and the maximum error is only 1.2%. Therefore, Eq. 6, which is based on the premise of the accurate circumferential velocity of the core region, can be used to calculate the clearance pressure distribution. Even though the pressure distribution calculated by Eq. 6 neglects the flow losses caused by the radial secondary flow and wall friction, and only takes the losses caused by the strong rotating shear flow into account, it is still relatively accurate because the strong rotational shear flow is the primary source for the energy consumption in the clearance cavity.

3.3 Sensitive factors of clearance flow patterns and pressure distributions

According to the aforementioned analysis, the flow patterns present a typical Batchelor turbulence in the rotating–stationary disk cavity, which means the circumferential velocity has a “core region + double boundary layers” distribution. However, the pump turbine is frequently subjected to a variety of off-design operations and frequent and quick transition processes. Under these operating conditions, the change of the runner rotational speed and the clearance inlet pressure change in real-time. Moreover, for the clearance flow channel sizes of the pump turbine, the radial size is determined by the runner diameter, while the height size (clearance height) is variable and largely dependent on the engineering experience. At present, the clearance height of the Francis pump turbine ranges from a few centimeters to tens of centimeters. Under these different conditions, how do the flow patterns evolve in the clearance cavity? Are the Batchelor flow characteristics still maintained? How does the rotating coefficient change in the core region? What is the relationship between flow patterns and pressure distribution? These questions need to be further investigated. Therefore, the effects of the disk rotating speed, clearance inlet pressure, and clearance height on the flow patterns and pressure distribution in the clearance cavity were studied in this study.

3.3.1 Effects of the disk rotating speed

The disk rotating speed was set as 200–400 rpm with a gradient of 50 rpm to analyze the influence of the disk rotating speed on the velocity and pressure distribution in the clearance cavity.

3.3.1.1 Flow patterns

Under different disk rotating speeds, the circumferential velocity in the cavity still presents a linear distribution in the radial direction, but it increases with the increase in the disk rotating speed (Figure 9A). Along the cavity height direction, the core regions of the circumferential speed are formed under all the disk rotating speeds (Figure 9B). However, the circumferential velocity of the core region increases with the rise of the disk rotating speed. The thickness of the boundary layer on the rotating and stationary disks decreases with the increase in the rotating speed, which is consistent with the law that the boundary layer thickness decreases with the increase of velocity (Cao and Qiu, 1998). Although the circumferential speed in the core region increases with the rise of the disk rotating speed, the rotating coefficient k in the core region remains constant under different disk rotating speeds (Figure 9C). The rotating coefficient k of numerical simulation is slightly larger than that of the model test, around 0.42 to 0.43 and 0.41 to 0.42, respectively (Figure 9D). We simulated the clearance flow patterns during the runaway transient process of a prototype pump turbine and discovered that the circumferential velocity in the core region had a positive correlation change with the rotating disk speed, while the rotating coefficient in the core region did not dramatically change with the disk rotating speed (Hou et al., 2021b).

FIGURE 9

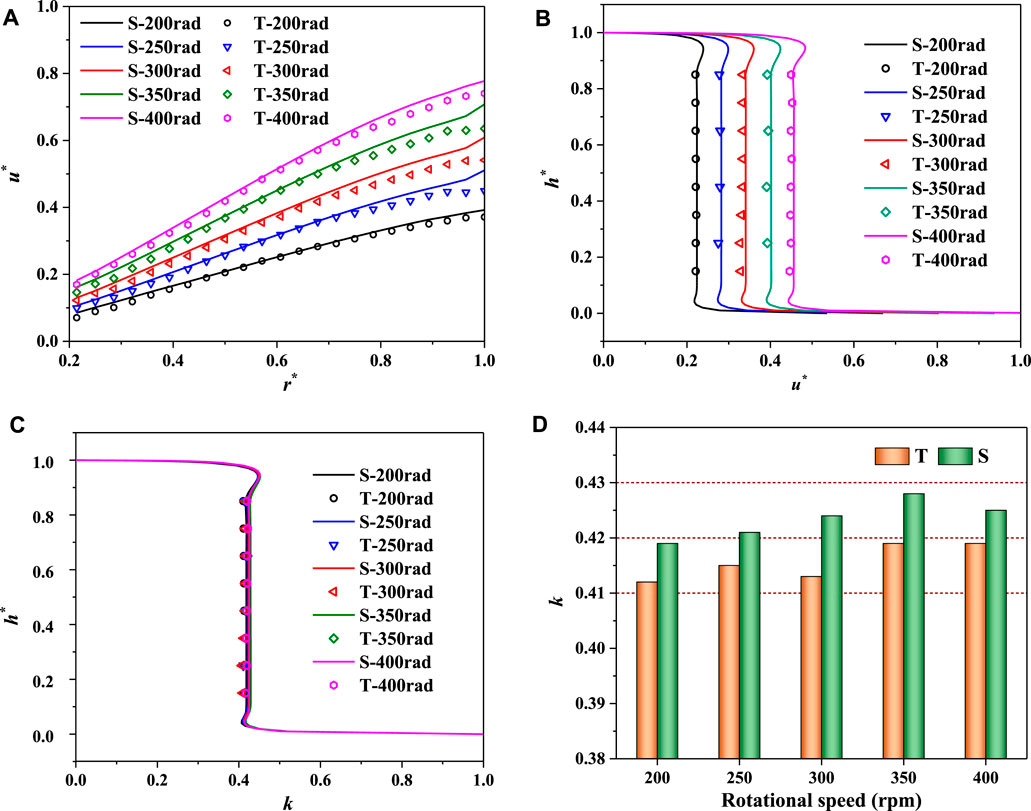
FIGURE 9. Circumferential velocity distributions under different disk rotating speeds. (A) Radial distribution ($0.45h_0$). (B) Height distribution ($r^{\ast }$=0.536 m). (C) Rotating coefficient k distribution. (D) Rotating coefficient k in the core region.

For the rotating–stationary disk cavity, the rotational Reynolds number, defined by Eq. 7, varies with the radius and rotating speed. When the rotating speed decreases to only 200 rpm, the average Reynolds number is 9.2 × 10⁵. Although the Reynolds number in the clearance cavity is not high enough, it is difficult to maintain laminar flow. For the clearance flow of the prototype pump turbine, it is more difficult to maintain laminar flow because of the larger radius and higher rotating speed. Therefore, Batchelor turbulence is the main flow pattern in the clearance flow channel of the pump turbine, and the core region rotates at a speed of around 41–42% of the rotating disk speed.

$Re={\omega }_0{r}^2/\nu ,(7)$

where $\nu$ is the kinematic viscosity.

3.3.1.2 Pressure distributions

According to the clearance flow patterns, the energy dissipation in the disk cavity is mostly caused by strong rotating shear flow. The stronger the rotating intensity, the greater the energy dissipation. Consistent with the aforementioned analysis, the cavity pressure decreases gradually inward radially, and the higher the disk rotating speed is, the greater will be the pressure drop (Figure 10A). The pressure drop $\mathrm{\Delta }p$ increases in a parabolic law with the disk rotating speed, which matches well with Eq. 5 (Figure 10B). $\mathrm{\Delta }p$ of numerical simulation is slightly larger than that of the model test, which can be attributed to the slightly higher rotating speed of the core region for the numerical simulation. However, the two are in good agreement with a difference of less than 5%.

FIGURE 10

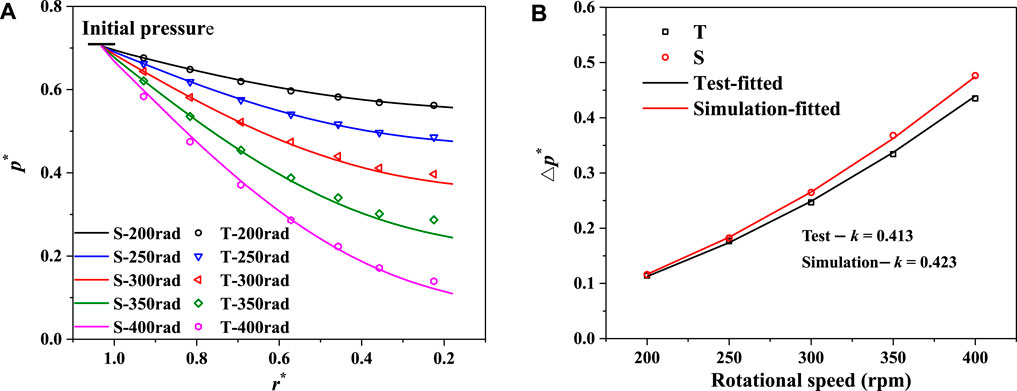
FIGURE 10. Pressure distributions under different disk rotating speeds. (A) Pressure distributions along the radial direction. (B) Variation laws of pressure drop $\mathrm{\Delta }p$.

Eq. 5 can be used to fit $\mathrm{\Delta }p$ acquired from the model test and numerical simulation, as shown by the black and red curves, respectively, in Figure 10B. The fitted k value of the model test and numerical simulation values are 0.413 and 0.423, respectively, which are in good agreement with the aforementioned flow pattern analysis (0.41–0.42 for the model test and 0.42–0.43 for the numerical simulation). Therefore, the core region rotates at a speed of around 41–42% of the rotating disk speed, which can accurately predict the pressure distribution in the clearance cavity based on Eq. 6 and the axial hydraulic thrust by integrating the cavity pressure.

3.3.2 Effects of the clearance inlet pressure

For the pump turbine, because the clearance regions are directly connected with the vaneless space of the main flow channel, the clearance pressure is closely related to the clearance inlet pressure (pressure in the main flow channel), which violently fluctuates during various transient processes. However, it is still unknown whether the inlet pressure affects the velocity and pressure distribution of the clearance cavity. With the help of the rotating–stationary disk test, the velocity and pressure distributions for the clearance inlet pressure ranging from 1.22–2.42 m with a gradient of 0.3 m were studied. Due to the limited inlet pressure in the model test, the inlet pressure of 30 m was increased for the numerical simulation to analyze the influences of the clearance inlet pressure on the velocity and pressure distributions.

3.3.2.1 Flow patterns

As shown in Figure 11A and Figure 11B, the clearance inlet pressure does not affect the circumferential velocity distribution in the rotating–stationary disk cavity. Because of the increased boundary impact, the circumferential velocity exhibits a little reduction at the disk boundary position when the clearance inlet pressure reaches 30 m. In the radial direction, the water flows outward near the rotating disk and inward near the stationary disk due to the imbalance between the pressure force and centrifugal force. When the centrifugal force remains constant, the larger the pressure force, the greater will be the radial force imbalance and the boundary effect, resulting in a slight decrease in the circumferential velocity at the boundary location. However, if the location is far from the boundary effect, the circumferential velocity in the core region is unaffected by the clearance inlet pressure, and still presents a “core region + double boundary layers” distribution.

FIGURE 11

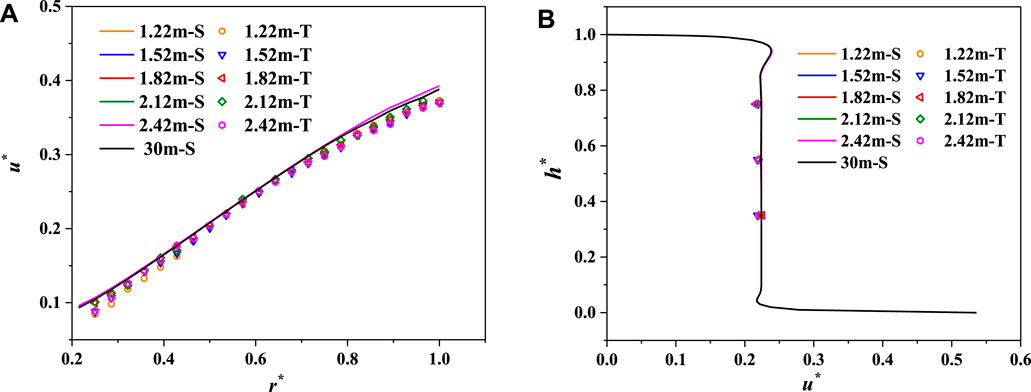
FIGURE 11. Circumferential velocity distribution under different clearance inlet pressures. (A) Radial distribution ($0.45h_0$). (B) Height distribution ($r^{\ast }$=0.536 m).

3.3.2.2 Pressure distributions

The pressure in the clearance cavity increases with the increases of the clearance inlet pressure, though it shows similar distributions and radially decreases inward the clearance cavity under different clearance inlet pressure conditions (Figure 12A). Although the pressure in the cavity is closely related to the clearance inlet pressure, the total pressure drop $\mathrm{\Delta }p$ in the cavity is unaffected (Figure 12B), which is consistent with the conclusions of Eq. 5 and Eq. 6. The pressure in the cavity can be expressed as the inlet pressure and the square of the circumferential velocity of the core region, while the pressure drop is only related to the latter. According to the circumferential velocity distribution in the core region, when the inlet pressure increases to 30 m, the circumferential velocity decreases slightly at the boundary position, resulting in a small decrease in the pressure drop due to the influence of the boundary effect.

FIGURE 12

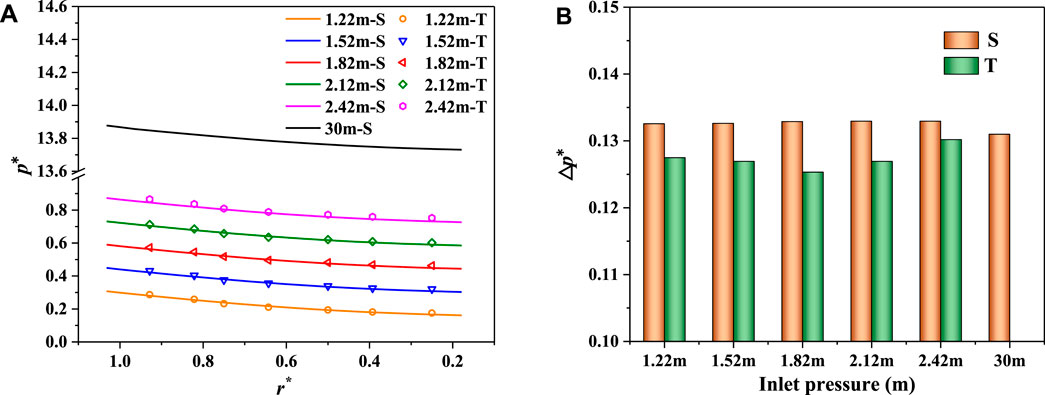
FIGURE 12. Pressure distributions under different clearance inlet pressures. (A) Pressure distributions along the radial direction. (B) Pressure drop $\mathrm{\Delta }p$.

3.3.3 Effects of the clearance height

The clearance flow channel of the pump turbine is a thin-layer cavity composed of the runner and the cover lower surface or bottom ring upper surface. Due to the lack of design specification, the clearance cavity height is largely dependent on experience. At present, most clearance heights range from a few centimeters to more than 10 cm, and even the cavity height changes along the radial direction. To investigate the effects of the clearance height on the flow patterns and pressure distribution in the cavity, the clearance height $h_0$ was set as 40–130 mm with a gradient of 30 mm.

3.3.3.1 Flow patterns

As shown in Figure 13A, the circumferential velocity gradually decreases with the increase of the clearance height at the outer edge of the rotating disk but remains invariable at the inner edge and middle position. Due to the strong centrifugal force near the rotating disk, the water flows outward in the radial direction and crashes against the boundary. After the collision, the water flows inward near the stationary wall. The larger the cavity height, the broader the collision interaction range, in which the circumferential speed was weakened to a great extent. Although it is greatly weakened, the circumferential velocity remains Batchelor turbulent flow (Figure 13B). However, the rotating coefficient k in the core region gradually decreases with the increase of the clearance height near the outer edge. Therefore, the clearance height has little effect on the circumferential velocity if the location is far from the influence range of boundary effects.

FIGURE 13

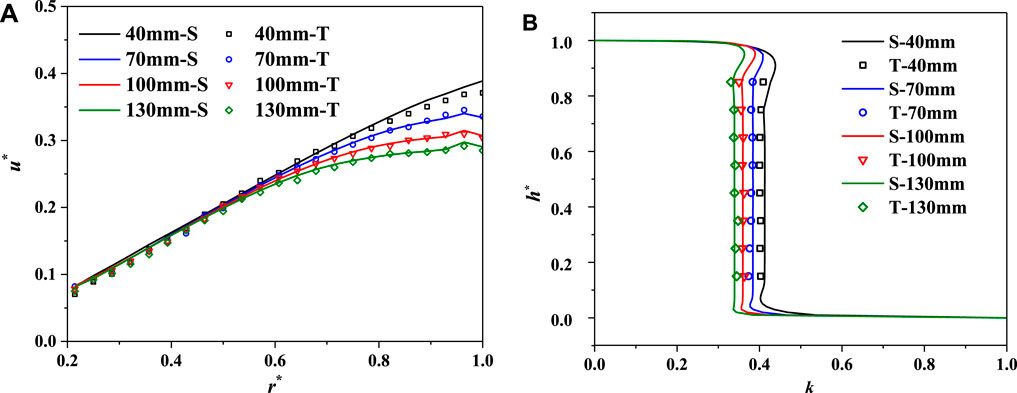
FIGURE 13. Circumferential velocity distribution under different clearance heights. (A) Radial distribution ($0.45h_0$). (B) Height distribution ($r^{\ast }$=0.821).

For the clearance flow channel of the pump turbine, the clearance cavity height is nearly equal to the height of this rotating–stationary disk model, while the clearance radial size is much larger than the influence range of the boundary effect. Therefore, we can assume that the clearance height has little effect on the clearance flow patterns of the pump turbine.

For the laminar flow in the rotating–stationary disk cavity, Singh (2014) demonstrated that the average circumferential velocity decreases with the increase of the clearance height. For the turbulence with large leakage flow, Poncet et al. (2005) discovered that the flow patterns in the rotating–stationary disk are not sensitive to the clearance height, which is consistent with our conclusion. Therefore, once the Batchelor turbulence flow with boundary layer separation is formed in the clearance cavity, the circumferential velocity of the core region is unaffected by the clearance height when the location is far away from the boundary. However, when the clearance height increases to a certain extent that the stationary disk no longer affects the flow near the rotating disk or the influence weakens, the Batchelor flow and the core region of circumferential velocity will no longer be formed. The flow patterns will eventually transform into a single free rotating disk flow. It cannot happen to the clearance flow of the pump turbine because of the limited space in the height direction. Therefore, once the Batchelor flow is formed in the clearance cavity, the clearance height has little effect on the circumferential velocity in the core region if the location is far from the boundary effect.

3.3.3.2 Pressure distributions

Under different clearance heights, the pressure distribution along the radial direction shows a substantial variation near the outer edge of the disk but remains unchanged at the inner edge and the middle position of the rotating disk (Figure 14A). Near the outer edge of the disk, the larger the clearance height, the smaller the circumferential velocity and the smaller the energy dissipation, resulting in a smaller pressure drop. Therefore, the total pressure drop $\mathrm{\Delta }p$ decreases with the increase of the clearance height (Figure 14B).

FIGURE 14

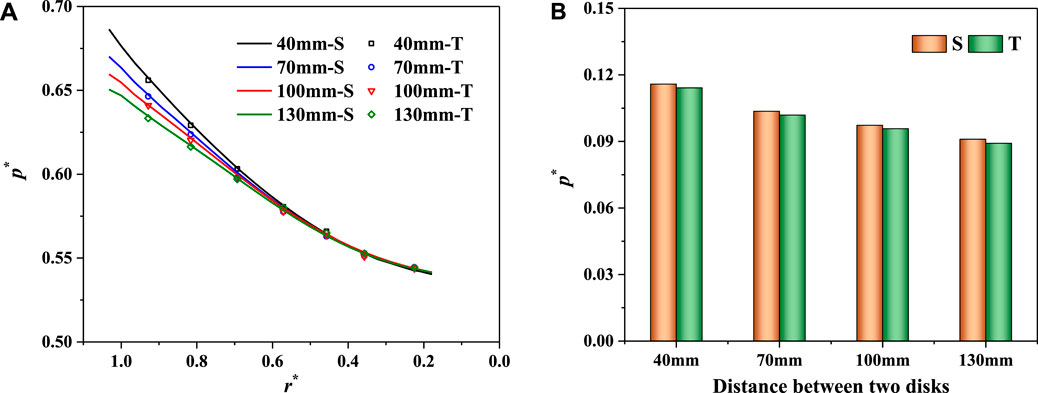
FIGURE 14. Pressure distributions under different clearance heights. (A) Pressure distributions along the radial direction. (B) Pressure drop $\mathrm{\Delta }p$.

We numerically simulated the pressure distributions of the clearance channel with different clearance heights for a pump turbine and found that the clearance height is not sensitive to the clearance pressure distribution (Hou et al., 2021a). Therefore, the clearance height has little effect on the pressure distribution in the clearance cavity of the pump turbine if the location is far from the boundary effect.

3.4 Clearance axial hydraulic thrust of the pump turbine

3.4.1 Clearance flow patterns

Compared with the rotating–stationary disk model test in this study, the clearance flow of the prototype pump turbine has a higher Reynolds number and larger radial size, which leads to Batchelor turbulence in the clearance flow channel. The circumferential velocity shows the “core region + double boundary layers” distribution. Though the fact that the circumferential velocity in the core region increases with the increased rotating disk speed, the core region rotates at a speed of around 41–42% of the rotating disk speed. In the meridian section, the water flows outward around the rotating disk, while flowing inward around the stationary wall, forming the secondary flow vortices.

3.4.2 Clearance axial hydraulic thrust

It is difficult to estimate the pressure distribution in the clearance cavity of the pump turbine by Eq. 6 before we recognize the clearance flow patterns and the rotating coefficient k. According to the analysis in this study, the k value of the core region can be quadratically fitted to 0.413 and does not dramatically change with relevant factors. Therefore, Eq. 6 can be modified as follows:

$p=p_1-0.085\rho {\omega }_0^2\left(R_1^2-r^2\right).(8)$

To verify the correctness of Eq. 8, we did a numerical simulation of a prototype pump turbine containing the clearance flow channel and obtained the pressure distributions in the clearance cavity (the related parameters were shown in reference (Hou et al., 2021b)). Due to the contradiction between calculation accuracy and calculation resources, the wall function method was used to solve the clearance flow channel of the pump turbine. As shown in Figure 15, the simulated pressure drops faster than that calculated by Eq. 8. However, the numerically simulated pressure matches well with that calculated by Eq. 6 when the circumferential velocity of the core region increases by 15% (k is equal to 0.413 × 1.15). The main reason is that the simulated circumferential velocity of the core region solved by the wall function method is 15% larger than the model test. The larger velocity consumes more energy and leads to a larger pressure drop in the clearance region. Therefore, Eq. 6 and Eq. 8 can be used to predict accurately the clearance pressure distributions of the pump turbine. Actually, k is about 0.413 in the clearance region both for the model test and fine numerical simulation, and the modified pressure distribution of Eq. 8 tends to be smaller, as shown in the red curve in Figure 15.

FIGURE 15

FIGURE 15. Clearance pressure distributions of a prototype pump turbine.

According to the pressure distribution law in Eq. 8, the clearance axial thrust acting on the runner can be expressed as a function of the clearance inlet pressure and the square of the runner rotating speed by integrating the pressure on the rotating wall.

$F_{\text{c}}=\pi \left(R_{1\mathrm{r}}^2-R_{2\mathrm{r}}^2\right)\left[p_{1\mathrm{r}}-0.043\rho {\omega }_{0\mathrm{r}}^2\left(R_{1\mathrm{r}}^2-R_{2\mathrm{r}}^2\right)\right],(9)$

where $F_{\text{c}}$ is the clearance axial hydraulic thrust; $R_{1r}$ and $R_{2r}$ are the outside and inside radius, respectively, of the clearance flow channel; $p_{1r}$ is the clearance inlet pressure; and ${\omega }_{0r}$ is the rotating speed of the runner.

4 Conclusion

In this study, a rotating–stationary disk model that was a simplified model of the pump turbine clearance flow was measured by PIV measurements and simulated by CFD simulation to study the clearance flow patterns and pressure distributions and the relationship between them. The results show that the circumferential velocity in the clearance region presents a distribution of “core region + double boundary layers.” The pressure in the clearance region has a circumferentially symmetric and radially quadratic distribution. Quantitatively, the clearance pressure and axial thrust can be expressed as a function of the clearance inlet pressure and the square of the runner rotating speed, which provides a basis for the axial force imbalance problems of pump turbine units.

(1) Driven by the rotating disk, the flow patterns in the clearance flow channel present a typical Batchelor turbulence flow with separated boundary layers. The circumferential velocity core region is formed in the middle region along the height direction, while Kármán and Bödewadt boundary layers are formed on the rotating and stationary disks. Due to the centrifugal force and boundary effects, the flow is radially outward around the rotating wall, while inward around the stationary wall in the meridian section, showing secondary flow vortices. Numerically, the strong rotating shear flow in the core region dominates the clearance flow patterns.

(2) The core region rotates at a speed of around 41–42% of the rotating disk speed for all conditions. The circumferential velocity in the core region is dominated by the rotating disk speed, while being unaffected by the clearance inlet pressure and the clearance height if the location is far from the boundary effect.

(3) Based on the liquid differential equilibrium equation and circumferential velocity in the core region, the clearance pressure and axial hydraulic thrust can be expressed as a function of the clearance inlet pressure and the square of the runner rotating speed, which provides a basis for the axial force imbalance problems of the pump turbine unit.

(4) In terms of CFD numerical calculation for clearance flow, although the circumferential velocity obtained by the empirical wall function method is 15% larger than the model test in value, their velocity distribution laws are similar. Therefore, it is still feasible to calculate the clearance flow of the prototype pump turbine by using the wall function method to reconcile the contradiction between calculation accuracy and resources.

For the theoretical analysis of the findings in the study, the accurate calculation of the two viscous boundary layers serves as the foundation for the core region. In fact, despite extensive research on the turbulent boundary layer, the relative theory is extremely immature, and most theories applied in engineering are summarized from experiments and calculations. In recent years, many numerical simulations based on the Reynolds-average method were used to numerically calculate the boundary layer. However, the turbulence boundary layer equation for the Reynolds-average approach has a pulsation item that is difficult to solve theoretically. Therefore, intensive studies in conjunction with numerical calculation techniques and tests will be required to calculate the turbulent boundary layer of the rotating disk in the future.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

XH and YC contributed to the conception and design of the study. XH and HL carried out the model test and CFD simulation. YC and KL contributed to the interpretation of the results. YC, HC, and DL contributed to the manuscript revision. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (Grant Nos. 51839008 and 51909226), the China Postdoctoral Science Foundation (Grant No. 2020M673568XB), and the Seed Fund Program for Sino-Foreign Joint Scientific Research Platform of Wuhan University.

Acknowledgments

The numerical simulations were conducted on the supercomputing system in the Supercomputing Center of Wuhan University.

Conflict of interest

Author DL was employed by Dongfang Electric Machinery Co., Ltd., and author HC was employed by CSG Power Generation Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Batchelor, G. K. (1951). Note on a class of solutions of the navier-stokes equations representing steady rotationally symmetric flow. Q. J. Mech. Appl. Math. 4, 29–41. doi:10.1093/qjmam/4.1.29

CrossRef Full Text | Google Scholar

Bech, K. H., Tillmark, N., Alfredsson, P. H., and Andersson, H. I. (2006). An investigation of turbulent plane Couette flow at low Reynolds numbers. J. Fluid Mech. 286, 291–325. doi:10.1017/s0022112095000747

CrossRef Full Text | Google Scholar

Bödewadt, U. T. (1940). Die drehstrmung bber festem grund. Z. Angew. Math. Mech. 20, 241–253. doi:10.1002/zamm.19400200502

CrossRef Full Text | Google Scholar

Brady, J., and Durlofsky, L. (1987). On rotating disk flow. J. Fluid Mech. 175, 363–394. doi:10.1017/s0022112087000430

CrossRef Full Text | Google Scholar

Cao, Y., and Qiu, X. (1998). Experimental heat transfer. Beijing: National Defense Industry Press.

Google Scholar

Cheah, S. C., Iacovides, H., Jackson, D. C., Ji, H., and Launder, B. E. (1994). Experimental investigation of enclosed rotor-Stator disk flows. Exp. Therm. Fluid Sci. 9, 445–455. doi:10.1016/0894-1777(94)90022-1

CrossRef Full Text | Google Scholar

Daily, J. W., and Nece, R. E. (1960). Chamber dimension effects on induced flow and frictional resistance of enclosed rotating disks. J. Basic Eng. 82, 217–230. doi:10.1115/1.3662532

CrossRef Full Text | Google Scholar

Elena, L., and Roland, S. (1996). Turbulence modeling of rotating confined flows. Int. J. Heat Fluid Flow 17, 283–289. doi:10.1016/0142-727x(96)00032-x

CrossRef Full Text | Google Scholar

Fu, X., Li, D., Wang, H., Zhang, G., Li, Z., and Wei, X. (2018). Influence of the clearance flow on the load rejection process in a pump-turbine. Renew. Energy 127, 310–321. doi:10.1016/j.renene.2018.04.054

CrossRef Full Text | Google Scholar

Gauthier, G., Gondret, P., Moisy, F., and Rabaud, M. (2002). Instabilities in the flow between co- and counter-rotating disks. J. Fluid Mech. 473, 1–21. doi:10.1017/s0022112002002525

CrossRef Full Text | Google Scholar

Gauthier, G., Gondret, P., and Rabaud, M. (1999). Axisymmetric propagating vortices inthe flow between a stationary and a rotating diskenclosed by a cylinder. J. Fluid Mech. 386, 105–126. doi:10.1017/s0022112099004346

CrossRef Full Text | Google Scholar

Goyal, R., and Gandhi, B. K. (2018). Review of hydrodynamics instabilities in Francis turbine during off-design and transient operations. Renew. Energy 116, 697–709. doi:10.1016/j.renene.2017.10.012

CrossRef Full Text | Google Scholar

Hendriks, F. (2010). On Taylor vortices and Ekman layers in flow-induced vibration of hard disk drives. Microsyst. Technol. 16 (1-2), 93–101. doi:10.1007/s00542-008-0765-2

CrossRef Full Text | Google Scholar

Hou, X., Cheng, Y., Hu, D., Xue, S., Wang, B., Zhang, X., et al. (2021a). Influence factors of clearance leakage flowrate and clearance hydraulic axial force of pump-turbine. IOP Conf. Ser. 1037, 012035. doi:10.1088/1755-1315/1037/1/012035

CrossRef Full Text | Google Scholar

Hou, X., Cheng, Y., Yang, Z., Liu, K., Zhang, X., and Liu, D. (2021b). Influence of clearance flow on dynamic hydraulic forces of pump-turbine during runaway transient process. Energies 14 (10), 2830. doi:10.3390/en14102830

CrossRef Full Text | Google Scholar

Kreiss, H., and Parter, S. (1983). On the swirling flow between rotating coaxial disks: existence and nonuniqueness. Commun. Pure Appl. Math. 36, 55–84. doi:10.1002/cpa.3160360104

CrossRef Full Text | Google Scholar

Kurokawa, J., Inagaki, M., Imamura, H., Taguchi, T., and Niikura, K. (2002). “Transient axial thrust of high-head pump-turbine at load rejection,” in 21st IAHR symposium, Lausanne, September 9-12, 2002, 361–371.

CrossRef Full Text | Google Scholar

Le, Z., and Kong, L. (2005). Cause analysis on rotating part lifting of unit 2 in tianhuangping pumped storage plant. Mech. Electr. Tech. Hydropower Stn. 28 (5), 11–14.

Google Scholar

Lopez, J. M. (1996). Flow between a stationary and a rotating disk shrouded by a co-rotating cylinder. Phys. Fluids 8 (10), 2605–2613. doi:10.1063/1.869047

CrossRef Full Text | Google Scholar

Lopez, J. M., and Weidman, P. D. (1996). Stability of stationary endwall boundary layers during spin-down. J. Fluid Mech. 326, 373–398. doi:10.1017/s0022112096008361

CrossRef Full Text | Google Scholar

Mao, Z., Tao, R., Chen, F., Bi, H., Cao, J., Luo, Y., et al. (2021). Investigation of the starting-up axial hydraulic force and structure characteristics of pump turbine in pump mode. J. Mar. Sci. Eng. 9 (2), 158. doi:10.3390/jmse9020158

CrossRef Full Text | Google Scholar

Mellor, G. L., Chapple, P. J., and Stokes, V. K. (1968). On the flow between a rotating and a stationary disk. J. Fluid Mech. 31 (01), 95. doi:10.1017/s0022112068000054

CrossRef Full Text | Google Scholar

Pirozzoli, S., Bernardini, M., and Orlandi, P. (2014). Turbulence statistics in Couette flow at high Reynolds number. J. Fluid Mech. 758, 327–343. doi:10.1017/jfm.2014.529

CrossRef Full Text | Google Scholar

Poncet, S., Chauve, M. P., and Le Gal, P. (2005). Turbulent rotating disk flow with inward throughflow. J. Fluid Mech. 522, 253–262. doi:10.1017/s0022112004002046

CrossRef Full Text | Google Scholar

Poncet, S., Serre, É., and Le Gal, P. (2009). Revisiting the two first instabilities of the flow in an annular rotor-stator cavity. Phys. Fluids 21 (6), 064106. doi:10.1063/1.3156859

CrossRef Full Text | Google Scholar

Savaş, O. (1983). Circular waves on a stationary disk in rotating flow. Phys. Fluids (1994). 26 (12), 3445. doi:10.1063/1.864124

CrossRef Full Text | Google Scholar

Serre, E., Crespo Del Arco, E., and Bontoux, P. (2001). Annular and spiral patterns in flows between rotating and stationary discs. J. Fluid Mech. 434, 65–100. doi:10.1017/s0022112001003494

CrossRef Full Text | Google Scholar

Singh, A. (2014). Inward flow between stationary and rotating disks. J. Fluids Eng. 136 (10), 101205. doi:10.1115/1.4027322

CrossRef Full Text | Google Scholar

Singh, A. (2017). Theoretical investigation on inflow between two rotating disks. J. Fluids Eng. 139 (11), 111202. doi:10.1115/1.4037058

CrossRef Full Text | Google Scholar

Singh, A., and Zosimovych, N. (2016). Laminar flow investigation between a stationary and a rotating disk with a source at centre. Eng. Sci./Mech. 1, 1–10.

Google Scholar

Stewartson, K. (1952). On the flow between two rotating coaxial disks. Math. Proc. Camb. Phil. Soc. 49 (2), 333–341. doi:10.1017/s0305004100028437

CrossRef Full Text | Google Scholar

van Eeten, K. M. P., van der Schaaf, J., van Heijst, G. J. F., and Schouten, J. C. (2013). Lyapunov-stability of solution branches of rotating disk flow. Phys. Fluids 25 (7), 073602. doi:10.1063/1.4812704

CrossRef Full Text | Google Scholar

Von Kármán, T. (1921). Uber laminare and turbulente reibung. Z. Angew. Math. Mech. 1, 233–252. doi:10.1002/zamm.19210010401

CrossRef Full Text | Google Scholar

Watanabe, T., Furukawa, H., Fujisawa, S., and Endo, S. (2016). Effect of axial clearance on the flow structure around a rotating disk enclosed in a cylindrical casing. J. Flow Control, Meas. Vis. 04 (01), 1–12. doi:10.4236/jfcmv.2016.41001

CrossRef Full Text | Google Scholar

Wu, G., Zhang, K., and Dai, Y. (2005). Influence of the runner gap and seal construction on the safety in operation of Francis water power sets. Large Electr. Mach. Hydraulic Turbine 1 (1), 44–52.

Google Scholar

Wu, G., Zhang, K., Dai, Y., and Sun, J. (2004). Influences of the leakage rate of low specific speed Francis runner on phenomenon of the lifting hydroelectric generator set. J. Hydroelectr. Eng. 23 (4), 106–111.

Google Scholar

Zandbergen, P., and Dijkstra, D. (1987). Von karman swirling flows. Annu. Rev. Fluid Mech. 19, 465–491. doi:10.1146/annurev.fl.19.010187.002341

CrossRef Full Text | Google Scholar

Zhang, J. (2017). Numerical simulation of multi-scale flows in Francis turbine and research on hydraulic stability of transient processes. Nanjing: Hohai University.

Google Scholar