Large-Scale Evolutionary Optimization Approach Based on Decision Space Decomposition

Introduction

The large-scale global optimization (LSGO) is of interest to researchers with the fast increase of complex optimization problems in applied engineering and science fields such as medicine and chemistry. The dimensionality of decision variables involved in various engineering fields problems has grown exponentially (Ma et al., 2021a; Li et al., 2022). There are many examples in large-scale optimization, such as the optimal design of satellite layout (Teng et al., 2010), the parameter identification in large-scale system models (Kimura et al., 2005), the inversion of seismic waveforms (Wang and Gao, 2012), and the parameter calibration of water supply systems (Wang et al., 2013). The common features of these problems are: the search scope of the objective problem exponentially expands as the dimensionality of decision variables grows, leading to an increasing number of locally optimal solutions for the optimization process; in addition, the coupling (or interaction) relationships between variables become more complex. Thus, the challenge of large-scale optimization problems can be summarized as the emergence of dimensional catastrophes as the number of decision variables grows exponentially and their coupling relationships become more complex (Liu, 2019).

Problems of complex engineering optimization systems generally use Evolutionary algorithm (EA) as a search engine to get the global optima in a complex high-dimensional search space. However, the EA is difficult or even impossible to deal with these problems with the increase of decision variables in the problem and the complexity of the inter-coupling relationship between variables. EA is a heuristic search algorithm based on the natural biological evolution mechanism, which does not require the gradient information of the target problem and has better robustness for solving complex NP-hard problems (Xue, 2021). For small and medium-scale optimization problems, EA has achieved excellent performance in various industrial application systems and can effectively handle various nonlinear, strongly coupled, mixed-variable, and other complex optimization scenarios (Xue, 2021; Xue and Jiang, 2021). However, when the scale of decision variables of the target problem exceeds a certain order of magnitude, conventional EA (Strasser et al., 2017; Ma et al., 2021b; Ma et al., 2021c; Zhang, 2022) are difficult to obtain satisfactory performances such as solution accuracy and convergence speed even with improved global optimization operator strategies due to their limited search capability (Fan et al., 2014; Ran Cheng and Yaochu Jin, 2015; Yang et al., 2017; Ma et al., 2019). Therefore, how to design efficient large-scale global optimization methods is an urgent problem to solve complex engineering system applications in big data environment.

Currently, a lot of excellent work has emerged to solve large-scale global optimization problems, such as dimensionality reduction (Bhowmik, 2016), local search (LaTorre, 2013; He et al., 2019; Ma et al., 2021d), and decomposition methods (Yang et al., 2008a), among which the method that has gained popularity is decomposition. Decomposition methods divide a complex large-scale optimization problem into several sets of small-size subproblems that are easier to handle. After conducting policy decomposition, the whole complex function can be optimized via optimizing each subproblem in a separate way. The role of this decomposition has been demonstrated in lots of optimization methods (Dantzig and Wolfe, 1960; Griewank and Toint, 1982; Bertsekas, 1995). Potter and De Jong (Potter and Jong, 1994) devised an effective Cooperative coevolution (CC) framework for decomposing complex large-scale problem. It has been shown that contribution-based Cooperative coevolutionary schemes (Omidvar, 2011) are superior to the traditional CC framework. The contribution-based CC scheme mainly lies in quantifying the importance level of a subcomponent over the entire fitness. When this contribution/importance information is computed, we can provide different computation resources among the subcomponents depending on their importance. The contribution-based CC scheme is not like the conventional CC framework, which distributes computational budget equally among the subcomponents. For CC and contribution-based CC frameworks, the decomposition strategy used in decomposing the decision variables into several subcomponents is important, because the final result of the optimization is extremely sensitive to the chosen decomposition strategy.

In this paper, we develop a decomposition strategy using min hash. The min hash method is a technique for quickly determining whether two collections are similar or not. This method was developed by Andrei Broder and was originally used in the AltaVista algorithm to find and remove duplicate Web pages in the obtained results. It can be employed for the large-scale clustering problems, such as clustering by the similarity of words contained between documents. It has the advantages of being simpler to compute and more efficient than comparison between two decision variables; being able to find similar decision variables quickly; and being able to cluster decision variables simply. In MHD, we use it to decompose the decision variables and improve the decomposition efficiency.

The most useful and innovative points of this work include:

1) We apply the min hash thought to the large-scale global optimization for decomposing high-dimensional decision space, i.e., decision variables. The efficiency of decision variable decomposition is improved due to the properties of the min hash itself.

2) From the experimental results, the proposed algorithm has potential advantages. The minimum hash incorporates the Jaccard similarity coefficient, which is more accurate for the splitting of decision variables and ensure an excellent optimization performance.

The rest of this paper is laid out as follows. In Background and Problem Statement, a partial summary and analysis of the large-scale decision variable interaction problem, decomposition strategies and min hash methods are given. In The Proposed Method, the specific contents of our proposed algorithm are described. Experimental Verification provides experimental results about the decomposition effect of the algorithm on the LSGO benchmark test function CEC 2013 (Li, 2013) and its performance, and compares it with several other classical algorithms. Conclusion concludes and summarizes the paper. Conclusion summarizes and concludes the paper.

Background and Problem Statement

LSGO Problems

The target LSGO problem can be defined as

$\underset{\text{x}\in R^n}{{\mathbf{x}}^{\ast }=\arg \min f\left(\mathbf{x}\right)}.(1)$

where f: Rⁿ $\to$ R is a real value objective function, x = (x₁, x₂, …, x_n) is a decision vector with n dimensions, n indicates the dimension of the variable, usually larger than 100 (Liu, 2019).

For the CC framework, the aim of decomposing the problem is to minimize the dependencies between subgroups (Omidvar et al., 2017), which is usually determined by the separable construction of the optimization function formulated as follows:

Definition 1. The function f (x) is said to be partially separable with m independent subgroups if:

$\underset{\text{x}}{\arg \min f\left(\mathbf{x}\right)}=\left(\underset{{\text{x}}_1}{\arg \min f({\mathbf{x}}_1,\mathrm{...}),}\underset{{\text{x}}_m}{\mathrm{...},\arg \min f(\mathrm{...},{\mathbf{x}}_m)}\right)(2)$

where x = (x₁, x₂, …, x_n) is an n-dimensional vector, x₁, … , x_m are the m disjoint sub-vectors of x, 1 < m $\le$ n. If m = n, f (x) is considered as completely separable (Omidvar et al., 2017).

Definition 2. The function f (x) is said to be fully non-separable if n decision variables are all interacting with each other and m = 1 (Omidvar et al., 2015).In fact, the partially additively separable problem is a special type of the partial separable, which usually shows the modular nature of the practical LSGO problems (Omidvar et al., 2015). Especially, it is formulated as below:

Definition 3. The function f (x) is partially additively separable if:

$f\left(\mathbf{x}\right)={\displaystyle \sum _{i=1}^m{f}_i\left({\mathbf{x}}_i\right)},m>1(3)$

where m is the number of independent subgroups, f_i (.) is a non-separable subfunction (Omidvar et al., 2017).

Decomposition Strategy

Cooperative coevolution framework is currently a useful approach to address LSGO. The effectiveness of this approach is attributed to the fact that it decomposes or divides a LSGO function into several sets of easier subfunctions. This thought of divide and conquer first appeared in a book called A Discourse on Method. Moreover, the validity of this idea has been verified in the paper (Weicker and Weicker, 1999; Liu et al., 2001). However, the disadvantage of CC framework lies in that the corresponding overall performance is highly relative to the selected decomposition strategy. Here, we briefly review the existing recognized and widespread decomposition strategies devised for CC, i.e., decomposition-based LSGO algorithms.

The key to applying the cooperative coevolution to handle LSGO problems is how to decompose a set of variables into a small number of subgroups. With no prior knowledge about the underlying constructions, we can decompose the specific problem using different methods. Ideally, we need to construct subcomponents according to a basic principle that the dependent effects among decision variables should be minimized. A cooperative coevolutionary technique proposed by Weicker (Chen et al., 2011) is used to analyze the interaction relations between variables. It is the first coevolutionary technique for automatic identifying interaction variables. However, it was not applied with a high-dimensional search space for the large-scale global optimization problems. Then, Chen (Chen et al., 2011) presented an improvement method for this technique and obtained well performance in handling LSGO problems. Another excellent method is the Delta grouping (Omidvar et al., 2010), which is an effective technique that automatically identifies interactive decision variables in the problem. However, the technique performs effectively especially in the scenario where only one set of interacting variables exists.

In addition to the above decomposition strategies, there are also grouping strategies where the size of the subcomponents is predetermined. For example, random grouping (Yang et al., 2008a), which decomposes an n-dimensional large problem into m s-dimensional smaller problems. The main disadvantage of this strategy lies in that it is required to specify an m or s value, which is inefficient for the use of the algorithm. For the optimization scenario where a large number of mutually interacting decision variables exist in the target large-scale problem, the algorithms do not achieve the desired performance metrics when s is small. Conversely, when few interacting decision variables exist in the problem, then the performance of the algorithm cannot be fully exploited when s is large. To address this problem, Yang (Yang et al., 2008b) suggested a multilevel cooperative coevolution (MLCC) algorithm. The algorithm is to provide an array with the possible s-values instead of using a fixed value. The evolutionary process allows measuring the performance of subcomponents of different sizes. The better value, in terms of performance indicator, is more likely to be chosen in the following evolution round. In this way, this strategy is able to address the issue of specifying s-values. However, this multilevel strategy suffers from an issue that if an s-value is selected, the variable is grouped into several subcomponents of equal size. In many practical problems, the specifications of the groups that appear to interact with each other are the same. Therefore, the most effective strategy is to adaptively find out the specification and the number of subcomponents.

Perturbation strategies are to some extent more convincing than random grouping. The key of the perturbation strategy is to use various methods to perturb the decision variables. Ultimately, the interaction between the decision variables is detected by detecting changes of the corresponding objective function. In most cases, the decomposition phase of the strategy is performed offline. When the interactions of all decision variables are detected, the decomposition phase is started, which in turn initiates the optimization process. In the background of cooperative coevolution, more and more decomposition algorithms that rely on perturbations have been developed, such as DG (Omidvar et al., 2014) and DG2 (Omidvar et al., 2017). DG is executed by first detecting the interaction information within each pair of the first decision variable and the other ones in the problem. When the algorithm finds the interaction within the pair of the first variable and any other decision variable, we can take this decision variable from the entire set of variables and puts it into one subgroup. Another key point of this strategy is the metric to be used in determining whether there is an interaction or not. In other words, what criteria determine whether they are interactions or not. DG uses a user-set threshold to determine whether there is an interaction or not. This approach is too intrusive in determining interactions, and human factors have a large influence on the decomposition results. Therefore, in 2017, Omidvar (Omidvar et al., 2017) et al. proposed DG2. One contribution of DG2 is to improve the shortcoming of DG that requires thresholding by eliminating the influence of human factors on interactions. It will automatically determine the threshold value based on the characteristics of the problem, having a higher practicality.

In addition, related scholars have proposed specifically threshold-based decomposition strategies: decomposition of decision variables by pre-setting the relevant thresholds for subgroups. Examples include RDG (Sun et al., 2018), RDG3 (Sun, 2019), and DGSC (Srinivas and Amgoth, 2022). RDG3 solves the overlapping LSGO problem by setting a threshold to specify the size of subcomponents. The DGSC algorithm predetermines the number of subcomponents and uses clustering to group the decision variables, which can avoid the grouping unevenness problem and save computational space. However, this type of algorithm ignores the coupling dependencies among decision variables, and it is difficult to place the closely dependent variables into same subgroups, which makes it difficult to achieve the desired optimization effect.

To the best of our knowledge, there are two decomposition-based strategies in addition to the methods described above. They are interaction adaptation and model building. The core of this strategy of interaction adaptation is to detect chromosomal interactions while optimizing the sequential evolution of genes. The variables involved in the function also need to be optimized. The main approaches in this category include the Linkage Evolving Genetic Operator (LEGO), proposed by Jim Smith in 1993. The focus of this algorithm is to exploit the recombination mechanism of genes. Combined with real-world problems, a new individual is the result of the free combination of genetic material from the parents. And the amount of genetic material that makes up the new individual is uncountable. Therefore, in the process of evolutionary optimization, the individuals in the population are also the result of the combination of genetic arrangements from the parents. If the genes of the parents are marked using a special linkage before the creation of new individuals, then the genes in the offspring will also have this special marker. There is a high probability that the linkage has changed position compared to the parent when generating the offspring. Individuals with more linkage position changes are considered to be more closely interacting. In the following evolutionary process, the more closely linked individuals can have a higher probability of reproduction (Cheng et al., 2022; Zhu et al., 2022).

The core idea of this strategy of model construction is to build a probabilistic model. This model is constructed based on the potential solutions of the population. This probabilistic model is also continuously optimized in the optimization process. New individuals are also generated from this model. Most of the more popular model building algorithms were proposed many years ago. They include mainly the compact Genetic Algorithm (cGA) proposed by Harik in 1999 and the Bayesian Optimization Algorithm (BOA) proposed by Pelikan and the Hierarchical Bayesian Optimization Algorithm (Hierarchical BOA) proposed by Pelikan in 2002. In addition to this, Griewank proposed partitioned quasi-Newton algorithms to handle certain LSGO challenges. The key point of this work is the partitioning of the matrix by approximating the quasi-Newton formulation. Specifically, they used the idea of decomposition to divide the matrix into blocks. The blocks are not connected to each other in any way. Let the component functions that use the quasi-Newton formula gradually approximate the decomposed blocks of the matrix. The sum of several matrix blocks constitutes the objective function value.

Jacquard Similarity Coefficient

Data mining tasks involve the similarity calculation of massive data, such as the similarity of retrieved documents, the similarity between users, and so on. These data are usually of high dimensionality, and the dimensionality of the document data encoded with one-hot is equal to the size of a dictionary. In the case of large data volume and high data dimensionality, it takes so much time to compute the similarity between two objects.

Min hash approximation algorithm can greatly improve the operation efficiency with similar accuracy. Before introducing the minimum hash, the Jaccard similarity coefficient is introduced. The Jaccard similarity coefficient is often utilized to compute out the similarity degree between individuals with symbolic or Boolean measures, since the feature attributes of these individuals are detected by symbolic or Boolean measures. Therefore, it is not possible to estimate the magnitude of the specific value of the difference, but only to obtain the result of “similarity or not”. Therefore, the Jaccard coefficient is only concerned with the consistency of the characteristics shared between individuals.

For two data sets A and B, the Jaccard coefficient is regarded as the quotient of the size of the intersection of the two data sets to the size of the union, defined as follows:

$J(A,B)=\frac{|A\cap B|}{|A\cup B|}=\frac{|A\cap B|}{\left|A\right|+\left|B\right|-|A\cap B|}(4)$

J (A, B) [0,1], if both A and B are sets that do not contain elements, J (A, B) is denoted as 1.

The metric associated with the Jaccard coefficient is called Jaccard distance. It expresses the dissimilarity of sets. The larger the Jaccard distance, the less similar the samples are. The expression of this formula is followed:

$d_j(A,B)=1-J(A,B)=\frac{|A\cup B|-|A\cap B|}{|A\cup B|}=\frac{A\text{Δ}B}{|A\cup B|}(5)$

A $\Delta$ B = |A $\cup$ B|-|A $\cap$ B| is symmetric difference. Therefore, the higher the Jaccard similarity coefficient, the greater the overlap of the samples.

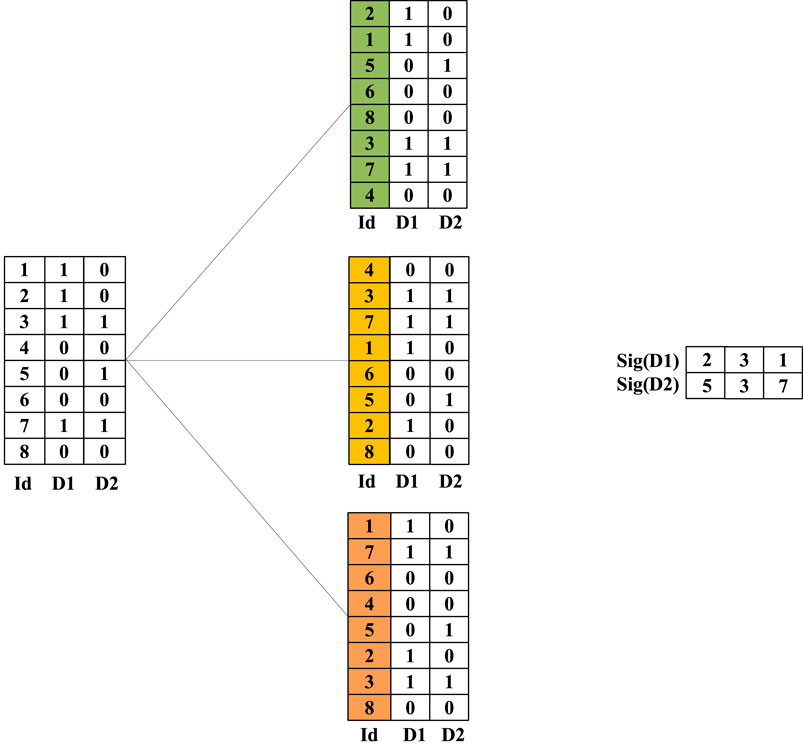
Suppose D1 and D2 are given two documents whose feature vectors are encoded in one-hot. If the position is 1, the document has the corresponding word, as shown in Table 1.

TABLE 1

TABLE 1. Document data vectors.

We can use the Jaccard coefficient to compute out the similarity of two vectors. The Jaccard coefficient is the specifications of elements in the intersection of A and B divided by the specifications of elements in the concatenation of A and B. Therefore, the similarity of documents D1 and D2 above is 2/5.

If p represents the number of dimensions in which both samples D1 and D2 are 1. q represents the dimension size or dimension number in which sample D1 is one and sample D2 is 0. r is the dimension size where sample D1 is 0 and sample D2 is 1. s denotes the number of dimensions in which both samples D1 and D2 are 0. Hence the Jaccard similarity coefficients of samples D1 and D2 can be rewritten as:

$J=\frac{p}{p+q+r}(6)$

(p + q + r) is denoted as the number of elements of the union of D1 and D2, while p is the number of elements of the intersection of D1 and D2.

Min Hash

Min hash, in short, is to randomly draw n items from all the items that the user likes. The few users for whom all the n items drawn are the same are considered to be users with similar interests and belong to the same cluster. The initial application of min hash includes clustering and eliminating near duplicates in Web documents, which is described by the set of words that appear in those documents. min hash in this case belongs to a clustering algorithm that clusters users based on them and their favorite goods, and clusters users who have the same favorite goods into one cluster. The advantages of the min hash clustering algorithm are: 1) it is relatively simple to compute and has a greater efficiency than comparing two users with each other; 2) it can quickly identify users with the same goods; 3) it can simply cluster the users.

Min hash is a method for approximating the Jaccard coefficient, and the main steps are as follows: a. Randomize the dimensions of vectors D1 and D2 m times; b. Find the index of the first non-zero row of D1 and D2 after rearrangement, which is represented by the functions h (D1), h (D2) (Function h () refers to the min hash function). After performing m random permutations, the new eigenvectors of D1 and D2 can be obtained as follows:

$\text{Sig}\left(D1\right)=[h_1\left(D1\right),h_2\left(D1\right),\mathrm{...},h_m\left(D1\right)](7)$

$\text{Sig}\left(D2\right)=[h_2\left(D2\right),h_2\left(D2\right),\mathrm{...},h_m\left(D2\right)](8)$

This process is shown in Figure 1, where m = 3.

FIGURE 1

FIGURE 1. Example of min hash process.

After obtaining the new feature vectors Sig (D1) and Sig (D2), we can calculate the probability p = 1/3 that each position is identical (i.e., the first non-zero row has the same index), which is an approximation of the Jaccard coefficient. This conclusion is based mainly on the following principle.

$P[h\left(D1\right)==h\left(D2\right)]=J(D1,D2)(9)$

The proof is as follows:

After rearranging the two vectors D1, D2, three possibilities exist in each dimension. 1) D1 and D2 are both one in this one dimension, which corresponds to p in Jaccard’s formula. 2) D1, D2 only one vector in this dimension is 1, which corresponds to (q + r) in Jaccard’s formula. 3) D1 and D2 are both 0 in this dimension.

The new vector Sig (D1) obtained by Min hash is the first non-zero row index of D1. Then the probability that Sig (D1) and Sig (D2) have the same index in the first non-zero row is p/(p + q + r), which is the Jaccard similarity coefficient formula.

If the full permutation is used (i.e., all permutations are considered), Min hash gives the exact Jaccard value. However, in practice, m permutations are usually used to improve efficiency, and the original vector can be transformed into a new vector of length m.

The Proposed Method

Framework of MHD

The framework of MHD includes the following procedures:

1) Initialization. First, the population best is initialized randomly (Line 1). The times of function evaluations Fes is the same to the population size. Next, the crossover rate is initialized for the optimization engine (Line 2), and the detailed parameter setting refers to the algorithm SaNSDE (Yang, 2008).

2) Min hash determination of decision variable interactions. In determining the interaction of decision variables, we use the minimum hash strategy, as shown in Figure 1. Before determining the interaction relationship, we normalize the decision vector to facilitate the minimum hashing (Line 3). We use Min-Max Normalization. It is also known as also known as outlier normalization. It makes the result map between 0 and 1. It has two major advantages such as improving the performance of the model. We obtain the similarity between the decision variables according to the process shown in Figure 1. The obtained data is stored and prepared for the next steps.

3) Variable grouping. This work combines a decomposition-based large-scale optimization strategy to find the global optimal solution. In this process, the decision space is decomposed into several subspaces. In this way, the variables that exhibit explicit interactions are divided into the same subgroups. In this critical step, we use a depth first search (DFS) strategy to cluster the decision variables with interaction relations. In fact, depth first search is one of the graph algorithms. The process is briefly described as going as deep as possible into each possible branching path, and each node can only be visited once. DG2 (Omidvar et al., 2017) uses a depth-first search strategy to achieve grouping of decision variables.

4) Population evolution. The contribution-based strategy is used to optimize subgroups. And the optimizer is SaNSDE in proposed method. First, it optimizes the initial value of the population best according to the grouping result, and obtains the new value (Line 7). Then, it calculates the contribution de of the current subgroup, and stores in array $\Delta$ (Line 8). The subgroup with the greatest impact on the fitness function (ie., largest contribution) is chosen as the optimization object (Line 11). Line 12 has the same effect as (Line 7). Third, the contribution of the current subgroup is updated (Sun et al., 2018) (Line 13) to start a new round of optimization.

Computational Complexity

The time complexity of min hash determination of decision variable interactions in Framework of MHD (Line 3) is O(N²), where N represents the specification of the decision search space. Time complexity of depth first search of graphs is O(N²). The complexity of optimize population based on the CC (Lines 5–15) in Framework of MHD is about O(N). Summarize all of the above, the computational complexity of MHD is O(N²) in the worst case.

Experimental Verification

To indicates the reasonableness of the proposed MHD algorithm, this section conducts a set of comparative experiments with some algorithms: 1) Accuracy comparison; 2) Convergence comparison; 3) Stability comparison. The compared algorithms include SaNSDE (Yang, 2008), which uses a transformation of differential evolution (DE) as optimizer used in CC framework; CBCC3-DG2 (Omidvar et al., 2017), which uses an improved difference grouping strategy and combines the grouping strategy with contribution-based CC approach; DECC-G (Yang et al., 2008a), which uses random strategy to achieve grouping and is also the most used comparison algorithm in other papers.

The algorithms are implemented on CEC 2013 (Li, 2013) test suit, where each test problem is invoked in 1000-dimensional test instances. CEC 2013 test suits includes 15 functions: Fully Separable Functions (f₁-f₃); Partially Separable Functions (f₄-f₁₁); Overlapping Functions (f₁₂-f₁₄) and Fully Non-separable Function (f₁₅).

The performance metric is the widely used the mean normalized scores (MNS) and standard normalized scores (SNS) (Liu, 2019), which is defined as:

$scor{e}_i\left(algo\right)=\log \left(\text{mean}\left(f_i\left(x\right)\right)\right)(10)$

$mean\_normalized\_scor{e}_i\left(algo\right)=\frac{scor{e}_i\left(algo\right)}{scor{e}_i\left(SaNSDE\right)}(11)$

$scor{e}_i\left(algo\right)=\log \left(\text{std}\left(f_i\left(x\right)\right)\right)(12)$

$std\_normalized\_scor{e}_i\left(algo\right)=\frac{scor{e}_i\left(algo\right)}{scor{e}_i\left(SaNSDE\right)}(13)$

Both our proposed algorithm and the comparison algorithm are run 25 times on each test problem. The maximum function evaluations used by all algorithms is 3,000,000. The size of population is also set to 100. Each algorithm uses simulated binary crossovers and polynomial variants common in the field (Molina, 2018). The crossover probabilities and variance probabilities are set according to the well-known optimization algorithm SaNSDE. The other parameters of the comparison algorithm in the article are the same as those set in the references (Yang et al., 2008a; Omidvar et al., 2017; Molina, 2018; Zhu et al., 2022) for the sake of fairness of comparison.

Results and Analysis on Accuracy Comparison

Table 2 reports the statistical results of the algorithms. MHD can still perform well in the first three test problem functions (f₁-f₃). In fact, FCA-G defeats CBCC3-DG2 and SaNSDE in the fourth to ninth test problem functions (f₄-f₉) and one-third of the overlapping test problems (f₁₄). On the last test function (f₁₅), MHD performs better than the compared algorithm. We can observe that MHD performs the best outstanding on most test instances, while DECC-G also obtains excellent performance on some test functions (f₁-f₃). Specifically, MHD achieves the greatest results on functions (f₄-f₁₁) and one overlapping functions (f₁₄). Compared to CBCC3-DG2, MHD performs very closely to SaNSDE. Compared to DECC-G, MHD performs better and more efficiently especially on the functions f₄-f₉. The above results validate the advantage of MHD in dealing with various LSGO problems.

TABLE 2

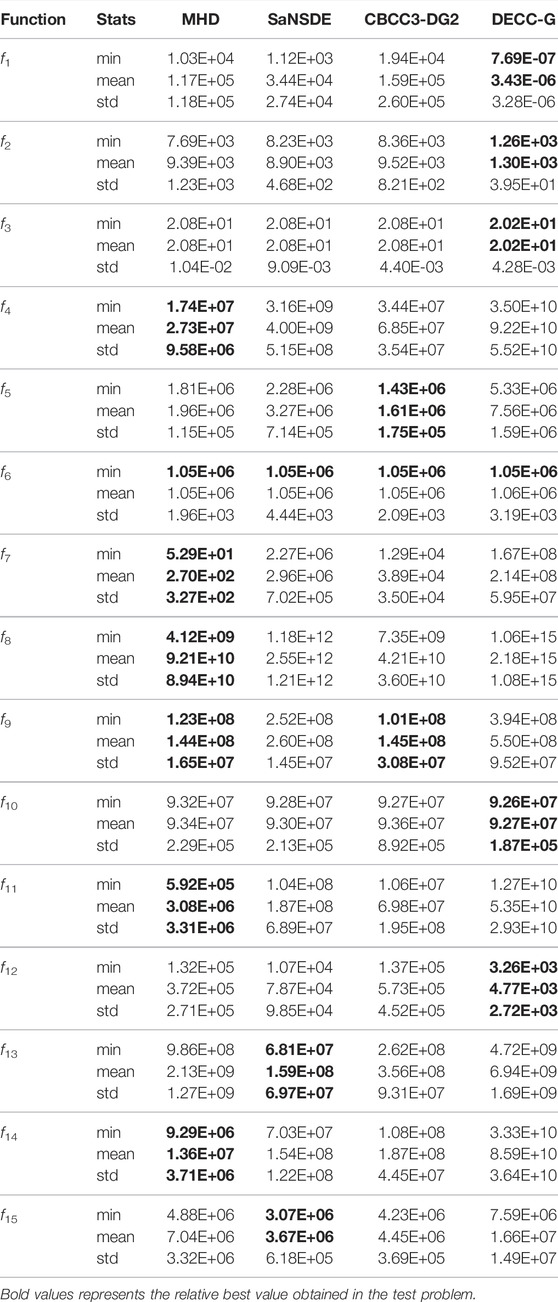
TABLE 2. The results of MHD, SaNSDE, CBCC3-DG2 and DECC-G run on CEC 2013 benchmarks. The best algorithm(s) are highlighted.

Compared to SaNSDE, CBCC3-DG2 and DECC-G, the grouping strategy used in MHD is more effective to deal with LSGO problems. The reason lies in that MHD uses a minimum hash strategy to determine the interaction between decision variables. It can further clarify the interaction relationship between decision variables by intersection and concatenation operations, and then decompose the variables with interactions to a subcomponent. In the evolutionary process, decomposing the decision variables facilitates the determination of the optimal solution. Decomposing variables according to the interactions between decision variables is a more convincing approach. There are many current methods to complete the decomposition of variables by analyzing the interactions of decision variables, and then seek the global optimal solution. Although algorithms such as SaNSDE, CBCC3-DG2 and DECC-G also use learning-based decomposition strategies, the decomposition process of DECC-G is too crude and ignores the interactions of decision variables. DECC-G decomposes variables with interactions to different subcomponents, and variables without interactions are forced to the same subcomponent.

Result Analysis on Convergence Comparison

Next, we make an extended experiment to show the convergence ability of MHD, as shown in Figure 2. In this figure, Figure 2 (f₁) - Figure 2 (f₁₅) denote the convergence process of MHD over functions f₁-f₁₅, respectively. In this experiment, we get 30 points at equal intervals to compare the convergence of each algorithm. All the points along the convergence curve are averaged by 25 independent runs.

FIGURE 2

FIGURE 2. The convergence curves of various algorithms on f₁-f₁₅ functions.

From Figure 2, we observe that MHD can converge quickly to a small value in most test functions. To be specific, MHD, SaNSDE and CBCC3-DG2 exhibit a similar convergence performance on functions f₁-f₃ and f₁₅. Since DECC-G adopts the random grouping strategy and cooperative coevolution, it fixes the size of the subgroup and implements an even distribution of computing resources. DECC-G has excellence performance on the first three functions (f₁-f₃). On the functions 4th to 11th (f₄-f₁₁), the convergence ability of MHD is doing well than the comparison algorithms. On the f₁₂-f₁₄ functions, each algorithm has its own advantages. DECC-G obtains the fasted convergence rate and the best values on function f₁₂. On function f₁₄, the three compared algorithms fall into the premature convergence dilemma. Although MHD does not perform well in the early stage, it can maintain a good convergence trend towards the optimum during the search. As a result, MHD obtains better solutions, as shown in Figure 2(f₁₄).

For the above excellent performance of MHD, we can give the following explanations: MHD allows for better grouping with accurate analysis of variable interactions. This approach can improve the feasibility of decomposing decision variables in the optimization process. In addition, we can conclude that the correct analysis of the interaction between decision variables provides good preconditions for the decomposition process and helps the search of optimal solutions. In other words, the min hash strategy has some effect in the problem of decision variable correlation analysis in large-scale global optimization.

Result Analysis on Stability Comparison

To access the stability of the algorithm, MHD is compared with SaNSDE, CBCC3-DG2 and DECC-G. Figure 3 shows the mean normalized scores (MNS) obtained by the four algorithms, where the vertical ordinate denotes mean normalized scores (the lower value indicates a better performance). Figure 4 compares the standard deviation normalized scores (SNS) results obtained by the algorithms. In this figure, the vertical ordinate denotes standard deviation normalized scores.

FIGURE 3

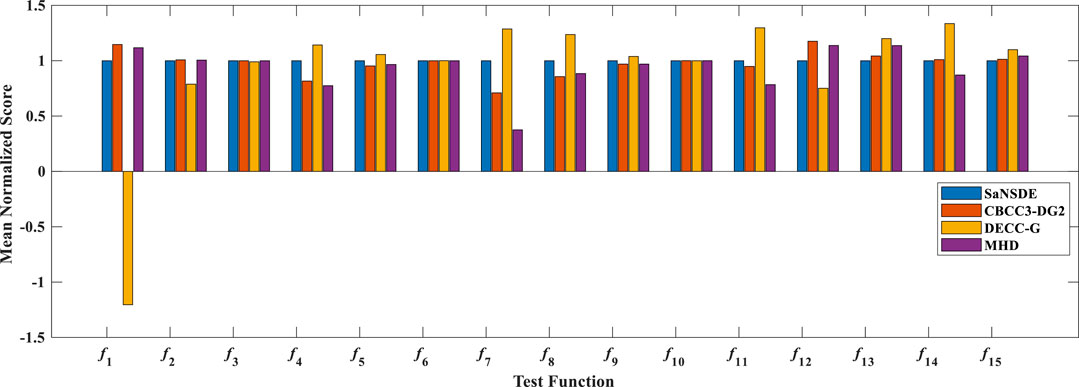
FIGURE 3. The mean normalized scores of the four algorithms. The lower the value indicates a better performance.

FIGURE 4

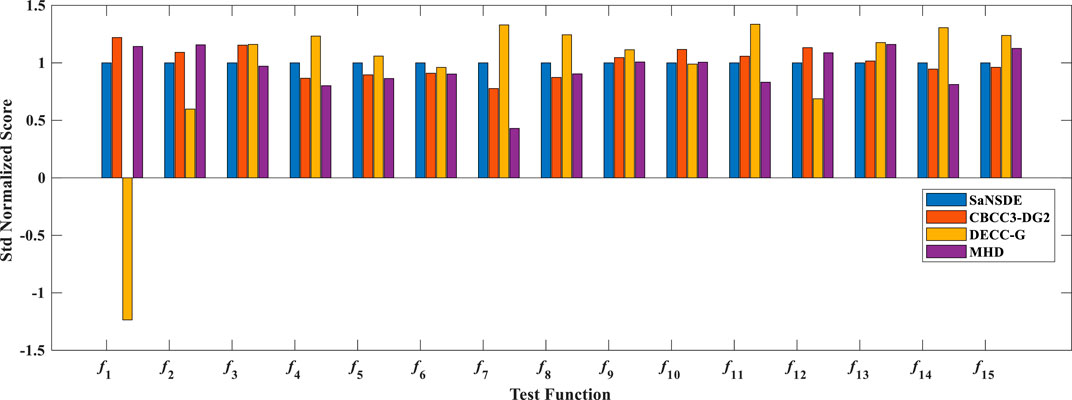
FIGURE 4. The standard deviation normalized scores of the four algorithms. The lower the value indicates a better performance.

From these figures, we can observe that the MNS and SNS results of MHD are better than its comparison algorithms on test problems f₄, f₅, f₇, f₈, f₉, f₁₁ and f₁₄. On test functions f₃, f₆ and f₁₀, the MNS of each algorithm are nearly the same. Functions f₄-f₁₁ are partially separable functions, which contain a variety of interactive variables, which play a positive or negative role in optimization results. MHD divides the variables that play an active role in the evolution process into a subgroup. Such Decomposition method is reasonable and helpful to determine the optimal solution during the search, and also improve the stability of the optimization.

The strategy used by MHD is effective in dealing with the LSGO problem compared to the three algorithms in SaNSDE, CBCC3-DG2 and DECC-G. The reason is that MHD uses the min hash strategy to determine the interaction between decision variables. It can further clarify the interaction relationship between decision variables through intersection and concatenation operations to draw more accurate conclusions. The comparison algorithm is simpler than MHD in determining the interaction relationships. Therefore, the algorithm achieves some advantages in terms of stability.

Conclusion

In this paper, we proposed a large-scale variable relationship analysis strategy called MHD to deal with the LSGO problems. MHD introduces the min hash principle to analysis interdependence between decision variables, and then group them adaptively. Specifically, the wide range decision space is decomposed into several small range search spaces according to the characteristics of the decision variables, using the minimum hash method to determine the interaction relationships between the decision variables. In this critical step, we use a depth first search (DFS) strategy to cluster the decision variables with interaction relations. In fact, depth first search is one of the graph algorithms. The process is briefly described as going as deep as possible into each possible branching path, and each node can only be visited once. DG2 uses a depth-first search strategy to achieve grouping of decision variables. The results of experimental proved that MHD shows significant advantages over its compared algorithms, especially on partially separable benchmark instances with up to 1,000 decision variables.

In the future work, we will combine MHD with more effective optimization strategies to improve the capabilities in all aspects of algorithms. In addition, applying the MHD algorithm to solve practical engineering problems is also the next research focus.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

JM is responsible for checking and revising the full text. FC is responsible for the conception and writing of the full text. XY is responsible for checking the format.

Funding

This work is provided help by Liaoning Social Science Planning Fund Key Project (L20CGL012); Liaoning Science and Technology Department Science Career Public Welfare Research Fund (2021JH4/10100026).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bertsekas, D. (1995). Optimization and Neural Computation Series. Athena Scientific.

Google Scholar

Bhowmik, T. (2016). Dimensionality Reduction-Based Optimization Algorithm for Sparse 3-D Image Reconstruction in Diffuse Optical Tomography. Sci. Rep., 6, 22242. doi:10.1038/srep22242

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, W., Weise, T., Yang, Z., and Tang, K. (2011). “Large-scale Global Optimization Using Cooperative Coevolution with Variable Interaction Learning,” in Proc. Of International Conference on Parallel Problem Solving from Nature (Berlin: Springer), 300–309.

Google Scholar

Cheng, L., Li*, X., Han, Z., Luo, T., Ma, L., and Zhu, P. (2022). Path-Based Multi-Sources Localization in Multiplex Networks. Chaos, Solit. Fractals 159, 112139. doi:10.1016/j.chaos.2022.112139

CrossRef Full Text | Google Scholar

Dantzig, G. B., and Wolfe, P. (1960). Decomposition Principle for Linear Programs. Operations Res. 8 (1), 101–111. doi:10.1287/opre.8.1.101

CrossRef Full Text | Google Scholar

Fan, J., Wang, J., and Han, M. (2014). Cooperative Coevolution for Large-Scale Optimization Based on Kernel Fuzzy Clustering and Variable Trust Region Methods. IEEE Trans. Fuzzy Syst. 22 (4), 829–839. doi:10.1109/tfuzz.2013.2276863

CrossRef Full Text | Google Scholar

Griewank, A., and Toint, P. L. (1982). Local Convergence Analysis for Partitioned Quasi-Newton Updates. Numer. Math. 39, 429–448. doi:10.1007/BF01407874

CrossRef Full Text | Google Scholar

He, Q., Wang, X., Lei, Z., Huang, M., Cai, Y., and Ma, L. (2019). TIFIM: A Two-Stage Iterative Framework for Influence Maximization in Social Networks. Appl. Math. Comput. 354, 338–352. doi:10.1016/j.amc.2019.02.056

CrossRef Full Text | Google Scholar

Kimura, S., Ide, K., Kashihara, A., Kano, M., Hatakeyama, M., Masui, R., et al. (2005). Inference of S-System Models of Genetic Networks Using a Cooperative Coevolutionary Algorithm. Bioinformatics 21 (7), 1154–1163. doi:10.1093/bioinformatics/bti071

PubMed Abstract | CrossRef Full Text | Google Scholar

LaTorre, A. (2013). “Large Scale Global Optimization: Experimental Results with MOS-Based Hybrid Algorithms,” in Proc (IEEE CEC), 2742–2749. doi:10.1109/cec.2013.6557901

CrossRef Full Text | Google Scholar

Li, X. (2013). Benchmark Functions for the CEC 2013 Special Session and Competition on Large-Scale Global Optimization. RMIT University, Tech. Rep. 23.

Google Scholar

Li, Y., Voulgaris, P. G., and Freris, N. M. (2022). A Communication Efficient Quasi-Newton Method for Large-Scale Distributed Multiagent Optimization. United States: Los Alamos National Laboratory. doi:10.48550/arXiv.2201.03759

CrossRef Full Text | Google Scholar

Liu, W. (2019). Cooperative Co-evolution with Soft Grouping for Large Scale Global Optimization. IEEE CEC, 318–325.

Google Scholar

Liu, Y., Yao, X., Zhao, Q., and Higuchi, T. (2001). Scaling up Fast Evolutionary Programming with Cooperative Coevolution. Proc. IEEE CEC, 1101–1108. doi:10.1109/CEC.2001.934314

CrossRef Full Text | Google Scholar

Ma, L., Cheng, S., and Shi, Y. (2021). Enhancing Learning Efficiency of Brain Storm Optimization via Orthogonal Learning Design. IEEE Trans. Syst. Man. Cybern. Syst. 51 (11), 6723–6742. doi:10.1109/tsmc.2020.2963943

CrossRef Full Text | Google Scholar

Ma, L., Huang, M., Yang, S., Wang, R., and Wang, X. (2021). An Adaptive Localized Decision Variable Analysis Approach to Large-Scale Multiobjective and Many-objective Optimization. IEEE Trans. Cybern., 1–13. doi:10.1109/TCYB.2020.3041212

CrossRef Full Text | Google Scholar

Ma, L., Li, N., Guo, Y., Wang, X., Yang, S., Huang, M., et al. (2021). Learning to Optimize: Reference Vector Reinforcement Learning Adaption to Constrained Many-objective Optimization of Industrial Copper Burdening System. IEEE Trans. Cybern., 1–14. doi:10.1109/TCYB.2021.3086501

CrossRef Full Text | Google Scholar

Ma, L., Wang, X., Huang, M., Lin, Z., Tian, L., and Chen, H. (2019). Two-Level Master-Slave RFID Networks Planning via Hybrid Multiobjective Artificial Bee Colony Optimizer. IEEE Trans. Syst. Man. Cybern. Syst. 49 (5), 861–880. doi:10.1109/tsmc.2017.2723483

CrossRef Full Text | Google Scholar

Ma, L., Wang, X., Wang, X., Wang, L., Shi, Y., and Huang, M. (2021). TCDA: Truthful Combinatorial Double Auctions for Mobile Edge Computing in Industrial Internet of Things. IEEE Trans. Mob. Comput., 1. doi:10.1109/TMC.2021.3064314

CrossRef Full Text | Google Scholar

Molina, D. (2018). SHADE with Iterative Local Search for Large-Scale Global Optimization. IEEE CEC, 1–8.

Google Scholar

Omidvar, M., Li, X., and Xin, Y. (2010). Cooperative Co-evolution with Delta Grouping for Large Scale Non-separable Function Optimization. Proc. IEEE CEC, 1762–1769. doi:10.1109/cec.2010.5585979

CrossRef Full Text | Google Scholar

Omidvar, M. N., Li, X., Mei, Y., and Yao, X. (2014). Cooperative Co-evolution with Differential Grouping for Large Scale Optimization. IEEE Trans. Evol. Comput. 18, 378–393. doi:10.1109/tevc.2013.2281543

CrossRef Full Text | Google Scholar

Omidvar, M. N., Li, X., and Tang, K. (2015). Designing Benchmark Problems for Large-Scale Continuous Optimization. Inf. Sci. 316, 419–436. doi:10.1016/j.ins.2014.12.062

CrossRef Full Text | Google Scholar

Omidvar, M. N., Li, X., and Yao, X. (2011). “Smart Use of Computational Resources Based on Contribution for Cooperative Co-evolutionary Algorithms,” in Proc. Of Genetic and Evolutionary Computation Conference, Dublin, Ireland, July 12-16, 2011 (New York, United States: ACM), 1115–1122. doi:10.1145/2001576.2001727

CrossRef Full Text | Google Scholar

Omidvar, M. N., Yang, M., Mei, Y., Li, X., and Yao, X. (2017). DG2: A Faster and More Accurate Differential Grouping for Large-Scale Black-Box Optimization. IEEE Trans. Evol. Comput. 21 (6), 929–942. doi:10.1109/tevc.2017.2694221

CrossRef Full Text | Google Scholar

Potter, M. A., and Jong, K. A. (1994). A Cooperative Coevolutionary Approach to Function Optimization. Proc. Int. Conf. Parallel Problem Solving Nat. 2, 249–257. doi:10.1007/3-540-58484-6_269

CrossRef Full Text | Google Scholar

Ran Cheng, R., and Yaochu Jin, Y. C. (2015). A Competitive Swarm Optimizer for Large Scale Optimization. IEEE Trans. Cybern. 45 (2), 191–204. doi:10.1109/tcyb.2014.2322602

PubMed Abstract | CrossRef Full Text | Google Scholar

Srinivas, M., and Amgoth, T. (2022). Data Acquisition in Large-Scale Wireless Sensor Networks Using Multiple Mobile Sinks: a Hierarchical Clustering Approach. Wirel. Netw. 28 (2), 603–619. doi:10.1007/s11276-021-02845-2

CrossRef Full Text | Google Scholar

Strasser, S., Sheppard, J., Fortier, N., and Goodman, R. (2017). Factored Evolutionary Algorithms. IEEE Trans. Evol. Comput. 21 (2), 281–293. doi:10.1109/tevc.2016.2601922

CrossRef Full Text | Google Scholar

Sun, Y. (2019). Decomposition for Large-Scale Optimization Problems with Overlapping Components. In Proceedings of the. IEEE CEC, 326–333. doi:10.1109/cec.2019.8790204

CrossRef Full Text | Google Scholar

Sun, Y., Kirley, M., and Halgamuge, S. K. (2018). A Recursive Decomposition Method for Large Scale Continuous Optimization. IEEE Trans. Evol. Comput. 22 (5), 647–661. doi:10.1109/tevc.2017.2778089

CrossRef Full Text | Google Scholar

Teng, H.-F., Yu, C., Wei, Z., Yan-jun, S., and Hu, Q-H. (2010). A Dual-System Variable-Grain Cooperative Coevolutionary Algorithm: Satellite-Module Layout Design. IEEE Trans. Evol. Comput. 14 (3), 438–455. doi:10.1109/tevc.2009.2033585

CrossRef Full Text | Google Scholar

Wang, C., and Gao, J. (2012). High-dimensional Waveform Inversion with Cooperative Coevolutionary Differential Evolution Algorithm. IEEE Geosci. Remote Sens. Lett. 9 (2), 297–301. doi:10.1109/lgrs.2011.2166532

CrossRef Full Text | Google Scholar

Wang, Y., Huang, J., Dong, W. S., Yan, J. C., Tian, C. H., Li, M., et al. (2013). Two-stage Based Ensemble Optimization Framework for Large-Scale Global Optimization. Eur. J. Operational Res. 228 (2), 308–320. doi:10.1016/j.ejor.2012.12.021

CrossRef Full Text | Google Scholar

Weicker, K., and Weicker, N. (1999). On the Improvement of Coevolutionary Optimizers by Learning Variable Interdependencies”. IEEE Press, 1627–1632.

Google Scholar

Xue, X. (2021). Matching Large-Scale Biomedical Ontologies with Central Concept Based Partitioning Algorithm and Adaptive Compact Evolutionary Algorithm. Appl. Soft Comput. 106, 1–11. doi:10.1016/j.asoc.2021.107343

CrossRef Full Text | Google Scholar

Xue, X., and Jiang, C. (2021). Matching Sensor Ontologies with Multi-Context Similarity Measure and Parallel Compact Differential Evolution Algorithm. IEEE Sensors J. 21 (21), 24570–24578. doi:10.1109/jsen.2021.3115471

CrossRef Full Text | Google Scholar

Yang, Q., Chen, W.-N., Gu, T., Zhang, H., Deng, J. D., Li, Y., et al. (2017). Segment-based Predominant Learning Swarm Optimizer for Large-Scale Optimization. IEEE Trans. Cybern. 47 (9), 2896–2910. doi:10.1109/tcyb.2016.2616170

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Ke, T., and Xin, Y. (2008). Multilevel Cooperative Coevolution for Large Scale Optimization. Proc. IEEE CEC, June, 1663–1670. doi:10.1109/cec.2008.4631014

CrossRef Full Text | Google Scholar

Yang, Z. (2008). Self-adaptive Differential Evolution with Neighborhood Search. IEEE CEC, 1110–1116.

Google Scholar

Yang, Z., Tang, K., and Yao, X. (2008). Large Scale Evolutionary Optimization Using Cooperative Coevolution. Inf. Sci. 178 (15), 2985–2999. doi:10.1016/j.ins.2008.02.017

CrossRef Full Text | Google Scholar

Zhang, Z. (2022). Large-scale Underwater Fish Recognition via Deep Adversarial Learning. doi:10.1007/s10115-021-01643-8

CrossRef Full Text | Google Scholar

Zhu, P., Cheng, L., Gao*, C., Wang*, Z., and Li, X. (2022). Locating Multi-Sources in Social Networks with a Low Infection Rate. IEEE Trans. Netw. Sci. Eng., 1. doi:10.1109/TNSE.2022.3153968

CrossRef Full Text | Google Scholar