MHD williamson nanofluid flow in the rheology of thermal radiation, joule heating, and chemical reaction using the Levenberg–Marquardt neural network algorithm

Various studies have been conducted on the topic of predicting the thermal conductivity of nanofluids. Here, the thermal conductivity of nanofluids is determined using artificial neural networks since this approach is rapid and accurate, as well as cost-effective. To forecast the thermal conductivity of magnetohydrodynamic Williamson nanofluids flow through a vertical sheet, a feed-forward neural network with various numbers of neurons has been evaluated, and the best network based on the performance is selected. The fluid model incorporates the effects of Joule heating, heat generation absorption, thermal radiation, and a chemical reaction (MHD-WNF-HGA). A combination of heat radiation and reactive species improves the energy and solute profiles. The magnetic Reynolds number is assumed to be so small; therefore, the generated magnetic field has no effect. A postulate of similarity variables is used to convert the physical model in the form of nonlinear partial differential equations to an ordinary differential equation system. A supervised Levenberg–Marquardt backpropagation algorithm possesses a multilayer perceptron that is used for training the network, which is one of the top algorithms in machine learning. The bvp4c numerical technique is adopted to build the datasets for the construction of continuous neural network mapping. Flow, energy, and concentration profiles of the fluidic flow are constructed by adjusting several physical quantities such as the Williamson parameter, thermal radiation parameter, magnetic parameter, Eckert number, Darcy number, Brownian motion, and thermophoresis parameter. Analytical techniques such as error histogram graphs and regression-based statistical graphs are used to examine the accuracy of a suggested method. It has been found that the Levenberg–Marquardt backpropagation neural network mappings’ derivation, convergence, authentication, and consistency have been proven. Furthermore, thermal radiation assists the energy distribution to increase smoothly. Fluid velocity drops with the Williamson parameter, whereas thermophoresis impact enhances the strength of the nanofluid density.

1 Introduction

Energy is a crucial physical property that must be transferred for any system to perform work. Work and heat may be used for energy transmission (Incropera et al., 1996). It is feasible for heat to transfer from one system to another when their temperatures vary (Cengel and Boles, 2015). Heat transfer is a subfield of physics concerned with the transmission of thermal (heat) energy. Heat transfer applications are encountered on a daily basis in the form of the human body’s constant heat output and its usage of clothing to adjust its internal temperature in reaction to external conditions (Cengel and Heat, 2003). In addition, heat transmission is used to regulate the temperature in our buildings and is necessary for cooking and drying. It is also used to control the temperature of car radiators and electrical equipment (Zhao et al., 2016). Heat transfer is used by solar thermal collectors (González et al., 2021) and thermal control components (Okonkwo et al., 2021) to convert solar energy into heat and power. Several of these components must quickly distribute heat in order for the system to work at its maximum effectiveness and efficiency (Okonkwo et al., 2018). Low gate size necessitates enhanced heat control. Generally, the smaller the gadget must be, the higher is the demand for efficient cooling technologies. Therefore, the improvement of heat transfer is a key priority in the area of thermal engineering. Different strategies are arising aim to enhance the heat transfer coefficient among working fluids and their contact surfaces (Das et al., 2006; Meseguer et al., 2012). The research development of heat transfer fluids has resulted from the enhancement of the thermal characteristics of these fluids by the inclusion of nanoscale particles. The dispersion of these solid particles in the host fluid improves the fluid’s energy transmission, resulting in enhanced thermal conductivity and heat transfer qualities. First of all, microscaled particles have been suspended in a fluid for more than a century by Maxwell (Choi et al., 1995). Research into fluid dispersion has been hampered by erosion and clogging caused by microparticles that settle quickly in the liquid. Colloidal dispersion in fids may now be studied in more detail due to the advent of nanoparticles. Later, the term “nanofluid” was coined in 1995 by Choi and Eastman (Maxwell, 1881). By incorporating a modest volumetric quantity of ultrafine nanomaterials into fluids, researchers have come up with many ideas for enhancing thermal efficiency and convective heat transfer. The thermal characteristics of fluids are improved when nanoparticles are scattered in them. Additionally, there are many features involved in the stability of nanofluids such as, Brownian motion, host fluid layer, particle’s nanolayers, and lower pumping power relative to pure liquids. The effect of different nanoparticles made of conducting materials on the improvement of thermal transfer is investigated in the research studies by Sheikholeslami et al. (2019a); Sheikholeslami et al. (2019b); Goodarzi et al. (2019); Sajid and Ali (2019); Alhowaity et al. (2022a); Alsallami et al. (2022); Elattar et al. (2022). Aluminum oxide nanoparticles in base fluid nanofluids past a sensor surface is studied by Mahdi et al. (2019). Three-dimensional magnetohydrodynamic squeezing flow of aluminum nanoparticle base in water type nanofluid is shown in the study by Khan et al. (2020). The rheological model through hybrid nanofluid flow is proposed in the study by Al-Mubaddel et al. (2022). Freezing temperature is studied in aluminum oxide nanofluid magnetic flow with a radiative effect in the study by AdnanKhan and Ahmed (2022). Nanofluids flow with a variety of forces and characteristics, which have been studied for the rate of heat transfer are in the research studies by Khan et al. (2019a); Shah et al. (2019); Ahmed et al. (2020); Khan et al. (2021a); Ashraf et al. (2022); Alhowaity et al. (2022b).

Non-Newtonian fluid models have been the subject of many experiments and theoretical studies cause of the wide variety of biological and industrial processes where they are applicable. Many industrial applications, such as emulsification, lubrication, nuclear fuel slurries, biofluids in cells and polymerization, and therapeutic fluid is in consideration of non-Newtonian fluids rather than Newtonian fluid theory. Many rheological models have been developed based on non-Newtonian fluids’ varied rheological characteristics such as power law model, Jeffery fluid model, Carreau model, Ellis–Sisko–Williamson model, cross-model, and other fluid models are the existing models. Among all, the Williamson fluid model is a basic model that may replicate the viscoelastic shear-thinning features of non-Newtonian fluids. Williamson (1929) established this idea in 1929, and he provided the experimental data. It is expected that the functional viscosity in the Williamson fluid model would decrease endlessly as the shear rate increases, which is nothing more than an infinite viscosity at rest (zero fluid motion) and zero-valued viscosity as the shear rate approaches infinity. In terms of fluid properties, Williamson nanofluid may be classified as visco-inelastic. When it came to investigating the issue of boundary layer flow over a flat surface, Blasius (1950), Sakiadis (1961), and others first looked into the theoretical aspects of approximation and precise methods. Few recent Williamson fluid research studies have been published in the study by Acharya et al. (2019); Khan et al. (2019b); Hamid and Khan (2019); Ibrahim and Gamachu (2019); Rasool et al. (2019); Zaman and Gul (2019); Pandya et al. (2020); Subbarayudu et al. (2020). Thermal radiation is the process through which the heat of a material induces the emission of electromagnetic waves (variation of its internal energy). It is one of the three ways different kinds of organisms may trade their own energy storage. The kind of radiation emitted might vary from ultraviolet to far-field infrared depending on the temperature of the substance. Every component of the body emits and absorbs thermal radiation continuously, and the absorbed radiation may have originated from a vast distance away. Each of these components transmits and receives heat in a manner that is directly influenced by their molecular structure. Connected to a body’s capability to transfer and store heat is its ability to radiate heat from its surface (specific temperatures). The two most important characteristics of thermal energy storage systems are heat transport performance and energy storage density. Nanotechnology may be effective for speeding both the melting and solidification of phase transition materials. Copper/water nanofluid is taken in a flat tube and numerically investigated for thermal transportation (She and Fan, 2018). Flow and energy transportation of metal oxide host water nanofluid is presented in the study by Ahmed et al. (2021) which is used in the PV/T system. For cooling purpose, the fluid is analyzed in the review of heat transfer science (Yang and Liu, 2018). MWCNT/water and Fe₃O₄/water-type hybrid nanofluids are studied to analyze the convective heat transfer and pumping power through perpendicular rib tabulators (Irandoost Shahrestani et al., 2021). Three-dimensional magnetic hybrid nanofluid along with chemical reaction and thermal radiation is passed an inclined rotating sheet is presented in the study by Umar et al. (2020). Numerical approach Lobatto IIIA is used to analyze heat transport of nanofluid in three-dimensional magnetic flow in the study by Ayub et al. (2021a). Similarly, the energy transport of magnetic Carreau nanofluid has been studied by Ayub et al. (2022) using the infinite rate of share viscosity condition. The nanofluid magnetic dipole flow is studied by Shah et al. (2022) under the effect of binary reaction and heat transportation through a cylindrical channel. The cubic autocatalytic chemical reaction has been studied for the unsteady cross nanofluid through a melting sheet in the study by Shah et al. (2021a). All the literature focused on enhancing thermal transportation using nanofluid in different circumstances and forces which is indeed the great demand of the advanced industry. Nanofluid with thermal radiation specification has been studied by Ayub et al. (2021b), Kumar et al. (2021), Raja et al. (2022), Khan et al. (2018), Raja et al. (2021), and Khan et al. (2021b). Artificial neural networks (ANNs) are computer networks that replicate the central nervous system by stimulating nerve cells or neurons. These have a self-organizing characteristic that aids them in solving a variety of issues, making them very convenient to use in computing and algorithmic kinds. Complex challenges, particularly nonanalytical, nonlinear, and nonstationary, may be solved with ANNs because of their ability to ease high-level programming in their crude mimicry of a biological network, which can be used to handle a wide range of problems. The experimental study is carried out using artificial neural networks strategies, to simulate energy and exergy of the evacuated solar-tubes is performed in the study by Sadeghi et al. (2020), thermal conductivity model nanofluid-based study is carried out in the study by Pare and Ghosh (2021), non-Newtonian hybrid nanofluid is taken to predict the dynamic viscosity (Toghraie et al., 2020), and statistical tools applied for thermos-physical properties of nanofluid (Esfe et al., 2022). The third-grade nanofluidic model along with convective conditions has been taken through a stretchable surface which is further solved by neural technique in the study by Shoaib et al. (2021). Furthermore, ANNs are important to forecast the findings of theoretical and numerical approximation studies of nanofluidic models (Sheikholeslami et al., 2019c; Sabir et al., 2022; Zuhra et al., 2022). Levenberg–Marquardt backpropagation neural network has been applied for the computational purpose of the nanofluid model (Vakili et al., 2016; Shah et al., 2021b; Shoaib et al., 2021; Umar et al., 2021; Botmart et al., 2022).

There have been several studies on the thermophysical characteristics of nanofluids, as mentioned earlier. ANNs, on the other hand, have been widely used in nanofluid-based thermal systems because of their ability to solve complicated problems at a lower cost and time. This research focuses on the ANN technique named Levenberg–Marquardt algorithm-based backpropagation to predict the physical parameters of Williamson nanofluids flow under the effects of Joule heating and thermal radiation.

Procedural study is highlighted as follows,

➢Williamson nanofluid is occupied in two-dimensional, magnetic flow stream that passes past a stretching surface in a porous medium.

➢Thermal radiation force, mass diffusion, energy transfer, heat generation/absorption, and Joule heat are imposed in a fluid.

➢Self-similar transformation is adopted to convert the physical model into a nonlinear differential system that has physical nondimensional variations to be computed.

➢The Bvp4c technique is used to find the numerical solutions in the form of a dataset. Which is further furnished through the neural network process for analysis.

➢In the NN process, the fitness functions are taken, that is, multiple responses are converted to a single response.

➢Designed backpropagation based neural networks by providing training and testing datasets. Levenberg–Marquardt algorithm is adapted to speed up the training.

➢The significance of the LMB-NN technique is illustrated through statistical tools such as mean square error, error histograms, correlation, and regression fitting graphs.

➢The analysis of variations that are Williamson parameter, Brownian motion, Prandtl number, thermophoresis, heat generation, Darcy number, Eckert number, and chemical reaction parameter velocity and temperature field are illustrated in the graphic structure.

In the remaining, a physical description of the flow model is presented in Section 2. Section 3 discusses the Levenberg–Marquardt strategy and step-by-step procedure in detail. Section 4 presents the findings of the proposed model via graphs and tables and discussion on each one. At last, a brief summary of the model via the ANN technique is presented.

2 Flow model and its mathematical construction

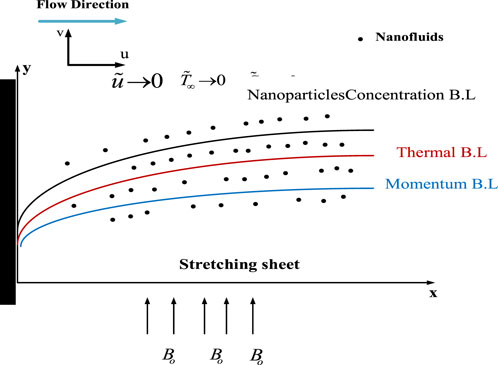
Let us consider a mathematical model for incompressible two-dimensional Williamson nanofluid past a stretched surface. Figure 1 depicts the design of the problem with Cartesian coordinates $\left(x,y\right)$ followed by velocity components $\left(u,v\right)$ with fluid flow arrangement. To observe mass diffusion and heat transfer, the interface of the applied magnetization field with dynamic viscosity and a porous medium are used. The transfer of heat is augmented by supposing the thermophysical characteristics of heat generation/absorption and Joule heating with a velocity of ${\tilde{U}}_w\left(x\right)=\tilde{B}x$ with $\tilde{B}$ is the extending parameter. The basic equations of the law of conservation of mass, momentum, heat, and nanoparticles concentration associated with the abovementioned stated assumptions are as follows (Bouslimi et al., 2021).

FIGURE 1

FIGURE 1. Geometry of the problem.

The governing equations of the flow model are as follows.

2.1 Continuity equation

The law of conservation of mass for continuity equation in vectorial form can be written as follows:

$\tilde{\nabla }.\overrightarrow{q}=0,(1)$

where $\overrightarrow{q}$ is denoted as the flow velocity vector, and $\tilde{\nabla }$ is known as the differential operator.

2.2 Momentum equation

According to Navier–Stokes’ equation, for the equilibrium of linear-momentum,

${\rho }_f\left[\frac{\partial \overrightarrow{\widehat{q}}}{\partial \tilde{t}}+\left(\overrightarrow{\widehat{q}}.\tilde{\nabla }\right)\overrightarrow{\widehat{q}}\right]+\frac{\mu }{K}\overrightarrow{\widehat{q}}=\overrightarrow{F_e}+\tilde{\nabla }.\tilde{S}.(2)$

2.3 Energy equation

The constitutive equation provides the following energy efficiency for heat conduction without the impact of viscous dissipation.

$\begin{array}{l}{\left(\rho c_p\right)}_f\left[\frac{\partial \overrightarrow{T}}{\partial \tilde{t}}+\left(\overrightarrow{q}.\tilde{\nabla }\right)\overrightarrow{T}\right]+\tilde{\nabla }\overrightarrow{q_r}=\overrightarrow{{\left(\rho c_p\right)}_p\left[\frac{{\tilde{D}}_{\tilde{T}}}{{\tilde{T}}_{\infty }}\left(\tilde{\nabla }\tilde{T}.\tilde{\nabla }\tilde{T}\right)+{\tilde{D}}_B\left(\tilde{\nabla }\tilde{C}.\tilde{\nabla }\tilde{T}\right)\right]}+\\ \tilde{\nabla }.\left(k\tilde{\nabla }\tilde{T}\right)+Q\left(\tilde{T}-{\tilde{T}}_{\infty }\right)+J_h.\end{array}(3)$

2.4 Conservation equation of the nanoparticle concentration

The nanoparticle concentration volume fraction equation in the occurrence of a homogeneous chemical reaction becomes

$\frac{\partial \overrightarrow{C}}{\partial \tilde{t}}+\left(\overrightarrow{q}.\tilde{\nabla }\right)\overrightarrow{C}+R^{\ast }\left(\tilde{C}-{\tilde{C}}_{\infty }\right)=\frac{{\tilde{D}}_{\tilde{T}}}{{\tilde{T}}_{\infty }}{\tilde{\nabla }}^2\tilde{T}+{\tilde{D}}_B{\tilde{\nabla }}^2\tilde{C}.(4)$

The Cauchy stress tensor $\left(\tilde{S}\right)$ for the Williamson nanofluid is defined as (Alhowaity et al., 2022b)

$\tilde{S}=\overline{\tau }-\tilde{P}\overline{I},(5)$

$\overline{\tau }=\left(\frac{{\mu }_0-{\mu }_{\infty }}{1-\mathrm{\Gamma }\stackrel{•}{\gamma }}+{\mu }_{\infty }\right){\overline{A}}_1,(6)$

where $\left({\mu }_0,{\mu }_{\infty }\right)\to$ limiting viscosity at zero and at an infinite shear rate, respectively, $\overline{\tau }\to$ extra stress tensor, $\overline{I}\to$ unit tensor, $\left(\mathrm{\Gamma }>0\right)\to$ time constant, ${\overline{A}}_1\to$ first Rivlin–Erickson tensor, $\tilde{P}\to$ pressure, and $\stackrel{•}{\gamma }\to$ is defined as:

$\pi =\text{trace}{\left({\overline{A}}_1\right)}^2,\stackrel{•}{\gamma }=\sqrt{\frac{\pi }{2}}.(7)$

Here, it is considered the case for $\mathrm{\Gamma }\stackrel{•}{\gamma }<1$ and ${\mu }_{\infty }=0$; thus, Eq. 6 can be transformed into the following form:

$\overline{\tau }=\left(\frac{{\mu }_0}{1-\mathrm{\Gamma }\stackrel{•}{\gamma }}\right){\overline{A}}_1={\mu }_0\left(1+\mathrm{\Gamma }\stackrel{•}{\gamma }\right){\overline{A}}_1.(8)$

According to Eq. 8, the binomial expression may be used. The two-dimensional boundary layer equations for the flow may be stated as follows:

$\frac{\partial \tilde{u}}{\partial x}+\frac{\partial \tilde{v}}{\partial y}=0,(9)$

$\frac{\partial \tilde{u}}{\partial x}\tilde{u}+\frac{\partial \tilde{u}}{\partial y}\tilde{v}+\frac{\nu }{K}\tilde{u}+\frac{\stackrel{⌢}{\sigma }{\stackrel{⌢}{B}}_0^2}{\stackrel{⌢}{\rho }}\tilde{u}=\nu \frac{{\partial }^2\tilde{u}}{\partial y^2}+\sqrt{2}\nu \mathrm{\Gamma }\frac{{\partial }^2\tilde{u}}{\partial y^2}\frac{\partial \tilde{u}}{\partial y},(10)$

$\begin{array}{l}\frac{\partial \tilde{T}}{\partial x}\tilde{u}+\frac{\partial \tilde{T}}{\partial y}\tilde{v}+\frac{1}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}\frac{\partial {\overrightarrow{q}}_r}{\partial y}=\alpha \frac{{\partial }^2\tilde{T}}{\partial y^2}+\frac{{\left(\tilde{\rho }{c}_p\right)}_p}{{\left(\tilde{\rho }{c}_p\right)}_f}\left[\frac{{\tilde{D}}_{\tilde{T}}}{{\tilde{T}}_{\infty }}{\left(\frac{\partial \tilde{T}}{\partial y}\right)}^2+{\tilde{D}}_B\left(\frac{\partial \tilde{C}}{\partial y}\frac{\partial \tilde{T}}{\partial y}\right)\right]+\\ \frac{Q}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}(\tilde{T}-{\tilde{T}}_{\infty })+\frac{\tilde{\sigma }{\tilde{B}}_0^2\left(\tilde{t}\right)}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}{\tilde{u}}^2,\end{array}(11)$

$\frac{\partial \tilde{C}}{\partial x}\tilde{u}+\frac{\partial \tilde{C}}{\partial y}\tilde{v}+R^{\ast }\left(\tilde{C}-{\tilde{C}}_{\infty }\right)=\frac{{\tilde{D}}_{\tilde{T}}}{{\tilde{T}}_{\infty }}\frac{{\partial }^2\tilde{T}}{\partial y^2}+{\tilde{D}}_B\frac{{\partial }^2\tilde{C}}{\partial y^2}.(12)$

Also, the following nomenclature is used: $\left(\tilde{u},\tilde{v}\right)\to$ velocity components, $\alpha \to$ thermal diffusivity, $\tilde{\rho }\to$ density of the fluid, $\nu \to$ kinematic viscosity of the fluid, ${\tilde{B}}_0\to$ uniform magnetic field, $\left(\tilde{T},{\tilde{T}}_{\infty }\right)\to$ fluid and ambient fluid temperature, respectively, ${\tilde{D}}_B\to$ coefficient of Brownian diffusion, ${\tilde{D}}_{\tilde{T}}\to$ thermophoretic diffusivity, $\tilde{\sigma }\to$ electrical-conductivity, ${\tilde{c}}_p\to$ specific thermal at fixed pressure, $R^{\ast }\to$ reaction rate of constructive/destructive, $\left(\tilde{C}\right)\to$ concentration nanoparticles, and $,{\tilde{C}}_{\infty }$ is ambient nanoparticle concentration.

Nonlinear thermal radiation and Joule heating are connected in the energy equation. In the energy equation, the viscous dissipation is expected to be very little that it may be ignored. Homogeneous chemical processes have an effect on concentration equations.

The corresponding boundary conditions for the present fluidic problem are given as follows:

$\text{At}\stackrel{⌢}{y}=0:\tilde{u}={\tilde{U}}_w\left(x\right),\tilde{v}=0,\tilde{T}={\tilde{T}}_w,{\tilde{D}}_B\frac{\partial \tilde{C}}{\partial y}+\frac{{\tilde{D}}_{\tilde{T}}}{{\tilde{T}}_{\infty }}\frac{\partial \tilde{T}}{\partial y},\}(13)$

$\text{As}\stackrel{⌢}{y}\to \infty \text{:}\tilde{u}\to 0,\tilde{v}\to 0,\tilde{T}\to {\tilde{T}}_{\infty },\tilde{C}\to {\tilde{C}}_{\infty },\}(14)$

where ${\tilde{U}}_w\left(x\right)=\tilde{B}x\to$ stretching surface velocity, $\left(\tilde{B}>0\right)\to$ stretching rate, and ${\tilde{q}}_r\to$ radiation heat flux and is defined as follows:

${\tilde{q}}_r=-\frac{\partial {\tilde{T}}^4}{\partial \stackrel{⌢}{y}}\frac{4{\tilde{\sigma }}^{\ast }}{3k^{\ast }}=-\frac{16{\tilde{\sigma }}^{\ast }}{3k^{\ast }}{\tilde{T}}^3\frac{\partial \tilde{T}}{\partial y},(15)$

$\therefore \frac{1}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}\frac{\partial }{\partial y}\left({\overrightarrow{q}}_r\right)=\frac{1}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}\frac{\partial }{\partial y}\left(-\frac{\partial {\tilde{T}}^4}{\partial y}\frac{4{\tilde{\sigma }}^{\ast }}{3k^{\ast }}\right)=-\frac{16{\tilde{\sigma }}^{\ast }}{3k^{\ast }{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}\frac{\partial }{\partial y}\left({\tilde{T}}^3\frac{\partial \tilde{T}}{\partial y}\right).(16)$

By substituting Eqs 15 and 16 in Eq. 11, we obtain

$\begin{array}{l}\frac{\partial \tilde{T}}{\partial x}\tilde{u}+\frac{\partial \tilde{T}}{\partial y}\tilde{v}=\alpha \frac{{\partial }^2\tilde{T}}{\partial y^2}+\frac{{\left(\tilde{\rho }{c}_p\right)}_p}{{\left(\tilde{\rho }{c}_p\right)}_f}\left[\frac{{\tilde{D}}_{\tilde{T}}}{{\tilde{T}}_{\infty }}{\left(\frac{\partial \tilde{T}}{\partial y}\right)}^2+{\tilde{D}}_B\left(\frac{\partial \tilde{C}}{\partial y}\frac{\partial \tilde{T}}{\partial y}\right)\right]+\frac{16{\tilde{\sigma }}^{\ast }}{3k^{\ast }{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}\frac{\partial }{\partial y}\left({\tilde{T}}^3\frac{\partial \tilde{T}}{\partial y}\right)\\ +\frac{Q}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}(\tilde{T}-{\tilde{T}}_{\infty })+\frac{\tilde{\sigma }{\tilde{B}}_0^2\left(\tilde{t}\right)}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}{\tilde{u}}^2.\end{array}(17)$

The nondimensional variables and similarity transformations listed as follows are introduced as

$\begin{array}{l}\eta =y\sqrt{\frac{{\tilde{U}}_w\left(x\right)}{\nu x}},\tilde{u}=\tilde{B}xf\prime \left(\eta \right),\tilde{v}=-{\left(\tilde{B}\nu \right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}f\left(\eta \right),\\ \theta \left(\eta \right)=\frac{\tilde{T}-{\tilde{T}}_{\infty }}{{\tilde{T}}_{\stackrel{⌢}{w}}-{\tilde{T}}_{\infty }},\varphi \left(\eta \right)=\frac{\tilde{C}-{\tilde{C}}_{\infty }}{{\tilde{C}}_{\infty }},\end{array}\}(18)$

The equation of continuity is identically satisfied by using Eq. 18 and Eqs 10, 12, 17, coupled with Eqs 13, 14; assume the form of ordinary differential equations shown as follows:

$\mathit{f}″\prime \left(\eta \right)\left(1+\lambda f″\left(\eta \right)\right)+f″\left(\eta \right)f\left(\eta \right)-f\prime \left(\eta \right)\left(f\prime \left(\eta \right)-M-Da\right)=0,(19)$

$\begin{array}{l}\theta ″\left(\eta \right)+\left(M\circ Ecf\left(\eta \right)+Nb\varphi \left(\eta \right)+Nt\theta \prime \left(\eta \right)\right)\theta \prime \left(\eta \right)+\mathrm{Pr}\left(R\left({\left(1+\left({\theta }_w-1\right)\theta \left(\eta \right)\right)}^3\right)\theta \prime \left(\eta \right)\right)\prime \\ +Ec\circ M{\left(f\left(\eta \right)\right)}^2+S\theta \left(\eta \right)=0,\end{array}(20)$

$\varphi ″\left(\eta \right)+\left(\raisebox{1ex}{$Nt$}\!\left/ \!\raisebox{-1ex}{$Nb$}\right.\right)\theta ″\left(\eta \right)+Le\left(f\left(\eta \right)\varphi \prime \left(\eta \right)-\gamma \varphi \left(\eta \right)\right)=0,(21)$

where the boundary conditions (13–14) after transforming into nondimensional form are given as

$f\left(0\right)=0,f\prime \left(0\right)=1,Nt\theta \prime \left(0\right)+Nb\varphi \prime \left(0\right)=0,\theta \left(0\right)=1,(22)$

$f^{\prime }\left(\infty \right)\to 0,\theta \left(\infty \right)\to 0,\varphi \left(\infty \right)\to 0.(23)$

With the nondimensional parameters given as $\left(M=\frac{\tilde{\sigma }{\tilde{B}}_0^2}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}\right)\to$ magnetic field parameter, $\left(R=\frac{16{\tilde{\sigma }}^{\ast }{\tilde{T}}_{\infty }^3}{3k{k}^{\ast }}\right)\to$ nonlinear thermal radiation parameter, $\left(\mathrm{Pr}=\frac{\mu }{\alpha }\right)\to$ Prandtl number, $\left(Nb=\frac{{\left(\tilde{\rho }{c}_p\right)}_p{\tilde{D}}_B{\tilde{C}}_{\infty }}{{\left(\tilde{\rho }{c}_p\right)}_f\nu }\right)\to$ Brownian motion parameter, $\left(Nt=\frac{{\left(\tilde{\rho }{c}_p\right)}_p{\tilde{D}}_T({\tilde{T}}_w-{\tilde{T}}_{\infty })}{{\left(\tilde{\rho }{c}_p\right)}_f\nu {\tilde{T}}_{\infty }}\right)\to$ thermophoresis parameter, $\left(S=\frac{Q}{{\left(\tilde{\rho }{\tilde{c}}_p\right)}_f}\tilde{B}\right)\to$ heat generation $\left(S>0\right)$ or absorption parameter $\left(S<0\right)$, $\left(Le=\frac{\nu }{{\tilde{D}}_B}\right)\to$ Lewis number, $\left(Da=\frac{\tilde{\mu }}{\tilde{\rho }}\tilde{B}K\right)\to$ Darcy number, $\left(Ec=\frac{{\tilde{U}}_w^2\left(x\right)}{{\tilde{c}}_p({\tilde{T}}_w-{\tilde{T}}_{\infty })}\right)\to$ Eckert number, $\left(\lambda =\mathrm{\Gamma }x\sqrt{\raisebox{1ex}{$2B^3$}\!\left/ \!\raisebox{-1ex}{$\nu $}\right.}\right)\to$ non-Newtonian Williamson parameter, and $\left(\gamma =\frac{R^{\ast }}{\tilde{B}}\right)\to$ chemical reaction parameter. Also, expressions for ${\rm N}{\tilde{u}}_x$ and $C{f}_x$ are shown as follows:

${\rm N}{\tilde{u}}_x=\frac{x{\overrightarrow{q}}_w}{{\tilde{k}}_f}({\widetilde{{\rm T}}}_w-{\widetilde{{\rm T}}}_{\infty }),(24)$

$C{f}_x=\frac{{\tau }_w}{\tilde{\rho }{\tilde{U}}_w^2\left(x\right)}.(25)$

The Sherwood number $S{h}_x$, which represents a nondimensional mass flow, is currently zero. Here, ${\overrightarrow{q}}_w$ indicates heat flux, and ${\tau }_w$ denotes shear stress of the wall along a stretching surface, respectively, and their mathematical expressions are given as follows:

${\overrightarrow{q}}_w\left(=-\alpha {\left(\frac{\partial \tilde{T}}{\partial y}\right)}_{y=0}+{\left({\overrightarrow{q}}_r\right)}_y\right),(26)$

${\tilde{\tau }}_w\left(={\tilde{\mu }}_f\left(1+\frac{\mathrm{\Gamma }}{2}\frac{\partial \tilde{u}}{\partial y}\right){\frac{\partial \tilde{u}}{\partial y}}_{\stackrel{⌢}{y}=0}\right).(27)$

The dimensionless formulation of Eqs 24 and 25 after substituting Eqs 26 and 27 are as follows:

$\frac{{\rm N}{u}_x}{\sqrt{{\mathrm{Re}}_x}}=-\left(1+R{\theta }_w^3\right)\theta \prime \left(0\right),(28)$

$C_{fx}\sqrt{{\mathrm{Re}}_x}=(1+\frac{\lambda }{2}f″\left(0\right))f″\left(0\right),(29)$

where $\sqrt{{\mathrm{Re}}_x}$ is the Reynolds number relative to the stretching velocity ${\tilde{U}}_w\left(x\right)$.

3 Design methodology/neural network modeling

Machine learning algorithms (MLAs) have been created to handle real-world problems arising in various fields of science, engineering, and mathematics. Depending on the training approach, these MLAs can be divided into three categories.

• Reinforcement learning algorithms (RLAs)

• Unsupervised learning algorithms (ULAs)

• Supervised learning algorithms (SLAs)

The supervised learning algorithm (SLA) is quite similar to how a human learns, by considering the fact that humans solve exercise problems or datasets to obtain new knowledge. The current study employs SLA in which adjustments of weights are constructed based on the comparison and correlation with some target output. For weight adjustment, a teaching signal is fed into the neural networks (NNs) which are called a training sample or training dataset. In SLA, the correct output is what the model is alleged to provide for the given input. Errors are backpropagated through the scheme, allowing the scheme to adjust the weights that supervise the neural networks (NNs).

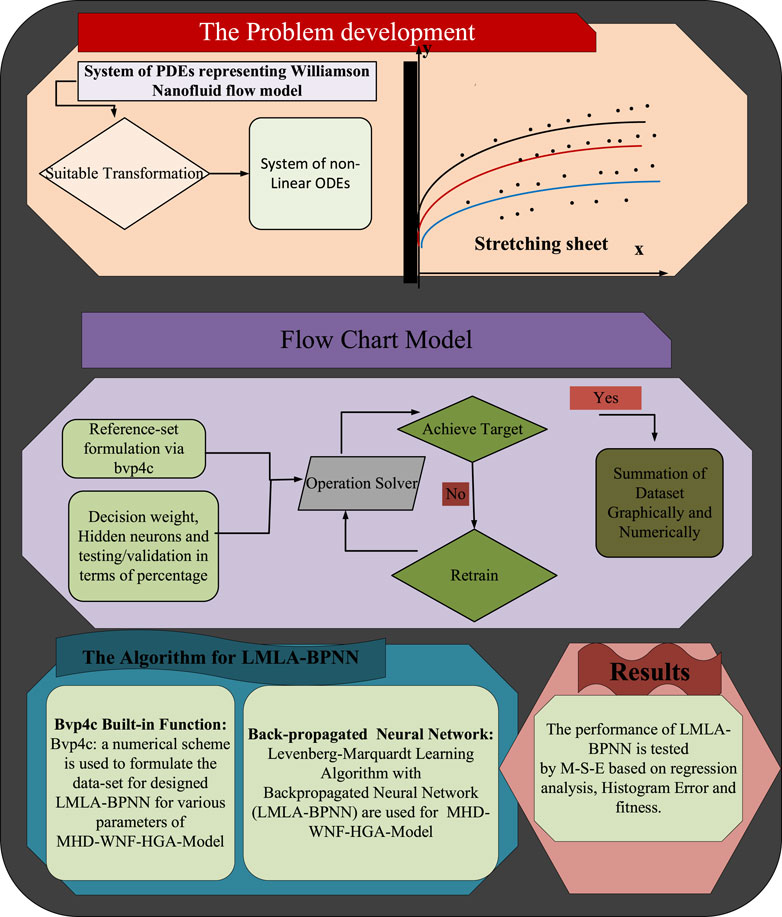
The brief deliberation of the results for the propose Levenberg–Marquardt learning algorithm for backpropagated neural networks (LMLA-BPNNs) subjected to the Joule’s heating effect of MHD Williamson nanofluid flow through a porous medium in the rheology of nonlinear thermal radiation and chemical reaction with variable heat generation/absorption (MHD-WNF-HGA) has been evaluated in this part. The partial differential equations (PDEs) prescribing MHD-WNF-HGA are converted to set ordinary differential equations (ODEs) by employing appropriate transformation. The set of differential Eqs 19–21 contains a detailed mathematical strategy for reproducing results employing a numerical scheme, and the fluidic problem MHD-WNF-HGA is tackled down with the help of “bvp4c” built-in function by MATLAB software for nine variants where higher order nondimensional system of ODEs are transformed to first-order ODEs.

$\mathit{f}″\prime \left(\eta \right)=\frac{\left(\left(f\prime \left(\eta \right)-M-Da\right)f\prime \left(\eta \right)-f\left(\eta \right)f″\left(\eta \right)\right)}{\left(1+\lambda f″\left(\eta \right)\right)},(30)$

$\theta ″\left(\eta \right)=-\frac{\mathrm{Pr}\left(\begin{array}{l}3R\left({\theta }_w-1\right){\left(1+\left({\theta }_w-1\right)\theta \left(\eta \right)\right)}^2{\left(\theta \prime \left(\eta \right)\right)}^2+S\theta \left(\eta \right)+Nb\theta \prime \left(\eta \right)\varphi \left(\eta \right)+\\ f\left(\eta \right)\theta \prime \left(\eta \right)+Nt{\left(\theta ″\left(\eta \right)\right)}^2+M\circ Ec{\left(f\left(\eta \right)\right)}^2\end{array}\right)}{\left(1+\mathrm{Pr}\circ R{\left(1+\left({\theta }_w-1\right)\theta \left(\eta \right)\right)}^3\right)},(31)$

$\varphi ″\left(\eta \right)=-\left(\left(\raisebox{1ex}{$Nt$}\!\left/ \!\raisebox{-1ex}{$Nb$}\right.\right)\theta ″\left(\eta \right)+Le\left(f\left(\eta \right)\varphi \prime \left(\eta \right)-\gamma \varphi \left(\eta \right)\right)\right),(32)$

$\begin{array}{l}f\left(\eta \right)={\mathrm{{\rm X}}}_1,\\ f\prime \left(\eta \right)={\mathrm{{\rm X}}}_2,\\ f″\left(\eta \right)={\mathrm{{\rm X}}}_3,\\ \mathrm{{\rm X}}{\prime }_3=\frac{\left(\left({\mathrm{{\rm X}}}_2-M-Da\right){\mathrm{{\rm X}}}_2-{\mathrm{{\rm X}}}_1{\mathrm{{\rm X}}}_3\right)}{\left(1+\lambda f″{\mathrm{{\rm X}}}_3\right)},\\ \theta \left(\eta \right)={\mathrm{{\rm X}}}_4,\\ \theta \prime \left(\eta \right)={\mathrm{{\rm X}}}_5,\\ \mathrm{{\rm X}}{\prime }_5=-\frac{\mathrm{Pr}\left(\begin{array}{l}3R\left({\theta }_w-1\right){\left(1+\left({\theta }_w-1\right){\mathrm{{\rm X}}}_4\right)}^2{\left({\mathrm{{\rm X}}}_5\right)}^2+S{\mathrm{{\rm X}}}_4+Nb{\mathrm{{\rm X}}}_4{\mathrm{{\rm X}}}_6+{\mathrm{{\rm X}}}_1{\mathrm{{\rm X}}}_5+\\ Nt{\left({\mathrm{{\rm X}}}_5\right)}^2+M\circ Ec{\left({\mathrm{{\rm X}}}_1\right)}^2\end{array}\right)}{\left(1+\mathrm{Pr}\circ R{\left(1+\left({\theta }_w-1\right){\mathrm{{\rm X}}}_4\right)}^3\right)},\\ \varphi \left(\eta \right)={\mathrm{{\rm X}}}_6,\\ \varphi \prime \left(\eta \right)={\mathrm{{\rm X}}}_7,\\ \mathrm{{\rm X}}{\prime }_7=-\left(\left(\raisebox{1ex}{$Nt$}\!\left/ \!\raisebox{-1ex}{$Nb$}\right.\right)\mathrm{{\rm X}}{\prime }_5+Le\left({\mathrm{{\rm X}}}_1{\mathrm{{\rm X}}}_7-\gamma {\mathrm{{\rm X}}}_6\right)\right).\end{array}(33)$

With the boundary conditions,

$\begin{array}{l}{\mathrm{{\rm X}}}_a\left(1\right)=0,{\mathrm{{\rm X}}}_a\left(2\right)=1,{\mathrm{{\rm X}}}_a\left(4\right)=1,Nt{\mathrm{{\rm X}}}_a\left(5\right)+Nb{\mathrm{{\rm X}}}_a\left(7\right)=0,\\ {\mathrm{{\rm X}}}_b\left(2\right)=0,{\mathrm{{\rm X}}}_b\left(4\right)=0,{\mathrm{{\rm X}}}_b\left(6\right)=0.\end{array}(34)$

Taking both into account,

$\mathit{f}″\prime \left(\eta \right)=\mathrm{{\rm X}}{\prime }_3,\theta ″\left(\eta \right)=\mathrm{{\rm X}}{\prime }_5,\varphi ″\left(\eta \right)=\mathrm{{\rm X}}{\prime }_7.(35)$

The dataset formation in the form of a numerical solution by employing “bvp4c” built-in function using MATLAB by variation of magnetic field quantity $\left(M\right)$, non-Newtonian Williamson parameter $\left(\lambda \right)$, nonlinear thermal radiation parameter $\left(R\right)$, Darcy number $\left(Da\right)$, heat generation/absorption parameter $\left(S\right)$, ratio-temperature $\left({\theta }_w\right)$, thermophoresis parameter $\left(Nt\right)$, chemical reaction parameter $\left(\gamma \right)$, and Lewis number $\left(Le\right)$. The transformed set of Eqs 19–21 which characterize the fluidic model representing MHD-WNF-HGA, the suggested LMLA-BPNN solver is accomplished by exerting neural network (NN) toolbox in MATLAB software by operating “nftool”, a built-in function. LMLA-BPNN receives knowledge via learning and stored that knowledge within interneuron connections “strengths”, which is expressed in the form of numerical values called “weights” which has a two-layered structure (input layer, hidden layer, and output layer). The output signal values for a newly testing input signal values are computed using these weights.

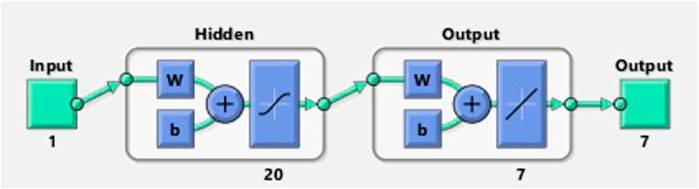
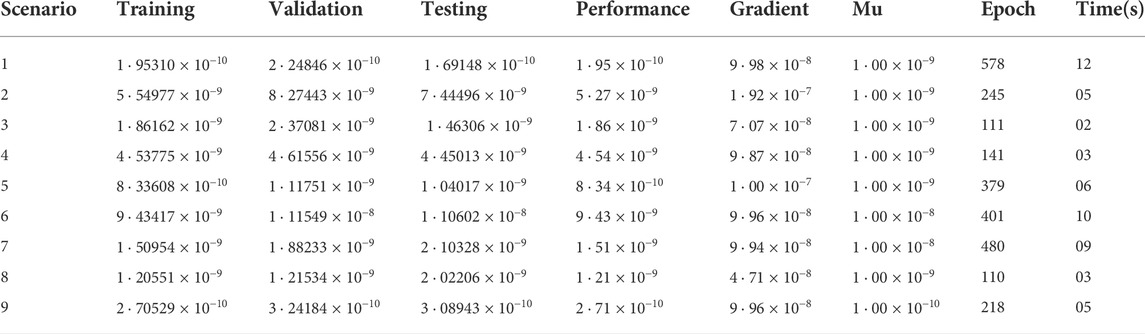
The “input layer” presents a pattern to the network, which then interconnects with one or more than one “hidden layer” where the actual computing is carried out via a system of weighted “connections”. The hidden layers then connect to an “output layer,” where the result is displayed as output. The artificial neural networks (ANNs) architecture is composed of 20 highly processing elements (neurons) interconnected in a parallel way to solve the fluidic problem with a sigmoid activation function. The sigmoid activation function is an S-shaped nonlinearly smooth function having input values ranging from +1 to 0, as illustrated in Figure 2. However, Figure 3 shows the block architecture of the process flow. The aim of determining the approximated solution of the proposed LMLA-BPNN is the reference dataset for training, validation, and testing purposes. The validity, reliability, and convergence of the LMLA-BPNN based on a comprehensive study of regression analysis, accuracy assessments, and histogram analysis supervised for the MHD-WNF-HGA fluidic model, which is sufficiently detailed graphically and numerically in Table 1.

FIGURE. 2

FIGURE. 2. Neural networks for MHD-WNF-HGA.

FIGURE 3

FIGURE 3. Flow architecture of the MHD-WNF-HGA model.

TABLE 1

TABLE 1. LMLA-BPBB’s outcomes for scenario Ⅰ of MHD-WNF-HGA.

For flow, energy, and nanoparticle concentration distribution of MHD-WNF-HGA, the reference dataset is built up that comprises nine scenarios with cases of LMLA-BPNN. The bvp4c built-in function technique is in collaboration with LMLA-BPNN for $\eta$ between 0 and 10 having equidistance of 0.01 s used in all processes of each case. The acquired datasets are determined as reference outcomes in terms of $\left(f\prime ,\theta ,\varphi \left(\eta \right)\right)$. Table 1 displays the numerical solutions of LMLA-BPNN for variants of $\left(f\prime ,\theta ,\varphi \left(\eta \right)\right)$ for MHD-WNF-HGA in terms of MSE, that is, training data (determine model parameters), validation data (yardstick to overfitting), testing data (final scoring of the model) and production (predict output), backpropagated networks, time taken, and total iterations/epochs, for all the scenarios connected with MHD-WNF-HGA.

4 Result interpretation

The designed LMLA-BPNN outcomes for the MHD-WNF-HGA fluid model have been illustrated in Figures 4–13 for various positions (scenarios) of I–IX. Figures 4A–13A is interpreting convergence of training data, validation data, and trying data progression through the epochs index for finding the cases of $M$, $Da$, and $\lambda$ for $f\prime \left(\eta \right)$; the case of $R$, $S$, and ${\theta }_w$ for $\theta \left(\eta \right)$; and finally, the cases of $Nt$, $\gamma$, and $Le$ $\varphi \left(\eta \right)$. The magnificent validation performance attained at epochs 578, 239, 111, 141, 379, 401, 480, 110, and 218 with mean squared error (MSE) almost $2.2485\times {10}^{-10}$, $8.2744\times {10}^{-9}$, $2.3708\times {10}^{-9}$, $4.6156\times {10}^{-9}$, $1.1175\times {10}^{-9}$, $1.1155\times {10}^{-8}$, $1.8823\times {10}^{-9}$, $1.2153\times {10}^{-9}$, and $3.2418\times {10}^{-10}$ in times 12, 05, 02, 03, 06, 10, 09, 03 and 05 s, respectively. It is estimated that the influence of all the obtained lines is smooth and leads to the stability point, indicating that the performance is perfect and ideal. According to the relative Table 1 and figures, the performance approach will be better by lowering MSE values. The smaller the MSE values, the more effective and precise the performance of the given approach is likely to be. Figures 4B–13B reveals the authenticity that LMLA-BPNN is precise, accurate, and efficiently convergent for solving the cases of $M$, $Da$, and $\lambda$ for $f\prime \left(\eta \right)$; the case of $R$, $S$, and ${\theta }_w$ for $\theta \left(\eta \right)$; and finally, the cases of $Nt$, $\gamma$, and $Le$ $\varphi \left(\eta \right)$. Figures 4B–13B demonstrates the gradient and Mu values for all the scenarios in the time duration for the training in recognizing another vector. The process is updating constantly during training. The training is terminated based on the number of validations checks and on the magnitude of the gradient. As the training approaches to a minimum level of performance, gradient will become very small. The training will stop if the magnitude of the gradient become less than $1.0\times {10}^{-5}$. Mu is the adaptive parameter of LMLA-BPNN, which is directly influenced on error convergence. The associated values of gradient are $9.9774\times {10}^{-8}$, $1.9235\times {10}^{-7}$, $7.0696\times {10}^{-8}$, $9.875\times {10}^{-8}$, $9.997\times {10}^{-8}$, $9.9587\times {10}^{-8}$, $9.9421\times {10}^{-8}$, $4.7068\times {10}^{-8}$, and $9.9582\times {10}^{-8}$, while Mu is $1\times {10}^{-9}$, $1\times {10}^{-9}$, $1\times {10}^{-9}$, $1\times {10}^{-9}$, $1\times {10}^{-9}$, $1\times {10}^{-8}$, $1\times {10}^{-8}$, $1\times {10}^{-9}$, and $1\times {10}^{-10}$ with epoch 578, 239, 111, 141, 379, 401, 480, 110, and 218, respectively. Result interpretation shows that enhancing the epoch can cause a reduction in Mu and gradient values.

FIGURE 4

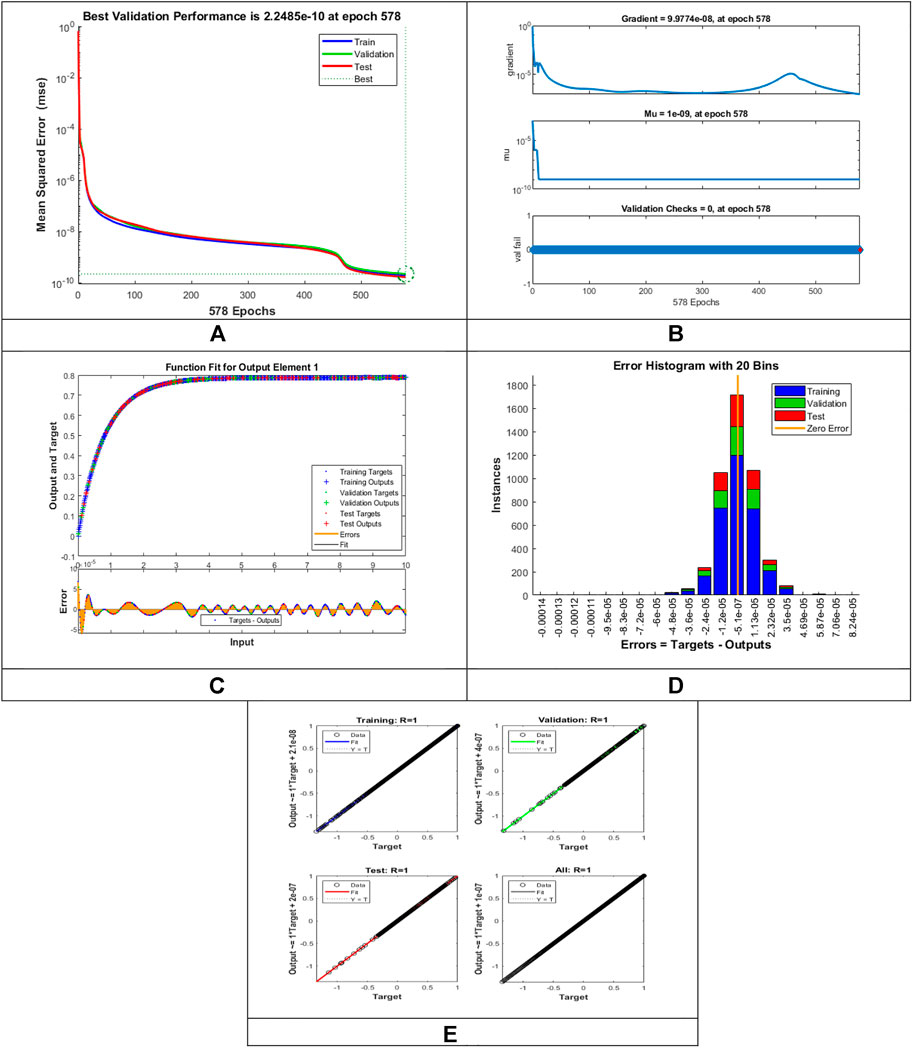
FIGURE 4. Pictorial illustration for the LMLA-BPNN base on variants of $Mvsf\prime \left(\eta \right)$ for MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, and (E) regression analysis.

FIGURE 5

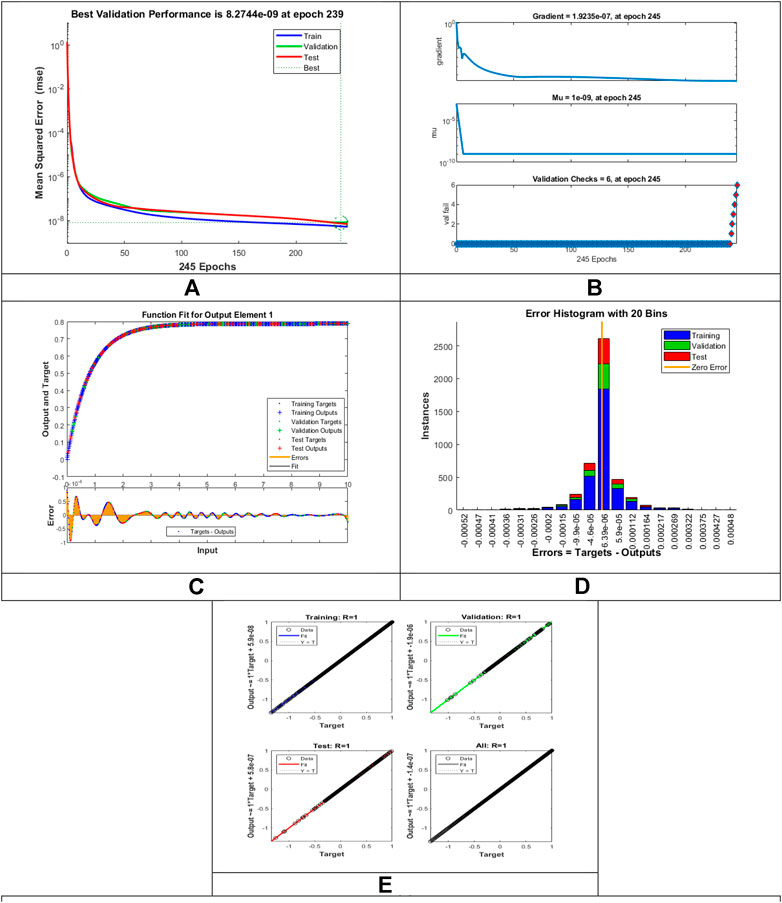
FIGURE 5. Pictorial illustration for the LMLA-BPNN base on variants of $Davsf\prime \left(\eta \right)$ MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, and (E) regression-analysis.

FIGURE 6

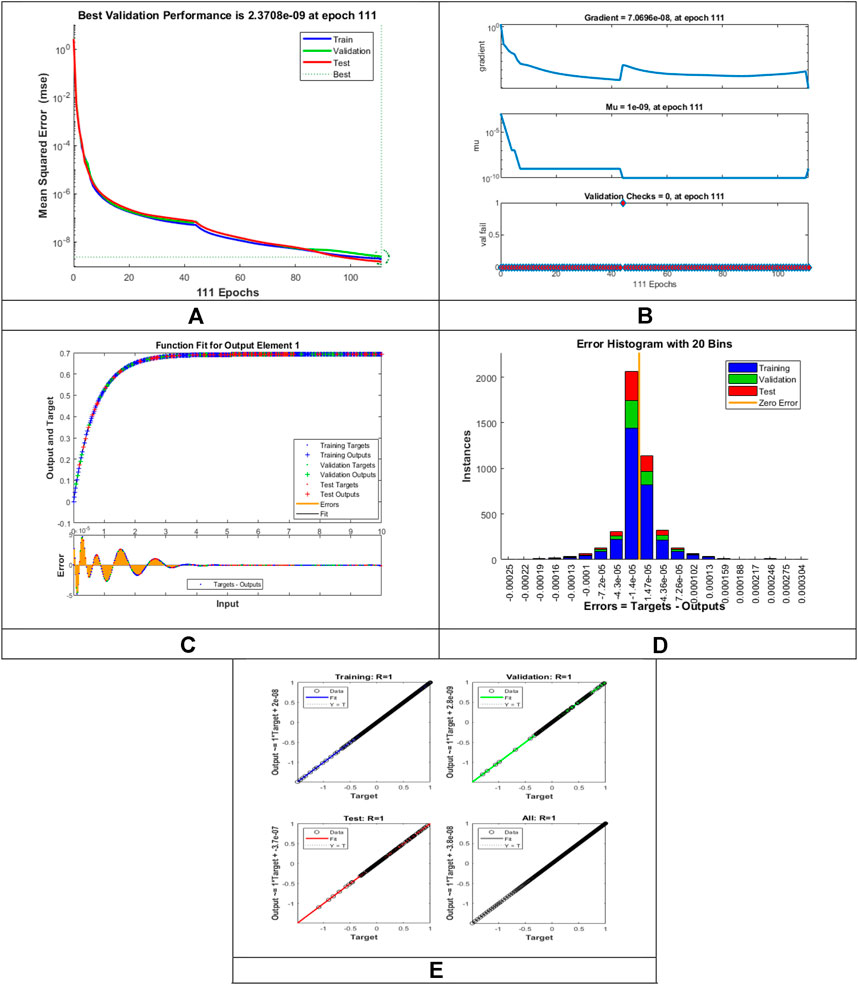
FIGURE 6. Pictorial illustration for the LMLA-BPNN base on variants of $\lambda vsf\prime \left(\eta \right)$ for MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, and (E) regression analysis.

FIGURE 7

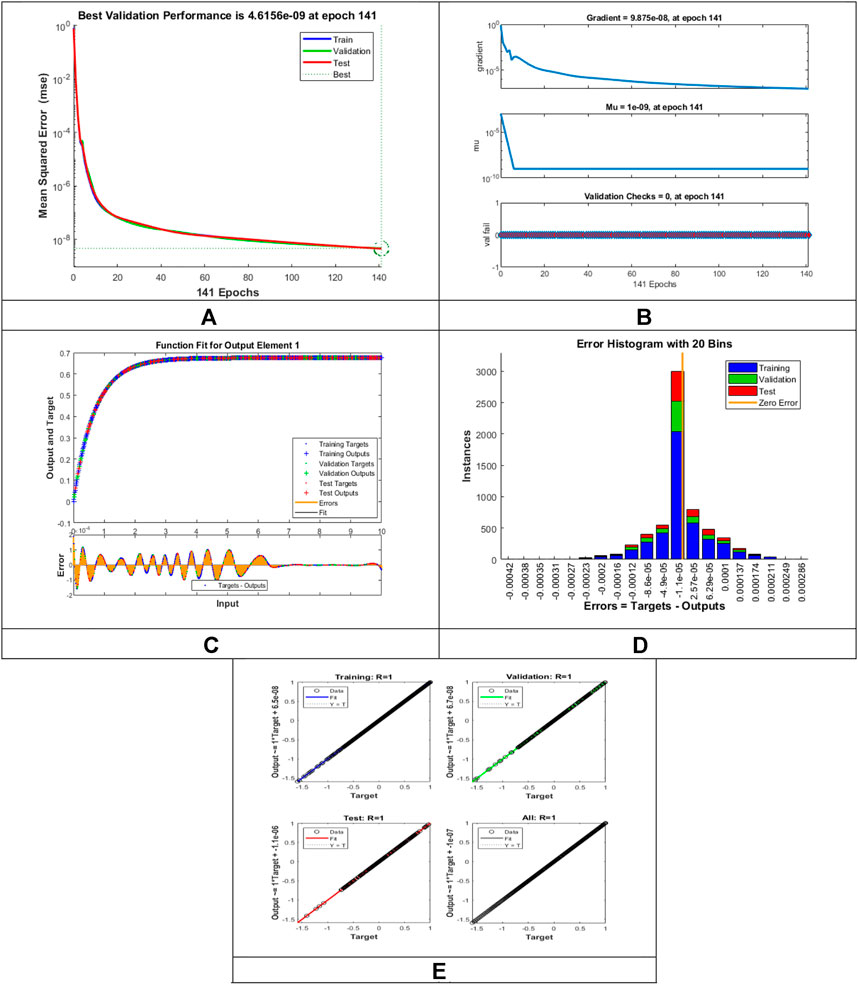
FIGURE 7. Pictorial illustration for the LMLA-BPNN base on variants of $Rvs\theta \left(\eta \right)$ for MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, and (E) regression analysis.

FIGURE 8

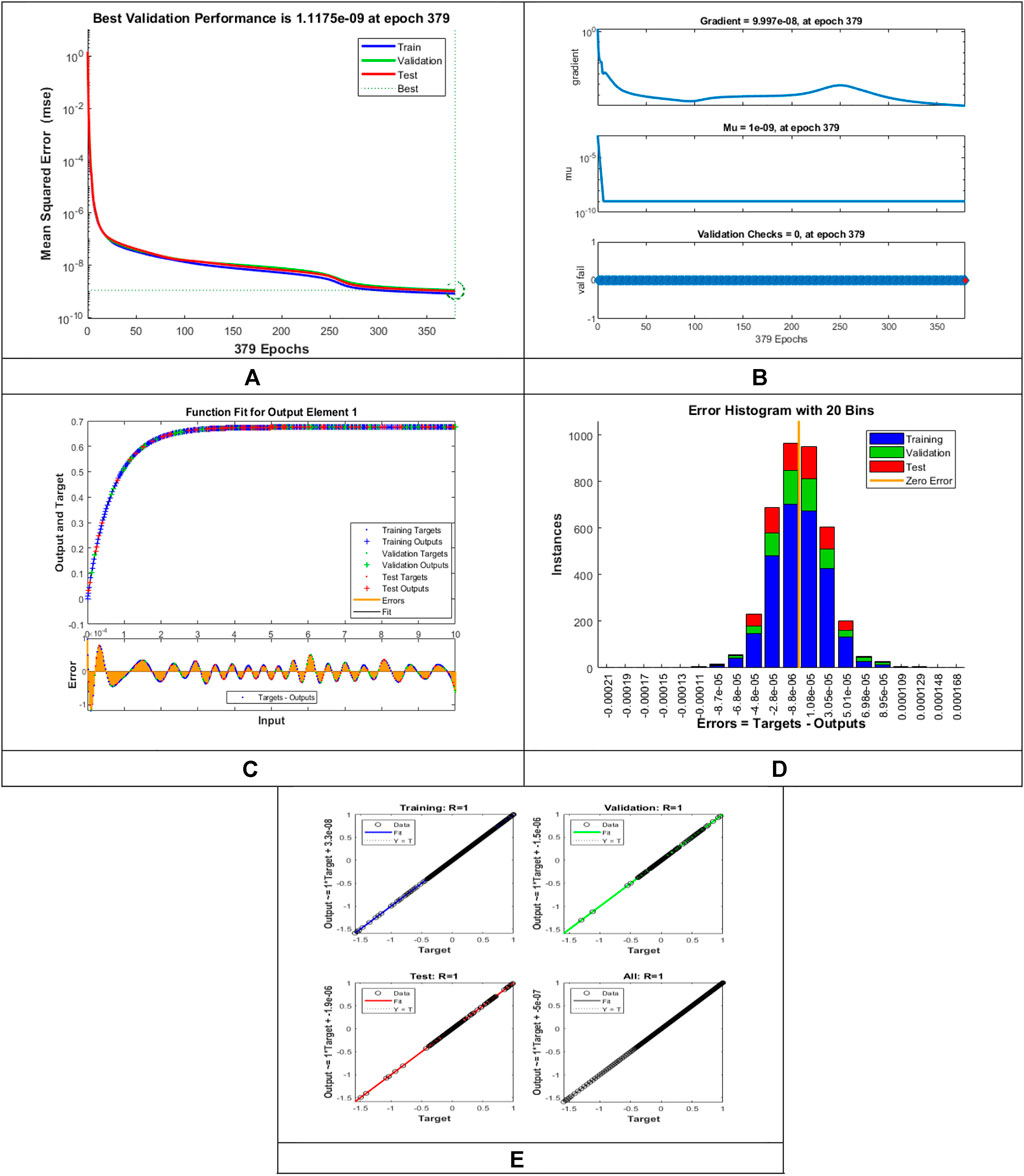
FIGURE 8. Pictorial illustration for the LMLA-BPNN base on variants of $Svs\theta \left(\eta \right)$ for MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, and (E) regression analysis.

FIGURE 9

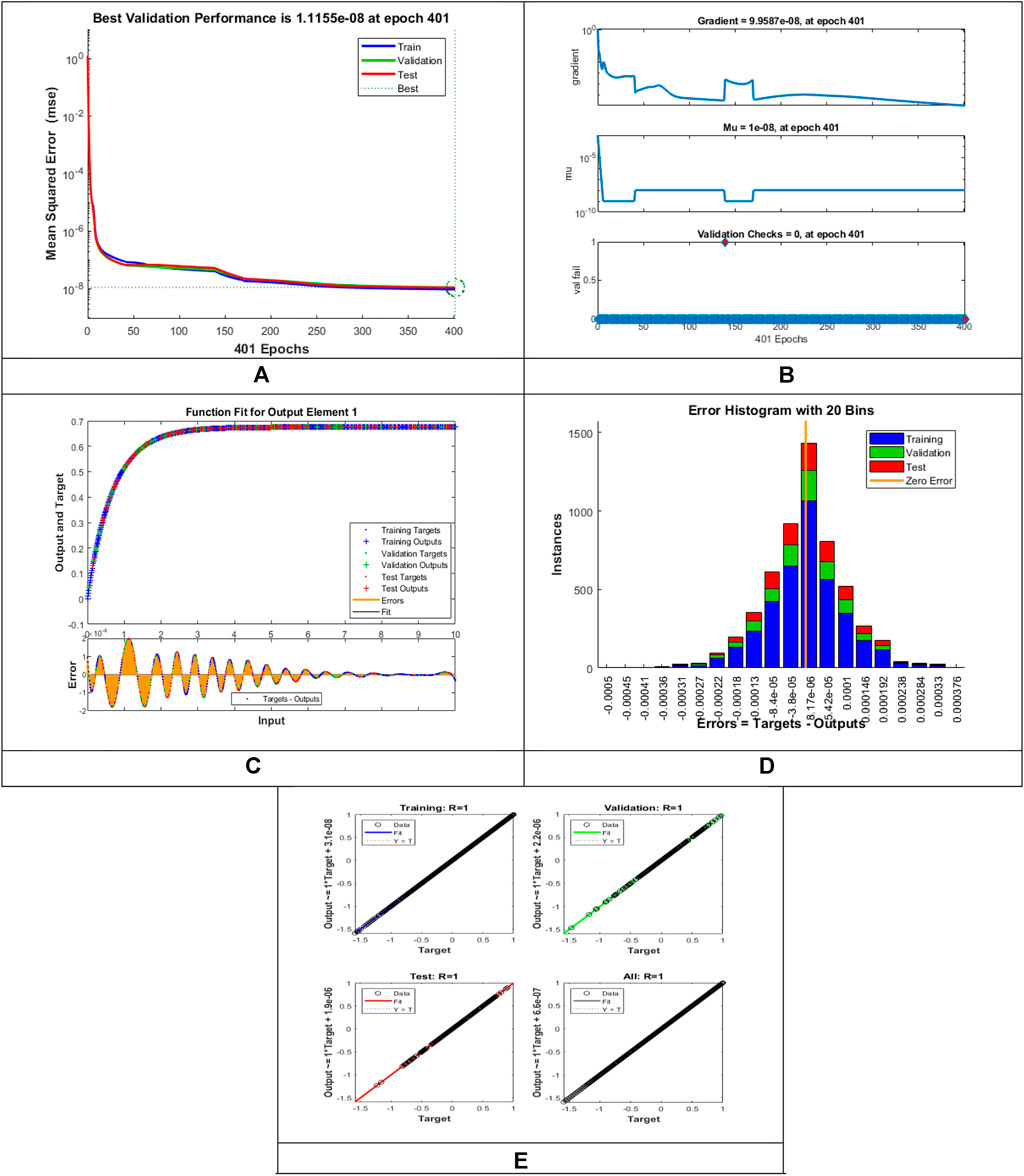
FIGURE 9. Pictorial illustration for the LMLA-BPNN base on variants of ${\theta }_{w}vs\theta \left(\eta \right)$ for MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, and (E) regression analysis.

FIGURE 10

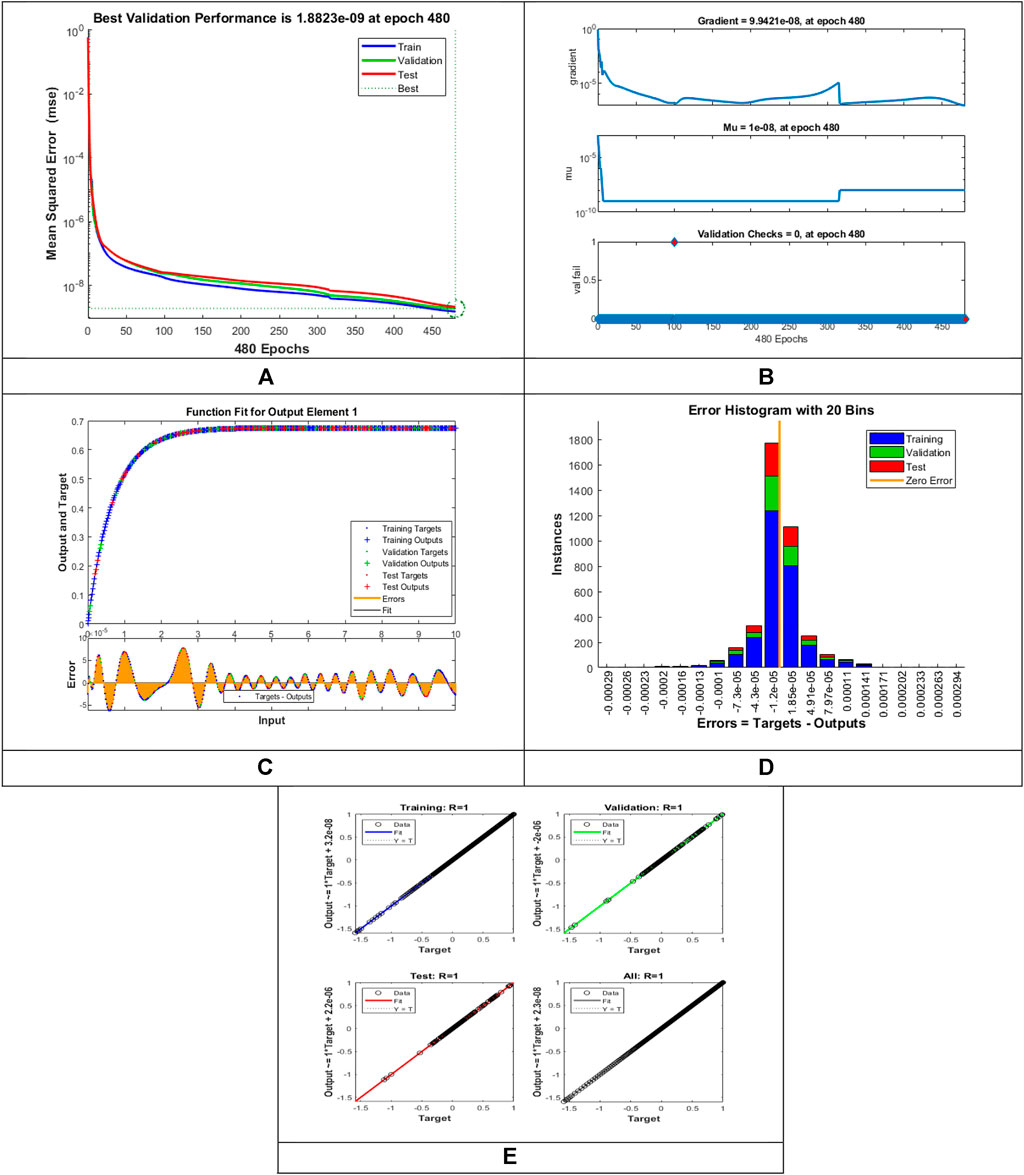
FIGURE 10. Pictorial illustration for the LMLA-BPNN base on variants of $Ntvs\varphi \left(\eta \right)$ for MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, and (E) regression analysis.

FIGURE 11

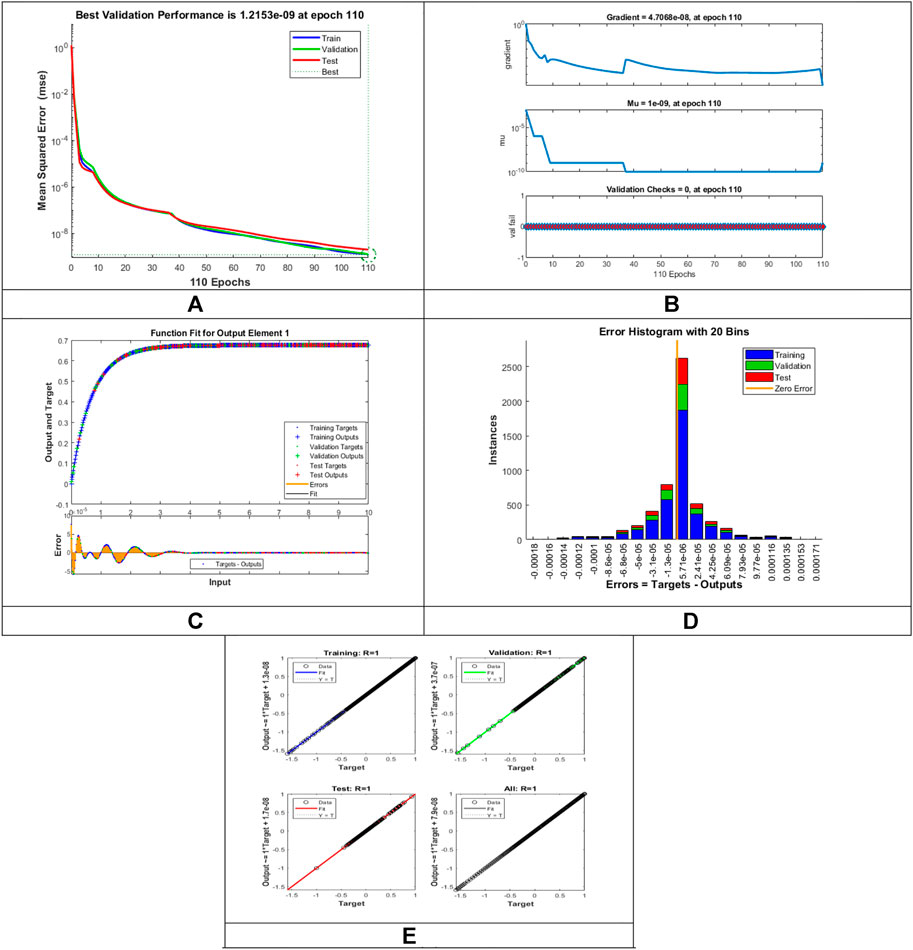
FIGURE 11. Pictorial illustration for the LMLA-BPNN base on variants of $\gamma vs\varphi \left(\eta \right)$ for MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, and (E) regression analysis.

FIGURE 12

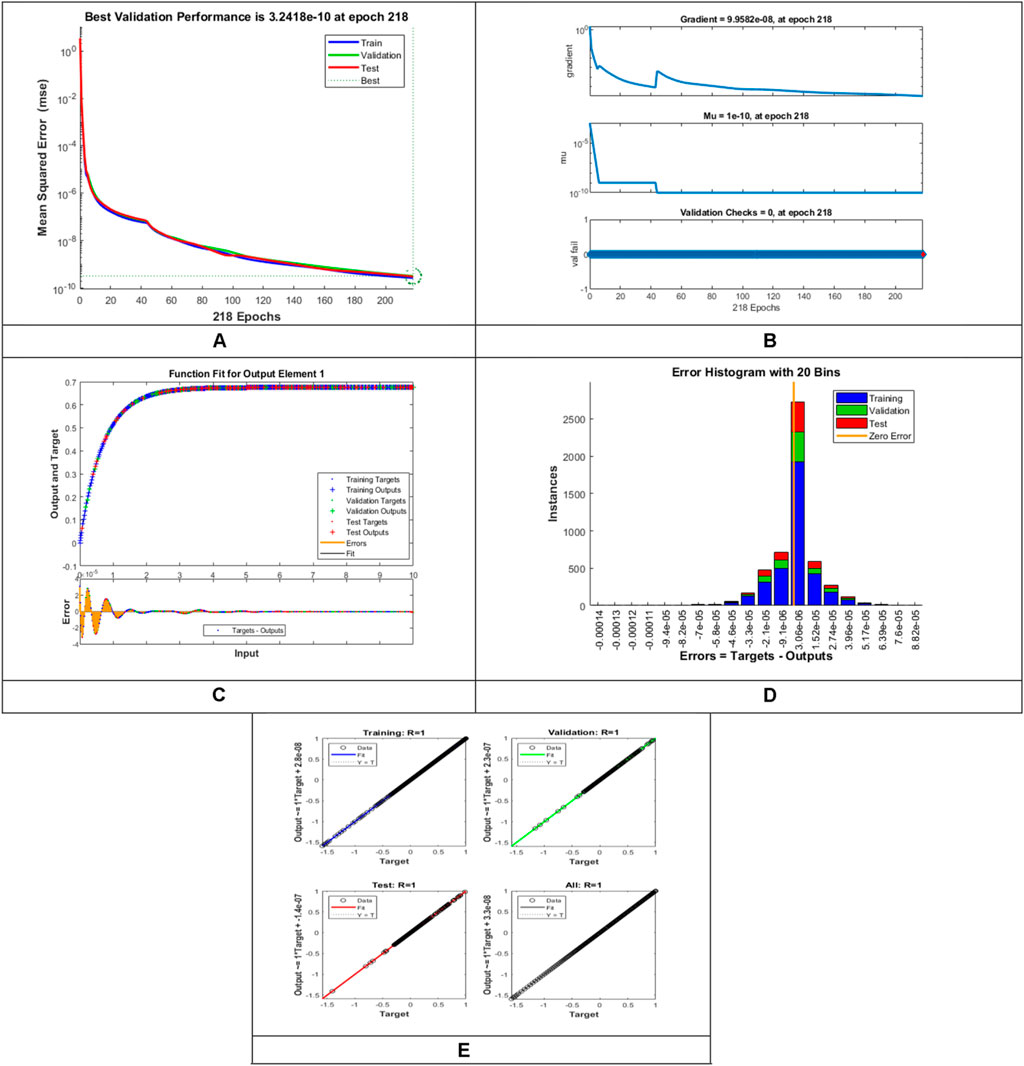
FIGURE 12. Pictorial illustration for the LMLA-BPNN base on variants of $Levs\varphi \left(\eta \right)$ for MHD-WNF-HGA. (A) M-S-E demonstration, (B) transition state analysis, (C) curve fitting, (D) error histogram, (E) and regression analysis.

FIGURE 13

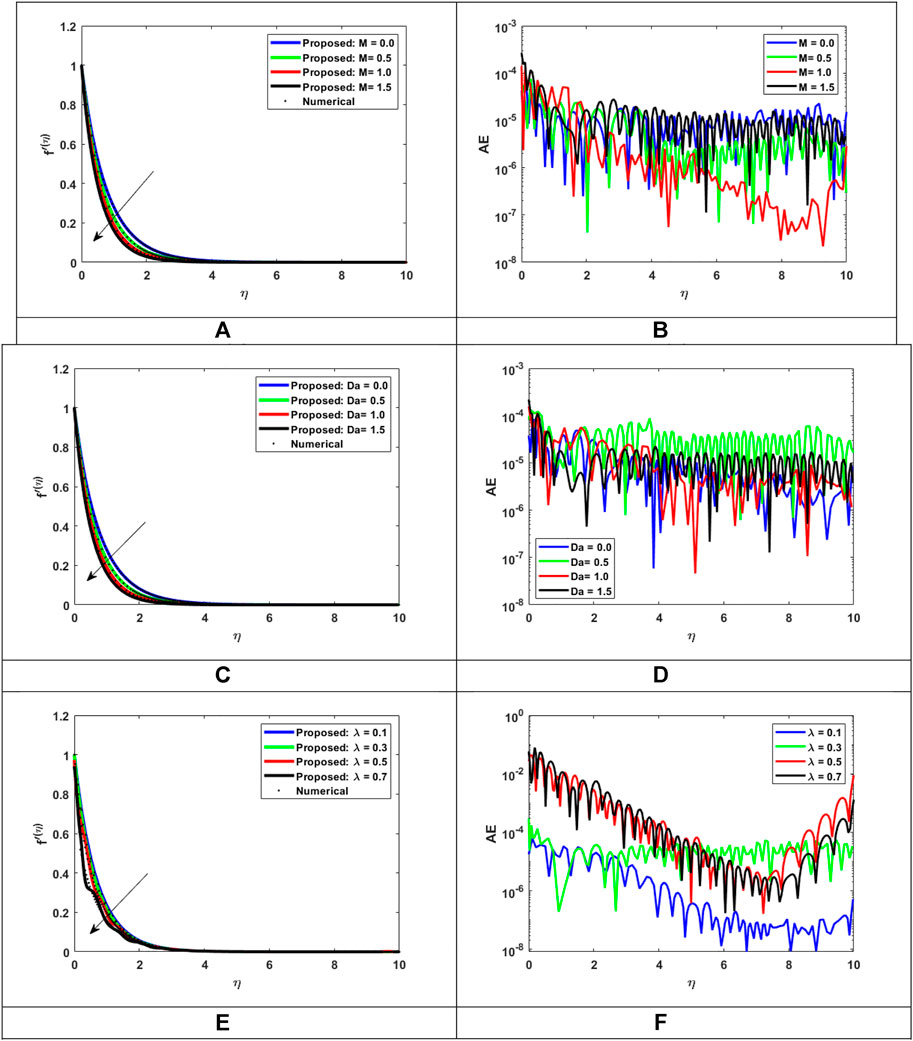
FIGURE 13. Assessment of LMLA-BPNN with reference dataset of MHD-WNF-HGA. (A) Variation of M for $f\prime \left(\eta \right)$, (B) AE for MHD-WNF-HGA, (C) Variation of $Da$ for $f^{\prime }\left(\eta \right)$, (D) AE for MHD-WNF-HGA, (E) Variation of $\lambda$ for $f\prime \left(\eta \right)$, (F) AE for MHD-WNF-HGA.

Figures 4C–13C represent the fitness analysis graphs for the proposed fluidic and the error occurred due to the variations of targeted solutions and reference solutions. The graphical representation indicates that the target result overlays the reference outlines of the LMLA-BPNN solver for all four cases with scenarios, indicating that the framework for the neural network (NN) design validates the accuracy of the solution.

After neural network training, the error histogram analysis plotted in Figures 4D–13D describes the distribution of error calculated from the zero axes. The error analysis and error values clarify the difference between the expected values and the targeted values. For six different scenarios of the LMLA-BPNN model, the average value of the error bin almost contrasts with the zero-line error adjoining. The average error bin comparing baseline line error which has surrounding errors for six different circumstances of the MHD-WNF-HGA model is $-5.1\times {10}^{-07}$, $6.39\times {10}^{-06}$, $1.47\times {10}^{-05}$, $-1.1\times {10}^{-05}$, $1.08\times {10}^{-05}$, $8.17\times {10}^{-06}$ $1.85\times {10}^{-05}$, $5.71\times {10}^{-06}$, and $3.06\times {10}^{-06}$. According to the error histogram analysis, the maximum number of error values collapse over the zero-line, indicating that LMLA-BPNN is an accurate algorithm for all the cases of each scenario. The network is next validated by creating a regression plot, which depicts the relationship between the network, outputs, and the target values. The network outputs and the target values would be exactly equal if the training is perfect. The results are shown in Figures 5E–13E. The three axes demonstrate the testing, validation, and training of the data. The perfect result-output = targets is shown in each axis of the dashed line. The solid line demonstrates the best fit linear regression line between the output values and target values, and the values of R indicate their relationship. During this computation, the regression analysis R = 1 indicates an exact linear relationship between the values of output and target values, which explains the effectiveness of LMLA-BPNN resolves the MHD-WNF-HGA fluidic model.

4.1 Velocity distributions

In the rheology of thermal radiation and chemical reaction with varying heat generation/absorption, the present work analyzes the Joule heating impact of MHD Williamson nanofluid flow through a porous layer. This research compares the effects of applied magnetic field, nonlinear thermal radiation, and heat generation/absorption. The system of partial differential equations (PDEs) is changed into a system of ordinary differential equations (ODEs) using the appropriate transformation to set an important nondimensional parameter arising in the physical fluid model and solved numerically by applying the “bvp4c” technique in MATLAB software to obtain the dataset. The numerical computation is performed for various nondimensional parameters, namely, non-Newtonian Williamson parameter $\left(\lambda \right)$, nonlinear thermal radiation parameter $\left(R\right)$, Eckert number $\left(Ec\right)$, ratio temperature $\left({\theta }_w\right)$, Darcy number $\left(Da\right)$, magnetic field parameter $\left(M\right)$, Brownian motion parameter $\left(Nb\right)$, heat generation/absorption parameter $\left(S\right)$, thermophoresis parameter $\left(Nt\right)$, Lewis number $\left(Le\right)$, Prandtl number $\left(\mathrm{Pr}\right)$, and chemical reaction parameter $\left(\gamma \right)$. For computation purpose, we have assumed default values for the physical quantities in all cases (unless, otherwise specified) as follows: $R=M=Da=Nt=Nb=0.5,$ $\lambda =0.3,$ $\gamma =Le=1.0,$ $Pr=5.0,$ and $S=-0.1$. The computational values of the diverse thermophysical properties are considered for fluid profiles, that is, momentum $\left(f\prime \left(\eta \right)\right)$, temperature $\left(\theta \left(\eta \right)\right)$, and concentration $\left(\varphi \left(\eta \right)\right)$ for magnetohydrodynamic (MHD) Williamson nanofluid flow over a stretching sheet, which is displayed in Figures 13–15. For numerical calculations, we used specific numerical values for parameters as shown in Table 2. The numerical finding of all the physical quantities with respect to flow distribution, energy distribution, and concentration distribution of nanoparticles along with their reference solution has been displayed with the help of graphical figures to obtain a good insight into the physical problem. The relative analysis of velocity distribution $f\left(\eta \right)$ with reference solution is displayed for magnetic field quantity $\left(M\right)$, non-Newtonian Williamson quantity $\left(\lambda \right)$, and Darcy number $\left(Da\right)$ in Figures 13A,C,E, respectively. A single surface’s flow rate is completely controlled by the velocity distribution. Velocity distribution plays a significant representation to analyze the occurrence of the flow rate of the fluid. Conversely, when external forces are applied to a flowing fluid, the behavior of the fluid changes, and one of these external forces is the magnetic force. Figure 13A displays the consequence of the influence of magnetic field $\left(M\right)$ on the flow profile $f\prime \left(\eta \right)$ of the fluid. It is observed that impact in this sense is lowered strongly due to an inverse relationship between velocity profile and magnetic field parameter. So by enhancing the influence of magnetic quantity means a decline in the flow speed of the fluid. When a magnetic field is used to influence a moving fluid, the particles of fluid stimulated causes a countervailing force called a resistive force, which slows and resists the motion of these fluids. Furthermore, this force is upright to both the magnetic field vector and the velocity vector which give rise to the resistive force, known as the Lorentz force generated in the direction of the fluid flow. As a result of the applied magnetic field, the Lorentz force emerges, opposing the flow and reducing fluid viscosity. The existence of a magnetic field causes a drag force, which causes to lower down the motion of the fluid. Figure 13C presents the impact of Darcy number $\left(Da\right)$ on velocity distribution. It is illustrated from the figure that the influence of larger values of $\left(Da\right)$ causes a decrease in velocity distribution. Physically, the porous media with a network of tiny voids known as pores that are disrupted by the fluids as it travels through this medium. Simultaneously, the porosity of a porous medium affects the permeability of the fluid through it. In addition, the higher the Darcy number $\left(Da\right)$, the larger the conflict of the porosity in permeable media which leads to the movement of fluid on one hand, and the fluid viscosity on the other hand, resulting a decline in fluid velocity. The association between the non-Newtonian Williamson parameter $\left(\lambda \right)$ and the velocity distribution is shown in Figure 13E. A rise in a non-Newtonian Williamson parameter $\left(\lambda \right)$ allows retardation in the velocity distribution $f\prime \left(\eta \right)$ which reduces the movement of fluid velocity. The absolute error (AE) analysis is shown in Figures 13B,D,F for $\left(M\right)$, $\left(Da\right)$, and $\left(\lambda \right)$ to verify the correctness criterion. The numeric output of AE for $\left(\epsilon \right)$ lies in the range ${10}^{-8}-{10}^{-3}$ , ${10}^{-8}-{10}^{-4}$, and ${10}^{-8}-{10}^{-1}$ for $\left(M\right)$, $\left(Da\right)$, and $\left(\lambda \right)$ with respect to $f\prime \left(\eta \right)$, respectively. The absolute error numeric result with the reference outputs shows the satisfactory accuracy criteria.

FIGURE 14

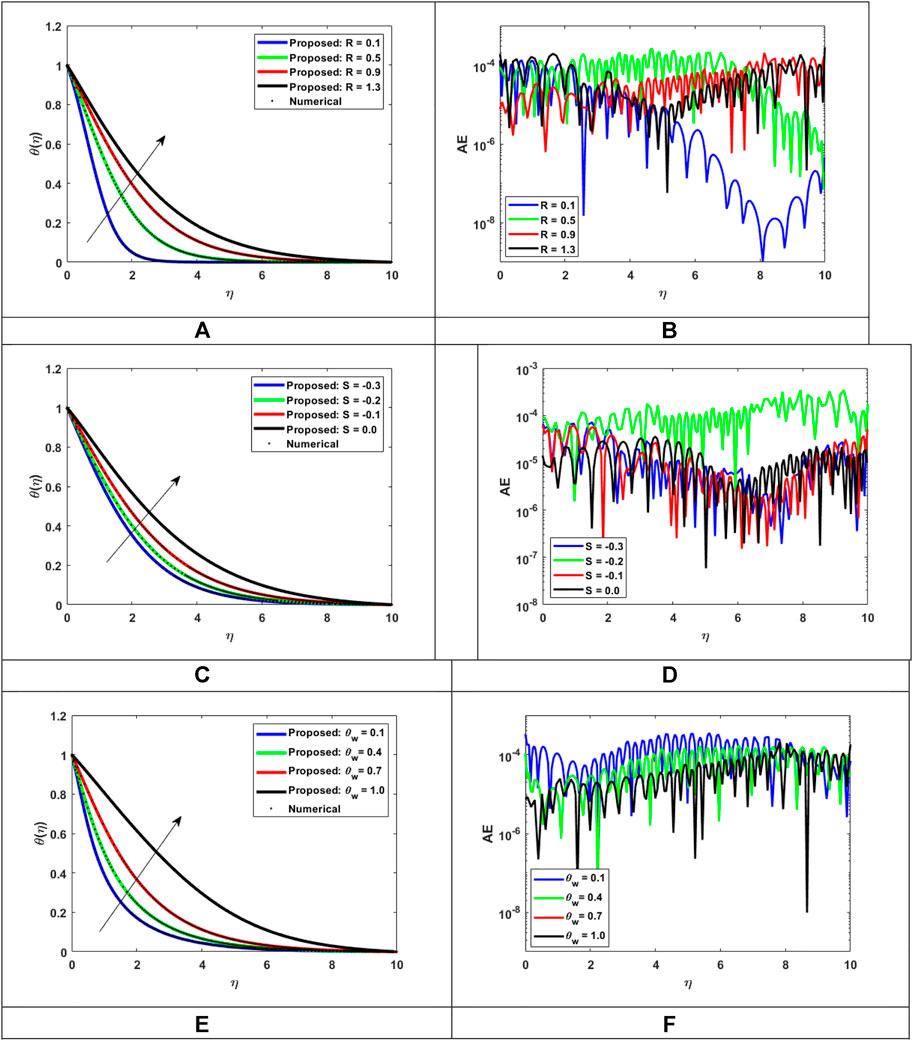
FIGURE 14. Assessment of LMLA-BPNN along the reference dataset of MHD-WNF-HGA. (A) Variation of $R$ for $\theta \left(\eta \right)$, (B) AE for MHD-WNF-HGA, (C) Variation of $S$ for $\theta \left(\eta \right)$, (D) AE for MHD-WNF-HGA, (E) Variation of ${\theta }_w$ for $\theta \left(\eta \right)$, (F) with AE for MHD-WNF-HGA.

FIGURE 15

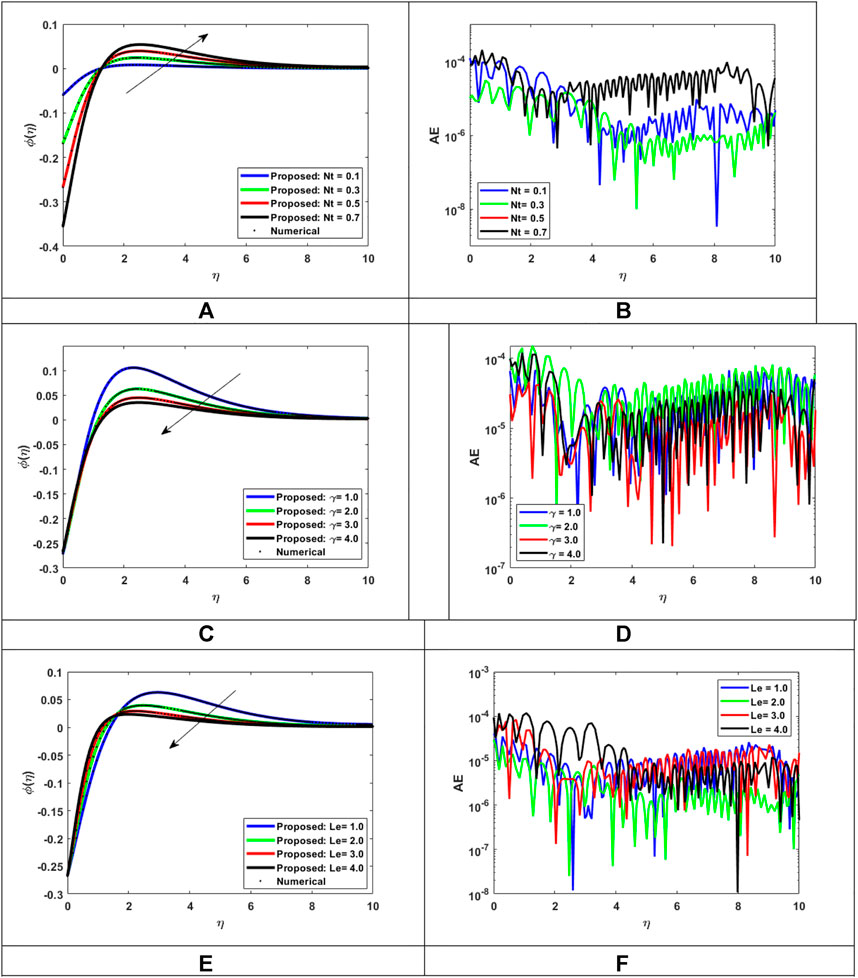
FIGURE 15. Assessment of LMLA-BPNN along the reference dataset of MHD-WNF-HGA. (A) Variation of $N_t$ for $\varphi \left(\eta \right)$, (B) AE for MHD-WNF-HGA, (C) Variation of $\gamma$ for $\varphi \left(\eta \right)$, (D) AE for MHD-WNF-HGA, (E) variation of $L_e$ for $\varphi \left(\eta \right)$, (F) AE for MHD-WNF-HGA.

TABLE 2

TABLE 2. Variant of MHD-WNF-HGA.

4.2 Temperature distributions

Fluid temperature distribution $\theta \left(\eta \right)$ has a considerable influence on the behavior of fluids and the impact on the particles within the fluid. Figures 14A,C,E show the comparison with a reference solution for various values of nonlinear thermal radiation parameter $\left(R\right)$, heat generation/absorption parameter $\left(S\right)$, and ratio temperature $\left({\theta }_w\right)$. Figure 14A exemplifies the differences in temperature distribution $\theta \left(\eta \right)$ with altered values of nonlinear thermal radiation parameter $\left(R\right)$. The temperature profile increased with upsurging values of the nonlinear thermal radiation parameter. The heat transfer rate inside the flow regime is higher and it works to simulate the fluid flow. The nonlinear thermal radiation parameter has three physical effects on the heat transmission of the nanofluid. First, the temperature of the boundary layer is raised on a regular basis. Second, the flow regime’s nanoparticles acquire thermal energy, enhancing thermal diffusion and heat transmission within the fluid owing to the thermal conductivity of the nanoparticles.

Finally, it aims to improve the thermal transfer techniques of nanofluids, specifically the thermal transfer method by load and by conduction. Figure 14C shows fluid temperature distribution $\theta \left(\eta \right)$ with different values of heat generation/absorption parameter $\left(S\right)$. Due to the rise in numerical values of the generation/absorption parameter, a huge rise in the fluid heat transfer is seen. There is a physical increase in the thermal dispersion and transfer of the fluids when heat is generated, which raises the temperature of the fluids. Also, with an increase in the heat source type $\left(S>0\right)$ values, the thickness of the boundary layer and the fluid temperature are likewise upsurges, while an opposite behavior occurs in the case of the heat absorption type $\left(S<0\right)$. However, when moving upward from the state of heat absorption to generation, there is reformation in boundary layer thickness and thermal diffusion. Figure 14E investigates the disparities in temperature distribution $\theta \left(\eta \right)$ with improved values of the ratio temperature parameter $\left({\theta }_w\right)$. The temperature profile increased with the enhancing ratio temperature parameter $\left({\theta }_w\right)$. This effect enhances the temperature of the boundary layer and increases its thickness. The absolute error tool is shown in Figures 14B,D,E for $\left(R\right)$, $\left(S\right)$, and $\left({\theta }_w\right)$ to check the accuracy criteria, respectively. The values of AE are in the ranges ${10}^{-9}-{10}^{-4}$ , ${10}^{-7}-{10}^{-3}$, and ${10}^{-7}-{10}^{-3}$ for $\theta \left(\eta \right)$. The absolute error numeric result with the reference outputs shows the satisfactory accuracy criteria.

4.3 Concentration of nanoparticle distribution

To examine the physical properties of the concentration of nanoparticles within the fluids, it is important to study the nomenclature and application of the fluids. The effectiveness and intensity of thermal and electrical conductivity, for instance, are correlated with the concentration of nanoparticles while studying fluid behavior. The relative analysis of nanoparticles concentration distribution $\varphi \left(\eta \right)$ with reference result is illustrated in Figures 15B,D,E) for $\left(Nt\right)$, $\left(\gamma \right)$, and $\left(Le\right)$. Figure 15A investigates the effect of the thermophoresis parameter $\left(Nt\right)$ with respect to the concentration of nanoparticle distribution $\varphi \left(\eta \right)$ within the flow regime of the fluid. As the thermophoresis parameter increases, the concentration of nanoparticle distribution enhances, the rate of heat transfer in the boundary layer increases, provoking particle deposition away from the fluid regime and therefore enhancing the concentration of the nanofluid particles. The effect of the chemical reaction parameter $\left(\gamma \right)$ and Lewis number $\left(Le\right)$ on the concentration of nanoparticles distribution $\varphi \left(\eta \right)$ is illustrated in Figures 15C,E, respectively. A significant decrease is observed with the rise in the chemical reaction parameter $\left(\gamma \right)$ and Lewis number $\left(Le\right)$. The absolute error (AE) analysis of $\left(Nt\right)$, $\left(\gamma \right)$, and $\left(Le\right)$ on nanoparticle concentration distribution $\varphi \left(\eta \right)$ are shown in Figures 11B,D,F to check the accuracy criteria, respectively. The AE values lies between ${10}^{-8}-{10}^{-3}$, ${10}^{-7}-{10}^{-3}$, and ${10}^{-8}-{10}^{-3}$ for $\varphi \left(\eta \right)$. The absolute error numeric result with the reference outputs shows the satisfactory accuracy criteria.

5 Conclusion

This research used the Levenberg–Marquardt neural network technique with backpropagation to solve the magnetohydrodynamic Williamson nanofluid flow through a stretched surface under the effects of nonlinear thermal radiation, Joule heating, heat generation/absorption, and chemical reaction (MHD-WNF-HGA). The solution of a mathematical model exhibiting (MHD-WNF-HGA) was examined with the adjustment of certain circumstances (scenarios). The bvp4c approach is used to build the dataset for the MHD-WNF-HGA model, which contains deviations from a variety of physical measurements such as the Williamson parameter, thermal radiation parameter, magnetic parameter, Eckert number, Darcy number, Brownian motion, and thermophoresis parameter. The MHD-WNF-HGA reference dataset is made up of various versions, with LMLA-BPNN training, testing, and validation accounting for 80, 10, and 10% of the dataset, respectively.

The important findings of the present investigations are as follows.

• Fluid flow speed drops when magnetic force and Darcy law are applied to the flow. Also, Williamson fluid velocity is high for the lower values but as the values rise, the velocity drop with speed.

• The temperature distribution elevates with the help of the thermal radiation parameter, heat generation absorption parameter, and temperature ration parameter.

• The thermophoresis effect enhances the strength of nanofluid concentration, while the chemical reaction quantity and Lewis number weaken the concentration strength.

Furthermore

The mean square error is anticipated to be in the average range of 10⁻⁵ for LMLA-BPNN when comparing the reference solution to the suggested data, which shows the close agreement between both.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The author would like to extend his appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through the Research Group Program under the grant No. RGP.2/12/43.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Acharya, N., Das, K., and Kundu, P. K. (2019). Influence of multiple slips and chemical reaction on radiative MHD Williamson nanofluid flow in porous medium: A computational framework. Multidiscip. Model. Mater. Struct. 15 (3), 630–658. doi:10.1108/MMMS-08-2018-0152

CrossRef Full Text | Google Scholar

Adnan, , Khan, U., and Ahmed, N. (2022). Thermal enhancement and entropy investigation in dissipative ZnO-SAE50 under thermal radiation: A computational paradigm. Waves Random Complex Media, 1–16. doi:10.1080/17455030.2022.2053243

CrossRef Full Text | Google Scholar

Ahmed, N., Khan, U., Mohyud-Din, S. T., Khan, I., Murtaza, R., Hussain, I., et al. (2020). A novel investigation and hidden effects of MHD and thermal radiations in viscous dissipative nanofluid flow models. Front. Phys. 8, 75. doi:10.3389/fphy.2020.00075

CrossRef Full Text | Google Scholar

Ahmed, S., Ahshan, K. H., Mondal, M., Alam, N., and Hossain, S. (2021). Application of metal oxides-based nanofluids in PV/T systems: A review. Front. Energy, 1–32. doi:10.1007/s11708-021-0758-8

CrossRef Full Text | Google Scholar

Al-Mubaddel, F. S., Allehiany, F. M., Nofal, T. A., Alam, M. M., Ali, A., Asamoah, J. K. K., et al. (2022). Rheological model for generalized energy and mass transfer through hybrid nanofluid flow comprised of magnetized cobalt ferrite nanoparticles. J. Nanomater. 2022, 1–11. doi:10.1155/2022/7120982

CrossRef Full Text | Google Scholar

Alhowaity, A., Bilal, M., Hamam, H., Alqarni, M. M., Mukdasai, K., Ali, A., et al. (2022a). Non-Fourier energy transmission in power-law hybrid nanofluid flow over a moving sheet. Sci. Rep. 12 (1), 10406. doi:10.1038/s41598-022-14720-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Alhowaity, A., Hamam, H., Bilal, M., and Ali, A. (2022b). “Numerical study of Williamson hybrid nanofluid flow with thermal characteristics past over an extending surface,” in Heat transfer (United States: Wiley Online Library). doi:10.1002/htj.22616

CrossRef Full Text | Google Scholar

Alsallami, S. A., Zahir, H., Muhammad, T., Hayat, A. U., Khan, M. R., and Ali, A. (2022). Numerical simulation of Marangoni Maxwell nanofluid flow with Arrhenius activation energy and entropy anatomization over a rotating disk. Waves Random Complex Media, 1–19. doi:10.1080/17455030.2022.2045385

CrossRef Full Text | Google Scholar

Ashraf, W., Khan, U., Al-Johani, A. S., Ahmed, N., Mohyud-Din, S. T., Khan, I., et al. (2022). Impact of freezing temperature (T_fr) of Al₂O₃ and molecular diameter (H₂O)_d on thermal enhancement in magnetized and radiative nanofluid with mixed convection. Sci. Rep. 12, 703. doi:10.1038/s41598-021-04587-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Ayub, A., Darvesh, A., Altamirano, G. C., and Sabir, Z. (2021). Nanoscale energy transport of inclined magnetized 3D hybrid nanofluid with Lobatto IIIA scheme. Heat. Transf. 50 (7), 6465–6490. doi:10.1002/htj.22188

CrossRef Full Text | Google Scholar

Ayub, A., Sabir, Z., Le, D. N., and Aly, A. A. (2021). Nanoscale heat and mass transport of magnetized 3-D chemically radiative hybrid nanofluid with orthogonal/inclined magnetic field along rotating sheet. Case Stud. Therm. Eng. 26, 101193. doi:10.1016/j.csite.2021.101193

CrossRef Full Text | Google Scholar

Ayub, A., Sabir, Z., Shah, S. Z. H., Mahmoud, S. R., Algarni, A., Sadat, R., et al. (2022). Aspects of infinite shear rate viscosity and heat transport of magnetized Carreau nanofluid. Eur. Phys. J. Plus 137 (2), 247. doi:10.1140/epjp/s13360-022-02410-6

CrossRef Full Text | Google Scholar

Blasius, H. (1950). The boundary layers in fluids with little friction. Zeitschrift für hermosct und hermo, 56(NACA-TM-1256).

Google Scholar

Botmart, T., Sabir, Z., Raja, M. A. Z., Weera, W., Sadat, R., Ali, M. R., et al. (2022). A numerical study of the fractional order dynamical nonlinear susceptible infected and quarantine differential model using the stochastic numerical approach. Fractal Fract. 6 (3), 139. doi:10.3390/fractalfract6030139

CrossRef Full Text | Google Scholar

Bouslimi, J., Omri, M., Mohamed, R. A., Mahmoud, K. H., Abo-Dahab, S. M., Soliman, M. S., et al. (2021). MHD Williamson nanofluid flow over a stretching sheet through a porous medium under effects of joule heating, nonlinear thermal radiation, heat generation/absorption, and chemical reaction. Adv. Math. Phys. 2021, 1–16. doi:10.1155/2021/9950993

CrossRef Full Text | Google Scholar

Cengel, Y. A., and Boles, M. A. (2015). Gas-vapor mixtures and air-conditioning. Thermodynamics and engineering approach. 8th ed. New York, NY, USA: McGraw-Hill, 725–729.

Google Scholar

Cengel, Y., and Heat, T. M. (2003). A practical approach. New York, NY, USA: McGraw-Hill.

Google Scholar

Choi, S. U. S., Singer, D. A., and Wang, H. P. (1995). Developments and applications of non-Newtonian flows. Asme Fed. 66, 99–105.

Google Scholar

Das, S. K., Choi, S. U., and Patel, H. E. (2006). Heat transfer in nanofluids—A review. Heat. Transf. Eng. 27 (10), 3–19. doi:10.1080/01457630600904593

CrossRef Full Text | Google Scholar

Elattar, S., Helmi, M. M., Elkotb, M. A., El-Shorbagy, M. A., Abdelrahman, A., Bilal, M., et al. (2022). Computational assessment of hybrid nanofluid flow with the influence of hall current and chemical reaction over a slender stretching surface. Alexandria Eng. J. 61 (12), 10319–10331. doi:10.1016/j.aej.2022.03.054

CrossRef Full Text | Google Scholar

Esfe, M. H., Kamyab, M. H., and Toghraie, D. (2022). Statistical review of studies on the estimation of thermophysical properties of nanofluids using artificial neural network (ANN). Powder Technol. 400 (5), 117210. doi:10.1016/j.powtec.2022.117210

CrossRef Full Text | Google Scholar

González, A., Ruz, O., and Castillo, E. (2021). Numerical study of the fluid dynamics and heat transfer for shear-thinning nanofluids in a micro pin-fin heat sink. Case Stud. Therm. Eng. 28, 101635. doi:10.1016/j.csite.2021.101635

CrossRef Full Text | Google Scholar

Goodarzi, H., Akbari, O. A., Sarafraz, M. M., Karchegani, M. M., Safaei, M. R., Sheikh Shabani, G. A., et al. (2019). Numerical simulation of natural convection heat transfer of nanofluid with Cu, MWCNT, and Al₂O₃ nanoparticles in a cavity with different aspect ratios. J. Therm. Sci. Eng. Appl. 11 (6), 061020. doi:10.1115/1.4043809

CrossRef Full Text | Google Scholar

Hamid, A., and Khan, M. (2019). Multiple solutions for MHD transient flow of Williamson nanofluids with convective heat transport. J. Taiwan Inst. Chem. Eng. 103, 126–137. doi:10.1016/j.jtice.2019.07.001

CrossRef Full Text | Google Scholar

Ibrahim, W., and Gamachu, D. (2019). Nonlinear convection flow of Williamson nanofluid past a radially stretching surface. AIP Adv. 9 (8), 085026. doi:10.1063/1.5113688

CrossRef Full Text | Google Scholar

Incropera, F. P., DeWitt, D. P., Bergman, T. L., and Lavine, A. S. (1996). Fundamentals of heat and mass transfer, 6. New York: Wiley, 116.

Google Scholar

Irandoost Shahrestani, M., Houshfar, E., Ashjaee, M., and Allahvirdizadeh, P. (2021). Convective heat transfer and pumping power analysis of MWCNT+ Fe3O4/water hybrid nanofluid in a helical coiled heat exchanger with orthogonal rib turbulators. Front. Energy Res. 9, 630805. doi:10.3389/fenrg.2021.630805

CrossRef Full Text | Google Scholar

Khan, M. I., Qayyum, S., Hayat, T., Khan, M. I., and Alsaedi, A. (2019). Entropy optimization in flow of Williamson nanofluid in the presence of chemical reaction and Joule heating. Int. J. Heat Mass Transf. 133, 959–967. doi:10.1016/j.ijheatmasstransfer.2018.12.168

CrossRef Full Text | Google Scholar

Khan, M. J., Duraisamy, B., Zuhra, S., Nawaz, R., Nisar, K. S., Jamshed, W., et al. (2021). Numerical solution of Catteno-Christov heat flux model over stretching/shrinking hybrid nanofluid by new iterative method. Case Stud. Therm. Eng. 28, 101673. doi:10.1016/j.csite.2021.101673

CrossRef Full Text | Google Scholar

Khan, N. S., Gul, T., Kumam, P., Shah, Z., Islam, S., Khan, W., et al. (2019). Influence of inclined magnetic field on Carreau nanoliquid thin film flow and heat transfer with graphene nanoparticles. Energies 12 (8), 1459. doi:10.3390/en12081459

CrossRef Full Text | Google Scholar

Khan, N. S., Zuhra, S., Shah, Z., Bonyah, E., Khan, W., Islam, S., et al. (2018). Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv. 8 (11), 115302. doi:10.1063/1.5055690

CrossRef Full Text | Google Scholar

Khan, U., Ahmed, N., Mohyud-Din, S. T., Hamadneh, N. N., Khan, I., and Andualem, M. (2021). The dynamics of H2O suspended by multiple Shaped Cu nanoadditives in rotating system. J. Nanomater. 2022, 1–11. doi:10.1155/2021/7299143

CrossRef Full Text | Google Scholar

Khan, U., Ahmed, N., and Mohyud-Din, S. T. (2020). Surface thermal investigation in water functionalized Al2O3 and γAl2O3 nanomaterials-based nanofluid over a sensor surface. Appl. Nanosci., 1–11. doi:10.1007/s13204-020-01527-3

CrossRef Full Text | Google Scholar

Kumar, M. A., Reddy, Y. D., Rao, V. S., and Goud, B. S. (2021). Thermal radiation impact on MHD heat transfer natural convective nano fluid flow over an impulsively started vertical plate. Case Stud. Therm. Eng. 24, 100826. doi:10.1016/j.csite.2020.100826

CrossRef Full Text | Google Scholar

Mahdi, J. M., Lohrasbi, S., and Nsofor, E. C. (2019). Hybrid heat transfer enhancement for latent-heat thermal energy storage systems: A review. Int. J. Heat Mass Transf. 137, 630–649. doi:10.1016/j.ijheatmasstransfer.2019.03.111

CrossRef Full Text | Google Scholar

Maxwell, J. C. (1881). “A treatise on electricity and magnetism: Pt. III,” in Magnetism. Pt. IV. Electromagnetism (England: Clarendon Press), 2.

Google Scholar

Meseguer, J., Pérez-Grande, I., and Sanz-Andrés, A. (2012). Spacecraft thermal control. Sawston, Cambridge: Elsevier.

Google Scholar

Okonkwo, E. C., Abid, M., and Ratlamwala, T. A. (2018). Numerical analysis of heat transfer enhancement in a parabolic trough collector based on geometry modifications and working fluid usage. J. Sol. Energy Eng. 140 (5). doi:10.1115/1.4040076

CrossRef Full Text | Google Scholar

Okonkwo, E. C., Wole-Osho, I., Almanassra, I. W., Abdullatif, Y. M., and Al-Ansari, T. (2021). An updated review of nanofluids in various heat transfer devices. J. Therm. Anal. Calorim. 145 (6), 2817–2872. doi:10.1007/s10973-020-09760-2

CrossRef Full Text | Google Scholar

Pandya, N. S., Shah, H., Molana, M., and Tiwari, A. K. (2020). Heat transfer enhancement with nanofluids in plate heat exchangers: A comprehensive review. Eur. J. Mech. - B/Fluids 81, 173–190. doi:10.1016/j.euromechflu.2020.02.004

CrossRef Full Text | Google Scholar

Pare, A., and Ghosh, S. K. (2021). A unique thermal conductivity model (ANN) for nanofluid based on experimental study. Powder Technol. 377, 429–438. doi:10.1016/j.powtec.2020.09.011

CrossRef Full Text | Google Scholar

Raja, M. A. Z., Khan, Z., Zuhra, S., Chaudhary, N. I., Khan, W. U., He, Y., et al. (2021). Cattaneo-christov heat flux model of 3D hall current involving biconvection nanofluidic flow with Darcy-Forchheimer law effect: Backpropagation neural networks approach. Case Stud. Therm. Eng. 26, 101168. doi:10.1016/j.csite.2021.101168

CrossRef Full Text | Google Scholar

Raja, M. A. Z., Shoaib, M., Khan, Z., Zuhra, S., Saleel, C. A., Nisar, K. S., et al. (2022). Supervised neural networks learning algorithm for three dimensional hybrid nanofluid flow with radiative heat and mass fluxes. Ain Shams Eng. J. 13 (2), 101573. doi:10.1016/j.asej.2021.08.015

CrossRef Full Text | Google Scholar

Rasool, G., Zhang, T., Chamkha, A. J., Shafiq, A., Tlili, I., Shahzadi, G., et al. (2019). Entropy generation and consequences of binary chemical reaction on MHD Darcy–Forchheimer Williamson nanofluid flow over non-linearly stretching surface. Entropy 22 (1), 18. doi:10.3390/e22010018

PubMed Abstract | CrossRef Full Text | Google Scholar

Sabir, Z., Raja, M. A. Z., Nguyen, T. G., Fathurrochman, I., Sadat, R., Ali, M. R., et al. (2022). Gudermannian neural networks using the optimization procedures of genetic algorithm and active set approach for the three-species food chain nonlinear model. J. Ambient. Intell. Humaniz. Comput., 1–10. doi:10.1007/s12652-021-03638-3

CrossRef Full Text | Google Scholar

Sadeghi, G., Nazari, S., Ameri, M., and Shama, F. (2020). Energy and exergy evaluation of the evacuated tube solar collector using Cu2O/water nanofluid utilizing ANN methods. Sustain. Energy Technol. Assessments 37, 100578. doi:10.1016/j.seta.2019.100578

CrossRef Full Text | Google Scholar

Sajid, M. U., and Ali, H. M. (2019). Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev. 103, 556–592. doi:10.1016/j.rser.2018.12.057

CrossRef Full Text | Google Scholar

Sakiadis, B. C. (1961). Boundary-layer behavior on continuous solid surfaces: I. Boundary-Layer equations for two-dimensional and axisymmetric flow. AIChE J. 7 (1), 26–28. doi:10.1002/aic.690070108

CrossRef Full Text | Google Scholar

Shah, S. L., Ayub, A., Dehraj, S., Wahab, H. A., Sagayam, K. M., Ali, M. R., et al. (2022). Magnetic dipole aspect of binary chemical reactive Cross nanofluid and heat transport over composite cylindrical panels. Waves Random Complex Media, 1–24. doi:10.1080/17455030.2021.2020373

CrossRef Full Text | Google Scholar

Shah, S. Z. H., Ayub, A., Sabir, Z., Adel, W., Shah, N. A., Yook, S. J., et al. (2021). Insight into the dynamics of time-dependent cross nanofluid on a melting surface subject to cubic autocatalysis. Case Stud. Therm. Eng. 27, 101227. doi:10.1016/j.csite.2021.101227

CrossRef Full Text | Google Scholar

Shah, Z., Raja, M. A. Z., Chu, Y. M., Khan, W. A., Abbas, S. Z., Shoaib, M., et al. (2021). Computational intelligence of Levenberg-Marquardt backpropagation neural networks to study the dynamics of expanding/contracting cylinder for cross magneto-nanofluid flow model. Phys. Scr. 96 (5), 055219. doi:10.1088/1402-4896/abe068

CrossRef Full Text | Google Scholar

Shah, Z., Tassaddiq, A., Islam, S., Alklaibi, A. M., and Khan, I. (2019). Cattaneo–Christov heat flux model for three-dimensional rotating flow of SWCNT and MWCNT Nanofluid with Darcy–Forchheimer porous medium induced by a linearly stretchable surface. Symmetry 11 (3), 331. doi:10.3390/sym11030331

CrossRef Full Text | Google Scholar

She, L., and Fan, G. (2018). Numerical simulation of flow and heat transfer characteristics of CuO-water nanofluids in a flat tube. Front. Energy Res. 6, 57. doi:10.3389/fenrg.2018.00057

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Gerdroodbary, M. B., Moradi, R., Shafee, A., and Li, Z. (2019). Application of Neural Network for estimation of heat transfer treatment of Al2O3-H2O nanofluid through a channel. Comput. Methods Appl. Mech. Eng. 344, 1–12. doi:10.1016/j.cma.2018.09.025

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Haq, R. U., Shafee, A., Li, Z., Elaraki, Y. G., Tlili, I., et al. (2019). Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchanger. Int. J. Heat Mass Transf. 135, 470–478. doi:10.1016/j.ijheatmasstransfer.2019.02.003

CrossRef Full Text | Google Scholar

Sheikholeslami, M., Jafaryar, M., Shafee, A., Li, Z., and Haq, R. U. (2019). Heat transfer of nanoparticles employing innovative turbulator considering entropy generation. Int. J. Heat Mass Transf. 136, 1233–1240. doi:10.1016/j.ijheatmasstransfer.2019.03.091

CrossRef Full Text | Google Scholar

Shoaib, M., Raja, M. A. Z., Zubair, G., Farhat, I., Nisar, K. S., Sabir, Z., et al. (2021). Intelligent computing with levenberg–marquardt backpropagation neural networks for third-grade nanofluid over a stretched sheet with convective conditions. Arab. J. Sci. Eng., 1–19. doi:10.1007/s13369-021-06202-5

CrossRef Full Text | Google Scholar

Subbarayudu, K., Suneetha, S., and Reddy, P. B. A. (2020). The assessment of time dependent flow of Williamson fluid with radiative blood flow against a wedge. Propuls. Power Res. 9 (1), 87–99. doi:10.1016/j.jppr.2019.07.001

CrossRef Full Text | Google Scholar

Toghraie, D. S., Sina, N., Mozafarifard, M., Alizadeh, A. A., Soltani, F., Fazilati, M. A., et al. (2020). Prediction of dynamic viscosity of a new non-Newtonian hybrid nanofluid using experimental and artificial neural network (ANN) methods. Heat. Transf. Res. 51 (15), 1351–1362. doi:10.1615/heattransres.2020034645

CrossRef Full Text | Google Scholar

Umar, M., Sabir, Z., Imran, A., Wahab, A. H., Shoaib, M., Raja, M. A. Z., et al. (2020). The 3-D flow of Casson nanofluid over a stretched sheet with chemical reactions, velocity slip, thermal radiation and Brownian motion. Therm. Sci. 24, 2929–2939. doi:10.2298/tsci190625339u

CrossRef Full Text | Google Scholar

Umar, M., Sabir, Z., Zahoor Raja, M. A., Gupta, M., Le, D. N., Aly, A. A., et al. (2021). Computational intelligent paradigms to solve the nonlinear SIR system for spreading infection and treatment using Levenberg–Marquardt backpropagation. Symmetry 13 (4), 618. doi:10.3390/sym13040618

CrossRef Full Text | Google Scholar

Vakili, M., Karami, M., Delfani, S., and Khosrojerdi, S. (2016). Experimental investigation and modeling of thermal radiative properties of f-CNTs nanofluid by artificial neural network with Levenberg–Marquardt algorithm. Int. Commun. Heat Mass Transf. 78, 224–230. doi:10.1016/j.icheatmasstransfer.2016.09.011

CrossRef Full Text | Google Scholar

Williamson, R. V. (1929). The flow of pseudoplastic materials. Ind. Eng. Chem. 21 (11), 1108–1111. doi:10.1021/ie50239a035

CrossRef Full Text | Google Scholar

Yang, X. H., and Liu, J. (2018). Liquid metal enabled combinatorial heat transfer science: Toward unconventional extreme cooling. Front. Energy 12 (2), 259–275. doi:10.1007/s11708-017-0521-3

CrossRef Full Text | Google Scholar

Zaman, S., and Gul, M. (2019). Magnetohydrodynamic bioconvective flow of Williamson nanofluid containing gyrotactic microorganisms subjected to thermal radiation and Newtonian conditions. J. Theor. Biol. 479, 22–28. doi:10.1016/j.jtbi.2019.02.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, N., Li, S., and Yang, J. (2016). A review on nanofluids: Data-driven modeling of thermalphysical properties and the application in automotive radiator. Renew. Sustain. Energy Rev. 66, 596–616. doi:10.1016/j.rser.2016.08.029

CrossRef Full Text | Google Scholar

Zuhra, S., Raja, M. A. Z., Shoaib, M., Khan, Z., Nisar, K. S., Islam, S., et al. (2022). Numerical analysis of Cattaneo–Christov heat flux model over magnetic couple stress Casson nanofluid flow by Lavenberg–Marquard backpropagated neural networks. Waves Random Complex Media, 1–28. doi:10.1080/17455030.2022.2062484

CrossRef Full Text | Google Scholar