- 1College of Electrical and Information Engineering, Hunan University, Changsha, China
- 2Industrial Training Centre, Shenzhen Polytechnic, Shenzhen, China
- 3College of Electrical and Power Engineering, Taiyuan University of Technology, Taiyuan, China
Introduction
Energy storage system (ESS) is a crucial part of intelligent grid. It plays a key supporting role in improving system efficiency. ESS has great potential applications in many scenarios, but it still faces challenges such as system framework design and operation strategy formulation in the future. In traditional framework design, consumers own and independently schedule the ESS, and have many difficulties with the high investment and management costs of the ESS (Dai et al., 2021). In general, shared energy storage system (SESS) can be treated as a problem of achieving efficiency and profit sharing (Noman et al., 2021). For example, a mainstream SESS structure, that is, installed in an energy community to serve many families was proposed (Müller and Welpe, 2018; Terlouw et al., 2019; Zhu and Ouahada, 2021). There are also many studies on the operation strategy of SESS. A strategy was proposed to manage SESS by aggregating controller to coordinate energy storage capacity (Dai and Charkhgard, 2018; Kalathil et al., 2019; Zhang et al., 2020). In (Terlouw et al., 2019; Murty and Kumar., 2020), an optimal method of SESS in grid-connected microgrid was proposed and the two-layer decision-making model to allocate the storage capacity was presented. Furthermore, multi-grade and multi-energy pricing and trading strategies were proposed in (Veeramsetty, 2021; Li et al., 2022; Zhang et al., 2022) to achieve the maximum of satisfaction and protection of participants’ privacy.
In this paper, an energy trading framework is proposed for shared energy storage provider (SESP) and multi-type consumers aiming at improving utilization efficiency of SESS and the benefits of all participants. The opinions of this paper are twofold as listed: 1) An energy trading framework is proposed for SESP and consumers. Within the proposed framework, a system consisting of multiple consumers and SESS built between consumers is considered. Then, the provider makes full use of the time similarity characteristics of consumer load by formulating electricity price and optimizing the energy storage scheduling, so as to promote the utilization efficiency of energy storage and optimize the benefits; 2) An optimal energy pricing strategy is developed by constructing the trading framework as a bi-level optimization model. The energy optimal pricing strategy can benefit both provider and consumers and improves utilization efficiency. The upper-level problem aims to maximize the profits of provider, while the lower-level problem aims to get the optimal energy consumptions. The bi-level optimization model can be transformed as a single-level by shifting the lower-level problem with its Karush-Kuhn-Tucker (KKT) conditions.
Hierarchical Trading Framework of Shared Energy Storage System
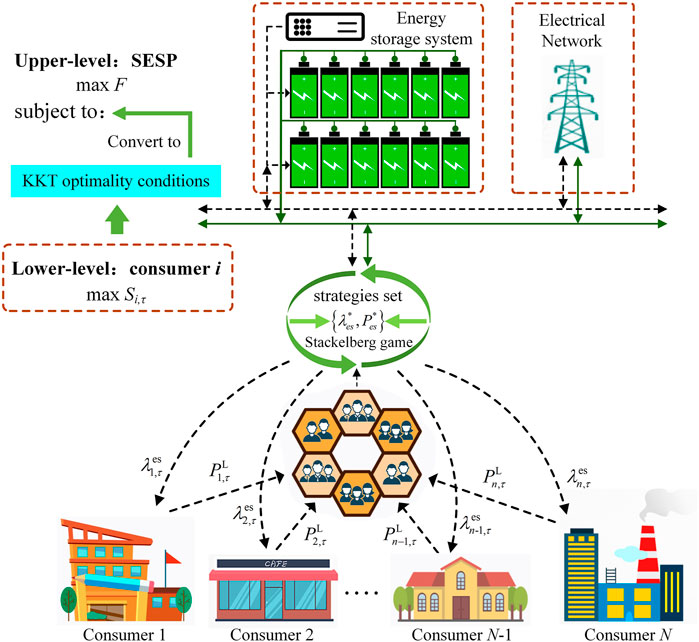
The hierarchical trading framework among SESP, power utilities, and multi-type consumers is depicted in Figure 1. For the provider, it takes advantage of their scale to establish large-scale SESS among consumers, and manage them uniformly to provide shared energy storage services for multi-type consumers in the same distribution network area (Li et al., 2019; Zhu and Ouahada, 2021). In terms of demand side, consumers are willing to purchase electricity from the provider due to its price superiority and would trade electricity with power utilities once the power price released by power utilities is lower than that released by the provider (Zhao et al., 2014). In addition, consumers will trade with power utilities for its power shortage when the demand of consumers surpasses the supply of the provider.
The service objects of shared energy storage include residents, commercial consumers, and large industrial consumers. The consumers send their demand information to SESP, the provider extends the consumption behavior of the consumers in time and space, and gathers multiple similar consumers together to form a number of consumers clusters with a certain similarity. According to the results of similarity analysis, the provider sends service price information to consumers on the premise of achieving its own optimal profit. However, both consumers and provider aim to maximize their own interests. Provider should supply consumers with suitable prices to compete with power utilities. For example, consumers reduce the power purchased from provider, so that provider passively reduces its electricity prices. The interest optimization process of provider and consumers forms a game relationship. Provider strategically provides consumers with electricity prices to maximize profits, while consumers influence provider by optimizing electricity consumption to maximize benefits. This is a sequential decision-making process, which constitutes a leader-follower game dominated by SESP, and can be expressed as a mathematical bi-level optimization model. The decision objective of upper model is to maximize the income of SESP to obtain the electricity price demanded by the provider. The decision objective of lower model is to maximize the satisfaction with energy consumption of consumers where the consumers adjust the strategy of their energy consumption according to the price. In the end, the optimal electricity price and the optimal discharge strategies set {λ*es, P*es} are obtained in this cycle.
Optimal Pricing Strategy Based on Stackelberg Game
From the perspective of consumers, different consumers choose to buy different amounts of energy according to their preferences for energy consumption. The utility can be defined as the satisfaction level of energy consumption. In this paper, a widely used quadratic function u is used to represent consumer’s utility (Wu et al., 2020; Liu et al., 2022), which is strictly concave and continuously differentiable. Then, the consumer satisfaction function S is introduced, defined as the difference between utility and electricity consumption cost. It can be described as a consumer satisfaction optimization problem. Since the demand of consumers is variable, consumers can always achieve optimal satisfaction by adjusting their demand to a point. When the marginal utility equals the energy prices, each consumer obtains the maximum satisfaction level based on optimality condition ∇S = 0. SESP, as the provider of electricity, will produce costs during operation, including the operation and maintenance costs of battery energy conversion process and power supply costs from the power utilities. Hence, the profit of SESP F can be expressed as the difference between electricity sales and operating costs.
The electricity trading problem between SESP and consumers can be described as a Stackelberg game G with the provider as the leader and consumers as followers. The game G is defined as a set of strategies, including provider and consumers, where {λes} is the strategy set of the provider; {Pes} is the strategy set of consumers; {S} is the satisfaction strategy set of consumers; {F} is the profit of the provider.
When all the participants in game G are at a Stackelberg equilibrium, SESP cannot improve its profit by adjusting energy prices from the Stackelberg equilibrium prices (λ*es), and similarly, no consumer can increase its satisfaction by adjusting its energy consumption (P*es). Based on the decision order, this game can be expressed as a bi-level optimizing model. In the upper-level, SESP finds the optimal energy prices (λ*es) by maximum F subjected to operational constraints. In the lower-level, consumers aim to get the optimal energy consumptions (P*es) by maximum S subjected to energy constraints. Note that consumers who have the approximate consumption energy similarity will get the same energy prices offered by the provider. Different group of consumers distinguished by consumption energy similarity will get different energy prices.
Due to its hierarchical structure and nonlinear objective function, the bi-level optimization problem cannot be directly solved by the available commercial solver. A common and accurate solution to this problem is to replace the lower-level problem by their KKT conditions. In this bi-level optimization problem, the optimal pricing strategy of SESP is composed of price variables, which are known parameters of the lower-level problem. In addition, when price constraints are given, the energy price set by the provider will always be lower than that set by the power utilities. Therefore, the bi-level optimization model can be transformed into a single-level optimization model by KKT conditions. The key solving process for this problem as follows:
1) Initialize consumer electricity demand and service price parameters; 2) Formulate the model of Stackelberg game in which the SESP acts as the leader and consumers are the followers, and transform it into a bi-level optimization model; 3) Convert the lower-level problem to upper-level constraints by KKT optimality conditions, then transform the bi-level problem to a single-level problem; 4) Solve the single-level problem and obtain optimal strategies of the provider and consumers, then calculate the profit of the provider and the satisfaction of consumers.
Discussion and Conclusions
In this paper, an energy trading framework is proposed for SESP and multiple consumers. In terms of pricing, the similarity analysis method based on consumer load characteristics is introduced. When the consumer’s load similarity is high, it means that the consumer’s energy demand is relatively similar. The high similarity collection will make the peak-valley difference of the overall load more obvious. The provider can use the proportional coefficient method based on similarity to raise the electricity price and play the load transfer ability of energy storage. When the consumer’s load similarity is low, the provider stimulates consumers’ willingness to use energy by reducing the electricity price during this period, and improves the utilization rate of energy storage. In the end, the bi-level optimization problem is solved by Stackelberg game method, and the optimal pricing strategy is obtained. The proposed framework can achieve market equilibrium between provider and consumers and is of practical significance.
Author Contributions
Writing the original draft and editing, SH; Conceptualization, XG and JC; Formal analysis, RC; Visualization and contributed to the discussion of the topic, ZS and JB.
Funding
This work is supported by the Scientific Research Startup Fund for Shenzhen High-Caliber Personnel of SZPT (No. 6022310042k).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Dai, R., and Charkhgard, H. (2018). Bi-objective Mixed Integer Linear Programming for Managing Building Clusters with a Shared Electrical Energy Storage. Comput. Operations Res. 96, 173–187. doi:10.1016/j.cor.2018.01.002
Dai, R., Esmaeilbeigi, R., and Charkhgard, H. (2021). The Utilization of Shared Energy Storage in Energy Systems: A Comprehensive Review. IEEE Trans. Smart Grid 12 (4), 3163–3174. doi:10.1109/TSG.2021.3061619
Kalathil, D., Wu, C., Poolla, K., and Varaiya, P. (2019). The Sharing Economy for the Electricity Storage. IEEE Trans. Smart Grid 10 (1), 556–567. doi:10.1109/TSG.2017.2748519
Li, J., Xu, D., Wang, J., Zhou, B., Wang, M., and Zhu, L. (2022). P2P Multi-Grade Energy Trading for Heterogeneous Distributed Energy Resources and Flexible Demand. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2022.3181703
Li, X., Wang, S., and Wang, S. (2019). A Review on Energy Management, Operation Control and Application Methods for Grid Battery Energy Storage Systems. Csee Jpes 7 (5), 1026–1040. doi:10.17775/CSEEJPES.2019.00160
Liu, N., Tan, L., Sun, H., Zhou, Z., and Guo, B. (2022). Bilevel Heat-Electricity Energy Sharing for Integrated Energy Systems with Energy Hubs and Prosumers. IEEE Trans. Ind. Inf. 18 (6), 3754–3765. doi:10.1109/TII.2021.3112095
Müller, S. C., and Welpe, I. M. (2018). Sharing Electricity Storage at the Community Level: An Empirical Analysis of Potential Business Models and Barriers. Energy Policy 118, 492–503. doi:10.1016/j.enpol.2018.03.064
Murty, V. V. S. N., and Kumar., A. (2020). RETRACTED ARTICLE: Multi-Objective Energy Management in Microgrids with Hybrid Energy Sources and Battery Energy Storage Systems. Prot. Control Mod. Power Syst. 5 (1), 1–20. doi:10.1186/s41601-019-0147-z
Noman, M., Li, G., Wang, K., and Han, B. (2021). Electrical Control Strategy for an Ocean Energy Conversion System. Prot. Control Mod. Power Syst. 6 (2), 160–177. doi:10.1186/s41601-021-00186-y
Terlouw, T., AlSkaif, T., Bauer, C., and van Sark, W. (2019). Multi-objective Optimization of Energy Arbitrage in Community Energy Storage Systems Using Different Battery Technologies. Appl. Energy 239 (APR-1), 356–372. doi:10.1016/j.apenergy.2019.01.227
Veeramsetty, V. (2021). Shapley Value Cooperative Game Theory-Based Locational Marginal Price Computation for Loss and Emission Reduction. Prot. Control Mod. Power Syst. 6 (4), 419–429. doi:10.1186/s41601-021-00211-0
Wu, C., Gu, W., Bo, R., MehdipourPicha, H., Jiang, P., Wu, Z., et al. (2020). Energy Trading and Generalized Nash Equilibrium in Combined Heat and Power Market. IEEE Trans. Power Syst. 35 (5), 3378–3387. doi:10.1109/TPWRS.2020.2973423
Zhang, K., Zhou, B., Chung, C. Y., Bu, S., Wang, Q., and Voropai, N. (2022). A Coordinated Multi-Energy Trading Framework for Strategic Hydrogen Provider in Electricity and Hydrogen Markets. IEEE Trans. Smart Grid, 1. doi:10.1109/TSG.2022.3154611
Zhang, W., Wei, W., Chen, L., Zheng, B., and Mei, S. (2020). Service Pricing and Load Dispatch of Residential Shared Energy Storage Unit. Energy 202, 117543. doi:10.1016/j.energy.2020.117543
Zhao, Z., Wu, L., and Song, G. (2014). Convergence of Volatile Power Markets with Price-Based Demand Response. IEEE Trans. Power Syst. 29 (5), 2107–2118. doi:10.1109/TPWRS.2014.2307872
Keywords: hierarchical optimization, pricing strategy, shared energy storage, stackelberg game, trading framework
Citation: Huang S, Gao X, Chen J, Chen R, Su Z and Bao J (2022) An Optimal Hierarchical Pricing Strategy for Shared Energy Storage Services. Front. Energy Res. 10:967998. doi: 10.3389/fenrg.2022.967998
Received: 13 June 2022; Accepted: 20 June 2022;
Published: 11 July 2022.
Edited by:
Jian Zhao, Shanghai University of Electric Power, ChinaReviewed by:
Qinran Hu, Southeast University, ChinaBo Yang, Kunming University of Science and Technology, China
Copyright © 2022 Huang, Gao, Chen, Chen, Su and Bao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiang Gao, Z2FveGlhbmdAc3pwdC5lZHUuY24=
 Shanhe Huang
Shanhe Huang Xiang Gao
Xiang Gao Jialin Chen1
Jialin Chen1