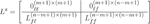Robust affine maneuver formation control based of second-order multi-agent grid inspection systems

Grid formation inspection is the future development trend of grid inspection. Aim to the robust control problem of multi-agent grid inspection system in complex environment, this paper proposes a formation control algorithm with prescribed performance. The dynamic model of follower distance error is given in the leader-follower framework using a symbolic Laplace matrix. Performance bounds are set on the sliding mode error by prescribed performance control. Then, the convergence and stability of the proposed control algorithm are not only proved by the Lyapunov stability theorem, but also the error state of the system converges to the prescribed performance bound. Finally, the simulation results show that the follower can follow the leader despite external interference and the validity of the proposed algorithm.

1 Introduction

In recent years, with the rapid development of smart grid, the use of mobile inspection robots instead of manual inspection has become a hot spot for research in the power industry (Wan et al. 2018). First, for dense grid system, multi-agent can decompose and simplify the complexity of the task when performing the task together, thus effectively shortening the execution time and improving the task completion efficiency. Second, the wide range of applications can be applied to the inspection of roads in harsh environments and off the beaten path, such as high altitude and alpine regions. Final, if a single inspection robot fails, it has less impact on the overall inspection. The results of multi-agent detection can be mutually verified to improve detection accuracy and avoid false detection. The structure of the multi-agent grid inspection systems is shown in Figure 1.

FIGURE 1

FIGURE 1. Multi-agent grid inspection systems application scenario diagram.

In order to realize the multi-agent inspection system, two main problems need to be solved, the first one is the flexibility, need to formations for different situations to achieve straight line driving, scaling, rotation and other movements. The second one is robustness, in the field environment the agent is easily subject to external interference.

Over the past 2 decades, multi-agents formation control has been investigated by various approaches. Depending on the definition of the target formation, existing formation control methods can be divided into displacement-based (Babazadeh and Selmic, 2018), distance-based (Cao et al. 2019) and orientation-based (Yang et al. 2020) methods, using constant inter-agent displacement, distance and orientation constraints to define the target formation respectively (Oh et al. 2015). Displacement-based formation control rates can be used to track target formations with time-varying translations (Zhao and Zelazo 2015), but it is difficult to control the scale or direction of the formation. Distance-based control rates can be used to track target formations with time-varying translations and directions (Ren 2007; Ren and Beard 2008), but it is difficult to track formations with time-varying sizes. Orientation-based control rates can track formations with time-varying translations and proportions (De Marina et al. 2016; Sun et al. 2017), but it is difficult to track time-varying orientations. Su et al. (2022) proposed a velocity-estimation-based control scheme to solve the time-varying orientations tracking problem (Su et al. 2022).

Because of the limitation of these traditional methods, researchers have proposed several methods for defining target formations using novel constant constraints, such as local orientation, center of gravity coordinates (Zelazo et al. 2015), complex Laplacian (Lin et al. 2014; Han et al. 2015), and stress matrix (Lin et al. 2015). Among these new methods, Zhao (2018) proposed a new control method for affine formation maneuvers that relies on the stress matrix. The proposed control law can track the target formation of time-varying affine transformations of any nominal configuration (Zhao 2018). Later, Xu et al. (2018) changed the undirected graph basis in the above algorithm to a directed graph to make it easier to implement in practice (Xu et al. 2018). Wang J. et al. (2021) studied the control problem of an affine formation algorithm for a multi-agents system with a given convergence time. By using a time-varying scale function, a distributed continuous control algorithm was designed (Wang J. et al. 2021). Ma et al. (2021b) proposes an adaptive reference vector reinforcement learning approach to many-objective optimization problem (Ma et al. 2021b). Ma et al. (2020) first analyzes the main factors that influence the performance of brain storm optimization and then proposes an orthogonal learning framework to improve its learning mechanism (Ma et al. 2020). Xie et al. (2022) solved the problem of convergence of the attitude tracking error in finite time by means of a prescribed performance function as well as an error compensation mechanism (Xie et al. 2022). However, the above formation algorithms are not resistant to external disturbances, so further improvement of the algorithm is needed.

Liu et al. (2018) eliminated the negative effects of external disturbances by using a method based on a radial basis function neural network combined with an artificial potential field approach (Liu et al. 2018). Ma et al. (2021c) proposed a truthful combinatorial double auction mechanism to guarantee desirable properties in constrained Mobile edge computing environments (Ma et al. 2021c). Doukhi and Lee (2019) combined an adaptive radial basis function neural network with a deterministic equivalent control technique to address the uncertainty of external disturbances as well as modeling errors (Doukhi and Lee 2019). Trindade et al. (2020) proposed a triple integrator-based consistency protocol for intelligences and incorporated the integration action into a formation tracking controller with double-integrating vehicles and gave sufficient necessary conditions for convergence (Trindade et al. 2020). Although the above algorithms solve the problem of external disturbances well, they increase the complexity of the algorithm and the integration term is difficult to implement in practical tests.

Bechlioulis and Rovithakis (2008) applied prescribed performance control to a multi-input, multi-output nonlinear system and proposed a robust adaptive controller with prescribed performance (Bechlioulis and Rovithakis 2008). Chen and Dimarogonas (2020) proposed to set prescribed performance for the leader’s error to drive followers so that the whole system can achieve the target formation (Chen and Dimarogonas 2020). Ma et al. (2017) proposed a specific multi-objective artificial bee colony optimizer and a adaptive local decision variable analysis method for large-scale multi-objective and multi-objective optimization problems, respectively (Ma et al. 2017; Ma et al. 2021a). Mehdifar et al. (2020) proposed a new distance-based robust formation control algorithm that also deals with connectivity maintenance and mutual collision between neighboring intelligences (Mehdifar et al. 2020). Jiang et al. solved the formation regulation problem for unmanned surface vehicle networks with disturbances by means of integral sliding mode control Wang Y. et al. (2021) proposed a novel predefined-time sliding-mode controller, this control scheme can guarantee that the tracking error converges to zero in a finite time (Wang Y. et al. 2021).

Although the algorithms in the aforementioned papers are robust, they are unable to implement the formation maneuver control. Therefore, it is necessary to consider a new algorithm that can have both robustness and formation transformation. Based on the above consideration, this paper proposes an robust affine maneuver formation control algorithm for multi-agent. The main contributions are summarized as follows:

$\left(1\right)$ Based on the directed graph basis, the followers only need to obtain the state information of their neighbors and do not need to obtain the global state information as well as the state information of the remaining followers.

$\left(2\right)$ Converting the maneuver control problem of formation into a control second-order integrator model follower tracking target formation problem using the nature of affine localization. Solve the flexibility problem of grid inspection system.

$\left(3\right)$ Sliding mode errors associated with position and velocity are designed, and then prescribed performance controls are used to achieve fast convergence of formation control as well as enhanced robustness of external disturbances to shape distortions. Solve the robustness problem of the grid inspection system.

The rest of the paper is organized as follows. Section 2, the preliminaries of the agents are introduced. The controller disign and stability analysis are given in Section 3. Section 4 shows the simulation results. Section 5 draws some conclusions.

2 Preliminaries

2.1 Notation and basic graph theory

A directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ contains a vertex set $\mathcal{V}$ and an edge set $\mathcal{E}$. If there exists an ordered pair $\left(j,i\right)\in \mathcal{E}$, the node j denotes the in-neighbour of i and the converse is called out-neighbour. The set of neighbors of vertex i is denoted by ${\mathcal{N}}_i=\{j:(j,i)\}\in \mathcal{E}$. Throughout this paper, it assumes that a directed graph does not have any self-loop and is a fixed topology.

Consider a set of n agents containing n_ℓ leaders and n_f followers in ${\mathbb{R}}^m$, where m ∈ {2, 3} and n ≥ m + 2. Thus the leaders’ subset is ${\mathcal{V}}_{\ell }$ and the subset of followers is ${\mathcal{V}}_f=\mathcal{V}\backslash {\mathcal{V}}_{\ell }$. For all followers, consider the following nonlinear dynamics

$\begin{array}{cc}\hfill & {\dot{p}}_i=v_i,\hfill \\ \hfill & {\dot{v}}_i=u_i+{\delta }_i,i\in {\mathcal{V}}_f.\hfill \end{array}(1)$

where $p_i\in {\mathbb{R}}^m$ denotes the position, v_i denotes agent i’s velocity, $u_i\in {\mathbb{R}}^m$ represents the control input of agent i, and ${\delta }_i(t)\in {\mathbb{R}}^m$ is an unknown, bounded and piece-wise continuous external disturbance vector. For simplicity, all the i in the paper belongs to ${\mathcal{V}}_f$. Let $p={[p_{\ell }^T,p_f^T]}^T\in {\mathbb{R}}^{mn}$ be the position of agents. The leaders do not need to access the information from these followers. Denote the constant configuration $r={[r_1^T,\dots ,r_n^T]}^T=[r_{\ell }^T,r_f^T]\in {\mathbb{R}}^{mn}$ as a nominaland configuration. Define the nominal formation as $(\mathcal{G},r)$. Then, the target formation with maneuvers can be described by p*(t) = [I_m ⊗ X(t)]r + 1_m ⊗ Y(t), where $X(t)\in {\mathbb{R}}^{m\times m}$, $Y(t)\in {\mathbb{R}}^m$ are time-varying. Y(t) controls formation translation and X(t) controls formation rotational, scaling and shearing manoeuvres relative to r.

2.2 Signed laplacian matrix

The matrix L^s of a directed graph is defined as follows:

$L^s\left(i,j\right)=\left\{\begin{array}{cc}-{\omega }_{ij}\hfill & ifi\ne jandj\in {\mathcal{N}}_i,\hfill \\ 0\hfill & ifi\ne jandj\notin {\mathcal{N}}_i,\hfill \\ \sum _{k\in {\mathcal{N}}_i}{\omega }_{ik}\hfill & ifi=j\hfill \end{array}\right.(2)$

where $\omega \in \mathbb{R}$ can be positive or negative real weights on edge $\left(j,i\right)$ and L^s is normally a nonsymmetric matrix.

A formation $(\mathcal{G},p)$ is a directed graph $\mathcal{G}$ with its vertex i of mapped to p_i. The affine image of the nominal configuration can be defined as

$\mathcal{A}\left(r\right)=\left\{p\in {\mathbb{R}}^{mn}:p=\left(I_n\otimes X\right)r+{\mathbf{1}}_n\otimes Y,\forall X\in {\mathbb{R}}^{m\times m},\forall Y\in {\mathbb{R}}^m\right\}(3)$

where (X, Y) is affine transformation.

Definition 1 (Affine Span). Given a set of points ${\{p_i\}}_{i=1}\in {\mathbb{R}}^m$, the affine span S of these points is

$S=\left\{\sum _{i=1}^n{a}_i{p}_i:a_i\in {\mathbb{R}}^m\text{for\hspace{0.17em}all}i\mathrm{a}\mathrm{n}\mathrm{d}\sum _{i=1}^n{a}_i=1\right\}(4)$

Definition 2 (Affine Localizability). The nominal formation $(\mathcal{G},p)$ is affinely localizable by leaders if for any $p={[p_{\ell }^T,p_f^T]}^T\in \mathcal{A}(r)$, p_f can be determined by p_ℓ uniquely.

Assumption 1. Assume that 1) The r has an m-dimensional affine span. 2) The $\left(\mathcal{G},r\right)$ has a signed Laplacian matrix L^s satisfying rank(L^s) = n − 1. 3) The nominal formation $\left(\mathcal{G},r\right)$ is affinely localizable by the leaders.

From Assumption 1, Eq. 2 can be rewritten in the following form

(5)

Under Assumption 1, for any $p={[p_{\ell }^T,p_f^T]}^T\in \mathcal{A}\left(r\right)$ satisfying $\left(L^s\otimes I_d\right)p=0$, it can be obtained

${\bar{L}}_{f\ell }^s{p}_{\ell }+{\bar{L}}_{ff}^s{p}_f=0(6)$

which ${\bar{L}}_{f\ell }^s=L_{f\ell }^s\otimes I_m$, and ${\bar{L}}_{ff}^s=L_{ff}^s\otimes I_m$.

We know that the control objective is $p_f\left(t\right)\to p_f^{*}\left(t\right)$ when t → ∞. From Eq. 6, it can be obtained $p_f^{*}\left(t\right)=-{\bar{L}}_{ff}^{s-1}{\bar{L}}_{f\ell }^s{p}_{\ell }^{*}\left(t\right)$.

The dynamic of the estimation error is as follows

$\begin{array}{cc}\hfill & e_{pf}\left(t\right)=p_f\left(t\right)-p_f^{*}\left(t\right)=p_f\left(t\right)+{\bar{L}}_{ff}^{s-1}{\bar{L}}_{f\ell }^s{p}_{\ell }^{*}\left(t\right),\hfill \\ \hfill & e_{vf}\left(t\right)=v_f\left(t\right)-v_f^{*}\left(t\right)=v_f\left(t\right)+{\bar{L}}_{ff}^{s-1}{\bar{L}}_{f\ell }^s{v}_{\ell }^{*}\left(t\right).\hfill \end{array}(7)$

The derivative of the above equation gives

$\begin{array}{cc}\hfill & {\dot{e}}_{pf}\left(t\right)=v_f\left(t\right)+{\bar{L}}_{ff}^{s-1}{\bar{L}}_{f\ell }^s{v}_{\ell }^{*}\left(t\right),\hfill \\ \hfill & {\dot{e}}_{vf}\left(t\right)=u+\delta +{\bar{L}}_{ff}^{s-1}{\bar{L}}_{f\ell }^s{\dot{v}}_{\ell }^{*}\left(t\right).\hfill \end{array}(8)$

3 Controller design and stability analysis

3.1 Sliding mode and prescribed performance control

Define the sliding mode error of the agent i as

$s_i=e_{pf}+\beta e_{vf}(9)$

where β > 0. A set of inequalities is usually applied to limit the upper and lower bounds on the system tracking error, the prescribed performance constraint function

$-{\underline{\eta }}_i{\rho }_i\left(t\right)<s_i\left(t\right)<{\bar{\eta }}_i{\rho }_i\left(t\right),i\in {\mathcal{V}}_f,\forall t⩾0(10)$

where ${\rho }_i(t)=({\rho }_0-{\rho }_{\infty })e^{-a_{i}t}+{\rho }_{\infty }$, ρ₀, ρ_∞ and a_i are the parameters to be set. The values of ${\bar{\eta }}_i$ and ${\underline{\eta }}_i$ are as follows

$\begin{array}{cc}\hfill & {\bar{\eta }}_i=\left\{\begin{array}{cc}{e}_{pi}+\beta e_{vi}\hfill & if{e}_{pi}>0,\hfill \\ 0.5\hfill & if{e}_{pi}\le 0,\hfill \end{array}\right.\hfill \\ \hfill & {\underline{\eta }}_i=\left\{\begin{array}{cc}0.5\hfill & if{e}_{pi}>0,\hfill \\ e_{pi}+\beta e_{vi}\hfill & if{e}_{pi}\le 0,\hfill \end{array}\right.\hfill \end{array}(11)$

To deal with the time-varying constraints in Eq. 10, the system Eq. 10 with constraints is transformed into a new equivalent unconstrained system using an error transformation technique. The modulation error is defined as

${\eta }_i\left(t\right)=\frac{s_i\left(t\right)}{{\rho }_i\left(t\right)}(12)$

where ρ_i(t) ≠ 0.

Then we introduce the error conversion function.

${\sigma }_i=T_i\left({\eta }_i\right)=\frac{1}{2}\ln \left(\frac{{\bar{\eta }}_i{\eta }_i+{\underline{\eta }}_i{\bar{\eta }}_i}{{{\bar{\eta }}_i\underline{\eta }}_i-{{\underline{\eta }}_i\eta }_i}\right)(13)$

where σ_i is the conversion error corresponding to η_i, $T_i(.):(-{\underline{\eta }}_i,{\bar{\eta }}_i)\to (-\infty ,+\infty )$ is a smooth strictly increasing bijective mapping satisfying $T_i\left(0\right)=0$. It can be seen that σ_i → 0 when and only when η_i → 0.

Next, taking the time derivative of σ_i, yields $\dot{{\sigma }_i}=\left(d{T}_i/d{\eta }_i\right)\dot{{\eta }_i}=0.5[1/({\eta }_i+{\underline{\eta }}_i)-1/({\eta }_i-{\bar{\eta }}_i)]\times [(\dot{s}/{\rho }_i)-(s\dot{{\rho }_i}/{\rho }_i^2)]=0.5{\xi }_i(\dot{s}-{\dot{\rho }}_i{\eta }_i)$, where

${\xi }_i=\frac{1}{{\rho }_i}\left[\frac{1}{{\eta }_i+\underline{{\eta }_i}}-\frac{1}{{\eta }_i-\overline{{\eta }_i}}\right](14)$

Then ${\dot{\rho }}_i$ is given in compact form as:

$\dot{\sigma }=\frac{1}{2}\xi \left(\dot{s}-\dot{\rho }\eta \right)(15)$

3.2 Control algorithm design for the followers

Theorem 1. Consider n agents with dynamics Eq. 1 in the mdimensional space (m ∈ 2, 3) with nominal formation $(\mathcal{G},r)$. Let the initial conditions be such that $-{\underline{\eta }}_i{\rho }_i(0)<s_i(0)<{\bar{\eta }}_i{\rho }_i(0),i\in {\mathcal{V}}_f$, and also ${\bar{\eta }}_i$, ${\underline{\eta }}_i$ are selected according to Eq. 11, then the control law is as follows:

$u_i=-k_i{\xi }_i{\sigma }_i,i\in {\mathcal{V}}_f(16)$

where k_i is control gain. The expressions for ξ_i and σ_i are shown in Eqs 13, 14, respectively, ensures prescribed performance in the sense of Eq. 10

Equation 16 can be abbreviated to the following form

$u=-\xi K\sigma (17)$

where ξ = diag (ξ_i) ⊗ I_m, K = diag (k_i) ⊗ I_m, $\sigma =col\left({\sigma }_i\right)$.

Proof. Differentiating η as well as employing Eq. 12, yields:

$\begin{array}{cc}\hfill \dot{\eta }& =h_{\eta }\left(t,\eta \right)=\left[\dot{s}-\dot{\rho }\left(t\right)\eta \right]/\rho \left(t\right)\hfill \\ \hfill & =\left[{\dot{e}}_{pf}+\beta {\dot{e}}_{vf}-\dot{\rho }\left(t\right)\eta \right]/\rho \left(t\right)\hfill \\ \hfill & =\left[v_f+{\bar{L}}_{ff}^{s-1}{\bar{L}}_{f\ell }^s{v}_{\ell }^{*}+\beta \left(-\xi K\sigma +\delta +{\bar{L}}_{ff}^{s-1}{\bar{L}}_{f\ell }^s{\dot{v}}_{\ell }^{*}\right)-\dot{\rho }\left(t\right)\eta \right]/\rho \left(t\right)\hfill \end{array}(18)$

Define the open set

${\mathrm{\Omega }}_{\eta }=\prod _{i\in {\mathcal{V}}_f}\left(-{\underline{\eta }}_i,{\bar{\eta }}_i\right)(19)$

Phase I. Since the initial error e_pf (0) and e_vf(0) is chosen to be within the performance bound, i.e., the proof set Ω_η is nonempty and open. Moreover, Eq. 19 ensures that η(0) ∈ Ω_η.

From Eq. 18 we obtain that h_η is continuous on t and locally Lipschitz on η_i over the set Ω_η. Therefore, the hypotheses of Theorem 54 in Sontag (2013) (p.476) hold and the existence and uniqueness of a maximal solution η(t) of Eq. 18 for a time interval [0, τ_max) such that η(t) ∈ Ω_η, ∀t ∈ [0, τ_max) is guaranteed.

Phase II. Consider the potential function: $V_i=0.5k_i{\sigma }_i^2,i\in {\mathcal{V}}_f$ and define the overall candidate Lyapunov function: V = 0.5σ^TKσ. Employing Eq. 15 and Eq. 17, we arrive at: $\dot{V}=0.5{\sigma }^{T}K\xi \dot{s}-0.5{\sigma }^{T}K\xi \dot{\rho }\eta =-0.5\beta {\sigma }^{T}K\xi \xi K\sigma +0.5{\sigma }^{T}K\xi (v_f+\delta +{\bar{L}}_{ff}^{s-1}{\bar{L}}_{f\ell }^s(v_{\ell }^{*}+\beta {\dot{v}}_{\ell }^{*})-\dot{\rho }\eta )$. Assume that the leader’s velocity $v_{\ell }^{*}$ and acceleration ${\dot{v}}_{\ell }^{*}$ are continuous and bounded, we have $\Vert v_f+\delta +{\tilde{L}}_{ff}^{s-1}{\tilde{L}}_{f\ell }^s(v_{\ell }^{*}+\beta {\dot{v}}_{\ell }^{*})\Vert \le ϵ$, where ϵ be an positive constant.

Invoking Young’s inequality, and exploiting the diagonality K, ξ, ρ matrices it can be obtained:

$\begin{array}{ll}\hfill \dot{V}& \le -\frac{1}{2}\beta {\sigma }^{T}K\xi \xi K\sigma +\frac{1}{2}{\sigma }^{T}K\xi ϵ\hfill \\ \hfill & \le -\frac{1}{4}\beta {\sigma }^{T}K\xi \xi K\sigma -\frac{1}{4}\beta \Vert {\sigma }^{T}K\xi {\Vert }^2+\frac{1}{2}{\sigma }^{T}K\xi ϵ\hfill \\ \hfill & \le -\frac{1}{4}\beta {\lambda }_{max}\left(K^2\right){\lambda }_{max}\left({\xi }^2\right)\Vert \sigma |{|}^2+\frac{{ϵ}^2}{4\beta },t\in \left[0,{\tau }_{max}\right)\hfill \end{array}(20)$

For $\dot{V}<0$ to hold, only

$-\frac{1}{4}\beta {\lambda }_{max}\left(K^2\right){\lambda }_{max}\left({\xi }^2\right)\Vert \sigma |{|}^2+\frac{{ϵ}^2}{4\beta }<0$

i.e.,

$\Vert \sigma \Vert >\frac{ϵ}{\beta {\lambda }_{\max }\left(K\right){\lambda }_{\max }\left(\xi \right)}$

Based on this result it is clear that Eq. 17 is also bounded for all t ∈ [0, τ_max). Now using σ and taking the inverse logarithmic function in Eq. 13, leads to:

$-{\underline{\eta }}_i<-\frac{{\bar{\eta }}_i-{\bar{\eta }}_i\exp \left(-2\bar{\sigma }\right)}{{\underline{\eta }}_i\exp \left(-2\bar{\sigma }\right)+{\bar{\eta }}_i}{\underline{\eta }}_i={\widehat{\underline{\eta }}}_i\le {\eta }_i\left(t\right)\le {\widehat{\bar{\eta }}}_i=\frac{{\underline{\eta }}_i\exp \left(2\bar{\sigma }\right)-{\underline{\eta }}_i}{{\underline{\eta }}_i\exp \left(2\bar{\sigma }\right)+{\bar{\eta }}_i}{\bar{\eta }}_i<{\bar{\eta }}_i(21)$

for all $t\in \left[0,{\tau }_{max}\right)$ and $i\in {\mathcal{V}}_f$.

Phase III. The following is proved by the method of counter evidence. The nonempty compact set of Ω_η is defined as ${{\mathrm{\Omega }}^{\prime }}_{\eta }=\prod ({\widehat{\underline{\eta }}}_i(t),{\widehat{\bar{\eta }}}_i(t))$. Hence, assuming τ_max ≤ ∞ and since ${{\mathrm{\Omega }}^{\prime }}_{\eta }\subset {\mathrm{\Omega }}_{\eta }$, Proposition C.3.6 in Sontag (2013) (p.381) dictates the existence of a time instant t′ ∈ [0, τ_max) such that $\eta (t^{\prime })\notin {{\mathrm{\Omega }}^{\prime }}_{\eta }$, which is a clear contradiction. Therefore (10) hold when τ_max = ∞.

4 Simulation

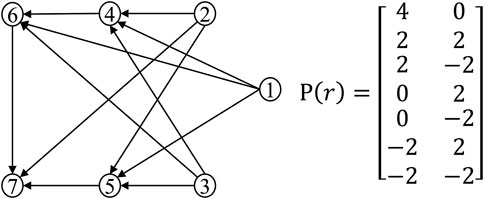
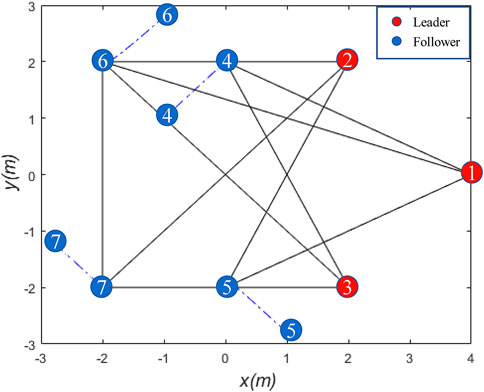
In this section, the proposed distributed control law is verified by simulation. As shown in Figure 2, given the nominal structure of seven agents $(\mathcal{G},r)$, its corresponding formation matrix is P(r). The arrow direction is the direction of directed graph interaction. The first three nodes denote leaders, and the remaining four nodes are followers. It is known that the number of leaders satisfies 3 = m+1, and the directed graph $\mathcal{G}$ can be judged as 3 reachable. The following symbolic Laplacian matrix L^s is obtained and satisfies its rank 4, while the corresponding stability matrix D = diag(1, 1, 1, − 1, − 1, − 1, − 1). Assume that the initial position: p = [4,0,2,2,2,−2,−0.6,1.8,0.5,−2.6,−1.6,2.6,−2.3,−2.6]^T and the control gain k_i = 0.3. ρ₀ = 1.1, ρ_∞ = 0.05 and a_i = 1. Assume the external disturbance is δ₁ = [0, 0], δ₂ = [0.3sin(0.6πt), 0.6sin(0.3πt)], δ₃ = [0.6sin(0.3πt), 0.3sin(0.6πt)], δ₄ = [0, 0].

$L^s=\left[\begin{array}{ccccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 1.5\hfill & \hfill 0.5\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0.5\hfill & \hfill 1.5\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 0.5\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill -1.5\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 1\hfill & \hfill -2\hfill \end{array}\right](22)$

FIGURE 2

FIGURE 2. Nominal formation of 7 agents.

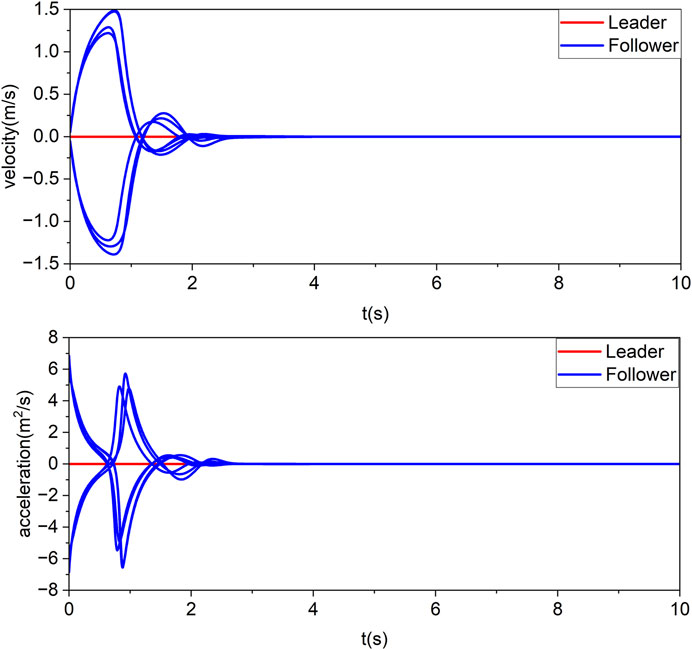
The next two simulation examples are presented in this paper. Consider first a simple case when the leader’s speed is 0. When the external disturbance is δ, the trajectory of the follower is shown in Figure 3, the sliding mode error of the follower is shown in Figure 4, and the velocity and acceleration changes are shown in Figure 5.

FIGURE 3

FIGURE 3. Trajectory of the agents when the leader speed is 0.

FIGURE 4

FIGURE 4. Sliding mode error of the agents when the leader speed is 0.

FIGURE 5

FIGURE 5. Velocity and acceleration of the agents when the leader speed is 0.

In order to adapt to the complex grid environment, agent need to change their formations according to the environment. With reasonable planning of the leader’s speed, the formation can be panned, rotated, scaled, etc. When the leader’s velocity is varied (As shown by the red line on Figure 8) and the other initial conditions are the same as above, the trajectory variation is shown in Figure 6, where the green part is assumed to be a grid tower. Some sliding mode error variation is shown in Figure 7, which shows that the error converges exactly within the prescribed performance bound, where the red line indicates the prescribed performance boundary. The velocity and acceleration changes are shown in Figure 8. It can be shown that the multi-agent is able to resist the effect of disturbance on shape distortion under the effect of Eq. 17.

FIGURE 6

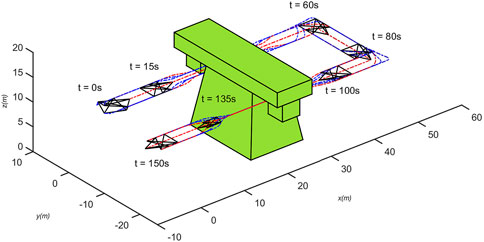
FIGURE 6. Trajectory using control law Eq. 17.

FIGURE 7

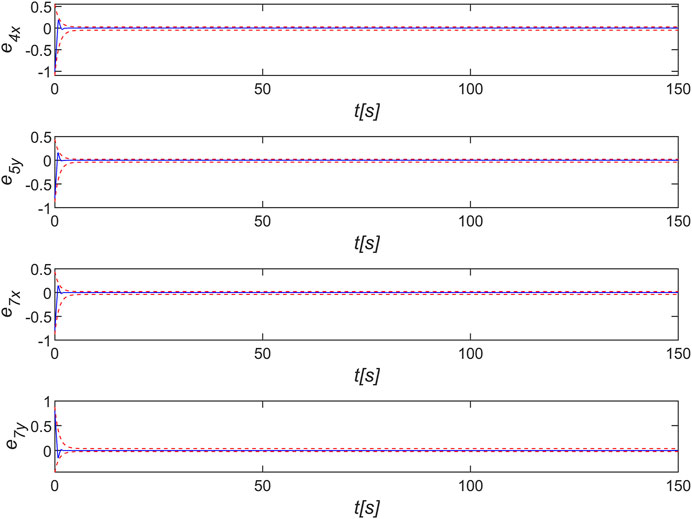
FIGURE 7. Sliding mode error of control law Eq. 17.

FIGURE 8

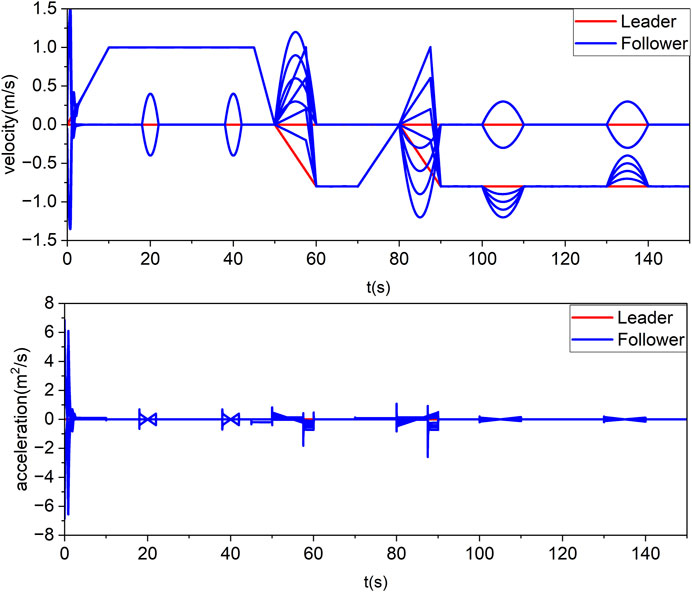
FIGURE 8. Velocity and acceleration of control law Eq. 17.

5 Conclusion

In this paper, we solve the problem of flexibility and robustness of multi-agent system in complex grid environments by using symbolic Laplace matrices and prescribed performance control. Then through Lyapunov stability analysis, it is verified that the proposed method is capable of ensuring asymptotic stability for tracking errors. Finally, it is verified by simulation that the designed algorithm can guarantee that all tracking errors in the system are eventually consistent and bounded, and the tracking errors can converge to a predefined region. The proposed control protocol increases formation robustness against shape distortions and can prevent formation convergence to incorrect shapes under the effect of external disturbances. In the future, the multi-agent grid inspection system under time-varying time delays needs to be studied and solved.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

PZ: conceptualization, writing—reviewing, and editing; DM: writing—original draft preparation and simulation; PL: supervision; and ML: contributed to the discussion of the topic.

Funding

This study was supported by the Technology Field Fund (2021-JCJQ-JJ-0726).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Babazadeh, R., and Selmic, R. (2018). “Anoptimal displacement-based leader-follower formation control for multi-agent systems with energy consumption constraints,” in 2018 26th Mediterranean Conference on Control and Automation (MED) (Zadar, Croatia: IEEE), 179–184.

CrossRef Full Text | Google Scholar

Bechlioulis, C. P., and Rovithakis, G. A. (2008). Robust adaptive control of feedback linearizable mimo nonlinear systems with prescribed performance. IEEE Trans. Autom. Contr. 53, 2090–2099. doi:10.1109/tac.2008.929402

CrossRef Full Text | Google Scholar

Cao, K., Li, D., and Xie, L. (2019). Bearing-ratio-of-distance rigidity theory with application to directly similar formation control. Automatica 109, 108540. doi:10.1016/j.automatica.2019.108540

CrossRef Full Text | Google Scholar

Chen, F., and Dimarogonas, D. V. (2020). Leader-follower formation control with prescribed performance guarantees. IEEE Trans. Control Netw. Syst. 8, 450–461. doi:10.1109/tcns.2020.3029155

CrossRef Full Text | Google Scholar

De Marina, H. G., Jayawardhana, B., and Cao, M. (2016). Distributed rotational and translational maneuvering of rigid formations and their applications. IEEE Trans. Robot. 32, 684–697. doi:10.1109/tro.2016.2559511

CrossRef Full Text | Google Scholar

Doukhi, O., and Lee, D. J. (2019). Neural network-based robust adaptive certainty equivalent controller for quadrotor uav with unknown disturbances. Int. J. Control Autom. Syst. 17, 2365–2374. doi:10.1007/s12555-018-0720-7

CrossRef Full Text | Google Scholar

Han, Z., Wang, L., Lin, Z., and Zheng, R. (2015). Formation control with size scaling via a complex laplacian-based approach. IEEE Trans. Cybern. 46, 2348–2359. doi:10.1109/tcyb.2015.2477107

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, Z., Wang, L., Chen, Z., Fu, M., and Han, Z. (2015). Necessary and sufficient graphical conditions for affine formation control. IEEE Trans. Autom. Contr. 61, 2877–2891. doi:10.1109/tac.2015.2504265

CrossRef Full Text | Google Scholar

Lin, Z., Wang, L., Han, Z., and Fu, M. (2014). Distributed formation control of multi-agent systems using complex laplacian. IEEE Trans. Autom. Contr. 59, 1765–1777. doi:10.1109/tac.2014.2309031

CrossRef Full Text | Google Scholar

Liu, Y., Huang, P., Zhang, F., and Zhao, Y. (2018). Distributed formation control using artificial potentials and neural network for constrained multiagent systems. IEEE Trans. Control Syst. Technol. 28, 697–704. doi:10.1109/tcst.2018.2884226

CrossRef Full Text | Google Scholar

Ma, L., Cheng, S., and Shi, Y. (2020). Enhancing learning efficiency of brain storm optimization via orthogonal learning design. IEEE Trans. Syst. Man. Cybern. Syst. 51, 6723–6742. doi:10.1109/tsmc.2020.2963943

CrossRef Full Text | Google Scholar

Ma, L., Huang, M., Yang, S., Wang, R., and Wang, X. (2021a). An adaptive localized decision variable analysis approach to large-scale multiobjective and many-objective optimization. IEEE Trans. Cybern. 2021, 1–13. doi:10.1109/tcyb.2020.3041212

CrossRef Full Text | Google Scholar

Ma, L., Li, N., Guo, Y., Wang, X., Yang, S., Huang, M., et al. (2021b). Learning to optimize: Reference vector reinforcement learning adaption to constrained many-objective optimization of industrial copper burdening system. IEEE Trans. Cybern. 2021, 1–14. doi:10.1109/tcyb.2021.3086501

CrossRef Full Text | Google Scholar

Ma, L., Wang, X., Huang, M., Lin, Z., Tian, L., Chen, H., et al. (2017). Two-level master-slave rfid networks planning via hybrid multiobjective artificial bee colony optimizer. IEEE Trans. Syst. Man. Cybern. Syst. 49, 861–880. doi:10.1109/tsmc.2017.2723483

CrossRef Full Text | Google Scholar

Ma, L., Wang, X., Wang, X., Wang, L., Shi, Y., Huang, M., et al. (2021c). Tcda: Truthful combinatorial double auctions for mobile edge computing in industrial internet of things. IEEE Trans. Mob. Comput. 2021, 1. doi:10.1109/tmc.2021.3064314

CrossRef Full Text | Google Scholar

Mehdifar, F., Bechlioulis, C. P., Hashemzadeh, F., and Baradarannia, M. (2020). Prescribed performance distance-based formation control of multi-agent systems. Automatica 119, 109086. doi:10.1016/j.automatica.2020.109086

CrossRef Full Text | Google Scholar

Oh, K.-K., Park, M.-C., and Ahn, H.-S. (2015). A survey of multi-agent formation control. Automatica 53, 424–440. doi:10.1016/j.automatica.2014.10.022

CrossRef Full Text | Google Scholar

Ren, W., and Beard, R. W. (2008). Distributed Consensus in Multi-vehicle Cooperative Control, 2008, 77–104.Consensus algorithms for double-integrator dynamicsTheory Appl.

Google Scholar

Ren, W. (2007). Multi-vehicle consensus with a time-varying reference state. Syst. Control Lett. 56, 474–483. doi:10.1016/j.sysconle.2007.01.002

CrossRef Full Text | Google Scholar

Sontag, E. D. (2013). Mathematical control theory: Deterministic finite dimensional systems, vol. 6. New York, U.S.: Springer Science & Business Media.

Google Scholar

Su, H., Chen, C., Yang, Z., Zhu, S., and Guan, X. (2022). Bearing-based formation tracking control with time-varying velocity estimation. IEEE Trans. Cybern. 2022, 1–13. doi:10.1109/tcyb.2022.3169891

CrossRef Full Text | Google Scholar

Sun, Z., Park, M.-C., Anderson, B. D., and Ahn, H.-S. (2017). Distributed stabilization control of rigid formations with prescribed orientation. Automatica 78, 250–257. doi:10.1016/j.automatica.2016.12.031

CrossRef Full Text | Google Scholar

Trindade, P., Cunha, R., and Batista, P. (2020). Distributed formation control of double-integrator vehicles with disturbance rejection. IFAC-PapersOnLine 53, 3118–3123. doi:10.1016/j.ifacol.2020.12.1045

CrossRef Full Text | Google Scholar

Wan, G., Yang, X., Cai, R., Li, H., Zhou, Y., Wang, H., et al. (2018). “Robust and precise vehicle localization based on multi-sensor fusion in diverse city scenes,” in 2018 IEEE international conference on robotics and automation (ICRA) (Manhattan, NY: IEEE), 4670–4677.

CrossRef Full Text | Google Scholar

Wang, J., Ding, X., Wang, C., Liang, L., and Hu, H. (2021a). Affine formation control for multi-agent systems with prescribed convergence time. J. Frankl. Inst. 358, 7055–7072. doi:10.1016/j.jfranklin.2021.07.019

CrossRef Full Text | Google Scholar

Wang, Y., Wang, Z., Chen, M., and Kong, L. (2021b). Predefined-time sliding mode formation control for multiple autonomous underwater vehicles with uncertainties. Chaos, Solit. Fractals 144, 110680. doi:10.1016/j.chaos.2021.110680

CrossRef Full Text | Google Scholar

Xie, S., Chen, Q., He, X., Tao, M., and Tao, L. (2022). Finite-time command-filtered approximation-free attitude tracking control of rigid spacecraft. Nonlinear Dyn. 107, 2391–2405. doi:10.1007/s11071-021-07091-x

CrossRef Full Text | Google Scholar

Xu, Y., Zhao, S., Luo, D., and You, Y. (2018). “Affine formation maneuver control of multi-agent systems with directed interaction graphs,” in 2018 37th Chinese Control Conference (CCC) (Wuhan, China: IEEE), 4563–4568.

CrossRef Full Text | Google Scholar

Yang, Z., Zhu, S., Chen, C., Feng, G., and Guan, X. (2020). Leader-follower formation control of nonholonomic mobile robots with bearing-only measurements. J. Frankl. Inst. 357, 1628–1643. doi:10.1016/j.jfranklin.2019.11.025

CrossRef Full Text | Google Scholar

Zelazo, D., Giordano, P. R., and Franchi, A. (2015). “Bearing-only formation control using an se(2) rigidity theory,” in 2015 54th IEEE Conference on Decision and Control (CDC) (Osaka, Japan: IEEE), 6121–6126.

CrossRef Full Text | Google Scholar

Zhao, S. (2018). Affine formation maneuver control of multiagent systems. IEEE Trans. Autom. Contr. 63, 4140–4155. doi:10.1109/tac.2018.2798805

CrossRef Full Text | Google Scholar

Zhao, S., and Zelazo, D. (2015). Bearing rigidity and almost global bearing-only formation stabilization. IEEE Trans. Autom. Contr. 61, 1255–1268. doi:10.1109/tac.2015.2459191

CrossRef Full Text | Google Scholar