Mathematical analysis of casson fluid flow with energy and mass transfer under the influence of activation energy from a non-coaxially spinning disc

A Casson fluid is the most suitable rheological model for blood and other non-Newtonian fluids. Casson fluids hold yield-stress and have great significance in biomechanics and polymer industries. In this analysis, a numerical simulation of non-coaxial rotation of a Casson fluid over a circular disc was estimated. The influence of thermal radiation, second-order chemical reactions, buoyancy, and heat source on a Casson fluid above a rotating frame was studied. The time evolution of secondary and primary velocities, solute particles, and energy contours were also examined. A magnetic flux of varying intensity was applied to the fluid flow. A nonlinear sequence of partial differential equations was used to describe the phenomenon. The modeled equations were reduced to a non-dimensional set of ordinary differential equations (ODEs) using similarity replacement. The obtained sets of ODEs were further simulated using the parametric continuation method (PCM). The impact of physical constraints on energy, concentration, and velocity profiles are presented through figures and tables. It should be noted that the effect of the Casson fluid coefficient, the Grashof number, and the magnetic field reduces the fluid’s primary velocity contour. The mass transfer field decreases with the action of constructive chemical reactions, but is augmented by the effects of destructive chemical reactions. The accelerating trend in Schmidt number lowers the mass profile, while it is enhanced by increasing values of activation energy and Soret number.

Introduction

Many natural and commercial processes use non-coaxial fluid motion. Non-coaxial and coaxial rotation of fluid and solids such as by discs, cylinders, and spheres are used in multiple industrial operations (Erdogan, 1977; Erdoḡan, 1997; Asghar et al., 2007). As a result of variations in temperature and chemical transmission, several types of non-coaxial and coaxial spinning of fluids in industrial systems arise. Swirling flows and spinning tubes while engaged in oil exploration and transit, and food manufacturing layouts are well-known instances of rotating mechanisms. In order to understand the underlying engineering mechanism, scientists and engineers have modeled the non-coaxial motion of fluids and calculated the results using a variety of approaches (Hayat et al., 2001; Hayat et al., 2004; Alharbi et al., 2022). Non-coaxial spinning of a disc has a wide range of uses, including food manufacturing and industrial production, jet turbines, squeeze bottles, hydrological flows, and chilling rotor blades, among others (Ullah et al., 2022a; Benhacine et al., 2022). Noranuar et al. (2021) used a computational approach to investigate the fluid flow and energy transport of MHD Casson ferrofluid affected by the coaxial rotation of a movable disc traveling through a permeable medium. Jabbar et al. (Jabbar et al., 2021) analyzed the influence of non-coaxial movement on the distribution of mass in a first-order biochemical reaction. It was discovered that the effect of buoyant force on secondary velocity was the polar opposite of its effect on primary velocity. Sharma et al. (Sharma et al., 2022) measured the thermal control of the flow of a hybrid nanoliquid over a stretchable rotating disc and discovered that a revolving disc with a static cone could attain the optimum condensation of disk-cone components while the exterior heat remained fixed. Das et al. (Das et al., 2018) determined the Hall impacts on MHD flow of an electrically charged particle induced by non-coaxial repetitions of a highly permeable disc and a fluid. The irregular flow of an oscillating disc in a Newtonian fluid about its own plane was reported by Ersoy (2017); when fluctuation occurred across the elliptical direction, the x- and y-terms exerted by the fluid on the disc varied in nearly opposite directions. The Darcy–Forchheimer hybrid nano-composite fluid flow across a permeable rotating disc was studied by Yaseen et al. (2022). Hassan et al. (2018) investigated the effects of a strong oscillating magnetic flux and a large concentration of nanoparticles on physical characteristics as well as energy and mass transport. Many researchers have recently reported on the study of non-coaxial motion of discs and fluids (Ali et al., 2020; Ali et al., 2022; Fei et al., 2022).

Thermal radiation is an electromagnetic wave-based heat transfer phenomenon. It is caused by a large temperature difference between two mediums. Many technological activities take place at extremely high temperatures. With regard to nuclear reactors, space technology, engineering and physics, glass production, power plants, furnace design, and other related areas, the contribution of thermal radiation to flow and thermal expansion may be observed. Satellites and other spacecraft, missiles, aircraft propulsion systems, atomic power plants, solar power plants, and combustion engines such as IC engines and furnaces are all dependent on radiation effects. Hassan et al. (2022) studied non-Newtonian fluid flows and determined their thermo-physical characteristics. In the presence of activation energy and a magnetic field, Rizwan and Hassan (2022), Raja et al. (2022), and Lin et al. (2014) documented the nanofluid flow of copper and cobalt nanocomposites under the influence of thermal radiation in different configurations. Hang et al. (2021) tested the ability of new smart materials to dynamically regulate thermal radiation and found that these materials could be employed in a variety of situations, resulting in better options and a significant increase in economic potential. Al and CuO nanoparticles were examined by Wakif et al. (2021) in the context of thermal radiation, and they concluded that the presence of convection cells was stabilized more by improving the strength of Lorentz forces, heat radiation, and surface roughness. The Jeffery hybrid nanofluid flow with thermal characteristics and magnetic effecst was studied by Ishtiaq et al. (2022), and their data showed that a $Cu-H_{2}O$ nanoliquid was more stable than one of $Ti{O}_2-H_{2}O$. Mabood et al. (2021) experimentally determined how hybrid nanoparticles influenced a variety of physical properties of hybrid nanoliquids across an overextended surface. The findings of their research were crucial in determining the influence of several key design elements on heat transmission and in improving industrial processes. The characteristics of fluid flow under the influence of thermal radiation and energy transmission over different geometries was reported by (Ahmed et al., 2018; Hassan et al., 2021a; Azam, 2022a; Azam, 2022b; Dadheech et al., 2022).

The minimum energy required to initiate an operation (such as a chemical reaction) is known as the activation energy, and the rate of a chemical reaction is directly proportional to its activation energy (Alsallami et al., 2022; Rehman et al., 2022). Punith et al. (2021) examined the effects of activation energy on the reactive species in a non-Newtonian nanofluid with energy and mass-exchange properties. The results showed that as the Marangoni number increased, the relative velocity improved, and the energy transmission decreased. Chemical processes, activation energy, and heat source/sink effects were used by Ramesh et al. (2022) to model the momentum and energy transport of a hybrid nanoliquid across two surfaces. The mass outlines were minimized by greater chemical reactions, whereas activation energy exhibited the reverse pattern. Hassan et al. (2021b) addressed the boundary layer behavior of the well-known non-Newtonian dilatant and pseudoplastic fluids over a moving belt. Ullah (Ullah et al., 2022b; Ullah et al., 2022c; Ullah, 2022) investigated the effects of activation energy and molten heat flux on an unstable Prandtl–Eyring model caused by a strained cylinder with varying thermal conductivity. It was discovered that increasing the reaction rate improved fluid temperature, while decreasing it had the opposite effect when activation energy and unsteadiness characteristics were considered. Many scholars have recently made significant contributions in this area (Azam and Abbas, 2021; Azam et al., 2021; Al-Mubaddel et al., 2022; Azam et al., 2022).

In reviewing the existing literature, we found that no analysis of combined transit of energy and mass in the flow caused by non-coaxial motion of a disc and surrounding fluid with respect to second-order chemical reactions, activation energy and buoyancy force had been performed. Therefore, we numerically simulated the non-coaxial rotation of a Casson fluid and disc under the influence of thermal radiation, second-order chemical reactions, buoyancy, and heat source in a rotating frame. A nonlinear sequence of partial differential equations was used to describe the phenomenon. The modeled equations were reduced to a non-dimensional set of ODEs using similarity replacement. The obtained sets of ODEs were further simulated using PCM methodology. The effect of physical constraints on energy, concentration and velocity profiles are presented in figures and tables. In the next section, the model is formulated, and in succeeding sections, we present the results and discussion.

Mathematical formulation

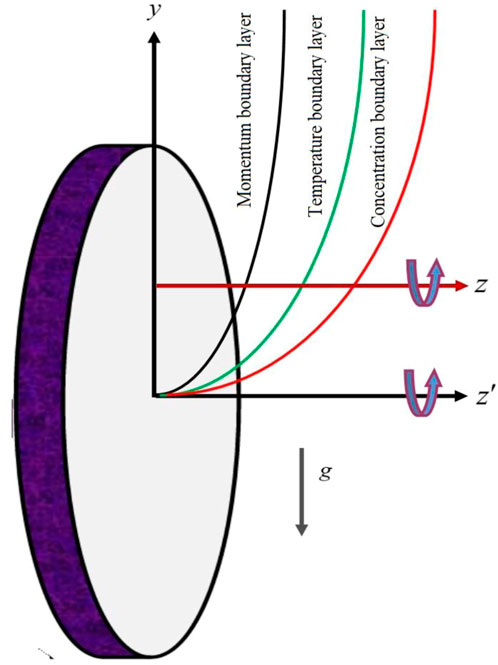
We considered the solute particles and thermal energy transmission in Casson fluid flow above a non-coaxial rotating disc with uniform angular velocity as displayed in Figure 1. The disk and ambient fluid both rotated on different axes under a fixed magnetic field, B₀. The disc temperature was higher than the heat energy. Initially, the temperature and concentration of the disc and the ambient fluid were assumed to be the same. After a period of time, the temperature of the disc was changed. We observed that the motion of the fluid was created by the surface motion of the disc. The disc wall stretched and shrank with the positive and negative values of $\Omega$. The gravitational and pressure effects are signified by g and p. In the proposed model, the opposing motions of the walls produced changes in vertical and horizontal velocities. The above-specified conditions produced results similar to (Erdogan, 1977; Benhacine et al., 2022)

$\begin{array}{l}u=-\left(y-1\right)\Omega ,T=T_{\infty },v=\Omega x,C=C_{\infty }at0=t\\ t>0,u=-\Omega y,T_w=T,v=\Omega x,C_w=C,z=0,\\ z\to \infty ,C=C_{\infty },u=-\Omega y+1,v=\Omega x,T_{\infty }=T\end{array}\}(1)$

FIGURE 1

FIGURE 1. Physical sketch of fluid flow across a vertical spinning disc.

Based on the above conditions, the following field was considered:

$V=f-\Omega y,g+\Omega x+0,C=C\left(z,t\right),T=T\left(z,t\right).(2)$

The basic equations were designed according to (Erdogan, 1977; Benhacine et al., 2022)

$\frac{1}{\rho }\frac{\partial p}{\partial x}=2{\Omega }^{2}x+v\left(\frac{1}{\beta }+1\right)\frac{{\partial }^{2}f}{\partial z^2}-\frac{\partial f}{\partial t}+\Omega g-\frac{\sigma B_0^2}{\rho }\left(f-\Omega l\right)-\frac{\mu }{\rho k}f+\frac{\mu \Omega }{\rho k}y,(3)$

$\frac{1}{\rho }\frac{\partial p}{\partial y}=2{\Omega }^{2}y+v\left(\frac{1}{\beta }+1\right)\frac{{\partial }^{2}g}{\partial z^2}-\frac{\partial g}{\partial t}-\Omega f-\frac{\sigma B_0^2}{\rho }g+{\beta }_T\left(-T_{\infty }+T\right)\overline{g}-\frac{\mu }{\rho k}g+\frac{\mu \Omega }{\rho k}x,(4)$

$\frac{\partial T}{\partial t}=\frac{K}{\rho C_p}\frac{{\partial }^{2}T}{\partial z^2}-\frac{1}{\rho C_p}\frac{16{\sigma }_1{T}_{\infty }^3}{3K^{*}}\frac{{\partial }^{2}T}{\partial Z^2}+\frac{Q_0}{\rho C_p}\left(T-T_{\infty }\right),(5)$

$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial z^2}+\frac{D{K}_T}{T_m}\frac{{\partial }^{2}T}{\partial Z^2}-k_r^2\left(C-C_0\right){\left(\frac{T}{T_{\infty }}\right)}^n\exp \left(-\frac{E_a}{\kappa T}\right),(6)$

Eliminating the pressure terms and employing the ambient conditions gives

$v\left(\frac{1}{\beta }+1\right)\frac{{\partial }^{2}f}{\partial z^2}-\frac{\partial f}{\partial t}+\Omega g-\frac{\sigma B_0^2}{\rho }\left(f-\Omega l\right)-\frac{\mu }{\rho k}f\left(\Omega l-f\right)=0,(7)$

$v\left(\frac{1}{\beta }+1\right)\frac{{\partial }^{2}g}{\partial z^2}-\frac{\partial g}{\partial t}-\Omega f-\frac{\sigma B_0^2}{\rho }g+{\Omega }^{2}l+{\beta }_T\left(-T_{\infty }+T\right)\overline{g}-\frac{\mu }{\rho k}g=0,(8)$

$\frac{\partial T}{\partial t}=\frac{K}{\rho C_p}\frac{{\partial }^{2}T}{\partial Z^2}+\frac{1}{\rho C_p}\frac{16{\sigma }_1{T}_{\infty }^3}{3K^{\ast }}\frac{{\partial }^{2}T}{\partial Z^2}+\frac{Q_0}{\rho C_p}\left(T-T_{\infty }\right),(9)$

$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial z^2}+\frac{D{K}_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial Z^2}-k_r^2\left(C-C_0\right){\left(\frac{T}{T_{\infty }}\right)}^n\exp \left(-\frac{E_a}{\kappa T}\right),(10)$

Resulting in

$\begin{array}{l}T=T,f=\Omega l,g=0,C=C_{\infty }t=0,\\ t>0,T=T_{\infty },C_w=C,g=0,f=0,z=0,\\ C=0,f=\Omega l,T=0,g=0z\to \infty .\end{array}\}(11)$

The similarity variables are as (Benhacine et al., 2022)

$\tau =\Omega t,\eta =\sqrt{\frac{\Omega }{v}}z,\theta \left(T_w-T_{\infty }\right)=T-T_{\infty },\phi \left(C_w-C_{\infty }\right)=C-C_{\infty },\Gamma =\frac{k\Omega }{v}.(12)$

In Eqs 7–10, we get

$\left(1+\frac{1}{\beta }\right)\frac{{\partial }^2\overline{F}}{\partial {\eta }^2}-\left(i\overline{F}+\frac{1}{\Gamma }\overline{F}+p\overline{F}\right)=-iGr\overline{\theta },-\frac{1}{p}=\overline{F}\left(0,p\right),0=\overline{F}\left(\infty ,p\right),(13)$

$\frac{{\partial }^2\theta }{\partial {\eta }^2}-\frac{\mathit{Pr}}{\lambda }\frac{\partial \theta }{\partial \tau }+Q\theta =0,\theta \left(0,\tau \right)=1,\theta \left(\infty ,\tau \right)=0,\theta \left(\eta ,0\right)=0,(14)$

$\frac{{\partial }^2\varphi }{\partial {\eta }^2}-Sc\frac{\partial \varphi }{\partial \tau }+ScSr\frac{{\partial }^2\theta }{\partial {\eta }^2}-Sc\gamma {\left(1+\delta \theta \right)}^n\phi \exp \left(-\frac{E}{1+\delta \theta }\right)=0,\varphi \left(0,\tau \right)=1,\varphi \left(\infty ,\tau \right)=0,\varphi \left(\eta ,0\right)=0.(15)$

The dimensionless parameters are

$\begin{array}{l}F\left(\eta ,\tau \right)=\frac{\left(f+ig\right)}{\Omega l-1},\lambda =1+\frac{4}{3N_R},N_R=\frac{K{K}^{\ast }}{4{\sigma }_1{T}_{\infty }^3},Gr=\frac{{\beta }_T\overline{g}\left(T_w-T_{\infty }\right)}{{\Omega }^{2}l},\mathit{Pr}=\frac{v_p{C}_p}{k},\\ M^2=\frac{\sigma B_0^2}{\rho \Omega },Sc=\frac{v}{D},Sr=\frac{D{K}_T\left(T_w-T_{\infty }\right)}{v{T}_m\left(C_w-C_{\infty }\right)},\gamma =\frac{K_1}{\Omega },\Gamma =\frac{k\Omega }{v}.\end{array}\}(16)$

Numerical solution

Different researchers have used various numerical and computational techniques to solve nonlinear PDEs (Tie-Hong et al., 2019; Chu et al., 2021; Zhao et al., 2021; Chu et al., 2022a; Chu et al., 2022b; Iqbal et al., 2022; Jin et al., 2022; Nazeer et al., 2022; Rashid et al., 2022; Wang et al., 2022). The main steps in employing the PCM method were taken from (Shuaib et al., 2020a; Shuaib et al., 2020b; Elattar et al., 2022):

Step 1: Simplifying Eqs 13–15 to first order:

$\begin{array}{l}{\mathrm{ƛ}}_1\left(\eta \right)=f\left(\eta \right),{\mathrm{ƛ}}_2\left(\eta \right)=f^{\prime }\left(\eta \right),{\mathrm{ƛ}}_3\left(\eta \right)=\theta \left(\eta \right),\\ {\mathrm{ƛ}}_4\left(\eta \right)={\theta }^{\prime }\left(\eta \right),{\mathrm{ƛ}}_5\left(\eta \right)=\varphi \left(\eta \right),{\mathrm{ƛ}}_6\left(\eta \right)={\varphi }^{\prime }\left(\eta \right).\end{array}\}(17)$

By putting Eq. 17 in Eqs 13–15, we get

$\left(1+\frac{1}{\beta }\right){\mathrm{ƛ}}_2^{\prime }-\left(i{\mathrm{ƛ}}_1+\frac{1}{\Gamma }{\mathrm{ƛ}}_1+p{\mathrm{ƛ}}_1\right)=-iGr{\mathrm{ƛ}}_3,-\frac{1}{p}={\mathrm{ƛ}}_1\left(0,p\right),0={\mathrm{ƛ}}_1\left(\infty ,p\right),(18)$

${\mathrm{ƛ}}_4^{\prime }-\frac{\mathit{Pr}}{{\lambda }^{*}}{\mathrm{ƛ}}_3+Q{\mathrm{ƛ}}_3=0,{\mathrm{ƛ}}_3\left(0,\tau \right)=1,{\mathrm{ƛ}}_3\left(\infty ,\tau \right)=0,{\mathrm{ƛ}}_3\left(\eta ,0\right)=0,(19)$

${\mathrm{ƛ}}_6^{\prime }-Sc{\mathrm{ƛ}}_5+ScSr{\mathrm{ƛ}}_4^{\prime }-Sc\sigma {\left(1+\delta {\mathrm{ƛ}}_3\right)}^n\phi \exp \left(-\frac{E}{1+\delta {\mathrm{ƛ}}_3}\right)=0,{\mathrm{ƛ}}_5\left(0,\tau \right)=1,{\mathrm{ƛ}}_5\left(\infty ,\tau \right)=0,{\mathrm{ƛ}}_5\left(\eta ,0\right)=0.(20)$

Step 2: Familiarizing the embedding term p in Eqs 18–20:

$\left(1+\frac{1}{\beta }\right){\mathrm{ƛ}}_2^{\prime }-\left(i{\mathrm{ƛ}}_1+\frac{1}{\Gamma }{\mathrm{ƛ}}_1+p{\mathrm{ƛ}}_1\right)+{\mathrm{ƛ}}_2-\left({\mathrm{ƛ}}_2-1\right)p=-iGr{\mathrm{ƛ}}_3,-\frac{1}{p}={\mathrm{ƛ}}_1\left(0,p\right),0={\mathrm{ƛ}}_1\left(\infty ,p\right),(21)$

${\mathrm{ƛ}}_4^{\prime }-\frac{\mathit{Pr}}{{\lambda }^{*}}{\mathrm{ƛ}}_3+{\mathrm{ƛ}}_4-\left({\mathrm{ƛ}}_4-1\right)p+Q{\mathrm{ƛ}}_3=0,{\mathrm{ƛ}}_3\left(0,\tau \right)=1,{\mathrm{ƛ}}_3\left(\infty ,\tau \right)=0,{\mathrm{ƛ}}_3\left(\eta ,0\right)=0,(22)$

$\begin{array}{l}{\mathrm{ƛ}}_6^{\prime }-Sc{\mathrm{ƛ}}_5+ScSr{\mathrm{ƛ}}_4^{\prime }+{\mathrm{ƛ}}_6-\left({\mathrm{ƛ}}_6-1\right)p-Sc\sigma {\left(1+\delta {\mathrm{ƛ}}_3\right)}^n\phi \exp \left(-\frac{E}{1+\delta {\mathrm{ƛ}}_3}\right)=0,{\mathrm{ƛ}}_5\left(0,\tau \right)=1,\\ {\mathrm{ƛ}}_5\left(\infty ,\tau \right)=0,{\mathrm{ƛ}}_5\left(\eta ,0\right)=0.\end{array}(23)$

Step 3: Apply the Cauchy principal and discretized Eqs 21–23.

After discretization, the obtained set of equations was computed through Matlab, using the code PCM.

Results and discussion

In this section, we present the trends and physical mechanism behind each figure. Table 1 compares our calculations to those in the published literature. It can be concluded that the proposed technique and results are reliable. The following explanations have been noticed from velocity, energy and concentration profiles:

Velocity Profile $\left(f^{\prime }\left(\eta ,\tau \right),g\left(\eta ,\tau \right)\right)$:

TABLE 1

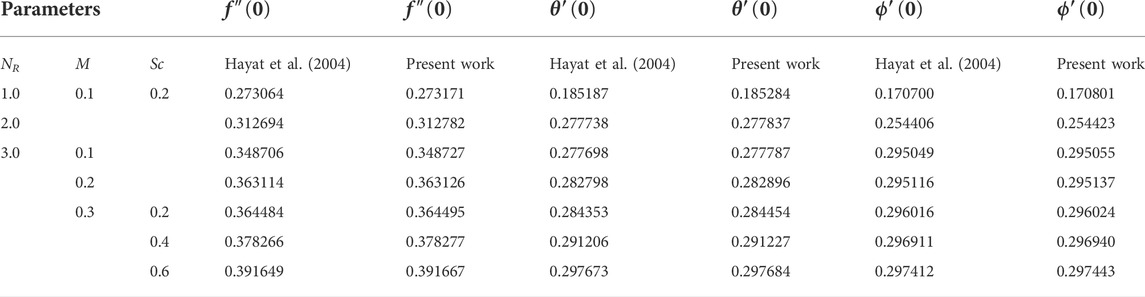
TABLE 1. Comparison of the present outcomes with published work for skin friction, Nusselt and Sherwood numbers, where $\beta =Gr=0.$

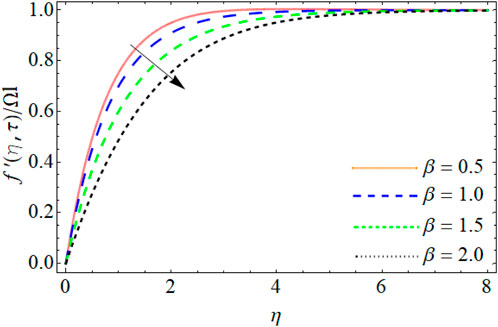
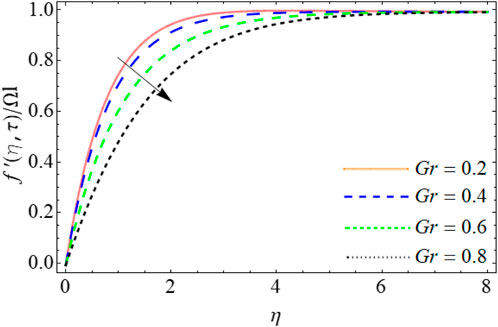
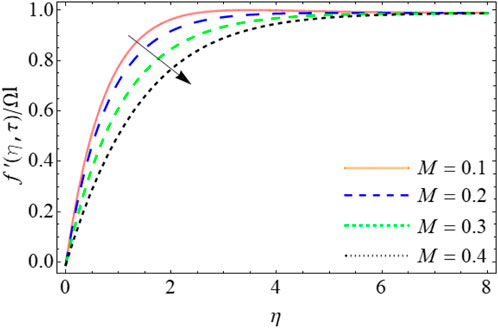
Figures 2–5 display the trend of velocity outlines $f^{\prime }\left(\eta ,\tau \right)$ versus the Casson fluid factor, $\beta$, Grashof number, Gr, magnetic term, M, and parameter,$\tau$, respectively. The primary velocity of the fluid significantly declines with the impact of Casson fluid factor, Grashof number, magnetic term and parameter $\tau$. It can be seen that the effect of Casson fluid factor lessens the fluid velocity $f^{\prime }\left(\eta ,\tau \right)$as presented in Figure 2. The gravitational force enhances, while the angular rotation of the spinning disc decreases the effect of Grashof number, which is why the increasing effect of Gr reduces the velocity field$f^{\prime }\left(\eta ,\tau \right)$as shown in Figure 3. The improving tendency of the magnetic field causes the generation of Lorentz forces, which resist the flow field and decrease its velocity (Figure 4). Figure 5 illustrated that the influence of parameter$\tau$declines the primary velocity contour.

FIGURE 2

FIGURE 2. Velocity outlines $f^{\prime }\left(\eta ,\tau \right)$ versus Casson fluid factor $\beta$.

FIGURE 3

FIGURE 3. Velocity outlines $f^{\prime }\left(\eta ,\tau \right)$ versus Grashof number Gr.

FIGURE 4

FIGURE 4. Velocity outlines $f^{\prime }\left(\eta ,\tau \right)$ versus magnetic term M.

FIGURE 5

FIGURE 5. Velocity outlines $f^{\prime }\left(\eta ,\tau \right)$ versus parameter$\tau$.

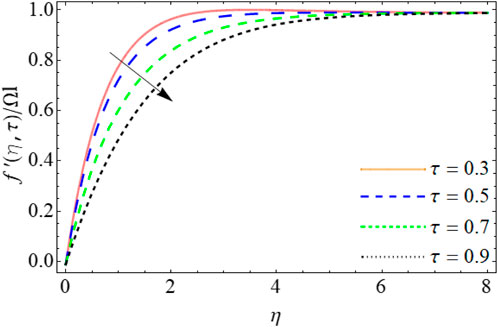
Figures 6–8 illustrate the velocity outlines $g\left(\eta ,\tau \right)$ versus Casson fluid factor $\beta$, Grashof number Gr, magnetic term M and parameter $\tau$ , respectively. It can be seen in Figure 6, that the Casson fluid factor lessens the fluid velocity $g\left(\eta ,\tau \right)$. The gravitational effect augments, while the angular revolution of revolving disc moderates, the value of the Grashof number, because the increasing effect of Gr boosts the secondary velocity field$g\left(\eta ,\tau \right)$as shown in Figure 7. Figures 8 and 9 illustrate that the secondary velocity frameworks decrease with the influence of magnetic field, while they increase with the increase in $\tau$. Physically, the repellant force of the magnetic flux resists the fluid motion, decreasing the velocity field, $g\left(\eta ,\tau \right)$.

Energy Profile $\left(\theta \left(\eta ,\tau \right)\right)$:

FIGURE 6

FIGURE 6. Velocity outlines $g\left(\eta ,\tau \right)$ versus Casson fluid factor $\beta$.

FIGURE 7

FIGURE 7. Velocity outlines $g\left(\eta ,\tau \right)$ versus Grashof number Gr.

FIGURE 8

FIGURE 8. Velocity outlines $g\left(\eta ,\tau \right)$ versus magnetic term M.

FIGURE 9

FIGURE 9. Velocity outlines $g\left(\eta ,\tau \right)$ versus parameter $\tau .$

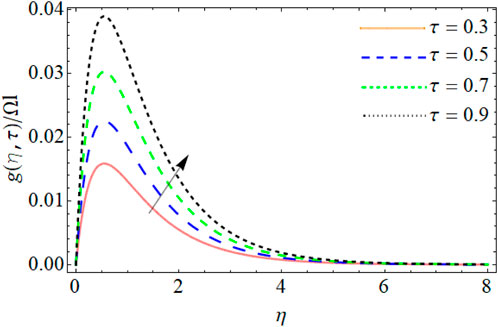
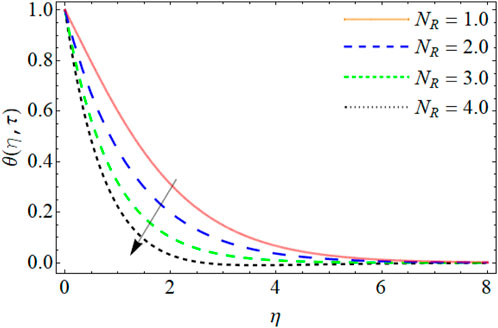
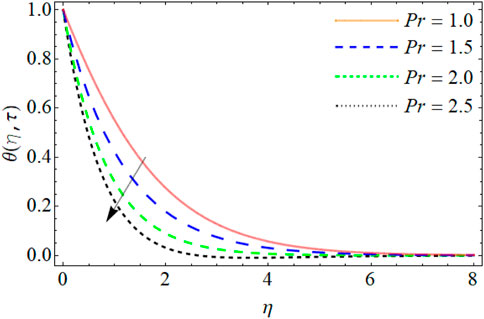
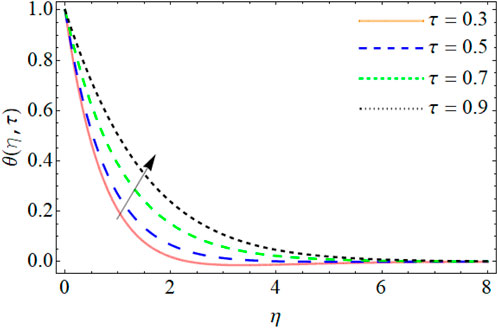
Figures 10–12 illustrate the mechanism behind the energy outlines $\theta \left(\eta ,\tau \right)$ versus the thermal radiation, N_R, the Prandtl number, Pr, and the parameter, $\tau$, respectively. Figures 10, 11 revealed that the energy contours decline with the rising values of thermal radiation and Prandtl number. Physically, radiation from the surface of the fluid transfers thermal energy to the surrounding system, which lowers the fluid temperature and results in the lessening of the energy outline $\theta \left(\eta ,\tau \right)$ as shown in Figure 10. Fluids with higher Prandtl numbers always have lower thermal diffusivity; therefore, an increase in Prandtl number decreases the energy field. Figure 12 shows that the action of parameter $\tau$ diminishes the thermal distribution, $\theta \left(\eta ,\tau \right)$.

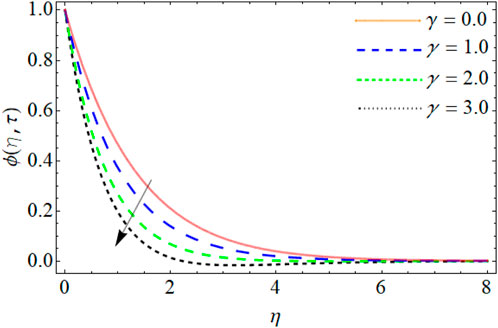
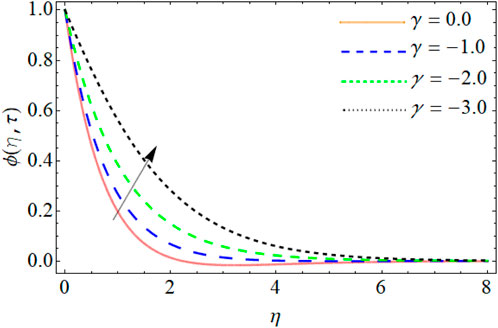
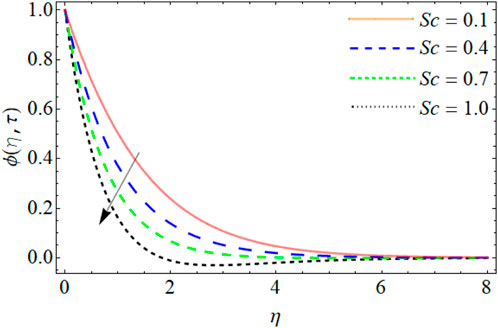
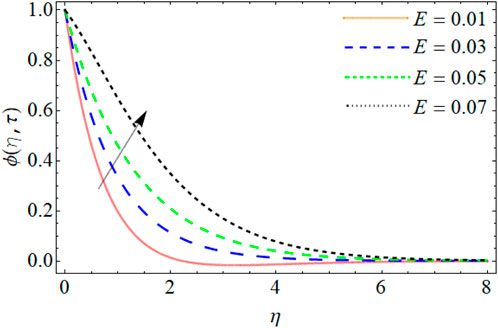
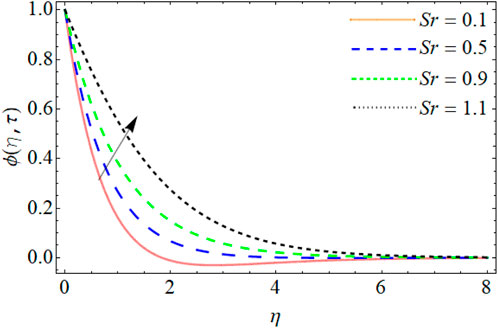
Concentration Profile $\left(\varphi \left(\eta ,\tau \right)\right)$:

FIGURE 10

FIGURE 10. Energy outlines $\theta \left(\eta ,\tau \right)$ versus thermal radiation N_R.

FIGURE 11

FIGURE 11. Energy outlines $\theta \left(\eta ,\tau \right)$ versus Prandtl number Pr.

FIGURE 12

FIGURE 12. Energy outlines $\theta \left(\eta ,\tau \right)$ versus parameter$\tau .$

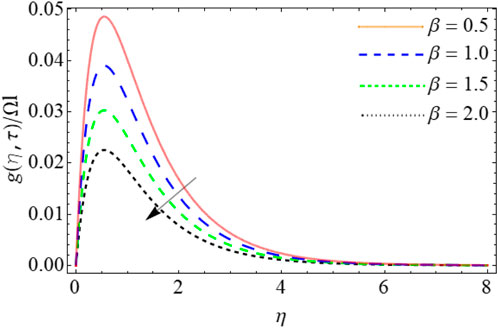
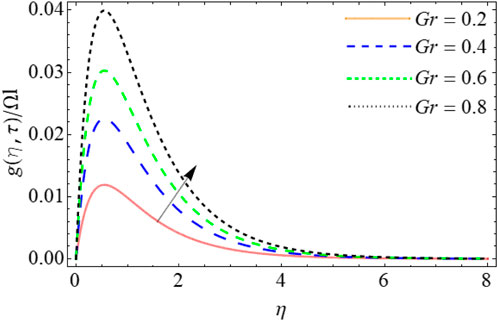
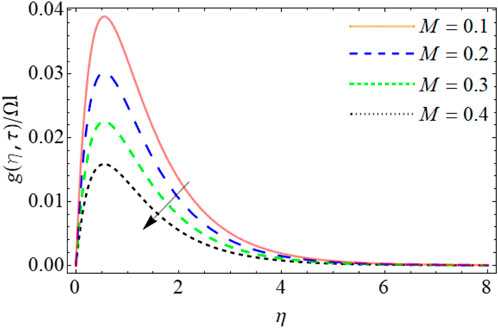
Figures 13–17 reveal the mass profile outlines $\varphi \left(\eta ,\tau \right)$ versus the constructive chemical reaction, $+\gamma ,$ the destructive chemical reaction, $-\gamma ,$ the Schmidt number, Sc, the activation energy, E, and the Soret number, Sr, respectively. Figures 13, 14 depict that the mass transfer field is reduced by the action of positive chemical reaction, $+\gamma$, but augmented by negative chemical reaction, $-\gamma$. The chemical reaction is inversely related to the angular rotation of the circular disk. The increase in chemical reaction regulates the angular motion of disc, as shown in Figures 13, 14. The kinetic viscosity of the fluid is increased, while the molecular diffusion of particles is reduced by the intensifying influence of Sc, which is why an increase in Sc reduces the mass field as presented in Figure 15. Figures 16, 17 show that the concentration contour increases with increasing activation energy and Soret number. The increased activation energy boosts the kinetic energy of fluid particles, which results in acceleration of mass transfer as depicted in Figure 16. Molecular diffusion is enhanced, while the kinetic viscosity increases at high Soret numbers, and, as a consequence, mass transition is enhanced (Figure 17).

FIGURE 13

FIGURE 13. Mass outlines $\varphi \left(\eta ,\tau \right)$ versus constructive chemical reaction$\gamma .$

FIGURE 14

FIGURE 14. Mass outlines $\varphi \left(\eta ,\tau \right)$ versus destructive chemical reaction$\gamma .$

FIGURE 15

FIGURE 15. Mass outlines $\varphi \left(\eta ,\tau \right)$ versus Schmidt number Sc.

FIGURE 16

FIGURE 16. Mass outlines $\varphi \left(\eta ,\tau \right)$ versus activation energy E.

FIGURE 17

FIGURE 17. Mass outlines $\varphi \left(\eta ,\tau \right)$ versus Soret number Sr.

Conclusion

We have examined the numerical simulation of non-coaxial rotation of a Casson fluid and disc. The influence of thermal radiation, second-order chemical reaction, buoyancy, and heat source in a Casson fluid over a rotating frame is also studied. A nonlinear sequence of partial differential equations was used to describe the phenomenon. The modeled equations were reduced to a non-dimensional set of ODEs using similarity replacement. The obtained sets of ODEs were simulated using PCM. The key findings are:

• The Casson fluid coefficient, Grashof number, and magnetic field reduce the fluid’s primary velocity contour$f^{\prime }\left(\eta ,\tau \right)$.

• The secondary velocity $g\left(\eta ,\tau \right)$outline decreases with the increasing value of magnetic field and Casson fluid parameter, but is increased from the effects of parameter $\tau$and the Grashof number.

• The energy field $\theta \left(\eta ,\tau \right)$ decays with the rising values of thermal radiation, parameter $\tau$, and Prandtl number.

• The mass transfer field is decreased by the action of the positive chemical reaction, $+\gamma$, but increases f tomhe effects of negative chemical reactions.

• An increase in the Schmidt number results in a decrease in the mass profile, while the mass profile is enhanced by increasing values of activation energy and Soret number.

• Our mathematical model may be modified for other types of non-Newtonian fluid models and may be solved through fractional and analytical techniques.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Large Groups [Project under grant number (RGP.2/116/43)]. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4350057DSR004.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, N., Khan, U., and Mohyud-Din, S. T. (2018). A theoretical investigation of unsteady thermally stratified flow ofγAl2O3−H2OandγAl2O3−C2H6O2nanofluids through a thin slit. J. Phys. Chem. Solids 119, 296–308. doi:10.1016/j.jpcs.2018.01.046

CrossRef Full Text | Google Scholar

Al-Mubaddel, F. S., Allehiany, F. M., Nofal, T. A., Alam, M. M., Ali, A., and Asamoah, J. K. K. (2022). Rheological model for generalized energy and mass transfer through hybrid nanofluid flow comprised of magnetized cobalt ferrite nanoparticles. J. Nanomater. 2022, 1–11. doi:10.1155/2022/7120982

CrossRef Full Text | Google Scholar

Alharbi, K. A. M., Ahmed, A. E. S., Ould Sidi, M., Ahammad, N. A., Mohamed, A., El-Shorbagy, M. A., et al. (2022). Computational valuation of Darcy ternary-hybrid nanofluid flow across an extending cylinder with induction effects. Micromachines 13 (4), 588. doi:10.3390/mi13040588

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, F., Hou, Y., Zahid, M., and Rana, M. A. (2020). Theoretical study of the reverse roll coating of non-isothermal magnetohydrodynamics viscoplastic fluid. Coatings 10 (10), 940. doi:10.3390/coatings10100940

CrossRef Full Text | Google Scholar

Ali, F., Zahid, M., Hou, Y., Manafian, J., Rana, M. A., and Hajar, A. (2022). A theoretical study of reverse roll coating for a non-isothermal third-grade fluid under lubrication approximation theory. Math. Problems Eng. 2022, 1–18. doi:10.1155/2022/5029132

CrossRef Full Text | Google Scholar

Alsallami, S. A., Zahir, H., Muhammad, T., Hayat, A. U., Khan, M. R., and Ali, A. (2022). Numerical simulation of Marangoni Maxwell nanofluid flow with Arrhenius activation energy and entropy anatomization over a rotating disk. Waves Random Complex Media, 1–19. doi:10.1080/17455030.2022.2045385

CrossRef Full Text | Google Scholar

Asghar, S., Hanif, K., and Hayat, T. (2007). The effect of the slip condition on unsteady flow due to non-coaxial rotations of disk and a fluid at infinity. Meccanica 42 (2), 141–148. doi:10.1007/s11012-006-9027-5

CrossRef Full Text | Google Scholar

Azam, M., and Abbas, Z. (2021). Recent progress in Arrhenius activation energy for radiative heat transport of cross nanofluid over a melting wedge. Propuls. Power Res. 10, 383–395. doi:10.1016/j.jppr.2021.11.004

CrossRef Full Text | Google Scholar

Azam, M. (2022). Bioconvection and nonlinear thermal extrusion in development of chemically reactive Sutterby nano-material due to gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 130, 105820. doi:10.1016/j.icheatmasstransfer.2021.105820

CrossRef Full Text | Google Scholar

Azam, M. (2022). Effects of Cattaneo-Christov heat flux and nonlinear thermal radiation on MHD Maxwell nanofluid with Arrhenius activation energy. Case Stud. Therm. Eng. 34, 102048. doi:10.1016/j.csite.2022.102048

CrossRef Full Text | Google Scholar

Azam, M., Mabood, F., and Khan, M. (2022). Bioconvection and activation energy dynamisms on radiative sutterby melting nanomaterial with gyrotactic microorganism. Case Stud. Therm. Eng. 30, 101749. doi:10.1016/j.csite.2021.101749

CrossRef Full Text | Google Scholar

Azam, M., Xu, T., Mabood, F., and Khan, M. (2021). Non-linear radiative bioconvection flow of cross nano-material with gyrotatic microorganisms and activation energy. Int. Commun. Heat Mass Transf. 127, 105530. doi:10.1016/j.icheatmasstransfer.2021.105530

CrossRef Full Text | Google Scholar

Benhacine, H., Mahfoud, B., and Salmi, M. (2022). Stability of conducting fluid flow between coaxial cylinders under thermal gradient and axial magnetic Field. Int. J. Thermofluid Sci. Technol. 9 (2). doi:10.36963/ijtst.2022090202

CrossRef Full Text | Google Scholar

Chu, Y. M., Bashir, S., Ramzan, M., and Malik, M. Y. (2022). Model‐based comparative study of magnetohydrodynamics unsteady hybrid nanofluid flow between two infinite parallel plates with particle shape effects. Math. Methods Appl. Sci. doi:10.1002/mma.8234

CrossRef Full Text | Google Scholar

Chu, Y. M., Nazir, U., Sohail, M., Selim, M. M., and Lee, J. R. (2021). Enhancement in thermal energy and solute particles using hybrid nanoparticles by engaging activation energy and chemical reaction over a parabolic surface via finite element approach. Fractal Fract. 5 (3), 119. doi:10.3390/fractalfract5030119

CrossRef Full Text | Google Scholar

Chu, Y. M., Shankaralingappa, B. M., Gireesha, B. J., Alzahrani, F., Khan, M. I., and Khan, S. U. (2022). Combined impact of Cattaneo-Christov double diffusion and radiative heat flux on bio-convective flow of Maxwell liquid configured by a stretched nano-material surface. Appl. Math. Comput. 419, 126883. doi:10.1016/j.amc.2021.126883

CrossRef Full Text | Google Scholar

Dadheech, P. K., Agrawal, P., Sharma, A., Nisar, K. S., and Purohit, S. D. (2022). Marangoni convection flow of γ–Al2O3 nanofluids past a porous stretching surface with thermal radiation effect in the presence of an inclined magnetic field. Heat. Trans. 51 (1), 534–550. doi:10.1002/htj.22318

CrossRef Full Text | Google Scholar

Das, S., Tarafdar, B., and Jana, R. N. (2018). Hall effects on magnetohydrodynamics flow of nanofluids due to non-coaxial rotation of a porous disk and a fluid at infinity. J. nanofluids 7 (6), 1172–1186. doi:10.1166/jon.2018.1527

CrossRef Full Text | Google Scholar

Elattar, S., Helmi, M. M., Elkotb, M. A., El-Shorbagy, M. A., Abdelrahman, A., Bilal, M., et al. (2022). Computational assessment of hybrid nanofluid flow with the influence of hall current and chemical reaction over a slender stretching surface. Alexandria Eng. J. 61 (12), 10319–10331. doi:10.1016/j.aej.2022.03.054

CrossRef Full Text | Google Scholar

Erdogan, M. E. (1977). Flow due to noncoaxial rotations of a porous disk and a fluid at infinity. Rev. Roum. Sci. Tech. Ser. Mec. Appl. 22, 171–178.

Google Scholar

Erdoḡan, M. E. (1997). Unsteady flow of a viscous fluid due to non-coaxial rotations of a disk and a fluid at infinity. Int. J. non-linear Mech. 32 (2), 285–290. doi:10.1016/s0020-7462(96)00065-0

CrossRef Full Text | Google Scholar

Ersoy, H. V. (2017). Unsteady flow due to a disk executing non-torsional oscillation and a Newtonian fluid at infinity rotating about non-coaxial axes. Sādhanā 42 (3), 307–315. doi:10.1007/s12046-017-0600-5

CrossRef Full Text | Google Scholar

Fei, J., Lin, B., Huang, T., and Xiao, J. (2022). Thin floor milling using moving support. Int. J. Adv. Manuf. Technol. 120 (1), 1385–1397. doi:10.1007/s00170-022-08814-z

CrossRef Full Text | Google Scholar

Hassan, M., Ali, S., Aich, W., Khlissa, F., Ayadi, B., and Kolsi, L. (2022). Transport pattern of Non-Newtonian mass and thermal energy under two diverse flow conditions by using modified models for thermodynamics properties. Case Stud. Therm. Eng. 29, 101714. doi:10.1016/j.csite.2021.101714

CrossRef Full Text | Google Scholar

Hassan, M., Al‐Khaled, K., Khan, S. U., Tlili, I., and Chammam, W. (2021). Assessment of boundary layer for flow of non‐Newtonian material induced by a moving belt with power law viscosity and thermal conductivity models. Numer. Methods Partial Differ. Equ. num, 22743. doi:10.1002/num.22743

CrossRef Full Text | Google Scholar

Hassan, M., El‐Zahar, E. R., Khan, S. U., Rahimi‐Gorji, M., and Ahmad, A. (2021). Boundary layer flow pattern of heat and mass for homogenous shear thinning hybrid‐nanofluid: An experimental data base modeling. Numer. Methods Partial Differ. Equ. 37 (2), 1234–1249. doi:10.1002/num.22575

CrossRef Full Text | Google Scholar

Hassan, M. (2018). Impact of iron oxide particles concentration under a highly oscillating magnetic field on ferrofluid flow. Eur. Phys. J. Plus 133 (6), 1–14. doi:10.1140/epjp/i2018-12045-7

CrossRef Full Text | Google Scholar

Hayat, T., Asghar, S., Siddiqui, A. M., and Haroon, T. (2001). Unsteady MHD flow due to non-coaxial rotations of a porous disk and a fluid at infinity. Acta Mech. 151 (1), 127–134. doi:10.1007/bf01272530

CrossRef Full Text | Google Scholar

Hayat, T., Ellahi, R., Asghar, S., and Siddiqui, A. M. (2004). Flow induced by non-coaxial rotation of a porous disk executing non-torsional oscillations and a second-grade fluid rotating at infinity. Appl. Math. Model. 28 (6), 591–605. doi:10.1016/j.apm.2003.10.011

CrossRef Full Text | Google Scholar

Iqbal, S. A., Hafez, M. G., Chu, Y. M., and Park, C. (2022). Dynamical Analysis of nonautonomous RLC circuit with the absence and presence of Atangana-Baleanu fractional derivative. jaac. 12 (2), 770–789. doi:10.11948/20210324

CrossRef Full Text | Google Scholar

Ishtiaq, F., Ellahi, R., Bhatti, M. M., and Alamri, S. Z. (2022). Insight in thermally radiative cilia-driven flow of electrically conducting non-Newtonian Jeffrey fluid under the influence of induced magnetic field. Mathematics 10 (12), 2007. doi:10.3390/math10122007

CrossRef Full Text | Google Scholar

Jabbar, N., Hafeez, M. B., Askar, S., and Nazir, U. (2021). Non-coaxially rotating motion in Casson martial along with temperature and concentration gradients via first-order chemical reaction. Energies 14 (22), 7784. doi:10.3390/en14227784

CrossRef Full Text | Google Scholar

Jin, F., Qian, Z. S., Chu, Y. M., and ur Rahman, M. (2022). On nonlinear evolution model for drinking behavior under Caputo-Fabrizio derivative. jaac. 12 (2), 790–806. doi:10.11948/20210357

CrossRef Full Text | Google Scholar

Lin, Y., Zheng, L., and Zhang, X. (2014). Radiation effects on Marangoni convection flow and heat transfer in pseudo-plastic non-Newtonian nanofluids with variable thermal conductivity. Int. J. Heat Mass Transf. 77, 708–716. doi:10.1016/j.ijheatmasstransfer.2014.06.028

CrossRef Full Text | Google Scholar

Mabood, F., Yusuf, T. A., and Khan, W. A. (2021). Cu–Al2O3–H2O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation. J. Therm. Anal. Calorim. 143 (2), 973–984. doi:10.1007/s10973-020-09720-w

CrossRef Full Text | Google Scholar

Nazeer, M., Hussain, F., Khan, M. I., El-Zahar, E. R., Chu, Y. M., Malik, M. Y., et al. (2022). Theoretical study of MHD electro-osmotically flow of third-grade fluid in micro channel. Appl. Math. Comput. 420, 126868. doi:10.1016/j.amc.2021.126868

CrossRef Full Text | Google Scholar

Noranuar, W. N. I. N., Mohamad, A. Q., Shafie, S., Khan, I., Jiann, L. Y., and Ilias, M. R. (2021). Non-coaxial rotation flow of MHD Casson nanofluid carbon nanotubes past a moving disk with porosity effect. Ain Shams Eng. J. 12 (4), 4099–4110. doi:10.1016/j.asej.2021.03.011

CrossRef Full Text | Google Scholar

Punith Gowda, R. J., Naveen Kumar, R., Jyothi, A. M., Prasannakumara, B. C., and Sarris, I. E. (2021). Impact of binary chemical reaction and activation energy on heat and mass transfer of marangoni driven boundary layer flow of a non-Newtonian nanofluid. Processes 9 (4), 702. doi:10.3390/pr9040702

CrossRef Full Text | Google Scholar

Raja, M. A. Z., Shoaib, M., Hussain, S., Nisar, K. S., and Islam, S. (2022). Computational intelligence of Levenberg-Marquardt backpropagation neural networks to study thermal radiation and Hall effects on boundary layer flow past a stretching sheet. Int. Commun. Heat Mass Transf. 130, 105799. doi:10.1016/j.icheatmasstransfer.2021.105799

CrossRef Full Text | Google Scholar

Ramesh, G. K., Madhukesh, J. K., Prasannakumara, B. C., and Roopa, G. S. (2022). Significance of aluminium alloys particle flow through a parallel plates with activation energy and chemical reaction. J. Therm. Anal. Calorim. 147 (12), 6971–6981. doi:10.1007/s10973-021-10981-2

CrossRef Full Text | Google Scholar

Rashid, S., Sultana, S., Karaca, Y., Khalid, A., and Chu, Y. M. (2022). Some further extensions considering discrete proportional fractional operators. Fractals 30 (01), 2240026. doi:10.1142/s0218348x22400266

CrossRef Full Text | Google Scholar

Rehman, S., Gul, T., Khan, W., Khan, A., and Zee, S. (2022). Effects of chemical reaction, viscosity, thermal conductivity, heat source, radiation/absorption, on MHD mixed convection nano-fluids flow over an unsteady stretching sheet by HAM and numerical method. Adv. Mech. Eng. 14 (1), 168781402210743. doi:10.1177/16878140221074301

CrossRef Full Text | Google Scholar

Rizwan, M., and Hassan, M. (2022). Feature of metallic oxide nanoparticles in the thermal efficiency and flow structure of non-Newtonian homogeneous nanofluid: Experimental data-based mathematical approach. Waves Random Complex Media, 1–20.

CrossRef Full Text | Google Scholar

Sharma, K., Kumar, S., Narwal, A., Mebarek-Oudina, F., and Animasaun, I. L. (2022). Convective MHD fluid flow over stretchable rotating disks with dufour and Soret effects. Int. J. Appl. Comput. Math. 8 (4), 159–212. doi:10.1007/s40819-022-01357-7

CrossRef Full Text | Google Scholar

Shuaib, M., Shah, R. A., and Bilal, M. (2020). Variable thickness flow over a rotating disk under the influence of variable magnetic field: An application to parametric continuation method. Adv. Mech. Eng. 12 (6), 168781402093638. doi:10.1177/1687814020936385

CrossRef Full Text | Google Scholar

Shuaib, M., Shah, R. A., Durrani, I., and Bilal, M. (2020). Electrokinetic viscous rotating disk flow of Poisson-Nernst-Planck equation for ion transport. J. Mol. Liq. 313, 113412. doi:10.1016/j.molliq.2020.113412

CrossRef Full Text | Google Scholar

Tie-Hong, Z., Zhou, B. C., Miao-Kun, W., and Yu-Ming, C. (2019). On approximating the quasi-arithmetic mean. J. Inequalities Appl. 2019 (1), 1–12.

Google Scholar

Ullah, I. (2022). Activation energy with exothermic/endothermic reaction and Coriolis force effects on magnetized nanomaterials flow through Darcy–Forchheimer porous space with variable features. Waves in random and complex media, 1–14.

CrossRef Full Text | Google Scholar

Ullah, I., Ali, R., Nawab, H., Uddin, I., Muhammad, T., Khan, I., et al. (2022). Theoretical analysis of activation energy effect on Prandtl–Eyring nanoliquid flow subject to melting condition. J. Non-Equilibrium Thermodyn. 47 (1), 1–12. doi:10.1515/jnet-2020-0092

CrossRef Full Text | Google Scholar

Ullah, I., Hayat, T., Aziz, A., and Alsaedi, A. (2022). Significance of entropy generation and the coriolis force on the three-dimensional non-Darcy flow of ethylene-glycol conveying carbon nanotubes (SWCNTs and MWCNTs). J. Non-Equilibrium Thermodyn. 47 (1), 61–75. doi:10.1515/jnet-2021-0012

CrossRef Full Text | Google Scholar

Ullah, Z., Ullah, I., Zaman, G., and Sun, T. C. (2022). A numerical approach to interpret melting and activation energy phenomenon on the magnetized transient flow of Prandtl–Eyring fluid with the application of Cattaneo–Christov theory. Waves in Random and Complex Media, 1–21.

CrossRef Full Text | Google Scholar

Wakif, A., Chamkha, A., Thumma, T., Animasaun, I. L., and Sehaqui, R. (2021). Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina–copper oxide hybrid nanofluids utilizing the generalized Buongiorno’s nanofluid model. J. Therm. Anal. Calorim. 143 (2), 1201–1220. doi:10.1007/s10973-020-09488-z

CrossRef Full Text | Google Scholar

Wang, F., Khan, M. N., Ahmad, I., Ahmad, H., Abu-Zinadah, H., and Chu, Y. M. (2022). Numerical solution of traveling waves in chemical kinetics: Time-fractional Fishers equations. Fractals 30 (2), 2240051–2240134. doi:10.1142/s0218348x22400515

CrossRef Full Text | Google Scholar

Wei, H., Gu, J., Ren, F., Zhang, L., Xu, G., Wang, B., et al. (2021). Smart materials for dynamic thermal radiation regulation. Small 17 (35), 2100446. doi:10.1002/smll.202100446

CrossRef Full Text | Google Scholar

Yaseen, M., Rawat, S. K., and Kumar, M. (2022). Cattaneo–Christov heat flux model in Darcy–Forchheimer radiative flow of MoS2–SiO2/kerosene oil between two parallel rotating disks. J. Therm. Anal. Calorim. 147, 10865–10887. doi:10.1007/s10973-022-11248-0

CrossRef Full Text | Google Scholar

Zhao, T. H., Khan, M. I., and Chu, Y. M. (2021). Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non‐Newtonian fluid between two rotating disks. Math. Methods Appl. Sci. doi:10.1002/mma.7310

CrossRef Full Text | Google Scholar