- Energy Storage & Electric Transportation Department, Energy and Environmental Science and Technology, Idaho National Laboratory, Idaho Falls, ID, United States
Electrochemical impedance spectroscopy (EIS) is a valuable technique to detect the health status and aging phenomena in lithium-ion batteries (LiB). Equivalent circuit modeling (ECM) is conventionally used when interpreting EIS data and gaining physical insights into the aging mechanisms. However, performing ECM is resource intensive and expert-level of knowledge is usually required to select suitable models and fitting parameters. This article presents a quick and user-friendly data analysis algorithm as an alternative to ECM by mathematically fitting geometric features in Nyquist plots and obtaining the growth trends of the features. The evolving trends in the Nyquist plots, such as chord lengths of the arcs and interception points, are consistent with the growth of resistance components obtained using ECM with R2 values from 0.67 to 0.99, and therefore can be used as indicators of battery aging. Our results show that the quick-fitting approach is suitable for analyzing a series of EIS data acquired during battery cycling and identifying the underlying aging mechanisms.
Introduction
Electrochemical impedance spectroscopy (EIS) is a fast and non-invasive characterization technique for understanding chemical and electrochemical phenomena occurring in electrochemical devices, such as Li-ion batteries (LiBs) (Meddings et al., 2020) and fuel cells (Tang et al., 2020). In EIS analysis, a current or voltage perturbation is applied to a cell across a wide range of frequencies from mHz to MHz, in which the corresponding response of voltage (or current) across the frequency range establishes the impedance spectrum (Choi et al., 2020). These impedance responses are the basis of isolating various conduction and transport phenomena at specific time scales in a cell, including charge transfer, diffusion, and molecule absorption (Park et al., 2010; Wang et al., 2021; Vivier and Orazem, 2022). In recent years, EIS has been recognized as a powerful tool for probing the health status in LiBs and solid-state electrolyte batteries (Gordon et al., 2016; Zhang et al., 2017; Frankenberger et al., 2019; Zhang et al., 2020) because changes in impedance are the direct consequences of degradation in the cells, such as electrode particle cracking and interlayer formation that slow down the charge transfer and diffusion processes (Westerhoff et al., 2016; Tatara et al., 2019; Iurilli et al., 2021; Vadhva et al., 2021). As battery lifetime and operational safety are heavily emphasized in electric vehicles and stationary storage systems, real-time EIS analysis will be advantageous to be integrated into battery management systems and detect degradation early, therefore ensures reliable and safe operations over extended lifespans (Pastor-Fernandez et al., 2016; Din et al., 2017). Rapid EIS measurement tools (Tanim et al., 2020; Hill et al., 2021) have also become available for scanning over broad ranges of frequencies within minutes to acquire EIS data promptly for real-time measurements.
While EIS data can be obtained fast, the interpretation of the data might not be as swift. Equivalent circuit modeling (ECM) is traditionally used to analyze and interpret EIS data. In ECM analysis, a LiB cell and all the electrochemical phenomena occurring within are converted into electrical circuits that consist of resistors, capacitors, and other circuit elements (Westerhoff et al., 2016). Constructing such an ECM is a resource- and time-intensive process. Depending on the battery architecture and use conditions, the ECM could vary from a simple resistor–capacitor (RC) circuit model to complex combinations of circuit components in series (Westerhoff et al., 2016; Choi et al., 2020). Multiple model candidates will usually need to be screened based on the cell’s physics, followed by mathematical fitting procedures to determine the optimized model and circuit parameters. Ambiguity may arise during the fitting process when multiple ECMs fit the data non-uniquely, adding uncertainties in data interpretation (Buteau and Dahn, 2019). For the reasons stated above, equivalent circuit analysis could be tedious and time-consuming. Experienced researchers and special software packages are usually involved in selecting reasonable fitting parameters and interpret the data unambiguously.
To lower the barrier and minimize uncertainties in EIS data analysis, computer- and machine learning-based methodologies have emerged in recent years (Buteau and Dahn, 2019; Zhu et al., 2019; Bredar et al., 2020; Murbach et al., 2020; Zhang et al., 2020; Babaeiyazdi et al., 2021; Huang et al., 2021; Bongiorno et al., 2022). These methods automate the equivalent circuit parameter search, make ECM screening efficient, and relieve the burden of human judgments for making initial guesses and data processing for non-experts (Buteau and Dahn, 2019; Zhu et al., 2019; Murbach et al., 2020). However, large datasets are usually required for establishing computer-based EIS analysis methodologies. Most of the computational methods involve data featurization, such as converting the Nyquist plots to mathematical features (Zhang et al., 2020; Babaeiyazdi et al., 2021; Jones et al., 2022), which allows computers to select fitting parameters based on the features. Hundreds to thousands of Nyquist plots and their corresponding ECMs will be required to accommodate various battery designs and gain reliability in the analysis (Buteau and Dahn, 2019; Zhang et al., 2020). Furthermore, the mathematical features recognized are usually not identifiable by humans and do not necessarily carry physical meanings, posing a challenge in linking the features in EIS data to specific aging phenomena.
In this work, we combine the advantages of ECM and computer-based methods to construct a non-expert-friendly approach to analyzing EIS data without involving extensive ECM fittings or large datasets. A least-square fitting approach is used to quickly capture geometric features that are related to battery aging in a Nyquist plot, such as intersection, radius, and chord lengths of the depressed semi-arcs. This quick-fitting method was demonstrated on a set of graphite/NMC532 single layer pouch cells, in which two distinctive aging behaviors exist, namely loss of active materials in the cathodes (LAMPE) and loss of Li inventory (LLI) (Birkl et al., 2017; Tanim et al., 2021a; Tanim et al., 2022). The quick-fitting algorithm shows that the intersections and chord lengths of the semi-arcs in the Nyquist plots are consistent with the growth trend of resistances, and that an increased chord length can serve as an indicator for distinguishing LAMPE from LLI.
Our quick-fitting algorithm complements the conventional ECM by quickly surveying the progression of series of EIS curves without extensive modeling efforts, therefore reducing the time consumption and complexity in evaluating larger sets of EIS data. The method will be advantageous for online battery management systems to perform automated data analysis during battery cycling. Moving forward, the quick-fitting algorithm has the potential to be combined with fast EIS data acquisition techniques (Tanim et al., 2020; Tanim et al., 2021b; Hill et al., 2021) and coupled with other machine learning-based aging-detection frameworks (Dubarry et al., 2017; Severson et al., 2019; Zhang et al., 2020; Chen et al., 2021; Kim et al., 2022) to aid the diagnosis of battery degradation and unraveling the underlying aging mechanisms.
Materials and methods
Cell fabrication and aging cycles
The cells are built using Graphite (1506T) and NMC532 (Toda America), fabricated at the Cell Analysis, Modeling, and Prototyping (CAMP) Facility at Argonne National Laboratory. The cells were designed using two different electrode active material loadings (denoted as Lmoderate and Llow), and were tested under various charge profiles. More details about the cell materials, designs, numberings, and charge profiles can be found in Supplementary Tables S1–S3 in Supporting Information 1.
The cells were tested using a MACCOR series 4000 Automated Test System at 30°C ± 1°C. During each life cycle, the cells were charged between 10 and 15 min with different charging protocols. All the cells were charged to 4.1 V, except in 2 cells lower cut-off voltages of 3.78 or 3.66 V were applied. Reference performance tests (RPTs) were conducted every 25–50 cycles initially, and every 100–125 cycles in the later stages over the course of aging. An RPT test includes a C/20 charge-discharge test between 3.0 and 4.1 V separated by 1 h rest time, followed by EIS measurement at selected RPTs. Before the EIS test, cells were charged to 3.8 V at C/1 and rested for 15 min. EIS was measured with an AC voltage amplitude of 10 mV over a frequency range of 500 kHz to 0.01 Hz. A Solartron 1287 potentiostat and analyzer (Model 1260) were used for EIS measurements. The cells were subjected to different numbers of aging cycles. The Lmoderate cells were cycled to 450 cycles. The Llow cells went up to 600 cycles, except two of them were charged to a lower cut-off voltage and cycled to 1000 cycles. Selected cells were disassembled for secondary post-testing characterizations to determine predominant aging modes. Detailed information about charging protocols can be referred to Supplementary Table S2 in Supporting Information 1.
Equivalent circuit modeling and fitting
The EIS data collected are processed using the ECM approach as a comparison to the mathematical quick-fitting approach that will be discussed later in this article. An basic ECM contains electrical components, i.e., resistors and capacitors, to simulate bulk, surface-interphase, and diffusion behaviors (Westerhoff et al., 2016). The model used in this article, as shown in Figure 1A is based on the most widely-accepted LiB system with minimized circuit elements for practical impedance analysis (Choi et al., 2020; Iurilli et al., 2021). The bulk resistance (ROhm) is a combined resistant effect from current collector, electrode, electrolyte, and separator. The constant phase elements (CPEs) are used to simulate non-ideal capacitances of LiBs to make the model more accurate. The CPESEI and CPEDL represent the capacitances of solid electrolyte interface (SEI) layer and double layer, respectively. RSEI and RCT represent the resistances of SEI layer and charge-transfer process, respectively. Warburg impedance describes diffusional effects of lithium-ion on the host material. Figure 1B shows a comparison between an experimental Nyquist plot from one of the graphite/NMC532 cells at 600 cycle and the fitting results. The result shows good match between measured data and fitted data. More discussion about the fitting approach, mathematical expressions, and quality of fitting can be found in Supporting Information 2.
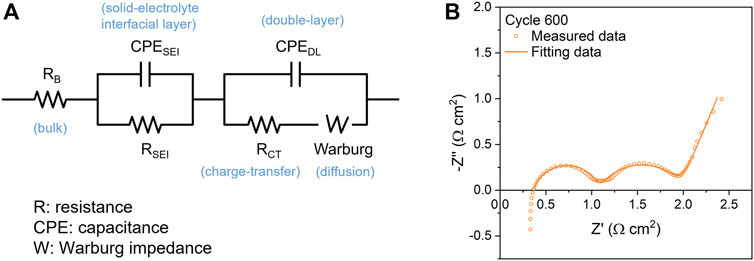
FIGURE 1. Equivalent circuit model and fitting results demonstration. (A) The equivalent circuit model used in this study. (B) A demonstration of the fitting results of a cell at the 600th cycle (P492 Cell 42), showing good consistency between raw data (dot) and fitted data (solid line).
Construction of quick EIS fitting algorithms
A typical Nyquist plot of the graphite/NMC532 cells in this study is shown in Figure 2. The Nyquist plot consists of two arcs located at higher (frequency range 105—103 Hz, referred as the first arc) and lower frequency domains (frequency range 103–1 Hz, referred as the second arc), followed by a tail. This type of EIS curve is common in LiBs (Choi et al., 2020; Iurilli et al., 2021). The impedance arc at higher frequency comes from the solid electrolyte interface (SEI) layer (RSEI), which is related to the resistance of anode materials and SEI layer. The arc at lower frequency is the response from charge transfer (RCT), which is linked to the kinetics of electrochemical reactions. RCT is heavily dependent on material properties such as phase transition, bandgap structure, particle integrity and size, and surface coating, making it an effective indicator to interpret reaction mechanisms in a cell. The longer tail following the arcs originates from Warburg diffusional effects.
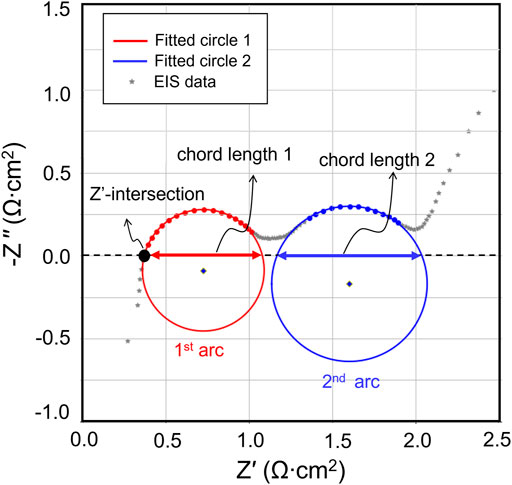
FIGURE 2. An example of quick EIS fitting. The raw EIS data is shown in the grey dots. The red and blue circles are the least square fitting results of the first and second arc, respectively. On each of the circles, the red and blue dots represent the range of fitting. Three geometry features of interest, Z′-intersection and chord length of 1st and 2nd arc, are marked accordingly in the diagram.
In our approach, the arcs in the EIS data (x, y files) are fitted directly to partial circles as a mathematical proxy to describe the shape of the Nyquist plot. The fitting algorithm is built using Python. We referenced an optimized least squares approach under the scipy package (Virtanen et al., 2020) to search the least square circle fit for the data. The input data range is changed along with the datapoints in the arc to determine the best fits and uncertainties. Detailed information regarding the fitting process and methods are discussed in Supporting Information 3. There are several mathematical features that can be extracted from the least square circle fitting, including the chord lengths of the semi-arcs, and intersection point with -Z′′ = 0. The chord length, determined by the radius and center of the fitted circle, will be an approximation for RSEI (chord length 1) and RCT (chord length 2). The -Z″ intersection represent the ROhm. In the following demonstrations, the chord length will be compared to the resistance obtained using ECM fitting.
Results and discussion
Lifetime behavior of the cells
The major aging modes of the cells in this study align with loss of Li inventory (LLI) and loss of active materials in the cathode (LAMPE). The aging behaviors were previously identified using various non-destructive (e.g., incremental capacity (IC) analysis) and destructive methods (e.g., optical and electron microscopy, ex situ X-ray scattering) (Paul et al., 2021a; Tanim et al., 2021a; Chinnam et al., 2021; Tanim et al., 2022). LLI is confirmed using both incremental capacity (IC) analysis (Dubarry et al., 2012) and disassembly of cell at the end of lifetime. The diagnosis of LAMPE is based on SEM images showing secondary particle cracking and on half-cells assembled from cathodes harvested after cycling, as well as IC analysis (Tanim et al., 2021a). Loss of active materials in the anode (LAMNE) was not included in the discussion because aging in the anode is minor.
IC analysis was performed to quantify the amounts of LLI and LAMPE of representative Lmoderate and Llow cells at the end of cycling life, and the amounts of LAMPE and LLI are summarized in Figure 3. The primary aging behavior can be correlated with the design of the cells and charging rates. In the Llow cases, cathode cracking induced LAMPE is the most significant aging mode (Tanim et al., 2021a) because of its higher charge acceptance and cathode utilization, causing more stress during cycling. When the charging cutoff voltage is reduced to 3.78 or 3.66 V, the amount of cracking and thus LAMPE is reduced even at 9C rate. In contrast, the Lmoderate series, in which the anode loading is higher, the dominant aging behavior becomes higher in LLI with less amount of LAMPE (Chinnam et al., 2021). For Lmoderate cells cycled with greater than 4.5C protocol, the cells suffer from Li plating, a severe form of LLI; whereas those cycled at 4C only exhibit minor LLI caused by SEI growth (Paul et al., 2021a; Paul et al., 2021b). This phenomenon is attributed to more severe electrolyte depletion at the anode during high C-rate, causing sluggish Li ion transport.
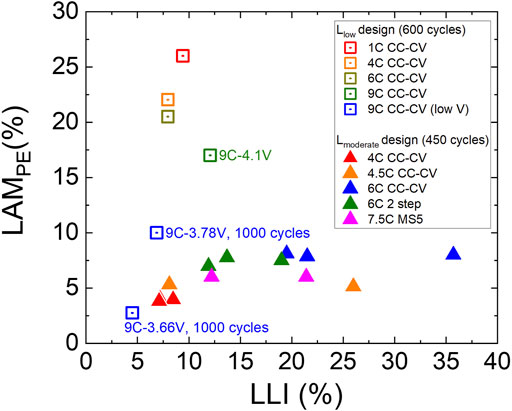
FIGURE 3. Scattering plot showing the amount of LLI and LAMPE at the end of cycling life of represented cells with different charge protocols. LAMPE is more significant in Llow designs, while LLI is prominent in the Lmoderate cells. CC-CV, 2 step, and MS5 represent various charge protocols, which is described in and Supporting Information 1. All the cells are charged to 4.1 V except for 2 cells are charged to 3.78 and 3.66 V, respectively (marked with “low V” in the legend). More details about the cell’s behavior can be found in previous publications (Paul et al., 2021a; Paul et al., 2021b; Chen et al., 2021; Chinnam et al., 2021).
EIS trends and primary aging behaviors
EIS data of five representative cells are selected based on their dominant aging modes (LLI or LAMPE) and the percentage of LAMPE and LLI are listed in Table 1. The cells and aging behaviors include:
• LAMPE dominated (Llow 1C and 9C)
• Mild aging due to a lower voltage cut-off during charging (Llow 9C-3.78 V)
• LLI dominated, in the form SEI-formation (Lmoderate 4C)
• LLI dominated, in the form of Li plating (Lmoderate 6C)

TABLE 1. Percentage of LAMPE and LLI of the cells in Figure 4 obtained using IC analysis.
The EIS as a function of cycle numbers are presented in Figure 4. Across the two electrode loadings and various cycling conditions, one common feature is that the first arc grows steadily over the course of aging, while the second arc evolves distinctively with higher or lower amount of LAMPE. As shown in Figures 4A, B, which are the high LAMPE cases, the second arc not only moves to the right, but the size also grows significantly at 600 cycles (as marked by the arrows). In contrast, when a lower cutoff voltage of (3.78 V) instead of 4.1 V is applied to the cell during charging, the second arc does not grow obviously even after 1000 cycles (Figure 4C). The link between growth of the second arc and LAMPE can be further rationalized by the behavior in Figures 4D, E. Both cells exhibit low amount of LAMPE and higher LLI, and the latter is caused by two different mechanisms, namely SEI-growth and Li plating. 4(d) ages through SEI-growth, a mild form of LLI, in which the capacity fade remains below 10%. The case in 4(e) suffered from heavy Li plating due to the interplay between a higher C-rate and greater anode thickness. In this case, Li plating causes ∼15% of capacity fade in the initial 100 cycles and close to ∼20% at the end of 450 cycles. Whether LLI is severe or not, the second arc in Figures 4D, E evolve similarly and does not exhibit significant growth at later stages of aging. Therefore, the growth of the second arc can be exclusively attributed to LAMPE instead of LLI. From an angle of electrochemical reactions, as LAMPE occurs in the form of cathode cracking, the overpotential for charge transfer reactions increases and therefore leads to an increased RCT For this reason, RCT is concluded to be exclusively correlated to LAMPE.
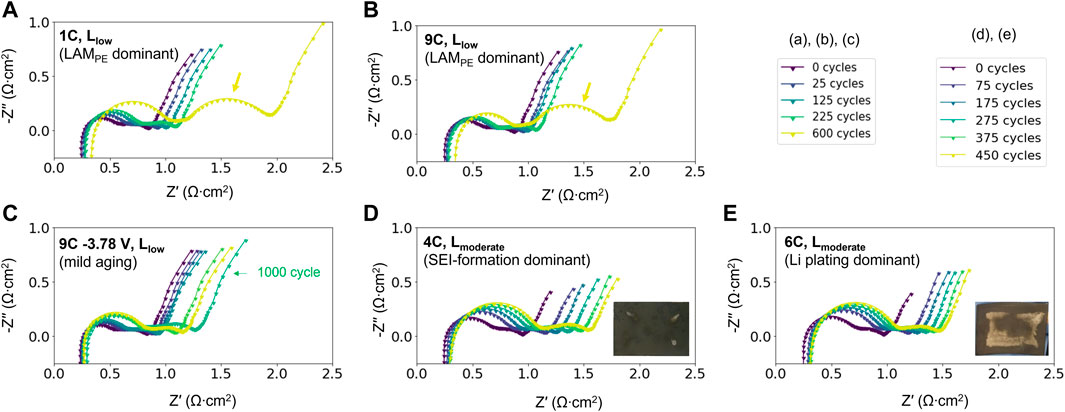
FIGURE 4. EIS trends for representative cell aging behaviors. (A, B) LAMPE dominant case cycled at 1C and 9C, (C) lower LAMPE cycled at 9C but with a lower cutoff voltage, (D) SEI-growth case at 4C with low LLI and LAM, and (E) Li plated case with heavy LLI but less LAM, cycled at 6C. In the LAMPE dominant cases (A, B), the second arc increases significantly at 600 cycles, as indicated by the arrows. The inserted optical images in (D, E) show the condition of the anodes at the end of 450 lifecycles. The metallic gray area is the plated Li.
Quick EIS fitting results
To validate our EIS fitting approach’s capability in catching the trend of aging, the fitting results are compared against the resistance values obtained using ECM. In the quick-fitting approach, the Zʹ-intersection and chord lengths are used as a proxy of resistances, as shown in Figure 5. The progression of Zʹ-intersection and cord lengths of the first and the second arc are consistent with the growth trend of ROhm, RSEI and RCT, respectively. Whether the cells are low or high in LAMPE, the first chord length and RSEI grows steadily along with aging cycles (red trends). In the high LAMPE cases, the second chord length and RCT stay around the same level before 225 cycles but increase almost by four times from 225 to 600 cycles (blue trends). In contrast, for the LAMPE cells, the chord length or RCT does not exhibit very significant growth trends. The trends in the 1st and 2nd chord lengths are also consistent with the percentages of LLI and LAMPE, respectively (Chinnam et al., 2021).
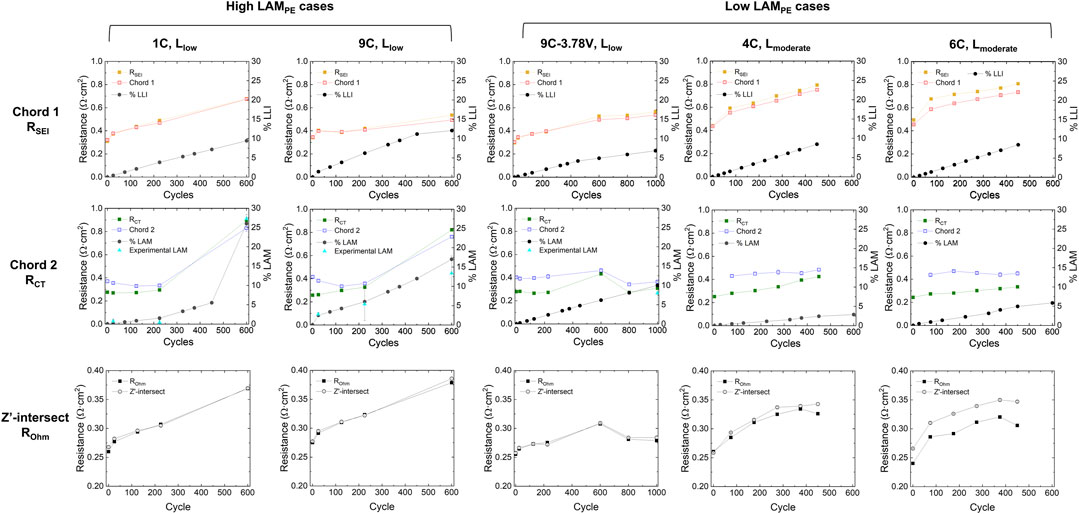
FIGURE 5. Comparison between representative results from the quick EIS fitting and conventional equivalent circuit fitting. The chord lengths were obtained using the quick EIS fitting method. The RSEI, RCT, and ROhm values were the fitting results using ECM. The %LAM and %LLI were obtained using IC analysis and half-cell tests. The growth trend between the chord length and resistance are consistent with each other. This trend is also in harmony with the %LLI and %LAMPE obtained from IC analysis and half-cell tests. The experimental LAMPE data points (light blue triangles) were based on half-cell test results using cathode materials retrieved from used pouch cells. Note that the second chord length (Chord 2) of 4C, Lmoderate and 6C, Lmoderate at the beginning of life (cycle 0) are not shown due to not-converged fitting results.
To investigate the mathematical correlation between the geometric metrices and resistances, ROhm, RSEI, and RCT are plotted against their corresponding features for all of the EIS data (16 cells in total) taken at different cycle numbers. As shown in Figures 6A, B, The Zʹ -intersection and ROhm exhibits a proportional trend (R2 = 0.949), as indicated by the regression results (see Supplementary Figure S6 in Supporting information 4). Similar relationship exists between the 1st chord length and RSEI (R2 = 0.989). However, the correlation between 2nd chord length and RCT in Figure 6C is not as obvious (R2 = 0.667), especially when 2nd chord length or RCT < 0.6 Ω cm2. This is due to the ill-defined second arcs especially at early stages of aging (less than 125 cycles), where the arcs are relatively flat due to insignificant LAMPE. Most of the fitted chord lengths fall in a range between 0.3 and 0.5 Ω cm2 compared to the corresponding RCT ranges roughly at the same scale between 0.2 and 0.4 Ω cm2. There also exists a few outliers as marked by black arrows in Figure 6C from early stages of aging at 0 or 25 cycles, where the shape of second arc is not yet well developed. As the arcs developed more defined shapes in later stages of aging (chord length >0.5 Ω cm2 or RCT > 0.4 Ω cm2) the linear correlation between the chord length and RCT can be seen more clearly. The consistency between the trends of geometric metrics and the resistances allows our EIS-fitting algorithm to quickly gauge the growth trend of resistance without the need of sophisticated ECM analysis. As discussed above, whether the arc is well-defined or not will be a limitation of the quick-fitting approach estimating the resistance values.
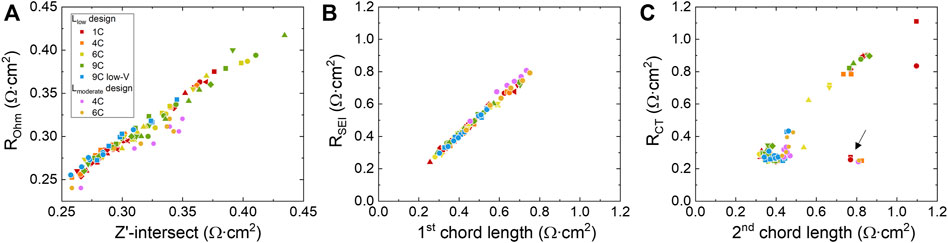
FIGURE 6. Correlations between the fitted geometric features and resistance components obtained using equivalent circuit fitting as (A) ROhm, (B) RSEI, and (C)RCT. The charge protocols and individual cells are marked by different colors and shapes, respectively. The Zʹ-intersect and first chord length progresses proportionally with ROhm and RSEI. For RCT, the correlation between the second chord length is not as obvious when RCT < 0.4 Ω. When RCT > 0.4 Ω, the proportional relationship becomes apparent. The outliers, which are data points from early stages of aging (0 or 25 cycles), are marked by the black arrow.
Conclusion
This work presents an approach to quickly analyzing EIS data by capturing the evolving trend of Nyquist plots during battery aging without using ECM extensively. This quick-fitting approach uses least square methods to fit the semi-arcs in the Nyquist plots and correlate the geometric features, such as chord lengths and intersects, to the resistance components (ROhm, RSEI, and RCT). The trend of geometric feature evolution captured by the quick-fitting approach is consistent with the resistance growth obtained using ECM, and therefore serves the purpose of aging mechanism diagnosis. For example, a significant growth in the low-frequency chord length is a sign of increased RCT and indicates LAMPE.
The quality of fitting will depend on the shape of the semi-arcs. In the cases that the semi-arcs are poorly defined, such as being flat due to multiple overlapped arcs, the fitting results will be accompanied with greater uncertainties or even fail to converge. Decoupling highly overlapped arcs can be challenging for both the quick-fitting algorithm and conventional ECM. Additional algorithms such as distribution of relaxation times (Dierickx et al., 2020) will be needed to decouple the overlapped semi-arcs.
Because ECM is not extensively involved in our quick-fitting algorithm, human engagement in data analysis is greatly reduced, allowing the quick-EIS fitting to become beginner-friendly and capable of expeditiously surveying large quantities of datasets generated during battery testing. The shape of Nyquist plots will serve as strong indicators for degradation mechanisms, because different aging mechanisms will impact specific frequency regions in the Nyquist plot and induce unique shape evolution during aging (Zhang et al., 2017; Frankenberger et al., 2019; Iurilli et al., 2021; Jones et al., 2022). Ultimately, this type of quick-EIS analysis algorithm has the potential to be combined with machine-learning-based battery lifetime prediction algorithms and degradation identification methodologies (Severson et al., 2019; Dubarry and Beck, 2020; Chen et al., 2021; Kim et al., 2022), as well as measurement tools for fast data acquisition (Tanim et al., 2020; Hill et al., 2021) to create a framework that automatically and quickly identify battery aging mechanisms.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
B-RC, YP, TT, and ED originated the research. PC and TT collected EIS data. B-RC, YP, P-RC, ML, and TT analyzed the EIS data. YP established the mathematical algorithm. The manuscript was primarily written by B-RC, YP, ML, and TT. All authors contributed to discussions of data and manuscript review.
Funding
Funding was provided from the U.S. Department of Energy (DOE) Office of Energy Efficiency and Renewable Energy (EERE) Vehicle Technologies Office (VTO). This research was supported by the Machine Learning for Accelerated Life Prediction and Cell Design. The cells were provided by the Extreme Fast Charge Cell Evaluation of Lithium-Ion Batteries (XCEL) program. This manuscript has been written by Battelle Energy Alliance under contract DE-AC07-05ID14517 for Idaho National Laboratory (INL). The U.S. Government retains, and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains, a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for U.S. Government purposes.
Acknowledgments
The authors thank Simon Thompson and Samuel Gillard from DOE for supporting this project under the Advanced Battery Cell Research Program. The authors also acknowledge the CAMP Facility at Argonne National Laboratory for providing cells; And Michael Evans and Ryan Jackman for data collection efforts at INL.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1132876/full#supplementary-material
References
Babaeiyazdi, I., Rezaei-Zare, A., and Shokrzadeh, S. (2021). State of charge prediction of ev Li-ion batteries using EIS: A machine learning approach. Energy 223, 120116. doi:10.1016/j.energy.2021.120116
Birkl, C. R., Roberts, M. R., McTurk, E., Bruce, P. G., and Howey, D. A. (2017). Degradation diagnostics for lithium ion cells. J. Power Sources 341, 373–386. doi:10.1016/j.jpowsour.2016.12.011
Bongiorno, V., Gibbon, S., Michailidou, E., and Curioni, M. (2022). Exploring the use of machine learning for interpreting electrochemical impedance spectroscopy data: Evaluation of the training dataset size. Corros. Sci. 198, 110119. doi:10.1016/j.corsci.2022.110119
Bredar, A. R. C., Chown, A. L., Burton, A. R., and Farnum, B. H. (2020). Electrochemical impedance spectroscopy of metal oxide electrodes for Energy applications. ACS Appl. Energy Mat. 3, 66–98. doi:10.1021/acsaem.9b01965
Buteau, S., and Dahn, J. R. (2019). Analysis of thousands of electrochemical impedance spectra of lithium-ion cells through a machine learning inverse model. J. Electrochem. Soc. 166, A1611–A1622. doi:10.1149/2.1051908jes
Chen, B.-R., Kunz, M. R., Tanim, T. R., and Dufek, E. J. (2021). A machine learning framework for early detection of lithium plating combining multiple physics-based electrochemical signatures. Cell Rep. Phys. Sci. 2, 100352. doi:10.1016/j.xcrp.2021.100352
Chinnam, P. R., Colclasure, A. M., Chen, B.-R., Tanim, T. R., Dufek, E. J., Smith, K., et al. (2021). Fast-charging aging considerations: Incorporation and alignment of cell design and material degradation pathways. ACS Appl. Energy Mat. 4, 9133–9143. doi:10.1021/acsaem.1c01398
Choi, W., Shin, H.-C., Kim, J. M., Choi, J.-Y., and Yoon, W.-S. (2020). Modeling and applications of electrochemical impedance spectroscopy (EIS) for lithium-ion batteries. J. Electrochem. Sci. Technol. 11, 1–13. doi:10.33961/jecst.2019.00528
Dierickx, S., Weber, A., and Ivers-Tiffée, E. (2020). How the distribution of relaxation times enhances complex equivalent circuit models for fuel cells. Acta 355, 136764. doi:10.1016/j.electacta.2020.136764
Din, E., Schaef, C., Moffat, K., and Stauth, J. T. (2017). A scalable active battery management system with embedded real-time electrochemical impedance spectroscopy. IEEE Trans. Power Electron 32, 5688–5698. doi:10.1109/TPEL.2016.2607519
Dubarry, M., and Beck, D. (2020). Big data training data for artificial intelligence-based Li-ion diagnosis and prognosis. J. Power Sources 479, 228806. doi:10.1016/j.jpowsour.2020.228806
Dubarry, M., Berecibar, M., Devie, A., Anseán, D., Omar, N., and Villarreal, I. (2017). State of health battery estimator enabling degradation diagnosis: Model and algorithm description. J. Power Sources 360, 59–69. doi:10.1016/j.jpowsour.2017.05.121
Dubarry, M., Truchot, C., and Liaw, B. Y. (2012). Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 219, 204–216. doi:10.1016/j.jpowsour.2012.07.016
Frankenberger, M., Singh, M., Dinter, A., and Pettinger, K.-H. (2019). EIS study on the electrode-separator interface lamination. Batteries 5, 71. doi:10.3390/batteries5040071
Gordon, I. J., Genies, S., Si Larbi, G., Boulineau, A., Daniel, L., and Alias, M. (2016). Original implementation of Electrochemical Impedance Spectroscopy (EIS) in symmetric cells: Evaluation of post-mortem protocols applied to characterize electrode materials for Li-ion batteries. J. Power Sources 307, 788–795. doi:10.1016/j.jpowsour.2016.01.036
Hill, B., Morrison, J., Sandefur, D., and Christophersen, J. P. (2021). Enhanced resolution for rapid broadband battery impedance measurements, in: IEEE Aerosp. Conf., IEEE: pp. 1–8.
Huang, J., Papac, M., and O’Hayre, R. (2021). Towards robust autonomous impedance spectroscopy analysis: A calibrated hierarchical bayesian approach for electrochemical impedance spectroscopy (EIS) inversion. Electrochim. Acta. 367, 137493. doi:10.1016/j.electacta.2020.137493
Iurilli, P., Brivio, C., and Wood, V. (2021). On the use of electrochemical impedance spectroscopy to characterize and model the aging phenomena of lithium-ion batteries: A critical review. J. Power Sources. 505, 229860. doi:10.1016/j.jpowsour.2021.229860
Jones, P. K., Stimming, U., and Lee, A. A. (2022). Impedance-based forecasting of lithium-ion battery performance amid uneven usage. Nat. Commun. 13, 4806. doi:10.1038/s41467-022-32422-w
Kim, S., Yi, Z., Chen, B.-R., Tanim, T. R., and Dufek, E. J. (2022). Rapid failure mode classification and quantification in batteries: A deep learning modeling framework. Energy Storage Mater 45, 1002–1011. doi:10.1016/j.ensm.2021.07.016
Meddings, N., Heinrich, M., Overney, F., Lee, J.-S., Ruiz, V., Napolitano, E., et al. (2020). Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Sources 480, 228742. doi:10.1016/j.jpowsour.2020.228742
Murbach, M., Gerwe, B., Dawson-Elli, N., and Tsui, L. (2020). impedance.py: A Python package for electrochemical impedance analysis. J. Open Source Softw. 5, 2349. doi:10.21105/joss.02349
Park, M., Zhang, X., Chung, M., Less, G. B., and Sastry, A. M. (2010). A review of conduction phenomena in Li-ion batteries. J. Power Sources 195, 7904–7929. doi:10.1016/j.jpowsour.2010.06.060
Pastor-Fernandez, C., Dhammika Widanage, W., Marco, J., Gama-Valdez, M.-A., and Chouchelamane, G. H. (2016). Identification and quantification of ageing mechanisms in Lithium-ion batteries using the EIS technique, in: IEEE transp. electrif. Conf. Expo, IEEE: pp. 1–6.
Paul, P. P., Cao, C., Thampy, V., Steinrück, H.-G., Tanim, T. R., Dunlop, A. R., et al. (2021). Using in situ high-energy X-ray diffraction to quantify electrode behavior of Li-ion batteries from extreme fast charging. ACS Appl. Energy Mat. 4, 11590–11598. doi:10.1021/acsaem.1c02348
Paul, P. P., Thampy, V., Cao, C., Steinrück, H.-G., Tanim, T. R., Dunlop, A. R., et al. (2021). Quantification of heterogeneous, irreversible lithium plating in extreme fast charging of lithium-ion batteries. Energy Environ. Sci. 14, 4979–4988. doi:10.1039/D1EE01216A
Severson, K. A., Attia, P. M., Jin, N., Perkins, N., Jiang, B., Yang, Z., et al. (2019). Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy. 4, 383–391. doi:10.1038/s41560-019-0356-8
Tang, Z., Huang, Q.-A., Wang, Y.-J., Zhang, F., Li, W., Li, A., et al. (2020). Recent progress in the use of electrochemical impedance spectroscopy for the measurement, monitoring, diagnosis and optimization of proton exchange membrane fuel cell performance. J. Power Sources 468, 228361. doi:10.1016/j.jpowsour.2020.228361
Tanim, T. R., Dufek, E. J., and Sazhin, S. V. (2021). Challenges and needs for system-level electrochemical lithium-ion battery management and diagnostics. MRS Bull. 46, 420–428. doi:10.1557/s43577-021-00101-8
Tanim, T. R., Dufek, E. J., Walker, L. K., Ho, C. D., Hendricks, C. E., and Christophersen, J. P. (2020). Advanced diagnostics to evaluate heterogeneity in lithium-ion battery modules. ETransportation 3, 100045. doi:10.1016/j.etran.2020.100045
Tanim, T. R., Yang, Z., Colclasure, A. M., Chinnam, P. R., Gasper, P., Lin, Y., et al. (2021). Extended cycle life implications of fast charging for lithium-ion battery cathode. Energy Storage Mater 41, 656–666. doi:10.1016/j.ensm.2021.07.001
Tanim, T. R., Yang, Z., Finegan, D. P., Chinnam, P. R., Lin, Y., Weddle, P. J., et al. (2022). A comprehensive understanding of the aging effects of extreme fast charging on high Ni NMC cathode. Adv. Energy Mat. 12, 2103712. doi:10.1002/aenm.202103712
Tatara, R., Karayaylali, P., Yu, Y., Zhang, Y., Giordano, L., Maglia, F., et al. (2019). The effect of electrode-electrolyte interface on the electrochemical impedance spectra for positive electrode in Li-ion battery. J. Electrochem. Soc. 166, A5090–A5098. doi:10.1149/2.0121903jes
Vadhva, P., Hu, J., Johnson, M. J., Stocker, R., Braglia, M., Brett, D. J. L., et al. (2021). Electrochemical impedance spectroscopy for all-solid-state batteries: Theory, methods and future outlook. ChemElectroChem 8, 1930–1947. doi:10.1002/celc.202100108
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., et al. (2020). SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods. 17, 261–272. doi:10.1038/s41592-019-0686-2
Vivier, V., and Orazem, M. E. (2022). Impedance analysis of electrochemical systems. Chem. Rev. 122, 11131–11168. doi:10.1021/acs.chemrev.1c00876
Wang, S., Zhang, J., Gharbi, O., Vivier, V., Gao, M., and Orazem, M. E. (2021). Electrochemical impedance spectroscopy. Nat. Rev. Methods Prim. 1, 41. doi:10.1038/s43586-021-00039-w
Westerhoff, U., Kurbach, K., Lienesch, F., and Kurrat, M. (2016). Analysis of lithium-ion battery models based on electrochemical impedance spectroscopy. Energy Technol. 4, 1620–1630. doi:10.1002/ente.201600154
Zhang, W., Weber, D. A., Weigand, H., Arlt, T., Manke, I., Schröder, D., et al. (2017). Interfacial processes and influence of composite cathode microstructure controlling the performance of all-solid-state lithium batteries. ACS Appl. Mat. Interfaces. 9, 17835–17845. doi:10.1021/acsami.7b01137
Zhang, Y., Tang, Q., Zhang, Y., Wang, J., Stimming, U., and Lee, A. A. (2020). Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 11, 1706. doi:10.1038/s41467-020-15235-7
Keywords: electrochemical impedance spectroscopy, battery aging and degradation, equivalent circuit fitting, lithium-ion batteries, batteries
Citation: Chen B-R, Police YR, Li M, Chinnam PR, Tanim TR and Dufek EJ (2023) A mathematical approach to survey electrochemical impedance spectroscopy for aging in lithium-ion batteries. Front. Energy Res. 11:1132876. doi: 10.3389/fenrg.2023.1132876
Received: 28 December 2022; Accepted: 20 February 2023;
Published: 28 February 2023.
Edited by:
Nada Zamel, Fraunhofer Institute for Solar Energy Systems (ISE), GermanyReviewed by:
Amani Al-Othman, American University of Sharjah, United Arab EmiratesGareth Hinds, National Physical Laboratory, United Kingdom
Copyright © 2023 Chen, Police, Li, Chinnam, Tanim and Dufek. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tanvir R. Tanim, VGFudmlyLlRhbmltQGlubC5nb3Y=; Bor-Rong Chen, Ym9ycm9uZy5jaGVuQGlubC5nb3Y=
 Bor-Rong Chen
Bor-Rong Chen Yugandhar R. Police
Yugandhar R. Police Tanvir R. Tanim
Tanvir R. Tanim Eric J. Dufek
Eric J. Dufek