Multi-armed bandit based device scheduling for crowdsensing in power grids

With the increase of devices in power grids, a critical challenge emerges on how to collect information from massive devices, as well as how to manage these devices. Mobile crowdsensing is a large-scale sensing paradigm empowered by ubiquitous devices and can achieve more comprehensive observation of the area of interest. However, collecting sensing data from massive devices is not easy due to the scarcity of wireless channel resources and a large amount of sensing data, as well as the different capabilities among devices. To address these challenges, device scheduling is introduced which chooses a part of mobile devices in each time slot, to collect more valuable sensing data. However, the lack of prior knowledge makes the device scheduling task hard, especially when the number of devices is huge. Thus the device scheduling problem is reformulated as a multi-armed bandit (MAB) program, one should guarantee the participation fairness of sensing devices with different coverage regions. To deal with the multi-armed bandit program, a device scheduling algorithm is proposed on the basis of the upper confidence bound policy as well as virtual queue theory. Besides, we conduct the regret analysis and prove the performance regret of the proposed algorithm with a sub-linear growth under certain conditions. Finally, simulation results verify the effectiveness of our proposed algorithm, in terms of performance regret and convergence rate.

Introduction

Nowadays, the development of smart power grids brings much convenience to human life and production. Meanwhile, more and more devices, such as sensors and actuators, are deployed in power grids, e.g., substations, transformers, and generators. Consequently, A critical challenge arises on how to collect information from massive devices and how to manage these devices. Mobile crowdsensing is a large-scale sensing paradigm empowered by ubiquitous devices. These devices interact with each other by sharing local knowledge according to the data they have perceived, and then the information can be further aggregated and fused in a central node for crowd intelligence extraction, decision-making, and service delivery (Guo et al., 2014).

However, collecting sensing data from massive devices is not easy due to the following reasons. Firstly, the scarce channel resource limits the number of devices that simultaneously access to an edge server. That is to say, the available wireless channels are fewer than the sensing devices. Secondly, the overlap of perception areas of different devices introduces sensing data redundancy. Besides, the system heterogeneity of sensing devices, such as processing capability, network connectivity, and battery capacity, leads to different processing capabilities (Xia et al., 2021). The system heterogeneity causes a drift of global statistical characteristics since the fast devices can collect more data according to their local observations. To achieve a more comprehensive observation of the area of interest, one should guarantee the participation fairness of sensing devices with different coverage regions. Therefore, the edge server has to perform device scheduling, i.e., choosing a part of sensing devices in each time slot, to collect more valuable sensing data. However, the lack of prior knowledge makes the device scheduling task hard, especially when the number of sensing devices is huge.

Actually, there have been some works on device scheduling in crowdsensing tasks. For example, The authors in (Chu et al., 2013) proposed a selection scheme of individual sensors to collect data in different regions in order to optimize some specified objective while satisfying constraints in the number and costs of sensors. The authors in (Han et al., 2016) chose from a set of available participants to maximize sensing revenue under a limited budget. The authors in (Sun and Tang, 2019) proposed a greedy scheduling algorithm to find data-giver vehicles for every subtask with minimized cost in vehicular crowdsensing. The work in (Han et al., 2015) considered an online scheduling problem that determined sensing decisions for smartphones that were distributed over different regions of interest. (Nguyen and Zeadally, 2021). studied a participant selection problem that aimed to maximize the number of event records reported by fewer users. Different from (Han et al., 2015; Han et al., 2016; Sun and Tang, 2019; Nguyen and Zeadally, 2021), the work in (Gendy et al., 2020) aimed to maximize the percentage of the accomplished sensing tasks in a given period, by modeling the interaction between the participating devices and sensing task publishers as auctions. However, these works did not take into account the effects of dynamic wireless channels on sensing performance. Besides, most of them performed sensing device scheduling under the assumption that some statistical information is available in advance, which is usually resource-consuming and even impractical especially when the number of sensing devices is huge. Motivated by this fact, we aim to propose an online scheduling algorithm to find device scheduling decisions in crowdsensing tasks.

Recently, the rapid development of reinforcement learning (RL) techniques sheds light on the considered problem. Among these RL techniques, the multi-armed bandit (MAB) program is thought of as an important tool and has been widely adopted for scheduling and resource allocation problems. For example, MAB has been applied to advertisement placement, multi-antenna beam selection (Cheng et al., 2019), packet routing, offloading (Sun et al., 2018; Chen and Xu, 2019), caching (Blasco and Gündüz, 2014; Sengupta et al., 2014), and so on. In this work, we reformulate the sensing device scheduling problem as an MAB program, based on which a device scheduling algorithm is also proposed. The contributions of this work are summarized as follows.

• Considering the scarcity of wireless channel resources, we formulate a device scheduling problem in crowdsensing scenarios. We take into account not only the availability of devices caused by dynamic wireless channels but also fairness among the devices for better comprehensive observation of the area of interest. Besides, no prior information about devices is available.

• Then, the device scheduling problem is reformulated as an MAB problem, based on which an online scheduling algorithm is also proposed. The proposed algorithm propose incorporates the upper confidence bound (UCB) policy and virtual queue theory, whose regret performance is also analyzed in this work.

• Finally, simulation results are conducted to verify the effectiveness of the proposed algorithm. The balance between the time used to reach a point that meets the fairness constraints of devices and the performance regret is revealed.

System model

Consider a system consisting of an edge server and a set $\mathcal{K}=\{\mathrm{1,2},\dots ,K\}$ of crowdsensing devices (e.g., sensors, cameras, and so on), as shown in Figure 1. These devices are responsible for collecting raw data from the observed events or objects and then pre-processing the raw data into samples, finally transmitting these samples to the edge server for processing tasks, such as statistical analysis and training a neural network for classification. For simplicity, we assume that the samples generated by different devices have the same size δ. Since the observed events can be periodic or aperiodic, or the observed objects have different activity characteristics, the amount of raw data collected by different devices is different. Other factors such as device location and perception ability also have influences on the amount of raw data collected by different devices. In addition, the processing capabilities of different devices are heterogeneous. Taking into account these facts mentioned above and for simplicity, we assume that time is slotted and the number of the newly generated samples of device $k\in \mathcal{K}$ in time slot τ, N_k(τ), is independently and identically distributed (i.i.d.) according to some unknown distribution whose expectation ν_k is also unknown a priori. Thus, the total number of the samples waiting for uplink transmission of device k at the beginning of time slot τ is

$M_k\left(\tau \right)=\text{min}\left\{M_{\text{max}},{\left[M_k\left(\tau -1\right)+N_k\left(\tau -1\right)-L_k\left(\tau -1\right)\right]}^{+}\right\},(1)$

where [x]⁺ = max{0, x}, M_max is the largest number of the samples that each device can store due to the limited storage space, and L_k(τ) is the number of the samples of device k has been transmitted the edge server in time slot τ, which will be specified in the following.

FIGURE 1

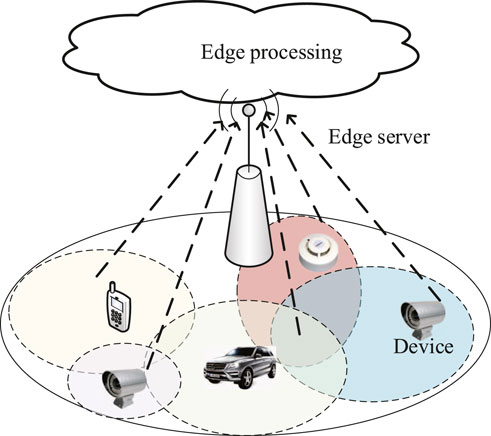
FIGURE 1. The considered system with an edge server and K devices. Different colored areas represent the perception areas of different devices.

Transmission model

The orthogonal frequency-division multiple access technique is adopted and there are F_max orthogonal channels, each with the same bandwidth w, that can be used for uplink transmission simultaneously. The channel h_k between the edge server and device k is i.i.d., which is assumed to be constant within a time slot but varies independently across different time slots. The achievable uplink rate of device k in time slot τ is computed as

$R_k\left(\tau \right)=w{\text{log}}_2\left(1+\frac{p_k|h_k\left(\tau \right){|}^2}{{\sigma }^2}\right),(2)$

where σ² denotes the noise power and p_k denotes the transmit power of device k. Then, the number of samples that can be transmitted to the edge server is

$l_k\left(\tau \right)=\text{min}\left\{\frac{\mathrm{\Delta }tR\left(\tau \right)}{\delta },M_k\left(\tau \right)+N_k\left(\tau \right)\right\},(3)$

where Δt is the duration length of a time slot.

Available channel constraint

When the edge server collects the generated samples from the devices, some devices can be unavailable for uplink transmission. For example, the devices experience poor channel conditions due to external interference, or the devices cannot work in the transmission mode when collecting raw data due to power constraints. We introduce the binary variable a_k(τ) to indicate the availability state of device k in time slot τ. Specifically, a_k(τ) = 1 represents that device k can work in the transmission mode in time slot τ, otherwise not. Let $\mathcal{Z}(\tau )=\{k\in \mathcal{K}|a_k(\tau )=1\}\in \mathcal{B}(\mathcal{K})$ denote the set of available devices that can work in the transmission mode in time slot τ where $\mathcal{B}(\mathcal{K})$ is the power set of $\mathcal{K}$. We assume the distribution of available devices, ${\widehat{P}}_{\mathcal{Z}}(e)=\widehat{P}(\mathcal{Z}(\tau )=e),e\in \mathcal{B}(\mathcal{K})$, is i.i.d. over time and unknown a priori, but $\mathcal{Z}(\tau )$ is unmasked to the edge server at the beginning of each time slot τ. Then, L_k is specified by

$L_k\left(\tau \right)=\left\{\begin{array}{cc}{l}_k\left(\tau \right)\hfill & \text{if}k\in \mathcal{Z}\left(\tau \right),\hfill \\ 0,\hfill & \text{else}.\hfill \end{array}\right.(4)$

In the considered system, there can be a huge number of devices, but the number of available channels at the same time is constrained. Due to the limited number of available channels, the edge server has to select a subset $\mathcal{W}(\tau )$ from the available devices, which should meet the available channel constraint, i.e.,

$\mathcal{W}\left(\tau \right)\triangleq \left\{\mathcal{W}\left(\tau \right)\subseteq \mathcal{Z}\left(\tau \right):|\mathcal{W}\left(\tau \right)|\le F_{\text{max}}\right\}\in \mathcal{B}\left(\mathcal{Z}\left(\tau \right)\right),(5)$

where $|\mathcal{W}(\tau )|$ denotes the cardinality of $\mathcal{W}(\tau )$.

Fairness constraint

In order to achieve more comprehensive observation of the area of interest or better performance of computational tasks such as training a neural network, besides collecting as many samples as possible, the edge server is required to collect samples from different devices to ensure the diversity of samples. Thus, fairness among the devices is also an important issue that should be addressed in many practical applications. Here, a binary variable b_k(τ) is introduced with b_k(τ) = 1 if device k is chosen to transmit its samples to the edge server in time slot τ, otherwise, b_k(τ) = 0. With the definition of b_k(τ), we formulate the fairness constraint as follows

$\underset{T\to \infty }{\text{lim}}\text{inf}\sum _{\tau =1}^T\mathbb{E}[b_k\left(\tau \right)]\ge c_k,\forall k\in \mathcal{K},(6)$

where T represents the total number of time slots, c_k ∈ (0, 1) represents the minimum of the portion of time slots required to transmit the samples of device k, and $\mathbb{E}[•]$ is the expectation operator. We incorporate $c_k,k\in \mathcal{K}$ into a vector $\mathbf{c}={[c_1,c_2,\dots ,c_K]}^T$ and c is thought of as a feasible fairness constraint if there is a policy which generates a decision sequence $\{\mathcal{W}(\tau ),\tau \ge 1\}$ such that the fairness constraint 6) is satisfied.

Problem formulation

In this work, we aim to optimize a time sequence $\{\mathcal{W}(\tau ),\tau \ge 1\}$ which maximizes the number of samples received at the edge server with a given time horizon of T time slots. The underlying problem with the fairness constraint and the available channel constraint can be formulated as

$\begin{array}{cc}\hfill \underset{\left\{\mathcal{W}\left(\tau \right),\tau \ge 0\right\}}{\text{max}}& \sum _{\tau =1}^T\sum _{k\in \mathcal{W}\left(\tau \right)}{L}_k\left(\tau \right)\hfill \\ \hfill \text{s.t.}& (5)\text{and}(6),\hfill \end{array}(7)$

which is hard to solve because we have no idea about the distribution of the number of newly generated samples, as well as the distribution of wireless channels. Besides, the fairness constraint and the available channel constraint make problem Eq. 7 more challenging. Thanks to the development of the MAB framework, which sheds light on solutions to problem Eq. 7.

Proposed algorithm

In this section, we first introduce a stationary policy optimization program to deal with the uncertainty of device availability. Then, the device scheduling problem is reformulated as an MAB program, based on which an arm-pull algorithm is proposed to determine the decision sequence.

Problem reformulation

In this work, to simplify the scheduling complexity, a stationary policy named $\mathcal{Z}$-only policies is introduced, in which a super arm $\mathcal{W}(\tau )\in \mathcal{Y}(\mathcal{Z}(\tau ))$ is selected according to the observed $\mathcal{Z}(\tau )$ only in each time slot τ (Neely, 2010), where $\mathcal{Y}(\mathcal{Z}(\tau ))$ denotes the set of all possible subsets when $\mathcal{Z}(\tau )$ is observed. According to Theorem 4.5 in (Neely, 2010), if c belongs to the maximum feasibility region $\mathcal{C}$ strictly, a $\mathcal{Z}$-policy which can meet the fairness constraint in Eq. 6 always exists.

We further use a vector of probability distributions $\mathbf{q}=[q_{\mathcal{W}}(e),\forall \mathcal{W}\in \mathcal{Y}(e),\forall e\in \mathcal{B}(\mathcal{K})]$ to describe an $\mathcal{Z}$-only policy π with ${\sum }_{\mathcal{W}\in \mathcal{Y}(e)}{q}_{\mathcal{W}}(e)=1,\forall e\in \mathcal{B}(\mathcal{K})$. Then, we compute the mean of b_k(τ) as

$\mathbb{E}\left[b_k^{\pi }\left(\tau \right)\right]=\sum _{e\in \mathcal{B}\left(\mathcal{K}\right)}{\widehat{P}}_{\mathcal{Z}}\left(e\right)\sum _{\mathcal{W}\in \mathcal{Y}\left(e\right):k\in \mathcal{W}}{q}_{\mathcal{W}}\left(e\right),(8)$

and have an equivalent expression of constraint 6), i.e., $\mathbb{E}[b_k^{\pi }(\tau )]\ge c_k$. Besides, we assume M_max is large enough and define ${\bar{l}}_k=\frac{1}{M_{\text{max}}}\mathbb{E}[l_k]\in [\mathrm{0,1}]$ as the normalized expectation of L_k. Then, problem Eq. 7 can be reformulated as

$\begin{array}{cc}\hfill \underset{\mathbf{\text{q}}}{\text{max}}& \sum _{e\in \mathcal{B}\left(\mathcal{K}\right)}{\widehat{P}}_{\mathcal{Z}}\left(e\right)\sum _{\mathcal{W}\in \mathcal{Y}\left(e\right)}{q}_{\mathcal{W}}\left(e\right)\sum _{k\in \mathcal{W}}{\bar{l}}_k\hfill \\ \hfill \text{s.t.}& \sum _{e\in \mathcal{B}\left(\mathcal{K}\right)}{\widehat{P}}_{\mathcal{Z}}\left(e\right)\sum _{\mathcal{W}\in \mathcal{Y}\left(e\right):k\in \mathcal{W}}{q}_{\mathcal{W}}\left(e\right)\ge c_k,\forall k\in \mathcal{K},\hfill \\ \hfill & \sum _{\mathcal{W}\in \mathcal{Y}\left(e\right)}{q}_{\mathcal{W}}\left(e\right)=1,\forall e\in \mathcal{B}\left(\mathcal{K}\right),\hfill \\ \hfill & q_{\mathcal{W}}\left(e\right)\in \left[\mathrm{0,1}\right],\forall \mathcal{W}\in \mathcal{Y}\left(e\right),\forall e\in \mathcal{B}\left(\mathcal{K}\right).\hfill \end{array}(9)$

which is a linear problem if the expectation ${\bar{L}}_k$ of L_k is known a priori. However, this assumption does not usually hold in practice and the edge server needs to estimate the average number of samples received from device k per time slot to make scheduling decisions. To address this issue, we introduce the MAB program.

Multi-armed bandit program

An MAB program is a machine learning framework where a player chooses a sequential of actions (arms) in order to maximize its cumulative reward in the long term (Lattimore and Szepesvári, 2020). Thankfully, we can model problem Eq. 7 as an MAB problem, in which the edge server and the devices play the roles of the player and the arms, respectively. Each subset $\mathcal{W}(\tau )$ of available arms is also treated as a super arm. Correspondingly, we can interpret the objective of problem Eq. 7 as determining a time sequence of the super arm to maximize the cumulative reward (i.e., the number of samples received at the edge server).

In the MAB program, there is an expected reward for each arm, but such statistical information is unknown by the player, which brings challenges to the arm selection of the player. The main basis that can be used to determine actions is some observation about the state in the current round and the experience gathered in previous rounds. More specifically, the arms which performed well in the past should be associated with higher priority. In the meantime, the player continues to explore the expected payoffs of the other arms. In other words, the player has to balance between the need to acquire more knowledge about the reward distributions of each arm (exploration) and the need to optimize rewards based on its current knowledge (exploitation) (Bubeck and Cesa-Bianchi, 2012). The exploration-exploitation dilemma inevitably causes performance loss and regret is the most popular metric for evaluating the learning performance in the MAB works, which is defined as the difference between the reward r* and the average reward in a given period of time (Lai and Robbins, 1985). Here, r* is the achievable maximum reward of problem Eq. 9 with the known ${\bar{L}}_k,\forall k\in \mathcal{K}$. Therefore, the original problem Eq. 7 can be reformulated as a cumulative regret minimization under policy π by determining a super arm $\mathcal{W}(\tau )$ in each time slot τ, i.e.,

$\begin{array}{cc}\hfill \underset{\left\{\mathcal{W}\left(\tau \right),\tau \ge 1\right\}}{\text{min}}& R^{\pi }={\mathrm{Tr}}^{*}-\mathbb{E}\left\{\sum _{\tau =1}^T\sum _{k\in \mathcal{W}\left(\tau \right)}{\widehat{l}}_k\left(\tau \right)\right\}\hfill \\ \hfill \text{s.t.}& (5)\text{and}(6),\hfill \end{array}(10)$

where ${\widehat{l}}_k(\tau )=l_k(\tau )/M_{\text{max}}$.

Algorithm design

When designing an algorithm for problem Eq. 10, three challenges need to be addressed: 1) how to maximize the cumulative reward when the reward expectation of each arm is unknown, 2) how to choose a super arm under the available channel constraint, and 3) how to meet the fairness constraint. The first two challenges can be dealt with with the extension of the classic UCB algorithm (Auer et al., 2002), but how to meet the fairness constraint requires the introduction of novel methods. Encouraged by (Neely, 2010; Li et al., 2019), the virtual queue technique has the potential to handle the fairness constraint. Specifically, a virtual queue is built for each arm k, i.e.,

$Q_k\left(\tau \right)={\left[Q_k\left(\tau -1\right)+c_k-b_k\left(\tau -1\right)\right]}^{+},(11)$

where [x]⁺ = max{0, x} and D_k(τ) represents the length of virtual queue of arm k at the beginning of time slot τ.

Define ${\varrho }_k(\tau )={\sum }_{{\tau }^{\prime }=1}^{\tau }{b}_k({\tau }^{\prime })$ as the number of times arm k has been chosen and υ_k(τ) as the empirical mean of the reward of arm k by the end of time slot τ. The update rules of v_k(τ) and ϱ_k(τ) are given as

${\upsilon }_k\left(\tau \right)=\left\{\begin{array}{cc}\frac{{\upsilon }_k\left(\tau -1\right){\varrho }_k\left(\tau -1\right)+{\widehat{l}}_k\left(\tau -1\right)}{{\varrho }_k\left(\tau -1\right)+1},\hfill & \text{if}k\in \mathcal{W}\left(\tau \right),\hfill \\ {\upsilon }_k\left(\tau -1\right),\hfill & \text{else},\hfill \end{array}\right.(12)$

and

${\varrho }_k\left(\tau \right)=\left\{\begin{array}{cc}{\varrho }_k\left(\tau -1\right)+1,\hfill & \text{if}k\in \mathcal{W}\left(\tau \right),\hfill \\ {\varrho }_k\left(\tau -1\right),\hfill & \text{else},\hfill \end{array}\right.(13)$

respectively. If ϱ_k(τ) = 0, we set υ_k(τ) = 0. Note that both ϱ_k (0) and υ_k (0) are initialized to be 0.

We estimate the mean reward of each arm k according to a truncated UCB method (Li et al., 2019), i.e.,

${\widehat{\upsilon }}_k\left(\tau \right)=\text{min}\left\{{\upsilon }_k\left(\tau -1\right)+\sqrt{\frac{2\text{ln}\tau }{{\varrho }_k\left(\tau -1\right)}},1\right\},(14)$

where ${\widehat{\upsilon }}_k(\tau )$ is set to be 1, if ϱ_k (τ − 1) = 0. Then, a super arm is selected in each time slot τ according to

${\mathcal{W}}^{*}\left(\tau \right)\in \underset{\begin{array}{c}\mathcal{W}\in \mathcal{Y}\left(\mathcal{Z}\left(\tau \right)\right),\\ |\mathcal{W}|=\text{min}\left\{N,|\mathcal{Z}\left(\tau \right)|\right\}\end{array}}{\text{arg max}}\sum _{k\in \mathcal{W}}\left(1-\alpha \right){\widehat{\upsilon }}_k\left(\tau \right)+\alpha Q_k\left(\tau \right)(15)$

where α ∈ (0, 1] is a weighting value.

Finally, the whole algorithm is summarised in Algorithm 1.

Algorithm 1. Proposed algorithm for problem Eq. 10.

1: Initialization: Set ${\varrho }_k(1)={\upsilon }_k(1)=Q_k(1)=0,\forall k\in \mathcal{K}$

2:for τ ∈ do

3: for $k\in \mathcal{K}$ do

4: if v_k(τ) > 0 then update ${\widehat{v}}_k(\tau )$ using (14)

5: else set ${\widehat{v}}_k(\tau )=1$ end if

6: Update Q_k using (11)

7: end for

8: Select $\mathcal{W}(\tau )$ using (15) and update $b_k(\tau ),\forall k\in \mathcal{K}$

9: Update v_k(τ) and ϱ_k(τ) using (12) and 13, respectively

10: end for

Regret analysis

We first introduce a lemma that specifies the upper bound on the expected regret of the proposed algorithm.

Lemma 1. The regret of the proposed algorithm is upper bounded by

$R^{\pi }\le \alpha \frac{KT}{2}+\left(1-\alpha \right)\left[\left(\frac{{\pi }^2}{3}+1\right)K+4\sqrt{2KFT\text{ln}T}\right].(16)$

Proof. Since similar proof has been presented in (Hsu et al., 2018; Li et al., 2019; Xia et al., 2021), here we only provide the sketch of the proof. Denote by ${\mathcal{W}}^{*}(\tau )$ the super arm selected according to the optimal $\mathcal{Z}$-policy π* and by $b_k^{*}(\tau )$’s the corresponding the indicator variables. Then, we have

$\begin{array}{cc}\hfill R^{\pi }& =\sum _{\tau =1}^T\mathbb{E}\left[\sum _{k\in {\mathcal{W}}^{*}\left(\tau \right)}{\widehat{l}}_k\left(\tau \right)-\sum _{k\in \mathcal{W}\left(\tau \right)}{\widehat{l}}_k\left(\tau \right)\right]\hfill \\ \hfill & =\sum _{\tau =1}^T\mathbb{E}\left[\sum _{k\in \mathcal{K}}\left(b_k^{*}\left(\tau \right)-b_k\left(\tau \right)\right){\bar{l}}_k\right]\hfill \\ \hfill & \le \frac{\alpha KT}{2}+\sum _{\tau =1}^T\mathbb{E}\left[{\mathrm{\Lambda }}_1\left(\tau \right)\right].\hfill \end{array}(17)$

in which ${\mathrm{\Lambda }}_1(\tau )={\sum }_{k\in \mathcal{K}}[\alpha Q_k(\tau )+(1-\alpha ){\bar{l}}_k]\left(b_k^{*}(\tau )-b_k(\tau )\right)$ (Li et al., 2019, Appednix C). Then, according to (Xia et al., 2021, Lemma 2), we have

${\mathrm{\Lambda }}_1\left(\tau \right)\le \left(1-\alpha \right)\left[{\mathrm{\Lambda }}_2\left(\tau \right)+{\mathrm{\Lambda }}_3\left(\tau \right)\right],(18)$

where ${\mathrm{\Lambda }}_2(\tau )={\sum }_{i\in \mathcal{W}(\tau )}\left({\widehat{\upsilon }}_k(\tau )-{\bar{l}}_k\right)$, ${\mathrm{\Lambda }}_3(\tau )={\sum }_{i\in {\mathcal{W}}^{‡}(\tau )}\left({\bar{l}}_k-{\widehat{\upsilon }}_k(\tau )\right)$, and ${\mathcal{W}}^{‡}(\tau )$ is chosen according to the following rule:

${\mathcal{W}}^{‡}\left(\tau \right)\in \underset{\mathcal{W}\in \mathcal{Y}\left(\mathcal{Z}\left(\tau \right)\right)}{\text{arg max}}\sum _{k\in \mathcal{W}}\alpha Q_k\left(\tau \right)+\left(1-\alpha \right){\bar{l}}_k.(19)$

Here, the upper bounds of Λ₂(τ) and Λ₃(τ) are directly given as follows:

$\begin{array}{cc}\hfill \sum _{\tau =1}^T\mathbb{E}\left[{\mathrm{\Lambda }}_2\left(\tau \right)\right]& \le \left(\frac{{\pi }^2}{6}+1\right)K+4\sqrt{2KFT\text{ln}T},\hfill \\ \hfill \sum _{\tau =1}^T\mathbb{E}\left[{\mathrm{\Lambda }}_3\left(\tau \right)\right]& \le \frac{{\pi }^2}{6}K.\hfill \end{array}(20)$

The corresponding analysis is similar to that in (Li et al., 2019; Appendices D and E). Finally, we finish the proof by substituting Eq. 20 into Eq. 18 and further into Eq. 17.

Remark 1. Given $0<\alpha \le \frac{1}{\sqrt{T}}$ and a large value T, then we can simplify the upper bound in Eq. 16 as

$R^{\pi }\le \frac{K\sqrt{T}}{2}+\left(\frac{{\pi }^2}{3}+1\right)K+4\sqrt{2KFT\text{ln}T},(21)$

which suggests that the time-average performance regret increases at a sub-linear rate (i.e., $\mathcal{O}(\sqrt{T\text{ln}T})$) over time.

Simulation results

In this section, we provide simulation results to verify the effectiveness of the proposed algorithm. We consider a disc area with a radius of 200 m and a single-antenna access point (AP) equipped with an edge server located in the center of the considered area. The transmit power of each sensing device k is set as 23 dBm and the noise power σ² is set as −107 dBm. The channel response h_k is computed as $h_k=\sqrt{{\beta }_k}{\tilde{h}}_k$ where ${\tilde{h}}_k$ and β_k stand for small-scale fading and large-scale fading, respectively. The small-scale fading is represented by i.i.d. zero-meaned complex Gaussian variables with unit variance. The large-scale fading is determined according to the path-loss model: PL [dB] = 128.1 + 37.6 log₁₀(d) where d stands for the distance in km (Dahrouj and Yu, 2010). The number of the newly generated samples N_k(τ) is assumed to be uniformly distributed in $[N_k^{\text{LB}},N_k^{\text{UB}}]$, where $N_k^{\text{LB}}$ and $N_k^{\text{UB}}$ are set as $N_k^{\text{LB}}=(0.5k+0.5)\times 20$ and $N_k^{\text{UB}}=(0.5k+1.5)\times 80,\forall k\in \mathcal{K}$. We also assume the availability of each sensing device to be i.i.d. using a binary random variable with a mean of 0.9. Besides, we assume M_max = 500 samples, δ = 100 bits/sample, and the length of a time slot Δt = 0.1 s.

We consider a system with K = 3 sensing devices randomly distributed within the coverage of the AP. However, only F = 2 channel links are available and the bandwidth of each orthogonal channel is set as 15 KHz. The fairness constraint factors are c₁ = 0.7, c₂ = 0.5, and c₃ = 0.6. Here, we define Ω₁ and Ω₂ as the cumulative performance gap and average performance gap, respectively, with Ω₁ = Σ^πM_max and Ω₂ = Ω₁/T, which are used to describe the difference between the optimal solution found by solving problem Eq. 9 and the solution found using the proposed algorithm (or baseline algorithms). Note that the optimal solution found by solving problem Eq. 9 satisfies the fairness constraint. For comparison, we introduce a modified version of the proposed algorithm, which does not take into account the fairness constraint. More specifically, the UCB algorithm for the modified version does not introduce the virtual queue technique. In Figure 2, we compare the proposed algorithms under different α values with the modified version. We find that the performance gap of the modified algorithm is the smallest, whose value is even negative because the modified algorithm does not need to meet the fairness constraint and may lead to biased observations of the area of interest. We also observe that the time-average performance gap of the proposed algorithm grows at a sub-linear trend. Besides, at first glance, the proposed algorithm with a smaller α value meets the fairness constraint but also enjoys better performance, which is more attractive. This is because a smaller α value makes the reward of each device dominant and the fairness constraint insignificant. However, what is missing in Figure 2 is the convergence time used to meet the fairness constraint, which is also an important metric that should be taken into account in practice.

FIGURE 2

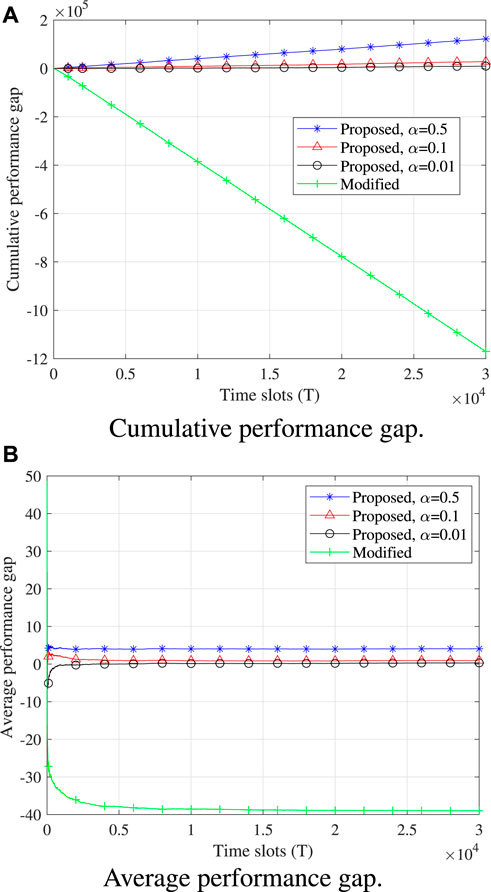
FIGURE 2. Performance comparison of different algorithms. (A) Cumulative performance gap over the time slots. (B) Average performance gap over the time slots.

Figure 3 shows the change in the selection fractions of different devices over the time slots. Here, the selection fraction is defined as the ratio of the chosen time of a certain device to the total number of time slots. We find that the curves of all the arms obtained by the proposed algorithm meet the fairness constraints eventually, no matter which α value is taken. The modified algorithm has no idea of the fairness constraints and thus does not need to meet the fairness constraints. In addition, it is observed that a smaller α value leads to more time consumption before the convergence is achieved and the convergence rate of the curve with α = 0.001 is the slowest.

FIGURE 3

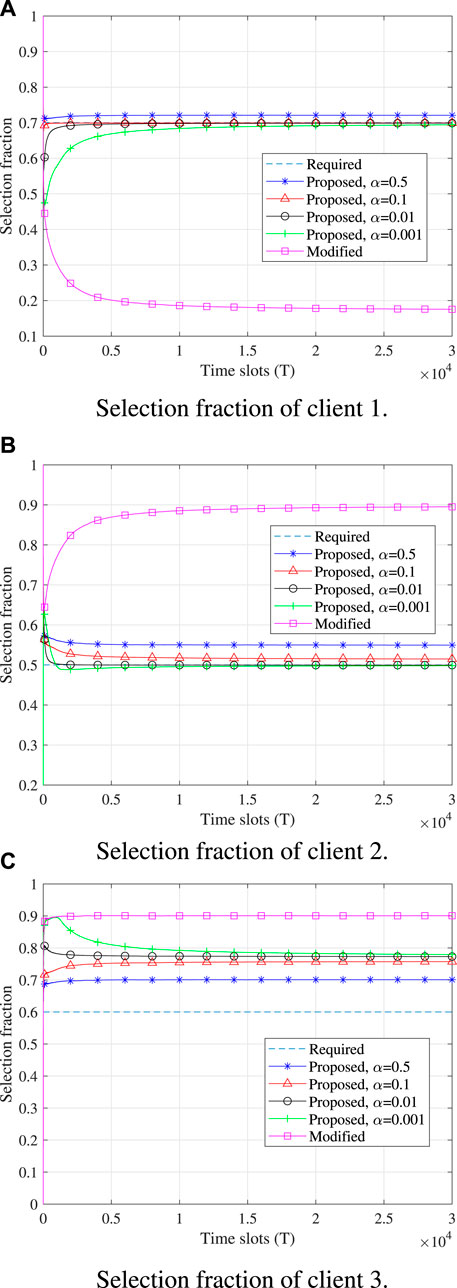
FIGURE 3. Client selection over the time slots. (A) Section fraction of client 1. (B) Section fraction of client 2. (C) Section fraction of client 3.

To further validate the effectiveness of the proposed algorithm, we consider a scenario with K = 20 devices and introduce the round-robin algorithm as a baseline, as shown in Figure 4. According to the results in Figure 4, we find that more samples are collected with the increase of the number of available channels. In addition, the proposed algorithm always achieves better performance than the round-robin algorithm.

FIGURE 4

FIGURE 4. Performance comparison of the proposed algorithm with the round-robin algorithm.

Conclusion

In this work, we considered sensing device scheduling problem in mobile crowdsensing tasks, which suffers from the scarcity of wireless channel resource and the lack of prior knowledge, as well as different capabilities among devices. To address these challenges, we reformulated the device scheduling problem as an MAB program, one should guarantee the participation fairness of sensing devices with different coverage regions. Then, we proposed a device scheduling algorithm on the basis of the UCB policy and virtual queue theory, whose performance regret was also analyzed. Finally, numerical results were conducted to verify the effectiveness of the proposed algorithm.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JZ contributed to the conception and prepared the first draft of the manuscript. YN performed the numerical simulations. HZ improved the writing of the manuscript. All authors approved the submitted version of the manuscript.

Funding

This work was supported in part by National Key R&D Program of China (2021ZD0140405), in part by Natural Science Foundation of Jiangsu Province (BK2021022532), in part by Jiangsu University Philosophy and Social Science Research Fund (2022SJYB0517).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Auer, P., Cesa-Bianchi, N., and Fischer, P. (2002). Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 47, 235–256. doi:10.1023/a:1013689704352

CrossRef Full Text | Google Scholar

Blasco, P., and Gündüz, D. (2014). “Learning-based optimization of cache content in a small cell base station,” in 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10-14 June 2014 (IEEE), 1897–1903.

CrossRef Full Text | Google Scholar

Bubeck, S., and Cesa-Bianchi, N. (2012). Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Found. Trends® Mach. Learn. 5, 1–122. doi:10.1561/2200000024

CrossRef Full Text | Google Scholar

Chen, L., and Xu, J. (2019). “Task replication for vehicular cloud: Contextual combinatorial bandit with delayed feedback,” in IEEE INFOCOM 2019 - IEEE Conference on Computer Communications, Paris, France, 29 April 2019 - 02 May 2019, 748–756.

CrossRef Full Text | Google Scholar

Cheng, M., Wang, J.-B., Wang, J.-Y., Lin, M., Wu, Y., and Zhu, H. (2019). “A fast beam searching scheme in mmwave communications for high-speed trains,” in IEEE Int. Conf. Commun. (ICC), Shanghai, China, 29 April 2019 - 02 May 2019, 1–6.

CrossRef Full Text | Google Scholar

Chu, E.-H., Lin, C.-Y., Tsai, P.-H., and Liu, J. (2013). Participant selection for crowdsourcing disaster information. WIT Trans. Built Environ. 133, 231–240.

CrossRef Full Text | Google Scholar

Dahrouj, H., and Yu, W. (2010). Coordinated beamforming for the multicell multi-antenna wireless system. IEEE Trans. Wirel. Commun. 9, 1748–1759. doi:10.1109/TWC.2010.05.090936

CrossRef Full Text | Google Scholar

Gendy, M. E., Al-Kabbany, A., and Badran, E. F. (2020). “Maximizing clearance rate by penalizing redundant task assignment in mobile crowdsensing auctions,” in Proc. IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Korea (South), 25-28 May 2020, 1–7.

CrossRef Full Text | Google Scholar

Guo, B., Yu, Z., Zhou, X., and Zhang, D. (2014). “From participatory sensing to mobile crowd sensing,” in Proc. IEEE International Conference on Pervasive Computing and Communication Workshops (PERCOM WORKSHOPS), Budapest, Hungary, 24-28 March 2014, 593–598.

CrossRef Full Text | Google Scholar

Han, K., Zhang, C., and Luo, J. (2016). Taming the uncertainty: Budget limited robust crowdsensing through online learning. IEEE/ACM Trans. Netw. 24, 1462–1475. doi:10.1109/tnet.2015.2418191

CrossRef Full Text | Google Scholar

Han, Y., Zhu, Y., and Yu, J. (2015). “Utility-maximizing data collection in crowd sensing: An optimal scheduling approach,” in Proc. IEEE Int. Conf. Sensing, Communication, and Networking (SECON), Seattle, USA, 22-25 June 2015, 345–353.

CrossRef Full Text | Google Scholar

Hsu, W., Xu, J., Lin, X., and Bell, M. R. (2018). “Integrating online learning and adaptive control in queueing systems with uncertain payoffs,” in Inf. Theory appli. Workshop (ITA) (San Diego, CA, USA, 1–9.

CrossRef Full Text | Google Scholar

Lai, T. L., and Robbins, H. (1985). Asymptotically efficient adaptive allocation rules. Adv. Appl. Math. 6, 4–22. doi:10.1016/0196-8858(85)90002-8

CrossRef Full Text | Google Scholar

Lattimore, T., and Szepesvári, C. (2020). Bandit algorithms. Cambridge: Cambridge University Press.

Google Scholar

Li, F., Liu, J., and Ji, B. (2019). Combinatorial sleeping bandits with fairness constraints. Proc. IEEE Conf. Comput. Commun. 7, 1702–1710.

CrossRef Full Text | Google Scholar

Neely, M. J. (2010). Stochastic network optimization with application to communication and queueing systems. Synth. Lect. Commun. Netw. 3, 1–211. doi:10.2200/s00271ed1v01y201006cnt007

CrossRef Full Text | Google Scholar

Nguyen, T. N., and Zeadally, S. (2021). Mobile crowd-sensing applications: Data redundancies, challenges, and solutions. ACM Trans. Internet Technol. 22, 1–15. doi:10.1145/3431502

CrossRef Full Text | Google Scholar

Sengupta, A., Amuru, S., Tandon, R., Buehrer, R. M., and Clancy, T. C. (2014). “Learning distributed caching strategies in small cell networks,” in Proc. Int. Symp. Wireless commun. Syst. (ISWCS) (Barcelona, Spain, 917–921.

CrossRef Full Text | Google Scholar

Sun, Y., Song, J., Zhou, S., Guo, X., and Niu, Z. (2018). “Task replication for vehicular edge computing: A combinatorial multi-armed bandit based approach,” in 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 09-13 December 2018, 1–7.

CrossRef Full Text | Google Scholar

Sun, Y., and Tang, Y. (2019). “Task-oriented data collection strategy in vehicular crowdsensing,” in Proc. Int. Conf. Computer Science and Education (ICCSE), Toronto, Canada, 19-21 August 2019, 761–766.

CrossRef Full Text | Google Scholar

Xia, W., Wen, W., Wong, K.-K., Quek, T. Q., Zhang, J., and Zhu, H. (2021). Federated-learning-based client scheduling for low-latency wireless communications. IEEE Wirel. Commun. 28, 32–38. doi:10.1109/mwc.001.2000252

CrossRef Full Text | Google Scholar