- Oak Ridge National Laboratory, Oak Ridge, TN, United States
An assessment of nuclear data performance for non-light-water reactor (non-LWR) reactivity calculations was performed at Oak Ridge National Laboratory that involved a thorough literature review to collect related observations made across different research institutions, an interrogation of the latest ENDF/B evaluated nuclear data libraries, and propagation of nuclear data uncertainties to key figures of merit associated with reactor safety for six non-LWR benchmarks. The outcome of this comprehensive study was published in a technical report issued by the US Nuclear Regulatory Commission. This paper provides a summary of the study’s key observations and conclusions and demonstrates with two examples how the various methods available in the SCALE code system were used to identify key cross section uncertainties for non-LWR reactivity analyses.
1 Introduction
Uncertainty analyses are an essential component in the design and computational analysis of advanced reactors, especially due to the growing interest in new reactor concepts for which scant operational data are available1. The advanced reactor concepts currently being developed throughout the industry (US, 2022) are significantly different from light-water reactor (LWR) designs with respect to geometry, materials, and operating conditions—and, consequently, with respect to their reactor physics behavior. An overview of different advanced reactor concepts is provided by the Gen IV International Forum (NEA, 2014), and the different technologies along with considerations around their fuel cycle are thoroughly discussed in a recent publication by the Academy of Sciences (National Academies of Sciences Engineering, and Medicine, 2023). Given the limited operating experience with non-LWRs, the accurate simulation of reactor physics and the quantification of associated uncertainties are critical for ensuring that advanced reactor concepts operate within the appropriate safety margins.
While nuclear data provide the fundamental basis for reactor physics calculations, they also provide the major source of input uncertainty. The nuclear interaction cross sections, fission yields, and decay data used in these calculations have uncertainty resulting from measurements and subsequent data evaluations. Nuclear data used with reactor physics codes result from extensive data evaluations, including validation studies performed with criticality experiments. The evaluated nuclear data libraries, such as the US Evaluated Nuclear Data File/B (ENDF/B) (Brown et al., 2018), undergo continuous modifications based on additional measurements or improved evaluations, and new revisions are being released on a regular basis to capture these additional improvements.
To improve understanding of the uncertainties that result from nuclear data in the calculation of safety-relevant output quantities and to determine where additional efforts should focus to reduce relevant nuclear data uncertainties, these uncertainties must be propagated to key figures of merit that impact nuclear safety. Furthermore, it must be considered that uncertainty information is not available for all nuclear data used in the simulation. Missing uncertainty data must be identified and, where possible, the impact of these gaps must be assessed to inform recommendations for further evaluations.
Although many studies assessing the impact of nuclear data uncertainties are available in the public literature, a comprehensive overview of the impact of nuclear data uncertainties for reactivity in the most relevant non-LWRs designs (in terms of reactor concepts for which license applications are expected in the near future in the United States) based on the same set of evaluated nuclear data libraries and using the same simulation approaches did not exist until recently. A recently concluded project at Oak Ridge National Laboratory (ORNL) sponsored by the US Nuclear Regulatory Commission (NRC) addressed this need by performing a thorough literature study to collect the observations made across different research institutions and by using SCALE [Wieselquist, W. A., Lefebvre, R. A., and Jessee, M. A. (Eds.), 2020] to systematically propagate nuclear data uncertainties to key figures of merit associated with reactor safety for five non-LWR types: high-temperature gas-cooled reactor (HTGR), molten salt reactor (MSR), fluoride salt–cooled high-temperature reactor (FHR), heat pipe reactor (HPR), and sodium-cooled fast reactors (SFRs). As part of this study, missing nominal nuclear data and nuclear data uncertainties were identified for reactivity analyses as well as for further fuel depletion analysis. This paper provides a summary of key observations and conclusions obtained during this study, while providing just two examples to demonstrate how the computational analyses were performed. Detailed analysis results are available in a comprehensive technical report (Bostelmann et al., 2021b) issued by the NRC. It is noted that the study focused on systems with 235U enriched or mixed uranium/plutonium fuel based on spent LWR fuel; 233U-fueled systems were not considered here.
After introducing the selected non-LWRs in Section 2, the applied approach used for the uncertainty analyses is briefly summarized (Section 3). As examples of the performed computational analyses, the propagation of nuclear data uncertainties is presented and discussed for reactivity assessments of the HPR and the FHR concepts (Section 4). Afterwards, an overview of key observations for all considered systems based on both the literature research and the SCALE analyses is given (Section 5).
2 Benchmarks
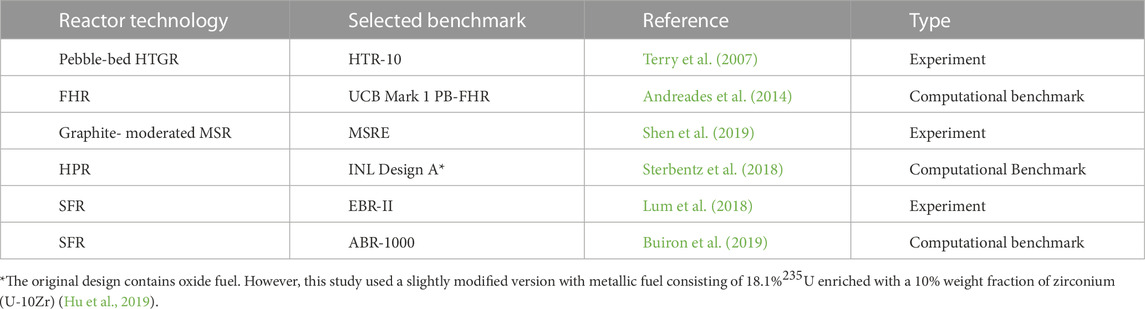
The benchmarks for uncertainty analyses with SCALE were identified by selecting reactors with available detailed specifications for which the geometry, materials, and neutron energy spectra are similar to those of the advanced reactor technologies of interest. Given the limited availability of measured data for advanced reactor systems, only theoretical or simplified descriptions were found for some reactor technologies. However, as long as the models include representative geometric dimensions and representative materials, uncertainty analyses of these models can serve well to provide an understanding of the impact of nuclear data uncertainties and to identify relevant nuclide reactions. Table 1 gives an overview of the selected benchmarks, and Figure 1 illustrates the developed SCALE models. Details of the models can be found in the references provided in Table 1.
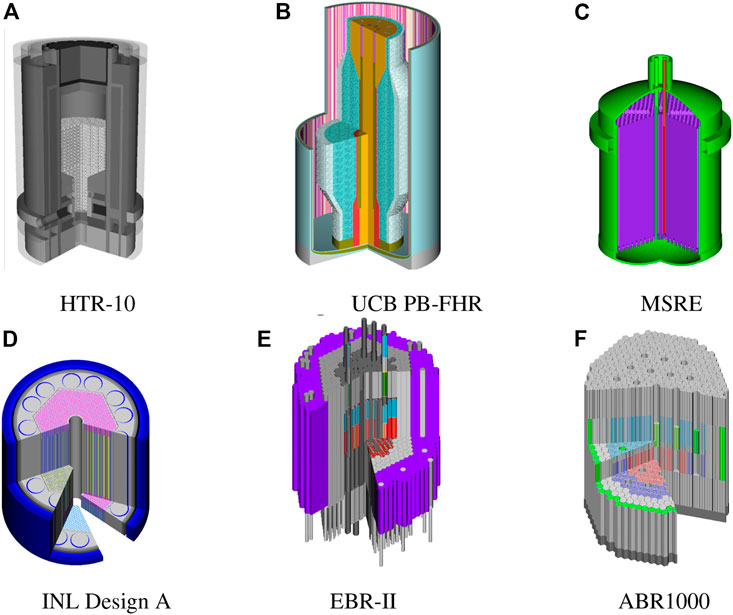
FIGURE 1. 3D visualizations of the non-LWR SCALE models. (A) HTR-10, (B) UCB PB-FHR, (C) MSRE, (D) INL Design A, (E) EBR-Ⅱ and (F) ABR 1000.
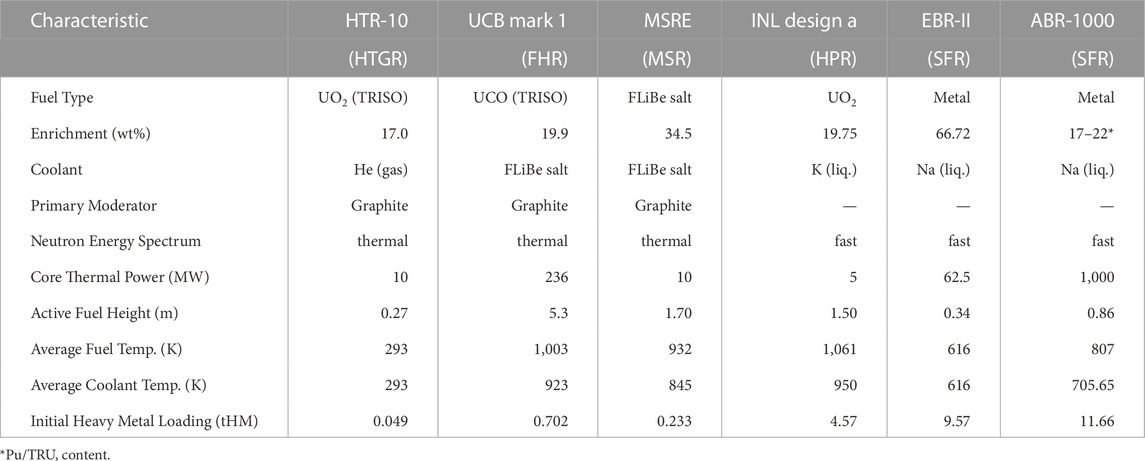
Many of the considered reactors share certain characteristics. Each of the thermal spectrum systems—HTR-10, the University of California Berkeley (UCB) PB-FHR, the Molten-Salt Reactor Experiment (MSRE)—rely on graphite as neutron moderator and reflector. Both the HTR-10 and the UCB PB-FHR are pebble-bed reactors that use graphite pebbles (of different size) in which tristructural isotropic (TRISO) fuel particles are distributed. The UCB PB-FHR uses molten salt FLiBe as coolant, which is a mixture of LiF and BeF2. Fluoride-based salt is also used in the MSRE for both the carrier salt and the fuel salt. The fast spectrum systems (INL Design A, EBR-II, ABR1000) operate in the absence of a moderator. EBR-II and ABR1000 include irradiated fuel: EBR-II includes high enriched uranium fuel assemblies at various burnups, and ABR1000 uses spent LWR fuel, i.e., uranium/transuranic (U/TRU) fuel, in its equilibrium core. Both these SFRs are cooled by sodium. The INL Design A is an HPR operated with high-assay low-enriched uranium (HALEU) and uses potassium as its working fluid. An overview of key characteristics of the selected benchmarks is provided in Table 2.
3 Uncertainty and sensitivity analysis approach
Uncertainty and sensitivity analyses of eigenvalues and reactivity coefficients were performed using two approaches: linear perturbation theory and random sampling approach. Both approaches relied on neutron transport calculations with SCALE’s Monte Carlo code KENO-VI in either multigroup (MG) or continuous-energy (CE) mode. Both approaches provided insights into the uncertainty of key metrics as well as the top-contributing nuclear data to the observed uncertainty. All analyses were performed using codes and nuclear data libraries from a pre-release version of SCALE 6.3.
3.1 Linear perturbation theory
Sensitivity analyses were performed for the eigenvalue and the reactivity effects using the perturbation theory–based approach implemented in SCALE’s TSUNAMI code (Broadhead et al., 2004). TSUNAMI calculates sensitivity coefficients for all nuclides included in the model of interest with all reactions in all energy groups (Williams, 1986; Williams et al., 2001). TSUNAMI was applied to calculate eigenvalue sensitivities. For reactivity differences such as temperature feedback and control rod worth, TSUNAMI calculations were performed at two different states, and SCALE’s module TSAR (Williams, 2007) was used to combine the two sets of sensitivity coefficients to obtain sensitivity coefficients for the reactivity difference.
The nuclear data uncertainties are given in energy-dependent covariance matrices for each nuclide reaction and for correlations between different nuclide reactions. The multiplication of these covariance matrices with the corresponding sensitivity coefficients determined using TSUNAMI in the so-called sandwich formula leads to the total output variance (Rearden et al., 2011). In addition to the total output uncertainty, TSUNAMI provides a list of the individual contributions of all relevant covariance matrices so that the top contributors to the output uncertainty can be identified.
Note that the output uncertainty is usually shown as the 1-sigma standard deviation of a normal distribution, due to the input nuclear data covariances being normal distributions.
3.2 Random sampling
For some reactor concepts, the random sampling approach as implemented in SCALE’s Sampler sequence (Williams et al., 2013) was used to study uncertainties resulting from nuclear data. The nuclear data are perturbed based on covariance data as provided in the ENDF/B nuclear data files. Sampler performs calculations multiple times based on the perturbed dataset. A statistical analysis of the output of interest yields the output’s uncertainty. To identify the top-contributing nuclide reactions to the output uncertainty, Sampler calculates the sensitivity index R2 (Bostelmann et al., 2022) of all reactions of all nuclides relevant for the model. On a level from 0 to 1, R2 provides a measure of the importance of an individual nuclear reaction to the observed output uncertainty.
Note that the output uncertainty is usually shown as the 1-sigma standard deviation using sample statistics. Although SCALE/Sampler can draw from many distributions, the fundamental nuclear data is specified as a normal distribution. To avoid generating non-physical nuclear data (such as negative cross sections), the normal distribution is truncated.
3.3 Applied nuclear data
Neutron transport calculations were performed using ENDF/B-VII.0 (Chadwick et al., 2006), ENDF/B-VII.1 (Chadwick et al., 2011), and ENDF/B-VIII.0 cross section libraries (Brown et al., 2018). For the uncertainty quantification, TSUNAMI applied the corresponding ENDF/B-VII.0–based, ENDF/B-VII.1–based, and ENDF/B-VIII.0–based covariance libraries, respectively. Sampler calculations were performed using perturbation factors that were generated based on these covariance libraries. More details on these libraries can be found in the SCALE manual (Wieselquist et al., 2020).
4 Nuclear data uncertainty propagation
Only the reactivity analysis of the INL Design A HPR and the FHR are presented here to demonstrate how the uncertainty and sensitivity analyses were performed. When considering the presented results, it is useful to keep in mind results usually obtained for the same quantities in LWR analysis. A keff uncertainty between 0.5% for fresh fuel and 0.8% for depleted fuel, and a fuel Doppler coefficient uncertainty between 1.2% and 1.8% is usually obtained (Aures et al., 2017; Delipei et al., 2021). Key contributors to these uncertainties are 238U and 239Pu radiative capture, as well as 235U and 239Pu neutron multiplicity.
4.1 INL design A
Based on a SCALE full core model initially developed for a different project (Walker et al., 2022), the sensitivity and uncertainty analyses for the fresh core of the INL Design A (Figure 1D) were performed with CE TSUNAMI for the following quantities of interest.
1 keff
2 Δρ fuel temperature: reactivity change from increasing fuel temperature by 500 K
3 Δρ grid radial expansion: reactivity change from radial expansion of the fuel element grid 0.08% into the surrounding gap
4 Δρ fuel axial expansion: reactivity change from axial expansion of the fuel by 0.5% into the lower gas plenum
The temperature increase and the relative expansions were chosen to obtain statistically distinguishable results with the Monte Carlo approach, but they do not correspond to actual changes during reactor operation. While the relative uncertainties obtained with the ENDF/B-VII.0 and ENDF/B-VII.1 libraries are fairly similar, a significant reduction in uncertainty was observed with the ENDF/B-VIII.0 library (Table 3). It is noted that even with the ENDF/B-VIII.0 library, the keff uncertainty is about twice as large as the typical keff uncertainty of an LWR system.
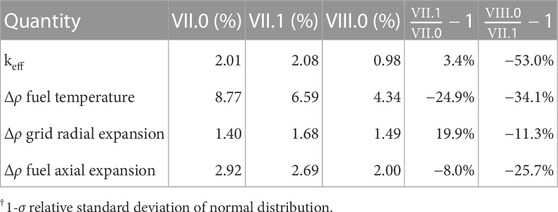
TABLE 3. INL Design A HPR uncertainties† in quantities of interest due to nuclear data uncertainty, for different ENDF/B library versions.
To understand which cross sections are the major contributors to the observed uncertainties and why there is this significant difference with the latest ENDF/B release, sensitivity analyses were performed by investigating the top contributions to the uncertainty provided by TSUNAMI. TSUNAMI determines these individual contributions through the multiplication of the cross section–specific sensitivity with the corresponding covariance matrix. Figure 2 presents these top contributions in the unit ΔR/R, R being the response of interest (e.g., keff).
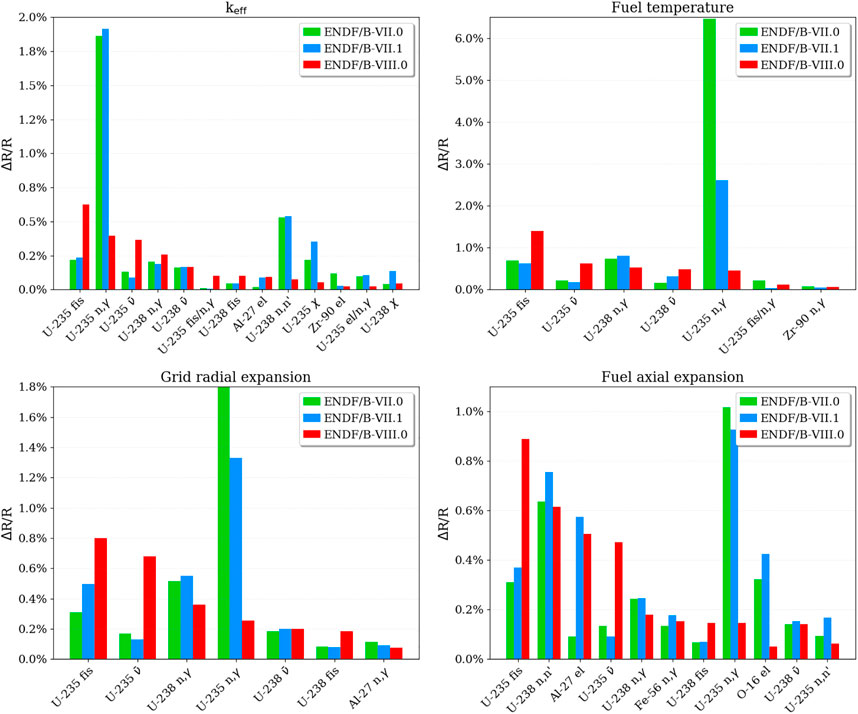
FIGURE 2. Relative contributions to the output uncertainties of the INL Design A HPR (as obtained with TSUNAMI in ΔR/R, R: response).
It is easily visible that the uncertainty in the 235U (n,γ) cross section is the top contributor to all output uncertainties in the ENDF/B-VII.0 and ENDF/B-VII.1 calculations. The associated uncertainty in this reaction was dramatically reduced in the ENDF/B-VIII.0 calculation, which led to a significant reduction in the overall output uncertainty. This reduction is the largest for keff because 235U (n,γ) was the dominating contributor to the keff uncertainty with ENDF/B-VII.0 and ENDF/B-VII.1. Slightly larger contributions from 235U fission and the neutron multiplicity
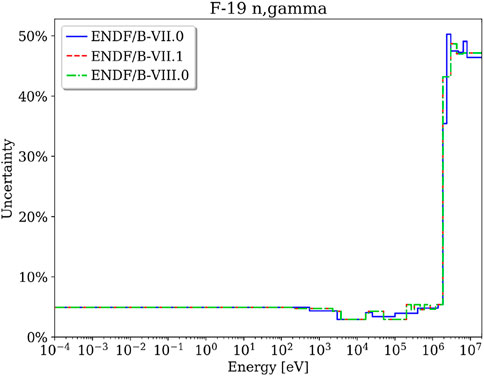
To further explain the large impact of the 235U (n,γ) cross section uncertainty on the INL Design A reactivity results, the uncertainty of this reaction and the neutron flux in this reactor were examined. Figure 3 shows that the 235U (n,γ) uncertainty is large, with up to 34% in the fast energy range; that is, in the energy range with many neutrons. Since the uncertainty is reduced in this energy range in ENDF/B-VIII.0, the overall contribution of this reaction to the output uncertainty is reduced. Figure 4 clearly illustrates the differences in the fast neutron spectrum in various regions of the reactor.
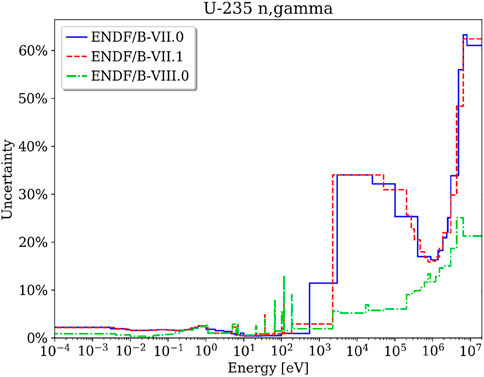
FIGURE 3. Relative uncertainty of the 235U (n,γ) cross section in different ENDF/B library releases.
FIGURE 4. Normalized neutron flux of the INL Design A HPR at the core axial midline, at different radial positions.
This example of analysis demonstrates 1) how to identify top-contributing nuclide reactions to an output uncertainty of interest and 2) the strong impact of reductions of important cross section uncertainties for the overall output uncertainty. Given that the 235U (n,γ) uncertainty was reduced in ENDF/B-VIII.0, the identification of top contributors in this case would result in recommendations for further measurements and evaluations of 235U fission, inelastic scattering (n,n′), and
4.2 UCB PB-FHR
Based on a SCALE full core model initially developed for a different project (Bostelmann et al., 2021a), the sensitivity and uncertainty analyses for the equilibrium core of the UCB PB-FHR were performed with Sampler and KENO-VI in MG mode for the following quantities of interest.
1 keff
2 Δρ fuel temperature: reactivity change from increasing fuel temperature by 500 K
3 Δρ coolant salt temperature: reactivity change from increasing salt temperature by 300 K
4 Δρ coolant salt density: reactivity change from increasing salt density by 50%
The temperature increases and the density multiplier were chosen to obtain statistically distinguishable results with the Monte Carlo approach, but they do not correspond to actual changes during reactor operation. Sampler was chosen due to convergence challenges of sensitivities for important scattering reactions of the graphite reflector and the salt components in the fast energy range when using the perturbation theory–based approach for this reactor. Furthermore, only this approach can be used for the analysis of output quantities such as a power distribution (not presented here). A sample size of 1,000 was used with Sampler to allow sufficient confidence in the obtained uncertainties of the reactivity differences. Sampler calculations were limited to ENDF/B-VII.1 and ENDF/B-VIII.0 since Sampler’s sensitivity analysis is currently enabled only for these two libraries.
The relative uncertainties obtained with these two libraries are fairly similar (Table 4). The relative uncertainty of the salt density reactivity stands out, with an uncertainty larger than 35%, and the keff uncertainty is about three times as large as the typical keff uncertainty of an LWR system.
TABLE 4. UCB PB-FHR uncertainties† in quantities of interest due to nuclear data uncertainty, for different ENDF/B library versions.
To understand which cross sections are the major contributors to the observed uncertainties and why the salt density uncertainty is significantly larger than the other uncertainties, sensitivity indices R2 were calculated for all reactions of all nuclides in the system. Figure 5 presents the largest obtained R2 values found to be statistically significant (above a statistical significance level).
FIGURE 5. Top contributor to the output uncertainties of the UCB PB-FHR in terms of R2 (as obtained with Sampler, accompanied by 95% confidence intervals).
It is easily visible that the top contributor to the keff and the salt density reactivity uncertainty is the uncertainty in the 7Li (n,γ) cross section. 7Li is one of the major components of the coolant salt; therefore, 7Li reactions have an especially large influence on the salt density reactivity. The uncertainty of this (n,γ) reaction is significant in the thermal region in which most of the neutrons can be found (Figure 6), with an approximate value in this energy range of 5% (Figure 7). The value for this uncertainty is identical between ENDF/B-VII.1 and ENDF/B-VIII.0. If the uncertainty of this single reaction could be reduced with further measurements and evaluations, then the uncertainties of these key reactivities would dramatically decrease. The relevant nuclide reactions for the other reactivity uncertainties are spread out over various reactions, mainly U and Pu reactions. Since many of these reactions’ uncertainties varied between ENDF/B-VII.1 and ENDF/B-VIII.0, their relative contributions and the total output uncertainties show larger variations.
FIGURE 6. Normalized neutron flux of the UCB PB-FHR at the core axial midline, at different radial positions.
In the ENDF/B-VIII.0 calculations of the fuel and salt temperature reactivities, large R2 values of the 239Pu elastic scattering reaction stand out. For the interpretation of R2, it has to be considered that R2 includes correlations between the different reactions. For example, in the case of 239Pu elastic scattering, this reaction is not itself contributing significant uncertainty to the total output uncertainty, but its R2 value is the result of correlations with both the 239Pu fission and (n,γ) reaction which show larger relative contributions in ENDF/B-VIII.0. In contrast, in the ENDF/B-VII.1 calculation, the R2 for 239Pu elastic scattering is below the statistical significance level because of the smaller importance of 239Pu fission and (n,γ) reaction relative to other contributors. More detailed explanations on the interpretation of R2 in such analyses can be found in (Bostelmann et al., 2022).
This example analysis demonstrates 1) how the large uncertainty of one cross section can dominate the uncertainty of important output quantities and that 2) analysis of non-LWRs can lead to the identification of unexpected, important cross section uncertainties of nuclides that were never found relevant for LWR analysis.
5 Key observations for the studied non-LWRs
The following provides an overview of the most relevant observations for the considered non-LWRs, focused on the ENDF/B evaluated data library. Comparisons of the data between the different ENDF/B libraries led to observations on important differences in cross sections and cross section uncertainties (e.g., 235U
5.1 Nuclear data for neutron transport calculations
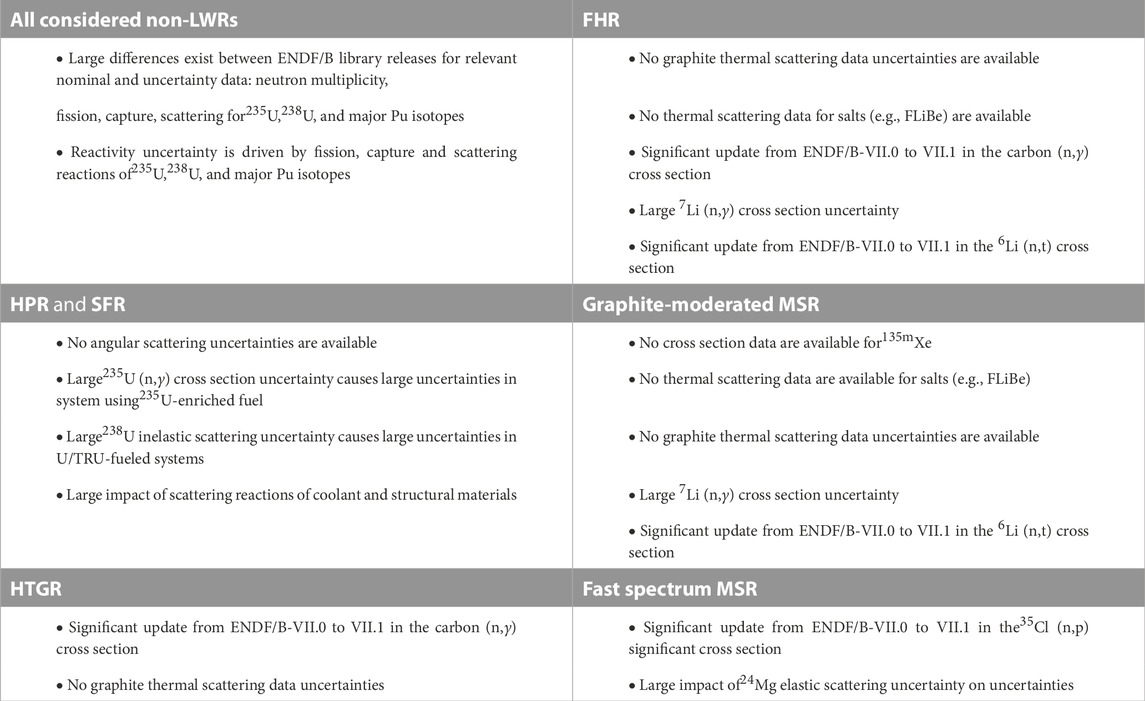
For neutron transport calculations to determine output quantities such as reactivity and power distributions, the observations with respect to nuclear data and non-LWRs are summarized in Table 5.
5.2 Nuclear data for time-dependent analyses
The time-dependent behavior of any reactor type requires more than just cross section data. For the following important data, limited or no data are available in the latest ENDF/B release.
• Fission yields: Uncertainties available, correlations not available
• Decay constants: Uncertainties available, correlations not available
• Branching ratios: No uncertainty or correlation data available
• Recoverable energy for fission and capture: No uncertainty or correlation data available
• Delayed neutron fractions and decay constants: No uncertainty or correlation data available
Data on recoverable energy for fission and capture reactions are in fact often hard-coded in neutron transport codes; this data is, for example, important to determine the material power. The same is valid for delayed neutron fractions and decay constants, which are especially important for transient analyses and which are further relevant in systems with flowing fuel (MSRs) due to the delayed neutron precursor drift.
6 Conclusion
This paper reviews an assessment of key nuclear data, nuclear data uncertainties, and nuclear data gaps that are relevant for reactor safety analysis in non-LWRs, recently concluded at ORNL. The study involved a literature review, examination of available evaluated nuclear data libraries, and sensitivity and uncertainty analyses with SCALE for six non-LWR benchmarks to quantify the impact of the identified key nuclear data on several key metrics. The nuclear data uncertainty propagation is highlighted herein for two of the six non-LWRs, and the summary of observations for all non-LWRs are presented.
SCALE’s approaches to study the impact of nuclear data uncertainties on the uncertainties of key metrics of interest—particularly the ranking of contributions to the output uncertainties—can be used to guide future measurement and evaluation efforts to reduce the significant nuclear data uncertainties and thereby significantly reduce the overall observed uncertainties. However, to perform such uncertainty assessments, SCALE (just as any other uncertainty analysis tool) relies on the availability of complete and reliable nuclear data.
Besides observing major cross section and uncertainty updates between the different ENDF/B nuclear data library releases that can have major influence on reactivities, various data gaps were identified, especially for missing uncertainties. These gaps must be addressed to improve prediction of key metrics and to avoid unknown biases. Furthermore, this study identified several large cross section uncertainties. A reduction of these specific large uncertainties is needed to significantly reduce the overall output uncertainty of key metrics. It is noted that no statement on the performance or recommendation of a specific ENDF/B library are made given the limited amount of experimental measurement data for non-LWRs to allow a thorough validation.
This study focused on key figures of merit obtained with neutron transport calculations at a single point in time. This type of systematic approach to assess nuclear data performance should be continued in the depletion simulations space to determine uncertainties in nuclide inventories, as well as in transient analysis space, in which key nuclear data include delayed neutron data. All of these studies will greatly benefit from the availability of additional non-LWR reactor physics benchmarks as a basis to fill in the gaps for validating computational tools and data for various safety relevant quantities.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
Author contributions
WW and GI provided the outline of study and provided supervision throughout. FB developed the models and performed the computational analyses. FB, GI, and WW collected the nuclear data gaps. FB wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work was supported by the US Nuclear Regulatory Commission.
Acknowledgments
The authors would like to acknowledge Cihangir Celik’s (ORNL) contribution during the development of the SCALE model of the pebble-bed fluoride salt-cooled high temperature reactor. The discussions with Andrew Holcomb (OECD/NEA) about ENDF/B nuclear data libraries and analysis results are much appreciated.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1This manuscript has been authored by UT-Battelle LLC, under contract DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
References
Andreades, C., Cisneros, A. T., Choi, J. K., Chong, A. Y. K., Fratoni, M., Hong, S., et al. (2014). Technical description of the “mark 1” pebble-bed fluoride-salt-cooled high-temperature reactor (PB-FHR) power plant. Berkeley, CA: University of California. Tech. Rep. UCBTH-14-002.
Aures, A., Bostelmann, F., Hursin, M., and Leray, O. (2017). Benchmarking and application of the state-of-the-art uncertainty analysis methods XSUSA and SHARK-X. Ann. Nucl. Energy 101, 262–269. doi:10.1016/j.anucene.2016.11.025
Bostelmann, F., Celik, C., Kile, R., and Wieselquist, W. (2021a). SCALE analysis of a fluoride salt cooled high temperature reactor in support of severe accident analysis. Oak Ridge, TN: Oak Ridge National Laboratory. Tech. Rep. ORNL/TM-2021/2273.
Bostelmann, F., Ilas, G., Celik, C., Holcomb, A. M., and Wieselquist, W. (2021b). Nuclear data assessment for advanced reactors. Oak Ridge, TN: Oak Ridge National Laboratory. ORNL/TM-2021/2002Tech. Rep. NUREG/CR-7289.
Bostelmann, F., Wiarda, D., Arbanas, G., and Wieselquist, W. A. (2022). Extension of SCALE/Sampler’s sensitivity analysis. Ann. Nucl. Energy 165, 108641. doi:10.1016/j.anucene.2021.108641
Broadhead, B. L., Rearden, B. T., Hopper, C. M., Wagschal, J. J., and Parks, C. V. (2004). Sensitivity- and uncertainty-based criticality safety validation techniques. Nucl. Sci. Eng. 146, 340–366. doi:10.13182/NSE03-2
Brown, D., Chadwick, M., Capote, R., Kahler, A., Trkov, A., Herman, M., et al. (2018). ENDF/B-VIII.0: The 8th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets 148, 1–142. doi:10.1016/J.NDS.2018.02.001
Buiron, L., Rimpault, G., Sciora, P., Stauff, N., Kim, T. K., Taiwo, T., et al. (2019). “Benchmark for uncertainty analysis in modeling (UAM) for design, operation and safety analysis of SFRs, core definitions,”. Version 1.6. Tech. rep., OECD/NEA.
Chadwick, M., Herman, M., Obložinský, P., Dunn, M., Danon, Y., Kahler, A., et al. (2011). ENDF/B-VII.1 nuclear data for science and technology: Cross sections, covariances, fission product yields and decay data. Nucl. Data Sheets 112, 2887–2996. doi:10.1016/j.nds.2011.11.002
Chadwick, M., Obložinský, P., Herman, M., Greene, N., McKnight, R., Smith, D., et al. (2006). ENDF/B-VII.0: Next generation evaluated nuclear data library for nuclear science and technology. Nucl. Data Sheets 107, 2931–3060. doi:10.1016/j.nds.2006.11.001
Delipei, G. K., Hou, J., Avramova, M., Rouxelin, P., and Ivanov, K. (2021). Summary of comparative analysis and conclusions from OECD/NEA LWR-UAM benchmark Phase I. Nucl. Eng. Des. 384, 111474. doi:10.1016/j.nucengdes.2021.111474
Hu, G., Hu, R., Kelly, J., and Ortensi, J. (2019). Multi-physics simulations of heat pipe micro reactor. Argonne, IL: Argonne National Laboratory. Tech. Rep. ANL-NSE-19/25.
Lum, E. S., Pope, C. L., Stewart, R., Byambadorj, B., and Beaulieu, Q. (2018). Evaluation of run 138B at experimental breeder reactor II, a prototypic liquid metal reactor. France: Organisation for Economic Co-operation and Development/Nuclear Energy Agency. Tech. Rep. EBR2-LMFR-RESR-001, CRIT, NEA/NSC/DOC(2006)1.
National Academies of Sciences Engineering, and Medicine (2023). Merits and viability of different nuclear fuel cycles and technology options and the waste aspects of advanced nuclear reactors. Washington, DC: Tech. rep.
NEA (2014). Technology roadmap update for generation IV nuclear energy systems. Tech. Rep. Paris, France: Nuclear Energy Agency.
Rearden, B. T., Williams, M. L., Jessee, M. A., Mueller, D. E., and Wiarda, D. A. (2011). Sensitivity and uncertainty analysis capabilities and data in SCALE. Nucl. Technol. 174, 236–288. doi:10.13182/NT174-236
Shen, D., Fratoni, M., Ilas, G., and Powers, J. J. (2019). “Molten-Salt Reactor Experiment (MSRE) zero-power first critical experiment with U-235. Tech,”. Rep. MSRE-MSR-EXP-001, NEA/NSC/DOC(2006)1, Rev. 0, OECD/NEA.
Sterbentz, J. W., Werner, J. E., Hummel, A. J., Kennedy, J. C., Brien, R. C. O., Dion, A. M., et al. (2018). “Preliminary assessment of two alternative core design concepts for the special purpose reactor,”. Tech. Rep. INL/EXT-17-43212, Rev. 1. Idaho National Laboratory, Idaho Falls, ID.
Terry, W. K., Montierth, L. M., Kim, S. S., Cogliati, J. J., and Ougouag, A. M. (2007). “Evaluation of the initial critical configuration of the HTR-10 pebble-bed reactor,”. Tech. Rep. HTR10-GCR-RESR-001, NEA/NSC/DOC(2006)1, Rev. 0, OECD/NEA.
Us, N. R. C. (2022). Pre-application activities for advanced reactors. https://www.nrc.gov/reactors/new-reactors/advanced/licensing-activities/pre-application-activities.html. (Accessed: 2022-09-07).
Walker, E., Skutnik, S., Wieselquist, W. A., Shaw, A., and Bostelmann, F. (2022). SCALE modeling of the fast-spectrum heat pipe reactor. Oak Ridge, TN: Oak Ridge National Laboratory. Tech. Rep. ORNL/TM-2021/2021.
Wieselquist, W. A., Lefebvre, R. A., and Jessee, M. A. (2020). SCALE code system. Oak Ridge, TN: Oak Ridge National Laboratory. Version 6.2.4. Tech. Rep. ORNL/TM-2005/39.
Williams, M. L., Broadhead, B. L., and Parks, C. V. (2001). Eigenvalue sensitivity theory for resonance-shielded cross sections. Nucl. Sci. Eng. 138, 177–191. doi:10.13182/NSE00-56
Williams, M. L., Ilas, G., Jessee, M. a., Rearden, B. T., Wiarda, D., Zwermann, W., et al. (2013). A statistical sampling method for uncertainty analysis with SCALE and XSUSA. Nucl. Technol. 183, 515–526. doi:10.13182/NT12-112
Williams, M. L. (1986). “Perturbation theory for nuclear reactor analysis,” in Handbook of nuclear reactors calculations. Editor Y. Ronen (United States: CRC Press).
Keywords: nuclear data, non-LWR, reactivity, scale, uncertainty analysis, sensitivity analysis
Citation: Bostelmann F, Ilas G and Wieselquist WA (2023) Key nuclear data for non-LWR reactivity analysis. Front. Energy Res. 11:1159478. doi: 10.3389/fenrg.2023.1159478
Received: 06 February 2023; Accepted: 10 April 2023;
Published: 20 April 2023.
Edited by:
Xiaojing Liu, Shanghai Jiao Tong University, ChinaReviewed by:
Tengfei Zhang, Shanghai Jiao Tong University, ChinaMohammad Alrwashdeh, Khalifa University, United Arab Emirates
Copyright © 2023 Bostelmann, Ilas and Wieselquist. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Friederike Bostelmann, Ym9zdGVsbWFubmZAb3JubC5nb3Y=
 Friederike Bostelmann
Friederike Bostelmann Germina Ilas
Germina Ilas William A. Wieselquist
William A. Wieselquist