A photovoltaic parameter identification method based on Pontogammarus maeoticus swarm optimization

Currently, the improvement of model parameter extraction accuracy is essential to research photovoltaic (PV) fields. In this study, a model parameter identification based on Pontogammarus maeoticus swarm optimization (PMSO) is proposed. The PMSO is used for parameter identification of mathematical models for PV modules. In the PMSO algorithm, by giving the ability of free exploration to particles that are far away from the optimal solution, the search scope is expanded to avoid falling into the local optimum. Besides, the local search for each Gammarus has a better convergence for PV parameter identification. Therefore, the accuracy of parameter identification for modeling PV modules is improved. The feasibility and superiority of the proposed method are verified by measured I-V characteristics of the PV array. The experimental results and error analysis verify that when compared with the conventional meta-heuristic algorithms, the proposed method achieves higher modeling accuracy. The proposed PMSO algorithm is suitable for engineering application of parameter identification and modeling of PV modules.

1 Introduction

In recent decades, with increasing concerns about resource depletion, climate change, and environmental pollution, the proportion of installed renewable energy has gradually increased (Renewables, 2022). Investment in renewable power and fuels has risen for the fourth consecutive year, and the record increase in global electricity generation has led to solar and wind power providing more than 10% of the world’s electricity for the first time ever (Renewables, 2022).

Therefore, in order to better estimate the generated power of photovoltaic (PV) power plants, many different types of PV models have been built, such as the single-diode model (SDM) (Kalliojärvi-Viljakainen et al., 2022; Javier Toledo et al., 2023), double-diode model (DDM) (Yahya-Khotbehsara and Ali, 2018), improved single-diode model (ISDM) (Abbassi et al., 2017), and triple-diode model (TDM) (Rezk and Ali Abdelkareem, 2022). The improvement of accuracy of parameter identification can enhance the simulation accuracy of PV models (Chouder et al., 2012). It can also help evaluate the performance of PV systems (Dabou et al., 2021), predict the output characteristics of PV arrays (Zhu et al., 2023), track the maximum power point (MPP) (Manna et al., 2023), and diagnose failure of PV arrays (Zhang and Huang, 2011), which directly affect the power generation efficiency and economic benefits of a PV power plant. Therefore, it is important to model the PV modules and accurately obtain the parameters of solar cells and PV modules.

The identification methods of PV model parameters can be divided into analytical and optimization methods. Many researchers have proposed to directly analyze the I-V curve to obtain parameters through the analysis method (Chan and Phang, 1987; Ortiz-Conde et al., 2006; Li Hong Idris Lim Ye et al., 2015; Torabi et al., 2017). This kind of method is direct and simple, but its accuracy depends on the correctness of the key information points selected on the I-V curve, i.e., short-circuit point, open-voltage point, and MPP. However, due to changes in outdoor ambient conditions, the I-V characteristic will have non-linear changes, so the analytical method cannot show good accuracy in practical applications.

Alternatively, with the progress of computer and artificial intelligence, many optimization methods based on the meta-heuristic algorithm to identify PV model parameters have been proposed. These methods are suitable for solving non-linear complex problems and improving the accuracy of solving. They are mainly divided into the following four categories: biology-based algorithms, physics-based algorithms, sociology-based algorithms, and mathematics-based algorithms (Yang et al., 2020). Many scholars have applied the meta-heuristic algorithm to identify PV model parameters. Mirjalili and Lewis (2016) proposed the whale optimization algorithm (WOA) in 2016. Xiong et al. (2018) soon applied the WOA to PV parameter identification. Zeng et al. (2021) proposed parameter identification of PV cells via the adaptive compass search (ACS) algorithm and when being compared with the WOA, the ACS algorithm showed better optimization accuracy and convergence rate. El-Dabah et al. (2023) proposed PV model parameter identification using the northern goshawk optimization (NGO) algorithm, and Kumar and Magdalin Mary (2022) proposed PV model parameter identification using the chaotic tuna swarm optimizer (CTSO) algorithm. Both methods have good results for the parameter identification of TDM. Wen et al. (2021) proposed the parameter identification of PV models by using an enhanced adaptive butterfly optimization algorithm (EABOA). The EABOA exhibits a precision superior to other methods in parameter extraction for the SDM and DDM. Nunes et al. (2020) proposed a novel multiswarm spiral leader particle swarm optimization (M-SLPSO) for PV parameter identification. The proposed M-SLPSO uses several swarms with different spiral trajectories, with population stagnation and premature convergence being alleviated. Alam et al. (2015) proposed a flower pollination algorithm (FPA)–based solar PV parameter estimation. Gude and Chandra Jana (2022) proposed the cuckoo search algorithm–based parameter identification of solar cells. Qais et al. (2019) proposed the coyote optimization algorithm (COA) for parameters extraction of three-diode PV models of PV modules. Lu et al. (2023) proposed the hybrid multi-group stochastic cooperative optimization algorithm (HMSCPSO), where the diversity of the population is increased to solve the problem of parameter identification. Shen et al. (2023) proposed the parameters of the discrete-time equivalent model (PDEM) of a PV system. The model parameters are identified using the least square method (LS) and bat algorithm (BA). Gu et al. (2023) proposed a simple and effective approach success-history adaptation differential evolution with linear population size reduction and decomposition (L-SHADED) to solve the problem of PV parameter identification, when the temperature and irradiance change. However, many problems still exist for the aforementioned algorithms, e.g., the adaptability of WOA parameters has to be improved. The NGO algorithm has worse accuracy considering noisy signals. The robustness of the FPA, CTSO, and EABOA should be enhanced for different temperature conditions. The accuracy of its identification is affected by the irradiance levels. Some algorithms do not take global search into account and may be easy to fall into local optimum.

This work proposes parameter identification of PV models by Pontogammarus maeoticus swarm optimization (PMSO). In the following experimental verification, the accuracy of the PV module parameter extraction by other conventional meta-heuristic algorithms and the proposed method is compared, which verifies the superiority of the proposed method. One of the advantages of the algorithm in comparison to others is that it can escape from local bests better for PV parameter identification. The local search for each Gammarus has a better convergence for PV parameter identification.

The contents of this article are organized as follows: the first section is the introduction. The second section introduces the SDM. The third section shows the detailed procedure of the PMSO algorithm. The fourth and fifth sections demonstrate the experimental verification and conclusions, respectively.

2 Single-diode model

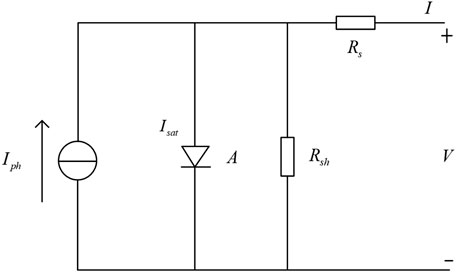
The SDM is the most popular PV model, which includes five parameters—photogeneration current I_ph, reverse saturation current I_sat, diode ideality factor A, equivalent series resistance R_s, and parallel resistance R_sh (Xu et al., 2023). Parameters of the SDM should vary according to module performance and environmental conditions, which is challenging for model parameter identification. In this work, the parameters of SDM are identified, and modeling results using the identified parameters are compared with several other conventional algorithms to verify the effectiveness and superiority of the proposed method.

The equivalent circuit of the SDM is shown in Figure 1. The mathematical expression of SDM is given as follows (Chen et al., 2023):

$I=I_{ph}-I_{sat}\left[\exp \left(\frac{V+I{R}_s}{A{V}_T}\right)-1\right]-\frac{V+I{R}_S}{R_{sh}},(1)$

$I_{ph}=\frac{\left(I_{sc}+K_i\Delta T\right)G}{G_s},(2)$

$I_{sat}=\frac{I_{sc}+K_i\Delta T}{e^{\left(V_{oc}+K_v\Delta T\right)/V_{T}N}-1},(3)$

where I is the output current; V is the output voltage; G is the measured irradiance; G_s is the irradiance under standard test conditions (STC); T is the absolute temperature of the solar cell; ΔT is the difference of temperature; V_T is the thermal voltage; I_sc is the shunt current; K_i is the temperature coefficient of I_sc; V_oc is the open-circuit voltage of the PV module; K_v is the temperature coefficient of V_oc; K is Boltzmann’s constant (1.380 × 1023 J/K); and q is the electron charge. The parameters to extract are I_ph photogenerated current, I_sat diode reverse saturation current, A diode quality factor, R_s equivalent series resistance, and R_sh parallel resistance. N is the number of solar cells connected in series. Besides, the predefined fitness function is required for parameter identification of the PV model. In this method, the fitness function takes the root mean square error of the measured current and theoretical current (Zhang et al., 2020), and is defined as follows:

$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(I_{mea,i}-I_{the,i}\right)}^2,}(4)$

where I_mea,i is the i-th measured current, I_the,i is the modeled theoretical current with the same voltage, and n represents the number of points in an I-V curve.

FIGURE 1

FIGURE 1. Single-diode model.

3 PMSO algorithm

3.1 Principle of Pontogammarus maeoticus swarm

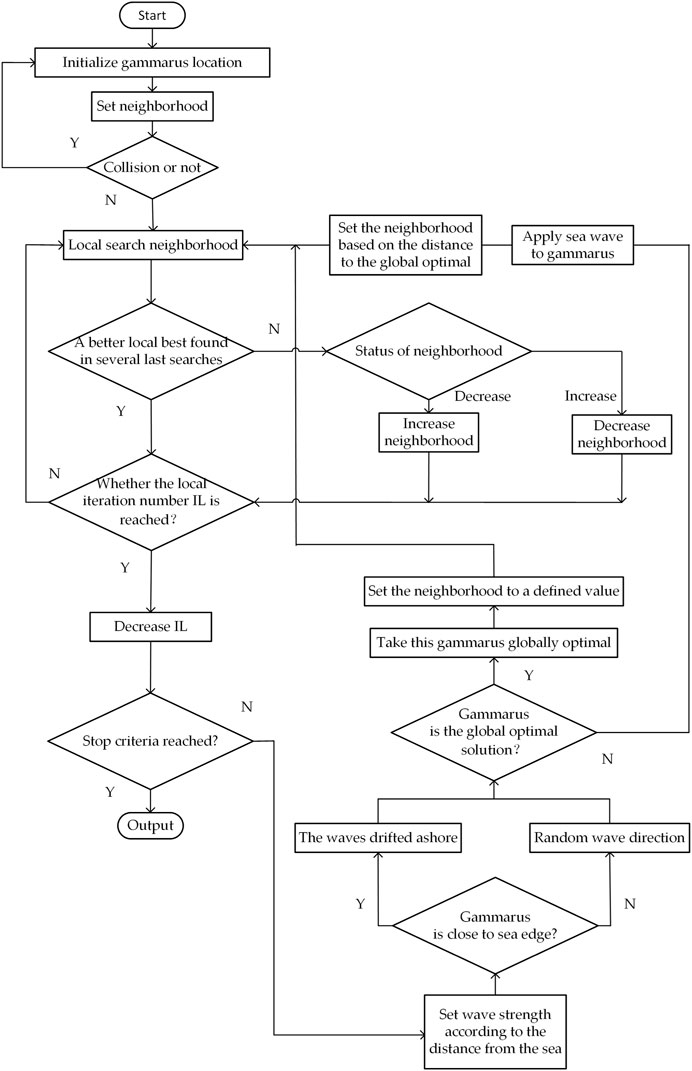
Gammarus is a kind of hard-shell creature, which belongs to the order Amphipoda. Pontogammarus maeoticus is one of the popular Gammarus. Two factors mainly help Gammarus searching for food (Ghojogh and Sharifian, 2018). The first one is the sea wave, as shown in Figure 2. The Gammarus that is far from the sea edge may be influenced strongly by the sea wave. This sea edge is modeled as the global best. Once the Gammarus has reached the sea edge, it would further search the local best at the vicinity of its position. Then, another action of the Gammarus starts, i.e., foraging, as shown in Figure 3. The foraging helps the Gammarus further search the local best. At last, the nutrients are foraged and the local best optimum is obtained.

FIGURE 2

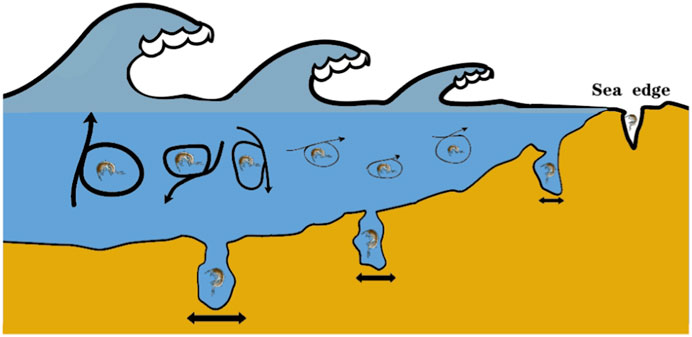
FIGURE 2. Sketch of sea waves, sea edge, sea bed, and Gammarus in sea and sea edge (Ghojogh and Sharifian, 2018).

FIGURE 3

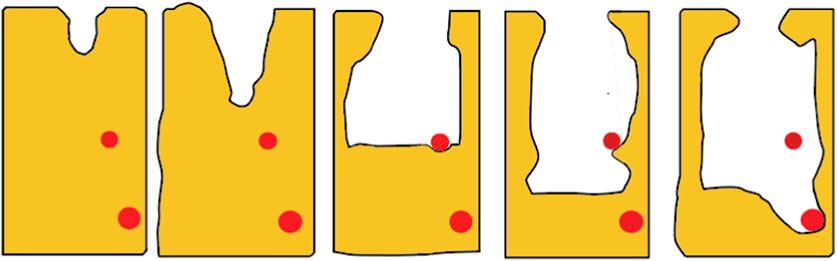
FIGURE 3. Sketch of local search by Gammarus for foraging, red dots are local bests (Ghojogh and Sharifian, 2018).

3.2 Initialization of Gammarus location

At first, the Gammarus is randomly generated for random exploration in the landscape, and its random initialization expression (Ghojogh and Sharifian, 2018) is given as follows:

$\begin{array}{l}{G}_i\left(d\right)=U\left(-l_d,l_d\right),\\ -l_d\le landscape\left(d\right)\le l_d,i=\left\{1,..,NG\right\},\end{array}(5)$

where G_i(d) is the location of the Gammarus, (−l_d,l_d) is the bound of search space in dimension d, and landscape (d) is dimension d of the landscape.

After randomly generating locations of the Gammarus, it should be checked whether collision occurs. If collision occurs, the Gammarus is repositioned. After repositioning, the collision should be checked again. For quantitatively measuring the collision, the distance between two Gammarus in a surrounding hyper-sphere or hyper-cube in the D-dimensional space is calculated. The distance calculation equation is as follows:

$distance\left(X_i,X_j\right)=\left|X_i-X_j\right|=\sqrt{{\displaystyle \sum _{d=1}^D}{\left(X_i\left(d\right)-X_j\left(d\right)\right)}^2,}(6)$

where X_i(d) and X_j(d) are the d-th decision variable for the position of i-th and j-th Gammarus, respectively. D is the number of all decision variables. Therefore, the collision distance is a hyper-parameter and should be set according to the specific problem. In this work, for the model parameter identification of the SDM, the five model parameters are determined as five decision variables. Furthermore, the distance between two Gammarus is calculated in a 5-D decision space.

3.3 Initial neighborhood settings

At the beginning of each global iteration, each Gammarus performs a local search of the domain. In the first global iteration, the initial domain N_i of all Gammarus is given as a constant. For the second and subsequent global iteration, the N_i of global optimal Gammarus is set as the initial neighborhood of founder of the global best (GB) at the first of every global iteration (NGB). Moreover, the N_i of other Gammarus will be determined by its distance from the global optimal solution. The greater the distance is, the greater will be the N_i. The equation is given as follows:

$N_i\leftarrow F\times \left|GB-G_i\right|,(7)$

where F is a hyperparameter to adjust the amplitude of distance, according to the distance between the GB and i-th Gammarus location in landscape, G_i.

3.4 Searching of optimal solution

The position of the Gammarus in the landscape is updated in each global iteration, except in the first. For each individual Gammarus, the moving distance is assigned according to the distance of the other Gammarus from the GB. The equation for updating positions is as follows:

$\left|W_i\right|\propto \left|GB-G_i\right|,(8)$

where W_i is the wave vector affecting the i-th Gammarus. On the other hand, all Gammarus are classified as the Gammarus close to the GB or that away from the GB, according to their distance from the GB. The criteria for judging and the number of close Gammarus are hyperparameters. For Gammarus close to the GB, the direction of its movement will be toward the GB. The angle calculation in different dimensions is as follows:

$\left\{\begin{array}{l}{\mathrm{\Theta }}_i\left(d\right)={\tan }^{-1}\frac{\sqrt{{\displaystyle {\sum }_{j=d+1}^D}{\left(v_i\left(j\right)\right)}^2}}{V_i\left(d\right)}\\ {\mathrm{\Theta }}_i\left(D-1\right)=2\times {\tan }^{-1}\frac{V_i\left(d\right)}{V_i\left(D-1\right)+\sqrt{{\left(V_i\left(D\right)\right)}^2+{\left(V_i\left(D-1\right)\right)}^2,}}\end{array}\right.(9)$

where V_i is the i-th Gammarus Gi vector to the GB. V_i(j) represents the j-th dimension component of this vector, $j=\left\{1,\dots ,D\right\}$. D is the number of dimensions of landscape. For Gammarus away from the GB, the direction of movement will be toward a random direction. The angle calculation is as follows:

${\theta }_i\left(d\right)=U\left(\mathrm{0,2}\pi \right),d=\left\{1,..,D-1\right\}.(10)$

Based on the moving distance and direction of the Gammarus, the vectors for moving are calculated as follows:

$\left\{\begin{array}{l}{W}_i={\left[W_i\left(1\right),W_i\left(2\right),..,W_i\left(D\right)\right]}^T\\ W_i\left(1\right)=\left|W_i\right|\cos \left({\mathrm{\Theta }}_i\left(1\right)\right),\\ W_i\left(d\right)=\left|W_i\right|\cos \left({\mathrm{\Theta }}_i\left(d\right)\right)\prod \begin{array}{l}d-1\\ j=1\end{array}\sin \left({\mathrm{\Theta }}_i\left(j\right)\right),d=\{2,..,D-.\\ W_i\left(D\right)=\left|W_i\right|\sin \left({\mathrm{\Theta }}_i\left(D-1\right)\right)\prod \begin{array}{l}D-2\\ j=1\end{array}\sin \left({\mathrm{\Theta }}_i\left(j\right)\right)\end{array}\right.(11)$

This prevents all Gammarus from moving toward the global and local best that have been found, allowing them to explore more of the landscape and find better solutions. The flowchart of the PMSO algorithm is shown in Figure 4. Then, PMSO is used to identify the model parameters based on the I-V curve. The identification results are obtained through continuous iterations by reducing the RMSE in (4) with the measured I-V curve. The framework of the proposed method is illustrated in Figure 5.

FIGURE 4

FIGURE 4. Flowchart of the PMSO algorithm.

FIGURE 5

FIGURE 5. Framework of the method flow.

4 Experiment and conclusion

4.1 Experiment

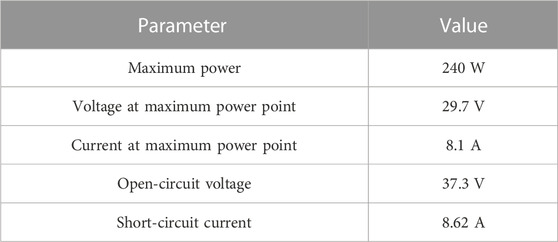
In order to verify the accuracy of the PMSO algorithm in the extraction of PV module parameters, in this work, a 5.28-kWp PV array composed of 22 poly-crystalline PV modules TSM-240 is used for experimental verification. The three-phase grid-connected inverter GW20KN-DT is used to measure the I-V curve of the PV array. The pyranometer is used to measure the in-plane irradiance of the PV array. The platinum-resistant Pt100 is pasted to the back of the PV module to measure the temperature. The data acquisition system for measuring the I-V curve and meteorological data is shown in Figure 6; Table 1 lists the specifications of the PV modules under STC, provided by the manufacturer.

FIGURE 6

FIGURE 6. Data acquisition system for measuring I-V curve and meteorological data.

TABLE 1

TABLE 1. Specification of PV module TSM-240.

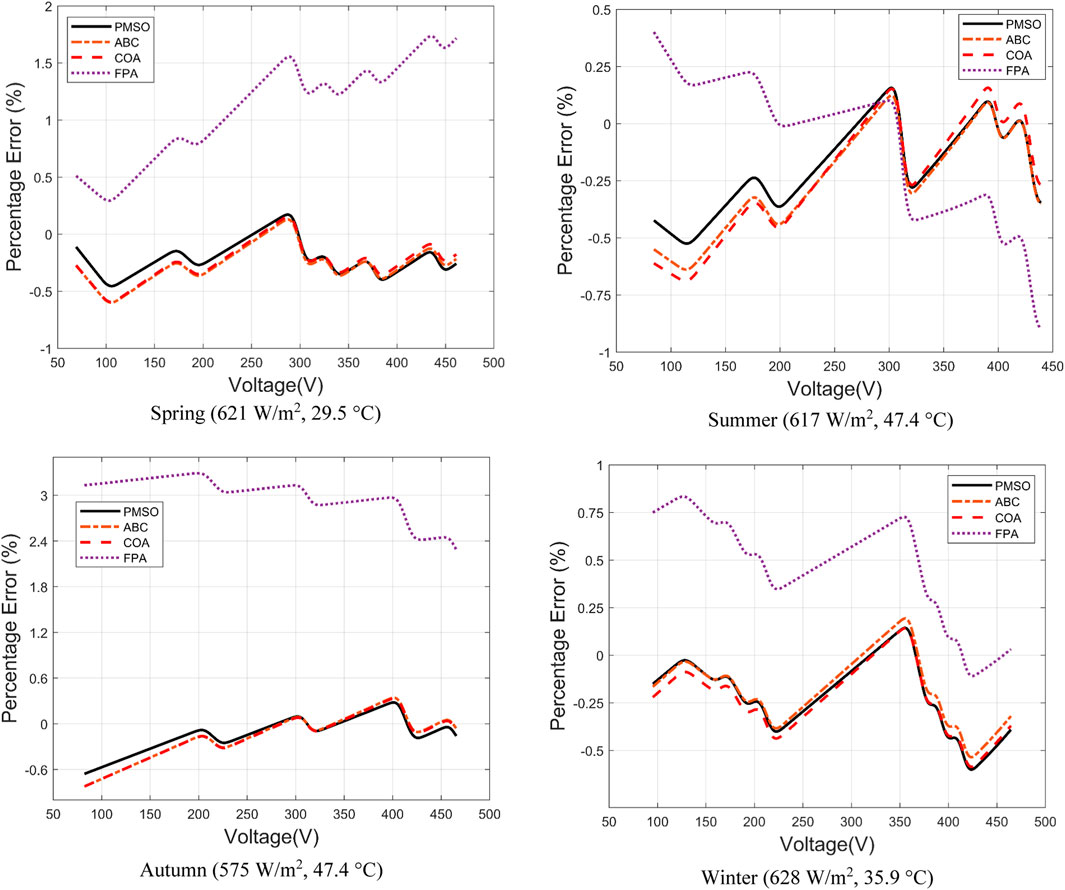
Modeling is carried out using the proposed extraction method based on the PMSO algorithm. The I-V curves, in-plane irradiance, and temperature of the PV array are transmitted to the indoor monitoring computer through the RS-485 bus for analysis and verification. In order to avoid excessive loss of PV plant by measuring the I-V curve, the sample interval is determined to be 2 min. Meanwhile, in order to reduce the measurement error, the measured I-V curves are preprocessed, and the measured data with amplitude less than 200 W/m² or curve distortion affected by local shadow are ignored. The number of local maximum and minimum values on the second derivative d²I/dV² of the curve is used as an indicator to identify abnormal I-V curves (Li et al., 2019). Then, the PMSO is used to estimate the model parameters. Finally, the extraction results of the PMSO are compared with those of other conventional parameter extraction methods, i.e., FPA (Alam et al., 2015), artificial bee colony (ABC) (Gude and Chandra Jana, 2022), and COA (Qais et al., 2019). Figure 7 presents the comparison results between the measured and modeled I-V characteristics based on the aforementioned parameter extraction methods in the typical days of four seasons. The comparison results between the measured and modeled P-V characteristics based on the aforementioned parameter extraction methods are shown in Figure 8. It can be seen from the experimental results shown in Figures 7, 8that when compared with other conventional meta-heuristic algorithms, the parameter extraction of PV modules on typical days of the four seasons is more consistent with the measured I-V curve. The corresponding values of the identified model parameters using the four parameter identification methods for the ambient conditions in spring (621 W/m², 29.5°C), summer (617 W/m², 47.4°C), autumn (575 W/m², 47.4°C), and winter (628 W/m², 35.9°C) are shown in Table 2.

FIGURE 7

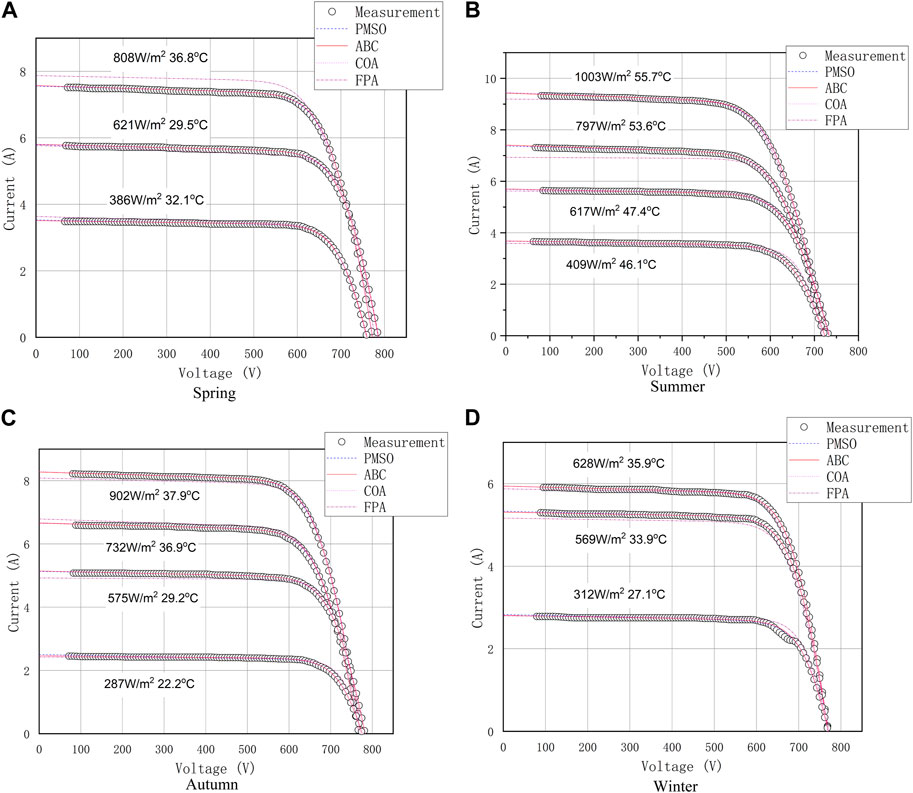
FIGURE 7. Comparison of measured and model estimated I-V characteristics in typical days in four seasons. (A) Spring, (B) Summer, (C) Autumn, and (D) Winter.

FIGURE 8

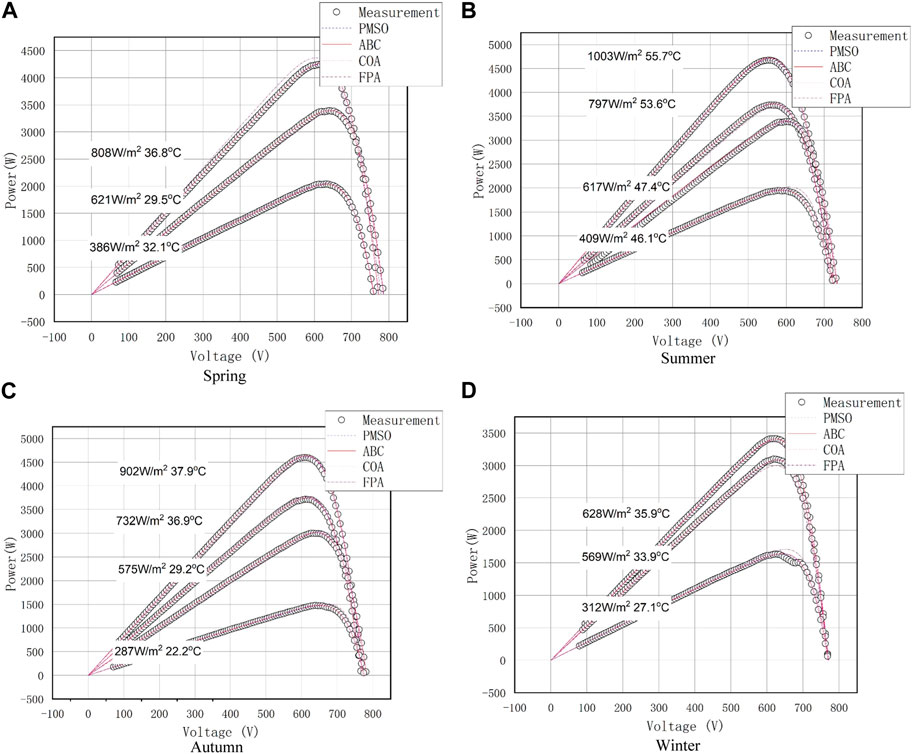
FIGURE 8. Comparison of measured and model estimated P-V characteristics in four seasons. (A) Spring, (B) Summer, (C) Autumn, and (D) Winter.

TABLE 2

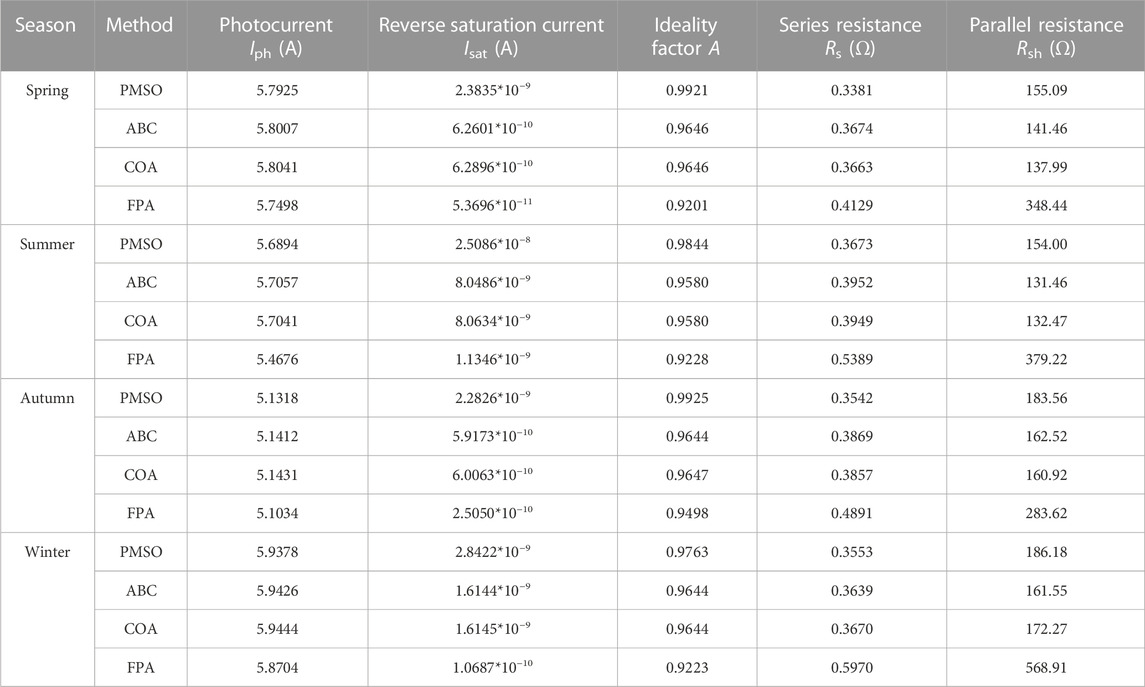
TABLE 2. Values of identified model parameters using four parameter identification methods for the ambient conditions in spring (621 W/m², 29.5°C), summer (617 W/m², 47.4°C), autumn (575 W/m², 47.4°C), and winter (628 W/m², 35.9°C).

4.2 Error analysis

In addition, the modeling error is analyzed by using model parameters identified by the proposed algorithm. Figure 9 shows the percentage error of the model based on the PMSO algorithm in four seasons at approximate 600 W/m². The percentage error for the model estimated by the proposed PMSO algorithm is relatively closer to 0 when compared with the other three algorithms. The reason is that the sea wave and foraging action of the Gammarus is effective for searching the global optimum of the identified model parameters. It validates that the proposed algorithm can achieve higher accuracy of parameter identification. Besides, the root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) are used to comprehensively assess the performance of different methods for model parameter identification. The RMSE is calculated via (4). The MAE and MAPE are calculated as follows:

$MAE=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left|I_{mea,i}-I_{the,i}\right|,(12)$

$MAPE=\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left|\frac{I_{mea,i}-I_{the,i}}{I_{mea,i}}\right|\times 100\%.(13)$

FIGURE 9

FIGURE 9. Percentage error of the estimated current based on PMSO in different seasons.

Table 3 shows the different error metrics of the four parameter identification methods for the ambient conditions in the four seasons. It reveals that the proposed PMSO algorithm achieves fewer errors than the other conventional meta-heuristic algorithms. Though, the RMSE of the model based on the proposed PMSO algorithm is greater in winter, the MAE of the modeled results is also the least. In most cases, the identification accuracy of the model parameters for the proposed PMSO algorithm is low enough for engineering applications.

TABLE 3

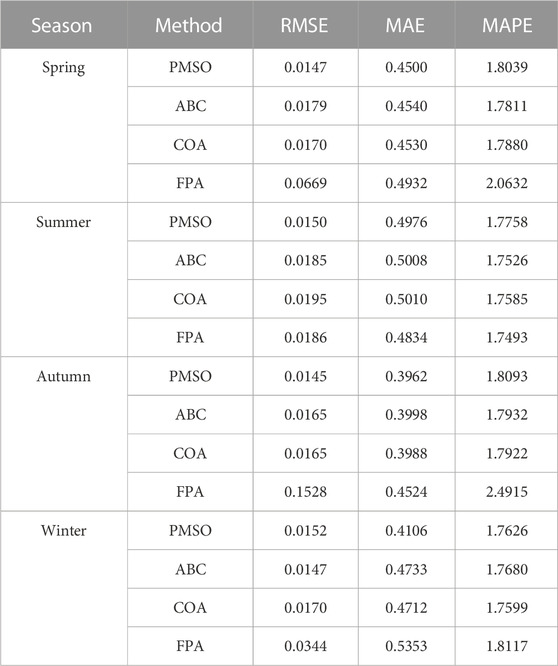
TABLE 3. Different error metrics of four parameter identification methods for the ambient conditions in spring (621 W/m², 29.5°C), summer (617 W/m², 47.4°C), autumn (575 W/m², 47.4°C), and winter (628 W/m², 35.9°C).

5 Conclusion

In this work, a model parameter identification method based on PMSO is proposed. In the PMSO algorithm, by giving the ability of free exploration to the particles that are far away from the optimal solution, the search scope is expanded to avoid falling into the local optimum. Therefore, the accuracy of parameter identification for modeling the PV module is improved. The feasibility and superiority of the proposed method are verified by the measured I-V characteristics of a PV array. Experimental results and error analysis verify that, compared with the conventional meta-heuristic algorithms, the proposed method achieves higher modeling accuracy. The proposed PMSO algorithm is suitable for engineering application of parameter identification of PV modules. Considering the advantage of the PMSO algorithm that it is not easy to fall into local optimum, the further research would focus on applying the PMSO algorithm for other different optimization problems, e.g., the maximum power point tracking of PV array with complicated shading.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LC, YS, and JZ contributed to the conception and design of the study. LC and WH organized the database. LC performed the statistical analysis. YS wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work is partially supported by the natural science research project of colleges and universities of Jiangsu (Grant Number: 21KJB470017).

Conflict of interest

Author WH was employed by State Grid Jiangsu Electric Power Co., Ltd., Huai’an Power Supply Branch.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbassi, A., Gammoudi, R., Ali Dami, M., Hasnaoui, O., and Mohamed, J. (2017). An improved single-diode model parameters extraction at different operating conditions with a view to modeling a photovoltaic generator: A comparative study. Sol. Energy 155, 478–489. ISSN0038-092X, 2017.06.057. doi:10.1016/j.solener.2017.06.057

CrossRef Full Text | Google Scholar

Alam, D. F., Yousri, D. A., and Eteiba, M. B. (2015). Flower Pollination Algorithm based solar PV parameter estimation. Energy Convers. Manag. 101, 410–422. ISSN 0196-8904, 2015.05.074. doi:10.1016/j.enconman.2015.05.074

CrossRef Full Text | Google Scholar

Chan, D. S. H., and Phang, J. C. H. (1987). Analytical methods for the extraction of solar-cell single- and double-diode model parameters from I–V characteristics. Electron Dev. IEEE Trans. 34, 286–293. doi:10.1109/t-ed.1987.22920

CrossRef Full Text | Google Scholar

Chen, X., Ding, K., Zhang, J., Yang, Z., Liu, Y., and Yang, H. (2023). A two-stage method for model parameter identification based on the maximum power matching and improved flow direction algorithm. Energy Convers. Manag. 278, 116712. ISSN 0196-8904. doi:10.1016/j.enconman.2023.116712

CrossRef Full Text | Google Scholar

Chouder, A., Silvestre, S., Sadaoui, N., and Rahmani, L. (2012). Modeling and simulation of a grid connected PV system based on the evaluation of main PV module parameters. Simul. Model. Pract. Theory 20 (1), 46–58. ISSN 1569-190X, 2011.08.011. doi:10.1016/j.simpat.2011.08.011

CrossRef Full Text | Google Scholar

Dabou, R., Bouraiou, A., Ziane, A., Necaibia, A., Sahouane, N., Blal, M., et al. (2021). Development of autonomous monitoring and performance evaluation system of grid-tied photovoltaic station. Int. J. hydrogen energy 46 (59), 30267–30287. doi:10.1016/j.ijhydene.2021.06.204

CrossRef Full Text | Google Scholar

El-Dabah, M. A., El-Sehiemy, R. A., Hasanien, H. M., and Saad, B. (2023). Photovoltaic model parameters identification using Northern Goshawk Optimization algorithm. Energy 262, 125522. ISSN 0360-5442, 2022.125522. doi:10.1016/j.energy.2022.125522Part B

CrossRef Full Text | Google Scholar

Ghojogh, B., and Sharifian, S. (2018). Pontogammarus maeoticus swarm optimization: A metaheuristic optimization algorithm. Available at: https://arxiv.org/pdf/1807.01844v1.pdf.

Google Scholar

Gu, Q., Li, S., Gong, W., Ning, B., Hu, C., and Liao, Z. (2023). L-SHADE with parameter decomposition for photovoltaic modules parameter identification under different temperature and irradiance. Appl. Soft Comput. 143, 110386. ISSN 1568-4946. doi:10.1016/j.asoc.2023.110386

CrossRef Full Text | Google Scholar

Gude, S., and Chandra Jana, K. (2022). A multiagent system based cuckoo search optimization for parameter identification of photovoltaic cell using Lambert W-function. Appl. Soft Comput. 120, 108678. ISSN 1568-4946. doi:10.1016/j.asoc.2022.108678

CrossRef Full Text | Google Scholar

Javier Toledo, F., Galiano, V., Blanes, J. M., Herranz, V., and Batzelis, E. (2023). Photovoltaic single-diode model parametrization. An application to the calculus of the Euclidean distance to an I–V curve. Math. Comput. Simul. ISSN0378-4754, 2023.01.005. doi:10.1016/j.matcom.2023.01.005

CrossRef Full Text | Google Scholar

Kalliojärvi-Viljakainen, H., Lappalainen, K., and Valkealahti, S. (2022). A novel procedure for identifying the parameters of the single-diode model and the operating conditions of a photovoltaic module from measured current–voltage curves. Energy Rep. 8, 4633–4640. ISSN 2352-4847, 2022.03.141. doi:10.1016/j.egyr.2022.03.141

CrossRef Full Text | Google Scholar

Kumar, C., and Magdalin Mary, D. (2022). A novel chaotic-driven Tuna Swarm Optimizer with Newton-Raphson method for parameter identification of three-diode equivalent circuit model of solar photovoltaic cells/modules. Optik 264, 169379. ISSN 0030-4026, 169379. doi:10.1016/j.ijleo.2022.169379

CrossRef Full Text | Google Scholar

Li, Y., Ding, K., Zhang, J., Chen, F., Chen, X., and Wu, J. (2019). A fault diagnosis method for photovoltaic arrays based on fault parametersidentification. Renew. Energy 143, 52–63. doi:10.1016/j.renene.2019.04.147

CrossRef Full Text | Google Scholar

Lu, Y., Liang, S., Ouyang, H., Li, S., and Wang, G.-G. (2023). Hybrid multi-group stochastic cooperative particle swarm optimization algorithm and its application to the photovoltaic parameter identification problem. Energy Rep. 9, 4654–4681. ISSN 2352-4847. doi:10.1016/j.egyr.2023.03.105

CrossRef Full Text | Google Scholar

Li Hong Idris Lim Ye, Z., Ye, J., Yang, D., and Du, H. (2015). A linear method to extract diode model parameters of solar panels from a single I–V curve. Renew. Energy 76, 135–142. ISSN 0960-1481, 2014.11.018. doi:10.1016/j.renene.2014.11.018

CrossRef Full Text | Google Scholar

Manna, S., Deepak Kumar Singh, Kumar Akella, A., Kotb, H., AboRas, K. M., Zawbaa, H. M., and Kamel, S. (2023). Design and implementation of a new adaptive MPPT controller for solar PV systems. Energy Rep. 9, 1818–1829. ISSN 2352-4847, 2022.12.152. doi:10.1016/j.egyr.2022.12.152

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. ISSN 0965-9978, 2016.01.008. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Nunes, H. G. G., Silva, P. N. C., Pombo, J. A. N., Mariano, S. J. P. S., and Calado, M. R. A. (2020). Multiswarm spiral leader particle swarm optimisation algorithm for PV parameter identification. Energy Convers. Manag. 225, 113388. ISSN 0196-8904, 2020.113388. doi:10.1016/j.enconman.2020.113388

CrossRef Full Text | Google Scholar

Ortiz-Conde, A., García Sánchez, F. J., and Muci, J. (2006). New method to extract the model parameters of solar cells from the explicit analytic solutions of their illuminated characteristics. Sol. Energy Mater Sol. Cells 90, 352–361. doi:10.1016/j.solmat.2005.04.023

CrossRef Full Text | Google Scholar

Qais, M. H., Hasanien, H. M., Alghuwainem, S., and Nouh, A. S. (2019). Coyote optimization algorithm for parameters extraction of three-diode photovoltaic models of photovoltaic modules. Energy 187, 116001. ISSN 0360-5442, 2019.116001. doi:10.1016/j.energy.2019.116001

CrossRef Full Text | Google Scholar

Renewables, R. E. N. (2022). 2022 global status report. Available at: https://www.ren21.net/wp-content/uploads/2019/05/GSR2022_Full_Report.pdf.

Google Scholar

Rezk, H., and Ali Abdelkareem, M. (2022). Optimal parameter identification of triple diode model for solar photovoltaic panel and cells. Energy Rep. 8, 1179–1188. Supplement 1. doi:10.1016/j.egyr.2021.11.179ISSN 2352-4847, 2021.11.179

CrossRef Full Text | Google Scholar

Shen, F., Zhang, W., Cao, Y., Wang, Z., Yang, G., Shan, J., et al. (2023). Parameter identification of photovoltaic discrete-time equivalent model using the bat algorithm. Energy Rep. 9, 449–458. Supplement 7. doi:10.1016/j.egyr.2023.04.166ISSN 2352-4847

CrossRef Full Text | Google Scholar

Torabi, K. E., Eddine, I. A., Obbadi, A., Errami, A., Rmaily, R., Sahnoun, S., et al. (2017). Parameters estimation of the single and double diode photovoltaic models using a gauss-seidel algorithm and analytical method: A comparative study. Energy Convers. Manage 148, 1041–1054. doi:10.1016/j.enconman.2017.06.064

CrossRef Full Text | Google Scholar

Wen, L., Wu, T., Xu, M., Tang, M., and Cai, S. (2021). Parameters identification of photovoltaic models by using an enhanced adaptive butterfly optimization algorithm. Energy 229, 120750. ISSN 0360-5442, 2021.120750. doi:10.1016/j.energy.2021.120750

CrossRef Full Text | Google Scholar

Xiong, G., Zhang, J., Shi, D., and Yu, H. (2018). Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 174, 388–405. ISSN 0196-8904, 2018.08.053. doi:10.1016/j.enconman.2018.08.053

CrossRef Full Text | Google Scholar

Xu, J., Zhou, C., and Li, W. (2023). Photovoltaic single diode model parameter extraction by dI/dV-assisted deterministic method. Sol. Energy 251, 30–38. ISSN 0038-092X, 2023.01.009. doi:10.1016/j.solener.2023.01.009

CrossRef Full Text | Google Scholar

Yahya-Khotbehsara, A., and Ali, S. (2018). A fast modeling of the double-diode model for PV modules using combined analytical and numerical approach. Sol. Energy 162, 403–409. ISSN 0038-092X, 2018.01.047. doi:10.1016/j.solener.2018.01.047

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Tao, Y., Yao, W., Shu, H., et al. (2020). Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 208, 112595. ISSN 0196-8904, 2020.112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Zeng, F., Shu, H., Wang, J., Chen, Y., and Yang, B. (2021). Parameter identification of PV cell via adaptive compass search algorithm. Energy Rep. 7, 275–282. Supplement 1. doi:10.1016/j.egyr.2021.01.069ISSN 2352-4847, 2021.01.069

CrossRef Full Text | Google Scholar

Zhang, J., Liu, Y., Li, Y., Ding, K., Feng, L., Chen, X., et al. (2020). A reinforcement learning based approach for on-line adaptive parameter extraction of photovoltaic array models. Energy Convers. Manage 214, 112875. doi:10.1016/j.enconman.2020.112875

CrossRef Full Text | Google Scholar

Zhang, L., and Huang, A. Q. (2011). Model-based fault detection of hybrid fuel cell and photovoltaic direct current power sources. J. Power Sources 196 (11), 5197–5204. ISSN 0378-7753, 2011.01.089. doi:10.1016/j.jpowsour.2011.01.089

CrossRef Full Text | Google Scholar

Zhu, H., Sun, S., Li, J., Pan, B., Jiang, T., and Sun, Y. (2023). Operation reference status selection for photovoltaic arrays and its application in status evaluation. Sol. Energy 250, 97–107. ISSN 0038-092X, 2022.12.034. doi:10.1016/j.solener.2022.12.034

CrossRef Full Text | Google Scholar