- 1China Huaneng Clean Energy Research Institute, Beijing, China
- 2Huaneng Jiuquan Wind Power Co., Ltd., Jiuquan, China
Wind power is one of the most representative renewable energy and has attracted wide attention in recent years. With the increasing installed capacity of global wind power, its nature of randomness and uncertainty has posed a serious risk to the safe and stable operation of the power system. Therefore, accurate wind power prediction plays an increasingly important role in controlling the impact of the fluctuations of wind power to in system dispatch planning. Recently, with the rapid accumulation of data resource and the continuous improvement of computing power, data-driven artificial intelligence technology has been popularly applied in many industries. AI-based models in the field of wind power prediction have become a cutting-edge research subject. This paper comprehensively reviews the AI-based models for wind power prediction at various temporal and spatial scales, covering from wind turbine level to regional level. To obtain in-depth insights on performance of various prediction methods, we review and analyze performance evaluation metrics of both deterministic models and probabilistic models for wind power prediction. In addition, challenges arising in data quality control, feature engineering, and model generalization for the data-driven wind power prediction methods are discussed. Future research directions to improving the accuracy of data-driven wind power prediction are also addressed.
1 Introduction
Along with the rapid advancements in both the economy and technology, human demand for energy is also on the rise (Wang Y. et al., 2019). However, overconsumption of fossil fuels will result in energy depletion, and the issue of environmental pollution is escalating rapidly. Therefore, the global must promote the conservation and sustainable use of fossil fuels and develop renewable energy vigorously. Wind energy is a typical representative of renewable energy and has characteristics of large reserves and easy development, it has been developed on a large scale and with high quality in recent years. Depending on the Global Wind Report 2023 (Williams et al., 2022), the global installed capacity of new wind power (WP) is 78 GW in 2022 (as shown in Figure 1), resulting in a total installed capacity of 906 GW in 2022. This represents a 9% increase compared to the previous year.
Currently, wind power has been a crucial contributor to electricity generation in numerous countries around the world. However, as wind power expands on a massive scale, its randomness and intermittent will bring great challenges for maintaining the stability of the power system. A promising solution for addressing the aforementioned challenges is to predict future WP accurately. In addition, the penalty mechanism for wind power prediction (WPP) errors by the electricity regulation department will affect the profits of wind farms. Therefore, accurate WPP is beneficial to relieve the peak load of the power system, ensuring reliable management of the power system, reducing the abandoned wind, and improving the wind farms’ revenue.
1.1 Literature review
In recent years, many scholars have proposed in-depth research and many approaches on WPP. According to classification standards, WPP models can be divided into several groups. According to the prediction types, they can be divided into deterministic models and probabilistic models. Depending on the prediction process, they can be grouped into two-phase models and end-to-end models. The two-phase models are to first predict wind speed (WS), and then get the WP depending on the WP curve. However, the end-to-end models are to predict the WP directly. This paper focuses on the end-to-end models.
Depending on the prediction time scale, they can be grouped into four types: ultra-short-term, short-term, medium-term, and long-term. According to the prediction space scale, they can be divided into three groups: the wind turbine, single wind farm, and regional wind farms.
Compared to WPP for single wind farm and regional wind farms, WPP for wind turbine has been studied earlier. In the prediction process, the model needs to pay attention to the operating status and data of the wind turbine itself, as well as micro meteorological data. The accurate WPP for the wind turbine can help characterize the power output of a single wind turbine. However, accurate prediction requires providing high-resolution micro meteorological data for each wind turbine, which makes it costly and almost impossible to achieve in practical engineering. Currently, the resolution of numerical weather prediction (NWP) data used in research is generally coarse. For example, Sobolewski et al. (2023) used historical turbine data collected by SCADA system, meteorological reanalysis data, and NWP data to predict power of wind turbine, but the spatial resolution of NWP data was 0.25°, which affected the prediction accuracy. In addition, with the development of wind power industry, wind farms have gradually developed into centralized and large-scale, so in the past few years, the demand for WPP for wind turbine gradually decreased. Based on the above reasons, there has been relatively little research on WPP for wind turbine in recent years, and there has been no significant breakthrough in related technical routes and methods. The research on methods is relatively less in-depth and cutting-edge, and most of them are relatively early traditional machine learning methods and deep learning methods, such as support vector machine (SVM), decision Tree (DT), recurrent neural network (RNN), long short-term memory (LSTM), etc. However, with the increasing attention paid to distributed wind turbines in recent years, the research on WPP for wind turbine can contribute to the development of distributed wind turbines (Riahy and Abedi, 2008; Zhang et al., 2019).
At present, most of the research on WPP worldwide is focused on the prediction for wind farm, so compared with WPP for wind turbine, research in this area is more in-depth, and related research methods and technical routes are also more diverse and cutting-edge. For example, some advanced methods proposed in recent years, such as attention mechanism (AM), Transformer, and its variants, have been applied to WPP for wind farms. Moreover, unlike WPP for wind turbine, the prediction for wind farm needs to pay attention to the overall information of the wind farm, and integrates information from multiple individual wind turbines to predict the overall power generation of the wind farm (Bigdeli et al., 2013; Yan et al., 2017b), so the WPP for wind farm is more difficult. One technical route for predicting the power of a wind farm is to draw on the technical route and methods of WPP for wind turbine. Firstly, the power of each wind turbine in the wind farm is predicted, and then the power of the entire wind farm is obtained by summing up. However, as the scale of wind farms increases, this technology route has high costs and low computational efficiency. Therefore, in most literature on WPP for wind farm, models generally do not finely analyze the information of each wind turbine, but rather pay more attention to the overall power of the wind farm, meteorological observation information and prediction information of the wind farm area. For example, Zhang et al. (2020c) used the NWP data and historical wind of actual wind farm as the input.
With the increase of wind farm scale, WPP for wind farm cannot meet the needs of power system scheduling. In addition, wind power are getting more deeply involved in electricity market transactions in recent years. Therefore, WPP for regional wind farms has also received increasing research. Unlike WPP for wind turbine and wind farm, the prediction for regional wind farms needs to analyze the information of multiple wind farms from both time and space perspectives comprehensively, and it places emphasis not only on the precision of point prediction but also on the accuracy of the overall prediction trend, so it is the most difficult type (Zhang J. et al., 2021; Pei et al., 2022). And the technical route of regional power prediction is not quite the same as that of WPP for wind turbine and wind farm. It is generally divided into accumulation method, upscaling method and spatial resources matching method. Moreover, in the literature on the prediction for regional wind farms, the models need to focus on the spatio-temporal dependencies between multiple wind farms, so methods that are good at extracting important spatial and spatiot-emporal information are often used, such as convolutional neural network (CNN), graph conventional network (GCN), stacked denoising auto-encoder (SDAE), convolutional LSTM (ConvLSTM), convolutional gated recurrent unit (ConvGRU), etc.
Based on the modeling theory, they can be classified into four types: physical models, traditional statistical models, AI-based models, and hybrid models.
The modeling processes of the physical models are complex and it is challenging to acquire the model parameters. When dealing with physical models, experts need to have rich professional knowledge. Since traditional statistical models have limited capability in nonlinear fitting and processing high-dimensional data, physical models and they are less welcomed now.
In recent years, AI technology with data-driven as the core has developed rapidly, gradually from shallow traditional machine learning to deep learning (Sun et al., 2021). Therefore, AI-based WPP models have developed rapidly and become a hot spot currently. Many previous research have demonstrated that AI-based models have superior prediction performance when compared to traditional statistical models. These models are expected to break through the technical bottleneck of WPP and achieve significant improvement in prediction accuracy.
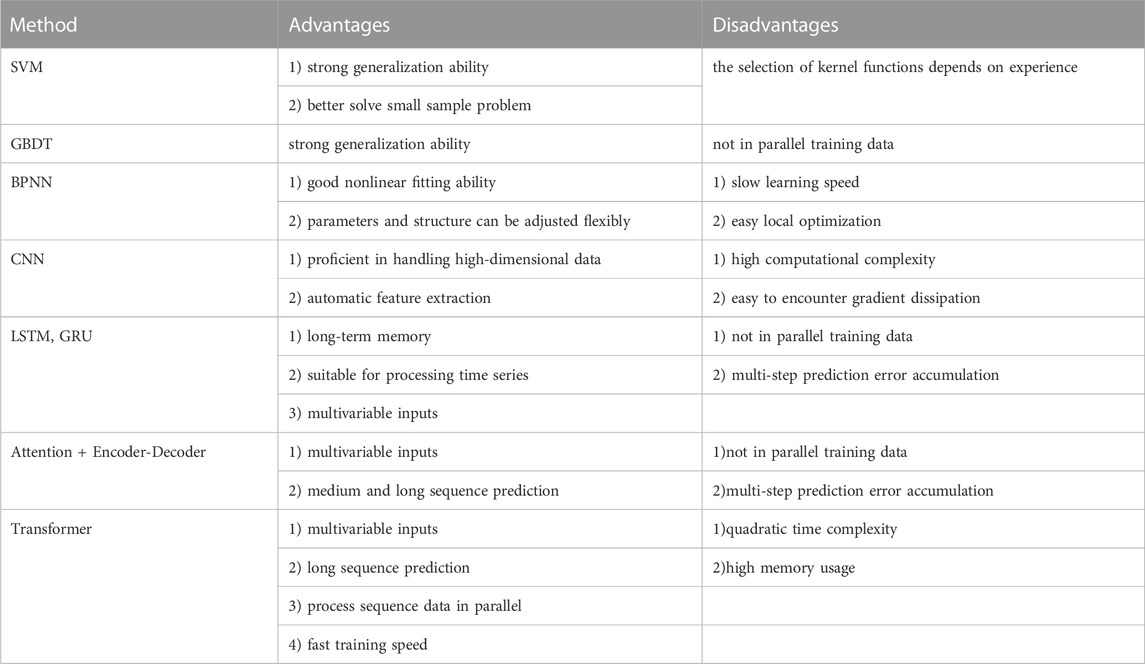
AI-based WPP models include traditional machine learning models, such as traditional artificial neural networks (ANNs), SVM, extreme learning machine (ELM), DT, etc. As AI technology advances, it has led to the increased adoption of deep learning models in WPP. These models, such as deep belief network (DBN), auto-encoder (AE), LSTM, CNN, gated recurrent unit (GRU), AM, and Transformer, are highly effective in solving complex nonlinear problems. Their advanced capabilities have made them a top choice for WPP applications. And the advantages and disadvantages of some major AI-based methods are shown in Table 1. Hybrid models can be built by combining various model types, including time series and traditional machine learning, or traditional machine learning and deep learning, or a combination of all of them, to thoroughly describe various facets of WP variation (Shi et al., 2012).
1.2 Contributions and paper organization
In recent years, a large number of scholars have reviewed the WPP methods. Lei et al. (2009) introduced physical models, traditional statistical models, spatial correlation models, and AI models for WPP. Shi et al. (2012) reviewed ARIMA, ANN, SVM and the hybrid models that combines them, and compared the prediction performance of models. Tascikaraoglu and Uzunoglu (2014) comprehensively surveyed hybrid models including data pre-processing, parameter selection and optimization, and error processing. Yan et al. (2015) analyzed the sources of prediction uncertainty and reviewed the WPP models in terms of model input, modeling principle, express way and prediction time-scale. Liu et al. (2020) reviewed the multi-objective optimization technologies in the field of WPP. González-Sopeña et al. (2021) proposed an overview of the performance evaluation methods used for assessing the prediction accuracy of short-term statistical WPP models. In addition, as AI technology has been widely studied in the field of WPP in recent years, some scholars have reviewed the AI-based WPP models. Sawant et al. (2022) gave a detailed overview of AI-based wind power prediction models from ultra short, short and long-term perspectives. Wang Y. et al. (2021) reviewed the deep learning models used for WPP, including the processes of data processing, feature extraction, and relationship learning. Zhu et al. (2023) discussed the base principle of AI technology in the application of renewable energy power prediction, and systematically summarized the application of AI technology in wind power and photovoltaic power prediction. However, the more popular and cutting-edge methods in the field of WPP in the past few years, such as AM, Transformer and its variants, are rarely mentioned in the previous review. Moreover, it can be seen from the above that there are great differences in the technical route and research depth of WPP methods in different prediction space scales, but the previous review literature gave scant attention to the AI-based WPP methods from the perspective of different prediction space scales. Thus, the main contribution of this paper is to comprehensively review the AI-based models for WPP at various spatial scales, covering from wind turbine level to regional level. The following are the key points of the contributions.
This paper systematically reviews the AI-based WPP models based on different prediction space scales, including some popular and cutting-edge models in recent years, such as AM, Generative adversarial networks (GAN), Transformer and its variants, And the advantages, disadvantages and the prediction performance of various methods are comprehensively discussed.
The performance evaluation metrics of deterministic models and probabilistic models for WPP are also reviewed and discussed, in order to gain comprehensive understanding of the performance of different prediction methods.
This paper discusses the challenges arising in data quality control, feature engineering, and model generalization for the data-driven WPP methods, and addresses the future work to improving the accuracy of data-driven WPP.
This review provides researchers with an understanding of the current research status and differences of AI-based methods in different prediction space scales, and the challenges and future work of data-driven WPP methods, thereby giving valuable guidance for researchers committed to developing optimized models for WPP.
The rest of the paper is structured as follows. Section 2, 3, and 4 are dedicated to reviewing the AI-based WPP models used for the different prediction objectives: the wind turbine, single wind farm, and regional wind farms. Section 5 presents the performance evaluation metrics of WPP. Section 6 provides the discussion and future work in WPP. Section 7 offers tentative conclusions of the paper.
2 AI-based wind power prediction models for wind turbine
Wind turbines can be divided into the off-grid wind turbine and grid-connected wind turbine. The WPP accuracy of off-grid wind turbines is required to be high in distributed WP generation, which will affect the reliability of wind turbines directly. For grid-connected wind turbines, the WPP error of a single wind turbine impacts the WPP of the whole cluster multiply (Peng et al., 2016). Thus, whether it is off-grid or grid-connected, the WPP accuracy is important for the popularity of WP (Guo et al., 2020). A single wind turbine covers a small area and can be disturbed or destroyed by meteorological conditions or local random disturbance factors easily. It is difficult to predict WP accurately (Li and Pan, 2017). Therefore, the research on WPP for a single wind turbine becomes particularly important, but in practice, the cost of WPP for every wind turbine in the whole wind farm is high, and many meteorological variables such as wind speed in the same range are highly similar, so at present, there are few types of research on AI-based WPP models for a wind turbine. Among these literature, traditional machine learning models including tree-based models, SVM, and traditional ANNs, are widely used; deep learning models include RNN and LSTM, but some of the more advanced methods in recent years, such as AM, GAN, and Transformer, have not been thoroughly studied. Overall, AI-based WPP models for wind turbine in the research are not very in-depth and there are no significant breakthroughs in recent years. However, with the increase in the demand for accurate and fast power supply of distributed wind turbines, AI-based WPP models for a wind turbine which will attract more attention.
2.1 Traditional machine learning models
Machine learning models have become increasingly popular in WPP because of their strong capability to learn complex nonlinear relationships among data. There are three distinct categories of machine learning models: Supervised learning, Unsupervised learning, and Semi-supervised learning. For predicting the WP of a single wind turbine, a wide range of supervised traditional machine learning models are applied, such as Regression Analysis (Rashid et al., 2020; Demir and Tasci, 2021; Sobolewski et al., 2023), SVM (Shi et al., 2010; Wang., 2013), Tree-based models, and traditional ANNs (Li et al., 2001; Nielson et al., 2020; Metodieva and Bozhkov, 2022).
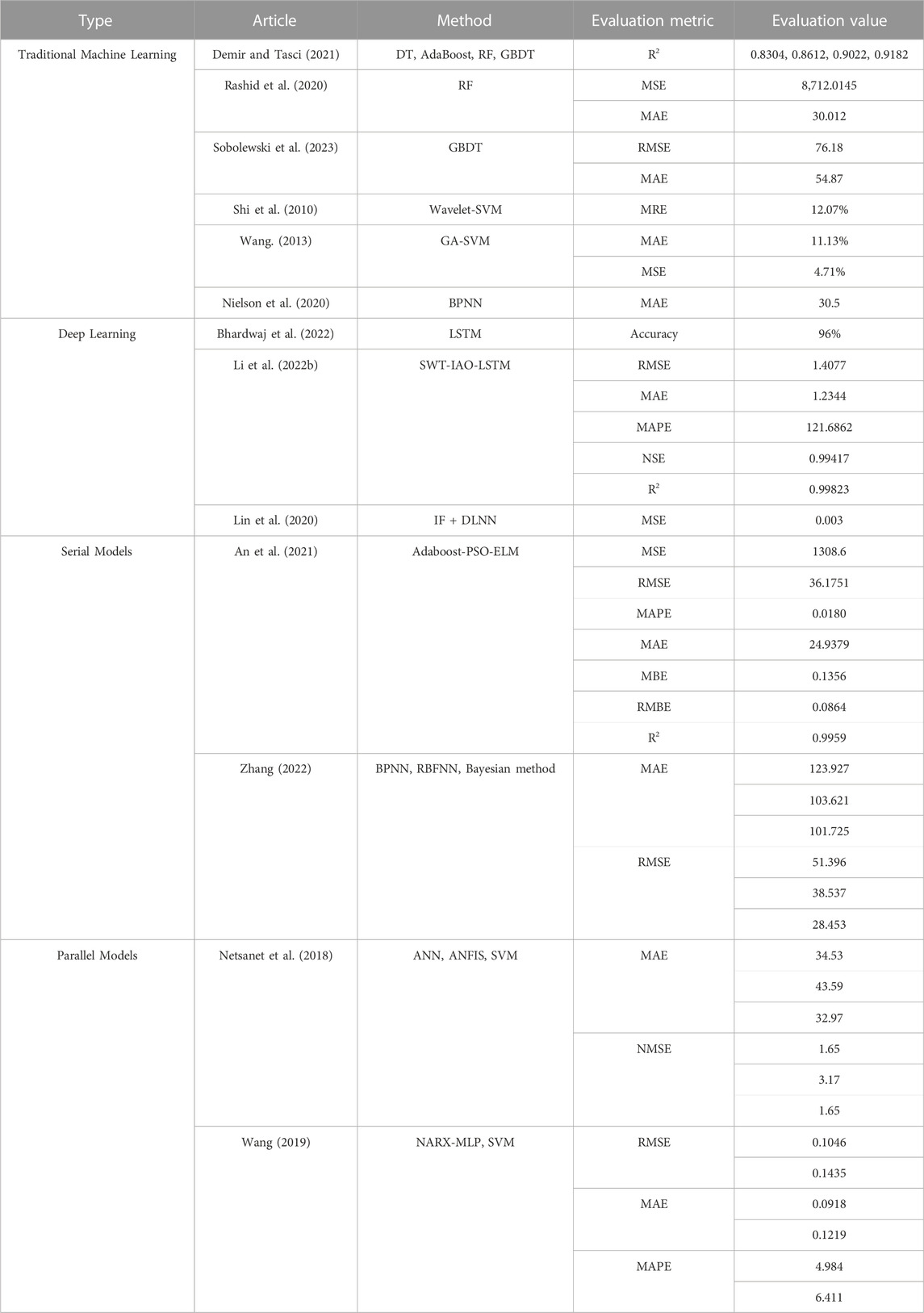
Tree-based models include DT, random forest (RF), AdaBoost, gradient boosting decision tree (GBDT), etc. They have been applied to tackle the problem of WPP for wind turbines. Generally speaking, the disadvantage of DT is that it has a large variance, and subtle changes in data distribution may lead to significant differences in tree structure, so compared with other tree-based models, its performance is generally the worst. Demir and Tasci (2021) confirmed this viewpoint in their research work. They used seven different regression algorithms to get the WPP of wind turbines. The algorithms included DT, AdaBoost, RF, GBDT, etc. According to the evaluation of R2, AdaBoost had the best performance and DT had the worst. RF is suitable for large datasets and has good computational efficiency and prediction accuracy, however, the prediction performance has some dependence on the quality of the original data. Rashid et al. (2020) used RF to predict the power of wind turbines. The capacity factor for real power output and annual affected power output was used to estimate the performance of wind turbines. GBDT has shown excellent performance in regression prediction problems with its efficient training speed and low memory consumption. Sobolewski et al. (2023) applied GBDT to WPP first. Compared with other AI-based models, such as LSTM, DT, and RF, the WPP accuracy based on GBDT was the highest, and with the increase in prediction time, the advantages of GBDT became more and more obvious.
SVM (Cortes and Vapnik, 1995) is a kernel-based machine learning model, which can better solve the small sample problem in practice. SVM has a simple structure, strong generalization ability, and is easy to be trained. It has achieved a better prediction effect than traditional ANNs in solving nonlinear and large-dimension problems. Some scholars have studied improved SVM to improve prediction accuracy. For example, Shi et al. (2010) proposed a WPP model based on wavelet SVM for a wind turbine. In wavelet SVM, the radial basis function (RBF) kernel function was replaced by the wavelet kernel function. However, the theory of SVM is quite complex, and its prediction effect is intricately linked to the choice of kernel functions and parameters. Therefore, some scholars have utilized some data-driven algorithms to optimize the parameters of SVM. For example, Wang., 2013 proposed to use genetic algorithm (GA) to optimize the parameters of SVM. This proposed model was more accurate and had better generalization in short-term WPP. But the selection of kernel functions has not been well supported by theory and mainly depends on experience so far, so it has certain randomness.
ANN has a good nonlinear fitting ability, and its parameters and structure can be adjusted flexibly, so it is widely used in WPP (Shuang et al., 2011). Common traditional ANNs include back propagation neural network (BPNN), radial basis function neural network (RBFNN), general regression neural network (GRNN), etc. Among them, BPNN is the most classic. Nielson et al. (2020) used BPNN to establish multi-parameter input models to predict the WP of the wind turbine, and the performance of BPNN in different atmospheric stability regimes was discussed. But the learning speed of BPNN is slow and cannot guarantee convergence to the global optimum. In addition, the prediction performance of traditional ANNs is greatly affected by the parameters of the models, resulting in unstable prediction accuracy. In recent years, with the exponential growth of AI technology, deep learning models based on traditional ANNs have attracted more attention in the field of WPP.
2.2 Deep learning models
Over the past few years, deep learning models have become the most popularly used machine learning models, owing to their intricate structures and potent nonlinear mapping capabilities. And they are increasingly being employed in a variety of applications, including WPP. Compared to traditional machine learning models, deep learning models can perform well on a relatively small dataset and in less time (Qin et al., 2016). Bhardwaj et al. (2022) compared the WPP performance of traditional machine learning models and deep learning models for a wind turbine. The polynomial regression and LSTM were used, and the polynomial regression could not predict the WP accurately, while the accuracy of LSTM could reach 96%.
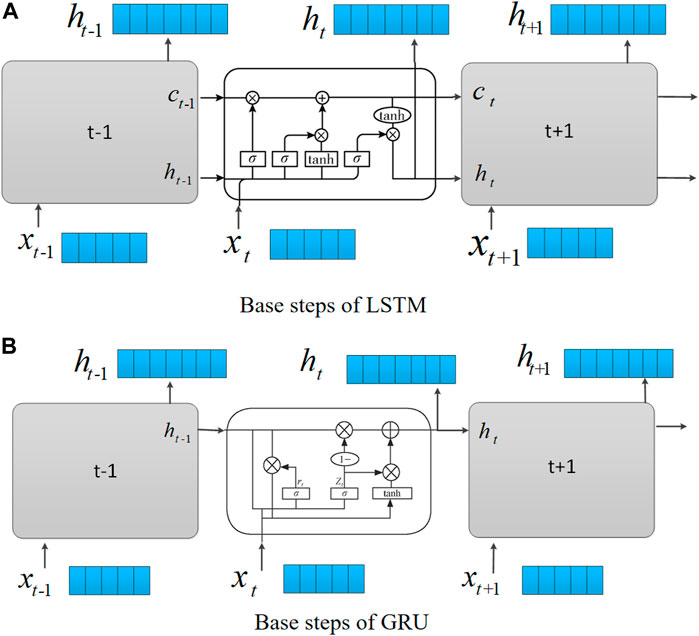
Since RNN has the ability of short-term memory, it has good performance when solving time series problems. RNN is widely used in WPP for a wind turbine, due to its structure, it is prone to the problem of gradient disappearance or explosion. LSTM is a variant of RNN and its base steps are shown in Figure 2A. LSTM introduces gating mechanism on the basis of RNN, replacing common neuron modules with special memory neuron modules, so it has the ability of long-term memory which perfectly fits our need to predict power for wind turbines (Yu et al., 2018). LSTM can achieve satisfactory results in multi-step WPP of wind turbines, but as the prediction time scale increases, the prediction accuracy will gradually decrease. In addition, some data-driven technologies are used to optimize the hyperparameter of LSTM, thus improving the prediction accuracy. For example, Li Z. et al. (2022) proposed a model combining isolated forest (IF), squeeze wavelet transform (SWT), aquila optimization (AO), and LSTM for WPP of new wind turbines. The WPP model was built based on LSTM, and its parameters were optimized by AO.
To sum up, there are few types of research on deep learning models for the WPP of a single wind turbine at present. Most of them are combined with outlier detection methods, noise reduction methods and optimization algorithms to further improve the accuracy and generalization ability of the models. This may be due to the small size of the single wind turbine samples and the decreasing application scenarios of WPP for a wind turbine.
2.3 Hybrid models
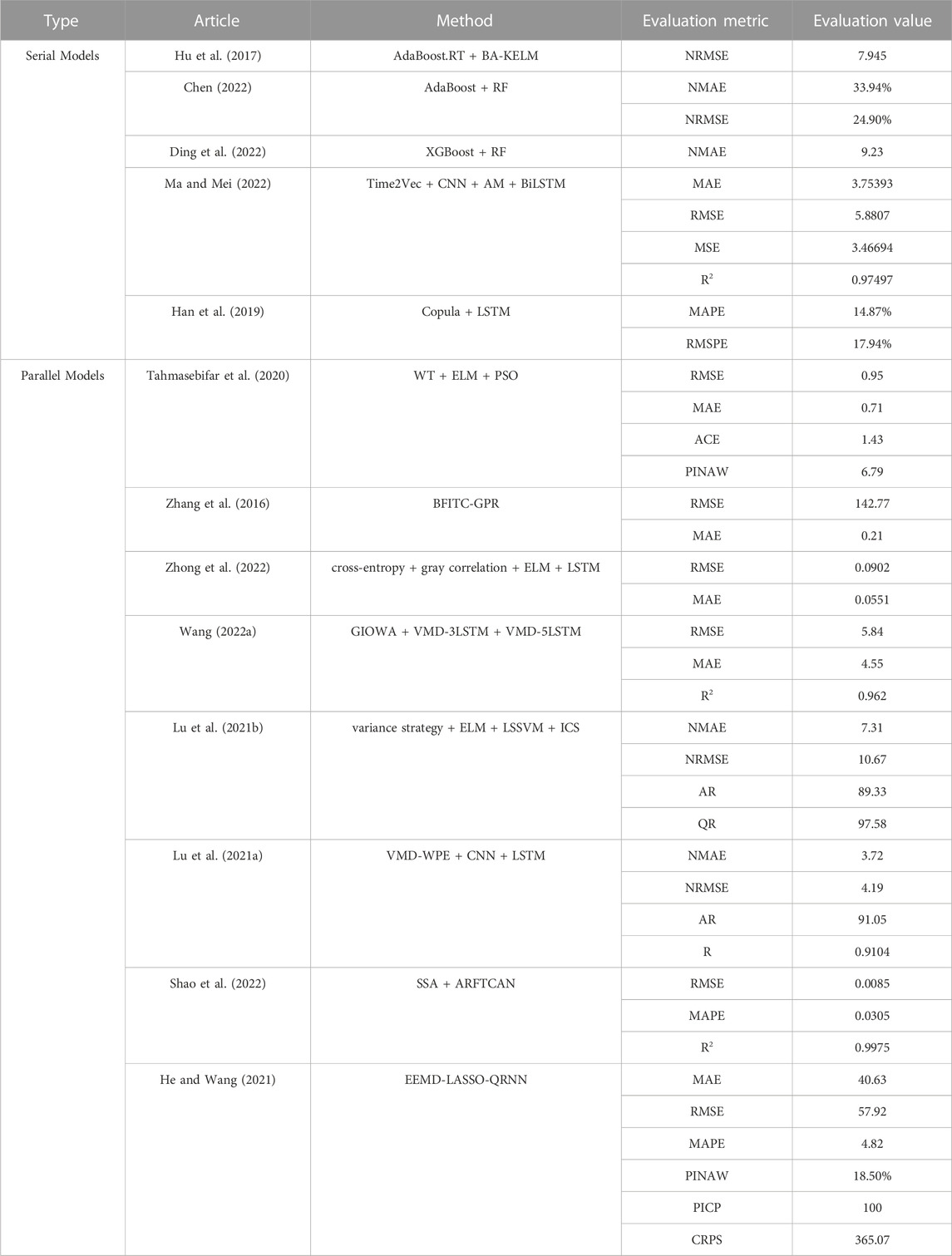
WPP is affected by multiple factors, and using a single prediction model may lose some useful information, resulting in low robustness and weak generalization of the model. In order to give full play to the advantages of different algorithms and make the most of all useful information, Bates and Granger (2001) first proposed the hybrid predicting theory in 1969. Hybrid models effectively overcome the inherent limitations of a single prediction model and reduce the probability of scenarios with large prediction errors (Tascikaraoglu and Uzunoglu, 2014). Therefore, as soon as they were proposed, they received extensive attention and research. With the continuous development of hybrid predicting theory, hybrid models have been divided into two categories: serial models and parallel models. In addition, with the rapid development of machine learning, ensemble learning has emerged. And the boosting algorithm and bagging algorithm are both widely used ensemble learning algorithms, which can be used to design hybrid models for WPP. Some hybrid models in the literature are showed in Table 2.
2.3.1 Serial models
In serial models, there is a strong dependency relationship between each prediction model or prediction process, and serial models include boosting algorithm in ensemble learning and fusion prediction models. Figure 3 shows their structures.
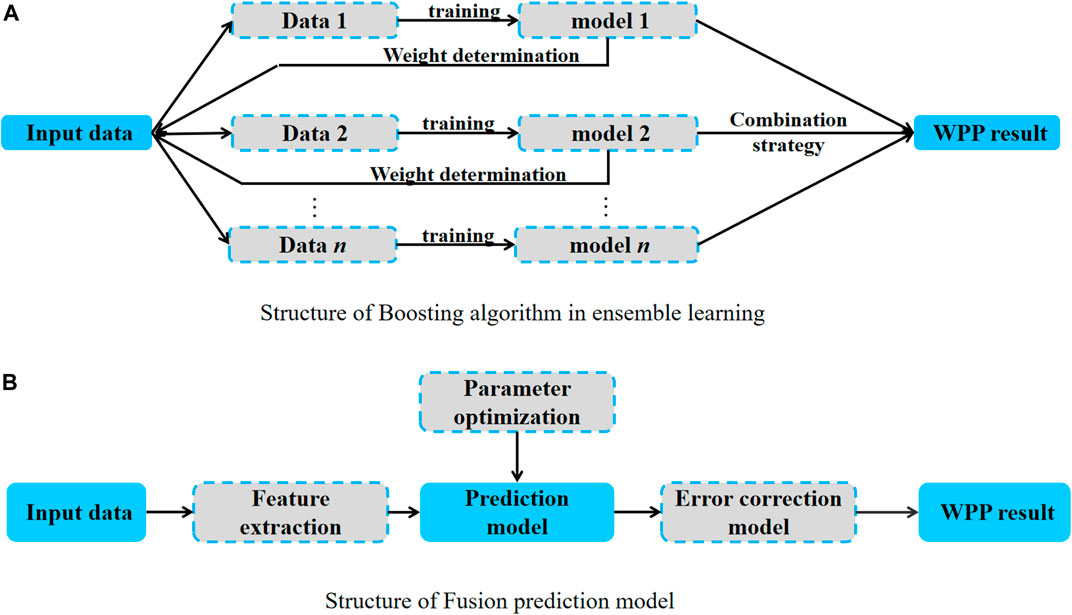
FIGURE 3. Structure of serial models. (A) Structure of Boosting algorithm in ensemble learning. (B) Structure of Fusion prediction model.
In Boosting algorithm, a series of weak learning models can be promoted to strong learning models and a sequential process is used. In addition, each subsequent model will be corrected and improved based on the previous model to improve the prediction accuracy. For example, An et al. (2021) established a WPP model that combined the Adaboost algorithm with particle swarm optimization-extreme learning machine (PSO-ELM) to improve the prediction performance and generalization ability of the model. A series of PSO-ELM weak predictors containing different hidden layer nodes were constructed with Adaboost. Finally, each weak predictor was weighted and fused into a strong WPP model. The results showed that Adaboost-PSO-ELM could better learn the variation trend of WS and wind direction in every season.
Fusion prediction models combine the processes of feature extraction, relationship learning, error correction, etc., which form the entire process of WPP. Each process uses a different model, which can give full play to the expertise of different technologies and achieve higher prediction accuracy. Zhang (2022) predicted the short-term power of wind turbines based on historical data. Compared to BPNN, RBFNN had a better prediction effect and was selected as the preliminary prediction model. Then the Bayesian dynamic linear model was used to predict the prediction error of RBFNN to achieve error correction, thereby improving the WPP accuracy.
2.3.2 Parallel models
In parallel models, there is no strong dependency relationship between each model, and model construction and training can be carried out simultaneously. Parallel models mainly include bagging algorithm in ensemble learning and weight-based models, and Figure 4 shows their structures.
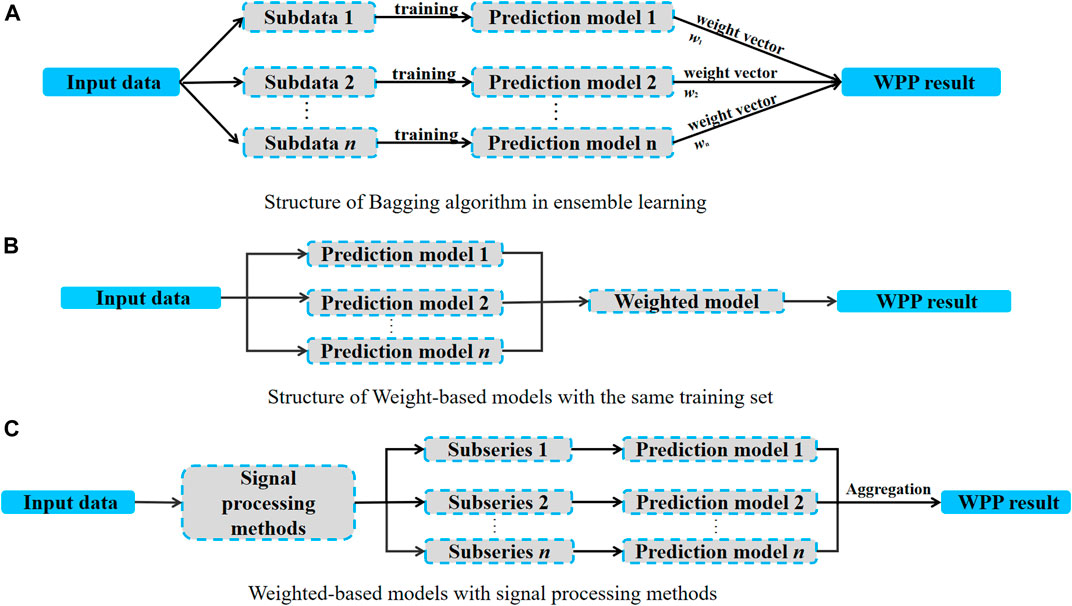
FIGURE 4. Structure of parallel models. (A) Structure of Bagging algorithm in ensemble learning. (B) Structure of Weight-based models with the same training set. (C) Weighted-based models with signal processing methods.
In the Bagging algorithm, several training sub-samples are constructed by extracting input data with playback. Then several sub-learning models are built in parallel, and the results of the sub-models are combined by means or weights to get the final prediction results. Currently, there are few studies on WPP for wind turbines based on the Bagging algorithm.
Unlike the Bagging algorithm, one way of weight-based models is to use the same training set for each model, and the final prediction results are got by weighting each model. At present, these models are commonly used in WPP for wind turbines. Netsanet et al. (2018) further divided the weight distribution methods into three categories: Simple Averaging, Regulation, and Outperformance. Simple averaging is the simplest hybrid method, and the final prediction result is the arithmetic average of all prediction results. It is very popular in many studies, especially in business prediction (Clemen, 1989). Although it is easy to implement and explain simple averaging, it has a disadvantage in that it assigns predefined weights to a single model, regardless of the relative performance of the models. Regression considers the prediction performance of a single model. It assigns optimal weights to the models by ignoring their Sum of squares due to error (SSE), which ensures that models with larger prediction errors receive smaller weights, and vice versa. In the Outperformance method, the relative past performance of the hybrid models is measured based on the square of the loss function, and the models are weighted based on this.
Overall, the AI-based methods currently used in the field of WPP for wind turbine are mainly traditional machine learning methods and a few early deep learning methods, including RNN and LSTM. The main hybrid models used are fixed weight-based models with the same training set. Therefore, the research on AI-based methods for predicting the power of wind turbines is not in-depth and cutting-edge, and there is significant room for development and research.
3 AI-based wind power prediction models for wind farm
Compared to power prediction for wind farms, the cost of power prediction for each single wind turbine is very high. Therefore, there is currently less research on AI-based WPP models for the single wind turbine, and more research focuses on the wind farm. Thus, the research on models and technical routes in WPP for wind farm are more in-depth and cutting-edge. For example, some improved traditional machine learning models, as well as the hot traditional machine learning and leading-edge deep learning methods in recent years, such as ELM, AE, AM, GAN, etc., have been studied in WPP for wind farm, but are less involved in WPP for wind turbine. Next, the application of traditional machine learning models, deep learning models, and hybrid models to WPP for the wind farm will be introduced.
3.1 Traditional machine learning models
K-means, hierarchical clustering, Gaussian mixture model (GMM), and Self-organizing maps (SOM) are widely used unsupervised algorithms in WPP for the wind farm, which are often applied to pattern recognition of prediction scenarios. K-means is a classical algorithm, and Sun et al. (2019) used K-means to split the data into an ensemble of components with a similar fluctuant level of each sub-layer. Wang et al. (2020) combined SOM clustering and K-fold cross-validation. And the training samples were classified according to data distribution characteristics, improving the prediction ability of different basis learners in WPP models.
The classical supervised learning models used in WPP for the wind farm are similar to those used for the wind turbine, such as traditional ANNs (Fan et al., 2008; Hu et al., 2022), SVM(Liu et al., 2009; Wu and Peng, 2016; Zhang H. et al., 2020), GBDT (Ren et al., 2022), and RF (Lahouar and Slama, 2017). Besides, some other methods which are rarely used for a wind turbine in the literature, such as GP, ELM, and Bayesian method, are usually used for wind farms.
As mentioned in Section 2.1, SVM is a commonly used and efficient algorithm. Compared with WPP for wind turbine, the research on SVM in WPP for wind farm is more in-depth. The improved SVM including piecewise support vector machine (PSVM) (Liu et al., 2009), least absolute shrinkage and selection operator (LSSVM) (Zhang H. et al., 2020), v-support vector regression with Gaussian noise (GN-SVR), and Noise-SVR, were proposed to improve the precision of WPP. For example, LSSVM has improved in terms of computational efficiency and convergence accuracy. Wu and Peng (2016) proposed a WPP model by combining LSSVM, principal component analysis (PCA), and bate algorithm (BA). And the proposed model had been demonstrated to outperform other models through comparative analysis. GN-SVR is optimal only when the noise follows a Gaussian distribution, while the noise of wind power usually follows a beta distribution, Laplace distribution, etc., but does not follow a Gaussian distribution. To solve this problem, Noise-SVR (Hu et al., 2014) was proposed to determine the loss function according to the probability distribution of noise.
ELM is a NN with a single hidden layer and can quickly obtain the optimal solution by optimizing the weights of input layer and the threshold of hidden layer; However, ELM is also prone to overfitting. Kernel ELM (KELM) is an improved ELM, which adds the kernel function to ELM, so KELM enhances the generalization and has a more stable performance, while also having the same solution speed as ELM. In research, optimization algorithms such as PSO and GA are often used to optimize the parameters of ELM and KELM, in order to avoid blindly training the model. For example, Shan et al. (2022) utilized the improved artificial bee colon to optimize the parameters of KELM. Then the model was used to predict short-term wind power. The optimization of parameters could effectively improve the prediction accuracy.
The Bayesian method adds the prior information of parameters to the likelihood function, so it makes full use of the prior information of model parameters in addition to the sample information, thus improving the prediction accuracy. In addition, the Bayesian method show good robustness when processing small sample problem, so it is commonly used in the probabilistic prediction of WP for wind farms. Yang et al. (2017) constructed the Rough Set-PSO-Naive Bayesian model for WPP. A Naive Bayesian classifier was built to obtain the prediction power class. PSO was applied to optimize the output weight of Naive Bayesian.
Gaussian Process (GP) is a method based on Bayesian theory and statistical theory. It is a non-parametric model, and its parameters can be independently obtained during the learning process (Yan et al., 2017a). Therefore, compared to many other machine learning methods, a significant advantage of GP is that it can integrate many machine learning tasks, including model training, parameter estimation, and uncertainty estimation, so the regression process of GP has been greatly simplified, and the outcomes are less influenced by subjectivity and more interpretable. Moreover, it has a strong generalization ability for nonlinear, high-dimensional, especially small sample complex problems. Liu et al. (2018) used GP to provide a new approach for short-term WPP under the missing data scenario. GP models were established to evaluate the performance of various missing patterns in WPP in the literature.
In summary, traditional machine learning models can adaptively learn the characteristics of data and predict nonlinear WP data accurately. Compared with physical models and traditional statistical models, it has a better prediction performance. However, these models have limitations in expressing complex data and fully reflecting the characteristics of data (Wei et al., 2023).
3.2 Deep learning models
In recent years, with the rapid development of big data technology, deep learning methods have demonstrated great potential in modeling and predicting. Many advanced models based on deep learning have emerged, and related technologies have become a hot spot in WPP for wind farms. Compared with the deep learning models used in WPP for wind turbines, these for wind farms are studied more deeply in the literature and have been applied in many processes of WPP, such as feature extraction and relationship learning. Deep learning models for wind farms mainly include AE-based models, RBM-based models, CNN-based models, RNN-based models, and Transformer, which will be introduced separately. And some traditional machine learning and deep learning WPP methods for wind farm in the literature are shown in Table 3.
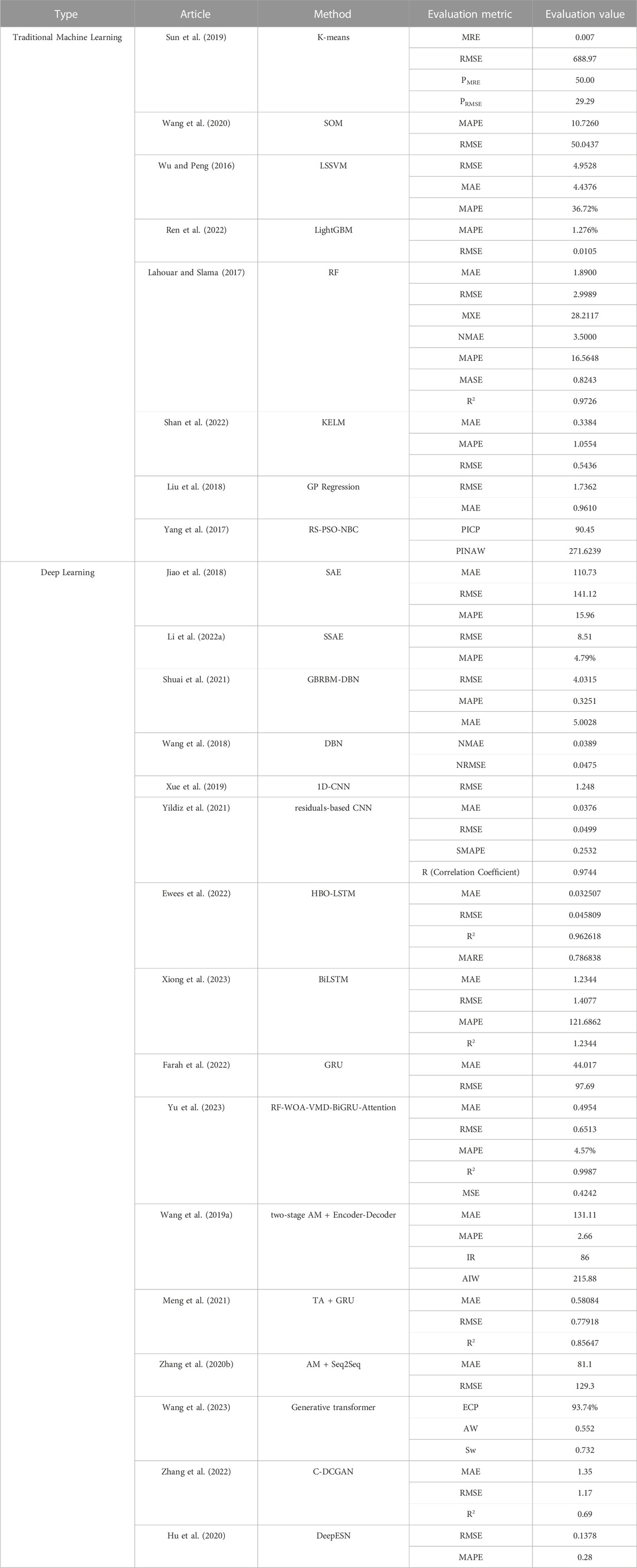
TABLE 3. Some traditional machine learning and deep learning WPP methods for wind farm in the literature.
AE is one of the most popular DNNs used in unsupervised learning. It compresses the original data into latent spatial features, and then reconstructs the output. Currently, the original form of AE is rarely employed for feature extraction in WPP for wind farms, and many variants of AE have been commonly used, such as stacked auto-encoder (SAE), stacked sparse auto-encoder (SSAE), SDAE, and so on. There are two major processes for training the variants of AE for feature extraction: unsupervised layer-wise pre-training and supervised fine-tuning (Khodayar et al., 2017). SAE is a deep multilayer NN formed by stacking multiple AEs (Jaseena and Kovoor, 2020). By extracting important information from features through SAE, the WPP results of models are more stable. For example, Jiao et al. (2018) established an SAE to extract features from the data sequence samples and used the subsequent loss function to obtain the optimal initial connection weights of the NN. SSAE has a structure in which different sparse AEs are stacked. Using the sparse constraint, SSAE can generate features that are both sparse and succinct, so it can obtain suitable features for WPP. Li D. et al. (2022) used SSAE to extract the spatial independent features of multi-dimensional WP, which were used as prediction objects to predict separately. Finally, the results of feature prediction were reconstructed and decoded to obtain the power prediction results of multiple wind farms. DAE adds noise to the input data of AE, and then DAE learns to denoise and regenerates undamaged input data to obtain more robust feature representations. By stacking several DAEs, SDAE is constructed. SDAE can simulate spatial correlation and interdependence among wind farms, improving NWP accuracy for WPP (Peng et al., 2020).
Restricted boltzmann machine (RBM) is an energy-based NN and has a strong capacity for unsupervised learning (Huang et al., 2018). DBN is a probability-generation model formed by stacking several RBMs. Every RBM in DBN is a feature extractor, so DBN can be employed for high-dimensional feature extraction and is also often used in WPP for wind farms. The training process of a DBN is similar to that of AE-based models. Besides, dropout can be used to prevent over-fitting in the training stage (Hinton et al., 2012). Some scholars have studied the improved DBN to improve the prediction accuracy. For example, Shuai et al. (2021) added Gaussian function to RBM and created the improved DBN to correct WS.
CNN has a powerful ability to extract features, and has been used for feature extraction and relationship learning in WPP for the wind farm. CNN models can be divided into 1D-CNN, 2D-CNN and, 3D-CNN. The kernels used in these networks move in one, two, and three directions, respectively. 1D-CNN is mainly used for vectors. Xue et al. (2019) proposed an ultra-short-term WPP model based on CNN and GRU. 1D-CNN was utilized to reduce the output of the calculation model and overcome the problem of gradient explosion and disappearance during training. Unlike 1D-CNN, the input and kernel of 2D-CNN are both matrices, so many methods have been proposed to form matrix inputs (Yu et al., 2019; Yu et al., 2020). A 3D-CNN can extract useful features from tensors. Therefore, the information obtained from 3D-CNN is more comprehensive than that got from 1D-CNN and 2D-CNN. Kazutoshi et al. (2018) proposed a model based on 3D-CNN to automatically extract the spatio-temporal features of NWP data. However, 2D-CNN extracts spatial features and 1D-CNN extracts simple pattern features from the data. But the training of 3D CNN incurs a higher computational cost compared to 1D-CNN and 2D-CNN (Hong and Satriani). Besides, some studies use CNN for relationship learning in WPP (Sheng et al., 2023). In recent studies, it has been found that some simple CNN-based models such as Temporal convolutional network (TCN) (Wang, 2021) and residuals-based CNN (Yildiz et al., 2021) are more effective than RNNs such as LSTM in different sequence modeling tasks. However, most of the above prediction models are still one-step predictions for WPP, and the results are insufficient to support practical applications (Wu et al., 2022).
Similar to WPP for wind turbines, LSTM is also widely used for wind farms. LSTM can well solve the long-term dependence problem of sequences, and many studies (Yuan et al., 2019; Ewees et al., 2022) have shown that compared to other prediction methods, LSTM has a higher accuracy in WPP, verifying that LSTM is feasible and valid in WPP for wind farms. Some scholars have proposed methods to optimize LSTM in order to overcome its shortcomings and improve the accuracy of WPP. For example, Ewees et al. (2022) used heap based optimizer (HBO) to optimize the super parameters of LSTM. To overcome the disadvantage of LSTM not being able to capture the correlation of long sequences well, the structure of RNN-skip was proposed in the LSTNet model (Lai et al., 2018). Moreover, other common types of RNNs, such as GRU, bidirectional LSTM (BiLSTM), and bidirectional GRU (BiGRU), are also used in WPP for wind farms. BiLSTM has two distinct hidden layers, which process sequential data in both forward and backward directions. By this structure, BiLSTM considers both past and future information from the time series, so generally speaking, it has better prediction performance than LSTM but requires more computational costs.
GRU is a variant of LSTM and its base steps are shown in Figure 2B, which also can solve the problem of gradient disappearance and explosion. And compared with LSTM, GRU does not have a dedicated memory cell, so GRU has a simpler structure, making it be trained faster than LSTM. But LSTM has a better performance for the dataset with longer sequences. Besides, the variants of GRU such as BiGRU and convolutional GRU (ConvGRU) have also been used in WPP for wind farms. BiGRU has a structure that is similar to that of BiLSTM. Besides, ConvGRU changes the calculation method of activation function δ and tanh from full connection to convolution, which can extract and utilize spatio-temporal information at the same time (Sun et al., 2022). Thus, ConvGRU is also suitable for power prediction for regional wind farms. Despite RNN and their variants can deeply mine and predict long-series WP, most of them are unable to efficiently remember important information of long-series historical data, leading to a decrease in accuracy of multi-step WPP. Thus, AM was proposed and studied by many scholars.
The common structure of AM is shown in Figure 5A. AM can focus on crucial information with a significant weight, ignore insignificant information with a low weight, and continuously adjust the weight to make it possible to facilitate the prioritization of relevant information in varied conditions, so AM has higher scalability and robustness (Hao et al., 2019). In recent years, AM has been widely used in various prediction tasks. In the field of WPP, AM is often combined with RNN, LSTM, GRU and their variants, and Encoder-Decoder. To effectively extract the long-term dependencies of multivariate data from NWP data, the Attention-GRU model (Niu et al., 2020) and multi-source and temporal attention network (Zhang H. et al., 2021) were proposed to improve the accuracy of multi-step WPP, but this led to new problems such as spatial complexity. In order to well deal with the nonlinear mapping relationship between WP and multiple meteorological factors and strengthen the trend characteristic of wind power, Wang X. et al. (2019) established a short-term WPP model based on two-stage AM and Encoder-Decoder. A feature AM was used in the Encoder and a temporal AM was applied in the Decoder. Some scholars combine AI technology to optimize model parameters. For example, Meng et al. (2021) combined Temporal attention (TA) and GRU to accelerate the early mining of the temporal correlation of input sequences. And Dynamic chatic crisscross optimization (DCCSO) was proposed to optimistic the initial weights and thresholds of TA-GRU. Considering the issue of excessive features from NWP data and historical wind data, Zhang Y. et al. (2020) used t-distributed stochastic neighbor embedding (t-SNE) to reduce the feature dimension. Then Encoder-Decoder with AM was built for each cluster for WPP. And the structure of Encoder-Decoder is shown in Figure 5B. Recent years, one of the representative models for multi-step WPP is Encoder-Decoder with AM, which can enhance the screening ability and memory level of important information over long distances, thereby improving the accuracy of multi-step WPP. Thus, the model is suitable for ultra-short-term and short-term WPP in practice. However, its training efficiency is low because the model cannot support parallel operations. To overcome the limitations of the aforementioned models, Transformer was proposed.

FIGURE 5. Structure of AM and encoder-decoder. (A) Attention common structure. (B) Encoder-Decoder common structure.
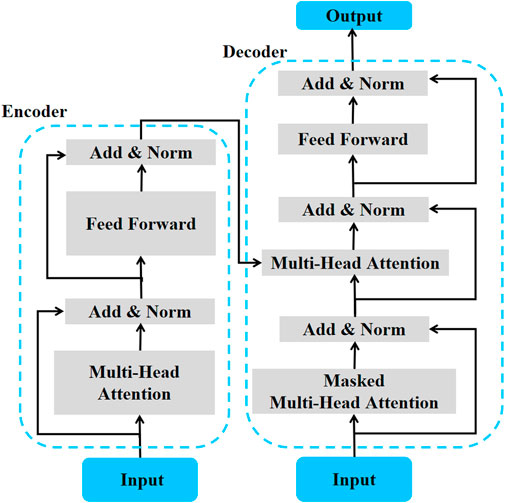
As shown in Figure 6, Transformer has the self-attention mechanism. By utilizing it, Transformer can fully utilize the dependency structure of the time series data, perceive global information, and achieve effective encoding of input sequences. This can preserve more effective information and improve training efficiency through parallel operations, so compared with LSTM and GRU, Transformer can model the time series features of both long-term and short-term, which has become a research hotspot in the multi-step WPP (Pan et al., 2022; Ye et al., 2023). Wang et al. (2023) proposed a conformal asymmetric multi-quantile generative transformer to obtain the Prediction intervals (PIs) of WP. The model effectively utilized the historical and future information by the Encoder-Decoder structure and reduced the prediction error by the generative output. However, Transformer still has some shortcomings in predicting long time series, such as quadratic time complexity, inherent limitations of Encoder-Decoder architecture, and high memory usage. Regarding these issues, Informer was proposed, which has sparse AM to reduce time complexity and spatial memory overhead, and the improvements of Encoder-Decoder architecture can enable the model to handle longer time series inputs and improve computational efficiency. For example, Wei et al. (2023) used Informer for ultra-short-term WPP in the big data environment and confirmed that Informer had higher prediction accuracy and computational efficiency than Transformer. Considering the superiority of Informer in long sequence prediction, Wang WG. (2022) proposed Informer for medium to long term WPP and combined GCN to capture the spatio-temporal dependencies of the data.
In addition to the popular DNN models above, some other deep learning models have also been employed for WPP. GAN is currently a hot spot in NNs for data generation. Its essence is the game learning of generators and discriminators, which makes the distribution of generated data approximate to the real data gradually until ‘false and true’ (Shao et al., 2023). GAN can perform well even with incomplete original data, but its generator is prone to generating multiple distributed data. In order to solve this problem, Yoon et al. (2018) proposed generative adversarial imputation nets (GAIN), which added “hints” to the GAN to provide additional information for the discriminator, so it can fully explore the distribution characteristics of the original data. However, GAIN does not consider the temporal characteristics between data, so it is not suitable for wind data. To address this issue, TimeGAN was proposed. It combined with an autoregression model, so the model can capture the progressive dependencies presented in real data, thereby preserving the dynamic time series dependency of the data (Yoon et al., 2019). Moreover, Luo et al. (2018) proposed GAN based on GRU for generating multivariate temporal data to address this issue.
In summary, AE-based models, RBM-based models, and CNN-based models are widely used for feature extraction in WPP for wind farms. CNN-based models only have one supervised training process, while AE-based models and RBM-based models have unsupervised layer-wise pre-training and supervised fine-tuning. Besides, various variants of RNNs, AM, and Transformer are usually used for relationship learning in WPP. LSTM and GRU are more commonly used for WPP in RNNs. And in practice, LSTM is more suitable when better prediction accuracy is desired, whereas GRU is preferable when less memory usage but the faster calculation speed is needed. AM is usually used to combine with different types of RNNs and Encoder-Decoder, which can improve the accuracy of multi-step WPP. With the development of AI technology, Transformer has the advantage of RNNs and improves training efficiency. It and its variant will be a hot spot in future research on multi-step WPP for wind farms.
3.3 Hybrid models
Similar to the hybrid models for the wind turbine, these for wind farm are also divided into serial models and parallel models. But the methods and technical routes have been studied more widely and deeply. For example, some dynamic weight-based models and weight-based models with signal processing are often used in WPP for wind farm, but are rarely used in WPP for wind turbine. And Some hybrid WPP methods for wind farm in the literature are shown in Table 4.
3.3.1 Serial models
The Boosting algorithm in ensemble learning is also included in the serial models for wind farms. Hu et al. (2017) proposed a WPP model based on improved AdaBoost.RT and KELM, to enhance the performance of weak learning algorithms effectively. And the prediction results proved excellent accuracy and generalization performance of the proposed approach. But the NWP data input to the model only included WP, WS, and temperature. To address this issue, Chen (2022) considered various wind meteorological characteristics and proposed a two-layer structure consisting of four clustering algorithms in the first layer and AdaBoost in the second layer for WPP. And the RF was utilized as a weak learner for AdaBoost.
Fusion prediction models for wind farms are more widely studied than those for wind turbines (Han et al., 2019; Ding et al., 2022; Ma and Mei, 2022; Xiang et al., 2022; Yin and Liu, 2022). In research, the process of error correction is often in the fusion prediction models, and statistical methods and machine learning methods are often used for error estimation. For example, Zhang et al. (2014) used Markov to modify the prediction results of fuzzy neural networks; Ding et al. (2022) first established a WPP model with XGBoost, then trained RF separately with WPP errors of different wind speed bands, and finally obtained short-term WPP results based on error correction. The process of error correction can quantify the magnitude of model error and the uncertainty of data noise, thereby improving the prediction accuracy. With the development of AI technology, hybrid deep learning models including different DNNs are widely studied, in which every DNN specializes in a specific aspect of the prediction task in order to optimize its unique strengths. Thus, hybrid deep learning models can integrate and streamline the laborious decomposition process, thereby improving the prediction accuracy and computational efficiency. For example, Ma and Mei (2022) combined Time2Vec, CNN, AM, and BiLSTM to propose a hybrid deep learning model for WPP, and the simulation demonstrated the validity and applicability of the proposed model.
3.3.2 Parallel models
Compared with the parallel models for a wind turbine, the classification of the models for the wind farm is similar but also has some differences.
The Bagging algorithm in ensemble learning is more used in WPP for wind farms. Tahmasebifar et al. (2020) established a Bagging ensemble model by combining WT and ELM to get prediction points and PIs of WP. Zhang et al. (2016) proposed a hybrid model based on GP and Bagging for WPP. And fully independent training conditional (FITC) was introduced to improve GP.
Weight-based models with the same training set are also widely used for wind farms. The challenge lies in determining the weight coefficients for each model. As described in Section 2.3, most weight-based models used for wind turbines are fixed weight-based models, while the models for wind farms not only include fixed weight-based models but also include dynamic weight-based models. For the fixed weight-based models for wind farms, not only some methods similar to those used for wind turbines have been adopted, but also optimal weight selection has been achieved through the application of rough set theory (Yan, 2021) and intelligent optimization approaches (Heng, 2020). Although fixed weight-based models can improve the accuracy of WPP to some extent, they cannot adjust the weights of hybrid methods in time and have certain limitations. In dynamic weight-based models, the weight assigned to each individual base prediction model is dependent on the data being analyzed. And the cross-entropy theory (Chen et al., 2012) and GIOWA (Wang S., 2022) have been used in the models. For example, Zhong et al. (2022) used historical similarity, the cross-entropy theory, and the gray correlation algorithm to allocate the weights of ELM and LSTM in the hybrid models for WPP.
In WPP for wind farms, in addition to the weight-based models with the same training set, it is also a common technical route to decompose the original sequence first, then model and predict the WP separately for different sub-sequences, and finally weight them. And Figure 4C shows the structure. In this technical route, wavelet decomposition (WD), variational modal decomposition (VMD), EMD, and singular spectrum analysis (SSA) are usually used. For example, Lu et al. (2021a) used VMD-Weighted permutation entropy to decompose the WP sequence and then input sub-sequences into four independent CNN-LSTM networks for deterministic prediction. In order to get more comprehensive and reliable outcomes for probabilistic prediction; He and Wang (2021) used ensemble empirical mode decomposition (EEMD) to decompose intricate original data and combined LASSO and quantile RNN (QRNN). So as to extract features automatically and obtain stable and robust performance for long sequence prediction, Shao et al. (2022) used SSA to decompose the WP sequence and integrated adaptive receptive field (ARF) into temporal convolutional attention network (TCAN).
In summary, hybrid models can integrate the characteristics of different prediction methods, making them widely used in WPP for wind farms. And hybrid models have many different structures. Serial models need higher computational expenses, while parallel models need less.
From the above description, it can be seen that there are various types of AI-based methods for WPP, but currently there is no unified optimization selection method and standard. In addition, there are differences in the construction time, geographical factors, and historical data accumulation of different wind farms, so it is easy to choose the prediction model improperly in practice. To address this issue, it is necessary to conduct experiments based on multiple methods and select appropriate methods based on the prediction results. However, preliminary selection of methods can be made based on wind data characteristics and different requirements for the prediction accuracy, computational cost, computational efficiency, etc. In practice, if the size of the dataset is small, more attention needs to be paid to the generalization of the prediction model. Therefore, the traditional machine learning models can be prioritized to predict the wind power. SVM and GBDT generally show better generalization ability, thus may have better prediction performance when the dataset is not sufficiently large. When the size of the dataset is large enough, different deep learning models and hybrid models can be selected. Generally speaking, Encoder-Decoder with AM, Transformer and Informer can achieve good prediction results in multi-step WPP. Therefore, in ultra short and short-term prediction, if there is a demand for fewer computational costs, Encoder-Decoder with AM can be prioritized, while the neural networks in Encoder and Decoder can prioritize GRU; if better prediction performance and computational efficiency are desired, priority can be given to Transformer, Informer, and hybrid models that combine them with other methods. In medium to long term prediction, Informer can have better prediction accuracy, so Informer and hybrid models that combine Informer with other methods can be given priority consideration.
4 Wind power prediction methods for regional wind farms
With the rapid development of wind power, the distribution scale of wind farms has gradually developed from small-scale and decentralized to large-scale and regional (Liu et al., 2014), and the demand for WPP will also gradually evolve from farm-based to regional. Although the WPP for regional wind farms can refer to the power prediction experience and method practice of wind turbines and wind farms, there are still special requirements and optimal practice methods for its power prediction.
Compared with wind turbines and wind farms, WPP for regional wind farms requires more data to support model training and prediction analysis. Because of the increasing number of wind turbines, the spatial dependence between different wind farms is more complex, so it is necessary to make a comprehensive analysis from the perspective of time and space to further improve the prediction accuracy. For the characteristics of power data, the regional data has good smoothness, while the power data of wind turbines have relatively large fluctuation. In terms of prediction accuracy, regional power prediction not only focuses on the accuracy of point prediction but also pays more attention to the accuracy of the overall prediction trend, which is more in line with the load distribution and scheduling arrangements of the power system (Gang et al., 2016). The WPP for regional wind farms is more challenging.
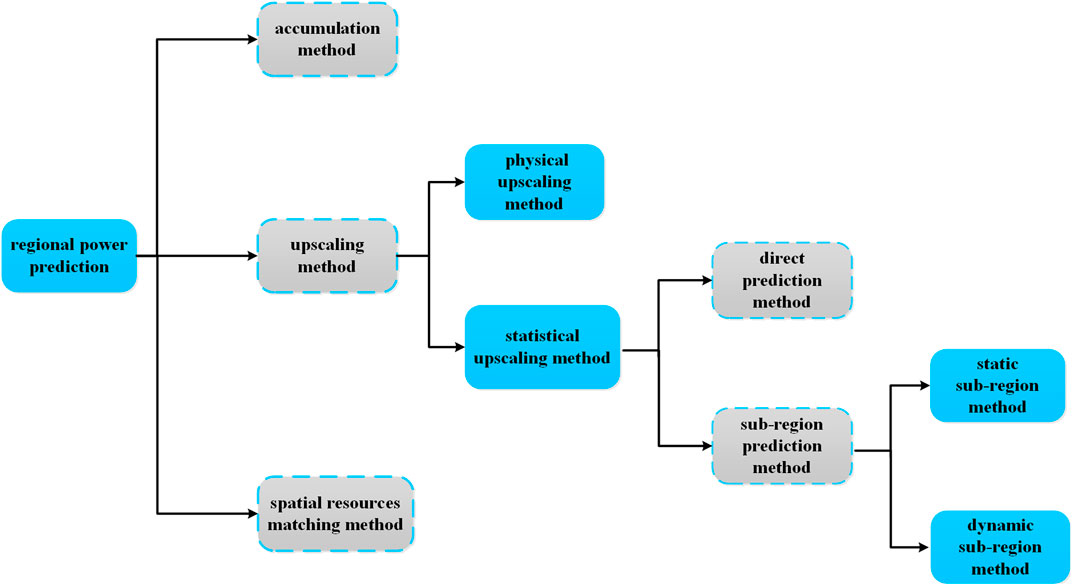
The methods and practices in WPP for regional wind farms are analyzed in detail in this section. The methods for regional wind farms mainly include the accumulation method, upscaling method, and spatial resources matching method (Ye and Zhao, 2014; Zhao and Ye, 2015; Peng X. et al., 2017) The upscaling method can be grouped into the physical upscaling method and statistical upscaling method, as shown in Figure 7.
4.1 Accumulation method
The accumulation method is the most classical in WPP for regional wind farms. The WPP results of wind turbines and wind farms are directly used, and the power prediction results of each wind farm are added to obtain the power prediction result of the regional. The WPP methods for wind turbines and wind farms can be directly used in the accumulation method. The process of the accumulation method is shown in Figure 8. Bai et al. (2010) used the accumulation method to study the problem of regional power prediction in Inner Mongolia. But the experiment showed that the prediction results had a strong dependence on the data quality, and the results were not satisfactory.
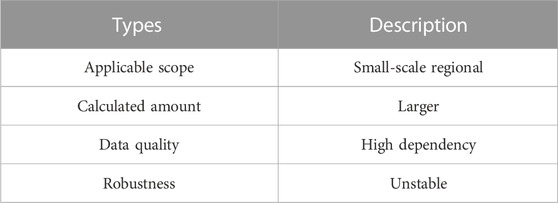
The accumulation method has obvious limitations (Wang et al., 2017). A separate WPP model for each wind farm needs to be established in the method, so when the regional scale is large, the storage of modeling data and model training consumes huge resources. Independent modeling of each wind farm has more stringent requirements on data quality, which requires each wind farm to have sufficient modeling data. Therefore, when wind farms have insufficient data, such as new wind farms or wind farms with poor data quality, the WPP models can not be established normally. In addition, the WPP results of regional wind farms are closely related to the WPP accuracy of each wind farm. The disturbance of any wind farm at any time will affect the fluctuation or mutation of the WPP results for regional wind farms, which leads to poor robustness of regional prediction results. Table 5 shows the advantages and disadvantages of the accumulation method for regional power prediction.
4.2 Upscaling method
To overcome the limitation of establishing one or more WPP models for each wind farm in the accumulation method, the upscaling method came into being. The core idea of the upscaling method is to establish fewer WPP models for a single wind farm and to obtain the accurate WP of the region through the mapping relationship between the WPP results of these fewer typical wind farms and the regional predicted power. In this way, the requirements for the data quality of each wind farm in the region and the accuracy of each prediction model are reduced. Therefore, when the data quality and performance of the WPP model are good in the wind farm, it can be selected as a typical wind farm. Furthermore, more accurate WPP results can also be obtained if the region contains wind farms with incomplete data (new wind farms) or substandard data quality.
The upscaling method is divided into a physical upscaling method and a statistical upscaling method (Tarroja et al., 2011; Wang et al., 2017; Wang K. et al., 2021). The physical upscaling method has a strong spatial dependence and generally requires the construction of a WS/WP prediction model for a typical wind turbine. Then, the WS/WP of multiple wind turbines is calculated according to the topography, spatial information, and wind turbine arrangement. Finally, the WPP result of the region is obtained. The physical upscaling method requires accurate spatial information, and the complexity of the algorithm increases with the increase of regional scale. Therefore, the Statistical upscaling method is more widely used.
The statistical upscaling method is divided into the direct prediction method and the sub-region prediction method. In the direct prediction method, the NWP data of a region are calculated by the downscaling method, and then the mapping relationship between the NWP data and the regional wind power is constructed.
The key to the direct prediction method is to establish the temporal and spatial correlation between different wind farms, to improve the prediction accuracy of the adjacent wind farm. Benefiting from the rapid development of deep learning, the model structure is constantly optimized and the model capacity is constantly increasing, so it can learn the spatiotemporal characteristics of different wind farms very efficiently. In addition, some methods that are good at capturing spatio-temporal information are more frequently used, such as spatio-temporal convolutional network (STCN), GCN, ConvLSTM, ConvGRU, etc. For example, Fan et al. (2020) studied WPP for regional wind farms based on GCN, then used multiple historical features as input and future regional power as a target to build a prediction model. Dong et al. (2022) proposed STCN based on the directed graph convolution structure. And it was formed by combing GCN and TCN and could better learn the spatial and temporal characteristics of multiple wind farms.
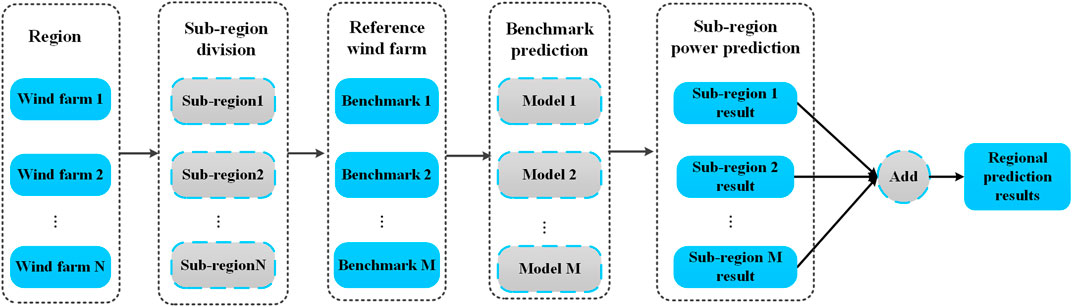
The detailed process of the sub-region prediction method is as follows and shown in Figure 9: 1) By dividing the region into sub-regions, the regional scale is further narrowed; 2) A typical wind farm is selected from each sub-region as a reference wind farm; (3) Building WPP models for the reference wind farm of each sub-region; 4) According to the correlation between the reference wind farm and each wind farm in the sub-region, the WPP result of each sub-region is obtained by referring to the WPP result of the reference wind farm; 5) The WPP results of each sub-region are summed to obtain the WPP result of the whole region.
By the above process, more accurate WPP results for regional wind farms can also be obtained when there are new wind farms in the region. When the data of each wind farm in the region is sufficient, the WPP models for each sub-region can be directly carried out. Therefore, the problem that it is difficult to determine the scaling factor in the process of getting the power of the sub-region through the power of the target wind farm can be avoided. Yu et al. (2022) divided the region into sub-regions based on the spatio-temporal correlation of the region and then used the 1D-CNN-BiLSTM model to predict the WP of each sub-region. After the WPP results of the sub-regions were obtained, the WPP result of the whole region was further obtained. Liu et al. (2021) used the regional hierarchical clustering algorithm to determine the sub-regional division of the region. And the local mode of the wind area was considered to select the optimal partition, which further improved the accuracy of region prediction.
Different from the direct prediction method, the sub-region prediction method needs to construct multiple models, and the number of models is determined by the sub-region division results. Although the sub-region division brings more modeling costs, the whole region can be managed more precisely through it, which reduces the difficulty of model training. In addition, when the region is large, the corresponding meteorological observation data are difficult to fully cover the entire region. And it has a certain impact on the accuracy of NWP data after downscaling. Through the sub-regional division, the wind farm which is close to the meteorological observation stations and has sufficient data can be selected as the reference wind farm, which increases the accuracy of the WPP models.
In addition, the sub-region prediction method has been improved in the studies, which is further divided into static sub-region prediction method and dynamic sub-region method (Yang et al., 2021; Tu et al., 2022; Yang et al., 2022). And the key difference is the sub-region division stage. The historical data are used to divide sub-regions in the static sub-region prediction method. The general division principles include the capacity of wind power, administrative region, geographical location, wind resource characteristics, etc. The sub-regions are divided according to the above characteristics, and remain unchanged after division Figure 10. The prediction data such as WS, wind direction, and temperature in the NWP data are used to divide sub-regions in the dynamic sub-region prediction method. That is to say, sub-regions are divided into the prediction stage, and then the reference wind farm selection and model training are started. Therefore, in the dynamic sub-region prediction method, the sub-region division results in the first prediction may be different from those in the second prediction, so model training needs to be carried out in the prediction stage. And it increases the frequency of model training and limits the application prospects of the dynamic sub-region prediction method. However, with the wide application of transfer learning, it is expected to reduce training frequency through transfer learning. Firstly, a whole model is trained, and then the model is fine-tuned after the dynamic sub-regions are obtained. On the premise of ensuring the accuracy of the model, the training speed of the model is accelerated, and then the bottleneck of the model training is broken through.
4.3 Spatial resources matching method
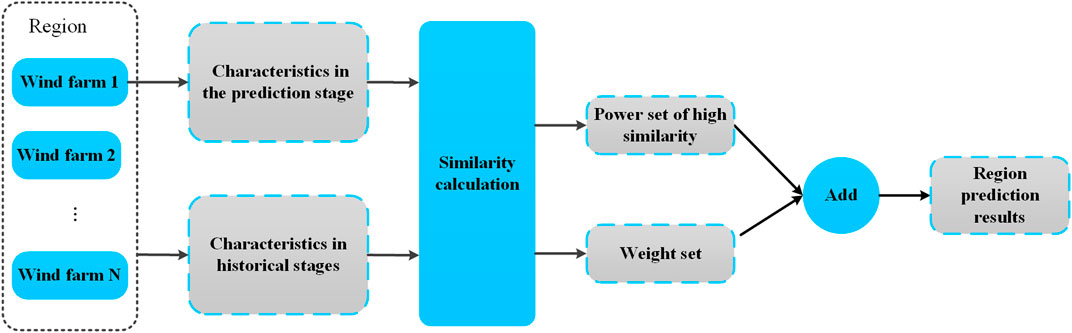
The spatial resources matching method was first proposed by Lobo and Sanchez (2012), and its basic assumption is that under the same spatial scale and similar wind resources, the WP of regions is also similar. The spatial resources matching method compares the similarity of wind resource characteristics of the region between the prediction period and the historical period. Then, the power with high similarity in the historical data is extracted, and the weights are assigned to the power according to the similarity. Finally, the WPP result of the region is obtained through the weighted summation method. The spatial resources matching method is a popular region prediction method in recent years. This method requires less computational resources and has high accuracy, but it is difficult to optimize model parameters. Peng XS. et al. (2017) proposed an improved method, which considers the parameter of the historical wind power output. And the selection method of equivalent measurement power and the optimization method of the model was proposed.
In summary, the main methods for regional power prediction include the accumulation method, upscaling method, and spatial resources matching method. Among them, the statistical upscaling method is widely used. The spatial resources matching method is newer and more popular in recent years. In practice, if the distribution of regional wind farms is sparse, the scale and capacity are small, and the data quality is good, the accumulation method can be prioritized; If the scale and capacity of the regional wind farms are large, priority can be given to the statistical upscaling method. In addition, employing dynamic spatio-temporal correlation analysis to cluster regional wind farms and developing precise spatio-temporal prediction models for sub-region can be effective strategies to predict regional power output. And some methods that are good at capturing spatio-temporal information can be prioritized, such as STCN, and convolutional structures or CNN, combined with LSTM, GRU, and their variants.
5 Performance evaluation metrics of WPP
As can be seen from the above, the new algorithms and models for WPP emerge endlessly at present, and there are various performance evaluation metrics for deterministic models and probabilistic models. And assessing the validity of a WPP model is a crucial stage in its evolution. The performance evaluation metrics of WPP which are most commonly used for deterministic and probabilistic methods are shown below.
5.1 Accuracy of deterministic models
Many different kinds of performance evaluation metrics are used in the literature to evaluate the prediction accuracy of deterministic models. The most commonly used metrics are shown below.
1. Mean absolute error (MAE)
MAE is the fundamental assessment metric of regression tasks.
Where y is the actual WP value,
2. Root mean square error (RMSE)
RMSE is also a primary metric commonly used in the field of WPP. In addition, NMAE and NRMSE are also usually used in the literature.
3. Mean absolute percentage error (MAPE)
MAPE is defined as a percentage of the error but results in disproportionately high values when the actual values approach zero, and is not applicable when the actual value is zero. In order to correct this disadvantage, improved versions of the MAPE have been proposed and they are shown down below.
4. Symmetric mean absolute percentage error (SMAPE)
SMAPE is based on the percentage errors to evaluate the prediction accuracy, and it has prevented the shortcomings of MAPE.
5. Mean arctangent absolute percentage error (MAAPE)
MAAPE (Kim and Kim, 2016) is another improved version of MAPE. Based on the arctangent function, MAAPE has retained the distinguishing features of MAPE while surmounting its shortcomings.
6. Coefficient of determination (R2)
R2 is used to describe the characteristics of data changes. The closer it is to 1, the better the model-fitting effect is.
Where
7. Standard Deviation Error (SDE)
SDE refers to the fluctuation amplitude of errors over a period, which can reflect the dispersion degree of the data.
Where
5.2 Accuracy of probabilistic models
Probabilistic models are also a hot spot in WPP. However, it is a more challenging task to assess the prediction performance of probabilistic models, as the prediction values cannot be straightforwardly compared to the actual values, and multiple criteria, including various properties of the prediction values, need to be considered to evaluate the reliability of such models. The most common evaluation metrics for probabilistic models are shown below.
1. Prediction interval nominal confidence (PINC)
Where α is the significance level.
2. Prediction interval coverage probability (PICP)
PICP measures exclusively the reliability of the PI. It accounts for the average of target values covered by the interval.
Where
3. Prediction interval normalized averaged width (PINAW)
PINAW represents the average of the PI width and also can be used as the primary measure for assessing the reliability of the prediction model.
Where R is the range of the target variable.
4. Coverage width based criterion (CWC)
CWC is merged by the PICP and the PINAW. η和 γ in Eq. 14 are two controlling hyper-parameters that determine the extent to which invalid PIs are penalized.
Where
5. ACE (Average coverage error)
ACE is a measure of the reliability of a PI, with lower values indicating a higher degree of reliability. This metric adds an extra layer of insight beyond the PICP, as a larger PICP does not always correspond to a more optimal PINC (Pinson, 2010).
In summary, MAE and RMSE are always used in the deterministic models, and NMAE, NRMSE, and MAPE are usually used. But MAPE has obvious shortcomings, so many variants of MAPE have been studied and proposed. In the probabilistic models, PICP and PINAW are always applied in the recent literature, and they provide direct information regarding coverage and width.
6 Discussion and future work
Over the past few decades, demand for more accurate WPP has driven more and more research work, and there is no sign that this trend is slowing down. It was observed that in recent years, the research on AI-based WPP models has focused on a single wind farm and regional wind farms, while the research on WPP for wind turbines is relatively few, which cannot meet the needs of accurate and fast power supply for the distributed wind turbine. For wind turbines and wind farms, hybrid models for WPP will be the hot research direction in the future. It can combine various advanced prediction models based on existing methods, improving the accuracy of WPP in different time scales and different environments. For regional wind farms, the prediction accuracy of the models for WPP needs to be analyzed from both time and space perspectives, and the main methods include the accumulation method, upscaling method, and spatial resources matching method. Among them, the statistical upscaling method is commonly used in WPP for regional wind farms. Besides, according to the performance evaluation metrics of WPP, MAE and RMSE are commonly used for deterministic models, while PICP and PINAW are often used in probabilistic models to evaluate the prediction accuracy of the model.
At present, there are still some problems in AI-based WPP models.
1. Poor quality of original data: AI technology is data-driven, so data quality determines the prediction performance of AI-based models. But in practical applications, the data obtained from wind turbines and farms may be incomplete due to various factors such as measurement errors, sensors malfunction, and operational errors. Hence, it is challenging to address the issue of WPP in the presence of missing data (Liu et al., 2018). In addition, the current NWP-based WPP models have become the mainstream, but it is difficult to provide accurate micro-meteorological data for each wind turbine and the wind farm in real practice, which results in poor prediction accuracy of the models;
2. Insufficient feature engineering:In real practice, the fluctuations of WP may be caused by many factors. But currently, WPP models always utilize WS, often wind directions, and sometimes temperature, air pressure, and humidity as the meteorological inputs in the literature, while more factors, such as the turbulence or stability measures, are rarely considered as input, but the impact that these factors have on the electricity generation of turbine and wind farm has been well documented in the literature (Martin et al., 2016);
3. Poor generalization of WPP models: Currently, although a large number of WPP models have been proposed, they tend to be highly dependent on data and prediction scenarios, and have poor robustness. When the environmental parameters and operating conditions of a wind turbine or wind farm change significantly, the prediction accuracy of the models may significantly reduce;
4. Lack of standardized validation methods for AI-based WPP models: As can be seen from the above, there are many different AI-based WPP models in the current research, but the datasets used in the models are different. And the prediction scenarios and evaluation metrics are also inconsistent, and the performance of the models may be over-fitted. Therefore, it is difficult to compare the actual generalization effects of prediction methods, and it is urgent to establish a unified evaluation standard.
Therefore, potential future research direction of AI-based WPP models can arise from the following aspects.
1. Data quality control: Because direct use of the original data for model training increases the uncertainty of the results, the original data needs to be processed before building the WPP models. In addition, it is necessary to consider as many prediction meteorological data sources as possible, realizing real-time prediction and using data assimilation techniques to improve the accuracy of input data, thereby reducing the error of prediction results;
2. More comprehensive feature engineering: many studies show that the choice of variables is very important, so exploring more candidate features that impact WP variations, such as topographical and meteorological features, will beneficial to improve the accuracy of WPP. To obtain this information, appropriate sensors can be installed at the wind turbine and wind farms for data collection;
3. Adaptive learning of WPP models: With the development of large data and AI technology, WPP models can adjust the parameters and structure of models adaptively and dynamically based on technologies such as automatic feature engineering and automatic machine learning, to keep high prediction accuracy even when the environment changes unexpectedly. For example, by introducing dynamic optimization algorithms such as reinforcement learning, the real-time interaction between model parameters and the environmental condition can be achieved. And the strategy of the models can be adjusted in time according to the feedback of the scene and the parameters can be dynamically learned, which will be a new research hotspot in the future;
4. Establishment of standardization validation methods for AI-based WPP models: Up to now, there is no more scientific method to test the generalization of the WPP models in the research, which is not beneficial to the rapid promotion of advanced models and methods in academia to the industry. Therefore, it will be an important direction in the future to establish standardization validation methods for WPP models. It can be used to validate and compare the actual prediction performance and generalization of various prediction models, to achieve standardized validation of prediction models.
Above all, this paper presents an overview of AI-based WPP models. Compared with other WPP models, AI-based WPP models have developed rapidly and gained more attention. The classification of WPP models in this paper is according to the spatial scale of the prediction problem. For wind turbines and wind farms, traditional machine learning models represented by traditional ANNs, SVM, and DT, deep learning models, and hybrid models combining multiple AI algorithms have been studied. And according to the literature, recent developments tend to favor hybrid models, which can generally have high performance; for regional wind farms, the application of the accumulation method, upscaling method, and spatial resources matching method are discussed. In addition, this paper analyzed the challenges and future development trends of AI-based WPP models. This review provides valuable guidance for researchers committed to developing optimized models for WPP.
Author contributions
Conceptualization, YL and QHW; methodology, YL; formal analysis, YL, KZ, and WQ; investigation, YL, YW and QW; resources, KZ and WQ; writing—original draft preparation, YL, YW, and QW; writing—review and editing, YL, YW, QW, and QHW; supervision, YL and QHW; project administration, QHW. All authors contributed to the article and approved the submitted version.
Funding
This research is supported by the Science and Technology Project of China Huaneng Group (HNKJ21-H52).
Conflict of interest
KZ and WQ were employed by Huaneng Jiuquan Wind Power Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
An, G., Jiang, Z., Cao, X., Liang, Y., and Sun, H. (2021). “Short-term wind power prediction based on particle swarm optimization-extreme learning machine model combined with Adaboost algorithm,” in IEEE access (New Jersey, United States: IEEE Access), 1.
Bai, Y. X., Fang, D. Z., Hou, Y. H., and Zhu, C. S. (2010). Regional wind power forecasting system for inner Mongolia power grid. Power Syst. Technol. 34 (10), 157–162.
Bates, J. M., and Granger, C. (2001). The combination of forecasts. OR 20, 451–468. doi:10.2307/3008764
Bhardwaj, T., Mehenge, S., and Revathi, B. S. (2022). “Wind_Turbine_Power_Output_Forecasting_Using_Artificial_Intelligence,” in 2022 international virtual conference on power engineering computing and control: Developments in electric vehicles and energy sector for sustainable future (PECCON) (Chennai, India: IEEE), 1–5.
Bigdeli, N., Afshar, K., Gazafroudi, A. S., and Ramandi, M. Y. (2013). A comparative study of optimal hybrid methods for wind power prediction in wind farm of Alberta, Canada. Renew. Sustain. Energy Rev. 27, 20–29. doi:10.1016/j.rser.2013.06.022
Chen, H. (2022). Cluster-based ensemble learning for wind power modeling from meteorological wind data. Renew. Sustain. Energy Rev. 167, 112652. doi:10.1016/j.rser.2022.112652
Chen, N., Sha, Q., Tang, Y., and Zhu, L. Z. (2012). A combination method for wind power predication based on cross entropy theory. Proc. CSEE 32 (04), 29–34+22.
Clemen, R. T. (1989). Combining forecasts: A review and annotated bibliography. Int. J. Forecast. 5, 559–583. doi:10.1016/0169-2070(89)90012-5
Cortes, C., and Vapnik, V. N. (1995). Support vector networks. Mach. Learn. 20 (3), 273–297. doi:10.1007/bf00994018
Demir, F., and Tasci, B. (2021). “Predicting the power of a wind turbine with machine learning-based approaches from wind direction and speed data,” in 2021 international conference on technology and policy in energy and electric power (ICT-PEP) (Jakarta, Indonesia: IEEE), 37–40.
Ding, T. T., Yang, M., Yu, Y. X., Si, Z. Y., and Zhang, Q. (2022). Short-term wind power integration prediction method based on error correction. High. Volt. Eng. 48 (02), 488–496.
Dong, X., Sun, Y., Li, Y., Wang, X., and Pu, T. (2022). Spatio-temporal convolutional network based power forecasting of multiple wind farms. J. Mod. Power Syst. Clean. Energy 10 (002), 388–398. doi:10.35833/mpce.2020.000849
Ewees, A. A., Al-Qaness, M. a. A., Abualigah, L., and Elaziz, M. A. (2022). HBO-LSTM: Optimized long short term memory with heap-based optimizer for wind power forecasting. Energy Convers. Manag. 268, 116022. doi:10.1016/j.enconman.2022.116022
Fan, G. F., Wang, W. S., and Liu, C. (2008). Artificial neural network based wind power short term prediction system. Power Syst. Technol. 32 (22), 72–76.
Fan, H., Zhang, X., Mei, S., Chen, K., and Chen, X. (2020). M2GSNet: Multi-Modal multi-task graph spatiotemporal network for ultra-short-term wind farm cluster power prediction. Appl. Sci. 10, 7915. doi:10.3390/app10217915
Farah, S., David, A. W., Humaira, N., Aneela, Z., and Steffen, E. (2022). Short-term multi-hour ahead country-wide wind power prediction for Germany using gated recurrent unit deep learning. Renew. Sustain. Energy Rev. 167, 112700. doi:10.1016/j.rser.2022.112700
Gang, W., Wu, X., Li, X., and Wang, C. (2016). “Study on optimal dispatch and control of active power for wind farm cluster based on the fusion information,” in 2016 IEEE PES asia-pacific power and energy engineering conference (APPEEC) (Xi'an: IEEE).
González-Sopeña, J. M., Pakrashi, V., and Ghosh, B. (2021). An overview of performance evaluation metrics for short-term statistical wind power forecasting. Renew. Sustain. Energy Rev. 138, 110515. doi:10.1016/j.rser.2020.110515
Guo, Q., Kuang, H. H., Wang, J. H., Zhou, Y. J., Gao, R. G., Qi, H. T., et al. (2020). Transcriptomic analysis of Bursaphelenchus xylophilus treated by a potential phytonematicide, punicalagin. Electr. Eng. 21 (02), 1–14. doi:10.21307/jofnem-2020-001
Han, S., Qiao, Y. H., Yan, J., Liu, Y. Q., Li, L., and Wang, Z. (2019). Mid-to-long term wind and photovoltaic power generation prediction based on copula function and long short term memory network. Appl. Energy 239, 181–191. doi:10.1016/j.apenergy.2019.01.193
Hao, S., Lee, D. H., and Zhao, D. (2019). Sequence to sequence learning with attention mechanism for short-term passenger flow prediction in large-scale metro system. Transp. Res. Part C Emerg. Technol. 107, 287–300. doi:10.1016/j.trc.2019.08.005
He, Y., and Wang, Y. (2021). Short-term wind power prediction based on EEMD–LASSO–QRNN model. Appl. Soft Comput. 105, 107288. doi:10.1016/j.asoc.2021.107288
Heng, J. N. (2020). Research and application of time series combined and hybrid forecasting model based on machine learning algorithm. Dalian, China: Dongbei University of Finance and Economics.
Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. R. (2012). Improving neural networks by preventing co-adaptation of feature detectors. arXiv e-prints.
Hu, D., Zhang, Z., and Zhou, H. (2022). “Research on wind power Prediction based on BP neural Network,” in 2022 second international conference on advances in electrical, computing, communication and sustainable technologies (ICAECT) (Bhilai, India: IEEE), 1–5.
Hu, H., Wang, L., and Lv, S-X. (2020). Forecasting energy consumption and wind power generation using deep echo state network. Renew. Energy 154, 598–613. doi:10.1016/j.renene.2020.03.042
Hu, M. Y., Hu, Z. J., Zhang, M. L., and Fu, C. Y. (2017). Research on wind power forecasting method based on improved AdaBoost.RT and KELM algorithm. Power Syst. Technol. 41 (02), 536–542.
Hu, Q., Zhang, S., Xie, Z., Mi, J., and Wan, J. (2014). Noise model based ν-support vector regression with its application to short-term wind speed forecasting. Neural Netw. 57, 1–11. doi:10.1016/j.neunet.2014.05.003
Huang, L. W., Jiang, B. T., Shou-Ye, L. V., Liu, Y. B., and De-Yi, L. I. (2018). Survey on deep learning based recommender systems. Chin. J. Comput. 41 (07), 1619–1647.
Jaseena, K. U., and Kovoor, B. C. (2020). A hybrid wind speed forecasting model using stacked autoencoder and LSTM. J. Renew. Sustain. Energy 12 (2), 023302. doi:10.1063/1.5139689
Jiao, R., Huang, X., Ma, X., Han, L., and Tian, W. (2018). A model combining stacked auto encoder and back propagation algorithm for short-term wind power forecasting. IEEE Access 6, 17851–17858. doi:10.1109/access.2018.2818108
Kazutoshi, Y., Higashiyama, F., and Yasuhiro, H. (2018). Feature extraction of NWP data for wind power ForecastingUsing 3D-convolutional neural networks. Energy Procedia 155, 350–358. doi:10.1016/j.egypro.2018.11.043
Khodayar, M., Kaynak, O., and Khodayar, M. E. (2017). Rough deep neural architecture for short-term wind speed forecasting. IEEE Trans. Industrial Inf. 13 (6), 2770–2779. doi:10.1109/tii.2017.2730846
Kim, S., and Kim, H. (2016). A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 32 (3), 669–679. doi:10.1016/j.ijforecast.2015.12.003
Lahouar, A., and Slama, J. (2017). Hour-ahead wind power forecast based on random forests. Renew. Energy 109, 529–541. doi:10.1016/j.renene.2017.03.064
Lai, G., Chang, W. C., Yang, Y., and Liu, H. (2018). Modeling long- and short-term temporal patterns with deep neural networks. arxiv, 95–104.
Lei, M., Shiyan, L., Chuanwen, J., Hongling, L., and Yan, Z. (2009). A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 13 (4), 915–920. doi:10.1016/j.rser.2008.02.002
Li, D., Wang, O., Yang, B. H., and Zhang, Y. H. (2022a). Tunable particle/cell separation across aqueous two-phase system interface by electric pulse in microfluidics. Proc. CSU-EPSA 34 (02), 23–34. doi:10.1016/j.jcis.2021.12.140
Li, J., and Pan, Y. (2017). A review of researches on wind power forecasting technology. Mod. Electr. Power 34 (03), 1–11.
Li, S., Wunsch, D., O'hair, E., and Glesselmann, M. (2001). Using neural networks to estimate wind turbine power generation. IEEE Trans. Energy Convers. 16, 276–282. doi:10.1109/60.937208
Li, Z., Luo, X., Liu, M., Cao, X., Du, S., and Sun, H. (2022b). Short-term prediction of the power of a new wind turbine based on IAO-LSTM. Energy Rep. 8, 9025–9037. doi:10.1016/j.egyr.2022.07.030
Lin, Z., Liu, X., and Collu, M. (2020). Wind power prediction based on high-frequency SCADA data along with isolation forest and deep learning neural networks. Int. J. Electr. Power & Energy Syst. 118, 105835. doi:10.1016/j.ijepes.2020.105835
Liu, C., Zhang, X., Mei, S., and Liu, F. (2021). Local-pattern-aware forecast of regional wind power: Adaptive partition and long-short-term matching. Energy Convers. Manag. 231, 113799. doi:10.1016/j.enconman.2020.113799
Liu, H., Li, Y., Duan, Z., and Chen, C. (2020). A review on multi-objective optimization framework in wind energy forecasting techniques and applications. Energy Convers. Manag. 224, 113324. doi:10.1016/j.enconman.2020.113324
Liu, T., Wei, H., and Zhang, K. (2018). Wind power prediction with missing data using Gaussian process regression and multiple imputation. Appl. Soft Comput. 71, 905–916. doi:10.1016/j.asoc.2018.07.027
Liu, Y. H., Liu, C., Li, W. H., and Zhang, D. Y. (2014). Multi-time scale power prediction of wind farm cluster based on profile pattern matching. Proc. CSEE 34 (25), 4350–4358.
Liu, Y., Shi, J., Yang, Y., and Han, S. (2009). Piecewise support vector machine model for short-term wind-power prediction. Int. J. Green Energy 6 (5), 479–489. doi:10.1080/15435070903228050
Lobo, M. G., and Sanchez, I. (2012). Regional wind power forecasting based on smoothing techniques, with application to the Spanish peninsular system. IEEE Trans. Power Syst. 27, 1990–1997. doi:10.1109/tpwrs.2012.2189418
Lu, P., Ye, L., Pei, M., and Li, Z. (2021a). Short-term wind power forecasting based on meteorological feature extraction and optimization strategy. Renew. Energy 184, 642–661. doi:10.1016/j.renene.2021.11.072
Lu, P., Ye, L., Zhao, Y., Dai, B., Pei, M., and Li, Z. (2021b). Feature extraction of meteorological factors for wind power prediction based on variable weight combined method. Renew. Energy, 1925–1939. doi:10.1016/j.renene.2021.08.007
Luo, Y., Cai, X., Zhang, Y., Xu, J., and Yuan, X. (2018). Multivariate time series imputation with generative adversarial networks, 1–12.
Ma, Z., and Mei, G. (2022). A hybrid attention-based deep learning approach for wind power prediction. Appl. Energy 323, 119608. doi:10.1016/j.apenergy.2022.119608
Martin, C., Lundquist, J. K., Clifton, A., Poulos, G. S., and Schreck, S. J. (2016). Wind turbine power production and annual energy production depend on atmospheric stability and turbulence. Wind Energy Sci. 1 (2), 221–236. doi:10.5194/wes-1-221-2016
Meng, A. B., Chen, S., Wang, C. E., Ding, W. F., Cai, Y. F., Fu, J. J., et al. (2021). Ultra-short-term wind power prediction based on chaotic CSO optimized temporal attention GRU model. Power Syst. Technol. 45 (12), 4692–4700.
Metodieva, I. H., and Bozhkov, S. H. (2022). “Neural network a way to forecast the generation of electricity from a wind turbine,” in 2022 8th international conference on energy efficiency and agricultural engineering (EE&AE) (Ruse, Bulgaria: IEEE), 1–4.
Netsanet, S., Zhang, J., Zheng, D., Agrawal, R. K., and Muchahary, F. (2018). “An aggregative machine learning approach for output power prediction of wind turbines,” in 2018 IEEE Texas power and energy conference (TPEC) (TX, USA: IEEE), 1–6.
Nielson, J., Bhaganagar, K., Meka, R., and Alaeddini, A. (2020). Using atmospheric inputs for Artificial Neural Networks to improve wind turbine power prediction. Energy 190, 116273. doi:10.1016/j.energy.2019.116273
Niu, Z., Yu, Z., Tang, W., Wu, Q., and Reformat, M. (2020). Wind power forecasting using attention-based gated recurrent unit network. Energy 196, 117081. doi:10.1016/j.energy.2020.117081
Pan, X., Wang, L., Wang, Z., and Huang, C. (2022). Short-term wind speed forecasting based on spatial-temporal graph transformer networks. Energy 253, 124095. doi:10.1016/j.energy.2022.124095
Pei, M., Ye, L., Li, Y., Luo, Y., Song, X., Yu, Y., et al. (2022). Short-term regional wind power forecasting based on spatial–temporal correlation and dynamic clustering model. Energy Rep. 8, 10786–10802. doi:10.1016/j.egyr.2022.08.204
Peng, X., Chen, Y., Che, J., and Wang, B. (2017a). “A dynamic adaptive algorithm for statistical up-scaling based short-term wind power prediction of regions,” in 2017 China international electrical and energy conference (CIEEC) (Beijing, China: IEEE), 644–647.
Peng, X. S., Fan, W. W., Wang, B., Zhang, T., Wen, J. Y., Deng, D. Y., et al. (2017b). A lifting spatial resources matching approach based wind power prediction of regions. Electr. Power Constr. 38 (07), 10–17.
Peng, X., Xiong, L., Wen, J., Cheng, S., and Wang, B. (2016). A summary of the state of the art for short-term and ultra-short-term wind power prediction of regions. Proc. CSEE.
Peng, X., Zhang, Z., Xu, Q., Wang, B., and Huang, Z. (2020). “A three-stage ensemble short-term wind power prediction method based on VMD-WT transform and SDAE deep learning,” in 2020 IEEE/IAS industrial and commercial power system asia (I&CPS asia) (Weihai: IEEE), 1350–1356.
Pinson, P. K, G., and Kariniotakis, G. (2010). Conditional prediction intervals of wind power generation. IEEE Trans. Power Syst. 25 (4), 1845–1856. doi:10.1109/tpwrs.2010.2045774
Qin, W., Martinez-Anido, C. B., Wu, H., Florita, A. R., and Hodge, B. M. (2016). Quantifying the economic and grid reliability impacts of improved wind power forecasting. IEEE Trans. Sustain. Energy 7 (4), 1525–1537. doi:10.1109/tste.2016.2560628
Rashid, H., Haider, W., and Batunlu, C. (2020). “Forecasting of wind turbine output power using machine learning,” in 2020 10th international conference on advanced computer information technologies (ACIT) (Germany: Deggendorf), 396–399.
Ren, J., Yu, Z., Gao, G., Yu, G., and Yu, J. (2022). A CNN-LSTM-LightGBM based short-term wind power prediction method based on attention mechanism. Energy Rep. 8, 437–443. doi:10.1016/j.egyr.2022.02.206
Riahy, G. H., and Abedi, M. (2008). Short term wind speed forecasting for wind turbine applications using linear prediction method. Renew. Energy 33 (1), 35–41. doi:10.1016/j.renene.2007.01.014
Sawant, M., Patil, R., Shikhare, T., Nagle, S., Chavan, S., Negi, S., et al. (2022). A selective review on recent advancements in long, short and ultra-short-term wind power prediction. Energies 15 (21), 8107. doi:10.3390/en15218107
Shan, J-N., Wang, H-Z., Pei, G., Zhang, S., and Zhou, W-H. (2022). Research on short-term power prediction of wind power generation based on WT-CABC-KELM. Energy Rep. 8, 800–809. doi:10.1016/j.egyr.2022.09.165
Shao, Z. G., Zhang, C. S., Chen, F. X., and Xie, Y. H. (2023). Generative adversarial networks for power system applications. CSEE J. Power Energy Syst. 43 (03), 987–1004.
Shao, Z., Han, J., Zhao, W., Zhou, K., and Yang, S. (2022). Hybrid model for short-term wind power forecasting based on singular spectrum analysis and a temporal convolutional attention network with an adaptive receptive field. Energy Convers. Manag. 269, 116138. doi:10.1016/j.enconman.2022.116138
Sheng, Y., Wang, H., Yan, J., Liu, Y., and Han, S. (2023). Short-term wind power prediction method based on deep clustering-improved Temporal Convolutional Network. Energy Rep. 9, 2118–2129. doi:10.1016/j.egyr.2023.01.015
Shi, J., Guo, J., and Zheng, S. (2012). Evaluation of hybrid forecasting approaches for wind speed and power generation time series. Renew. Sustain. Energy Rev. 16 (5), 3471–3480. doi:10.1016/j.rser.2012.02.044
Shi, J., Liu, Y., Yang, Y., Han, S., and Wang, P. (2010). “The research and application of wavelet-support vector machine on short-term wind power prediction,” in 2010 8th world congress on intelligent control and automation (China: Jinan), 4927–4931.
Shuai, H. A., Yue, X. A., Da, H. B., Sj, A., and Jl, A. (2021). An improved deep belief network based hybrid forecasting method for wind power. Energy 124, 120185. doi:10.1016/j.energy.2021.120185
Shuang, H., Liu, Y., and Jie, Y. (2011). “Neural network ensemble method study for wind power prediction,” in 2011 asia-pacific power and energy engineering conference (Wuhan, China: IEEE).
Sobolewski, R. A., Tchakorom, M., and Couturier, R. (2023). Gradient boosting-based approach for short- and medium-term wind turbine output power prediction. Renew. Energy 203, 142–160. doi:10.1016/j.renene.2022.12.040
Sun, C., Zhang, Y., Huang, G., Liu, L., and Hao, X. (2022). A soft sensor model based on long&short-term memory dual pathways convolutional gated recurrent unit network for predicting cement specific surface area. ISA Trans. 130, 293–305. doi:10.1016/j.isatra.2022.03.013
Sun, R., Zhang, T., He, Q., and Xu, H. (2021). Review on key technologies and applications in wind power forecasting. High. Volt. Eng. 47 (04), 1129–1143.
Sun, Z., Zhao, S., and Zhang, J. (2019), Short-term wind power forecasting on multiple scales using VMD decomposition, K-means clustering and LSTM principal computing. IEEE access. New York City: IEEE, 1.
Tahmasebifar, R., Moghaddam, M. P., Sheikh-El-Eslami, M. K., and Kheirollahi, R. (2020). A new hybrid model for point and probabilistic forecasting of wind power. Energy 211, 119016. doi:10.1016/j.energy.2020.119016
Tarroja, B., Mueller, F., Eichman, J. D., Brouwer, J., and Samuelsen, S. (2011). Spatial and temporal analysis of electric wind generation intermittency and dynamics. Renew. Energy 36 (12), 3424–3432. doi:10.1016/j.renene.2011.05.022
Tascikaraoglu, A., and Uzunoglu, M. (2014). A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 34, 243–254. doi:10.1016/j.rser.2014.03.033
Tu, Q. Y., Miao, S. H., Lin, Y. J., Zhang, D., Yao, F. X., and Han, J. (2022). Ultra-short-term interval forecasting method for regional wind farms based on dynamic R-vine copula model. High. Volt. Eng. 48 (02), 456–470.
Wang, G., Jia, R., Liu, J., and Zhang, H. (2020). A hybrid wind power forecasting approach based on Bayesian model averaging and ensemble learning. Renew. Energy 145 (Jan.), 2426–2434. doi:10.1016/j.renene.2019.07.166
Wang, J. X. (2019). Short-term wind power forecasting method for single turbine. Master. Shandong: Shandong Jianzhu University.
Wang, K., Qi, X., Liu, H., and Song, J. (2018). Deep belief network based k-means cluster approach for short-term wind power forecasting. Energy 165, 840–852. doi:10.1016/j.energy.2018.09.118
Wang, K., Zhang, Y., Lin, F., and Xu, Y. (2021a). “Regional wind power forecasting based on hierarchical clustering and upscaling method,” in 2021 3rd asia energy and electrical engineering symposium (AEEES) (Chengdu, China: IEEE), 713–718.
Wang, Q. (2013). A research of SVM short-term wind power prediction based on GA optimization. J. Guizhou Normal Univ. Sci. 31 (01), 103–106.
Wang, S. (2022a). “Research on wind power combination prediction method based on physical data fusion,” in Master. Shenyang (Liaoning, China: Shenyang University of Technology).
Wang, W., Feng, B., Huang, G., Guo, C., Liao, W., and Chen, Z. (2023). Conformal asymmetric multi-quantile generative transformer for day-ahead wind power interval prediction. Appl. Energy 333, 120634. doi:10.1016/j.apenergy.2022.120634
Wang, W. G. (2022b). Research on medium and long term wind power prediction based on Informer. Master: Beijing Jiaotong University.
Wang, X., Li, P., and Yang, J. (2019a). Short-term wind power forecasting based on two-stage attention mechanism. IET Renew. Power Gener. 14 (2), 297–304. doi:10.1049/iet-rpg.2019.0614
Wang, Y. (2021). Combined model of short-term wind speed prediction for wind farms based on deep learning. Doctor: Hefei: University of Science and Technology of China.
Wang, Y., Hu, Q., Li, L., Foley, A. M., and Srinivasan, D. (2019b). Approaches to wind power curve modeling: A review and discussion. Renew. Sustain. Energy Rev. 116, 109422. doi:10.1016/j.rser.2019.109422
Wang, Y. J., Lu, Z. X., Qiao, Y., Wang, L. L., and Xu, H. X. (2017). Short-term regional wind power statistical upscaling forecasting based on feature clustering. Power Syst. Technol. 41 (05), 1383–1389.
Wang, Y., Zou, R., Liu, F., Zhang, L., and Liu, Q. (2021b). A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 304, 117766. doi:10.1016/j.apenergy.2021.117766
Wei, H., Wang, W-S., and Kao, X-X. (2023). A novel approach to ultra-short-term wind power prediction based on feature engineering and informer. Energy Rep. 9, 1236–1250. doi:10.1016/j.egyr.2022.12.062
Williams, R., Zhao, F., and Lee, J. (2022). Global wind report 2022. Brussels: Global Wind Energy Council.
Wu, Q., and Peng, C. (2016). Wind power generation forecasting using least squares support vector machine combined with ensemble empirical mode decomposition, principal component analysis and a bat algorithm. Energies 9 (4), 261. doi:10.3390/en9040261
Wu, Y. H., Wang, Y. S., Xu, H., Chen, Z., Zhang, Z., and Guan, S. J. (2022). Survey of wind power output power output power forecasting technology. J. Front. Comput. Sci. Technol. 16 (12), 2653–2677.
Xiang, L., Liu, J., Yang, X., Hu, A., and Su, H. (2022). Ultra-short term wind power prediction applying a novel model named SATCN-LSTM. Energy Convers. Manag. 252, 115036. doi:10.1016/j.enconman.2021.115036
Xiong, J., Peng, T., Tao, Z., Zhang, C., Song, S., and Nazir, M. S. (2023). A dual-scale deep learning model based on ELM-BiLSTM and improved reptile search algorithm for wind power prediction. Energy 266, 126419. doi:10.1016/j.energy.2022.126419
Xue, Y., Wang, L., Wang, S., and Zhang, Y. F. (2019). Thermal conductivity of protein-based materials: A review. Renew. Energy 37 (03), 456–462. doi:10.3390/polym11030456
Yan, J., Li, K., Bai, E. W., Deng, J., and Foley, A. M. (2017a). Hybrid probabilistic wind power forecasting using temporally local Gaussian process. IEEE Trans. Sustain. Energy 7 (1), 87–95. doi:10.1109/tste.2015.2472963
Yan, J., Liu, Y., Han, S., Wang, Y., and Feng, S. (2015). Reviews on uncertainty analysis of wind power forecasting. Renew. Sustain. Energy Rev. 52, 1322–1330. doi:10.1016/j.rser.2015.07.197
Yan, J. (2021). Research on short-term wind power forecasting method based on multi-dimensional clustering and Markov chain combination model. Yinchuan: North Minzu University. Master.
Yan, J., Zhang, H., Liu, Y., Han, S., Li, L., and Lu, Z. (2017b). Forecasting the high penetration of wind power on multiple scales using multi-to-multi mapping. IEEE Trans. Power Syst. 33, 3276–3284. doi:10.1109/tpwrs.2017.2787667
Yang, M., Peng, T., and Su, X. (2022). Ultra-short term wind power prediction based on two-dimensional coordinate dynamic division of prediction information. Proc. CSEE 42 (24), 8854–8864.
Yang, X., Guo, F., Zhang, Y., Ning, K., and Feng, G. (2017). A naive bayesian wind power interval prediction approach based on rough set attribute reduction and weight optimization. Energies 10 (11), 1903. doi:10.3390/en10111903
Yang, Z. M., Peng, X. S., Lang, J. X., Wang, H. Y., Wang, B., and Liu, C. (2021). Short-term wind power prediction based on dynamic cluster division and BLSTM deep learning method. High. Volt. Eng. 47 (04), 1195–1203.
Ye, L., Li, Y. L., Pei, M., Li, Z., Xu, X. J., and Lu, J. Z. (2023). Combined approach for short-term wind power forecasting under cold weather withSmall sample. Proc. CSEE 43 (02), 543–555.
Ye, N., and Zhao, Y. N. (2014). A review on wind power prediction based on spatial correlation approach. Automation Electr. Power Syst. 38 (14), 126–135.
Yildiz, C., Acikgoz, H., Korkmaz, D., and Budak, U. (2021). An improved residual-based convolutional neural network for very short-term wind power forecasting. Energy Convers. Manag. 228, 113731. doi:10.1016/j.enconman.2020.113731
Yin, S., and Liu, H. (2022). Wind power prediction based on outlier correction, ensemble reinforcement learning, and residual correction. Energy 250, 123857. doi:10.1016/j.energy.2022.123857
Yoon, J., Jordon, J., and Schaar, M. (2018). Gain: Missing data imputation using generative adversarial nets. Stockholm, Sweden: Stockholmsmassan, 5689–5698.
Yu, G., Liu, C., Tang, B., Chen, R., Lu, L., Cui, C., et al. (2022). Short term wind power prediction for regional wind farms based on spatial-temporal characteristic distribution. Renew. Energy 199, 599–612. doi:10.1016/j.renene.2022.08.142
Yu, M., Niu, D., Gao, T., Wang, K., Sun, L., Li, M., et al. (2023). A novel framework for ultra-short-term interval wind power prediction based on RF-WOA-VMD and BiGRU optimized by the attention mechanism. Energy 269, 126738. doi:10.1016/j.energy.2023.126738
Yu, R., Gao, J., Yu, M., Lu, W., Xu, T., Zhao, M., et al. (2018). LSTM-EFG for wind power forecasting based on sequential correlation features. Future Gener. Comput. Syst. 93, 33–42. doi:10.1016/j.future.2018.09.054
Yu, R., Liu, Z., Li, X., Lu, W., Ma, D., Yu, M., et al. (2019). Scene learning: Deep convolutional networks for wind power prediction by embedding turbines into grid space. Appl. Energy 238, 249–257. doi:10.1016/j.apenergy.2019.01.010
Yu, Y., Han, X., Yang, M., and Yang, J. (2020). Probabilistic prediction of regional wind power based on spatiotemporal quantile regression. United States: IEEE Transactions on Industry Applications, 1.
Yuan, X., Chen, C., Jiang, M., and Yuan, Y. (2019). Prediction interval of wind power using parameter optimized Beta distribution based LSTM model. Appl. Soft Comput. 82, 105550. doi:10.1016/j.asoc.2019.105550
Zhang, C. S., Shao, Z. G., Chen, F. X., Jiang, C. X., and Feng, J. B. (2022). Renewable power generation data transferring based on conditional DeepConvolutions generative adversarial network. Power Syst. Technol. 46 (06), 2182–2190.
Zhang, H., Yan, J., Liu, Y., Gao, Y., Han, S., and Li, L. (2021a). Multi-source and temporal attention network for probabilistic wind power prediction. IEEE Trans. Sustain. Energy 12 (4), 2205–2218. doi:10.1109/tste.2021.3086851
Zhang, H., Yang, Y., Zhang, Y., He, Z., Yuan, W., Yang, Y., et al. (2020a). A combined model based on SSA, neural networks, and LSSVM for short-term electric load and price forecasting. LSSVM short-term Electr. load price Forecast. Neural Comput. Appl. 33 (2), 773–788. doi:10.1007/s00521-020-05113-0
Zhang, J., Liu, D., Li, Z., Han, X., Liu, H., Dong, C., et al. (2021b). Power prediction of a wind farm cluster based on spatiotemporal correlations. Appl. Energy 302, 117568. doi:10.1016/j.apenergy.2021.117568
Zhang, J., Yan, J., Infield, D., Liu, Y., and Lien, F-S. (2019). Short-term forecasting and uncertainty analysis of wind turbine power based on long short-term memory network and Gaussian mixture model. Appl. Energy 241, 229–244. doi:10.1016/j.apenergy.2019.03.044
Zhang, L. (2022). “Research on short-term wind power prediction based on error compensation neural network model,” in . Master. Inner Mongolia (China: Inner Mongolia University of Science & Technology).
Zhang, Y. C., Guo, X. J., and Deng, H. (2016). A combination method of short-term wind power forecasting based on improved GPR and Bagging. Power Syst. Prot. Control 44 (23), 46–51.
Zhang, Y., Li, Y., and Zhang, G. (2020b). Short-term wind power forecasting approach based on Seq2Seq model using NWP data. Energy 213, 118371. doi:10.1016/j.energy.2020.118371
Zhang, Y., Wang, J., and Wang, X. (2014). Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 32, 255–270. doi:10.1016/j.rser.2014.01.033
Zhao, Y. N., and Ye, L. (2015). A numerical weather prediction feature selection approach based on minimal–redundancy–maximal–relevance strategy for short-term regional wind power prediction. Proc. CSEE 35 (23), 5985–5994.
Zhong, W. Z., Li, C. G., Cui, Y., Li, F., and Wang, D. D. (2022). Combined prediction of ultra-short term wind power considering weighted historical similarity. Acta energiae Solaris Sin. 43 (06), 160–168.
Keywords: wind power prediction, artificial intelligence, data-driven method, machine learning, deep learning
Citation: Liu Y, Wang Y, Wang Q, Zhang K, Qiang W and Wen QH (2023) Recent advances in data-driven prediction for wind power. Front. Energy Res. 11:1204343. doi: 10.3389/fenrg.2023.1204343
Received: 12 April 2023; Accepted: 30 May 2023;
Published: 12 June 2023.
Edited by:
Juan P. Amezquita-Sanchez, Autonomous University of Queretaro, MexicoReviewed by:
Ning Li, Xi’an University of Technology, ChinaSrete Nikolovski, Josip Juraj Strossmayer University of Osijek, Croatia
Kaiping Qu, China University of Mining and Technology, China
Copyright © 2023 Liu, Wang, Wang, Zhang, Qiang and Wen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qiuzi Han Wen, cXpfd2VuaGFuQHFueS5jaG5nLmNvbS5jbg==
 Yaxin Liu
Yaxin Liu Yunjing Wang1
Yunjing Wang1