Network-constrained flexible ramping product provision of prosumer aggregator: a data-driven stochastic bi-level optimization

Prosumers are expected to provide the flexible ramping product (FRP) in the power system. However, voltage violations and line congestion may arise in the distribution network, when FRP delivered by prosumers. Hence, this paper proposes a data-driven stochastic bi-level optimization model to coordinate the prosumer aggregator to decide FRP-offering while ensuring distribution network security under FRP delivery. In the proposed bi-level model, the upper-level is a min-max problem, representing the minimum expected cost under the worst-case scenario probability distribution for the prosumer aggregator. The lower-level is the operation cost minimization within the distribution network security for distribution network operator. The proposed model is converted into a single-level model using the Karush-Kuhn-Tucker condition and strong duality theory, and applied to the modified IEEE 33-bus network with three prosumers. The results demonstrate the effectiveness of the proposed model.

1 Introduction

The expansion of renewable energy integration into the power grid has led to the de-committed of conventional units, exacerbating the scarcity of ramping resources in the power system (Wang and Hodge, 2017). According to the CAISO daily report dated 23 June 2023, the requirement of FRP during the 3 hours following 6 a.m. accounted for 40.4% of the peak load for that day (California Independent System Operator, 2023). Addressing this pressing issue requires urgent exploration of demand-side ramping capability (Yamujala et al., 2022). With the implementation of low-carbon policies and smart control technologies in distribution system, an increasing number of passive low-voltage consumers with distributed resources are being transformed into active prosumers, resulting in unprecedented improvements of flexibility in distribution system (Kubli et al., 2018). While significant improvements have been made in enhancing flexibility, its value cannot be fully realized without proper organization and coordination. As a crucial link between decentralized flexibility and economically scalable electricity services, research on prosumer aggregator has rapidly gained momentum (Olivella-Rosell et al., 2018). However, the deliverability and availability challenges associated with FRP (Fang et al., 2020), coupled with the voltage violations and line congestion in prosumer active responses, pose additional challenges for prosumer aggregator in providing FRP. Therefore, this paper investigate how prosumer aggregator can provide FRP while ensuring the security of the distribution network.

The current definition of prosumer is broad, encompassing subjects such as electric vehicle aggregators, smart buildings, and grid-connected microgrids, which are also considered as prosumers (Gonzalez-Romera et al., 2019; Hu et al., 2019; Huang et al., 2020; Nizami et al., 2020). In order to comprehensively analyze the current state of research, this paper also considers the provision of FRP by this broad category of prosumer. Studies on the provision of FRP by prosumer aggregators can be categorized into two group.

The first group focuses solely on the economic strategy developed based on the portfolio model without considering distribution system security. For instance, the author in the literature (Kim et al., 2021) proposes a FRP offering strategy for electric vehicles considering travel chain uncertainty. Similarly, The literature (Wang et al., 2017; Hu et al., 2018) propose a FRP offering strategy for microgrid and battery energy storage aggregator, respectively. The literature (Zhang et al., 2022) develops a method to allocate ramping capacity in electric-gas systems. The literature (Zhu et al., 2020) proposes a decision framework for residential-level energy hubs considering the provision of FRP for arbitrage. The literature (Khoshjahan et al., 2020) develops a stochastic FRP offering strategy for energy storage systems. Likewise, The literature (Khoshjahan et al., 2022) presents a robust optimal strategy for prosumer aggregators to provide FRP in the real-time market. In summary, the studies have explored the prosumers that encompass various types of flexible resources based on the optimal offering model within forecast market clearing prices. This group of bidding decision models focuses only on the optimal power allocation of resources within the prosumer and ignores the interaction relationship with the market clearing price, which can lead to an underestimation of the prosumer’s flexibility. Moreover, strategies formulated using predicted market clearing prices resemble passive time-of-use tariff demand response strategies. Such approaches do not fully showcase the proactive advantages inherent to the prosumer.

The second group considers the security of the distribution network when submitting an offering strategy but ignores the potential security issues when FRP is activated. For example, the literature (Zhang et al., 2020) proposes an extended ACOPF model that integrates electric vehicles and calculates the marginal benefit value of FRP. The literature (Bahramara et al., 2022) presents a method for considering distribution network line congestion when microgrids provide services to system-independent operators. The literature (Ghaemi et al., 2021a) proposes a bi-level model for DNO purchasing microgrid’s FRP in the distribution network, while the literature (Allahmoradi et al., 2021) suggests a stochastic optimal strategy for reducing the net load ramping rate of active distribution networks. The literature (Ghasemi et al., 2021) introduces a bi-level optimal approach to incorporate distributed resources for providing FRP. Although the bi-level model described above effectively captures the interaction between the distribution network and prosumer aggregators, the upper models are not aggregator which are not suitable for bidding decisions. Although all of the work mentioned above considers distribution system security when the prosumer aggregator submit FRP, they only consider the energy strategy to satisfy distribution network security when the FRP is not activated. The power flow in the distribution network will change when the distribution network operator activates the FRP of the prosumer, which may cause distribution network security issues such as voltage violations and line congestions. In addition, the value of flexibility for each prosumer cannot be accounted for correctly because of the ignorance of the network security constraints during FRP delivery.

Moreover, the volatility of distributed renewable energy (DRE) indirectly affects the bidding/offering decision of prosumer aggregators. The optimization strategies developed in the aforementioned literature, based on stochastic optimization (Wang et al., 2017; Khoshjahan et al., 2020; Allahmoradi et al., 2021; Bahramara et al., 2022) and robust optimization (Zhu et al., 2020; Ghasemi et al., 2021b; Khoshjahan et al., 2022; Zhang et al., 2022) for uncertainty modeling in the DRE output and market clearing prices. Robust optimization does not rely on probability distribution characteristics and makes decisions based only on worst-case uncertainty scenarios. In optimal scheduling problems where uncertainty extreme scenarios have a low probability of occurring, robust models tend to result in overly conservative strategies. It is a characteristic more suited to the study of stable control and planning problems (Ma et al., 2023). Stochastic optimization assumes that the decision-making has a comprehensive understanding of uncertainty through known probability distributions, and often empirical or data-driven approaches are used to construct probability distributions (Fu et al., 2023a). However, due to the finiteness of the sample, the constructed probability distribution may be far from the true probability distribution, which can lead to an under-conservative strategy. Selecting representative discrete scenarios to characterize the probability distribution is also an issue, which a large set of scenarios will greatly increase the computational burden. The literature (Fu et al., 2023b) proposes an approach to select the representative scenarios by neural networks to reduce the size of scenarios. Distributionally robust methods have attracted much attention in recent years, which combine the advantages of stochastic optimization and robust optimization by formulating expected optimal decisions under robust probability distributions, and have been applied to power system optimal scheduling (Shi et al., 2023) and control (Xu et al., 2023) issues. Among them, a stochastic optimization method based on a mixed-norm model was firstly proposed in the literature (Zhao and Guan, 2016), which can achieve expectation-optimal decision-making under robust probability distribution. The method can adjust the conservativeness of uncertainty modeling and is particularly applicable to the formulation of bid-offer strategy. The prosumer aggregator can improve its response to the future development of the complex distribution grid market by employing external data and adopting a risk-averse willingness to dynamically adjust its bidding and offering strategy. Therefore, embedding this model into the problem of FRP decision-making by prosumer aggregators is also within the scope of research interest in this paper.

In this context, the paper proposes a bidding/offering model based on a data-driven stochastic bi-level optimization for prosumer aggregator. The major contributions of this paper are presented as follows.

1) Proposing a novel data-driven stochastic bi-level optimization framework for prosumer aggregator, which effectively incorporates the value of external data and proactively develops energy and FRP bidding/offering strategy that strike a better balance between economy and conservativeness.

2) Proposing an extended linearized ACOPF model that avoids technical violations of the distribution system after the delivery of FRP and enables the derivation of more detailed marginal prices of nodes. More importantly, the linearization greatly improves the model’s applicability, especially in the construction of the bi-level programming.

The remainder of this paper is organized as follows. Section 2 presents the problem description. In Section 3, the proposed model and solution technique is formulated. The numerical results are analyzed in Section 4. Finally, Section 5 concludes the paper.

2 Problem description

2.1 Stochastic bi-level optimization structure for bid and offer strategy of prosumer aggregator

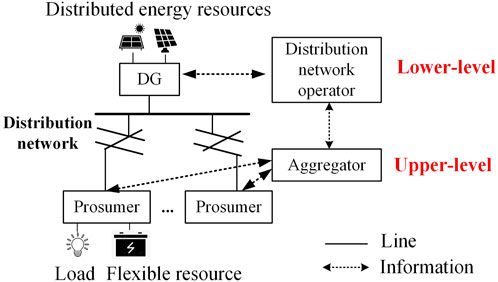
The proposed model presents a data-driven, stochastic bi-level optimization problem. This captures the interactive decision-making between the prosumer aggregator managing the prosumers and the DNO scheduling the DRE. The structure is illustrated in Figure 1. We assume that all prosumers within the distribution network can be managed by a single aggregator. The interactive decision-making of prosumer aggregator and DNO is a stochastic bi-level optimization problem that can be modeled based on the scenario approach. The upper-level problem represents the formulation of energy bidding and FRP offering at the distribution locational marginal price for prosumer aggregator, and the lower-level problem represents the energy and FRP clearing out locally for DNO receiving the upper-level decision, the structure of which is shown in Figure 2. In fact, the proposed model is also a Stackelberg Game problem, where the prosumer aggregator acts as the leader while the DNO acts as the follower. The proactive superiority of the prosumer aggregator is emphasized. DRE are common in distribution networks, and their energy management strategy affect the energy and FRP clearing of DNO, and subsequently the strategies of prosumers. The conservativeness of uncertainty modeling is corrected using a data-driven approach. The prosumer aggregator searches for the worst-case probability distribution in the optimization space of the scenario probability distribution, and ultimately achieves the minimum expected cost of the bidding/offering strategy under the worst probability distribution.

FIGURE 1

FIGURE 1. Coordinated operational framework for aggregator and DNO.

FIGURE 2

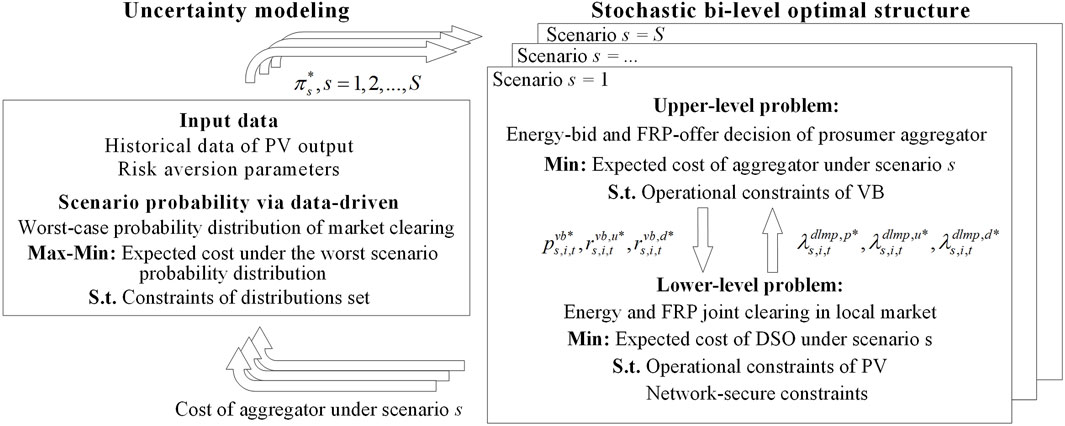
FIGURE 2. A data-driven stochastic bi-level optimization framework for prosumer aggregator decision bid-offer.

The KKT condition and strong dual theory are used to solve the model. The KKT condition can replace the lower-level optimization problem with an equilibrium constraint. The strong dual theory can replace the bi-linear term in the upper level objective. The linearization of the complementary relaxation constraints is done by the big-M method. The model can eventually be transformed into a mixed-integer linear programming problem that can be easily solved by commercial software.

2.2 Uncertainty modeling of DRE

DRE are widely deployed in distribution networks, and their stochastic output characteristics have a substantial influence on the energy and FRP locally clearing of DNO. The uncertainty model proposed in the literature (Zhao and Guan, 2016) is able to take into account the uncertainty of the probability distribution of random variables. In this paper, this model is integrated into the proposed stochastic bi-level programming problem.

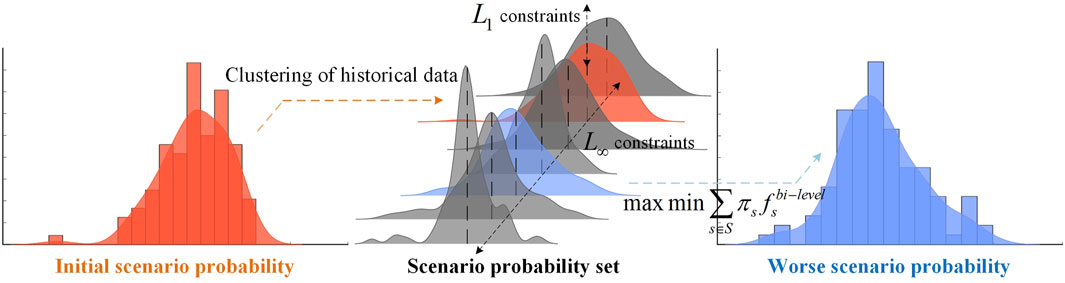
The process of uncertainty modeling, as illustrated in Figure 3, comprises several steps. Firstly, historical data is clustered to obtain an initial probability distribution. Subsequently, the $L_1$ norm and $L_{\infty }$ norm are utilized to construct the set of probability distributions. It is worth noting that the mix-norm captures the risk-averse of the prosumer aggregator, influencing the level of conservativeness within the ensemble. Lastly, a bi-level stochastic optimization model is employed to identify the worst-case distribution from the set, facilitating the formulation of an optimal decision that is both economically viable and conservative.

FIGURE 3

FIGURE 3. A data-driven framework for uncertainty modeling.

3 Method development of FRP provision by prosumer aggregator

3.1 Scenario probability distribution set

${\displaystyle \sum _{\mathit{s}\in \mathit{S}}}\left|{\mathit{\pi }}_{\mathit{s}}-{\mathit{\pi }}_{\mathbf{0}}\right|\le \frac{\mathit{S}}{\mathbf{2}{\mathit{N}}_{\mathit{s}}}\mathit{ln}\frac{\mathbf{2}\mathit{S}}{\mathbf{1}-{\mathit{\alpha }}_{\mathbf{1}}}(1)$

${\mathit{max}}_{\mathit{s}=\mathbf{1},\dots ,\mathit{S}}\left|{\mathit{\pi }}_{\mathit{s}}-{\mathit{\pi }}_{\mathbf{0}}\right|\le \frac{\mathbf{1}}{\mathbf{2}{\mathit{N}}_{\mathit{s}}}\mathit{ln}\frac{\mathbf{2}\mathit{S}}{\mathbf{1}-{\mathit{\alpha }}_{\mathit{s}}}(2)$

${\displaystyle \sum _{\mathit{s}\in \mathit{S}}}{\mathit{\pi }}_{\mathit{s}}=\mathbf{1}(3)$

${\mathit{\pi }}_{\mathit{s}}\ge \mathbf{0},\mathit{s}=\mathbf{1},\dots ,\mathit{S}(4)$

Equation 1 sets the limits of the overall uncertainty of the probability distribution while Eq. 2 sets the limits on the maximum probability uncertainty (Zhao and Guan, 2016). Eqs. 3-4 denotes the basic properties of discrete probabilities.

3.2 Optimization model of prosumer aggregator

3.2.1 Objective function

The upper-level problem aims to minimize operating cost under the worst-case scenario probability distribution, which comprises two terms. The first term represents the cost of purchasing energy while the second term corresponds to the revenue from providing the FRP, encompassing both upward FPR and downward FRP, respectively.

$\mathit{m}\mathit{i}\mathit{n}\mathit{m}\mathit{a}\mathit{x}∆\mathit{t}{\displaystyle \sum _{\mathit{s}\in \mathit{S}}}{\mathit{\pi }}_{\mathit{s}}{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{\lambda }}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{l}\mathit{m}\mathit{p},\mathit{p}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}-\left({\mathit{\lambda }}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{l}\mathit{m}\mathit{p},\mathit{u}}{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}+{\mathit{\lambda }}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{l}\mathit{m}\mathit{p},\mathit{d}}{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\right)(5)$

3.2.2 Operational constraints of prosumer

The energy management problem within the prosumer could be deal with the portfolio model previously reviewed, which is outside the scope of this paper. Therefore, the virtual battery model is used here to represent the prosumer flexibility, referring to the authors’ previous work (Hou et al., 2019; Hu et al., 2019; Wu et al., 2019).

${\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}\le {\overline{\mathit{p}}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}(6)$

${\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}-{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}\ge \mathbf{0}(7)$

${\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}+{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}\le {\overline{\mathit{p}}}_{\mathit{i}}^{\mathit{v}\mathit{b}}(8)$

${\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}},{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}},{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\ge \mathbf{0}(9)$

${\mathit{e}}_{\mathit{s},\mathit{i},\mathit{t}+\mathbf{1}}^{\mathit{v}\mathit{b}}={\mathit{e}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}+{\mathit{\eta }}^{\mathit{c}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}∆\mathit{t}(10)$

${\overline{\mathit{e}}}_{\mathit{i}}^{\mathit{v}\mathit{b}}-{\mathit{e}}_{\mathit{s},\mathit{i},\mathit{t}+\mathbf{1}}^{\mathit{v}\mathit{b}}\ge {\mathit{\eta }}^{\mathit{c}}{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}∆\mathit{t}(11)$

${\mathit{e}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}\le {\overline{\mathit{e}}}_{\mathit{i}}^{\mathit{v}\mathit{b}}(12)$

${\mathit{e}}_{\mathit{i}}^{\mathit{v}\mathit{b},\mathit{i}\mathit{n}\mathit{i}}={\mathit{e}}_{\mathit{s},\mathit{i},\mathbf{1}}^{\mathit{v}\mathit{b}}(13)$

${\mathit{e}}_{\mathit{i}}^{\mathit{v}\mathit{b},\mathit{e}\mathit{x}}={\mathit{e}}_{\mathit{s},\mathit{i},\mathit{T}}^{\mathit{v}\mathit{b}}(14)$

The amount of energy and FRP of each prosumer is limited using Eqs.6–14. Eqs. 10–14 demonstrate the dynamic behavior of prosumer at each time step, which depends on the amount of stored energy in the previous time step.

3.3 Optimization model of DNO

3.3.1 Objective function

The lower-level problem aims to minimize the operating costs of the DNO and represents the energy and FRP clearing out within the distribution network, as described in Eq.15. The first term in Eq.15 represents the cost of energy purchased by the DNO from the retail market to maintain power balance within the distribution system. The second term corresponds to the revenue from providing FRP to the market by the DNO, which is determined by the quantities offered from DRE and the prosumers.

$\mathit{min}∆\mathit{t}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{\gamma }}_{\mathit{t}}^{\mathit{p}}{\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}}-\left({\mathit{\gamma }}_{\mathit{t}}^{\mathit{u}}{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{u}}+{\mathit{\gamma }}_{\mathit{t}}^{\mathit{d}}{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{d}}\right)(15)$

${\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{u}}={\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}+{\displaystyle \sum _{\mathit{j}\in \mathit{J}}}{\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}:{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{u}}(16)$

${\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{d}}={\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}+{\displaystyle \sum _{\mathit{j}\in \mathit{J}}}{\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}:{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{d}}(17)$

Where ${\mathit{\gamma }}_{\mathit{t}}^p$ is the day-ahead energy price in the retail market, ${\mathit{\gamma }}_{\mathit{t}}^{\mathit{u}}$ and ${\mathit{\gamma }}_{\mathit{t}}^{\mathit{d}}$ are the upward and downward FRP price. The right-hand side of Eqs. 16, 17 denote the dual multiplier variables of the constraints. The expressions of the same form in the later section carry the same meaning as described here.

3.3.2 Operational constraints of PV

The selection of distributed PV as the representative DRE here is motivated by its widespread prevalence and common usage. Other DRE operational models can be extended on this basis easily.

${\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}\le {\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{f}\mathit{o}\mathit{r}\mathit{e}}:{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{p}+}(18)$

${\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}\le {\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}:{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{d}+}(19)$

${\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}+{\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}\le {\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{f}\mathit{o}\mathit{r}\mathit{r}}:{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}+}(20)$

${\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}},{\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}},{\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}\ge \mathbf{0}:{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{p}-},{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}-},{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{d}-}(21)$

Eqs. 18–21 represent that the DRE providing energy and FRP within the forecasting power limits of the operating.

3.3.3 Network secure constraints

Inspired by the literature (Yuan et al., 2018), this paper proposes an extended linearized ACOPF model which can simultaneously optimize the system cost of providing energy and FRP.

${\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}}+{\displaystyle \sum _{\mathit{j}\in \mathit{J}}}{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}-{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}-{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{p}}_{\mathit{b},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}-{\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{s}\mathit{s}}=\mathbf{0}:{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{p}}(22)$

${\underset{\_}{\mathit{p}}}^{\mathit{d}\mathit{s}\mathit{o}}\le {\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}}\le {\overline{\mathit{p}}}^{dso}:{\mathit{\mu }}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{p}-},{\mathit{\mu }}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{p}+}(23)$

${\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{s}\mathit{s}}\approx {\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{s}\mathit{s}*}-{\displaystyle \sum _{\mathit{j}\mathit{ϵ}\mathit{J}}}{\mathit{z}}_{\mathit{j}}^{\mathit{d}}\left({\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}-{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}*}\right)+{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{z}}_{\mathit{i}}^{\mathit{d}}\left({\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}-{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}*}\right)(24)$

Eq. 22 represents the energy balance at system-level. Eq. 23 shows the acceptable range of exchanging power between the DNO and grid. Eq. 24 represents the linearized expression of distribution network losses, where the matrix $z^d$ is the partial derivatives of bus power of the distribution network with respect to the losses (Yuan et al., 2018).

${\mathit{p}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{n}\mathit{e}\mathit{t}}={\mathit{p}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v}}-{\mathit{p}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b}}-{\mathit{p}}_{\mathit{w},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}(25)$

${\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}={\mathit{\nu }}_{\mathbf{1}}+{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{b}}^{\mathit{p}}{\mathit{p}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{n}\mathit{e}\mathit{t}}-{\displaystyle \sum _{\mathit{i}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{i}}^{\mathit{q}}{\mathit{q}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}(26)$

$\underset{\_}{\mathit{\nu }}\le {\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}\le \overline{\mathit{\nu }}:{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}-},{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}+}(27)$

$\underset{\_}{\mathit{\nu }}\le {\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}+{\displaystyle \sum _{w\in B}}{\mathit{z}}_{\mathit{b},\mathit{w}}^{\mathit{p}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}\right)\le \overline{\mathit{\nu }}:{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-},{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}(28)$

$\underset{\_}{\mathit{\nu }}\le {\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}-{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{w}}^{\mathit{p}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\right)\le \overline{\mathit{\nu }}:{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-},{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}(29)$

Eqs. 25–27 represent the maximum and the minimum permissible voltage magnitude of each bus. Eqs. 28, and 29 define the allowable operating range of voltage magnitude after the delivery of FRP, where the matrix $z^p$ and $z^q$ are the partial derivatives of active power and reactive power each bus respect to voltage magnitude respectively (Yuan et al., 2018).

${\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}\approx {\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}*}-{\displaystyle \sum _{\mathit{j}\in \mathit{J}}}{\mathit{z}}_{\mathit{j}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}-{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}*}\right)+{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}}-{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}*}\right)(30)$

${\underset{\_}{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}\le {\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}\le {\overline{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}:{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}-},{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}+}(31)$

${\underset{\_}{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}\le {\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}-{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{w}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}\right)\le {\overline{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}:{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}-},{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}+}(32)$

${\underset{\_}{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}\le {\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}+{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{w}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\right)\le {\underset{\_}{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}:{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}-},{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}+}(33)$

Eqs. 30, and 31 represent the operating boundary of the branch power flow. Eqs. 32, and 33 define the allowable operating range of branch power flow after the delivery of FRP, where the matrix $z^{l_k}$ is the partial derivatives of active power each bust respect to branch flow (Yuan et al., 2018).

3.4 Solution methodology

3.4.1 KKT conditions

The first-order optimality condition on the lower-level decision variable ${\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}},{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{u}},{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{d}},{{\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{p}\mathit{v}},\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}},{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{d}}$ are sequentially presented in Eqs. 34–39.

${\mathit{\gamma }}_{\mathit{t}}^{\mathit{p}}+{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{p}}-{\mathit{\mu }}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{p},\mathit{p}-}+{\mathit{\mu }}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}.\mathit{p}+}=\mathbf{0}(34)$

$-{\mathit{\gamma }}_{\mathit{t}}^{\mathit{u}}+{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{u}}=\mathbf{0}(35)$

$-{\mathit{\gamma }}_{\mathit{t}}^{\mathit{d}}+{\mathit{\lambda }}_{\mathit{t}}^{\mathit{d}}=\mathbf{0}(36)$

${\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{p}+}-{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{d}+}+{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}+}-{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{p}-}+{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{p}}\left(\mathbf{1}+{\mathit{z}}_{\mathit{j}}^{\mathit{p}}\right)$

$+\left.{\displaystyle \sum _{\mathit{ϵ}}}{\mathit{z}}_{\mathit{b},\mathit{j}}^{\mathit{p}}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}+}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}+}\right)$

$+{\displaystyle \sum _{\mathit{ϵ}}}{\mathit{z}}_{\mathit{j}}^{{\mathit{l}}_{\mathit{k}}}\left(-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}+}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}+}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}+}\right)=\mathbf{0}(37)$

${\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}+}\left.-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}-}-{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{u}}+{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{j}}^{\mathit{p}}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}+}\right)$

$+{\displaystyle \sum _{\mathit{k}\in \mathit{K}}}{\mathit{z}}_{\mathit{j}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}-}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}+}\right)=\mathbf{0}(38)$

${\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{d}+}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}+}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{d}-}-{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{d}}+{\displaystyle \sum _{\mathit{b}\mathit{ϵ}\mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{j}}^{\mathit{p}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}\right)$

$+{\displaystyle \sum _{\mathit{ϵ}}}{\mathit{z}}_{\mathit{j}}^{{\mathit{l}}_{\mathit{k}}}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}+}=\mathbf{0}(39)$

The resulting complementary conditions Eqs 40–59 are non-linear equations, but they can be linearized using the Big-M method.

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{p}+}\perp {\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{f}\mathit{o}\mathit{r}\mathit{e}}-{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}\ge \mathbf{0}(40)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{d}+}\perp {\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}-{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}\ge \mathbf{0}(41)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}+}\perp {\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}+\mathbf{1}}^{\mathit{p}\mathit{v},\mathit{f}\mathit{o}\mathit{r}\mathit{e}}-{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}-{\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}+{\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}\ge \mathbf{0}(42)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{p}-}\perp {\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}}\ge \mathbf{0}(43)$

$\mathbf{0}\ge {\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}-}\perp {\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}\le \mathbf{0}(44)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{d}-}\perp {\mathit{r}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}\ge \mathbf{0}(45)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{p}-}\perp {\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}}-{\underset{\_}{\mathit{p}}}^{\mathit{d}\mathit{s}\mathit{o}}\ge \mathbf{0}(46)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{p}+}\perp {\overline{\mathit{p}}}^{\mathit{d}\mathit{s}\mathit{o}}-{\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}}\ge \mathbf{0}(47)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}-}\perp {\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}-\underset{\_}{\mathit{\nu }}\ge \mathbf{0}(48)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}+}\perp \overline{\mathit{\nu }}-{\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}\ge \mathbf{0}(49)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-}\perp {\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}+{\displaystyle \sum _{\in }}{\mathit{z}}_{\mathit{z},\mathit{w}}^{\mathit{p}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}\right)-\underset{\_}{\mathit{\nu }}\ge \mathbf{0}(50)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}+}\perp \overline{\mathit{\nu }}-{\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}-{\displaystyle \sum _{\in }}{\mathit{z}}_{\mathit{z},\mathit{w}}^{\mathit{p}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}\right)\ge \mathbf{0}(51)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-}\perp {\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}-{\displaystyle \sum _{\in }}{\mathit{z}}_{\mathit{z},\mathit{w}}^{\mathit{p}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\right)-\underset{\_}{\mathit{\nu }}\ge \mathbf{0}(52)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}\perp \overline{\mathit{\nu }}-{\mathit{\nu }}_{\mathit{s},\mathit{b},\mathit{t}}+{\displaystyle \sum _{\in }}{\mathit{z}}_{\mathit{z},\mathit{w}}^{\mathit{p}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\right)\ge \mathbf{0}(53)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}-}\perp {\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}-{\underset{\_}{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}\ge \mathbf{0}(54)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}+}\perp {\mathit{p}}^{{\mathit{l}}_{\mathit{k}}}-{\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}\ge \mathbf{0}(55)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}-}\perp {\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}-{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{w}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}\right)-{\underset{\_}{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}\ge \mathbf{0}(56)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}+}\perp {\overline{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}-{\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}+{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{w}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{u}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}\right)\ge \mathbf{0}(57)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}-}\perp {\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}+{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{w}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\right)-{\underset{\_}{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}\ge \mathbf{0}(58)$

$\mathbf{0}\le {\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}+}\perp {\overline{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}-{\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}-{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{w}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{d}}+{\mathit{r}}_{\mathit{s},\mathit{w},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\right)\ge \mathbf{0}(59)$

3.4.2 Strong duality property

The lower-level model is formulated as a linear programming problem thus exhibits strong duality property. Eqs. 60, 61 refers to the strong duality condition corresponding to lower-level problem under each scenario.

$\begin{array}{ll}\hfill {\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{\gamma }}_{\mathit{t}}^{\mathit{p}}{\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}}-{\mathit{\gamma }}_{\mathit{t}}^{\mathit{u}}{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{u}}-{\mathit{\gamma }}_{\mathit{t}}^{\mathit{d}}{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{d}}& ={\displaystyle \sum _{\in }}[{\displaystyle \sum _{\in }}\left[{-\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{p}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v},\mathit{b}}\left(\mathbf{1}+{\mathit{z}}_{\mathit{i}}^{\mathit{d}}\right)-{\displaystyle \sum _{\in }}\left({\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{u}}{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}+{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{d}}{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}\right)\right]\hfill \\ \hfill & +{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v},\mathit{b}}{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{i}}^{\mathit{p}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}+}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}+}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}\right)\hfill \\ \hfill & +{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v},\mathit{b}}{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}\left(-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}+}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}+}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}+}\right)\hfill \\ \hfill & +{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{u}}{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{i}}^{\mathit{p}}\left(-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}+}\right)+{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}-}{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}+}\right)\hfill \\ \hfill & +{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b},\mathit{d}}{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{i}}^{\mathit{p}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}\right)+{\mathit{r}}_{\mathit{s},\mathit{i},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}-}{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}+}\right)]+\mathit{X}\hfill \end{array}(60)$

$\begin{array}{ll}\hfill \mathit{X}& ={\displaystyle \sum _{\mathit{t}\in \mathit{T}}}[-{\displaystyle \sum _{\mathit{j}\in \mathit{J}}}\left({\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{p}+}{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{f}\mathit{o}\mathit{r}\mathit{e}}+{\mathit{\mu }}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{r}\mathit{u}+}{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v},\mathit{f}\mathit{o}\mathit{r}\mathit{e}}\right)+{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{p}}\left(-{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{p}}_{\mathit{b},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}-{\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{s}\mathit{s}*}-{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{z}}_{\mathit{i}}^{\mathit{d}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}*}+{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{z}}_{\mathit{i}}^{\mathit{d}}{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{v}\mathit{b}*}\right)\hfill \\ \hfill & +{\mathit{\mu }}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{p}-}{\underset{\_}{\mathit{p}}}^{\mathit{d}\mathit{s}\mathit{o}}-{\mathit{\mu }}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{p}+}{\overline{\mathit{p}}}^{\mathit{d}\mathit{s}\mathit{o}}+{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-}\right)\left(\underset{\_}{\mathit{\nu }}-{\mathit{\nu }}_{\mathbf{1}}+{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{w}}^{\mathit{p}}{\mathit{p}}_{\mathit{w},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}+{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{w}}^{\mathit{q}}{\mathit{p}}_{\mathit{w},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}\right)\hfill \\ \hfill & +{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}+}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{b}\mathit{u}+}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}\right)\left({\mathit{\nu }}_{\mathbf{1}}-{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{w}}^{\mathit{p}}{\mathit{p}}_{\mathit{w},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}-{\displaystyle \sum _{\mathit{w}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{w}}^{\mathit{q}}{\mathit{p}}_{\mathit{w},\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}-\overline{\mathit{\nu }}\right)\hfill \\ \hfill & +{\displaystyle \sum _{\mathit{k}\in \mathit{K}}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{p}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{r}\mathit{u}-}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{r}\mathit{d}-}\right)\left({\underset{\_}{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}-{\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}*}-{\displaystyle \sum _{\mathit{j}\in \mathit{J}}}{\mathit{z}}_{\mathit{j}}^{{\mathit{l}}_{\mathit{k}}}{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}*}+{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}*}\right)\hfill \\ \hfill & +{\displaystyle \sum _{\mathit{k}\in \mathit{K}}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{p}+}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{r}\mathit{u}+}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{r}\mathit{d}+}\right)\left({\mathit{p}}_{\mathit{s},\mathit{t}}^{{\mathit{l}}_{\mathit{k}}}+{\displaystyle \sum _{\mathit{j}\in \mathit{J}}}{\mathit{z}}_{\mathit{j}}^{{\mathit{l}}_{\mathit{k}}}{\mathit{p}}_{\mathit{s},\mathit{j},\mathit{t}}^{\mathit{p}\mathit{v}*}-{\displaystyle \sum _{\mathit{i}\in \mathit{N}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}{\mathit{p}}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{v}\mathit{b}*}-{\overline{\mathit{p}}}^{{\mathit{l}}_{\mathit{k}}}\right)]\hfill \end{array}(61)$

3.4.3 Linearized objective

The corresponding DLMP expressions can be obtained by taking partial derivatives of the Lagrangian function associated with the lower-level model, as shown by the following Eqs. 62–64.

${\mathit{\lambda }}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{i}\mathit{m}\mathit{p},\mathit{p}}=-{\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{p}}\left(\mathbf{1}+{\mathit{z}}_{\mathit{i}}^{\mathit{d}}\right)+{\displaystyle \sum _{\mathit{b}\in \mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{t}}^{\mathit{p}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v}+}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}+}+{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}\right)$

$+{\displaystyle \sum _{\mathit{k}\in \mathit{K}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}\left(-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{p}+}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}+}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}-}+{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}+}\right)(62)$

${\mathit{\lambda }}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{l}\mathit{m}\mathit{p},\mathit{u}}={\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{u}}-{\displaystyle \sum _{\mathit{b}\mathit{ϵ}\mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{j}}^{\mathit{p}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}+}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{u}-}\right)-{\displaystyle \sum _{\mathit{k}\mathit{ϵ}\mathit{K}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}-}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{u}+}\right)(63)$

${\mathit{\lambda }}_{\mathit{s},\mathit{i},\mathit{t}}^{\mathit{d}\mathit{l}\mathit{m}\mathit{p},\mathit{d}}={\mathit{\lambda }}_{\mathit{s},\mathit{t}}^{\mathit{d}}-{\displaystyle \sum _{\mathit{b}\mathit{ϵ}\mathit{B}}}{\mathit{z}}_{\mathit{b},\mathit{j}}^{\mathit{p}}\left({\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}-}-{\mathit{\mu }}_{\mathit{s},\mathit{b},\mathit{t}}^{\mathit{v},\mathit{r}\mathit{d}+}\right)-{\displaystyle \sum _{\mathit{k}\mathit{ϵ}\mathit{K}}}{\mathit{z}}_{\mathit{i}}^{{\mathit{l}}_{\mathit{k}}}\left({\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}+}-{\mathit{\mu }}_{\mathit{s},{\mathit{l}}_{\mathit{k}},\mathit{t}}^{\mathit{r}\mathit{d}-}\right)(64)$

Finally, the linear equivalent expression of the objective function Eq. 5 can be driven from the strong duality condition Eq. 60 and the DLMP expressions Eqs. 62–64. The linear objective function can be substituted by Eq. 5 is stated below:

$\mathit{m}\mathit{i}\mathit{n}\mathit{m}\mathit{a}\mathit{x}{\displaystyle \sum _{\mathit{s}}}{\mathit{\pi }}_{\mathit{s}}△\mathit{t}{\displaystyle \sum _{\mathit{t}}}{\mathit{\gamma }}_{\mathit{t}}^{\mathit{p}}{\mathit{p}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o}}-{\mathit{\gamma }}_{\mathit{t}}^{\mathit{u}}{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{u}}-{\mathit{\gamma }}_{\mathit{t}}^{\mathit{d}}{\mathit{r}}_{\mathit{s},\mathit{t}}^{\mathit{d}\mathit{s}\mathit{o},\mathit{d}}-\mathit{X}(65)$

4 Numerical studies

4.1 Input data

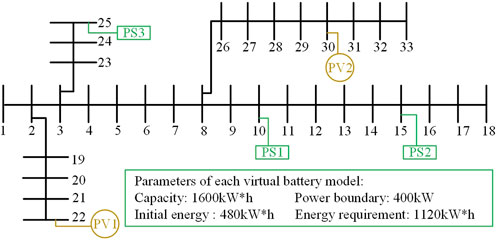
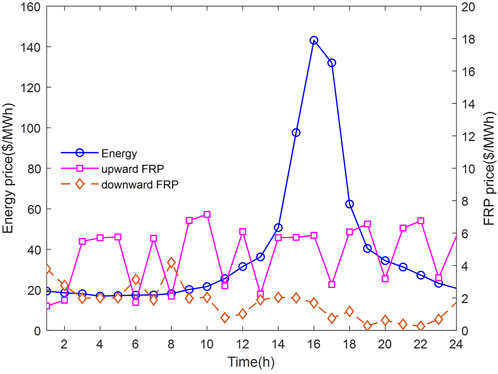
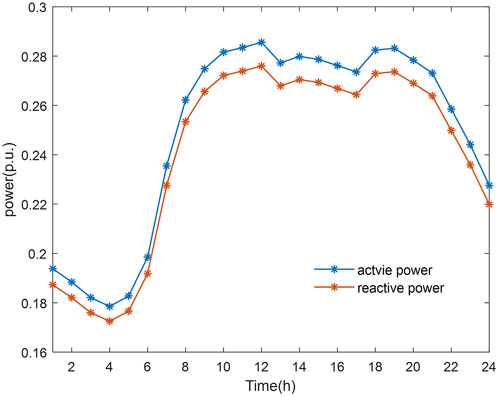
A modified IEEE-33 bus power system is employed to demonstrate the effectiveness of the proposed model. Figure 4 shows the specific access locations and capacities of the prosumers. The exchange power limit between the DNO and grid sets 5 MW. The simulation is presented in the form of per-unit value with a base value of 10 MW. The market prices for energy and FRP are displayed in Figure 5, derived from the case in the literature (Wang et al., 2017). The active and reactive loads demand of the distribution network is shown in Figure 6. All cases studies are performed on a PC with Inter Core 7 CPU (3.40 GHz) and 24.0 GB RAM with the commercial solver GUROBI 10.0.1 for MILP problems.

FIGURE 4

FIGURE 4. Topology of the modified IEEE 33 bus power system.

FIGURE 5

FIGURE 5. Energy, FRT market prices.

FIGURE 6

FIGURE 6. Load curve.

To demonstrate the effectiveness of the proposed model, two numerical case are designed here. In both cases, a total of 1,000 historical scenarios of PV’s output are utilized, and the mix-norm constraint is applied with a confidence level of 90%.

1) Case 1: Aggregator provide FRP without considering the security of the distribution network after FRP delivery.

2) Case 2: The proposed model.

To demonstrate the effectiveness of the data-driven model in adjusting offers conservativeness, two additional case are designed based on Case 2.

1) Case 3: The mix-norm constraint is applied with a confidence level of 80%.

2) Case 4: The mix-norm constraint is applied with a confidence level of 100%.

4.2 Distribution network security analysis

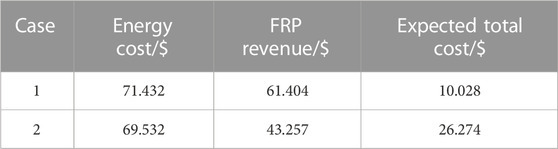
The energy-bidding and FRP-offering costs of the prosumer aggregator for different cases are shown in Table 1. Each type cost of Case 1 is better than that of Case 2. When comparing the energy costs of Case 1 and Case 2, it is clear that without considering the security constraint related to FRP delivery, the prosumer aggregator often prioritizes higher FRP benefit over energy costs. Obviously ignoring the security constraint related to FRP delivery will cause the prosumer flexibility value to be overestimated and affect the energy bidding decision.

TABLE 1

TABLE 1. Bid-offer decision of prosumer aggregator in case 1 and case 2.

The voltage magnitude of each bus for Case 1 and Case 2 at time slot 18:00 are shown in Figure 7. It can be seen that the voltage magnitude of bus 12–17 in case 1 violates the low bound after the delivery of the downward FRP. On the contrary, the voltage magnitude of each node in Case 2 remains within the safety boundary after the delivery of the downward FRP. In addition, it can be seen that the voltage magnitude boost is less in Case 2 than in Case 1 after delivering the upward FRP, because the quantity of FRP in Case 2 is less than that of Case 1.

FIGURE 7

FIGURE 7. Cases results of voltage magnitudes.

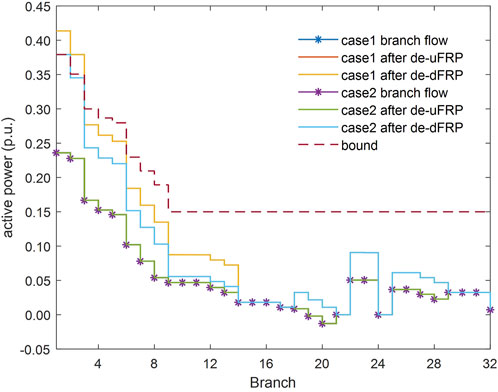
The power flow of each line of Case 1 and Case 2 in time slot 12:00 are shown in Figure 8. The congestion occurs in Case 1 after the delivery of downward FRP in line 1–3. On the contrary, there is no line occurring congestion after delivering the downward FRP. The power of each line does not change significantly in both cases after delivery of upward climbing because the quantity of upward FRP accounts for too small a proportion of the distribution network load demand.

FIGURE 8

FIGURE 8. Case results of line congestion.

The above analysis provides that the prosumer aggregator can offer FRP while enable distribution network security.

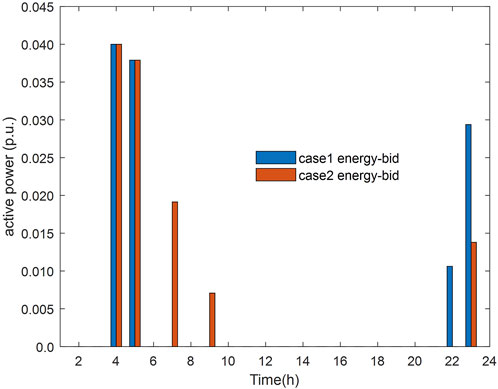
The full-time energy and FRP bidding/offering strategies of prosumer 2 in Case1 and Case2 are shown in Figure 9 and Figure 10, respectively. Comparing Figure 5 and Figure 6, it can be found that both energy and FRP cater better to the price and the peak-valley characteristics of the distribution grid load to minimize the operating cost. Case 2 purchases energy and offers downward FRP in periods 7 and 9, which differ significantly from Case1. Between the time periods 07:00–22:00, downward FRP of Case 2 is significantly less than that of Case 1, which is caused by the constraints related to post-delivery FRP.

FIGURE 9

FIGURE 9. Case results of energy-bid od prosumer 2.

FIGURE 10

FIGURE 10. Cases results of FRP-offer of prosumer 2.

4.3 Economic and conservative analysis

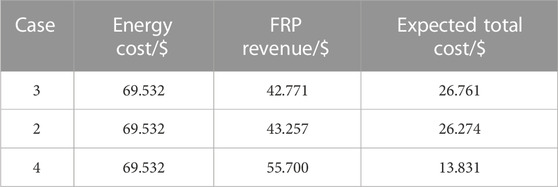
The costs of prosumer aggregator for Case3-4 are shown in Table 2. The expected total cost of the bidding/offering strategy increases with increasing confidence due to the consideration of greater distributional uncertainty, which makes the strategy more conservative and therefore less economical. It reflects the adjustment of the conservativeness of the strategy by the subjective risk-averse of the prosumer aggregator in the FRP-offer.

TABLE 2

TABLE 2. Bid-offer decision of prosumer aggregator in cases 2–4.

5 Conclusion

This paper addresses the problem of providing FRP by a prosumer aggregator within distribution network security. For this purpose, a data-driven bi-level stochastic optimization approach is proposed to model the process of active interaction between the prosumer and the DNO for decision making. The stochastic decision problem of adjustable conservativeness of the prosumer aggregator is solved by a data-driven scenario approach. The portfolio problem of the prosumer aggregator and the problem of security-constrained economic dispatch of the distribution network are solved in the upper-level and lower-level model, respectively.

The simulation results show that through the optimal scheduling of aggregator, prosumers can actively purchase energy from DNO and provide the upward and downward FRP, and ensure that the distribution network does not occur voltage violations and line congestion. The prosumer aggregator is able to take advantage of the peak-valley characteristics of prices and adjust the conservativeness of its decisions based on confidence levels. The reduction in FRP available to the prosumer due to distribution network security constraints leads to higher costs for the prosumer.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XA: Project administration, Supervision, Writing–review and editing. HH: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Validation, Writing–original draft, Writing–review and editing. JH: Funding acquisition, Project administration, Supervision, Writing–review and editing. ZW: Formal Analysis, Investigation, Writing–review and editing. KW: Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (52177080, 2021YFB4000104).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allahmoradi, S., Moghaddam, M., Bahramara, S., and Sheikhahmadi, P. (2021). Flexibility-constrained operation scheduling of active distribution networks. Int. J. Electr. Power & Energy Syst. 131, 107061. doi:10.1016/j.ijepes.2021.107061

CrossRef Full Text | Google Scholar

Bahramara, S., Sheikhahmadi, P., Mazza, A., and Chicco, G. (2022). Day-ahead self-scheduling from risk-averse microgrid operators to provide reserves and flexible ramping ancillary services. Int. J. Electr. Power & Energy Syst. 142, 108381. doi:10.1016/j.ijepes.2022.108381

CrossRef Full Text | Google Scholar

California Independent System Operator (2023). The net-demand trend. Available at: https://www.caiso.com/TodaysOutlook/Pages/default.aspx (Accessed June 23, 2023).

Google Scholar

Fang, X., Sedzro, k., Yuan, H., Ye, H., and Hodge, B. (2020). Deliverable flexible ramping products considering spatiotemporal correlation of wind generation and demand uncertainties. IEEE Trans. Power Syst. 35 (4), 2561–2574. doi:10.1109/TPWRS.2019.2958531

CrossRef Full Text | Google Scholar

Fu, X., Wu, X., Zhang, C., Fan, S., and Liu, N. (2023b). Planning of distributed renewable energy systems under uncertainty based on statistical machine learning. Prot. Control Mod. Power Syst. 7 (1), 41. doi:10.1186/s41601-022-00262-x

CrossRef Full Text | Google Scholar

Fu, X., Zhou, Y., Wei, Z., and Wang, Y. (2023a). Optimal operation strategy for a rural microgrid considering greenhouse load control. CSEE J. Power Energy Syst., 1–11. doi:10.17775/CSEEJPES.2022.06200

CrossRef Full Text | Google Scholar

Ghaemi, S., Salehi, J., and Moeini-Aghtaie, M. (2021a). Developing a market-oriented approach for supplying flexibility ramping products in a multimicrogrid distribution system. IEEE Trans. Industrial Inf. 17 (10), 6765–6775. doi:10.1109/TII.2020.3047600

CrossRef Full Text | Google Scholar

Ghaemi, S., Salehi, J., and Moeini-Aghtaie, M. (2021b). Estimating abilities of distributed energy resources in providing flexible ramp products for active distribution networks. Sustain. Cities Soc. 65, 102593. doi:10.1016/j.scs.2020.102593

CrossRef Full Text | Google Scholar

Gonzalez-Romera, E., Ruiz-Cortes, M., Milanes-Montero, M., Barrero-Gonzalez, F., Barrero-Gonzalez, E., Lopes, R., et al. (2019). Advantages of minimizing energy exchange instead of energy cost in prosumer microgrids. Energies 12 (4), 719. doi:10.3390/en12040719

CrossRef Full Text | Google Scholar

Hou, P., Hu, J., and Yang, G. (2019). Convex optimization of virtual storage system scheduling in market environment. J. Mod. Power Syst. Clean Energy 7 (6), 1744–1748. doi:10.1007/s40565-019-0548-z

CrossRef Full Text | Google Scholar

Hu, J., Sarker, M., Wang, J., Wen, F., and Liu, W. (2018). Provision of flexible ramping product by battery energy storage in day-ahead energy and reserve markets. IET Generation, Transm. Distribution 12 (10), 2256–2264. doi:10.1049/iet-gtd.2017.1522

CrossRef Full Text | Google Scholar

Hu, J., Yang, G., Ziras, C., and Kok, K. (2019). Aggregator operation in the balancing market through network-constrained transactive energy. IEEE Trans. Power Syst. 34 (5), 4071–4080. doi:10.1109/TPWRS.2018.2874255

CrossRef Full Text | Google Scholar

Huang, Z., Fang, B., and Deng, J. (2020). Multi-objective optimization strategy for distribution network considering V2G-enabled electric vehicles in building integrated energy system. Prot. Control Mod. Power Sysyem 5 (1), 7. doi:10.1186/s41601-020-0154-0

CrossRef Full Text | Google Scholar

Khoshjahan, M., and Kezunovic, M. (2022). Robust bidding strategy for aggregation of distributed prosumers in flexiramp market. Electr. Power Syst. Res. 209, 107994. doi:10.1016/j.epsr.2022.107994

CrossRef Full Text | Google Scholar

Khoshjahan, M., Moeini-Aghtaie, M., Fotuhi-Firuzabad, M., Dehghanian, P., and Mazaheri, H. (2020). Advanced bidding strategy for participation of energy storage systems in joint energy and flexible ramping product market. IET Generation, Transm. Distribution 14 (22), 5202–5210. doi:10.1049/iet-gtd.2020.0224

CrossRef Full Text | Google Scholar

Kim, D., Kwon, K., and Kim, M. (2021). Application of flexible ramping products with allocation rates in microgrid utilizing electric vehicles. Int. J. Electr. Power & Energy Syst. 133, 107340. doi:10.1016/j.ijepes.2021.107340

CrossRef Full Text | Google Scholar

Kubli, M., Loock, M., and Wuestenhagen, R. (2018). The flexible prosumer: measuring the willingness to co-create distributed flexibility. Energy Policy 144, 540–548. doi:10.1016/j.enpol.2017.12.044

CrossRef Full Text | Google Scholar

Ma, G., Li, J., and Zhang, X. (2023). Energy storage capacity optimization for improving the autonomy of grid-connected microgrid. IEEE Trans. Smart Grid 14 (4), 2921–2933. doi:10.1109/TSG.2022.3233910

CrossRef Full Text | Google Scholar

Nizami, M., Hossain, M., Amin, B., and Fernandez, E. (2020). A residential energy management system with bi-level optimization-based bidding strategy for day-ahead bi-directional electricity trading. Appl. Energy 261, 114322. doi:10.1016/j.apenergy.2019.114322

CrossRef Full Text | Google Scholar

Olivella-Rosell, P., Lloret-Gallego, P., Munne-Collado, I., Villafafila-Robles, R., Sumper, A., Ottessen, S., et al. (2018). Local flexibility market design for aggregators providing multiple flexibility services at distribution network level. Energies 11 (4), 822. doi:10.3390/en11040822

CrossRef Full Text | Google Scholar

Shi, X., Xu, Y., Guo, Q., Sun, H., and Zhang, X. (2023). Day-Ahead Distributionally Robust Optimization-Based Scheduling for Distribution Systems With Electric Vehicles. Electr. Veh. 14 (4), 2837–2850. doi:10.1109/TSG.2022.3223332

CrossRef Full Text | Google Scholar

Wang, J., Zhong, H., Tang, W., Rajagopal, R., Xia, Q., Kang, C., et al. (2017). Optimal bidding strategy for microgrids in joint energy and ancillary service markets considering flexible ramping products. Appl. Energy 205, 294–303. doi:10.1016/j.apenergy.2017.07.047

CrossRef Full Text | Google Scholar

Wang, Q., and Hodge, B. (2017). Enhancing power system operational flexibility with flexible ramping products: A review. IEEE Trans. Industrial Inf. 13 (4), 1652–1664. doi:10.1109/TII.2016.2637879

CrossRef Full Text | Google Scholar

Wu, J., Hu, J., Ai, X., Zhang, Z., and Hu, H. (2019). Multi-time scale energy management of electric vehicle model-based prosumers by using virtual battery model. Appl. Energy 251, 113312. doi:10.1016/j.apenergy.2019.113312

CrossRef Full Text | Google Scholar

Xu, X., Li, Y., Ma, H., and Shahidehpour, M. (2023). Hierarchical Central-Local Inverter-Based Voltage Control in Distribution Networks Considering Stochastic PV Power Admissible Range. Stoch. p. v. Power Admissible Range 14 (3), 1868–1879. doi:10.1109/TSG.2022.3213776

CrossRef Full Text | Google Scholar

Yamujala, S., Jain, A., Sreekumar, S., Bhakar, R., and Mathur, J. (2022). Enhancing power systems operational flexibility with ramp products from flexible resources. Electr. Power Syst. Res. 202, 107599. doi:10.1016/j.epsr.2021.107599

CrossRef Full Text | Google Scholar

Yuan, H., Li, F., Wei, Y., and Zhu, J. (2018). Novel linearized power flow and linearized OPF models for active distribution networks with application in distribution LMP. IEEE Trans. Smart Grid 9 (1), 438–448. doi:10.1109/TSG.2016.2594814

CrossRef Full Text | Google Scholar

Zhang, M., Zhou, M., Wu, Z., Yang, H., and Li, G. (2022). A ramp capability-aware scheduling strategy for integrated electricity-gas systems. Energy 241, 122813. doi:10.1016/j.energy.2021.122813

CrossRef Full Text | Google Scholar

Zhang, X., Hu, J., Wang, H., Wang, G., Chan, K., and Qiu, J. (2020). Electric vehicle participated electricity market model considering flexible ramping product provisions. IEEE Trans. Industry Appl. 56 (5), 5868–5879. doi:10.1109/TIA.2020.2995560

CrossRef Full Text | Google Scholar

Zhao, C., and Guan, Y. (2016). Data-driven stochastic unit commitment for integrating wind generation. IEEE Trans. Power Syst. 31 (4), 2587–2596. doi:10.1109/TPWRS.2015.2477311

CrossRef Full Text | Google Scholar

Zhu, X., Zeng, B., Dong, H., and Liu, J. (2020). An interval-prediction based robust optimization approach for energy-hub operation scheduling considering flexible ramping products. Energy 194, 116821. doi:10.1016/j.energy.2019.116821

CrossRef Full Text | Google Scholar

Nomenclature