Process models and model-data fusion in dendroecology

1. Introduction

Relationships between tree-ring proxies (width, density, isotopes) and climate have usually been estimated with statistical approaches (Fritts, 1976; Cook and Kairiukstis, 1990). More or less complex statistical relationships have been calibrated to large datasets either to understand the response of the proxy to climatic changes or to reconstruct past climates. In both cases, these statistical approaches often reduce the problem to linear relationships; they assume that there were no major changes in the tree environment other than the climatic factors considered; finally they consider the underlying processes as a black box. Process-based models developed for tree-growth (Fritts et al., 1991; Berninger et al., 2004; Misson, 2004; Rathgeber et al., 2005; Anchukaitis et al., 2006) and isotope fractionation (Danis et al., 2012) studies give an opportunity to go beyond these limitations. Used in a forward mode, process-based models are driven by climate and other environmental factors (such as CO₂ concentration, nutrient availability and soil moisture) (Gaucherel et al., 2008b), they can take into account competition between individual, and they enable one to better understand the functioning of the trees and the effect of the interaction of different environmental forcings. In an inverse mode, climate information can be extracted by relaxing the above-mentioned constraints (Boucher et al., 2014).

After a rapid overview of the models used or potentially useable in dendroecology, we succinctly present the approaches of Model-Data Fusion (MDF). We then present different ways to merge data with these models depending on the objective, basically calibration of parameters or inversion to estimate input data such as climate. We conclude with the possibilities offered by data assimilation.

2. Tree-Growth Process Models

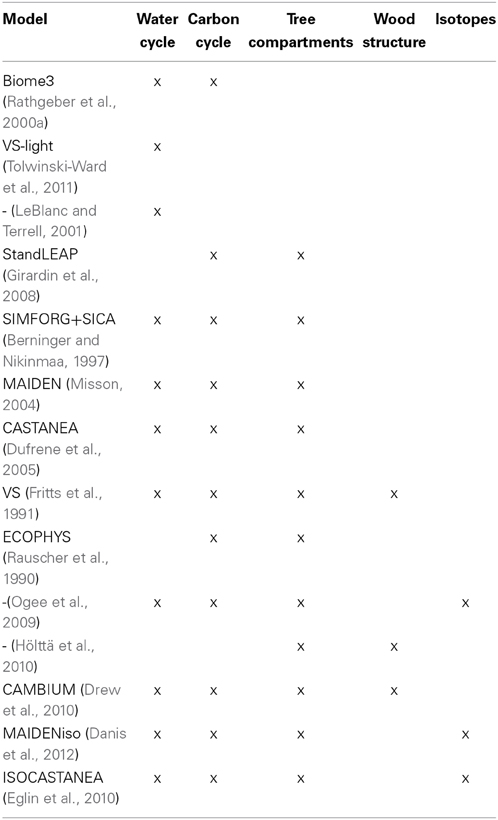
Growth models usually assume that the growth of forests is ultimately limited by the capacity of trees to photosynthesize and acquire nutrients to maintain growth. These models are here roughly classified in four categories related to the processes taken into account (Table 1). (Rathgeber et al., 2000a) used dendroecological data with a biogeochemistry model (BIOME3, Haxeltine and Prentice, 1996) to provide a realistic evaluation of the impact of global change on the productivity of forest stands. By using BIOME3, they applied a global model at a local scale. In such an approach, the spatial and temporal scales at which some vegetative processes were mathematically described did not correspond to the scales at which the data were acquired. This scale issue is overcome by other carbon-based models that take into account tree-growth processes in varying detail and degrees of complexity: (Federer et al., 1989; Fritts et al., 1991; LeBlanc and Foster, 1992; Foster and Leblanc, 1993; Medlyn et al., 1999; Roux et al., 2001; Berninger et al., 2004; Girardin et al., 2008). In their review, (Roux et al., 2001) raised two critical issues for tree-growth models that call for the development and testing of original modeling schemes: the representation of carbon allocation, storage and remobilization. These linked processes possibly explain why the stem growth of trees is often linked from 1 year to the next, producing autocorrelation in tree-ring series (Desplanque et al., 1998; Berninger et al., 2004). The model of (Misson et al., 2004), i.e., MAIDEN, is particularly well adapted to reproduce these temporal correlations.

TABLE 1

Table 1. Rough classification of the models cited according to the main processes included.

A simplified approach is provided by models representing the water cycle where tree-growth is correlated with soil moisture (LeBlanc and Terrell, 2001) or where soil moisture is combined with temperature and light through the most limiting factor principle (Tolwinski-Ward et al., 2011). Bioclimatic models (Rathgeber et al., 2005), in which tree-growth is correlated with several climatic variables assumed to drive tree-growth (e.g., soil moisture, chilly temperature, growing season temperature) are of the same type. They are not really ecophysiological models, as important ecophysiological processes such as photosynthesis, respiration and cell multiplication are not implemented. These models can be useful when applied on a large scale where the inclusion of a large number of species and biotopes makes it difficult to apply higher order models.

True ecophysiological models try to represent the interaction between the carbon and the water cycles in the tree (see columns 2 and 3 in Table 1). Several phases in the tree growth are distinguished according to the phenology, from no activity in winter to leaf and root expansion in spring, biomass production in summer, carbohydrate reserve accumulation at the beginning of autumn and leaf and root senescence during late autumn. Photosynthesis and stomatal conductance are often based on the Farquhar biochemical model (Farquhar et al., 1980). Daily temperatures and precipitation drive the estimates of photosynthetic production, respiration and carbon allocation in four compartments (leaf, bole, root and storage) (see column 4 in Table 1). The water cycle includes transpiration, interception, soil evaporation, drainage and runoff. All these processes are explicitly represented in MAIDEN (Misson, 2004), but also in various models such as VS (Fritts et al., 1991), CASTANEA (Davi et al., 2005; Dufrene et al., 2005), ECOPHYS (Rauscher et al., 1990) or SIMFORG (Berninger and Nikinmaa, 1997). The final output of these models is generally tree productivity but other physiological proxies such as those reflected by cellulose isotopic composition are also simulated by some of these models (column 6 in Table 1, Panek and Waring, 1997; Ogee et al., 2009; Eglin et al., 2010; Danis et al., 2012).

These models are used to project the impact of climatic changes on forests, but they are far from being perfect, in particular when management practices and non-climatic factors must be taken into account. Several processes are not yet included, e.g., the mortality of trees and associated stand dynamics, as in Pedersen (1998) or Bigler and Bugmann (2004). They often assume monospecific forests. Disturbances by insects (Hogg, 1999) or fires (Covington et al., 2001) are not explicitly included. Nutrient availability, which may limit tree productivity, or the influence of hydraulics on the tree performance, are other gaps in several models. Most of them (e.g., Pietsch and Hasenauer, 2002) predict an increase in biomass production proportional to photosynthesis production and then to CO₂ assimilation (Rathgeber et al., 2003; Gaucherel et al., 2008b). The results of Berninger et al. (2004) show that, although photosynthesis increases in response to increasing CO₂ concentrations, tree growth rate cannot parallel the increase in photosynthesis because the potential growth rate is limited directly by temperature through nitrogen mineralization. The apparent fertilization effect of the models, related to water use efficiency (WUE) enhancement, itself due to a decrease in stomatal area, has not been observed in experimental chambers or in tree-ring series (Gedalof and Berg, 2010; Silva and Horwath, 2013). There is therefore much controversy as to whether the increase in CO₂ since the beginning of the industrial period has enhanced growth, with much recent evidence reporting changes in plant physiological processes but not in growth (Huang et al., 2007; Andreu-Hayles et al., 2011; Peñuelas et al., 2011; Girardin et al., 2012; Lévesque et al., 2014). Experiments are often done on young trees while the CO₂ effect is a long term process which cannot be easily investigated by short-term experiments (Medlyn et al., 1999). Even when these experiments are done on old trees (30 years old for Alpine conifers, Handa et al., 2005), the duration of the experiments is necessarily limited in time (3 years in the FACE experiment (Handa et al., 2005). Even when an increased WUE is observed, it is not necessarily related to a tree-growth enhancement (Andreu-Hayles et al., 2011; Peñuelas et al., 2011). Nevertheless some studies have acknowledged that WUE enables a better resistance to drought (Linares and Camarero, 2012; Girardin et al., 2012) and thus a strong fertilization effect (Keenan et al., 2013).

Most models presented in the previous paragraphs simulate biomass production but not cell and wood composition. These processes cannot be ignored when we are interested in wood quality (Houllier et al., 1995). In dendrochronology, the Vaganov-Shashkin (VS) model (Fritts et al., 1991) was a pioneer in this domain. It simulates cambial activity as observed by the number of cells, their size, wall thickness and wood density. In this model, these processes at the level of the cell are described as a function of environmental conditions. (Hölttä et al., 2010) proposed a model where the processes of cell enlargement and cambium activity are related to the short-term carbon dynamics. The CAMBIUM model links productivity to cambium activity and tries to mimic the spatial distribution of the xylem cell structures (Downes et al., 2009; Drew et al., 2010). The first block of the standard VS model is the estimation of the growth rate related to photosynthesis production. The second block is the dynamics of cell growth. The first block has been recently simplified and called VS-light (Tolwinski-Ward et al., 2011): it has been reduced to a product of three limiting climatic factors, i.e., temperature, soil water balance and solar radiation, and is therefore no longer a true process model.

3. Model-Data Fusion Methods

Basically, model-data fusion (MDF) does not concern the huge field of standard statistical modeling which is based on the use of data to calibrate the parameters of a probabilistic model. MDF, in its present meaning, concerns complex process models and encompasses calibration, model inversion and data assimilation techniques (Evensen, 2004; Raupach et al., 2005; Tarantola, 2005).

The methods have been reviewed for ecological applications by Peng et al. (2011). They are used to improve the performance of a model by either optimizing/refining the values of unknown parameters and initial conditions or by improving the predictive capacity of a model by constraining the model by data. All the MDF methods reported in the literature have the following features: (i) a model is used to describe the temporal evolution of output variables; (ii) observations correlated with model outputs are available; (iii) an objective function is defined that combines model outputs and observations with any associated prior information and error structure; and (iv) optimization techniques are used to adjust forward model parameters or output variables to minimize the discrepancy between model estimates and observations. The general principle of MDF is a selection of model properties that minimizes the gap between model system representation and real systems based on observations and prior characteristics. An objective or cost function is then constructed to quantify the mismatch between model predictions and observations by also taking the model-data errors into account. Discovering optimal parameters can help to improve predictions or test alternative hypotheses embedded in models. A key feature of MDF schemes is how they incorporate information that pertains to uncertainty for both the model and the observations, providing a best estimate of the true state of a system. As this is also at the core of the Bayesian paradigm, recent approaches are increasingly using Bayesian statistics.

Any optimization technique can operate either on data batches (i.e., all the data available are processed in one batch) or sequential data (i.e., data are used sequentially to update the optimization). Variational data assimilation operates in a batch processing manner over a given time window that contains observational time points (Kalnay, 2003). The four-dimension variational method uses historical observations and requires computation of the adjoint model, i.e., a transformation of the model which makes it possible to go backwards in time (a forward model is used to go forwards in time).

One of the most popular examples of a sequential method is the Kalman filter (KF) (Kalman, 1960). KF is a recursive algorithm that estimates the state of a system at each iteration using a state-space model in combination with (noisy) measurements. The objective of KF is to reduce the influence of noise that occurs in measurements. It provides a convenient representation of model, data and parameter errors (Williams et al., 2005; Wang et al., 2009). KF has two distinct phases: the prediction phase and the updating phase. The prediction phase uses the state estimate from the previous time step to produce an estimate of the state at the current time step. For the updating phase, the current a priori prediction is combined with current observational data to refine the state estimate. The Ensemble Kalman filter (EnKF) is an extension of the traditional KF. EnKF is now used in ecology (Williams et al., 2005; Fox et al., 2009) to optimize model parameters (Quaife et al., 2008; Mo et al., 2008).

Bayesian statistics were conceptually introduced in paleoclimatology by Korhola et al. (2002) and Haslett et al. (2006), but without any reference to a mechanistic model and by Guiot et al. (2000) with a mechanistic model. The idea of the approach is to define an a priori distribution of the parameters (calibration) or the input variables (inversion) based on accumulated expert knowledge or on results obtained with independent data and to calculate their a posteriori distribution based on available data and model simulations. The objective is not to obtain the “best fit” estimations but to integrate the parameter or input variable space to obtain a robust estimation of their probability distribution. These approaches are based on intensive calculation algorithms. A popular type of such algorithms is known as the Monte Carlo Markov Chain (MCMC) algorithm. Let us consider a multi-dimensional mathematical space where each dimension represents a parameter or an input variable (depending on whether the objective is calibration or inversion). We define a vector of parameters as an element of this multi-dimensional climate space. Then the Metropolis-Hastings iterative algorithm is used to browse the climate space according to an acceptance-rejection rule (Metropolis et al., 1953; Hastings, 1970). The output of this algorithm is a path or chain of climate parameters describing the posterior distribution of climate parameters. In the domain of climate reconstruction, the approach is still not widely used (Wu et al., 2007, 2009).

3.1. Calibration and Prediction

All models, from the simplest to the most complex, contain parameters that are often set by knowledge of the underlying processes and/or from information contained in the literature. When this information is not available, it is necessary to directly estimate the parameters by fitting the model simulations to data. This is the calibration step of modeling. The choice of an applicable calibration technique is necessary for successful model parameter estimation. Techniques range in complexity from manual calibration to algorithms such as global optimization, MCMC and data assimilation techniques. Manual calibration consists in a user inspecting the performance from a model and comparing it to the observations in order to determine the best parameters (Misson, 2004). This method is often time-consuming and sometimes difficult to implement. Global optimization techniques, which attempt to find the most accurate set of parameters with respect to data, are more automatic. Optimization is achieved by maximum likelihood approaches where the model parameters are adjusted by maximizing a likelihood function depending on the data and model parameters. See for example the PEST method in hydrology (Doherty, 2003). This provides accurate, reproducible parameters for a model, but lacks the ability to take into account the uncertainties of the model and data. Bayesian methods are useful to circumvent this problem. MCMC offer the opportunity to estimate the (a posteriori) parameter distribution once the calibration has been done, starting from their predefined (a priori) statistical distributions (Gelman et al., 1995; Andrieu et al., 2001). Such approaches can nevertheless lead to unrealistic results, in the event of inappropriate a priori information or non-relevant parameter distribution extractions. To bypass this difficulty, other kinds of procedures such as Particle Filtering (PF) have been recently proposed on the basis of genetic algorithms (Doucet et al., 2001; Pelletier et al., 2006). Unlike MCMC approaches, the procedure still consists in going though the parameter-space, but with a high number of initial choices, called particles, that are defined by their parameter values (their coordinates).

We present here the comparison of three methods, namely the PEST, MCMC and PF algorithms (Gaucherel et al., 2008a,b), to estimate 11 parameters of the MAIDEN model (Misson, 2004). The study is applied to Pinus halepensis ring width and xylem density series and climatic series from the Aix-en-Provence and Istres weather stations, all from Southern France (Nicault, 1999; Rathgeber et al., 2000b). The process-based model MAIDEN uses daily precipitation, minimum and maximum temperatures as input and was implemented for the 1950–1994 period. The model output of interest is the biomass allocated to the tree bole which is assumed to be comparable to the annual increment index based on wood density and ring width. The 11 parameters were calibrated on the 1962–1994 period using the Aix-en-Provence data and verified on the independent 1950–1961 period using the Istres station. In fact, several parameters were calibrated with daily physiological measurements, but we focus here on the dendrochronological calibration.

Figure 1 shows the interest of having a method able to provide uncertainties on the parameters. Some parameters have a Gaussian shape, which indicates that the parameter has an optimum value with a reasonable uncertainty, but the others are not really sensitive as they have a uniform distribution over a large interval: this means that these parameters can have relatively different values without really changing the simulation of the bole biomass increment. The PEST optimum values, the MCMC and PF probability modes of the eleven parameters are used in MAIDEN to estimate the bole biomass increments which are compared to the measured values. Figure 2 compares the three estimated curves with the observed curve for both the calibration period and the verification period. The agreement between the three methods and the observations is good, except for the 1956-1958 interval. In fact February 1956 was extremely cold and this seriously injured the trees which took 3 years to recover. This process is not included in the model so the 1956-1958 interval has been removed from the verification. The PEST optimization gives a r² = 0.46. This optimum fit is in good agreement with the MCMC final fit distribution, as the maximum MCMC fit value reached is r² = 0.52, while its modal value is 0.37. PEST needed only 16 iterations to reach this value. For the PF algorithm, the final fit gives a r² = 0.25 ± 0.02 with 1000 particles, a fit lower than that for the other calibration techniques. When applied to independent meteorological data, the three calibration parameter sets lead to rather similar bole biomass increment variations. Residuals between the standardized final simulations and the observations over the 11 years of validation show that the MAIDEN model has difficulty in simulating some years: namely the freezing years 1956 and 1985 and following, the rainy year 1963 and years 1993–1994 (Figure 2). When considering the residuals between the three final bole increment series and the corresponding observations, it appears that MCMC and PEST present rather similar behavior, distinct from that of the PF algorithm.

FIGURE 1

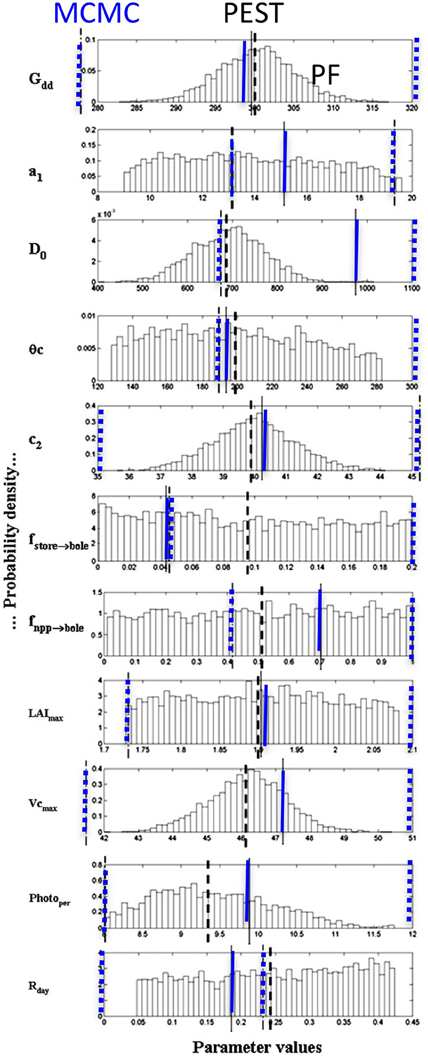
Figure 1. The eleven MAIDEN parameter probability distributions using the particle filter technique for Pinus halepensis. The heavy black dashed lines indicate the PEST optimum parameter value, the blue dashed lines indicate the 5 and 95% percentiles, while the blue continuous lines show the MCMC parameter modes for comparison. Meaning of the abbreviations: G_dd, Growing degree-days in C; a₁, Leuning factor, linking stomatal conductance and photosynthesis; D_o, coefficient linking the stomatal conductance and the humidity deficit at the leaf surface, in P_a; θ_c, Soil water stress parameter, in mm; c₂, Temperature function coefficient controlling the fraction of daily net primary production allocated to the store reservoir during fall; f_{fstore→bole} Fraction of carbon stored in the bole during summer; f_npp→bole, Fraction of net primary production of the tree bole during summer; LAI_max, Maximum Leaf Area Index of the site; VC_max, species maximum carboxylation capacity limited by Rubisco availability; Photo_per, Threshold of day-light duration necessary to trigger growth; R_day, Leaf dark respiration rate. Adapted from Gaucherel et al. (2008a).

FIGURE 2

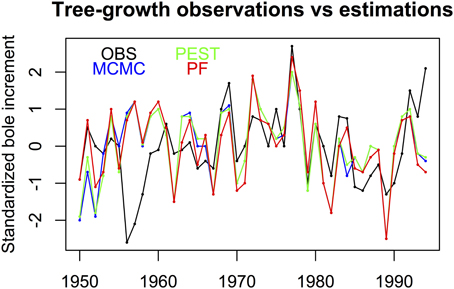
Figure 2. The Pinus halepensis bole biomass increments measured (mean earlywood density multiplied by earlywood width plus mean latewood density multiplied by latewood width) (Rathgeber et al., 2003) and simulated by MAIDEN, using three calibration methods (green PEST, blue MCMC, red PF); All the variables are standardized to be unitless. Adapted from Gaucherel et al. (2008a).

PEST is an extremely fast method, but its main disadvantage is that it does not provide any information on the uncertainty of the parameters. The main disadvantage of PF is that the particle number has to be high (from 10² to 10⁶) for the algorithm to be efficient, which is computationally costly. However PF has several advantages over MCMC and PEST (Gaucherel et al., 2008a): (i) it is easy to develop and to implement; (ii) it does not need any burning period (i.e., period necessary to reach equilibrium between inputs and outputs) nor parameter distribution filtering to calculate the a posteriori distributions; (iii) it can be parallelized; (iv) almost no tuning algorithm is necessary. As a sequential approach, the PF algorithm has the ability to indicate the highly constraining years, i.e., those which poorly fit simulations and observations. The final advantage of PF is that as it is based on the law of large numbers, it obtains smoother and more regular (Gaussian) parameter distributions, making it easier to analyze and interpret.

In a second step, using the parameter set obtained from MCMC, the model was applied to climate simulations provided by the ARPEGE climate model driven by the IPCC-B2 scenario (Gibelin and Deque, 2003) after statistical downscaling (Gaucherel et al., 2008b). The CO₂ atmospheric concentration has an influence on the climate and is taken into account by the climate model simulation, but it also has a direct effect through fertilization (already mentioned in section 2). Figure 3 shows the projection of Pinus halepensis growth for the next century with and without taking into account this fertilization effect (Gaucherel et al., 2008b). It appears clearly that ecophysiological models such as MAIDEN can be very sensitive to this effect. The main reason is that the model does not include any nutrient limiting factor, particularly to link the influence of nitrogen and photosynthetic capacity. Without the fertilization effect, tree growth will decrease because of lack of water (the precipitation deficit is amplified by more evapotranspiration), but if the latter effect is included, tree-growth will increase. As mentioned in the literature review in the introduction section, this fertilization effect is not always observed on living trees and is subject to controversy (Gedalof and Berg, 2010; Silva and Horwath, 2013).

FIGURE 3

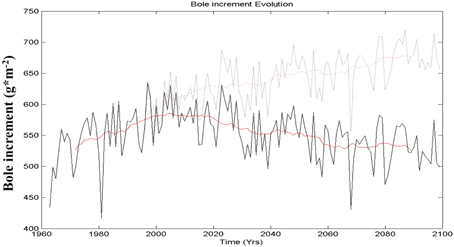
Figure 3. Evolution of the mean annual production of Pinus halepensis for southeast France simulated by MAIDEN on the basis of the ARPEGE B2 scenario, with (dark line) and without (dotted line) the fertilization effect of CO₂ (MCMC calibration). The black lines are the non smoothed values and the red lines are the smoothed values. Vertical axis represents bole annual increment in grams of carbon per square meter. Adapted from Gaucherel et al. (2008b).

3.2. Inversion and Reconstruction

Inverse modeling is a statistical method that can be used to estimate variables that are directly or indirectly related to the measured quantity. An inverse model differs from forward modeling in that it uses dependent variables (e.g., bole increment) to constrain input climate variables rather than using climate to predict dependent variable distributions. It is not an analytical inversion, but an iterative procedure which converges progressively toward the climate probability distribution compatible with the observations. The climatic space is randomly sampled to produce a large variety of climatic scenarios which are introduced in the vegetation model to simulate the corresponding vegetation composition and productivity. In dendroecological applications, the simulated bole increments from the process-based inversion are compared to the tree-ring data and those matching reasonably well are retained. These scenarios are used to build histograms, which are estimates of probability distribution functions of a climate able to generate such bole increments. This implies a measure of coherence between outputs of the model and tree-ring proxies.

Inversion of the model is done under the paradigm of the Bayesian theory (Robert and Casella, 1999). The main concepts used are prior and posterior probability distributions. The prior is the information, summarized in the form of a distribution, which is available before data analysis. The posterior is the information that will be deduced from the combination of data and the hierarchical model. In that respect, the hierarchical model is not restricted to the tree-growth model, but it is the function which relates the prior to the posterior. In statistical terms, it is the probability of climate C conditional to tree-ring data (Y). It is noted, according to Bayes' law:

$\begin{array}{ll}p(C\mid Y)\propto f(Y\mid C)p(C)\hfill & \left(1\right)\hfill \end{array}$

where p(C) is the prior distribution of climate C and f(Y | C) is the likelihood function of tree-ring variables given the climate (as provided by the model from the climate). The prior is an initial guess of the probability distribution of the climate. It can be given by the knowledge we have from modern climate variability or, if we work on periods that are very different from the present one, from the knowledge which has been accumulated in palaeclimatology. The distribution law is then a uniform law defined on the range so defined. The likelihood function is provided by comparing tree-growth model simulations given a large set of climate scenarios to observed tree-growth data.

The above-mentioned inversion approach has been developed in the context of a multi-proxy reconstruction in Fontainebleau forest, near Paris, France (Boucher et al., 2014). At this location, different tree-ring proxies (ring widths, carbon and oxygen stable isotopes) have been measured and their sensitivity to climate has been demonstrated (Etien et al., 2008). Furthermore, from the modeling perspective, MAIDENiso was successfully parametrized and developed (in the forward mode) for this specific site (Danis et al., 2012). Thus, running MAIDENiso in the inverse mode allowed (Boucher et al., 2014) to retrieve, for each year since 1850 AD, a probability distribution of climatic inputs. Additionally, since MAIDENiso equations are constrained not only by meteorological conditions, but also by atmospheric CO₂ concentrations (e.g., via stomatal conductance modeling), it was possible to isolate the contribution of CO₂ to the overall reconstruction, and to point out a possible divergence effect associated with a CO₂ enriched atmosphere since the beginning of the industrial era. The idea behind the inversion performed at Fontainebleau was quite simple. For each year in which proxies were measured (but where climate was not available), we modified a reference year to fit the tree ring proxies as well as possible. The reference year (here 1984) was chosen to be as similar as possible to an “average year.” The modification of the reference year was performed using the delta method. Deltas are additive (temperature) or multiplicative (precipitation) values that modify the reference year, producing alternative meteorological scenarios that are iteratively injected into MAIDENiso. It is precisely the posterior distribution for these deltas that needs to be found by the inversion algorithm, for each year of the reconstruction.

As a first step in the inversion, a uniform prior is set on both temperature and precipitation delta values (Figure 4). A uniform prior means that only the bounds of paleo-temperature [−5,5] and precipitation [0.25,2] variability are fixed and all the values have equal probability. In a second step, using the MCMC procedure, we iteratively modify the delta values (called proposals) within the bounds of the uniform distribution. Proposals are accepted if two main conditions are met: (1) the proposal must be within the bounds of the prior distribution, and (2) the proposal must result in some gain in simulation accuracy (here, measured by a simple Euclidian distance between simulations and observations). A negative gain is accepted if it is above a small negative threshold. Otherwise, the proposal is rejected. The MCMC algorithm stops when the chain reaches a stable state, meaning that the successive accepted proposals are not correlated with one another (stationarity). All the accepted proposals are used to build a posterior distribution that represents the range of possible delta values required to simulate tree rings that resemble real-world proxies.

FIGURE 4

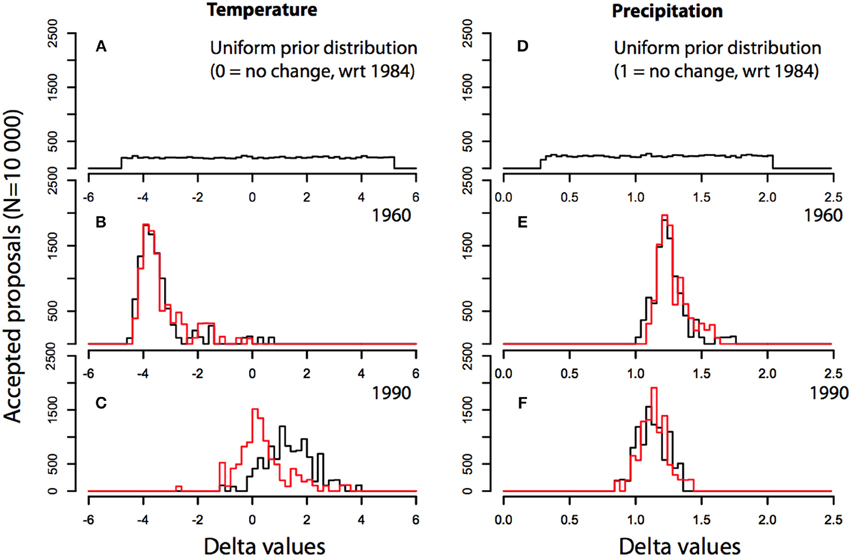
Figure 4. Prior and posterior distributions (N = 10 000 accepted proposals) of delta values for temperature (left) and precipitation (right). Deltas are additive (temperature) or multiplicative (precipitation) constants that are applied to the reference year (here 1984) to produce alternative meteorological scenarios that are iteratively injected in MAIDENiso, through the inversion algorithm. Prior distributions for temperature and precipitation are shown in the upper panels (A,D). Posterior distributions for temperature (B,C) and precipitation (E,F) are shown in the middle and lower panels, respectively. Black curves are posterior distributions obtained when the inversion is forced by realistic CO₂ data, while red curves are posterior distributions obtained when constrained by CO₂ levels fixed at pre-industrial levels (280 ppmv).

For each year of the reconstruction, delta posterior distributions differ because proxies, themselves, are different (Figures 4B,C). For example, the years 1960 and 1990 yield quite different summer temperature and precipitation estimates (black curves). Summer 1960 was relatively cold (median temperature delta = −3.4C) and wetter than normal (median precipitation delta = 1.35, i.e., +35%). In contrast, summer 1990 was warmer than normal (median temperature delta = 1.9C), while precipitation was close to average (median precipitation delta = 1.15, i.e., +15%). However, it is interesting to note that posterior distribution also changes depending on the CO₂ scenario used to constrain the inversion. In the preceding simulations, a realistic CO₂ scenario was used (Robertson et al., 2001), meaning that CO₂ variations are coherent with the increasing trend observed on the global scale [280 to 400 ppmv]. However, if CO₂ concentrations are fixed at preindustrial levels for the whole reconstruction period (1850–1999), then overall temperature reconstructions differ considerably in the low-frequency domain (red curves). This effect is partly visible on Figure 4C, where it is clear that the summer temperature reconstructed for year 1990 is colder by about 2C if pre-industrial CO₂ concentration (280 ppmv) is used instead of actual 1990 concentrations (370 ppmv). This difference becomes even more apparent when the full reconstructions are compared Figure 5. When pre-industrial CO₂ levels are used for the whole time period (red), a colder climate is reconstructed, and most importantly, the warming trend clearly observed in climatic records at Fontainebleau cannot be reproduced.

FIGURE 5

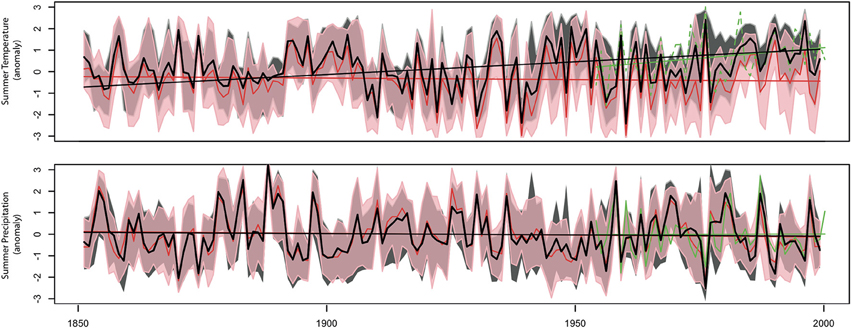
Figure 5. Summer temperature (A) and precipitation (B) reconstruction in Fontainebleau, France, obtained from the inversion of MAIDENiso. Black curves (and the associated 90% uncertainty range) are median reconstructed values obtained when the inversion is constrained by realistic CO₂ concentrations. The red curve (and the associated 90% confidence intervals) are median reconstructed values obtained when the inversion is forced by CO₂ concentrations fixed at pre-industrial levels (280 ppmv). The dashed green line represents observed climate series (1953–1999). Linear lines with corresponding colors were added to each series to evaluate linear trends in reconstructed and observed climates. Adapted from Boucher et al. (2014).

Although, as we have previously discussed, isolating the net effect of CO₂ on the forest response is likely to be more complex than the effect we modeled, our results suggest that CO₂ is an important driver for tree growth in Fontainebleau forest, and that the constraint of inversion with a realistic CO₂ scenario makes the reconstruction better converge toward observed climate variability. Abnormally low pre-industrial CO₂ concentrations force the model to compensate by too cold a climate. In the case of Fontainebleau forest, this compensation effect by a colder climate can be explained by links and feedbacks between climate, stomatal conductance and photosynthesis. With lower atmospheric CO₂ concentrations, stomata have to maximize carbon gains by increasing their area to match real-world growth rates. However, by doing so, water losses by evapotranspiration and evaporation at the leaf surface also increase. So, in order to compensate for water losses, reconstructed temperatures need to be lower, a situation that ultimately minimizes evapotranspiration and evaporation fluxes.

4. Discussion

4.1. Toward Better Ecophysiological Models

The inversion of mechanistic dendroecological models offers a great framework for dendroclimatologists to incorporate and deal with non-stationarity (i.e., the so-called divergence D'Arrigo et al., 2008) and with interactions between climate, tree growth and CO₂ concentrations, among other things. This well-known ”divergence” problem which is related to the fact that the climate-tree-growth relationship was modified after the 1960s or later, is possibly an artifact of inadequate detrending (D'Arrigo et al., 2008; Esper and Frank, 2009) or an effect of CO₂ fertilization or change in water availability (Daux et al., 2011). The problem of tree-growth trend is often discussed in dendrochronology (Melvin and Briffa, 2008; Nicault et al., 2010). Trends in tree-growth time-series may be caused by long-term variations in climate, long-term CO₂ or nitrogen increases, and various factors related to the tree physiology and wood structure. Numerous techniques have been used to try to separate the climate trend from other factors, with more or less success. (Melvin, 2004) showed that the extensive use of concepts taken from tree-growth models and based on the assumption that common external growth forcing operates through its influence on photosynthesis may solve the problem. The example of model inversion shown in the previous section confirms the relevance of this approach.

Increasing atmospheric CO₂ concentration enhances biomass production in MAIDEN as in most ecophysiological models (Berninger et al., 2004). Under elevated CO₂ concentrations, stomatal area may be reduced without reducing internal carbon concentrations (Keenan et al., 2013). Partial stomatal closure increases water retention and increases biomass production per unit of water absorbed by the plant (better WUE). So, less precipitation is required to sustain growth rates. This rate of increase in WUE might be downgraded by various acclimation processes to long term CO₂ increases (Drake et al., 1997): a decrease in Rubisco, a rise in carbohydrate solubility, increases in light use efficiency, or lower rates of dark respiration. These processes are not really integrated in most of the models discussed. Clearly, additional research is required to better understand these processes so that they can be included and accounted for in simulations in both forward and inverse mode. On the one hand, the meta-analysis of Medlyn et al. (1999) showed that current models were adequate to model photosynthesis in elevated CO₂. On the other hand, (Berninger et al., 2004) concluded that additional processes such as those that control acclimation to CO₂ in the long term as well as other limiting factors (e.g., nitrogen availability) need to be integrated in upcoming model generations to improve the realism of climate reconstructions. A recent study (Li et al., 2014) that CO₂ fertilization over the past 50 years is too small to be distinguished in the ring-width data given ontogenetic trends and interannual variability in climate.

Finally, what is clear is that ecophysiological models of tree-growth still need more development, but that their use instead of oversimplified statistical methods (response functions or transfer functions) has enabled significant progress. It is clear that our understanding of mechanistic dendroecological processes and their integration in deterministic models is a continually evolving and rapidly changing area of research. For that reason, it would be unwise to apply the approach to a wide range of environments and species, without first going through a thorough examination of underlying dendroecological processes and achieving a clear assessment of the model's ability to simulate at least the most fundamental ones.

4.2. Toward a More General Data Assimilation Scheme

Data assimilation sensu stricto has been used extensively in various disciplines (meteorology, oceanography …), where many observational datasets, both in-situ and remotely sensed, are available. A spectacular application can be found in climatology with the so-called climate reanalysis (Kalnay et al., 1996). As ecology cannot call on such massive datasets, more appropriate techniques are those based on Bayesian statistics. Dubinkina et al. (2011) introduced particle filters in paleoclimatological modeling. We propose here to use a similar approach in dendroecology with MAIDENiso.

Models need to state the initial conditions to start the runs. MAIDENiso (Danis et al., 2012) needs several years of daily climate data (minimum and maximum temperature, precipitation). For simplicity, we consider the current and previous years. The scheme of the method is presented in Figure 6. We start the simulations at the year t₀ + 1, using climate at time t₀ + 1 and t₀. By introducing small perturbations in this 2-year climate vector, we generate an ensemble of N simulations of tree proxies (tree-growth and isotopes) for year t₀ + 1. These simulated proxies are the particles which need to be compared to the observed proxies. A weight w_i, proportional to the likelihood of the model state (simulation of the proxies), conditional to the observations, is attributed to them according to their similarities to the observations (in Figure 6 the closest particle has the largest bullet). A posterior probability distribution is thus generated (2):

$\begin{array}{ll}p(c\mid d)={\displaystyle \sum _{i=1}^N{w}_i}\delta (c-c_i)with{w}_i=\frac{kexp(-{(d-H(c_i))}^2/2{\sigma }^2)}{{\displaystyle \sum _{i=1}^{N}p}(d\mid c_i)}\hfill & \left(2\right)\hfill \end{array}$

where p(c | d) is the posterior distribution of the climate c given the proxies d, i.e., the probability distribution of the reconstructed climate; k is a normalization constant; H is the measurement model (MAIDENiso simulation); is the observation error; c is the input climate. H(c_i) is the modeled proxies which depend on the climate c_i; the weight w_i measures the distance between the i^th particle and the observed value. The posterior distribution is resampled, providing M new equal weight particles by propagation using the model. These particles are compared to the observed proxies at year t₀+2. The procedure is repeated until the end of the observed proxies series.

FIGURE 6

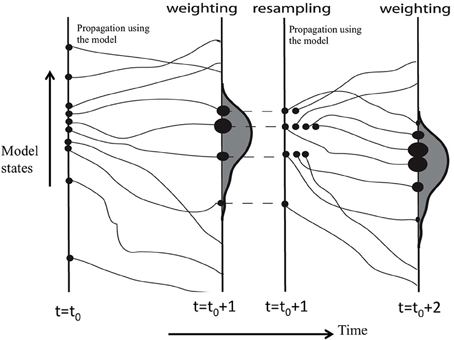
Figure 6. Scheme of the particle filter technique for assimilation of data in a process model (H. Goosse, pers. comm.).

This is the theory, but some difficulties remain to be solved before the method is operational. First the input climate is a large dimension vector. The model needs daily values of three variables, so that the number of possible combinations of the parameters is much larger than the number of particles. In reality, daily values can be derived from a relatively small number of parameters, namely the parameters of the probability distribution of the seasonal temperatures and precipitations. These large dimension vectors can also be reduced by a few principal components. Another problem is the comparison of the simulation H(c_i) to the proxies d. In reality we have here three proxies (bore increment, carbon and oxygen isotopes). They must be combined in Equation 2 and they must be simulated in the same units by the model. For the isotopes, this is the case, but the bore increment—related to the area and the density of the ring in a section, i.e., which is not a mass—must be compared to the annual biomass increment simulated by the model. In a previous section, this was solved by standardizing simulated and observed values. This is not the only solution and maybe not the best one.

This scheme of data assimilation must be considered as an avenue of research. To be useful, this approach must be applicable to long series, to provide climate reconstructions over several centuries of the past and projections to the future. As at each step we produce climate reconstructions and these reconstructions are used in the following step, there is a danger of drift. It is not certain that the link between observed and simulated proxies is sufficiently strong to foil the possible drifts. Studies on the stationarity of the process must then be conducted. A more complex but promising approach is given by coupling a climate model like LOVECLIM (Goosse et al., 2010) to a tree-growth model like MAIDENiso (Danis et al., 2012) and by assimilating data to this coupled system. In this case, the observed proxies are used to constrain the climate simulations to make them more realistic. As the climate model is global, this needs a network of proxies and not only a single site, and also a downscaling method (Vrac et al., 2007) to adapt the climate simulations to the dimension of the studied forests.

4.3. Some Perspectives

In contrast to empirical-statistical models, forward models of tree-growth can explicitly account for non-climatic factors, which reduces the risk of attributing to climate some tree-growth changes that are in fact related to internal processes. This extends their applicability and reduces the risk of violating the uniformitarian principle (which assumes stationarity of the relationships between tree-rings and abiotic factors). These forward models have another advantage: they are excellent tools to simulate proxies in various abiotic conditions and hence to better understand their sensitivity to various factors and evaluate biases and errors associated with reconstructions of past climate. These approaches do not imply that present empirical-statistical methods should be adandoned, but rather that our toolkitsshould be extended to analyze the proxies. The approaches used in dendroclimatology were developed 30 or 40 years ago, and were creative and productive responses to the situation we faced then. We now have a much richer set of records, a more diverse and powerful set of tools for analyzing and using them, and benefit from great advances in understanding tree functioning and climate variations on the long term.

Author Contributions

All authors contributed equally to the work with ideas, interpretations, and discussion. Joël Guiot supervised and wrote most of the paper, Etienne Boucher wrote the inversion section and Guillermo Gea-Izquierdo thoroughly revised the initial draft.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Support for Joël Guiot and Guillermo Gea-Izquierdo was provided by the Labex OT-Med (ANR-11-LABEX-0061) funded by the “Investissements dAvenir,” French Government program of the French National Research Agency (ANR) through the A*Midex project (ANR-11-IDEX-0001-02). Support for Etienne Boucher was provided by the Fonds de Recherche Quebecois -Nature et Technologies (FRQNT) and the ARCHIVES project through the funding of the National Sciences and Engineering Council (NSERC) and the participation of the Ouranos consortium. This paper is a contribution to the MISTRALS/PALEOMEX program. Fontainebleau data were kindly provided by V. Daux (LSCE, Saclay) and Pinus halepensis data by A. Nicault (ECCOREV, Aix-en-Provence). The english of the manuscript has been much improved by Elizabeth Rowley.

References

Anchukaitis, K. J., Evans, M. N., Kaplan, A., Vaganov, E. A., Hughes, M. K., Grissino-Mayer, H. D., et al. (2006). Forward modeling of regional scale tree-ring patterns in the southeastern United States and the recent influence of summer drought. Geophys. Res. Lett. 33:L04705. doi: 10.1029/2005GL025050

CrossRef Full Text

Andreu-Hayles, L., Planells, O., Gutierrez, E., Muntan, E., Helle, G., Anchukaitis, K., et al. (2011). Long tree-ring chronologies reveal 20th century increases in water-use efficiency but no enhancement of tree growth at five iberian pine forests. Global Change Biol. 17, 2095–2112. doi: 10.1111/j.1365-2486.2010.02373.x

CrossRef Full Text

Andrieu, C., Djurić, P. M., and Doucet, A. (2001). Model selection by mcmc computation. Signal Process. 81, 19–37. doi: 10.1016/S0165-1684(00)00188-2

CrossRef Full Text

Berninger, F., Hari, P., Nikinmaa, E., Lindholm, M., and Merilainen, J. (2004). Use of modeled photosynthesis and decomposition to describe tree growth at the northern tree line. Tree Physiol. 24, 193–204. doi: 10.1093/treephys/24.2.193

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Berninger, F., and Nikinmaa, E. (1997). Implications of varying pipe model relationships on scots pine growth in different climates. Funct. Ecol. 11, 146–156. doi: 10.1046/j.1365-2435.1997.00067.x

CrossRef Full Text

Bigler, C., and Bugmann, H. (2004). Predicting the time of tree death using dendrochronological data. Ecol. Appl. 14, 902–914. doi: 10.1890/03-5011

CrossRef Full Text

Boucher, E., Guiot, J., Hatte, C., Daux, V., Danis, P., and Dussouillez, P. (2014). An inverse modeling approach for tree-ring-based climate reconstructions under changing atmospheric co₂ concentrations. Biogeosciences 11, 3245–3258. doi: 10.5194/bg-11-3245-2014

CrossRef Full Text

Cook, E., and Kairiukstis, L. (1990). Methods of Dendrochronology. Applications in the Environmental Sciences. Dordrecht: Kluwer Academic Publishers. doi: 10.1007/978-94-015-7879-0

CrossRef Full Text

Covington, W., Fule, P., Hart, S., and Weaver, R. (2001). Modeling ecological restoration effects on ponderosa, pine forest structure. Restorat. Ecol. 9, 421–431. doi: 10.1046/j.1526-100X.2001.94011.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Danis, P., Hatte, C., Misson, L., and Guiot, J. (2012). MAIDENiso: a multiproxy biophysical model of tree-ring width and oxygen and carbon isotopes. Can. J. Forest Res. 42, 1697–1713. doi: 10.1139/x2012-089

CrossRef Full Text

D'Arrigo, R., Wilson, R., Liepert, B., and Cherubini, P. (2008). On the ‘divergence problem’in northern forests: a review of the tree-ring evidence and possible causes. Global Planet. Change 60, 289–305. doi: 10.1016/j.gloplacha.2007.03.004

CrossRef Full Text

Daux, V., Edouard, J. L., Masson-Delmotte, V., Stievenard, M., Hoffmann, G., Pierre, M., et al. (2011). Can climate variations be inferred from tree-ring parameters and stable isotopes from larix decidua? Juvenile effects, budmoth outbreaks, and divergence issue. Earth Planet. Sci. Lett. 309, 221–233. doi: 10.1016/j.epsl.2011.07.003

CrossRef Full Text

Davi, H., Dufrene, E., Granier, A., Le Dantec, V., Barbaroux, C., Francois, C., et al. (2005). Modelling carbon and water cycles in a beech forest part ii: validation of the main processes from organ to stand scale. Ecol. Model., 185. 387–405. doi: 10.1016/j.ecolmodel.2005.01.003

CrossRef Full Text

Desplanque, C., Rolland, C., and Michalet, R. (1998). Comparative dendroecology of the silver fir (Abies alba) and the Norway spruce (Picea abies) in an Alpine valley of France. Can. J. For. Res. 28, 737–748. doi: 10.1139/x98-025

CrossRef Full Text

Doherty, J. (2003). Ground water model calibration using pilot points and regularization. Ground Water 41, 170–177. doi: 10.1111/j.1745-6584.2003.tb02580.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Doucet, A., de Freitas, N., and Gordon, N. (2001). Sequential Monte Carlo Methods in Practice. Statistics for Engineering and Information Science. New York, NY: Springer-Verlag. doi: 10.1007/978-1-4757-3437-9

CrossRef Full Text

Downes, G., Drew, D., Battaglia, M., and Schulze, D. (2009). Measuring and modelling stem growth and wood formation: an overview. Dendrochronologia 27, 147–157. doi: 10.1016/j.dendro.2009.06.006

CrossRef Full Text

Drake, B., Gonzalez-Meler, M., and Long, S. (1997). More efficient plants: A consequence of rising atmospheric CO₂? Annu. Rev. Plant Physiol. Plant Mol. Biol. 48, 609–639.

Pubmed Abstract | Pubmed Full Text

Drew, D. M., Downes, G. M., and Battaglia, M. (2010). CAMBIUM, a process-based model of daily xylem development in Eucalyptus. J. Theor. Biol. 264, 395–406. doi: 10.1016/j.jtbi.2010.02.013

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dubinkina, S., Goosse, H., Sallaz-Damaz, Y., Crespin, E., and Crucifix, M. (2011). Testing a particle filter to reconstruct climate changes over the past centuries. Int. J. Bifurcat. Chaos 21, 3611–3618. doi: 10.1142/S0218127411030763

CrossRef Full Text

Dufrene, E., Davi, H., François, C., Maire, G. l., Dantec, V. L., and Granier, A. (2005). Modelling carbon and water cycles in a beech forest: Part i: model description and uncertainty analysis on modelled nee. Ecol. Modell. 185, 407–436. doi: 10.1016/j.ecolmodel.2005.01.004

CrossRef Full Text

Eglin, T., Francois, C., Michelot, A., Delpierre, N., and Damesin, C. (2010). Linking intra-seasonal variations in climate and tree-ring delta C-13: a functional modelling approach. Ecol. Modell. 221, 1779–1797. doi: 10.1016/j.ecolmodel.2010.04.007

CrossRef Full Text

Esper, J., and Frank, D. (2009). Divergence pitfalls in tree-ring research. Climatic Change 94, 261–266. doi: 10.1007/s10584-009-9594-2

CrossRef Full Text

Etien, N., Daux, V., Masson-Delmotte, V., Stievenard, M., Bernard, V., Durost, S., et al. (2008). A bi-proxy reconstruction of fontainebleau (france) growing season temperature from ad 1596 to 2000. Climate Past 4, 91–106. doi: 10.5194/cp-4-91-2008

CrossRef Full Text

Evensen, G. (2004). The ensemble kalman filter: theoretical formulation and practical implementation. Ocean Dyn. 53, 343–367. doi: 10.1007/s10236-003-0036-9

CrossRef Full Text

Farquhar, G. D., Caemmerer, S., and Berry, J. A. (1980). A biochemical model of photosynthetic CO₂ assimilation in leaves of c3 species. Planta 149, 78–90. doi: 10.1007/BF00386231

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Federer, C., Tritton, L., Hornbeck, J., and Smith, R. (1989). Physiologically based dendroclimate models for effects of weather on red spruce basal-area growth. Agricul. Forest Meteorol. 46, 159–172. doi: 10.1016/0168-1923(89)90119-6

CrossRef Full Text

Foster, J., and Leblanc, D. (1993). A physiological approach to dendroclimatic modeling of oak radial growth in the midwestern united-states. Can. J. Forest Res. 23, 783–798. doi: 10.1139/x93-103

CrossRef Full Text

Fox, A., Williams, M., Richardson, A. D., Cameron, D., Gove, J. H., Quaife, T., et al. (2009). The reflex project: comparing different algorithms and implementations for the inversion of a terrestrial ecosystem model against eddy covariance data. Agricul. Forest Meteorol. 149, 1597–1615. doi: 10.1016/j.agrformet.2009.05.002

CrossRef Full Text

Fritts, H. (1976). Tree Rings and Climate. London: Academic Press.

Fritts, H., Vaganov, E., Scviderskaya, I., and Shashkin, A. (1991). Climate variation and tree-ring structure in conifers. empirical and mechanistic models of tree-ring width, number of cells, cell size, cell-wall thickness and wood density. Climate Res. 1, 97–116. doi: 10.3354/cr001097

CrossRef Full Text

Gaucherel, C., Campillo, F., Misson, L., Guiot, J., and Boreux, J. J. (2008a). Parameterization of a process-based tree-growth model: Comparison of optimization, mcmc and particle filtering algorithms. Environ. Modell. Softw. 23, 1280–1288. doi: 10.1016/j.envsoft.2008.03.003

CrossRef Full Text

Gaucherel, C., Guiot, J., and Misson, L. (2008b). Changes of the potential distribution area of french mediterranean forests under global warming. Biogeosciences 5, 1493–1504. doi: 10.5194/bg-5-1493-2008

CrossRef Full Text

Gedalof, Z., and Berg, A. A. (2010). Tree ring evidence for limited direct CO₂ fertilization of forests over the 20th century. Global Biogeochem. Cycles 24:GB3027. doi: 10.1029/2009GB003699

CrossRef Full Text

Gelman, A., Carlin, J., Stern, H., and Rubin, D. (1995). Bayesian Data Analysis. London: Chapman and Hall.

Gibelin, A. L., and Deque, M. (2003). Anthropogenic climate change over the mediterranean region simulated by a global variable resolution model. Climate Dyn. 20, 327–339. doi: 10.1007/s00382-002-0277-1

CrossRef Full Text

Girardin, M., Bernier, P., Raulier, F., Tardif, J., Conciatori, F., and Guo, X. (2012). Testing for a CO₂ fertilization effect on growth of canadian boreal forests. J. Geophys. Res. Biogeosci. 9, 2523–2536. doi: 10.1029/2010JG001287

CrossRef Full Text

Girardin, M. P., Raulier, F., Bernier, P. Y., and Tardif, J. C. (2008). Response of tree growth to a changing climate in boreal central Canada: a comparison of empirical, process-based, and hybrid modelling approaches. Ecol. Modell. 213, 209–228. doi: 10.1029/2010JG001287

CrossRef Full Text

Goosse, H., Brovkin, V., Fichefet, T., Haarsma, R., Huybrechts, P., Jongma, J., et al. (2010). Description of the earth system model of intermediate complexity loveclim version 1.2. Geosci. Model Dev. 3, 603–633. doi: 10.5194/gmd-3-603-2010

CrossRef Full Text

Guiot, J., Torre, F., Jolly, D., Peyron, O., Borreux, J., and Cheddadi, R. (2000). Inverse vegetation modeling by monte carlo sampling to reconstruct paleoclimate under changed precipitation seasonality and CO₂ conditions: application to glacial climate in mediterranean region. Ecol. Model. 127, 119–140. doi: 10.1016/S0304-3800(99)00219-7

CrossRef Full Text

Handa, I. T., Körner, C., and Hättenschwiler, S. (2005). A test of the treeline carbon limitation hypothesis by in situ CO₂ enrichment and defoliation. Ecology 86, 1288–1300. doi: 10.1890/04-0711

CrossRef Full Text

Haslett, J., Whiley, M., Bhattacharya, S., Salter-Townshend, M., Wilson, S., Allen, J., et al. (2006). Bayesian paleoclimate reconstruction. J. R. Stat. Soc. A 169, 395–438. doi: 10.1111/j.1467-985X.2006.00429.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hastings, W. (1970). Monte carlo sampling methods using markov chains and their application. Biometrika 57, 97–109. doi: 10.1093/biomet/57.1.97

CrossRef Full Text

Haxeltine, A., and Prentice, I. (1996). Biome3: an equilibrium terrestrial biosphere model based on ecophysiological constraints, resource availability, and competition among plant functional types. Global Biogeochem. Cycles 10, 693–709. doi: 10.1029/96GB02344

CrossRef Full Text

Hogg, E. (1999). Simulation of inter-annual responses of trembling aspen stands to climatic variation and insect defoliation in western Canada. Ecol. Model. 114, 175–193. doi: 10.1016/S0304-3800(98)00150-1

CrossRef Full Text

Hölttä, T., Mäkinen, H., Nöjd, P., Mäkelä, A., and Nikinmaa, E. (2010). A physiological model of softwood cambial growth. Tree Physiol. 30, 1235–1252. doi: 10.1093/treephys/tpq068

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Houllier, F., Leban, J., and Colin, F. (1995). Linking growth modelling to timber quality assessment for norway spruce. Forest Ecol. Manage. 74, 91–102. doi: 10.1016/0378-1127(94)03510-4

CrossRef Full Text

Huang, J., Bergeron, Y., Denneler, B., Berninger, F., and Tardif, J. (2007). Response of forest trees to increased atmospheric CO₂. Crit. Rev. Plant Sci. 26, 265–283. doi: 10.1080/07352680701626978

CrossRef Full Text

Kalman, R. (1960). A new approach to linear filtering and prediction problems. Trans. ASME J. Basic Eng. 82, 35–45. doi: 10.1115/1.3662552

CrossRef Full Text

Kalnay, E. (2003). Atmospheric Modelling, Data Assimilation and Predictability. Cambridge: Cambridge University Press.

Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., et al. (1996). The ncep/ncar 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–471.

Keenan, T. F., Hollinger, D. Y., Bohrer, G., Dragoni, D., Munger, J. W., Schmid, H., et al. (2013). Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature 499, 323–327. doi: 10.1038/nature12291

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Korhola, A., Vasko, K., Toivonen, H., and Olandor, H. (2002). Holocene temperature changes in northern fennoscandia reconstructed from chironomids using bayesian modelling. Quat. Sci. Rev. 21, 1841–1860. doi: 10.1016/S0277-3791(02)00003-3

CrossRef Full Text

LeBlanc, D., and Foster, J. (1992). Predicting effects of global warming on growth and mortality of upland oak species in the midwestern united states-a physiologically based dendroecological approach. Can. J. Forest Res. 22, 1739–1752. doi: 10.1139/x92-228

CrossRef Full Text

LeBlanc, D., and Terrell, M. (2001). Dendroclimatic analysis using thornwaite-mather-type evapotranspiration models: A bridge between dendroevology and forest simulation models. Tree Ring Res. 57, 55–66.

Lévesque, M., Siegwolf, R., Saurer, M., Eilmann, B., and Rigling, A. (2014). Increased water-use efficiency does not lead to enhanced tree growth under xeric and mesic conditions. New Phytol. 203, 94–109. doi: 10.1111/nph.12772

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Li, G., Harrison, S. P., Prentice, I. C., and Falster, D. (2014). Simulation of tree ring-widths with a model for primary production, carbon allocation and growth. Biogeosci. Discuss. 11, 10451–10485. doi: 10.5194/bgd-11-10451-2014

CrossRef Full Text

Linares, J. C., and Camarero, J. J. (2012). From pattern to process: linking intrinsic water-use efficiency to drought-induced forest decline. Global Change Biol. 18, 1000–1015. doi: 10.1111/j.1365-2486.2011.02566.x

CrossRef Full Text

Medlyn, B. E., Badeck, F. W., De Pury, D. G. G., Barton, C. V. M., Broadmeadow, M., Ceulemans, R., et al. (1999). Effects of elevated [CO₂] on photosynthesis in european forest species: a meta-analysis of model parameters. Plant Cell Environ. 22, 1475–1495. doi: 10.1046/j.1365-3040.1999.00523.x

CrossRef Full Text

Melvin, T. (2004). Historical Growth Rates and Changing Climatic Sensitivity of Boreal Conifers. Ph.D. thesis, University of East Anglia, Norwich.

Melvin, T., and Briffa, K. (2008). A “signal-free” approach to dendroclimatic standardisation. Dendrochronologia 26, 71–86. doi: 10.1016/j.dendro.2007.12.001

CrossRef Full Text

Metropolis, N., Rosenbluth, A., Rosenbluth, M., Teller, A., and Teller, E. (1953). Equations of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1093.

Misson, L. (2004). Maiden: a model for analyzing ecosystem processes in dendroecology. Can. J. Forest Res. 34, 874–887. doi: 10.1139/x03-252

CrossRef Full Text

Misson, L., Rathgeber, C., and Guiot, J. (2004). Dendroecological analysis of climatic effects on Quercus petraea and Pinus halepensis radial growth using the process-based MAIDEN model. Can. J. Forest Res. 34, 888–898. doi: 10.1139/x03-253

CrossRef Full Text

Mo, X., Chen, J., Ju, W., and Black, T. (2008). Optimization of ecosystem model parameters through assimilating eddy covariance flux data with an ensemble kalman filter. Ecol. Model. 217, 157–173. doi: 10.1016/j.ecolmodel.2008.06.021

CrossRef Full Text

Nicault, A. (1999). Analyse de l'influence du Climat sur les variations inter et intra annuelles de la croissance radiale du pin d'Alep (Pinus halepensis, Mill.) en Provence calcaire. Ph.D. thesis, Université Aix-Marseille III, Marseille.

Nicault, A., Guiot, J., Edouard, J., and Brewer, S. (2010). Preserving long-term fluctuations in standardisation of tree-ring series by the adaptative regional growth curve (argc). Dendrochronologia 28, 1–12. doi: 10.1016/j.dendro.2008.02.003

CrossRef Full Text

Ogee, J., Barbour, M. M., Wingate, L., Bert, D., Bosc, A., Stievenard, M., et al. (2009). A single-substrate model to interpret intra-annual stable isotope signals in tree-ring cellulose. Plant Cell Environ. 32, 1071–1090. doi: 10.1111/j.1365-3040.2009.01989.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Panek, J., and Waring, R. (1997). Stable carbon isotopes as indicators of limitations to forest growth imposed by climate stress. Ecol. Appl. 7, 854–863. doi: 10.1890/1051-0761(1997)007[0854:SCIAIO]2.0.CO;2

CrossRef Full Text

Pedersen, B. (1998). The role of stress in the mortality of midwestern oaks as indicated by growth prior to death. Ecology 79, 79–93. doi: 10.1890/0012-9658(1998)079[0079:TROSIT]2.0.CO;2

CrossRef Full Text

Pelletier, G., Chapra, S., and Tao, H. (2006). Qual2kw –a framework for modeling water quality in streams and rivers using a genetic algorithm for calibration. Environ. Model. Softw. 21, 419–425. doi: 10.1016/j.envsoft.2005.07.002

CrossRef Full Text

Peng, C., Guiot, J., Wu, H., Jiang, H., and Luo, Y. (2011). Integrating models with data in ecology and palaeoecology: advances towards a model–data fusion approach. Ecol. Lett. 14, 522–536. doi: 10.1111/j.1461-0248.2011.01603.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Peñuelas, J., Canadell, J. G., and Ogaya, R. (2011). Increased water-use efficiency during the 20th century did not translate into enhanced tree growth. Global Ecol. Biogeogr 20, 597–608. doi: 10.1111/j.1466-8238.2010.00608.x

CrossRef Full Text

Pietsch, S., and Hasenauer, H. (2002). Using mechanistic modeling within forest ecosystem restoration. Forest Ecol. Manag. 159, 111–131. doi: 10.1016/S0378-1127(01)00714-9

CrossRef Full Text

Quaife, T., Lewis, P., De Kauwe, M., Williams, M., Law, B., Disney, M., et al. (2008). Assimilating canopy reflectance data into an ecosystem model with an ensemble kalman filter. Remote Sens. Environ. 112, 1347–1364. doi: 10.1016/j.rse.2007.05.020

CrossRef Full Text

Rathgeber, C., Guiot, J., and Edouard, J. (2000a). Utilisation d'un modèle biogéochimique en dendroécologie. application au pin cembro. CR Acad. Sci. 323, 489–497. doi: 10.1016/S0764-4469(00)00154-2

CrossRef Full Text

Rathgeber, C., Misson, L., Nicault, A., and Guiot, J. (2005). Bioclimatic model of tree radial growth: application to the French Mediterranean Aleppo pine forests. Tree Struct. Funct. 19, 162–176. doi: 10.1007/s00468-004-0378-z

CrossRef Full Text

Rathgeber, C., Nicault, A., Guiot, J., Keller, T., Guibal, F., and Roche, P. (2000b). Simulated responses of pinus halepensis forest productivity to climatic change and CO₂ increase using a statistical model. Global Planetary Change, 26, 405–421. doi: 10.1016/S0921-8181(00)00053-9

CrossRef Full Text

Rathgeber, C., Nicault, N., Kaplan, J., and Guiot, J. (2003). Using a biogeochemistry model in simulating forests productivity responses to climatic change and [CO₂] increase: example of pinus halepensis in provence (south-east france). Ecol. Model. 166, 239–255. doi: 10.1016/S0304-3800(03)00161-3

CrossRef Full Text

Raupach, M., Rayner, P., Barrett, D., DeFries, R., Heimann, M., Ojima, D., et al. (2005). Model–data synthesis in terrestrial carbon observation: methods, data requirements and data uncertainty specifications. Global Change Biol. 11, 378–397. doi: 10.1111/j.1365-2486.2005.00917.x

CrossRef Full Text

Rauscher, H. M., Isebrands, J. G., Host, G. E., Dickson, R. E., Dickmann, D. I., Crow, T. R., et al. (1990). Ecophys: An ecophysiological growth process model for juvenile poplar. Tree Physiol. 7, 255–281. doi: 10.1093/treephys/7.1-2-3-4.255

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Robert, C., and Casella, G. (1999). Monte Carlo Statistical Methods. New-York, NY: Springer-Verlag; Springer Texts in Statistics. doi: 10.1007/978-1-4757-3071-5

CrossRef Full Text

Robertson, A., Overpeck, J., Rind, D., Mosley-Thompson, E., Zielinski, G., Lean, J., et al. (2001). Hypothesized climate forcing time series for the last 500 years. J. Geophys. Res. Atmos. 106, 14783–14803. doi: 10.1029/2000JD900469

CrossRef Full Text

Roux, X. L., Lacointe, A., Escobar-Gutiérrez, A., and Dizès, S. L. (2001). Carbon-based models of individual tree growth: a critical appraisal. Ann. For. Sci. 58, 469–506. doi: 10.1051/forest:2001140

CrossRef Full Text

Silva, L. C. R., and Horwath, W. (2013). Explaining global increases in water use efficiency: Why have we overestimated responses to rising atmospheric co₂ in natural forest ecosystems? PLoS ONE 8:e53089. doi: 10.1371/journal.pone.0053089

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Tarantola, A. (2005). Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia, PA: SIAM, Society for Industrial and Applied Mathematics. doi: 10.1137/1.9780898717921

CrossRef Full Text

Tolwinski-Ward, S., Evans, M., Hughes, M., and Anchukaitis, K. (2011). An efficient forward model of the climate controls on interannual variation in tree-ring width. Clim. Dyn. 36, 2419–2439. doi: 10.1007/s00382-010-0945-5

CrossRef Full Text

Vrac, M., Marbaix, P., Paillard, D., and Naveau, P. (2007). Non-linear statistical downscaling of present and lgm precipitation and temperatures over europe. Climate Past 3, 669–682. doi: 10.5194/cp-3-669-2007

CrossRef Full Text

Wang, Y., Trudinger, C., and Enting, I. (2009). A review of applications of model-data fusion to studies of terrestrial carbon fluxes at different scale. Agr. Forest Meteorol. 149, 1829–1842. doi: 10.1016/j.agrformet.2009.07.009

CrossRef Full Text

Williams, M., Schwarz, P., Law, B., Irvine, J., and Kurpius, M. (2005). An improved analysis of forest carbon dynamics using data assimilation. Global Change Biol. 11, 89–105. doi: 10.1111/j.1365-2486.2004.00891.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wu, H., Guiot, J., Brewer, S., Guo, Z., and Peng, C. (2007). Dominant factors controlling glacial and interglacial variations in the treeline elevation in tropical africa. Proc. Natl. Acad. Sci. U.S.A. 104, 9720–9724. doi: 10.1073/pnas.0610109104

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wu, H., Guiot, J., Peng, C., and Guo, Z. (2009). New coupled model used inversely for reconstructing past terrestrial carbon storage from pollen data: validation of model using modern data. Global Change Biol. 15, 82–96. doi: 10.1111/j.1365-2486.2008.01712.x

CrossRef Full Text