Sustaining diversity in trait-based models of phytoplankton communities

It is well-established that when equilibrium is attained for two species competing for the same limiting resource in a stable, uniform environment, one species will eliminate the other due to competitive exclusion. While competitive exclusion is observed in laboratory experiments and ecological models, the phenomenon seems less common in nature, where static equilibrium is prevented by the fluctuating physical environment and by other factors that constantly change species abundances and the nature of competitive interactions. Trait-based models of phytoplankton communities appear to be useful tools for describing the evolution of large assemblages of species with aggregate group properties such as total biomass, mean trait, and trait variance, the latter representing the functional diversity of the community. Such an approach, however, is limited by the tendency of the trait variance to unrealistically decline to zero over time. This tendency to lose diversity, and therefore adaptive capacity, is typically “solved” by fixing the variance or by considering exogenous processes such as immigration. Exogenous processes, however, cannot explain the maintenance of adaptive capacity often observed in the closed environment of chemostat experiments. Here we present a new method to sustain diversity in adaptive trait-based models of phytoplankton communities based on a mechanism of trait diffusion through subsequent generations. Our modeling approach can therefore account for endogenous processes such as rapid evolution or transgenerational trait plasticity.

1. Introduction

Phytoplankton are a group of mainly single-celled primary producers widespread in aquatic ecosystems. Although phytoplankton represent only 1% of the Earth's photosynthetic biomass, they account for more than 45% of our planet's annual net primary production (Falkowski et al., 2004). Given that phytoplankton community composition and diversity play important roles in the functioning of aquatic ecosystems (Ptacnik et al., 2008; Eggers et al., 2014) and global climate (Falkowski et al., 1998), it is important to understand the factors that drive assembly and dynamics of such communities. Modeling provides an important tool for addressing these problems.

Early models of marine ecosystems (Fasham et al., 1990) were relatively simple (so-called NPZD-type models comprising nutrient, phytoplankton, zooplankton, and detritus) partly due to the constraints set by the available computing facilities. Although recent modeling approaches have begun to resolve more complex community structures by explicitly incorporating different functional groups of phytoplankton, significant challenges remain (Anderson, 2005), in particular concerning the formulation of valid models for describing plankton diversity and the adaptive responses of phytoplankton communities to a changing environment. The marine microbial environment is, in fact, spectacularly diverse, with an estimated 25,000 morphologically distinct forms of phytoplankton (Falkowski and Oliver, 2007). It is neither feasible nor effective to account explicitly for all these different types in plankton models, because this would require far too many equations and free parameters.

Although adaptive responses are expected to be more robust for more diverse ecosystems, we still lack mechanistic models that can capture the observed degree of biodiversity. For example, because of competitive exclusion (Hardin, 1960), modeled biodiversity tends to collapse over time both for “adaptive dynamics” models (Norberg et al., 2001; Merico et al., 2009) and for models that explicitly resolve many different species under variable environmental forcing in spatially resolved settings (Bruggeman and Kooijman, 2007; Follows et al., 2007).

A myriad of ideas and mechanisms have been proposed as potentially suitable to sustain species diversity (Chesson, 2000). High diversity has been alternatively attributed both to intense competition, which forces niche restriction, and to reduced competition resulting from predation. Diversity has also been found to be in some cases positively, and in other cases negatively correlated with productivity (Huston, 1979). Mechanisms proposed to sustain diversity in mathematical models include density dependence, where the growth rates of different types of organisms depend on the density of each type itself, or frequency dependence, where the growth rates of types depend on their relative frequency (Levin, 1981). More recently, a mechanism based on metabolic and physiological trade-offs in a simple, single-resource chemostat system has been proposed (Beardmore et al., 2011). This model, however, requires a mutation rate in combination with multiple convex trade-offs in order to produce sufficiently complex fitness landscapes to enable co-maintenance.

Exogenous processes such as immigration have also been considered as a potential solution for maintaining biodiversity in phytoplankton models (Norberg et al., 2001; Bruggeman and Kooijman, 2007; Savage et al., 2007; Tirok et al., 2011). However, treating immigration as part of the explanation for coexistence ultimately leads to circular reasoning when immigration rates are fixed and are not themselves explained (Chesson, 2000). The continuous migration of species into an area of interest depends on diversity maintenance in the areas that are the source of the immigrants (Chesson, 2000). A non-circular explanation for the maintenance of biodiversity in terms of immigration may be possible for meta-communities (Leibold and Norberg, 2004) consisting of distinct yet connected local sub-communities, which as a whole behave as a Complex Adaptive System (Levin, 2003). In such meta-communities, biodiversity at the large scale could result from the diversity of adaptive responses among the local communities. However, this mechanism may still not contribute much to biodiversity in relatively well-mixed environments such as large regions of the ocean (Leibold and Norberg, 2004).

Nevertheless, and quite surprisingly, microbial communities appear able to maintain a considerable level of adaptive capacity even within the confined and stable environment of chemostat systems (for which immigration cannot be invoked as a viable explanation), either in the simple case of bacterial cultures (Maharjan et al., 2006) or in relatively more complex communities comprising nutrient, algae, and rotifers (Fussmann et al., 2007; Kinnison and Hairston, 2007; Ellner and Becks, 2010).

Here we present a new mathematical method to sustain diversity in adaptive, trait-based models of phytoplankton communities based on the mechanism of trait diffusion through subsequent generations. This endogenous mechanism can be thought to be driven either by genetic mutation, via rapid evolution, or by trans-generational phenotypic plasticity, i.e., expressed independently of changes in the offspring genotype. We develop the method in the idealized context of a simple nutrient-phytoplankton-zooplankton (NPZ) chemostat system and apply it to examine the consequences of different levels of trait diffusivity for the ecological dynamics and adaptive capacity of a phytoplankton community.

2. Methods

2.1. Trait Diffusion

We consider the evolution of a community of phytoplankton species which differ in a single trait represented by a numerical value x. The number of species per unit interval on the trait scale at time t shall be denoted c(x, t). We further write r(x, t) and d(x, t) to denote the reproduction rate and the death rate per species. Since we are only concerned with unicellular organisms that reproduce by cell division here, we will use the term reproduction as synonym of growth. We start from a trait-time discrete model where x and t are restricted to integer values. We assume that the offspring of a parent with trait value x will have trait value x+1 with probability p, trait value x − 1 with probability q, and remain at trait value x with probability 1 − p − q. At time t + 1,

$\begin{array}{cc}\begin{array}{l}c(x,t+1)\text{}=\text{}[1-\text{}d(x,t)\text{}+\text{}(1-p-q)r(x,t)]c(x,t)\text{}+pr(x-1,t)\hfill \\ c(x-1,t)+qr(x+1,t)c(x+1,t).\hfill \end{array}& (1)\end{array}$

We now consider the limit (rescaling x and t as necessary) where c, r, and d change little over one mesh cell of the trait-time grid. Taylor-expanding the above expression about (x, t), keeping only terms up to first order in time and up to second order in trait, we obtain

$\begin{array}{cc}\begin{array}{l}c+c_t=[1-d+(1-p-q)r]c+p[rc-(rc)x+\frac{1}{2}(rc)xx]\hfill \\ +q[rc+(rc)x+\frac{1}{2}(rc)xx].\hfill \end{array}& (2)\end{array}$

In the following, we treat the trait space as unbounded with the implicit assumption that extreme trait values would be ecologically meaningless. This is expressed by the boundary conditions c(x, t) → 0 for every t ≥ 0 as x → ±∞. Introducing now the net growth rate a = r − d, the trait drift parameter μ = q − p, and the trait diffusion parameter ν = (p + q)/2, we finally obtain the Fokker–Planck equation

$\begin{array}{cc}{c}_t=ac+\mu {(rc)}_x+\nu {(rc)}_{xx}.& (3)\end{array}$

The trait drift parameter μ is proportional to the bias and the trait diffusion parameter ν is proportional to the variability with which the trait is passed from one generation to the next. In particular, when μ is non-zero, there is a tendency for the trait to change in a certain direction in the absence of environmental pressure; in most of the following we will assume that there is no such bias. The overall diffusion coefficient ν r, being a classical diffusivity, must have units of trait²/time. Here, we use a dimensionless abstract trait scale and r, as a rate, has units of 1/time, so that the trait diffusion parameter ν is a dimensionless quantity.

Fokker–Planck equations appear generically as evolution equations for the probability density of state-dependent random walks. In our case, however, we do not enforce normalization, so that c represents the macroscopic trait space number density, which is proportional to the trait probability function for an individual organism in the limit of large population size. We further remark that the above derivation has numerous precursors in different areas of modeling: a similar Fokker–Planck equation arises, for example, in the continuum limit of the Becker–Döring model for the nucleation of liquid precipitates (Clement and Wood, 1980).

To solve the Fokker–Planck Equation (3) directly, one could choose a sufficiently large bounded region of the trait space endowed with homogeneous Dirichlet boundary conditions and discretize the quation using standard methods for the numerical solution of partial differential equations. But rather than solving the underlying trait discrete model directly, we shall adopt a different and more efficient approach. In the following, however, we reduce the model complexity further by deriving simplified aggregate equations for the evolution of the first three moments of c. In much of the prior literature, the moment equations are derived directly from the discrete model (Clement and Wood, 1980; Norberg et al., 2001; Merico et al., 2009). Here, we find it more convenient to match the time-dependent Gaussian ansatz function

$\begin{array}{cc}c(x,t)=\frac{P(t)}{\sqrt{2\pi \sigma (t)}}{e}^{-\frac{{(x-\overline{x}(t))}^2}{2\sigma (t)}},& (4)\end{array}$

with the Fokker–Planck dynamics. This can be done in several ways. We choose to approximate the equation locally near the mean trait x, i.e., we pursue a local matching of Taylor coefficients. Inserting the Gaussian ansatz into (3), computing i = 0, 1, 2 derivatives in x, and evaluating at x = x(t) yields

$\begin{array}{cc}\frac{2\sigma \dot{P}-P\dot{\sigma }}{\sqrt{8\pi }{\sigma }^{3/2}}=\frac{P\left[\sigma \left(a+\mu r_x+\nu r_{xx}\right)-\nu r\right]}{\sqrt{2\pi }{\sigma }^{3/2}},& (5\text{a})\end{array}$

$\begin{array}{cc}\frac{P\dot{\overline{x}}}{\sqrt{2\pi }{\sigma }^{3/2}}\text{}=\text{}\frac{P\left[\sigma \left(a_x\text{}+\text{}\nu r^{(3)}\text{}+\text{}\mu r_{xx}\right)\text{}-\text{}3\nu r_x\text{}-\text{}\mu r\right]}{\sqrt{2\pi }{\sigma }^{3/2}}\text{},& (5\text{b})\end{array}$

$\begin{array}{cc}\begin{array}{l}\frac{3P\dot{\sigma }-2\sigma \dot{P}}{\sqrt{8\pi }{\sigma }^{5/2}}=\frac{3\nu Pr}{\sqrt{2\pi }{\sigma }^{5/2}}-\frac{P\left(a+3\mu r_x+6\nu r_{xx}\right)}{\sqrt{2\pi }{\sigma }^{3/2}}\\ +\frac{P\left(a_{xx}+\nu r^{(4)}+\mu r^{(3)}\right)}{\sqrt{2\pi \sigma }},\end{array}& (5\text{c})\end{array}$

with r⁽³⁾ and r⁽⁴⁾ indicating respectively third and fourth derivatives with respect to x. This system of equations is linear in the time derivatives, for which we can easily solve:

$\begin{array}{cc}\dot{P}=\frac{1}{2}P\left[\sigma \left(a_{xx}+\mu r^{(3)}+\nu r^{(4)}\right)+2a-3\nu r_{xx}\right],& (6\text{a})\end{array}$

$\begin{array}{cc}\dot{\overline{x}}=\sigma \left(a_x+\nu r^{(3)}+\mu r_{xx}\right)-3\nu r_x-\mu r,& (6\text{b})\end{array}$

$\begin{array}{cc}\begin{array}{l}\dot{\sigma }=\sigma [\sigma \left(a_{xx}+\mu r^{(3)}+\nu r^{(4)}\right)\\ \text{}-5\nu r_{xx}-2\mu r_x]+2\nu r.\end{array}& (6\text{c})\end{array}$

These equations describe the temporal evolution of three macroscopic properties of the phytoplankton community: (i) the total abundance P, (ii) the mean trait x, and (iii) the trait variance σ. When there is no trait drift, that is when μ = 0, which we shall assume henceforth, the model reduces to

$\begin{array}{cc}\dot{P}=\frac{1}{2}P\left[\sigma \left(a_{xx}+\nu r^{(4)}\right)+2a-3\nu r_{xx}\right],& (7\text{a})\end{array}$

$\begin{array}{cc}\dot{\overline{x}}=\sigma \left(a_x+\nu r^{(3)}\right)-3\nu r_x,& (7\text{b})\end{array}$

$\begin{array}{cc}\dot{\sigma }=\sigma \left[\sigma \left(a_{xx}+\nu r^{(4)}\right)-5\nu r_{xx}\right]+2\nu r.& (7\text{c})\end{array}$

We close this section with two remarks. First, the Gaussian ansatz (4) can be seen as an instance of “collective coordinates,” which have been widely used in the study of solitary waves and later applied in a dissipative context (Gottwald and Kramer, 2004). That approach, however, is based on minimizing the least-square distance to the solution template. In contrast, we pursue local matching which leads to simpler expressions involving only derivatives of the coefficient functions. Second, the coefficients d and r may implicitly depend on c and couple to other dynamical quantities in a more complex model without change to the derivation above.

2.2. NPZ Model

We will now study the trait diffusion approach in the context of a previously published chemostat model (Merico et al., 2009), which describes the adaptive dynamics of a phytoplankton community P, via temporal changes in the mean trait edibility, subject to a constant nutrient input N and to variable grazing pressure by zooplankton Z. P, N, and Z are expressed as concentrations. The phytoplankton abundance P evolves according to the trait diffusion Equation (7), in which we assume that the loss rate per unit of phytoplankton is given by

$\begin{array}{cc}d(x,t)=m_P+\delta +g(\overline{x}(t),P(t))& (8)\end{array}$

with m_P a generic, constant rate of mortality, δ the rate of dilution, and g the rate of zooplankton grazing. As mentioned, the trait value x characterizes the edibility of phytoplankton from the point of view of zooplankton. For simplicity, we assume that zooplankton graze uniformly across the whole phytoplankton community at a rate which depends on the mean edibility via the Michaelis–Menten response

$\begin{array}{cc}g(\overline{x},P)=\frac{{\mu }_Z}{\epsilon }\left(\frac{\overline{x}}{\overline{x}P+K_P}\right)& (9)\end{array}$

with μ_Z the maximum zooplankton growth rate, ε the zooplankton assimilation efficiency and K_P the half-saturation constant for zooplankton growth.

The reproduction rate r(x, t) is limited by the nutrient concentration and follows the Michaelis–Menten growth response

$\begin{array}{cc}r(x,t)=\frac{{\mu }_{P}N(t)}{N(t)+K_N(x)}& (10)\end{array}$

with maximum reproduction rate μ_P and half-saturation K_N(x) = K*_N/(1 − κ − x⁻¹). The half-saturation is a function of the trait x and reflects a trade-off relationship between nutrient harvesting abilities and edibility of phytoplankton. This relationship was mechanistically derived by Merico et al. (2009) by assuming that phytoplankton partition assimilated energy over three pools: (1) generic biomass, (2) nutrient harvesting biomass, with allocation coefficient α, and (3) defense biomass, with allocation coefficient β. The fraction of energy allocated to generic biomass is indicated with κ, while the remaining fraction (1 − κ) is partitioned between nutrient harvesting and defense pools. This leads to 1 − κ = α + β. Edibility x is then assumed to be inversely proportional to the relative amount of defense biomass β so that α(x) = 1 − κ − x⁻¹. With the analogous assumption that K_N is proportional to the relative amount of nutrient harvesting biomass α(x), i.e., K_N = K*_N/α(x), the trade-off equation K_N(x) = K*_N/(1 − κ − x⁻¹) follows. This equation implies that the higher the nutrient harvesting ability (i.e., the lower the half-saturation K_N), the more edible the phytoplankton (i.e., the higher the trait x), and vice versa. A more comprehensive discussion and a plot of the trade-off relationship is provided by Merico et al. (2009), their Figure 2, for different values of the parameter κ. Under a changing environment (i.e., under changing nutrient concentration and grazing pressure), this trade-off function drives the changes in the mean edibility trait and therefore in phytoplankton community composition.

The total rate of nutrient uptake is proportional to the rate of reproduction of phytoplankton as given by (7a). Nutrients are released back into the pool via the generic mortality term proportional to m_P. Finally, zooplankton follows a simple growth model with growth rate per unit of zooplankton g, rate of mortality constant m_Z, and rate of dilution constant δ. Thus, the following equations for nutrient and zooplankton complete the model dynamics:

$\begin{array}{cc}\begin{array}{l}\dot{N}=\delta (N_0-N)\hfill \\ -\frac{P}{\kappa }[r-m_P+\frac{\sigma }{2}(r_{xx}+\nu r^{(4)})-\frac{3}{2}\nu r_{xx}],\end{array}& (11\text{a})\end{array}$

$\begin{array}{cc}\dot{Z}=\left[\frac{{\mu }_Z}{\kappa }\right(\frac{\overline{x}P}{\overline{x}P+K_P})-m_Z-\delta ]Z.& (11\text{b})\end{array}$

Without trait diffusion, i.e., when ν = 0, this model reduces to the conventional adaptive dynamics formulation of Merico et al. (2009) in which the trait variance, and therefore the functional diversity of the phytoplankton community, is not sustained.

2.3. Simulations

Our aim is now to explore the NPZ dynamics with and without trait diffusion. Therefore, we take as our base case one previously defined and well tested parameter configuration that leads to limit cycles (Merico et al., 2009); all relevant variables and parameters along with their units and values are reported in Table 1. We then compare the following three methods for expressing diversity in the NPZ model.

1. Standard model. This corresponds to the conventional adaptive dynamics formulation (Merico et al., 2009) in which the functional diversity of the model system is not sustained by the inclusion of any specific mechanism, neither endogenous nor exogenous. The system is given by Equations (7) through (11) with ν = 0.

2. Fixed trait variance. In the model of case 1 above, we additionally keep the functional diversity constant by setting the rate of change of the trait variance (i.e., the right hand side of (7c)) to zero.

3. Trait diffusion. The functional diversity of the system is sustained by trait diffusion; we solve the full model Equations (7) through (11).

TABLE 1

Table 1. State variables and parameters used in the model.

We note that, according to Merico et al. (2009), the NPZ system can shift its dynamic behavior from limit cycles to equilibrium as the trait variance changes. While a comprehensive exploration of the different dynamical regimes of the new trait-diffusion model is beyond the scope of this work, we shall examine its behavior in different previously identified regimes with a particular focus on its transient behavior. Specifically, we compare and discuss the three model cases under the following scenarios.

(a) Limit cycle dynamics under states of low and high initial adaptive capacities.

(b) Transitions from limit cycle dynamics to equilibrium and vice versa under shock perturbations in K_P and N₀.

(c) Response of the trait-diffusion model to varying ν and K_P.

3. Results

The results for scenario (a), limit cycle dynamics under states of low and high initial adaptive capacities (i.e., trait variances) are displayed in Figures 1, 2 and in Supplementary Figures 1, 2. In all three models, N, P, and Z reach an oscillatory state whose amplitude and period depend on the trait variance. At low initial variance, the trait variance converges to zero in the standard model, it is constant by construction in the model with fixed variance, and turns out to be only weakly oscillatory under trait-diffusion. The rate of change of the mean trait (i.e., rate of adaptation) is proportional to the trait variance, as specified by Equation (7b). Thus, the standard model loses adaptive capacity in the long term. At high initial variance, the model with fixed variance shows high-amplitude oscillations in the mean trait (Figure 2), a strikingly different dynamics than in the other models. Such strong and undesired sensitivity on the initial variance is also expressed by the different cycle dynamics (higher amplitude and longer periodicity) in N, P, and Z (Supplementary Figure 2) emerging in this model as compared to the other two.

FIGURE 1

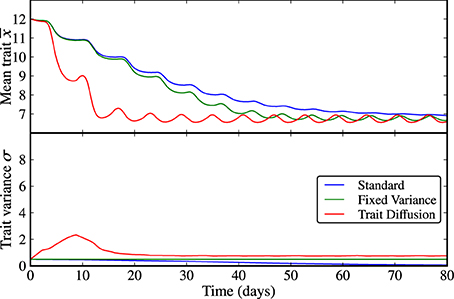
Figure 1. Limit cycle dynamics from a state of low initial diversity (σ(0) = 0.5). The trait variance converges to zero in the standard model (blue line), it is constant by construction in the model with fixed variance (green line), and it shows an initial increase followed by a relaxation to a steady-state with almost imperceptible superimposed oscillations under in the trait diffusion model (red line). The standard model clearly loses adaptive capacity in the long term (i.e., oscillations in the mean trait becomes weaker as the trait variance approaches zero). The corresponding NPZ dynamics is shown in Supplementary Figure 1.

FIGURE 2

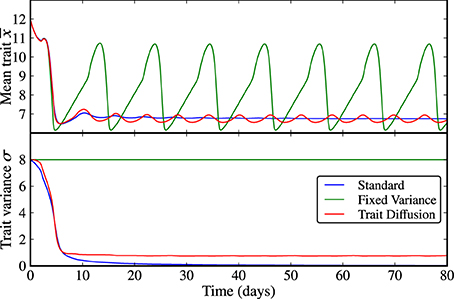
Figure 2. Limit cycle dynamics from a state of high initial diversity (σ(0) = 8). Analogously to the case of low initial diversity (Figure 1), the trait variance converges to zero in the standard model (blue line), it is constant by construction in the model with fixed variance (green line), and it shows an initial relaxation to a steady-state with almost imperceptible superimposed oscillations in the trait diffusion model (red line). The model with fixed variance shows high-amplitude oscillations in the mean trait. The standard model clearly loses adaptive capacity in the long term (i.e., oscillations in the mean trait become weaker as the trait variance approaches zero). The corresponding NPZ dynamics is shown in Supplementary Figure 2.

With the chosen parameterization, the trait-diffusion model relaxes to moderate mean-trait oscillations. Noticeably, this does not limit the adaptive capacity of the model. The driving factor of the trait variance is trait diffusivity (the last term in (7c)), which is proportional to reproduction. Thus, under low initial adaptive capacity (Figure 1), the trait variance initially grows because, at the beginning of the simulation, reproduction rates are relatively high and the mean trait changes rapidly.

Scenario (b), the transition from limit cycle dynamics to equilibrium and vice versa under shock perturbations in grazing pressure and nutrient availability, further illustrates the different adaptive capabilities of the three models. As described by Merico et al. (2009), the chemostat system can undergo a Hopf bifurcation either as a function of the half-saturation parameter for zooplankton growth K_P or as function of nutrient input N₀.

The first set of results in Figure 3 shows a shock perturbation in K_P from 1000 to 200 μmolNl⁻¹ and back, which corresponds to a sudden, temporary increase in grazing pressure. Expectedly, at the beginning of the simulation when the grazing pressure is low, the system approaches equilibrium in all three models. The rapid increase in grazing pressure leads to emerging limit cycles in N, P, and Z with different amplitudes, see Supplementary Figure 3. When the grazing pressure is relaxed again, the dynamics return to equilibrium. However, the rate of adaptation, being linked to the trait variance, is different for the three models. In the standard model, the collapse of the trait variance prevents adequate adaptation as time progresses; the return to equilibrium is far slower than the natural time scales of the dynamics. The model with fixed variance is fastest to adapt, and the trait-diffusion model adapts sufficiently fast. We note that the behavior of the trait-diffusion model is not fully symmetric—the trait variance lags behind adaptation in the mean trait. As a result, adaptation from a state of large mean trait to a state of low mean trait is faster than vice versa, which suggests a hysteresis effect in the adaptive behavior.

FIGURE 3

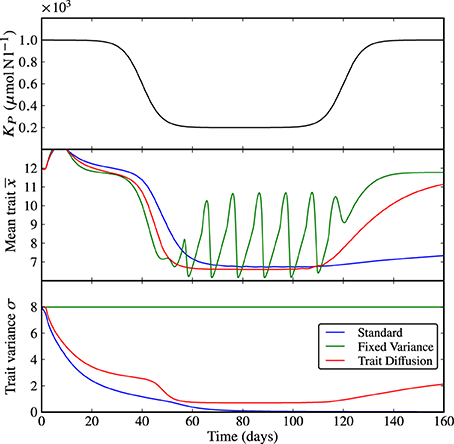
Figure 3. K_P shock. As K_P transitions from a state of low grazing pressure (i.e., high K_P) to an intermediate period of high grazing pressure (i.e., low K_P), the underlying dynamics shifts from equilibrium to limit cycles. When the grazing pressure is relaxed again (i.e., back to high K_P), the three models show different rates of adaptations. In the standard model, the collapse of the trait variance prevents adequate adaptation as time progresses. Adaptation is fastest in the model with fixed variance and sufficiently fast in the trait-diffusion model. The corresponding NPZ dynamics is shown in Supplementary Figure 3.

The same bifurcation behavior is observed when perturbing the environmental nutrient concentration N₀. Here, we simulate a rapid increase of N₀ from 20 to 80 μmol l⁻¹ and back (see Figure 4 and the corresponding Supplementary Figure 4). This experiment demonstrates once again (i) the critical dependence of the fixed variance model on the arbitrary choice in the degree of functional diversity set for the system, which is then “frozen” throughout the simulation and (ii) the dependence of the standard model on the initial conditions and on the choice of initial time. Only the trait diffusion model is capable of responding to the environmental perturbations with a dynamical change in trait variance.

FIGURE 4

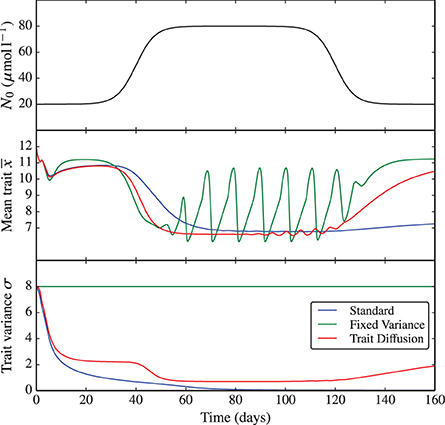
Figure 4. N₀ shock. As nutrient input N₀ is varied from low to high concentrations and back, the underlying dynamics shifts, similarly to the K_P shock, from equilibrium to limit cycles and back. The trait diffusion model responds to the environmental perturbation with a dynamical change in trait variance. The corresponding NPZ dynamics is shown in Supplementary Figure 4.

Being proportional to reproduction, the trait diffusivity parameter ν affects the adaptive capacity of the phytoplankton community as the probability of generating offspring with “new” trait values increases. As explained above, the limit of ν = 0 represents the standard case in which functional diversity is not sustained. The larger the trait diffusivity, the more pronounced are the oscillations in the mean edibility and the larger is the trait variance, see Figure 5. Analogously, ν also influences the amplitude and frequency of the oscillations in N, P, and Z (Supplementary Figure 5).

FIGURE 5

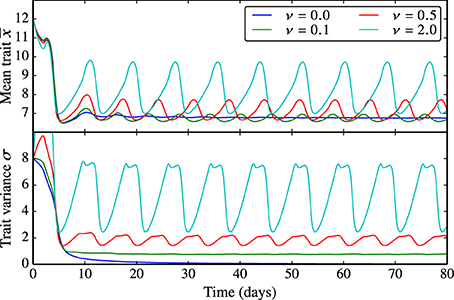
Figure 5. Behavior of the trait-diffusion model for different values of ν. Being proportional to reproduction, the trait diffusivity parameter ν affects the adaptive capacity of the phytoplankton community as the probability of generating offspring with new trait values increases. ν = 0 represents the standard case in which functional diversity is not sustained. The larger ν, the more pronounced are the oscillations in the mean edibility and the larger is the trait variance. The corresponding NPZ dynamics is shown in Supplementary Figure 5.

Obviously, ν is not the only parameter that influences the functional diversity of the phytoplankton community. In Figure 6, we show the combined effect of grazing pressure (as represented by different values of K_P) and ν on the average trait variance at steady-state. In the standard case where ν = 0, K_P has no impact on the trait variance. When ν > 0, the increase of the adaptive capacity is amplified at higher K_P.

FIGURE 6

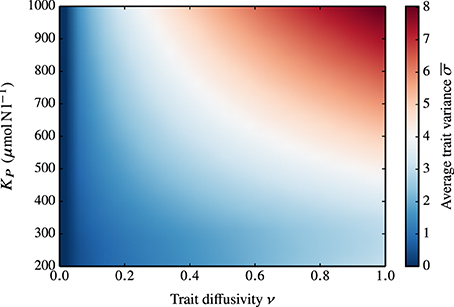
Figure 6. Dependence of the average, steady-state trait variance on K_P and ν. In the standard case (ν = 0), K_P has no impact on the trait variance (i.e., the average trait variance at steady-state is zero for all K_P values). At increasing ν corresponds an increase in the adaptive capacity, which is amplified at higher K_P.

4. Discussion

We have presented here a modeling approach that addresses the problem of maintaining phytoplankton functional diversity based on the mechanism of trait diffusion through subsequent generations. The method does not require exogenous processes, such as immigration, or the consideration of meta-communities. Analogous to the approach of Merico et al. (2009), the new model is developed for an idealized chemostat system in which the phytoplankton community is described in terms of total abundance, mean trait edibility, and trait variance, and is subject to an environment defined by nutrient availability and grazing pressure. A trade-off between the competitive ability of phytoplankton for harvesting nutrient and its value as food for zooplankton (or edibility) governs inter-specific differences within the community. We have then presented and compared three cases of differing functional diversity.

In the standard model, functional diversity expectedly declines over time. Although this behavior is consistent with the competitive exclusion principle (Hardin, 1960), chemostat experiments do not show decreases in the adaptive capacity of phytoplankton communities (Yoshida et al., 2003; Becks et al., 2010). In this case, lacking any mechanism for sustaining diversity, the model clearly cannot capture the adaptive capacity of communities, neither in the laboratory nor in the natural environment.

The simplest and perhaps most common way of sustaining diversity in adaptive dynamics models is to fix the trait variance to a constant value (Fussmann et al., 2003, 2007; Wirtz, 2013). This approach was recently adopted by Norberg et al. (2012) in a multi-species model application for studying the effects of climate change on biodiversity. Each species had a fixed trait variance assigned, therefore changes in the trait distribution occurred due to changes in the mean trait value of each species and inter-specific competition; i.e., the dynamics of intra-specific diversity were excluded. The variance was then set to zero for any species reaching very low abundance. While this assumption prevented that almost extinct populations reshaped toward fitter trait values and throve again, it did not allow for a mechanistic and dynamic treatment of the trait variance and therefore of functional diversity. Consistently with previous findings of richer dynamics in models that dynamically calculate the trait variance as opposed to assuming constant variance (Fussmann et al., 2003; Nuismer and Doebeli, 2004), our work shows clearly that functional diversity can dynamically impact the ecological interactions. Moreover, we consider a constant trait variance unrealistic, except in quite rare uniform and stable environments.

Our method of trait diffusion introduces a specific mechanism for maintaining diversity. The method is based on the assumption of a small probability ν that the trait value of an offspring slightly diverts from the parent's trait value. The source of trait variance in this case is made proportional to reproduction. This approach is able to successfully prevent competitive exclusion by maintaining the adaptive capacity of the community. An emergent and compelling body of literature suggests that many organisms can undergo adaptive phenotypic evolution over just a few generations (Carroll et al., 2007). Evolution may occur quickly enough to alter the outcomes of ecological interactions (Yoshida et al., 2003; Fussmann et al., 2007). The parameter ν of our model can be interpreted in this context of rapid evolutionary processes. Alternatively, given that the environment can impose trans-generational effects and generate heritable variation for many traits in animals, plants, and other organisms (Bonduriansky and Day, 2009), ν can account for trans-generational phenotypic plasticity (Agrawal et al., 1999; Holeski et al., 2012). Such trans-generational effects have been recently observed (Pomati and Nizzetto, 2013) in natural phytoplankton communities (Synechococcus sp. and Scenedesmus sp.) subject to triclosan, an antibacterial and antifungal agent common in disinfecting and personal care products and thus widely spread as environmental pollutant in waste, surface and coastal waters. Our method can therefore find useful applications in those studies aiming at predicting the rate of adaptation of species under different scenarios of environmental change (Visser, 2008).

A key advantage of the trait-diffusion approach is that the trait diffusivity ν depends only on phytoplankton reproduction. Thus, it could be measured in the laboratory under different predator-prey dynamics. The trait variance σ, instead, is highly dependent on the actual state of the system and therefore must be inferred from “real world” observations for applications modeling the ocean. From a theoretical point of view, ν could be derived from microscopic models of the reproductive process, much as constants of diffusivity in other modeling situations relate to parameters of random walks at the microscopic level.

Alternative mechanisms are of course conceivable for sustaining diversity. The flattening of the “fitness landscape” by the combined effects of multiple, convex trade-offs (Beardmore et al., 2011) is one of those. Recently, a model combining approximations of mechanistic and tested relations between traits and growth functions (Wirtz, 2013) has been shown to produce multiple maxima in the fitness landscape. The impact of the shape of trade-offs deserves further investigations given that models typically postulate linear trade-offs for the sake of simplicity, and also because of the limited empirical evidence available (Smith et al., 2014).

In conclusion, our mechanistic formulation, which does not require exogenous factors, is able to prevent competitive exclusion and thus maintain the adaptive capacity of a phytoplankton community in the confined environment of a chemostat system. This is accomplished by introducing a trans-generational trait variation mechanism proportional to reproduction in the context of a trait-based, adaptive dynamics model. This mechanism can reflect the maintenance of biodiversity via rapid evolution or trans-generational phenotypic plasticity. An obvious next step would be to apply our method in the context of a real ocean.

Author Contributions

Agostino Merico and Marcel Oliver conceived the idea of the study; Marcel Oliver developed the mathematical model; Gunnar Brandt coded the model and performed the numerical experiments; Agostino Merico wrote the first draft of the manuscript; all authors contributed to interpret the results and to revise the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgment

We thank Georg Gottwald for pointing out the connection between the aggregate trait-diffusion model and the method of collective coordinates. Agostino Merico and S. Lan Smith gratefully acknowledge support provided by a CREST project (Principal Investigator, S. Lan Smith) funded by the Japan Science and Technology Agency. Marcel Oliver further thanks the German Science Foundation for support.

Supplementary Material

The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fevo.2014.00059/abstract

References

Agrawal, A. A., Laforsch, C., and Tollrian, R. (1999). Transgenerational induction of defences in animals and plants. Nature 401, 60–63. doi: 10.1038/43425

CrossRef Full Text | Google Scholar

Anderson, T. R. (2005). Plankton functional type modelling: running before we can walk?. J. Plankton Res. 27, 1073–1081. doi: 10.1093/plankt/fbi076

CrossRef Full Text | Google Scholar

Beardmore, R., Gudelj, I., Lipson, D., and Hurst, L. (2011). Metabolic trade-offs and the maintenance of the fittest and the flattest. Nature 472, 342–346. doi: 10.1038/nature09905

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Becks, L., Ellner, S., Jones, L., and Hairston, N. Jr. (2010). Reduction of adaptive genetic diversity radically alters eco-evolutionary community dynamics. Ecol. Lett. 13, 989–997. doi: 10.1111/j.1461-0248.2010.01490.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bonduriansky, R., and Day, T. (2009). Nongenetic inheritance and its evolutionary implications. Ann. Rev. Ecol. Evol. Syst. 40, 103–125. doi: 10.1146/annurev.ecolsys.39.110707.173441

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bruggeman, J., and Kooijman, S. A. L. M. (2007). A biodiversity-inspired approach to aquatic ecosystem modeling. Limnol. Oceanogr. 52, 1533–1544. doi: 10.4319/lo.2007.52.4.1533

CrossRef Full Text | Google Scholar

Carroll, S., Hendry, A., Reznick, D., and Fox, C. (2007). Evolution on ecological time-scales. Funct. Ecol. 21, 387–393. doi: 10.1111/j.1365-2435.2007.01289.x

CrossRef Full Text | Google Scholar

Chesson, P. (2000). Mechanisms of maintenance of species diversity. Ann. Rev. Ecol. Syst. 31, 343–366. doi: 10.1146/annurev.ecolsys.31.1.343

CrossRef Full Text | Google Scholar

Clement, C., and Wood, M. (1980). Moment and Fokker-Planck equations for the growth and decay of small objects. Proc. R. Soc. Lond. Math. Phys. Sci. 371, 1747. doi: 10.1098/rspa.1980.0096

CrossRef Full Text | Google Scholar

Eggers, S. L., Lewandowska, A. M., Barcelos e Ramos, J., Blanco-Ameijeiras, S., Gallo, F., and Matthiessen, B. (2014). Community composition has greater impact on the functioning of marine phytoplankton communities than ocean acidification. Global Change Biol. 20, 713–723. doi: 10.1111/gcb.12421

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ellner, S., and Becks, L. (2010). Rapid prey evolution and the dynamics of two-predator food webs. Theor. Ecol. 4, 133–152. doi: 10.1007/s12080-010-0096-7

CrossRef Full Text | Google Scholar

Falkowski, P., Barber, R., and Smetacek, V. (1998). Biogeochemical controls and feedbacks on ocean primary production. Science 281, 200–206. doi: 10.1126/science.281.5374.200

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Falkowski, P. G., Katz, M. E., Knoll, A. H., Quigg, A., Raven, J. A., Schofield, O., et al. (2004). The evolution of modern eukaryotic phytoplankton. Science 305, 354–360. doi: 10.1126/science.1095964

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Falkowski, P. G., and Oliver, M. J. (2007), Mix and match: how climate selects phytoplankton. Nat. Rev. Microbiol. 5, 813–819. doi: 10.1038/nrmicro1751

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Fasham, M. J. R., Ducklow, H. W., and McKelvie, S. M. (1990). A nitrogen-based model of plankton dynamics in the oceanic mixed layer. J. Mar. Res. 48, 591–639. doi: 10.1357/002224090784984678

CrossRef Full Text | Google Scholar

Follows, M. J., Dutkiewicz, S., Grant, S., and Chisholm, S. W. (2007). Emergent biogeography of microbial communities in a model ocean. Science 315, 1843–1846. doi: 10.1126/science.1138544

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Fussmann, G. F., Ellner, S. P., and Hairston, N. G. Jr. (2003). Evolution as a critical component of plankton dynamics. Proc. R. Soc. Lond. B 270, 1015–1022. doi: 10.1098/rspb.2003.2335

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Fussmann, G. F., Loreau, M., and Abrams, P. A. (2007). Eco-evolutionary dynamics of communities and ecosystems. Funct. Ecol. 21, 465–477. doi: 10.1111/j.1365-2435.2007.01275.x

CrossRef Full Text | Google Scholar

Gottwald, G., and Kramer, L. (2004). On propagation failure in one- and two-dimensional excitable media. Chaos 14, 855–863. doi: 10.1063/1.1772552

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hardin, G. (1960). The competitive exclusion principle. Science 131, 1292–1297. doi: 10.1126/science.131.3409.1292

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Holeski, L. M., Jander, G., and Agrawal, A. A. (2012). Transgenerational defense induction and epigenetic inheritance in plants. Trends Ecol. Evol. 27, 618–626. doi: 10.1016/j.tree.2012.07.011

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Huston, M. (1979). A general hypothesis of species diversity. Am. Natural. 113, 81–101. doi: 10.1086/283366

CrossRef Full Text | Google Scholar

Kinnison, M., and Hairston, N. J. (2007). Eco-evolutionary conservation biology: contemporary evolution and the dynamics of persistence. Funct. Ecol. 21, 444–454. doi: 10.1111/j.1365-2435.2007.01278.x

CrossRef Full Text | Google Scholar

Leibold, M. A., and Norberg, J. (2004). Biodiversity in metacommunities: Plankton as complex adaptive systems? Limnol. Oceanogr. 49, 1278–1289. doi: 10.4319/lo.2004.49.4-part-2.1278

CrossRef Full Text | Google Scholar

Levin, S. (1981). “Mechanisms for the generation and maintenance of diversity,” in The Mathematical Theory of the Dynamics of Biological Populations, eds R. Hiorns and D. Cooke (London: Academic Press), 173–194.

Google Scholar

Levin, S. (2003). Complex adaptive systems: exploring the known, the unknown and the unknowable. Bull. Am. Math. Soc. 40, 3–19. doi: 10.1090/S0273-0979-02-00965-5

CrossRef Full Text | Google Scholar

Maharjan, R., Seeto, S., Notley-McRobb, L., and Ferenci, T. (2006). Clonal adaptive radiation in a constant environment. Science 313, 514–517. doi: 10.1126/science.1129865

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Merico, A., Bruggeman, J., and Wirtz, K. (2009). A trait-based approach for downscaling complexity in plankton ecosystem models. Ecol. Model. 220, 3001–3010. doi: 10.1016/j.ecolmodel.2009.05.005

CrossRef Full Text | Google Scholar

Norberg, J., Swaney, D. P., Dushoff, J., Lin, J., Casagrandi, R., and Levin, S. A. (2001). Phenotypic diversity and ecosystem functioning in changing environments: a theoretical framework. Proc. Natl. Acad. Sci. U.S.A. 98, 11376–11381. doi: 10.1073/pnas.171315998

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Norberg, J., Urban, M., Vellend, M., Klausmeier, C., and Loeuille, N. (2012). Eco-evolutionary responses of biodiversity to climate change. Nat. Clim. Change 2, 747–751. doi: 10.1038/nclimate1588

CrossRef Full Text | Google Scholar

Nuismer, S., and Doebeli, M. (2004). Genetic correlations and the coevolutionary dynamics of three-species systems. Evolution 58, 1165–1177. doi: 10.1111/j.0014-3820.2004.tb01697.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pomati, F., and Nizzetto, L. (2013). Assessing triclosan-induced ecological and trans-generational effects in natural phytoplankton communities: a trait-based field method. Ecotoxicology 22, 1–16. doi: 10.1007/s10646-013-1068-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ptacnik, R., Solimini, A. G., Andersen, T., Tamminen, T., Brettum, P., Lepistö, L., et al. (2008). Diversity predicts stability and resource use efficiency in natural phytoplankton communities. Proc. Natl. Acad. Sci. U.S.A. 105, 5134–5138. doi: 10.1073/pnas.0708328105

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Savage, V. M., Webb, C. T., and Norberg, J. (2007). A general multi-trait-based framework for studying the effects of biodiversity on ecosystem functioning. J. Theor. Biol. 247, 213–229. doi: 10.1016/j.jtbi.2007.03.007

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Smith, S. L., Merico, A., Wirtz, K. W., and Pahlow, M. (2014). Leaving misleading legacies behind in plankton ecosystem modelling. J. Plankton Res. 36, 613–620. doi: 10.1093/plankt/fbu011

CrossRef Full Text | Google Scholar

Tirok, K., Bauer, B., Wirtz, K., and Gaedke, U. (2011). Predator-prey dynamics driven by feedback between functionally diverse trophic levels. PLoS ONE 6:e27357. doi: 10.1371/journal.pone.0027357

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Visser, M. (2008). Keeping up with a warming world; assessing the rate of adaptation to climate change. Proc. R. Soc. B Biol. Sci. 275, 649–659. doi: 10.1098/rspb.2007.0997

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Wirtz, K. W. (2013). Mechanistic origins of variability in phytoplankton dynamics: Part i: Niche formation revealed by a size-based model. Mar. Biol. 160, 2319–2335. doi: 10.1007/s00227-012-2163-7

CrossRef Full Text | Google Scholar

Yoshida, T., Jones, L. E., Ellner, S. P., Fussmann, G. F., and Hairston, N. G. Jr. (2003). Rapid evolution drives ecological dynamics in a predator-prey system. Nature 424, 303–306. doi: 10.1038/nature01767

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar