- Department of Biological Sciences, University of South Florida St. Petersburg, St. Petersburg, FL, USA
Regulatory agencies often rely on paleolimnological studies for models that predict variables pertinent to nutrient loading or to public perception. Limitations of statistical approaches often pose significant challenges. We present a case study from Florida USA that involves diatom-based inference models derived from two calibration sets. Spatial autocorrelation conclusions differed with methods and approaches, and h block cross validation was unduly pessimistic. Calibration sets and temporal sets represent fundamentally different populations. The accuracy and precision of temporal inferences for specific lakes can be affected by site-specific factors, and are not likely to be known with the certainty suggested by models. Error terms can provide a false sense of knowledge about the reliability of inferences for temporal samples. Broad error terms for limnetic total phosphorus models have little or no utility in any event. Limnetic total P models can perform poorly when applied to N-limited lakes. Transfer functions should be regarded more as qualitative indicators of past water quality rather than methods with known precision, and more emphasis should be placed on multiple lines of evidence and ecological interpretations.
Introduction
Transfer functions are common tools for quantifying changes in limnetic nutrient concentrations and primary-producer standing crops in lakes that have been subject to eutrophication (Brooks et al., 2001; Vermaire and Gregory-Eaves, 2007; Guilizzoni et al., 2010). Models are derived that relate recent biological remains in sediments to the measured water quality of overlying waters for a large set of lakes on the landscape. The goal is to construct defensible models that can provide inferences for passive (sediment-core) samples when historic water-quality data are lacking. Models typically are tested with cross-validation procedures that are intended to provide realistic estimates of error terms. Inferences based on assemblages in sediment cores are used to help define reference conditions and restoration goals for lake-management programs (Smol, 1992; Brenner et al., 1993; Battarbee, 1999). This paper focuses on diatoms as historic indicators, but the concepts are applicable to other biological indicators used for eutrophication assessment.
Modern quantitative methods (CCA: ter Braak, 1986; ML and WA: Birks et al., 1990; WA-PLS: ter Braak and Juggins, 1993) were first used to assess water-quality change in acid-rain studies. Study regions were sometimes remote, and lakes were often similar in water quality (e.g., Davis et al., 1983; Dixit et al., 1988; Charles et al., 1990). Calibration and core lakes were generally acidic, poorly buffered, and low in nutrient content. Lakes were affected by relatively few aspects of human influence, so inferences were subject to minimal covariant influence. Because, pH was never de-transformed from its logarithm expression, error terms were small with respect to inferred means, and models appeared to have high precision. The same modeling approaches have been applied to eutrophication assessment, but this application involves greater limnological complexity, so it merits careful scrutiny.
Several factors contribute to greater environmental complexity in eutrophication studies than in acid-rain studies. Eutrophication is not regionally uniform, but it depends on unique combinations of local influences that include agricultural runoff, storm-water inputs, septic and sewage-treatment inputs, and industrial wastes. Nutrient inputs of nitrogen and phosphorus vary depending on specific sources (Riedinger-Whitmore et al., 2005; Davidson and Jeppesen, 2013). Lakes that undergo eutrophication in urban settings can be subject to simultaneous changes in alkalinity or pH (Ramstack et al., 2003; Brenner et al., 2006; Whitmore et al., 2006). Even within a given study region, factors that induce trophic-state changes can vary.
Lakes of greatest management concern often lie in areas where there is high population density and diverse environmental influences. Lakes in historic studies might have been subject to unexpected influences, such as contaminants, which affected biological indicators in ways that could not be anticipated with a calibration set. The complex nature of urban lakes and eutrophication introduces many sources of variance that potentially create substantial differences between populations of spatial (calibration) and temporal (core) samples.
This paper addresses issues related to the practical aspects of modeling trophic-state changes for lake-management programs. We discuss some statistical approaches, use examples to illustrate potential concerns, and show why knowledge about specific lakes, their history, and ecology can be important for evaluating quantitative inferences. We also examine generalizations about models and eutrophication assessments in regions with shallow lakes.
Purpose-designed Models for Lake Management Programs and Their Challenges
Lake-management agencies typically have well-defined concerns about water-quality issues within their jurisdictions. Paleolimnologists are sometimes called on to construct calibration sets and transfer functions to address criteria within a specific range of water quality. Agencies might intend to regulate water quality for chlorophyll a concentrations or cyanobacteria because these factors are evident to the public. In other cases, agencies focus on limnetic nutrient concentrations in order to regulate nutrient loading. Variables of management concern are likely to determine the choice of dependent variables for models. Agencies might have preconceived ideas about reference conditions or calibration designs, and sometimes might not be well-informed about the necessary size or range of calibration sets, or how transfer functions work. Paleolimnologists often must work actively with agencies to inform them about appropriate project design and methods.
A case study from Florida, USA illustrates typical management needs, and how paleolimnological studies often work within constraints imposed by agencies. Florida Department of Environmental Protection (FDEP) asked us to create a calibration set and transfer function to assess nutrient criteria standards proposed by the U.S. Environmental Protection Agency (EPA). FDEP was concerned that the maximum acceptable chlorophyll a concentration (20 μg/L) promulgated by the EPA for lakes with color > 40 PCU and alkalinity >20 mg/L CaCO3 was subject to a high Type I error rate, so the proposed federal standard would incorrectly describe naturally productive lakes as impaired.
FDEP requested a model to infer past chlorophyll a, but because this is a response variable, we advocated for inclusion of a limnetic total phosphorus (P) inference model. FDEP selected lakes in the color range of 20–100 PCU and alkalinity range of 20–200 mg/L, which mitigated that lakes would have pH values >~6.5. We had concern that reference conditions for some lakes might lie outside of this range. FDEP initially proposed 30 calibration lakes and 30 historic application lakes. We advocated for appropriate calibration size (Reavie and Juggins, 2011) by invoking expert opinion through the Paleolimnology Forum listservice, after which the agency agreed to a 70-lake calibration design with a 5-lake application. The agency provided 5-year means of water-quality data from 2005 to 2010 to match sediment surface samples, but our research team was contractually required to collect the surface samples in 2012–2013. Record-low water levels in 2012–2013 changed solute concentrations and introduced a source of error between diatoms in surface samples and the older water-quality values.
As we anticipated, the chlorophyll a transfer function (r2 = 0.51, RMSE = 0.224 log10 chlorophyll a, n = 72) had less predictive capability than the total P model (r2 = 0.62, RMSE = 0.183 log10 total P). Analog matching showed that reference conditions for 4 of the 5 historical lakes were outside the calibration range, which substantiated our initial concern. Our report was redeemed somewhat by inclusion of a previous model based on a broader calibration design that had stronger predictive capability (r2 = 0.88, RMSE = 0.177 log10 total P, r2boot = 0.77, n = 69). We interpreted lake histories using multiple lines of evidence in addition to water-quality inferences.
This example shows that studies designed to address specific needs of lake-management agencies often must be conducted within imposed constraints that can create practical challenges for paleolimnologists. Investigators must use judgment and advocate for appropriate project design when necessary.
Spatial Autocorrelation, Cross Validation, and the Comparability of Spatial and Temporal Sets
Agencies often seek precision estimates for water-quality inferences. There are inherent problems, however, with defining appropriate error terms for temporal samples based on spatial calibration sets. The following example illustrates potential difficulties.
For needs of the FDEP project, we used expert statistical consultation (Steve Juggins, Newcastle University) for model development and testing. Despite apparent reasonable predictive capability of the total P model (r2 = 0.62), spatial dependency in environmental data was indicated by Mantel correlograms (Oden and Sokal, 1986) at 10-km distances. RMSE estimates increased significantly at 20-km distances, so h block cross validation (Telford and Birks, 2009) was used to exclude samples at a critical cutoff distance of 20 km during cross-validation cycles. As a result, the r2 of the total P model dropped to 0.27 with an RMSEP of 0.27 log10 μg/L. At this level of performance, a total P inference of 50 μg/L had a 68% confidence interval of 27–93 μg/L, and a 95% confidence interval of 15–169 μg/L, rendering inferences useless for lake-management purposes. The chlorophyll a model was deemed to have no practical predictive power.
This assessment proved untenable for the agency. Following the above assessment, the present authors sought other perspectives about model utility. We cross validated the total P model with surface samples from 41 independent lakes that had known water quality. The r2 was 0.48, less than the ostensible r2 of 0.62, distinctly better than the h-block estimate of 0.27, and comparable to the bootstrap estimate of 0.46. We interpret that spatial autocorrelation in environmental data alone might not have posed a problem as serious as h block cross validation suggested. Autocorrelation must occur in both response and environmental variables for regression coefficients to be adversely affected (Legendre et al., 2002). In addition, calibration lakes were 1–5 km apart, so the elimination distance of 20 km in h block testing probably led to removal of too many lakes and caused performance estimates to deteriorate. With h block cross validation, there are evident risks of determining that potentially useful models have reduced or little practical utility.
Telford and Birks (2009) showed that pseudoreplication from spatial dependency can lead to underestimation of prediction errors. Similar lakes in one or more regions can create apparent strength in predictive ability, and cause overly optimistic error estimates. If a model is applied to a lake from a dissimilar region, actual error terms for inferences might be larger than the model suggests. By removing pseudoreplicate samples, h block cross validation provides more pessimistic error estimates to compensate for that tendency. If a passive sample is well-centered in the calibration set, however, h block might provide error estimates that are too pessimistic. We question whether potentially overly optimistic or overly pessimistic error estimates are preferable, and suggest that neither might be objectively more correct.
In some calibration sets, regional geology might contribute to spatial relationships in water quality. Judgements about the inclusion of environmental variables might affect conclusions about autocorrelation. For example, Secchi depth and chlorophyll a are highly correlated and interdependent, as are alkalinity and specific conductance. All such correlated variables were included in the assessment that found the FDEP models of no value because of spatial environmental patterns. For additional insight about lakes in this region, we tested for spatial autocorrelation in our older calibration set (r2 = 0.88, n = 69 lakes) using multivariate Mantel correlograms and multiscale ordination (MSO: Borcard et al., 2011). For these tests, we used a priori knowledge based on exploratory analyses to select only environmental variables that exert significant influence on diatom assemblages, and we avoided redundant environmental variables. These tests showed no spatial dependency in diatom or environmental data, including at the 20-km distance. Spatial autocorrelation appears to be influenced by lakes in the calibration set and by the selection of variables. Our conclusions from this experience were that no single method of assessing model performance or error terms seems distinctly more correct or defensible, but the outcome of testing might discount models that could be informative for lake management programs.
Another important concern is the potential distinction between spatial and temporal data sets. Cross validation tests evaluate relationships among environmental and biological data from the landscape, but they don't necessarily provide accurate error estimates for samples in a given sediment core. An RMSEP estimate is determined using separate lakes, whereas samples in a core are temporally correlated. In two lakes for which we have >20 years of modern water-quality values, limnetic total P and pH have no significant correlation (r = 0.17, p = 0.78; r = 0.08, p = 0.50) whereas in the calibration set, they are significantly correlated (r = 0.44, p < 0.001). Samples in calibration and historic sets represent different populations, and can have incomparable types of variance and relationships among environmental variables.
The Site-Specific Nature of Model Response in Complex Systems
Secondary variables might change over time in given study lakes, and might unpredictably exert covariant effects on biological indicators and inferences for variables of interest. As a case example, Lakes Lochloosa and Little Jackson in Florida have been subject to substantial increases in P loading during the twentieth century. Lochloosa experienced an 8-fold increase in P deposition (Kenney et al., 2014), and Little Jackson sustained an approximate 5-fold increase (Whitmore et al., 2006). Diatom-based limnetic total P inferences reflect increased P loading in Lochloosa, but they do not in Little Lake Jackson (Figure 1).
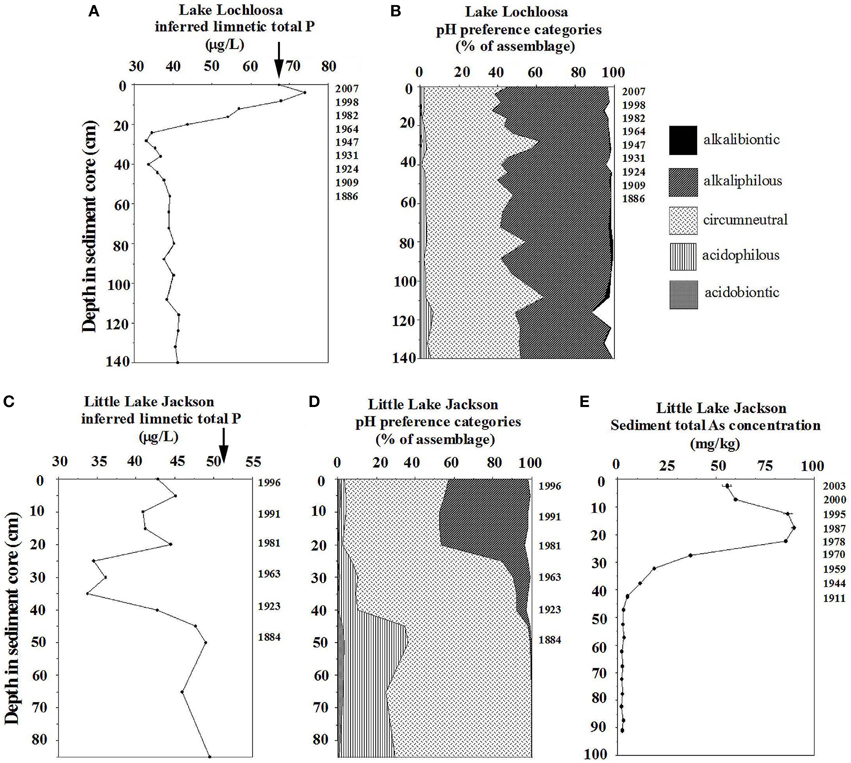
Figure 1. Diatom-based inferred limnetic total P values for Lakes Lochloosa and Little Jackson, with summary pH autecological preference information, and sedimented arsenic concentrations in Little Lake Jackson. Summary pH autecological information was calculated as in Whitmore et al. (1996). Arrows on total P panels indicate means of modern measured water quality. (A) Inferred limnetic total P for Lake Lochloosa (modified from Kenney et al., 2014). (B) Summary pH preference data for diatoms in Lake Lochloosa. (C) Inferred limnetic total P for Little Lake Jackson. (D) Summary pH preference data for diatoms in Little Jackson (updated from Whitmore et al., 2006). (E) Net sedimented total As concentrations from Little Lake Jackson (modified from Whitmore et al., 2008).
The difference in model response might result from effects of pH on diatom assemblages. Little Lake Jackson underwent significant alkalization during the twentieth century because of wetland destruction and ionic loading (Whitmore et al., 2006: Figure 1). The lake also was subject to substantial inputs of arsenical pesticides (Whitmore et al., 2008; Figure 1), which might have affected diatom communities. In contrast, Lake Lochloosa showed no change in pH during increased P loading (Kenney et al., 2014; Figure 1). Limnetic total P inferences at the base of the Lochloosa core were consistent with reference conditions for the region, and the modern total P inference (67.2 μg/L) was nearly identical to the modern measured mean (67.4 μg/L, Figure 1). Differences in model performance did not result from an abundance of fragilarioid diatoms, an often generalized explanation for model inaccuracy in shallow lakes (Bennion et al., 2001; Sayer, 2001; Heathcote et al., 2015). In surface sediments of both lakes, benthic fragilarioid taxa represent ~ 30% of the assemblage, and species of Aulacoseira represent ~ 20%, along with various other taxa. Lochloosa, which had more tenable total P inferences, is 44 times larger in size and is shallower (max. depth = 3 m) than Little Jackson (max. depth = 6.9 m). Lochloosa might have been expected to yield worse inferences than Little Jackson because of benthic diatom proliferation or wind-generated mixing of sediments, but this was not the case. In short, we can not generalize whether models are likely to work well or fail based on lake depth or other broad characteristics.
Generalizations about Fragilarioid Taxa in Shallow Lakes
In many of our studies in Florida, fragilarioid taxa are not so much ubiquitous or responding to light in shallow water with indifference to nutrients (e.g., Bennion et al., 2001) as they are indicative of hypereutrophic conditions, where light penetration is poor. Their survival in low-light conditions is probably possible because of tychoplanktonic lifestyles (Sayer, 2001). In our more reliable calibration set, limnetic total P optima of Pseudostaurosira brevistriata (127 μg/L), Staurosira construens var. venter (89 μg/L), and Staurosirella pinnata (87 μg/L) are significantly higher, for example, than those of Aulacoseira ambigua (49 μg/L), A. granulata (44 μg/L), or A. distans (50 μg/L). Lakes in the range of fragilarioid optima often are dominated by cyanobacteria. P. brevistriata is significantly correlated with log10 limnetic total P (r = 0.51, p < 0.001, n = 25) but not with mean water depth (r = 0.06). Temporal shifts to fragilarioid dominance in Florida often mark the onset of advanced eutrophication. Florida lakes in this range tend to be N limited (Kratzer and Brezonik, 1981; Paulic et al., 1996), causing models to underestimate limnetic total P because it is available in excess of biological needs. N-limited lakes often must be eliminated from our total P calibration sets (Brenner et al., 1993; Riedinger-Whitmore et al., 2005; Kenney et al., 2014) because total P is underestimated in those lakes. Elimination of fragilarioid taxa from diatom profiles would remove important ecological information about water-quality change in many cases, and their presence in our region can not be generalized as non-informative.
Impractically Large Error Expressions Serve Little Useful Purpose
Because agencies regulate variables such as limnetic total P rather than log10 total P, eutrophication studies don't have the luxury of leaving inferences log transformed, as with acidification studies. When confidence intervals become so broad that they span several trophic-state categories, which often occurs when log total P inferences are de-transformed, they serve no practical use for lake-management purposes. Figure 2 shows confidence intervals for limnetic total P reconstructions in Lake Lochloosa. Despite accurate inferences with respect to reference and modern conditions and a fairly robust model (r2 = 0.88, RMSE = 0.177 log10 total P, n = 69, r2boot = 0.77), confidence intervals are uninformative: it is impossible to demonstrate water-quality change based on error terms from the de-transformed total P inferences. Many published studies report RMSE for limnetic total P models in log-transformed units to avoid unreasonably broad confidence limits. We note that even for strong limnetic P models, investigators might do well to intentionally disregard error terms and treat inferences as qualitative guidelines.
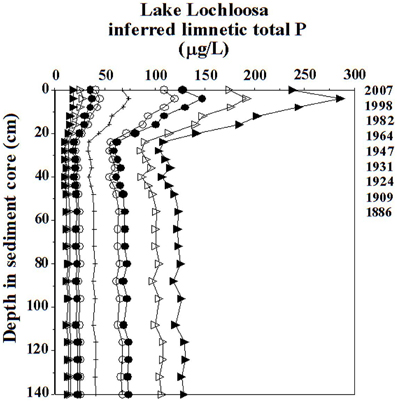
Figure 2. Confidence intervals for diatom-based inferred limnetic total P values for the Lake Lochloosa core. Hatched lines: inferred means. Open circles: 68% confidence intervals (± 1 SE) for the model. Closed circles: 95% confidence intervals (± 1.96 SE) for the model. Open triangles: 68% confidence intervals based on bootstrapping. Closed triangles: 95% confidence intervals based on bootstrapping.
Are Univariate Models the Best We Can Offer?
Statistical approaches for univariate models typically involve removing less common taxa to minimize noise. Eliminating “non-informative” taxa (Juggins et al., 2015) to narrow confidence intervals might provide greater precision, but it can remove information about factors other than the specific variable of interest. Removing taxa shifts the focus to species that serve a singular purpose. Taxa that appear non-informative for a univariate model can reflect other aspects of a lake's history, such as past hydrological influences, macrophyte presence, or changes in water depth. When taxa are removed from an assessment, it narrows the focus of interpretation. Is this potentially “throwing out the baby with the bath water”?
Prediction models typically involve acceptance of basic assumptions that potentially limit the thinking of paleolimnologists about historical changes. One is that system response can be meaningfully understood by focusing on one variable of interest. Another is that by studying the general, we can better understand the specific. A third is that by eliminating less common taxa, we obtain more information about a system. To quote a comment by Deevey (1988) regarding assumptions of hydrological modeling, “If this confidence is misplaced, most limnologists would probably prefer not to hear about it.”
Conclusions and Recommendations
Environmental protection and conservation agencies deal with considerable financial and legal obligations related to lake management, so paleolimnological investigators must help address their needs while endeavoring to apply defensible scientific practices. Investigators often are required to work within constraints of project designs, and to actively inform agencies about appropriate study design, optimal approaches, and expected outcomes.
We suggest that calibration sets and temporal sets of data are potentially different populations. The accuracy and precision of temporal inferences for a given lake can be affected largely by site-specific factors, and they are not likely to be known with the objective certainty that modeling usually implies. The effects of local influences can vary over time as well. Using a deductive approach to quantify precision is tenuous for temporal samples in lakes that have unique histories and arrays of environmental influences. Error terms in some cases might underestimate the informativeness of inferences, and in other cases might imply accuracy that is not warranted because of site-specific influences that can't be anticipated through the calibration. As a result, statements about statistical precision can mislead lake managers about the certainty or usefulness of reference estimates. Broad error terms for limnetic total P models generally have little or no utility. In view of these considerations, we recommend that limnetic total P inferences should be regarded as qualitative guidelines rather than values with known precision. To do otherwise involves some degree of misrepresentation.
The accuracy of inferences for reference conditions are best judged in terms of reasonableness with respect to benchmark lakes and edaphic conditions for a given region. Trajectories should be compared with multiple lines of evidence to evaluate patterns and timing, and inferences should be compared with periods of known water quality when data are available. Compelling arguments have been made about the need to incorporate contemporary ecology into assessments of lake ecosystem change (Battarbee et al., 2005; Sayer et al., 2010), and paleolimnologists should consider this advice. The most comprehensive historical reconstructions are those that address multiple system responses (Davidson et al., 2010), and those that combine assessments of floristic change and known ecologies of taxa with quantitative estimates (e.g., Bennion et al., 2011). We recommend that studies addressing trophic-state assessment for lake-management purposes should avoid heavy reliance on univariate models. Statistical modeling does not provide an adequate substitute for a more comprehensive knowledge about the ecology and limnology of the systems being studied.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Battarbee, R. W. (1999). The importance of palaeolimnology to lake restoration. Hydrobiologia 395/396, 149–159. doi: 10.1023/A:1017093418054
Battarbee, R. W., Anderson, N. J., Jeppesen, E., and Leavitt, P. R. (2005). Combining paleolimnological and limnological approaches in assessing lake ecosystem response to nutrient reduction. Freshw. Biol. 50, 1772–1780. doi: 10.1111/j.1365-2427.2005.01427.x
Bennion, H., Appleby, P. G., and Phillips, G. L. (2001). Reconstructing nutrient histories in the Norfolk Broads, UK: implications for the role of diatom-total phosphorus transfer functions in shallow lake management. J. Paleolimnol. 26, 181–204. doi: 10.1023/A:1011137625746
Bennion, H., Simpson, G. L., Anderson, N. J., Clarke, G., Dong, X., Hobæk, A., et al. (2011). Defining ecological and chemical reference conditions and restoration targets for nine European lakes. J. Paleolimnol. 45, 415–431. doi: 10.1007/s10933-010-9418-4
Birks, H. J. B., Line, J. M., Juggins, S., Stevenson, A. C., and ter Braak, C. J. F. (1990). Diatoms and pH reconstruction. Philos. Trans. R. Soc. Lond. B Biol. Sci. 327, 263–278. doi: 10.1098/rstb.1990.0062
Borcard, D., Gillet, F., and Legendre, P. (2011). Numerical Ecology with R. New York, NY: Springer Press.
Brenner, M., Whitmore, T. J., Flannery, M. S., and Binford, M. W. (1993). Paleolimnological methods for defining target conditions in lake restoration: Florida case studies. Lake Reserv. Manag. 7, 209–217. doi: 10.1080/07438149309354272
Brenner, M., Whitmore, T. J., Riedinger-Whitmore, M. A., DeArmond, B., Leeper, D. A., Kenney, W. F., et al. (2006). Geochemical and biological consequences of groundwater augmentation in lakes of west-central Florida (USA). J. Paleolimnol. 36, 371–383. doi: 10.1007/s10933-006-9008-7
Brooks, S. J., Bennion, H., and Birks, H. J. B. (2001). Tracing lake trophic history with a chironomid-total phosphorus inference model. Freshw. Biol. 46, 513–533. doi: 10.1046/j.1365-2427.2001.00684.x
Charles, D. F., Binford, M. W., Furlong, E. T., Hites, R. A., Mitchell, M. J., Norton, S. A., et al. (1990). Paleoecological investigations of recent lake acidification in the Adirondack Mountains, N. Y. J. Paleolimnol. 3, 195–241. doi: 10.1007/BF00219459
Davidson, T. A., and Jeppesen, E. (2013). The role of palaeolimnology in assessing eutrophication and its impact on lakes. J. Paleolimnol. 49, 391–410. doi: 10.1007/s10933-012-9651-0
Davidson, T. A., Sayer, C. D., Perrow, M., and Jeppesen, E. (2010). The simultaneous inference of zooplanktivorous fish and macrophyte density from sub-fossil cladoceran assemblages: a multivariate regression tree approach. Freshw. Biol. 55, 546–564. doi: 10.1111/j.1365-2427.2008.02124.x
Davis, R. B., Norton, S. A., Hess, C. T., and Brakke, D. F. (1983). Paleolimnological reconstruction of the effects of atmospheric deposition of acids and heavy metals on the chemistry and biology of lakes in New England and Norway. Hydrobiologia 103, 113–123. doi: 10.1007/BF00028438
Deevey, E. S. (1988). Estimation of downward leakage from Florida lakes. Limnol. Oceanogr. 33, 1308–1320. doi: 10.4319/lo.1988.33.6.1308
Dixit, A. S., Dixit, S. S., and Evans, R. D. (1988). The relationship between sedimentary diatom assemblages and lakewater pH in 35 Quebec lakes, Canada. J. Paleolimnol. 1, 23–38. doi: 10.1007/bf00202191
Guilizzoni, P., Marchetto, A., Lami, A., Gerli, S., and Musazzi, S. (2010). Use of sedimentary pigments to infer past phosphorus concentration in lakes. J. Paleolimnol. 45, 433–445. doi: 10.1007/s10933-010-9421-9
Heathcote, A. J., Ramstack Hobbs, J. M., Anderson, N. J., Frings, P., Engstrom, D. R., and Downing, J. A. (2015). Diatom floristic change and lake paleoproduction as evidence of recent eutrophication in shallow lakes of the midwestern USA. J. Paleolimnol. 53, 17–34. doi: 10.1007/s10933-014-9804-4
Juggins, S., Simpson, G. L., and Telford, R. J. (2015). Taxon using statistical learning techniques to improve transfer function prediction. Holocene 25, 130–136. doi: 10.1177/0959683614556388
Kenney, W. F., Whitmore, T. J., Buck, D. J., Brenner, M., Curtis, J. H., Di, J. J., et al. (2014). Whole-basin, mass-balance approach for identifying critical phosphorus-loading thresholds in shallow lakes. J. Paleolimnol. 51, 515–528. doi: 10.1007/s10933-014-9771-9
Kratzer, C. R., and Brezonik, P. L. (1981). A Carlson-type trophic state index for nitrogen in Florida lakes. Water Resour. Bull. 17, 713–715. doi: 10.1111/j.1752-1688.1981.tb01282.x
Legendre, P., Dale, M. R. T., Fortin, M.-J., Gurevitch, J., Hohn, M., and Myers, D. (2002). The consequences of spatial structure for the design and analysis of ecological, field surveys. Ecography 25, 601–615. doi: 10.1034/j.1600-0587.2002.250508.x
Oden, N. L., and Sokal, R. R. (1986). Directional autocorrelation: an extension of spatial correlograms to two dimensions. Syst. Zool. 35, 608–617. doi: 10.2307/2413120
Paulic, M., Hand, J., and Lord, L. (1996). Water-quality Assessment for the State of Florida. Section 305(b) Main Report. Tallahassee, FL: Florida Department of Environmental Protection.
Ramstack, J. M., Fritz, S. C., Engstrom, D. R., and Heiskary, S. A. (2003). The application of a diatom-based transfer function to evaluate regional water-quality trends in Minnesota since 1970. J. Paleolimnol. 29, 79–94. doi: 10.1023/A:1022869205291
Reavie, E. D., and Juggins, S. (2011). Exploration of sample size and diatom-based indicator performance in three North American phosphorus training sets. Aquat. Ecol. 45, 529–538. doi: 10.1007/s10452-011-9373-9
Riedinger-Whitmore, M. A., Whitmore, T. J., Smoak, J., Brenner, M., Moore, A. M., Curtis, J., et al. (2005). Cyanobacterial proliferation is a recent response to eutrophication in many Florida lakes: a paleolimnological assessment. Lake Reserv. Manag. 21, 423–435. doi: 10.1080/07438140509354447
Sayer, C. D. (2001). Problems with the application of diatom-total phosphorus transfer functions: examples from a shallow English lake. Freshw. Biol. 46, 743–757. doi: 10.1046/j.1365-2427.2001.00714.x
Sayer, C. D., Davidson, T. A., Jones, J. I., and Langdon, P. G. (2010). Combining contemporary ecology and palaeolimnology to understand shallow lake ecosystem change. Freshw. Biol. 55, 487–499. doi: 10.1111/j.1365-2427.2010.02388.x
Smol, J. P. (1992). Paleolimnology: an important tool for effective ecosystem management. J. Aquat. Ecosyst. Health 1, 49–58. doi: 10.1007/BF00044408
Telford, R. J., and Birks, H. J. B. (2009). Evaluation of transfer functions in spatially structured environments. Quat. Sci. Rev. 28, 1309–1316. doi: 10.1016/j.quascirev.2008.12.020
ter Braak, C. J. F. (1986). Canonical correspondence analysis: a new eigenvector technique for multivariate direct gradient analysis. Ecology 67, 1167–1179. doi: 10.2307/1938672
ter Braak, C. J. F., and Juggins, S. (1993). Weighted average partial least squares regression (WA-PLS): an improved method for reconstructing environmental variables from species assemblages. Hydrobiologia 269/270, 485–502. doi: 10.1007/BF00028046
Vermaire, J. C., and Gregory-Eaves, I. (2007). Reconstructing changes in macrophyte cover in lakes across the northeastern United States based on sedimentary diatom assemblages. J. Paleolimnol. 39, 477–490. doi: 10.1007/s10933-007-9125-y
Whitmore, T. J., Brenner, M., Curtis, J. H., Dahlin, B. H., and Leyden, B. (1996). Holocene climatic and human influences on lakes of the Yucatan Peninsula, Mexico: an interdisciplinary, palaeolimnological approach. Holocene 6, 273–287. doi: 10.1177/095968369600600303
Whitmore, T. J., Brenner, M., Kolasa, K. V., Kenny, W. F., Riedinger-Whitmore, M. A., Curtis, J. H., et al. (2006). Inadvertent alkalization of a Florida lake caused by increased nutrient and solute loading to its watershed. J. Paleolimnol. 36, 353–370. doi: 10.1007/s10933-006-9000-2
Keywords: transfer functions, phosphorus, lake management, diatoms, paleolimnology
Citation: Whitmore TJ, Lauterman FM, Smith KE and Riedinger-Whitmore MA (2015) Limnetic total phosphorus transfer functions for lake management: considerations about their design, use, and effectiveness. Front. Ecol. Evol. 3:107. doi: 10.3389/fevo.2015.00107
Received: 01 May 2015; Accepted: 31 August 2015;
Published: 16 September 2015.
Edited by:
Isabelle Larocque-Tobler, The L.A.K.E.S. Institute, SwitzerlandReviewed by:
Jesse C. Vermaire, Carleton University, CanadaCarl Sayer, University College London, UK
Copyright © 2015 Whitmore, Lauterman, Smith and Riedinger-Whitmore. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thomas J. Whitmore, Department of Biological Sciences, University of South Florida St. Petersburg, 140 7th Avenue South, St. Petersburg, FL 33701, USA,d2hpdG1vcmVAdXNmc3AuZWR1
 Thomas J. Whitmore
Thomas J. Whitmore Francesca M. Lauterman
Francesca M. Lauterman Kathryn E. Smith
Kathryn E. Smith Melanie A. Riedinger-Whitmore
Melanie A. Riedinger-Whitmore