- Department of Ecology and Evolutionary Biology, University of California, Los Angeles, Los Angeles, CA, United States
Cooperative groups can increase fitness either by helping kin or interacting with unlike individuals to produce social heterosis. They cannot, however, simultaneously maximize both benefits. This tradeoff between nepotism and diversity is modeled using Hamilton's rule (rb–c > 0), by allowing benefit and cost to be dynamic functions of relatedness (i.e., social heterosis predicts b and c depend on r). Simulations show that evolutionary outcomes tend to maximize either nepotism (with high genetic relatedness), or social heterosis (with low relatedness) rather than produce an intermediate outcome. Although genetic diversity can arise through multiple mating, a second possible mechanism—the exchanging of individuals across groups—is similarly effective. Such worker “drifting” is common in many species of social Hymenoptera and may be a form of indirect reciprocity. Drifting individuals increase an unrelated group's productivity by enhancing its genetic diversity, with this effect being reciprocated by other unrelated drifters entering their natal group. The benefits from social heterosis and indirect reciprocity are robust against cheating and show that it is possible to evolve stable cooperation between individuals that are genetically distant or unrelated. As drifting becomes more prevalent colony boundaries may become weakly discriminated, which may predispose toward the evolution of unicoloniality in some species.
Introduction
Cooperative life histories bring two potential benefits to group members. The first can be to gather close kin together such that group living benefits are shared among individuals likely to have genes in common. Thus, even if a given group member's behavior has a cost in reducing their own reproduction, such traits can still spread if the benefits of kin-directed nepotism are large enough. Hamilton (1964) clearly delineated that such nepotism can be evolutionarily favored when the benefit of cooperation (b, and > 0) directed toward kin (defined as the level of relatedness, r, and > 0) is greater than the cost to self (c, and < 0). This is commonly known as Hamilton's rule for kin selection, where cooperation becomes favored whenever rb–c > 0.
Models derived from the rule have predicted a number of outcomes across the social Hymenoptera based on differences in r. Daughters working for their mothers are predicted to be more likely to evolve with monogamy (Boomsma, 2009). Destruction of male eggs laid by unmated workers (i.e., policing) is predicted based on r-values of brothers, full nephews, and half-nephews (Ratnieks and Wenseleers, 2005). Relatedness is a key variable in reproductive skew models for predicting how reproduction is best apportioned within cooperative groups (Nonacs and Hager, 2011). In each case relatedness predicts kin nepotism—the differential treatment of individuals based on their perceived degree of genetic similarity. Daughters are more likely to stay as helpers if they can assist full rather than half siblings. Workers destroy half sibling's eggs, when by doing so they can create more reproductive opportunities for their mother. Dominants may allow less-related subordinates a greater share of reproduction to maintain their cooperation. For a numerical example, plotting the value of rb + c shows that cooperation is increasingly selectively favored over non-cooperation as relatedness increases (Figure 1A).
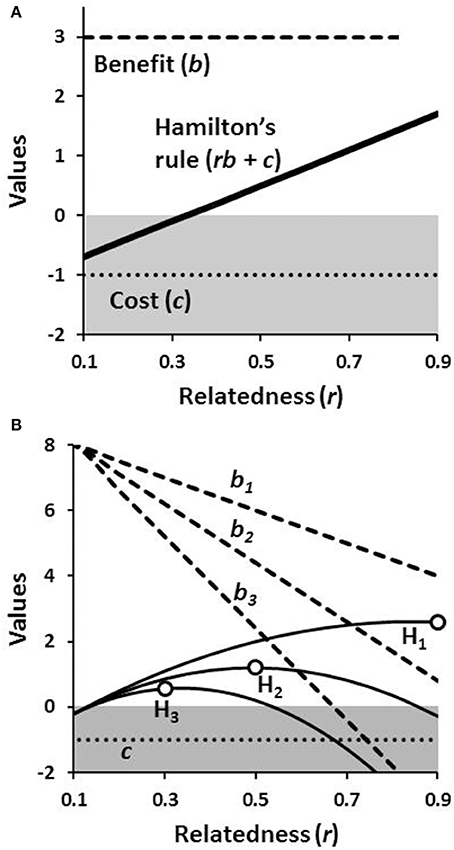
Figure 1. Hamilton's rule for cooperation in relation to relatedness. Invocations of the rule often implicitly assume that benefit and cost are constant across relatedness values (A). Cooperation is evolutionarily favored wherever rb + c > 0 and selection for cooperative behavior always increases with r. Alternatively with social heterosis the value of b is a function of the relatedness of the group members relative to a random sample drawn from the population (B). Therefore, by Hamilton's rule (H1−3) with differing declining payoff functions for b, cooperation can still be the most rewarding with closest relatives, but also alternatively, with less closely related individuals (shown by the open circles on the solid lines).
The second potential benefit of a cooperative life history is to affiliate with dissimilar individuals who have complementary skills or attributes. Greater synergisms that arise within groups of unlike individuals and result in increased survival or productivity for the whole group is social heterosis (Nonacs and Kapheim, 2007, 2008). Hamilton's rule can be similarly instructive for understanding how social heterosis works. The significant difference from the previous kin selective formulation is that with social heterosis the magnitudes of b and c can be functions of r rather than fixed, independent values. Phenotypically more similar individuals, as would be expected of close kin, would produce less benefit (b) for the group, as a whole, which results in a negative relationship between b and r (Nonacs and Kapheim, 2014). A set of numerical examples illustrates how a dynamic relationship of r to b can alter the demographics of the optimal group membership (Figure 1B). When social heterosis provides great benefit (b1) to the group, the outcome is kin selective, where individuals have the highest fitness in groups composed of the closest kin. With lower levels of benefit, the optimal group members become increasingly distant kin (b2 and b3).
Given that kin selection favors higher r-values while social heterosis likely favors lower or even negative values, the two processes intrinsically drive the evolution of cooperation in opposite directions as regards group composition and genetic structure. They cannot be simultaneously maximized and the tradeoffs therein suggest that if cooperation evolves to realize one benefit, it is at the expense or loss of the other (Nonacs and Kapheim, 2007).
The social Hymenoptera (ants, bees, and wasps) are an excellent model taxonomic group for comparing how nepotism vs. social heterosis structures life histories. Hymenopteran species exemplify every level of sociality, ranging from cooperating groups composed of one female and a single daughter, to societies that interact peaceably on continental scales. Furthermore, across these species there is also great variability in levels of relatedness ranging from 100% clonal societies to societies that are near random collections of kin and non-kin. Historically, multiple aspects of social Hymenoptera behavior and life history are considered as the best examples of nepotistic kin selection in action (Bourke, 2014), while simultaneously genetic diversity within groups has been found to significantly increase both group survival and reproduction across a variety of taxa (see multiple examples reviewed in Nonacs and Kapheim, 2007). As a particular example, genetically diverse societies of ants are more productive than homogeneous ones (Modlmeier et al., 2012).
A question to answer is under what conditions does kin selection or social heterosis win out? This requires first focusing on the mechanisms that create high or low relatedness groups, with a particular emphasis on the under-appreciated phenomenon of worker exchanges between nests or groups (known as “drifting”). The next step is to quantitatively model selection under conditions where either acting nepotistically or favoring diversity can increase fitness.
Determinates of Within-Colony Relatedness: Mating Behavior and Worker Drifting
A social insect nest can have one queen (monogyny), or multiple reproductive queens either simultaneously present and laying (polygyny) or sequentially replacing each other over a relatively short period of time (sequential monogyny). A queen can mate with just one male (monandry) or multiple males (polyandry). Therefore, monogamy (monogyny plus monandry) would favor nepotism by creating the maximum non-clonal relatedness between all full sister workers, while genetic diversity is increased through polygyny and polyandry. The effects that number of reproductive mothers and fathers per colony have on colony genetic structure have been extensively considered elsewhere and need not be reviewed once more here (Nonacs, 1988; Hughes et al., 2008).
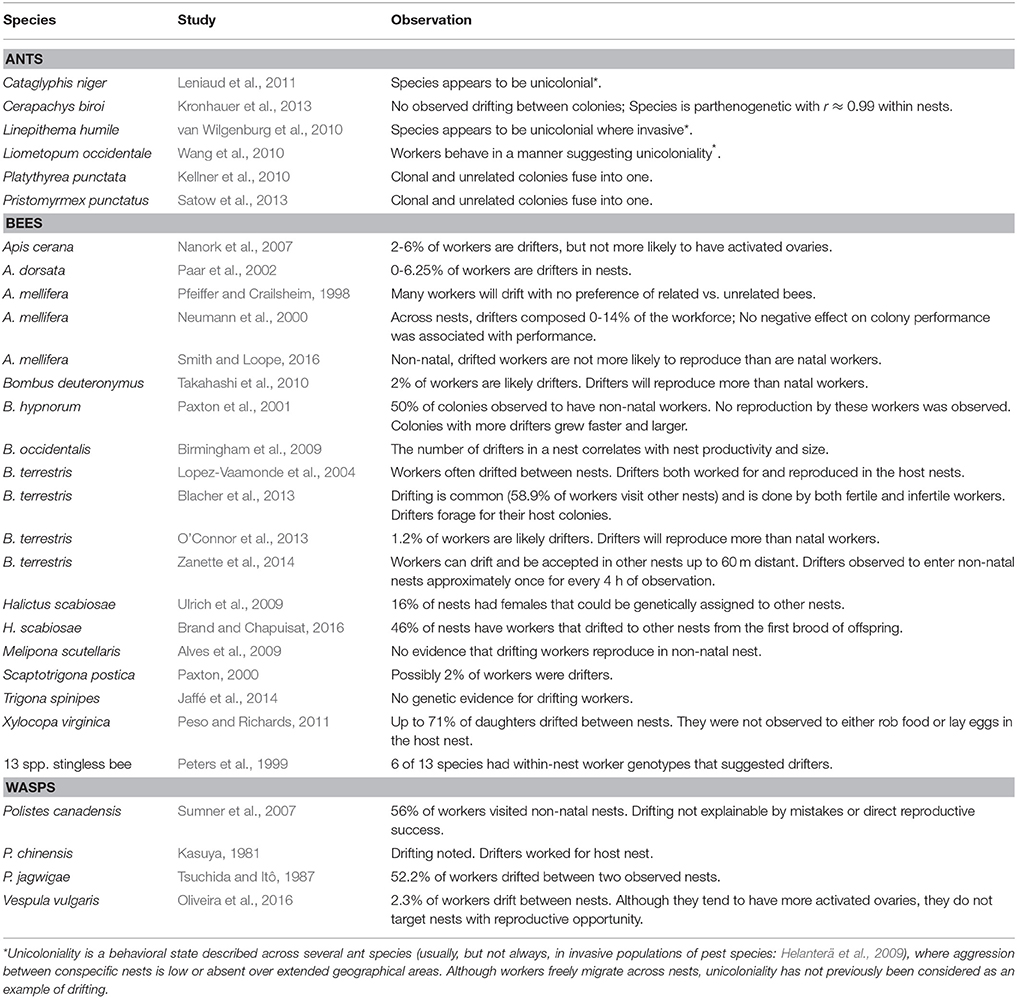
Within-nest genetic diversity also increases when unrelated nests exchange workers. Known as “drifting,” in many species mature workers leave their natal nest and join a different nest, either temporarily or permanently (Beekman and Oldroyd, 2008). A greater propensity for workers to drift, therefore, correlates with increased within-group genetic diversity. A review of the literature, however, finds drifting common across all branches of the social Hymenoptera, and often occurring at high frequency (Table 1: ants, bees and wasps). Several explanations for drifting are possible.
One explanation for worker drifting is individual-level mistakes. Young workers intending to return to their natal colony get lost and enter the wrong nest. Then, if the species is error-prone in nestmate vs. non-nestmate recognition (e.g., Reeve, 1989), this would result in acceptance and addition to the nest's workforce. Drifting as a byproduct of getting lost would predict that it ought to be a relatively rare phenomenon as one would expect more error-prone genotypes to be selected against.
A second explanation is that drifting is a selfish, individual-level strategy where drifters escape reproductive suppression in their natal colony and reproductively parasitize an unrelated nest (Beekman and Oldroyd, 2008; Smith and Loope, 2016). Drifters do seem especially attracted to failing colonies, such as ones with no viable queen, and once there actively and successfully compete to lay eggs (e.g., in Apis cerana; Nanork et al., 2007). “Selfish” drifting is also found in otherwise healthy colonies (Table 1), but at usually lower frequencies and with less obvious consequences (e.g., in A. mellifera non-natal workers do significantly less of certain tasks, but the effects on colony productivity are not obvious; Pfeiffer and Crailsheim, 1999).
Thus, the key point across the examples in Table 1 is that while seeking reproductive opportunities may partially explain drifting by some individuals, a large fraction of drifters appear to adopt worker roles and behaviors that are indistinguishable from the actual daughters of resident queens. Therefore, a third explanation for drifting would be that drifters can increase their fitness without directly reproducing. In P. canadensis drifting females often join nearby nests with genetic relatives and therefore gain indirect fitness (Sumner et al., 2007). Clearly, drifting also increases the genetic diversity in the workforce population and this can through social heterosis positively affect a variety of group-level characters (Oldroyd and Fewell, 2007, 2008). In grasshoppers, groups of mixed relatedness survive better than groups composed of only sibs (Caesar et al., 2010). In harvester ants, intracolonial relatedness and colony growth are significantly negatively correlated which indicates that multiple mating by queens produces fitness advantages (Wiernasz et al., 2004). Diverse societies are also more productive in the ant, Temnothorax longispinosus (Modlmeier et al., 2012). In paper wasps, genetic relatedness does not predict aggressive interactions between female foundresses (Nonacs et al., 2004), and a new analysis of that data shows that between-female relatedness does negatively correlate with nest size (R2 = 0.519; N = 8; P < 0.05). Also, diversity in terms of size differences between nest foundresses correlates with nest productivity (Nonacs and Reeve, 1995). Many more examples of potential social heterosis are reviewed in Nonacs and Kapheim (2007).
A population of unrelated nests exchanging helpful workers can, therefore, be considered to indulge in a form of positive indirect reciprocity (Alexander, 1987). The interaction would be indirect because no nest's action would be predicated on the response of an identified partner. It would be reciprocating because all participating nests could reap the benefits of increased group productivity. Drifting would increase inclusive fitness for all group members, because what matters is the overall number of produced kin and not that they be directly raised by kin. However, cooperative networks based on indirect reciprocity can collapse due to cheating where individuals accept beneficial acts but never reciprocate (Nowak and Sigmund, 2005). For example, a cheater in the current scenario might be a nest that only accepts drifters (gaining an increased and more diverse workforce).
If it is plausible that social evolution can be driven by either nepotistic kin favoritism or genetically diversifying social heterosis, it becomes important to determine how probable each pathway may be. This is best approached initially through a simulation model that allows populations to evolve to favor high relatedness (i.e., monogamy and strong bias against drifting), or to evolve to favor high genetic diversity (i.e., multiple-mating by queens and weak discrimination against non-natal workers). Additionally, the evolution of drifting needs to examine how the behavior is expressed when a potential for selfishness to arise in populations is also possible.
The Evolution of Cooperation by Kin Selection vs. Social Heterosis
Model Description
The model is a genetic algorithm where simulations allow the best combination of traits to evolve and spread through populations (Mitchell, 1996). Simulations begin with initial populations of 400 nests of a haplodiploid species, with each nest having a single, mated queen and beginning with a group size (ni) of 100 workers (Figure 2). A group's reproductive success can potentially increase due to either high relatedness or greater genetic diversity within the colony. These group-level characteristics are a function of five loci that are under potential selection. One is the mating locus which determines queen mating behavior (m) and ranges from monandry to a maximum polyandry level of seven mates. The second is the diversity locus, which has a maximum of 10 possible alleles in the population (with each allele being a proportion of the population: a1–a10). A third locus determines the level of self-identity which affects propensity to drift (d), which ranges from a value of 0 (the individual repels the entry of all non-nestmates into its nest and never drifts), to 1 (individuals will randomly drift across nests and never repel any other individual). These three loci interact to determine the genetic relatedness and diversity found within each colony. However, although these three loci set the amount of benefit that is potentially available, whether or not such benefits are gained depends on the values at the other two “realization” loci. These determine the ability of workers to actuate the potential benefits of either high relatedness or genetic diversity. Conceptually, it can be thought of as a worker has the probabilities, x and y, to do “something” in order to gain nepotistic and social heterosis benefits, respectively. Thus, these last two loci determine the probabilities of doing that something, and they range from zero (the worker never does it) to one (the worker always does it). The model does not define the specific kind of acts which must be done to realize benefits. At the nest level, the probability to do the acts that gain benefits is the mean across all workers for nepotistic, x, and social heterosis, y, action. All loci in females act additively (e.g., a queen with alleles for mating once and seven times, will mate with four males).
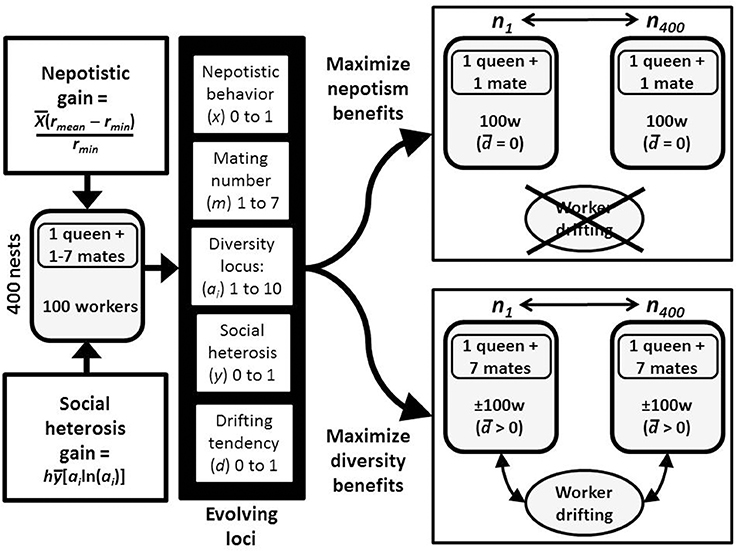
Figure 2. Flowchart for the model and evolution by nepotism vs. social heterosis. In response to the availability of benefits from both nepotism and genetic diversity, there are 5 possible loci that can evolve. These are the number of times a queen will mate, a diversity locus that produces social heterosis, two loci for behaviors (unspecified in the model) that result in gaining the nepotistic or genetic diversity benefits, and a locus for a between-nest drifting predisposition. Because nepotism and social heterosis are likely to be mutually exclusive, populations will tend to evolve along one of the two pathways.
Simulations run for 10,000 time steps, with given scenarios repeated 25–50 times. Simulations proceed within a time period in the following order of four steps.
(1) Ten existing workers in every nest are randomly replaced by new daughters of the queen. This mimics worker turnover due to birth and death.
(2) All workers are given an opportunity to drift that depends on their genotype. As an example, a worker homozygous for 0.05 alleles would have d = 5% chance per time step of leaving its natal nest (Figure 2). If a worker does drift, a potential recipient nest is randomly chosen from the entire population. The probability that a drifter is accepted is determined by the self-identity value of the targeted nest, which is the mean across all worker genotypes at that locus. A drifting worker can attempt to enter up to 20 randomly chosen nests (note, this is mathematically equivalent to 20 attempts on one randomly chosen nest). If it fails to be accepted, it returns to its natal nest. Drifting workers can also potentially leave but randomly choose its own nest to enter. Individual nests can have a net outflow or inflow of drifters and thus over multiple time periods group size can decrease or increase from the original 100. The propensity to drift is therefore also prorated by multiplying an individual's genotype by its resident relative group size (ni/100). Hence the likelihood of drifting positively correlates to group size, but likelihood of accepting a drifter does not. Overall, the structure of the model is such that the expressed range of group sizes in the population will not be large, and the existing variance will be closely correlated to the level of genetic diversity. Therefore, ni by itself has no direct fitness consequences.
(3) Nests reproduce with their relative fitness determined by the sum total of their gain through nepotism and social heterosis: Nepotistic gain = x [(rmean–rmin)/rmin], where rmean is the individual colony-specific average of within-group relatedness across all workers. Workers in this model are either full sisters (sharing both parents), half sisters (sharing only the same mother), or unrelated (accepted drifters). The nepotistic gain is scaled relative to a global value of least possible within-nest relatedness in the absence of drifting (rmin = 0.3214), where the queen has mated with seven males (i.e., 86% of the workers are half sisters). Thus, an individual colony's maximum nepotistic gain is set relative to its rmean, which scales from 0 with maximal polyandry to 1.333 with monandry. With drifting it is possible that rmean < rmin, in which case nepotistic gain is set to zero. What this assumes is that nepotism occurs only with a certain minimal level of relatedness within the nest. As all simulations begin with all colonies having the highest genetic relatedness possible, any evolution within simulations toward increasing social heterosis must occur with a loss of potential benefit gain from exploiting nepotism.
Social heterosis gain = hy [-Σailn(ai)], where ai is the non-zero proportion that allele i composes of the entire population of diversity alleles in the colony. The term within the brackets is the Shannon diversity index, and is sensitive to both the number of alleles present and their frequency. In the simulations it can vary from 0 (only one allele is present in the nest) to 2.303 (all 10 alleles are present at equal frequency). A scaling constant, h, is varied from 0 to 1.50 in order to alter the relative potential gains from nepotism vs. social heterosis across scenarios. A scaling constant is required in that numerically nepotism and social heterosis benefits arise via differing functions.
The model does not specify a particular mechanism through which colony-level productivity is enhanced by either genetic diversity or acting more altruistically in the presence of closer kin. Numerous expressions of benefit are possible. A more diverse colony may exploit a wider variety of resources, such as nectar vs. pollen gathering in bees. Similarly, there could be variance in genetic proclivity or ability to do certain tasks, such as tending brood, nest hygiene, or comb construction. In a more closely related colony, individuals may be less likely to contest for reproduction, more likely to recognize and protect against usurpers, risk lives in colony defense, and enforce punishment on lazy individuals or cheaters (Bourke, 2011).
All simulations start with x = y = 0; such that all colonies gain no benefit from either nepotism or diversity. Over time x and y should evolve to higher values as this results in higher colony fitness. The need to have the gain from relatedness or diversity determined by a second independent factor is to avoid the results always reflecting the sociobiology of the starting conditions. All simulations start with all colonies having the highest possible within-nest relatedness such that if they also immediately gained large nepotism benefits, one would never get evolution toward diversifying the colony. An initial condition of x = y = 0 is the mechanism to create an initially neutral evolutionary arena.
(4) For each time period every nest, with all its inhabitants, has a 10% chance of dying and is replaced by a new nest with a new queen and 100 workers that are her offspring. The new queen is a daughter drawn randomly from one of the surviving nests (relative to the differential fitness as calculated above). Similarly, her mates are the sons drawn randomly from surviving nests. The number of mates is determined by the new queen's mating number genotype. A new queen could potentially experience a mutation at any or all of the five loci (at a rate of 0.01). For the mating number and diversity loci, a mutation was randomly drawn from the set range of values: 1–7 for mates, and 1–10 for diversity alleles. For the self-identity locus and two realization loci, mutations increased or decreased expression by 0.05 increments (with boundary limits of 0 and 1). Mutation rates for all loci are set to zero for the last 10% of the time periods to let selection act most strongly.
Initial Conditions
Queen and male genotypes were initially randomly drawn with respect to mating and diversity alleles. Therefore, across the 400 nests mating behavior ranged from monogamy to mating with seven males, and each diversity allele had an approximate frequency of 0.1. The drifting locus and realization loci were all set to zero. This means that initially all workers neither moved between nests nor did the acts that would gain benefit through nepotism or genetic diversity. All nests were, therefore, equally reproductively fit.
Cheating and Strategic Behavior in Drifters
The base case simulation model assumes that a drifting worker is reciprocating and as helpful to non-natal nests as it is at home. This leads to a question of whether or not such a system of indirect reciprocity could be destabilized by non-cooperative genotypes. Therefore, the simulations were replicated where drifting could also evolve to cheat in one of three ways:
1. Nest strategic behavior. Workers are 50% less likely to drift from their natal nest, and are also twice as likely to admit drifters to their nest. Such nests would tend to grow in size and be relatively more likely to accumulate beneficial genetic diversity, while at the same restricting the number of drifters available to other nests.
2. Individually strategic behavior. In non-natal nests, workers express social heterosis at only 50% of the level at which they would in their natal nest (e.g., as in A. mellifera nests where non-natal drifters did less of some brood care tasks; Pfeiffer and Crailsheim, 1999).
3. Spiteful behavior. Workers in their home nest create social heterosis, but in non-natal nests reduce social heterosis (and therefore group-level fitness) in relation to the magnitude of their social heterosis genotype (e.g., as in Bombus deuteronymus and B. terrestris where drifters may compete for reproduce rather than forage; Takahashi et al., 2010; O'Connor et al., 2013).
Model Results: Initial Conditions
In all cases the simulations resulted in the evolution of either strong realization of nepotistic or genetic diversity benefits (Figure 2). As the scaling constant (h) increased, a tipping point was crossed, where populations went from almost entirely monandrous to mating with more four males, on average (Figure 3A). In 250 individual simulation runs, there was only one outcome where the mean number of matings was >1, but <4. The lack of intermediate outcomes was further evident in simulations with intermediate values of h (0.5–1.00). In these cases, most simulations followed a track to either monandry or polyandry. However, occasionally an initial invasion advantage developed for the alternative pathway, and a positive feedback loop drove the expression to higher levels and suppressed the more common result (Figure 3A).
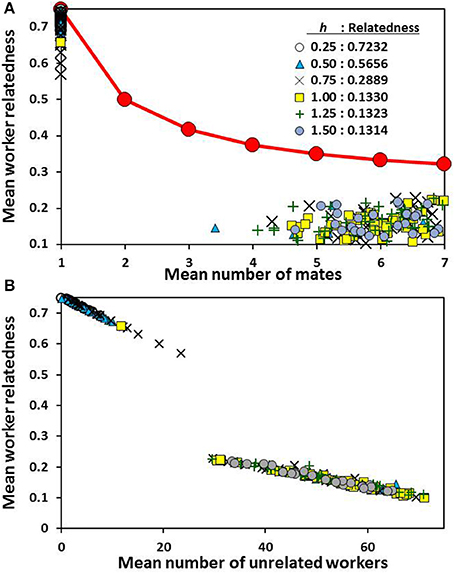
Figure 3. Mean within-group relatedness of workers as a function of the mean number of mates (A) and the number of unrelated workers averaged across all colonies (B). Every point is for a single simulation run at a given level of relative strength of social heterosis expression (h). The red line is the expected relatedness between workers based on the number queen mates. The observed relatednesses, averaged across simulations for a given h value, are given in the legend.
The same pattern held for drifting behavior as found in mate number (Figure 3B): individual simulations resulted in either very little drifting or a substantial amount. An intermediate level was never the outcome. Positive selection for drifting meant that the average worker-worker relatedness within nests was substantially lower than predicted by the queen's matedness status (Figure 3A).
All simulations began with no expression or realization of either nepotistic benefits, social heterosis, or tendency to drift. When h biased selection toward favoring nepotism, populations evolved over 10,000 generations to strongly express nepotism and colony self-identity remained strong with little drifting (Figure 4: top panel). As h increased, nepotistic expression was weak and workers became genotypically more likely to drift and accept drifters into their nest (Figure 4: middle and bottom panels). This combination of increasing drifting and higher levels of polyandry results in nests maintaining significantly more genetic diversity (Figure 5). In contrast to nepotism and drifting expression, social heterosis expression was always positively selected over time, independent of h (Figure 4). Thus, the group-level productivity gains through social heterosis maintain significantly increased genetic diversity even when social selection produces monandry with little worker drifting (Figure 5).
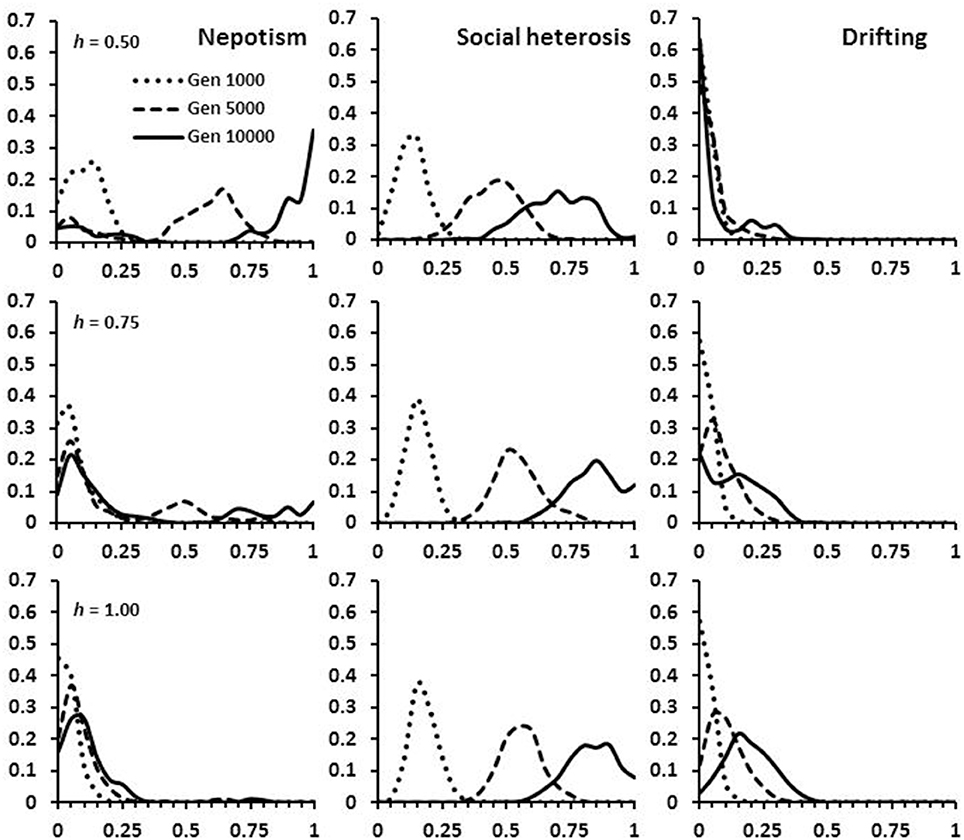
Figure 4. Frequency of alleles at the expression loci for nepotism, social heterosis and drifting. The distributions are given at time periods 1,000, 5,000, and 10,000 in the simulations. The three panels show the effects on allele distribution as selection goes from favoring monandry and high relatedness (h = 0.50), to favoring polyandry, drifting and low relatedness (h = 1.00).
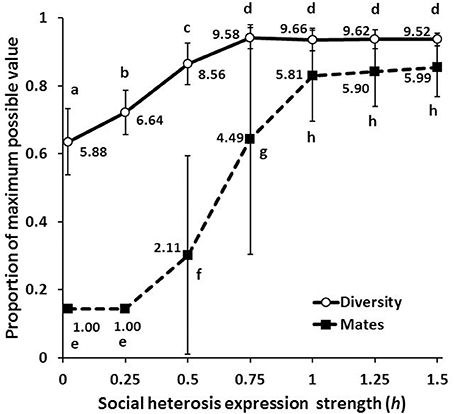
Figure 5. Diversity and mate number (mean ± SD) as the relative strength of social heterosis expression (h) increases. Numbers give the means for each measure, letters indicate means that are not significantly different from each other by a Bonferroni-Dunn post-hoc comparison.
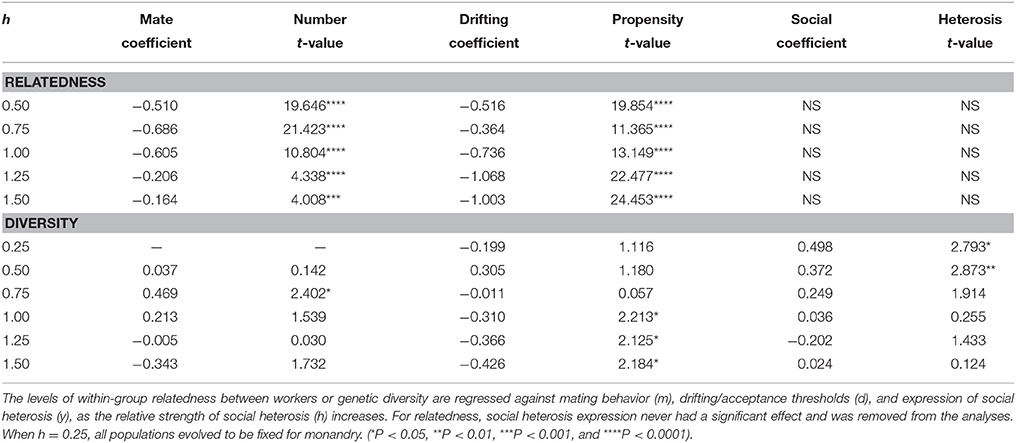
The relative influence of social heterosis, matedness, and proclivity for drifting on relatedness and within-colony genetic diversity were examined through multiple regression (Table 2). For relatedness, both the number of mates and propensity to drift were highly significant, with the latter having perhaps the stronger effect with higher h. The level of social heterosis expression had no significant consequences for relatedness. For diversity, social heterosis expression was the only significant factor when monandry was strongly favored. As h increased (and along with it the likelihood that polyandry would be eventual outcome), diversity was significantly enhanced by the number of mates, but became unaffected by social heterosis expression. As polyandry became strongly favored, then only the level of drifting had a significant effect.
Model Results: Cheating and Strategic Behavior in Drifters
One potential form of cheating at a nest level is for nests to accumulate genetic diversity by being more willing to accept unrelated workers, and having their own workers be less likely to drift. Interestingly, this form of cheating is initially as prevalent as complete reciprocity (i.e., nests that do not differentially accept drifters), but by 10,000 generations has become rare (Figure 6). The overall consequences are reduced within-group relatedness, despite a reduced level of polyandry (Figure 7). Note that the diversity index used in the model returns slightly higher values for the same number of alleles in a smaller colony than in a larger colony (see Supplementary Material). However, this bias is very small and clearly does not prevent the initial spread of this type of cheating.
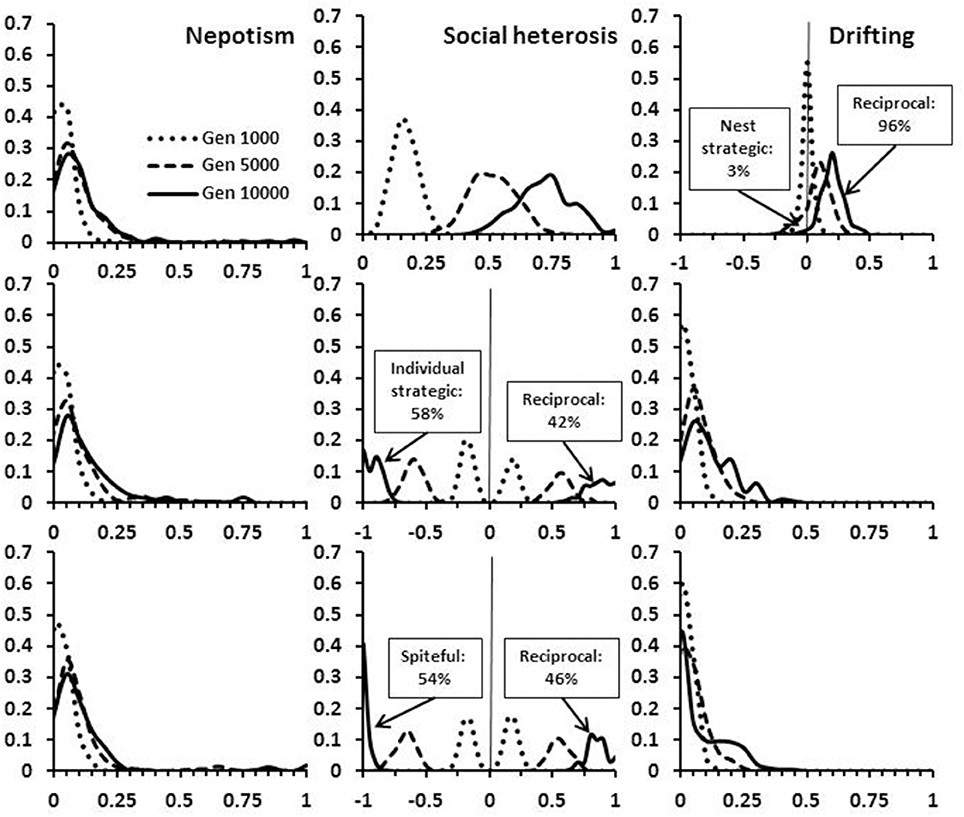
Figure 6. Frequency of alleles at the expression loci for nepotism, social heterosis and drifting when cheating is possible. The distributions are given at time periods 1,000, 5,000, and 10,000 in the simulations, with h = 1.00. In the top panel cheating produces nests that differentially collect drifters. In the middle panel, individual drifters behave strategically and provide less social heterosis to non-natal nests. In the bottom panel, drifters act spitefully in non-natal nests. For demonstration purposes, reciprocating alleles are shown as positive values and cheating alleles as negative values (ranges 0 ± 1).
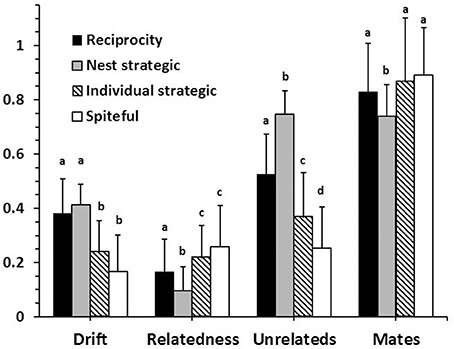
Figure 7. Mean (±SD) colony genotypes with and without cheating being possible. Drift is the mean level of acceptance on unrelated individuals. Relatedness is the mean between workers in a nest. The mean numbers of unrelated individuals in a nest and queen mates are given as proportional values relative to the maximum possible. Letters indicate means within categories that are not significantly different by a Bonferroni-Dunn post-hoc comparison.
Two other forms of cheating would be manifest at the individual worker level where workers in non-natal nests provide a lower level of benefit (strategic), or actively reduce gains in diversity benefits (spiteful). Both types of cheating are present in populations in slightly higher proportions than reciprocating behavior (Figure 6). The overall consequences are fewer drifters and higher within-group relatedness in comparison to a completely reciprocating population (Figure 7). With all forms of cheating, however, populations still evolve to have high levels of polyandry, significant numbers of drifting workers, and within-group relatedness that is less than expected by the observed level of polyandry. The results shown for cheating are all with h = 1.00. Quantitatively similar results were obtained with h < 1.00 (not shown).
Discussion
Social Hymenoptera are often considered a model taxon for evidence supportive of kin selection favoring cooperation (Bourke, 2014). Indeed with constant benefits and costs, Hamilton's rule predicts causative relationships between high relatedness and the propensity to evolve cooperation (Boomsma, 2009). However, low-relatedness societies are both common and evolutionarily derived from higher relatedness life histories (Hughes et al., 2008), without any noticeable increase in dysfunction. An alternative view is that lower relatedness favors social heterosis where groups act as a cooperative social genome composed of dissimilar individuals contributing unique skills and capabilities (Nonacs and Kapheim, 2007, 2012). This evolutionary tradeoff in the benefits of low vs. high genetic relatedness for sociality also follows from Hamilton's rule when b or c vary as a function of r (Figure 1). Not surprisingly, an evolutionary genetic algorithm finds that most often populations stabilize to either maximize nepotism or genetic diversity and not an intermediate outcome (Figures 3, 4). These results do emphasize, however, that simply having an advantage to nepotistic behavior is not always sufficient for it to be selectively favored.
The more interesting result arising from the simulations is that social Hymenoptera can increase colony-level genetic diversity not only by queens employing a top-down control mechanism (number of mates they have), but also by a bottom-up mechanism of workers forming an indirectly-reciprocating network of drifters. A community wide “pool” of genetically heterogeneous workers to which colonies both contribute to and draw from is a type of a public good (i.e., a source from which genetic diversity can be acquired). Significant levels of contribution to this public good are also stable in the presence of cheating or spiteful behavior, supporting previous models of the effects of social diversity for stabilizing cooperation through indirect reciprocity (Santos et al., 2008). The simulation results further suggest that not all types of cheating are equally evolutionarily viable. For example, if nests accept more workers than drift away, individual thresholds initially evolve to create a net influx of drifters into the natal colony. Once there are sufficient numbers of drifting workers in the population, however, reciprocating genotypes (i.e., those with equal likelihoods of both drifting and accepting drifters), strongly predominate, to the extent of being 96% of the population after 10,000 time steps (Figure 6). In contrast, individual-level cheating persists in populations at frequencies slightly greater than wholly reciprocating genotypes and does reduce the overall occurrence of drifting (Figures 6, 7). Nevertheless, neither drifters that are strategic in behavior (behaving less altruistically in non-natal colonies) nor spiteful; (reducing fitness of non-natal colonies) prevent drifting from evolving through gains from indirect reciprocity. Previously cheating has been shown to be less likely when the cost of the beneficial act is small and reciprocators can be identified by an honest phenotypic marker or “tag” (Riolo et al., 2001; Colman et al., 2012). In the case of worker drifting, the cost is arguably trivial to nonexistent. A sterile drifter sacrifices no direct fitness and the cost of lost labor for its natal nest can be more than offset by admitting an unrelated replacement producing social heterosis. Also, the tag in this case is simple and honest: a willingness to accept drifters. Reciprocating nests would be evident in the population by their relaxed acceptance threshold levels (Reeve, 1989; Masuda and Ohtsuki, 2007; Colman et al., 2012). There would be no need to evolve specific phenotypic markers, learn to recognize reciprocators, or to punish cheaters.
To date, “worker drifting” has been a bee- or wasp-centric concept. In contrast, observed large scale exchanges of unrelated workers across multiple species of ants are viewed in the context of “unicoloniality” and loss of nest-level identity over greater geographic areas (Helanterä et al., 2009). As a descriptive phenomenon, however, drifting and unicoloniality differ quantitatively and not qualitatively. Indeed, drifting in some species of bees and wasps reaches levels that may be barely distinguishable from unicoloniality in ants (e.g., 42% of workers in A. mellifera nests are aliens; Pfeiffer and Crailsheim, 1998, 59% of marked workers in B. terrestris at least visit a foreign nest; Blacher et al., 2013, and 56% of female Polistes canadensis drift; Sumner et al., 2007). Overall, one evolutionary pathway to unicoloniality may be as simple as strong selection through social heterosis for high levels of drifting. The outcomes of the simulations and the fact that there may be more naturally-occurring unicolonial species than previously appreciated (Wang et al., 2010; Nonacs, 2011), strongly suggests that earlier predictions (e.g., Helanterä et al., 2009), of unicoloniality being destabilized by kin selection and nepotism may not hold up.
One final point is about the mechanistic expressions of kin selective or social heterosis benefits. As a theoretical or conceptual exercise, it is not necessary for models to be specific on how fitness gains are achieved. Nevertheless, the proximate “how” question may critically affect whether nepotism or genetic diversity is the stronger evolutionary force. For instance, close kinship can be imposed on groups through strict monogamy, but selection for high relatedness must have correlated consequences: offspring are more likely to become workers; to work harder; or to sacrifice more direct reproduction than otherwise (Boomsma, 2009). However, in societies with large group sizes and workers that are already almost completely altruistic (i.e., sterile and willing to die for the good of the group) there remains little more to gain through greater enforced nepotism. Conversely, in large groups genetic diversity can be both highly variable and malleable. One obvious mechanism, multiple mating, has repeatedly arisen in eusocial Hymentopera (Hughes et al., 2008). A heretofore not well appreciated second mechanism is worker drifting. Drifting to produce indirect reciprocity for alloparenting can be anthropomorphized as, “I'll raise more of your kin, and you'll raise more of mine.” If the resultant genetic diversity from exchanging individuals allows all groups to be more successful, then the evolution of low-relatedness societies can be an expected consequence.
In conclusion, both nepotism for helping close kin and advantages of genetic diversity are likely to affect the evolution of cooperation. The effects of genetic relatedness are demonstrable across multiple contexts (Bourke, 2011, 2014). Likewise, genetic diversity is often an advantageous group-level trait (Oldroyd and Fewell, 2007, 2008), that can produce social heterosis (Nonacs and Kapheim, 2007). Both benefits, however, cannot be maximized simultaneously and gaining in one means losing in the other. It is especially important that future models on cooperation consider that nepotism may not evolve if it loses social heterosis, and vice versa. One can draw several testable predictions from the model results. First, selection for nepotism or diversity should produce positive feedbacks such that species should either exhibit high within-group relatedness on the order of full sisterhoods, or low relatedness, such as at a half-sib or less level. Intermediate levels should be rare (e.g., as in Figure 3). Second, colonies that accept drifting workers should also tend to produce drifters (i.e., nest-level strategic behavior that would uncorrelate acceptance from movement should be rare). Third, in species where selfish drifters invade colonies in order to reproduce, one should still find a significant fraction of drifters that behave entirely altruistically. The presence of cheaters should not cause the collapse of a network of indirect reciprocity. Finally as a point to consider, the arguments derived here are applied to the social Hymenoptera, but consider that humans also meet a number of the criteria of a unicolonial species (Moffett, 2012), in that individuals can relatively freely drift between a wide variety of often barely definable groups. The degree to which human sociality is structured by forces other than kin selection is a fertile field for future exploration (Nonacs and Kapheim, 2014; Richerson et al., 2016).
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fevo.2017.00087/full#supplementary-material
References
Alves, D. A., Imperatriz-Fonseca, V. L., Francoy, T. M., Santos-Filho, P. S., Nogueira-Neto, P., Billen, J., et al. (2009). The queen is dead-long live the workers: intraspecific parasitism by workers in the stingless bee Melipona scutellaris. Mol. Ecol. 18, 4102–4111. doi: 10.1111/j.1365-294X.2009.04323.x
Beekman, M., and Oldroyd, B. P. (2008). When workers disunite: intraspecific parasitism by eusocial bees. Ann. Rev. Entomol. 53, 19–37. doi: 10.1146/annurev.ento.53.103106.093515
Birmingham, A. L., Hoover, S. E., Winston, M. L., and Ydenberg, R. C. (2009). Drifting bumble bee (Hymenoptera: Apidae) workers in commercial greenhouses may be social parasites. Can. J. Zool. 82, 1843–1853. doi: 10.1139/z04-181
Blacher, P., Yagound, B., Lecoutey, E., Devienne, P., Chameron, S., and Chaline, N. (2013). Drifting behaviour as an alternative reproductive strategy for social insect workers. Proc. R. Soc. Lond. B 280:20131888. doi: 10.1098/rspb.2013.1888
Boomsma, J. J. (2009). Lifetime monogamy and the evolution of eusociality. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 364, 3191–3207. doi: 10.1098/rstb.2009.0101
Bourke, A. F. G. (2011). The validity and value of inclusive fitness theory. Proc. R. Soc. Lond. B 278, 3313–3320. doi: 10.1098/rspb.2011.1465
Bourke, A. F. G. (2014). Hamilton's rule and the causes of social evolution. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 369:2013036. doi: 10.1098/rstb.2013.0362
Brand, N., and Chapuisat, M. (2016). Low relatedness and frequent inter-nest movements in a eusocial sweat bee. Insect. Soc. 63, 249–256. doi: 10.1007/s00040-015-0460-0
Caesar, S., Karlsson, M., and Forsman, A. (2010). Diversity and relatedness enhance survival in colour polymorphic grasshoppers. PLoS ONE 5:e10880. doi: 10.1371/journal.pone.0010880
Colman, A. M., Browning, L., and Pulford, P. D. (2012). Spontaneous similarity discrimination in the evolution of cooperation. J. Theor. Biol. 299, 162–171. doi: 10.1016/j.jtbi.2011.05.022
Hamilton, W. D. (1964). The genetical evolution of social behaviour. I and II. J. Theor. Biol. 7, 1–52. doi: 10.1016/0022-5193(64)90038-4
Helanterä, H., Strassmann, J. E., Carrillo, J., and Queller, D. C. (2009). Unicolonial ants: where do they come from, what are they and where are they going? Trends Ecol. Evol. 24, 341–349. doi: 10.1016/j.tree.2009.01.013
Hughes, W. O. H., Oldroyd, B. P., Beekman, M., and Ratnieks, F. L. W. (2008). Ancestral monogamy shows kin selection is key to the evolution of eusociality. Science 320, 1213–1216. doi: 10.1126/science.1156108
Jaffé, R., Pioker-Hara, F. C., dos Santos, C. F., Santiago, L. R., Alves, D. A., de Kleinert, A., et al. (2014). Monogamy in large bee societies: a stingless paradox. Naturwissen 101, 261–264. doi: 10.1007/s00114-014-1149-3
Kasuya, E. (1981). Internidal drifting of workers in the Japanese paper wasp. Polistes chinensis antenallis (Vespidae, Hymenoptera). Insect. Soc. 28, 343–346. doi: 10.1007/BF02224191
Kellner, K., Barth, B., and Heinze, J. (2010). Colony fusion causes within-colony variation in a parthenogenetic ant. Behav. Ecol. Sociobiol. 64, 737–746. doi: 10.1007/s00265-009-0891-6
Kronhauer, D. J. C., Tsuji, K., Pierce, N. E., and Keller, L. (2013). Non–nest mate discrimination and clonal colony structure in the parthenogenetic ant Cerapachys biroi. Behav. Ecol. 24, 617–622. doi: 10.1093/beheco/ars227
Leniaud, L., Heftez, A., Grumiau, L., and Aron, S. (2011). Multiple mating and supercoloniality in Cataglyphis desert ants. Biol. J. Linn. Soc. 104, 866–876. doi: 10.1111/j.1095-8312.2011.01772.x
Lopez-Vaamonde, C., Koning, J. W., Brown, R. M., Jordan, W. C., and Bourke, A. F. G. (2004). Social parasitism by male-producing reproductive workers in a eusocial insect. Nature 430, 557–560. doi: 10.1038/nature02769
Masuda, N., and Ohtsuki, H. (2007). Tag-based indirect reciprocity by incomplete social information. Proc. R. Soc. Lond. B 274, 689–695. doi: 10.1098/rspb.2006.3759
Modlmeier, A. P., Liebmann, J. E., and Foitzik, S. (2012). Diverse societies are more productive: a lesson from ants. Proc. R. Soc. Lond. B 279, 2142–2150. doi: 10.1098/rspb.2011.2376
Moffett, M. W. (2012). Supercolonies of billions in an invasive ant: what is a society? Behav. Ecol. 23, 925–933. doi: 10.1093/beheco/ars043
Nanork, P., Chapman, N. C., Wongsiri, S., Lim, J., Gloag, R. S., and Oldroyd, B. P. (2007). Social parasitism by workers in queenless and queenright Apis cerana colonies. Mol. Ecol. 16, 1107–1114. doi: 10.1111/j.1365-294X.2006.03207.x
Neumann, P., Moritz, R. F. A., and Mautz, D. (2000). Colony evaluation is not affected by drifting of drone and worker honeybees (Apis mellifera L.) at a performance testing apiary. Apidologie 31, 67–79 doi: 10.1051/apido:2000107
Nonacs, P. (1988). Queen number in colonies of social Hymenoptera as a kin-selected adaptation. Evolution 42, 566–580. doi: 10.1111/j.1558-5646.1988.tb04161.x
Nonacs, P. (2011). Kinship, greenbeards, and runaway social selection in the evolution of social insect cooperation. Proc. Natl. Acad. Sci. U.S.A. 108, 10808–10815. doi: 10.1073/pnas.1100297108
Nonacs, P., and Hager, R. (2011). The past, present and future of reproductive skew theory and experiments. Biol. Rev. 86, 271–298. doi: 10.1111/j.1469-185X.2010.00144.x
Nonacs, P., and Kapheim, K. M. (2007). Social heterosis and the maintenance of genetic diversity. J. Evol. Biol. 20, 2253–2265. doi: 10.1111/j.1420-9101.2007.01418.x
Nonacs, P., and Kapheim, K. M. (2008). Social heterosis and the maintenance of genetic diversity at the genome level. J. Evol. Biol. 21, 631–635. doi: 10.1111/j.1420-9101.2007.01489.x
Nonacs, P., and Kapheim, K. M. (2012). Modeling disease evolution with multilevel selection: HIV as a quasispecies social genome. J. Evol. Med. 1:235553. doi: 10.4303/jem/235553
Nonacs, P., and Kapheim, K. M. (2014). Cultural evolution and emergent group-level traits through social heterosis. Behav. Brain Sci. 37, 266–267. doi: 10.1017/S0140525X1300294X
Nonacs, P., and Reeve, H. K. (1995). The ecology of cooperation in wasps: causes and consequences of alternative reproductive decisions. Ecology 76, 953–967. doi: 10.2307/1939359
Nonacs, P., Reeve, H. K., and Starks, P. T. (2004). Optimal reproductive-skew models fail to predict aggression in wasps. Proc. R. Soc. Lond. B 271, 811–817. doi: 10.1098/rspb.2003.2668
Nowak, M. A., and Sigmund, K. (2005). Evolution of indirect reciprocity. Nature 437, 1291–1298. doi: 10.1038/nature04131
O'Connor, S., Park, K. J., and Goulson, D. (2013). Worker drift and egg dumping by queens in wild Bombus terrestris colonies. Behav. Ecol. Sociobiol. 67, 621–627. doi: 10.1007/s00265-013-1481-1
Oldroyd, B. P., and Fewell, J. (2007). Genetic diversity promotes homeostasis in insect colonies. Trends Ecol. Evol. 22, 408–413. doi: 10.1016/j.tree.2007.06.001
Oldroyd, B. P., and Fewell, J. (2008). Large fitness benefits from polyandry in the honey bee, Apis mellifera. Trends Ecol. Evol. 23, 59–60. doi: 10.1016/j.tree.2007.10.012
Oliveira, R. C., Oi, C. A., Vollet-Neto, A., and Wenseleers, T. (2016). Intraspecific worker parasitism in the common wasp, Vespula vulgaris. Anim. Behav. 113, 79–85. doi: 10.1016/j.anbehav.2015.12.025
Paar, J., Oldroyd, B. P., Huettinger, E., and Kastberger, G. (2002). Drifting of workers in nest aggregations of the giant honeybee Apis dorsata. Apidologie 33, 553–561. doi: 10.1051/apido:2002040
Paxton, R. J. (2000). Genetic structure of colonies and a male aggregation in the stingless bee Scaptotrigona postica, as revealed by microsatellite analysis. Insect. Soc. 47, 63–69. doi: 10.1007/s000400050010
Paxton, R. J., Thoren, P. A., Estoup, A., and Tengo, J. (2001). Queen-worker conflict over male production and the sex ratio in a facultatively polyandrous bumblebee, Bombus hypnorum: the consequences of nest usurpation. Mol. Ecol. 10, 2489–2498. doi: 10.1046/j.0962-1083.2001.01377.x
Peso, M., and Richards, M. H. (2011). Not all who wander are lost: nest fidelity in Xylocopa virginica examined by mark recapture. Insect. Soc. 58, 127–133. doi: 10.1007/s00040-010-0125-y
Peters, J. M., Queller, D. C., Imperatriz-Fonseca, V. L., Roubik, D. W., and Strassmann, J. E. (1999). Mate number, kin selection and social conflicts in stingless bees and honeybees. Proc. R. Soc. Lond. B 266, 379–384. doi: 10.1098/rspb.1999.0648
Pfeiffer, K. J., and Crailsheim, K. (1998). Drifting of honeybees. Insect. Soc. 45, 151–167. doi: 10.1007/s000400050076
Pfeiffer, K. J., and Crailsheim, K. (1999). The behaviour of drifted nurse honey bees. Insect. Soc. 46, 34–40. doi: 10.1007/s000400050109
Ratnieks, F. L. W., and Wenseleers, T. (2005). Policing insect societies. Science 307, 54–56. doi: 10.1126/science.1106934
Reeve, H. K. (1989). The evolution of conspecific acceptance thresholds. Am. Nat. 133, 407–435. doi: 10.1086/284926
Richerson, P., Baldini, R., Bell, A. V., Demps, K., Frost, K., Hillis, V., et al. (2016). Cultural group selection follows Darwin's classic syllogism for the operation of selection. Behav. Brain Sci. 39:e58. doi: 10.1017/S0140525X15000606
Riolo, R. L., Cohen, M. D., and Axelrod, R. (2001). Evolution of cooperation without reciprocity. Nature 414, 441–443. doi: 10.1038/35106555
Santos, F. C., Santos, M. D., and Pacheco, J. M. (2008). Social diversity promotes the emergence of cooperation in public goods games. Nature 454, 213–216. doi: 10.1038/nature06940
Satow, S., Satoh, T., and Hirota, T. (2013). Colony fusion in a parthenogenetic ant, Pristomyrmex punctatus. J. Insect Sci. 13:8. doi: 10.1673/031.013.3801
Smith, M. L., and Loope, K. J. (2016). Caught in an evolutionary trap: worker honey bees that have drifted into foreign colonies do not invest in ovary activation. Insect. Soc. 63, 61–65. doi: 10.1007/s00040-015-0434-2
Sumner, S., Lucas, E., Barker, J., and Isaac, N. (2007). Radio-tagging technology reveals extreme nest-drifting behavior in a eusocial insect. Curr. Biol. 17, 140–145. doi: 10.1016/j.cub.2006.11.064
Takahashi, J., Martin, S. J., Ono, M., and Shimizu, I. (2010). Male production by non-natal workers in the bumblebee, Bombus deuteronymus (Hymenoptera: Apidae). J. Ethol. 28, 61–66. doi: 10.1007/s10164-009-0155-y
Tsuchida, K., and Itô, Y. (1987). Internidal drifting and dominance behaviour in Polistes jadwigae Dalla Torre workers (Hymenoptera: Vespidae). J. Ethol. 5, 83–85. doi: 10.1007/BF02347898
Ulrich, Y., Perrin, N., and Chapusiat, M. (2009). Flexible social organization and high incidence of drifting in the sweat bee, Halictus scabiosae. Mol. Ecol. 18, 1791–1800. doi: 10.1111/j.1365-294X.2009.04154.x
van Wilgenburg, E., Torres, C. W., and Tsutsui, N. D. (2010). The global expansion of a single ant supercolony. Evol. Appl. 3, 136–143. doi: 10.1111/j.1752-4571.2009.00114.x
Wang, T. B., Patel, A., Vu, F., and Nonacs, P. (2010). Natural history observations on the velvety tree ant (Liometopum occidentale): unicoloniality and mating flights. Sociobiology 55, 787–794.
Wiernasz, D. C., Perroni, C. L., and Cole, B. J. (2004). Polyandry and fitness in the western harvester ant, Pogonomyrmex occidentalis. Mol. Ecol. 13, 1601–1606. doi: 10.1111/j.1365-294X.2004.02153.x
Keywords: hymenoptera, social evolution, genetic diversity, kin selection, reciprocity, social heterosis
Citation: Nonacs P (2017) Go High or Go Low? Adaptive Evolution of High and Low Relatedness Societies in Social Hymenoptera. Front. Ecol. Evol. 5:87. doi: 10.3389/fevo.2017.00087
Received: 06 December 2016; Accepted: 17 July 2017;
Published: 02 August 2017.
Edited by:
Seirian Sumner, University College London, United KingdomReviewed by:
Heikki Helanterä, University of Helsinki, FinlandPau Carazo, Universitat de València, Spain
Copyright © 2017 Nonacs. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter Nonacs, cG5vbmFjc0BiaW9sb2d5LnVjbGEuZWR1
 Peter Nonacs
Peter Nonacs