- 1Helmholtz Institute for Functional Marine Biodiversity at the University Oldenburg (HIFMB), Oldenburg, Germany
- 2Fisheries and Aquatic Sciences, School of Forest Resources and Conservation, University of Florida, Gainesville, FL, United States
- 3Alfred Wegener Institute Helmholtz Centre for Polar and Marine Research, Bremerhaven, Germany
Introduction
Classifications may be defined as the result of the process by which similar objects are recognized and categorized through the separation of elements of a system into groups of response (Everitt et al., 2011). This is done by submitting variables to a classifier, that first quantifies the similarity between samples according to a set of criteria and then regroups (or classifies) samples in order to maximize within-group similarity and minimize between-group similarity (Everitt et al., 2011).
Classifications have become critical in many disciplines. In spatial ecology, for example, grouping locations with similar features may help the detection of areas driven by the same ecological processes and occupied by same species (Fortin and Dale, 2005; Elith et al., 2006), which can support conservation actions. In fact, classifications have been used with the aim of investigating the spatial distribution of target categories such as habitats (Coggan and Diesing, 2011), ecoregions (Fendereski et al., 2014), sediment classes (Hass et al., 2017), or biotopes (Schiele et al., 2015). Sometimes such classifications were found to act as surrogates for biodiversity in data-poor regions (e.g., Lucieer and Lucieer, 2009; Huang et al., 2012), some class being known for supporting higher biodiversity. Many of the traditional classification methods were developed in order to reduce system complexity (Fortin and Dale, 2005) by imposing discrete boundaries between elements of a system; it is easier for the human mind to simplify complex systems by identifying discrete patterns (Eysenck and Keane, 2010), and grouping similar elements together (Everitt et al., 2011). However, in natural environments, spatial and temporal transitions between elements of a system are often gradual (e.g., an intertidal flat transitioning from land to sea) (Farina, 2010). Those transitions may display distinct properties from those of the two elements they separate. Despite the particularities and importance of such transitions, they are often disregarded in ecological research (Foody, 2002), leading to the adoption of approaches that, by defining sharp boundaries, may fail to appropriately describe natural patterns and groups of a system. Such approaches have become the norm, despite the existence of approaches such as, fuzzy logic (Zadeh, 1965) and machine learning (Kuhn and Johnson, 2013) that are able to offer a more representative description of those natural transitional zones. In ecology for instance, machine learning approaces have gained some traction because of their ability to predict classes distribution (area-wide) in data-poor conditions (e.g., sparse punctual information) with a relative high performance and with no particular assumption in building the relationship between targetted classes and physical parameters (e.g., Barry and Elith, 2006; Brown et al., 2011; Fernández-Delgado et al., 2014).
In the present contribution, we aim at highlighting the limitations associated with classification techniques that are based on Boolean logic (i.e., true/false) and that impose discrete boundaries to systems. We propose to shift practices toward techniques that learn from the system under study by adopting soft classification to support uncertainty evaluation.
Discrete Classifications
The increasing availability of tools and software to semi-automatically perform classifications has reduced the amount of critical thoughts put into the exercise. Classification results are sensitive to a variety of decisions made when establishing the methodology of a particular application (Lecours et al., 2017). For instance, (1) the method to compare the objects to be classified (e.g., distance-based method), (2) whether or not the method assigns each object to one single class (i.e., Boolean approach) or assigns a membership for one or multiple classes (e.g., fuzzy logic approach), (3) whether or not the method uses samples to train the classification (i.e., supervised or unsupervised approach), and (4) the evaluation methods (see Foody, 2002; Borcard et al., 2011). Furthermore, a number of other potential sources of errors resulting in potentially misleading classifications remains: variation in the data collection methods, the spatial, temporal, and thematic scales (i.e., the way the data are categorized/identified), the spatial and temporal stability of the observations and the goodness of model fit (Barry and Elith, 2006).
One of the most challenging parts of using classifications is to evaluate how representative of real patterns the classification is. Due to the cumulative effect of the factors listed above (Rocchini et al., 2011), classification results may not adequately represent natural patterns, making the classified patterns artificial, and misleading, for instance when used to assist decision-making (Lecours et al., 2017; see Fiorentino et al., 2017). Even when a robust method is developed to reduce the impact of these factors, the concept of discrete classes may in itself be misleading; this type of classes can provide an incomplete, oversimplified representation of complex natural patterns, and thus misrepresent the reality to be described. In spatial ecology, using discrete classes involves establishing “hard” boundaries between them, which has been shown to cause misclassification errors (Sweeney and Evans, 2012; Lecours et al., 2017). For instance, an object may not always belong to one of the defined classes, thus being forced into one of those defined classes by the classifier. When doing so, the interpretation that is often made is that the object was misclassified or that there was an error of the algorithm, while in fact, it is a consequence of the often-erroneous assumption that all objects must belong to a specific class. A solution that has been proposed to avoid those errors is to shift practices toward “soft” classifications instead of “discrete” classifications.
Soft Classifications
It has been argued in the literature that soft classification approaches better represent and describe natural patterns, including transitional areas (Ries et al., 2004). Soft classification approaches, which include fuzzy logic (Zadeh, 1965) Bayesian, neural networks, support vector machines, decision trees, boosting, bagging, generalized linear models, and multiple adaptive regression splines, among others (see Fernández-Delgado et al., 2014 for a comprehensive review on classification and associated problems), acknowledge that one object may belong to more than one class This enables the recognition of elements of the real world that are between classes (i.e., do not belong to one specific pre-defined class), such as transitional zones and fine-scale natural heterogeneity.
While hard classifiers assign an object to a class following a Boolean, binary system (true/false, in a class or not), soft classifiers assign memberships to objects. Memberships are the estimated probabilities of objects to belong to a class (Everitt et al., 2011). Each object will have as many membership values as there are classes. Membership varies along the continuum ranging from 0 (not a member) to 1 (definitely a member). An object that has relatively high membership values for more than one class is thus said to be not clearly associated with one specific class. This may be an indication that no class adequately describes this particular object, which could inform and guide further analyses in order to explain that pattern. Those analyses may for instance highlight that this data object is an error, or if there are many objects in the same situation, that a new class needs to be defined.
Can Soft Classifications be Used to Estimate Uncertainty?
In remote sensing, traditional pixel-based classifications use image pixels as objects to be classified. The use of discrete classifiers in land cover studies often oversimplifies the actual land cover (Foody, 2000). For instance, forested wetlands, which in nature mark the transition between forested areas and waters bodies, would most likely be classified as a “forest” land cover or a “water” land cover by a hard classifier. For the purpose of this example, we assume that it classifies it as “forest.” On the other end, a soft classifier might assign to that same pixel a “forest” membership of 0.65 and a “water” membership of 0.35. As a result, different users could interpret those classifications according to the following statements:
A) Based on the hard classification result, the pixel represents “forest” land cover. In the absence of a ground-truth point data for that particular pixel, it could be assumed that this result is 100% certain.
B) Based on the soft classification result, the pixel represents a mixture of “forest” land cover and “water” land cover.
C) Based on the multiple memberships from the soft classification, the pixel has an associated level of ambiguity (e.g., it is 35% ambiguous that the pixel represents a “forest” land cover and 65% ambiguous that it represents a “water” land cover).
D) Based on the multiple memberships from the soft classification, it is possible that the pixel belongs to a distinct class characterized by a mixture of forest and water (the transition), perhaps “wetland.” After validation or a re-run of the soft classification with a new class, it could potentially be possible to say that the pixel represents a “wetland” land cover with much less ambiguity. While we argue that soft classifications are more appropriate than hard classifications, we note that a re-run of the hard classification with a class corresponding to wetlands would also be more accurate than the initial hard classification.
The interpretation in “A” is not fully representative of the reality as the water component of the pixel is not reported or acknowledged at all. In “B” a nuance is added to the interpretation as the potentially mixed nature of the pixel is acknowledged. In “C,” that nuance is interpreted as a measure of ambiguity, i.e., that it is acknowledged that the classifier could not distinguish between the two classes. Finally, in “D,” the mixed nature of the pixel is used to redefine the classification based on ecological knowledge (e.g., that wetlands can be a mixture of forest and water from a remote sensor's perspective), and to guide further analyses about the nature of the land cover. That simple example illustrates uncertainty as defined by Zhang and Goodchild (2002), i.e., as the ambiguity of a classification. Since membership quantifies the probability of an object to belong to multiple classes, it can be used as a measure of ambiguity, and therefore as a measure of uncertainty (Yager, 2016).
Depending on the nature of the analysis, the spatial representation of membership can be used to display spatial uncertainty of classifications, or to identify transitions between existing classes. Traditional fuzzy and model-based approaches thus acknowledge transitions among classes.
However, such approaches have the limitation to be algorithmic, i.e., not explicitly accounting for data statistical properties such as randomness (Warton et al., 2015) and mean-variance trends (Warton et al., 2012)–although resampling or finite mixture approaches may provide likelihood-based foundations to the clustering (Pledger and Arnold, 2014). In fact, methods based on a single classifier offer only one piece of evidence, which does not provide any confidence interval of the membership estimation (Huang and Lees, 2004; Liu et al., 2004). In turn, ensemble modeling approaches overcome such problems in a consistent environment (Elder IV, 2003). Despite some criticisms to ensemble modeling approaches like the lack of interpretation capability and some tendency to overfit (see Elder IV, 2003 for a discussion on the topic), ensemble modeling approaches were shown to outperform other methods (Elder IV, 2003; Fernández-Delgado et al., 2014). The confidence interval around the membership values provided by such models may be used to acknowledge natural transitions in addition to the error estimates around those membership values.
The Advantage of Mapping Uncertainty
The concepts of uncertainty and error have often mistakenly been used interchangeably (Zhang and Goodchild, 2002; Jager and King, 2004). As a consequence, uncertainty is often perceived negatively because of its association with the idea of error and inaccuracy. Uncertainty is inherent to any and all data and cannot necessarily be removed or minimized to get closer to the truth the same way errors can (Zhang and Goodchild, 2002; Beale and Lennon, 2012). Uncertainty is part of our perception of natural patterns (e.g., temporal dynamics, spatial variability), data representation (e.g., positional uncertainty, measurement uncertainty, thematic uncertainty), and modeling (e.g., error introduced by the model) (e.g., Barry and Elith, 2006).
Maps of uncertainty, or maps of ignorance, help to identify areas where the classification has a stable, consistent, and distinct solution and can be used further to target the areas where uncertainty is higher, thus highlighting the need to deepen the investigation in those areas (Rocchini et al., 2011). It has been demonstrated that maps of uncertainty enhance decision-making in conservation contexts by solving issues that often appear when hard classifications are applied (Regan et al., 2005; Langford et al., 2009). In fact, maps of uncertainty permit a more realistic and natural delineation of boundaries between classes (Zhang and Goodchild, 2002).
Soft classifications and ensemble models allow users' knowledge of the system to grow by providing an estimation of uncertainty. When classes cannot provide an appropriate description of the system under study (for example in cases of high fuzziness), the investigator can choose to change the classifier or deepen the investigation to better understand the patterns in the system and how it translates into the data representation. On the opposite, Boolean (true/false) approaches only offer a static view, and while measures of accuracy can be calculated to quantify misclassifications, they have been shown to sometimes misrepresent the amplitude of the misclassifications (e.g., Lecours et al., 2016) and often cannot guide further investigations to better understand the dynamics at play.
To assist with the interpretation of uncertainty resulting from the application of a soft classifier, at least three solutions based on membership assignations of objects to classes can be used (Table 1). These solutions can be used to display uncertainty spatially in a map, which can be interpreted, discussed, and then used to further enhance the classification in an iterative process (Figure 1).

Table 1. Methods for synthesizing membership values (p) resulting from soft classifications at each location (i) for a given number of classes (K).
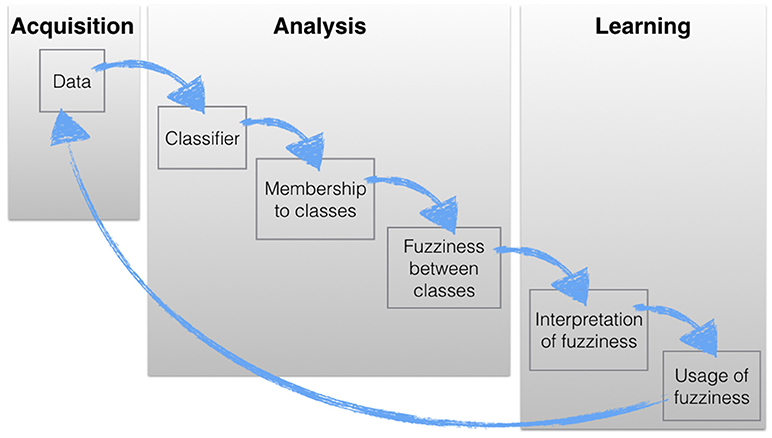
Figure 1. Example of learning classifier workflow using a fuzzy clustering. The learning phase is linked to the data acquisition because fuzziness may highlight data weakness, thereby areas where new data acquisition is required. Note that the same workflow can be translated to any other methods that allow uncertainty.
Conclusion
We acknowledge that classification methods need to be reliable and appropriate for the intended use, and adequately represent the natural complexity of the systems under study. However, we think that the main challenge of classifications is the proper and meaningful interpretation of the associated uncertainty rather than the method itself.
The use of soft classifiers to provide the visual and spatial display of classification uncertainty enhances the value of classifications. Providing a measure of uncertainty associated with classes leads to the fulfillment of classifications' potential, which goes beyond the simple identification and separation of classes. Classifications based on concepts of fuzzy logic, model-based approaches, and ensemble modeling approaches, will help move away from classes with hard, discrete boundaries, yielding better solutions to represent accurately and better understand complex systems. Acknowledging uncertainty encourages learning from the classification process by encouraging further investigation and hypothesizing about its causes (e.g., inappropriate spatial resolution, data quality, inappropriate number of classes).
Whether the aim of an exercise is to communicate results or to start the investigation of a system through exploratory analyses, the spatial display of uncertainty provides directions on which actions need to be undertaken. While stakeholders may use map of uncertainty to find for instance the proper conservation measure and therefore to better handle areas where high uncertainty is displayed, scientists may use the same information to build new hypotheses and shed light on processes that underpin such uncertainty.
Author Contributions
DF conceived and organized the manuscript. DF, VL, and TB wrote and reviewed the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank the reviewer and Dr. Casper Kraan whose comments helped to improve the manuscript.
References
Barry, S., and Elith, J. (2006). Error and uncertainty in habitat models. J. Appl. Ecol. 43, 413–423. doi: 10.1111/j.1365-2664.2006.01136.x
Beale, C. M., and Lennon, J. J. (2012). Incorporating uncertainty in predictive species distribution modelling. Philos. Trans. R. Soc. Lond. B Biol. Sci. 367, 247–258. doi: 10.1098/rstb.2011.0178
Borcard, D., Gillet, F., and Legendre, P. (2011). Numerical Ecology With R, 1st Edn. New York, NY: Springer.
Brown, C. J., Smith, S. J., Lawton, P., and Anderson, J. T. (2011). Benthic habitat mapping: a review of progress towards improved understanding of the spatial ecology of the seafloor using acoustic techniques. Estuar. Coast. Shelf Sci. 92, 502–520. doi: 10.1016/j.ecss.2011.02.007
Burrough, P. A., van Gaans, P. F. M., and Hootsmans, R. (1997). Continuous classification in soil survey: spatial correlation, confusion and boundaries. Geoderma 77, 115–135. doi: 10.1016/S0016-7061(97)00018-9
Coggan, R., and Diesing, M. (2011). The seabed habitats of the central english channel: a generation on from holme and cabioch, how do their interpretations match-up to modern mapping techniques? Cont. Shelf Res. 31, 132–150. doi: 10.1016/j.csr.2009.12.002
Elder IV, J. F. (2003). The generalization paradox of ensembles. J. Comput. Graph. Stat. 12, 853–864. doi: 10.1198/1061860032733
Elith, J. H., Graham, C. P., Anderson, R., Dudík, M., et al. (2006). Novel methods improve prediction of species' distributions from occurrence data. Ecography 29, 129–151. doi: 10.1111/j.2006.0906-7590.04596.x
Everitt, B. S., Landau, S., Leese, M., and Stahl, D. (2011). Cluster Analysis, 5th Edn. London: John Wiley & Sons. Available online at: http://onlinelibrary.wiley.com/book/10.1002/9780470977811 (Accessed April 24, 2013).
Eysenck, M. W., and Keane, M. T. (2010). Cognitive Psychology: A Student's Handbook, 6 Student Edn. New York, NY: Taylor & Francis.
Farina, A. (2010). Ecology, Cognition and Landscape: Linking Natural and Social Systems, 2009 edn. Dordrecht; New York, NY: Springer.
Fendereski, F., Vogt, M., Payne, M. R., Lachkar, Z., Gruber, N., Salmanmahiny, A., et al. (2014). Biogeographic classification of the Caspian Sea. Biogeosciences 11, 6451–6470. doi: 10.5194/bg-11-6451-2014
Fernández-Delgado, M., Cernadas, E., Barro, S., and Amorim, D. (2014). Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 15, 3133–3181. Available online at: http://jmlr.org/papers/v15/delgado14a.html
Fiorentino, D., Pesch, R., Guenther, C.-P., Gutow, L., Holstein, J., Dannheim, J., et al. (2017). A ‘fuzzy clustering’ approach to conceptual confusion: how to classify natural ecological associations. Mar. Ecol. Prog. Ser. 584, 17–30. doi: 10.3354/meps12354
Foody, G. M. (2000). Mapping land cover from remotely sensed data with a softened feedforward neural network classification. J. Intell. Robotic Syst. 29, 433–449. doi: 10.1023/A:1008112125526
Foody, G. M. (2002). Status of land cover classification accuracy assessment. Remote Sens. Environ. 80, 185–201. doi: 10.1016/S0034-4257(01)00295-4
Fortin, M.-J., and Dale, M. R. T. (2005). Spatial Analysis: A Guide for Ecologists. Cambridge; New York, NY: Cambridge University Press.
Hass, H. C., Mielck, F., Fiorentino, D., Papenmeier, S., Holler, P., and Bartholom,ä, A. (2017). Seafloor monitoring west of Helgoland (German Bight, North Sea) using the acoustic ground discrimination system RoxAnn. Geo Mar. Lett. 37, 125–136. doi: 10.1007/s00367-016-0483-1
Huang, Z., and Lees, B. G. (2004). Combining non-parametric models for multisource predictive forest mapping. Photogr. Eng. Remote Sens. 70, 415–425. doi: 10.14358/PERS.70.4.415
Huang, Z., Nichol, S. L., Siwabessy, J. P. W., Daniell, J., and Brooke, B. P. (2012). Predictive modelling of seabed sediment parameters using multibeam acoustic data: a case study on the Carnarvon Shelf, Western Australia. Int. J. Geograph. Inform. Sci. 26, 283–307. doi: 10.1080/13658816.2011.590139
Jager, H. I., and King, A. W. (2004). Spatial uncertainty and ecological models. Ecosystems 7, 841–847. doi: 10.1007/s10021-004-0025-y
Kuhn, M., and Johnson, K. (2013). Applied Predictive Modeling. New York, NY; Heidelberg; Dordrecht; London: Springer.
Langford, W. T., Gordon, A., and Bastin, L. (2009). When do conservation planning methods deliver? Quantifying the consequences of uncertainty. Ecol. Inform. 4, 123–135. doi: 10.1016/j.ecoinf.2009.04.002
Lecours, V., Brown, C. J., Devillers, R., Lucieer, V. L., and Edinger, E. N. (2016). Comparing selections of environmental variables for ecological studies: a focus on terrain attributes. PLoS ONE 11:e0167128. doi: 10.1371/journal.pone.0167128
Lecours, V., Devillers, R., Edinger, E. N., Brown, C. J., and Lucieer, V. L. (2017). Influence of artefacts in marine digital terrain models on habitat maps and species distribution models: a multiscale assessment. Remote Sens. Ecol. Conserv. 3, 232–246. doi: 10.1002/rse2.49
Liu, W., Gopal, S., and Woodcock, C. E. (2004). Uncertainty and confidence in land cover classification using a hybrid classifier approach. Photogram. Eng. Remote Sens. 70, 963–971. doi: 10.14358/PERS.70.8.963
Lucieer, V., and Lucieer, A. (2009). Fuzzy clustering for seafloor classification. Mar. Geol. 264, 230–241. doi: 10.1016/j.margeo.2009.06.006
Pledger, S., and Arnold, R. (2014). Multivariate methods using mixtures: correspondence analysis, scaling and pattern-detection. Comput. Stat. Data Anal. 71, 241–261. doi: 10.1016/j.csda.2013.05.013
Regan, H. M., Ben-Haim, Y., Langford, B., Wilson, W. G., Lundberg, P., Andelman, S. J., et al. (2005). Robust decision-making under severe uncertainty for conservation management. Ecol. Appl. 15, 1471–1477. doi: 10.1890/03-5419
Ries, L., Robert, J., Fletcher, J., Battin, J., and Sisk, T. D. (2004). Ecological responses to habitat edges: mechanisms, models, and variability explained. Annu. Rev. Ecol. Evol. Syst. 35, 491–522. doi: 10.1146/annurev.ecolsys.35.112202.130148
Rocchini, D., Hortal, J., Lengyel, S., Lobo, J. M., Jiménez-Valverde, A., Ricotta, C., et al. (2011). Accounting for uncertainty when mapping species distributions: the need for maps of ignorance. Prog. Phys. Geogr. 35, 211–226. doi: 10.1177/0309133311399491
Schiele, K. S., Darr, A., Zettler, M. L., Friedland, R., Tauber, F., von Weber, M., et al. (2015). Biotope map of the German Baltic Sea. Mar. Pollut. Bull. 96, 127–135. doi: 10.1016/j.marpolbul.2015.05.038
Sweeney, S. P., and Evans, T. P. (2012). An edge-oriented approach to thematic map error assessment. Geocarto Int. 27, 31–56. doi: 10.1080/10106049.2011.622052
Warton, D. I., Foster, S. D., De'ath, G., Stoklosa, J., and Dunstan, P. K. (2015). Model-based thinking for community ecology. Plant Ecol. 216, 669–682. doi: 10.1007/s11258-014-0366-3
Warton, D. I., Wright, S. T., and Wang, Y. (2012). Distance-based multivariate analyses confound location and dispersion effects. Methods Ecol. Evolut. 3, 89–101. doi: 10.1111/j.2041-210X.2011.00127.x
Yager, R. (2016). Uncertainty modeling using fuzzy measures. Knowl. Based Syst. 92, 1–8. doi: 10.1016/j.knosys.2015.10.001
Keywords: uncertainty, spatial ecology, discrete classification, soft boundaries, mapping transitions
Citation: Fiorentino D, Lecours V and Brey T (2018) On the Art of Classification in Spatial Ecology: Fuzziness as an Alternative for Mapping Uncertainty. Front. Ecol. Evol. 6:231. doi: 10.3389/fevo.2018.00231
Received: 28 June 2018; Accepted: 10 December 2018;
Published: 21 December 2018.
Edited by:
Miles David Lamare, University of Otago, New ZealandReviewed by:
Zhi Huang, Geoscience Australia, AustraliaCopyright © 2018 Fiorentino, Lecours and Brey. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dario Fiorentino, ZGFyaW8uZmlvcmVudGlub0Bhd2kuZGU=
 Dario Fiorentino
Dario Fiorentino Vincent Lecours
Vincent Lecours Thomas Brey
Thomas Brey