The Metabolic Basis of Fat Tail Distributions in Populations and Community Fluctuations

Introduction

Deciphering the links between community structure and dynamics is a long-standing question in ecology. Scaling theories are an appealing approach to unify community size structure and population variability (Marquet et al., 2007; Cohen et al., 2012; Segura et al., 2017; Zaoli et al., 2017). Fundamental principles driving energy and mass conversion by organisms constrain processes at higher levels of biological organization and have therefore been useful to characterize community structure and dynamics (Brown et al., 2004).

Four scaling functions are ubiquitous in ecology: (i) the scaling of metabolic rates (B_i) with body mass (M_i); (B_i∞${\text{M}}_{\text{i}}^{\alpha }$; generally 0.5 < α < 2) (Damuth, 1981; Brown et al., 2004; DeLong et al., 2010), (ii) the scaling of population density (N_i) with body mass (size-density relationship, SDR; ${\mathrm{\text{N}}}_{\mathrm{\text{i}}}\propto {{\mathrm{\text{M}}}_{\mathrm{\text{i}}}}^{{\mathrm{\text{e}}}_{\mathrm{\text{SDR}}}}$; generally e_SDR < 0) (Damuth, 1981; Agustí et al., 1987; Blackburn and Gaston, 1997; White et al., 2007); (iii) the Taylor's scaling law, relating the average population abundance (mean(N)) with population variance (var(N_i)) (TL; var(N_i)∝ mean(N_i)${ }^{{\text{e}}_{\text{TL}}}$; e_TL~1–2), and (iv) the scaling of population variance (var(N_i)) with body-mass (variance mass allometry, VMA; Var(N_i)$\propto {{\mathrm{\text{M}}}_{\mathrm{\text{i}}}}^{{\mathrm{\text{e}}}_{\mathrm{\text{VMA}}}}$; generally e_VMA < 0) (Marquet, 2005; Cohen et al., 2012). Multiple mechanisms have been proposed to explain these scaling relationships, and how they are interrelated (Zaoli et al., 2017), but the debate is far from being settled.

The form of the SDR varies with spatial scale and with the method of estimating population density (Blackburn and Gaston, 1997; White et al., 2007). At regional to global scales, the SDR often yields an exponent of approximately −α, indicating that populations of different size can flux similar amounts of energy per unit area (Lawton, 1989), a phenomenon referred to as energy equivalence (Damuth, 1981). By contrast, density estimates obtained for all species present in local communities often produce weak triangular or polygonal (i.e., constraint envelope) relationships with exponents shallower than −α, indicating that that larger-bodied species flux more energy (Marquet et al., 1995; White et al., 2007; Barneche et al., 2016). Under the hypothesis that only the abundance of dominant species are constrained by resource availability (Barneche et al., 2016; Ghedini et al., 2018), it is possible to derive some general predictions about population and community dynamics (Figure 1).

FIGURE 1

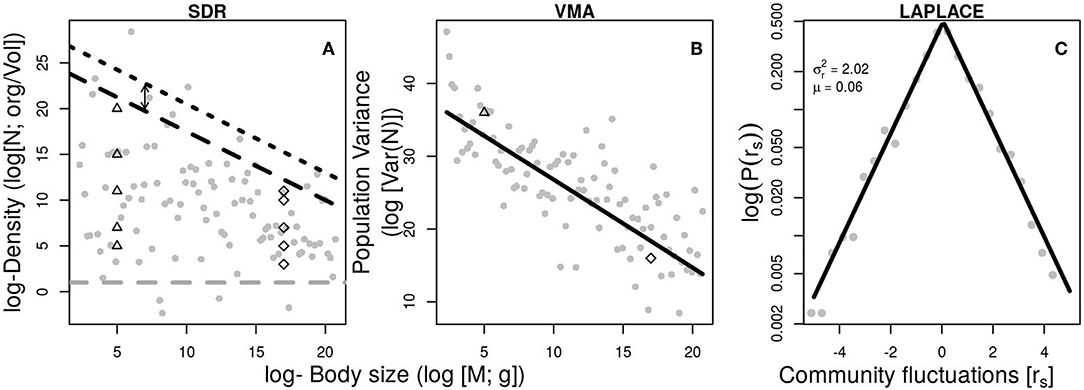
Figure 1. Examples of relevant macroscopic community patterns simulated following Equations 5,6, 7, and 10. (A) The scaling of population density with body size (SDR) where maximum popupulation density (n_max; black dashed lines) scales as the inverse of the metabolic scaling (–α = −0.75) and its intercepts increase with increasing resources supply from R_tot = 0.1 (dashed line) to R_tot = 3 (dotted line). Remaining parameters from Equation 5 are a = 1, T = 15°C. Minimum population abundance (gray dashed line) is assumed to have no relationship with body size (β = 0, b = 1 in Equation 6). Examples of possible temporal changes in the SDR space of a small sized (log(M) = 5; upper triangles) and large-sized (log(M) = 17; open diamond) species. (B) The variance mass allometry (VMA) showing a decrease in population variance with body size (Equation 10; α = 0.75, β = 0, b = 1, a = 1, R_tot = 0.1, T = 15°C, E = 0.65). The hypothetical positions of a small sized and a large-sized species from (A) are shown for comparison. (C) The Laplace distribution of aggregated population fluctuations. The Laplace distribution is the resulting distribution of aggregate temporal fluctuations of single populations (Equation 1). Simulated random normal variation (gray points) has been added to the equations.

Fluctuations in abundance of single populations from time t to time t+1 can be expressed as:

$\begin{array}{ll}{r}_i=\text{log}\left(\frac{N_i^{t+\text{1}}}{N_i^t}\right)& (1)\end{array}$

The distribution of fluctuations often show departures from the expected log-normal to fat-tailed distributions, implying reduced predictability for population outbreaks and extinctions (Halley and Inchausti, 2002; Lan and Chandran, 2011; Segura et al., 2013; Anderson et al., 2017a), but a mechanistic explanation for this phenomenon is currently lacking. At the community level, the aggregation of fluctuations of single populations across species (r_i) often follows a double exponential or Laplace distribution (Figure 1) which is a power law when the exponential of fluctuations (exp(r_i) = ${\text{N}}_{\text{i}}^{\text{t}+1}/N_{\text{i}}^{\text{t}}$) are evaluated (Keitt and Stanley, 1998; Allen et al., 2001; Marquet et al., 2007; Kalyuzhny et al., 2014; Segura et al., 2017). If the distribution of r_i values is centered on zero, it implies that an increase in one species is compensated by the decrease in another, consistent with zero-sum dynamics, which has important consequences for community dynamics (Marquet, 2005; Segura et al., 2017). Differently, VMA is a scaling law relating population variability with body size. Its scaling exponent has been theoretically predicted by combining the TL scaling exponent (e_TL~ 2) and the SDR exponent (e_SDR~ −0.75) giving an exponent e_VMA ~ e_TL ${ }_{{ }^{*}}$ e_SDR ~ −3/2 (Marquet, 2005; Cohen et al., 2012). The VMA was succesfully evaluated using empirical data sets (Cohen et al., 2012; Xu, 2016) but the TL has been questioned as a statistical result of sampling from skewed distributions (Cohen and Xu, 2015). However, the ecological mechanisms generating skewed distributions remains unclear. Finding an expression for the VMA without invoking the Taylor's law would help to advance in the understanding of mechanisms behind populations and community variability (Figure 1).

Here, under the hypothesis that metabolic requirements constraint the maximum abundance of dominant species in a local community (Agustí et al., 1987; Belgrano et al., 2002; Brown et al., 2004; Barneche et al., 2016; Ghedini et al., 2018), we provide a formal link between body size, the distributions of population abundance, and population and community fluctuations in abundance. These links will help to advance our understanding of determinants of size structure, and population and community variability in natural communities. Based on the influence of body size, temperature, and resource flux on the metabolic limit to maximum population abundance, we derive a constraint envelope model that establishes: (i) a formal link with single-population variability that generates a fat-tailed distribution of fluctuations, (ii) an explicit relationship with the Laplace distribution of community fluctuations, and (iii) a general form of variance-mass allometry which, in a particular case, includes the VMA previously proposed by Marquet (2005) and Cohen et al. (2012).

The Metabolic Restriction to Maximum Population Abundance

The model is based on fundamental principles of resource network transport and enzyme kinetics and should therefore be applicable to many ecological systems (Brown et al., 2004). The basal metabolic rate (B_i) scale as a power law with body size (M_i) and have a near-exponential dependence with temperature (T in Kelvin)

$\begin{array}{ll}{B}_i=b_{\text{0}}\text{exp}\left(\frac{-E}{kT}\right)M_i^{\alpha }& (2)\end{array}$

where b₀ is the size and temperature independent taxon specific constant, exp() is the exponential function, E is the activation energy (E ~ 0.65 eV for heterotrophs and E ~ 0.32 eV for autotrophs) and k is the Boltzmann constant (8.62 × 10⁻⁵ eV K⁻¹). Ideally, the scaling of field metabolic rate should be used, however, field metabolic data are not yet available for many groups (Nagy, 2005) and thus the scaling of basal metabolic rate is assumed. The allometric scaling of metabolism (α) showed variations among major evolutionary transitions (~0.75–2; DeLong et al., 2010), but for the remaining of the article we will use the prototypical value found for metazoans (α ~ 0.75). This choice does not modify the qualitative predictions of the theoretical model, as long as the scaling of metabolism is larger than that of the minimum population size (see below).

Total resource use (R_tot) in a local ecosystem (e.g., light or nutrients in case of autotrophs) is equal to the sum of the population-level rates of resource use per unit area or volume, R_i, across S cohabiting species ($R_{tot}={\sum }_{i=1}^s{R}_i$). R_i, in turn, is proportional to the product of metabolic rate (B_i) and the population density per unit area or volume (N_i),

$\begin{array}{ll}{R}_i=N_i{B}_i& (3)\end{array}$

Our interest is in understanding the upper limit to population density, max(N_i). We assume that a dominant species can use no more than a fraction γ of R_tot. For simplicity, we further assume that this fraction is a constant independent of body size (i.e., γ ∝ M⁰). Given these assumptions, we can combine Equations 2 and 3, and then substituting γR_tot for R_i (Belgrano et al., 2002; Deng et al., 2012) for maximum population density:

$\begin{array}{ll}max(N_i)=\gamma R_{tot}{b}_{\text{0}}^{-\text{1}}\text{exp}\left(\frac{E}{kT}\right)M_i^{-\alpha }& (4)\end{array}$

and its logarithm:

$\begin{array}{ll}{n}_{max}=\text{log}(max(N_i))=\left[a+\text{log}(R_{tot})+\frac{E}{kT}\right]-\alpha \text{log}(M_i)& (5)\end{array}$

where a = log(γ ${\text{b}}_0^{-1}$). As defined, n_max represents the upper limit for population density on the natural logarithmic scale. Similarly, we can define the equation for the lower population abundance bound on the logarithmic scale n_min:

$\begin{array}{ll}{n}_{min}=b-\beta \text{log}(M_i)& (6)\end{array}$

We will assume for simplicity that n_min is independent of body size (β = 0), and of temperature and resources (i.e., b is constant) (Pimm, 1991; Marquet and Taper, 1998). In the present context n_min is interpreted as the lower bound a local population can reach before getting locally extinct. For example, in the case of phytoplankton with asexual reproduction, the minimum abundance is one organism (thus exp(n_min) = 1). We recall that this is not a metabolic scaling, and later we will discuss the qualitative effects of a different scaling exponent (β > 0) on specific predictions.

Equations 5 and 6 allow us to set the limits on local population abundance of a species in an ecosystem given its body size, resource supply rate and temperature (Figure 1; Lawton, 1989). In the following sections, we will derive a formal theoretical model relating the metabolic rate (Equations 2, 5, and 6) to the scope for single population fluctuations, the emergence of fat tails and the distribution of aggregated community fluctuations. The model predicts the potential limits of fluctuations (conditional to body size) within the boundaries imposed by metabolic restrictions, but it does not analyze the specific mechanisms that generates the variability (e.g., predation, environmental perturbations).

Single Population Abundance Distribution

Because reproduction is a multiplicative process, a reasonable assumption for the distribution of abundances (N_i) through time for a single species in a local community is that it follows a Lognormal distribution (Halley and Inchausti, 2002). This implies that the logarithm of abundance follows a normal distribution with a mean μ and standard deviation σ (MacArthur, 1955; Halley and Inchausti, 2002). Defining n_max and n_min (in Equations 5 and 6) as the expected 5th and 95th quantiles of the size-dependent (i.e., conditional) distribution of log abundances, the following formal relationship can be derived using Equations 2–6:

$\begin{array}{ll}\begin{array}{c}\mu =\frac{n_{max}+n_{min}}{\text{2}}=\frac{a+\text{log}(R_{tot})+\frac{E}{kT}+b}{\text{2}}-\frac{(\alpha +\beta )}{\text{2}}\text{log}(M_i)\\ {\sigma }^{\text{2}}=\frac{n_{max}-n_{min}}{\text{3.28}}=\frac{a+\text{log}(R_{tot})+\frac{E}{kT}-b}{\text{3.28}}-\frac{(\alpha -\beta )}{\text{3.28}}\text{log}(M_i)\end{array}& (7)\end{array}$

These equations predict that μ will be negatively related to body size, consistent with empirical local size-abundance distributions (Damuth, 1981; Agustí et al., 1987; Blackburn and Gaston, 1997; Belgrano et al., 2002; White et al., 2007). If lower population limit is independent of body size (β = 0), as observed in most local size density relationships (Lawton, 1989; Blackburn and Gaston, 1997), the predicted average slope would be the half of the scaling exponent of metabolism (e.g., –α/2 ~ −0.375) closer to the observed average in local communities of animals (−0.25; Blackburn and Gaston, 1997). In the particular case when there is a strong scaling of lower population limit with body size (e.g., β ~ α) (e.g., Silva and Downing, 1994), the equations recover the energetic equivalence rule, as the predicted exponent of the SDR is the opposite to the metabolic scaling exponent (e_SDR ~ –α) (Brown et al., 2004; White et al., 2007; Deng et al., 2012).

A novel explicit prediction is the link between metabolic constraints and the variance σ² of log-population abundance (Figure 2). Equation 7 predicts a decreasing function of σ² with body size (unless the extreme case β = α), an inverse relationship with temperature and a positive relationship with the logarithm of resource supply. It provides the ecological conditions to observe a linear (α = β) or a triangular (α > β) relationship between log-size and log-abundance as has been observed (Lawton, 1989; Marquet et al., 1995; Blackburn and Gaston, 1997; White et al., 2007; Barneche et al., 2016). The decrease in population variance might be related to longer generation times in larger-sized organisms, which is closely related to body size. Those equation combine the physiological effect of the metabolic transport network (α, M_i) with the effect of local ecosystem properties (temperature and resource supply; T and R_tot) on population fluctuations. With the formal theoretical predictions on the mean and standard deviation of population abundance, it is possible to explore their role on populations and community fluctuations.

FIGURE 2

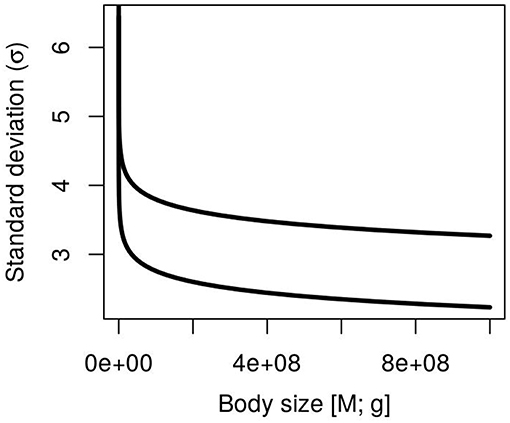
Figure 2. Body size dependence of population standard deviation (Equation 7) at different resource levels (R_tot = 3 upper curve and R_tot = 0.1 lower curve). Remaining parameters used to draw the curve are α = 0.75, β = 0, a = 1, b = 0, T = 15°C, E = 0.65.

Emergence of fat Tails in Single Population Fluctuations

The magnitudes of abundance fluctuations for a single population can be characterized as the log of the ratio of abundances, r_i, for two successive time periods, t and t+1 (Equation 1) (Keitt and Stanley, 1998; Halley and Inchausti, 2002; Segura et al., 2013). The ratio of two lognormal distributions is itself a lognormal and in the long run, covariance of population abundance between successive times is zero, thus, the mean (μ_ri) and variance (${\sigma }_{\text{ri}}^2$) of the fluctuations (r_i) are estimated as:

$\begin{array}{ll}\begin{array}{c}{\mu }_{ri}={\mu }_{t+\text{1}}-{\mu }_t\\ {\sigma }_{ri}^{\text{2}}={\sigma }_{t+\text{1}}^{\text{2}}+{\sigma }_t^{\text{2}}\end{array}& (8)\end{array}$

If mean abundance in successive times are similar, the expected mean of fluctuations μ_ri is on average zero, but the variance is the sum of the two variances (Equation 8), which amplifies the effect of size, temperature and resources on it (from Equation 7). The periodic changes in temperature or resources which naturally occur in natural ecosystems will shift the upper metabolic limit (n_max) and thus modify the scope for fluctuations of each population (${\sigma }_{\text{ri}}^2$ in Equation 8 and Figure 1). If the abundance of a single population is estimated over long periods (relative to its generation time), the fluctuations for a single species will follow a lognormal distribution with zero mean, but time-varying variances. This can be described as a mixture of lognormal distributions with different variances, which is a mechanism able to generate fat tail distribution of fluctuations (Halley and Inchausti, 2002; Segura et al., 2013; Anderson et al., 2017a). This provides a plausible metabolic-based explanations for the fat tails in the population fluctuations. This explanation is complementary to previous explanations based on environmentally-driven population crashes (Anderson et al., 2017a), migration (Anderson et al., 2017b) antropogenic disturbances (Quiroz-Martinez et al., 2012), or the long-range propagation of interaction among species in a food web (Keitt and Stanley, 1998; Allen et al., 2001). However, for a given community in a particular ecosystem in a defined period of time, present model allows to estimate quantitative predictions about the mixture of normal distributions and the resulting “fat-tailed” distribution for each species given their body size.

According to the present model, fat tails will be easily detectable in small-sized highly-abundant species because of their larger scope for fluctuations as opposed to large-sized species (Figure 1). If a short period of time is evaluated or if resources or temperature present a temporal trend as registered under antropogenic eutrophication or climate change, asymmetric distributions of population fluctuations could result as has been noted early (Halley and Inchausti, 2002; Segura et al., 2013; Anderson et al., 2017a). Short datasets might preclude detecting statistical differences between lognormal or their fat-tailed counterparts. Moreover, the ability to detect substantial differences would decrease with the size of the organism as the scope for fluctuations (${\sigma }_{\text{ri}}^2$) is reduced. The patterns predicted by Equations 7 and 8 should be treated as the extreme limits into where population dynamics could act (Lawton, 1989). Finding deviations from the theoretically predicted scope for fluctuations could provide interesting clues about other ecological mechanisms reducing (e.g., predator-prey coupling) or amplifying (e.g., fishing) population variability.

Link With the Laplace Distribution of Community Fluctuations

When the fluctuation (r_i) of multiple populations whitin a community spanning a large range in body sizes are aggregated, the Laplace distribution is the expected outcome as has been observed in empirical studies (Keitt and Stanley, 1998; Allen et al., 2001; Kalyuzhny et al., 2014; Segura et al., 2017). The link of single population fluctuations (Equation 8) to the community level is straightforward. There is a proposition that states that the aggregation of Lognormal distributions with mean zero and stochastic variance which has an exponential distribution generates a Laplace random variable (proposition 2.2.1 in Kotz et al., 2001). Single population fluctuations are approximately normal in the log space and its average is expected to be zero (μ_rs = 0) and independent of body size (Equation 8) which fullfills the former criteria. The variance of the fluctuations (${\sigma }_{\text{rs}}^2$) can be approximated as twice the variance of single population fluctuation (Equation 8; ${\sigma }_{\text{rs}}^2$ ~ 2σ²) which is related to metabolic rates and present a left skewed distribution with multiple shapes (Figure 2). When β = 0, the variances (σ²) of populations distributed uniformly in the log body-size space are power laws with a scaling ~−α/3.28, and at the other end they are independent of size (when α = β), and present an inverse relationship with absolute temperature and an exponenetial dependence on resource flux (R_tot). This distributions are close to an average of zero and an exponential distribution of the variances necessary to obtain a Laplace distribution of community fluctuations (Kotz et al., 2001).

Deviations from Laplace are expected because the distribution of variances (σ²) are not strictly exponential, but this patterns have not been investigated yet (Kalyuzhny et al., 2014). Another source of discrepancies from the expected Laplace could arise if the fluctuations are estimated in a reduced period of time, where aperiodic fluctuations in abiotic conditions caused by nutrient pulses or systematic trends in temperature regimes modify the variance structure of fluctuations (Equation 7). Overall, Laplace distribution serves as a null model to test community fluctuations in real ecosystems or to analyze deviations from theoretical assumptions. This framework allows to generate theoretical predictions on the specific effect of increasing temperature or resource variability on population and community fluctuations.

A General Model for the Link Between Population Variance and Body Size

The variance-mass allometry has been defined theorethicaly by combining SDR and TL (Marquet, 2005; Cohen et al., 2012) and states that population variance (Var(N)) is a decreasing power function of body mass (M) which was supported by empirical tests (Cohen et al., 2012; Lagrue et al., 2015). However, the TL has been critiziced in statistical and biological grounds (Cohen and Xu, 2015). An alternative procedure to derive theoretical predictions on the variance-mass relationship without relying on fitting the Taylor's law can be performed based on the metabolic limits to density (Equations 5–8). The variance of population abundance (Var(N_i)) is defined in terms of μ and σ (Equation 7) as follows:

$\begin{array}{ll}Var(N)=e^{\text{2}\mu +{\sigma }^{\text{2}}}\left(e^{{\sigma }^{\text{2}}}-\text{1}\right)& (9)\end{array}$

Substituting Equations 7 into Equation 9 and then rearranging for M, we obtain an explicit relationship between organisms size and population variance as follows:

$\begin{array}{ll}Var(N)=M^{-\text{1.6}\alpha -\text{0.4}\beta }+e^{\text{1.6}c+\text{0.4}b}-M^{-\text{1.3}\alpha -\text{0.7}\beta }+e^{\text{1.3}c+\text{0.7}b}& (10)\end{array}$

This equation includes the effect of resources and temperature into the term c = a+ log(R_tot) + E/kT. It is a combination of two power laws that generates a steeper slope toward large-sized organisms (Figure 3). In the special case in which the scaling of maximum and minimum population abundance are the same (α = β) the Equation 10 is reduced to:

$\begin{array}{ll}Var(N)\propto M^{-\text{2}\alpha }& (11)\end{array}$

Equivalent to the variance-mass allometry (VMA) proposed using a different derivation by Marquet (2005) and Cohen et al. (2012). The exponent equal to minus twice the scaling of metabolism (e.g., −0.75*2 = −3/2) match exactly their predicted theoretical value (Marquet, 2005; Cohen et al., 2012). Moreover, results showed that the metabolic limit to maximum population abundance generates a skewed distribution of species abundances, a necessary condition to generate TL (Cohen and Xu, 2015) but the model (Equation 11) does not depend on fitting Taylor's law to empirical data (Taylor, 1961). Therefore, our present method provides an advantage to conduct empirical tests, because contrary to TL, it does not require time series of population abundances to estimate temporal mean and variance.

FIGURE 3

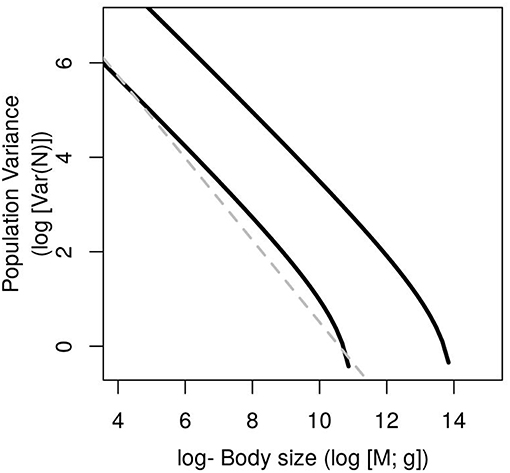
Figure 3. General variance mass allometry (VMA) under different resource supply concentrations (R_tot = 3 upper line and R_tot = 0.1 lower line). The special case when α = β is a straight line (dashed line) whose slope is twice the opposite of the metabolic exponent e_VMA = −2α.

The explicit link with metabolic scaling presented in Equation 10 could help to explain why free-living, free-living infested, and parasitic species exhibit different VMA relationships (Lagrue et al., 2015). It is expected theoretically that both the intercept and slope of metabolic scaling (b₀ and α in Equation 2) differ between parasites and free-living species with direct implications in the VMA (Equation 10; Lagrue et al., 2015). Similarly, a fraction of the metabolic power of free-living species infested with parasites is not used to reproduce and increase population abundance, but to feed parasites, diminishing their effective scope for fluctuations with size as have been observed (Lagrue et al., 2015).

Model Assumptions and Alternative Models for the Size Dependence of Maximum Population Abundance (n_max)

There are three main assumptions required to derive specific predictions on variability of population and community fluctutations, namely: (i) there is a maximum to population abundance determined by body size, and ecosystem properties (T, R_tot), (ii) there is a lower bound to population abundance, and (iii) the distribution of population abundances is lognormal.

An important assumption in our proposed model is the existence of a metabolic determinant of maximum population density. While this assumption has received empirical support (Damuth, 1981; Belgrano et al., 2002; Deng et al., 2012) it has also been questioned and alternative models for the SDR have been suggested (e.g., Carbone and Gittleman, 2002; DeLong and Vasseur, 2012; Pawar et al., 2012). How do alternative SDR models fit into the framework propossed here? A group of consumer-resource models whose parameters are estimated based on scaling relationships provide quantitative predictions on the shape of the SDR by finding the body-size scaling of non-trivial steady-state consumer density (DeLong and Vasseur, 2012; Pawar et al., 2012). These models assume that the feeding processes (e.g., handling time, attack rate) and not the internal metabolic transport network determine the maximum population density of a consumer population. For example, under a simplified Lotka-Volterra predator-prey model, it was found that the SDR scaling exponent (e_SDR) was related to maximum population growth rate, attack rate efficiency and predator-prey size scaling, with specific body size-scalings exponents (ρ,δ,ω, respectively). A formal prediction of the body-size density scaling relationship was constructed (e_SDR = ρω−δ) (DeLong and Vasseur, 2012). Temperature will affect the normalization constant for each of these scaling rates, generating potentially more complex responses than the near-exponential response suggested in Equation 2. The quantitative predictions of consumer-resource models about n_max and its effects on the populations and communities fluctuations are able to be directly incorporated into the present framework (e.g., in Equation 4) and tested against empirical data. Any other quantitative model with formal predictions on the distribution of the SDR (e.g., Irwin et al., 2006; Pawar et al., 2012, among others) can be plugged into Equation 4 to generate specific testable hypothesis about the determinants of natural variability. However, the information on scaling relationships of feeding proceses required is sometimes not available and thus the metabolic approach here presented might serve as a first aproximation. We advocate for the empirical evaluation of alternative models on the determinants of SDR and its effect in the variability of populations and the community.

The limit of the lower population abundance (Equation 5) requires further exploration both in theoretical and empirical grounds (Traill et al., 2007). There is evidence for some groups suggesting that this pattern is flat (Marquet and Taper, 1998; Traill et al., 2007), after accounting for trophic group, temperature, species richness, and sampling area, the size scaling of population abundance is negligible for populations that are rare (Barneche et al., 2016). However, negative scaling exponents have been found for mammals (Silva and Downing, 1994) but the pattern is restricted to particular groups (Nagy, 2005) and we lack a robust theoretical framework to explain it (Lawton, 1989). As a first approximation and without further information, we suggest assuming β is independent of body size and temperature or resources. In the absence of information on the scaling of b, the parameter could be estimated by fitting a slope to the 5% quantile of the size-abundance distribution for the community under different resources or temperature regimes. More theoretical and empirical evaluations on the scaling of minimum population abundance is required to advance in the determinants of population and community variability.

The distribution of single species abundances following a Lognormal seems to be reasonable and have been proposed as a simple and ecologically meaningfull distribution to model population abundances (Halley and Inchausti, 2002). Present results are not sensitive to departures from the Lognormal, as long as the distribution of abundances be symetric in the log-scale. Under any other symetric distribution, the constant dividing standard deviation in Equation 7 will change, but will not qualitatively alter the results about the Laplace distribution. It will however change the derivation of a VMA which is based on the relationship between variance of the Lognormal and μ and σ. However, the lognormal is a reasonable first step and provides analytical results able to be tested with empirical data.

Final remarks

Our model is an asymptotic time model that defines the statistical boundaries for fluctuations in the long run and derive predictions on the shape of the distribution of fluctuations (conditional to body-size) at multiple ecological levels. Results present quantitative predictions of the fluctuation of population and community abundance with body size derived from the metabolic limits to maximum population abundance. Larger organisms are limited by metabolic constraints which defines maximum population density and limit population fluctuations. First, results showed how the metabolic constraints and the fluctuation of resources and temperature are able to generate fat tails in the fluctuation of single populations. Second, we derive a model for whole community fluctuations able to reproduce the observed double exponential or Laplace distribution. We also derived a variance-mass allometry independent from the fitting the Taylors' law and that recuperates the VMA previously proposed as a special case. Our approach provides a general framework to mechanistically link universal patterns observed in ecology, namely the metabolic scaling, species density distribution, and the Variance mass allometry.

Grounded on first principles our model provides a novel quantitative link between size structure and variability, two central tenets of ecological agenda. The universality of the patterns suggests that explanations should be rooted on first principles, and a great candidate is the scaling of the metabolic activity (Gillooly et al., 2001; Brown et al., 2004; Savage et al., 2004). An important aspect of our model framework is that parameters values can be fully assigned independently of size-variance data and have clear ecological interpretation. While α represents the scaling of metabolic rate with size, the relationship with temperature and resources is explicit. Empirical test of present model and alternative formulations for the maximum population abundance are required to advance in the comprehension of the mechanisms determining natural variability.

Author Contributions

AS designed research and write the first draft. GP provided analytical tools and derived the equations. Both authors contributed to the writing of the final manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to specially thank the two reviewers of a previous version of this manuscript, whose comments and corrections greatly improved the quality of present manuscript. AS thanks Fondo Carlos Vaz Ferreira de Apoyo a Proyectos de Investigación en todas las Áreas del Conocimiento (D2C2) for economical support.

References

Agustí, S., Duarte, C., and Kalff, J. (1987). Algal cell size and the maximum density and biomass of phytoplankton. Limnol. Oceanogr. 32, 983–986.

Google Scholar

Allen, A. P., Li, B. L., and Charnov, E. L. (2001). Population fluctuations, power laws and mixtures of lognormal distributions. Ecol. Lett. 4, 1–3. doi: 10.1046/j.1461-0248.2001.00194.x

CrossRef Full Text | Google Scholar

Anderson, S. C., Branch, T. A., Cooper, A. B., and Dulvy, N. K. (2017a). Black-swan events in animal populations. Proc. Natl. Acad. Sci. U.S.A. 114, 3252–3257. doi: 10.1073/pnas.1611525114

PubMed Abstract | CrossRef Full Text | Google Scholar

Anderson, S. C., Branch, T. A., Cooper, A. B., and Dulvy, N. K. (2017b). Reply to youngflesh and lynch: migration and population growth rate in animal black-swan events. Proc. Natl. Acad. Sci. U.S.A. 114, E8955–E8956. doi: 10.1073/pnas.1714157114

PubMed Abstract | CrossRef Full Text | Google Scholar

Barneche, D. R., Kulbicki, M., Floeter, S. R., Friedlander, A. M., and Allen, A. P. (2016). Energetic and ecological constraints on population density of reef fishes. Proc. Royal Soc. B Biol. Sci. 283:20152186. doi: 10.1098/rspb.2015.2186

PubMed Abstract | CrossRef Full Text | Google Scholar

Belgrano, A., Allen, A. P., Enquist, B. J., and Gillooly, J. F. (2002). Allometric scaling of maximum population density: a common rule for marine phytoplankton and terrestrial plants. Ecol. Lett. 5, 611–613. doi: 10.1046/j.1461-0248.2002.00364.x

CrossRef Full Text | Google Scholar

Blackburn, T. M., and Gaston, K. J. (1997). A critical assessment of the form of the interspecific relationship between abundance and body size in animals. J. Anim. Ecol. 66:233. doi: 10.2307/6025

CrossRef Full Text | Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Carbone, C., and Gittleman, J. L. (2002). A common rule for the scaling of carnivore density. Science 295, 2273–2276. doi: 10.1126/science.1067994

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, J. E., and Xu, M. (2015). Random sampling of skewed distributions implies Taylor's power law of fluctuation scaling. Proc. Natl. Acad. Sci. U.S.A. 112, 7749–7754. doi: 10.1073/pnas.1503824112

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, J. E., Xu, M., and Schuster, W. S. F. (2012). Allometric scaling of population variance with mean body size is predicted from Taylor's law and density-mass allometry. Proc. Natl. Acad. Sci. U.S.A. 109, 15829–15834. doi: 10.1073/pnas.1212883109

PubMed Abstract | CrossRef Full Text | Google Scholar

Damuth, J. (1981). Population density and body size in mammals. Nature 290, 699–700.

Google Scholar

DeLong, J. P., Okie, J. G., Moses, M. E., Sibly, R. M., and Brown, J. H. (2010). Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. U.S.A. 107, 12941–12945. doi: 10.1073/pnas.1007783107

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLong, J. P., and Vasseur, D. A. (2012). Size-density scaling in protists and the links between consumer-resource interaction parameters. J. Animal Ecol. 81, 1193–1201. doi: 10.1111/j.1365-2656.2012.02013.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Deng, J., Zuo, W., Wang, Z., Fan, Z., Ji, M., Wang, G., et al. (2012). Insights into plant size-density relationships from models and agricultural crops. Proc. Natl. Acad. Sci. U.S.A. 109, 8600–8605. doi: 10.1073/pnas.1205663109

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghedini, G., White, C. R., and Marshall, D. J. (2018). Metabolic scaling across succession: do individual rates predict community-level energy use? Funct. Ecol. 32, 1447–1456. doi: 10.1111/1365-2435.13103

CrossRef Full Text | Google Scholar

Gillooly, J. F., Brown, J. H., West, G. B., Savage, V. M., and Charnov, E. L. (2001). Effects of size and temperature on metabolic rate. Science 293, 2248–2251. doi: 10.1126/science.1061967

PubMed Abstract | CrossRef Full Text | Google Scholar

Halley, J., and Inchausti, P. (2002). Lognormality in ecological time series. Oikos 99, 518–530. doi: 10.1034/j.1600-0706.2002.11962.x

CrossRef Full Text | Google Scholar

Irwin, A. J., Finkel, Z. V., Schofield, O. M. E., and Falkowski, P. G. (2006). Scaling-up from nutrient physiology to the size-structure of phytoplankton communities. J. Plankton Res. 28, 459–471. doi: 10.1093/plankt/fbi148

CrossRef Full Text | Google Scholar

Kalyuzhny, M., Seri, E., Chocron, R., Flather, C. H., Kadmon, R., and Shnerb, N. M. (2014). Niche versus neutrality: a dynamical analysis. Am. Nat. 184, 439–446. doi: 10.1086/677930

PubMed Abstract | CrossRef Full Text | Google Scholar

Keitt, T. H., and Stanley, H. E. (1998). Dynamics of North American breeding bird populations. Nature 393, 257–260. doi: 10.1038/30478

CrossRef Full Text | Google Scholar

Kotz, S., Kozubowski, T. J., and Podgórski, K. (2001). The Laplace Distribution and Generalizations: A Revisit With Applications to Communications, Economics, Engineering, and Finance. New York: Springer.

Google Scholar

Lagrue, C., Poulin, R., and Cohen, J. E. (2015). Parasitism alters three power laws of scaling in a metazoan community: Taylor's law, density-mass allometry, and variance-mass allometry. Proc. Natl. Acad. Sci. U.S.A. 112, 1791–1796. doi: 10.1073/pnas.1422475112

PubMed Abstract | CrossRef Full Text | Google Scholar

Lan, B. L., and Chandran, P. (2011). Distribution of animal population fluctuations. Phys. A Stat. Mech. Appl. 390, 1289–1294. doi: 10.1016/j.physa.2010.11.015

CrossRef Full Text | Google Scholar

Lawton, J. H. (1989). What is the relationship between population density and body size in animals? Oikos 55:429. doi: 10.2307/3565606

CrossRef Full Text | Google Scholar

MacArthur, R. (1955). Fluctuations of animal populations and a measure of community stability. Ecology 36:533. doi: 10.2307/1929601

CrossRef Full Text | Google Scholar

Marquet, P. A. (2005). Scaling and power-laws in ecological systems. J. Exp. Biol. 208, 1749–1769. doi: 10.1242/jeb.01588

PubMed Abstract | CrossRef Full Text | Google Scholar

Marquet, P. A., Abades, S. R., and Labra, F. A. (2007). “Biodiversity power laws,” in Scaling Biodiversity, ed P. A. M. J. H. B. D. Storch (Cambridge: Cambridge University Press), 441–461.

Google Scholar

Marquet, P. A., Navarrete, S. A., and Castilla, J. C. (1995). Body size, population density, and the energetic equivalence rule. J. Anim. Ecol. 64:325. doi: 10.2307/5894

CrossRef Full Text | Google Scholar

Marquet, P. A., and Taper, M. L. (1998). On size and area: Patterns of mammalian body size extremes across landmasses. Evol. Ecol. 12, 127–139. doi: 10.1023/A:1006567227154

CrossRef Full Text | Google Scholar

Nagy, K. A. (2005). Field metabolic rate and body size. J. Exp. Biol. 208, 1621–1625. doi: 10.1242/jeb.01553

PubMed Abstract | CrossRef Full Text | Google Scholar

Pawar, S., Dell, A. I., and Savage, V. M. (2012). Dimensionality of consumer search space drives trophic interaction strengths. Nature 486, 485–489. doi: 10.1038/nature11131

PubMed Abstract | CrossRef Full Text | Google Scholar

Pimm, S. L. (1991). The Balance of Nature? Ecological Issues in the Conservation of Species and Communities. Chicago: University of Chicago Press.

Google Scholar

Quiroz-Martinez, B., Schmitt, F. G., and Dauvin, J.-C. (2012). Statistical analysis of polychaete population density: dynamics of dominant species and scaling properties in relative abundance fluctuations. Nonlinear Process. Geophys. 19, 45–52. doi: 10.5194/npg-19-45-2012

CrossRef Full Text | Google Scholar

Savage, V. M., Gillooly, J. F., Brown, J. M., West, G. B., and Charnov, E. L. (2004). Effects of body size and temperature on population growth. Am. Nat. 163, 429–441. doi: 10.1086/381872

PubMed Abstract | CrossRef Full Text | Google Scholar

Segura, A. M., Calliari, D., Lan, B. L., Fort, H., Widdicombe, C. E., Harmer, R., et al. (2017). Community fluctuations and local extinction in a planktonic food web. Ecol. Lett. 20, 471–476. doi: 10.1111/ele.12749

PubMed Abstract | CrossRef Full Text | Google Scholar

Segura, C. D., Fort, H., and Lan, B. L. (2013). Fat tails in marine microbial population fluctuations. Oikos 122, 1739–1745. doi: 10.1111/j.1600-0706.2013.00493.x

CrossRef Full Text | Google Scholar

Silva, M., and Downing, J. A. (1994). Allometric scaling of minimal mammal densities. Conserv. Biol. 8, 732–743. doi: 10.1046/j.1523-1739.1994.08030732.x

CrossRef Full Text | Google Scholar

Taylor, L. R. (1961). Aggregation, variance and the mean. Nature 189, 732–735. doi: 10.1038/189732a0

CrossRef Full Text | Google Scholar

Traill, L. W., Bradshaw, C. J. A., and Brook, B. W. (2007). Minimum viable population size: a meta-analysis of 30 years of published estimates. Biol. Conserv. 139, 159–166. doi: 10.1016/j.biocon.2007.06.011

CrossRef Full Text | Google Scholar

White, E. P., Ernest, S. K. M., Kerkhoff, A. J., and Enquist, B. J. (2007). Relationships between body size and abundance in ecology. Trends Ecol. Evol. 22, 323–330. doi: 10.1016/j.tree.2007.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, M. (2016). Ecological scaling laws link individual body size variation to population abundance fluctuation. Oikos 125, 288–299. doi: 10.1111/oik.03100

CrossRef Full Text | Google Scholar

Zaoli, S., Giometto, A., Maritan, A., and Rinaldo, A. (2017). Covariations in ecological scaling laws fostered by community dynamics. Proc. Natl. Acad. Sci. U.S.A. 114, 10672–10677. doi: 10.1073/pnas.1708376114

PubMed Abstract | CrossRef Full Text | Google Scholar