- 1The Santa Fe Institute, Santa Fe, NM, United States
- 2Department of Integrative Biology, University of California, Berkeley, Berkeley, CA, United States
- 3Department of Mathematics, Imperial College, London, United Kingdom
Organisms are subject to the laws of physics, so the process of evolution by genetic variation and natural selection is constrained by these fundamental laws. Classic and recent studies of the biophysical limits facing organisms have shown how fundamental physical constraints can be used to predict broad-scale relationships between body size and organismal biomechanics and physiology. These relationships often take the form of power laws across a wide range of body sizes for organisms sharing a common body plan. However, such biophysical perspectives have not been fully connected with the detailed dynamics of evolution by natural selection, nor with the variation between species around the central scaling relationships. Here we first discuss what a general biophysical theory of evolution would require and provide a mathematical framework for constructing such a theory. We discuss how the theory can predict not only scaling relationships, but also of identifying the types of tradeoffs made by different species living in particular niches. In addition, we discuss how a key higher-order requirement of a biophysical theory of evolution is its ability to predict asymptotic behavior and the limits of a particular body plan. We use several examples to illustrate how dominant physical constraints can be used to predict the minimum and maximum body sizes for a particular body plan, and we argue that prediction of these limits is essential for identifying the dominant physical constraints for a given category of organisms. Our general framework proposes that a major portion of fitness should be the overlay of how all traits of a particular body plan interact with fundamental physical constraints. To illustrate this concept, we investigate multiple physical limits on particular traits, such as insect legs, and show how the interaction of a number of traits determines the size limits on entire body plans, such as those of vascular plants. We use bacteria as an example of the shifts in which physiological traits and physical constraints are most limiting at various organism sizes. Finally, we address the effects of environmental conditions and ecological interactions in determining which of the physical constraints faced by organisms are most likely to affect their growth, survival, and reproduction, and hence their fitness. We consider such ecological effects on our examples of bacteria, insects, mammals and trees, and we nest the constraints-perspective in the broader picture of evolutionary processes.
1. Introduction
The classic view of evolution is that individual species become adapted to specific niches through the process of genetic variation and natural selection, where the temporal trajectories of particular populations are noisy and often unpredictable in detail. From this perspective, the myriad physiological functions performed by one species can only be fully understood through the lens of a specific evolutionary history and the numerous selective pressures in a particular ecological setting that lead to selection for one physiological/morphological local optimum (of potentially many). A contrasting perspective to focusing on these detailed processes that lead to speciation is that evolution occurs in the physical world, and that the consistency of basic physical laws produces broad-ranging regularities across biological diversity (Thompson, 1917; Rashevsky, 1944, 1960; Brown et al., 1993; Alexander, 1996; Niklas and Hammond, 2013). A prime example of such regularities is the observation of scaling relationships such as the metabolic power law relationship between body size and metabolic rate noted by Kleiber (1932). This type of systematic behavior has been shown to be the consequence of the global optimum configuration of a trait within a range of possibilities with respect to a particular physical law or constraint (e.g., Brown et al., 2004). How much of detailed evolution can we predict from such a constraints-first perspective, and how do we reconcile such a perspective with the detailed processes of the evolution of a particular species?
Here we review constraint-based perspectives on evolution, and show how they are nested within the broader framework of evolutionary biology. We discuss contexts under which certain physical constraints are dominant and/or independent of other constraints, thus producing scaling relationships across diverse species. In particular, we focus on the ultimate limits of particular categories of organisms as prime examples of where physical constraints dominate. We define a limit as the point where the optimal performance of a physiological function or morphological trait is not effective enough to allow an organism to survive. These limits set a minimum or maximum allowable body size. Such limits are known for microbes, arthropods, vascular plants, and mammals, each of which we will later discuss as detailed examples. These limits illustrate how the constraints perspective on evolution is useful, not only for predicting regular trends within a category of organisms (such as allometric scaling), but also for predicting higher-order features such as the size limits of a body plan or a transition to an alternate body plan that allows for expansion into bigger or smaller body sizes.
Understanding or predicting such limits gives us insight into macroevolutionary processes, including major evolutionary transitions (e.g., DeLong et al., 2010; Kempes et al., 2016), and is the first step in building a more detailed perspective on how physical constraints shape microevolution. In addition, another reason to focus on these constraints is as a test of theories for scaling relationships. If a particular theory proposes that a dominant constraint predicts a particular scaling relationship, then it should also predict at what scales that constraint becomes asymptotically limiting to organism physiology and architecture. That is, the scaling theory should also predict the minimal and maximal sizes for organisms that share a body plan.
2. Evolution, Physical Constraints, and the Body Plan
One could think of evolution from the perspective of overlaying multiple physical constraints (e.g., constraints arising from immutable physical laws such as gravitational force). This could be done from the perspective of evolutionary history in which life sequentially encounters new constraints with increasing complexity or body size, or from the perspective of distinct physical constraints that each lead to scaling relationships, all of which apply to an organism simultaneously. In this latter case the overall physiology of an organism can be seen as the overlay and interaction of multiple constraints and associated scaling relationships (Figure 1). This combination can lead to more complex evolutionary optimizations if many constraints are equally consequential, as will be discussed formally below.
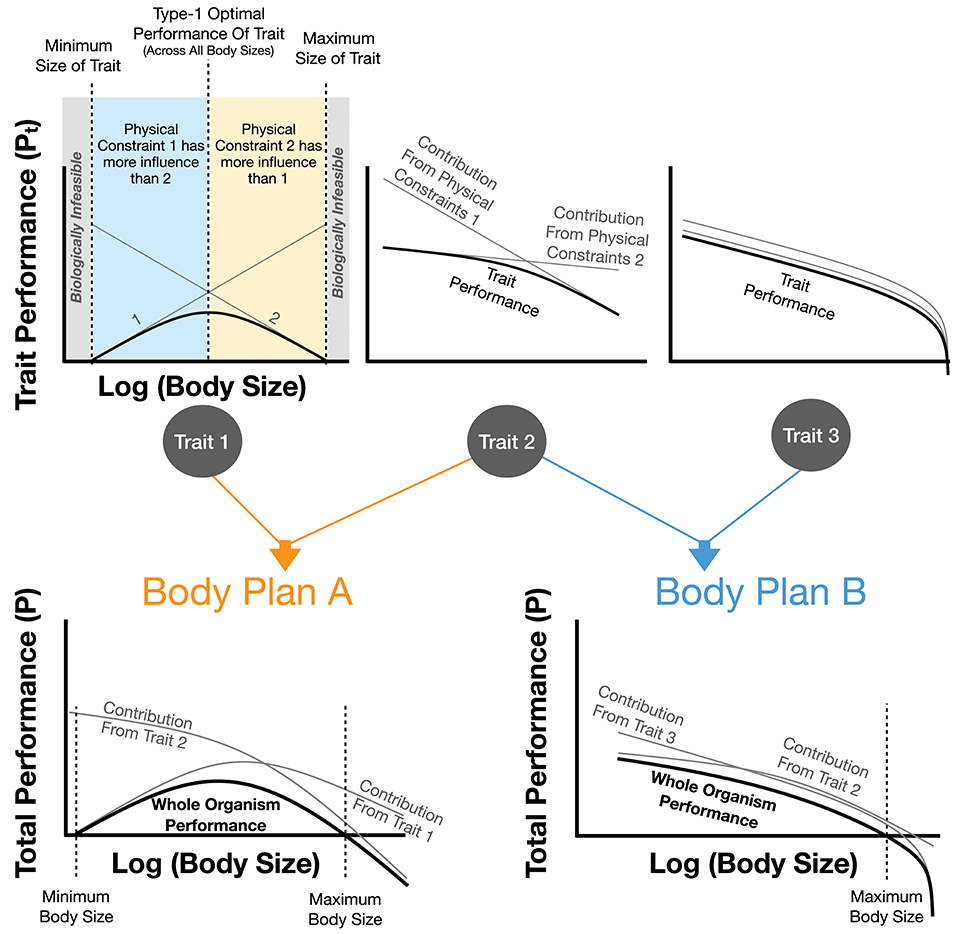
Figure 1. The impact of physical constraints on trait performance and body plan performance. Each trait is the sum of the performance costs, Pt, from individual physical effects. It is assumed that each physical effect curve and the overall summed trait performance are all optimized. For trait 1 it can be seen that the optimal trait performance has a maximum value at intermediate body sizes representing the best performance across all individuals of this body plan (an example of a type-2 optimum in Figure 3). Trait 1 also illustrates a minimum and maximum body size for this trait, both of which are the point at which the cost of the trait would equal total metabolism. This figure also shows how combinations of traits combine to form overall body plans which in turn may illustrate a type-2 optimum (see Body Plan A) along with minimum and maximum body sizes where the cost of the overall body plan exceeds total metabolism. It should be noted that this figure is representative, and real organisms would combine an arbitrary number of traits with a wide variety of performance-curve shapes. In many cases one or two traits could dictate the total value of P.
Studying evolution using the constraints perspective is further complicated by the fact that, although a specific feature of an organism is constrained by a number of physical laws that may scale differently with size, the selection pressure on that feature is ultimately based on how the interaction of many such interrelated features affects the fitness of the entire organism. The way that traits affect the fitness of an organism depends on the physical environment in which the organism must function and its ecological interactions with other organisms, both of which can change over a life span. Thus, the organism is the product of a history of adaptation to particular physical constraints and ecological conditions, as well as of the evolutionary constraints of its structural components and physiological machinery. Indeed, it should be noted that the constraints that affect organism performance represent a subset of the overall evolutionary process. The full picture of evolution is one in which genes are mapped into a phenotype, that phenotype defines the performance of an organism, and performance ultimately becomes fitness via many interactions with a particular ecological context where factors such as predation, likelihood of reaching reproductive maturity, resource availability, parental nurturing, and niche construction all play important and complicated roles (Figure 2). Classic and well-developed models of trait evolution typically consider the heritability, covariation, and rate of change in traits to assess how traits affect fitness and are genetically connected (e.g., see Lynch et al., 1998 for a broad review and Lande (1979) for an allometric application). This traditional perspective has been successful in predicting a wide variety of evolutionary regularities and in uncovering genetic correlations. The overall dynamics of trait evolution in traditional evolutionary models (such as the Price equation) can, in principle, be partitioned into the contributions from each of the processes described in Figure 1 (Queller, 2017).
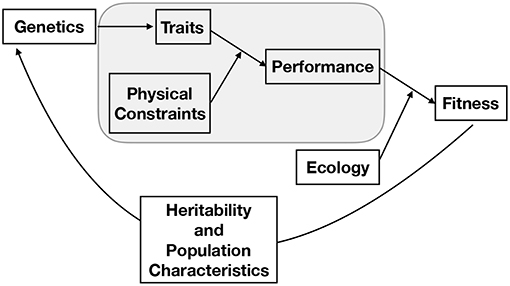
Figure 2. A conceptual representation of the full process of evolution, where the gray box represents the main focus of this paper. From this perspective, genes produce a phenotype, that phenotype defines the performance of an organism given a set of physical constraints, performance becomes fitness through the many features of an ecological context, and the population of genetics evolves given this fitness and the nature of the population, mechanisms of heredity, and mutation. It should be noted that the connection between traits and physical constraints may become the dominant component of fitness in particular contexts. For example, we illustrate here that in many cases the ultimate limit of a particular body plan occurs when one physical constraint becomes asymptotically challenging taking fitness to zero.
Our focus in this paper is mainly on one such component, the mechanistic determination of performance from the set of physical constraints and organism traits (phenotype), without consideration of how those traits are genetically determined (including correlations between gene effects), which processes influence inheritance, or how the performance fully interacts with the complicated set of ecological constraints described above. We show that physical constraints can be used to determine the intrinsic growth rate of an individual, which is a major component of fitness. Furthermore, we consider cases in which particular constraints become asymptotically challenging so that performance of an organism goes to zero, thereby dominating fitness and predicting the ultimate limits of a body plan, independent of other ecological considerations. In considering these examples throughout the paper we suggest that the constraints perspective could eventually be integrated into a broader framework incorporating the underlying genetics, ecological considerations, and population structure in order to determine overall fitness and evolutionary dynamics (Figure 2). For example, the connection between traits, physical constraints, and fitness could be nested within adaptive dynamics models (e.g., Abrams, 2001; McGill and Brown, 2007), which are aimed at determining evolutionary stable strategies of complex trait combinations within a population (e.g., see Falster and Westoby, 2003; Falster et al., 2016 for considerations of plant traits). We also discuss the contexts in which the physical optimizations can be performed without an explicit treatment of the evolutionary dynamics, and why such optimizations can be, and have been, successful in predicting allometric scaling relationships and ultimate limits.
2.1. Abstract Formalism of Constraints and Fitness
With the complications and caveats listed above in mind, we provide a simple formalism for evolution in the context of physical constraints. Below we connect this formalism to the aspects of fitness that can be directly calculated, specifically, the growth rate of an individual. There are a wide variety of models for evolutionary dynamics which typically connect the rate of change in the abundance of a gene or specific genome to its fitness given specific assumptions about inheritance and mutation (e.g., Lynch et al., 1998; Nowak, 2006; Frank, 2011a,b, 2012a,b,c; Queller, 2017). All of these frameworks rest on the ability to quantify the fitness, fj of each genotype and/or phenotype j in the population, and in each case we can connect a particular model to constraints so long as we can specify the physical determinants of fitness. A classic example of an earlier attempt to connect physical constraints and fitness comes from McNeil Alexander, where he formalized the evolution of safety factors using the equation ϕ(s) = l(s)F + U(s), where ϕ(s) is the overall cost of a trait given a safety factor s, F is the cost of failure, l(s) is the probability of failure, and U(s) is the cost of growing, using, and maintaining a trait as a function of the safety factor (Alexander, 1996). From this perspective, trait evolution is the minimization of this total cost where an increasing safety factor typically decreases the likelihood of failure but increases the cost of production, use, and maintenance. Our approach is to further generalize this concept and connect it to fitness, rather than just safety factors, by defining the interconnection between all organism traits and physical constraints. Take tt to be the contribution of a particular trait to overall fitness, then
or
where pp is a particular physical constraint, gt, p is the net benefit attributed to a particular trait due to physiology interacting with a physical constraint, and is the portion of the net benefit that strongly depends on ecological interactions in combination with physical constraints (e.g., predator avoidance given the density of predators; see Appendix A.1 for a more detailed treatment). The first subscript, t, refers to the trait of interest, and the second, p, to a particular physical constraint. Here lowercase subscripts refer to an arbitrary element of a matrix or vector, such that tt is an arbitrary element of , and uppercase subscripts refer to the last element where P is the length of , T is the length of , and g is a T × P matrix.
It is important to note that this formalism could be setup to address traits at various levels of organization—ranging from detailed considerations of the functional proteins to entire morphological features—depending on the questions of interest. For example, the first column of the matrix g might be the relationship that describes whether a hollow cylinder will develop a local kink over its length. The second column might be the relationship for how far a cylinder bends, and the third column might be the relationship for the weight of the cylinder. In this same matrix the rows would then describe different traits, so that the first row could be the trait of a leg and the second the trait of a wing. Thus, in this example, g1,1 relates to the performance of a leg resisting kinking, and g2,1 to the performance of a wing resisting kinking, both in combination with p1. Similarly, g1,2 and g2,2 relate to the performance of a leg and wing, respectively, in resisting bending, and g1,3 and g2,3 relate, respectively, to the performance of the weight of a leg and wing.
In this formalism, performance, as described by gt, p, refers to a net consideration of both the cost and return to fitness for a particular trait, where gt, p could be either positive or negative depending on a trait's current form (e.g., the current genotype and phenotype of an organism). Fitness is then defined as
It is important to note a few features of this formalism. First, tt is meant to represent the lifetime contribution to fitness such that g, , and e should be constructed as lifetime quantities. Second, the main challenge of this formalism is in constructing the matrix g and also deciding on the level of granularity with which to describe the traits t. For example, should one consider all properties of a bone together or should one partition a bone into its various sub-traits such as its of cross-sectional shape, material composition, and dimensional ratios? Constructing the lifetime values of e is equally challenging given a particular ecological setting. As already emphasized, the focus of this paper is on investigating the consequences of the physical contribution, , to fitness, ignoring ecological effects, . However, it should be noted that future efforts that attempt to systematize the variation around scaling relationships will often need to quantify .
2.2. Dominant Constraints and Scaling Relationships
In light of the complicated dynamics of overlapping physical and evolutionary constraints for organism evolution discussed earlier, it is perhaps surprising that any scaling relationships exist relating diverse organisms. For example, one can imagine contexts in which many physiological traits are equally consequential, and organisms with different combinations of traits have equivalent fitness. In other contexts, ecological processes might be more important than physiological effects and might shift unpredictably across body size. In some cases the interrelation of traits (e.g., due to the underlying genetics) might produce very complicated relationships across body sizes that cannot be easily interpreted and would include signals of phylogenetic relatedness. In contrast, scaling relationships for a particular trait highlight that a single constraint (or possibly a small set of constraints) dominates over a wide range of sizes and is consistently optimized, and/or that the optimization of one trait to a particular physical constraint is independent from other traits. In this paper, the term “optimization” here has two interrelated meanings: (1) A type-1 optimum, which is determined for one body size and is the best functionality that can be achieved by a single trait, or set of traits, in organisms with a particular body plan (Figure 3). We hold body size constant and optimize across different values of the parameters that determine the performance of that trait, or set of traits. An allometric scaling law is the set of type-1 optima, each performed at a particular body size. (2) A type-2 optimum, which is the best functionality that can be achieved for a particular body plan considering all body sizes. The procedure for finding a type-2 optimum is to first find the type-1 optimum at each body size for a trait or set of traits, and then to find the body size that has the best type-1 optimum. A type-2 optimum represents the body size that outperforms all others. The type-2 optimum would be the best point along the relationship between body size and the type-1 optima. In the case of a power-law for the set of type-1 optima, the type-2 optimum would occur at the smallest or largest size. In other cases, performance may not change with body size (i.e., the type-1 optima are all equivalent across different body sizes for a given measure of performance).
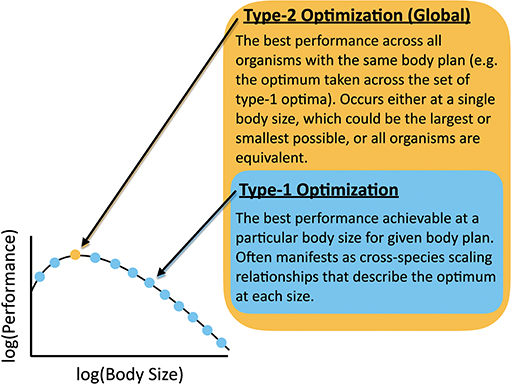
Figure 3. Definition of Type-1 and Type-2 optimizations with reference to a body-size performance curve.
In the context of the formalism that we have introduced above, the layered hierarchy of constraints that define a single species is represented by the relative size of the entries of g (e.g., gt, p). The existence of scaling laws indicate that a small subset of elements in g are significantly larger than all other elements across a range of body sizes for a class of organisms. Formally, this situation can be expressed as
where s represents a subset of g. Ultimate limits would indicate that a subset of entries of g become increasingly or asymptotically large and negative at a particular scale and tt∈s → 0. In this context the type-1 optimization has vanishingly small fitness at a particular body size and this body size then represents either an upper or lower bound on the possibilities for a particular body plan.
3. Applying the Constraints Framework
3.1. Explicit Connections to Growth
The preceding formalism is meant to be an abstract representation of the evolution of organism traits with body size under a set of physical constraints considering both physiological and ecological effects. As such we have assumed a linear form for the determination of fitness. More generally, we should expect that the contribution of an individual trait to fitness should follow , where gt is a function of fitness contribution for a particular trait given the entire set of traits, , physical constraints, , and other species in the same environment, , and may not be representable as a linear combination of the form of Equation (1). This general relationship makes it clear that there may be many traits with fitness contributions that are contingent on the value of other traits. Although the physiological optimization problem may not be of the form of Equation (1), that does not mean that it cannot be fully quantified and solved.
To make such optimizations more explicit we should first concretely connect traits with aspects of fitness. A variety of recent efforts have shown that the growth curves of a variety of organisms can be predicted from a model that considers the budgeting of total metabolic rate, B, into growth and maintenance purposes as (where Em and Bm are the unit costs of synthesizing and maintaining biomass, respectively, and τ is time) (West et al., 2001; Kempes et al., 2012). Typically this model is solved by rearranging for dm/dτ and recognizing that B scales as a power law with mass. However, the power law of B is the result of an optimization and we can relax this assumption and instead specify this budget in terms of the effect of each individual organism trait
where Bi(τ) (W) is the contribution of trait i to total metabolic power, Ci(τ) (W) is the metabolic cost of each trait, and Em (J/g) is the energy to synthesize biomass given all of the current traits. Each of these terms is taken as a function of time as an organism progresses through a life cycle. In connection with our general framework we have that
and
where , , and g = b − c in connection with the notation in Equations (1) and (2).
As written, these equations describe the growth rate of an organism along ontogeny. These equations are often converted into population growth rates by first solving Equation (5) for the growth trajectory m(τ) and then using this to find the time to reach reproductive maturity G (e.g., West et al., 2001; Kempes et al., 2012). From this generation time the specific growth rate of the population is given by μ = ln(k)/G, where k represents the expected number of offspring produced by an adult and could in principle be a complicated function of the traits themselves and thus parameterize the variety of ecological features discussed earlier (e.g., for bacteria without any mortality k = 2). In general, one could combine our framework for the growth rate of an individual with a complicated model for the expected offspring to reach maturity, , to form a μ that represents total fitness in an evolutionary model. Here 〈k〉 is a function of the set of current traits, , and all effects from the environment and other species, . Given a body plan, our goal is to find the set of trait values that maximize the population growth rate for each organism size, or
The optimization procedure should hold adult size fixed (type-1 optimization) and solve for the b and c that maximize population growth rate which integrates over the full life-history. As a result, the optimum population growth rate μopt(m) is a function of size, and the b and c that produce this optimum will also change with body size. In many cases it may be more practical to consider lifetime averages for all of the traits and optimize the average individual growth rate, , which is what we consider in our examples. Note that for a fixed k optimizing is equivalent to optimizing μ. Again each of these optimization problems may not have analytically tractable forms, but it should be possible to perform the numerical optimization using a wide variety of known techniques.
3.2. A Single-Cell Example
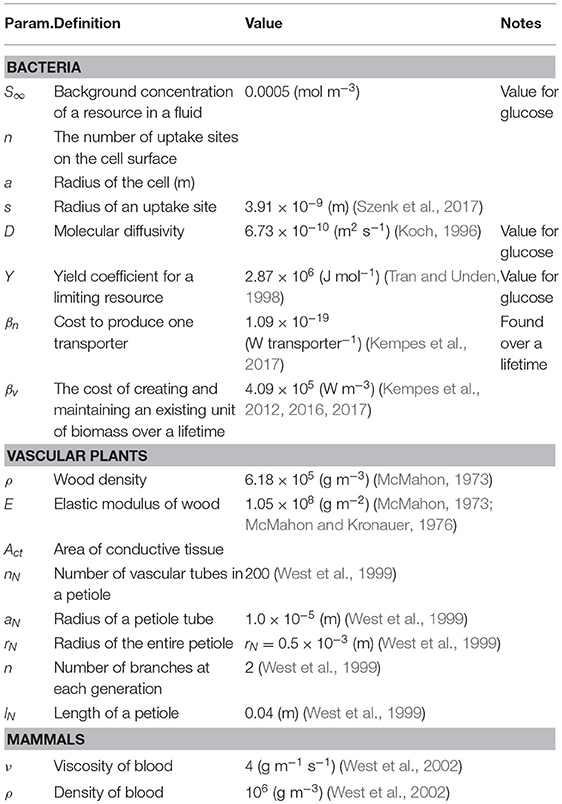
There are many cases where it is possible to concretely and simply calculate the tradeoffs associate with investment in various traits for an organism along with the optimization of those traits. To illustrate how this procedure is done, along with some of the challenges of operationalizing the conceptual framework outlined in Equation (1), we begin with the simple example of optimizing a single trait. Consider the case of a non-motile spherical bacterium that is acquiring resources via diffusion through the cellular surface followed by active transport via membrane-bound protein structures. The total metabolic energy available to the organism is proportional to the number of molecules, say O2 during respiration, acquired by the cell. It has been shown that the diffusive uptake rate is given by where n is the number of uptake sites, a is the radius of the cell, s is the radius of an uptake site, and S∞ is the background concentration of the resource in the fluid (e.g., Fiksen et al., 2013). This implies that
where Y is the yield coefficient (Joules per mole) for the limiting resource. We also know that each of these transporters requires some amount of energy, βn to produce, and thus the total cost of n transporters is
Taken together, these two relationships imply that the average growth rate over a lifetime is given by and can be rewritten in the form of our framework as
where we are considering the trait to be uptake sites and to be composed of terms related to the limits of diffusive uptake and the costs of protein construction. Since we are only considering a single trait, is a simple scalar and already represents the entire sum for fitness. Figure 4 gives the energetic values of each term along with the resulting growth rate for a single cell of size a = 10−6 (m), and shows that as a cell adds transporters there is an increase in up to the point where uptake saturates for any additional transporters. In fact this sum gives rise to an optimal number of transporters which can be easily shown to be
It can be seen in Figure 4B that for a cell of a = 10−6 m this optimal value occurs before the entire cell is covered in transporters. For a cell of this size the optimal solution is achievable. However, this may not be possible for all cell sizes. Figure 4C gives the scaling of nopt with cell size (type-1 optima) and shows that there is a size, a = 1.14 × 10−6 (m), at which the total surface area is entirely covered in transporters. This represents a minimum cell size at which the optimal solution is feasible; any smaller cells would have fewer than the optimal number of transporters. In this example, the type-2 optimum for the number of transporters occurs at the largest possible cell size.
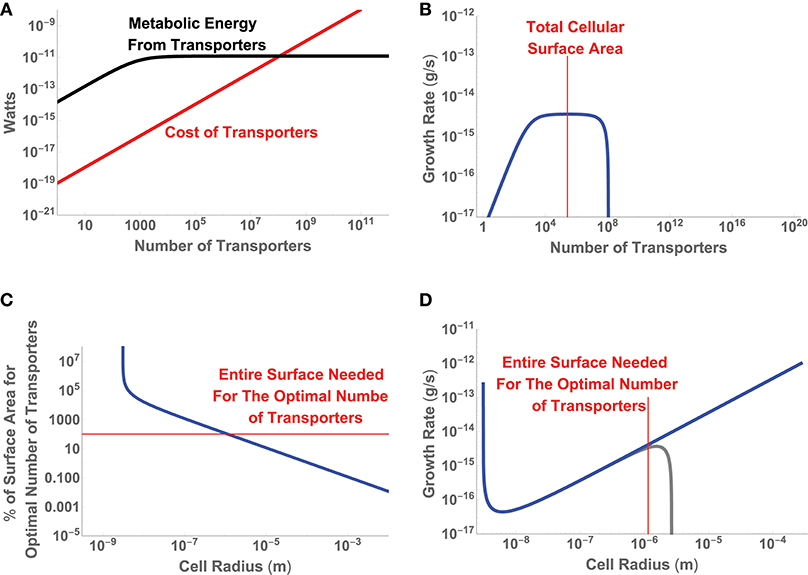
Figure 4. (A) The relative energetic uptake and cost of transporters for a cell of size a = 10−6 (m), along with (B) the inferred growth rate of that cell. (C) The percentage of cellular surface area devoted to nopt, the optimal number transporters from Equation (13), as a function of cell size. (D) The inferred growth rate given the optimal number of transporters as a function of cell size. The blue curve considers only the cost of the transporters in the optimization, while the gray curve includes the cost of the cellular volume.
We could allow for smaller cells to have suboptimal performance by, for example, keeping a fixed fraction of the surface area covered in transporters. However, these suboptimal cells would run into another limitation, where the total surface area becomes less than the area of a single transporter. The point where the cell surface area is equal to the area of a single transporter is given by
and occurs when a = 1.95 × 10−9 (m). There are other limitations facing the cell that we have not considered. For example, its entire surface area cannot be covered in transporters both for structural reasons and because other functions must be imbedded in the membrane (e.g., the machinery for ATP synthesis).
In general, this single trait optimization could be interacting with a variety of other traits. For example, we have only considered the requirement that uptake meets the costs of the transporters themselves, and in this scenario it is not the return on investment of a transporter that ultimately limits the cell. For all cell sizes we can determine the number of transporters beyond which uptake exceeds the cost of producing those transporters (until surface area limits at the small end). However, this analysis does not consider the internal metabolic requirements of the cell, where the volume to total surface area ratio is scaling proportional to a and we would expect the transporters, even if they cover the entire surface area, to be increasingly unable to support larger cells. These other limitations could be added to Equation (12) by, in the simplest case, adding a cost term proportional to overall volume. Consequently,
where βv is the unit cost per volume of creating and maintaining an existing unit of biomass over a lifetime (see Kempes et al., 2016, 2017 for a more in depth accounting of cellular composition and the costs that would form βv). In this example the first row represents the trait of uptake while the second row represents the trait of cytoplasmic volume.
This addition does not change the value of nopt, but will shift the overall growth rate. In this case the added cost is negligible for small cell sizes but eventually becomes the dominant cost for large cells and sets an upper bound on cell size at a = 2.67 × 10−6 (m) (Figure 4D). This upper bound occurs because the cost of the cellular volume eventually outpaces uptake and growth goes to zero. It should be noted that in this example we have not considered the physiological and metabolic functions within the cellular volume that interact with the uptake of resources to provide the metabolic power available to the cell. Such considerations would add interconnections between the first and second rows (e.g., how the cellular volume produces energy given the uptake rate), adjust the structure of , and would require a more complicated optimization of . Similarly, we could add a consideration of the tradeoffs between two traits, say the investment in the number of transporters and investment in chemotaxis (see Appendix A.2). In this case the two traits, swimming velocity and the number of uptake sites, are fundamentally interconnected and must be co-optimized to maximize . However, the point is that ultimately we are trying to optimize the linear combination that makes up even if individual terms in that sum are complicated and interrelated functions, which should at least be numerically achievable.
This single-cell case study demonstrates how our general framework can be applied to a specific context and explicitly illustrates the three main features that we are interested in, those being:
1. The change in optimal performance across many different sizes (e.g., the maximum growth rate per unit mass increases for larger cells Figure 4D).
2. The size at which optimal performance becomes impossible (e.g., the optimal number of transporters exceeds the total surface area of the cell Figure 4C).
3. The ultimate limit of size where any functionality is impossible (e.g., a single transporter covers the entire surface area of the cell Equation 14).
3.3. Independent Trait Optimization
The framework that we have proposed gives a general perspective for the co-optimization of physiological constraints, appearance of scaling relationships, and prediction of ultimate constraints. However, constructing the complete set of physiological traits and their interactions with physical constraints (the complete g = b − c and ) is a daunting task and an important area of future effort. Yet it is important to note that within our general framework there can be traits that are unrelated to other traits. In such a case optimizing a trait's contribution to fitness can be done in isolation. Since is a linear sum, optimizing one trait increases a portion of overall fitness so long as this trait is not connected to other traits and thus does not have competing consequences in the overall sum. It should also be noted that a trait can be effectively independent of all other traits if the contribution it makes to one is much larger than its influence on all other for j ≠ i. In general, if all of the traits are independent we have that
implying that each trait can be optimized individually. If we have a mix of independent traits and traits with complicated interdependencies, then we have that
where j represents all of the traits that are effectively independent of other traits (and can be individually optimized), and k the set of traits which contain interdependencies. It should be noted that sums like amount to summing and combining rows in Equation A4 (see Appendix), which then form new “effective traits.”
These representations make it clear that if enough trait independence exists, then single trait optimizations will accurately predict the observed scaling of a trait with body size. This helps explain past successes in deriving and predicting allometric relationships by focusing on a few dominant constraints and performing type-1 optimizations (e.g., West et al., 1997, 1999).
3.4. Simplified Metrics of Performance and Ultimate Limits
In light of the formalism above we can see why single-trait optimizations often predict allometric relationships and much past attention has already been given to these optimizations and scaling relationships. One of our primary interests here is to use these concepts to predict ultimate limitations, one of the main types of higher-order behavior that we can extract from a constraints-based perspective of evolution. These limits are important because they predict the range of body sizes achievable for a given body plan. We are also interested in how organism performance shifts across this range of body sizes as this informs aspects of selection.
In order to make these ideas more explicit we introduce several systematic metrics that capture the essence of our earlier framework but focus on a reduced set of traits and allow us to predict ultimate limits for particular categories of organisms. We introduce two types of common biological currency for assessing performance and for understanding the ultimate limits on a particular body plan, both of which were employed in our single-cell example in section 3.2.
For the ultimate limits of a particular body plan we are interested in the size where growth ceases (dm/dτ = 0 in Equation 5), which is realized when the costs of all of the traits are equal to their metabolic return: . In this context, a natural metric for performance is the ratio of costs to metabolic return, . It is also natural to set the highest value of performance, P, to unity, and define . If we are interested in considering the constraints imposed by a single trait, then we can simplify this metric to
where Cf(m) is the cost of a particular trait, B(m) is the total metabolic rate of an organism (), and where we have made the dependence on organism mass, m, explicit for the metric and subcomponents. This metric will either determine when one trait would be limiting, even if other traits impose more serious limits on organisms, or will define the ultimate limit in the case where Cf is the most dominant constraint (e.g., ). It should be noted that this equation could be parameterized in terms of other measures of organism size such as volume rather than mass.
It should also be noted that an evolutionary optimization to particular physical constraints at each scale may lead to a scaling in both B(m) and Cf(m), implying that 1 − P(m) scales allometrically. If Cf(m) scales in the same way as B(m), then 1 − P(m) will be a constant implying scale-independent performance. If Cf(m) and B(m) each scale as a power law with body size, but with different exponents, then 1 − P(m) will be defined by a positive or negative scaling exponent indicating decreasing or increasing performance, respectively, as body size increases (larger P indicates greater performance). In connection with our earlier and more general framework, the point at which P(m*) = 0 corresponds to fi → 0 and represents the point where the type-1 optimum is infeasible. At this point m* is either the maximum of minimum size for organisms with a particular body plan.
It is not always straightforward to calculate the energy consumption of a particular organismal trait Cf(m), nor is this always the most relevant indication of a limit as features can fundamentally limit an organism without consuming much metabolic power. For example, the construction and maintenance of particular arteries is insubstantial compared to overall metabolic rate, but what does matter for arteries is the likelihood of rupture under expected forces, or the likelihood of blockage under the normal range of physiological conditions. While the metabolic cost of rupture could be converted into energetic terms (e.g., pumping energy becomes infinite once the vessel is no longer connected) it is often more meaningful and practical to simply recognize that a rupture causes death, and to calculate the requirements of rupture avoidance. These are direct physical limits, and are topics with rich histories in the biophysical literature (e.g., Currey, 1970; McMahon, 1973; McMahon and Kronauer, 1976; Wainwright et al., 1976; Peters, 1986; Berg, 1993; Alexander, 1996; Calder, 1996; West et al., 1999; Gere, 2003; Niklas and Spatz, 2004, 2006; Vogel, 2004; Niklas, 2007; Niklas and Hammond, 2013). Such constraints often manifest in the dimensional and morphological requirements of particular organism features, such as the ratios of thickness to surface area and volume or of lengths to radii. Instead of P(m) a more useful dimensionless metric is to consider is M(m), which is the ratio of the minimal requirements of the size of a feature, Sf(m), compared with maximum allowable size S(m),
More specifically, Sf(m) is the size of a trait, such as a leg, that is required to work at all in performing a defined function (e.g., not breaking under the typical forces experienced over an organism's lifetime). S(m) is the space allowable for that trait given other constraints of the physiology and geometry of the organism. For example, if the cross-section of the leg is completely filled by the skeleton, then this represents an extreme upper-bound as there would be no space for muscles. More realistically, we can define the space allowable for the skeleton based on the space needed to accommodate the muscles that operate the leg, which are defined by the force required to move the leg, all of which leads to a smaller value for S(m) than the entire volume of the leg.
It is thus clear that M(m) allows for choices in the dimensions of Sf(m) and S(m), which could be volumes or linear dimensions, and where S(m) can be chosen at the feature or organism scale. As mentioned above for P(m), when S(m) is the volume of the entire organism, then M(m*) represents the extreme upper bound to an organism's size, which often gives us intuition about which constraints are most limiting for specific categories of organisms.
We apply these metrics to several examples for insects, bacteria, vascular plants, and mammals, as classes of organisms with extensive biophysical predictions for scaling relationships and well-developed perspectives on the ultimate limits of particular biophysical processes. Our goal is to understand how physical constraints have shaped the ultimate limits for particular classes of organisms. Within each class we take as a given the known body plan and do not consider how this architecture evolved, which is an interesting area for future research. Within each example our focus is on the point where type-1 optima become infeasible. In the context of the metrics that we have developed, for an upper bound on a particular body plan this is defined either as M(mmax) = 0, or P(mmax) = 0, and for a lower bound we are looking for M(mmin) = 0, or P(mmin) = 0. We will also discuss when there is a well-defined optimum body size for a class of organisms between the limiting sizes (e.g., a type-2 optimum), as for example at the large end of mammals (Yeakel et al., 2018). As mentioned above, in some cases P or M is more appropriate for highlighting limits. For bacteria, we are able to show that P and M occur at similar scales for particular features and the energy and dimensional requirements are interconnected. In arthropods we primarily rely on M in connection with the limits of exoskeletons. In vascular plants and mammals we rely on both P and M as metrics.
4. Examples Within Groups of Organisms
4.1. Insect Biomechanics and the Interplay of Different Physical Constraints
Insect appendages provide an example of how the structure of a trait is phylogenetically constrained, and how the performance of different functions by that trait is determined by physical laws. A critical phylogenetic constraint on insects is that the body is surrounded by an exoskeleton. Therefore, all organs and muscles must operate inside a container of fixed dimensions. Exoskeletons are scratched and punctured as animals move around in natural habitats and interact with other organisms, unlike endoskeletons that are protected from such surface damage by the surrounding soft tissues. Furthermore, insects must shed their exoskeleton (molt) in order to grow to larger size. Another phylogenetic constraint that limits the mechanical performance of insects is that the exoskeleton is composed of chitin fibers in a protein matrix.
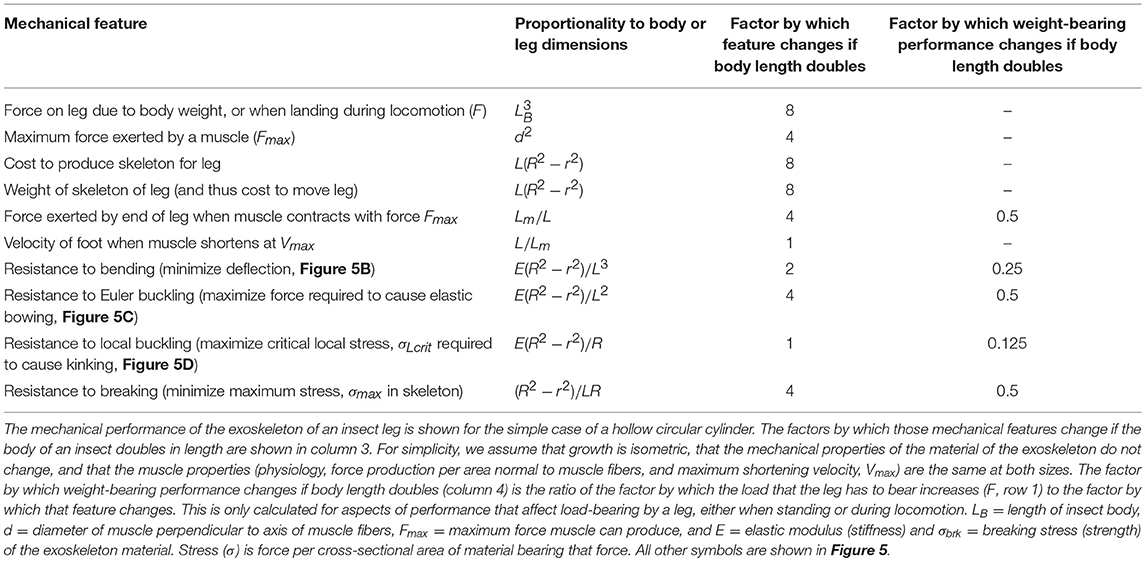
Insect appendages illustrate how the dimensions of a structure (in this case an appendage is the trait) can affect different aspects of mechanical performance (each of which is a column in Equation 1). The motions of and forces exerted by jointed appendages of insects (e.g., legs, wings, mouthparts, antennae, each being a row in Equation 1) can be analyzed by treating these structures as lever systems (Alexander, 2003). Appendages that are short are better at exerting large forces on the environment (e.g., for crushing prey or digging) for a given muscle force. In contrast, appendages that are long are better at rapid motions (e.g., running) for a given rate of muscle shortening. If we consider the exoskeleton of a stiff segment of an insect leg as a hollow, circular cylinder (Figure 5A), we can examine the consequences of changes in the cylinder's dimensions on other aspects of mechanical performance using standard beam theory (e.g., Currey, 1970), as described in biomechanics and engineering textbooks (e.g., Wainwright et al., 1976; Gere, 2003; Vogel, 2004). Some examples of how different aspects of leg performance depend on body and leg dimensions are given in Table A2 (Appendix). The cost to produce and move the exoskeleton depends on its volume. However, the ability of the leg's exoskeleton to resist deformation (Figures 5B,C) and breakage also depend in different ways on its length (L) as well as its radius (R) and the radius (r) of the space inside the exoskeleton. A hollow exoskeleton can also fail by undergoing local buckling (kinking like a bent soda straw, Figure 5D), which can damage the tissue inside the exoskeleton. The critical local stress (σLcrit) to cause a kink not only depends on the dimensions of a hollow cylinder (Table A2 in Appendix), but is much lower if the surface is scratched, as exoskeletons are prone to be.
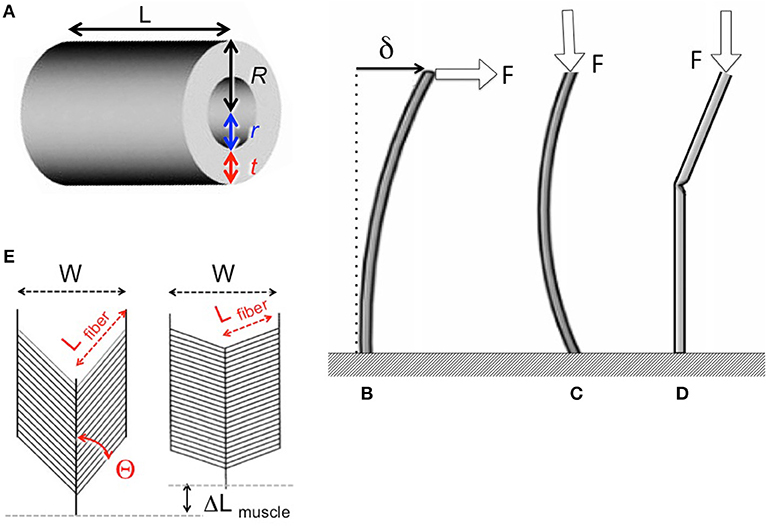
Figure 5. (A) Dimensions of a hollow cylindrical exoskeletal element: L = length, R = outer radius, r = inner radius, t = wall thickness. (B) Diagram of the deflection (δ) of the free end of an exoskeletal element being bent like a cantilever by a force (F) acting laterally on the end of the of the cantilever. (C) Elastic Euler buckling of an exoskeletal element acting like a column bearing an axial load (F). (D) Local buckling (kinking) of an exoskeletal element acting like a column bearing an axial load (F). (E) Diagram of a pennate muscle when relaxed (left) and after the muscle fibers have contracted (right): θ = angle between muscle fibers and the line of action of the muscle, Lfiber = length of the muscle fibers, W = width of the muscle, ΔLmuscle = distance muscle shortened when fibers contracted. Muscle bulging is not in the radial direction, and a greater number of shorter muscle fibers can fit into the volume of a pennate muscle than into a parallel-fibered muscle of the same size. However, the component of the force produced by the contracting fibers (Ffibers) in a pennate muscle that acts parallel to the line of action of the muscle (Fmuscle) depends on the angle (θ) of the fibers (Fmuscle = Ffibers cos θ), so Fmuscle decreases as the muscle shortens and θ becomes more oblique (Azizi et al., 2008).
The mechanical properties of the material composing the exoskeleton of an insect appendage also constrain its performance. For example, resistance to bending, bowing, and kinking by the exoskeleton of an appendage depends on the stiffness (elastic modulus, E) of the material (Table A2 in Appendix). Whether a stress (force per cross-sectional area of material bearing a load) in the exoskeleton will cause breakage depends on the strength (breaking stress, σbrk) of that material. These mechanical properties of insect exoskeleton are determined by the amount and orientation of the chitin fibers, the degree of cross-linking (tanning) and of hydration of the protein matrix, and the relative thickness of the heavily-tanned outer layer (exocuticle) and the less-tanned inner layer (endocuticle) (e.g., Wigglesworth, 1948; Wainwright et al., 1976;Parle et al., 2017).
The radius (r) of the space within the exoskeleton limits the force production and shortening of the muscles it contains, and thus can limit the ability of the appendage to perform various functions. The force that a muscle can produce depends on its cross-sectional area normal to the long axis of the muscle fibers. Because the r of the exoskeleton constrains muscle cross-sectional area, r limits the maximum force that can be exerted by a muscle; r also limits how much a contracting muscle can bulge radially, thereby limiting the distance that the muscle can shorten. The force exerted by a contracting muscle is a complex function of its change in length (Rassier et al., 1999; Nishikawa et al., 2018), so by limiting muscle shortening, r also affects force production. These constraints are mitigated in insects because most of their muscles are pennate, with fibers that are oriented at an angle to the muscle's line of action (Figure 5E). Thus, a pennate muscle can exert higher forces, but also shortens less (ΔLmuscle, Figure 5E) than a parallel-fibered muscle (Vogel, 2003). These constraints of the exoskeleton on muscle force and shortening can limit the performance of activities (e.g., running, pushing) that affect the competitive success and survival of insects in the environment, and can thus determine Sf(m) of the trait (leg) in Equation (20).
Using these physical rules described above, the type-1 optimal morphology for a leg can be determined for an insect of a given size if the aspects of leg performance (e.g., rapid running, forceful digging) can be identified that are most likely to affect the insect's fitness in its ecological setting. By examining the type-1 optima for the legs of insects across a range of body sizes, the type-2 optimum can be determined, and the physical limits on body size can be explored.
The effect of body size on different aspects of appendage performance are illustrated in Table A2 (Appendix). In this example, we assume for simplicity that the exoskeleton of a leg is a hollow circular cylinder, that the insect grows isometrically, and that the mechanical properties of the exoskeleton material and the behavior of the muscle (force production per area normal to muscle fibers, and maximum shortening velocity) do not change with size. The consequences to leg mechanics of an isometric doubling of body dimensions illustrate how different functions vary with size. The load that a leg must bear (F) and the cost of producing and moving the exoskeleton increase 8-fold, while the force produced by a muscle only increases 4-fold. Relative to the F's that must be resisted, the maximum force exerted by the appendage per muscle force exerted is only half of that at the smaller size. Resistance to bending and to breaking while bearing body weight or locomoting are also reduced by 50% if size doubles, whereas resistance to bowing is reduced by 75% and to kinking by 87.5%. This suggests that leg failure by kinking may determine the maximum allowable size, S(m) in Equation (20), for a given insect body plan. This S(m) can be increased by selection for allometric growth (e.g., smaller r relative to R) or for increased stiffness and strength of the material composing the exoskeleton.
Insects have to molt their exoskeleton to grow. The mechanical properties of the exoskeleton material change during this process (e.g., Wigglesworth, 1948; Parle et al., 2017). After the old exoskeleton is shed, the new exoskeleton is thinner (lower t) and less cross-linked (lower E and σbrk) than the older shed exoskeleton. With time after molting, the new exoskeletal material becomes more cross-linked and the thickness of the wall of the exoskeleton increases as more endocuticle is secreted. Therefore, resistance to bending and resistance to failure (by breaking or kinking) are lower right after molting. This poor mechanical performance of the soft, thin exoskeleton right after molting might be the factor that limits the overall body size of insects. Furthermore, insects are more vulnerable to predators right after a molt because locomotory appendages may buckle and bend too easily for effective escape maneuvers, and the exoskeleton may be easier to break or puncture by the predator. Therefore, while vulnerability to the predators in the environment of an insect may set the Sf(m) required for survival, molting reduces S(m) and the performance metric M(m).
In addition to the biomechanical constraints of an exoskelton and molting, other limits to the size of insects have been proposed and debated, including the supply of oxygen via the tracheal system, the power requirements for flight, and the effect of size on maneuverability of flying insects after bird and bat predators evolved (e.g., Kaiser et al., 2007; Kirkton, 2007; Okajima, 2008; Harrison et al., 2010; Clapham and Karr, 2012). We suggest that the approach illustrated in Figure 1 would be a fruitful way to evaluate the body sizes at which the various proposed mechanisms are likely to be most important and to identify which are most likely to constrain the size of insects.
While the exoskeleton of an insect appendage provides an example of a trait that does a number of physical tasks whose performance varies with size (as illustrated in the top row of Figure 1), the physiology of bacteria provide an example of how several traits together affect the performance of an organism as a function of its size (bottom row of Figure 1).
4.2. Bacterial Physiology and Ultimate Limits
Prokaryotes represent the oldest and morphologically simplest forms of self-reproducing life, although their metabolic and genetic diversity far exceeds the eukaryotes. We can consider their morphology, in a first approximation, as a membrane with embedded protein complexes enclosing a solution of DNA, carbohydrates, RNA, and proteins of various complexity. We are interested in how this physiology and architecture inform the evolutionary possibilities for bacteria in terms of the physics of both internal physiology and interaction with an external environment.
Considering interactions with the external environment, bacteria live in a world characterized by a low Reynolds number. That is, in conditions where viscous forces dominate over inertial forces. Within this low-Reynolds world one of the most common forms of motility is run/tumble chemotaxis, in which bacteria swim linearly for a variable time and then perform a random reorientation before swimming again. This form of motility is an asymmetric process, and allows for both a random-walk search and gradient following through biasing the random walk by dynamically adjusting the probability of tumbling (Berg, 1993). Within the context of motility it is also possible to calculate our metric P. It has been shown that the minimum power required for run-tumble chemotaxis is approximately given by
where k is the Boltzmann constant, T is absolute temperature, a is again the cell radius, and D is the molecular diffusivity (Mitchell, 2002). This result follows from considerations of the rotational and translational diffusion of cells, combined with the required distance a cell must move to detect a change in the concentration of a resource (Purcell, 1977; Mitchell, 1991, 2002; Berg, 1993). This cost must be a fraction of the total metabolic power, which in bacteria is known to scale with cell volume, V, according to
with α = 1.76 and (DeLong et al., 2010). The ultimate limit of motility is the point where its costs equal the total available metabolic energy, which can be found by setting Equation (22) equal to Equation (21) and substituting a = (3V/4π)1/3. Taking D = 5.19 ×10−10 (m2 s−1) and T = 298.15 K, the numerical solution for this lower limit is (m3). This limit can also be defined in terms of our metric for performance, P = 1 − Bmot/B, where Figure 6A illustrates that for most of the range of bacterial sizes P ≈ 1 and Bmot is a negligible fraction of total metabolic power. This calculation also illustrates that before reaching the ultimate limit described above (P = 0 at Vmin), P decreases sharply (Figure 6A), thus defining an intermediate size at which motility costs become radically more expensive, and may become selected against. This precipitous decrease occurs as Bmot increases sharply, due to the increasing significance of overcoming molecular diffusion.
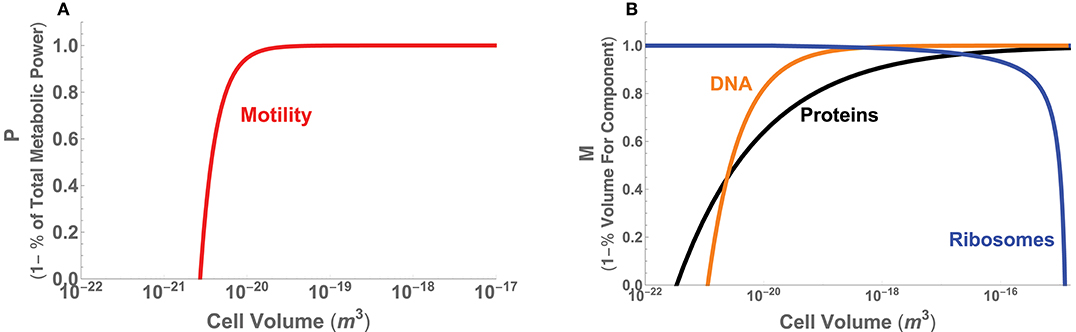
Figure 6. (A) The minimal power requirements for motility in bacteria as a function of total cell volume and given as the metric P, which is 1 minus the percentage of total metabolic power. (B) The volume requirements for DNA, protein, and ribosomes in bacteria as a function of cell volume and given as the metric M = 1−Vc/V, where Vc is the volume of each component.
Turning to the internal constraints of the bacterial body plan, recent efforts have shown that there are significant changes in the physiological processes and composition of bacterial cells across the range of cell size (Kempes et al., 2016). Many of these follow power-law relationships with asymptotic behavior that arise at distinct scales. It has been shown that the partitioning of total metabolic power between growth and maintenance purposes predicts the scaling of population growth rate across bacteria, including a lower-bound on cell size where maintenance metabolism exceeds total metabolic rate. This lower bound on size also agrees with considerations of physical space, where the combined scaling of all cellular macromolecules entirely fills the cell at a similar size and further constrains this lower bound. The total macromolecular pool is dominated by DNA and protein content at the small end of bacteria due to a sub-linear scaling of both. This same scaling causes these two macromolecules to be diluted in concentration with increasing bacterial cell volume. However, other theory has shown that the requirements for ribosomes can be predicted to scale roughly linearly with cell volume over a large range of cell volumes, up to a point where the requirement for ribosomes increases rapidly and exceeds total cell volume, thus setting an upper limit of bacterial cell sizes. This limiting behavior occurs because there is finite-volume singularity—at a distinct cell volume an infinite number of ribosomes are required—caused by the point where the cell division time is faster than the time it takes a ribosome to replicate itself.
These set of space limitations can be easily translated into our metric M by taking S to be the total volume of a cell and Sf to be the known scaling of protein, DNA, and ribosome volumes (see Appendix A.3 for the details of each of these scaling relationships). For example, given the total protein volume in the cell, Vp, the morphological metric is defined by Mp = 1 − Vp/V. Figure 6B provides the overlay of the performance curves for each of the three components, illustrating that at the small end of cell size proteins and DNA cause M to go to zero, and at the large end ribosomes have the same effect. Similar to our considerations of motility, we observe that over a wide range of intermediate cell sizes M ≈ 1 for considerations of the proteins and ribosomes, up to, for example, the point where the previously described “ribosome catastrophe” occurs.
4.3. Vascular Organisms
4.3.1. Trees
Terrestrial vascular plants are defined by a body plan that couples photosynthesis in leaves suspended in the atmosphere to nutrient and water acquisition from the soil. As such, the vascular system—which transports sugars from the leaves and nutrients from the roots to the rest of the tissues—is of central importance. Trees are also characterized by the need to effectively fill the entire canopy space in order to collect as much sunlight as possible and consequently to be as tall as possible to outcompete other plants for sunlight and avoid being shaded. These various constraints have led to a variety of perspectives for understanding plant allometry together with an extensive set of theories, calculations, and measurements.
Given the competitive importance of tree height, there have been many proposed mechanisms for determining its ultimate limit. These mechanisms have focused on both mechanical and hydraulic constraints. The mechanical constraints were originally addressed quantitatively by McMahon (McMahon, 1973; McMahon and Kronauer, 1976) who pointed out that the maximum possible height of a tree was set by the buckling limit (small lateral displacements cause failure) of its trunk, and this could be calculated using a formula first derived by Greenhilll from the classic bending moment equations for solid materials:
where ρ (g m−3) is the density of wood, E (g m−1 s−2) is the elastic modulus, d (m) is the trunk diameter, and C = 0.792 (s2/3 m−1/3) when the force is distributed over the entire column (e.g., this model considers a single beam with a uniform radius over its height) (McMahon, 1973; McMahon and Kronauer, 1976). This relationship has the same scaling between height and radius, h ∝ d2/3, as that for trees across all sizes and is in good agreement with data. However, using measured value of E (g m−1 s−2) ≈ 1.05 × 105 (McMahon, 1973; McMahon and Kronauer, 1976), this relationship leads to a critical height which is roughly 3 to 4 times larger than the observed scaling. Trees exist in a region of parameter space far below this upper bound and these mechanical constraints don't seem to limit the tallest possible trees at any size nor set an upper bound on the ultimate tallest possible vascular plant.
If no other physical constraints predicted this same scaling, then one could argue that trees have simply evolved to be a fixed safety factor from the mechanical limit and, provided that they conform to the h ∝ d2/3 scaling of height to diameter, there is no upper bound on tree height. However, arguments related to hydraulic limits and space-filling predict the same scaling relationship between height and radius as that from the mechanical constraints and, at the same time, set an upper bound on the tallest possible trees as discussed below (West et al., 1999; Niklas and Spatz, 2004, 2006; Niklas, 2007). Nevertheless, the buckling arguments are important in the broader space of all evolutionary possibilities. For example, these constraints could be relevant to vascular plants with alternate body plans, alternate evolutionary trajectories, or at earlier stages of vascular plant evolution compared with those that seem to conform to hydraulic limits.
There are several approaches to considering the hydraulic limits to tree height centered either on the requirements for conductive tissue or the feasibility of pumping fluid over the length of a single vascular tube. For the conductive tissues arguments there are two main perspectives. The first uses the observations and/or assumptions that (i) annual growth scales with leaf mass, (ii) annual growth scales with total plant mass to the 3/4 power, (iii) the flux of water through the leaves must match the flux through the conductive tissue so that leaf mass scales with the hydraulically functional cross-section, and (iv) the mass of the roots scales isometrically with the mass of the stems which in turn is proportional to the cross-sectional area times length. From these assumptions it can be shown that tree height, h, is related to diameter, d, as
where a good fit to data is obtained with k1 = 34.64 (m1/3) and k2 = 0.475 (m) (Niklas and Spatz, 2004, 2006; Niklas, 2007). For large trees this relationship parallels the Euler-Greenhill predictions, but also does a better job of capturing observed curvature in the data away from a power law at the small end of trees. While this relationship does not predict an upper bound on tree size it does predict a lower bound of for h = 0, which is roughly the diameter of petioles (the segment of the plant that attaches leaves to the stem) suggesting that this smallest size agrees with the minimal vascular plant of a single leaf and stem. This limit can also be understood in terms of our metric M, where we can define M(h) = 1 − dpetiole/d. Here M is defined in terms of h as the overall measure of size, d is the required diameter, and its ratio to the petiole diameter, dpetiole, defines performance. Given the above relationships, , which quickly approximates unity for h > 0. The above derivation of the equation for h shows that this lower bound is due to differences in the observed scaling of the leaf mass and trunk diameter with total plant mass, representing underlying hydraulic constraints. However, since this relationship relies on several empirical scaling relationships it is difficult to see exactly which physical constraints are being optimized.
The second perspective on hydraulic limits uses the assumptions of (i) canopy space filling, (ii) mechanical stability, and (iii) hydraulic resistance minimization within a fractal-like architecture to optimize the overall plant body plan (West et al., 1999). The optimization is performed in terms of the various ratios of the vessel and branch sizes and a detailed calculation of the total resistance of the entire vascular network. Similar to the perspective above, the results predict that h ∝ d2/3, but also predict a maximum height where the entire trunk becomes conductive tissue. This can be seen by choosing , the total area of connective tissue in the trunk, where nN is the total number of vascular tubes in a petiole, aN is the radius of a petiole tube, and rN is the radius of the entire petiole. If we take S to be the total area of the trunk, then we have that or
which is plotted in Figure 7 using the typical values of nN = 200, (m), and (m) (West et al., 1999).
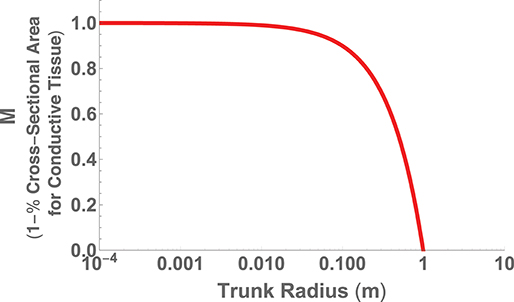
Figure 7. The fraction of trunk cross sectional area required for conductive tissue as a function of trunk radius and represented as the metric M.
The maximum trunk radius and associated height is given by M = 0, which corresponds to ,
and
where n ≈ 2 is the number of branches at each generation and lN ≈ 0.04 (m) is the length of a petiole. Given the values listed above, these relationships predict rmax ≈ 1(m) and hmax ≈ 100(m) in good agreement with record trees. This approach thus predicts the fundamental limit on vascular plants, in addition to the cross-species scaling, by co-optimizing the dominant physical constraints of both hydraulic resistance and mechanical stability. This is a case where the accurate prediction of the limit corroborates that the dominant constraints of the system have been identified.
4.3.2. Mammals
Similar to vascular plants, a theory of fractal vascular networks regulating metabolic supply has been developed for the metabolic scaling of mammals and broadly predicts a variety of observed allometries and scaling relationships (West et al., 1997). This theory considers transport to be the rate-limiting step for metabolism and that optimizing the transport network by minimizing its cost predicts overall metabolic rate and a host of downstream effects. This theory is impressive not only in its ability to predict interspecific scaling relationships across a wide range of body sizes, but also for its ability to predict asymptotic limits to the mammalian body plan. This is possible because the theory provides a detailed description of the coupling of the body plan to the underlying physical and geometric constraints. For example, for very small mammals, the pulsatile waves emanating from the heart are unable to reach the capillaries because of the dissipation of energy due to hydraulic resistance along the path of the branching vascular tubes. Previous work has shown that in all mammalian vascular systems there is a point in the network where pulsatile flow becomes laminar flow, and this cross over occurs at , where rc and lc are the critical radius and length of a vascular segment at the branching generation in the network where the cross over occurs, ν = 4 (g m−1 s−1) is the viscosity of blood, ρ = 106 (g m−3) is the density of blood, and (m s−1), where E is the modulus of elasticity of the vessel with a wall of thickness w (West et al., 2002). As mammals become smaller the branching generation at which this cross-over occurs decreases and eventually becomes the aorta itself, and corresponding to a dramatic decrease in efficiency due to an overdamped vascular system. From this perspective, we can define the metric M in terms of the system damping by taking , where r0 and l0 are the dimensions of the initial segment (aorta) of the vascular network. The lower limit of mammal size is given by . Noting that the aorta allometry of and , where a1 and a2 are allometric normalization constants, the preceding equality is equivalent to , which defines the minimum size as . Given that a mammal of m = 10, 000 (g) has the vessel dimensions of r0 = 0.0075 (m) and l0 = 0.2 (m), then (g m−2), and the minimum mammal size is predicted to be mmin ≈ 3.6 (g) (West et al., 2002). This lower limit is close to observed sizes of several species of shrew which are the smallest mammals. Similar to many of the other analyses above, this example illustrates that even when a type-1 physiological optimization is performed at every body size, there will still be a body size where even optimal performance represents an impossible physiology.
5. Discussion
We propose that it will eventually be possible to enhance our understanding of the complex selective factors involved in evolution by analyzing the overlay and co-optimization of physical constraints for a particular body plan at a given size scale. Here we have suggested that the first step is to understand the limits of a body plan that is optimized to a particular set of dominant constraints. Moving forward we need theories that establish a hierarchy of physical constraints for identified types of body plans of organisms. We also need theories that can predict the interconnected temporal evolution of physiology, body size, and physical constraints.
Implicit in a full theory of evolution under constraints is the need to identify and integrate the ecological constraints that organisms face in addition to the phylogenetic and physical constraints discussed above. Ecological constraints emerge, for instance, from interactions among the set of coexisting organisms through predator-prey dynamics, competition for overlapping resources, and via more complicated symbioses, coevolution, and niche construction. For example, recent theoretical work on the population dynamics of foragers using a single shared resource has connected basic allometric physiology with the dynamics of resource consumption, as well as consumer starvation, growth, and reproduction (Yeakel et al., 2018). This work shows that Damuth's law—the observation that the population density (Individuals m−2) of a species is proportional to body mass to the −3/4 power (Damuth, 1987)—is predicted as the natural steady state of the complicated dynamics of reproduction, starvation, and mortality, where the rate of each of these processes is based on the underlying energetics of allometric metabolism. More importantly for our considerations here, this model of interacting foragers also shows that larger mammals should outcompete smaller mammals up to a maximum mammalian size. This maximum mammalian size occurs at a point where the population consumes all available resources and perishes. This limit is supported by data, where the predicted maximum size of a mammal is roughly 3.5 times larger than the largest observed terrestrial mammals, which are in the fossil record (Yeakel et al., 2018). In contrast to our analyses here of single-organism physiology, this maximum size limit emerges as an ecological-scale interaction between an entire population and available resources.
Environments may also introduce additional constraints through the expected variation of conditions. For example, one would expect selection on breaking resistance (e.g., Table A2 in Appendix) in trees to depend not on typical wind speeds, but rather on the probability of unusually high wind speeds over the lifetime of a tree. Earlier we introduced the formalism presented by McNeil Alexander in which the evolution of safety factors is dictated by the equation ϕ(s) = l(s)F + U(s) (Alexander, 1996). As noted earlier, trees seem to have a safety factor of roughly four which has also been directly verified in detailed analyses of bending under wind stress. A broader literature on the economy of wood density has quantified the variation of safety factor in response to a variety of competing evolutionary considerations including life-history strategies for resource acquisition (e.g., quick growth for sunlight), adult stature, wood production cost, and wood resistance to decay and herbivores. The effect of decay and herbivory on the strength of the wood in trees also varies during the lifetime of a tree. The formalism of Alexander can thus be expanded to encapsulate all of these limits, which goes beyond our focus on the physiology and biomechanics of individual organisms. An important challenge of such an approach is defining l(s) and U(s) under a complex set of species interactions and distributions that occur under various changing environmental conditions and stresses. In our formalism, the challenge becomes defining the matrix g in such a way that each entry represents an entire life-cycle value that integrates the probabilities of various environmental and competitive effects. Future efforts should focus on developing new, and expanding existing, compendia of constraints for particular body plans and integrating these into detailed evolutionary models. If this is done, it may be possible to make ever more specific evolutionary and ecological predictions from physical constraints.
Finally, since the framework presented here only requires the specification of organism structure and physical constraints, it is amenable to general considerations of life for origins of life and astrobiology research.
Author Contributions
CK: conceived of the project. CK, GW, and MK: developed mathematical formalisms, conducted analyses, and wrote the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
CK and GW thank CAF Canada for generously supporting this work. We also are also grateful for grants from the National Aeronautics Space Administration, 80NSSC18K1140 (supporting CK), the National Science Foundation, IOS-1655318 (to MK) and PHY1838420 (to GW), and from the Gene & Clare Thaw Charitable Trust (to GW). We also thank the 4 reviewers of this paper whose feedback greatly improved the manuscript.
References
Abrams, P. (2001). Modelling the adaptive dynamics of traits involved in inter-and intraspecific interactions: an assessment of three methods. Ecol. Lett. 4, 166–175. doi: 10.1046/j.1461-0248.2001.00199.x
Alexander, R. M. (2003). Principles of Animal Locomotion. Princeton, NJ: Princeton University Press.
Azizi, E., Brainerd, E. L., and Roberts, T. J. (2008). Variable gearing in pennate muscles. Proc. Natl. Acad. Sci. U.S.A. 105, 1745–1750. doi: 10.1073/pnas.0709212105
Bremer, H., Dennis, P. P., and Neidhardt, F. (1996). “Modulation of chemical composition and other parameters of the cell by growth rate,” in Escherichia coli and Salmonella typhimurium: cellular and molecular biology, 2nd Edn. (American Society for Microbiology).
Brown, J., Marquet, P., and Taper, M. (1993). Evolution of body size: consequences of an energetic definition of fitness. Am. Nat. 142, 573–584. doi: 10.1086/285558
Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000
Calder, W. A. (1996). Size, Function, and Life History. Toronto, ON: General Publishing Company, Ltd.
Clapham, M. E., and Karr, J. A. (2012). Environmental and biotic controls on the evolutionary history of insect body size. Proc. Natl. Acad. Sci. U.S.A. 109, 10927–10930. doi: 10.1073/pnas.1204026109
Damuth, J. (1987). Interspecific allometry of population density in mammals and other animals: the independence of body mass and population energy-use. Biol. J. Linn. Soc. 31, 193–246. doi: 10.1111/j.1095-8312.1987.tb01990.x
DeLong, J. P., Okie, J. G., Moses, M. E., Sibly, R. M., and Brown, J. H. (2010). Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. U.S.A. 107, 12941–12945. doi: 10.1073/pnas.1007783107
Dill, K. A., Ghosh, K., and Schmit, J. D. (2011). Physical limits of cells and proteomes. Proc. Natl. Acad. Sci. U.S.A. 108, 17876–17882. doi: 10.1073/pnas.1114477108
Erickson, H. P. (2009). Size and shape of protein molecules at the nanometer level determined by sedimentation, gel filtration, and electron microscopy. Biol. Proc. Online 11, 32–51. doi: 10.1007/s12575-009-9008-x
Falster, D., and Westoby, M. (2003). Plant height and evolutionary games. Trends Ecol. Evol. 18, 337–343. doi: 10.1016/S0169-5347(03)00061-2
Falster, D. S., FitzJohn, R. G., Brännström, Å., Dieckmann, U., and Westoby, M. (2016). plant: a package for modelling forest trait ecology and evolution. Methods Ecol. Evol. 7, 136–146. doi: 10.1111/2041-210X.12525
Fiksen, Ø., Follows, M. J., and Aksnes, D. L. (2013). Trait-based models of nutrient uptake in microbes extend the michaelis-menten framework. Limnol. Oceanogr. 58, 193–202. doi: 10.4319/lo.2013.58.1.0193
Frank, S. A. (2011a). Natural selection. I. Variable environments and uncertain returns on investment. J. Evol. Biol. 24, 2299–2309. doi: 10.1111/j.1420-9101.2011.02378.x
Frank, S. A. (2011b). Natural selection. II. Developmental variability and evolutionary rate. J. Evol. Biol. 24, 2310–2320. doi: 10.1111/j.1420-9101.2011.02373.x
Frank, S. A. (2012a). Natural selection. III. Selection versus transmission and the levels of selection. J. Evol. Biol. 25, 227–243. doi: 10.1111/j.1420-9101.2011.02431.x
Frank, S. A. (2012b). Natural selection. IV. The price equation. J. Evol. Biol. 25, 1002–1019. doi: 10.1111/j.1420-9101.2012.02498.x
Frank, S. A. (2012c). Natural selection. V. How to read the fundamental equations of evolutionary change in terms of information theory. J. Evol. Biol. 25, 2377–2396. doi: 10.1111/jeb.12010
Gabashvili, I. S., Agrawal, R. K., Spahn, C. M., Grassucci, R. A., Svergun, D. I., Frank, J., et al. (2000). Solution structure of the E. coli 70s ribosome at 11.5 a° resolution. Cell 100, 537–549. doi: 10.1016/S0092-8674(00)80690-X
Harrison, J. F., Kaiser, A., and VandenBrooks, J. M. (2010). Atmospheric oxygen level and the evolution of insect body size. Proc. R. Soc. B Biol. Sci. 277, 1937–1946. doi: 10.1098/rspb.2010.0001
Kaiser, A., Klok, C. J., Socha, J. J., Lee, W.-K., Quinlan, M. C., and Harrison, J. F. (2007). Increase in tracheal investment with beetle size supports hypothesis of oxygen limitation on insect gigantism. Proc. Natl. Acad. Sci. U.S.A. 104, 13198–13203. doi: 10.1073/pnas.0611544104
Kempes, C. P., Dutkiewicz, S., and Follows, M. J. (2012). Growth, metabolic partitioning, and the size of microorganisms. Proc. Natl. Acad. Sci. U.S.A. 109, 495–500. doi: 10.1073/pnas.1115585109
Kempes, C. P., van Bodegom, P. M., Wolpert, D., Libby, E., Amend, J., and Hoehler, T. (2017). Drivers of bacterial maintenance and minimal energy requirements. Front. Microbiol. 8:31. doi: 10.3389/fmicb.2017.00031
Kempes, C. P., Wang, L., Amend, J. P., Doyle, J., and Hoehler, T. (2016). Evolutionary tradeoffs in cellular composition across diverse bacteria. ISME J. 10, 2145–2157. doi: 10.1038/ismej.2016.21
Kirkton, S. D. (2007). Effects of insect body size on tracheal structure and function. Adv. Exp. Med. Biol. 618, 221–228. doi: 10.1007/978-0-387-75434-5_17
Koch, A. L. (1996). What size should a bacterium be? a question of scale. Annu. Rev. Microbiol. 50, 317–348. doi: 10.1146/annurev.micro.50.1.317
Lande, R. (1979). Quantitative genetic analysis of multivariate evolution, applied to brain: body size allometry. Evolution 33(1 Pt. 2):402–416. doi: 10.1111/j.1558-5646.1979.tb04694.x
Lynch, M.Walsh, B., et al. (1998). Genetics and Analysis of Quantitative Traits, Vol. 1. Sunderland, MA: Sinauer.
McGill, B. J., and Brown, J. S. (2007). Evolutionary game theory and adaptive dynamics of continuous traits. Annu. Rev. Ecol. Evol. Syst. 38, 403–435. doi: 10.1146/annurev.ecolsys.36.091704.175517
McMahon, T. (1973). Size and shape in biology: elastic criteria impose limits on biological proportions, and consequently on metabolic rates. Science 179, 1201–1204. doi: 10.1126/science.179.4079.1201
McMahon, T. A.M and Kronauer, R. E. (1976). Tree structures: deducing the principle of mechanical design. J. Theor. Biol. 59, 443–466. doi: 10.1016/0022-5193(76)90182-X
Mitchell, J. G. (1991). The influence of cell size on marine bacterial motility and energetics. Microb. Ecol. 22, 227–238. doi: 10.1007/BF02540225
Mitchell, J. G. (2002). The energetics and scaling of search strategies in bacteria. Am. Nat. 160, 727–740. doi: 10.1086/343874
Neidhardt, F., Umbarger, H., and Neidhardt, F. (1996). “Chemical composition of Escherichia coli,” in Escherichia coli and Salmonella typhimurium: Cellular and Molecular Biology, 2nd Edn. (Washington, DC: American Society for Microbiology).
Niklas, K. J. (2007). Maximum plant height and the biophysical factors that limit it. Tree Physiol. 27, 433–440. doi: 10.1093/treephys/27.3.433
Niklas, K. J., and Hammond, S. T. (2013). Biophysical effects on plant competition and coexistence. Funct. Ecol. 27, 854–864. doi: 10.1111/j.1365-2435.2012.02035.x
Niklas, K. J., and Spatz, H.-C. (2004). Growth and hydraulic (not mechanical) constraints govern the scaling of tree height and mass. Proc. Natl. Acad. Sci. U.S.A. 101, 15661–15663. doi: 10.1073/pnas.0405857101
Niklas, K. J., and Spatz, H.-C. (2006). Allometric theory and the mechanical stability of large trees: proof and conjecture. Am. J. Bot. 93, 824–828. doi: 10.3732/ajb.93.6.824
Nishikawa, K. C., Monroy, J. A., and Tahir, U. (2018). Muscle function from organisms to molecules. Integr. Compar. Biol. 58, 194–206. doi: 10.1093/icb/icy023
Okajima, R. (2008). The controlling factors limiting maximum body size of insects. Lethaia 41, 423–430. doi: 10.1111/j.1502-3931.2008.00094.x
Parle, E., Dirks, J.-H., and Taylor, D. (2017). Damage, repair and regeneration in insect cuticle: the story so far, and possibilities for the future. Arthropod Struct. Dev. 46, 49–55. doi: 10.1016/j.asd.2016.11.008
Peters, R. H. (1986). The Ecological Implications of Body Size. Cambridge, UK: Cambridge University Press.
Phillips, R., Kondev, J., Theriot, J., and Garcia, H. (2012). Physical Biology of the Cell. New York, NY: Garland Science.
Queller, D. C. (2017). Fundamental theorems of evolution. Am. Nat. 189, 345–353. doi: 10.1086/690937
Rashevsky, N. (1944). Studies in the physicomathematical theory of organic form. Bull. Math. Biophys. 6, 1–59.
Rashevsky, N. (1960). Mathematical Biophysics: Physico-Mathematical Foundations of Biology, Volume One, Third Edition. New York, NY: Dover Publications Incorporated.
Rassier, D., MacIntosh, B., and Herzog, W. (1999). Length dependence of active force production in skeletal muscle. J. Appl. Physiol. 86, 1445–1457. doi: 10.1152/jappl.1999.86.5.1445
Szenk, M., Dill, K. A., and de Graff, A. M. R. (2017). Why do fast-growing bacteria enter overflow metabolism? testing the membrane real estate hypothesis. Cell Syst. 5, 95–104. doi: 10.1016/j.cels.2017.06.005
Tran, Q. H., and Unden, G. (1998). Changes in the proton potential and the cellular energetics of Escherichia coli during growth by aerobic and anaerobic respiration or by fermentation. Eur. J. Biochem. 251, 538–543. doi: 10.1046/j.1432-1327.1998.2510538.x
Vogel, S. (2004). Comparative Biomechanics: Life's Physical World. Princeton, NJ: Princeton University Press.
Wainwright, S. A., Biggs, W., Currey, J. D., and Gosline, J. (1976). Mechanical Design in Organisms. London: Edward Arnold Ltd.
West, G. B., Brown, J. H., and Enquist, B. J. (1997). A general model for the origin of allometric scaling laws in biology. Science 276, 122–126. doi: 10.1126/science.276.5309.122
West, G. B., Brown, J. H., and Enquist, B. J. (1999). A general model for the structure and allometry of plant vascular systems. Nature 400, 664–667. doi: 10.1038/23251
West, G. B., Brown, J. H., and Enquist, B. J. (2001). A general model for ontogenetic growth. Nature 413, 628–631. doi: 10.1038/35098076
West, G. B., Woodruff, W. H., and Brown, J. H. (2002). Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc. Natl. Acad. Sci. U.S.A. 99(Suppl. 1):2473–2478. doi: 10.1073/pnas.012579799
Wigglesworth, V. (1948). The insect cuticle. Biol. Rev. 23, 408–451. doi: 10.1111/j.1469-185X.1948.tb00566.x
Yeakel, J. D., Kempes, C. P., and Redner, S. (2018). Dynamics of starvation and recovery predict extinction risk and both damuth's law and cope's rule. Nat. Commun. 9:657. doi: 10.1038/s41467-018-02822-y
Zhu, J., Penczek, P. A., Schröder, R., and Frank, J. (1997). Three-dimensional reconstruction with contrast transfer function correction from energy-filtered cryoelectron micrographs: procedure and application to the 70s Escherichia coli ribosome. J. Struct. Biol. 118, 197–219. doi: 10.1006/jsbi.1997.3845
Appendix
A.1. Connection to Ecological Constraints
The full treatment of fitness considers how all traits are constrained by the interaction of both physiological and ecological factors with physical constraints. Ecological effects consist of all of the features affecting the effective number of offspring such as predation, likelihood of diseases, or starvation risk. From this perspective fitness can be written as
which can be rewritten as
where pp is a particular physical constraint, gt, p is a term representing the net benefit attributed to a particular trait due an organism's physiology interacting with a physical constraint, and et, p is the net benefit attributed to a particular trait due to an ecological interaction with a physical constraint. It should be noted that et, p will generally depend on complicated ecological quantities such as the density of predators. In all of these cases, lowercase subscripts refer to to an arbitrary element of a matrix or vector, such that tt is an arbitrary element of , and uppercase subscripts refer to the last element where P is the length of , T is the length of , and g is a T × P matrix.
It should be noted that the sort of linear separation performed in Equation (A2) is only possible if there are not traits that can only be described in terms of functions of both gt, p and et, p together. In addition, an implicit assumption in optimizing a particular trait according to maximizing only is that the physiological effects on fitness are larger than the ecological effects, or that , for a particular trait t. It could be the case that for some other trait, t′, the fitness effects are determined by , in which case the ecological optimization would be most relevant for understanding the trait and overall fitness. In some cases, considering both terms may be required for understanding a trait. Here we mostly focus on traits where the physiological effects dominate.
A.2. Detailed Example of Trait Co-optimization
The ultimate goal of the general framework is to consider the tradeoffs amongst multiple traits in optimizing growth rate. To illustrate this procedure we can analyze the tradeoffs between two traits within our single-cell example. Consider the investment in the number of transporters and investment in chemotaxis and competing and complementary ways to increase total resource uptake to the cell. In such a situation, we would have that
where g(a, vs, n, S∞, D) is a complicated function parameterizing diffusion through a boundary layer and the characteristics of the fluid. The power output required for swimming at a particular speed is given by where vs is the swimming speed and η is the viscosity of the fluid. In this example the first row represents the trait of uptake through transporters and the third row the trait of swimming. However, since these two traits must be co-optimized given the mutual dependence on swimming speed, vs, we could combine them into a single row representing the combined trait of resource uptake:
The trait of resource uptake could then be optimized independently to find the ideal combinations of n and vs across a range of cell sizes. The cost of the cellular volume would only matter again in terms of solving for an upper bound on cell size where dm/dτ = 0.
It should be noted that in all of our illustrative examples, the matrices involved can be condensed into a single row where the summation of costs and benefits is simply the dot product of vectors. This scenario would not be the case for more complicated trait optimizations, and, in general, summations of the form of Equation (5) will allow for optimizations where constructing the matrices is not simple or useful.
A.3. Bacterial Composition
Previous efforts have characterized the scaling of the major macromolecular components of bacteria (Kempes et al., 2016), where the volume of the DNA follows
where () and βD = 0.21 ± 0.03, while the volume of expressed proteins scales more steeply with cell size following
where (), and βp = 0.70 ± 0.06. Taken together with the known scaling of growth rate, defined by , the volume of expressed proteins determines the required volume of ribosomes which follow
where βμ ≈ 0.64, (), m−3 is the average volume of a ribosome (Zhu et al., 1997; Gabashvili et al., 2000), is the average volume of a protein (Neidhardt et al., 1996; Erickson, 2009; Phillips et al., 2012), bp is the average length of a the combined ribosomal protein transcripts (Bremer et al., 1996), and rr = 63 bp s−1 is the transcript processing rate (Bremer et al., 1996), and bp is the average length of a protein transcript (Dill et al., 2011).
A.4. Definitions and Parameter Values
Table A1 provides a list of definitions for the main features of our general framework, Table A2 provides definitions for insects, and Table A3 provides parameter definitions and values for bacteria, trees, and mammals.
Keywords: biophysical constraints, allometry, metabolic scaling, safety factors, evolutionary transitions
Citation: Kempes CP, Koehl MAR and West GB (2019) The Scales That Limit: The Physical Boundaries of Evolution. Front. Ecol. Evol. 7:242. doi: 10.3389/fevo.2019.00242
Received: 24 December 2018; Accepted: 11 June 2019;
Published: 07 August 2019.
Edited by:
Diego Barneche, University of Exeter, United KingdomReviewed by:
Daniel Padfield, University of Exeter, United KingdomJames ODwyer, University of Illinois at Urbana-Champaign, United States
Alex Brummer, University of California, Los Angeles, United States
Colin Olito, Lund University, Sweden
Copyright © 2019 Kempes, Koehl and West. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christopher P. Kempes, Y2tlbXBlc0BzYW50YWZlLmVkdQ==
 Christopher P. Kempes
Christopher P. Kempes M. A. R. Koehl
M. A. R. Koehl Geoffrey B. West
Geoffrey B. West