- 1School of Informatics, Computing, and Engineering, Indiana University, Bloomington, IN, United States
- 2Pacific Ecoinformatics and Computational Ecology Lab, Berkeley, CA, United States
A well-known parable is that of the blind men studying an elephant each of which assert the elephant is the part they first hold in their hands, e.g., “rope!” says the tail holder while the leg holder asserts “tree!” The various subdisciplines of ecology appear similar in that we each engage in our enthusiastic but at least somewhat myopic study with remarkably limited agreement or even discussion about the overall system which we all study. Allometric trophic network (ATN) theory offers a path out of this dilemma by integrating across scales, taxa, habitats and organizational levels from physiology to ecosystems based on consumer-resource interactions among co-existing organisms. The network architecture and the metabolic and behavioral processes that determine the structure and dynamics of these interactions form the first principles of ATN theory, which in turn provides a synthetic overview and powerfully predictive framework for ecology from organisms to ecosystems. Beyond ecology, ATN theory also synthesizes eco-evolutionary and socio-ecological research still largely based on consumer-resource mechanisms but respectively integrated with different processes including natural selection and market mechanisms. This paper briefly describes foundations, advances, and future directions of ATN theory including predicting an ecosystem’s phenotype from its community’s genotype in order to accelerate more predictive and unified understanding of the complex systems studied by ecologists and other environmental scientists.
Introduction
The parable of the blind men and the elephant (Saxe, 2016) describes one of the most compelling and widely known metaphors for scientific unification (e.g., Himmelfarb et al., 2002; Cohen et al., 2003). The millennia-old parable ridicules the different religions that adamantly maintained disparate theologies about a single god on the Indian subcontinent. Probably the most famous English version of the parable is the poem written by J. G. Sax in the mid 1800’s (Figure 1) that concludes “And so these men of Indostan disputed loud and long, …though each was partly in the right, and all were in the wrong!” Ecology and its many subdisciplines share disconcertingly many similarities with this parable. Perhaps most strikingly is the lack of explicit discussion among subdisciplines of how different subdomains of ecology fit together to form a more unified concept of ecological systems. Allometric Trophic Network (ATN) theory (Brose et al., 2006b; Martinez et al., 2006; Otto et al., 2007; Berlow et al., 2009; Boit et al., 2012) helps fill this void by providing a synthetic mechanistic description of ecological systems that integrates the physiology and behavior of organisms with their interactions among other organisms scaled up to the many species and interactions that determine the behavior of complex communities and ecosystems (Figure 2).
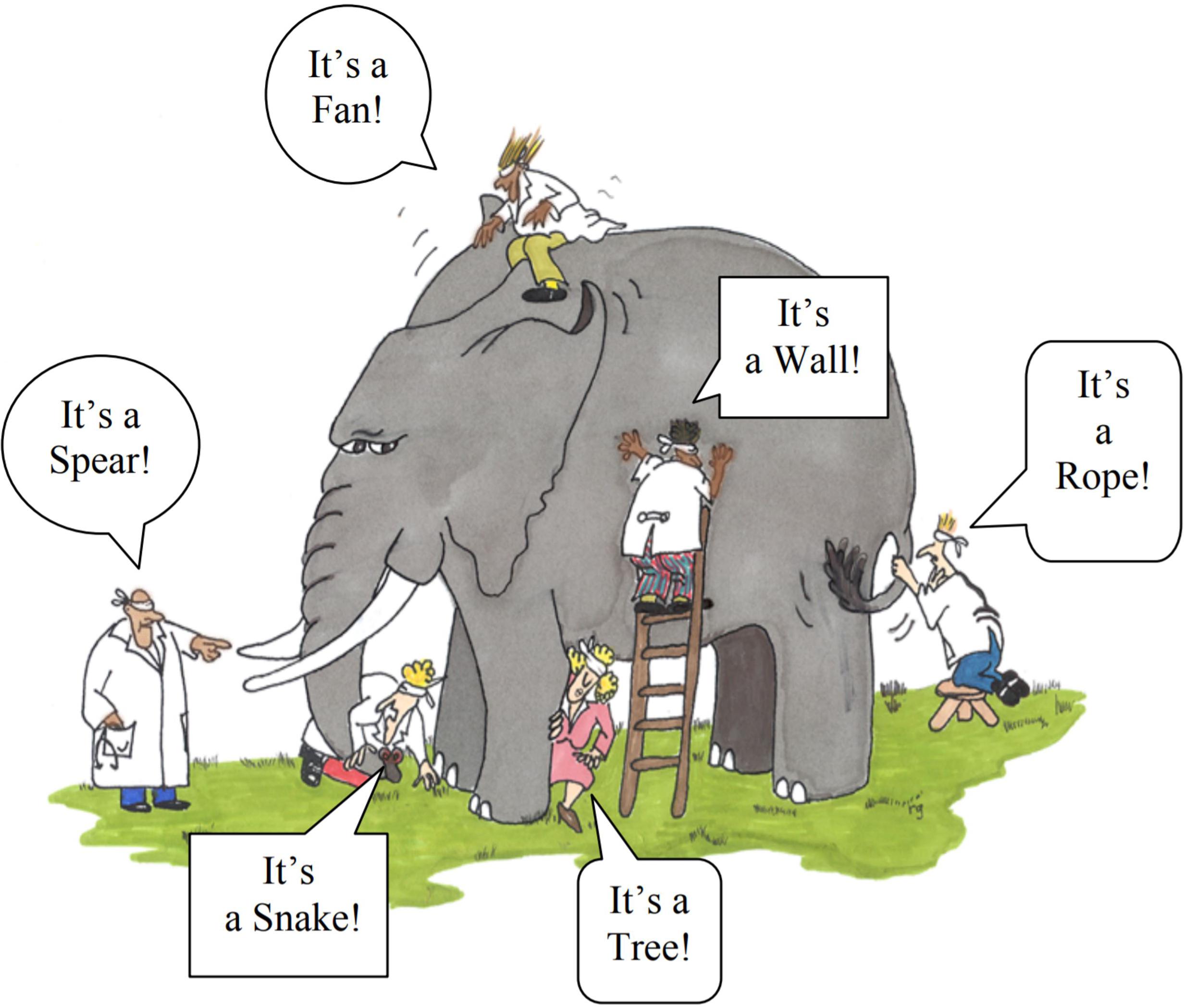
Figure 1. Blind people “seeing” the elephant (reproduced with permission from Himmelfarb et al., 2002).
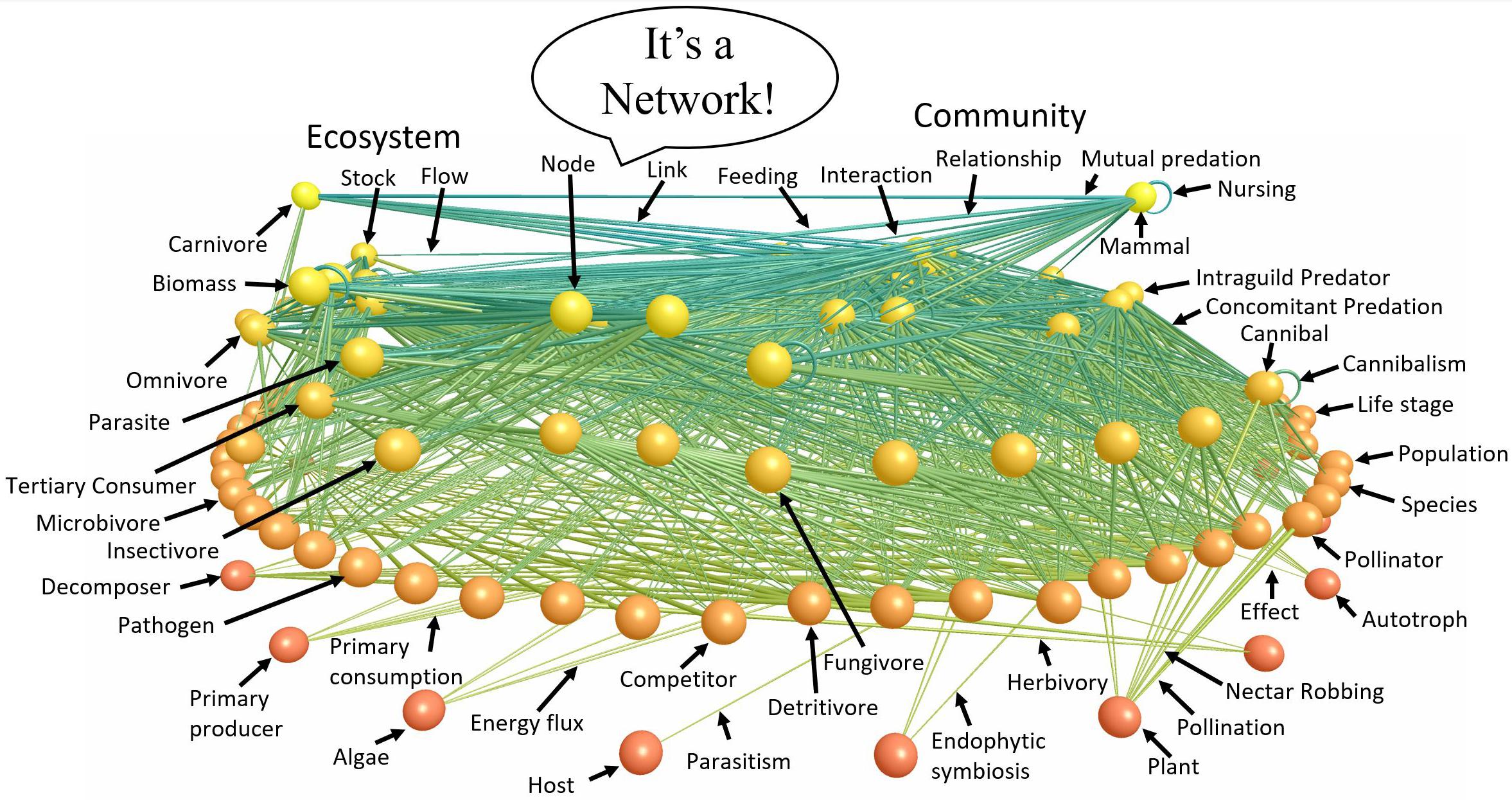
Figure 2. A food web labeled with terms describing different components and aspects of the network. Nodes of the network are vertically arranged according to trophic level with autotrophs at the bottom and upper level carnivores at the top. Links between nodes represent feeding relationships. The various terms characteristic of ecology’s various subdisciplines that point to the parts of the ecological network emphasize that ecological subdisciplines study very similar entities from different perspectives. ATN theory helps synthesize these subdisciplines by focusing on the structure (Figure 3) and dynamics (Box A) of ecological networks such as that of Little Rock Lake (Martinez, 1991) visualized (Yoon et al., 2004) and figuratively labeled here.
ATN theory (Figure 3 and Box A) pursues such advances by building upon the metabolic theory of ecology and its emphasis on unification across scales (Brown et al., 2004). ATN theory does this by integrating metabolic theory with a theory of trophic networks comprised of organisms consuming resources produced by other organisms (e.g., food) and, in case of autotrophs, the environment (e.g., sunlight, water and inorganic chemicals). This theory holds that organisms’ existence, abundance and dynamics critically depend on these same properties of their consumers and resources. ATN theory also embraces the importance of metabolic rates in determining the rates of organismal activity and the central tendency of mass-specific metabolic and production rates to consistently scale with body size over 20 orders of magnitude (Brown et al., 2004). This range includes practically all the organisms disparately studied by subdisciplines separated according to taxonomy (e.g., microbial, plant, animal etc.), habitat (terrestrial, freshwater, marine, etc.) and geography (temperate, tropical, montane, etc.). However, in contrast to its name, the metabolic theory of ecology appears to be primarily a theory of organismal physiology controversially based on how nutrients and waste are transported within organisms (Price et al., 2012). Though metabolism closely relates to many phenomena from organismal locomotion to the global carbon cycle (Marquet et al., 2004; Allen et al., 2005; Schramski et al., 2015), the role of the metabolic theory of ecology in the ‘elephant’ (Figure 1) that is ecology (Figure 2) deserves more active and explicit attention. A description of what the science of ecology is and its need for scientific unification provides important context for such attention.
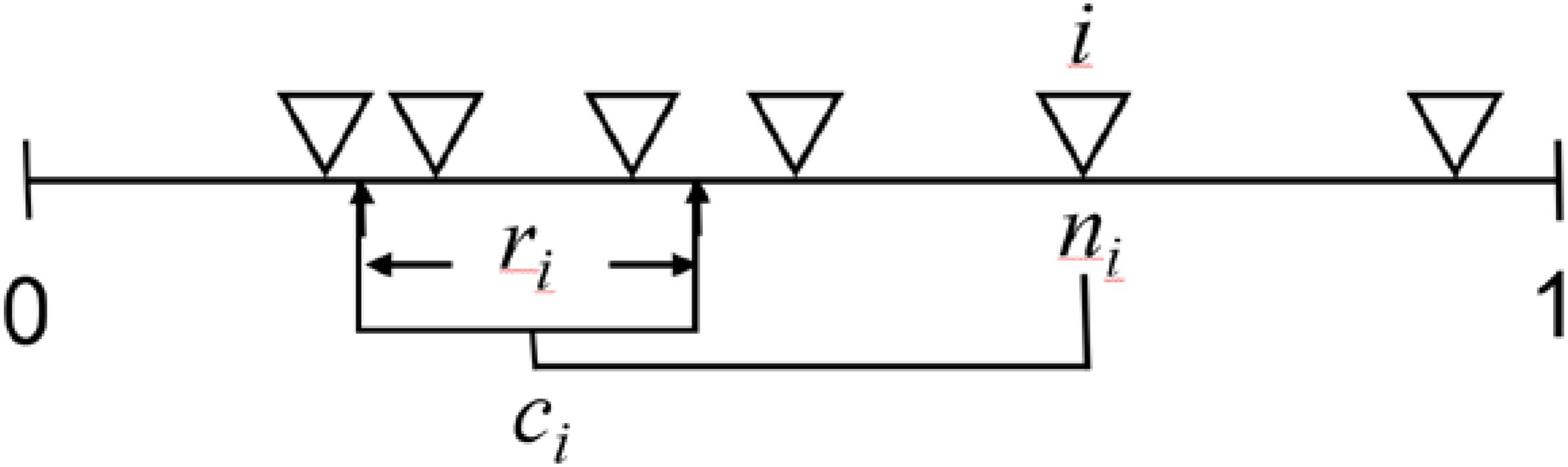
Figure 3. Diagram of the niche model from Williams and Martinez (2000). This model formalizes the theory that the primary mechanisms responsible for food-web structure are the bioenergetic processes that create a trophic hierarchy based on autotrophs from herbivory through omnivory and carnivory and biophysical processes that constrain consumers to feed on species within a contiguous section of this hierarchical niche space. The one-dimensional axis from 0 to 1 represents this community niche space. The model’s two input parameters are the number of species (S) and complexity in terms of directed connectance (C = # of links/S2). Each of S species (e.g., S = 6, each shown as ∇) is assigned a random “niche value” (ni) drawn uniformly from the interval [0,1]. Species higher on axis tend to be at higher trophic levels than species lower on the axis because species i consumes all species within a range (ri) that is placed by uniformly drawing the center of the range (ci) from ri/2 to the lesser of ni or 1- ri/2. This placement keeps all of ri on the niche axis and permits looping and cannibalism by allowing up to half ri to include values ≥ ni. Species lower (higher) on the axis tend to be more specialized (general) because the size of ri is assigned by using a beta function to randomly draw values from [0,1] whose expected value is 2C and then multiplying that value by ni, expected E(ni) = 0.5, to obtain the desired C. A beta distribution with α = 1 has the form f(x| 1,β) = β(1-x)β−1, 0 < x < 1, 0 otherwise, and E(X) = 1/(1 + β). In this case, x = 1-(1-y)1/β is a random variable from the beta distribution if y is a uniform random variable and β is chosen to obtain the desired expected value. This form was chosen for of its simplicity and ease of calculation and it provides for a large number of different network structures similar to the number expected due to maximizing entropy (Williams, 2010). The fundamental generality of species i is measured by ri. The number of species falling within ri measures realized generality. The species with the lowest niche value and other species who happen to have no species that fall within their feeding range are assigned to the first trophic level. Assuming species tend to be larger than their resource species, the niche model gives rise to allometric degree distributions where larger bodied species tend to be at higher trophic levels, more generalized, and have fewer consumer species than species at lower trophic levels. Such degree distributions have been found to be highly stabilizing which allows for coexistence for many more species than food webs without such degree distributions (Brose et al., 2006b; Otto et al., 2007; Kartascheff et al., 2010; Digel et al., 2011; Yan et al., 2017). Overall, the niche model has been widely used to generate realistically structured and dynamically stable food webs while developing and testing allometric trophic network theory.
BOX A | Allometric trophic network (ATN) theory’s master equations.
ATN theory asserts that population size is primarily determined by balancing losses to consumers and metabolic costs with gains from autotrophic production and heterotrophic food consumption. As such, the architecture of consumer-resource interactions among species and their rates of resource consumption and production are the central focus of ATN theory. This core theory is formalized as a set of ordinary differential equations (ODEs) originally developed and applied to a 2-species food chain (Yodzis and Innes, 1992), and later extended to n-species (Williams and Martinez, 2004a; Williams et al., 2007), plant nutrient dynamics (Brose et al., 2005a, b), and then further extended to include age-structured populations (Kuparinen et al., 2016), nutrient recycling through detritus (Boit et al., 2012), growth inefficiencies (Boit et al., 2012; Kath et al., 2018), and pollinator’s reproductive services to plants (Hale et al., 2020). The following ATN equations and description was developed for fisheries applications (Kuparinen et al., 2016) and lacks the explicit dynamics of plant nutrients. These equations and several key parameter values are presented to describe their basic structure as well as their flexibility in being developed for different applications e.g., the addition of population structure needed for modeling fishing pressure on adults within populations. These three ODEs model the dynamics of (1) producers, (2) consumers, and (3) detritus:
where B refers to the matrix of all biomasses, Bi is the biomass of species i; ri is intrinsic growth rate of producer i, Gi(B) is logistic growth [1−(∑j = producersBj)/K] where carrying capacity K is shared by all autotrophs; si is the fraction of exudation and/or exfoliation; xi is the mass-specific metabolic rate of consumer i usually estimated by allometric scaling; yij is the maximum consumption rate of species i feeding on j; and eji is the assimilation efficiency describing the fraction of ingested biomass that is actually assimilated; fm is the fraction of assimilated carbon respired for the maintenance of basic bodily functions; and fa is the fraction of assimilated carbon that comprises consumers’ net biomass production (1- fa is respired). Fij (B) in Eqn. 3 is the consumers’ normalized functional response
where ωij is the relative prey preference of consumer species i feeding on resource species j; qij = 1.2 which forms a relatively stable functional response intermediate between the Holling Type-II and Type-III functional responses (Williams and Martinez, 2004b); B0ij is the half saturation constant of resource species j at which consumer species i achieves half its maximum feeding rate on species j; dkj is the coefficient of feeding interference of species k with i while feeding on species j; pik = the fraction of resource species shared between species i and k. dkj also accounts for prey resistance to consumption that may increase with increasing abundance of consumers of species j. The fishing mortality of the fully selected individuals (Fmax) depends on age-specific fishing selectivity (Sage). For fish juveniles (age = 1) and larvae (age = 0) as well as all the organisms that are not fished, Sage = 0. For fish 2 years or older (age > 1), selectivity varies logistically according to Sage = 1/[1 + e-2(age-ageF50)] (Sage is 0.12, 0.50, and 0.88 for age-classes 2, 3, and 4 years and older, respectively), where ageF50 is the age at which 50% of individuals each year are caught and was set to 3 years for two fish species (Kuparinen et al., 2016). This selectivity scenario was chosen to mimic the standard attempt of fisheries management (and gear regulations) to set targets for fishing pressure so that fish may adequately reproduce prior to being caught. See Kuparinen et al. (2016) and Bland et al. (2019) for treatment of intraspecific variation among different life stages of fishes.
Ecology and Scientific Unification
A straightforward definition of ecology is a biological science focused on the study of organisms interacting within their environment (Odum, 1969). This defines ecology and its focus on interacting organisms much like cellular and molecular biologists define their discipline as the study of biological cells and their molecules and physiology defines itself as the study of organisms and their parts. While including environment in definitions of ecology may seem gratuitous, such inclusion emphasizes that ecology’s focal entities, i.e., organisms, appear more exposed to, and driven by, the spatial and temporal variation in their abiotic environment than are organisms’ physiological and molecular components whose biotic environment helps buffer these components from such variation. The influential Cary Institute extends ecology’s focus to this abiotic variability by defining ecology as: “The scientific study of the processes influencing the distribution and abundance of organisms, the interactions among organisms, and the interactions between organisms and the transformation and flux of energy and matter” (Cary Institute Definition of Ecology, 2019). While this broad definition usefully emphasizes abiotic processes such as climate and hydrological mechanisms, ATN theory focuses on the biological core of ecology involving interacting organisms and then considers abiotic and other mechanisms beyond simple forcing functions as interdisciplinary extensions beyond this core.
However defined, few see ecology as scientifically unified (Scheiner and Willig, 2008) and instead many see ecology as “a mess” (Lawton, 1999; Vellend, 2010) with only a “few fuzzy generalizations” (Simberloff, 2004). To some, this suggests that ecologists should embrace the “elegant chaos” of ecological systems along with the “non-predictive side of their science” (Anonymous, 2014) that purportedly achieves understanding without the power to successfully predict (Pickett et al., 2010). Such perspectives effectively set ecology, especially community ecology, not only apart from other biological disciplines but also apart from natural sciences in general and what distinguishes science from other social activities (Evans et al., 2012). Eschewing such exceptionalism, ecology needs scientific synthesis and predictive success simply because it is our mission as scientists to create and test generally predictive theory about the entities we study (Evans et al., 2013; Marquet et al., 2014). Physics achieved it with Newton’s laws of motion. Chemistry achieved it with the periodic table of elements. Molecular biology achieved it with the transcription and translation paradigm. Evolutionary biology achieved it with Darwin’s theory of natural selection. In each of these cases, an evolving theoretical core has been identified that synthesizes and clarifies the nature of vast swaths of the entities each discipline studies and the mechanisms responsible for the behavior of these entities. Such rigor and understanding allows these disciplines to generally understand and precisely predict phenomena within their domains from the creation of the universe to healing humans from inherited diseases. Few would claim that ecology has achieved such scientific success but a good first step may be more fully acknowledging the success it has achieved (Scheiner and Willig, 2008).
Scientific unification is perhaps best indicated by theory that achieves both broad and precise predictive power within a discipline’s domain (Kitcher, 1989). Given this perspective, humans have already achieved much ecological understanding as indicated by the incredible success of humans in becoming the most abundant and widely distributed animal species on the planet (Bar-On et al., 2018). We have achieved this by developing an increasingly powerful theory of consumer-resource interactions among organisms within many different environments. Indeed, we define our earliest societies in terms of these interactions as hunter-gatherers. These societies developed sophisticated understanding of interactions among organisms and the environment that determine the distribution and abundance of organisms that they consumed and were consumed by. This understanding critically included creating and manipulating fire as a means of increasing the variety and palatability of humans’ food and of protecting humans from predation. Early human societies also used fire as a means of increasing the abundance of their food by burning forests and grasslands in order to provide more resources for our prey and clear habitats of hiding places for our predators. Our understanding of consumer-resource theory continued to progress through the development of agriculture and the green revolution through to current advances in epidemiology, vaccines and other medicines that help prevent our microbial consumers from decimating our populations.
This is all to say that purported limits to ecological understanding appear unduly limited (Scheiner and Willig, 2008) by a myopic and somewhat narcissistic focus on the last century or less of what western science explicitly labels as “ecology” but exclusive of much of that within its defined domain of organisms interacting within the environment. While our understanding lacks much of the rigor and general precision that theory has achieved in other physical and biological sciences, our perhaps excessive fitness suggests that what ecology may not lack is basic understanding of which mechanisms are responsible for the structure and function of ecological systems including the distribution and abundance of organisms. Such basic understanding of physics was held by farmers before Newton who knew the force of two horses could carry a cart up a hill faster than one horse. Similarly, humans centuries ago knew well how interacting organisms maintain themselves within their environment and accurately predicted the behavior of organisms based on mechanistic understanding of consumers and their resources. Beyond this broad and somewhat imprecise yet powerful understanding of the critical need for organisms to consume essential resources, the lack of a rigorous theory that formalizes consumer-resource or other mechanisms into a more general and precisely predictive framework is what distinguishes ecology from more unified sciences.
Allometric Trophic Network Theory to the Rescue?
Allometric trophic network (ATN) theory pursues such rigor and synthesis by asserting that the mechanisms responsible for the basic structure (Figures 2, 3) and dynamics (Box A) of ecological networks concerning trophic hierarchy from plants through carnivores and their feeding niches can be described in terms of “simple rules [that] yield complex food webs” (Williams and Martinez, 2000). A theory of network dynamics was built upon this simple theory of network architecture (Williams and Martinez, 2004b) by pursuing the strategy of a relatively simple bioenergetic theory whose “ultimate goal is to use these consumer-resource models as building blocks … for more complicated systems involving many interacting species” (Yodzis and Innes, 1992, p. 1152). This strategy was pursued both theoretically (Williams and Martinez, 2000; Brose et al., 2006b; Martinez et al., 2006; Otto et al., 2007; Schneider et al., 2016) and empirically (Dunne et al., 2008, 2013; Berlow et al., 2009; Boit et al., 2012; Banks et al., 2017; Jonsson et al., 2018; Curtsdotter et al., 2019). Theoretically, it built upon broader mechanistic consumer-resource theory of few interacting populations (Rosenzweig and MacArthur, 1963; Yodzis and Innes, 1992; Holland and DeAngelis, 2010; Lafferty et al., 2015) by scaling up such interactions to many species within whole systems represented as complex networks (Pascual and Dunne, 2006; Thompson et al., 2012). This formalizes relationships among diverse populations and different ecological subdisciplines while describing an overall vision of the ‘elephant’ that unifies the different parts studied by different ecologists (Figure 2). This vision is, given the essential metabolic requirements for life, that a network of the consumer-resource relationships forms a more general and precisely predictive framework for understanding organisms interacting within their environment. Philosophically, this vision holds that “The key to prediction and understanding lies in the elucidation of mechanisms underlying observed patterns” (Levin, 1992, p. 1943). Conceptually, ATN mechanisms involve networks with more or less contiguous diets hierarchically structured according to trophic level (Williams and Martinez, 2008) and body-size (Dunne et al., 2013; Brose et al., 2019a) whose consumer-resource interactions proceed largely at metabolically determined rates with consumption rates saturating at high levels of resource abundance (Yodzis and Innes, 1992; Williams et al., 2007). The tractability and empirical base of this vision rests on the major efforts ecologists focus on identifying organisms along with their body sizes and interactions within practically all habitats ecologists study. Broad agreement among ecologists about organisms and their interactions facilitates frequent and relatively consistent collection of these data. For example, ecologists generally aggregate organisms into functionally or taxonomically identified populations (Martinez, 1991), record their body size and type (e.g., vascular plant, vertebrate endotherm, etc.), and typically link these aggregates according to their consumer-resource interactions. The links most often document direct feeding interactions (McCann, 2011) between prey and their predators, plants and their herbivores and mutualistic partners (Bascompte and Jordano, 2013), and other biophysical consumer-resource interactions responsible for negative (Tilman, 1982; McPeek, 2019) and positive (Bruno et al., 2003; Holland and DeAngelis, 2010) effects species have on one another. Such general agreement about the nodes and links increases the rigor of quantitative comparison of ecological networks among almost all habitats (Figure 2) by increasing methodological consistency among the data compared. A major challenge to the completeness of such data involves the “dark matter” of biodiversity comprised of microbes that are invisible to the naked eye and feed without engulfing (Purdy et al., 2010; Weitz et al., 2015). Still, this is a unifying challenge, at least methodologically, due to the presence of microbes in all habitat types and the ability of tools such as protein sequencers to similarly address the challenges among these different environments (Purdy et al., 2010; Pompanon et al., 2012; Nielsen et al., 2018).
Based on such broad insights and consistencies among ecologists and ecological systems, food webs, the most iconic of ecological networks which depict organisms’ roles within the architecture of feeding relationships relative to primary producers, have long formed a fundamental cornerstone of ecological thought (Dunne, 2006). From their embrace in one of the first texts in ecology (Elton, 1927) which emphasized trophic levels and pyramids throughout the development of ecology including its current resurgence as complex ecological networks integrated with metabolic ecology (Humphries and McCann, 2014) and engagement with network science (Dunne et al., 2002a; Newman, 2010; Barabási, 2012), the trophic relationships that comprise food webs have been central to addressing major ecological questions. These questions addressed diversity and stability (May, 1973; McCann, 2000; Brose et al., 2006b; Stouffer and Bascompte, 2010, Stouffer and Bascompte, 2011), top–down vs. bottom–up control (Power, 1992; Schneider et al., 2016), trophic levels (Cousins, 1987; Williams and Martinez, 2004a), trophic cascades (Polis and Strong, 1996; Wang and Brose, 2018), keystone species (Paine, 1966; Power et al., 1996; Brose et al., 2005b), biodiversity-ecosystem function (Naeem et al., 1994; Martinez, 1996; Loreau, 2010; Cardinale et al., 2012; Thompson et al., 2012; Miele et al., 2019), and tipping points (Barnosky et al., 2012).
Food webs play such central roles largely because the first principles and foci embraced by food-web research are also central to the major subdisciplines of ecology (Box B). Two of these principles are: (1) organisms require energetic and other resources to live, grow and reproduce and, in fulfillment of these needs, (2) organisms consume other organisms and their products. Organisms’ physiology, behavior, and abundance largely determine rates of consumption and population growth. In order to specify these rates, the metabolic theory of ecology (Brown et al., 2004; Humphries and McCann, 2014) has been integrated with trophic network theory by using body size to assign metabolic maintenance costs and maximum consumption and production rates to populations within the networks. ATN theory multiplies these rates by the biomass (Brose et al., 2006b) or numerical abundance (Schneider et al., 2016) of species’ populations processing and interacting at these rates in order to generate a systems-level predictive understanding of population, energetic, and nutrient dynamics within ecosystems (Lindeman, 1942; Chapin et al., 2011; Boit et al., 2012).
BOX B | Organizational levels integrated with ecological networks.

The central concepts and principles involving feeding interactions and food webs have motivated a synthesis of network and consumer-resource theory (Martinez, 1995; Thompson et al., 2012) that integrates organismal (Holland and Deangelis, 2009), population (Turchin, 2003), community (Bascompte, 2009) and ecosystem ecology (Getz, 2011, Box B). The synthesis also integrates subdisciplines focused on trophic interactions within different aquatic and terrestrial habitats and among different organisms involving plant-animal, predator-prey, parasite-host, and pathogen-host interactions and also involving symbiotic relationships such as those between plants and fungi and between plants and pollinators (Martinez, 1995; Hale et al., 2020). Such synthetic integration is achieved in no small part by quantitative comparison of the architecture of trophic interactions in terms of network properties (e.g., Cohen, 1978; Bascompte et al., 2003; Dunne et al., 2013) that describe distributions of specialists and generalists, food chain lengths, degrees of separation, relative prevalence of motifs, along with the flows within this network structure (Shurin et al., 2006) that can be surprisingly well estimated from network structure alone (Williams and Martinez, 2004b; Carscallen et al., 2012). Beyond this pervasive core including virtually all types of organisms within all types of habitats, research on ecological networks extends consideration of consumer-resource interactions to evolutionary scales (Martinez, 2006; Dunne et al., 2008; Allhoff and Drossel, 2013, 2016; Allhoff et al., 2015a; Edger et al., 2015; Romanuk et al., 2019) and plant-nutrient (Brose et al., 2005a), reproductive (Hale et al., 2020), and other non-feeding interactions (Kéfi et al., 2012).
ATN theory builds upon major advances in ecology over the last half century that, in contrast to much of that progress that has led to increasingly disparate subdisciplines (Martinez, 1995; Loreau, 2010), weaves the disparate threads back together into a more coherent fabric (Thompson et al., 2012). This fabric illustrates, for example, how fisheries dynamics, infectious disease epidemics, competition and mutualism among plants and animals may be understood as different parameterizations and functional forms of consumer-resource interactions (Holland and DeAngelis, 2010; Lafferty et al., 2015) that comprise food webs and their more broadly powerful offspring; ecological networks (Pascual and Dunne, 2006) that also include non-feeding interactions such as plant nutrient consumption (Brose et al., 2005b), ecosystem engineering (Kéfi et al., 2012), and reproductive services (Hale et al., 2020). Such research has shown how scientific feats once thought difficult or impossible have been achieved (Box C). For example, the unlikely stability of many species coexisting within complex ecosystems appears largely due to allometric degree distributions (Brose et al., 2006b; Otto et al., 2007; Gross et al., 2009) where species’ generality (number of species eaten) increases and vulnerability (number of consumer species) decreases with increasing body size and trophic level (Figure 3) combined with non-linearities in feeding behavior (Williams and Martinez, 2004a; Hale et al., 2020) from which increases in highly stabilizing intraspecific competition (Chesson, 2000; Chesson and Kuang, 2008) emerge (Kartascheff et al., 2010). Also, while ecologists have argued that even a field guide to which species may strongly interact with others may be permanently out of reach (Power et al., 1996), ATN theory has gone much further by accurately predicting interaction strength (Paine, 1992) including how much the experimental removal of a species alters the abundance of other species in field (Berlow et al., 2009) and lab (Jonsson et al., 2018; Curtsdotter et al., 2019) experiments. For example, ATN theory accurately predicted that the effects of removing a species on the abundance of a species remaining a field experiment is a simple function of biomass of the two species and the body mass of the removed species (Berlow et al., 2009). ATN theory has also shown how verbal theory describing the classic seasonal population dynamics of complex lake ecosystems as well as their component populations (Sommer et al., 2012) may be surprisingly well quantified and forecasted (Boit et al., 2012). This paves the way for direct application to ecosystem management of fisheries (Martinez et al., 2012; Gilarranz et al., 2016; Kuparinen et al., 2016). Important steps in this direction includes disentangling different ecological, evolutionary and economic causes of the destabilization of fished populations and their ecosystems by fishing (Gilarranz et al., 2016; Kuparinen et al., 2016) as well has how thermal stress and (Gilarranz et al., 2016) and environmental noise (Kuparinen et al., 2018) affects fishery and other ecosystems. Finally, consumer-resource network theory has helped resolve prominent debates regarding the implications of observed network architecture for the stability of mutualistic networks (Valdovinos et al., 2016) and ecosystems (Hale et al., 2020) while successfully predicting novel foraging behavior of pollinators in the field (Valdovinos et al., 2016). This suggests that, well beyond agreement about the centrality of a conceptual framework, a substantial body of evolving theory is steadily advancing toward a simultaneously general, accurate and precise understanding and prediction of the structure and function of complex ecological systems. The following discussion of the foundations, current status, and future directions of ATN theory helps illuminate these claims further and the basis for making them.
BOX C | Allometric trophic network milestones.

Allometric Trophic Network Theory, Past and Present
Conceptual Foundations
Allometric trophic network (ATN) theory asserts that that the behavior of ecological systems is primarily determined by the organismal production and consumption of resources that provide the energy organisms require to live, grow and reproduce. Central to this theory is the network structure of consumer-resource interactions, especially the feeding interactions needed to supply organisms’ metabolic requirements, that form food webs. This focus on the production and consumption of food forms a more narrow conceptual core than do other broad theories of ecology (Reiners, 1986; Scheiner and Willig, 2008; Vellend, 2010) while also answering Reiners’s (1986) call for a theory of causal networks of population interactions to complement energy and matter theories of ecosystems. Extending beyond this core are other often limiting resources such as various services that organisms produce. These include services consumed by plants such as the reproductive services of pollinators and seed dispersers as well as nutrient provisioning services produced by mycorrhizal fungi and other detritivores (Hale et al., 2020). Other services consumed by a fuller range of organisms include habitat provisioning services produced by ecosystem engineers such as beavers, coral, and trees (Jones et al., 1994; Kéfi et al., 2012). The emerging broad interest in multiplex networks in the general field of network science may contribute much to understanding how diversity types of links affect ecological networks (Kéfi et al., 2017; Pilosof et al., 2017; Barner et al., 2018) and continue the practice of network science (Barabási, 2012) of contributing to, and benefiting from, research on ecological networks (Dunne et al., 2002a; Williams et al., 2002) including their controllability (Liu et al., 2011; Li et al., 2017; Jiang and Lai, 2019) and resilience (Gao et al., 2016).
Whereas the network architecture of consumer-resource interactions constitutes much of the structure of ecological systems formalized by ATN theory (Figure 3), the function of these networks is largely determined by the dynamics of the closely related rates of metabolism, production and consumption of organisms engaged in the consumer-resource interactions depicted by the network’s structure (Figures 2, 3). Given the diversity and complexity of these networks, ‘allometric’ merely refers to role of body size in constraining feeding relations such as those among predators and prey (Brose et al., 2019a) and hosts and parasites (Dunne et al., 2013) and the tactical decision to embrace the metabolic theory of ecology (Brown et al., 2004) by using organismal traits including body size and type (e.g., invertebrate) as the most general, powerful, and efficient way of estimating metabolic rates in lieu of more direct measurements when unavailable or inconvenient. Similarly, the niche model (Figure 3) is typically used to estimate realistic food web architectures (e.g., Domínguez-García et al., 2019) in lieu of more direct observations of particular food webs (Boit et al., 2012) and food web patterns (Riede et al., 2010). Several prominent variants of the niche model with different strengths and weaknesses (Martinez and Cushing, 2006; Williams and Martinez, 2008) have also been created that elucidate roles of body size (Beckerman et al., 2006; Petchey et al., 2008; Williams et al., 2010; Allhoff et al., 2015a; Schneider et al., 2016), phylogeny (Cattin et al., 2004; Stouffer et al., 2012; Allhoff et al., 2015a) and the contiguity of feeding niches (Stouffer et al., 2005, 2011; Allesina et al., 2008; Williams and Martinez, 2008; Williams et al., 2010) in generating empirically observed food webs. While the genesis of ATN theory began with allometrically scaled metabolism and feeding operating within networks structured according to the niche model, ATN theory is not restricted to these simple origins and continues to develop well beyond them.
Key to such development is the basis of ATN theory on the two previously mentioned principles of biology that provide a mechanistic foundation for integrating the several scales and organizational levels from organisms to ecosystems. Those principles include organisms’ need for energy and other resources and the production of those resources by organisms. These two principles locate a basic foundation of ATN theory primarily at the physiological level of metabolism as determined by fundamental biochemical reactions such as photosynthesis and the Krebs cycle which create biochemical energy and controls the ability of organisms to live and the rates that they can function. These functions include consumption, production, movement, and reproduction. While the physiology of metabolism both enables and constrains the basic ability for these functions to occur, organismal behavior mediates this potential by largely determining how much of the potential is realized. Compared to physiology, behavior also more clearly drives the production of services such as reproductive services performed by pollinators (Hale et al., 2020) and habitat modification performed by ecosystem engineers (Jones et al., 1994). By aggregating organismal behaviors among organisms, ATN theory scales up physiological and organismal behaviors to the population level in order to determine population dynamics and abundance. By focusing on consumer-resource relationships between populations coexisting within a habitat, ATN theory scales up populations and their interactions to the community and ecosystem levels. Whereas community ecology often focuses on the diversity and nature of interactions among populations, ecosystem ecology focuses on the stocks and flows of energy and nutrients involved in these interactions (Loreau, 2010). ATN theory scales up population ecology to both community and ecosystem levels by focusing on the biomass of populations typically measured in units of carbon that can be simply converted into the number of organisms in a population using the distribution of body sizes of organisms within a population (Thompson et al., 2012). While these distributions are typically characterized by the mean body size of adults, more sophisticated measures that account for the abundance of immature individuals may also be used. Populations of different organisms may be aggregated or otherwise summed at will to match the functional foci of ecosystem ecologists (e.g., plant, herbivore, omnivore, carnivore, decomposer, etc.) and phylogenetic foci of community ecologists (e.g., species, family, order, etc.) as well as combinations of these foci (e.g., bacterial decomposers, insect pollinators, fungal symbionts, etc.). The seamless integration of community and ecosystem ecology based on physiological, behavioral, and population mechanisms forms one of the most powerful contributions of ATN theory (Reiners, 1986; Thompson et al., 2012).
Antecedents and Chronology of ATN Theory
ATN theory has its beginning over a half century ago in theory about the structure and dynamics of food webs that were first described at least a century ago (Dunne, 2006). Early theory held that more links stabilized these networks by providing more options for resources to reach consumers if a particular species within a food chain was disrupted by drastically decreasing in abundance or going extinct (MacArthur, 1955). Later theory held that additional links increases the probability of positive feedback loops which would destabilize ecological networks such as food webs (May, 1972). Key to such considerations is the scaling of links with species diversity within such networks. Large increases of links with increased diversity increases niche overlap in consumer-resource networks. As Darwin (1859) and then Gause (Hardin, 1960) articulated, increased overlap could increase resource competition which could cause less fit species to go extinct. Such theory motivated the search for how linkage patterns in food webs within compilations of food webs from different habitats might alleviate such risks (Cohen, 1978). A key finding among these data was a constant “scale-invariant” ratio of the number of links per species in terms of feeding links per network node (Pimm et al., 1991). Such constancy causes network complexity in terms of the faction of all possible links or directed “connectance” (links per species2, Martinez, 1992) to hyperbolically decrease as the number of species increases. This decrease helps to avoid destabilizing effects of increasing links with the number of species on ecological networks (May, 1972). This pattern also inspired an elegant theory of food web structure that proposed a trophic hierarchy of species where species on average ate a fixed number of species below them on the hierarchy (Cohen et al., 1990). As such, a first generation (Dunne, 2006) of mechanistic theory was established by which the dynamic processes of population variability and trophic energy transfer led to a food-web pattern that avoided destabilizing effects of positive feedbacks and competitive exclusion and allowed complex ecosystems with many species to persist (Pimm et al., 1991).
This initial generation of food-web research led to a new generation first of food-web data and then of food-web theory (Dunne, 2006). The new and improved data exhibited more complexity with new “scale-dependent” theory being generated to better explain and predict this complexity (Martinez, 1994). Perhaps most significantly, the second generation data exhibited much more rapid increases of links as species richness increases leading to the “constant connectance hypothesis” (Martinez, 1992) which challenged the first generation’s “link-species scaling law” (Pimm et al., 1991) by asserting links increased approximately as the square of species diversity. This new pattern and others motivated new generation of theory asserting a trophic hierarchy that was more relaxed than the earlier one (Cohen et al., 1990) where species on average ate a fixed fraction of species within a contiguous range (Cohen, 1978) of the hierarchy that were on average below the consumer (Williams and Martinez, 2000). The relaxation accommodated previously excluded processes such as cannibalism and loops in food chains while the contiguity added mechanisms associated with physiological constraints such as digestive capabilities or gape size which forces species to consume resources within a contiguous range of trophic levels or body sizes, respectively (Figure 3). This second generation “niche model” (Figure 3) much more precisely predicted a much wider range of network properties in improved second generation food-web data (Dunne, 2006; Williams and Martinez, 2008). These data include ancient food webs over a half billion years old back in the Cambrian (Dunne et al., 2008) and other food webs including the many parasite species typically excluded from earlier data (Dunne et al., 2013). While this second-generation theory based on the mechanisms of trophic transfer and physiological constraints greatly increased the precision and generality over that of the first generation, the conflict between the dynamical considerations of the first-generation theory and the complexity of second-generation data had yet to be addressed.
Much of the first generation theory of ecological network dynamics (May, 1973) was based on representing direct and indirect interactions between two species as interspecific effects. For example, direct effects of a predator on a prey are typically negative and that of a prey on a predator are positive while indirect interactions such as competition between two species consuming a common resource are often considered direct negative effects both species have on each other (McPeek, 2019). A second generation of network dynamics emerged from avoiding such phenomenological representations and instead focusing on more easily measured and estimated processes such as consumer-resource interactions (Yodzis and Innes, 1992) between predators and prey from which intraspecific and interspecific effects emerge. This later generation scaled up these consumer-resource interactions into complex networks to discover the stabilizing effects of realistic foraging behaviors (Williams and Martinez, 2004a), network structure (Martinez et al., 2006), and body-size ratios between consumer and resource species (Brose et al., 2006a, 2019a). Rather than stability emerging from limiting niche overlap by decreasing connectance while increasing diversity (Pimm et al., 1991), second generation theory found that allometric degree distributions stabilized networks with high niche overlap (Williams and Martinez, 2000, 2008), complexity, and diversity (Brose et al., 2006b; Otto et al., 2007). These large overlaps in trophic niches and degree distributions where larger bodied species at higher trophic levels had fewer consumer species and more resource species than smaller bodied species at lower trophic levels (Cohen et al., 2003) emerge (Figure 3) from the constraints of hierarchy and contiguity in the niche model (Williams and Martinez, 2000, Williams and Martinez, 2008; Stouffer et al., 2011). Highly but not completely contiguous feeding niches that enhance overlap also enhance stability (Yan et al., 2017; Romanuk et al., 2019). Rather than achieving stability by simply limiting the number of interactions, ATN theory arranges many more interactions in more precisely described locations among species with varying body sizes which explains the remarkable stability of realistically structured networks over more randomly structured networks (Brose et al., 2006b; Martinez et al., 2006; Kartascheff et al., 2010).
Compared to the difficulty of measuring competition coefficients (Hart et al., 2018; Ellner et al., 2019), the relative ease of measuring consumer-resource interactions such as metabolic and consumption rates (Brose et al., 2008; Vucic-Pestic et al., 2010; Marx et al., 2019) and the even easier estimation of the rates of these interactions based on body size (Brose et al., 2006b, 2019a; Otto et al., 2007) opened up a wide range of ecological research to be addressed by ATN theory (Box C). Key to this increased breadth is parameterizing maximum feeding rates as a multiple of metabolic rate which appears surprisingly constant among organisms within metabolic groups such as invertebrates and ectotherm and endotherm vertebrates (Yodzis and Innes, 1992; Williams et al., 2007). Such rates indicate, e.g., that invertebrates may generally consume a maximum of eight times their metabolic rate over the long term while ectotherm vertebrates are limited to consuming only four times their metabolic rate (Brose et al., 2006b). Basing ATN theory on metabolic rates enables ATN theory to leverage the chief focus of the metabolic theory of ecology (Brown et al., 2004) i.e., the relationship between body size and metabolic rate, to vastly reduce the parameter space and focus it more specifically on complex networks of consumer-resource interactions found in nature (Hudson and Reuman, 2013). A key fulcrum of this lever is the observed body-size ratios between consumer and resource species (Brose et al., 2019a) broadly suggesting regularities such as invertebrate predators being an order of magnitude larger than their prey while vertebrates tend to be two orders of magnitude larger (Brose et al., 2006a, b, 2019a). Once the body size and type and therefore the metabolic rate of species at the base of the food web are set, combining these ratios and their huge variability (Brose et al., 2019a) with the structure of the food web generates fully and realistically parameterized networks for further research. Computational experiments that removed species from these networks enabled ATN theory to elucidate how traits of species generally affect the impacts of their loss (Brose et al., 2017), and more specifically predict the population dynamics (Curtsdotter et al., 2019) and quantitative effects of species removal experiments observed in the field (Berlow et al., 2009) and the lab (Jonsson et al., 2018) as well as help develop less empirically demanding methods for predicting such effects (Eklöf et al., 2013). Similarly, ATN species-invasion experiments helped generate empirically corroborated theory predicting generalists with few predators more effectively invade ecological networks and that low-connectance networks are more susceptible to species invasions while high-connectance networks experience larger extinction cascades resulting from the invasions (Romanuk et al., 2009, 2017) as well as other predictions of how temperature and species’ traits affect food web assembly (Gounand et al., 2016).
Other key advances in ecological theory build upon ATN theory’s synthesis of community and ecosystem ecology by elucidating effects of biodiversity on ecosystem function (Schneider et al., 2016; Miele et al., 2019). Having largely been confined to a single trophic level in terrestrial systems, primarily vascular plants (Hector and Bagchi, 2007), ATN theory has advanced such early research on biodiversity and ecosystem function to a much fuller range of organisms at many trophic levels (Schneider et al., 2016; Miele et al., 2019). Such advances emphasize that the way ecological systems function is determined much more by how their parts interact than the number of types of parts they have. That is, while many correlations between the number of nodes in a network and the network’s function are evident, the mechanisms responsible for the correlation intimately involve the interactions among the nodes rather than the mere existence of the nodes (Cardinale et al., 2012).
Early biodiversity and ecosystem function research embraced this mechanistic premise by explaining positive biodiversity-ecosystem function correlations as a result of the complementarity of resource use that may occur when more plant species with different resource needs and consumption strategies inhabit an ecosystem (Cardinale et al., 2012). However, such interactions involve a very limited albeit critical part of the much larger networks that comprise complex natural ecosystems. Classic theory about plant communities asserts the species best able to consume the most limiting shared resource out competes other species and therefore excludes them from the community (Tilman, 1982). Higher trophic levels could prevent such loses of biodiversity by preferentially feeding on competitive dominants (Paine, 1969) or, more generally, if the dominants exchanged their high growth rates for increased vulnerability to consumers (Chase et al., 2002). However, such preferences and tradeoffs proved unnecessary to maintain coexistence in ATN networks (Brose, 2008). Instead, preference-free consumers of resource species free of growth-vulnerability tradeoffs are sufficient to maintain coexistence within realistically structured food webs (Brose, 2008). A broad density-dependent dynamic emerges whereby abundance is its own enemy and rarity is its own refuge respectively due to “kill-the-winner” dynamics among abundant organisms (Thingstad, 2000) and “ignore-the-scraps” dynamics among consumers of rare species very few of which are single species specialists (Srinivasan et al., 2007). Such insights and dynamics allow ATN theory to more simply and rigorously address biodiversity and ecosystem function of a much larger proportion of ecological diversity without parameterizing or even asserting preferences or tradeoffs (Schneider et al., 2016). Recent advances in ATN theory employing these insights find support for a “vertical diversity hypothesis” that asserts increasing the trophic levels of species along with maximum body sizes given observed consumer-resource body-size ratios increases primary productivity within ecological networks subjected to constant inputs of plant nutrients (Wang and Brose, 2018). Such research suggests that broadly focusing on energy flux across trophic levels illuminates general consumer-resource mechanisms by which biodiversity may determine ecosystem function (Barnes et al., 2018).
Other more applied advances of ATN theory involve the structure, function, and ecosystem management of fisheries. These advances build upon some of the firmest foundations of ATN theory, especially aquatic food-web structure (Martinez, 1991, 1993b) that appears more tightly constrained by size structure due to gape limited feeding than above-ground terrestrial systems (Cohen et al., 2003, 2005; Brose, 2010; Brose et al., 2019a). Another important contribution to such work is the sociological factor of aquatic ecologists synergistically focusing on particular systems such as certain lakes or ocean areas explored by large research vessels. Terrestrial researchers appear more able and willing to diffuse their focus among many geographically dispersed systems due to their relative ease of access. This distinction results in more holistic empirical and theoretical research on particular aquatic ecosystems including viruses to vertebrates compared to terrestrial research. Systems such as Lake Constance north of the European Alps illustrate this phenomenon well. For example, study by the lake’s phytoplankton, zooplankton, and fish ecologists have resulted in multiple decade-long time series of the population abundances of dozens of these species observed every 2 weeks or less (Boit and Gaedke, 2014). An ATN model parameterized by the observed network structure and allometrically estimated metabolic rates of the organisms successfully simulates the overall seasonal dynamics of species’ abundance and production within the lake’s complex food web (Boit et al., 2012). Further development of this model to include ontogenetic size structure of fishes enabled ATN theory to illuminate how evolutionary and other mechanisms may be responsible for the increased variability of fished populations as well as the destabilization and degradation of fishery ecosystems due to fishing (Kuparinen et al., 2016; Bland et al., 2019) and how food webs buffer environmental variability (Kuparinen et al., 2018). This work shows how widely observed decreases in body size of fished populations may cause losses of ecosystem function and services that persist centuries after fishing has ceased (Kuparinen et al., 2016). Similar findings emerged from other similarly parameterized ATN analyses where fishing pressure and thermal stress decrease persistence among hundreds of simulated fisheries throughout the Caribbean (Gilarranz et al., 2016).
Extensions of ATN theory to fishery ecosystems is one of several approaches that incorporate humans into complex ecological networks. Research on a fuller range of species consumed by indigenous humans found that humans were “super generalists” in that they consumed more species than almost any other species within their food web (Dunne et al., 2016). Simulated invasions of ecological networks found that generalists were especially successful invaders that caused the most extinctions in food webs (Romanuk et al., 2009). Similar ATN studies of human-like species found reducing the fraction of super generalists’ many links to resource species that were strong links greatly reduced the number of extinctions caused by their presence in the food web (Dunne et al., 2016). This may explain traditions of seasonally restricting harvests to few of the many species that indigenous peoples consume as a management strategy to prevent such destructive extinction cascades to occur (Dunne et al., 2016). Given that current consumption of species is often driven much more by economics than human demographics, work has begun to incorporate market mechanisms into ATN models in order to better understand human effects on ecological networks and how economic policies can better manage extractive exploitation of coupled human-natural networks (Martinez et al., 2012). Initial results suggest that fished populations go extinct beyond tipping points at levels of fishing effort near levels predicted to be optimal by the logistic growth theory underlying most fisheries management and that increasing costs of fishing could cause much higher yields and revenue than predicted by logistic theory to be realized with much lower effort (Martinez et al., 2012).
Such integration of social sciences including anthropology and economics extends ATN theory to the socio-ecosystem level. This extension empowers ATN theory to mechanistically address the sustainability of socio-ecosystems where their dynamics critically depend on how human consumption and other human behaviors depend on price and the price elasticity that indicates how readily people substitute one item, e.g., hamburger, for another, e.g., salmon (Martinez et al., 2012). While ATN theory emerged from a focus on mechanisms involving biotic and abiotic material and energy, this extension to socio-ecosystems firmly integrates mechanisms involving price, capital and markets which represents information (O’Connor et al., 2019) much more than these quantities represent material or energy. As such, ATN theory incorporates a full breath of processes from biochemical reactions within cells to information about cultural predilections of human societies. Formalization of these mechanisms as complex dynamic networks enables ATN theory to effectively advance our ability to understand, predict, and potentially manage a full range of ecological phenomenon determining the ability of species including humans to thrive or whither or, more dramatically, persist or perish.
Changes in the global environment involve less direct anthropogenic impacts than the extirpation and exploitation of species due to habitat loss and fishing but these changes form perhaps the most significant threat to the sustainability of humans and other species on the planet. This threat includes both early and more recently recognized changes such as eutrophication caused by the deposition of plant nutrients in aquatic and terrestrial ecosystems and warming caused by the deposition of greenhouse gasses into the atmosphere. One of the more powerful applications of ATN theory has been to examine how these two changes, both separate and in combination, impact ecosystems. The first of such applications leveraged ATN theory’s explicit consideration of nutrient dynamics to find that eutrophication may increase interaction strength by increasing the maximum abundances of species responding to the loss of keystone predators from simple and complex food webs (Brose et al., 2005b). Higher maximum abundances enable larger changes in abundance to occur due to disturbances which often extirpate species. Later research leveraged the acceleration of metabolism by heat (Gillooly et al., 2001; Brown et al., 2004; Vasseur and McCann, 2005) to find that, while warming could conceivably just accelerate metabolism and behavior and largely leave ecosystems otherwise unaffected (Zhou et al., 2011), warming may instead decrease the efficiency of predation by increasing metabolism more than consumption (Vucic-Pestic et al., 2011) and stabilize population dynamics by increasing intraspecific interference (Lang et al., 2012). This leads to a rich range of predictions on the combined effects of eutrophication and warming depending on nutrient status and organisms involved (Binzer et al., 2016). For example, Binzer et al. (2016) found that warming may increase diversity in eutrophic systems while decreasing diversity in oligotrophic systems. They also found that body-size effects can cause warming to stabilize parasitoid-host systems while destabilizing predator-prey networks (Fussmann et al., 2014; Binzer et al., 2016). The sophistication and mechanistic bases of such ATN predictions of responses to novel environments greatly benefit from theoretically and empirically robust estimates of the effects of warming on network complexity (Petchey et al., 2010), body size (Sheridan and Bickford, 2011; Forster et al., 2012) and interactions of different rates such as nutrient supply and plant growth (Marx et al., 2019) and heat supply and feeding rates (Rall et al., 2012; Fussmann et al., 2014).
Beyond elucidating effects of separate and combined perturbations of biotic and abiotic components of ecosystems, ATN theory has elucidated system-level effects of perturbations more generally. For example, dozens of widely used measures of stability against episodic and sustained disturbances of ecosystems were recently found to map onto three largely independent dimensions of stability including “early response to pulse, sensitivities to press, and distance to threshold” dimensions (Domínguez-García et al., 2019). Such work illuminates a more integrated notion of ecological stability in general that articulates how different stability measures complement and contrast with each other when describing broader and more focused aspects of ecological responses to change. Combined with earlier investigations of how the more inherent stability of ecological networks’ ability to maintain their integrity in the absence of disturbance depends on their architecture (Brose et al., 2006b; Martinez et al., 2006), functional responses (Williams and Martinez, 2004b) and body sizes (Brose et al., 2006b; Otto et al., 2007), ATN theory provides a relatively comprehensive overview of how complex ecosystems manage to dynamically persist or not in constant and more variable environments.
One of the most significant recent advances in ATN theory has been the integration of evolutionary mechanisms into the structure and dynamics of ecological networks (Martinez, 2006; Dunne et al., 2008; Brännström et al., 2012; Ritterskamp et al., 2016b). Early work in this area employed somewhat arbitrary network structures that emerged from stochastically adding species to communities and focused on which dynamical equations and rules resulted more realistic networks structures (McKane, 2004; McKane and Drossel, 2005; Rossberg et al., 2006). More recent work (Allhoff et al., 2015a) employed ATN theory by structuring food webs according to body size and rules of the niche model (Williams and Martinez, 2000, 2008) and simulating the non-linear dynamics of the network using allometrically parameterized differential equations to calculate bioenergetic stocks and flows within the network (Brose et al., 2006b). This work formalizes phylogenetic niche conservation of trophic interactions (Cattin et al., 2004; Stouffer et al., 2012) by stochastically varying or “mutating” each species’ location and diet represented by the niche model’s three parameters describing each species’ fundamental trophic niche (Figure 3). Such work found that speciation events representing evolving species traits such as body size, metabolic rate and diet results in large realistically structured networks (Romanuk et al., 2019) with continuous turnover of species (Allhoff et al., 2015a) but little long-term changes in ecosystem function despite larger changes in functional diversity (Allhoff and Drossel, 2016). More specifically, ATN investigations (Romanuk et al., 2019) recently found that speciation results in surprisingly stable and complex networks with species sharing tightly packed feeding niches similar to empirical observations (Morlon et al., 2014; Romanuk et al., 2019) but unexpected based on competition (Ponisio et al., 2019) and more neutral (Morlon et al., 2014) theory.
Explorations of more subtle eco-evolutionary dynamics found fishing-induced evolution toward smaller and earlier maturing fishes degrades fishery yields and destabilize fished populations and their ecosystems (Kuparinen et al., 2016). Other explorations attempting to look for more dramatic changes in food webs over deep time found that food-web architecture changed relatively little over the half billion years recognizably complex ecosystems have been present on Earth (Dunne et al., 2008, 2014). Such research demonstrates the ability of ATN theory to integrate a range of evolutionary mechanisms including natural selection from seasonal (Yoshida et al., 2003; Boit et al., 2012; Hiltunen et al., 2014) to decadal (Kuparinen et al., 2016, 2018) to geologic (Dunne et al., 2008, 2014) time scales into the structure and dynamics of ecological networks.
Future Directions
While ATN theory has developed a relatively comprehensive framework for addressing complex ecological systems, much research needs to further test its predictions in order to understand and extend the limits of the framework along with its applications to pressing issues such as ecosystem management and the sustainability of human-natural systems. Key to these advances is a rich dialogue between theory and empiricism to better understand: (1) fundamental factors such as levels of network complexity (Petchey et al., 2010), metabolic rates (Kath et al., 2018; Quévreux and Brose, 2019), and consumer-resource body-size ratios (Brose et al., 2019a), (2) more nuanced behaviors such as migration and functional responses (Williams and Martinez, 2004a; Martinez et al., 2006; Williams, 2008; Heckmann et al., 2012; Rall et al., 2012; Pawar et al., 2019), and (3) more holistic comparisons between ATN models of ecosystems in computers and biological models of ecosystems in the lab (Jonsson et al., 2018; Blasius et al., 2020) and field (Berlow et al., 2009; Boit et al., 2012; Curtsdotter et al., 2019). Longer term observations of food web dynamics in the lab (Yoshida et al., 2003, 2007; Meyer et al., 2006; Blasius et al., 2020), mesocosms, and the field (Boit and Gaedke, 2014) are particularly needed. Such work helps illuminate whether and how ATN theory can effectively forecast ecosystem behaviors further into the future (Petchey et al., 2015; Brose et al., 2019b). Other important work includes refining the representation of the physiology of metabolism (Kath et al., 2018) and its sensitivity to abiotic and biotic environmental variation such as that in temperature (Vucic-Pestic et al., 2010, 2011; Rall et al., 2012) associated with climate change or the presence of predators associated with the ecology of fear (Sih, 1980; Ho et al., 2019). For example, accounting for anabolic efficiencies of biomass production appear critical to the ability to forecast complex ecological dynamics (Boit et al., 2012; Kath et al., 2018) and to predict positive effects of mutualism on the diversity, stability and functions of complex ecosystems (Hale et al., 2020). A particularly fascinating opportunity to study this may be to apply the systems biology of seagrass metabolism and production (Kumar and Ralph, 2017; Malandrakis et al., 2017) toward understanding the costs and benefits of rewarding animal pollinators (Hale et al., 2020) within these critically important marine ecosystems (Van Tussenbroek et al., 2016).
The important frontier of functional responses includes developing and testing models of how consumptive behaviors vary with the densities of resources (Gentleman et al., 2003; Vallina et al., 2014; Flynn and Mitra, 2016; Rosenbaum and Rall, 2018) and consumers of those resources (Skalski and Gilliam, 2001) as well as predators of the consumers (Sih, 1980; Schmitz and Suttle, 2001; Skalski and Gilliam, 2002) against individual based models (Katz et al., 2011) and empirical observations (Rall et al., 2009, 2012) of such behaviors. Such work helps to ensure the critically important functional responses within ATN models (Williams and Martinez, 2004b) accurately scale up the consumptive behaviors of individuals to behaviors of populations. This scaling would strongly benefit from incorporating recent advances in the allometry of organismal movement (Hirt et al., 2017, 2018) along with the preference for (Williams, 2008; Heckmann et al., 2012), searching for (Pawar et al., 2012, 2019), and handling of prey (Pawar et al., 2012, 2019) and other resources (Brose, 2010). Key to improving ATN theory in general and functional responses in specific is discovering when processes are better represented as functions, such as those representing adaptive foraging (Valdovinos et al., 2010, 2016; Heckmann et al., 2012), rather than constants. For example, ATN theory typically employs functional responses that assume constant search efficiency and handling times relative to metabolic rate whereas each process depends on temperature (Vasseur and McCann, 2005), allometry (Kalinkat et al., 2013) and whether the interactions occur in 3D environments such as pelagic and aerial habitats or 2D environments such as benthic habitats (Pawar et al., 2012, 2019). Such improvements may be unnecessary where e.g., temperature varies little, or critical e.g., when considering responses to climate warming (Binzer et al., 2016). For example, much ATN research employs logistically growing plants with a community level carrying capacity (Box A) due to its simplicity and qualitatively similar behavior to networks based on more sophisticated models of plant growth based on dynamically varying nutrient pools (Huisman and Welssing, 1999; Brose et al., 2005b). Deciding between simpler and more sophisticated theoretical treatments critically depends on the specific goal of applying all theory (e.g., Bauer et al., 2015) and ATN theory is no exception.
Further work scaling populations to communities involves the inclusion of more species and interactions in the architecture of consumer-resource interactions (Williams and Martinez, 2008). While earlier work has advanced the empirical basis of these networks from inclusion of tens of species to including hundreds of species (Jacob et al., 2011), molecular analyses of DNA in the environment and within organisms are leading to even more dramatic increases of biodiversity within food-web data (Pompanon et al., 2012; Roslin et al., 2016; Nielsen et al., 2018). A vast number of cryptic species and interactions including parasitic, symbiotic, and other interactions within organisms’ microbiomes are sure to challenge ATN and food-web theory in the near future. Initial progress in this direction includes research on incidental predation upon parasites by predators of their hosts which appears to mount relatively subtle challenges to structural food-web theory (Dunne et al., 2013). More dramatic challenges may emerge from including incidental predation on species’ entire microbiomes (Dunne et al., 2013) and the function of microbiomes within species. For example, a substantial amount of biomass consumed by purportedly herbivorous ungulates is produced by microbes within their multi-chambered gut system (Russell and Rychlik, 2001). Recognition of these ungulates as omnivores and quantification of their consumption of plant and microbial biomass could significantly revise understanding of major energy fluxes through food webs. Further attention on nursing by mammals including ungulates elucidates cannibalistic interactions, the feeding upon biomass of other individuals belonging to one’s own species, among all mammals. Cannibalistic, predatory, and mutualistic feeding among plants emerge from the increasing realization that plant individuals exchange energetic resources through their roots with other plants (Klein et al., 2016). The recognition of such feeding among plants challenges the long-assumed generalization that the base of food webs is composed of autotrophic species that do not feed upon other species. The recognition of more widely occurring cannibalism among many more species suggests pursuing further research on how cannibalism generally affects the structure and dynamics of ecological networks (Holt and Polis, 1997). For example, density-dependent cannibalism could buffer population oscillations and increase cannibals’ persistence by converting biomass from an energy sink into an energy supply when cannibals are abundant and their other resources are rare.
Another key frontier in ecological network research at the community level is the continued addition of non-feeding interactions to food webs (Kéfi et al., 2012). Early advances in this area involve the consumption of abiotic nutrients by plants (Brose et al., 2005b; Brose, 2008), nutrient recycling (Boit et al., 2012), bioaccumulation of toxics (Garay-Narváez et al., 2013, 2014), and the effects of environmental variability on the productivity of autotrophs (Boit et al., 2012; Kuparinen et al., 2018). More recent progress includes intraspecific variation addressed via links between age classes representing maturation and ontogenetic niche shifts in structured populations (Kuparinen et al., 2016, 2018; Bland et al., 2019). Other recent advances involve explicit consideration of facilitation (Kéfi et al., 2012; Valdovinos et al., 2016; Hale et al., 2020) and habitat modification also known as ecosystem engineering (Jones et al., 1994; Kéfi et al., 2012). Initial results show that the structure of these non-feeding interactions is highly predictable in terms of the overall architecture of these networks (Thébault and Fontaine, 2010) and more specifically, which subset of species within a community are involved different types of interactions (Kéfi et al., 2015). Further research shows how these non-feeding consumer-resource interactions can help stabilize the dynamics (Kéfi et al., 2016) and increase the positive effect of species diversity on ecosystem function (Miele et al., 2019) within ATN models of multiplex networks containing both feeding and non-feeding relationships. A key consideration in such extensions involves distinguishing feeding from non-feeding mechanisms occurring within an interspecific link. For example, pollination involves pollinators feeding on floral rewards produced by plants and plants consuming reproductive services produced by pollinators (Valdovinos et al., 2013). Explicit consideration of both interaction types as consumer-resource processes enabled ecological network theory to help resolve debate regarding whether the nestedness of mutualistic networks stabilizes (Bascompte et al., 2006) or destabilizes (James et al., 2012; Staniczenko et al., 2013) pollination networks (Valdovinos et al., 2016). The resolution holds that nestedness alone appears to destabilize mutualistic networks while also stabilizing these networks in the presence of adaptive foraging by pollinators who prefer partners with more floral rewards. The power of this resolution is perhaps best evidenced by its prediction that generalist pollinators prefer feeding on plants with fewer pollinator species to the same degree as such differential preferences are observed in the field (Valdovinos et al., 2016). Further progress in ATN theory involves incorporating such mutualistic mechanisms more broadly by including the production of plant rewards (floral rewards, nectaries, root exudate, etc.) and products of plant partners such as pollinators, seed dispersers, and mycorrhizal fungi providing reproductive and nutrient transport services in exchange for those rewards (Hale et al., 2020). Even broader advances may incorporate mutualistic and non-mutualistic facilitation such as those provided by coral polyps, shade plants, and barnacles that maintain the diversity and function of ecosystems as different as deserts are from the marine benthos. In each of these advances, classic notions of antagonistic, competitive, mutualistic, etc. effects species have on each other would be replaced by focusing on more empirically tractable and successfully predictive mechanisms that dynamically generate these effects (Hale et al., 2020).
A final frontier of ATN theory discussed here involves more explicit consideration of space (Holt, 1996, 2002). Early considerations addressed effects of spatial extent on food web architecture in terms of connectance and found this measure of network complexity decreases as area increases such that populations’ spatial niches within habitats do not all overlap (Brose et al., 2004). This reduction in spatial co-occurrence prevents some species from directly interacting. Adding a spatial dimension (Ritterskamp et al., 2016a) to the trophic dimension of niche space (Williams and Martinez, 2000, Williams and Martinez, 2008) can address such effects on food-web architecture. Further research has incorporated environmental gradients (Tylianakis and Morris, 2017; Pellissier et al., 2018; Baiser et al., 2019; Gravel et al., 2019) along with experimental (Piechnik et al., 2008; Piechnik, 2013) and theoretical (Holt et al., 1999; Gravel et al., 2019) effects of island biogeography on food-web structure. While such work elucidates key aspects (e.g., species-area relationships, community assembly, etc.) of the architectural framework for ATN theory, dynamical aspects have also been explored examining effects of spatial configurations of ATN models coupled by migration between the models (Allhoff et al., 2015b). This research paves the way for ATN-based meta-ecosystem models (Loreau et al., 2003; Gravel et al., 2010) of large landscapes with many interacting species analogous to global circulation models where the dynamics within a bounded area are determined by ATN theory coupled to neighboring areas by migration either due to random or bounded diffusion (Allhoff et al., 2015b; Ritterskamp et al., 2016a) or more realistic considerations of higher migration rates of relatively large-bodied species at high trophic levels due to resource quality and quantity (Hawn et al., 2018) that help stabilize coupled networks (McCann et al., 2005; Rooney et al., 2006, 2008). Global circulation models of atmospheric (e.g., weather) and aquatic (e.g., ocean circulation) dynamics similarly contain highly parameterized cells representing particular geographic areas where thermodynamic and other forces determine dynamics within each cell and Navier-Stokes equations model the migration of air and water among neighboring cells (Chassignet et al., 2014; Bauer et al., 2015). Navier-Stokes equations may also model plankton movement in aquatic systems supplemented by models of more mobile organisms migrating among neighboring ecological networks (McCann et al., 2005; Rooney et al., 2006, 2008) whose internal dynamics behave according to the bioenergetic equations of ATN theory (Yodzis and Innes, 1992; Williams and Martinez, 2004a; Williams et al., 2007). Such similarities suggest that research on spatial network ecology in aquatic and terrestrial systems could gain much from similar but much more advanced research in the earth sciences (Chassignet et al., 2014; Bauer et al., 2015).
An exciting and perhaps more immediate alternative to extending ATN theory by coupling networks in a spatially explicit manner is coupling ATN and macroecological theory. Whether assembled by evolution, migration or invasion (Rominger et al., 2016) or disassembled by eliminating certain species (Dunne et al., 2002b; Srinivasan et al., 2007) or simply failing to maintain densities above an extinction threshold (Brose et al., 2006b), ATN theory predicts the numbers, biomass, and metabolism of coexisting organisms and species within complex ecosystems. These outputs (e.g., total amounts of biomass and metabolism of all organisms and the total numbers of organisms and species) of ATN theory are the input or “state” variables for the recently developed Maximum Entropy theory of ecology (METE). METE successfully predicts a remarkable variety of empirically observed spatial and non-spatial macroecological patterns such as species-area and species-abundance relationships based on asserting that that organisms will be distributed in space and among species in the least biased way possible (Harte et al., 2008; Harte, 2011). Highly biased distributions occur, for example, when organisms are perfectly evenly distributed in space and among all species and if all but one species had only one organism with all remaining organisms belonging to one species restricted to one small area within a landscape. Instead of these biased distributions, METE predicts organisms are arranged into the distributions that are most likely given the constraints defined the theory’s input variables. By analogy, if one rolls two six-sided dice, Max-Ent predicts from these inputs that the most likely sum of a roll is 7 because the largest number of combinations (6) out of the 36 possible combinations add to 7 compared to, for example, only 1 combination that adds to 2 or 12, the least likely sums to be observed. Of course, calculating the number of combinations that a certain number of organisms or amount of metabolism are distributed among a certain number of species and within a certain amount of area is much more involved, but it is still conceptually quite similar to the dice example. The remarkable ability of METE to unify and successfully predict patterns as different as species-area relationships are from species-abundance distributions based on constraints provided by the values of its state variables could extend local ATN predictions to macroecological scales from regions to continents. In contrast to the biological mechanisms underpinning ATN theory, this extension would be based on statistical and information theory (O’Connor et al., 2019) that essentially describes the most probable macroecological patterns to be observed given the constraints provided by ATN theory (Harte, 2011). Beyond enabling the predictions of spatial patterns based on ATN model outputs, the species-abundance distributions emerging from both theories can be tested against each other and the data such as those from simulating Lake Constance (Boit et al., 2012; Boit and Gaedke, 2014). Similar to testing ATN theory’s functional responses of feeding against individual-based models of resource consumption, such tests of ATN theory’s species-abundance distributions could help build and improve bridges among ecological subdisciplines as well as improve the subdisciplines themselves.
Predicting Ecosystem Phenotype From Community Genotype: A Grand Challenge for Network Ecology
To the skeptic, the many directions described here could suggest a Quixotic pursuit of scientific exactitude as parodied by Jorge Luis Borges’ “life size map” subsequently reprised by Lewis Carroll as a cartographer’s fantasy that was built but abandoned because the map was too big to ever be unfolded. Despite the freedom of computational science from such spatial constraints, the cautionary tale deserves consideration. Systems biology faced similar skepticism when proposing the simulation of the overall behavior of a whole cell involving the detailed functioning of the genome, proteome, transcriptome and metabolome as a grand challenge of the 21st century (Tomita, 2001). This grand challenge was largely met a decade later with a computational model that predicted phenotype from genotype of a human pathogen (Karr et al., 2012). This achievement not only illustrates the tractability of a highly complex project based on computationally synthesizing different types of biological networks (Palsson, 2006), it also provides strategies and tactics for meeting similar challenges (Palsson, 2015). Central among these strategies are “the enumeration of network components, the reconstruction of networks, the mathematical representation of networks and their mathematical interrogation to assess their properties, and experiments to verify or refute computational predictions” (Palsson, 2004). Tactics to achieve this include developing software standards (Hucka et al., 2003; Waltemath et al., 2016) and integrating Boolean network modeling and constraint-based modeling with ordinary differential equations to reduce the need for parameter estimation (Karr et al., 2012). ATN researchers have already started adopting such tactics by developing software packages to make ATN research easier to conduct and reproduce (Delmas et al., 2017; Gauzens et al., 2017).
Continuing further on a similar path could embrace predicting ecosystem phenotype from community genotype as a grand challenge to advance environmental biology. Meeting this grand challenge would develop the understanding of how the overall behavior of a complex ecological system emerges from the genetic potential of organisms within nominal environments in the lab and eventually less controlled environments in the field. Such work would extend research on biodiversity and ecosystem function to a more comprehensive assessment of diversity for which all taxa surveys (Lawton et al., 1998) and population diversity (Luck et al., 2003) form important starts toward more comprehensive metagenomes of specific habitats (Leray et al., 2012; McCliment et al., 2012). This challenge also integrates the study of ecosystem function beyond material and energy flows to include quantitative effects of species loss (Brose et al., 2005b; Berlow et al., 2009; Brose, 2011) and invasions (Romanuk et al., 2009, 2017) as well and environmental and anthropogenic impacts (Kuparinen et al., 2016) on much finer measures of function such as the ecological and evolutionary fates of individual populations. ATN theory embraces much of the conceptual foundation of systems biology including mechanistic first principles scaled up into data driven networks formalized as empirically parameterized ordinary differential equations empowered by ecoinformatics and computation. ATN theory bases research at different scales upon such foundations (Box A). Instead of metabolic networks linking different biochemical species, ATN theory links metabolic energy exchanged among taxonomic species (Brose et al., 2006b). And instead of biochemical species emerging from signaling among networks of genes, ecological species emerge from evolution among phylogenetic networks of taxa (Allhoff et al., 2015a). Integrating a full range of empirically informed ecological and evolutionary processes and interactions in this way could do much to advance a more comprehensive and predictive understanding of environmental biology focused on the structure, function, and evolution of multi-organismic systems in nature (Martinez, 1995, 1996).
Many less grand but no less scientifically important challenges to ATN theory need to be addressed to more broadly test and extend ATN theory. For example, more generic forms of stochasticity often employed in ATN studies need to better focus on specific forms known to greatly affect the structure, functional and evolution of ecological systems. The generic forms mimic the variability among systems found in nature and the disturbances they experience (Domínguez-García et al., 2019) such as species loss (Dunne and Williams, 2009) and invasion (Romanuk et al., 2009, 2017). More specific forms of stochasticity include prominent cases such as marine larval dispersal (Cowen and Sponaugle, 2009) and tree masting (Koenig and Knops, 2005). Initial advances in this direction integrated environmental stochasticity into ATN’s deterministic equations via primary producers’ carrying capacity and found that such stochasticity is dampened in realistically parameterized ecological networks, especially at higher trophic levels (Kuparinen et al., 2018). Further progress may be achieved similarly by characterizing the magnitudes and frequencies of the specific forms of stochasticity and applying it to the components directly affected in order to evaluate how such stochasticity propagates through ecological systems and determine its ecological consequences. In contrast to such specificity, ATN studies more often deemphasize stochasticity by focusing on mean behaviors among replicates of experiments conducted within restricted time periods (Berlow et al., 2009) or temporal replicates within long time periods (Boit et al., 2012). For example, Boit et al. (2012) averaged decades of time series to create a mean seasonal progression of a temperate lake for ATN forecasts to be tested against. Such averaging helps minimize effects such as stochastic year-to-year variations in weather. A straightforward extension toward focusing on individual years would help illuminate how ATN theory could integrate annual stochasticity in temperature, light, and wind in order to better forecast complex dynamics for individual years. Another broad challenge is more precisely parameterizing ATN equations (Banks et al., 2017). While strong systematic trends and variability about these trends in metabolic rates with body size enable ATN theory to elucidate broad generalities that can be applied to specific systems, more precise parameterization would enable ATN theory to be more specifically and powerfully tested. While this could be achieved by more directly measuring rather than estimating metabolic and functional response parameters, for example in laboratory feeding trials of relatively few species (Rall et al., 2011), the discovery of systematic variations among different taxa (Rall et al., 2011), interaction types (Dunne et al., 2013), and habitat types (Digel et al., 2011) could provide more precise estimates of key parameters with much less effort (Brose et al., 2019a). Such efforts need to be expanded to better understand the capabilities of ATN theory and its limits (Williams and Martinez, 2008).
Conclusion
Food-web theory has been developing at least as long as ecology has formally developed as science and forms a key conceptual core of ecology. ATN theory (Brose et al., 2006b; Otto et al., 2007; Berlow et al., 2009) has emerged out of that core based on the architecture (Williams and Martinez, 2000, 2008) and non-linear dynamics (Yodzis and Innes, 1992; Williams and Martinez, 2004a) of organisms consuming primarily food but also other critical resources such as abiotic nutrients (Brose et al., 2005a, b) and services (Kéfi et al., 2012; Hale et al., 2020) produced by other organisms. Metabolism controls the rates of these dynamics by determining the costs of maintaining and building biomass and speed at which resources can be produced and consumed. While ATN theory often embraces the niche model (Figure 3) and the metabolic theory of ecology (Brown et al., 2004) to generally explore the consequences of the structure and rates of these interactions, more direct measures of structure and rates can facilitate application of ATN theory, especially with respect to specific ecosystems (Boit et al., 2012) and types of ecosystems (Digel et al., 2014; Brose et al., 2019a). ATN theory has advanced well beyond answering broad qualitative questions about stability (Dunne et al., 2005; Martinez et al., 2006; Stouffer and Bascompte, 2010, 2011), species coexistence (Brose, 2008; Kartascheff et al., 2010), and functioning (Kuparinen et al., 2016; Schneider et al., 2016; Miele et al., 2019) of complex ecosystems to the accurate and detailed quantitative prediction (Dunne et al., 2008; Berlow et al., 2009) and forecasting (Boit et al., 2012) of the structure and dynamics of specific systems in nature. Mechanisms other than consumer-resource interactions such as evolution, migration, maturation, and economics are increasingly integrated into ATN research. As such, this body of theory forms a rigorous example and mechanistic framework for multi-scale predictive understanding of ecological systems from physiological to socio-ecological scales. A particularly intriguing example is the ability to mechanistically bridge the physiological and behavioral understanding of organisms to continental scales of macroecological species-area and species-abundance distributions. Such sub-disciplinary and disciplinary bridge building combines detailed mechanistic understanding and a holistic vision of the proverbial elephant (Figure 1), parts of which are studied by ecological subdisciplines in specific (Figure 2) and even more parts of which are studied by sustainability scientists in general.
Overall, ATN theory helps unify ecology by integrating diverse perspectives into a successfully predictive whole that ecologists from virtually all subdisciplines studying all organisms in all habitats at all scales from molecules to the biosphere have contributed to (Figure 2). The many active frontiers of ecology in general and ATN theory in specific ensure that these synergisms will continue well into the future. Much ATN research pursues a data-rich form of theory more similar to systems biology (Purdy et al., 2010; Evans et al., 2013) than to physics from which several of the most prominent theoretical ecologists have emerged. This suggests that future ATN research may be more like Darwin’s extensive natural history expeditions and systems biologists’ expansive characterization of DNA, genetic signaling networks, and kinetic coefficients of enzymes than Netwon’s contemplation of a falling apple or Einstein imagining riding on a beam of light. In contrast to such brilliant advances in the physical sciences, the biological focus of ATN theory suggests ecologists attend more to spectacular advances and grand challenges of systems biology achieved by computational approaches (Holland, 2012) to integrating big data and diverse mechanisms using networks as a central organizing principle (Palsson, 2006) as have many other non-biological sciences (Barabási, 2012). Such work could well transform the theoretical core of ecology concerned with effects species have on one another to formalizing the mechanisms from which such effects emerge (Hale et al., 2020). Such a paradigm shift could result in future ecologists viewing our current preoccupation with antagonism, competition, mutualism and facilitation similar to alchemists’ preoccupation with earth, air, fire, and water. Ecologist’s ability to explain much but predict relatively little invoking these effects may share remarkably many similarities with the alchemists of old. Most hopefully, moving to a more mechanistic and data-rich focus would provide a much firmer foundation for sustainability science to help solve several of humanity’s most pressing problems.
Author Contributions
NM conceived of and wrote the manuscript.
Funding
This work was funded by the USA Department of Energy grant DE-SC0016247 and National Science Foundation grants 1241253, 1313830, 1642894, 1754207, and 1934817 to NM.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer, DG, declared a past collaboration with the author to the handling Editor.
Acknowledgments
This work was made possible by collaborations with many individuals most importantly lab members and visitors including B. Feifarek, D. Piechnik, R. Williams, U. Brose, J. Dunne, E. Berlow, K. Harrison, B. Harvey, C. Puleston, E. Vaccaro, I. Yoon, P. Yoon, R. Rael, T. Romanuk, L. Cushing, T. Srinivasan, H. Morlon, P. Tonin, A. Boit, B. Bauer, A. Kuparinen, A. Martín González, H. Ko, K. Salau, F. Valdovinos, K. Sale-Hale, K. Allhoff, and N. Kappler. Special thanks to the reviewers and Lelu Musick for artistic advice.
References
Allen, A. P., Gillooly, J. F., and Brown, J. H. (2005). Linking the global carbon cycle to individual metabolism. Funct. Ecol. 19, 202–213. doi: 10.1111/j.1365-2435.2005.00952.x
Allesina, S., Alonso, D., and Pascual, M. (2008). A general model for food web structure. Science 320, 658–661. doi: 10.1126/science.1156269
Allhoff, K. T., and Drossel, B. (2013). When do evolutionary food web models generate complex networks? J. Theor. Biol. 334, 122–129. doi: 10.1016/j.jtbi.2013.06.008
Allhoff, K. T., and Drossel, B. (2016). Biodiversity and ecosystem functioning in evolving food webs. Philos. Trans. R. Soc. B Biol. Sci. 371:20150281. doi: 10.1098/rstb.2015.0281
Allhoff, K. T., Ritterskamp, D., Rall, B. C., Drossel, B., and Guill, C. (2015a). Evolutionary food web model based on body masses gives realistic networks with permanent species turnover. Sci. Rep. 5, 1–12. doi: 10.1038/srep10955
Allhoff, K. T., Weiel, E. M., Rogge, T., and Drossel, B. (2015b). On the interplay of speciation and dispersal: an evolutionary food web model in space. J. Theor. Biol. 366, 46–56. doi: 10.1016/j.jtbi.2014.11.006
Baiser, B., Gravel, D., Cirtwill, A. R., Dunne, J. A., Fahimipour, A. K., Gilarranz, L. J., et al. (2019). Ecogeographical rules and the macroecology of food webs. Glob. Ecol. Biogeogr. 28, 1204–1218. doi: 10.1111/geb.12925
Banks, H. T., Banks, J. E., Bommarco, R., Curtsdotter, A., Jonsson, T., and Laubmeier, A. N. (2017). Parameter estimation for an allometric food web model. Int. J. Pure Appl. Math. 114, 143–160. doi: 10.12732/ijpam.v114i1.12
Barner, A. K., Pilosof, S., Bramon Mora, B., Hutchinson, M. C., Thébault, E., Kéfi, S., et al. (2018). Seeing the forest for the trees: putting multilayer networks to work for community ecology. Funct. Ecol. 33, 206–217. doi: 10.1111/1365-2435.13237
Barnes, A. D., Eisenhauer, N., Barnes, A. D., Jochum, M., Lefcheck, J. S., Eisenhauer, N., et al. (2018). Energy Flux: the link between multitrophic biodiversity and ecosystem functioning energy flux: the link between multitrophic biodiversity and ecosystem functioning. Trends Ecol. Evol. 33, 186–197. doi: 10.1016/j.tree.2017.12.007
Barnosky, A. D., Hadly, E. A., Bascompte, J., Berlow, E. L., Brown, J. H., Fortelius, M., et al. (2012). Approaching a state shift in Earth’s biosphere. Nature 486, 52–58. doi: 10.1038/nature11018
Bar-On, Y. M., Phillips, R., and Milo, R. (2018). The biomass distribution on Earth. Proc. Natl. Acad. Sci. U.S.A. 115, 6506–6511. doi: 10.1073/pnas.1711842115
Bascompte, J. (2009). Disentangling the web of life. Science 325, 416–419. doi: 10.1126/science.1170749
Bascompte, J., and Jordano, P. (2013). Mutualistic Networks. Princeton, NJ: Princeton University Press.
Bascompte, J., Jordano, P., Melian, C. J., and Olesen, J. M. (2003). The nested assembly of plant-animal mutualistic networks. Proc. Natl. Acad. Sci. U.S.A. 100, 9383–9387. doi: 10.1073/pnas.1633576100
Bascompte, J., Jordano, P., and Olesen, J. M. (2006). Asymmetric coevolutionary networks facilitate biodiversity maintenance. Science 312, 431–433. doi: 10.1126/science.1123412
Bauer, P., Thorpe, A., and Brunet, G. (2015). The quiet revolution of numerical weather prediction. Nature 525, 47–55. doi: 10.1038/nature14956
Beckerman, A. P., Petchey, O. L., and Warren, P. H. (2006). Foraging biology predicts food web complexity. Proc. Natl. Acad. Sci. U.S.A. 103, 13745–13749. doi: 10.1073/pnas.0603039103
Berlow, E. L., Dunne, J. A., Martinez, N. D., Stark, P. B., Williams, R. J., and Brose, U. (2009). Simple prediction of interaction strengths in complex food webs. Proc. Natl. Acad. Sci. U.S.A. 106, 187–191. doi: 10.1073/pnas.0806823106
Binzer, A., Guill, C., Rall, B. C., and Brose, U. (2016). Interactive effects of warming, eutrophication and size structure: impacts on biodiversity and food-web structure. Glob. Chang. Biol. 22, 220–227. doi: 10.1111/gcb.13086
Bland, S., Valdovinos, F. S., Hutchings, J. A., and Kuparinen, A. (2019). The role of fish life histories in allometrically scaled food-web dynamics. Ecol. Evol. 9, 1–10. doi: 10.1002/ece3.4996
Blasius, B., Rudolf, L., Weithoff, G., Gaedke, U., and Fussmann, G. F. (2020). Long-term cyclic persistence in an experimental predator–prey system. Nature 577, 226–230. doi: 10.1038/s41586-019-1857-0
Boit, A., and Gaedke, U. (2014). Benchmarking successional progress in a quantitative food web. PLoS One 9:e90404. doi: 10.1371/journal.pone.0090404
Boit, A., Martinez, N. D., Williams, R. J., and Gaedke, U. (2012). Mechanistic theory and modelling of complex food-web dynamics in Lake Constance. Ecol. Lett. 15, 594–602. doi: 10.1111/j.1461-0248.2012.01777.x
Brännström, Å, Johansson, J., Loeuille, N., Kristensen, N., Troost, T. A., Hille, R., et al. (2012). Modelling the ecology and evolution of communities: a review of past achievements, current efforts, and future promises. Evol. Ecol. Res. 14, 601–625.
Brose, U. (2008). Complex food webs prevent competitive exclusion among producer species. Proc. R. Soc. B Biol. Sci. 275, 2507–2514. doi: 10.1098/rspb.2008.0718
Brose, U. (2010). Body-mass constraints on foraging behaviour determine population and food-web dynamics. Funct. Ecol. 24, 28–34. doi: 10.1111/j.1365-2435.2009.01618.x
Brose, U. (2011). Extinctions in complex, size-structured communities. Basic Appl. Ecol. 12, 557–561. doi: 10.1016/j.baae.2011.09.010
Brose, U., Archambault, P., Barnes, A. D., Bersier, L.-F., Boy, T., Canning-Clode, J., et al. (2019a). Predator traits determine food-web architecture across ecosystems. Nat. Ecol. Evol. 3, 919–927. doi: 10.1038/s41559-019-0899-x
Brose, U., Rosenbaum, B., Petchey, O. L., Tabi, A., Gaedke, U., Matthews, B., et al. (2019b). The intrinsic predictability of ecological time series and its potential to guide forecasting. Ecol. Monogr. 89:e01359. doi: 10.1002/ecm.1359
Brose, U., Berlow, E. L., and Martinez, N. D. (2005a). “From food webs to ecological networks: linking non-linear trophic interactions with nutrient competition,” in Dynamic Food Webs, eds P. de Ruiter, V. Wolters, J. C. Moore, and K. B. T.-D. F. W. Melville-Smith (Burlington: Elsevier), 27–36. doi: 10.1016/B978-012088458-2/50005-9
Brose, U., Berlow, E. L., and Martinez, N. D. (2005b). Scaling up keystone effects from simple to complex ecological networks. Ecol. Lett. 8, 1317–1325. doi: 10.1111/j.1461-0248.2005.00838.x
Brose, U., Blanchard, J. L., Eklöf, A., Galiana, N., Hartvig, M., Hirt, M. R., et al. (2017). Predicting the consequences of species loss using size-structured biodiversity approaches. Biol. Rev. 92, 684–697. doi: 10.1111/brv.12250
Brose, U., Ehnes, R. B., Rall, B. C., Vucic-Pestic, O., Berlow, E. L., and Scheu, S. (2008). Foraging theory predicts predator-prey energy fluxes. J. Anim. Ecol. 77, 1072–1078. doi: 10.1111/j.1365-2656.2008.01408.x
Brose, U., Jonsson, T., Berlow, E. L., Warren, P., Banasek-Richter, C., Bersier, L.-F., et al. (2006a). Consumer-resource body-size relationships in natural food webs. Ecology 87, 2411–2417. doi: 10.1890/0012-9658(2006)87[2411:cbrinf]2.0.co;2
Brose, U., Williams, R. J., and Martinez, N. D. (2006b). Allometric scaling enhances stability in complex food webs. Ecol. Lett. 9, 1228–1236. doi: 10.1111/j.1461-0248.2006.00978.x
Brose, U., Ostling, A., Harrison, K., and Martinez, N. D. (2004). Unified spatial scaling of species and their trophic interactions. Nature 428, 167–171. doi: 10.1038/nature02297
Brown, H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.2106/JBJS.J.01311
Bruno, J. F., Stachowicz, J. J., and Bertness, M. D. (2003). Incorporating facilitation into ecological theory. Trends Ecol. Evol. 18, 119–125. doi: 10.1016/S0169-5347(02)00045-9
Cardinale, B. J., Duffy, J. E., Gonzalez, A., Hooper, D. U., Perrings, C., Venail, P., et al. (2012). Biodiversity loss and its impact on humanity. Nature 486, 59–67. doi: 10.1038/nature11148
Carscallen, W. M. A., Vandenberg, K., Lawson, J. M., Martinez, N. D., and Romanuk, T. N. (2012). Estimating trophic position in marine and estuarine food webs. Ecosphere 3, art25. doi: 10.1890/ES11-00224.1
Cary Institute Definition of Ecology (2019). Cary Institute of Ecosystem Studies. Available online at: https://www.caryinstitute.org/discover-ecology/definition-ecology (accessed March 4, 2019).
Cattin, M. F., Bersier, L. F., Banasek-Richter, C., Baltensperger, R., and Gabriel, J. P. (2004). Phylogenetic constraints and adaptation explain food-web structure. Nature 427, 835–839. doi: 10.1038/nature02327
Chapin, F. S. III, Matson, P. A., and Vitousek, P. (2011). Principles of Terrestrial Ecosystem Ecology. Berlin: Springer Science & Business Media.
Chase, J., Abrams, P. A., Grover, J., Diehl, S., Chesson, P., Holt, R. D., et al. (2002). The interaction between predation and competition:a review and synthesis. Ecol. Lett. 5, 302–3015. doi: 10.1038/nature07248
Chassignet, E. P., Sommer, J., and Wallcraft, A. J. (2014). “General circulation models,” in Encyclopedia of Environmental Change, eds J. K. Cochran, H. J. Bokunewicz, and P. L. Yager (Thousand Oaks, CA: SAGE Publications, Ltd), 486–490. doi: 10.4135/9781446247501.n1605
Chesson, P. (2000). Mechanisms of Maintenance of Species Diversity. Annu. Rev. Ecol. Syst. 31, 343–366. doi: 10.1146/annurev.ecolsys.31.1.343
Chesson, P., and Kuang, J. J. (2008). The interaction between predation and competition. Nature 456, 235–238. doi: 10.1038/nature07248
Cohen, J. E. (1978). Food Webs and Niche Space. Princeton, NJ: Princeton University Press, doi: 10.1016/0025-5564(79)90090-7
Cohen, J. E., Briand, F., and Newman, C. M. (1990). Community Food Webs: Data And Theory. Berlin: Springer Verlag.
Cohen, J. E., Jonsson, T., and Carpenter, S. R. (2003). Ecological community description using the food web, species abundance, and body size. Proc. Natl. Acad. Sci. U.S.A. 100, 1781–1786. doi: 10.1073/pnas.232715699
Cohen, J. E., Jonsson, T., Muller, C. B., Godfray, H. C. J., and Savage, V. M. (2005). Body sizes of hosts and parasitoids in individual feeding relationships. Proc. Natl. Acad. Sci. U.S.A. 102, 684–689. doi: 10.1073/pnas.0408780102
Cousins, S. (1987). The decline of the trophic level concept. Trends Ecol. Evol. 2, 312–316. doi: 10.1016/0169-5347(87)90086-3
Cowen, R. K., and Sponaugle, S. (2009). Larval Dispersal and Marine Population Connectivity. Ann. Rev. Mar. Sci. 1, 443–466. doi: 10.1146/annurev.marine.010908.163757
Curtsdotter, A., Banks, H. T., Banks, J. E., Jonsson, M., Jonsson, T., Laubmeier, A. N., et al. (2019). Ecosystem function in predator-prey food webs-confronting dynamic models with empirical data. J. Anim. Ecol. 88, 196–210. doi: 10.1111/1365-2656.12892
Darwin, C. (1859). On the Origin of the Species. Peterborough, ON: Broadview Press, doi: 10.1016/S0262-4079(09)60380-8
Delmas, E., Brose, U., Gravel, D., Stouffer, D. B., and Poisot, T. (2017). Simulations of biomass dynamics in community food webs. Methods Ecol. Evol. 8, 881–886. doi: 10.1111/2041-210X.12713
Digel, C., Curtsdotter, A., Riede, J., Klarner, B., and Brose, U. (2014). Unravelling the complex structure of forest soil food webs: higher omnivory and more trophic levels. Oikos 123, 1157–1172. doi: 10.1111/oik.00865
Digel, C., Riede, J. O., and Brose, U. (2011). Body sizes, cumulative and allometric degree distributions across natural food webs. Oikos 120, 503–509. doi: 10.1111/j.1600-0706.2010.18862.x
Domínguez-García, V., Dakos, V., and Kéfi, S. (2019). Unveiling dimensions of stability in complex ecological networks. Proc. Natl. Acad. Sci. U.S.A. 116, 25714–25720. doi: 10.1073/pnas.1904470116
Dunne, J. A. (2006). “The network structure of food webs,” in Ecological Networks: Linking Structure to Dynamics in Food Webs, eds M. Pascual and J. A. Dunne (Oxford: Oxford University Press), 27–86.
Dunne, J. A., Brose, U., Williams, R. J., and Martinez, N. D. (2005). “Modeling food-web dynamics: complexity–stability implications,” in Aquatic Food Webs, eds A. Belgrano, U. M. Scharler, J. Dunne, and R. E. Ulanowicz (Oxford: Oxford University Press), 117–129. doi: 10.1093/acprof:oso/9780198564836.003.0011
Dunne, J. A., Labandeira, C. C., Williams, R. J., Dunne, J. A., Labandeira, C. C., and Williams, R. J. (2014). Highly resolved early Eocene food webs show development of modern trophic structure after the end-Cretaceous extinction. Proc. R. Soc. B 281:20133280. doi: 10.1098/rspb.2013.3280
Dunne, J. A., Lafferty, K. D., Dobson, A. P., Hechinger, R. F., Kuris, A. M., Martinez, N. D., et al. (2013). Parasites affect food web structure primarily through increased diversity and complexity. PLoS Biol. 11:e1001579. doi: 10.1371/journal.pbio.1001579
Dunne, J. A., Maschner, H., Betts, M. W., Huntly, N., Russell, R., Williams, R. J., et al. (2016). The roles and impacts of human hunter-gatherers in North Pacific marine food webs. Sci. Rep. 6, 1–9. doi: 10.1038/srep21179
Dunne, J. A., and Williams, R. J. (2009). Cascading extinctions and community collapse in model food webs. Philos. Trans. R. Soc. B Biol. Sci. 364, 1711–1723. doi: 10.1098/rstb.2008.0219
Dunne, J. A., Williams, R. J., and Martinez, N. D. (2002a). Food-web structure and network theory: the role of connectance and size. Proc. Natl. Acad. Sci. U.S.A. 99, 12917–12922. doi: 10.1073/pnas.192407699
Dunne, J. A., Williams, R. J., and Martinez, N. D. (2002b). Network structure and biodiversity loss in food webs: robustness increases with connectance. Ecol. Lett. 5, 558–567. doi: 10.1046/j.1461-0248.2002.00354.x
Dunne, J. A., Williams, R. J., Martinez, N. D., Wood, R. A., and Erwin, D. H. (2008). Compilation and network analyses of Cambrian food webs. PLoS Biol. 6:e60102. doi: 10.1371/journal.pbio.0060102
Edger, P. P., Heidel-Fischer, H. M., Bekaert, M., Rota, J., Glöckner, G., Platts, A. E., et al. (2015). The butterfly plant arms-race escalated by gene and genome duplications. Proc. Natl. Acad. Sci. U.S.A. 112, 8362–8366. doi: 10.1073/pnas.1503926112
Eklöf, A., Tang, S., and Allesina, S. (2013). Secondary extinctions in food webs: a Bayesian network approach. Methods Ecol. Evol. 4, 760–770. doi: 10.1111/2041-210X.12062
Ellner, S. P., Snyder, R. E., Adler, P. B., and Hooker, G. (2019). An expanded modern coexistence theory for empirical applications. Ecol. Lett. 22, 3–18. doi: 10.1111/ele.13159
Evans, M. R., Bithell, M., Cornell, S. J., Dall, S. R. X., Díaz, S., Emmott, S., et al. (2013). Predictive systems ecology. Proc. R. Soc. B Biol. Sci. 280:20131452. doi: 10.1098/rspb.2013.1452
Evans, M. R., Norris, K. J., and Benton, T. G. (2012). Predictive ecology: systems approaches. Philos. Trans. R. Soc. B Biol. Sci. 367, 163–169. doi: 10.1098/rstb.2011.0191
Flynn, K. J., and Mitra, A. (2016). Why plankton modelers should reconsider using rectangular hyperbolic (Michaelis-Menten, Monod) descriptions of predator-prey interactions. Front. Mar. Sci. 3:165. doi: 10.3389/fmars.2016.00165
Forster, J., Hirst, A. G., and Atkinson, D. (2012). Warming-induced reductions in body size are greater in aquatic than terrestrial species. Proc. Natl. Acad. Sci. U.S.A. 109, 19310–19314. doi: 10.1073/pnas.1210460109
Fussmann, K. E., Schwarzmüller, F., Brose, U., Jousset, A., and Rall, B. C. (2014). Ecological stability in response to warming. Nat. Clim. Chang. 4, 206–210. doi: 10.1038/nclimate2134
Gao, J., Barzel, B., and Barabási, A. L. (2016). Universal resilience patterns in complex networks. Nature 530, 307–312. doi: 10.1038/nature16948
Garay-Narváez, L., Arim, M. M., Flores, J. D., and Ramos-Jiliberto, R. (2013). The more polluted the environment, the more important biodiversity is for food web stability. Oikos 122, 1247–1253. doi: 10.1111/j.1600-0706.2012.00218.x
Garay-Narváez, L., Flores, J. D., Arim, M., and Ramos-Jiliberto, R. (2014). Food web modularity and biodiversity promote species persistence in polluted environments. Oikos 123, 583–588. doi: 10.1111/j.1600-0706.2013.00764.x
Gauzens, B., Barnes, A., Giling, D., Jochum, M., Lefcheck, J. S., Wang, S., et al. (2017). fluxweb: a R package to easily estimate energy fluxes in food webs. Methods Ecol. Evol. 10, 270–279.
Gentleman, W., Leising, A., Frost, B., Strom, S., and Murray, J. (2003). Functional responses for zooplankton feeding on multiple resources: a review of assumptions and biological dynamics. Deep Res. Part II Top. Stud. Oceanogr. 50, 2847–2875. doi: 10.1016/j.dsr2.2003.07.001
Getz, W. M. (2011). Biomass transformation webs provide a unified approach to consumer-resource modelling. Ecol. Lett. 14, 113–124. doi: 10.1111/j.1461-0248.2010.01566.x
Gilarranz, L. J., Mora, C., and Bascompte, J. (2016). Anthropogenic effects are associated with a lower persistence of marine food webs. Nat. Commun. 7, 1–5. doi: 10.1038/ncomms10737
Gillooly, J. F., Brown, J. H., West, G. B., Savage, V. M., and Charnov, E. L. (2001). Effects of size and temperature on metabolic rate. Science 293, 2248–2251. doi: 10.1126/science.1061967
Gounand, I., Kéfi, S., Mouquet, N., and Gravel, D. (2016). Trait selection during food web assembly: the roles of interactions and temperature. Theor. Ecol. 9, 417–429. doi: 10.1007/s12080-016-0299-7
Gravel, D., Baiser, B., Dunne, J. A., Kopelke, J. P., Martinez, N. D., Nyman, T., et al. (2019). Bringing Elton and Grinnell together: a quantitative framework to represent the biogeography of ecological interaction networks. Ecography 42, 401–415. doi: 10.1111/ecog.04006
Gravel, D., Guichard, F., Loreau, M., and Mouquet, N. (2010). Source and sink dynamics in meta-ecosystems. Ecology 91, 2172–2184. doi: 10.1890/09-0843.1
Gross, T., Rudolf, L., Levin, S. A., and Dieckmann, U. (2009). Generalized models reveal stabilizing factors in food webs. Science 325, 747–750. doi: 10.1126/science.1173536
Hale, K. R. S., Valdovinos, F. S., and Martinez, N. D. (2020). Mutualism increases diversity, stability, and function of multiplex networks that integrate pollinators into food webs. Nat. Commun. 11:2182. doi: 10.1038/s41467-020-15688-w
Hart, S. P., Freckleton, R. P., and Levine, J. M. (2018). How to quantify competitive ability. J. Ecol. 106, 1902–1909.
Harte, J. (2011). Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics. Oxford: OUP.
Harte, J., Zillio, T., Conlisk, E., and Smith, A. B. (2008). Maximum entropy and the state-variable approach to macroecology. Ecology 89, 2700–2711. doi: 10.1890/07-1369.1
Hawn, C. L., Herrmann, J. D., Griffin, S. R., and Haddad, N. M. (2018). Connectivity increases trophic subsidies in fragmented landscapes. Ecol. Lett. 21, 1620–1628. doi: 10.1111/ele.12958
Heckmann, L., Drossel, B., Brose, U., and Guill, C. (2012). Interactive effects of body-size structure and adaptive foraging on food-web stability. Ecol. Lett. 15, 243–250. doi: 10.1111/j.1461-0248.2011.01733.x
Hector, A., and Bagchi, R. (2007). Biodiversity and ecosystem multifunctionality. Nature 448, 188–190. doi: 10.1038/nature05947
Hiltunen, T., Hairston, N. G., Hooker, G., Jones, L. E., and Ellner, S. P. (2014). A newly discovered role of evolution in previously published consumer-resource dynamics. Ecol. Lett. 17, 915–923. doi: 10.1111/ele.12291
Himmelfarb, J., Stenvinkel, P., Ikizler, T. A., and Hakim, R. M. (2002). Perspectives in renal medicine: the elephant in uremia: oxidant stress as a unifying concept of cardiovascular disease in uremia. Kidney Int. 62, 1524–1538. doi: 10.1046/j.1523-1755.2002.00600.x
Hirt, M. R., Grimm, V., Li, Y., Rall, B. C., Rosenbaum, B., and Brose, U. (2018). Bridging scales: allometric random walks link movement and biodiversity research. Trends Ecol. Evol. 33, 701–712. doi: 10.1016/j.tree.2018.07.003
Hirt, M. R., Jetz, W., Rall, B. C., and Brose, U. (2017). A general scaling law reveals why the largest animals are not the fastest. Nat. Ecol. Evol. 1, 1116–1122. doi: 10.1038/s41559-017-0241-4
Ho, H., Tylianakis, J. M., Zheng, J. X., and Pawar, S. (2019). Predation risk influences food-web structure by constraining species diet choice. Ecol. Lett. 22, 1734–1745. doi: 10.1111/ele.13334
Holland, J. H. (2012). Signals and Boundaries: Building Blocks for Complex Adaptive Systems. Cambridge: MA, MIT Press.
Holland, N. J., and Deangelis, D. L. (2009). Consumer-resource theory predicts dynamic transitions between outcomes of interspecific interactions. Ecol. Lett. 12, 1357–1366. doi: 10.1111/j.1461-0248.2009.01390.x
Holland, N. J., and DeAngelis, D. L. (2010). A consumer–resource approach to the density-dependent population dynamics of mutualism. Ecology 91, 1286–1295. doi: 10.1890/09-1163.1
Holt, R. D. (1996). “Food webs in space: an island biogeographic perspective,” in Food Webs, eds G. A. Polis and K. O. Winemiller (Boston, MA: Springer), 313–323. doi: 10.1007/978-1-4615-7007-3_30
Holt, R. D. (2002). Food web in space: on the interplay of dynamic instability and spatial processes. Ecol. Res. 17, 261–273. doi: 10.1046/j.1440-1703.2002.00485.x
Holt, R. D., Lawton, J. H., Polis, G. A., and Martinez, N. D. (1999). Trophic rank and the species-area relationship. Ecology 80, 1495–1504.
Holt, R. D., and Polis, G. A. (1997). A theoretical framework for intraguild predation. Am. Nat. 149, 745–764.
Hucka, M., Finney, A., Sauro, H. M., Bolouri, H., Doyle, J. C., Kitano, H., et al. (2003). The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics 19, 524–531. doi: 10.1093/bioinformatics/btg015
Hudson, L. N., and Reuman, D. C. (2013). A cure for the plague of parameters: constraining models of complex population dynamics with allometries. Proc. R. Soc. B Biol. Sci. 280:20131901. doi: 10.1098/rspb.2013.1901
Huisman, J., and Welssing, F. J. (1999). Biodiversity of plankton by species oscillations and chaos. Nature 402, 407–410. doi: 10.1038/46540
Humphries, M. M., and McCann, K. S. (2014). Metabolic ecology. J. Anim. Ecol. 83, 7–19. doi: 10.1111/1365-2656.12124
Jacob, U., Thierry, A., Brose, U., Arntz, W. E., Berg, S., Brey, T., et al. (2011). The role of body size in complex food webs. Adv. Ecol. Res. 45, 181–223. doi: 10.1016/B978-0-12-386475-8.00005-8
James, A., Pitchford, J. W., and Plank, M. J. (2012). Disentangling nestedness from models of ecological complexity. Nature 487, 227–230. doi: 10.1038/nature11214
Jiang, J., and Lai, Y.-C. (2019). Irrelevance of linear controllability to nonlinear dynamical networks. Nat. Commun. 10:3961. doi: 10.1038/s41467-019-11822-5
Jones, C. G., Lawton, J. H., and Shachak, M. (1994). Organisms as ecosystem engineers. Oikos 69, 373–386. doi: 10.2307/3545850
Jonsson, T., Kaartinen, R., Jonsson, M., and Bommarco, R. (2018). Predictive power of food web models based on body size decreases with trophic complexity. Ecol. Lett. 21, 702–712. doi: 10.1111/ele.12938
Kalinkat, G., Schneider, F. D., Digel, C., Guill, C., Rall, B. C., and Brose, U. (2013). Body masses, functional responses and predator-prey stability. Ecol. Lett. 16, 1126–1134. doi: 10.1111/ele.12147
Karr, J. R., Sanghvi, J. C., MacKlin, D. N., Gutschow, M. V., Jacobs, J. M., Bolival, B., et al. (2012). A whole-cell computational model predicts phenotype from genotype. Cell 150, 389–401. doi: 10.1016/j.cell.2012.05.044
Kartascheff, B., Heckmann, L., Drossel, B., and Guill, C. (2010). Why allometric scaling enhances stability in food web models. Theor. Ecol. 3, 195–208. doi: 10.1007/s12080-009-0063-3
Kath, N. J., Boit, A., Guill, C., and Gaedke, U. (2018). Accounting for activity respiration results in realistic trophic transfer efficiencies in allometric trophic network (ATN) models. Theor. Ecol. 11, 1–11. doi: 10.1007/s12080-018-0378-z
Katz, Y., Tunstrøm, K., Ioannou, C. C., Huepe, C., and Couzin, I. D. (2011). Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl. Acad. Sci. U.S.A. 108, 18720–18725. doi: 10.1073/pnas.1107583108
Kéfi, S., Berlow, E. L., Wieters, E. A., Joppa, L. N., Wood, S. A., Brose, U., et al. (2015). Network structure beyond food webs: mapping non-trophic and trophic interactions on Chilean rocky shores. Ecology 96, 291–303. doi: 10.1890/13-1424.1
Kéfi, S., Berlow, E. L., Wieters, E. A., Navarrete, S. A., Petchey, O. L. O. L., Wood, S. A., et al. (2012). More than a meal. integrating non-feeding interactions into food webs. Ecol. Lett. 15, 291–300. doi: 10.1111/j.1461-0248.2011.01732.x
Kéfi, S., Miele, V., Wieters, E. A., Navarrete, S. A., and Berlow, E. L. (2016). How structured is the entangled bank? The surprisingly simple organization of multiplex ecological networks leads to increased persistence and resilience. PLoS Biol. 14:e1002527. doi: 10.1371/journal.pbio.1002527
Kéfi, S., Thébault, E., Eklöf, A., Lurgi, M., Davis, A. J., Kondoh, M., et al. (2017). “Toward multiplex ecological networks: accounting for multiple interaction types to understand community structure and dynamics,” in Adaptive Food Webs: Stability and Transitions of Real and Model Ecosystems, eds J. C. Moore, P. C. de Ruiter, K. S. McCann, and V. Wolters (Cambridge: Cambridge University Press), 73.
Kitcher, P. (1989). Explanatory Unification and the Causal Structure of the World. Minneapolis: University of Minnesota Press.
Klein, T., Siegwolf, R. T. W., and Körner, C. (2016). Belowground carbon trade among tall trees in a temperate forest. Science 352, 342–344. doi: 10.1126/science.aad6188
Koenig, W. D., and Knops, J. M. H. (2005). The mystery of masting in trees. Am. Sci. 93, 340–347. doi: 10.1511/2005.4.340
Kuparinen, A., Boit, A., Valdovinos, F. S., Lassaux, H., and Martinez, N. D. (2016). Fishing-induced life-history changes degrade and destabilize harvested ecosystems. Sci. Rep. 6:22245. doi: 10.1038/srep22245
Kuparinen, A., Perälä, T., Martinez, N. D., and Valdovinos, F. S. (2018). Environmentally-induced noise dampens and reddens with increasing trophic level in a complex food web. Oikos 128, 1–13. doi: 10.1111/oik.05575
Lafferty, K. D., DeLeo, G., Briggs, C. J., Dobson, A. P., Gross, T., and Kuris, A. M. (2015). A general consumer-resource population model. Science 349, 854–857. doi: 10.1126/science.aaa6224
Lang, B., Rall, B. C., and Brose, U. (2012). Warming effects on consumption and intraspecific interference competition depend on predator metabolism. J. Anim. Ecol. 81, 516–523. doi: 10.1111/j.1365-2656.2011.01931.x
Lawton, J. H., Bignell, D. E., Bolton, B., Bloemers, G. F., Eggleton, P., Hammond, P. M., et al. (1998). Biodiversity inventories, indicator taxa and effects of habitat modification in tropical forest. Nature 391, 72–76.
Leray, M., Boehm, J. T., Mills, S. C., and Meyer, C. P. (2012). Moorea BIOCODE barcode library as a tool for understanding predator-prey interactions: insights into the diet of common predatory coral reef fishes. Coral Reefs 31, 383–388. doi: 10.1007/s00338-011-0845-0
Li, A., Cornelius, S. P., Liu, Y. Y., Wang, L., and Barabási, A. L. (2017). The fundamental advantages of temporal networks. Science 358, 1042–1046. doi: 10.1126/science.aai7488
Liu, Y. Y., Slotine, J. J., and Barabási, A. L. (2011). Controllability of complex networks. Nature 473, 167–173. doi: 10.1038/nature10011
Loreau, M. (2010). Linking biodiversity and ecosystems: towards a unifying ecological theory. Philos. Trans. R. Soc. B Biol. Sci. 365, 49–60. doi: 10.1098/rstb.2009.0155
Loreau, M., Mouquet, N., and Holt, R. D. (2003). Meta-ecosystems: a theoretical framework for a spatial ecosystem ecology. Ecol. Lett. 6, 673–679. doi: 10.1046/j.1461-0248.2003.00483.x
Luck, G. W., Daily, G. C., and Ehrlich, P. R. (2003). Population diversity and ecosystem services. Trends Ecol. Evol. 18, 331–336. doi: 10.1016/S0169-5347(03)00100-9
MacArthur, R. (1955). Fluctuations of animal populations and a measure of community stability. Ecology 36, 533–536.
Malandrakis, E. E., Danis, T., Iona, A., and Exadactylos, A. (2017). “Abiotic stress of seagrasses: recent advances in transcriptomics, genomics, and systems biology,” in Systems Biology of Marine Ecosystems, eds M. Kumar and P. Ralph (Berlin: Springer), 119–132.
Marquet, P. A., Allen, A. P., Brown, J. H., Dunne, J. A., Enquist, B. J., Gillooly, J. F., et al. (2014). On theory in ecology. Bioscience 64, 701–710. doi: 10.1093/biosci/biu098
Marquet, P. A., Labra, F. A., and Maurer, B. A. (2004). Metabolic theory: linking individuals to ecosystem. Ecology 85, 1794–1796. doi: 10.1890/03-0694
Martinez, N. D. (1991). Artifacts or Attributes? Effects of Resolution on the Little Rock Lake Food Web. Ecol. Monogr. 61, 367–392. doi: 10.2307/2937047
Martinez, N. D. (1992). Constant connectance in community food webs. Am. Nat. 139, 1208–1218. doi: 10.1086/285382
Martinez, N. D. (1993a). Effects of resolution on food web structure. Oikos 66, 403–412. doi: 10.2307/3544934
Martinez, N. D. (1993b). Effect of scale on food web structure. Science 260, 242–243. doi: 10.1126/science.260.5105.242
Martinez, N. D. (1995). “Unifying ecological subdisciplines with ecosystem food webs,” in Linking Species and Ecosystems, ed. C. G. Jones (Berlin: Springer Science & Business Media), 166–175. doi: 10.1007/978-1-4615-1773-3_17
Martinez, N. D. (1996). “Defining and measuring functional aspects of biodiversity,” in Biodiversity: A Biology of Numbers and Difference, ed. K. J. Gaston (Hoboken, NJ: Wiley), 114–148.
Martinez, N. D. (2006). “Network evolution: exploring the change and adaptation of complex ecological systems over deep time,” in Ecological Networks from Structure to Dynamics in Food Webs, eds M. Pascual and J. A. Dunne (Oxford: Oxford University Press), 287–302.
Martinez, N. D., and Cushing, L. J. (2006). “Additional model complexity reduces fit to complex food-web structure,” in Ecological Networks: Linking Structure to Dynamics in Food Webs, eds M. Pascual and J. A. Dunne (Oxford: Oxford University Press), 87–89.
Martinez, N. D., Tonnin, P., Bauer, B., Rael, R. C., Singh, R., Yoon, S., et al. (2012). “Sustaining economic exploitation of complex ecosystems in computational models of coupled human-natural networks,” in Proceedings of the National Conference on Artificial Intelligence, Pittsburgh, PA, 326–334.
Martinez, N. D., Williams, R. J., and Dunne, J. A. (2006). “Diversity, complexity, and persistence in large model ecosystems,” in Ecological Networks: Linking Structure to Dynamics in Food Webs, eds M. Pascual and J. A. Dunne (Oxford: Oxford University Press), 163–184. doi: 10.1111/j.1469-7998.1982.tb03499.x
Marx, J. M., Rall, B. C., Phillips, H. R. P., and Brose, U. (2019). Opening the black box of plant nutrient uptake under warming predicts global patterns in community biomass and biological carbon storage. Oikos 128, 1503–1514. doi: 10.1111/oik.06141
May, R. M. (1973). Stability and Complexity in Model Ecosystems. Princeton, NJ: Princeton University Press.
McCann, K., Hastings, A., and Huxel, G. R. (1998). Weak trophic interactions and the balance of nature. Nature 395, 794–798. doi: 10.1038/27427
McCann, K. S., Rasmussen, J. B., and Umbanhowar, J. (2005). The dynamics of spatially coupled food webs. Ecol. Lett. 8, 513–523. doi: 10.1111/j.1461-0248.2005.00742.x
McCliment, E. A., Nelson, C. E., Carlson, C. A., Alldredge, A. L., Witting, J., and Amaral-Zettler, L. A. (2012). An all-taxon microbial inventory of the Moorea coral reef ecosystem. ISME J. 6, 309–319. doi: 10.1038/ismej.2011.108
McKane, A. J. (2004). Evolving complex food webs. Eur. Phys. J. B 38, 287–295. doi: 10.1140/epjb/e2004-00121-2
McKane, A. J., and Drossel, B. (2005). “Models of food web evolution,” in Ecological Networks: Linking Structure to Dynamics in Food Webs, eds M. Pascual and J. A. Dunne (Oxford: Oxford University Press), 223–243.
McPeek, M. A. (2019). Mechanisms influencing the coexistence of multiple consumers and multiple resources: resource and apparent competition. Ecol. Monogr. 89, 1–22. doi: 10.1002/ecm.1328
Meyer, J. R., Ellner, S. P., Hairston, N. G., Jones, L. E., and Yoshida, T. (2006). Prey evolution on the time scale of predator-prey dynamics revealed by allele-specific quantitative PCR. Proc. Natl. Acad. Sci. U.S.A. 103, 10690–10695. doi: 10.1073/pnas.0600434103
Miele, V., Guill, C., Ramos-Jiliberto, R., and Kéfi, S. (2019). Non-trophic interactions strengthen the diversity—functioning relationship in an ecological bioenergetic network model. PLoS Comput. Biol. 15:e1007269. doi: 10.1371/journal.pcbi.1007269
Morlon, H., Kefi, S., and Martinez, N. D. (2014). Effects of trophic similarity on community composition. Ecol. Lett. 17, 1495–1506. doi: 10.1111/ele.12356
Naeem, S., Thompson, L. J., Lawler, S. P., Lawton, J. H., and Woodfin, R. M. (1994). Declining biodiversity can alter the performance of ecosystems. Nature 368, 734–737.
Newman, M. (2010). Networks: An Introduction. Oxford: Oxford University Press, doi: 10.1093/acprof:oso/9780199206650.001.0001
Nielsen, J. M., Clare, E. L., Hayden, B., Brett, M. T., and Kratina, P. (2018). Diet tracing in ecology: method comparison and selection. Methods Ecol. Evol. 9, 278–291. doi: 10.1111/2041-210X.12869
O’Connor, M. I., Pennell, M. W., Altermatt, F., Matthews, B., Melián, C. J., and Gonzalez, A. (2019). Principles of ecology revisited: integrating information and ecological theories for a more unified science. Front. Ecol. Evol. 7:219. doi: 10.3389/fevo.2019.00219
Odum, E. P. (1969). The strategy of ecosystem development. Science 164, 262–270. doi: 10.1126/science.164.3877.262
Otto, S. B., Rall, B. C., and Brose, U. (2007). Allometric degree distributions facilitate food-web stability. Nature 450, 1226–1229. doi: 10.1038/nature06359
Paine, R. T. (1966). Paine, 1966, food web complexity and species diversity. Am. Nat. 100, 65–75. doi: 10.1086/282400
Paine, R. T. (1992). Food-web analysis through field measurement of per capita interaction strength. Nature 355:73.
Palsson, B. O. (2015). Systems Biology. Cambridge: Cambridge University Press, doi: 10.1017/CBO9781139854610
Palsson, B. Ø (2004). In silico biotechnology. Curr. Opin. Biotechnol. 15, 50–51. doi: 10.1016/j.copbio.2004.01.006
Palsson, B. Ø (2006). Systems Biology: Properties of Reconstructed Networks. Cambridge: Cambridge university press.
Pascual, M., and Dunne, J. A. (eds) (2006). Ecological Networks: Linking Structure to Dynamics in Food Webs. Oxford: Oxford University Press.
Pawar, S., Dell, A. I., Lin, T., and Wieczynski, D. J. (2019). Interaction dimensionality scales up to generate bimodal distributions in ecological communities. Front. Ecol. Evol. 7:202. doi: 10.3389/fevo.2019.00202
Pawar, S., Dell, A. I., and Savage, V. M. (2012). Dimensionality of consumer search space drives trophic interaction strengths. Nature 486, 485–489. doi: 10.1038/nature11131
Pellissier, L., Albouy, C., Bascompte, J., Farwig, N., Graham, C., Loreau, M., et al. (2018). Comparing species interaction networks along environmental gradients. Biol. Rev. 93, 785–800. doi: 10.1111/brv.12366
Petchey, O. L., Beckerman, A. P., Riede, J. O., and Warren, P. H. (2008). Size, foraging, and food web structure. Proc. Natl. Acad. Sci. U.S.A. 105, 4191–4196. doi: 10.1073/pnas.0710672105
Petchey, O. L., Brose, U., and Rall, B. C. (2010). Predicting the effects of temperature on food web connectance. Philos. Trans. R. Soc. B Biol. Sci. 365, 2081–2091. doi: 10.1098/rstb.2010.0011
Petchey, O. L., Pontarp, M., Massie, T. M., Kéfi, S., Ozgul, A., Weilenmann, M., et al. (2015). The ecological forecast horizon, and examples of its uses and determinants. Ecol. Lett. 18, 597–611. doi: 10.1111/ele.12443
Pickett, S. T. A., Kolasa, J., and Jones, C. G. (2010). Ecological Understanding: the Nature of Theory and the Theory of Nature. Amsterdem: Elsevier.
Piechnik, D. A. (2013). Trophic levels colonize sequentially but effects of habitat size and quality are transient. Acta Oecol. 47, 85–94. doi: 10.1016/j.actao.2012.11.002
Piechnik, D. A., Lawler, S. P., and Martinez, N. D. (2008). Food-web assembly during a classic biogeographic study: species’ “trophic breadth” corresponds to colonization order. Oikos 117, 665–674. doi: 10.1111/j.0030-1299.2008.15915.x
Pilosof, S., Porter, M. A., Pascual, M., and Kéfi, S. (2017). The multilayer nature of ecological networks. Nat. Ecol. Evol. 1, 1–9. doi: 10.1038/s41559-017-0101
Pimm, S. L., Lawton, J. H., and Cohen, J. E. (1991). Food web patterns and their consequences. Nature 350:669.
Polis, G. A., and Strong, D. R. (1996). Food web complexity and community dynamics. Am. Nat. 147, 813–846. doi: 10.1007/s00442-006-0505-1
Pompanon, F., Deagle, B. E., Symondson, W. O. C., Brown, D. S., Jarman, S. N., and Taberlet, P. (2012). Who is eating what: diet assessment using next generation sequencing. Mol. Ecol. 21, 1931–1950. doi: 10.1111/j.1365-294X.2011.05403.x
Ponisio, L. C., Valdovinos, F. S., Allhoff, K. T., Gaiarsa, M. P., Barner, A., Guimarães, P. R., et al. (2019). A network perspective for community assembly. Front. Ecol. Evol. 7:103. doi: 10.3389/fevo.2019.00103
Power, M. E. (1992). Top-down and bottom-up forces in food webs: do plants have primacy. Ecology 73, 733–746. doi: 10.1007/s00442-010-1802-2
Power, M. E., Tilman, D., Estes, J. A., Menge, B. A., Bond, W. J., Mills, L. S., et al. (1996). Challenges in the quest for keystones. Bioscience 46, 609–620. doi: 10.2307/1312990
Price, C. A., Weitz, J. S., Savage, V. M., Stegen, J., Clarke, A., Coomes, D. A., et al. (2012). Testing the metabolic theory of ecology. Ecol. Lett. 15, 1465–1474. doi: 10.1111/j.1461-0248.2012.01860.x
Purdy, K. J., Hurd, P. J., Moya-Laraño, J., Trimmer, M., Oakley, B. B., and Woodward, G. (2010). Systems biology for ecology. Mol. Ecosyst. 43, 87–149. doi: 10.1016/B978-0-12-385005-8.00003-4
Quévreux, P., and Brose, U. (2019). Metabolic adjustment enhances food web stability. Oikos 128, 54–63. doi: 10.1111/oik.05422
Rall, B. C., Brose, U., Hartvig, M., Kalinkat, G., Schwarzmüller, F., Vucic-Pestic, O., et al. (2012). Universal temperature and body-mass scaling of feeding rates. Philos. Trans. R. Soc. B Biol. Sci. 367, 2923–2934. doi: 10.1098/rstb.2012.0242
Rall, B. C., Kalinkat, G., Ott, D., Vucic-Pestic, O., and Brose, U. (2011). Taxonomic versus allometric constraints on non-linear interaction strengths. Oikos 120, 483–492. doi: 10.1111/j.1600-0706.2010.18860.x
Rall, B. C., Vucic-Pestic, O., Ehnes, R. B., Emmerson, M. C., and Brose, U. (2009). Temperature, predator-prey interaction strength and population stability. Glob. Chang. Biol. 16, 2145–2157. doi: 10.1111/j.1365-2486.2009.02124.x
Reiners, W. A. (1986). Complementary models for ecosystems. Am. Nat. 127, 59–73. doi: 10.1086/284467
Riede, J. O., Rall, B. C., Banasek-Richter, C., Navarrete, S. A., Wieters, E. A., Emmerson, M. C., et al. (2010). Scaling of Food-Web Properties with Diversity and Complexity Across Ecosystems. Adv. Ecol. Res. 42, 139–170. doi: 10.1016/B978-0-12-381363-3.00003-4
Ritterskamp, D., Bearup, D., and Blasius, B. (2016a). A new dimension: evolutionary food web dynamics in two dimensional trait space. J. Theor. Biol. 405, 66–81. doi: 10.1016/j.jtbi.2016.03.042
Ritterskamp, D., Feenders, C., Bearup, D., and Blasius, B. (2016b). Evolutionary food web models: effects of an additional resource. Theor. Ecol. 9, 501–512. doi: 10.1007/s12080-016-0305-0
Romanuk, T. N., Binzer, A., Loeuille, N., Carscallen, W. M. A., and Martinez, N. D. (2019). Simulated evolution assembles more realistic food webs with more functionally similar species than invasion. Sci. Rep. 9:18242. doi: 10.1038/s41598-019-54443-0
Romanuk, T. N., Zhou, Y., Brose, U., Berlow, E. L., Williams, R. J., and Martinez, N. D. (2009). Predicting invasion success in complex ecological networks. Philos. Trans. R. Soc. B Biol. Sci. 364, 1743–1754. doi: 10.1098/rstb.2008.0286
Romanuk, T. N., Zhou, Y., Valdovinos, F. S., and Martinez, N. D. (2017). Robustness trade-offs in model food webs: invasion probability decreases while invasion consequences increase with connectance. Adv. Ecol. Res. 56, 263–291. doi: 10.1016/bs.aecr.2016.11.001
Rominger, A. J., Goodman, K. R., Lim, J. Y., Armstrong, E. E., Becking, L. E., Bennett, G. M., et al. (2016). Community assembly on isolated islands: macroecology meets evolution. Glob. Ecol. Biogeogr. 25, 769–780. doi: 10.1111/geb.12341
Rooney, N., McCann, K., Gellner, G., and Moore, J. C. (2006). Structural asymmetry and the stability of diverse food webs. Nature 442, 265–269. doi: 10.1038/nature04887
Rooney, N., McCann, K. S., and Moore, J. C. (2008). A landscape theory for food web architecture. Ecol. Lett. 11, 867–881. doi: 10.1111/j.1461-0248.2008.01193.x
Rosenbaum, B., and Rall, B. C. (2018). Fitting functional responses: direct parameter estimation by simulating differential equations. Methods Ecol. Evol. 9, 2076–2090. doi: 10.1111/2041-210X.13039
Rosenzweig, M. L., and MacArthur, R. H. (1963). Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 97, 209–223.
Roslin, T., Majaneva, S., and Clare, E. (2016). The use of DNA barcodes in food web construction—terrestrial and aquatic ecologists unite! 1. Genome 59, 603–628. doi: 10.1139/gen-2015-0229
Rossberg, A. G., Matsuda, H., Amemiya, T., and Itoh, K. (2006). Food webs: experts consuming families of experts. J. Theor. Biol. 241, 552–563. doi: 10.1016/j.jtbi.2005.12.021
Russell, J. B., and Rychlik, J. L. (2001). Factors that alter rumen microbial ecology. Science 292, 1119–1122. doi: 10.1126/science.1058830
Scheiner, S. M., and Willig, M. R. (2008). A general theory of ecology. Theor. Ecol. 1, 21–28. doi: 10.1007/s12080-007-0002-0
Schmitz, O. J., and Suttle, K. B. (2001). Effects of top predator species on direct and indirect interactions in a food web. Ecology 82, 2072–2081.
Schneider, F. D., Brose, U., Rall, B. C., and Guill, C. (2016). Animal diversity and ecosystem functioning in dynamic food webs. Nat. Commun. 7, 1–8. doi: 10.1038/ncomms12718
Schramski, J. R., Dell, A. I., Grady, J. M., Sibly, R. M., and Brown, J. H. (2015). Metabolic theory predicts whole-ecosystem properties. Proc. Natl. Acad. Sci. U.S.A. 112, 2617–2622. doi: 10.1073/pnas.1423502112
Sheridan, J. A., and Bickford, D. (2011). Shrinking body size as an ecological response to climate change. Nat. Clim. Chang. 1, 401–406. doi: 10.1038/nclimate1259
Shurin, J. B., Gruner, D. S., and Hillebrand, H. (2006). Review All wet or dried up? Real differences between aquatic and terrestrial food webs. Proc. R. Soc. B Biol. Sci. 273, 1–9. doi: 10.1098/rspb.2005.3377
Sih, A. (1980). Optimal behavior: can foragers balance two conflicting demands? Science 210, 1041–1043. doi: 10.1126/science.210.4473.1041
Simberloff, D. (2004). Community ecology: is it time to move on? Am. Nat. 163, 787–799. doi: 10.1086/420777
Skalski, G. T., and Gilliam, J. F. (2001). Functional responses with predator interference: viable alternatives to the Holling type II model. 82, 3083–3092. doi: 10.1890/0012-96582001082[3083:FRWPIV]2.0.CO;2
Skalski, G. T., and Gilliam, J. F. (2002). Feeding under predation hazard: testing models of adaptive behavior with stream fish. Am. Nat. 160, 158–172. doi: 10.1086/341012
Sommer, U., Adrian, R., De Senerpont Domis, L., Elser, J. J., Gaedke, U., Ibelings, B., et al. (2012). Beyond the Plankton Ecology Group (PEG) Model: mechanisms Driving Plankton Succession. Annu. Rev. Ecol. Evol. Syst. 43, 429–448. doi: 10.1146/annurev-ecolsys-110411-160251
Srinivasan, U. T., Dunne, J. A., Harte, J., and Martinez, N. D. (2007). Response of complex food webs to realistic extinction sequences. Ecology 88, 671–682. doi: 10.1890/06-0971
Staniczenko, P. P. A., Kopp, J. C., and Allesina, S. (2013). The ghost of nestedness in ecological networks. Nat. Commun. 4, 1391–1396. doi: 10.1038/ncomms2422
Stouffer, D., Camacho, J., Guimera, R., Ng, C., and Nunes Amaral, L. (2005). Quantitative patterns in the structure of model and imperical food webs. Ecology 86, 1301–1311. doi: 10.1890/04-0957
Stouffer, D. B., and Bascompte, J. (2010). Understanding food-web persistence from local to global scales. Ecol. Lett. 13, 154–161. doi: 10.1111/j.1461-0248.2009.01407.x
Stouffer, D. B., and Bascompte, J. (2011). Compartmentalization increases food-web persistence. Proc. Natl. Acad. Sci. U.S.A. 108, 3648–3652. doi: 10.1073/pnas.1014353108
Stouffer, D. B., Rezende, E. L., and Amaral, L. A. N. (2011). The role of body mass in diet contiguity and food-web structure. J. Anim. Ecol. 80, 632–639. doi: 10.1111/j.1365-2656.2011.01812.x
Stouffer, D. B., Sales-Pardo, M., Sirer, M. I., and Bascompte, J. (2012). Evolutionary conservation of species’ roles in food webs. Science 335, 1489–1492. doi: 10.1126/science.1216556
Thébault, E., and Fontaine, C. (2010). Stability of ecological communities and the architecture of mutualistic and trophic networks. Science 329, 853–856. doi: 10.1126/science.1188321
Thingstad, T. F. (2000). Elements of a theory for the mechanisms controlling abundance, diversity, and biogeochemical role of lytic bacterial viruses in aquatic systems. Limnology 45, 1320–1328.
Thompson, R. M., Brose, U., Dunne, J. A., Hall, R. O., Hladyz, S., Kitching, R. L., et al. (2012). Food webs: reconciling the structure and function of biodiversity. Trends Ecol. Evol. 27, 689–697. doi: 10.1016/j.tree.2012.08.005
Tilman, D. (1982). Resource Competition and Community Structure. Princeton, NJ: Princeton university press.
Tomita, M. (2001). Whole-cell simulation: a grand challenge of the 21st century. Trends Biotechnol. 19, 205–210. doi: 10.1016/S0167-7799(01)01636-5
Turchin, P. (2003). Complex Population Dynamics: A Theoretical/Empirical Synthesis. Princeton university press.
Tylianakis, J. M., and Morris, R. J. (2017). Ecological networks across environmental gradients. Annu. Rev. Ecol. Evol. Syst. 48, 25–48. doi: 10.1146/annurev-ecolsys-110316-022821
Valdovinos, F. S., Brosi, B. J., Briggs, H. M., Moisset de Espanés, P., Ramos-Jiliberto, R., and Martinez, N. D. (2016). Niche partitioning due to adaptive foraging reverses effects of nestedness and connectance on pollination network stability. Ecol. Lett. 19, 1277–1286. doi: 10.1111/ele.12664
Valdovinos, F. S., Moisset de Espanés, P., Flores, J. D., and Ramos-Jiliberto, R. (2013). Adaptive foraging allows the maintenance of biodiversity of pollination networks. Oikos 122, 907–917. doi: 10.1111/j.1600-0706.2012.20830.x
Valdovinos, F. S., Ramos-Jiliberto, R., Garay-Narváez, L., Urbani, P., and Dunne, J. A. (2010). Consequences of adaptive behaviour for the structure and dynamics of food webs. Ecol. Lett. 13, 1546–1559. doi: 10.1111/j.1461-0248.2010.01535.x
Vallina, S. M., Ward, B. A., Dutkiewicz, S., and Follows, M. J. (2014). Maximal feeding with active prey-switching: a kill-the-winner functional response and its effect on global diversity and biogeography. Prog. Oceanogr. 120, 93–109. doi: 10.1016/j.pocean.2013.08.001
Van Tussenbroek, B. I., Villamil, N., Márquez-Guzmán, J., Wong, R., Monroy-Velázquez, L. V., and Solis-Weiss, V. (2016). Experimental evidence of pollination in marine flowers by invertebrate fauna. Nat. Commun. 7, 1–6. doi: 10.1038/ncomms12980
Vasseur, D. A., and McCann, K. S. (2005). A mechanistic approach for modeling temperature dependent consumer resource dynamics. Am. Nat. 166, 184–198. doi: 10.1086/431285
Vellend, M. (2010). Conceptual synthesis in community ecology. Q. Rev. Biol. 85, 183–206. doi: 10.1086/652373
Vucic-Pestic, O., Ehnes, R. B., Rall, B. C., and Brose, U. (2011). Warming up the system: higher predator feeding rates but lower energetic efficiencies. Glob. Chang. Biol. 17, 1301–1310. doi: 10.1111/j.1365-2486.2010.02329.x
Vucic-Pestic, O., Rall, B. C., Kalinkat, G., and Brose, U. (2010). Allometric functional response model: body masses constrain interaction strengths. J. Anim. Ecol. 79, 249–256. doi: 10.1111/j.1365-2656.2009.01622.x
Waltemath, D., Karr, J. R., Bergmann, F. T., Chelliah, V., Hucka, M., Krantz, M., et al. (2016). Toward community standards and software for whole-cell modeling. IEEE Trans. Biomed. Eng. 63, 2007–2014. doi: 10.1109/TBME.2016.2560762
Wang, S., and Brose, U. (2018). Biodiversity and ecosystem functioning in food webs: the vertical diversity hypothesis. Ecol. Lett. 21, 9–20. doi: 10.1111/ele.12865
Weitz, J. S., Stock, C. A., Wilhelm, S. W., Bourouiba, L., Coleman, M. L., Buchan, A., et al. (2015). A multitrophic model to quantify the effects of marine viruses on microbial food webs and ecosystem processes. ISME J. 9, 1352–1364. doi: 10.1038/ismej.2014.220
Williams, R. J. (2008). Effects of network and dynamical model structure on species persistence in large model food webs. Theor. Ecol. 1, 141–151. doi: 10.1007/s12080-008-0013-5
Williams, R. J. (2010). Simple MaxEnt models explain food web degree distributions. Theor. Ecol. 3, 45–52. doi: 10.1007/s12080-009-0052-6
Williams, R. J., Anandanadesan, A., and Purves, D. (2010). The probabilistic niche model reveals the niche structure and role of body size in a complex food web. PLoS One 5:e12092. doi: 10.1371/journal.pone.0012092
Williams, R. J., Berlow, E. L., Dunne, J. A., Barabási, A.-L., and Martinez, N. D. (2002). Two degrees of separation in complex food webs. Proc. Natl. Acad. Sci. U.S.A. 99, 12913–12916. doi: 10.1073/pnas.192448799
Williams, R. J., Brose, U., and Martinez, N. D. (2007). “Homage to Yodzis and Innes, 1992: scaling up feeding-based population dynamics to complex ecological networks,” in From Energetics to Ecosystems: The Dynamics and Structure of Ecological Systems, ed. N. Rooney (Berlin: Springer), 37–51. doi: 10.1007/978-1-4020-5337-5_2
Williams, R. J., and Martinez, N. D. (2000). Simple rules yield complex food webs. Nature 404, 180–183. doi: 10.1038/35004572
Williams, R. J., and Martinez, N. D. (2004a). Limits to trophic levels and omnivory in complex food webs: theory and data. Am. Nat. 163, 458–468. doi: 10.1086/381964
Williams, R. J., and Martinez, N. D. (2004b). Stabilization of chaotic and non-permanent food-web dynamics. Eur. Phys. J. B 38, 297–303. doi: 10.1140/epjb/e2004-00122-1
Williams, R. J., and Martinez, N. D. (2008). Success and its limits among structural models of complex food webs. J. Anim. Ecol. 77, 512–519. doi: 10.1111/j.1365-2656.2008.01362.x
Yan, G., Martinez, N. D., and Liu, Y. (2017). Degree heterogeneity and stability of ecological networks. J. R. Soc. Interface 14:20170189. doi: 10.1098/rsif.2017.0189
Yodzis, P., and Innes, S. (1992). Body size and consumer-resource dynamics. Am. Nat. 139, 1151–1175.
Yoon, I., Williams, R., Levine, E., Yoon, S., Dunne, J., and Martinez, N. (2004). “Webs on the web (WOW): 3D visualization of ecological networks on the WWW for collaborative research and education,” in Proceedings of SPIE - The International Society for Optical Engineering, Bellingham, doi: 10.1117/12.526956
Yoshida, T., Ellner, S. P., Jones, L. E., Bohannan, B. J. M., Lenski, R. E., and Hairston, N. G. (2007). Cryptic population dynamics: rapid evolution masks trophic interactions. PLoS Biol. 5:e50235. doi: 10.1371/journal.pbio.0050235
Yoshida, T., Jones, L. E., Ellner, S. P., Fussmann, G. F., and Hairston, N. G. (2003). Rapid evolution drives ecological dynamics in a predator-prey system. Nature 424, 303–306. doi: 10.1038/nature01767
Zhou, Y., Brose, U., Kastenberg, W., and Martinez, N. D. (2011). “A new approach to ecological risk assessment: simulating effects of global warming on complex ecological networks,” in Unifying Themes in Complex Systems, eds A. J. Morales, C. Gershenson, D. Braha, A. A. Minai, and B. -Y. Yaneer (Berlin: Springer), 342–350.
Keywords: ecological networks, synthesis, prediction, consumer resource dynamics, allometry, food webs, mutualistic networks, stability
Citation: Martinez ND (2020) Allometric Trophic Networks From Individuals to Socio-Ecosystems: Consumer–Resource Theory of the Ecological Elephant in the Room. Front. Ecol. Evol. 8:92. doi: 10.3389/fevo.2020.00092
Received: 28 March 2019; Accepted: 20 March 2020;
Published: 27 May 2020.
Edited by:
Angelica L. Gonzalez, Rutgers, The State University of New Jersey, Camden, United StatesReviewed by:
Dominique Gravel, Université de Sherbrooke, CanadaVan Savage, UCLA Health System, United States
Copyright © 2020 Martinez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Neo D. Martinez, bmVvQHBlYWNlbGFiLm5ldA==
 Neo D. Martinez
Neo D. Martinez