Delineating Conservation Areas for Cohabiting Species: An Example of Vernal Pond Conservation From Fort Stewart in Georgia, United States

Military installations are valuable in global biodiversity conservation as they secure representative ecosystems from land conversion and protect many threatened or endangered species. Selecting suitable areas for biodiversity conservation within military installations is a challenging problem as this must not impede military training activities. The issue gets more complicated when considering multiple cohabiting species in a metacommunity with species dependency. In this paper, we present an example for the conservation of two cohabiting species, Gopher Tortoise (GT) and Gopher Frog (GF), located within the boundaries of a military installation, Fort Stewart, Georgia, United States. The GF depends on both locations of GT habitat (burrows) and ephemeral vernal ponds (for breeding). We develop a model that identifies the cost-efficient areas for the conservation of these two species while taking into account the dependency of GF on GT burrows. The model selects a specified number of conservation areas for the two species, where each GF conservation area covers an adequate number of vernal ponds for the GFs to accommodate their reproduction, and each GT conservation area provides adequate habitat quality to sustain a viable GT population. The model also requires each GF site to be located close to GT sites so that the GFs could find refuge after they leave the water. We use the total distance of selected sites to the main roads in the military installation as a proxy for the conservation cost. We achieve contiguity of each conservation area by selecting sites that are adjacent to a central site of the conservation area to ensure undisrupted travel for both the GFs and the GTs. Using the model, we generated alternative configurations of conservation areas that could be considered by the land managers of Fort Stewart. Our methods are general and can be applied to other reserve site selection and land management problems with cohabiting interrelated species.

Introduction

Military training areas are estimated to cover 5–6% of the Earth’s land surface and they have the potential to make a significant contribution to global biodiversity conservation (Aycrigg et al., 2015; Zentelis and Lindenmayer, 2015). This is because most military training areas sustain diverse ecological systems and many threatened or endangered species by protecting them from land conversion to agriculture and urban uses. Conservation of these ecosystems and species has yet to be planned systematically by identifying the most suitable areas in such a way that the biodiversity conservation goals could be achieved without impeding the military training activities.

Among the military installations in the continental United States, Fort Stewart in Georgia has the greatest number of federally and state-listed amphibian and reptile species (Petersen et al., 2016). One of those species is Gopher Tortoise (Gopherus polyphemus), hereafter referred to as GT or the GTs, which is native to the southeastern United States and has a status of vulnerable according to IUCN (2021). The GTs are a keystone species currently listed as state-threatened in Georgia and a candidate to be listed as federally-threatened. Another important species in the region is Gopher Frog (Lithobathes capito), hereafter referred to as GF or the GFs. The GFs have an imperiled status according to NatureServe (2020). The GFs breed in vernal ponds which are numerous throughout the installation. Vernal ponds are seasonal wetlands covered by shallow water in wet seasons of the year and may be completely dry at other times. These ponds, ranging in size from small puddles to shallow lakes, provide habitat for many threatened or endangered plants and animals, including the GFs. Due to road-building, re-grading of land, industrial and residential development, or other human activities, vernal ponds and the ecological communities and species they sustain have been damaged or threatened. Protecting these vernal ponds, therefore, has received a substantial amount of attention in the past two decades (see, e.g., Compton et al., 2007; Gamble et al., 2007; Joly, 2019; Sterrett et al., 2019; Kieran et al., 2021). The GFs spend their larval period in vernal ponds, which is estimated to last approximately 3–4 months, then the juveniles and adults travel to and live in upland areas around these ponds. When open-air conditions become unfavorable, the GFs seek shelter in nearby GT burrows to avoid fire, extreme heat, cold, and dry weather (Alexy et al., 2003; Roznik and Johnson, 2009; Smith et al., 2021)¹. In the past decade, Fort Stewart has been expanding its military training areas within the installation Protecting these two ecologically important species while not impeding the military training activities has become an important problem for the land managers. The conservation problem requires a site selection approach that accounts for the dependency of the GFs on GT burrows.

We extend methods from the reserve design/site selection literature that use integer programming approaches to optimize site selection for conservation of species (Cocks and Baird, 1989; Ando et al., 1998; Williams et al., 2005; Billionnet, 2013). For our application, at least two important features, among others, need to be considered. These are the contiguity of selected conservation areas and the dependency of GF on the GT burrows. Contiguity is one of the spatial attributes that has long been acknowledged to be important in sustaining the functioning of conservation reserves (see, e.g., Diamond, 1975; Simberloff, 1988; Margules and Pressey, 2000). Several methods and models to achieve reserve contiguity have been developed (Williams et al., 2005; Moilanen et al., 2009; Billionnet, 2013). The conservation of multiple species has been addressed in several studies, with (Beier et al., 2011; Alagador et al., 2012; Jafari and Hearne, 2013; LeBras et al., 2013; Wang and Önal, 2016) or without (McCarthy et al., 2006; Nicholson and Possingham, 2006; Nicholson et al., 2006; Jantke and Schneider, 2010) the consideration of spatial attributes, contiguity in particular, of conservation areas. In those studies, species are usually considered collectively but independently, that is they are treated as a whole with the dependency between them being largely ignored. Recently Wang et al. (2020) presented an optimization method to design conservation areas for these two species in Fort Stewart. In their model they required that a selected GF site must also be a selected GT site, that is, the conservation areas for the GFs must be completely located within the conservation areas for the GTs. Since the GFs have some capacity to travel (usually up to 2 km), that requirement may be relaxed as long as the GFs can travel to some nearby GT burrows to seek refuge.

In this paper, we present a modified optimization model, specifically a mixed-integer programming (MIP) model to address the problem of conservation planning of these two species in Fort Stewart. Rather than locating the GFs’ conservation areas within those of the GTs’, we hypothesize that the GFs’ chance of survival could be promoted by securing a specified number of ponds in each GF conservation area and explicitly model the dependency of the GFs on the GT burrows nearby the GF sites. For this purpose, we have extended one of our previous models which employed the classical p-median formulation for the conservation of a single species (Önal et al., 2016). We require that a specified number of conservation areas for each species is to be configured, each covering an adequate number of vernal ponds for the GFs and/or providing adequate habitat quality for the GTs. We also require that around each GF site there must be some GT sites wherein the GFs could find refuge after they leave the water. We use the model to identify potential conservation areas for both of these two cohabiting species in Fort Stewart military installation. We conclude by discussing some possible extensions of the model.

Methods and the Model

We use integer programming methods from the site selection/reserve design literature to solve the above problem of identifying sites for conservation of the GTs and the GFs. For our specific application in this study, we start by dividing the entire planning area into disjoint spatial units each of which will or will not be selected for conservation. In the general case, each selected unit must protect at least one species, preferably multiple species simultaneously. In the particular application that will be presented here, each selected unit must serve as a protected habitat site for either GT or GF or both. A collection of the selected units that serve a viable population of GT or GF is called a conservation area. The overall conservation plan may include multiple detached conservation areas each serving a particular population of the two species. The spatial units, called sites or cells, may have regular or irregular shapes. In this particular application, we consider regular grid squares as spatial units. Two sites are adjacent if they share a common edge or corner. A conservation area is contiguous if any pair of sites in it can be linked through a chain of adjacent sites all of which are included in the same conservation area. Both the GFs and the GTs need fairly large habitat areas that may range up to several hundred hectares (NatureServeExplorer, 2020). Therefore, we suppose that a site plus the sites adjacent to it (at most nine sites for a grid partition) is large enough for a viable population of each species. We configure each conservation area around a central site where the selection of the central sites and the assignment of selected sites to the individual conservation areas will both be determined endogenously by the model. We require that each conservation area sustains a viable population of the target species either by including an adequate number of ponds for the GFs or by including an adequate amount of carrying capacity for the GTs. We incorporated the dependency of the GFs on the GT burrows by requiring that adjacent to each selected GF site there must be some selected GT site(s) to provide a specified number of burrows. We designed a specified number of conservation areas for each species to promote the likelihood of these species’ long-term survival.

The notation used in the model is as follows. i, j: indexes of candidate sites; s: index of target species, s1 represents the GF, and s2 represents the GT; d_i: the distance from site i to the nearest main road in the military installation; r_s: the number of populations (conservation areas) to be protected for species s; p_i: the number of ponds in site i for the GFs; b_i: the carrying capacity of site i for the GTs; P_f: the minimal number of ponds in a conservation area (to ensure successful reproduction of the GFs in that area); B_t: the minimal carrying capacity of a conservation area for GT (to sustain a viable GT population in that area); B_f: the minimal carrying capacity of the GT sites adjacent to any GF site (to provide burrows to the GFs); N_i: the set of sites adjacent to site i (including site i itself); U_si: a binary variable which takes the value of 1 if site i is selected for species s and 0 otherwise; V_i: a binary variable which takes the value of 1 if site i is selected (for whichever species) and 0 otherwise; X_sji: a binary variable which takes the value of 1 if site j is the center of a conservation area designated to species s and site i belongs to that area.

The algebraic model below configures the specified number of conservation areas for each of these two species. Note that there can be numerous spatial configurations satisfying the conservation requirements outlined above. Here, in addition to the conservation targets, we aim to find the economically most preferable configuration(s). In most conservation planning situations, this normative objective can be measured by the cost of purchasing or leasing the selected sites. In the application we present in this study, the entire planning area is owned by the military, thus no such economic cost is involved. However, there is an operation/maintenance cost involved depending on the location and size of the individual conservation areas. The conservation managers visit individual sites at certain times to perform certain operations such as thinning or burning undesirable bushes, cutting certain trees, or seeding the understory. The cost of manpower to be allocated to such operations can be substantial. A good proxy for those costs could be the distance from the nearest main road, which reflects the burden of having a maintenance tour to the site as the further the selected sites are from the main road, the more difficult it would be to do management works in the conservation area. Therefore, as a proxy to the overall economic cost, we consider the total distance of selected sites to the main roads in the military installation. This simplified proxy measure does not reflect the true cost of conservation tasks to be performed, but it is operational. Each GF conservation area must contain an adequate number of ponds, each GT conservation area must have an adequate GT carrying capacity, and around each GF site, there must be a specified number of GT sites for GFs to find burrows to shelter. The following mathematical model incorporates all these considerations:

$$Min\sum _i{d}_i{V}_i(1)$$

$$\sum _j{X}_{sjj}=r_s\mathrm{for}\mathrm{all}s(2)$$

$$X_{sji}\le X_{sjj}\mathrm{for}\mathrm{all}s,i,j\in N_i(3)$$

$$\sum _{i\in N_j}{p}_i{}^{*}X_{s1ji}\ge P_f{}^{*}X_{s1jj}\mathrm{for}\mathrm{all}j(4)$$

$$\sum _{i\in N_j}{b}_i{}^{*}X_{s2ji}\ge B_t{}^{*}X_{s2jj}\mathrm{for}\mathrm{all}j(5)$$

$$\sum _{j\in N_i}{X}_{sji}=U_{si}\mathrm{for}\mathrm{all}s,i(6)$$

$$\sum _{j\in N_i}{b}_j{}^{*}U_{s2j}\ge B_f{}^{*}U_{s1i}\mathrm{for}\mathrm{all}i(7)$$

$$U_{si}\le V_i\mathrm{for}\mathrm{all}s,i(8)$$

The objective function (1) minimizes the total distance between selected sites and their nearest main road. Constraint (2) specifies the number of populations (or equivalently the number of conservation areas) to be protected for each target species. When X_sjj = 1, site j is a center for species s, and a viable population or equivalently a conservation area sustaining the viable population will be protected around it. Constraint (3) states that if a site i is selected into the conservation area which is centered at site j and designated for the conservation of species s (X_sji = 1), then site j must be a central site for that species (X_sjj = 1). Constraints (4) and (5) are viable population requirements for the GFs and the GTs, respectively. Constraint (4) states that if a site j is selected as the center for a GF conservation area (X_s1jj = 1) then some of its adjacent sites i must be selected and these sites, including site j, collectively cover at least P_f ponds. Constraint (5) is interpreted similarly except that it is stated for the GTs and burrows instead of ponds. Constraint (6) states that if a site i is selected for species s (U_si = 1), then that site belongs to exactly one conservation area for that species (∑_{j ∈ Ni} X_sji = 1); this prevents multiple counting of a site’s contribution to the protection of the same species. A site, however, can be assigned to different conservation areas when these areas are designated for different species. Constraint (7) states that if a site i is selected for the GFs (U_s1i = 1), then within it and the sites adjacent to it there must be some selected GT sites (U_s2j = 1) to provide at least B_f burrows to the GFs. Finally, constraint (8) states that if a site is to be included in a conservation area for one of the two species (U_si = 1), then it must be a selected site (V_i = 1) and will be accounted for in the objective function.

Empirical Application

We applied the model presented above to the dataset of the Fort Stewart military installation in Georgia, United States, considering the GF and GT as target species. The data about the location of the military installation was obtained from Ft. Stewart. The data on the suitability and carrying capacity for the GTs were obtained from National Biological Information Infrastructure (Elliott et al., 2003). The location of vernal ponds were obtained from Ft. Stewart. We overlaid the installation area with a square grid partition that includes 30 rows and 55 columns where each square in the partition (cells or sites) has an edge of 1 km. In the data, the carrying capacity of individual cells ranges between 0 and 601 GTs per cell, and the number of ponds in each cell ranges between 0 and 13. Figure 1 shows the locations of the ponds, the density of GT carrying capacity, and the cells’ distances to the nearest road. We first designed conservation areas for these two species with no consideration of the dependency of GF on GT burrows, that is, we solved the model without constraint (7) (Plan A). We then generated alternative site selections by varying the number of conservation areas for individual species (r_s), the minimum number of ponds in individual GF conservation area (P_f), the minimum value of carrying capacity of the individual GT conservation area (B_t), and the minimum value of carrying capacity of GT sites adjacent to GF sites (B_f). The sites that have at least one pond in each have an average value of 25 ponds in their adjacent sites (including the site itself). Similarly, those sites that have a non-zero GT carrying capacity have an average of 578 GT carrying capacity in their adjacent sites (including the site itself), and the average GT carrying capacity across those sites is 68. We set the values of P_f, B_t, and B_f higher than these values so that the model will select high-quality sites. Here we present the results with r_s = 2, P_f = 40, and B_t = 700, that is, we design two conservation areas for each species and require each GF conservation area to contain at least 40 ponds and each GT conservation area to have a carrying capacity of at least 700 individuals. We set the values of B_f at 100 (Plan B) then at 200 (Plan C) to investigate the sensitivity of results to the number of burrows in the sites adjacent to a selected GF site. We used Gurobi (9.0.2) integrated in GAMS (32.1.0) to solve the model (GAMS, 2021). Our computer was a Lenove Desktop with an Intel Pentium CPU of 2.8 GHz and a RAM of 8.0 GB.

FIGURE 1

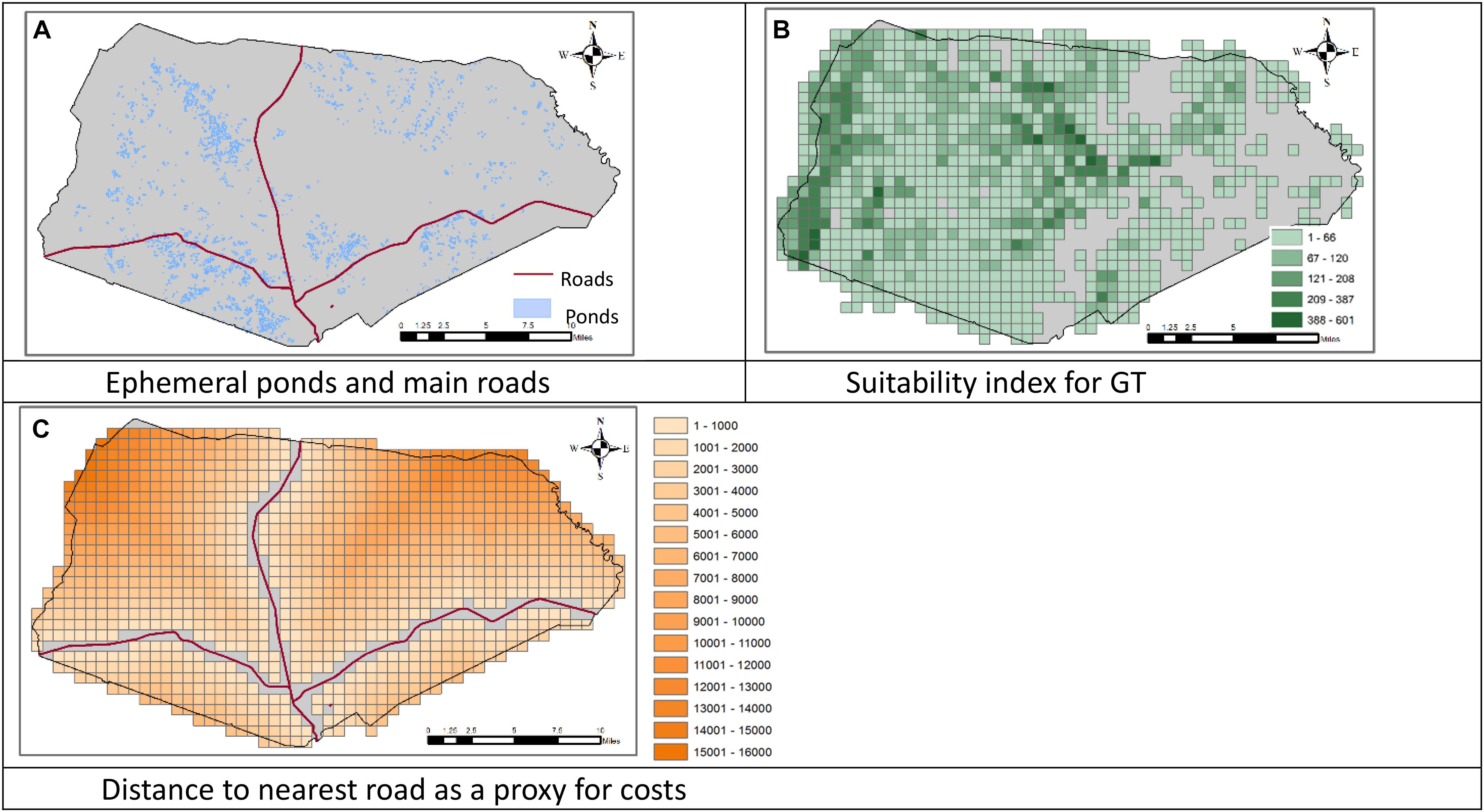
Figure 1. Locations of the ephemeral ponds and roads, the suitability of the land to support the Gopher Tortoise (GT), and the distance to nearest road in the Fort Stewart military installation in Georgia, United States. (A) Ephemeral ponds and main roads. (B) Suitability index for GT. (C) Distance to nearest road as a proxy for costs.

Figure 2 displays the locations and spatial layouts of the selection results for the three conservation plans described above. Table 1 summarizes those selection results, including the number of selected sites in each conservation plan, the total and average distances between the selected sites and the nearest main roads to them, and the extent of overlapping of the GF sites with the GT sites.

FIGURE 2

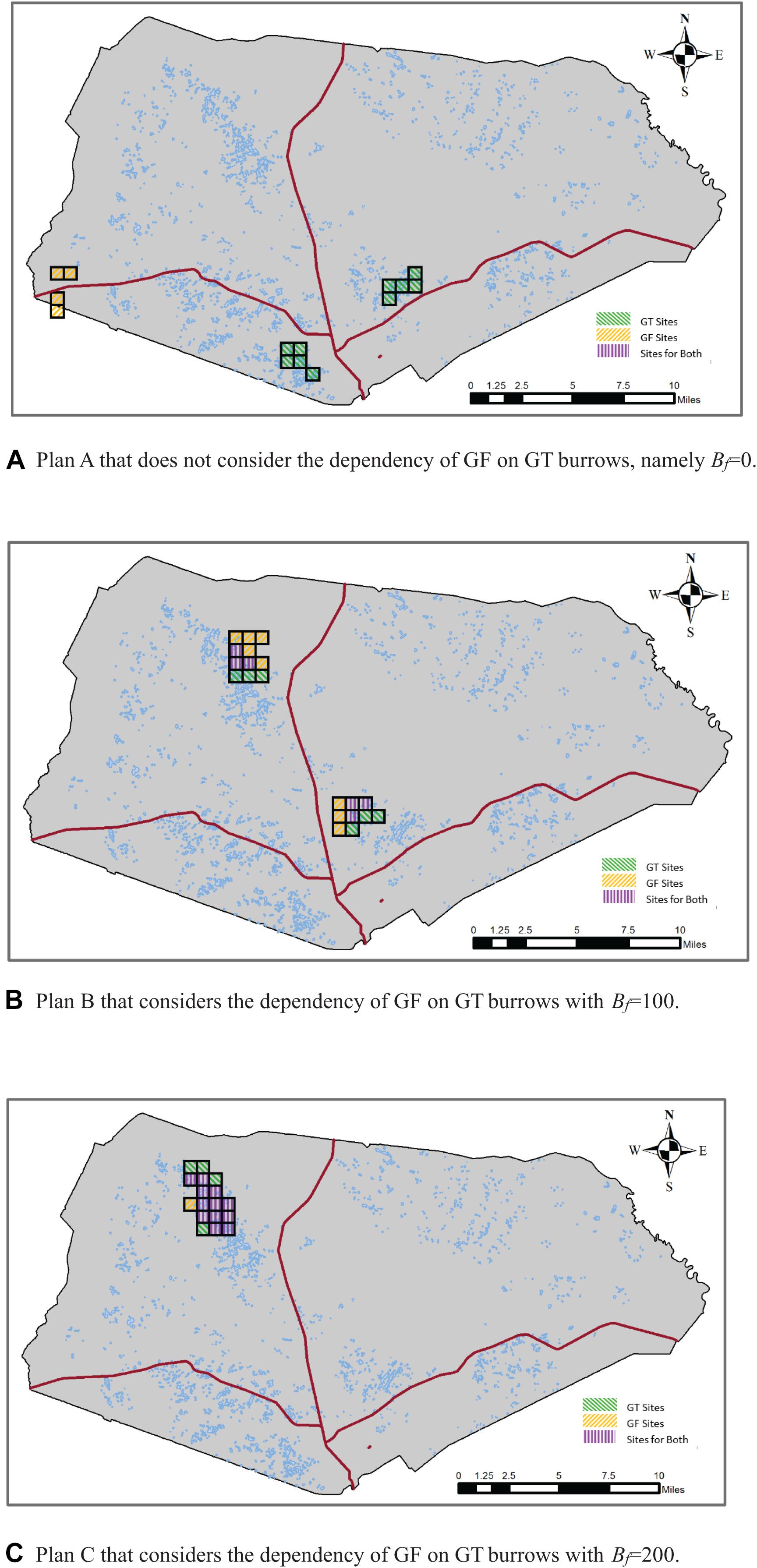
Figure 2. Selection results of alternative conservation plans with r_s = 2, P_f = 40, and B_t = 700. (A) Plan A that does not consider the dependency of Gopher Frog (GF) on GT burrows, namely B_f = 0. (B) Plan B that considers the dependency of GF on GT burrows with B_f = 100. (C) Plan C that considers the dependency of GF on GT burrows with B_f = 200.

TABLE 1

Table 1. Summary of selected results for alternative conservation plans.

In Plan A where we did not consider the dependency of GF on GT burrows, a total of 14 sites were selected (Table 1). The conservations areas for GF and GT were separated and far apart from each other (Figure 2A), with no overlap of the GF sites with the GT sites. In Plan B, where we considered the dependency of GF on GT burrows and required that around each GF site there must be some GT sites to provide at least 100 burrows, a total of 20 sites were selected, among those 12 were GF sites. Of those 12 GF sites, six sites were also GT sites, thus resulting in a 50% overlap of the GF sites with the GT sites. In Plan C, where we increased the minimum number of burrows (B_f) to 200, a total of 17 sites were selected for the two species. Those sites were clustered and formed one big conservation area located in the northwest of the installation. Of the 17 selected sites, 13 were GF sites of which 12 were also GT sites, resulting in a 92% overlap. As the conservation goal was made more ambitious, the cost of the conservation program, namely the total distance between the selected sites to the nearest main roads, increased. These results are intuitive because when the dependency of GF on GT burrows was not considered, the model selected the GF sites and the GT sites nearest to the main roads to minimize the total distance. When the dependency of GF on GT burrows was considered, the selected GF and GT sites must be either overlapping or adjacent to each other so that the GFs could find burrows in those GT sites. When a greater number of burrows was required, a higher percentage of the selected GF sites were overlapping with the GT sites, as can be expected. We note that it is just a coincidence that in this particular application the conservation areas for the two species were clustered to form one big conservation area in Plan C. This is a matter of the data set used here, in particular the distances between those sites to the nearest main roads and the distributions of ponds and burrows across those sites. It is possible that when a greater number of burrows are required to be adjacent to the GF sites, the model could configure two separate conservation areas as shown in Figure 2B.

Our empirical results suggest that the model is solvable without serious computational difficulty, which is an important concern when working with mixed-integer programming models. In the model, we allowed the selection of all of the 1,650 sites included in the partition (30 rows and 55 columns) except those sites that include part of a main road in them. This resulted in a fairly large-scale model including 35,402 equations and 33,639 variables. Yet, the model could be solved in less than 1 s under all the scenarios described above. This is a clear indication that the model could be an extremely useful computational tool even in larger empirical applications (more interacting species to protect and more sites to choose). The solution times were very small in this particular application possibly because only a small number of selected sites could satisfy the conservation goals. We speculate that the solution time could increase significantly with the number of sites to be selected under stringer conservation goals, which is yet to be tested.

Conclusion and Discussion

We have developed a MIP model for the conservation site selection problem of two important species, GT and GF in the military installation of Fort Stewart in Georgia, United States. The model selects a specified number of conservation areas for each species, with each area satisfying a specified conservation goal to promote the long-term survival of the two target species. We integrated the dependency of the GFs on GT burrows by selecting GT sites around each GF site to ensure the GFs’ accessibility to GT burrows. The methods are generalizable to other reserve site selection and land management settings with cohabiting interrelated species.

In our previous work where the same area and species were used in the empirical application (Dissanayake et al., 2014; Wang et al., 2020), we incorporated the dependency of the GFs on GT burrows when targeting to conserve these two species. In this paper, we emphasized the importance of considering this interspecies dependency and showed that the results could be dramatically different if this dependency was ignored (compare panel A with panels B and C in Figure 2). Also, based on the fact that the GFs have some capacity to travel, we relaxed the requirement that all selected GF sites be GT sites. Instead, we required that a selected GF site must have some selected GT sites adjacent to it to provide an adequate number of burrows so that the GFs can find refuge in those burrows when weather conditions are not favorable in and around seasonal ponds that they normally rely on. This permits some level of non-overlapping of the GF conservation areas with the GT conservation area and offers additional flexibility in conservation planning. As the required number of these burrows becomes larger, one would expect the GF conservation areas to overlap more with those of the GTs. Our empirical results confirm this intuitive expectation.

In most cases, spatial considerations play a crucial role in the effective functioning of nature conservation areas. Contiguity and compactness, in particular, are given special emphasis by conservation planners. This is the case also when designing economically and ecologically effective conservation planning strategies for the GFs and GTs considered in this paper. Although we did not include a direct mechanism to impose contiguity and compactness in the model, both the contiguity and compactness of the joint conservation areas are promoted by selecting sites adjacent to central sites (both the selected areas and their centers are determined by the model). This is because neither of these species needs a very large home range to sustain a viable population, and therefore a central site along with the sites adjacent to it would be large enough (about 900 ha) to meet the specified conservation goals. This renders us the convenience in model building as we can omit the contiguity requirement. If, however, a larger conservation area is to be established and some sites not necessarily adjacent to the center sites need to be included in the selection, the contiguity of selected sites has to be enforced explicitly. The model presented here can be modified for that purpose by introducing explicit constraints to achieve contiguity of the conservation areas. We note, however, that spatial contiguity is a difficult issue to address in an optimization framework. Although a few alternative modeling approaches have been presented in the literature (see, e.g., Önal et al., 2016; Wang et al., 2020), those approaches suffer from computational inefficiency. In general, MIP models become difficult to solve to exact optimality as the model size becomes larger. This is the case when spatial attributes, such as contiguity and compactness, are considered because incorporating these attributes requires additional constraints and discrete variables, which can be numerous when a large number of sites are involved in the analysis. It is highly likely that the super computational efficiency of the model we present here would also be compromised if we explicitly imposed contiguity. Readers who are interested in modeling spatial attributes, contiguity in particular, and the computational performance aspects of those models, are referred to Wang et al. (2018).

Due to the data availability, we have used the number of ponds as a proxy for the likelihood of successful breeding of the GFs in each conservation area, without considering other data features such as the area of each pond and its probability of going dry. Ideally, those data should be obtained as they probably are more relevant in describing the conservation planning goals. The model presented here could be modified to incorporate those data when they are available. For example, instead of conserving a specified number of ponds in each conservation area for the GFs, we may secure a certain amount of total pond area, or ensure a specified threshold probability of having water in at least some GF sites within the conservation area. Incorporating such uncertainties into the model would require a nonlinear model which may be difficult to solve to optimality. However, the difficulty may be overcome by using linearization techniques that transform the nonlinear model into a linear one (see, e.g., Wang and Önal, 2016). We are planning to utilize the pond area and/or survival probability in our future research.

Pond-breeding species such as the GFs used in this paper generally have very limited abilities to disperse and often form metapopulations that may be scattered across the landscape and far apart from each other (Marsh and Trenham, 2001; Smith and Green, 2005). In conservation planning for such species, it may be desirable to consider the metapopulation dynamics of species. One way to promote the likelihood of species’ long-term persistence would be achieving some level of connectivity for those metapopulations (Hanski, 1998; Baguette, 2004). Although the model presented in this paper configures multiple conservation areas (specified by the parameter r_s) for individual target species, it does not consider the metapopulation dynamics of the species. The model can be modified to encourage interactions between species populations by requiring that around the center site (represented in the model as the binary variable X_sjj) of each conservation area there should be, for example, at least one other center site around which another conservation area is formed. The model may also be modified to discourage interactions between species populations by requiring that two sites could not both serve as center sites if the distance between them is under a distance threshold.

Finally, our model has been static in the sense that it selects conservation areas that, once selected, would presumably exist for at least a quite long period. Because military training may take different forms over the year and may require different geographic conditions in different locations, it may be reasonable to integrate the conservation selections with military training requirements by taking into account the life cycle of target species, such as breeding, larval, and dispersal periods. More data including species life cycle and military training activities would be needed. We did not explore this thread of thoughts in the present paper, but our model provides a basis on which a more realistic and applicable conservation selection model may be developed.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

SD, HÖ, and YW contributed to the conception and design of the study. HÖ and YW created the model. YW conducted the simulation, generated results, and wrote the first draft of the manuscript. SD provided the application data. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

Publication of this article in an open access journal was funded by the Portland State University Library’s Open Access Fund.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^ The dependency of the GFs on GT burrows is not strict as the GFs can also use other burrows or tree stumps (Smith et al., 2021). However, the dependency is believed to be high. Smith et al. (2021) conducted a scientific sampling of GT burrows and found 274 GFs in 1,097 GT burrows located at four different sites with GF occupancy rates ranging from 0.17 to 0.25 across the four sites. They also note that the GF occupancy rate in GT burrows occupied by GTs is even higher, in the range of 0.49–0.79.

References

Alagador, D., Trivino, M., Cerdeira, J., Bras, R., Cabeza, M., and Araújo, M. (2012). Linking like with like: optimising connectivity between environmentally-similar habitats. Landsc. Ecol. 27, 291–301. doi: 10.1007/s10980-012-9704-9

CrossRef Full Text | Google Scholar

Alexy, K. J., Brunjes, K. J., Gassett, J. W., and Miller, K. V. (2003). Continuous remote monitoring of gopher tortoise burrow use. Wildl. Soc. Bull. 31, 1240–1243.

Google Scholar

Ando, A., Camm, J. D., Polasky, S., and Solow, A. (1998). Species distributions, land values and efficient conservation. Science 279, 2126–2128. doi: 10.1126/science.279.5359.2126

PubMed Abstract | CrossRef Full Text | Google Scholar

Aycrigg, J., Belote, R., Dietz, M., Aplet, G., and Fischer, R. (2015). Bombing for biodiversity in the United States: response to Zentelis & Lindenmayer 2015. Conserv. Lett. 8, 306–307. doi: 10.1111/conl.12197

CrossRef Full Text | Google Scholar

Baguette, M. (2004). The classical metapopulation theory and the real, natural world: a critical appraisal. Basic Appl. Ecol. 5, 213–224. doi: 10.1016/j.baae.2004.03.001

CrossRef Full Text | Google Scholar

Beier, P., Spencer, W., Baldwin, R. F., and McRae, B. H. (2011). Toward best practices for developing regional connectivity maps. Conserv. Biol. 25, 879–892. doi: 10.1111/j.1523-1739.2011.01716.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Billionnet, A. (2013). Mathematical optimization ideas for biodiversity conservation. Eur. J. Oper. Res. 231, 514–534. doi: 10.1016/j.ejor.2013.03.025

CrossRef Full Text | Google Scholar

Cocks, K. D., and Baird, I. A. (1989). Using mathematical programming to address the multiple reserve selection problem: an example from the Eyre Peninsula. South Australia. Biol. Conserv. 49, 113–130. doi: 10.1016/0006-3207(89)90083-9

CrossRef Full Text | Google Scholar

Compton, B. W., McGarigal, K., Cushman, S. A., and Gamble, L. R. (2007). A resistant-kernel model of connectivity for amphibians that breed in vernal pools. Conserv. Biol. 21, 788–799. doi: 10.1111/j.1523-1739.2007.00674.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Diamond, J. M. (1975). The island dilemma: lessons of modern biogeographic studies for the design of natural reserves. Biol. Conserv. 7, 129–146. doi: 10.1016/0006-3207(75)90052-x

CrossRef Full Text | Google Scholar

Dissanayake, S. T. M., Önal, H., Westervelt, J. D., and Balbach, H. (2014). “Optimal selection of clustered conservation lands using integer programming: the case of Fort Stewart in Georgia, USA,” in Handbook on the Economics of Ecosystem Services and Biodiversity, eds P. A. L. D. Nunes, P. Kumar, and T. Dedeurwaerdere (Cheltenham: Edward Elgar Publishing), 193–207. doi: 10.4337/9781781951514.00018

CrossRef Full Text | Google Scholar

Elliott, M., Anderson, L., Bumback, B., Schmidt, J. P., and Kramer, L. (2003). Gap Analysis Project: Georgia GAP Reptile Models 2008. Athens, GA: USGS and University of Georgia Institute of Ecology. Available online at: http://gapanalysis.nbii.gov

Google Scholar

Gamble, L. R., McGarigal, K., and Compton, B. W. (2007). Fidelity and dispersal in the pond-breeding amphibian, ambystoma opacum: implications for spatio-temporal population dynamics and conservation. Biol. Conserv. 139, 247–257. doi: 10.1016/j.biocon.2007.07.001

CrossRef Full Text | Google Scholar

GAMS (2021). GAMS Development Corporation, GAMS Software GmbH. Available online at: http://www.gams.com/ (accessed June 6, 2021).

Google Scholar

Hanski, I. (1998). Metapopulation dynamics. Nature 396, 41–49.

Google Scholar

IUCN (2021). International Union for Conservation of Nature Red List. Available online at: https://www.iucnredlist.org/species/9403/12983629 (accessed July 20, 2021).

Google Scholar

Jafari, N., and Hearne, J. (2013). A new method to solve the fully connected reserve network design problem. Eur. J. Oper. Res. 231, 202–209. doi: 10.1016/j.ejor.2013.05.015

CrossRef Full Text | Google Scholar

Jantke, K., and Schneider, U. A. (2010). Multiple-species conservation planning for European wetlands with different degrees of coordination. Biol. Conserv. 143, 1812–1821. doi: 10.1016/j.biocon.2010.04.036

CrossRef Full Text | Google Scholar

Joly, P. (2019). Behavior in a changing landscape: using movement ecology to inform the conservation of pond-breeding amphibians. Front. Ecol. Evol. 7:155. doi: 10.3389/fevo.2019.00155

CrossRef Full Text | Google Scholar

Kieran, S. R. C., Hull, J. M., and Finger, A. J. (2021). Environmental DNA sampling provides new management strategies for vernal pool branchiopods in California. PLoS One 16:e0243338. doi: 10.1371/journal.pone.0243338

PubMed Abstract | CrossRef Full Text | Google Scholar

LeBras, R., Dilkina, B., Xue, Y., Gomes, C. P., McKelvey, K. S., Schwartz, M. K., et al. (2013). “Robust network design for multispecies conservation,” in Proceedings of the 27th AAAI Conference on Artificial Intelligence (Bellevue, Was).

Google Scholar

Margules, C. R., and Pressey, R. L. (2000). Systematic conservation planning. Nature 405, 243–253.

Google Scholar

Marsh, D. M., and Trenham, P. C. (2001). Metapopulation dynamics and amphibian conservation. Conserv. Biol. 15, 40–49. doi: 10.1111/j.1523-1739.2001.00129.x

CrossRef Full Text | Google Scholar

McCarthy, M. A., Thompson, C. J., and Williams, N. S. G. (2006). Logic for designing nature reserves for multiple species. Am. Nat. 167, 717–727. doi: 10.2307/3844778

CrossRef Full Text | Google Scholar

Moilanen, A., Wilson, K. A., and Possingham, H. P. (2009). Spatial Conservation Prioritization: Quantitative Methods and Computational Tools. Oxford: Oxford University Press.

Google Scholar

NatureServeExplorer. (2020). NatureServeExplorer. Available online at: https://explorer.natureserve.org/Taxon/ELEMENT_GLOBAL.2.105963/Lithobates_capito (accessed October 8, 2020).

Google Scholar

Nicholson, E., and Possingham, H. P. (2006). Objectives for multiple-species conservation planning. Conserv. Biol. 20, 871–881. doi: 10.1111/j.1523-1739.2006.00369.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicholson, E., Westphal, M. I., Frank, K., Rochester, W. A., Pressey, R. L., Lindenmayer, D. B., et al. (2006). A new method for conservation planning for the persistence of multiple species. Ecol. Lett. 9, 1049–1060. doi: 10.1111/j.1461-0248.2006.00956.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Önal, H., Wang, Y., Dissanayake, S. T., and Westervelt, J. D. (2016). Optimal design of compact and functionally contiguous conservation management areas. Eur. J. Oper. Res. 251, 957–968. doi: 10.1016/j.ejor.2015.12.005

CrossRef Full Text | Google Scholar

Petersen, C., Lovich, R. E., and Stallings, S. (2016). Herpetofauna Biodiversity on United States Army Installations. Final Report. Jefferson, MO: Department of Defense Legacy Resource Management Program.

Google Scholar

Roznik, E. A., and Johnson, S. A. (2009). Burrow use and survival of newly metamorphosed Gopher Frogs (Rana capito). J. Herpetol. 43, 431–437. doi: 10.1670/08-159r.1

CrossRef Full Text | Google Scholar

Simberloff, D. (1988). The contribution of population and community biology to conservation science. Annu. Rev. Ecol. Syst. 19, 473–511. doi: 10.1146/annurev.es.19.110188.002353

CrossRef Full Text | Google Scholar

Smith, L. L., Howze, J. M., Staiger, J. S., Sievers, E. R., Burr, D., and Enge, K. M. (2021). Added value: gopher tortoise surveys provide estimates of Gopher Frog abundance in tortoise burrows. J. Fish Wildl. Manag. 12, 3–11.

Google Scholar

Smith, M. A., and Green, D. M. (2005). Dispersal and the metapopulation paradigm in amphibian ecology and conservation: are all amphibian populations metapopulations? Ecography 28, 110–128. doi: 10.1111/j.0906-7590.2005.04042.x

CrossRef Full Text | Google Scholar

Sterrett, S. C., Katz, R. A., Fields, W. R., and Grant, E. H. C. (2019). The contribution of road-based citizen science to the conservation of pond-breeding amphibians. J. Appl. Ecol. 56, 988–995. doi: 10.1111/1365-2664.13330

CrossRef Full Text | Google Scholar

Wang, Y., Fang, Q., Dissanayake, S. T. M., and Önal, H. (2020). Optimizing conservation planning for multiple cohabiting species. PLoS One 15:e0234968. doi: 10.1371/journal.pone.0234968

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., and Önal, H. (2016). Optimal design of compact and connected nature reserves for multiple species. Conserv. Biol. 30, 413–424. doi: 10.1111/cobi.12629

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Önal, H., and Fang, Q. (2018). How large spatially-explicit optimal reserve design models can we solve now? An exploration of current models’ computational efficiency. Nat. Conserv. 27, 17–34. doi: 10.3897/natureconservation.27.21642

CrossRef Full Text | Google Scholar

Williams, J. C., ReVelle, C. S., and Levin, S. A. (2005). Spatial attributes and reserve design models: a review. Environ. Model. Assess. 10, 163–181. doi: 10.1007/s10666-005-9007-5

CrossRef Full Text | Google Scholar

Zentelis, R., and Lindenmayer, D. (2015). Bombing for biodiversity-enhancing conservation values of military training areas. Conserv. Lett. 8, 299–305. doi: 10.1111/conl.12155

CrossRef Full Text | Google Scholar