Theoretical perspectives on reproductive aging

Age patterns of female reproduction vary widely among iteroparous animal species with determinate growth. Often fertility declines with age, but in other cases, it may be flat or rise across age. Sometimes fertility ceases altogether, leaving a substantial post-reproductive life span. In this article, we discuss theories that may provide some insights into how these diverse patterns might evolve. We present a simple optimal life history model and consider circumstances in which fertility might rise or fall with age. In our model, without assuming that costs per birth rise with age, that foraging efficiency declines, or that net intergenerational transfers increase, we find that optimal fertility would tend to rise rather than decline. This happens because less energy would be allocated to survival at older ages, leaving more to allocate to fertility. In our analysis, optimal fertility could decline at older ages when an older female makes heavy net intergenerational transfers to multiple offspring or grandoffspring, reducing resources for her own reproduction. This pattern is more likely to evolve when costs of fertility at older ages are higher, when costs of reducing juvenile mortality are low, and when the level of juvenile mortality is high. We also derive conditions for the evolution of menopause, for determinate growth, and for juvenile mortality that declines with age. The optimal life history can exhibit a variety of age patterns of fertility, rising, flat, or falling, depending on the constraints and opportunities faced.

1. Introduction

Why do humans and other animals age and die? This question has attracted much theoretical and empirical attention in recent decades. The question of why fertility declines with age in so many species has attracted far less attention (Monaghan et al., 2008).

Empirical studies have found a wide variety of age patterns of fertility across the animal kingdom. For most but not all mammals fertility declines at older ages (Jones et al., 2014; Lemaître et al., 2020), although in some species, it is flat or rises with age. Non-mammalian vertebrates often have flat or rising fertility with age. Birds have slow or negligible reproductive aging (Holmes et al., 2003). Reptiles, tortoises, and amphibians often have slow or negligible aging (da Silva et al., 2022; Reinke et al., 2022). Invertebrates show all patterns, but most often fertility declines at older ages (Jones et al., 2014). A number of species besides humans and toothed whales have substantial post-reproductive survival, including nematodes and rotifers (Jones et al., 2014).

A theory of reproductive aging must be sufficiently flexible to accommodate these many different possible age patterns. Here, we explore how and why evolution might sometimes lead to reproductive senescence, but at other times to flat or rising fertility and at still other times to menopause or lifetime infertility. Fertility is centrally important in evolutionary theory, but we suggest that it cannot be analyzed in isolation from other key aspects of life history such as survival, growth, foraging efficiency, parental and grandparental transfers, and broader social organization. For this reason, we begin with a review of some topics in life history theory and their relation to fertility.

Medawar (1952/1957) and Williams (1957) initiated modern evolutionary thinking on senescence and death. Hamilton (1966) formalized one of their central insights, that deleterious mutations that raised mortality at older ages would reduce reproductive fitness less than those raising it at younger ages, and so natural selection would remove them from the population more weakly and slowly at older ages, causing mortality to rise with age. This approach, emphasizing mutation accumulation, has been developed further (Charlesworth, 1994; Caswell and Salguero-Gómez, 2013; Wachter et al., 2014). According to this approach, senescence is “purely maladaptive” (Partridge and Barton, 1993) and occurs because the forces of selection are not sufficiently powerful at older ages to rid the population of continuously occurring deleterious mutations.

If applied to fertility in the same way, the mutation accumulation approach implies that fertility should decline with age in proportion to declining survivorship as measured by the life table l_x function (Hamilton, 1966). However, Hamilton (1966) warned us that this approach would be less useful for fertility: “…it is not so plausible that a gene could simply add an element of fertility at a given age without affecting the rest of the schedule as it is that a gene might cause the elimination of a single element of mortality.” Raising survival by eliminating a deleterious mutation would not necessarily require additional energy. However, adding a birth would certainly require nutritional energy taken either from siblings or from the mother’s own bodily reserves, which would adversely affect fertility and survival at other ages. A mutation accumulation approach can still be adopted but these energetic tradeoffs would need to be taken into account and would make the theory more complicated (Lee, 2003).

A very different approach develops the idea that senescence is adaptive. If an organism was to allocate more energy to maintaining its soma and postponing death, it would require energy that could otherwise be used for reproduction earlier in life, perhaps reducing fitness. This is the disposable soma theory of Kirkwood (1977) which has been developed in formal models of optimal life history theory. In these models, an organism acquires energy at each age and allocates it among somatic maintenance and survival, fertility, and growth. Under natural selection, the organism moves toward the pattern of energy allocation by age which maximizes its lifetime reproductive fitness as beneficial mutations are positively selected rather than through the negative selection of deleterious mutations, as emphasized by Hamilton.

Mutation accumulation theory cannot explain or predict age patterns of fertility and mortality de novo. Its predictions about mortality depend on a given age pattern of fertility and conversely. Optimal life history theory does provide an initial age pattern of rates (based on many assumptions), but it ignores the insights of mutation accumulation theory. A full account would require attention to both. Partridge and Barton (1993) provided worked-out examples and a useful diagram that illustrates the interaction of the two evolutionary processes. Mutation accumulation would blur and modify the optimal life history results, but the basic shapes of the age schedules would reflect the optimal patterns. Danko et al. (2012) concluded that mutation accumulation could raise old age mortality but would have very little effect on the evolved mean age at reproductive maturity, which was very largely determined by adaptive (optimizing) forces. These considerations suggest the value of an approach that can derive the evolutionarily optimal age profiles themselves that reflect tradeoffs in energetic allocations across the life history.

Others have applied the optimal life history approach to age patterns of fertility when there are tradeoffs with mortality and fertility at later ages, a topic called “the general life history problem” (Charlesworth and Leon, 1976; Stearns, 1992, 2000; Charlesworth, 1994). The main result, as summarized by Stearns (2000), is that when mortality is higher at a range of adult ages, optimal reproduction will be higher before those ages and lower after those ages.

Our approach is related to the general life history problem, but we impose more structure. We develop a simple optimal life history model to consider the joint evolution of age patterns of fertility, mortality, growth, and intergenerational transfers. We use variations on our basic optimal life history model to investigate interrelated topics relevant to reproductive senescence. Tradeoffs between fertility and mortality occur through the energy budget equation at each age and intergenerational transfers are also explicitly taken into account. This formulation makes the results easier to interpret (we hope) but also reduces their generality.

We now briefly introduce the main topics or scenarios that we will consider.

1.1. Menopause

Hamilton (1966), of course, realized that extensive post-reproductive survival in women was inconsistent with his analysis of senescence, but he noted “As remarked by Williams, an obvious excuse for this discrepancy is to be found in the factor of parental care,” a point closely related to the “Grandmother Hypothesis” (Hawkes et al., 1998), and the thrust of our model and analysis here. While we realize there are many theories of the evolution of menopause, for example, as reviewed in a game theory framework by Thouzeau and Raymond (2017), we believe that intergenerational transfers are central. The budget constraint of an isolated individual is constrained by the energy it acquires itself at each age through foraging, which it then allocates at that age among growth, survival, and reproduction. However, in many species, females (and sometimes males) make significant investments in their offspring after birth, e.g., feeding, guarding, sheltering, training, or warming them. When such investments extend over time, perhaps leading to multiple simultaneously dependent offspring (as with humans), then later life fertility could be affected. The extreme case here is menopause with lengthy post-reproductive survival. We analyze the conditions under which this menopause pattern would be optimal. Due to the costs of supporting multiple dependent offspring, this typically occurs in a broader social context in which grandmothers and other kin, and possibly non-kin as well, help invest in the offspring. A study of the Tsimane, a contemporary Amazon Basin forager-horticulturalist group, illustrates this point (Hooper et al., 2015:S3). Average total net caloric transfers to children and grandchildren are nearly as high at ages in the 50s as in the 30s and 40s and they remain substantial through the 60 s before declining. Distant kin and non-kin also make transfers. Another recent study draws on data from multiple hunter-gatherers and horticulturalist groups to estimate the direct fitness from own fertility and indirect fitness from transfers, taking relatedness into account. It concludes that “Under reasonable assumptions, these [indirect fitness] benefits are the equivalent to having up to several more offspring after age 50.” (Davison and Gurven, 2022, text in square brackets added).

1.2. The age pattern of juvenile mortality

Hamilton (1966) wrote “None of the schedules of forces of selection … can account for the rise in mortality in younger and younger pre-reproductive ages.” Indeed his analysis implies that mortality at all ages before reproductive maturity should be constant and very low because death at any pre-reproductive age entails a loss of 100% of reproductive fitness, whether the age is younger or older. This predicted low and flat mortality pattern is inconsistent with observed juvenile mortality as Hamilton was well aware, paralleling the problem with human post-reproductive survival. Again, he suggests that “…parental care brings the necessary trend,” although he did not include it in his model. As we incorporate intergenerational transfers in our model, we can show that juvenile mortality should instead decline with age (Lee, 2003; Chu et al., 2008), here demonstrated in a new way. However, we recognize that these transfers can be only one among a number of reasons why infant/juvenile mortality declines with age since this also occurs in species that do not make transfers after birth.

1.3. Determinate growth vs. indeterminate growth with lifelong reproduction

An earlier study (Taylor et al., 1974) showed that with a linear budget constraint, the optimal life history would initially invest solely in survival and growth and then, after a certain age, switch to investing solely in survival and fertility, a pattern known as “determinate growth.” With a non-linear budget constraint, however, the optimal outcome could instead be “indeterminate growth” in which resources are allocated to growth, survival, and fertility throughout the entire life span. This can result in “negative senescence” in the sense that body size grows over a life span leading to declining mortality and increasing fertility (Vaupel et al., 2004; Baudisch, 2008). Mammals (with some possible exceptions) and birds exhibit determinate growth, while many fish, amphibians, and reptiles exhibit indeterminate growth. The distinction is very important since reproductive senescence is not to be expected in species with indeterminate growth. In this study, we will derive the determinate growth result in a new way.

1.4. Reproductive senescence in determinate growth species

We address the conditions under which evolved fertility may rise, fall, or be flat in determinate growth iteroparous species like mammals and birds. Our analysis, which builds on the preceding topics, includes the roles of intergenerational transfers, foraging efficiency, and the energetic costs of fertility and survival. We believe that our analysis and results here are new. Perhaps, most strikingly, we find that if none of these just-listed factors varies with age (e.g., if net transfers do not rise with age and if foraging efficiency does not decline), then optimal fertility would rise with age, the opposite of reproductive senescence. Later, we will discuss the interpretation of this result and suggest an alternative approach for future research.

2. Formal analysis of reproductive aging in optimal life histories

We focus on female fertility in iteroparous animal species with determinate growth. Our models are generally single sex. For simplicity of exposition, our models have at most three age classes that are sufficient to see whether fertility rises or declines with age and to derive other useful results. Readers interested in similar treatments with many age classes or with continuous age distributions will find them in our other articles such as Chu et al. (2008) and Chu and Lee (2013). Our modeling approach is conceptual in the sense that we do not try to derive realistic age schedules of fertility and mortality in contrast, for example, to the explicit results in Drenos and Kirkwood (2005) (who assume parametric fertility schedules that decline with age). Instead, our goal is to see under what conditions evolutionary forces might lead to different qualitative age patterns of fertility: decreasing or increasing with age or ceasing altogether as with menopause.

2.1. Optimal life history models

We consider several different one-sex (female) models in which each individual lives either one, two, or at most three periods. Everyone dies after period three. We call these periods age-0, age-1, and age-2. We interpret them as childhood, young adulthood, and old age, or sometimes as childhood, youth (Juvenilehood), and adulthood. We start with the most general version of the model, before considering special cases.

An individual starts life at age-0 with an initial body mass, w₀, provided by its mother out of her energy budget based on her evolved life history. With a given body mass w_a at age a, an individual can acquire energy γw_a through foraging or hunting, where γ is a coefficient expressing the way foraging efficiency (energy generation) is related to body size. If the foraging/hunting activity is carried out cooperatively with other co-residing kin members, the setting is different, and we will consider this case elsewhere. At each age x ∈ {0, 1, 2}, the individual may acquire energy both through foraging (γw_x) and through a net transfer of energy from older individuals aged a > x. T_a is the possible net energy transfer received or given at age a; T_a > 0 if one is receiving net energy at age a, and T_a > 0 if one is transferring net energy to others at age a.

We use the three-age scenario because it is the simplest structure needed to explain some age patterns of fertility and mortality. With an appropriate interpretation, this three-age setting is, in fact, quite general. If there are more than three ages, conventional dynamic programming says that individuals can always first optimize from age-3 onward, and then do the second-stage optimization by taking the optimized fitness value at the end of period 3 as given. Thus, age-3 can be thought of as including “the remaining life periods from age-3 onward.”

In some cases to be discussed, we do not need three ages to tell the story, and then we will simplify the model accordingly. Sometimes we will need a minor modification to illustrate a point, and then we will introduce this modification only for that illustration.

Let us begin with an organism that after its birth must rely entirely on the energy it acquires on its own. At each age a, the organism acquires energy, γw_a, and allocates it either to maintenance or reproduction. Reproduction requires energy to build and maintain the necessary organs, to produce eggs and provide nutrients, to find and acquire a breeding site, and to find and choose a mate (in more complicated two-sex models). Maintenance requires energy to avoid and repair somatic damage and avoid illness and predation raising the probability of survival to the end of the period. Specifically, for each individual, we have the following energy constraint:

$b_a{p}_a+c_a{m}_a+d_a{z}_a=\mathrm{\gamma }{w}_{a}a=0,1(1)$

where b_a and c_a are cost coefficients, p_a is the probability the agent survives to the end of period a, and m_a is the number of live births successfully produced.¹ The interpretation of Eq. 1 is that at age a, in order to increase p_a (probability of surviving) by △p_a, it needs b_a△p_a of energy input, and similarly for fertility m_a. The cost of providing the initial body mass for each offspring is included in the individual’s cost per birth, c_a.

In this 3-age setting, the optimal life history in the evolutionary sense can be viewed as maximizing expected lifetime births,

$max\left\{l_0{m}_0+l_1{m}_1+l_2{m}_2\right\}(2)$

where $l_x={\prod }_{i=0}^x{p}_i$. For any given w_a, a = 0, 1, 2, the control variables are p_a and m_a. Therefore, the problem is to choose p_a and m_a to maximize {l₀m₀ + l₁m₁ + l₂m₂}. Let an * indicate the optimal value, so the optimal controls are written as ${\text{l}}_{\text{a}}^{*}$, ${\text{p}}_{\text{a}}^{*}$, and $m_a^{*}$.²

Now, we consider possible transfers. Given any transfers T_a, a = 0, 1, 2, the available energy on the right-hand side of Eq. 1 becomes E_a = γw_a + T_a. The same maximization can be applied, and let us write the maximum as,

$\mathrm{\pi }(T_0,T_1,T_2)\equiv l_0^{*}{m}_0^{*}+l_1^{*}{m}_1^{*}+l_2^{*}{m}_2^{*}(3)$

If transfers are also to be chosen, evolution will drive the life history to choose the optimal transfers (T₀, T₁, T₂), subject to some additional constraints.

The most common transfers are between kin. In our one-sex, 3-age, stationary population setting, the equilibrium age structure evaluated at the period’s end must be proportional to the following factors: l₀ for age-0, l₁ for age-1, and l₂ for age-2. This age distribution can be interpreted either as averages for generations of a given kin group or as averages for the population as a whole. The sum of net transfers given within the kin group or within the population must equal the sum of net transfers received, so net transfers must satisfy the following constraint:

$l_0{T}_0+l_1{T}_1+l_2{T}_2=0(4)$

Thus, the optimal transfer problem is to maximize π (T₀, T₁, T₂) in Eq. 3, subject to the constraint in Eq. 4 (for a fuller discussion of this constraint and its interpretation at the family level, refer to Lee, 2008).

To summarize, we separate the optimal life history exercise into two steps, namely, the first step is to maximize over {p_a, m_a} for any given transfers (T₀, T₁, T₂) and the second step is to choose the optimal $T_a^{\prime }$s.

Now, we consider some specific scenarios.

2.2. Scenario 1: Menopause

We interpret menopause as an optimal corner solution (i.e., at the zero-fertility lower bound) of old-age fertility and will explain when and why this unique optimality may arise in our simple model. To focus on the discussion of m₂, we consider the scenario $m_0^{*}=0$ and T₀ > 0, T₁ < 0, and T₂ < 0, meaning that the age-0 needs energy transfers from older ages and is not sexually mature. We skip the conditions that generate these scenarios for the time being³ and focus the discussion on the age-3’s (grandmother’s) decisions.

If the optimal solution involves $p_2^{*}>0$ and $m_2^{*}=0$, then it says that it is optimal for the grandmother to survive but not reproduce. Intuitively, this is more likely to happen when γw₂ is large (the grandmother is more capable of foraging, perhaps due to her accumulated knowledge) so that she produces a lot of energy, and c₂ is large so that it is costly for the grandmother to reproduce, so some of her acquired energy may be transferred out. However, what exactly are the mathematical conditions for $p_2^{*}>0,m_2^{*}$ = 0 to happen?

Given $m_0^{*}=0$, the objective function becomes,

$\mathrm{\pi }\equiv \max \left\{p_0{p}_1{m}_1+p_0{p}_1{p}_2{m}_2\right\}$

We consider a small perturbation in the grandmother’s net transfers such that |T₂| becomes marginally larger, with the increased transfers all going to age-0, and correspondingly m₂ becomes marginally smaller, with all other control variables held unchanged. Since m₀ = 0, the increased transfer to age-0 would only increase p₀. Thus, the change in fitness is,

$d\mathrm{\pi }=p_1{m}_{1}d{p}_0+\left(p_1{p}_2{m}_2\right)d{p}_0+\left(p_0{p}_1{p}_2\right)d{m}_2\mathrm{or}$

$\frac{d\mathrm{\pi }}{d{m}_2}=p_1{m}_1\frac{d{p}_0}{d{m}_2}+\left(p_1{p}_2{m}_2\right)\frac{d{p}_0}{d{m}_2}+p_0{p}_1{p}_2$

The energy saved by a fertility change of dm₂ at age-2 is −c₂dm₂. Referring to the equilibrium population age distribution earlier, we see that the proportion of individuals at age-2 divided by the proportion of individuals at age-0 is p₁p₂. This implies that each individual at age-0 would receive −p₁p₂c₂dm₂ energy, that is, gain energy if dm₂ is negative and fertility at age-2 declines. Therefore, age-0 would increase her survival probability by,⁴

$\frac{d{p}_0}{d{m}_2}=\frac{-p_1{p}_2{c}_2}{b_0}$

Thus,

$\frac{d\mathrm{\pi }}{d{m}_2}=-p_1{m}_1\frac{p_1{p}_2{c}_2}{b_0}\left(-p_1{p}_2{m}_2\right)\frac{p_1{p}_2{c}_2}{b_0}+p_0{p}_1{p}_2$

$=-p_1{p}_2\left[p_1{m}_1\frac{c_2}{b_0}+\left(p_1{p}_2{m}_2\right)\frac{c_2}{b_0}-p_0\right]$

$=-\frac{p_1{p}_2}{p_0}\left\{\frac{c_2}{b_0}\left[p_0{p}_1{m}_1+{\text{p}}_0{\text{p}}_1{p}_2{m}_2\right]-p_0^2\right\}.$

Recall our assumption that at an optimum, the population is in a stationary equilibrium. The abovementioned expressions do not necessarily refer to an optimum, but if the life history moves slowly along an evolutionary trajectory, then the population is always near a stationary equilibrium which implies that π (the net reproduction ratio) will be near 1.0. Note that the first two terms in the square brackets equal π. Using this, and substituting 1.0, we find,

$\frac{d\mathrm{\pi }}{d{m}_2}=-\frac{p_1{p}_2}{p_0}\left\{\frac{c_2}{b_0}-p_0^2\right\}=\frac{p_1{p}_2}{p_0}\left\{p_0^2-\frac{c_2}{b_0}\right\}.$

This derivative will continue to be negative as long as $p_0^2<\frac{c_2}{b_0}$, and age-2 will continue to evolve in the direction of reducing its fertility m₂ and transferring more to the age-0, gradually raising p₀ until finally an interior optimum is reached where $p_0=\sqrt{\frac{c_2}{b_0}}$ or, alternatively, arrives at a corner due to one of two possible boundaries. One boundary occurs at p₀ = 1 when $\frac{c_2}{b_0}>1$. Another possible boundary occurs if m₂ reaches zero.

While p₀ = 1 is a possible outcome in our model, we believe it has never been observed in nature so we will focus on the possible corner outcome for fertility. We consider the possibility of reaching the fertility boundary while $\frac{d\mathrm{\pi }}{d{m}_2}$ is still negative, indicating that lower fertility, were it possible, would lead to greater fitness. From the result earlier, this is more likely to happen when $\frac{c_2}{b_0}$ is large, that is, the cost of raising fertility for an older female is substantially greater than the cost of reducing the mortality of a young offspring or grandoffspring. It is also more likely to happen when p₀ is low so that despite the transfers from older women as their fertility falls, the survival of young grandoffspring has remained low.

A positive value for $\frac{d\text{π}}{d{m}_2}{|}_{m_2=0,\mathrm{ }d{m}_2<0}$ tells us that fitness would be raised even more if it were possible for fertility at age-2 to become negative. Since this is not possible, m₂ = 0, a corner solution, will give the highest feasible fitness. If dπ/dm₂ = 0 when m₂ = 0 that would indicate an interior solution optimum that just happened by chance to occur at the corner.

It is also important to note that a trajectory ending in menopause is possible only if the fertility of younger adult women can rise high enough to achieve a net reproduction ratio of 1. As older women increase their transfers to their grandoffspring, their daughters can reduce theirs and raise their fertility. We will return to this point later.

Menopause occurs when the fitness curve has a non-positive slope around the vertical axis. Figure 1 illustrates this situation, plotting the fitness index against m₂. As drawn, the fitness curve crosses the vertical axis (at m₂ = 0) with a negative slope, indicating that the optimum is a corner solution. This corresponds to the life-history interpretation of “menopause.” If dπ/dm₂ = 0 at m₂ = 0, then the slope of the fitness curve around the vertical axis is exactly zero.

FIGURE 1

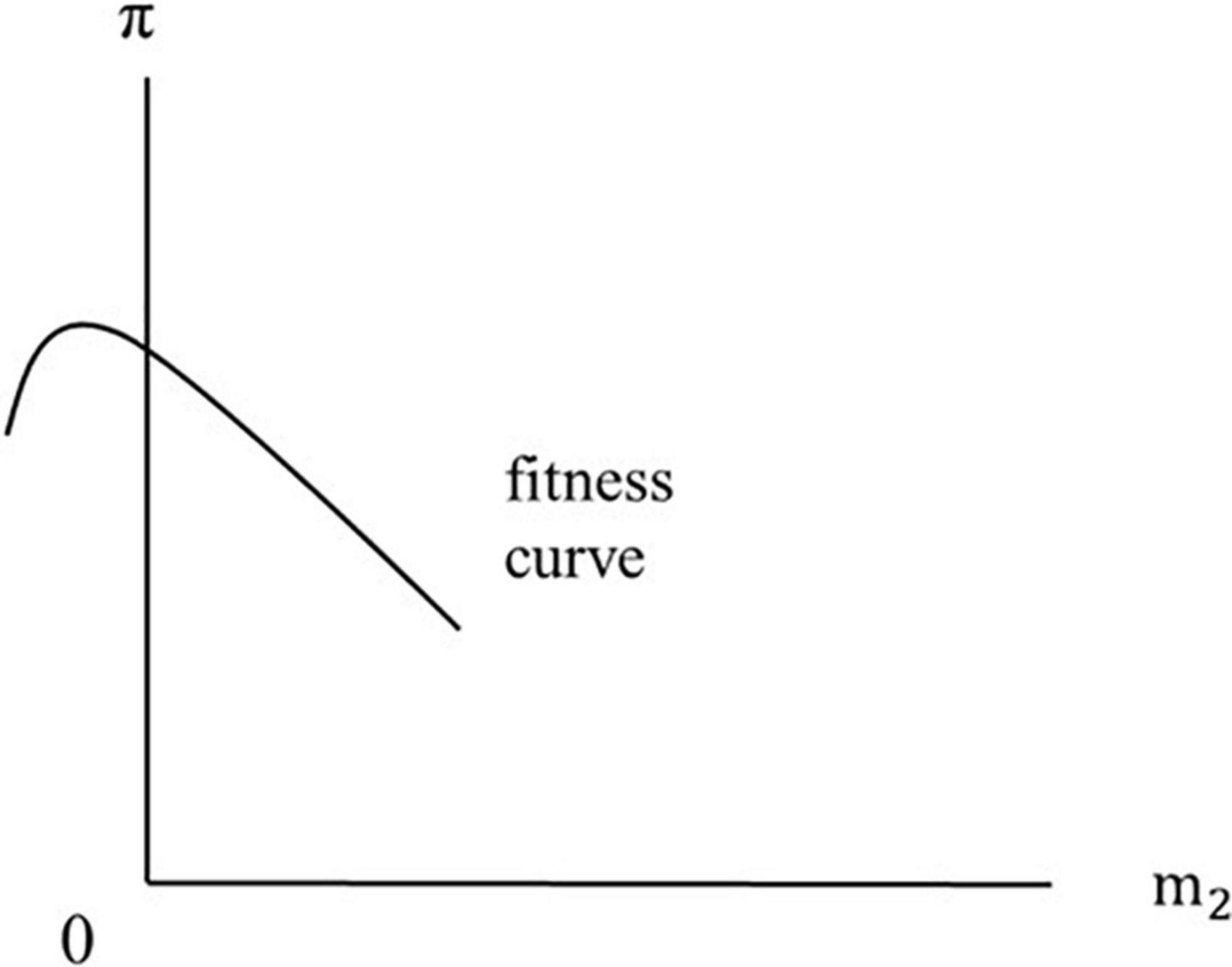
Figure 1. Menopause occurs when the fitness curve has a non-positive slope around the vertical axis. If the slope around the vertical axis is exactly zero, then dπ/dm₂ = 0.

Here, in our simple model, menopause evolves as the end point of declining fertility at older ages. However, in a more flexible model, the same forces at work could equally well apply to unchanged fertility at older ages together with the evolution of longer post-reproductive survival. Menopause is known to occur in humans and four species of toothed whale (Ellis et al., 2018). Transfers in human hunter-gatherer-horticulturalist groups have been extensively studied (Hooper et al., 2015; Davison and Gurven, 2022).

2.3. Scenario 2: The age pattern of mortality from birth to maturity

In this scenario, we interpret the three ages as childhood, youth, and adulthood. Suppose c₀ and c₁ are large, then the first two ages may not be appropriate for reproducing. In this case, age-2 is the age of sexual maturity. Or, using the alternative interpretation we discussed earlier (for additional age groups using dynamic programming), the individual is sexually mature from age-2 onward. We also assume that only the age-2 is strong enough to acquire sufficient energy to transfer to ages 0 and 1.

For species without parental transfers, Hamilton’s theory predicts that the probability of surviving to the next age should be the same for age-0 and age-1 (in fact, for all ages before reproductive maturity). If there are parental transfers to children and youth, we will argue that mortality should instead be higher at the younger ages and survival lower than later in youth, that is, p₀ < p₁. This implies there is high childhood (infant) mortality followed by a decline. If there are more than three ages, then the survival probability will decline after the age of sexual maturity due to the usual senescence argument. Thus, p₀ < p₁ constitutes a sufficient condition for U-shape (in our 3-age setting, V-shape) mortality of species with parental transfers. In what follows, we derive conditions for this to happen.

Given m₀ = m₁ = 0, we have the following simplified objective function:

$\mathrm{\pi }\equiv \max \left\{p_0{p}_1{p}_2{m}_2\right\}$

Let the giving-end age-2 transfer to age-1 be $T_1^{\prime }$ and to age-0 be $T_0^{\prime }$. The energy received by an individual at age-1 is $p_2{T}_1^{\prime }$ and at age-0 is $p_1{p}_2{T}_0^{\prime }$. Again, these are obtained by dividing the ratio of the proportion of individuals at age-2 by that at age-1. Thus, the corresponding survival probability is,

${\text{p}}_0=\frac{\left({\mathrm{\gamma }}_0{\text{w}}_0+{\text{p}}_1{\text{p}}_2{\text{T}}_0^{{}^{\prime }}\right)}{{\text{b}}_0}$

${\text{p}}_1=\frac{\left({\mathrm{\gamma }}_1{\text{w}}_1+{\text{p}}_2{\text{T}}_1^{{}^{\prime }}\right)}{{\text{b}}_1}$

Now suppose age-2 individuals change their strategy for transferring energy, reallocating energy from age-0 to age-1 ($d{T}_0^{\prime }=-d{T}_1^{\prime }$), holding all other controls unchanged. We can see the change in survival probability would be

${\text{dp}}_0=\frac{{\text{p}}_1{\text{p}}_2{\text{dT}}_0^{{}^{\prime }}}{{\text{b}}_0}$

${\text{dp}}_1=\frac{-{\mathrm{p}}_2{\text{dT}}_0^{{}^{\prime }}}{{\text{b}}_1}$

The change in the fitness index is,

$\frac{\text{d}\mathrm{\pi }}{{\text{dT}}_0^{{}^{\prime }}}=\left(\frac{{\text{p}}_0{\text{p}}_2}{{\text{b}}_1}-\frac{{\text{p}}_1^2{\text{p}}_2}{{\text{b}}_0}\right){\text{p}}_2{\text{m}}_2$

If we are at an optimum, then this perturbation must have zero effect on fitness, π, so,

$\frac{{\text{p}}_1^2}{{\text{b}}_0}-\frac{{\text{p}}_0}{{\text{b}}_1}=0$

This equation implies that $p_1=\sqrt{\frac{b_0{p}_0}{b_1}}$.

If we make the neutral assumption that b₀ = b₁, that is that the energetic costs of improving survival in childhood and youth are equal, then we have $p_1=\sqrt{p_0}$ in which case p₁ > p₀ since p₀ < 1. This means that mortality before adulthood declines with age, as, in fact, it generally does. Even if b₀ < b₁, there would still be a range of values of p₀ for which mortality would be declining with age.

This result says that if sexually mature adults transfer energy to offspring at more than one immature age, then it is always more efficient for the younger age to face a higher mortality rate than the older. The intuition of our result is that since our objective function is p₀p₁p₂m₂ and there are costs b₀ and b₁ for raising p₀ and p₁, maximization of p₀p₁ would always lead to p₀ = p₁ because costs would be the least when the two are equal. However, cross-age transfers introduce additional cost concerns, making a death at age-1 costlier than one at age-0, because a death at age-1 would also waste the earlier transfers to the offspring at age-0. This “accumulation effect” creates a product term on the cost side, which is the reason why we have p₁ as a square root of p₀. In more general cases with many ages before sexual maturity, this accumulation effect would be amplified for ages closer to zero and farther from the age of sexual maturity. Thus, unless there are specific assumptions about the b_a coefficients, for species with transfers from adults-to-children, it is likely mortality declines with age and survival increases up to sexual maturity. As noted earlier, this cannot be the whole story since mortality also declines in species without intergenerational transfers.

2.4. Scenario 3: Determinate growth

The objective of this scenario is to explain why a determinate growth pattern occurs. Let us forget about the transfers for a moment and consider life with only two ages, namely, age-0 and age-1. The individual invests energy z_a in growth, raising body size by d_az_a. The objective function is to maximize,

$p_0{m}_0+p_0{p}_1{m}_1.$

We assume that the energy constraint is also linear in z_a:

$b_a{p}_a+c_a{m}_a+d_a{z}_a=\mathrm{\gamma }{w}_{a}a=0,1$

where w₁ = w₀ + z₀, characterizing the somatic growth occurring through investment at the previous age, z₀.

Energy production increases with body mass as described by γ (body mass may also be interpreted more broadly here to include investment in the brain or in the acquisition of knowledge). Evidently, age-1 would never invest in z₁ because it is the last period of life, so z₁ = 0. Given the above, we will have determinate growth if at age-0 z₀ and m₀ are not both positive, since determinate growth is characterized by growth without reproduction followed by reproduction without growth.

Consider a marginal change of dm₀ < 0. This saves the age-0 individual an amount c₀ |dm₀| of energy, which can be used to create dz₀ = c₀|dm₀|/d₀ of somatic growth. Then, the corresponding body growth can generate γdz₀ = γc₀|dm₀|/d₀ energy at age-1. This energy will allow an additional [γc₀|dm₀|/d₀]/c₁ age-1 births. Is this marginal change worthwhile? We check it by investigating the sign of,⁵

$\text{d}\mathrm{\pi }=-{\mathrm{p}}_0{\text{dm}}_0+{\text{p}}_0{\text{p}}_1\frac{\mathrm{\gamma }{\text{c}}_0}{{\text{d}}_0{\text{c}}_1}{\text{dm}}_0$

$\frac{\text{d}\mathrm{\pi }}{{\text{dm}}_0}={\text{p}}_0\left({\text{p}}_1\frac{\mathrm{\gamma }{\text{c}}_0}{{\text{d}}_0{\text{c}}_1}-1\right).$

Note that c₀, c₁, γ, and d₀ are all constants. For any given p₀ and p₁, since the above expression is independent of the perturbation dm₀, (dπ/dm₀) = 0 will hold only by accident. Thus, with a linear budget constraint, it is impossible to have indeterminate growth: m₀ should either increase with a corresponding decrease in z₀ (which would mean that an organism reproduced over the rest of its life without growing at all following birth), or decrease with a corresponding increase in z₀, until a constraint boundary is hit, which corresponds to determinate growth as it is observed in nature.

Indeterminate growth, with both growth and fertility occurring together from the start, could occur in this model only with a non-linear budget constraint in which the incremental (marginal) fitness gains from energy spent on fertility or growth were not constant, but rather declined as the energy devoted to each increased. It is certainly plausible that this would be the case. For example, Metcalf et al. (2003) comparatively analyzed monocarpic perennial plants to test life history theories, reporting that rapid growth and low mortality tradeoffs in small plants are consistent with the budget constraint approach. However, they also find that growth is a decreasing function of size which suggests a non-linear budget constraint. Non-linearity in somatic growth could also arise if more rapid growth is less efficient. For example, suppose at age-0 growth is related to investment by w₁ = w₀ + ζ(δ) where ζ(δ) is non-linear and ${\mathrm{\zeta }}^{\prime }\left(\mathrm{\delta }\right)>0,\mathrm{\zeta }{}^{\prime }{}^{\prime }\left(\mathrm{\delta }\right)<0$, with growth becoming less efficient at higher rates. Then, an interior solution is possible with both growth and reproduction occurring. Other possibilities will be discussed later.

2.5. Scenario 4: Reproductive senescence

In this scenario, we study when fertility will decline with age. We consider a 3-period lifetime with determinate growth. At age-0, the body grows, and age-1 and age-2 are mature ages. The mature individual has a somatic capital w*, which is a constant for age-1 and age-2, but different ages have different efficiency parameters (γ_a, a = 1, 2) to generate energy. The reason behind different ${\mathrm{\gamma }}_a^{\prime }s$ might be depreciation or wearing out; for example, the age-2 may have the same body size as age-1 but be less healthy or agile than age-1, so that γ₁ > γ₂ (Lemaître et al., 2020: p. 8). We assume that age-0 generates 0 energy, but that is just for simplicity and convenience; it need not be so.

Let the giving-end transfer from age a (a = 1,2) to age-0 be |T_a|. The net energy left for the age-a adult to allocate is, therefore, γ_aw* |T_a| E_a.

The total energy received at age-0 is p₁ |T₁| + p₁p₂ |T₂|. Using this, the corresponding survival probability for age-0 is p₀ = (p₁ |T₁| + p₁p₂ |T₂|)/b₀ (because age-0 is not reproductive, all her energy is used in maintenance). For any given |T₁|, |T₂|, and p₀, we concentrate on the fertility decision of the adult:

$\max p_0\left[p_1{m}_1+p_1{p}_2{m}_2\right]$

subject to the constraints b_ap_a + c_am_a = E_a. The choice variables are p_a and m_a. Dynamic programming tells us that we should first solve the age-2 maximization:

$\text{Max}{p}_2{m}_2\mathrm{subject}\mathrm{to}{b}_2{p}_2+c_2{m}_2=E_2.$

This generates $m_2^{*}=\frac{E_2}{2c_2}$ and $p_2^{*}=\frac{E_2}{2b_2}$. Then, we substitute the optimized value $p_2^{*}{m}_2^{*}$ back to the age-1 formulation and solve the following problem:

$\text{Max}\left[p_1{m}_1+p_1{p}_2^{*}{m}_2^{*}\right]\mathrm{subject}\mathrm{to}{b}_1{p}_1+c_1{m}_1=E_1.$

Straightforward maximization shows that the age-1 solution is

$m_1^{*}=\frac{1}{2c_1}\left[E_1-E_2^2\frac{c_1}{4b_2{c}_2}\right].$

To see whether there is reproductive senescence, we look at the difference,

$m_1^{*}-m_2^{*}=\frac{E_1}{2c_1}-\left[\frac{E_2}{2c_2}+\frac{E_2^2}{8b_2{c}_2}\right].(5)$

Evidently, reproductive senescence ($m_1^{*}>m_2^{*}$) is more likely to occur if (1) c₁ is small or c₂ is larger (age-1 is more efficient in reproducing than age-2), or (2) E₁ is large or E₂ is small due to reduced foraging efficiency with aging (age-1 has more disposable energy than age-2), (3) E₂ is small because |T₂| is large (age-2 is an important supporter of age-0), or (4) high cost (large b₂) of achieving higher old age survival.

Case (1) occurs if the reproductive system tends to deteriorate with age, for example, the declining quantity and quality of ova in mammals and birds, raising the cost of reproduction with age. This deterioration could perhaps be offset by increased spending on maintenance. However, while that might reduce c₂ − c₁, it would also add the energetic cost of maintenance to the total cost of reproducing at age-2. Case (2) occurs if the productive soma tends to deteriorate and lose efficiency, so that γ₁ > γ₂, as reviewed by Lemaître et al. (2020: p. 8) (for simplicity, we have not subscripted γ in the previous model but the meaning here should be clear).

Therefore, this condition, large c₂/b₀, would underly the result in Scenario 4 which found that small E₂ brings reproductive senescence. As T₂ is endogenous, this argument explains what is likely to make it larger and E₂ smaller.

In case (3), an older female’s energy available for reproduction is depleted by her large net transfers to younger descendants, |T₂|, as she relies more heavily on investment in indirect fitness by using energy transfers to raise the fitness of grandoffspring rather than to reproduce herself. These transfers are themselves evolving as we discussed in Scenario 1. The greater the ratio $\frac{c_2}{b_0}$, the greater will be the evolved transfers from T₂ to T₀ and the lower, therefore, will be E₂. The polar case is menopause or m₂ = 0.

Case (4) occurs when for any reason such as higher extrinsic mortality or smaller body size survival at older ages is more costly to attain, consistent with a result by Charlesworth and Leon (1976).

In any event, it is important to note that reproductive senescence does not necessarily appear in optimal life history. Suppose that there is no change with age in the cost of fertility c_a, or foraging efficiency γ_a, or net transfers T_a so that available energy is also the same at both ages. Setting all these equal in Eq. 5, we find that,

${\text{m}}_2^{*}-{\text{m}}_1^{*}=\frac{{\text{E}}_2^2}{8{\text{b}}_2{\text{c}}_2}>0.$

That is, in this case, optimal fertility would rise with age rather than decline, because at older ages, investment in survival brings less fitness payoff (particularly when b₂ is large), unlike investment in fertility. Optimal energy expenditures are shifted from maintenance to fertility, which rises relative to age-1. This would also be true under somewhat weaker assumptions. In addition, these same forces would be at work to generate this result in a model with more ages. This equation seems consistent with the slow or negligible reproductive aging in birds since older birds do not make transfers to grandoffspring and, therefore, retain more energy for their own reproduction, and their cost of survival (b₂) is low since they fly.

3. Discussion

We will consider our results in a broader context, starting with menopause. Should menopause be considered an example of extreme reproductive senescence? Some analysts see it resulting from the evolution of longer life while reproductive senescence remained unchanged. For example, Ellison and Ottinger (2014) wrote: “But the Chu and Lee (2006) hypotheses assume that the evolved characteristic in humans is an early termination of reproduction relative to its ancestral state, whereas it seems clear that the evolved characteristic is prevalent and extended post-reproductive life, not premature reproductive cessation.” Since our models, including here in Scenario 1, assume a preexisting life span and then analyze the optimal level of fertility in predefined old age, their criticism appears well-founded. Furthermore, our verbal interpretations of results typically have asserted the evolutionary ordering of change suggested in this quote (Chu and Lee, 2013), which in retrospect is unfortunate. It is unfortunate because in the mathematical theory, the ordering of change is irrelevant, and all that matters is the relative lengths of dependent childhood, fertility, and life span, not which trait is fixed and which one changes. We view the system of intergenerational transfers, menopause, and post-reproductive life as coevolving along with the development of the brain and the long period of maturation and dependence of offspring as described in the theoretical framework of Hawkes et al. (1998) or Kaplan et al. (2000) (which are not very different for a single sex model). We view menopause as an adaptive part of an optimal life history strategy. Accepting Ellison and Ottinger’s (2014) conclusion that age at reproductive senescence remained fixed while longer life evolved still requires an explanation of fitness benefits derived from this lengthening post-reproductive period.

Consider the circumstances we find to be conducive to the evolution of menopause. First is the high fertility of younger adult females. For humans, it is well-known that reproductive-age women have short birth intervals and high fertility relative to other great apes (Thompson and Sabb, in press), made possible by transfers from others (Kaplan et al., 2000). Second, the energetic cost of a birth to an older woman should be high and the cost of raising the survival of young offspring through transfers to them should be low. How costly would it be for increased fertility at older female ages to evolve? The mammalian and avian reproductive systems with a fixed supply of oocytes at birth might make it more difficult and costly to continue fertility to higher ages. Elephants and some whales maintain fertility to far higher ages than humans, so it would arguably be possible. Nonetheless, it seems plausible that continuing fertility to high ages would be more costly for mammals than for other non-avian species. The cost of raising infant/juvenile survival for mammals might be lower than for other species because of the ability to feed infants efficiently over an extended period through lactation. Grandparents could indirectly contribute to infant nutrition by helping to feed the mother. Among mammals, humans with pair bonding and a long history of food sharing in social groups might again be well-situated to improve the survival of post-lactation juveniles. This is all speculative, of course, but perhaps a case could be made that c₂/b₀ is generally high for mammals and within mammals is possibly higher for humans.

Regarding mortality decline within the juvenile period, we have already discussed the difficulties with Hamilton’s demonstration that mortality should be constant until reproductive maturity, which he himself did not believe, although as a refutation of Fisher’s argument based on reproductive value, Hamilton’s analysis remains convincing. Once intergenerational transfers (or “parental care,” in his words) are introduced, Hamilton’s argument no longer holds. Now, the older the juvenile the more has been invested in her so the greater the fitness loss if she should die (a corresponding forward-looking story can also be told). This seems correct so far as it goes. One difficulty is that mortality also declines in species that do not make transfers following birth. Orzack and Levitis (in press) present a further critique.

As we showed, a linear budget constraint leads to determinate growth and is inconsistent with indeterminate growth. However, the condition is sufficient but not necessary; some non-linear budget constraints would also lead to determinate growth. Indeed, even if a budget constraint were locally linear, it is difficult to imagine that it could remain linear over the entire evolutionary range, even as upper or lower bounds on variables were approached. The insight from the model is a useful starting point but is not the end of the story. A little later we will suggest a different approach in which the budget constraint is inherently nonlinear.

As noted earlier, reproductive senescence in the optimal life history is far from inevitable. If we make the neutral assumption that the costs of survival and fertility and the efficiency of foraging for a given body weight as well as intergenerational transfer behavior all remain unchanged in the adult life history, then fertility will rise with age rather than decline, for reasons already discussed. We certainly could assume a tendency to senesce in any one of the three fundamental parameters in our model (b, c, or γ) which could lead to fertility decline, but that leaves open the question of why there was an insufficient investment to maintain these capabilities in the face of wear and tear. More important, in our analysis, is the possibility that intergenerational transfer behavior evolves in such a way as to reduce fertility at older ages while boosting the survival (and in a full model, growth as well) of young offspring. This possibility is contained within our model as we have discussed earlier, and is more likely to evolve when the ratio of the cost of raising old age fertility to the cost of improving survival for young offspring is high and the level of early life survival is low. While menopause is one polar outcome, intermediate outcomes with interior solutions with reduced old age fertility are also possible.

We also have some thoughts about future studies for ourselves or others on this topic. As we noted at the beginning, wear-and-tear has rightly been rejected as an adequate explanation of aging and senescence, because an organism could offset it by allocating resources to maintenance, repair, and replacement. To quote Williams (1957), “It is true, of course, that some parts of organisms do literally wear out. Human teeth, for instance, show wear similar to that of any tool subjected to friction, but this wear is no more a part of senescence than is the wearing away of replaceable epidermal cells. The senescence of human teeth consists not of their wearing out but of their lack of replacement when worn out.”

It is possible, however, that current analytic approaches to reproductive aging, including ours in this article, go too far in the direction of banishing wear and tear from consideration. In our specification, for example, a unit of energy expended on reproduction at age a will produce 1/c_a births. Nothing here says that c_a, the energy cost of reproduction at age a, does not vary with age. However, unless there is some theoretical reason to expect c to rise with age, we cannot very well assume it does without smuggling in by the backdoor the very thing we want to show may exist.

In this regard, it could be useful to distinguish the somatic reproductive machinery as one variable, call it K, from the current energy allocated to reproduction and fed into the reproductive machinery, call it f. Then, fertility at age a, m_a, is a function m_a = g(K_a, f_a) for which a specific example would be $m_a=h{K}_a^{\mathrm{\alpha }}{f}_a^{1-\mathrm{\alpha }}$. What we call the reproductive machinery, K, tends to wear out over time at the rate δ and the organism can offset some or all of this decay by investing energy i, giving K_a = (1 − δ)K_a−1 + i_a−1. An investment in K at any age will also raise all future levels of K at subsequent ages, other things equal. These future benefits of investment in K will be large for a young organism with its whole future ahead of it, but small for an older organism that is closer to the end of life. For this reason, in the optimal life history, K will be at a peak early in life but then will decline because it becomes less worthwhile to offset the wear-and-tear at older ages. As a result, for any given expenditure of energy on current reproduction f_a, the increase in the birthrate will be less at older ages than at younger because the machinery has become less efficient or, we might say, the energy cost per birth c_ahas risen with age. It rises not by assumption but due to the optimal investment strategy. While maintenance of reproductive organs affects all future reproductive ages, the future is shorter for older than for younger females, so the incentive to invest at older ages is also less. This reasoning is very similar to that for rising mortality. Now, in a symmetric way, we have the possibility of reproductive senescence. We speculate that a model of this sort could account for the different patterns of fertility that rise, fall, or hold steady across age, as observed in nature. We think it is a promising avenue for future research.

4. Conclusion

The balance of these and perhaps other forces will determine age patterns of fertility and reproductive senescence. The weights received by each of these forces will in turn depend on many other aspects of the life history and sociality of the species, and perhaps on the environment as well. There is no single theoretical insight that will clarify reproductive senescence in the way that insights of Medawar, Williams, and Hamilton seemed, for a time, to show that rising mortality in adulthood would be inevitable. Reproductive life histories are far too complex and variable.

Data availability statement

This manuscript is theoretical and does not analyze data. There is one chart but it is mathematical and does not use data.

Author contributions

CC contributed more to the mathematical modeling. RL contributed more to the plan, structure, and writing of the manuscript. Both authors contributed to all parts of the manuscript and approved the submitted version.

Funding

Funding for RL from U.S. National Institute of Aging through a grant to the Center for the Demography and Economics of Aging at University of California, Berkeley, P30AG012839.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^ In a discrete-time setting, we must be careful about interpreting the order of events. Energy is a “flow” (measured for a period of time), whereas survival and reproduction are measured at the period’s end, which corresponds to a stock (measured at a point in time). Different specifications of the order of events may involve slight changes in the formulation.
2. ^ The more general form of the optimal life history (see Chu et al., 2008) is λ³ = max_{pa, ma} {λ²l₀m₀ + λl₁m₁ + l₂m₂}, where λ is the implicit population growth rate. In stationary equilibrium, λ would be driven to 1 (zero net growth), so that the problem is equivalent to solving Eq. 2. In what follows, we adopt the stationary scenario implicitly, and treat Eq. 2 as the objective function.
3. ^ These conditions are not difficult to imagine: For instance, if c₀ is very large, then it is very costly for the age-0 to reproduce, therefore $m_0^{*}=0$ must appear. And if E₀ = γw₀ is very small, then the age-0 must rely on transfers from seniors to survive.
4. ^ Alternatively, one can combine Eqs. 1 and 4 and use the assumption m₀ = 0 to obtain,
   ${\text{p}}_0=\frac{\mathrm{\gamma }{\text{w}}_0}{{\text{b}}_0}-\frac{{\text{p}}_1\left[{\text{T}}_1+{\text{p}}_2\left({\text{b}}_2{\text{p}}_2+{\text{c}}_2{\text{m}}_2-\mathrm{\gamma }{\text{w}}_2\right)\right]}{{\text{b}}_0}.$
   Taking derivative yields dp₀/ dm₂ in the text.
5. ^ Note that in order to evaluate the tradeoff between age-0 fertility and somatic growth, we design a specific direction of perturbation. This makes the derivatives look cleaner.

References

Baudisch, A. (2008). Inevitable Aging? Contributions to Evolutionary-Demographic Theory. Cham: Springer.

Google Scholar

Caswell, H., and Salguero-Gómez, R. (2013). Age, stage and senescence in plants. J. Ecol. 101, 585–595. doi: 10.1111/1365-2745.12088

PubMed Abstract | CrossRef Full Text | Google Scholar

Charlesworth, B. (1994). Evolution in Age-Structured Populations, 2nd Edn. Cambridge, MA: Cambridge University Press.

Google Scholar

Charlesworth, B., and Leon, J. A. (1976). The relation of reproductive effort to age. Am. Nat. 110, 449–459.

Google Scholar

Chu, C. Y., Chien, H. K., and Lee, R. D. (2008). Explaining the optimality of U-shaped age-specific mortality. Theoret. Popul. Biol. 73, 171–180. doi: 10.1016/j.tpb.2007.11.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Chu, C. Y., and Lee, R. (2006). The co-evolution of intergenerational transfers and longevity: an optimal life history approach. Theoret. Popul. Biol. 69, 193–201. doi: 10.1016/j.tpb.2005.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Chu, C. Y., and Lee, R. D. (2013). On the evolution of intergenerational division of labor, menopause and transfers among adults and offspring. J. Theoret. Biol. 332, 171–180. doi: 10.1016/j.jtbi.2013.04.031

PubMed Abstract | CrossRef Full Text | Google Scholar

da Silva, R., Conde, D. A., Baudisch, A., and Colchero, F. (2022). Slow and negligible senescence among testudines challenges evolutionary theories of senescence. Science 376, 1466–1470. doi: 10.1126/science.abl7811

PubMed Abstract | CrossRef Full Text | Google Scholar

Danko, M. J., Kozłowski, J., Vaupel, J. W., and Baudisch, A. (2012). Mutation accumulation may be a minor force in shaping life history traits. PLoS One 7:e34146. doi: 10.1371/journal.pone.0034146

PubMed Abstract | CrossRef Full Text | Google Scholar

Davison, R., and Gurven, M. (2022). The importance of elders: Extending Hamilton’s force of selection to include intergenerational transfers. Proc. Natl. Acad. Sci. 28. doi: 10.1073/pnas.2200073119

PubMed Abstract | CrossRef Full Text | Google Scholar

Drenos, F., and Kirkwood, T. B. L. (2005). Modelling the disposable soma theory of ageing. Mech. Age. Dev. 126, 99–103. doi: 10.1016/j.mad.2004.09.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellis, S., Franks, D. W., Nattrass, S., Currie, T. E., Cant, M. A., Giles, D., et al. (2018). Analyses of ovarian activity reveal repeated evolution of post-reproductive lifespans in toothed whales. Sci. Rep. 8:12833. doi: 10.1038/s41598-018-31047-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellison, P. T., and Ottinger, M. A. (2014). “A comparative perspective on reproductive aging, reproductive cessation, post-reproductive life, and social behavior,” in Sociality, Hierarchy, Health: Comparative Biodemography: A Collection of Papers, eds M. Weinstein and M. A. Lane (Washington, DC: National Academies Press).

Google Scholar

Hamilton, W. D. (1966). The moulding of senescence by natural selection. J. Theoret. Biol. 12, 12–45.

Google Scholar

Hawkes, K., O’Connell, J. F., Jones, N. G. B., Alvarez, H., and Charnov, E. L. (1998). Grandmothering, menopause, and the evolution of human life histories. Proc. Natl. Acad. Sci. U.S.A. 95, 1336–1339.

Google Scholar

Holmes, D. J., Thomson, S. L., Wu, J., and Ottinger, M. A. (2003). Reproductive aging in female birds. Exp. Gerontol. 38, 751–756. doi: 10.1016/S0531-5565(03)00103-7

CrossRef Full Text | Google Scholar

Hooper, P. L., Gurven, M., Winking, J., and Kaplan, H. S. (2015). Inclusive fitness and differential productivity across the life course determine intergenerational transfers in a small-scale human society. Proc. R. Soc. B Biol. Sci. 282:20142808. doi: 10.1098/rspb.2014.2808

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, O. R., Scheuerlein, A., Salguero-Gómez, R., Camarda, C. G., Schaible, R., Casper, B. B., et al. (2014). Diversity of ageing across the tree of life. Nature 505, 169–173.

Google Scholar

Kaplan, H., Hill, K., Lancaster, J., and Hurtado, A. M. (2000). A theory of human life history evolution: diet, intelligence, and longevity. Evol. Anthropol. Issues News Rev. 9, 156–185.

Google Scholar

Kirkwood, T. (1977). Evolution of ageing. Nature 270, 301–304. doi: 10.1038/270301a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, R. (2003). Rethinking the evolutionary theory of aging: transfers, not births, shape senescence in social species. Proc. Natl. Acad. Sci. U.S.A. 100, 9637–9642. doi: 10.1073/pnas.1530303100

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, R. (2008). Sociality, selection and survival: simulated evolution of mortality with intergenerational transfers and food sharing. Proc. Natl. Acad. Sci. U.S.A. 105, 7124–7128. doi: 10.1073/pnas.0710234105

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemaître, J. F., Ronget, V., and Gaillard, J. M. (2020). Female reproductive senescence across mammals: a high diversity of patterns modulated by life history and mating traits. Mech. Ageing Dev. 192:111377. doi: 10.1016/j.mad.2020.111377

PubMed Abstract | CrossRef Full Text | Google Scholar

Medawar, P. B. (1952/1957). “An Unsolved Problem of Biology” reprinted as Chapter 2 in P. Medawar (1957) The Uniqueness of the Individual. London: HK Lewis and Co.

Google Scholar

Metcalf, J. C., Rose, K. E., and Rees, M. (2003). Evolutionary demography of monocarpic perennials. Trends Ecol. Evol. 18, 471–480.

Google Scholar

Monaghan, P., Charmantier, A., Nussey, D. H., and Ricklefs, R. E. (2008). The evolutionary ecology of senescence. Funct. Ecol. 22, 371–378. doi: 10.1111/j.1365-2435.2008.01418.x

CrossRef Full Text | Google Scholar

Partridge, L., and Barton, N. H. (1993). Optimality, mutation and the evolution of ageing. Nature 362, 305–311. doi: 10.1038/362305a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Reinke, B. A., Cayuela, H., Janzen, F. J., Lemaître, J. F., Gaillard, J. M., Lawing, A. M., et al. (2022). Diverse aging rates in ectothermic tetrapods provide insights for the evolution of aging and longevity. Science 376, 1459–1466. doi: 10.1126/science.abm0151

PubMed Abstract | CrossRef Full Text | Google Scholar

Stearns, S. C. (1992). The Evolution of Life Histories. Oxford: Oxford University Press.

Google Scholar

Stearns, S. C. (2000). Life history evolution: successes, limitations, and prospects. Naturwissenschaften 87, 476–486.

Google Scholar

Orzack, H. O., and Levitis, D. (in press). “Human mortality from beginning to end: what does naturalselection have to do with it?,” in Human Evolutionary Demography, eds O. Burger, R. Lee, and R. Sear (Charlottesville: Open Science Framework).

Google Scholar

Taylor, H. M., Gourley, R. S., Lawrence, C. E., and Kaplan, R. S. (1974). Natural selection of life history attributes: an analytical approach. Theor. Popul. Biol. 5, 104–122.

Google Scholar

Thompson, M. E., and Sabb, K. (in press). “Evolutionary demography of the great apes,” in Human Evolutionary Demography, eds O. Burger, R. Lee, and R. Sear (Charlottesville: Open Science Framework).

Google Scholar

Thouzeau, V., and Raymond, M. (2017). Emergence and maintenance of menopause in humans: a game theory model. J. Theoret. Biol. 430, 229–236. doi: 10.1016/j.jtbi.2017.07.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Vaupel, J. W., Baudisch, A., Dolling, M., Roach, D. A., and Gampe, J. (2004). The case for negative senescence. Theoret. Popul. Biol. 65, 339–351.

Google Scholar

Wachter, K. W., Steinsaltz, D., and Evans, S. H. (2014). Evolutionary shaping of demographic schedules. Proc. Natl. Acad. Sci. U.S.A. 111, 10846–10853. doi: 10.1073/pnas.1400841111

PubMed Abstract | CrossRef Full Text | Google Scholar

Williams, G. C. (1957). Natural selection and the evolution of senescence. Evolution 11, 398–411.

Google Scholar