Pesticide control, physical control, or biological control? How to manage forest pests and diseases more effectively

The frequent occurrence of forest diseases and insect pests has a significant impact on the forest ecosystem. The government needs to take measures to protect the forest ecosystem. The common management modes for forest pests and diseases include pesticide control, physical control, and biological control. In the process of governance, governments need to consider not only cost-effectiveness but also the impact on the ecosystem. In this article, the differential game model under these three modes is constructed, and the equilibrium results are compared and analyzed. Finally, the research conclusion is drawn that under the biological control mode, the income generated by the unit control quantity is inversely proportional to the balanced control quantity. However, under pesticide control and physical control modes, the revenue generated by the unit control quantity is proportional to the balanced control quantity. At the same time, under the biological control mode, the unit governance cost is proportional to the balanced control quantity. Under the pesticide control and physical control modes, the unit control cost is inversely proportional to the balanced control quantity. Social forces tend to adopt pesticide control. The government prefers physical control.

1 Introduction

1.1 Background and research significance

The world’s total forest area is 4.06 billion hectares (ha), or 31% of the total land area (Food and Agricultural Organization, 2020). Forests are also home to many kinds of animals and many kinds of plants. It is the most biologically active region on Earth. Forests have the functions of producing oxygen, purifying air, regulating climate, and maintaining ecological balance. Forests regulate the air and water in nature and affect climate change. At the same time, forests provide various resources for human production and life. It has played a vital role in the reproduction and survival of human civilization.

In recent years, due to the influence of human activities, the global temperature has kept rising. This causes the forest ecosystem to lose balance. This provides climatic support for forest pests to thrive. This gradually increasing temperature is suitable for the propagation and spread of forest pests. The occurrence of pests and diseases seriously endangers the health of forests. The destruction of forest ecosystems is also increasing. If the forest ecosystems are destroyed, it will cause the temperature to rise further, which will aggravate forest pests and diseases. At the same time, the world’s human afforestation area keeps increasing (Bai et al., 2021). Compared with natural forests, artificial forests have the following characteristics: higher density, fewer species, and more artificial intervention. Due to limited attention to adverse environmental impacts, plantation forests are devoted almost exclusively to wood production (Dragicevic, 2019a). Therefore, plantation forests are more susceptible to pests and diseases. Strengthening the management of forest pests and diseases has become the focus of ecosystem protection.

In order to deal with forest pests and diseases, multiple approaches to management are needed. This requires the participation of the government and social forces in society. The “social power” of forest pest management refers to the support and participation of nongovernmental organizations from all aspects of society. It includes the active actions and efforts of enterprises, nongovernmental organizations, the media, academia, and the public. These forces can contribute to the management of forest pests and diseases by developing regulations, promoting pest prevention technologies and innovations, conducting information and education on forest pest control, and implementing environmental regulation (Lei et al., 2021). Government and social forces can spray pesticides in forests, set up physical facilities, release natural enemies, and invest in bioeconomic activities that are less susceptible to pests and diseases (Dragicevic, 2019b). These methods can effectively control forest pests and diseases. Although the increase in forest pests and diseases in recent years is mainly due to global temperature rise and other factors, the solution to global temperature rise cannot be achieved overnight (Tandon and Verma, 2021). Instead, more effective results can be achieved using direct measures to control forest pests and diseases. At the same time, in the process of managing forest pests and diseases, governments and social forces should not only consider cost-effectiveness but also try their best to protect forest ecosystems. How to choose an effective management mode for forest pests and diseases and protect forest resources is an important issue in this article.

1.2 Literature review

The causes of forest pests and diseases are varied. For example, Ayres and Lombardero (2018) believe that the main causes of forest diseases and pests are global climate change, land use, and biological distribution. Popkin (2020) believes that the invasion of foreign pests is the main cause of forest diseases and insect pests in the USA. Canelles et al. (2021) believed that pests and diseases in one forest were mainly transmitted by other forests. Jentsch et al. (2020) believed that wood transportation is an important cause of forest diseases and insect pests. These scholars explained the causes of forest pests, mainly global climate change, natural invasion of pests, human-caused invasion, and other factors.

Some scholars have mainly studied the effects of forest pests and diseases. For example, Ozkan (2022) believed that forest diseases and insect pests could lead to a continuous reduction of forest area. Turner et al. (2007) believed that forest pests and diseases could have adverse effects on the foreign trade of wood. Niquidet et al. (2015) believed that the effects of some diseases and pests could be controlled, while others would have persistent and disastrous effects. These scholars mainly analyzed the natural impact, economic impact, and time span of the impact of forest pests and diseases.

Some scholars have mainly studied how to control forest pests and diseases. For example, Yang et al. (2014) studied the weather hostility of pests, which plays a significant role in the control of forest pests. Sheremet et al. (2018) studied how to introduce corresponding policies to encourage private forest owners to participate in forest pest control. Lovett et al. (2016) believed that it was necessary to control the circulation channels of wood products. These scholars analyzed how to manage forest pests and diseases mainly from the perspectives of biological control, national policies, and logistics management.

In order to make up for the shortcomings of the above studies, this article studied how to protect the forest ecosystem from the perspective of different forest pest management modes. The management modes of common forest pests and diseases are mainly divided into pesticide management, physical management, and biological management. In this article, based on setting the corresponding assumptions and defining the parameters of the model, three kinds of differential game models are established. The HJB formula is then used to solve the differential game model. This article obtains the optimal governance quantity and social utility of government and social forces. Comparative analysis of social utility is carried out through numerical analysis. Finally, this article discusses the relevant conclusions. In this article, the factors influencing the amount of forest pest management and the applicable scope of different forest pest control modes are identified.

1.3 Problem description

Rising global temperatures are causing serious forest pests and diseases. The effective control of forest diseases and insect pests by the government can protect forest resources. It is very important to promote the development of forestry and maintain the balance of natural ecology. In order to clearly depict the problems of forest pests and diseases that exist all the time, this article uses a differential game, which is a game with continuous time. Pesticide control tends to damage ecosystems and lead to pest resistance, but it is low-cost and has quick results. Physical containment facilities can be reused, but they are costly and vulnerable to extreme weather. Biological control can better protect the ecosystem, but introduced natural enemies are prone to problems of adaptability and infestation.

Game theory explores what strategies each player should adopt in different situations and the consequences and effects of these strategies (Valizadeh and Gohari, 2021). There are players in game theory. This article divides the game players into government and social forces. When there are several governments in reality, two governments can be discussed separately according to the method and conclusion of this article to get the desired result. In order to effectively control forest pests and diseases, government and social forces can adopt the following three control modes:

(1) Pesticide control. There are many kinds of pesticides, and the pesticides referred to in this article mainly refer to chemical pesticides. Compared with biological pesticides, chemical pesticides have the advantages of high efficacy and an immediate effect. In controlling forest pests, pesticides with good control effects should be selected according to the characteristics of the control objects. This can achieve targeted, tailored medicine, which is the key to good prevention and control effects. In the process of pesticide control, it is necessary to choose the weakest stage of pest development to control. In this way, pesticides can be used to achieve the best control effect. However, this type of management can also adversely affect natural enemies of forest pests (Palma-Onetto et al., 2021).

(2) Physical control. This method of prevention and control begins by placing a certain number of mechanical facilities. It mainly includes artificial killing, the use of simple devices and instruments, and even the application of modern devices and equipment. Some forest pests are sensitive to radiation, sound, electricity, light, temperature, and other physical factors. Physical management mainly uses the sensitivity of forest pests to eliminate forest pests. For example, light trapping is a physical way to control pests. This is mainly to take advantage of the phototaxis of some forest pests and then artificially set up insect lights. The trap light can be used to trap and kill pests. The use of light to induce killing is one of the most common physical control measures.

(3) Biological control. This method of control is mainly based on biological control of forest pests. Natural enemies of forest pests mainly include natural enemies of insects, microorganisms, birds, and so on. The natural enemies of insects are mainly bees, ladybugs, praying mantises, and so on. Microorganisms mainly refer to bacteria, fungi, and viruses. Birds are mainly cuckoos, woodpeckers, great tit, and so on. In addition, another approach is to cultivate plants that possess natural resistance to invasive species without necessarily being their natural enemies (Dragicevic, 2015). Biological control has a certain effect on pest control and is economical (Janssen and Rijn, 2021). At the same time, the organisms themselves can reproduce, so this method also has the characteristics of environmental protection and efficiency. Biological control is one of the important methods of forest pest control.

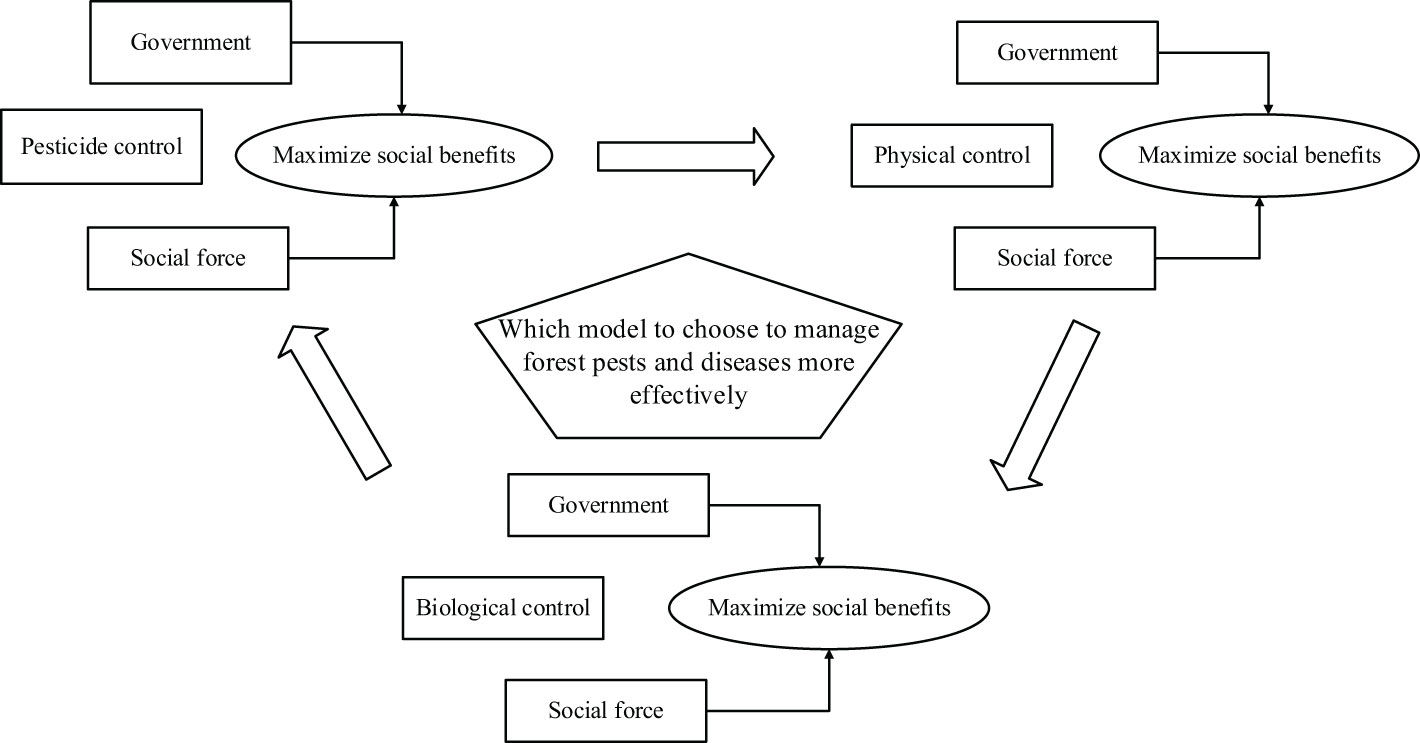
The relationship between the three forest pests and disease control modes is shown in Figure 1.

FIGURE 1

Figure 1 Relationship between three different forest pests and disease control modes.

In Figure 1, there are two players (the government and social forces) and three forest pest and disease control modes. In order to maximize their own benefits, each player can choose the forest pest and disease control mode to be adopted. The arrows in the figure show that the players are constantly choosing between different forest pests and disease control modes.

2 Methodology

2.1 Hypothesis

(1) The pest management decisions of the government and social forces are constantly changing. With the increase in global temperature, the propagation and spreading ability of forest pests are further enhanced. In the absence of natural enemies, once the forest is infected by pests and diseases, it is easy to spread such pests throughout the forest. In the face of the destruction of the forest ecosystem, the government and social forces will carry out forest pest control. After a period of management, forest pests and diseases have been reduced. At this point, the government and social forces will reduce the intensity of governance. The severity of forest pests and diseases has increased as they have been neglected. At this time, the government and social forces will increase efforts to control pests and diseases. Over time, the cycle continues. Forest pest management decisions by governments and social forces are in flux.

(2) The government and social forces can fully grasp the information about forest pests and diseases. There are many kinds of forest pests. Forests are infested by many kinds of pests and diseases. If forest pests and diseases are not dealt with in time, large areas of forest are likely to be affected. In some cases, governments do not understand some exotic insects and cannot make timely decisions conducive to forest pest management (Pirtle et al., 2021). In other cases, monitoring and early warning agencies of the government and social forces are located far from forest pests and diseases. This is not conducive to government and social forces grasping information about forest pests. In order to enable government and social forces to make optimal decisions, this article assumes that government and social forces have comprehensive access to forest pest and disease information.

(3) The forest ecosystem has an important impact on national production and management activities. Forests can conserve water, conserve soil, sequester carbon, release oxygen, and purify the atmosphere (Food and Agricultural Organization, 2020). If the forest is far from a densely populated area, then forest pests and diseases have less impact on people’s lives and production and management activities. When pests and diseases occur in an area, the government does not take measures to control them. That is because forest pests and diseases cost money to control. On the other hand, if the forest is close to the country’s population concentration, people will be more affected when the forest is destroyed. At this time, people will be concerned about the state of the forest ecosystem.

2.2 Variable definition

In Table 1, the discount factor ρ is a number used to calculate the value of future cash flows at the current point in time. It is a tool that reduces future cash flows to the current point in time in order to calculate the value of time. Decay of reputation δ is the process by which, over time, the quality of the reputation earned by governments and social forces as a result of environmental protection gradually declines. The decay of reputation is a natural phenomenon as people’s perceptions and attitudes towards things change and evolve over time. At the same time, for governments and social forces, there can be unexpected events or negative news, which can affect the quality of their environmental reputation. The management of forest pests and diseases can protect forest resources, improve forest economic benefits, and stop the deterioration of the ecological environment. In this article, the income obtained from the unit management volume is defined as b_F. Under the long-term application of insecticides, the genetic variation of pests gradually weakens their virulence to insecticides and eventually cannot be effectively controlled by insecticides. This article defines this resistance of pests as d. Once forest pests have resistance, it will increase the difficulty of controlling them, which is defined as k_d.

TABLE 1

Table 1 Definition of variables and parameters used in this article.

Each mode of forest pest management has a cost. In this article, the cost of forest pest management at the unit level is defined as c_P, c_H, c_B, respectively. Once a forest is infested with pests and diseases, it is difficult to fully recover. On the contrary, there is a certain control rate for forest pests and diseases. This article defines the control rate as s. The reputation of the government and social forces will enhance the image of the country, enhance the sense of trust and support among the people in the country, and so on. This article defines the unit impact of this reputation as l. Compared with pesticide management of forest pests and diseases, physical control and biological control can play a better role in protecting the environment. These two control modes can have an additional impact on reputation, which this article defines as I_Hand I_E. Social forces are mainly non-governmental organizations. These organizations are often underfunded. These organizations usually receive a certain amount of subsidy in the process of managing forest pests and diseases. This article defines the proportion of these subsidies as p. Extreme weather (such as typhoons, rainstorms, heat waves, hail, etc.) will affect the effectiveness of forest pest management. In this article, the occurrence times of forest pests and diseases are defined as e_H. The impact coefficient of these extreme weather events on forest pest management facilities is k_e. Physical facilities for forest pest management (e.g., trap lights, slime boards, bark strips, infrared detectors, etc.) can be reused. The number of times these physical facilities are reused is defined as α. The number of reuses affects the cost of managing forest pests and diseases. The impact of repeated use of these physical facilities on governance costs is defined as k_α.

The social welfare function is a tool used to measure the level of social welfare. This function is the sum of utility values over a period of time to represent social welfare over that period of time. Social benefit refers to the benefits or values generated by society under a certain decision made at a certain point. These effects can be positive, negative, or neutral. This article defines the social welfare function as J. At the same time, this article defines social benefits as V.

2.3 Differential games of different forest pest control modes

The differential game has the goal of optimizing the independence and conflict of each player and can finally obtain the strategy of each player as it evolves over time and reaches the Nash equilibrium. At present, the differential game is mainly applied in the fields of advertising decisions (Viscolani and Zaccour, 2009), logistics management (Bai et al., 2022), supply chain (Zhu et al., 2021), etc. Meanwhile, some scholars also use differential games to study the field of forest protection (Fredj et al., 2004).

In the context of differential games, the strategies adopted by the government and social forces are time-dependent functions. The actions taken by each participant are influenced by the strategies employed by other participants, leading to an ongoing evolutionary process wherein participants search for optimal strategies. This dynamic interaction can be described using differential equations that capture the rate of change in the relationship between variables, typically with respect to time or space variables (Arnone et al., 2022). In the specific context of this study, both forest pests and diseases, as well as the decisions made by the government and social forces, are subject to constant change. Therefore, the application of differential game theory is highly relevant and suitable.

When compared to alternative methods such as differential equations or stochastic strategies, differential games exhibit strong applicability in this study. While differential equations fail to account for the strategic interactions and outcomes among decision-makers, differential games effectively capture the conflicts and cooperation that occur between the government and social forces in the context of forest pest management. On the other hand, stochastic game models focus primarily on probability information regarding potential future events, emphasizing randomness rather than the continuous nature of time (Wu and Zhang, 2022). As such, the applicability of stochastic strategies in this paper is limited.

Forest pests and diseases are constantly changing with the changing climate. At the same time, forest pests and diseases will be constantly changed by the governance decisions of governments and social forces. In order to describe this change clearly, this article uses differential games to study forest pest management.

In the mode of pesticide control of forest pests and diseases, the social benefits obtained by the government and social forces are composed of the benefits of pest control, economic costs, ecological costs, and reputation gained. The specific expression can be expressed as:

$\begin{array}{ll}{J}_{P1}={\displaystyle {\int }_0^{\infty }[b_F{F}_{P1}(t)\frac{1}{\ln (e+k_{d}d)}-\frac{c_P}{2}{F}_{P1}^2(t)-\frac{c_E}{2}{F}_{P1}^2(t)+l{x}_{P1}(t)]e^{-\rho t}\text{d}t}& (1)\end{array}$

$\begin{array}{ll}{J}_{P2}={\displaystyle {\int }_0^{\infty }[b_F{F}_{P2}(t)\ln (e+k_{s}s)-\frac{c_P}{2}(1-p)F_{P2}^2(t)+l{x}_{P2}(t)]e^{-\rho t}\text{d}t}& (2)\end{array}$

In the above formula, $b_F{F}_{P1}(t)\frac{1}{\ln (e+k_{d}d)}$ represents the benefit to the government from the pesticide control mode. $\ln (e+k_{d}d)$ represents the development of resistance to pesticides by forest pests. $\frac{c_P}{2}{F}_{P1}^2(t)$ represents how much it costs the government to buy pesticides. $\frac{c_E}{2}{F}_{P1}^2(t)$ represents the negative impact of pesticide use on the ecological environment. $l{x}_{P1}(t)$ represents the positive effect of a government’s reputation on the social good. $b_F{F}_{P2}(t)\ln (e+k_{s}s)$ represents the benefits to social forces in the pesticide control mode. $\frac{c_P}{2}(1-p)F_{P2}^2(t)$ represents the cost of social forces under the pesticide control mode. $\frac{c_P}{2}p{F}_{P2}^2(t)$ represents government subsidies accepted by social forces. $l{x}_{P2}(t)$ represents the positive effect of the reputation of social power on social good.

Under the pesticide control mode, the changes in reputation gained by the government are as follows:

$\begin{array}{ll}{\dot{x}}_{P1}(t)=(a_F-a_E)F_{P1}(t)-\delta x_{P1}(t)& (3)\end{array}$

Under the pesticide control mode, the changes in reputation gained by the social power are as follows:

$\begin{array}{ll}{\dot{x}}_{P2}(t)=a_F{F}_{P2}(t)-\delta x_{P2}(t)& (4)\end{array}$

In the above formula, $a_F{F}_{P1}(t)$ shows the government’s reputation increased in the pesticide control mode. $a_E{F}_{P1}(t)$ shows the government’s reputation that is destroyed and reduced by biological diversity. $\delta x_{P1}(t)$ shows the attenuation of the government’s reputation. $a_F{F}_{P2}(t)$ shows the reputation of social forces in biological control modes. $\delta x_{P2}(t)$ shows the attenuation of the reputation of social forces.

In the mode of physical control of forest diseases and insect pests, the social benefits obtained by the government and social forces are:

$\begin{array}{ll}{J}_{H1}={\displaystyle {\int }_0^{\infty }[\frac{b_F}{1+k_e{e}_H}{F}_{H1}(t)-\frac{c_H}{2}\ln (1+k_{\alpha }\alpha )F_{H1}^2(t)+l{x}_{H1}(t)]e^{-\rho t}\text{d}t}& (5)\end{array}$

$\begin{array}{ll}{J}_{H2}={\displaystyle {\int }_0^{\infty }[b_F{F}_{H2}(t)\ln (1+k_{s}s)-\frac{c_H}{2}(1+k_{\alpha }\alpha )(1-p)F_{H2}^2(t)+l{x}_{H2}(t)]e^{-\rho t}\text{d}t}& (6)\end{array}$

In the above formula, $\frac{b_F}{1+k_e{e}_H}{F}_{H1}(t)$ means the government gain under the physical control of forest pests. $1+k_e{e}_H$ means the adverse effects of extreme weather on physical facilities. $\frac{c_H}{2}\ln (1+k_{\alpha }\alpha )F_{H1}^2(t)$ means government governance costs under the physical governance of forest pests. $\ln (1+k_{\alpha }\alpha )$ represents the changes in the cost caused by the repetitive use of physical facilities. $l{x}_{H1}(t)$ means the social benefits increased by the government’s reputation. $b_F{F}_{H2}(t)\ln (1+k_{s}s)$ represents the benefits of social forces to govern forest pests. $\frac{c_H}{2}(1+k_{\alpha }\alpha )(1-p)F_{H2}^2(t)$ means the cost of governing the forest pests in social forces. $\frac{c_H}{2}(1+k_{\alpha }\alpha )p{F}_{H2}^2(t)$ indicates subsidies obtained by social forces. $l{x}_{H2}(t)$ means the benefits of the reputation of social forces.

Under the physical control mode, the changes in reputation gained by the government are as follows:

$\begin{array}{ll}{\dot{x}}_{H1}(t)=a_F\ln (e+I_H)F_{H1}(t)-\delta x_{H1}(t)& (7)\end{array}$

Under the physical control mode, the changes in reputation gained by the social forces are as follows:

$\begin{array}{ll}{\dot{x}}_{H2}(t)=a_F\ln (e+I_H)F_{H2}(t)-\delta x_{H2}(t)& (8)\end{array}$

Among them, $a_F\ln (e+I_H)F_{H1}(t)$ indicates the increase in the government’s reputation in the physical control mode. $\delta x_{H1}(t)$ shows the attenuation of the government’s reputation. $a_F\ln (e+I_H)F_{H2}(t)$ shows the reputation of social forces in physical control modes. $\delta x_{H2}(t)$ shows the attenuation of the reputation of social forces.

In the mode of biological control of forest diseases and insect pests, the income obtained by the government and social forces is:

$\begin{array}{ll}{J}_{B1}={\displaystyle {\int }_0^{\infty }[b_F{F}_{B1}^2(t)-(c_B+k_m{c}_m+k_o{c}_o)F_{B1}^2(t)+l{x}_{B1}(t)]e^{-\rho t}\text{d}t}& (9)\end{array}$

$\begin{array}{ll}{J}_{B2}={\displaystyle {\int }_0^{\infty }[b_F{F}_{B2}^2(t)-c_B(1-p)F_{B2}^2(t)+l{x}_{B2}(t)]e^{-\rho t}\text{d}t}& (10)\end{array}$

Among them, $b_F{F}_{B1}^2(t)$ represents the income obtained by the government under the biological management of forest pests. $(c_B+k_m{c}_m+k_o{c}_o)F_{B1}(t)$ represents the cost of government control of forest pests under the biological control of forest pests. $k_m{c}_m{F}_{B1}(t)$ represents the loss caused by the inadaptation of introduced species. $k_o{c}_o{F}_{B1}(t)$ represents loss due to the proliferation of introduced species. $l{x}_{B1}(t)$ represents the social benefit increased by the government’s reputation. $b_F{F}_{B2}^2(t)$ represents the benefits to social forces from the biological management of forest pests. $c_B(1-p)F_{B2}(t)$ represents the cost of social forces under the biological management of forest pests. $l{x}_{B2}(t)$ represents the increased benefit of a reputation for social power.

Under the biological control mode, the changes in reputation gained by the government are as follows:

$\begin{array}{ll}{\dot{x}}_{B1}(t)=\left[a_F+a_E\ln (e+I_E)\right]F_{B1}(t)-\delta x_{B1}(t)& (11)\end{array}$

Under the biological control mode, the changes in reputation gained by the social power are as follows:

$\begin{array}{ll}{\dot{x}}_{B2}(t)=a_F{F}_{B2}(t)-\delta x_{B2}(t)& (12)\end{array}$

Among them, $[a_F+a_E\ln (e+I_E)]F_{B1}(t)$ represents the increased government reputation under the biocontrol mode. $a_F{F}_{B1}(t)$ represents an increase in the government’s reputation as a result of the introduction of organisms. $F_{B1}(t)a_E\ln (e+I_E)$ says improved biodiversity has led to an increase in the government’s reputation. $\delta x_{B1}(t)$ represents a decline in the government’s reputation. $a_F{F}_{B2}(t)$ represents the increased reputation of social forces under the biological control mode. $\delta x_{B2}(t)$ represents a decline in the reputation of social forces.

3 Results

In the differential game, the social welfare of the government and social forces when forest pests and diseases occur is not only affected by control variables and parameters but also changes over time. In order to better calculate the amount of control and social benefits, the HJB formula was adopted. The HJB formula is a partial differential equation, which is the core of optimal control.

3.1 HJB formula

Under the pesticide control mode, the HJB equation of the social welfare function of the government and social forces is:

$\begin{array}{ll}\begin{array}{l}\rho V_{P1}=\underset{F_{P1}(t)}{\max }\{[b_F{F}_{P1}(t)\frac{1}{\ln (e+k_{d}d)}-\frac{c_P}{2}{F}_{P1}^2(t)-\frac{c_E}{2}{F}_{P1}^2(t)+l{x}_{P1}(t)]\\ +\frac{\partial V_{P1}}{\partial x_{P1}}[(a_F-a_E)F_{P1}(t)-\delta x_{P1}(t)]\}\end{array}& (13)\end{array}$

$\begin{array}{ll}\begin{array}{l}\rho V_{P2}=\underset{F_{P2}(t)}{\max }\{[b_F{F}_{P2}(t)\ln (e+k_{s}s)-\frac{c_P}{2}(1-p)F_{P2}^2(t)+l{x}_{P1}(t)]\\ +\frac{\partial V_{P2}}{\partial x_{P2}}\left[a_F{F}_{P2}(t)-\delta x_{P2}(t)\right]\}\end{array}& (14)\end{array}$

Under the physical control mode, the HJB equation of the social welfare function of the government and social forces is:

$\begin{array}{ll}\begin{array}{l}\rho V_{H1}=\underset{F_{H1}(t)}{\max }\{[\frac{b_F}{1+k_e{e}_H}{F}_{H1}(t)-\frac{c_H}{2}\ln (1+k_{\alpha }\alpha )F_{H1}^2(t)+l{x}_{H1}(t)]\\ +\frac{\partial V_{H1}}{\partial x_{H1}}\left[a_F\ln (e+I_H)F_{H1}(t)-\delta x_{H1}(t)\right]\}\end{array}& (15)\end{array}$

$\begin{array}{ll}\begin{array}{l}\rho V_{H2}=\underset{F_{H2}(t)}{\max }\{[b_F{F}_{H2}(t)\ln (1+k_{s}s)-\frac{c_H}{2}(1+k_{\alpha }\alpha )(1-p)F_{H2}^2(t)+l{x}_{H2}(t)]\\ +\frac{\partial V_{H2}}{\partial x_{H2}}\left[a_F\ln (e+I_H)F_{H2}(t)-\delta x_{H2}(t)\right]\}\end{array}& (16)\end{array}$

Under the biological control mode, the HJB equation of the social welfare function of the government and social forces is:

$\begin{array}{ll}\begin{array}{l}\rho V_{B1}=\underset{F_{B1}(t)}{\max }\{[b_F{F}_{B1}^2(t)-(c_B+k_m{c}_m+k_o{c}_o)F_{B1}^{}(t)+l{x}_{B1}(t)]\\ +\frac{\partial V_{B1}}{\partial x_{B1}}\left[(a_F+a_E\ln (e+I_E))F_{B1}(t)-\delta x_{B1}(t)\right]\}\end{array}& (17)\end{array}$

$\begin{array}{ll}\begin{array}{l}\rho V_{B2}=\underset{F_{B2}(t)}{\max }\{[b_F{F}_{B2}^2(t)-c_B(1-p)F_{B2}^2(t)+l{x}_{B2}(t)]\\ +\frac{\partial V_{B2}}{\partial x_{B2}}\left[a_F{F}_{B2}(t)-\delta x_{B2}(t)\right]\}\end{array}& (18)\end{array}$

3.2 Result of equilibrium

Proposition 1: Under the pesticide control mode, the control quantities of government and social forces are, respectively (the specific solving procedure is shown in Appendix 1):

$\begin{array}{ll}{F}_{P1}^{*}(t)=\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{l}{\rho +\delta }\frac{a_F-a_E}{c_P+c_E}& (19)\end{array}$

$\begin{array}{ll}{F}_{P2}^{*}(t)=\frac{b_F\ln (e+k_{s}s)+\frac{l}{\rho +\delta }{a}_F}{c_P(1-p)}& (20)\end{array}$

In Eqs. (19) and (20), the resistance d of forest pests and the degree c_E of damage of pesticides to forest ecosystems are inversely proportional to the degree $F_{P1}^{*}(t)$ of government control. The rate s of forest pest control is proportional to the degree $F_{P2}^{*}(t)$ of social force input. The cost c_P of pest control is inversely proportional to the degree $F_{Pi}^{*}(t)(i=1,2)$ of control by government and social forces. The amount b_F of revenue generated per unit of governance is directly proportional to the degree $F_{Pi}^{*}(t)(i=1,2)$ of control of both government and social forces.

Conclusion 1: Under the pesticide control mode, the stronger the resistance to forest pests, the lower the balanced management degree of the government. The higher the damage degree of pesticides to the forest ecosystem, the lower the balanced governance degree of government. The faster the pest control speed, the more balanced the control amount of social force input. The greater the cost of pest control, the smaller the amount of balanced control input of government and social forces. The greater the income generated by the amount of unit governance, the greater the amount of government and social forces invested in governance.

Proposition 2: Under the physical control mode, the control quantities of government and social forces are, respectively (the specific solving procedure is shown in Appendix 2):

$\begin{array}{ll}{F}_{H1}^{*}(t)=\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}& (21)\end{array}$

$\begin{array}{ll}{F}_{H2}^{*}(t)=\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}& (22)\end{array}$

In Eqs. (21) and (22), the number e_H of extreme weather events is inversely proportional to the degree $F_{H1}^{*}(t)$ of control by the government. The number α of times physical facilities can be reused and the cost c_H of physical control are inversely proportional to the degree $F_{Hi}^{*}(t)$of control by government and social forces. The rate s of forest pest control is proportional to the degree $F_{Hi}^{*}(t)$ of balanced control of social forces. The amount b_F of revenue generated by a unit of control is proportional to the degree $F_{Hi}^{*}(t)$ of balanced control of government and social forces.

Conclusion 2: Under the physical control mode, the more extreme weather occurs, the lower the balanced governance degree of the government. The more physical facilities are reused, the lower the balance of government and social forces. The higher the cost of physical governance, the lower the degree of balanced governance of government and social forces. The faster the speed of forest pest control, the more balanced control amount of social forces input. The greater the income generated by the amount of unit governance, the greater the amount of government and social forces invested in governance.

Proposition 3:

$\begin{array}{ll}{F}_{B1}^{*}(t)=\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F+a_E\ln (e+I_E)}{2b_F}& (23)\end{array}$

$\begin{array}{ll}{F}_{B2}^{*}(t)=\frac{c_B(1-p)}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F}{2b_F}& (24)\end{array}$

In Eqs. (23) and (24), the cost c_m and c_o caused by the introduction of biological inadaptation or flooding is proportional to the government’s balanced control degree $F_{B1}^{*}(t)$. The income b_F generated by the amount of governance per unit is inversely proportional to the degree $F_{Bi}^{*}(t)$ of balanced governance between government and social forces. The unit governance cost c_B is proportional to the balanced governance degree of government and social force input.

Conclusion 3: Under the biological control mode of forest pests, the more cost caused by the inadaptation or flooding of introduced organisms, the more balanced management amount the government will invest. Different from the previous two governance modes, in this biological governance mode, the greater the income generated by the unit amount of governance, the smaller the amount of balanced governance input by the government and social forces. At the same time, under the biological control mode, the larger the unit governance cost, the larger the balanced governance amount of government and social force input.

4 Numerical analysis

In order to more clearly depict the change in social benefits of government and social power, numerical analysis is used in this article. This article assumes that the discount factor ρ is 0.9. The decay δ of reputation is 0.1. The resistance d produced by forest pests is 0.2. The influence coefficient k_d of pest resistance on the difficulty of control is 1. The destruction degree c_E of forest ecosystems per unit control amount is 0.5. The added cost c_m of inadaptability of introduced organisms is 0.4. The increased cost c_o of imported organisms is 0.8. The coefficient k_m of inadaptation of introduced organisms is 0.5. The coefficient k_o associated with the influx of introduced organisms is 1. The positive impact I_H of physical governance on reputation is 1.5. The positive impact I_E of biological governance on reputation is 2. The rate s of forest pest control is 0.5. The effect k_s of unit governance speed is 2. The positive influence l of the reputation of government or social power on earnings is 1. The proportion p of subsidies to social forces is 0.3. The positive effect a_F per unit of forest pest control on reputation is 1.5. The negative impact a_E of unit number of ecological damage on reputation is 1.2. The number e_H of extreme weather events is 2. The impact k_e of each extreme weather on pest management facilities was 0.5. The number α of reuse of physical facilities is 3. The effect k_α of reuse on cost is 0.3. The state variable is 1.

Therefore, this article can calculate:

$\begin{array}{ll}{V}_{P1}^{*}=1+\frac{2.85}{c_P+0.5}& (25)\end{array}$

$\begin{array}{ll}{V}_{H1}^{*}=1+\frac{1}{c_H}\times 8.68& (26)\end{array}$

$\begin{array}{ll}{V}_{B1}^{*}=-0.14c_B^2+0.65c_B+0.23& (27)\end{array}$

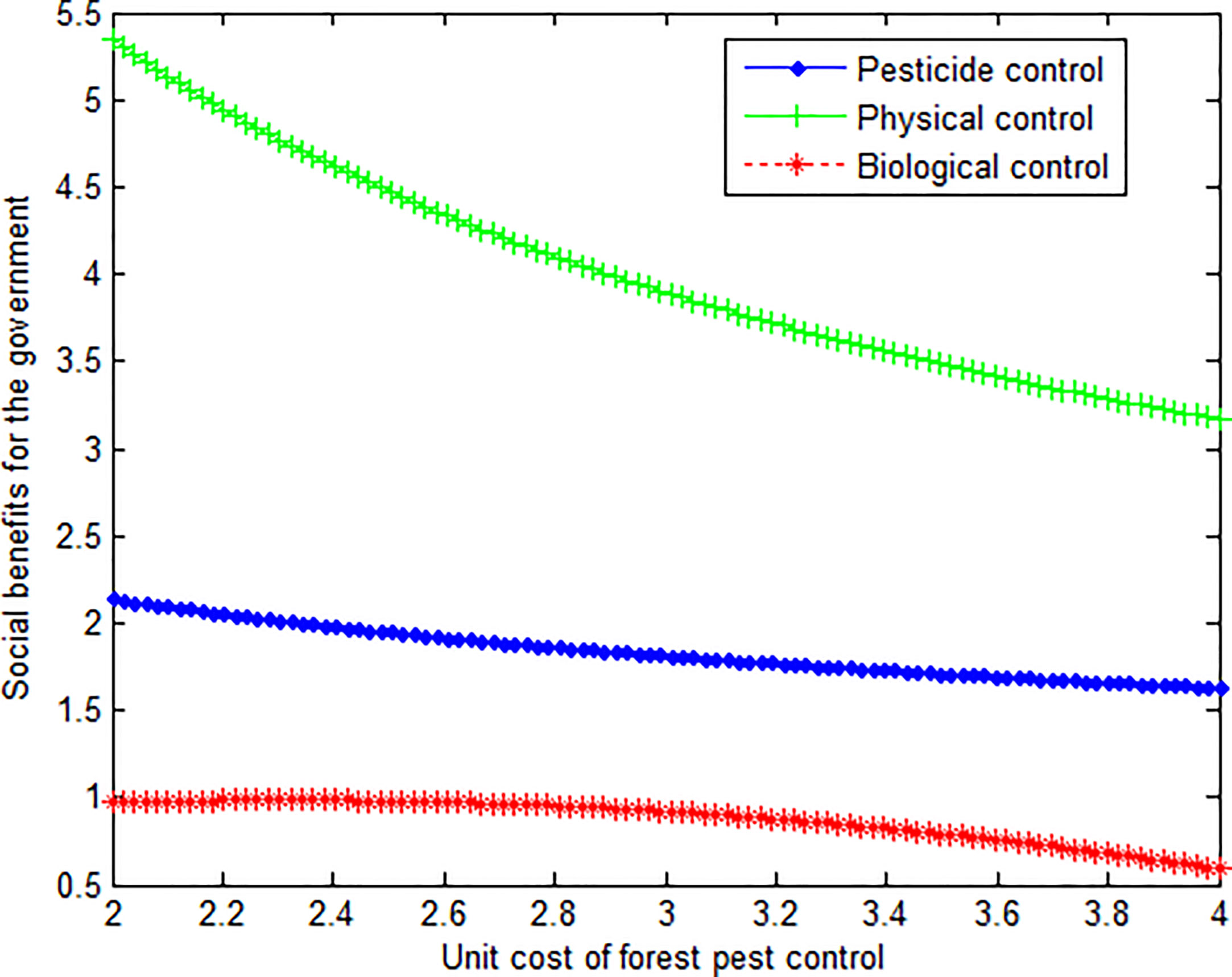
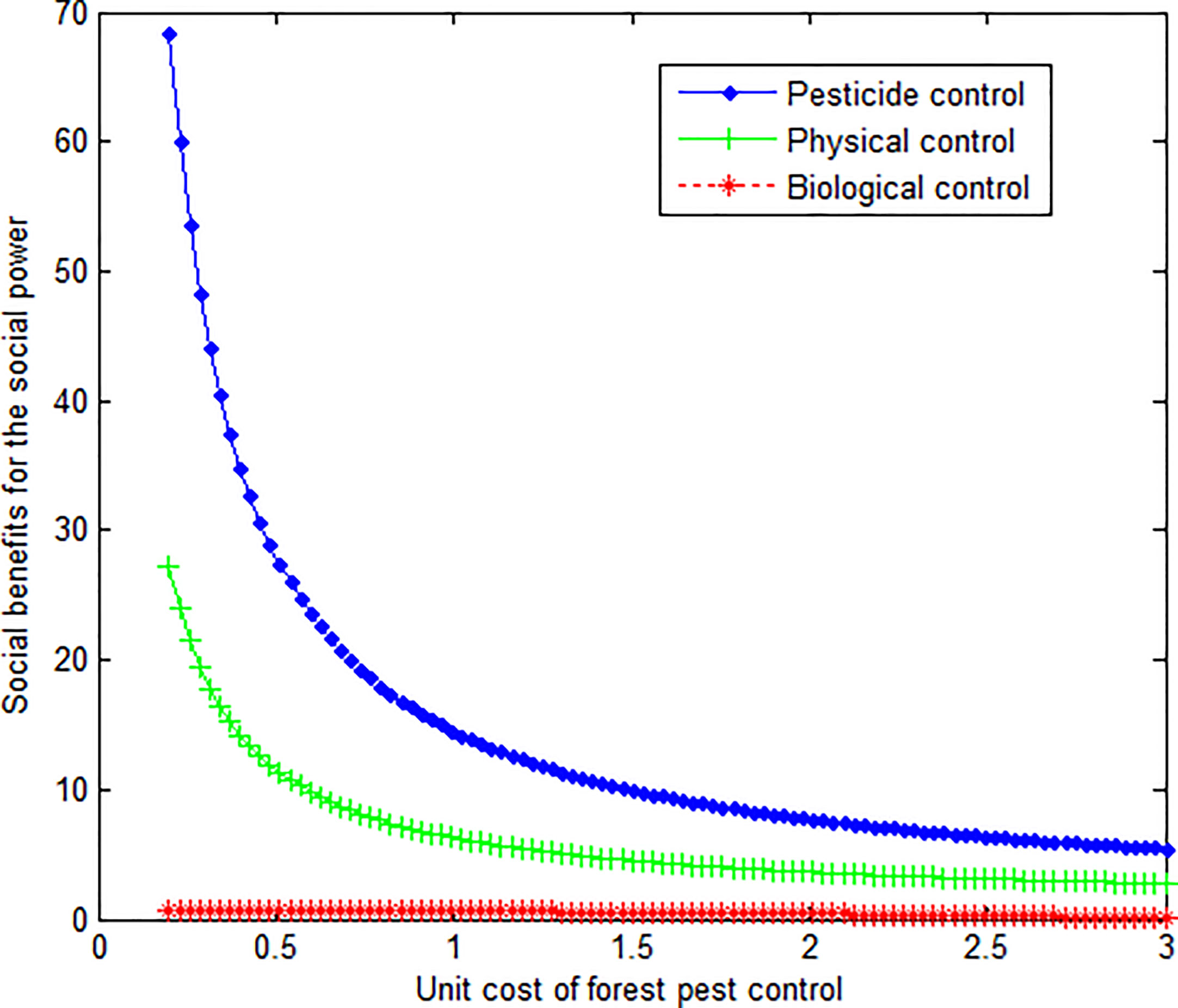
This article can produce the graph shown in Figure 2.

If the income b_F generated by the unit control quantity is 3, this article can calculate:

$\begin{array}{ll}{V}_{P1}^{*}=1+\frac{5.84}{c_P+0.5}& (28)\end{array}$

$\begin{array}{ll}{V}_{H1}^{*}=1+\frac{1}{c_H}\times 11.63& (29)\end{array}$

$\begin{array}{ll}{V}_{B1}^{*}=-0.09c_B^2+0.43c_B+0.49& (30)\end{array}$

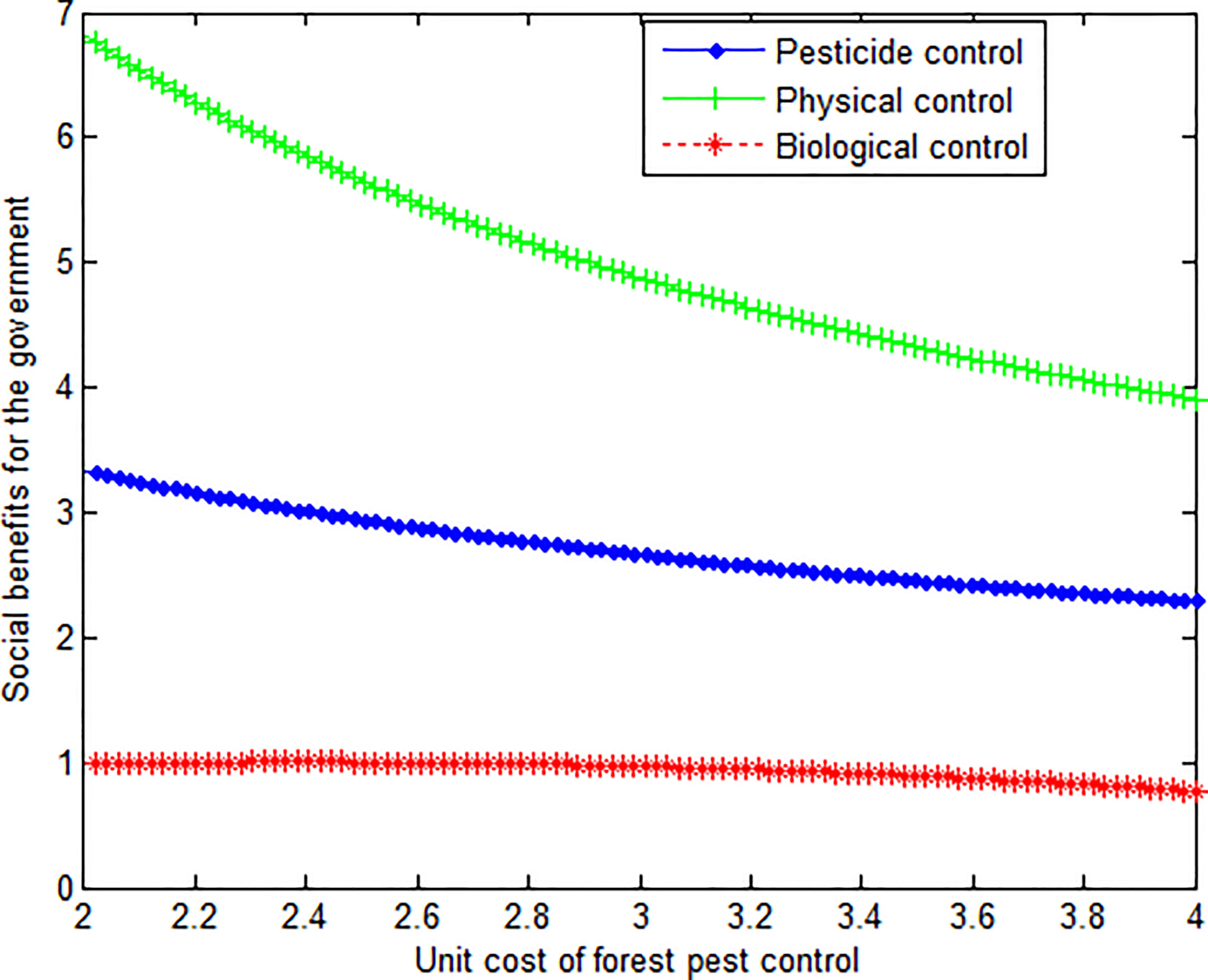
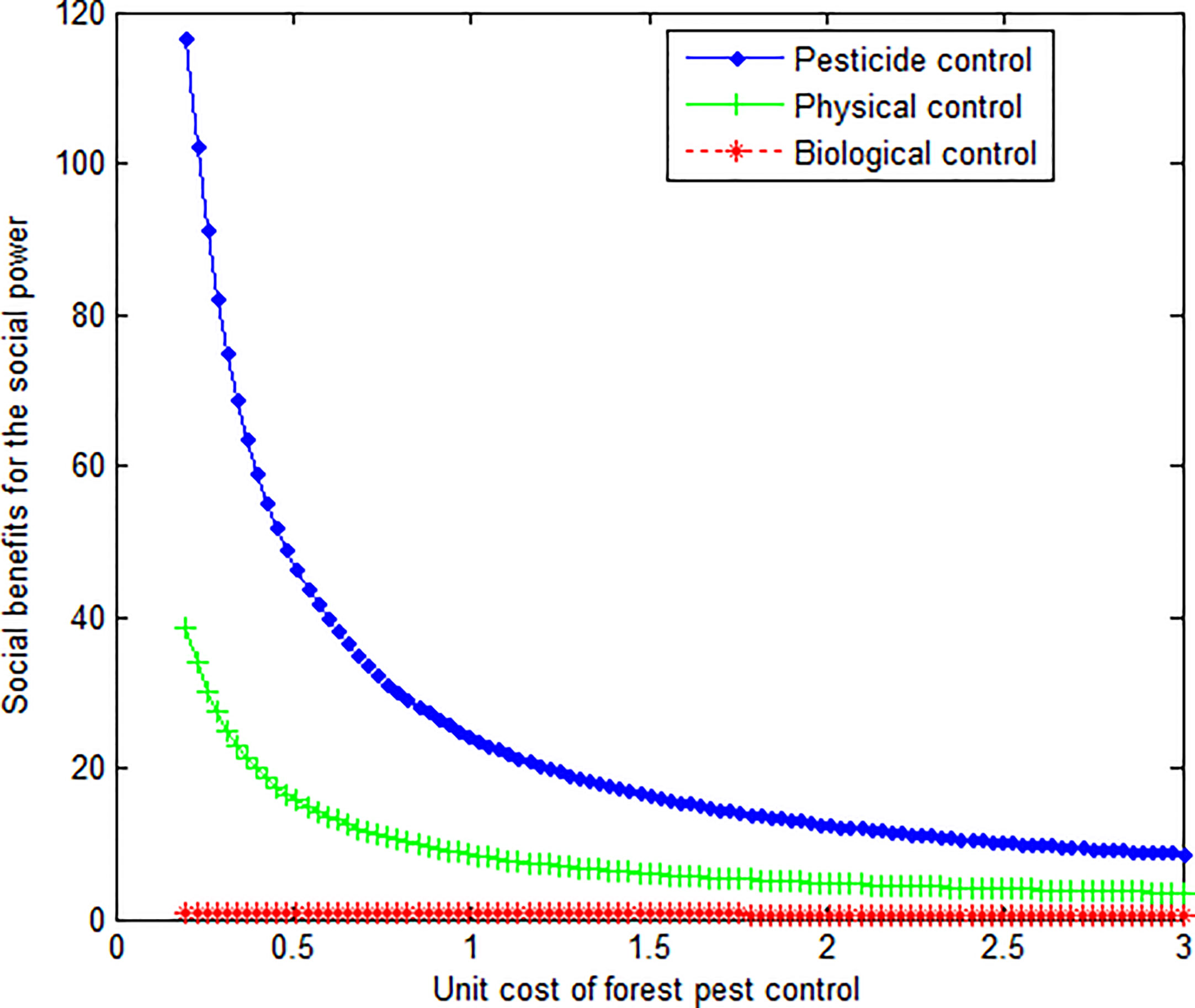
This article can produce the graph shown in Figure 3.

As can be seen from Figures 2 and 3, regardless of the change in governance benefits, the social benefits of physical control by the government are the largest. At the same time, the curve of biological governance is smoother.

FIGURE 2

Figure 2 The influence of control cost on the government’s social benefits.

FIGURE 3

Figure 3 The influence of control cost on the government’s social benefits.

Conclusion 4: When the unit management cost is the same, the government can get the maximum benefit from the physical management of forest pests. However, compared with the other two control modes, with the change of governance costs, the change of social benefits for the government under the biological control mode is relatively gentle.

If the income b_F generated by the unit control quantity is 2, this article can calculate:

$\begin{array}{ll}{V}_{P2}^{*}=1+\frac{1}{c_P}\times 13.49& (31)\end{array}$

$\begin{array}{ll}{V}_{H2}^{*}=1+\frac{1}{c_H}\times 5.26& (32)\end{array}$

$\begin{array}{ll}{V}_{B2}^{*}=-0.068c_B^2+0.682& (33)\end{array}$

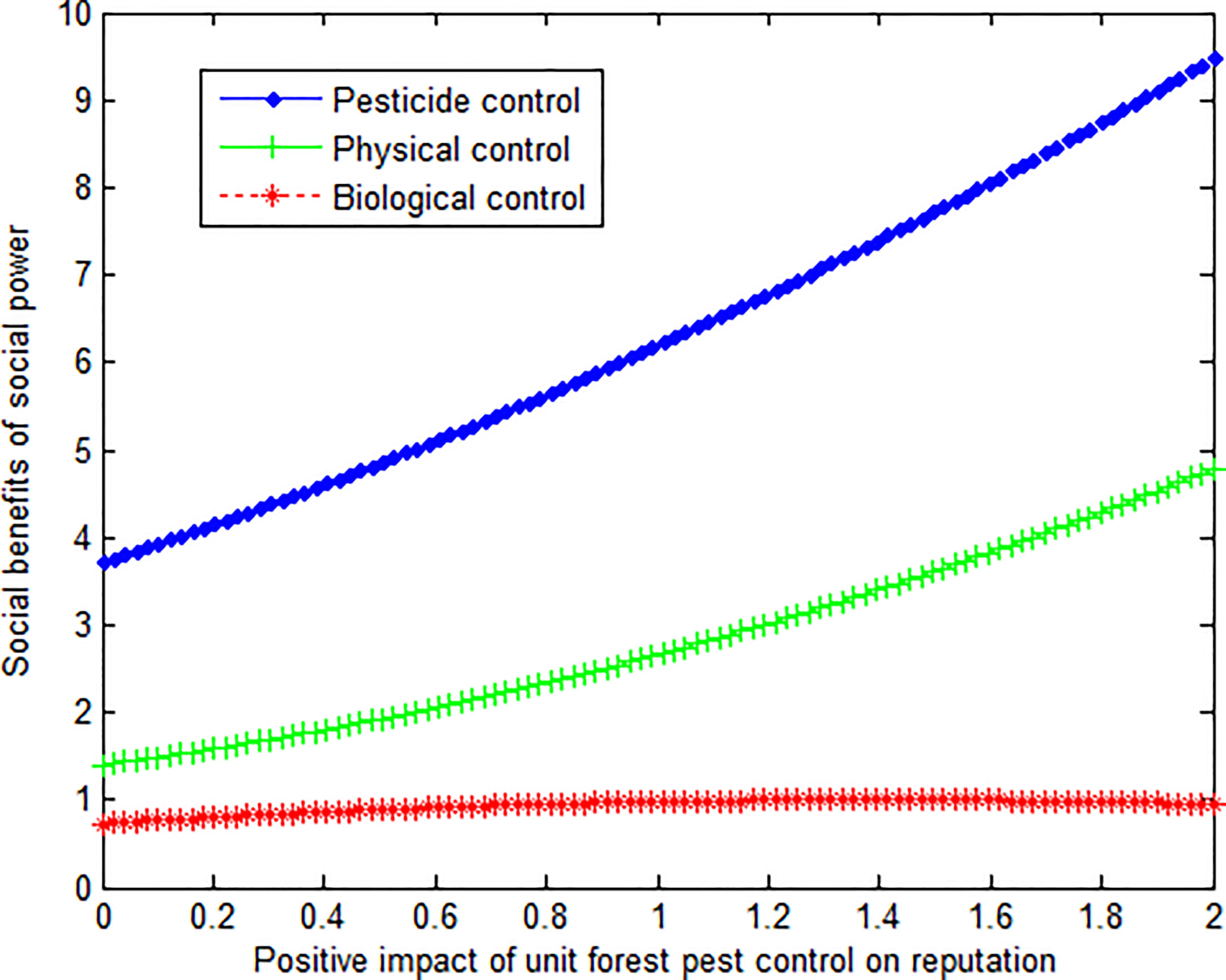
This article can produce the graph shown in Figure 4.

If the income b_F generated by the unit control quantity is 3, this article can calculate:

$\begin{array}{ll}{V}_{P2}^{*}=1+\frac{1}{c_P}\times 23.13& (34)\end{array}$

$\begin{array}{ll}{V}_{H2}^{*}=1+\frac{1}{c_H}\times 7.50& (35)\end{array}$

$\begin{array}{ll}{V}_{B2}^{*}=-0.045c_B^2+0.792& (36)\end{array}$

This article can produce the graph shown in Figure 5.

As can be seen from Figures 4 and 5, regardless of the change of governance benefits, the social benefits of pesticide control by the social power are the largest. At the same time, the curve of biological governance is smoother.

FIGURE 4

Figure 4 The influence of control cost on social power’s social benefits.

FIGURE 5

Figure 5 The influence of control cost on social power’s social benefits.

Conclusion 5: When the unit control cost is the same, social forces gain the most benefits from pesticide control of forest pests. However, compared with the other two governance modes, with the change in governance costs, the benefits of social forces under the biological governance mode change more gently.

In Figures 2–5, this article makes a visual presentation of the change in control cost. In order to show the changes in more parameters, this article then makes a visual presentation of the changes in the positive effects of control and the negative effects of ecological destruction.

Other parameters remain unchanged; redefine the following parameters. The income b_F generated by the unit control quantity is 2. The unit cost of managing forest pests and diseases is 2. That is, c_p = c_H = c_B = 2. The positive effect a_F per unit of forest pest control on reputation is changing. This article can calculate:

$\begin{array}{ll}{V}_{P1}^{*}=0.22a_F^2+0.29a_F+1.1& (37)\end{array}$

$\begin{array}{ll}{V}_{H1}^{*}=0.89a_F^2+1.24a_F+1.43& (38)\end{array}$

$\begin{array}{ll}{V}_{B1}^{*}=-0.14a_F^2+0.317a_F+0.819& (39)\end{array}$

$\begin{array}{ll}{V}_{P2}^{*}=0.4a_F^2+2.08a_F+3.72& (40)\end{array}$

$\begin{array}{ll}{V}_{H2}^{*}=0.43a_F^2+0.83a_F+1.40& (41)\end{array}$

$\begin{array}{ll}{V}_{B2}^{*}=-0.14a_F^2+0.39a_F+0.73& (42)\end{array}$

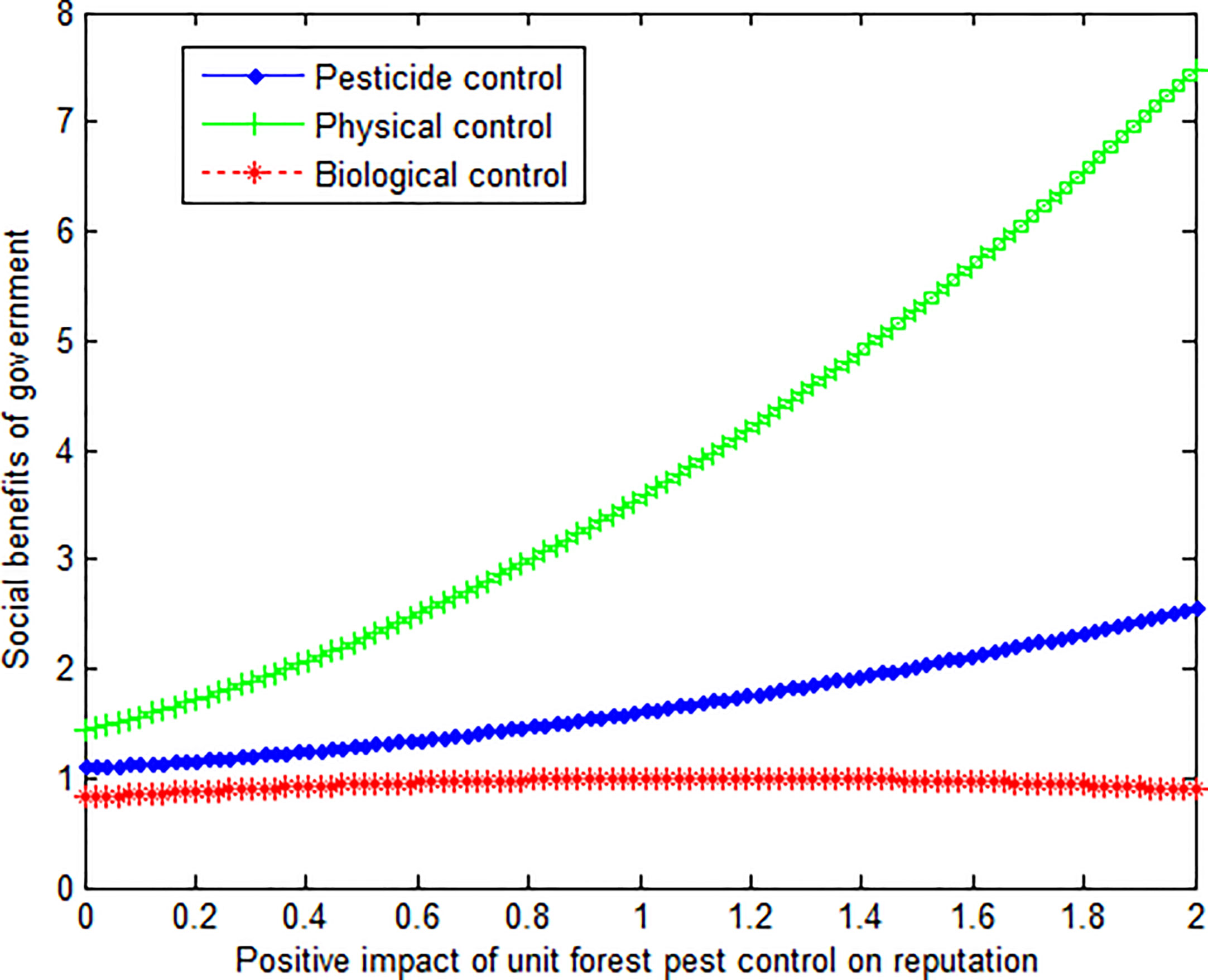
This article can produce the graphs shown in Figures 6 and 7.

As can be seen from Figures 6 and 7, as the reputation of controlling forest pests and diseases increases, the social benefits of both pesticide control and physical control by government and social forces increase. However, the social benefits of government and social forces change very gently under biological control.

FIGURE 6

Figure 6 The influence of positive impact on the government’s social benefits.

FIGURE 7

Figure 7 The influence of positive impact on social power’s social benefits.

Conclusion 6: Under pesticide control and physical control, the social benefits of government and social forces are directly proportional to the reputation generated by pest control.

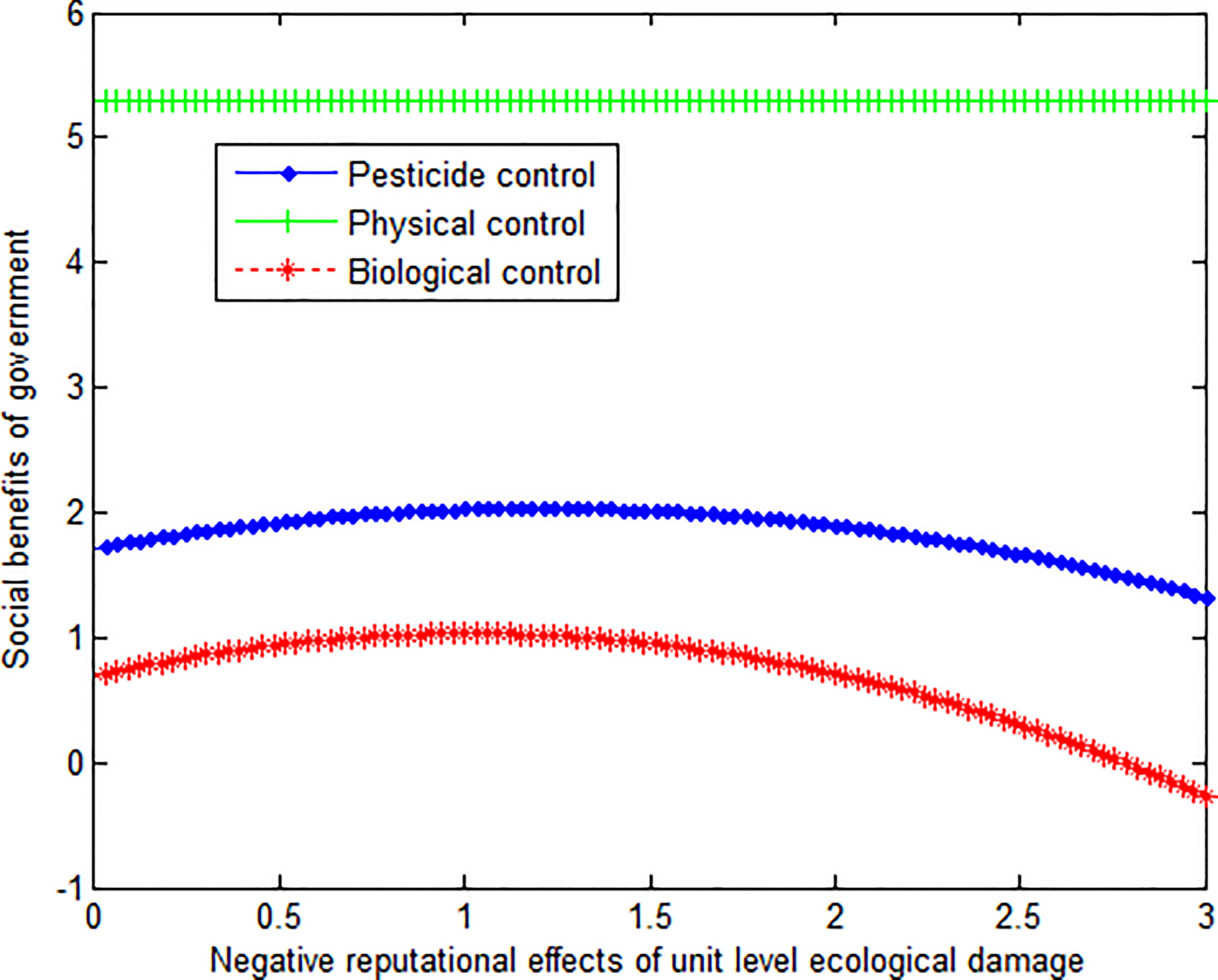
Other parameters remain unchanged; redefine the following parameters: The negative impact a_E of unit number of ecological damage on reputation is changing. The income b_F generated by the unit control quantity is 2. The unit cost of managing forest pests and diseases is 2. That is, c_p = c_H = c_B = 2. The positive effect a_F per unit of forest pest control on reputation is 1.5. This article can calculate:

$\begin{array}{ll}{V}_{P1}^{*}=-0.22a_E^2+0.53a_E+1.72& (43)\end{array}$

$\begin{array}{ll}{V}_{H1}^{*}=5.29& (44)\end{array}$

$\begin{array}{ll}{V}_{B1}^{*}=-0.33a_E^2+0.67a_F+0.69& (45)\end{array}$

This article can produce the graph shown in Figure 8.

FIGURE 8

Figure 8 The influence of negative reputational effects on the government’s social benefits.

Conclusion 7: As the adverse effects of ecological damage on reputation continue to increase, the social benefits of the government under pesticide control and biological control modes are first increased and then decreased.

5 Discussion

In recent years, the global temperature has been gradually rising, and forest pests are frequently harmful and very easy to spread. Governments and social forces need to take measures to control forest pests and diseases. Pesticide control tends to damage ecosystems and lead to pest resistance, but it is low cost and has quick results. Physical containment facilities can be reused, but they are costly and vulnerable to extreme weather. Biological control can better protect the ecosystem, but introduced natural enemies are prone to problems of adaptability and infestation. Therefore, how to control forest pests and diseases is an important issue in this article. As most of the existing studies use traditional methods such as data analysis and field investigation, there is no research on forest pests and diseases using differential games. In this article, the differential game is applied to forest pest management, especially considering the advantages and disadvantages of various prevention and control modes and how the government and social forces achieve effective forest pest management.

In the process of forest pest management, we must pay attention to the reasonable rotation and mixing of pesticides. Long-term use of a pesticide will cause resistance to pests and diseases. Pesticide rotation and mixing can reduce the development of resistance to pests and diseases. At the same time, we also need to have a reasonable grasp of the dosage. Since reducing the number of drugs cannot reach the control effect, delay the best control period. If the amount of medicine is increased, there will be a waste of pesticides, an increase in cost, harm to the natural enemies of pests, increased environmental pollution, and other problems. In the process of pesticide use, attention should be paid to the extent of damage to the ecosystem.

Mechanical control mainly includes artificial killing, the use of simple appliances, instruments, and other devices, and even the application of modern devices and equipment. Mechanical control devices can be reused, and the more they are used, the less physical equipment is required. For example, pest traps are easy to operate, nontoxic, safe, and low-cost (Kecskeméti et al., 2021). If they can be reused after they are released, forest pests can be hunted continuously. However, in recent years, extreme weather has occurred more frequently around the world. Physical prevention and control measures are easily affected by extreme weather. When extreme weather such as typhoons and rainstorms occurs frequently, the number of physical facilities installed should be reduced to reduce the damage to physical facilities.

The goal of artificial mass breeding and release of natural enemies of insects is clear. Predators used for breeding and release should be much targeted. Only targeted natural enemies can play a better role in controlling forest pests. Moreover, predators are living things that can reproduce themselves. The offspring of natural enemies can also have an impact on forest pests. However, the more targeted the predator, the higher the cost. For example, in order to control forest pests, a variety of egg-parasitic wasps of Trichotropis (Zang, 2021) are the most studied and utilized in feeding and releasing natural enemies in China. This has been commercialized, and Trichogramma can be used to control major lepidopteran pests.

Pesticides are disposable and can easily affect the environment. The natural enemies of pests are easily restricted by environmental adaptability and flooding (Mandal et al., 2023). Physical facilities can be reused. As a result, governments tend to prefer physical prevention. Governments pay more attention to ecological sustainability than social forces. Governments focus on long-term interests, while social forces tend to focus on short-term interests (Dragicevic, 2019c). Social forces generally focus on the number of forest pests eliminated in the short term. The effects of pesticides on ecosystems are often not visible in the short term. As a result, social forces are more inclined to use pesticide control.

6 Conclusion

In order to study the application scope of different management modes for forest pests and diseases, differential game models of pesticide management, physical management, and biological management were constructed in this article. Also, the equilibrium results are compared and analyzed. Finally, the research conclusion is drawn that under the biological control mode, the income generated by the unit control quantity is inversely proportional to the balanced control quantity. However, under the pesticide control and physical control modes, the income generated by the unit control quantity is proportional to the balanced control quantity. At the same time, under the biological control mode, the unit governance cost is proportional to the balanced governance quantity. Under the pesticide control and physical control modes, the unit control cost is inversely proportional to the balanced control quantity. Social forces tend to adopt pesticide control. The government prefers physical control.

This article has some shortcomings. For example, this article is based on the analysis of mathematical modeling, and the relevant specific data are limited. At the same time, the problem of pests and diseases in specific forests has not been studied, and the specific conditions faced by different forests may not be exactly the same. In future studies, relevant specific data can be added to carry out research on specific forest pests and diseases. The research in this article can be extended to some extent. For example, this article only considers the situation that the government’s decision-making is constantly changing, the government can grasp the information on forest diseases and pests in a more comprehensive way, and the forest affects national production and management. In future studies, it is possible to consider the situation that the government’s decision is unchanged, the government cannot grasp the comprehensive information of pests and diseases, the forest has little impact on economic development, etc., and carry out relevant studies. In addition, this study is not only applicable to the study of forest pests and diseases but also has certain reference significance for forest fire control, forest wildlife protection, and other related issues.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

YB: Model building, problem description, writing – first draft, result analysis; LW: Figure preparation, literature collection; XY: Quality control, writing – review & editing. All authors contributed to the article and approved the submitted version.

Funding

This research is funded by the Doctoral Research Foundation of Shandong Management University, sdmud2023001. This research is financially supported by Social Science Planning Foundation of Chongqing in China, 2021BS080.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arnone E., Kneip A., Nobile F., Sangalli L. M. (2022). Some first results on the consistency of spatial regression with partial differential equation regularization. Statistica Sin. 1, 32. doi: 10.5705/ss.202019.0346

CrossRef Full Text | Google Scholar

Ayres M. P., Lombardero M. J. (2018). Forest pests and their management in the Anthropocene. Can. J. For. Res. 48, 292–301. doi: 10.1139/cjfr-2017-0033

CrossRef Full Text | Google Scholar

Bai Y., Gao Y., Li D., Liu D. (2022). Coordinated distribution or client introduce? Analysis of energy conservation and emission reduction in Canadian logistics enterprises. Sustainability 14, 16979. doi: 10.3390/su142416979

CrossRef Full Text | Google Scholar

Bai X., Jia X., Zhao C., Shao M. (2021). Artificial forest conversion into grassland alleviates deep-soil desiccation in typical grass zone on China's loess plateau: regional modeling. Agriculture Ecosyst. Environ. 320, 107608. doi: 10.1016/j.agee.2021.107608

CrossRef Full Text | Google Scholar

Canelles Q., Aquilue N., James P. M. A., Lawler J., Brotons L. (2021). Global review on interactions between insect pests and other forest disturbances. Landscape Ecol. 36 (4), 945–972. doi: 10.1007/s10980-021-01209-7

CrossRef Full Text | Google Scholar

Dragicevic A. (2015). Bayesian population dynamics of spreading species. Environ. Model. Assess. 20, 17–27. doi: 10.1007/s10666-014-9416-4

CrossRef Full Text | Google Scholar

Dragicevic A. (2019a). Comparing forest control modes against invasive biological threats. J. Theor. Biol. 462, 270–282. doi: 10.1016/j.jtbi.2018.11.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Dragicevic A. Z. (2019b). Concentric framework for sustainability assessment. J. Cleaner Production 248, 119268. doi: 10.1016/j.jclepro.2019.119268

CrossRef Full Text | Google Scholar

Dragicevic A. (2019c). Rethinking the forestry in the aquitaine massif through portfolio management. For. Policy Econo. 109, 102020. doi: 10.1016/j.forpol.2019.102020

CrossRef Full Text | Google Scholar

Food and Agricultural Organization (2020). Global forest resources assessment 2020 – key findings (Rome, Italy: Food and Agricultural Organization).

Google Scholar

Fredj K., Martıín-Herrán G., Zaccour G. (2004). Slowing deforestation pace through subsidies: a differential game. Automatica 40, 301–309. doi: 10.1016/j.automatica.2003.10.020

CrossRef Full Text | Google Scholar

Janssen A., Rijn P. (2021). Pesticides do not significantly reduce arthropod pest densities in the presence of natural enemies. Ecol. Lett. 24, 2010–2024. doi: 10.1111/ele.13819

PubMed Abstract | CrossRef Full Text | Google Scholar

Jentsch P. C., Bauch C. T., Yemshanov D., Anand M. (2020). Go big or go home: a model-based assessment of general strategies to slow the spread of forest pests via infested firewood. PloS One 15, e0238979. doi: 10.1371/journal.pone.0238979

PubMed Abstract | CrossRef Full Text | Google Scholar

Kecskeméti S., Gesel A., Fail J., Egri D. (2021). In search of the spectral composition of an effective light trap for the mushroom pest Lycoriella ingenua (Diptera: Sciaridae). Sci. Rep. 11, 12770. doi: 10.1038/s41598-021-92230-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei M., Yuan X., Yao X. (2021). Synthesize dual goals: a study on China's ecological poverty alleviation system. J. Integr. Agr. 20, 1042–1059. doi: 10.1016/S2095-3119(21)63635-3

CrossRef Full Text | Google Scholar

Lovett G. M., Weiss M., Liebhold A. M., Holmes T. P., Leung B., Lambert K. F., et al. (2016). Nonnative forest insects and pathogens in the united states: impacts and policy options. Ecol. Appl. 26, 1437–1455. doi: 10.1890/15-1176

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandal D. S., Samanta S., Parshad R. D., Chekroun A., Helal M., Chattopadhyay J. (2023). Study of a crop-pest-natural enemy model with z-type control – an approach to pest management. Int. J. Biomathematics 16, 2240099. doi: 10.1142/S1793524522500991

CrossRef Full Text | Google Scholar

Niquidet K., Tang J., Peter B. (2015). Economic analysis of forest insect pests in Canada. Can. Entomologist 148, S357–S366. doi: 10.4039/tce.2015.27

CrossRef Full Text | Google Scholar

Ozkan S. N. (2022). Management of the control against forest pests in Artvin spruce forests. Int. J. Trop. Insect Sci. 42, 527–534. doi: 10.1007/s42690-021-00568-7

CrossRef Full Text | Google Scholar

Palma-Onetto V., Oliva D., González-Teuber M. (2021). Lethal and oxidative stress side effects of organic and synthetic pesticides on the insect scale predator Rhyzobius lophanthae. Entomologia Generalis 41, 345–355. doi: 10.1127/entomologia/2021/1045

CrossRef Full Text | Google Scholar

Pirtle E. I., Umina P. A., Hauser C. E., Maino J. L. (2021). Using mock surveillance to quantify pest detectability prior to establishment of exotic leafminers. Crop Prot. 148, 105713. doi: 10.1016/j.cropro.2021.105713

CrossRef Full Text | Google Scholar

Popkin G. (2020). Deadly imports: in one US forest, 25% of tree loss caused by foreign pests and disease. Science. doi: 10.1126/science.abc7624

CrossRef Full Text | Google Scholar

Sheremet O., Ruokamo E., Juutinene A., Svento R., Hanley N. (2018). Incentivising participation and spatial coordination in payment for ecosystem service schemes: forest disease control programs in Finland. Ecol. Economics 152, 260–272. doi: 10.1016/j.ecolecon.2018.06.004

CrossRef Full Text | Google Scholar

Tandon A., Verma P. R. (2021). Human population induced urban developments and their effects on temperature rise: a nonlinear mathematical model. Ecol. Complexity 47, 100947. doi: 10.1016/j.ecocom.2021.100947

CrossRef Full Text | Google Scholar

Turner J. A., Buongiorno J., Zhu S., Prestemon J. P., Bulman L. S. (2007). Modelling the impact of the exotic forest pest nectria on the New Zealand forest sector and its major trading partners. New Z. J. Forestry Sci. 37, 383–411.

Google Scholar

Valizadeh M., Gohari A. (2021). Simulation of a random variable and its application to game theory. Math. Oper. Res. 46, 452–470. doi: 10.1287/moor.2020.1067

CrossRef Full Text | Google Scholar

Viscolani B., Zaccour G. (2009). Advertising strategies in a differential game with negative competitor’s interference. J. Optim. Theory Appl. 140, 153–170. doi: 10.1007/s10957-008-9454-7

CrossRef Full Text | Google Scholar

Wu Z., Zhang F. (2022). Maximum principle for discrete-time stochastic optimal control problem and stochastic game. Math. Control Related Fields 12 (2), 475–493. doi: 10.3934/mcrf.2021031

CrossRef Full Text | Google Scholar

Yang Z., Wang X., Zhang Y. (2014). Recent advances in biological control of important native and invasive forest pests in China. Biol. Control 68, 117–128. doi: 10.1016/j.biocontrol.2013.06.010

CrossRef Full Text | Google Scholar

Zang F. (2021). Biological control with Trichogramma in China: history, present status, and perspectives. Annu. Rev. Entomology 66, 463–484. doi: 10.1146/annurev-ento-060120-091620

CrossRef Full Text | Google Scholar

Zhu S., Xie K., Cui P. (2021). Dynamic adjustment mechanism and differential game model construction of mask emergency supply chain cooperation based on covid-19 outbreak. Sustainability 13, 1115. doi: 10.3390/su13031115

CrossRef Full Text | Google Scholar

Appendix 1

Take the derivatives of F_P1 with respect to Eq. (13), take the derivatives of F_P2 with respect to Eq. (14), and set them equal to zero, we can get:

$\begin{array}{ll}{F}_{P1}^{*}(t)=\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{\partial V_{P1}}{\partial x_{P1}}\frac{a_F-a_E}{c_P+c_E}& (46)\end{array}$

$\begin{array}{ll}{F}_{P2}^{*}(t)=\frac{b_F\ln (e+k_{s}s)+\frac{\partial V_{P2}}{\partial x_{P2}}{a}_F}{c_P(1-p)}& (47)\end{array}$

Substituting Eq. (46) into Eq. (13) and substituting Eq. (47) into Eq. (14), we can get:

$\begin{array}{ll}\begin{array}{l}\rho V_{P1}=[b_F\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{\partial V_{P1}}{\partial x_{P1}}\frac{a_F-a_E}{c_P+c_E}\right)\frac{1}{\ln (e+k_{d}d)}-\left(\frac{c_P}{2}+\frac{c_E}{2}\right)\\ {\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{\partial V_{P1}}{\partial x_{P1}}\frac{a_F-a_E}{c_P+c_E}\right)}^2+l{x}_{P1}(t)]\\ +\frac{\partial V_{P1}}{\partial x_{P1}}\left[(a_F-a_E)\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{\partial V_{P1}}{\partial x_{P1}}\frac{a_F-a_E}{c_P+c_E}\right)-\delta x_{P1}(t)\right]\end{array}& (48)\end{array}$

$\begin{array}{ll}\begin{array}{l}\rho V_{P2}=[b_F\frac{b_F\ln (e+k_{s}s)+\frac{\partial V_{P2}}{\partial x_{P2}}{a}_F}{c_P(1-p)}\ln (e+k_{s}s)-\frac{c_P}{2}(1-p){\left(\frac{b_F\ln (e+k_{s}s)+\frac{\partial V_{P2}}{\partial x_{P2}}{a}_F}{c_P(1-p)}\right)}^2+l{x}_{P1}(t)]\\ +\frac{\partial V_{P2}}{\partial x_{P2}}[a_F\frac{b_F\ln (e+k_{s}s)+\frac{\partial V_{P2}}{\partial x_{P2}}{a}_F}{c_P(1-p)}-\delta x_{P2}(t)]\end{array}& (49)\end{array}$

Let $V_{P1}^{*}=m_1{x}_{P1}+m_2$ and $V_{P2}^{*}=m_3{x}_{P2}+m_4$ , wherein, m₁, m₂, m₃, and m₄ are all constants. The parameters of the optimal social welfare function can be obtained by calculation as follows:

$\begin{array}{ll}\{\begin{array}{l}{m}_1=\frac{l}{\rho +\delta }\\ m_2=\frac{1}{\rho }[b_F\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{l}{\rho +\delta }\frac{a_F-a_E}{c_P+c_E}\right)\frac{1}{\ln (e+k_{d}d)}-\left(\frac{c_P}{2}+\frac{c_E}{2}\right)\\ {\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{l}{\rho +\delta }\frac{a_F-a_E}{c_P+c_E}\right)}^2]\\ +\frac{1}{\rho }\frac{l}{\rho +\delta }\left[(a_F-a_E)\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{l}{\rho +\delta }\frac{a_F-a_E}{c_P+c_E}\right)\right]\end{array}& (50)\end{array}$

$\begin{array}{ll}\{\begin{array}{l}{m}_3=\frac{l}{\rho +\delta }\\ m_4=\frac{1}{\rho }[b_F\frac{b_F\ln (e+k_{s}s)+\frac{l}{\rho +\delta }{a}_F}{c_P(1-p)}\ln (e+k_{s}s)-\frac{c_P}{2}(1-p){\left(\frac{b_F\ln (e+k_{s}s)+\frac{l}{\rho +\delta }{a}_F}{c_P(1-p)}\right)}^2]\\ +\frac{1}{\rho }\frac{l}{\rho +\delta }{a}_F\frac{b_F\ln (e+k_{s}s)+\frac{l}{\rho +\delta }{a}_F}{c_P(1-p)}\end{array}& (51)\end{array}$

Therefore, it can be concluded that:

$\begin{array}{ll}\begin{array}{l}{V}_{P1}^{*}=\frac{l}{\rho +\delta }{x}_{P1}+\frac{1}{\rho }[b_F\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{l}{\rho +\delta }\frac{a_F-a_E}{c_P+c_E}\right)\frac{1}{\ln (e+k_{d}d)}-\left(\frac{c_P}{2}+\frac{c_E}{2}\right)\\ {\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{l}{\rho +\delta }\frac{a_F-a_E}{c_P+c_E}\right)}^2]\\ +\frac{1}{\rho }\frac{l}{\rho +\delta }\left[(a_F-a_E)\left(\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{l}{\rho +\delta }\frac{a_F-a_E}{c_P+c_E}\right)\right]\end{array}& (52)\end{array}$

$\begin{array}{ll}\begin{array}{l}{V}_{P2}^{*}=\frac{1}{\rho }[b_F\frac{b_F\ln (e+k_{s}s)+\frac{l}{\rho +\delta }{a}_F}{c_P(1-p)}\ln (e+k_{s}s)-\frac{c_P}{2}(1-p){\left(\frac{b_F\ln (e+k_{s}s)+\frac{l}{\rho +\delta }{a}_F}{c_P(1-p)}\right)}^2]\\ +\frac{l}{\rho +\delta }{x}_{P2}+\frac{1}{\rho }\frac{l}{\rho +\delta }{a}_F\frac{b_F\ln (e+k_{s}s)+\frac{l}{\rho +\delta }{a}_F}{c_P(1-p)}\end{array}& (53)\end{array}$

In this case,

$\begin{array}{ll}{F}_{P1}^{*}(t)=\frac{b_F}{(c_P+c_E)\ln (e+k_{d}d)}+\frac{l}{\rho +\delta }\frac{a_F-a_E}{c_P+c_E}& (54)\end{array}$

$\begin{array}{ll}{F}_{P2}^{*}\left(t\right)=\frac{b_F\ln \left(e+k_{s}s\right)+\frac{l}{\rho +\delta }{a}_F}{c_P\left(1-p\right)}& (55)\end{array}$

Appendix 2

Take the derivatives of FH1 with respect to Eq. (15), take the derivatives of FH2 with respect to Eq. (16), and set them equal to zero, we can get:

$\begin{array}{ll}{F}_{H1}^{*}(t)=\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{\partial V_{H1}}{\partial x_{H1}}\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}& (56)\end{array}$

$\begin{array}{ll}{F}_{H2}^{*}(t)=\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{\partial V_{H2}}{\partial x_{H2}}\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}& (57)\end{array}$

Substituting Eq. (56) into Eq. (15) and substituting Eq. (57) into Eq. (16), we can get:

$\begin{array}{ll}\begin{array}{l}\rho V_{H1}=\{\frac{b_F}{1+k_e{e}_H}\left[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{\partial V_{H1}}{\partial x_{H1}}\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}\right]-\frac{c_H}{2}\ln (1+k_{\alpha }\alpha )\\ {\left[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{\partial V_{H1}}{\partial x_{H1}}\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}\right]}^2+l{x}_{H1}(t)]\\ +\frac{\partial V_{H1}}{\partial x_{H1}}{a}_F\ln (e+I_H)\left[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{\partial V_{H1}}{\partial x_{H1}}\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}\right]-\delta x_{H1}(t)\frac{\partial V_{H1}}{\partial x_{H1}}\}\end{array}& (58)\end{array}$

$\begin{array}{ll}\begin{array}{l}\rho V_{H2}=\{b_F\left[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{\partial V_{H2}}{\partial x_{H2}}\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}\right]\ln (1+k_{s}s)-\\ \frac{c_H}{2}(1+k_{\alpha }\alpha )(1-p){\left[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{\partial V_{H2}}{\partial x_{H2}}\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}\right]}^2+l{x}_{H2}(t)\\ +\frac{\partial V_{H2}}{\partial x_{H2}}{a}_F\ln (e+I_H)\left[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{\partial V_{H2}}{\partial x_{H2}}\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}\right]-\delta x_{H2}(t)\frac{\partial V_{H2}}{\partial x_{H2}}\}\end{array}& (59)\end{array}$

Let $V_{H1}^{*}=m_5{x}_{H1}+m_6$ and $V_{H2}^{*}=m_7{x}_{H2}+m_8$ , wherein, m₅, m₆, m₇, and m₈ are all constants. The parameters of the optimal social welfare function can be obtained by calculation as follows:

$\begin{array}{ll}\{\begin{array}{l}{m}_5=\frac{l}{\rho +\delta }\\ m_6=\frac{1}{\rho }\{\frac{b_F}{1+k_e{e}_H}\left[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}\right]-\frac{c_H}{2}\ln (1+k_{\alpha }\alpha )\\ {\left[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}\right]}^2\\ +\frac{l}{\rho +\delta }{a}_F\ln (e+I_H)[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}]\}\end{array}& (60)\end{array}$

$\begin{array}{ll}\{\begin{array}{l}{m}_7=\frac{l}{\rho +\delta }\\ m_8=\frac{1}{\rho }\{b_F\left[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}\right]\ln (1+k_{s}s)-\\ \frac{c_H}{2}(1+k_{\alpha }\alpha )(1-p){\left[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}\right]}^2\\ +\frac{l}{\rho +\delta }{a}_F\ln (e+I_H)[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}]\}\end{array}& (61)\end{array}$

Therefore, it can be concluded that:

$\begin{array}{ll}\begin{array}{l}{V}_{H1}^{*}=\frac{l}{\rho +\delta }{x}_{H1}+\frac{1}{\rho }\{\frac{b_F}{1+k_e{e}_H}\left[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}\right]-\frac{c_H}{2}\ln (1+k_{\alpha }\alpha )\\ {\left[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}\right]}^2\\ +\frac{l}{\rho +\delta }{a}_F\ln (e+I_H)[\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}]\}\end{array}& (62)\end{array}$

$\begin{array}{ll}\begin{array}{l}{V}_{H2}^{*}=\frac{l}{\rho +\delta }{x}_{H2}+\frac{1}{\rho }\{b_F\left[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}\right]\ln (1+k_{s}s)-\\ \frac{c_H}{2}(1+k_{\alpha }\alpha )(1-p){\left[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}\right]}^2\\ +\frac{l}{\rho +\delta }{a}_F\ln (e+I_H)[\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}]\}\end{array}& (63)\end{array}$

In this case,

$\begin{array}{ll}{F}_{H1}^{*}(t)=\frac{b_F}{(1+k_e{e}_H)c_H\ln (1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H\ln (1+k_{\alpha }\alpha )}& (64)\end{array}$

$\begin{array}{ll}{F}_{H2}^{*}(t)=\frac{b_F\ln (1+k_{s}s)}{c_H(1-p)(1+k_{\alpha }\alpha )}+\frac{l}{\rho +\delta }\frac{a_F\ln (e+I_H)}{c_H(1-p)(1+k_{\alpha }\alpha )}& (65)\end{array}$

Appendix 3

Take the derivatives of FB1 with respect to Eq. (17), take the derivatives of FB2 with respect to Eq. (18), and set them equal to zero, we can get:

$\begin{array}{ll}{F}_{B1}^{*}(t)=\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{\partial V_{B1}}{\partial x_{B1}}\frac{a_F+a_E\ln (e+I_E)}{2b_F}& (66)\end{array}$

$\begin{array}{ll}{F}_{B2}^{*}(t)=\frac{c_B(1-p)}{2b_F}-\frac{\partial V_{B2}}{\partial x_{B2}}\frac{a_F}{2b_F}& (67)\end{array}$

Substituting Eq. (66) into Eq. (17) and substituting Eq. (67) into Eq. (18), we can get:

$\begin{array}{ll}\begin{array}{l}\rho V_{B1}=b_F{\left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{\partial V_{B1}}{\partial x_{B1}}\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]}^2-(c_B+k_m{c}_m+k_o{c}_o)\\ \left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{\partial V_{B1}}{\partial x_{B1}}\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]+l{x}_{B1}(t)-\delta x_{B1}(t)\frac{\partial V_{B1}}{\partial x_{B1}}\\ +\frac{\partial V_{B1}}{\partial x_{B1}}\left(a_F+a_E\ln (e+I_E)\right)\left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{\partial V_{B1}}{\partial x_{B1}}\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]\end{array}& (68)\end{array}$

$\begin{array}{ll}\begin{array}{l}\rho V_{B2}=b_F{\left[\frac{c_B(1-p)}{2b_F}-\frac{\partial V_{B2}}{\partial x_{B2}}\frac{a_F}{2b_F}\right]}^2-c_B(1-p)\left[\frac{c_B(1-p)}{2b_F}-\frac{\partial V_{B2}}{\partial x_{B2}}\frac{a_F}{2b_F}\right]+l{x}_{B2}(t)\\ +\frac{\partial V_{B2}}{\partial x_{B2}}{a}_F\left[\frac{c_B(1-p)}{2b_F}-\frac{\partial V_{B2}}{\partial x_{B2}}\frac{a_F}{2b_F}\right]-\delta x_{B2}(t)\frac{\partial V_{B2}}{\partial x_{B2}}\end{array}& (69)\end{array}$

Let $V_{B1}^{*}=m_9{x}_{B1}+m_{10}$ and $V_{B2}^{*}=m_{11}{x}_{B2}+m_{12}$, wherein, m₉, m₁₀, m₁₁, and m₁₂ are all constants. The parameters of the optimal social welfare function can be obtained by calculation as follows:

$\begin{array}{ll}\{\begin{array}{l}{m}_9=\frac{l}{\rho +\delta }\\ m_{10}=\frac{1}{\rho }{b}_F{\left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]}^2-\frac{1}{\rho }(c_B+k_m{c}_m+k_o{c}_o)\\ \left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]\\ +\frac{1}{\rho }\frac{l}{\rho +\delta }(a_F+a_E\ln (e+I_E))\left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]\end{array}& (70)\end{array}$

$\begin{array}{ll}\{\begin{array}{l}{m}_{11}=\frac{l}{\rho +\delta }\\ m_{12}=\frac{1}{\rho }{b}_F{\left[\frac{c_B(1-p)}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F}{2b_F}\right]}^2-\frac{1}{\rho }{c}_B(1-p)\left[\frac{c_B(1-p)}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F}{2b_F}\right]\\ +\frac{1}{\rho }\frac{l}{\rho +\delta }{a}_F\left[\frac{c_B(1-p)}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F}{2b_F}\right]\end{array}& (71)\end{array}$

Therefore, it can be concluded that:

$\begin{array}{ll}\begin{array}{l}{V}_{B1}^{*}=\frac{l}{\rho +\delta }{x}_{B1}+\frac{1}{\rho }{b}_F{\left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]}^2-\frac{1}{\rho }(c_B+k_m{c}_m+k_o{c}_o)\\ \left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]\\ +\frac{1}{\rho }\frac{l}{\rho +\delta }\left(a_F+a_E\ln (e+I_E)\right)\left[\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F+a_E\ln (e+I_E)}{2b_F}\right]\end{array}& (72)\end{array}$

$\begin{array}{ll}\begin{array}{l}{V}_{B2}^{*}=\frac{l}{\rho +\delta }{x}_{B2}+\frac{1}{\rho }{b}_F{\left[\frac{c_B(1-p)}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F}{2b_F}\right]}^2-\frac{1}{\rho }{c}_B(1-p)\left[\frac{c_B(1-p)}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F}{2b_F}\right]\\ +\frac{1}{\rho }\frac{l}{\rho +\delta }{a}_F\left[\frac{c_B(1-p)}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F}{2b_F}\right]\end{array}& (73)\end{array}$

In this case,

$\begin{array}{ll}{F}_{B1}^{*}(t)=\frac{c_B+k_m{c}_m+k_o{c}_o}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F+a_E\ln (e+I_E)}{2b_F}& (74)\end{array}$

$\begin{array}{ll}{F}_{B2}^{*}(t)=\frac{c_B(1-p)}{2b_F}-\frac{l}{\rho +\delta }\frac{a_F}{2b_F}& (75)\end{array}$