- 1Quantitative Life Sciences, The Abdus Salam International Centre for Theoretical Physics (ICTP), Trieste, Italy
- 2Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM, United States
- 3Alexander Silberman Institute for Life Sciences, Faculty of Science, Hebrew University of Jerusalem, Jerusalem, Israel
- 4Department of Ecology, Evolution and Behavior, Hebrew University of Jerusalem, Jerusalem, Israel
- 5School of Engineering Mathematics and Technology, University of Bristol, Bristol, United Kingdom
The ability to quantify when and where animals interact is key to the understanding of a plethora of ecological processes, from the structure of social communities and predator–prey relations to the spreading of pathogens and information. Despite the ubiquity of interaction processes among animals and the revolution in tracking technologies that now allows for the monitoring of multiple individuals simultaneously, a common theoretical framework with which to analyze movement data and extract interaction events is still lacking. Given the wide spectrum of mechanisms that governs how a biological organism detects the proximity of other organisms, most of the proposed theoretical approaches have been tailored to specific species or empirical situations and so far have been lacking a common currency with which to evaluate and compare findings across taxa. Here, we propose such general framework by borrowing techniques from statistical physics, specifically from the theory of reaction diffusion processes. Some of these techniques have already been employed to predict analytically pathogen transmission events between pairs of animals living within home ranges, but have not yet pervaded the movement ecology literature. Using both continuous and discrete variables, we present the mathematical framework and demonstrate its suitability to study interaction processes. By defining interactions whenever a token of information is transferred from one individual to another, we show that the probability of transferring information for the first time is equivalent to the first-passage probability of reacting in a multi-target environment. As interaction events reduce to encounter events when information transfer is perfectly efficient, we compare our formalism to a recently proposed approach to study encounters. Such approach takes the joint occupation probability of two animals over a region of interaction as a measure of the probability of encounter, rather than the first-encounter probability. We show the discrepancy of the two approaches by analytically comparing their predictions with continuous variables, while with discrete space–time variables, we quantify their difference over time. We conclude by pointing to some of the open problems that the reaction diffusion formalism, alternatively, the reaction motion formalism, as it should be more appropriately called, might be able to tackle.
1 Introduction
A vast number of studies in animal ecology aims at linking behavior at the level of the individuals to the processes governing the dynamics of a group or an entire population (Levin, 1992). Underlying this fundamental tenet is the search for general laws that link the interactions between animals to the patterns that emerge at much larger scales. A renewed interest in such perspective has surfaced in the last decades following the introduction of the movement ecology framework (Nathan et al., 2008) and the advances in sensor technologies that allow to track animals in space and time at unprecedented resolution (Matley et al., 2022; Nathan et al., 2022). It is the ability to follow simultaneously multiple individuals and infer when and how they interact that will be instrumental to the understanding of this micro-to-macro connection. Notably, despite the pervasiveness of interaction processes between moving organisms, models in the animal ecology literature of how individuals interact or more simply when and where they encounter or are in proximity of one another have been limited.
While theoretical approaches that aim at quantifying interaction processes have appeared (Hutchinson and Waser, 2007; Bartumeus et al., 2008; McKenzie et al., 2009; Gurarie and Ovaskainen, 2013; Martinez-Garcia et al., 2020), efforts to develop a general framework have been stymied by two main factors: semantic issues, due in part to the different ways in which animals may interact, and the apparent absence of analytical “null” models in the movement ecology literature. As animals interact by relying on their sensory biases, by using their cognitive mechanisms and by exploiting their motor abilities, finding a general definition of interaction has been challenging and the rationale has often resulted in specific choices based on the biological questions and the species under observation.
In collective movement studies, a classic example is the use of delays in motor response to determine leadership roles. This approach has been employed to construct social ranks in a flock of pigeons based on their global delayed response in following each other’s trajectories (Nagy et al., 2010), and to extract time-dependent delays during coordinated maneuvers of foraging bat pairs to identify leaders (Giuggioli et al., 2015) or to classify the influential neighbors during collective turns of a shoal of laboratory fish (Jiang et al., 2017). Examples in animal social studies also abound (Farine and Whitehead, 2015). In that context, a social interaction network for a group of individuals is constructed based on the occurrence per sampling period of well-defined events (Whitehead, 2008), e.g., grooming, or parent and offspring associations, and has been used to predict how processes such an infection or some form of information is spread over the network. While these and other approaches provide practical tools to estimate specific forms of relatedness, they often lack a common currency with which to make comparison across species.
Even in the simplest scenario in which an interaction is defined as an encounter, i.e., a co-location or a proximity event, model estimations differ greatly depending on how the movement is represented. The assumption that animals move deterministically, i.e., perform ballistic motion, has led to the so-called ideal gas model prediction of an exponential time dependence in the encounter probability with mean π/(8dbv) (Hutchinson and Waser, 2007), whereby in a population of density d, a focal individual moves with constant speed v and encounters other individuals when within a distance b. The cornerstone of the ideal gas model is the law of mass action. It posits that encounters are directly proportional to the concentration of individuals and neglects any dependence on the statistical properties of the trajectories of the moving entities. In essence, it is a mean field approximation and deviates further from the actual predictions the more winding are the movement paths and the lower the density of individuals.
In the extreme limit of very diluted systems, e.g., one randomly moving organism searching for static targets, a large literature on random biological encounters have emerged in the last 20 years. The focus of that literature has been the study of target encounter efficiency when an animal’s straight movement paths follow a power law distance function as compared to a sharply decaying one (Viswanathan et al., 2011; Reynolds, 2015), the latter characteristics of Brownian motion. Various scenarios have been considered including the distinction between destructive searches, for which a target is consumed upon encounter, and non-destructive searches, for which the target is uninfluenced by the searcher (Santos et al., 2004; Bartumeus et al., 2005), as well as the difference between hard encounters, which occur whenever a searcher is within a threshold distance from a target, and soft encounters whose occurrence depends on some smooth functional dependence of the searcher–target distance. Given the vast number of animal interactions, an important study that has brought clarity to the literature is the one by Gurarie and Ovaskainen (2013), which has provided a classification of the different types of animal encounter interactions and has reviewed and compared many of the theoretical results, in particular of interest to us here, the findings on what is generally referred to as random search statistics (see, e.g., Bartumeus et al., 2014; Bartumeus et al., 2016).
In comparison to the vast literature on search of static targets, past ecological investigations on moving targets, that is on actual animal encounters, have been limited, with the exceptions of a couple of analytic studies in one dimension (Tejedor et al., 2011; Giuggioli et al., 2013), and two-dimensional simulation studies on animal encounters when moving as Lévy walkers both in terms of encounter efficiency (Bartumeus et al., 2008) and in terms of survival advantage when the energy content of the prey is accounted for (Faustino et al., 2007; Faustino et al., 2012). Lately, following the improved resolution in tracking technology (Nathan et al., 2022), there has been an upsurge of interest on encounter processes (Martinez-Garcia et al., 2020; Albery et al., 2021; Noonan et al., 2021; Yang et al., 2023). Yet, the animal ecology literature seems to have missed out a body of work in statistical physics on the theoretical investigations of encounter and transmission events, normally referred to as the theory of reaction diffusion processes. That theory was laid out in the 1980s by Kenkre in the context of exciton annihilation in molecular crystals as well as in the general field of exciton capture in sensitized luminescence (Kenkre, 1980; Kenkre, 1982a; Kenkre, 1982b). Originally, the theoretical formalism was developed for movement in unbounded discrete lattices with focus on coherence in exciton motion (Kenkre and Wong, 1981; Kenkre, 1982b), but specific problems were also solved in bounded systems (Kenkre and Wong, 1980). A focused aim of those investigations was the resolution of annoying paradoxes that had been encountered in the field of molecular crystals regarding both magnitude and temperature dependence of exciton diffusion constants extracted from experimental data in aromatic hydrocarbon crystals (Kenkre and Schmid, 1983; Kenkre et al., 1985). A decisive demonstration of the errors made in previous analyses in molecular crystals was given by Kenkre and Schmid in the papers referenced. This was done in the context of the extraction of motion parameters from mutual annihilation observations on the one hand and sensitized luminescence observations on the other. A study of that demonstration would be highly useful in any encounter context whether molecular or ecological.
The techniques used to interpret empirical observations on exciton annihilation have actually been extended to spatially continuous domains to study hard encounters in an ecological context, more precisely to predict the probability of interaction for animals living within separate home ranges in one (Kenkre and Sugaya, 2014) and two dimensions (Sugaya and Kenkre, 2018). By representing the tendency of an animal to remain close to its burrow or nest via an Ornstein–Uhlenbeck process (Giuggioli et al., 2006; Giuggioli and Kenkre, 2014), i.e., by tethering its motion using a spring force, an exact analytic representation of the encounter and transmission probability when interaction occurs within a cutoff distance has been derived (Kenkre and Sugaya, 2014; Sugaya and Kenkre, 2018). The formalism that Kenkre developed with Sugaya in this context towards the implementation of the reaction diffusion theory has been given in detail in the recent publication of a book by two of the coauthors (see chapter 6 in ref (Nitant Kenkre and Giuggioli, 2021). Even though these analytical techniques clearly represent the most appropriate and powerful starting point from which to study a broad range of encounter and interaction processes, surprisingly they have not been exploited in the animal ecology literature.
Following Kenkre’s reaction diffusion approach, a novel analytic formalism to study movement on discrete lattices and in discrete time (Giuggioli, 2020) has allowed to analytically derive the so-called splitting probabilities, that is, the probability for interaction events to occur in a set of locations and not others (Giuggioli and Sarvaharman, 2022). Knowledge of these splitting probabilities allows one to predict interactions in a multi-target environment, and has led to analytic predictions of the spatiotemporal dynamics of random transmission events in arbitrary dimensions and arbitrary (lattice) topology (Giuggioli and Sarvaharman, 2022), including hexagonal and honeycomb lattices (Daniel et al., 2023), as well as when individuals undergo a resetting dynamics (Das and Giuggioli, 2022) or when the environment is spatially heterogeneous (Sarvaharman and Giuggioli, 2023). All these developments, both with continuous and discrete variables, should form the backbone of a general theory of animal interaction and encounter processes and, given their analytic formulation, should become part of the arsenal of “null” models in movement ecology.
Here, we present evidence of the need of a reaction diffusion formalism to study encounter and transmission events between animals, interchangeably referred to as walkers in this study. We define a transmission event as the first occurrence when information is successfully transferred between two individuals. With continuous variables, we consider the spatiotemporal dynamics of two diffusing animals (Brownian walkers) living in two separate home ranges undergoing Onrstein-Uhlenbeck motion and show the analytic formalism that has been developed in that case (Sugaya and Kenkre, 2018) to represent the probability of first transmission. With perfect efficiency of information transfer, the first-transmission event reduces to a first-encounter event, hence aligning our definition of an encounter event to that of a first-hitting event that has been used in the ecological literature (Gurarie and Ovaskainen, 2011). In this limit, we compare the formalism to the one presented in a recent theoretical investigation by Martinez-Garcia and collaborators (Martinez-Garcia et al., 2020) where a pairwise distance threshold probability has been proposed as a tool to study animal encounters. For the Ornstein–Uhlenbeck case considered, we analytically derive the mathematical equation that relates the two probabilities.
For the discrete space–time formulation, we also consider two diffusing animals (lattice random walkers) living in separate home ranges. We choose two scenarios to represent the characteristic reduction in movement range. In the first one, we impose a hard constraint on the movement range of the animals (reflected lattice walkers). In the second one, we account for the animal tendency to return to a den or a burrow by resetting its location at random times to its own focal point in space (resetting random walkers). For these two cases, for simplicity, we restrict the interactions to when animals are co-located on the same site and we quantify the time dependence of the first-encounter probability (maximal information transfer efficiency). We compare this dependence to the one obtained by spatially integrating the animal joint occupation probability of all possible interaction co-locations, a quantity analogous to the pairwise distance threshold probability examined with continuous space–time variables. For the discrete case, we also show the exact formalism to extract mean first-transmission times.
In the present study, we make various assumptions about the animals’ behavior, their environment, and how we characterize their movement. In choosing very simple representations of how animals move within a home range in one and two dimensions, we have purposely sacrificed ecological complexity to gain in conceptual and mathematical transparency. We have disregarded that animals may engage in activities other than foraging (see, e.g., examples in refs Morales et al., 2004; Ovaskainen et al., 2008; Gurarie et al., 2009 and for relevant techniques developed to infer behavioral shifts from tracking data). We have also assumed that animals move in a homogeneous environment and have represented in a simple manner how the presence of a home range in one and two dimensions affects their motion. A third assumption is that we have neglected correlations in the movement steps, which means that when animals move with some degree of persistence, our estimation of encounter and transmission rates are valid for time scales longer than the correlation or persistence time (Gurarie et al., 2009).
2 Materials and methods
2.1 The continuous space–time formalism
To bypass any potential semantic issues, we restrict our study and define an interaction when a measurable unit of information is being passed from one individual to the other. Examples include an infectious disease, which is transmitted through the transfer of a pathogen, or the passing of knowledge, e.g., food source location. In these cases, when the movement statistics is Markov and the information being transferred is a binary variable (presence/absence), transmission events can be modeled as a first-absorption process (Spendier and Kenkre, 2013). In other words, by defining interactions based on the transfer of a token of information from one animal to another, it is possible to mathematically model interaction events as a function of the movement statistics and the ability of the uninformed individual to receive information from the informed one, as exemplified pictorially in Figure 1. Modeling and quantifying such events and identifying the underlying principles under which randomly moving particles or more generally biological agents react with each other is an important area of investigation in statistical physics and is referred to as the theory of reaction diffusion processes.
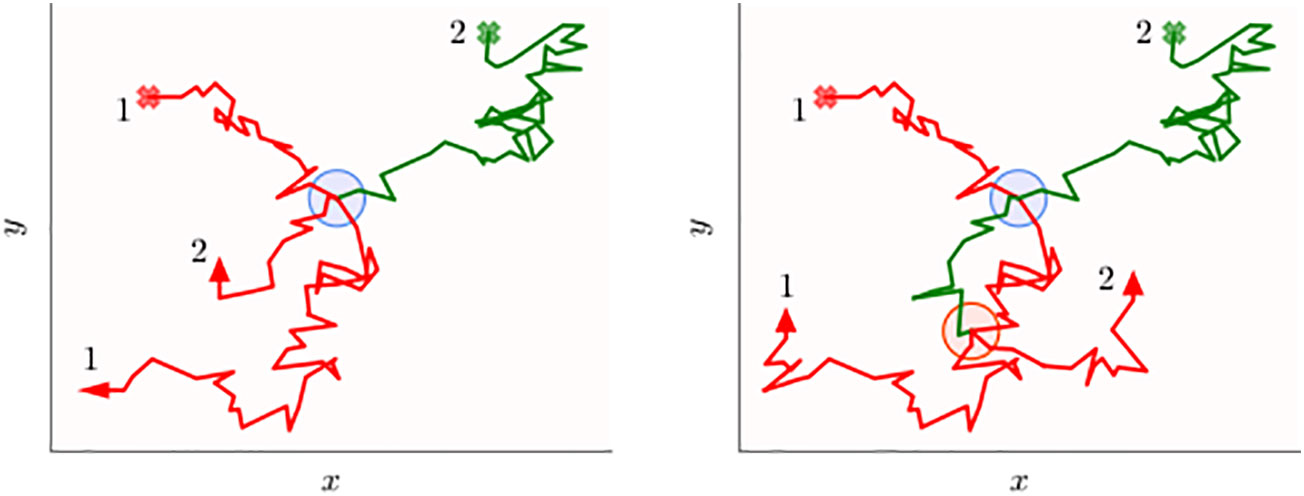
Figure 1 Schematics of the two-dimensional movement paths of two animals tracked over a certain period of time that may transfer information when they are within a certain distance threshold. The circular disks represent all the spatial locations when the two individuals are simultaneously within a threshold distance from each other. Animal 1 (red trajectory) carries information, while animal 2 (green trajectory) initially does not. Both the walkers start from their respective initial points shown as the cross marks, and when information is transferred from the first to the second animal, the green trajectory turns red. In the left panel, the information transfer process occurs early on (blue disk), which is on the first occasion in which they are within interaction distance, while in the right panel, transfer occurs on the second occasion (red disk). The inefficiency of the transfer process is evident in both panels because the green trajectory does not turn red when on the disk boundaries (first encounter), but only after some time the animals are within the disk. Note that time stamps of the trajectory are not explicitly indicated and the animal paths should not be thought of representing movement with constant speed. In other words, the disks aim to display direct interactions, i.e., when individuals are within a threshold distance at the same time, rather than indirect ones when spatial coincidence may occur at different times.
A well-known assumption to estimate interaction times consists of summing the average time for two individuals to be in proximity, T, and the average reaction time or information transfer time upon proximity, I. Such assumption goes under different names in different disciplines, e.g., the inverse addition law in chemical reactions (Soustelle, 2011), or Matthiessen’s rule in solid-state physics (Ziman, 2001). Kenkre and his collaborators showed the limitations of such an assumption (Kenkre et al., 1985), whose validity is restricted to the so-called reaction limited case (T/I → 0) and the motion limited case (I/T → 0), and developed an analytic formalism to predict the time-dependent first-transmission probability between randomly moving entities in unbounded lattices (Kenkre, 1980; Kenkre, 1982a; Kenkre, 1982b). With a similar theoretical construct, it is possible to analyze the transmission problem of two animals, one informed and the other one uninformed, living in separate home ranges. By representing them as two Brownian walkers biased towards their respective focal points in space, i.e., their home range centers, through a spring force (Ornstein–Uhlenbeck process), Kenkre and Sugaya (Kenkre and Sugaya, 2014; Sugaya and Kenkre, 2018) have analytically derived the transmission probability, that is, the probability that the uninformed (susceptible) individual has become informed (infected) at time t.
To understand what are the key ingredients necessary to quantify reaction diffusion processes, in particular the time-dependent transmission probability of a token of information from one individual to another, we report here some of the necessary mathematical details with continuous variables. We start by considering the partial differential equation (PDE) governing the dynamics of the joint occupation probability of the two tethered Brownian walkers, one susceptible and one infected, subject to an interaction rate upon proximity (Kenkre and Sugaya, 2014; Sugaya and Kenkre, 2018). The PDE of the time-dependent joint occupation probability of walkers 1 and 2 to be at and , respectively, contains a Smoluchowski term to describe the movement to which a transmission interaction term in the form of a loss is added (Kenkre and Sugaya, 2014; Sugaya and Kenkre, 2018). A variable transformation from the coordinates of the two animals (a center of mass coordinate would be ) and a relative position (in ref (Sugaya and Kenkre, 2018), are defined with a multiplicative factor ) allows one to write the joint PDE governing equation as (Sugaya and Kenkre, 2018)
where D is the diffusion constant of both animals, ∇± represents the partial differential operator in radial coordinates for r±, δ(z) is the Dirac delta function, R± = R1 ± R2 are the transformed coordinates of the two animals’ home range centers, γ is the strength of the attraction (spring force constant) towards their respective home range centers, and the prime symbol of the integral means that integration is over a given range of values to be specified.
Note that in Equation (1), which describes the dynamics in a four-dimensional space, is the spatiotemporal dependence of the joint occupation probability (distribution) of the informed and uninformed individual. When a transmission event occurs, the uninformed individual disappears, and thus the probability is identically zero. This aspect is captured by the last term of Equation (1), which indicates that there is a probability loss over time at rate when the two animals are within the interaction distance, indicated by the prime integration with respect to the separation distance variable. When the rate , there is no interaction, while an encounter event is represented with . Note also that the presence of the integration allows one to specify the spatial locations where interactions may occur (integration over ) and at what distance it may occur (integration over the relative coordinate, ).
With being non-zero when both the informed and the uninformed individuals are present, the first-transmission probability, (t), that is, the probability (density) that a first-transmission event has occurred anywhere in the interaction region, is simply given by
where the symbols indicate the dependence on the initial conditions via , which represents the solution of Equation (1) when; the two animals are localized at at time t=0. In Equation (2), we have dropped the prime superscript on the integration over , since we consider it over the entire two-dimensional space, while we have kept it for the relative coordinates since that is only over the interaction region.
To proceed further, one needs to find the solution of Equation (1) and then insert it in Equation (2) to obtain the first-transmission probability. In some situations, like the one we are analyzing here, the solution can be found analytically in terms of quantities that can be derived from the dynamics in the absence of interactions ( = 0). This is accomplished by employing the so-called Montroll’s defect technique (Montroll and Potts, 1955; Nitant Kenkre, 2021), which allows one to find analytically the Laplace transformed , which represents the Laplace transform of a function f(t), i.e., being the Laplace variable. More precisely, one may express the first-transmission probability analytically as a ratio of quantities in Laplace domain defined independently of the transmission phenomenon, namely (Sugaya and Kenkre, 2018)
whose time dependence can be found numerically by performing an inverse Laplace transform. In Equation (3), the quantity represents the probability, in the absence of any interaction, that the two animals are within the interaction region at time starting from the initial coordinates ,
where Π is the joint occupation probability solution of Equation (1), when , given the initial conditions and , referred to as the propagator (solution). It is simply given by the product of two-dimensional Ornstein–Uhlenbeck propagators for each animal centered around their respective focal point or home range center (Sugaya and Kenkre, 2018). While depends on the animal initial conditions (to lighten the formalism, we have omitted this aspect from the notation), the function does not have any spatial dependence and is the probability, in the absence of any interaction, that the locations of the two animals are within the interaction region at a time after starting within it,
Note that while is normalized in time and has units of inverse of time, and are dimensionless quantities, but are not normalized in time, thus are not time probability density per se. One may notice in fact that, since is normalized in space, by integrating Equation (4) over all relative distance values, , would equal exactly 1. This mathematical remark is equivalent to stating that, in the absence of interactions, there is certainty that the two animals are somewhere in space.
2.2 The discrete space–time formalism
The recent development of the discrete space–time approach follows in the footsteps of the original studies on exciton annihilation in unbounded and periodic lattices (Kenkre, 1982b) and has extended that formalism to bounded domains with reflecting boundaries (Giuggioli and Sarvaharman, 2022), to scenarios when the movement is altered by random resetting to a given location (Das and Giuggioli, 2022), to dynamics in presence of spatial heterogeneities such as global biases (Sarvaharman and Giuggioli, 2020), variable diffusivities in space (Sarvaharman and Giuggioli, 2023), permeable barriers (Kay and Giuggioli, 2022; Sarvaharman and Giuggioli, 2023), and different media and interfaces (Das and Giuggioli, 2023).
The equation governing the transmission problem between two lattice random walkers is similar to the continuous version, but with the notable difference that the dynamics for the informed and uninformed individuals are governed by a difference equation rather than an integro-differential equation as in Equation (1). By calling the joint occupation probability at discrete time for one walker to be at site and the other at site , one has
In Equation (6), the elements of the tensor represent the transition probabilities at each time step for the first walker to move from site to site and for the second walker to move from site to site . As we consider that the two individuals move independently of one another, , where and control, respectively, the movement steps of walker 1 and walker 2. Compared to the continuous case, the interaction term in Equation (6) is now a summation rather than an integral, with a Kronecker delta and the prime symbol indicating all lattice sites where interaction may occur, while represents the transfer probability once the two walkers are within the interaction range, and it is in place of the rate of the transfer of the continuous case.
Note that while we use discrete time variables, it is straightforward to convert Equation (6) to continuous time and changing accordingly jump probabilities to rates. There is, however, a computational convenience in using discrete versus continuous time in our context, and that is in the ease to invert to discrete time a generating function (i.e., a discrete Laplace transform) as compared to inverting to continuous time a function defined in the Laplace domain (Giuggioli, 2020).
One of the advantages of the spatially discrete formalism over the spatially continuous one is that it allows one to analytically quantify the so-called splitting probability of interaction, that is, the (time-dependent) joint probability that a transmission event occurs in a set of lattice sites or nodes and not in others. This prescription is naturally constructed in discrete space given the ease with which to associate the joint presence or absence of individuals at a set of locations with coordinates (), where the first and second coordinates refer, respectively, to the first and second animal. Given the (unordered) set where the two individuals may transfer information, the probability that a transmission event (in any of the possible locations) occurs at time for the first time (first-transmission probability) is given by (Giuggioli and Sarvaharman, 2022)
where represents the initial location of the two animals, and is the time-dependent probability that the transmission event occurs when the animals are at the lattice coordinates and not at any of the other sites of interaction, the so-called splitting probabilities.
If is the propagator of Equation (6) in the absence of any interaction (), one can write the generating function— for a generic function —of the splitting probabilities, i.e., as the following ratio (Giuggioli and Sarvaharman, 2022)
with and , and the same as but with the vector replacing the -th column (the symbol indicates transpose). Note that is the discrete analog of the joint occupation probability used in the continuous variable section, which was expressed in terms of the transformed variable .
To represent animals roaming within their own home ranges, we consider two cases. In the first, the home ranges have partial overlap and the range where animals move is bounded by impenetrable boundaries (reflected random walkers). In the second, the domain is periodic, but large enough to be effectively unbounded, and each animal resets at random times to its own focal point (resetting random walkers). In both cases, we consider the individuals to move independently, leading to a product form of the propagator for the process without transmission (), namely, , where are the occupation probabilities for each independent walker.
For computational convenience, we consider that an interaction event may occur only when the animals are co-located and we study both the one and two-dimensional scenarios. For the one-dimensional case, we focus on the first-encounter probability, that is, we set , and we compute, through a numerical inversion of the generating function, the time dependence of the first-encounter probability, offering a quantitative comparison with the corresponding discrete equivalent of in Equation (18), which is given by
Note that also in this discrete case, could be rewritten in terms of relative coordinates, but since we are considering only co-locations as encounters, it has no advantage.
For the two-dimensional case, we limit ourselves to the analysis of the mean first-transmission time with reflected random walkers, but no comparison can be made to a corresponding mean for given that it is not a normalized probability function and the evaluation of an average, via , is not finite.
Diffusion in partially overlapping range-limited one-dimensional domains
We consider that each animal diffuses within its own one-dimensional lattice domain, both of size , and that the two domains overlap only partially. In this case, the tensors (m =1 and 2) reduce to matrices and their elements are , when away from the boundary sites and . The actual dimension of the overlap region, that is, the number of lattice sites where the animals may transmit information or encounter one another, is directly related to the distance between the central locations of the home ranges and . The individual walker propagator in this case is given by (Giuggioli, 2020)
where
with and for , and
for the first animal, and with for the second animal.
From, it is easy to obtain the generating function , and use it to construct .
Diffusion with resetting in one-dimensional domains
For the case of the resetting random walkers, one requires to modify Equation (6) by adding on the right-hand side the terms and , with and representing the probability for the first and second walker to relocate at random times to site and , respectively. In this case, the tridiagonal matrices are given by and .
By taking periodic boundary conditions , the propagator for an individual resetting random walker is given by (Das and Giuggioli, 2022)
where is the resetting site, with given in Equation (12) and . Analogously to the reflecting case above, the propagator for both walkers, that is, the solution of Equation (6) in the absence of transmission events, is given by .
Diffusion in two-dimensional range-limited home ranges
For a two-dimensional setting, we consider animals living in home ranges of rectangular shape of identical size. The range limitation of the animals is ensured by reflecting boundary conditions. The two home ranges are aligned along the vertical axis, but are shifted by an amount equal to sites along the horizontal axis. In the absence of interactions, for each animal the propagator is given by (Giuggioli, 2020)
where and represent, respectively, the number of sites along the two directions and with and given, respectively, in Equations (11) and (12).
To determine the mean transmission time at any of the co-locations, one requires knowledge of the mean first-passage time between the initial location and the co-location sites, the mean first-passage between all co-location sites (all permutations), and the mean return time to the co-location sites. For that, we use Equation (14) to build the product of the individual propagators in time by shifting by sites the coordinates of the horizontal axis for the second individual. For an initial condition with coordinates along the horizontal and vertical axes and with , we construct the generating function of the four-dimensional propagator,
with the range in and being, respectively, and , while the range for both and is .
From Equation (15), it is straightforward to obtain the mean (first) return time (Kac, 1947) to a site ,
and through a simple differentiation (Redner, 2001), i.e., , the mean first-passage
between a starting site and a target site .
3 Results
3.1 Difference between first-encounter probability and distance threshold probability
We consider the case of perfect transfer efficiency, in Equation (3), and focus on the so-called hard encounter events, that is, those instances when animals reach a relative distance . By integrating over all possible angles and separation up to radius in Equations (4) and (5), following Kenkre and Sugaya (Sugaya and Kenkre, 2018), one obtains
and
where , with and , respectively, being the distance and relative angle between the home range centers, where , and where is the Marcum Q-function of order 1. Given that is a spatial integration of the (time-dependent) joint occupation probability over the relative distance , we refer to it in the following as the distance threshold probability.
Equation (18), with a rate constant multiplying it, has been called the mean encounter rate (Equation (14) in ref Martinez-Garcia et al., 2020) and has been proposed to explore how the interplay between the scale of perception and home-range size affects encounter rates. Although the discrepancy with Equation (3) when is self-evident, it is instructive to rewrite Equation (3) in that limit as , renaming first transmission as first encounter, , and through a Laplace inversion obtain
Equation (20) shows the relation between the first-encounter probability, , and the distance threshold probability, and its structure is quite revealing. It represents a generalization of the well-known renewal equation for Markov processes (Redner, 2001), , that relates the occupation probability to be at x at time t starting at with the first-passage or first-hitting probability, , to reach x from . While it may seem always possible to write an equation such as Equation (20), with and representing a spatially integrated version, or more precisely integration over a given range, of and , respectively, it turns out to be true only when is independent of , something that occurs only when certain spatial symmetries are present. While it is difficult to visualize the geometry of these special cases with animals moving in two and three dimensions, given that the set of locations where encounters may occur are part of a four- or six-dimensional space, it may help to think about a one-dimensional encounter problem. The simplest scenario is that of two Brownian walkers that diffuse without any spatial constraint on a line and come into “contact” once they are at a distance b. Their encounter dynamics can be mapped onto the search dynamics of a two-dimensional Brownian walker that hits for the first time a radial target of radius b centered around the origin. The associated Equation (20) becomes equivalent to an effective one-dimensional renewal equation since a first hitting event is controlled only by the radial coordinate of the Brownian walker being equal to b. More intuitively, whenever a set of interaction locations are arranged spatially as a single big target, then one may potentially write equations such as Equations (3) and (20) where and are spatially integrated representation of the animals’ occupation probability in the absence of any interaction.
In general, in all scenarios that lack high spatial symmetries, the interaction locations have a complicated geometry and parameterizing the resulting shape with multiple variables becomes a complicated task. In addition, when a first-hitting event requires to specify the threshold value of many variables, one needs to construct splitting probabilities, practically separating the space into multiple areas. In these situations, identifying these separate areas where interactions may occur is easily met by mapping the dynamics into discrete space and studying the first transmission to a set of multiple targets on a lattice, which is the subject of the next subsections.
3.2 First-encounter probability with overlapping home ranges in one dimension
Having formally shown in the example studied in Section 3.1 the relation between and , we now proceed to quantify their difference with the discrete formalism. For simplicity and computational convenience, we start by considering animals living in one-dimensional domain bounded by reflecting boundaries, as depicted in the left panel of Figure 2. Past analyses to determine the transmission dynamics in this one-dimensional problem has led to analytic expressions only for the mean transmission time (Giuggioli et al., 2013), whereas we are now able to capture the exact dynamics for the entire transmission probability . We consider two different home range overlaps with the two animals starting, respectively, at and , and use standard inversion routines (i.e., a one dimensional integration) for generating functions (Abate and Whitt, 1992; Abate et al., 1999) to plot the first-encounter probability in the right panel of Figure 2.
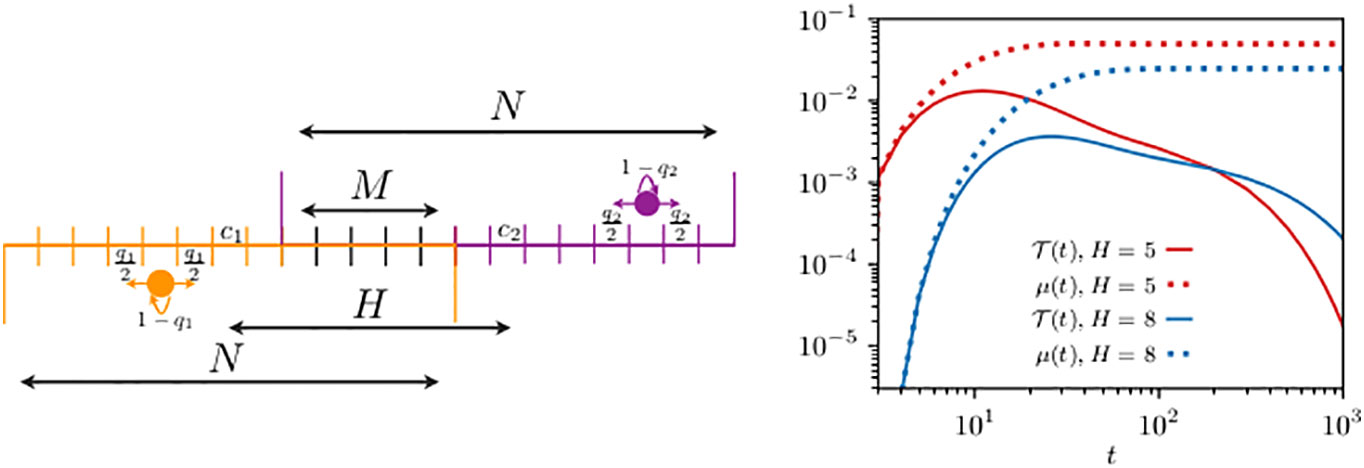
Figure 2 Schematics of two animals roaming within separate one-dimensional home ranges with partial overlap (left panel) and their first-encounter probability (right panel). On the left panel, the circle displays an animal while the arrows indicate the movement probability at each time step: the left and right horizontal arrows represent the probability to move, respectively, left and right, while the bent arrow is the probability of remaining at the same site. Although not shown in the schematics, the movement rules at the boundary sites are slightly different with the probability of staying modified to , while the probability to move outside of the domain is suppressed. The size of the two home ranges is equal to . The first walker diffuses within a domain centered at , is limited by reflecting boundaries at sites 1 and 11, and starts from , while for the second walker, there are two cases: the allowed range is either (i) [6,16] or (ii) [9,19], and in both cases with reflecting boundaries at the end sites. The two animals may encounter each other when they simultaneously occupy a site in the overlap region, made up of a total of M sites. In case (i), the distance between the two home range centers is and the second walker starts from , while in case (ii), we have and . The quantities n0(t) (in the legend, we have omitted the subscript n0 for clarity), from Equation (7), and , from Equation (9), are shown by the continuous and dotted lines [in red for case (i) and in blue for case (ii)], respectively. For both walkers, we take diffusivity .
As a comparison, we plot the discrete analog of the function , namely, Equation (9). While decays to zero at long times, reaches a finite non-zero value, making it evident why the former is a normalized probability function, while the latter is not. The long time saturation value of indicates that once the memory of the initial placement vanishes, the chance that two individuals are found in any of the possible co-locations is constant and equals the integral over the interaction region of the steady-state joint occupation probability.
3.3 First-encounter probability with one-dimensional resetting dynamics
We take the so-called resetting random walker as another representation of an animal that moves within a home range. As the walker resets at random times to a focal point in space, the range of movement is effectively bounded, with the resetting sites representing the den or burrow where animals tend to return to. At long times, the spatial occupation probability is in fact equivalent to a steady-state probability if the walker were to move with a constant bias towards the resetting location (Giuggioli et al., 2019). For computational convenience, we take a periodic spatial domain for both walkers.
Even though the movement of the walkers is effectively bounded, and differently from the reflected walker case above, we need to specify a finite number M of interacting locations given that the discrete formalism requires to evaluate a determinant of size M. With the appropriate choice of the movement model parameters and the placement and number of interacting locations around the home range centers, we ensure that the probability of transmission at the sites excluded from the M selected is negligible.
We consider perfect transfer efficiency and compare the first-encounter probability, with , to in Figure 3. Compared to the previous case with reflecting walkers, one can see that the dynamics is relatively quicker. The first-encounter mode is reached after 10 and 12 steps when, respectively, H = 5 and H = 8 in Figure 2, while it is reached after 3 steps when H = 2 and after 8 steps when H = 4 in Figure 3. This faster time dependence can be explained by the choice of the parameters of the problem. In the resetting case at each time step, the chance of a walker to move can be shown to be 3/10 relative to the reflecting walkers. This fast dynamics is also noticeable in , when compared to Figure 2.
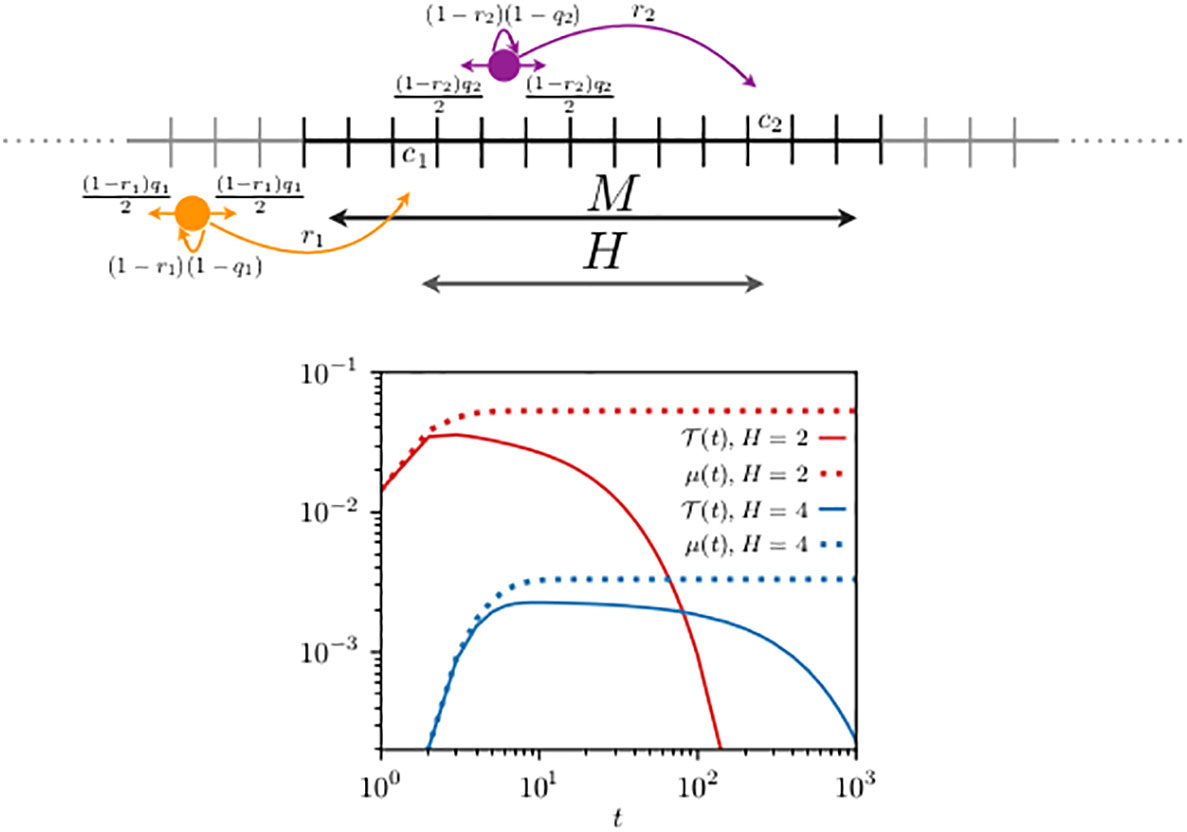
Figure 3 Schematics of two resetting random walkers (top panel) and their first-encounter probability (bottom panel). Compared to Figure 2, the movement rules are modified by the fact that at each time step the animal may reset its location to its own home range center, indicated in the schematics by the long arrows with probability and . To mimic unbounded space the boundary conditions are periodic and the domain size (), diffusivity (), and resetting probability () are chosen to ensure that the contributions to the encounters of those trajectories that exploit the lattice periodicity are negligible. For two cases analyzed, the home range centers are located at and , giving, respectively, a relative distance H between their home range center of 2 and 4. We have used Equation (13) to construct n0 (t) in Equation (7) and in Equation (9), and display them with the continuous and dotted lines [in red for case (i) and in blue for case (ii)], respectively. In both cases, the walkers start from their corresponding home range centers () and interact when they simultaneously occupy a site within the domain [7,13], consisting of sites.
3.4 Mean first-transmission times between animals diffusing in two-dimensional home ranges
As mentioned earlier, the reaction diffusion approach allows one to map the first-transmission problem with transfer efficiency ρ to a first-absorption problem with multiple static partially absorbing targets located at () in a spatial domain of double the original dimensions. Since it is now theoretically possible to predict exactly the mean first-absorption time to any of a set of partially absorbing targets (Giuggioli and Sarvaharman, 2022), we exploit here that advance for our transmission problem. We examine the case of two reflected lattice walkers moving in two dimensions in partially overlapping home ranges (see the top panel of Figure 4). If we call the mean transmission time to a set of M co-location sites starting from a site , we have (Giuggioli and Sarvaharman, 2022)
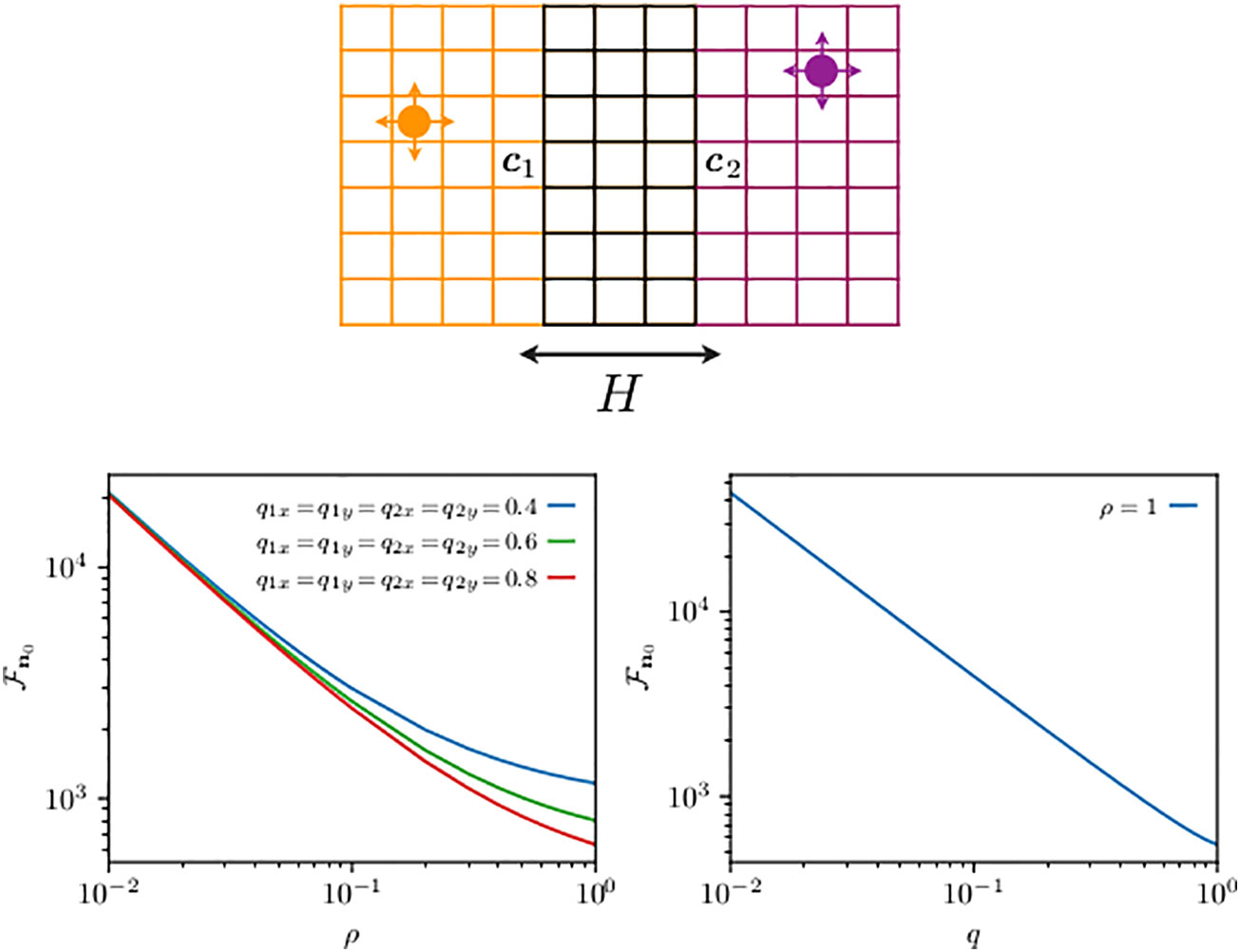
Figure 4 Schematics of two animals roaming within separate two-dimensional home ranges with partial overlap along one direction (top panel) and their mean first-transmission time (bottom panel). On the top panel, the circle displays an animal while the arrows indicate the movement probability at each time step: the left, right, up, and down arrows represent the probability to move, respectively, left, right, up, and down. Although not shown by an arrow, the th animal while not at any of the boundaries can stay at the same site with probability , where and denote the diffusivities in the x- and y-directions, respectively. The probability of staying at sites (except four corners) on boundaries along the x- and y-directions is and , respectively, while at the four corners, it is . The size of the two home ranges is equal to with and . The first walker diffuses within a domain centered at c1 = (6, 3) is limited by reflecting boundaries at sites 1 and 11 in the x-direction and at sites 1 and 5 in the y-direction, and it starts from n10. For the second walker, the allowed range is [9,19] in the x-direction and [1,5] in the y-direction, and in both cases with reflecting boundaries at the end sites. Hence, the domain for the second walker is centered at c2 = (6, 3), which is also its starting point, i.e., n20. The distance between the two home range centers is . The two animals may encounter each other when they simultaneously occupy a site in the overlap region, made up of a total of M sites. The quantity n0 from Equation (21) is shown on the panels at the bottom. The bottom left panel shows n0 as a function of ρ for the same diffusivities for both walkers in both directions. The bottom right panel shows the mean encounter time n0 () as a function of diffusivity q such that .
where the elements of the matrix are expressed exactly in terms of mean first-passage times , mean return times , and the transfer efficiency . More specifically, we have (, with ), while the diagonal elements are given by , where is the mean return time to site . The other two matrices are obtained from as follows: .
We use Equations (16) and (17) to build the elements of the matrices in Equation (21), and in Figure 4, we plot , the mean transmission time, as a function of ρ for different diffusion constants in the bottom left panel, and the mean encounter time () as a function of the diffusion constant, expressed via the (dimensionless) diffusivity parameters and . As approaches 1, the dynamics become motion limited, because the slowest process, the time to reach the targets in this case, governs the time scale of the interaction. From Equation (21), one can extract a perturbation expansion in (Giuggioli and Sarvaharman, 2022), and the shape of the slowing down in the decrease of in the left panel can be quantitatively explained as the first-order correction to the zeroth order (motion limited) term. The plot in the right panel shows that the encounter rate is mainly linearly proportional to the animal diffusion constant (Bénichou and Voituriez, 2014). While such dependence is somewhat expected, what is unexpected is the very limited deviation from an inverse dependence of , because one can show that for any element . The right panel thus points to a negligible dependence of the function on .
4 Summary and discussion
The ability to track simultaneously with high resolution a large number of animals both in laboratory settings and in the field demands the development of modeling approaches to predict when, where, and how animals interact. As some of the theoretical challenges to represent animal interactions have already been tackled in analyzing physical and chemical systems, our aim here has been to make the movement ecology community profit from insights already gained in other fields. To do so, we have opened up the modeling literature from statistical physics, both past and present, on reaction diffusion processes and we have studied the transmission and encounter problem between two animals leaving within separate home ranges.
We have presented the mathematical details that allow to predict over time first-transmission and first-encounter probability in both continuous and discrete variables. With continuous variables, we have considered two Brownian walkers that may interact with an information transfer rate when within a threshold distance and have modeled their motion via a Ornstein–Uhlenbeck process. With discrete variables, we have instead considered that interactions may occur with probability upon co-location and have taken reflected and resetting lattice random walkers to represent animals that roam within distinct home ranges.
With perfect transfer efficiency ( or ), the interaction events reduce to encounter events. In this case, we have compared the continuous formulation to study first-encounter probability to the one proposed recently in the literature using a distance threshold probability and we have been able to derive a mathematical equation that connects the two quantities. To quantify the difference in the two probabilities, we have used discrete variables and looked at the dynamics of two animals living in separate home ranges and moving and interacting on constrained one-dimensional lattices. That comparison allows us to visualize why one is a normalized probability function with all finite moment, while the other is not normalized and possesses infinite moments.
We recognize that the first-encounter probability and the distance threshold probability capture different aspects of the animal dynamics, and we thus believe that there should be scope for employing both, or either, especially in light of the various mechanisms with which animals may interact in an ecological setting. If an encounter event affects detectable characteristics of the animals, then clearly the first instance when that happens is the relevant observable. Examples include the transfer of an infectious pathogen or a parasite, a predator capturing a prey, or an animal passing knowledge about food sources by being observed or smelled by a nearby conspecific. In all these circumstances, the first-transmission probability is a necessary tool to predict the dynamics based on the interplay between the transfer efficiency and the rate of movement. If, on the other hand, information transfer upon interaction is not binary (presence/absence) or it is hard to detect, then knowledge of when animals are within a given distance becomes useful, as shown in the very recent developments (Albery et al., 2021; Noonan et al., 2021; Yang et al., 2023) following ref (Martinez-Garcia et al., 2020).
While we have focused here on destructive searches, this does not preclude the use of the reaction formalism in non-destructive studies, and more specifically the one with discrete space–time variables. In non-destructive scenarios, as the evaluation of the forager efficiency is based on the cumulative encounter of targets, the quantity of interest becomes the (multiple) visitation statistics to any of the lattice sites where targets are located, coupled with a resetting of the walker to a neighboring site upon a target capture. Such dynamics can be studied analytically with the discrete formalism, which has general validity for any Markov movement process and irrespective of the choice of spatial constraint or boundary conditions or the presence of spatial heterogeneities. It could be exploited to provide some useful insights into some of the ongoing debate about the efficiency of stochastic searches when targets get replenished and walkers move as Lévy walkers (Viswanathan et al., 1999; Benhamou, 2007; Reynolds, 2008; Levernier et al., 2020; Buldyrev et al., 2021) and to explore the dependence on the density (James et al., 2008), boundary conditions (Buldyrev et al., 2001; James et al., 2010), and the spatial distribution of the resources (Humphries and Sims, 2014) without using time-consuming stochastic simulations. As the discrete formalism allows one to include any type of heterogeneities, it could also bring insights into the timely studies about species survival following habitat fragmentation and habitat loss as a function of the animal foraging statistics (Wosniack et al., 2014; Niebuhr et al., 2015). Another advantage of the discrete spatial formalism in comparison to the diffusion equation is also worth mentioning. With the latter, it is well known that one describes an ensemble of spatiotemporal trajectories that include (with some exponentially small probability) those that move infinitely fast from a localized initial condition. This limitation, on the other hand, is not present when using random walks on a lattice.
Despite the limitation of our Markov assumption, which considers the movement to be diffusive, extensions of encounter estimations to situations where the assumption about persistence is relaxed are possible. The effects of correlations in the movement steps, also called motion coherence, can be incorporated in a general reaction-motion formalism using the so-called generalized master equation (Kenkre et al., 1973; Kenkre, 1977), which possesses a non-local memory kernel with one extreme (never decaying memory) reducing to a wave equation, that is, to ballistic motion, and the other extreme to an infinitely fast decaying memory, that is, diffusive motion. The intermediate situation, with an exponentially decaying memory, represents coherent motion at short times, and incoherent motion at long times, and was shown to be identical to the telegraphers’ equation in one dimension (Kenkre, 1977). In the context of exciton annihilation, an example of how motion coherence has been included using a generalized master equation can be found in ref (Gülen et al., 1988).
Accounting for correlations in the discrete formalism is also possible and can be accomplished by representing a movement process with correlated steps as a vectorial Markov process with components (see, e.g., Ernst, 1988). The formal difference from the cases analyzed here consists of the need to deal with larger matrices since the set of interaction locations would become possible interaction sites in the higher-dimensional space.
Overall, while there is still much development to be done, an important contribution of our study is that, using a reaction motion formalism, it is possible to predict time-dependent first-transmission and, in the limit, first-encounter probability in terms of the animal movement statistics and the geometric constraints of the space.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Author contributions
VK, RN, and LG developed the idea of the work. DD and LG developed the math. DD prepared the figures. LG wrote the initial draft with contributions from all authors; and all authors contributed to reviewing and editing. All authors contributed to the article and approved the submitted version.
Funding
LG acknowledges funding from the Biotechnology and Biological Sciences Research Council (BBSRC) Grant No. BB/T012196/1, and the National Environment Research Council (NERC) Grant No. NE/W00545X/1. RN acknowledges funding from the Minerva Center for Movement Ecology, the Minerva Foundation, and the Adelina and Massimo Della Pergola Chair of Life Sciences. All authors would like to thank the Isaac Newton Institute for Mathematical Sciences for support and hospitality during the programme “Mathematics of Movement: an interdisciplinary approach to mutual challenges in animal ecology and cell biology”, when part of the work on this paper was undertaken, supported by the EPSRC Grant Number EP/R014604/1.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abate J., Choudhury G. L., Whitt W. (1999). “An introduction to numerical transform inversion and its application to probability models,” in Computational probability. Ed. Grassman W. K. (Boston: Kluwer), 257–323.
Abate J., Whitt W. (1992). Numerical inversion of probability generating functions. Oper. Res. Lett. 12 (4), 245–251. doi: 10.1016/0167-6377(92)90050-D
Albery G. F., Kirkpatrick L., Firth J. A., Bansal S. (2021). Unifying spatial and social network analysis in disease ecology. J. Anim. Ecol. 90 (1), 45–61. doi: 10.1111/1365-2656.13356
Bartumeus F., Campos D., Ryu W. S., Lloret-Cabot R., Méndez V., Catalan J. (2016). Foraging success under uncertainty: search tradeoffs and optimal space use. Ecol. Lett. 19 (11), 1299–1313. doi: 10.1111/ele.12660
Bartumeus F., da Luz M. G. E., Viswanathan G. M., Catalan J. (2005). Animal search strategies: a quantitative random-walk analysis. Ecology 86 (11), 3078–3087. doi: 10.1890/04-1806
Bartumeus F., Fernandez P., Da Luz M. G. E., Catalan J., Solé R. V., Levin S. A. (2008). Superdiffusion and encounter rates in diluted, low dimensional worlds. Eur. Phys. J. Special Topics 157, 157–166. doi: 10.1140/epjst/e2008-00638-6
Benhamou S. (2007). How many animals really do the Lévy walk? Ecology 88 (8), 1962–1969. doi: 10.1890/06-1769.1
Bénichou O., Voituriez R. (2014). From first-passage times of random walks in confinement to geometry-controlled kinetics. Phys. Rep. 539 (4), 225–284. doi: 10.1016/j.physrep.2014.02.003
Buldyrev S. V., Havlin S., Ya Kazakov A., Da Luz M. G. E., Raposo E. P., Stanley H. E., et al. (2001). Average time spent by Lévy flights and walks on an interval with absorbing boundaries. Phys. Rev. E 64 (4), 041108. doi: 10.1103/PhysRevE.64.041108
Buldyrev S. V., Raposo E. P., Frederic Bartumeus S., Rusch F. R., Da Luz M. G. E., Viswanathan G. M. (2021). 'Inverse Square Lévy Walks are not Optimal Search Strategies for d ≥ 2? Phys. Rev. Lett. 126 (4), 048901. doi: 10.1103/PhysRevLett.126.048901
Das D., Giuggioli L. (2022). Discrete space-time resetting model: application to first-passage and transmission statistics. J. Phys. A: Math. Theor. 55 (42), 424004. doi: 10.1088/1751-8121/ac9765
Das D., Giuggioli L. (2023). Dynamics of lattice random walk within regions composed of different media and interfaces. J. Stat. Mech: Theor. Exp. 2023 (1), 013201. doi: 10.1088/1742-5468/aca8f9
Ernst M. H. (1988). Random walks with short memory. J. Stat. Phys. 53, 191–201. doi: 10.1007/BF01011552
Farine D. R., Whitehead H. (2015). Constructing, conducting and interpreting animal social network analysis. J. Anim. Ecol. 84 (5), 1144–1163. doi: 10.1111/1365-2656.12418
Faustino C. L., Da Silva L. R., Da Luz M. G. E., Raposo E. P., Viswanathan G. M. (2007). Search dynamics at the edge of extinction: Anomalous diffusion as a critical survival state. Europhysics Lett. 77 (3), 30002. doi: 10.1209/0295-5075/77/30002
Faustino C. L., Lyra M. L., Raposo E. P., Viswanathan G. M., da Luz M. G. E. (2012). The universality class of random searches in critically scarce environments. Europhysics Lett. 97 (5), 50005. doi: 10.1209/0295-5075/97/50005
Giuggioli L. (2020) Exact spatiotemporal dynamics of confined lattice random walks in arbitrary dimensions: A century after Smoluchowski and Pólya. Phys. Rev. X 10 (2), 021045. doi: 10.1103/PhysRevX.10.021045
Giuggioli L., Abramson G., Kenkre V. M., Parmenter R. R., Yates T. L. (2006). Theory of home range estimation from displacement measurements of animal populations. J. Theor. Biol. 240 (1), 126–135. doi: 10.1016/j.jtbi.2005.09.002
Giuggioli L., Gupta S., Chase M. (2019). Comparison of two models of tethered motion. J. Phys. A: Math. Theor. 52 (7), 075001. doi: 10.1088/1751-8121/aaf8cc
Giuggioli L., Kenkre V. M. (2014). Consequences of animal interactions on their dynamics: emergence of home ranges and territoriality. Movement Ecol. 2, 1–22. doi: 10.1186/s40462-014-0020-7
Giuggioli L., McKetterick T. J., Holderied M. (2015). Delayed response and biosonar perception explain movement coordination in trawling bats. PloS Comput. Biol. 11 (3), e1004089. doi: 10.1371/journal.pcbi.1004089
Giuggioli L., Pérez-Becker S., Sanders D. P. (2013). Encounter times in overlapping domains: application to epidemic spread in a population of territorial animals. Phys. Rev. Lett. 110 (5), 058103. doi: 10.1103/PhysRevLett.110.058103
Giuggioli L., Sarvaharman S. (2022). Spatio-temporal dynamics of random transmission events: from information sharing to epidemic spread. J. Phys. A: Math. Theor. 55 (37), 375005. doi: 10.1088/1751-8121/ac8587
Gülen D., Kenkre V. M., Knox R. S., Parris P. E. (1988). Effects of transport coherence on the mutual annihilation of excitons. Phys. Rev. B 37 (4), 1839. doi: 10.1103/PhysRevB.37.1839
Gurarie E., Andrews R. D., Laidre K. L. (2009). A novel method for identifying behavioural changes in animal movement data. Ecol. Lett. 12 (5), 395–408. doi: 10.1111/j.1461-0248.2009.01293.x
Gurarie E., Ovaskainen O. (2011). Characteristic spatial and temporal scales unify models of animal movement. Am. Nat. 178 (1), 113–123. doi: 10.1086/660285
Gurarier E., Ovaskainen O. (2013). Towards a general formalization of encounter rates in ecology. Theor. Ecol. 6, 189–202. doi: 10.1007/s12080-012-0170-4
Humphries N. E., Sims D. W. (2014). Optimal foraging strategies: Lévy walks balance searching and patch exploitation under a very broad range of conditions. J. Theor. Biol. 358, 179–193. doi: 10.1016/j.jtbi.2014.05.032
Hutchinson J. M. C., Waser P. M. (2007). Use, misuse and extensions of “ideal gas” models of animal encounter. Biol. Rev. 82 (3), 335–359. doi: 10.1111/j.1469-185x.2007.00014.x
James A., Pitchford J. W., Plank M. J. (2010). Efficient or inaccurate? analytical and numerical modelling of random search strategies. Bull. Math. Biol. 72 (4), 896. doi: 10.1007/s11538-009-9473-z
James A., Plank M. J., Brown R. (2008). Optimizing the encounter rate in biological interactions: ballistic versus Lévy versus brownian strategies. Phys. Rev. E 78 (5), 051128. doi: 10.1103/PhysRevE.78.051128
Jiang L, Giuggioli L., Perna A., Escobedo R, Lecheval V., Sire C, et al. (2017). Identifying influential neighbors in animal flocking. PloS Comput. Biol. 13 (11), e1005822. doi: 10.1371/journal.pcbi.1005822
Kac M. (1947). On the notion of recurrence in discrete stochastic processes. Bull. Amer. Math. Soc 53 (10), 1002–1010. doi: 10.1090/S0002-9904-1947-08927-8
Kay T., Giuggioli L. (2022). Diffusion through permeable interfaces: fundamental equations and their application to first-passage and local time statistics. Phys. Rev. Res. 4 (3), L032039. doi: 10.1103/PhysRevResearch.4.L032039
Kenkre V. M. (2021). Memory functions, projection operators, and the defect technique: some tools of the trade for the condensed matter physicist. Vol. 982. Cham, Switzerland: Springer Nature. doi: 10.1007/978-3-030-68667-3
Kenkre V. M. (1977). “The generalized master equation and its applications,” in Landman U. ed. Statistical mechanics and statistical methods in theory and application (New York: Plenum), 441–461.
Kenkre V. M. (1980). Theory of exciton annihilation in molecular crystals. Phys. Rev. B 22 (4), 2089. doi: 10.1103/PhysRevB.22.2089
Kenkre V. M. (1982a). A theoretical approach to exciton trapping in systems with arbitrary trap concentration. Chem. Phys. Lett. 93 (3), 260–263. doi: 10.1016/0009-2614(82)80135-8
Kenkre V. M. (1982b). “The master equation approach: Coherence, energy transfer, annihilation, and relaxation,” in Exciton Dynamics in Molecular Crystals and Aggregates, Springer Tracts in Modern Physics. Eds. Kenkre V. M., Reineker P. (Berlin: Springer), 1–109.
Kenkre V. M., Giuggioli L. (2021). Theory of the spread of epidemics and movement ecology of animals: an interdisciplinary approach using methodologies of physics and mathematics (Cambridge, UK: Cambridge University Press).
Kenkre V. M., Montroll E. W., Shlesinger M. F. (1973). Generalized master equations for continuous time random walks. J. Stat. Phys. 9, 45–50. doi: 10.1007/BF01016796
Kenkre V. M., Parris P. E., Schmid D. (1985). Investigation of the appropriateness of sensitized luminescence to determine exciton motion parameters in pure molecular crystals. Phys. Rev. B 32 (8), 4946. doi: 10.1103/PhysRevB.32.4946
Kenkre V. M., Schmid D. (1983). Comments on the exciton annihilation constant and the energy transfer rate in naphthalene and anthracene. Chem. Phys. Lett. 94 (6), 603–608. doi: 10.1016/0009-2614(83)85066-0
Kenkre V. M., Sugaya S. (2014). Theory of the transmission of infection in the spread of epidemics: Interacting random walkers with and without confinement. Bull. Math. Biol. 76 (12), 3016–3027. doi: 10.1007/s11538-014-0042-8
Kenkre V. M., Wong Y. M. (1980). Theory of exciton migration experiments with imperfectly absorbing end detectors. Phys. Rev. B 22 (12), 5716. doi: 10.1103/PhysRevB.22.5716
Kenkre V. M., Wong Y. M. (1981). Effect of transport coherence on trapping: Quantum-yield calculations for excitons in molecular crystals. Phys. Rev. B 23 (8), 3748. doi: 10.1103/PhysRevB.23.3748
Levernier N., Textor J., Bénichou O., Voituriez R (2020). Inverse square Lévy walks are not optimal search strategies for d ≥ 2. Phys. Rev. Lett. 124 (8), 080601. doi: 10.1103/PhysRevLett.124.080601
Levin S. A. (1992). The problem of pattern and scale in ecology: the Robert H. MacArthur award lecture. Ecology 73 (6), 1943–1967. doi: 10.2307/1941447
Marris D., Sarvaharman S., Giuggioli L. (2023) Exact spatio-temporal dynamics of lattice random walks in hexagonal and honeycomb domainss. Phys. Rev. E 07 (5), 054139. doi: 10.1103/PhysRevE.107.054139
Martinez-Garcia R., Fleming C. H., Seppelt R., Fagan W. F., Calabrese J. M. (2020). How range residency and long-range perception change encounter rates. J. Theor. Biol. 498, 110267. doi: 10.1016/j.jtbi.2020.110267
Matley J. K., Klinard N. V., Martins A. P.B., Aarestrup K., Aspillaga E., Cooke S. J., et al. (2022). Global trends in aquatic animal tracking with acoustic telemetry. Trends Ecol. Evol. 37 (1), 79–94. doi: 10.1016/j.tree.2021.09.001
McKenzie H. W., Lewis M. A., Merrill E. H. (2009). First passage time analysis of animal movement and insights into the functional response. Bull. Math. Biol. 71, 107–129. doi: 10.1007/s11538-008-9354-x
Montroll E. W., Potts R. B. (1955). Effect of defects on lattice vibrations. Phys. Rev. 100 (2), 525–543. doi: 10.1103/PhysRev.100.525
Morales J. M., Haydon D. T., Frair J., Holsinger K. E., Fryxell J. M. (2004). Extracting more out of relocation data: building movement models as mixtures of random walks. Ecology 85 (9), 2436–2445. doi: 10.1890/03-0269
Nagy M, Ákos Z., Biro D., Vicsek T (2010). Hierarchical group dynamics in pigeon flocks. Nature 464 (7290), 890–893. doi: 10.1038/nature08891
Nathan R., Getz W. M., Revilla E., Holyoak M., Kadmon R., Saltz D., et al. (2008). A movement ecology paradigm for unifying organismal movement research. Proc. Natl. Acad. Sci. 105 (49), 19052–19059. doi: 10.1073/pnas.0800375105
Nathan R., Monk C. T., Arlinghaus R., Adam T., Alós J., Assaf M., et al. (2022). Big-data approaches lead to an increased understanding of the ecology of animal movement. Science 375 (6582), eabg1780. doi: 10.1126/science.abg1780
Niebuhr B. B. S., Wosniack M. E., Santos M. C., Raposo E. P., Viswanathan G. M., Da Luz M. G. E., et al. (2015). Survival in patchy landscapes: the interplay between dispersal, habitat loss and fragmentation. Sci. Rep. 5 (1), 11898. doi: 10.1038/srep11898
Noonan M. J., Martinez-Garcia R., Davis G. H., Crofoot M. C., Kays R., Hirsch B. T., et al. (2021). Estimating encounter location distributions from animal tracking data. Methods Ecol. Evol. 12 (7), 1158–1173. doi: 10.1111/2041-210X.13597
Ovaskainen O., Rekola H., Meyke E., Arjas E. (2008). Bayesian methods for analyzing movements in heterogeneous landscapes from mark–recapture data. Ecology 89 (2), 542–554. doi: 10.1890/07-0443.1
Reynolds A. (2008). How many animals really do the Lévy walk? Ecology 89 (8), 2347–2351. doi: 10.1890/07-1688.1
Reynolds A. (2015). Liberating Lévy walk research from the shackles of optimal foraging. Phys. Life Rev. 14, 59–83. doi: 10.1016/j.plrev.2015.03.002
Santos M. C., Raposo E. P., Viswanathan G. M., Da Luz M. G. E. (2004). Optimal random searches of revisitable targets: crossover from superdiffusive to ballistic random walks. Europhysics Lett. 67 (5), 734. doi: 10.1209/epl/i2004-10114-9
Sarvaharman S., Giuggioli L. (2020). Closed-form solutions to the dynamics of confined biased lattice random walks in arbitrary dimensions. Phys. Rev. E 102 (6), 062124. doi: 10.1103/PhysRevE.102.062124
Sarvaharman S., Giuggioli L. (2023). Particle-environment interactions in arbitrary dimensions: a unifying analytic framework to model diffusion with inert spatial heterogeneities. arXiv:2209.09014. Available at: https://arxiv.org/pdf/2209.09014.pdf.
Spendier K., Kenkre V. M. (2013). Analytic solutions for some reaction-diffusion scenarios. J. Phys. Chem. B 117 (49), 15639–15650. doi: 10.1021/jp406322t
Sugaya S., Kenkre V. M. (2018). Analysis of transmission of infection in epidemics: Confined random walkers in dimensions higher than one. Bull. Math. Biol. 80 (12), 3106–3126. doi: 10.1007/s11538-018-0507-2
Tejedor V., SChad M., Voituriez O. B. R., Metzler R. (2011). Encounter distribution of two random walkers on a finite one-dimensional interval. J. Phys. A: Math. Theor. 44 (39), 395005. doi: 10.1088/1751-8113/44/39/395005
Viswanathan G. M., Buldyrev S. V., Havlin S., Da Luz M. G. E., Raposo E. P., Stanley H.E. (1999). Optimizing success random searches. Nature 401 (6756), 911–914. doi: 10.1038/44831
Viswanathan G. M., Da Luz M. G. E., Raposo E. P., Stanley H.E. (2011). The physics of foraging: an introduction to random searches and biological encounters (Cambridge, UK: Cambridge University Press).
Whitehead H. (2008). Analyzing animal societies: quantitative methods for vertebrate social analysis (Chicago, USA: University of Chicago Press).
Wosniack M. E., Santos M. C., Pie M. R., Marques M. C. M., Raposo E. P., Viswanathan G. M., et al. (2014). Unveiling a mechanism for species decline in fragmented habitats: fragmentation induced reduction in encounter rates. J. R. Soc. Interface 11 (91), 20130887. doi: 10.1098/rsif.2013.0887
Yang A., Wilber M. Q., Manlove K. R., Miller R. S., Boughton R., Beasley J., et al. (2023). Deriving spatially explicit direct and indirect interaction networks from animal movement data. Ecol. Evol. 13 (3), e9774. doi: 10.1002/ece3.9774
Keywords: animal interactions, encounter problems, movement ecology, random walks and Brownian motion, reaction diffusion processes
Citation: Das D, Kenkre VM, Nathan R and Giuggioli L (2023) Misconceptions about quantifying animal encounter and interaction processes. Front. Ecol. Evol. 11:1230890. doi: 10.3389/fevo.2023.1230890
Received: 29 May 2023; Accepted: 18 July 2023;
Published: 04 October 2023.
Edited by:
Danish Ali Ahmed, Gulf University for Science and Technology, KuwaitReviewed by:
Marcos Gomes Eleuterio da Luz, Federal University of Paraná, BrazilAndy Reynolds, Rothamsted Research, United Kingdom
Copyright © 2023 Das, Kenkre, Nathan and Giuggioli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Luca Giuggioli, bHVjYS5naXVnZ2lvbGlAYnJpc3RvbC5hYy51aw==
 Debraj Das
Debraj Das V. M. Kenkre2
V. M. Kenkre2 Ran Nathan
Ran Nathan Luca Giuggioli
Luca Giuggioli