Evolution of parental roles in phase portraits of bimatrix asymmetric games

In this paper, we address the evolutionary dynamic of parental roles using game theory. The main purpose of the article was to expand a classical list of evolutionary dynamic parental conflicts by adding some important cases which hitherto have not been intensively studied. Our models are apt to deliver some novel insights into the evolution of parental care. We also introduced several hypothetical events that served as illustrations of an arising alteration in cost-benefits for both parents and simulated a subsequent evolutionary endpoint. Our models revealed that evolutionary outcomes for reproductive decisions of both parents could be completely predicted by certain payoff matrices, which serve as proxies for a Darwinian fitness gain. In this sense, the result of a frequency-dependent selection on reproductive traits would inevitably depend on fitness costs and benefits arising for both parents in various circumstances. We demonstrated that population division could be a plausible evolutionary consequence for any human mating game where ‘reproductive defection’ represents the best response to any action by the reproductive opponent. We conclude that future evolutionary studies of human reproductive behavior should be more oriented on estimating a sex-biased asymmetry in potential fitness gains obtained by cooperative and deceptive parents in diverse environments and cultures.

1. Introduction

Parental care requires a sufficient amount of bioenergetical resources and time (Kaplan et al., 2000). The innate goal of any living creature is to gain the individual and inclusive fitness through successful reproduction resulting in viable and fertile offspring, while the absence of reproduction would soon lead to the extinction of life forms. Nevertheless, from biological perspectives there is a potential for intense reproductive conflict that can lead to maladaptive outcome. Because each parent could gain certain fitness benefits by saving energy, meanwhile their partner devotes to successful common reproduction relatively more efforts (Lessells, 2006; Royle et al., 2016). Apparently, this conflict has various intensity levels in different taxa. Although females are more frequently the caregivers, diversification of parental roles can take a variety of forms (Kokko et al., 2012). In its extremum, an intense parental conflict could be resolved in favor of one sex or another by establishing male-only or female-only care practices. Observed inequality in parental efforts between males and females in different taxa reflects the essence and nature of sexual disputes over parental care and results in a profound dimorphism of sexual, parental and behavioral roles. Revealing mechanisms underlying the resolution of evolutionary conflict over parental care is still an important research task in biology (Royle et al., 2016).

A generally accepted explanation for sexually dimorphic roles implying the prevalence of female care is based on the theoretical concept of the initial difference in the female and male gametes’ size–anisogamy (Lehtonen and Kokko, 2011). Dimorphism at the gamete size and their level results in competition among gametes, and in the scarcity (or abundance) of gametes of the opposite mating type (Lehtonen et al., 2016). Hence, sexual selection among members of the sex with the more numerous gametes (typically males) is stronger than in sex with larger but limited in number gametes (typically females). In connection with the above, it was supposed that the probability of paternal care was significantly lower (Trivers and Campbell, 1972). It is evidenced by the fact that male care practices are relatively seldom observed in mammals (Eisenberg and Gould, 1970). However, the initial anisogamy, as a mechanism, that sets classical sexual roles, is not universally realized in various taxa and biological classes of animals if we consider the entire subtype of vertebrates. For instance, in fish, amphibians and birds, parental care, defined as investment in offspring after fertilization, is not an exception at all but an ordinary phenomenon (Salthe and Mecham, 1974); likewise, the majority of species diversity of birds demonstrate variation of social monogamy and biparental effort for a clutch (Lack, 1968).

In this paper, we are using gamy theory to illustrate a dynamic shaping parental role and thus to reveal a potential mechanism specifying a share of care each parent should provide to common offspring. Nowadays, evolutionary game theory is widely used to explain the distribution of parental investments and diversification in sexual roles (Maynard Smith, 1982, 1984; McNamara and Weissing, 2010) via modeling optimal reproductive solutions for each sex in terms of fitness (McNamara et al., 2000, 2003; Johnstone and Hinde, 2006). An important feature of this approach is that evolutionary game theory allows to simulate a parental conflict which has been acting during the evolutionary time in a given population, describe an iterative (evolutionary) change in strategies for two groups of players, and predict a final outcome of a continuous selection pressure acting on each sex separately (Dawkins and Carlisle, 1976; Schuster and Sigmund, 1981; Maynard Smith, 1982; Maynard Smith and Hofbauer, 1987; McNamara and Weissing, 2010).

Sexual, and parental dimorphism is ubiquitous (Lehtonen et al., 2016), and therefore interactions between females and males are almost always asymmetric. Asymmetry can be caused by physiological (genetic) differences among two groups of players (sexes) or due to preexisting environmental heterogeneity, including inequality in the social environment, or it could be a combination of both factors. Such asymmetric interactions are recognized as an important application in evolutionary game theory. Asymmetric evolutionary games correspond to the realm of bimatrix games in classical game theory. In game theory, a bimatrix game is a simultaneous two-player game in which each player has a finite number of possible decisions. It is generally thought, that in the case of reproduction, each agent (parent) can make two decisions: either caring for the offspring or refusing to care (deserting; McNamara and Weissing, 2010).

The first and most complete classification of evolutionarily stable strategies for asymmetric games was carried out by Maynard Smith (1982). He also examined cases with paradoxical solutions of mutual rejection of cooperation and cyclical dynamics in players strategies.

Our paper expands a classical list of evolutionary dynamic parental conflicts by adding some important cases which hitherto have not been intensively studied. To understand parental behavior, we also propose several hypothetical events that may serve as illustrations for certain changes in matrix payoffs for two-player games. Proposed mathematical calculations and phase portraits can also be useful in analyzes of various interactions in a wide range of two interacting classes of players, such as: parent-offspring, host–parasite, owner-intruder, etc.

2. Methods

2.1. Mathematical calculation and graphical representations

Mathematical calculations and graphical representation of phase portraits were realized using Wolfram Mathematica 13.0 (and 13.2.0) computational software program.

2.2. Methodology

An evolution of strategies in a conflict of the sexes over parental investment could be elucidated by means of a simple dynamic system using the game-theoretic approach (Schuster and Sigmund, 1981).

Considering that, for each subsequent generation the rate increase in the quantity of cooperative males adopted first strategy, $\frac{d{x}_1\left(t\right)}{dt}$ , given by $a_{11}{y}_1+a_{12}{y}_2$ , will be the difference between the payoff obtained by caring males and average males’ payoff in a previous generation, given by $a_{11}{x}_1{y}_1+a_{12}{x}_1{y}_2+a_{21}{x}_2{y}_1+a_{22}{x}_2{y}_2$ . A similar argument applies to changing in the proportion of females applying two different strategies, $\frac{d{y}_1\left(t\right)}{dt}$ .

By solving the equations $f\left(x\mathrm{,}y\right)=0$ , and $g\left(x\mathrm{,}y\right)=0$ , for $\frac{d}{dt}x\left(t\right)=f\left(x\mathrm{,}y\right)$ ,

$\frac{d}{dt}y\left(t\right)=g\left(x\mathrm{,}y\right)$ , the fixed points could be obtained. To analyze the stability, the Jacobian matrix at this fixed point was performed.

2.3. Strategies specification

Taking into account substantial variation across different species (Royle et al., 2016), in most parental desertion games, the first strategy constitutes a cooperative tactic implies successful reproduction followed by care. By contrast, the second strategy is a deceptive tactic implying exploitation of the other’s investment. Usually, a defecting parent avoids any sort of care (desert). Considering internal fertilization, in mammals a defecting female can also exploit her social partner’s investment and benefit from extra-pair maternity.

Absence of care could also be manifested through reproductive reluctance avoiding pregnancy, refusing to have sexual intercourse, also getting rid of the fetus or infanticide a newborn; for a review, (see Hrdy and Hausfater, 1984), which could be more applicable for females.

2.4. Payoff matrices

In classical game theory models’ matrices payoffs are proxies for a Darwinian fitness (Maynard Smith and Price, 1973).

$A:\mathrm{}\mathrm{}=\left(\begin{array}{c}aiiaij\\ ajiajj\end{array}\right);$ $B:\mathrm{}\mathrm{}=\mathrm{}\left(\begin{array}{c}biibij\\ bjibjj\end{array}\right);$

Where a_ij is the payoff for a male using strategy X _i against a female playing strategy Y _j , with b _ji corresponding to payoff for a female using second strategy Y _j against a male playing strategy X _i.

Let fitness payoffs for males be in matrix A, and females’ payoffs in matrix B. The upper row of each matrix corresponds to fitness costs for a cooperative and caring parent; the lower one reflects benefits for a deceptive strategy. The left column corresponds to changes in the individual fitness gains in cases of interacting with a cooperative partner; the right column corresponds to instances when an individual interacts with a defecting partner.

2.5. Phase portrait characteristics

Modeled phase portraits represent a one-unit square posed on a coordinate system, where zero denotes a deserting strategy, and one corresponds to a cooperation and care strategy. Any point inside the portrait could be seen as a stage in an ongoing evolutionary dynamic. For instance, within any evolutionary moment the share of males adopting the first strategy (childcare) could be traced on the x-axis; it could be obtained by drawing the vertical line through a point on the x-axis. Similarly, the proportion of caring females can be seen on the y-axis. The arrows indicate selections direction over an evolutionary time scale and the expected shift in the proportions of males and females that adopted these two strategies.

3. Models and phase portraits

Evolution of a novel function starts from random genetic changes as a precondition for a Darwinian natural selection which further operates on a given spontaneous variation (Darwin, 1871; Nei, 2013). These evolutionary innovations can equip individuals with “tools” that would have been favored by Darwinian selection. Hence, a spread of a novel persistent trait/allele enables bearers with a sufficient reproductive fitness advantage. The most striking example is the occurrence of lactation in mammals. Phase-portraits presented in Figure 1A demonstrated such a selection force which guided the evolution of female-only care as a pervasive reproduction model in a given population. The point (0;1) here constitutes an evolutionary attractor (see McNamara and Weissing, 2010).

FIGURE 1

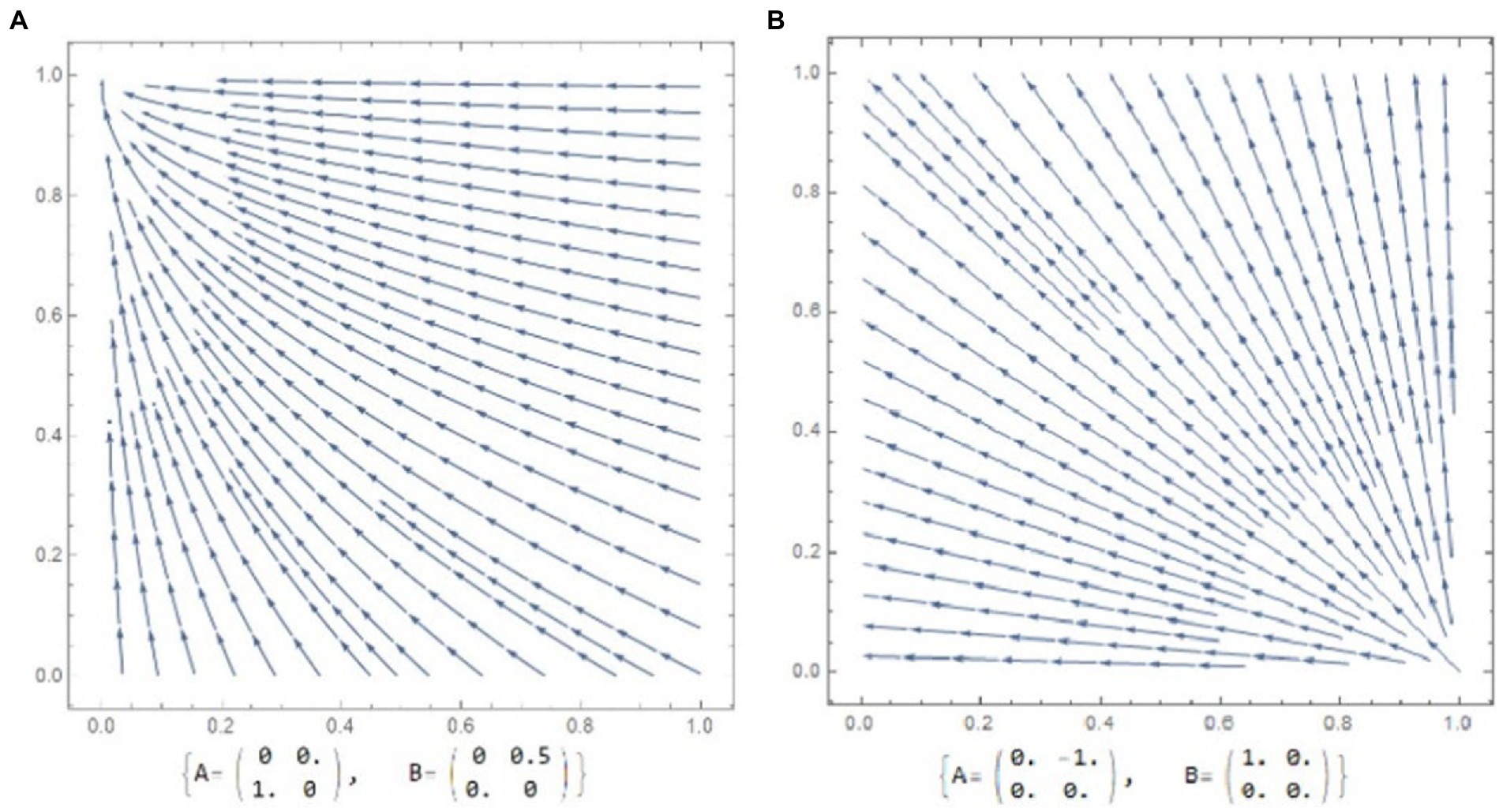
Figure 1. Phase portrait and corresponding payoff matrices for males and females. The arrowheads depict evolutionary trajectories. (A) An evolutionary dynamic directed toward female-only care. (B) An evolutionary dynamic where male population would be specifically selected against male-only care.

The phase portrait in Figure 1A illustrates the Dawkins and Carlisle theoretical prediction on parental dispute resolution: a deserting partner probably would be the one who could do it first (Dawkins and Carlisle, 1976). Later, Maynard Smith (1982) supposed that the sharing of parental burden would depend on whether the players had information about the intentions and stable roles of each sex (see also McNamara and Weissing, 2010). In this regard, internal fertilization and lactation could be the key factors that determine female form of care in mammals.

The next model (Figure 1B) represents a dynamic of decreasing the propensity for paternal care; males may lose if they do cooperate, so male cooperation should be punished (− 1 point). The parenting evolution will lead away from the male-only care point. This point is called an evolutionary repellor (McNamara and Weissing, 2010). Interestingly, there is always an increase in female cooperation, independent of the starting point, but it will only reach 100% female-care if in the starting point proportions of cooperating males and females in sum were higher than 1.

A selection dynamic is very similar to the previous example is shown in Figure 2A. However, the interactions here are more complicated. After the initial tendency toward female-only care and male defection, the model achieves the only possible outcome of a continuously stable strategy–biparental care (Figure 2A).

FIGURE 2

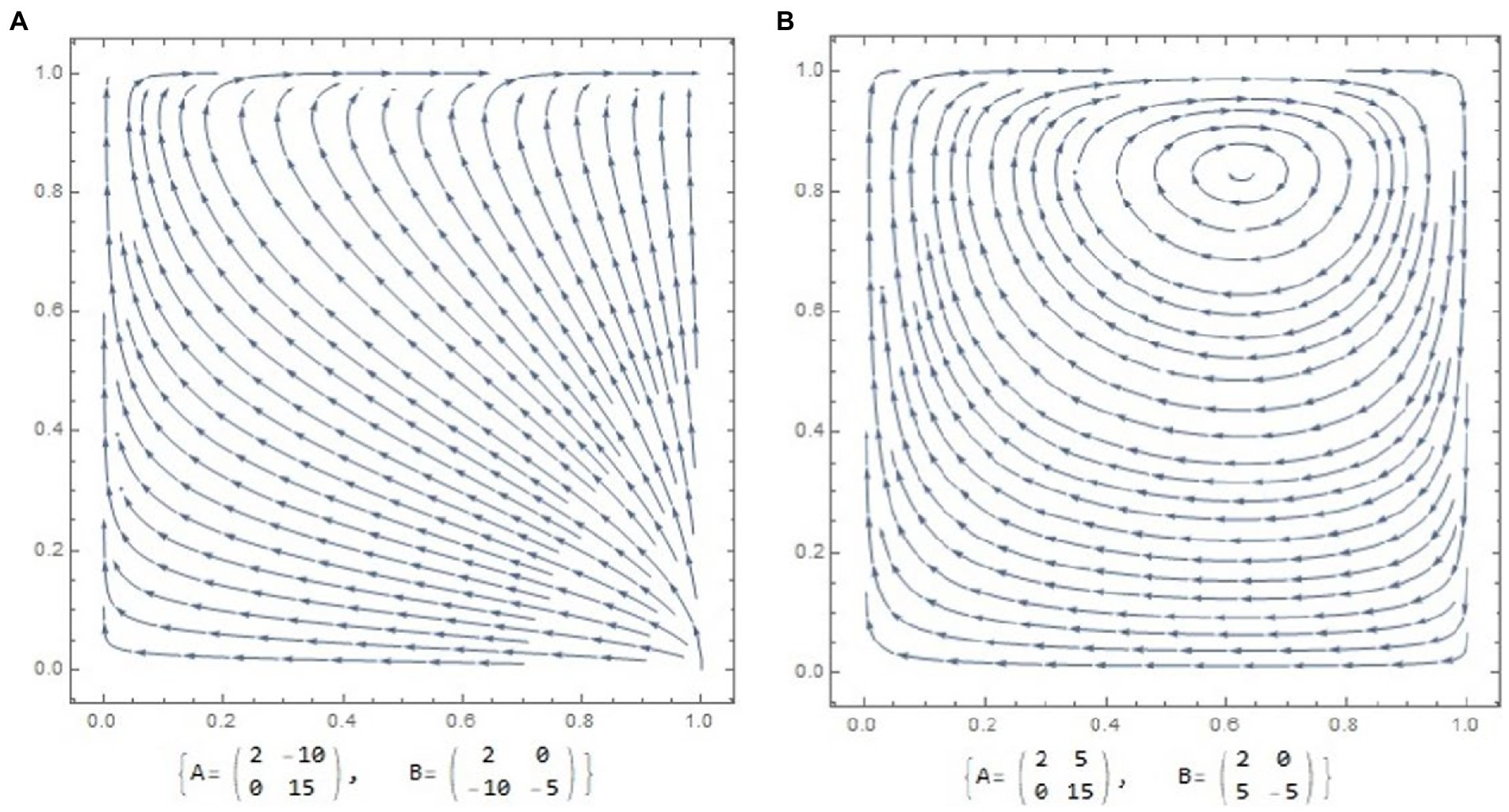
Figure 2. Phase portrait and corresponding payoff matrices for males and females. The arrowheads depict evolutionary trajectories. (A) selection favors cooperative parental strategies; hence population evolves toward the equilibrium state–biparental care. While male populations would be specifically selected against male-only care practice. (B) Phase portrait of dynamical forces, describing battle of the sexes according to payoff matrix proposed by R. Dawkins. The model leads to endless oscillations.

The next famous example of nonlinear relationships between the two players was described in the classical example of an asymmetric conflict, the battle of the sexes by Dawkins (1978). This model has become classical for biological and ecological studies of sexual conflicts (see Schuster and Sigmund, 1981; Figure 2B).

Figure 3A shows mutual refusal of cooperation. Here reproductive defection could become an adaptive strategy for both sexes. These paradoxical dynamics, as it was defined by Maynard Smith (1982), dominate when a partner’s cheating reduces an individual’s fitness more than in the case of mutual rejection of reproduction and care (see Figure 3A, asymmetric Prisoners Dilemma game).

FIGURE 3

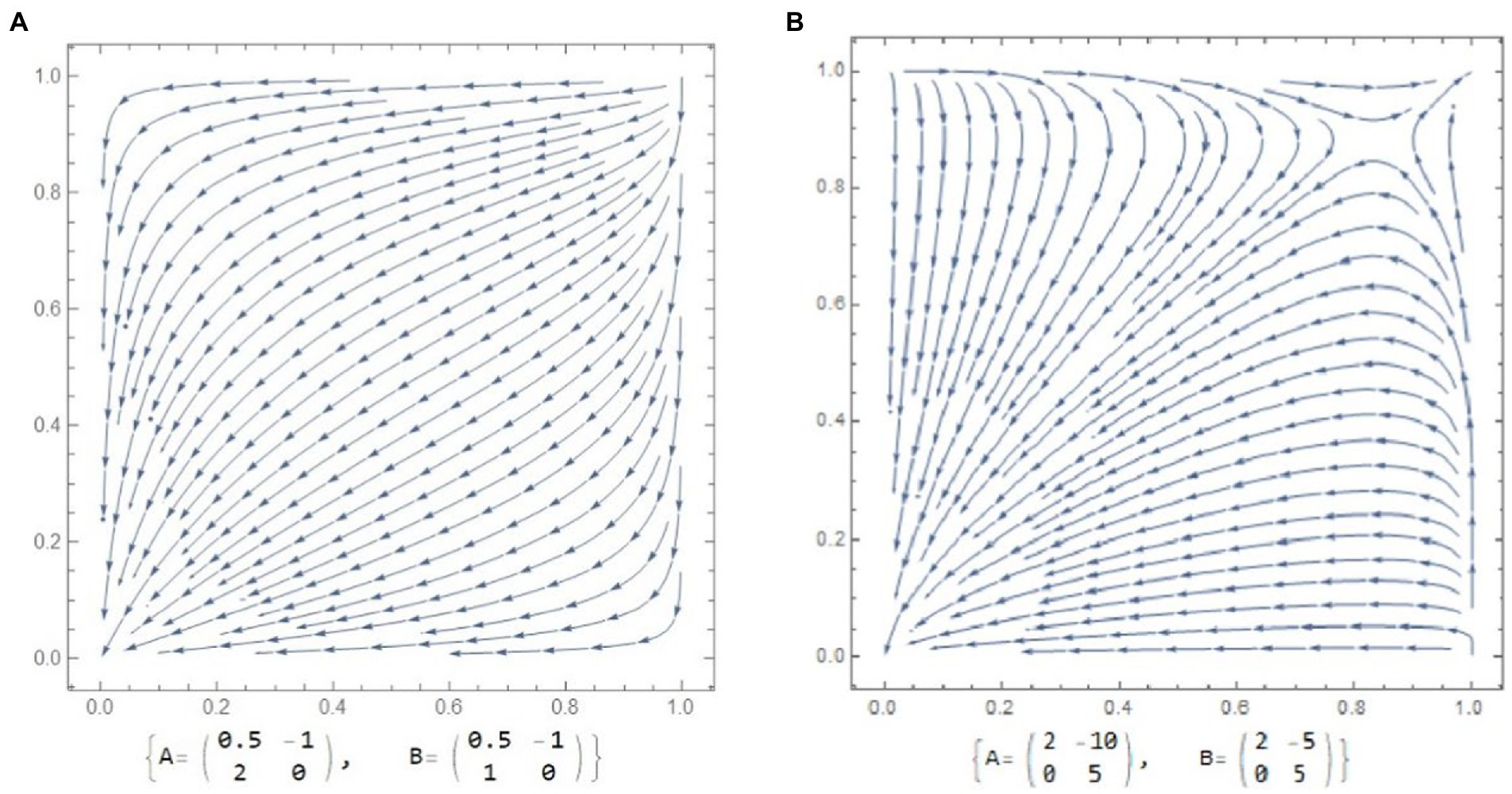
Figure 3. Phase portrait and corresponding payoff matrices for males and females. The arrowheads depict evolutionary trajectories. (A) Evolution of care avoidance and mutual reproductive rejection as equilibrium state. Even if the system had started at biparental care, small mutations would have sent it into a state of mutual defection. (B) population is disruptively selected for opposite parenting strategies. This would lead to populations with either exclusively biparental care or populations with a mutual defection strategy (care avoidance).

The next case is called evolutionary branching (McNamara and Weissing, 2010), where a disruptive selection becomes a possible outcome (Figure 3B).

Of the many possible scenarios of bimatrix asymmetric games, here we have discussed six. Depending on the payoff matrix, different evolutionary trajectories and outcomes are possible, leading to stable female care only (Figure 1A), stable defecting strategy (Figure 3A), stable biparental care (Figure 2A), to all possible outcomes except paternal care only (Figure 1B), to vortices of mixed strategies (Figure 2B) and to mixed strategy (Figure 3B). It is interesting to note, that the outcomes of the four figures (Figures 1A, 2A, 3A,B) are all individual cases among plenty of possible outcomes contained in Figure 1B. Hence, the currently observed outcomes (prevalent strategies) of any population do not allow any conclusion about the evolutionary trajectory, while latter could be completely predicted by a certain payoff matrix.

4. Discussion

Parental care is costly for parents, because care expends resources that parents would otherwise allocate to their own somatic effort and future reproduction (Alexander, 1987; Morita et al., 2016; Royle et al., 2016). Inequality in parenting costs for males and females leads to profound variation in parental care patterns and creates prerequisites for a sexual conflict through diversification of selection pressures on each sex.

Previous attempts to determine the share of care each parent provides utilizing the concept of an initial anisogamy, had not contributed exhaustive answers to the origins of the variety of observed parental roles in different taxa (Royle et al., 2016). To disclose a complex dynamic within a parenting dispute over care, we turned to an evolutionary game theory (Maynard Smith, 1982, 1984; McNamara and Weissing, 2010).

Of particular interest to this paper is the notion that alteration in fitness gains could lead to remarkable evolutionary consequences. For instance, in different models’ iterative evolutionary changes and corresponding social dynamics could be highly similar. However, the final evolutionary outcomes would be entirely different (Figures 1B, 2B). In this sense, mating system evolution under a frequency-dependent selection would inevitably depend on certain asymmetry preexisting in males’ and females’ reproductive positions substantially varying in different circumstances. The resulting outcome is not always obvious, and sometimes even contradicts the logical conclusions (McNamara and Weissing, 2010) drawn using the classical analysis of the linear interaction of cause (predictor) and effect (response value). Rational fitness-maximizing individual decisions can sometimes lead to apparently maladaptive reproductive behavior – mutual rejection of care and parenting (Kokko and Jennions, 2014).

Paradoxical solutions of mutual deception as equilibrium states are presented in Figure 3A.

Gaming conditions for a case of mutual rejection of parenting imply that in terms of fitness there always would be a high risk of deception for caring parents of both sexes (Morita et al., 2016). In this example (Figure 3A) the costs for being the only care giver are high, whereas defecting is rewarded. In the next figure (Figure 3B), the payoff of not providing any parental care is positive for both parents and higher then when both cooperate. Both scenarios could be applied to sexual conflict in humans, where child rearing is long and costly, and this dynamic is created by extremely destructive risks of partner defection. For women partner defection bring a serious burden of single parenting. Firstly, production of ovum, gestation, and lactation is still a biologically taxing process for women. And if women do not receive male support, they will practice “gene shopping” (Marlowe, 2000). Prevalence of deceptive tactic in females (e.g., extra-pair conception) intensifies males’ selection against care, making it more and more difficult for females to count on partners help. On the other hand, increasing costs of raising a child, forcing woman to become more persistent in searching male investment, which will prolong birth intervals. In the model presented on Figure 3A, the selection force will counteract the cooperation of the players and potentially oppress reproduction (Semenova and Butovskaya, 2021). And if care is essential for offspring’s survival, there would be the only option for successful reproduction–relay on help of various kin or non-relative alloparents (Hrdy and Hausfater, 1984).

Theory predicts that intense sexual conflict over care (е.g. mismatching males and females interests in reproductive payoffs) leads to a fitness minimum, which could reinforce the rate of evolutionary novelty and potentially promote speciation (for a review; Parker and Partridge, 1998; Gavrilets, 2000). An invasion of a novel mutant with a sustain cooperative strategy could facilitate an establishment of two opposite evolutionarily stable outcomes (McNamara et al., 2000): biparental care or mutual deception (Figure 3B). The last model suggest that cooperators could survive by forming clusters within which they interact more often with their own type and hence lowering the probability of meeting an opponent’s defection (Axelrod, 1984). In this sense, population division with the emergence of strict norms of reproductive practices (e.g. moral and marriage norms) should be seen as a plausible evolutionary consequence for any mating game where ‘reproductive defection’ represents the best response to any action by the opponent. Clusterization in groups of individuals which had adopted cooperative reproductive strategies could occur in geographically (Hauert, 2006) or even in religiously structured populations (Alexander, 1987), for instance, via imposing monogamy.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material: www.wolframcloud.com/obj/9930a448-532f-4551-8d08-9ce712cbea4e.

Author contributions

МB conceived of the presented original idea. OS and MB outlined the theoretical framework. AB developed the theory. AB performed the mathematical calculations. AB made numerical simulations and resulting phase portraits. All authors discussed the results. OS wrote the manuscript with confirmation from AB and MB. AB verified the analytical methods. All authors and approved the final version of this paper.

Funding

The article was prepared in the framework of a research grant funded by the Ministry of Science and Higher Education of the Russian Federation (grant ID: 075-15-2022-328).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alexander, R. D. (1987). The Biology of Moral Systems. Aldine de Gruyter, New York.

Google Scholar

Axelrod, R. (1984). The Evolution of Cooperation. Basic Books, New York.

Google Scholar

Darwin, C. (1871). The Descent of Man, and Selection in Relation to Sex. London: William Clowes and Sons, p. 456.

Google Scholar

Dawkins, R. (1978). The Selfish Gene. New York: Oxford University Press

Google Scholar

Dawkins, R., and Carlisle, T. R. (1976). Parental investment, mate desertion and a fallacy. Nature 262, 131–133. doi: 10.1038/262131a0

CrossRef Full Text | Google Scholar

Eisenberg, J. F., and Gould, E. (1970). The Tenrecs: A Study in Mammalian Behavior and Evolution. Washington, DC: Smithsonian Institution Press.

Google Scholar

Gavrilets, S. (2000). Rapid evolution of reproductive barriers driven by sexual conflict. Nature 403, 886–889. doi: 10.1038/35002564

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauert, C. (2006). Spatial effects in social dilemmas. J. Theor. Biol. 240, 627–636. doi: 10.1016/j.jtbi.2005.10.024

CrossRef Full Text | Google Scholar

Hrdy, S. B., and Hausfater, G. (1984). Comparative and Evolutionary Perspectives on Infanticide: Introduction and Overview. Infanticide: Comparative and Evolutionary Perspectives, pp. xiii-xxxv.

Google Scholar

Johnstone, R. A., and Hinde, C. A. (2006). Negotiation over offspring care–how should parents respond to each other's efforts? Behav. Ecol. 17, 818–827. doi: 10.1093/beheco/arl009

CrossRef Full Text | Google Scholar

Kaplan, H., Hill, K., Lancaster, J., and Hurtado, A. M. (2000). A theory of human life history evolution: diet, intelligence, and longevity. Evol. Anthropol. 9, 156–185. doi: 10.1002/1520-6505(2000)9:4<156::AID-EVAN5>3.0.CO;2-7

CrossRef Full Text | Google Scholar

Kokko, H., and Jennions, M. D. (2014). The relationship between sexual selection and sexual conflict. Cold Spring Harb. Perspect. Biol. 6:a017517. doi: 10.1101/cshperspect.a017517

PubMed Abstract | CrossRef Full Text | Google Scholar

Kokko, H., Klug, H., and Jennions, M. D. (2012). Unifying cornerstones of sexual selection: operational sex ratio, Bateman gradient and the scope for competitive investment. Ecol. Lett. 15, 1340–1351. doi: 10.1111/j.1461-0248.2012.01859.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lack, D. L. (1968). Ecological Adaptations for Breeding in Birds. London: Methuen, p. 409.

Google Scholar

Lehtonen, J., and Kokko, H. (2011). Two roads to two sexes: unifying gamete competition and gamete limitation in a single model of anisogamy evolution. Behav. Ecol. Sociobiol. 65, 445–459. doi: 10.1007/s00265-010-1116-8

CrossRef Full Text | Google Scholar

Lehtonen, J., Kokko, H., and Parker, G. A. (2016). What do isogamous organisms teach us about sex and the two sexes? Philos. Trans. R. Soc. B Biol. Sci. 371:20150532. doi: 10.1098/rstb.2015.0532

PubMed Abstract | CrossRef Full Text | Google Scholar

Lessells, C. K. M. (2006). The evolutionary outcome of sexual conflict. Philos. Trans. R. Soc. B Biol. Sci. 361, 301–317. doi: 10.1098/rstb.2005.1795

PubMed Abstract | CrossRef Full Text | Google Scholar

Marlowe, F. (2000). Paternal investment and the human mating system. Behav. Proc. 51, 45–61. doi: 10.1016/s0376-6357(00)00118-2

CrossRef Full Text | Google Scholar

Maynard Smith, J. M. (1982). Evolution and the Theory of Games. Cambridge: Cambridge University Press.

Google Scholar

Maynard Smith, J. M. (1984). Game theory and the evolution of behaviour. Behav. Brain Sci. 7, 95–101. doi: 10.1017/S0140525X00026327

CrossRef Full Text | Google Scholar

Maynard Smith, J. M., and Hofbauer, J. (1987). The “battle of the sexes”: a genetic model with limit cycle behavior. Theor. Popul. Biol. 32, 1–14. doi: 10.1016/0040-5809(87)90035-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Maynard Smith, J. M., and Price, G. R. (1973). The logic of animal conflict. Nature 246, 15–18. doi: 10.1038/246015a0

CrossRef Full Text | Google Scholar

McNamara, J. M., Houston, A. I., Barta, Z., and Osorno, J. L. (2003). Should young ever be better off with one parent than with two? Behav. Ecol. 14, 301–310. doi: 10.1093/beheco/14.3.301

CrossRef Full Text | Google Scholar

McNamara, J. M., Szekely, T., Webb, J. N., and Houston, A. I. (2000). A dynamic game-theoretic model of parental care. J. Theor. Biol. 205, 605–623. doi: 10.1006/jtbi.2000.2093

PubMed Abstract | CrossRef Full Text | Google Scholar

McNamara, J. M., and Weissing, F. J. (2010). “Evolutionary game theory” in Social Behaviour: Genes, Ecology and Evolution. eds. T. Székeley, A. J. Moore, and J. Komdeur (Cambridge: Cambridge University Press), 109–133.

Google Scholar

Morita, M., Ohtsuki, H., and Hiraiwa-Hasegawa, M. (2016). Does sexual conflict between mother and father Lead to fertility decline? Hum. Nat. 27, 201–219. doi: 10.1007/s12110-016-9254-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Nei, M. (2013). Mutation-Driven Evolution. Oxford: Oxford University Press.

Google Scholar

Parker, G. A., and Partridge, L. (1998). Sexual conflict and speciation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 353, 261–274. doi: 10.1098/rstb.1998.0208

PubMed Abstract | CrossRef Full Text | Google Scholar

Royle, N. J., Alonzo, S. H., and Moore, A. J. (2016). Co-evolution, conflict and complexity: what have we learned about the evolution of parental care behaviours? Curr. Opin. Behav. Sci. 12, 30–36. doi: 10.1016/j.cobeha.2016.08.004

CrossRef Full Text | Google Scholar

Salthe, S. N., and Mecham, J. S. (1974). Reproductive and courtship patterns. Physiol. Amphib. 2, 309–521. doi: 10.1016/B978-0-12-455402-3.50010-3

CrossRef Full Text | Google Scholar

Schuster, P., and Sigmund, K. (1981). Coyness, philandering and stable strategies. Anim. Behav. 29, 186–192. doi: 10.1016/S0003-3472(81)80165-0

CrossRef Full Text | Google Scholar

Semenova, O. V., and Butovskaya, M. L. (2021). Theoretical reproductive outcomes of the sexual conflict in humans. Dokl. Biol. Sci. 500, 138–144. doi: 10.1134/S0012496621050094

CrossRef Full Text | Google Scholar

Trivers, R. L., and Campbell, B. (1972). Sexual Selection and the Descent of Man. Chicago: Aldine.

Google Scholar