Elastic Wave Control Beyond Band-Gaps: Shaping the Flow of Waves in Plates and Half-Spaces with Subwavelength Resonant Rods

In metamaterial science, local resonance and hybridization are key phenomena strongly influencing the dispersion properties; the metasurface discussed in this article created by a cluster of resonators, subwavelength rods, atop an elastic surface being an exemplar with these features. On this metasurface, band-gaps, slow or fast waves, negative refraction, and dynamic anisotropy can all be observed by exploring frequencies and wavenumbers from the Floquet–Bloch problem and by using the Brillouin zone. These extreme characteristics, when appropriately engineered, can be used to design and control the propagation of elastic waves along the metasurface. For the exemplar we consider, two parameters are easily tuned: rod height and cluster periodicity. The height is directly related to the band-gap frequency and, hence, to the slow and fast waves, while the periodicity is related to the appearance of dynamic anisotropy. Playing with these two parameters generates a gallery of metasurface designs to control the propagation of both flexural waves in plates and surface Rayleigh waves for half-spaces. Scalability with respect to the frequency and wavelength of the governing physical laws allows the application of these concepts in very different fields and over a wide range of lengthscales.

1. Introduction

Recent years have witnessed the increasing popularity of metamaterial concepts, based on the so-called local resonance phenomenon, to control the propagation of electromagnetic (Pendry et al., 1999; Smith et al., 2004b; Ramakrishna and Grzegorczyk, 2008; Werner, 2016), acoustic, and elastic (Liu et al., 2000; Craster and Guenneau, 2012) waves in artificially engineered media. Initially, attention focused on the existence of subwavelength band-gaps generated by the resonators (Pendry et al., 1998; Movchan and Guenneau, 2004; Achaoui et al., 2011; Lemoult et al., 2011; Colombi et al., 2014), and resulting frequency-dependent effective material parameters for negative refraction and focusing effects (Pendry, 2000; Smith et al., 2000; Yang et al., 2002; Li and Chan, 2004), and now consideration is transitioning to methods for achieving more complete forms of wave control by encompassing tailored graded designs to obtain spatially varying refraction index (Pendry et al., 2006), wide band-gaps and mode conversion. In the fields of photonics and acoustics, this transition has already taken place and new graded designs allow for the tailored control of the propagation of light (Kadic et al., 2011; Maradudin, 2011), micro-waves (Schurig et al., 2006), water waves (Farhat et al., 2008), and sound (Cummer and Schurig, 2007; Zhang et al., 2011; Romero-Garcia et al., 2013; Chen et al., 2014). Elastodynamic media have, in contrast to acoustic and electromagnetic systems, additional complexity such as supporting both compressional and shear wave speeds that differ and which mode converts at interfaces (Craster and Guenneau, 2012). On the one hand, this makes elastic metamaterials complex to model and require the use of computational elastodynamic techniques (Colombi et al., 2016b), on the other hand, it offers new control possibilities not achievable in the electromagnetic or acoustic cases. Wave control has implications in several disciplines and the discoveries of metasurface science are currently being translated into several applications. If we limit our discussion to elastic metamaterials, potential applications could be implemented at any lengthscale. On the large scale, seismic metamaterials have become very popular (Brûlé et al., 2014; Finocchio et al., 2014; Dertimanis et al., 2016; Miniaci et al., 2016; Achaoui et al., 2017). At smaller scale, in mechanical engineering, applications based on wave redirection and protection are currently being explored (Colombi, 2016; Colombi et al., 2017) to reduce vibrations in high precision manufacturing and in laboratories for high precision measurements (e.g., interferometry) or in the field of ultrasonic sensing to amplify signal to noise ratio. In the field of acoustic imaging, the tailored control of hypersound (elastic waves at GHz frequencies), used for cell or other nano-compound imaging or energy conversion and harvesting (Davis and Hussein, 2014; Della Picca et al., 2016), is emerging as one of the most promising applications of energy trapping and signal enhancement through metamaterials. Furthermore, at this small scale, novel nanofabrication techniques deliver the tailoring possibilities required for graded devices (e.g., Alonso-Redondo et al., 2015; Rey et al., 2016).

Among the possible resonant metasurface designs for elastic waves proposed in recent years (e.g., Baravelli and Ruzzene, 2013; Miniaci et al., 2015; Lee et al., 2016; Matlack et al., 2016; Galich et al., 2017; Tallarico et al., 2017), the one made of a cluster of rods (the resonators) (Pennec et al., 2008; Wu et al., 2008; Achaoui et al., 2011; Colombi et al., 2016c) on an elastic substrate has revealed superior characteristics and versatility of use in particular toward the fabrication of graded design. The physics of this metasurface is well described through a Fano-like resonance (Miroshnichenko et al., 2010). A single rod attached to an elastic surface couples with the motion of both the A₀ mode in a plate or the Rayleigh wave on a thick elastic substrate (half-space). This coupling is particularly strong at the longitudinal resonance frequencies of the rod. At this point, the eigenvalues of the equation describing the motion of the substrate and the rod are perturbed by the resonance and become complex leading to the formation of a band-gap (Landau and Lifshitz, 1965; Perkins and Mote, 1986). When the resonators are arranged on a subwavelength cluster (i.e., with λ, the wavelength ≫ than the resonator spacing), as in the metasurface discussed here, the resonance of each rod acts constructively enlarging the band-gap until, approximately, the rod’s anti-resonance (Rupin et al., 2014; Colombi et al., 2016c). Thus, the resulting band-gap is broad and subwavelength. Because the resonance frequency of the rod drives the band-gap position, a spatially graded metasurface is simply obtained by varying the length of the rods, which directly underpins the resonance frequency. Thus, the length of the rod appears to be the key parameter for the metasurface tunability, although the periodicity and distribution of the rods cannot be ignored as they also influence the dispersion curves leading to zone characterized by dynamic anisotropy and negative refraction (Kaina et al., 2015). These effects are important as they may be used to generate highly collimated waves or for subwavelength imaging. Our purpose in this work is to complement the research on local resonance and slow and fast waves, with the study of the dynamic anisotropy effect (Colquitt et al., 2011) when the rods are periodically arranged on the elastic surface.

In fact, it has been recently realized that many novel features of hyperbolic metamaterials such as superlensing and enhanced spontaneous emission (Poddubny et al., 2013) could be achieved thanks to dynamic anisotropy in photonic (Ceresoli et al., 2016) and phononic crystals (Colquitt et al., 2011; Antonakakis et al., 2014b). For instance, the high-frequency homogenization theory (Craster et al., 2010) establishes a correspondence between anomalous features of dispersion curves on band diagrams with effective tensors in governing wave equations: flat band and inflection (or saddle) points lead to extremely anisotropic and indefinite effective tensors, respectively, that change the nature of the wave equations (elliptic partial differential equations can turn parabolic or hyperbolic depending upon effective tensors). This makes analysis of dynamic anisotropy a potentially impactful work.

The first half of the article is dedicated to the review of the state of the art on the control of flexural and Rayleigh waves with rods on an elastic substrate. This part will collect the major achievements and milestones obtained by our research group in the past 3 years. In the second part, we will present another characteristic of this metasurface analyzing the 2D dispersion curves and the effect of dynamic anisotropy in the subwavelength regime. The results (Figures 1 and 2) are presented using state of the art 2D or 3D time domain spectral element simulations (SPECFEM2D/3D, for an extensive introduction (Komatitsch and Martin, 2007; Peter et al., 2011; Rietmann et al., 2012)), while dispersion curves have been computed analytically for 1D cells (Figure 1), or via COMSOL Multiphysics for 2D elementary cells (Figures 3 and 4).

FIGURE 1

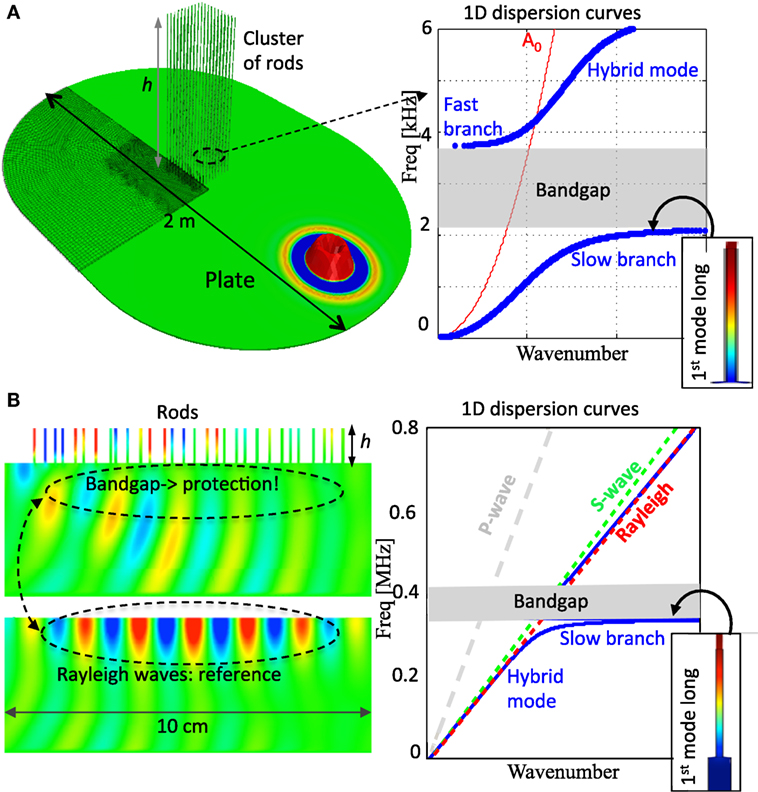
Figure 1. (A) The metamaterial discussed in this article is made of a plate and a cluster of closely spaced rods in the same material. It is characterized by a hybrid dispersion curve (blue line), very different from the A₀ mode (red line) that propagates in a reference pristine plate excited by a vertical force. The plate and the rods are made of aluminum. The inset shows the fundamental longitudinal mode shape that generates the hybrid curve and the band-gap (shaded region). In this formulation, flexural modes are neglected and the colorcode represents the vertical displacement. (B) Same as (A) but for the second type of metamaterial discussed here: a 2D elastic half-space where rods are attached to the top surface creating a band-gap for Rayleigh waves. Contrarily to the plate case, the reference half-space is characterized by non-dispersive Rayleigh (red), S-wave (green), and P-wave (gray) dispersion curves.

FIGURE 2

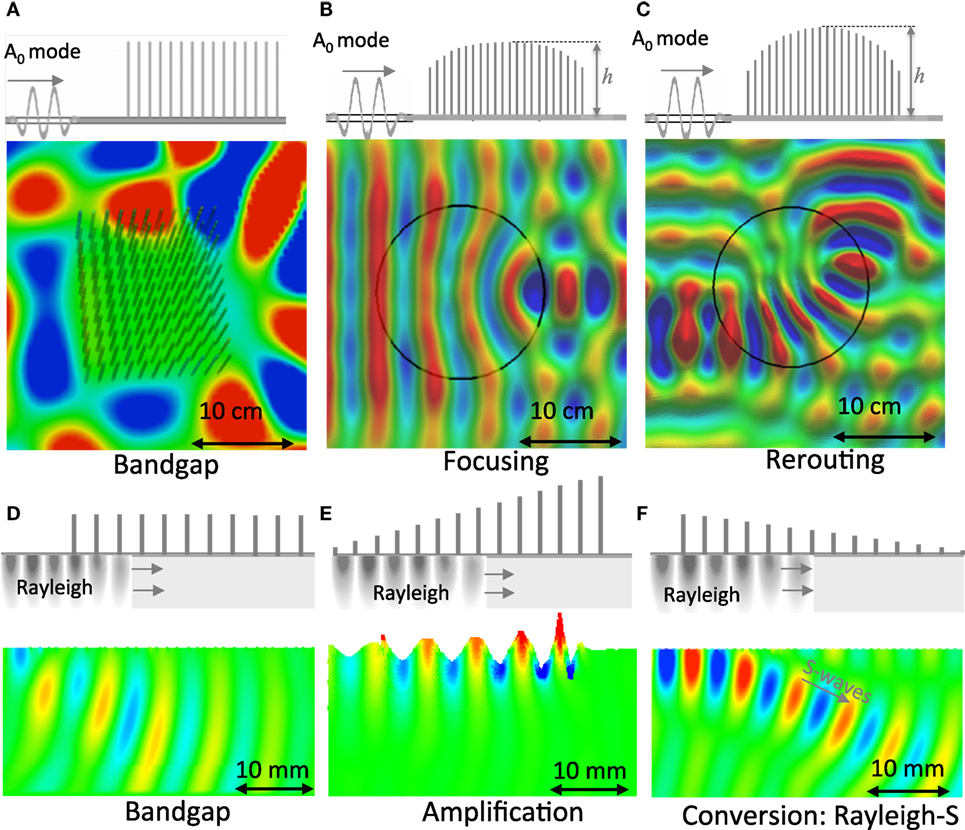
Figure 2. Examples of control achieved through this resonant metamaterial for different types of waves (Flexural or Rayleigh) and lengthscale. Colorcode represents the vertical displacement calculated from time domain numerical simulations. (A) Band-gaps can stop the propagation of flexural and Rayleigh waves leaving desired regions free of vibrations. (B,C) Elastic energy can be guided or focused with gradient index lenses. (D) Rayleigh wave band-gap created by the constant height resonators. (E) Waves can be spatially segregated depending on the frequency and strongly amplified. (F) Rayleigh waves can be converted to S-waves and redirected in the bulk. The aspect ratio of the rods and the height gradient are not in scale to better present the concept.

FIGURE 3

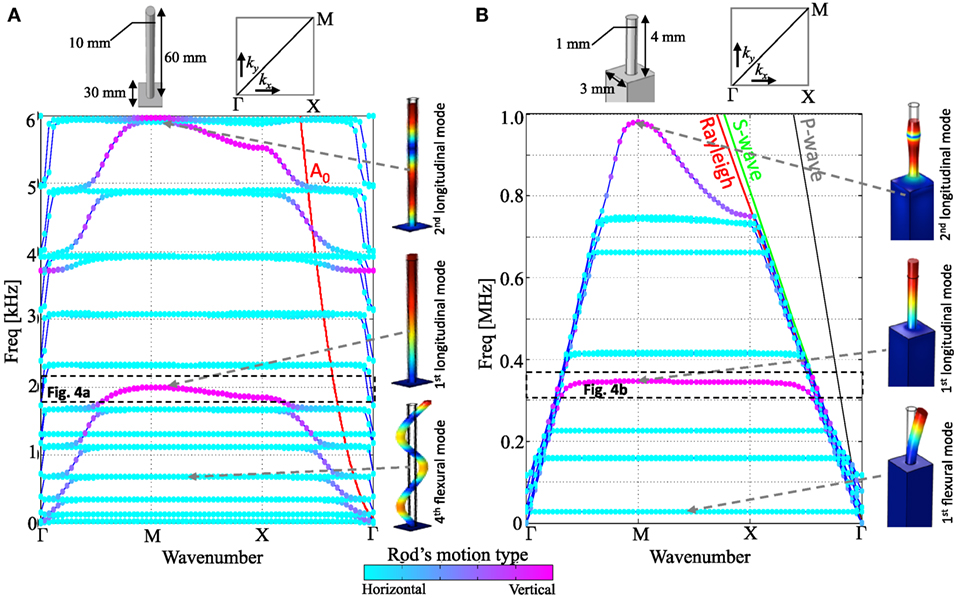
Figure 3. (A) Complete dispersion curves for an infinitely periodic 2D layout of rods on an elastic plate. The size of the unit-cell and the irreducible Brillouin zone (Γ − M − X − Γ) is given at the top. The colorcode superimposed on the dispersion curves represents the motion polarization of the rod. The bare-plate reference A₀ has been relocated in the same crystallographic direction as Figure 1A. Snapshots from frequency domain numerical simulation clarify the modal deformation associated with each resonance. (B) Same as (A) but for the half-space. Here, the propagative zone is bounded by the S-wave (green) maximum velocity (analogous of the so-called light-line in plasmonics).

FIGURE 4

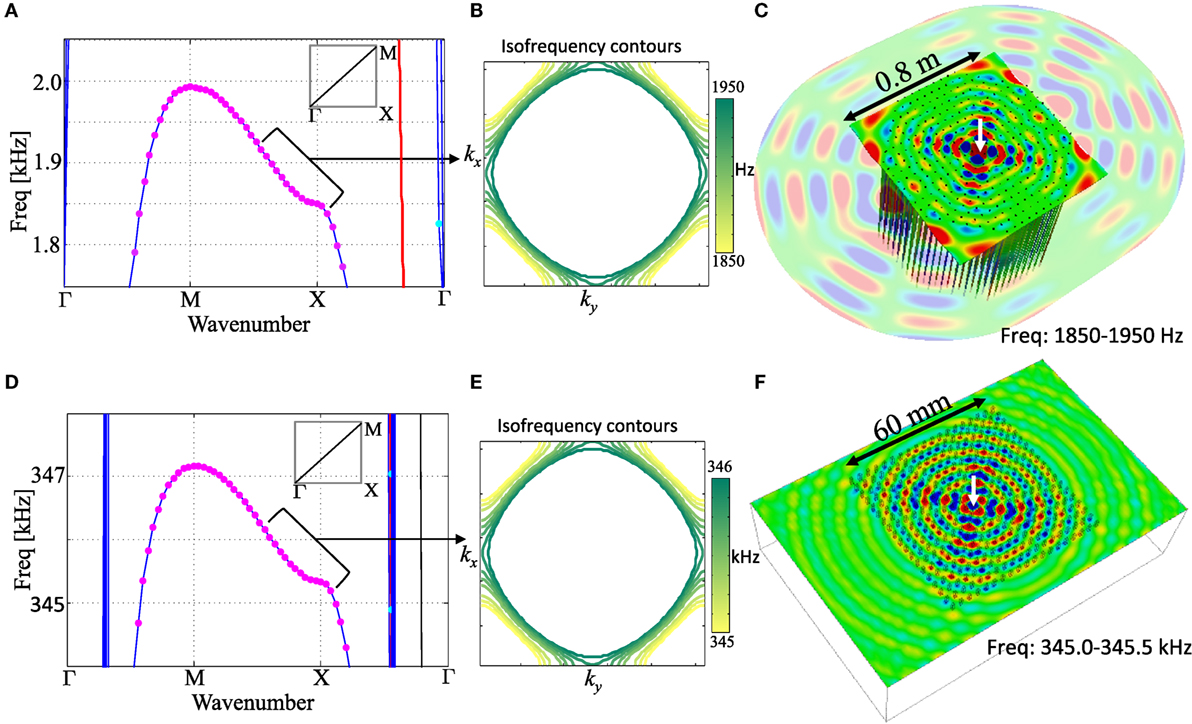
Figure 4. (A) A zoomed section around the first longitudinal resonance of the dispersion curves in Figure 3A reveals the strong dynamic anisotropy of this region. (B) The isofrequency contours in the k_y = (− π/d, π/d) and k_y = (− π/d, π/d) space show the hyperbolic behavior of the system around the inflection point. (C) Snapshot taken from a time domain numerical simulation with the source located at the center of a cluster of rods. The field has been filtered in the band point by the arrow in the dispersion curve plot. The colorscale represents the vertical component of the displacement field. To ease the visualization of the anisotropic pattern, the plate is represented from the backside and a transparency filter is applied outside the metamaterial to show both the rods and the field in the bare plate. (D–F) Same as (A–C) but for the rods cluster on a half-space. In this case, we only show the vertical displacement field on the top surface. While the actual shape and dimension of the numerical model is sketched with thin black lines.

2. Early Results: Plate vs. Infinite Half-Space Metamaterial

We start by recalling results obtained with a metamaterial, introduced in 2014, made from a thin elastic plate and a cluster of closely spaced resonators (see model in Figure 1A) both made of aluminum. At that time, despite the limited knowledge of the metasurface dispersion properties, the cluster of resonators immediately showed surprising phenomena such as the presence, in the Fourier spectra, of large subwavelength band-gaps (Rupin et al., 2014) affecting the propagation of the A₀ mode in the thin plate in the kHz range. Around the same time, Colombi et al. (2014) demonstrated that by exploiting the stop band, waves can be trapped in a very subwavelength cavity and that energy could be tunneled through the metasurface by inserting a defect, with an approach reminiscent of phononic crystal applications. These early attempts to compute the dispersion curves of the metasurface for a given rod size and spacing were based on array methods that projected the time series recorded from either experiment or numerical simulation on the frequency wavenumber plane (f − k plane). These preliminary results confirmed the resonant nature of the band-gap and uncovered another striking characteristic of the metamaterial: the nearly flat branches occurring at edges of the Brillouin zone before and after the band-gap. These flat branches represent, for high wavenumbers, very slow modes. Conversely for k approaching the origin, these modes travel very fast. The analytical calculation of the dispersion properties by Williams et al. (2015) (e.g., the plot in Figure 1A), means we can now fully harness the power of this metasurface and use the concept of fast and slow modes to fully control the propagation of waves in a plate (Colombi, 2016). For completeness, we report that similar dispersion curves could be computed using the plate with sprung masses developed in Xiao et al. (2012) and Torrent et al. (2013). Before showing the effects of the tailored wave control, we continue our digression into the important applications of elastic resonators on an elastic surface. It has been known since Khelif et al. (2012) that short pillars (or other type of resonators (Boechler et al., 2013)) on an elastic half-space can alter the dispersion curves by introducing Bragg and resonant band-gaps for Rayleigh waves. However, the use of longitudinally elongated resonators, such as the rods shown in Figure 1B, allow for a much clearer separation of the longitudinal mode (responsible for the band-gap) from other flexural resonances that will be discussed in the last section of this article. This has the twofold advantage of pushing the band-gap to the subwavelength scale, simultaneously increasing its breadth, and also simplifying the analytical description of the metamaterial. From an analytical point of view, the thin elastic plate metasurface can still be treated as a scalar problem as one can use Kirchhoff’s plate theory coupled with a longitudinal wave equation for the rod. In an elastic half-space, this is no longer possible and the full elastic equation must be used to describe its physics. With this concept in mind, Colquitt et al. (2017) constructed an analytical formulation for the dispersion curve of a 1D array of resonators on the half-space considering only the longitudinal modes of the rods. From visual inspection of the plot in Figure 1B, besides the obvious lack of dispersion for body and Rayleigh waves in the half-space (by contrast, the A₀ mode in Figure 1A is strongly dispersive) and the different frequency and size of the model (meters and kHz for the plate and centimeters and MHz for the half-space), a similar hybridization mechanism (Miroshnichenko et al., 2010) creates the band-gap in both systems. However, in the half-space, the maximum speed of the system is bounded by the shear S-wave line. These observations are consistent with the physical interpretation that the vertical component of the elliptically polarized Rayleigh waves, usually traveling slower than the shear wave, couples with the longitudinal motion of the resonator. The presence of these band-gaps have inspired the development of seismic metamaterials for Rayleigh waves (Colombi et al., 2016c) where the close relationship between shear S- and Rayleigh waves in the half-space lead to unexpected wave phenomena in the metamaterial. As chiefly demonstrated in Colombi et al. (2016a) and Colquitt et al. (2017), the resonance creates a hybrid branch bridging the Rayleigh line with the S-wave line. Through a graded resonators design (e.g., decreasing or increasing rod’s height), the conversion becomes ultra-broadband, a key requirement for practical engineering applications.

3. Gallery of Control Possibilities Achieved by Tuning the Rod Length

The rich physics encoded within the hybrid dispersion curves that we have just described for the plate and half-space cases can be translated into extraordinary wave propagation phenomena. Furthermore, scalability is one of the strong characteristics of metamaterials which makes them applicable in different wave realms and lengthscales. With the following examples, we demonstrate that applications for the two different settings and lengthscale introduced in Figures 1A,B, namely the elastic plate and the half-space. This choice is made to remain coherent with our previous laboratory and numerical studies on these structures (Rupin et al., 2014; Colombi et al., 2017). The description starts from Figure 2A, snapshots extracted from a numerical simulation (Colombi et al., 2014) show the band-gap created by a small cluster of resonators located on top of a thin elastic plate. The field has been filtered inside the band-gap at a frequency between 2 and 3 kHz (6-mm-thick plate and 60-cm-long rods, both made of aluminum). The band-gap frequency f directly depends on the resonator length h and, therefore, can be easily tuned by selecting longer or shorter rods using the well known formula:

$f=\frac{1}{4h}\sqrt{\frac{E}{\rho }},$ (1)

where E its Young’s modulus and ρ its density. This formula is valid when the substrate is sufficiently stiff, for seismic metamaterials, where the resonator might be supported by a soft sediment layer, the contribution of the substrate must be taken into account when calculating the resonance frequency (Colombi et al., 2016c).

In Figures 2B,C, we exploit the effective wave velocity (slow waves) that is locally achieved in the metamaterial. In these figures, we show two types of the so-called graded index lenses (Sarbort and Tyc, 2012) well known for their capacity to focus and re-route waves without aberration and reflection. These lenses are characterized by a radially varying velocity profile decreasing from the outside to the inside. By considering 4-kHz flexural waves, h varies approximately between 60 and 80 cm while in Figure 2B while between 60 and 90 cm for the case in Figure 2C (full details as well as refraction, velocity, and height profiles for these and other lenses are available in Colombi (2016)). In practice, such a material is very difficult to fabricate unless one uses layers of different material (Torrent et al., 2014) or a graded thickness profile for the plate case (Dubois et al., 2013; Climente et al., 2014). For the half-space, this is clearly not possible. By using the slow modes of the flat branch occurring before the band-gap (see dispersion curves in Figures 1A,B), these velocity gradients can be achieved by tailoring the resonator height distribution to the velocity profile required by the lens. This step is better achieved using the analytical form of the dispersion curve as shown in Colombi (2016) derived using the theory from Williams et al. (2015). Although only the results for the plate have been currently published (Colombi, 2016), the same method can be applied to Rayleigh waves too with the theory developed by Colquitt et al. (2017).

In the remaining three figures, the description moves to the control of Rayleigh waves. Unlike the plate case where the physics can be captured in the plane, here it is important to describe the whole wavefield inside the half-space. For this reason, 2D simulations in the P − SV plane (plane strain) are now shown. Technical details on how these simulations have been implemented can be found in previous studies (Peter et al., 2011; Colombi et al., 2015, 2016a). As already anticipated in Figure 1B, the first snapshot shows the band-gap (here the field is filtered between 0.35 and 0.4 MHz) produced by an array of resonators of constant height. In Figure 2E, we show the well-known phenomena of rainbow trapping (Tsakmakidis et al., 2007; Romero-Garcia et al., 2013; Zhu et al., 2013) for elastic waves (Colombi et al., 2016a). The combined graded and resonant structure allows the incoming Rayleigh waves to be slowed down selectively at different propagation distances inside the metasurface, and eventually to be trapped in a subwavelength area. The trapping process culminates with a strong signal amplification followed by a reflection (in a lossless media) (Colombi et al., 2017). As for the lens case, this effect is completely due to the slow branch occurring below the band-gap. The graded array of resonators (resonant metawedge) enhances this effect and makes this device completely broadband (inversely proportional to the height). Note that, compared to the band-gap described in Figure 2D, here the Rayleigh wave remains confined to the surface while a broadband band-gap is produced after the wedge; for clarity of presentation, we have used a monochromatic source of Rayleigh waves at 0.5 MHz (Colquitt et al., 2017). When the wedge orientation is reversed, as in Figure 2F, the surprising phenomenon of modal conversion is obtained and the graded profile enhances the conversion on a large frequency band; in the previous section, this was already anticipated from the analysis of the dispersion curves. An alternative but straightforward description of trapping and conversion can be derived by plotting the dispersion curves as a function of the resonator length versus frequency as demonstrated in Colombi et al. (2016a). The control possibilities emerging from this discussion suggest tremendous potential for applications of these metamaterials toward vibration reduction and enhanced sensing. In this section, we have not specified yet whether these phenomena depend, or not, on the periodicity of the resonator distribution in the metamaterial. Because local resonance is at the origin of the effects presented, so far the answer is no for all of them. However, in the next section, we will explore the important implications of periodicity.

4. Periodicity, Dynamic Anisotropy, and Hyperbolic Behavior

The height of the rods is not the only parameter available in terms of design of the metasurface. Solid-state physics informs us that the lattice periodicity and spacing also matter as that generates, in particular, Bragg-type scattering. Dynamic anisotropy, which is anisotropy observed in the wavefield, which changes as frequency varies, is a common feature in phononic crystals with the most extreme situation being that where the wave energy is confined to “rays” with the field taking a cross-like form. Despite this, it has only marginally been associated with subwavelength metamaterials (Kaina et al., 2015; Maznev et al., 2015) with most work carried out in the context of phononic crystals. This section explores how anisotropy is obtained with this metasurface design. We introduce in Figures 3A,B the dispersion curves for a 2D array of resonators, respectively, on a plate and on an infinite elastic support (half-space). The analysis is carried out inside the well-known irreducible Brillouin zone defined on the wavevector plane k = (k_x, K_y) by the three points of coordinates: Γ = (0, 0), M = (π/d, π/d), and X = (π/d, 0) where d is the pitch of the array of resonators. Given the complexity of the 3D problem, the model is solved numerically and includes all the admissible modes of the unit cell, not only, as previously done, the elongation of the rods. The resulting dispersion curves are characterized by several resonances that make it hard to distinguish the longitudinal one. To aid interpretation we plot, along with the curve, the ratio between the vertical value and the longitudinal value of the eigenfunction measured at the top of the resonator (where for all modes, the displacement reach a maximum (Ewins, 2000)). High values mean that the motion is vertically polarized, conversely low value means that motion is horizontal; this interpretation is further confirmed associating with each resonance its modal deformation.

The size of the unit cell in Figure 3A is chosen to be similar to the cluster configuration in our previous work (Colombi et al., 2014; Rupin et al., 2014), where we have used a 6 mm plate and 60 cm rods both made of aluminum. The eigenvalue analysis is done using COMSOL and we make use of the built-in Bloch–Floquet boundary conditions to mimic an infinite 2D array of rods that are 3-cm-spaced. The bare plate dispersion curve is shown in red for the Γ-X direction that is equal to the configuration in Figure 1A (although without flexural resonances). Thanks to the colorcode used, the longitudinal modes are clearly identified in the dispersion curves. Given the lattice size, the first longitudinal mode is very subwavelength ~λ/8. While the zoomed detail around this resonance is shown in Figure 4, we can already distinguish the change in curvature that is responsible for the dynamic anisotropy behavior. The other flat branches are mainly flexural modes (except for some breathing mode of the resonator). These are all double modes because the resonator is free to move in both directions. In Figure 3B, we repeat the same analysis for the half-space. The dimensions of the unit cell are similar to those for the plate although the spacing is slightly larger to improve the visualization of the anisotropy in Figure 4B. A technical detail is that, to mimic the infinite character of the half-space, we have applied an absorbing boundary at the lower side of the computational cell (see COMSOL Structural Mechanics Module documentation). The physics of the wave propagation in the half-space differs from the plate case mainly because of the lack of dispersion (see the straight dispersion curves for the bare half-space) and the higher speed of the waves. In this configuration however, the longitudinal resonance is only slightly subwavelength ~λ/3. Clearly, by using a longer resonator, the band-gap can be pushed to a much lower frequency but the curvature of the longitudinal resonance is then shrunk down to a fraction of the Hertz, making the visualization of the anisotropy practically impossible as the effect is so sensitive that small numerical or manufacturing variations would spoil the expected result.

We now focus on the anisotropic behavior by zooming in to frequencies close to the longitudinal modes. A detailed view of the first mode of the plate is depicted in Figure 4A. We can clearly appreciate the slope change that occurs before the resonance. A spectral element simulation in the time domain shows a snapshot of the wavefield filtered around the inflection point of the mode. An array of 20 × 20 resonators, spaced and sized according to Figure 3A, is placed at the center of the plate. Because the plate boundaries are reflecting, to improve the visualization despite the reverberations, we have smoothed the square array removing the corner. The cluster is in fact octagonal. The shape and size of the plate are identical to the one used in Rupin et al. (2014), so this phenomenon could be easily verified experimentally. The source is located in the middle of the array and, in our case, it is broadband Gaussian pulse. The cross-shaped anisotropic profile, as well as the strong contrast between the wavelength inside and outside the plate, is clearly visible, and reminiscent of wave patterns in negatively refracting and hyperbolic metamaterials.

Using the same modeling technique, dynamic anisotropy also characterizes the half-space and it is indeed visible in the numerical results of Figure 4B. The half-space is simulated applying perfectly matched layers on the side and on the bottom surface. The snapshot show the vertical component of the displacement filtered at the inflection point. As for the case of the plate, a similar cross is visible. However, here we observe a strong spatial attenuation of the field due to the fact that waves are free to propagate or scatter downward, while in the plate they were guided (e.g., Figure 2D).

At this stage, we note that there is a vast literature on electromagnetic hyperbolic metamaterials, which were theorized by David Smith and David Schurig almost 15 years ago in the context of negatively refracting media described by electric permittivity and magnetic permeability tensors with eigenvalues of opposite signs (Smith and Schurig, 2003; Smith et al., 2004a). These media originally thought of as an anisotropic extension of John Pendry’s perfect lens (Pendry, 2000; Luo et al., 2002) take their name from the topology of the isofrequency surface. In an isotropic homogeneous medium (e.g., vacuum in electromagnetics and air in acoustics), the linear dispersion and isotropic behavior of transversely propagating (electromagnetic or sound) waves implies a circular isofrequency contour given by the dispersion equation $k_x^2+k_y^2={\omega }^2/c^2$ with k = (k_x, k_y) the wavevector, ω the angular wave frequency, and c the wavespeed of light or sound waves. In a transversely anisotropic effective medium, one has $T_{yy}{k}_x^2+T_{xx}{k}_y^2={\omega }^2/c^2$, where T_xx and T_yy are entries of the (inverse of) effective tensor of permittivity or mass density, shear or Young’s moduli, etc. depending on the wave equation. It is well known that the circular isofrequency contour of vacuum distorts to an ellipse for the anisotropic case. However, when we have extreme anisotropy such that T_xxT_yy < 0 the isofrequency contour opens into an open hyperbole. In electromagnetics, such a phenomenon requires the metamaterial to behave like a metal in one direction (along which waves are evanescent) and a dielectric in the other and similarly, in acoustics and platonics. A hallmark of hyperbolic media is an X-shape wave pattern for emission of a source located therein (Poddubny et al., 2013), reminiscent of the hyperboles arising from the dispersion relations. Note, of course, that if both entries of the effective tensor are negative, this means that waves are evanescent in all directions, what corresponds to a metal in electromagnetics.

In the case of structured Kirchhoff–Love plates, one can apply the method of high-frequency homogenization in the vicinity of the inflection point indicated in Figure 4A to obtain a homogenized partial differential equation describing the effective behavior of the plate in the neighborhood of such resonances. Remarkably, although the governing equation for Kirchhoff–Love plates involves the fourth-order biharmonic operator (Graff, 1975), it was shown in Antonakakis and Craster (2012) and Antonakakis et al. (2014b) that the effective partial differential equation describing the long-scale behavior of the structured plate near such resonances is of the form $T_{yy}{k}_x^2+T_{xx}{k}_y^2={\omega }^2/c^2$, where T_xxT_yy < 0. The fact that the effective rigidity tensor is diagonal and negative-definite results in the structured plate being strongly anisotropic in the dynamic regime and Lamb waves propagate through the plate as if propagating in a hyperbolic medium, as discussed above.

Even more remarkably, for the case of linear elasticity, it was shown in Antonakakis et al. (2014a) that one can use the method of high-frequency homogenization to obtain effective partial differential equations of precisely the same form as above for Kirchhoff–Love plates; this, together with the fact that similar features exist in Figure 4B, corresponding to an inflection point on the dispersion curves for Rayleigh waves propagating on structured half-spaces, suggests that analogous effects may be obtained for surface waves traveling over suitably structured elastic half-spaces.

5. Future Perspectives

Devices based on exploiting band-gap phenomena, as seismic shields using ideas from Bragg-scattering (Brûlé et al., 2014; Miniaci et al., 2016) or zero-frequency stop-bands (Achaoui et al., 2017), are gaining in popularity. At this large scale, an important analogy may exist between the metamaterial discussed here and clusters of high-rise buildings in urban areas. During an earthquake, the combined effects of building–soil interactions (Wong and Trifunac, 1975) and site–city effects (Guéguen et al., 2002) may lead to buildings acting as local resonators spatially modifying the distribution of the ground motion intensity. Given the nuisance of ground vibration, and the importance of elastic wave control, for the urban environment, this will be an area of growing importance; the additional degrees of freedom, control over sub-wavelength behavior, and the broadband features that can be utilized using the resonant sub-wavelength structures discussed herein make them very attractive alternatives. At smaller scale, one moves toward the manipulation of mechanical waves in vibrating structures, again it is the long wave and low-frequency waves that one often wants to control and, again, these are precisely the waves that are targeted by sub-wavelength resonator array devices. The ability to spatially segregate waves by frequency, the field enhancement, and potential to mode convert surface to bulk waves, Figures 2D–F, are all phenomena with practical importance. Similarly, the ability to control surface waves to create concentrators and surface lenses, and the ability to redirect waves, using sub-wavelength arrays, Figures 2A–C, are powerful examples to draw upon for devices. The combined features of a flat band and a change of curvature near the inflection point in Figure 4 mean that we are in a position to achieve effective parameters with eigenvalues of opposite sign exhibiting very different absolute values. So one can imagine controlling Rayleigh waves that would undergo simultaneously positive and negative refraction on the subwavelength scale, and this could lead to cloaking devices analogous to hyperbolic cloaks in electromagnetics (Kim et al., 2015). At the geophysics scale, applications of hyperbolic cloaks for Rayleigh waves are in seismic protection. It has been also suggested that one can achieve black hole effects (Krylov, 2014) in hyperbolic metamaterials (Smolyaninov et al., 2012), and this would have interesting applications in energy harvesting for Rayleigh waves propagating through arrays of rods at critical frequencies. Regardless of the application, these advanced control concepts exploiting slow waves will be better studied also considering losses and non-linearity in the propagation (e.g., Krushynska et al., 2016; Schwan et al., 2017).

Given the relative youth of metamaterials, as a field, and the very recent translation of metamaterial concepts to elastic plate, and elastic bulk, media, there are undoubtedly many phenomena that will translate across from the more mature optical metamaterial field. Metasurfaces have become popular in optics as they can be created to combine the vision of sub-wavelength wave manipulation, with the design, fabrication, and size advantages associated with surface excitation. These powerful concepts, and the degree of control available, are driving progress in optics toward flat optical lenses and devices (Yu and Capasso, 2014); the elastic analogs of these optical metasurfaces are those we describe here and we anticipate similar progress in the design of mechanical devices.

Author Contributions

AC initiated the project, carried out the numerical studies, and created the figures. DC helped with the analytical part of the study. RC, YA, and SG helped with the isofrequency and dynamic anisotropy study. PR and MR carried out the initial laboratory experiment on the plate laying out the milestone for this study. AC, RC, and SG wrote the article. All authors contributed to the editing of the article.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

All of the computations presented in this paper were performed using the Froggy platform of the CIMENT infrastructure (https://ciment.ujf-grenoble.fr), supported by the Rhone-Alpes region (GRANT CPER07_13 CIRA), the OSUG2020 labex (reference ANR10 LABX56) and the EquipMeso project (reference ANR-10-EQPX-29-01) of the programme Investissements d’Avenir supervised by the Agence Nationale pour la Recherche. AC and RC thanks the EPSRC for their support through research grant EP/L024926/1. AC was supported by the Marie Curie Fellowship “Metacloak.” AC, PR, SG, and RC acknowledge the support of the French project Metaforet (reference ANR) that facilitates the collaboration between Imperial College, ISTerre and Institut Fresnel.

References

Achaoui, Y., Antonakakis, T., Brule, S., Craster, R., Enoch, S., and Guenneau, S. (2017). Clamped seismic metamaterials: ultra-low frequency stop bands. New J. Phys. 19, 063022. doi: 10.1088/1367-2630/aa6e21

CrossRef Full Text | Google Scholar

Achaoui, Y., Khelif, A., Benchabane, S., Robert, L., and Laude, V. (2011). Experimental observation of locally-resonant and bragg band gaps for surface guided waves in a phononic crystal of pillars. Phys. Rev. B 83, 10401. doi:10.1103/PhysRevB.83.104201

CrossRef Full Text | Google Scholar

Alonso-Redondo, E., Schmitt, M., Urbach, Z., Hui, C. M., Sainidou, R., Rembert, P., et al. (2015). A new class of tunable hypersonic phononic crystals based on polymer-tethered colloids. Nat. Commun. 6, 8039. doi:10.1038/ncomms9309

PubMed Abstract | CrossRef Full Text | Google Scholar

Antonakakis, T., and Craster, R. (2012). High-frequency asymptotics for microstructured thin elastic plates and platonics. Proc. R. Soc. A 468, 1408–1427. doi:10.1098/rspa.2011.0652

CrossRef Full Text | Google Scholar

Antonakakis, T., Craster, R., and Guenneau, S. (2014a). Homogenisation for elastic photonic crystals and dynamic anisotropy. J. Mech. Phys. Solids 71, 84–96. doi:10.1016/j.jmps.2014.06.006

CrossRef Full Text | Google Scholar

Antonakakis, T., Craster, R. V., and Guenneau, S. (2014b). Moulding and shielding flexural waves in elastic plates. Eur. Phys. Lett. 105, 54004. doi:10.1209/0295-5075/105/54004

CrossRef Full Text | Google Scholar

Baravelli, E., and Ruzzene, M. (2013). Internally resonating lattices for bandgap generation and low-frequency vibration control. J. Sound Vib. 332, 6562–6579. doi:10.1016/j.jsv.2013.08.014

CrossRef Full Text | Google Scholar

Boechler, N., Eliason, J. K., Kumar, A., Maznev, A. A., Nelson, K. A., and Fang, N. (2013). Interaction of a contact resonance of microspheres with surface acoustic waves. Phys. Rev. Lett. 111, 036103. doi:10.1103/PhysRevLett.111.036103

PubMed Abstract | CrossRef Full Text | Google Scholar

Brûlé, S., Javelaud, E. H., Enoch, S., and Guenneau, S. (2014). Experiments on seismic metamaterials: molding surface waves. Phys. Rev. Lett. 112, 133901. doi:10.1103/PhysRevLett.112.133901

PubMed Abstract | CrossRef Full Text | Google Scholar

Ceresoli, L., Abdeddaim, R., Antonakakis, T., Maling, B., Chmiaa, M., Sabouroux, P., et al. (2016). Dynamic effective anisotropy: asymptotics, simulations, and microwave experiments with dielectric fibers. Phys. Rev. B 92, 174307. doi:10.1103/PhysRevB.92.174307

CrossRef Full Text | Google Scholar

Chen, Y., Liu, H., Reilly, M., Bae, H., and Yu, M. (2014). Enhanced acoustic sensing through wave compression and pressure amplification in anisotropic metamaterials. Nat Commun. 5, 5247. doi:10.1038/ncomms6247

PubMed Abstract | CrossRef Full Text | Google Scholar

Climente, A., Torrent, D., and Sánchez-Dehesa, J. (2014). Gradient index lenses for flexural waves based on thickness variations. Appl. Phys. Lett. 105, 064101. doi:10.1063/1.4893153

CrossRef Full Text | Google Scholar

Colombi, A. (2016). Resonant metalenses for flexural waves. J. Acoust. Soc. Am. 140, EL423. doi:10.1121/1.4967179

CrossRef Full Text | Google Scholar

Colombi, A., Ageeva, V., Clare, A., Craster, R., Patel, R., Roux, P., et al. (2017). Enhanced sensing and conversion of ultrasonic rayleigh waves by elastic metasurfaces. Sci. Rep. 7, 6750. doi:10.1038/s41598-017-07151-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombi, A., Colquitt, D., Roux, P., Guenneau, S., and Craster, R. V. (2016a). A seismic metamaterial: the resonant metawedge. Sci. Rep. 6, 27717. doi:10.1038/srep27717

CrossRef Full Text | Google Scholar

Colombi, A., Guenneau, S., Roux, P., and Craster, R. (2016b). Transformation seismology: composite soil lenses for steering surface elastic rayleigh waves. Sci. Rep. 6, 25320. doi:10.1038/srep25320

CrossRef Full Text | Google Scholar

Colombi, A., Roux, P., Guenneau, S., Gueguen, P., and Craster, R. (2016c). Forests as a natural seismic metamaterial: Rayleigh wave bandgaps induced by local resonances. Sci. Rep. 5, 19238. doi:10.1038/srep19238

CrossRef Full Text | Google Scholar

Colombi, A., Roux, P., Guenneau, S., and Rupin, M. (2015). Directional cloaking of flexural waves in a plate with a locally resonant metamaterial. J. Acoust. Soc. Am. 137, 1783–1789. doi:10.1121/1.4915004

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombi, A., Roux, P., and Rupin, M. (2014). Sub-wavelength energy trapping of elastic waves in a meta-material. J. Acoust. Soc. Am. 136, EL192–EL198. doi:10.1121/1.4890942

CrossRef Full Text | Google Scholar

Colquitt, D., Colombi, A., Craster, R., Roux, P., and Guenneau, S. (2017). Seismic metasurfaces: sub-wavelength resonators and rayleigh wave interaction. J. Mech. Phys. Solids 99, 379–393. doi:10.1016/j.jmps.2016.12.004

CrossRef Full Text | Google Scholar

Colquitt, D., Jones, I., Movchan, N., and Movchan, A. (2011). Dispersion and localization of elastic waves in materials with microstructure. Proc. R. Soc. Lond. A 467, 2874–2895. doi:10.1098/rspa.2011.0126

CrossRef Full Text | Google Scholar

Craster, R., and Guenneau, S. (2012). Acoustic Metamaterials: Negative Refraction, Imaging, Lensing and Cloaking. London: Springer.

Google Scholar

Craster, R. V., Kaplunov, J., and Postnova, J. (2010). High-frequency asymptotics, homogenisation and localisation for lattices. Q. J. Mech. Appl. Math. 63, 497–519.

Google Scholar

Cummer, S., and Schurig, D. (2007). One path to acoustic cloaking. N. J. Phys. 9, 45. doi:10.1088/1367-2630/9/3/045

CrossRef Full Text | Google Scholar

Davis, B. L., and Hussein, M. I. (2014). Nanophononic metamaterial: thermal conductivity reduction by local resonance. Phys. Rev. Lett. 112, 055505. doi:10.1103/PhysRevLett.112.055505

PubMed Abstract | CrossRef Full Text | Google Scholar

Della Picca, F., Berte, R., Rahmani, M., Albella, P., Bujjamer, J., Poblet, M., et al. (2016). Tailored hypersound generation in single plasmonic nanoantennas. Nano Lett. 16, 1428–1434. doi:10.1021/acs.nanolett.5b04991

PubMed Abstract | CrossRef Full Text | Google Scholar

Dertimanis, V., Antoniadis, I., and Chatzi, E. (2016). Feasibility analysis on the attenuation of strong ground motions using finite periodic lattices of mass-in-mass barriers. J. Eng. Mech. 142, 04016060. doi:10.1061/(ASCE)EM.1943-7889.0001120

CrossRef Full Text | Google Scholar

Dubois, M., Farhat, M., Bossy, E., Enoch, S., Guenneau, S., and Sebbah, P. (2013). Flat lens for pulse focusing of elastic waves in thin plates. Appl. Phys. Lett. 103, 071915. doi:10.1063/1.4818716

CrossRef Full Text | Google Scholar

Ewins, D. J. (2000). Modal Testing: Theory, Practice and Application, 2nd Edn. Baldock, UK: Research Studies Press.

Google Scholar

Farhat, M., Enoch, S., Guenneau, S., and Movchan, A. B. (2008). Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Phys. Rev. Lett. 101, 134501. doi:10.1103/PhysRevLett.101.134501

PubMed Abstract | CrossRef Full Text | Google Scholar

Finocchio, G., Casablanca, O., Ricciardi, G., Alibrandi, U., Garescì, M. F., Chiappini, M., et al. (2014). Seismic metamaterials based on isochronous mechanical oscillators. Appl. Phys. Lett. 104, 191903. doi:10.1063/1.4876961

CrossRef Full Text | Google Scholar

Galich, P. I., Fang, N. X., Boyce, M. C., and Rudykh, S. (2017). Elastic wave propagation in finitely deformed layered materials. J. Mech. Phys. Solids 98, 390–410. doi:10.1016/j.jmps.2016.10.002

CrossRef Full Text | Google Scholar

Graff, K. (1975). Wave Motion in Elastic Solids. Oxford: The Clarendon Press.

Google Scholar

Guéguen, P., Bard, P.-Y., and Chávez-García, F. J. (2002). Site-city seismic interaction in mexico city–like environments: an analytical study. Bull. Seism. Soc. Am. 92, 794–811. doi:10.1785/0120000306

CrossRef Full Text | Google Scholar

Kadic, M., Dupont, G., Chang, T.-M., Guenneau, S., and Enoch, S. (2011). Curved trajectories on transformed metal surfaces: beam-splitter, invisibility carpet and black hole for surface plasmon polaritons. Photon. Nanostruct. 9, 302–307. doi:10.1016/j.photonics.2011.06.002

CrossRef Full Text | Google Scholar

Kaina, N., Lemoult, F., Fink, M., and Lerosey, G. (2015). Negative refractive index and acoustic superlens from multiple scattering in single negative metamaterials. Nature 525, 77–81. doi:10.1038/nature14678

PubMed Abstract | CrossRef Full Text | Google Scholar

Khelif, A., Achaoui, Y., and Aoubiza, B. (2012). Surface acoustic waves in pillars-based two-dimensional phononic structures with different lattice symmetries. J. Appl. Phys. 112, 033511. doi:10.1063/1.4737780

CrossRef Full Text | Google Scholar

Kim, K., No, Y., Chang, S., Choi, J., and Par, H. (2015). Invisible hyperbolic metamaterial nanotube at visible frequency. Sci. Rep. 5, 16027. doi:10.1038/srep16027

PubMed Abstract | CrossRef Full Text | Google Scholar

Komatitsch, D., and Martin, R. (2007). An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics 72, SM155–SM167. doi:10.1190/1.2757586

CrossRef Full Text | Google Scholar

Krushynska, A., Kouznetsova, V., and Geers, M. (2016). Visco-elastic effects on wave dispersion in three-phase acoustic metamaterials. J. Mech. Phys. Solids 96, 29–47. doi:10.1016/j.jmps.2016.07.001

CrossRef Full Text | Google Scholar

Krylov, V. (2014). Acoustic black holes: recent developments in the theory and applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61, 1296–1306. doi:10.1109/TUFFC.2014.3036

PubMed Abstract | CrossRef Full Text | Google Scholar

Landau, L. D., and Lifshitz, E. M. (1965). Quantum Mechanics Non-Relativistic Theory. Oxford: Pergamon Press.

Google Scholar

Lee, H., Oh, J. H., Seung, H. M., Cho, S. H., and Kim, Y. Y. (2016). Extreme stiffness hyperbolic elastic metamaterial for total transmission subwavelength imaging. Sci. Rep. 6, 24026. doi:10.1038/srep24026

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemoult, F., Fink, M., and Lerosey, G. (2011). Acoustic resonators for far-field control of sound on a subwavelength scale. Phys. Rev. Lett. 107, 064301. doi:10.1103/PhysRevLett.107.064301

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., and Chan, C. (2004). Double-negative acoustic metamaterial. Phys. Rev. E 70, 055602. doi:10.1103/PhysRevE.70.055602

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Mao, Y., Zhu, Y., Yang, Z., Chan, C., et al. (2000). Locally resonant sonic materials. Science 289, 1734–1736. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, C., Johnson, S., Joannopoulos, J., and Pendry, J. (2002). All-angle negative refraction without negative effective index. Phys. Rev. B 65, 201104. doi:10.1103/PhysRevB.65.201104

CrossRef Full Text | Google Scholar

Maradudin, A. A. (2011). Structured Surfaces as Optical Metamaterials. Cambridge: Cambridge University Press.

Google Scholar

Matlack, K. H., Bauhofer, A., Krodel, S., Palermo, A., and Daraio, C. (2016). Composite 3D-printed metastructures for low-frequency and broadband vibration absorption. Proc. Natl. Acad. Sci. U.S.A. 113, 8386–8390. doi:10.1073/pnas.1600171113

PubMed Abstract | CrossRef Full Text | Google Scholar

Maznev, A., Gu, G., Sun, S., Xu, J., Shen, Y., Fang, N., et al. (2015). Extraordinary focusing of sound above a soda can array without time reversal. New J. Phys. 17, 042001. doi:10.1088/1367-2630/17/4/042001

CrossRef Full Text | Google Scholar

Miniaci, M., Krushynska, A., Bosia, F., and Pugno, N. M. (2016). Large scale mechanical metamaterials as seismic shields. New J. Phys. 18, 083041. doi:10.1088/1367-2630/18/8/083041

CrossRef Full Text | Google Scholar

Miniaci, M., Marzani, A., Testoni, N., and Marchi, L. D. (2015). Complete band gaps in a polyvinyl chloride (pvc) phononic plate with cross-like holes: numerical design and experimental verification. Ultrasonics 56, 251–259. doi:10.1016/j.ultras.2014.07.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Miroshnichenko, A. E., Flach, S., and Kivshar, Y. S. (2010). Fano resonances in nanoscale structures. Rev. Mod. Phys. 82, 2257–2298. doi:10.1103/RevModPhys.82.2257

CrossRef Full Text | Google Scholar

Movchan, A., and Guenneau, S. (2004). Split-ring resonators and localized modes. Phys. Rev. B 70, 125116. doi:10.1103/PhysRevB.70.125116

CrossRef Full Text | Google Scholar

Pendry, J., Holden, A., Robbins, D., and Stewart, W. (1998). Low frequency plasmons in thin-wire structures. J. Phys. Condens. Matter 10, 4785.

Google Scholar

Pendry, J., Holden, A. J., Robbins, D. J., and Stewart, W. J. (1999). Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microwave Theory Tech. 47, 2075–2084. doi:10.1109/22.798002

CrossRef Full Text | Google Scholar

Pendry, J. B. (2000). Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969. doi:10.1103/PhysRevLett.85.3966

PubMed Abstract | CrossRef Full Text | Google Scholar

Pendry, J. B., Schurig, D., and Smith, D. R. (2006). Controlling electromagnetic fields. Science 312, 1780–1782. doi:10.1126/science.1125907

PubMed Abstract | CrossRef Full Text | Google Scholar

Pennec, Y., Djafari-Rouhani, B., Larabi, H., Vasseur, J. O., and Hladky-Hennion, A. C. (2008). Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate. Phys. Rev. B 78, 104105. doi:10.1103/PhysRevB.78.104105

CrossRef Full Text | Google Scholar

Perkins, N. C., and Mote, C. D. (1986). Comments on curve veering in eigenvalue problems. J. Sound Vib. 106, 451–463. doi:10.1016/0022-460X(86)90191-4

CrossRef Full Text | Google Scholar

Peter, D., Komatitsch, D., Luo, Y., Martin, R., Le Goff, N., Casarotti, E., et al. (2011). Forward and adjoint simulations of seismic wave propagation on fully unstructured hexahedral meshes. Geophys. J. Int. 186, 721–739. doi:10.1111/j.1365-246X.2011.05044.x

CrossRef Full Text | Google Scholar

Poddubny, A., Iorsh, I., Belov, P., and Kivshar, Y. (2013). Hyperbolic metamaterials. Nat. Photonics 7, 948–957. doi:10.1038/nphoton.2013.243

CrossRef Full Text | Google Scholar

Ramakrishna, S., and Grzegorczyk, T. (2008). Physics and Applications of Negative Refractive Index Materials. Boca-Raton, FL: CRC Press.

Google Scholar

Rey, M., Elnathan, R., Ditcovski, R., Geisel, K., Zanini, M., Fernandez-Rodriguez, M.-A., et al. (2016). Fully tunable silicon nanowire arrays fabricated by soft nanoparticle templating. Nano Lett. 16, 157–163. doi:10.1021/acs.nanolett.5b03414

PubMed Abstract | CrossRef Full Text | Google Scholar

Rietmann, M., Messmer, P., Nissen-Meyer, T., Peter, D., Basini, P., Komatitsch, D., et al. (2012). “Forward and adjoint simulations of seismic wave propagation on emerging large-scale gpu architectures,” in Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, SC ’12, Vol. 38, (Salt Lake City, UT: IEEE Computer Society Press), 1–38.

Google Scholar

Romero-Garcia, V., Pico, R., Cebrecos, A., Sanchez-Morcillo, V. J., and Staliunas, K. (2013). Enhancement of sound in chirped sonic crystals. Appl. Phys. Lett. 102, 091906. doi:10.1063/1.4793575

CrossRef Full Text | Google Scholar

Rupin, M., Lemoult, F., Lerosey, G., and Roux, P. (2014). Experimental demonstration of ordered and disordered multi-resonant metamaterials for lamb waves. Phys. Rev. Lett. 112, 234301. doi:10.1103/PhysRevLett.112.234301

CrossRef Full Text | Google Scholar

Sarbort, M., and Tyc, T. (2012). Spherical media and geodesic lenses in geometrical optics. J. Opt. 14, 075705. doi:10.1088/2040-8978/14/7/075705

CrossRef Full Text | Google Scholar

Schurig, D., Mock, J., Justice, B., Cummer, S., Pendry, J., Starr, A., et al. (2006). Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980. doi:10.1126/science.1133628

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwan, L., Geslain, A., Romero-Garca, V., and Groby, J.-P. (2017). Complex dispersion relation of surface acoustic waves at a lossy metasurface. Appl. Phys. Lett. 110, 051902. doi:10.1063/1.4975120

CrossRef Full Text | Google Scholar

Smith, D. R., Kolinko, P., and Schurig, D. (2004a). Negative refraction in indefinite media. J. Opt. Soc. Am. B 21, 1032–1043. doi:10.1364/JOSAB.21.001032

CrossRef Full Text | Google Scholar

Smith, D., Pendry, J., and Wiltshire, M. (2004b). Metamaterials and negative refractive index. Science 305, 788–792. doi:10.1126/science.1096796

CrossRef Full Text | Google Scholar

Smith, D. R., Padilla, W. J., Vier, D. C., Nemat-Nasser, S. C., and Schultz, S. (2000). Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 84, 4184–4187. doi:10.1103/PhysRevLett.84.4184

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, D. R., and Schurig, D. (2003). Electromagnetic wave propagation in media with indefinite permittivity and permeability tensors. Phys. Rev. Lett. 90, 077405. doi:10.1103/PhysRevLett.90.077405

PubMed Abstract | CrossRef Full Text | Google Scholar

Smolyaninov, I., Hwang, E., and Narimanov, E. (2012). Hyperbolic metamaterial interfaces: Hawking radiation from rindler horizons and spacetime signature transitions. Phys. Rev. B 85, 235122. doi:10.1103/PhysRevB.85.235122

CrossRef Full Text | Google Scholar

Tallarico, D., Movchan, N. V., Movchan, A. B., and Colquitt, D. J. (2017). Tilted resonators in a triangular elastic lattice: chirality, bloch waves and negative refraction. J. Mech. Phys. Solids 103, 236–256. doi:10.1016/j.jmps.2017.03.007

CrossRef Full Text | Google Scholar

Torrent, D., Mayou, D., and Sánchez-Dehesa, J. (2013). Elastic analog of graphene: Dirac cones and edge states for flexural waves in thin plates. Phys. Rev. B 87, 115143. doi:10.1103/PhysRevB.87.115143

CrossRef Full Text | Google Scholar

Torrent, D., Pennec, Y., and Djafari-Rouhani, B. (2014). Omnidirectional refractive devices for flexural waves based on graded phononic crystals. J. Appl. Phys. 116, 224902. doi:10.1063/1.4903972

CrossRef Full Text | Google Scholar

Tsakmakidis, K. L., Boardman, A. D., and Hess, O. (2007). Trapped rainbow storage of light in metamaterials. Nature 450, 397–401. doi:10.1038/nature06285

CrossRef Full Text | Google Scholar

Werner, D. (2016). Broadband Metamaterials in Electromagnetics: Technology and Applications. Singapore: Pan Stanford Publishing.

Google Scholar

Williams, E. G., Roux, P., Rupin, M., and Kuperman, W. A. (2015). Theory of multiresonant metamaterials for A₀ lamb waves. Phys. Rev. B 91, 104307. doi:10.1103/PhysRevB.91.104307

CrossRef Full Text | Google Scholar

Wong, H. L., and Trifunac, M. D. (1975). Two-dimensional, antiplane, building-soil-building interaction for two or more buildings and for incident planet sh waves. Bull. Seismol. Soc. Am. 65, 1863–1885.

Google Scholar

Wu, T.-T., Huang, Z.-G., Tsai, T.-C., and Wu, T.-C. (2008). Evidence of complete band gap and resonances in a plate with periodic stubbed surface. Appl. Phys. Lett. 93, 111902. doi:10.1063/1.2970992

CrossRef Full Text | Google Scholar

Xiao, Y., Wen, J., and Wen, X. (2012). Flexural wave band gaps in locally resonant thin plates with periodically attached spring–mass resonators. J. Phys. D Appl. Phys. 45, 195401. doi:10.1088/0022-3727/45/19/195401

CrossRef Full Text | Google Scholar

Yang, S., Page, J. H., Liu, Z., Cowan, M. L., Chan, C. T., and Sheng, P. (2002). Ultrasound tunneling through 3d phononic crystals. Phys. Rev. Lett. 88, 104301. doi:10.1103/PhysRevLett.88.104301

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, N., and Capasso, F. (2014). Flat optics with designer metasurfaces. Nat. Mater. 13, 139–149. doi:10.1038/nmat3839

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., Xia, C., and Fang, N. (2011). Broadband acoustic cloak for ultrasound waves. Phys. Rev. Lett. 106, 024301. doi:10.1103/PhysRevLett.106.024301

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, J., Chen, Y., Zhu, X., Garcia-Vidal, F. J., Yin, X., Zhang, W., et al. (2013). Acoustic rainbow trapping. Sci. Rep. 3, 1728. doi:10.1038/srep01728

CrossRef Full Text | Google Scholar