Condensation on Surfaces With Biphilic Topography: Experiment and Modeling

Optimization of the efficiency of the condensers via different surface engineering techniques is a subject of interest due to its wide range of application in thermal management for aerospace vehicles, power generation systems, and etc., which will further result in considerable savings in annual investments and operating costs by millions of dollars. However, the current technologies are lacking either the necessary condensation enhancements or cost-effective, large-scale fabrication method. In this work, we present a new surface topography to enhance drop-wise condensation at low manufacturing costs. These surfaces consist of macro-scale hydrophobic patterns on hydrophilic structures. Due to their high wettability contrast, the biphilic surfaces enhance drop-wise condensation with long-term functionality, and more importantly, they can be easily manufactured in large-scale using conventional methods as no nano- or micro-features are needed.

Introduction

One of the main technical challenges in a variety of industrial fields including aircrafts, power plants, and water desalination systems is the effective discharge of excessive heat generated inside the system. From thermal management point of view, condensation or phase change in general is considered the most optimum way of removing waste heat from the system due to its high heat transfer rate. Efficiency of the thermal transfer during condensation strongly depends on the mode of condensation, namely drop-wise and film-wise condensation (Schmidt et al., 1930; Song et al., 1991; Rose, 1998, 2002; Leach et al., 2006). The current industrial condensers, however, are very inefficient because they rely on film-wise condensation for waste heat removal. The film-wise condensation offers low heat transfer coefficient due to thermal resistance imposed by the liquid layer as when the film is formed, it acts as a barrier to thermal transfer and impedes the continuous heat transfer from the condensing surface.

Several researchers have tried to address this issue and find ways to improve the heat transfer efficiency by enhancing drop-wise condensation on the condensing surfaces (Miljkovic et al., 2012; Xiao et al., 2013; Paxson et al., 2014). Unlike film-wise condensation, the drop-wise condensation is achieved on a surface that is not wetted by the condensate. In drop-wise condensation, there is a continuous surface renewal by falling drops resulting in at least 10-fold enhancement in heat transfer rate compared to the film-wise condensation (Welch and Westwater, 1961; Le Fevre and Rose, 1964; Carey, 1992; Kandlikar et al., 1999; Ma et al., 2000; Rose, 2002; Kim and Kim, 2011).

The current technology to promote drop-wise condensation is mostly limited to hydrophobic coatings (Das et al., 1999; Lara and Holtzapple, 2011; Alizadeh et al., 2013; Zamuruyev et al., 2014) or nano-engineered textured surfaces (Chen et al., 2011; Anderson et al., 2012; Cheng et al., 2012; Miljkovic et al., 2012; Lo et al., 2013; Hou et al., 2015). The hydrophobic coatings have short life span and tend to come off depending on the working conditions in a few hours. These coatings are mainly polymer based with low thermal conductivity; thus, covering the condensing surface with the coating impedes the heat transfer and reduces the overall efficiency.

The superhydrophobic nano-patterned surfaces allow sustained drop-wise condensation and have shown considerably higher enhancements in heat transfer compared to hydrophobic coatings due to variety of reasons. For example, superhydrophobic surfaces can significantly increase the mobility of the droplets leading to a combination of both gravity-driven falling droplets as well as self-propelled jumping droplets. These surfaces are mostly metal substrates with nano-features, hence high thermal conductivity. However, the nucleation energy barrier is much higher on superhydrophobic surfaces compared to hydrophilic surfaces, which causes a significant reduction in droplet number density, and more importantly the manufacturing process for nano-engineered surfaces is neither cost-effective nor scalable.

Therefore, the state-of-the-art condensing surfaces cannot be applied to industrial applications due to their high manufacturing costs and difficulty in maintaining drop-wise condensation in long run. In order to tune the advantage of lower energy barrier accompanied with hydrophilic surfaces and higher drop mobility of super-hydrophobic surfaces, Kumagai et al. (1991) entertained the possibility of using biphilic patterning of surfaces. Results showed a great potential of using such surfaces with heat transfer performance bounded by the two extreme cases, i.e., film and drop wise condensation. After this work, several researchers studied different configurations, such as biphilic strips (Drelich et al., 1996; Morita et al., 2005; Megaridis et al., 2016; Zou et al., 2018), biphilic dotted surfaces (Raj et al., 2012) and biphilic pillars (Kita et al., 2018).

This paper focuses on development of biphilic surfaces with high wettability contrast to boost drop wise condensation, while maintaining high conduction rate through the surface at low manufacturing costs. Previously engineered biphilic surfaces are different arrangements of superhydrophobic designs on hydrophilic substrates that despite their high heat transfer efficiency, cannot overcome the large-scale fabrication challenges and are inapplicable to industrial systems (Narhe and Beysens, 2007; Chatterjee et al., 2013; Hou et al., 2015). The unique aspect of our work is to design a hybrid hydrophilic hydrophobic surface in which the variation in interfacial energy is achieved through crafting millimeter-sized hydrophobic patterns on metal substrates that not only leads to high thermal transfer efficiency but also can be manufactured using scalable fabrication techniques.

Biphilic surfaces consist of hydrophobic patterns on hydrophilic structures as shown in Figure 1. The hydrophilic base provides high thermal conductivity and low nucleation activation energy resulting in enhanced vapor condensation rate, and the hydrophobic patterns inhibit transition to film-wise condensation and enhance the rate of droplet removal from the condensing surface, all of which increases the overall heat transfer efficiency.

FIGURE 1

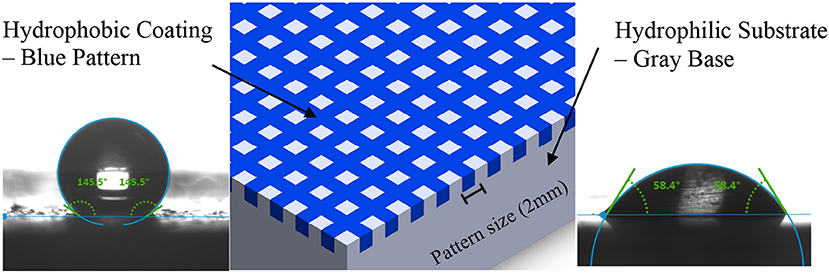
Figure 1. Schematic drawing of biphilic surface showing the hydrophobic pattern on a hydrophilic base. The contact angle of water on the hydrophobic and hydrophilic sites are 145° and 58°, respectively.

Mathematical Modeling

Understanding the mechanism of drop-wise condensation is essential in design and optimization of durable surfaces with enhanced drop-wise condensation for industrial applications. There are several theories on drop formation and heat and mass transport during drop-wise condensation (Jakob, 1936; McCormic and Baer, 1963; Song et al., 1991; Leipertz, 2010). The most commonly used theory for modeling of drop-wise condensation was first introduced by Eucken (1937), which is based on small droplet formation by direct condensation on nucleation sites randomly distributed over the condensing surface. According to this theory, as the clusters of vapor reach a maximum size adjacent to the condensing surface, they form small drops of stable thermodynamically minimum radius at sites with the smallest free energy barrier. The small drops grow by direct condensation only until they reach the mean nucleation site spacing at which the neighboring drops start to coalescence. The large droplets then fall-off of the condensing surface reaching the critical drop size due to the force instabilities at the contact-line. To properly model the drop-wise condensation and calculate the overall heat flux and heat removal efficiency via different condensing surfaces, a comprehensive understanding of all the sub-processes is necessary. Drop-wise condensation consists of a series of random fundamentally unsteady sub-processes over a wide range of time- and length-scales, viz. initial nucleation, droplet growth by direct condensation, coalescence, droplet instability and fall-off, and renucleation of fresh droplets (Sikarwar et al., 2013).

The first step in drop-wise condensation process is the heterogeneous nucleation, which depends on the number of active nucleation sites on the condensing surface. The nucleation site density, N_s, varies with surface topography and thermodynamic properties of fluid, and extent of subcooling (Rose, 1976; Sikarwar et al., 2013). Based on the experimental data, the nucleation site density was found to be within the range of 10⁹-10¹⁵ m⁻² (Khandekar and Muralidhar, 2014; Liu and Cheng, 2015). For the purpose of the heat transfer modeling of drop-wise condensation, we assume the nucleation site density to be at 10¹⁰ m⁻².

The small drops that are formed by nucleation continue to grow by direct condensation. The smallest stable droplet radius, r_min, can be found using the classical nucleation theory (Schmidt et al., 1930; Kim and Kim, 2011).

$\begin{array}{ll}{r}_{min}=\frac{2T_{sat}\sigma }{h_{fg}\rho (T_{sat}-T_w)}& (1)\end{array}$

For small non-interacting droplets, the droplet size distribution is calculated following the population balance theory. The population balance theory is based on the droplet number conservation in a certain droplet radius range. In other words, for an arbitrary size range of (r₁−r₂), the number of droplet entering the size range minus the number of droplet leaving the size range is equal to the number of droplet fall-off of the surface (AbuOrabi, 1998; Kim and Kim, 2011; Miljkovic et al., 2013):

$\begin{array}{ll}A{n}_1{G}_{1}dt=A{n}_2{G}_{2}dt+S{n}_{1-2}dtdr& (2)\end{array}$

$\begin{array}{ll}G=\frac{dr}{dt}& (3)\end{array}$

where A, G, n₁, n₂, S, and n₁₋₂ are the surface area, droplet growth rate, number density of the droplet of radius r₁, number density of the droplet of radius r₂, sweeping (or falling) rate, and average population density in the size range. In the limit of infinitesimally small size range, Equation (2) reduces to:

$\begin{array}{ll}\frac{d(Gn)}{dr}=\frac{-n}{\tau }& (4)\end{array}$

where $\tau =\frac{A}{S}$ is the sweeping period. The number density for small droplets can be eventually obtained by solving Equation (4), which requires additional information discussed in the following steps.

The next step is the large droplet growth by coalescence of the neighboring drops. There is a well-known equation for number distribution of large droplets derived by Le Fevre and Rose (1966) and Glicksman and Hunt (1972).

$\begin{array}{ll}N\left(r\right)=\frac{1}{3{\pi }^2{r}_{max}}{\left(\frac{r}{r_{max}}\right)}^{\frac{-2}{3}}& (5)\end{array}$

where r_max is the maximum radius beyond which the drop falls off of the surface. The maximum droplet radius is where the tangential component of droplet weight reaches the interfacial force at the contact-line. Following the force balance equation, the fall-off radius can be determined as Dimitrakopoulos and Higdon (1999).

$\begin{array}{ll}{r}_{max}=\sqrt{\frac{6\sigma \left(cos{\theta }_r-cos{\theta }_a\right)sin{\theta }_{avg}}{\rho \pi \left(2-3cos{\theta }_{avg}+co{s}^3{\theta }_{avg}\right)sin\alpha }}& (6)\end{array}$

Where ρ, σ, θ_r, θ_a, θ_avg, and α are liquid density, surface tension, receding contact angle, advancing contact angle, equilibrium contact angle, and the substrate inclination angle, which is 90° for vertical substrate, respectively. The fall-off radius, as seen in Equation (6), strongly depends on the contact angle of the liquid droplet on the condensing surface, for example, for hydrophobic substrates, the fall-off radius is smaller than hydrophilic surfaces. It should be noted the reduction in fall-off radius is equivalent to better thermal transfer as large droplets are removed and replaced by small droplets at a faster rate.

The overall heat transfer through the condensing surface is calculated by integrating the heat flux through one single droplet over the condenser surface area for all the droplets both large and small based on the number densities calculated earlier (Wu and Maa, 1976; Carey, 1992; AbuOrabi, 1998). The heat transfer rate for a single droplet, q_d, is determined using the standard thermal resistive model (Miljkovic et al., 2013; Sikarwar et al., 2013) shown in Figure 2. The temperature drop from the saturated vapor, T_sat, to the substrate, T_w, is calculated considering all the thermal resistances in between namely the vapor-liquid interface resistance, the droplet curvature resistance, conduction resistance, coating resistance, and finally resistance through the substrate. The equation for the total temperature drop, T_t, is given by:

$\begin{array}{ll}{T}_t=T_{sat}-T_w=T_{int}+T_{cur}+T_{cond}+T_{coat}+T_{sub}& (7)\end{array}$

$\begin{array}{l}{T}_{sat}-T_w=\frac{q_d}{2{\pi }^2{h}_{int}\left(1-cos{\theta }_{avg}\right)}+\frac{r_{min}\left(T_{sat}-T_w\right)}{r}\\ +\frac{q_d{\theta }_{avg}}{4vr{k}_{l}sin{\theta }_{avg}}+\frac{q_d{\delta }_{coat}}{{\pi }^2{k}_{coat}\left(1-co{s}^2{\theta }_{avg}\right)}\\ +\frac{q_d{\delta }_{base}}{{\pi }^2{k}_{base}\left(1-co{s}^2{\theta }_{avg}\right)}& (8)\end{array}$

where δ_coat, δ_base, h_fg, h_int, k_l, k_coat, and k_base are the coating thickness, the base thickness, the latent heat of vaporization, the interfacial heat transfer coefficient, liquid thermal conductivity, the coating thermal conductivity, and the base thermal conductivity. The heat transfer rate through a single droplet can be replaced using the latent heat equation for a droplet of growing radius and changing contact angle:

$\begin{array}{l}{q}_d=\pi \rho h_{fg}{r}^{2}G\{\left(1-co{s}^2{\theta }_{avg}\right)sin{\theta }_{avg}\frac{d{\theta }_{avg}}{dr}r\\ +{\left(1-cos{\theta }_{avg}\right)}^2\left(2+cos{\theta }_{avg}\right)\}& (9)\end{array}$

It should be noted that the first term in Equation (9) associated with the change in contact angle across the surface is only zero for surfaces with constant wettability. By plugging in Equation (8) back into Equation (7), the droplet growth rate can be found in terms of the temperature drop and the liquid and substrate properties.

$\begin{array}{l}G=\left(\frac{\left(1-cos{\theta }_{avg}\right)\times \left(\frac{T_{sat}-T_w}{{\rho }_{fg}}\right)}{\left(1-co{s}^2{\theta }_{avg}\right)sin{\theta }_{avg}\frac{d\theta }{dr}r+{\left(1-cos{\theta }_{avg}\right)}^2\left(2+cos{\theta }_{avg}\right)}\right)\\ \times \left(\frac{\left(1-\frac{r_{min}}{r}\right)}{\frac{1}{2h_{int}}+\frac{r\left(1-cos{\theta }_{avg}\right){\theta }_{avg}}{4k_{l}sin{\theta }_{avg}}+\frac{{\delta }_{coat}}{k_{coat}\left(1+cos{\theta }_{avg}\right)}+\frac{{\delta }_{base}}{k_{base}\left(1+cos{\theta }_{avg}\right)}}\right)& (10)\end{array}$

Finally, the number density for small droplets can be calculated from integrating Equation (4) by replacing the droplet growth rate using Equation (10). As the number density function has to be continuous, the value for number density of the small drops at its upper limit should be equal to the lower limit of the number density of large drops. The radius where the large and small number density functions meet is called effective radius, r_e, which is equal to the half of the spacing between the active nucleation sites, l_c, beyond which neighboring droplets can merge.

$\begin{array}{ll}{r}_c=\frac{l_c}{2}=\frac{1}{\sqrt{4N_s}}& (11)\end{array}$

$\begin{array}{ll}N\left(r_e\right)=n\left(r_e\right)& (12)\end{array}$

Therefore, the overall heat transfer rate, q′, through the condensing surface can be calculated via the following equation (Wu and Maa, 1976):

$\begin{array}{ll}{q}^{\prime }={\displaystyle {\int }_{r_{min}}^{r_e}{q}_d\left(r\right)n\left(r\right)dr+}{\displaystyle {\int }_{r_e}^{r_{max}}{q}_d\left(r\right)N\left(r\right)dr}& (13)\end{array}$

FIGURE 2

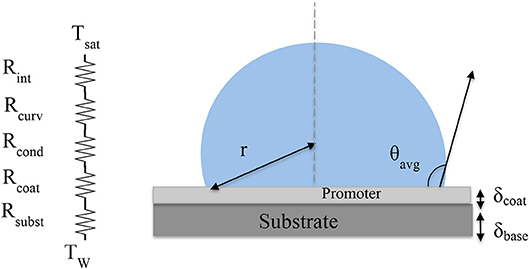
Figure 2. Drawing of droplet on a condenser surface with the related thermal resistance network that includes the liquid-vapor interface resistance, the curvature resistance, the droplet conduction resistance, the hydrophobic promoter resistance, and finally the thermal resistance in the substrate. The hydrophobic promoter has the thickness of δ_coat on hydrophobic sites and zero on hydrophilic base.

Biphilic vs. Hydrophobic and Hydrophilic

Here, we are going to numerically compare the performance of the biphilic surfaces to all-hydrophobic and all-hydrophilic substrates. The previous models on condensation heat transfer are mostly applicable to substrates with constant wettability across the surface area; hence zero contact angle gradient with respect to droplet radius. However, for biphilic surfaces, the contact angle changes throughout the surface depending on the pattern size γ. Another important thing to consider when studying biphilic surfaces is the maximum or fall-off radius. For biphilic surfaces, first of all, the fall-off radius for droplets on hydrophobic site is different than fall-off radius on hydrophilic base due to the change in dynamic and equilibrium contact angles on these surfaces, and secondly, the fall-off radius is not determined by Equation (6) solely, but it also depends on the pattern size as for example, droplets growing on hydrophilic base cannot extend past the hydrophobic boundary on account of the reduction in adhesion forces. Thus, the maximum droplet radius on biphilic surfaces is found using the contact-line force balance combined with the pattern spacing.

We have incorporated the details, listed above, specific to biphilic surfaces in our model to provide a more accurate heat transfer analysis for these surfaces. To assess the quality of the biphilic surfaces compared to all-hydrophobic and all-hydrophilic substrates, first thing to consider is the number density of small and large droplets on these surfaces, shown in Figure 3. The hydrophobic surface seems to have the highest number densities for both the large and small droplets, the hydrophilic surface has the lowest number densities, and finally the biphilic surface sits somewhere in between. It should be noted that higher number densities especially for small droplets are more favorable in terms of enhancing the rate of heat transfer. Therefore, to this point, merely based on the number densities, the hydrophobic substrate appears to be the better option.

FIGURE 3

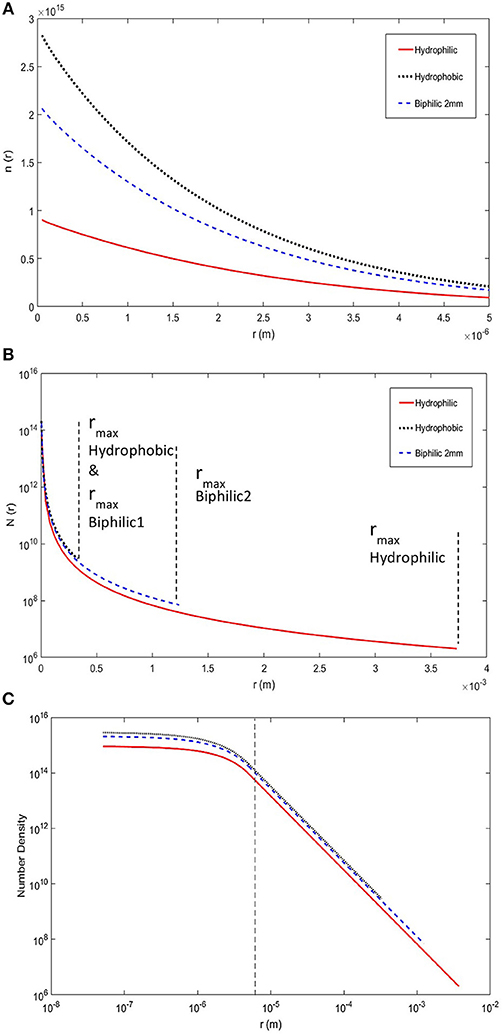
Figure 3. Droplet size distribution as a function of droplet radius for hydrophilic, hydrophobic, and 2 mm biphilic substrates. (A) The number densities are shown for small droplets formed by direct condensation. (B) The number densities are shown for large droplets formed by coalescence. The fall-off radii are shown for each substrate. The biphilic surface has two separate fall-off radii corresponding to the hydrophobic sites and hydrophilic base marked as biphilic1 and biphilic2, respectively. (C) The log-log graph of combined number densities for all droplets from initial nucleation to fall-off. The dashed line shows the borderline between small droplets and large droplets. The associated model parameters are: T_sat = 20°C, T_w = −10°C, δ_coat = 1 μm, k_coat = 0.15 W/m.K, γ = 2 mm, hydrophobic θ_a and θ_r are 150° and 144°, and hydrophilic θ_a and θ_r are 73° and 34°.

The fall-off radius is another important quantity that should be considered. The smaller fall-off radius represents a better thermal transfer for rapid droplet removal from the surface makes room for fresh small droplet formation and consequently continual heat removal from the condensing surface. The values for fall-off radii are shown in Figure 3. The hydrophobic surface has smaller fall-off radius compared to hydrophilic surface as expected. The biphilic surface, on the other hand, has two fall-off radii, one for the droplet sitting on hydrophobic pattern and one for hydrophilic base. The hydrophobic pattern fall-off radius is same as all-hydrophobic substrate only if the pattern spacing is bigger than the fall-off diameter because the droplet would fall-off of the surface before it can grow outside the pattern. For the hydrophilic base, however, the fall-off radius is limited by the pattern spacing, which is much smaller than fall-off radius on the all-hydrophilic surface.

The third important factor is the rate of heat transfer for droplets of specific radius, single drop heat transfer rate multiplied by number density at that desired radius, and finally the overall rate of heat transfer through the surface. Figure 4 shows the heat transfer rate vs. the droplet radius. As you can see, the heat transfer rate strongly depends on the value of contact angle as increase in contact angle imposes a barrier to thermal transport through the droplet by changing the profile of the isotherms within the drop (Alizadeh-Birjandi and Kavehpour, 2017). As a result, the rate of heat transfer for drops of specific radius is much smaller on hydrophobic substrate all around the range of droplet radius, and the hydrophilic surface has the highest values at all points. Although the hydrophobic surfaces had very high number densities, their local heat transfer rate is comparably small. However, biphilic surfaces have the number density and fall-off radius close to those of hydrophobic surface and the local rate of heat transfer close to hydrophilic surface; hence best of the two categories.

FIGURE 4

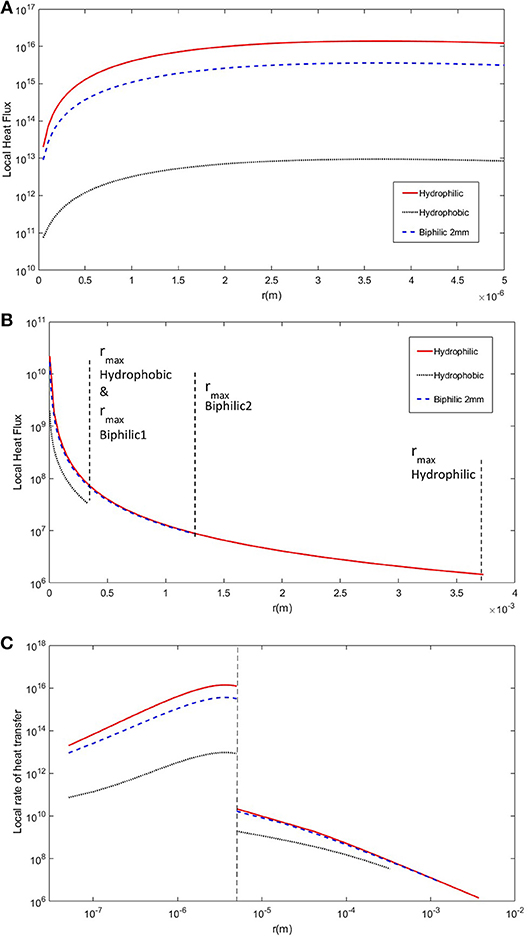
Figure 4. The steady-state single droplet condensation heat flux as a function of droplet radius for hydrophilic, hydrophobic, and 2 mm biphilic substrates. (A) The heat flux is shown for small droplets formed by direct condensation. (B) The heat flux is shown for large droplets formed by coalescence. The fall-off radii are shown for each substrate. The biphilic surface has two separate fall-off radii corresponding to the hydrophobic sites and hydrophilic base marked as biphilic1 and biphilic2, respectively. (C) The log-log graph of combined heat flux for all droplets from initial nucleation to fall-off. The dashed line shows the borderline between small droplets and large droplets. The associated model parameters are: T_sat = 20°C, T_w = −10°C, δ_coat = 1 μm, k_coat = 0.15 W/m.K, γ = 2 mm, hydrophobic θ_a and θ_r are 150° and 144°, and hydrophilic θ_a and θ_r are 73° and 34°.

The overall heat transfer rate is calculated using Equation (13) or measuring the area underneath the plot in Figure 4, and based on the results in Table 1, as already predicted, the biphilic surfaces have the highest heat transfer rate compared to all-hydrophobic and all-hydrophilic substrates. It should be noted that although the hydrophobic surfaces have smaller local heat flux compared to the hydrophilic surfaces, their overall heat flux is almost twice as large as that of hydrophilic substrate simply because their fall-off radius is small and drops tend to roll-off of these surface quickly making room for small droplet formation via nucleation with orders-of-magnitude larger local heat flux. The biphilic substrate with 2 mm pattern spacing has the highest overall heat flux making it a good candidate for enhancing high efficiency drop-wise condensation. Another advantage of using biphilic surfaces, as mentioned before, is their ability to be mass-produced. Since the size of the patterns are in millimeters as opposed to nano-scale features on superhydrophobic surfaces, their manufacturing process is scalable and cost-effective; hence applicable to industrial applications.

TABLE 1

Table 1. The overall heat flux through the condenser surface for hydrophilic, hydrophobic, and 2 mm biphilic substrates.

The analysis performed to this point were based on pattern spacing of 2 mm, which was chosen arbitrarily. To obtain an optimum pattern spacing is essential in designing an efficient thermal system at reasonable manufacturing cost, that is, the smaller pattern size is favorable for heat transfer as it decreases the fall-off radius, but the fabrication technology for small pattern size is limited and highly costly. The overall heat flux is calculated and presented in Table 2 for surfaces of different pattern spacings. As shown, for surfaces of pattern spacing higher than 4 mm, the biphilic substrate loses its advantage as the overall heat flux drops below the all-hydrophobic surface heat flux. Therefore, there exists an upper boundary to how large the pattern spacing can be, while to determine the lower boundary or a definite optimum, a comprehensive cost analysis is necessary which is part of the future work for this study.

TABLE 2

Table 2. The overall heat flux through the condenser surface for 2, 3, 4, 5, and 6 mm biphilic substrates.

Materials and Methods

Next, we have performed experiments on these surfaces to visually compare condensing droplets mobility and condensation behavior. It should be emphasized that the experiments are not designed to make any direct heat transfer measurements. The experimental setup consists of three main components, the condenser, the cooling module, and an environmental chamber. The condensing surface was attached vertically, using thermally conductive paste, to a cooling module, which consists of a series of Peltier plates and a temperature controller unit. The sample surface temperature was recorded by thermocouples. The vapor generation system was an automatic humidifier with controlled humidity. Finally, a high-speed camera was used to capture real-time videos of the experiments for further image analysis. All experiments were performed inside the environmental chamber to regulate and maintain consistent humidity and temperature at 80% relative humidity and 20°C saturated temperature. The chamber has a vent to atmosphere to mitigate the buildup of pressure and therefore inaccurate humidity measurements.

Three different samples, hydrophilic, biphilic, and hydrophobic, are placed on the same substrate for comparison. All substrates are made of aluminum with thermal conductivity of 205 W/K.m and thickness of 5 mm. The hydrophobicity, however, is achieved by spraying a 50-micron thick layer of the WX2100™ spray on the aluminum substrate everywhere on the surface for all-hydrophobic surface and on precisely positioned patterns for biphilic surface. The dynamic and equilibrium contact angles on each of these substrates are measured using Krüss DSA 100 machine. The DSA 100 is equipped with high-resolution camera and a controlled dispensing system that allows measuring the contact angles with precision. The advancing and receding contact angles on the hydrophobic and hydrophilic sites are θ_a = 150°, θ_r = 144°, θ_a = 73°, and θ_r = 34°, respectively.

Experimental Results and Discussion

Experiments are performed to compare the condensation heat transfer efficiency of biphilic surfaces to all-hydrophobic and all-hydrophilic substrates and to test our analytical predictions of the condensation behavior of the biphilic surfaces. To qualitatively assess the efficiency of condensation, five important factors, corresponding to condensation sub-processes, should be considered namely, nucleation, the droplet growth rate, coalescence, the droplet removal rate, and finally renucleation. Even though the experimental work does not include any heat transfer measurements, it assumes the enhancement of the afore-mentioned sub-processes as indications of enhanced condensation heat transfer. Figure 5 shows images of condensation experiment on a sample at −10°C for hydrophobic, 2 mm-biphilic, and hydrophilic substrates. These images are taken every 15 min during the experiment. Initially, the condensate starts forming on the hydrophilic sites on both biphilic and hydrophilic substrates. Droplets on biphilic substrate grow and merge at a quicker rate compared to the hydrophilic and hydrophobic substrates. The wettability contrast on the biphilic substrate appears to decrease the maximum droplet size, which leads to faster droplet removal and renucleation, the key components in efficient drop-wise condensation. The condensation experiments are repeated for samples at −5, −10, and −15°C for all of which the biphilic substrate shows better condensation efficiency. The videos of the experiments are provided in Supplementary Information section. It can be seen that the drops tend to form, grow, and fall rapidly on biphilic substrate with no sign of liquid film formation. On hydrophobic substrates, although the number densities are visually higher than the other substrates, the slow droplet coalescence and departure limit their performance and cause ice formation in some cases. The reason of reducing the substrate temperature below the freezing point, while below-dew point would be sufficient, is to increase the condensation rate, which would be consistent with the case for pure vapor condensation. Because this work does not evaluate heat transfer quantities, the effect of latent heat of fusion effect does not affect droplet dynamic.

FIGURE 5

Figure 5. The comparison of time evolution of condensation process on hydrophobic (left), 2 mm biphilic (center), and hydrophilic (right) regions. The images are taken every 10 min. The biphilic substrate shows better droplet nucleation and removal throughout the experiment. The experimental parameters are: T_sat = 20°C, T_w = −10°C, humidity = 80%RH, γ = 2 mm, hydrophobic θ_a and θ_r are 150° and 144°, and hydrophilic θ_a and θ_r are 73° and 34°. The complete videos of the experiments are presented in Supplementary Information section.

Conclusion

The previously established mathematical model for drop-wise condensation was modified to study the heat transfer performance of textured surfaces with high wettability contrast, biphilic surfaces, compared to hydrophilic, and hydrophobic surfaces. The analytical model predictions show that the biphilic surfaces of pattern spacing below 5 mm can achieve a higher drop-wise condensation heat transfer rate via continuous droplet nucleation and consistent and controlled droplet removal. The experimental results also verify the advantage of using biphilic structures over the conventional hydrophilic or hydrophobic surfaces. However, there are still challenges and unknown aspects to this technology; hence room for improvements and future study. For instance, the sustainability of the hydrophobic promoter should be studied by calculating the wall-shear stress to assess whether or not these substrates can withstand long-term continuous droplet formation and removal. In addition, the shape and size of the wettability patterns, as mentioned before, need to be optimized for both manufacturing and thermal transfer purposes.

Author Contributions

EA-B and HK both contributed to the design of the study. EA-B performed the experiments and data analysis and wrote the first draft of the manuscript. EA-B, AA, and HK contributed and were involved in manuscript revision and submission.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2019.00038/full#supplementary-material

Video S1. The time-lapse video recording of condensation process on hydrophobic (left), 2mm biphilic (center), and hydrophilic (right) regions. The videos are played at 60× speed. The experimental parameters are: T_sat = 20°C, T_w = −5°C, humidity = 80%RH, γ = 2mm, hydrophobic θ_a and θ_r are 150° and 144°, and hydrophilic θ_a and θ_r are 73° and 34°.

Video S2. The time-lapse video recording of condensation process on hydrophobic (left), 2mm biphilic (center), and hydrophilic (right) regions. The videos are played at 60× speed. The experimental parameters are: T_sat = 20°C, T_w = −10°C, humidity = 80%RH, γ = 2mm, hydrophobic θ_a and θ_r are 150° and 144°, and hydrophilic θ_a and θ_r are 73° and 34°.

Video S3. The time-lapse video recording of condensation process on hydrophobic (left), 2mm biphilic (center), and hydrophilic (right) regions. The videos are played at 60× speed. The experimental parameters are: T_sat = 20°C, T_w = −15°C, humidity = 80%RH, γ = 2mm, hydrophobic θ_a and θ_r are 150° and 144°, and hydrophilic θ_a and θ_r are 73° and 34°.

References

AbuOrabi, M. (1998). Modeling of heat transfer in dropwise condensation. Int. J. Heat Mass Transf. 41, 81–87. doi: 10.1016/S0017-9310(97)00094-X

CrossRef Full Text | Google Scholar

Alizadeh, A., Bahadur, V., Kulkarni, A., Yamada, M., and Ruud, J. A. (2013). Hydrophobic surfaces for control and enhancement of water phase transitions. MRS Bull. 38, 407–411. doi: 10.1557/mrs.2013.104

CrossRef Full Text | Google Scholar

Alizadeh-Birjandi, E., and Kavehpour, H. P. (2017). Plant leaves icephobicity. J. Coat. Technol. Res. 14, 1061–1067. doi: 10.1007/s11998-017-9988-4

CrossRef Full Text | Google Scholar

Anderson, D. M., Gupta, M. K., Voevodin, A. A., Hunter, C. N., Putnam, S. A., Tsukruk, V. V., et al. (2012). Using amphiphilic nanostructures to enable long-range ensemble coalescence and surface rejuvenation in dropwise condensation. ACS Nano 6, 3262–3268. doi: 10.1021/nn300183d

PubMed Abstract | CrossRef Full Text | Google Scholar

Carey, V. P. (1992). Liquid-Vapor Phase-Change Phenomena. Philadelphia, PA: Hemisphere Publishing Corporation, 413–472.

Google Scholar

Chatterjee, A., Derby, M. M., Peles, Y., and Jensen, M. K. (2013). Condensation heat transfer on patterned surfaces. Int. J. Heat Mass Transf. 66, 889–897. doi: 10.1016/j.ijheatmasstransfer.2013.07.077

CrossRef Full Text | Google Scholar

Chen, X., Wu, J., Ma, R., Hua, M., Koratkar, N., Yao, S., et al. (2011). Nanograssed micropyramidal architectures for continuous dropwise condensation. Adv. Funct. Mater. 21, 4617–4623. doi: 10.1002/adfm.201101302

CrossRef Full Text | Google Scholar

Cheng, J. T., Vandadi, A., and Chen, C. L. (2012). Condensation heat transfer on two-tier superhydrophobic surfaces. Appl. Phys. Lett. 101, 131909-1–131909-4. doi: 10.1115/IMECE2012-85841

CrossRef Full Text | Google Scholar

Das, A. K., Kilty, H. P., Marto, P. J., Andeen, G. B., and Kumar, A. (1999). The use of an organic self-assembled monolayer coating to promote dropwise condensation of steam on horizontal tubes. J. Heat Transf. 122, 278–286. doi: 10.1115/1.521465

CrossRef Full Text | Google Scholar

Dimitrakopoulos, P., and Higdon, J. (1999). On the gravitational displacement of three-dimensional fluid droplets from inclined solid surfaces. J. Fluid Mech. 395, 181–209. doi: 10.1017/S0022112099005844

CrossRef Full Text | Google Scholar

Drelich, J., Wilbur, J. L., Miller, J. D., and Whitesides, G. M. (1996). Contact angles for liquid drops at a model heterogeneous surface consisting of alternating and parallel hydrophobic/hydrophilic strips. Langmuir 12, 1913–1922. doi: 10.1021/la9509763

CrossRef Full Text | Google Scholar

Eucken, A. (1937). Energie- und stoffaustausch an grenzflächen. Die Naturwissenschaften 25, 209–218. doi: 10.1007/BF01490886

CrossRef Full Text | Google Scholar

Glicksman, R. L., and Hunt, W. A. (1972). Numerical simulation of dropwise condensation. Int. J. Heat Mass Transf. 15, 2251–2269. doi: 10.1016/0017-9310(72)90046-4

CrossRef Full Text | Google Scholar

Hou, Y., Yu, M., Chen, X., Wang, Z., and Yao, S. (2015). Recurrent filmwise and dropwise condensation on a beetle mimetic surface. ACS Nano 9, 71–81. doi: 10.1021/nn505716b

PubMed Abstract | CrossRef Full Text | Google Scholar

Jakob, M. (1936). Heat transfer in evaporation and condensation. Mech. Eng. 58, 643–660.

Google Scholar

Kandlikar, S. G., Shoji, M., and Dhir, V. K. (1999). Handbook of Phase Change: Boiling and Condensation. Boca Raton, FL: Taylor & Francis Group.

Google Scholar

Khandekar, S., and Muralidhar, K. (2014). Dropwise Condensation on Inclined Textured Surfaces. New York, NY: Springer.

Google Scholar

Kim, S., and Kim, K. J. (2011). Dropwise condensation modeling suitable for superhydrophobic surfaces. ASME J. Heat Transf. 133:081502. doi: 10.1115/1.4003742

CrossRef Full Text | Google Scholar

Kita, Y., Mackenzie-Dover, C., Askounis, A., Takata, Y., and Sefiane, K. (2018). Drop mobility on superhydrophobic microstructured surfaces with wettability contrasts. Soft Matter 14, 9418–9424. doi: 10.1039/C8SM01762J

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumagai, S., Tanaka, S., Katsuda, H., and Shimada, R. (1991). On the enhancement of filmwise condensation heat transfer by means of the coexistence with dropwise condensation sections. Exp. Heat Transf. Int. J. 4, 71–82. doi: 10.1080/08916159108946406

CrossRef Full Text | Google Scholar

Lara, J. R., and Holtzapple, M. T. (2011). Experimental investigation of dropwise condensation on hydrophobic heat exchangers. Part II: effect of coatings and surface geometry. Desalination 280, 363–369. doi: 10.1016/j.desal.2011.07.017

CrossRef Full Text | Google Scholar

Le Fevre, E. J., and Rose, J. W. (1964). Heat-transfer measurements during dropwise condensation of steam. Int. J. Heat Mass Transf. 7, 272–273. doi: 10.1016/0017-9310(64)90095-X

CrossRef Full Text | Google Scholar

Le Fevre, E. J., and Rose, J. W. (1966). “A theory of heat transfer by dropwise condensation,” in International Heat Transfer Conference Digital Library (Danbury, CT: Begel House Inc.).

Google Scholar

Leach, R. N., Stevens, F., Langford, S. C., and Dickinson, J. T. (2006). Dropwise condensation: experiments and simulations of nucleation and growth of water drops in a cooling system. Langmuir 22, 8864–8872. doi: 10.1021/la061901+

PubMed Abstract | CrossRef Full Text | Google Scholar

Leipertz, A. (2010). “Dropwise condensation,”in VDI Heat Atlas VDI-GVC, ed P. Stephan (New York, NY: Springer, 933–937.

Google Scholar

Liu, X., and Cheng, P. (2015). Dropwise condensation theory revisited Part II. Droplet nucleation density and condensation heat flux. Int. J. Heat Mass Transf. 83, 842–849. doi: 10.1016/j.ijheatmasstransfer.2014.11.008

CrossRef Full Text | Google Scholar

Lo, C. W., Wang, C. C., and Lu, M. C. (2013). Spatial control of heterogeneous nucleation on the superhydrophobic nanowire array. Adv. Funct. Mater. 21, 1211–1217. doi: 10.1002/adfm.201301984

CrossRef Full Text | Google Scholar

Ma, X., Rose, J. W., Xu, D., Lin, J., and Wang, B. (2000). Advances in dropwise condensation heat transfer: Chinese research. Chem. Eng. J. 78, 87–93. doi: 10.1016/S1385-8947(00)00155-8

CrossRef Full Text | Google Scholar

McCormic, J. L., and Baer, E. (1963). On the mechanism of heat transfer in dropwise condensation. J. Collide Sci. 18, 208–216. doi: 10.1016/0095-8522(63)90012-6

CrossRef Full Text | Google Scholar

Megaridis, C., Mahapatra, P. S., Ghosh, A., and Ganguly, R. (2016). Key design and operating parameters for enhancing dropwise condensation through wettability patterning. Int. J. Heat Mass Transf. 92, 877–883. doi: 10.1016/j.ijheatmasstransfer.2015.08.106

CrossRef Full Text | Google Scholar

Miljkovic, N., Enright, R., Nam, Y., Lopez, K., Dou, N., Sack, J., et al. (2012). Jumping-droplet-enhanced condensation on scalable superhydrophobic nanostructured surfaces. Nano Lett. 13, 179–187. doi: 10.1021/nl303835d

PubMed Abstract | CrossRef Full Text | Google Scholar

Miljkovic, N., Enright, R., and Wang, E. N. (2013). Modeling and optimization of superhydrophobic condensation. J. Heat Transf. 135:111004. doi: 10.1115/1.4024597

CrossRef Full Text | Google Scholar

Morita, M., Koga, T., Otsuka, H., and Takahara, A. (2005). Macroscopic-wetting anisotropy on the line-patterned surface of fluoroalkylsilane monolayers. Langmuir 21, 911–918. doi: 10.1021/la0485172

PubMed Abstract | CrossRef Full Text | Google Scholar

Narhe, R. D., and Beysens, D. A. (2007). Growth dynamics of water drops on a square-pattern rough hydrophobic surface. Langmuir 23, 6486–6489. doi: 10.1021/la062021y

PubMed Abstract | CrossRef Full Text | Google Scholar

Paxson, A. T., Yagüe, J. L., Gleason, K. K., and Varanasi, K. K. (2014). Stable dropwise condensation for enhancing heat transfer via the initiated chemical vapor deposition (iCVD) of grafted polymer films. Adv. Mater. 26, 418–423. doi: 10.1002/adma.201303065

PubMed Abstract | CrossRef Full Text | Google Scholar

Raj, R., Enright, R., Zhu, Y., Adera, S., and Wang, E. N. (2012). Unified model for contact angle hysteresis on heterogeneous and superhydrophobic surfaces. Langmuir 28, 15777–15788. doi: 10.1021/la303070s

PubMed Abstract | CrossRef Full Text | Google Scholar

Rose, J. W. (1976). Further aspects of dropwise condensation theory. Int. J. Heat Mass Transf. 19, 1363–1370. doi: 10.1016/0017-9310(76)90064-8

CrossRef Full Text | Google Scholar

Rose, J. W. (1998). Condensation heat transfer fundamentals. Chem. Eng. Res. Design 76, 143–152. doi: 10.1205/026387698524712

CrossRef Full Text | Google Scholar

Rose, J. W. (2002). Dropwise condensation theory and experiment: a review. Proc. Inst. Mech. Eng. Part A J. Power Energy 216, 115–128. doi: 10.1243/09576500260049034

CrossRef Full Text | Google Scholar

Schmidt, E., Schurig, W., and Sellschopp, W. (1930). Versuche über die kondensation von wasserdampf in film- und tropfenform. Tech. Mech. Thermodyn. 1, 53–63. doi: 10.1007/BF02641051

CrossRef Full Text | Google Scholar

Sikarwar, B. S., Khandekar, S., and Muralidhar, K. (2013). Mathematical modeling of dropwise condensation on textured surfaces. Sadhana 38, 1135–1171. doi: 10.1007/s12046-013-0190-9

CrossRef Full Text | Google Scholar

Song, Y., Xu, D., Lin, J., and Tsian, S. (1991). A study on the mechanism of dropwise condensation. Int. J. Heat Mass Transf. 34, 2827–2831. doi: 10.1016/0017-9310(91)90243-8

CrossRef Full Text | Google Scholar

Welch, J., and Westwater, J. W. (1961). Microscopic study of dropwise condensation. ASME Int. Dev. Heat Transf. 2, 302–309.

Google Scholar

Wu, W. H., and Maa, J. R. (1976). On the heat transfer in dropwise condensation. Chem. Eng. J. 12, 225–231. doi: 10.1016/0300-9467(76)87016-5

CrossRef Full Text | Google Scholar

Xiao, R., Miljkovic, N., Enright, R., and Wang, E. N. (2013). Immersion condensation on oil-infused heterogeneous surfaces for enhanced heat transfer. Sci. Rep. 3:1988. doi: 10.1038/srep01988

PubMed Abstract | CrossRef Full Text | Google Scholar

Zamuruyev, K. O., Bardaweel, H. K., Carron, C. J., Kenyon, N. J., Brand, O., Delplanque, J. P., et al. (2014). Continuous droplet removal upon dropwise condensation of humid air on a hydrophobic micropatterned surface. Langmuir 30, 10133–10142. doi: 10.1021/la5004462

PubMed Abstract | CrossRef Full Text | Google Scholar

Zou, L., Wang, H., Zhu, X., Ding, Y., Chen, R., and Liao, Q. (2018). Droplet splitting on chemically striped surface. Colloids Surf. A Physicochem. Eng. Aspects 537, 139–148. doi: 10.1016/j.colsurfa.2017.09.052

CrossRef Full Text | Google Scholar