Air Permeability of the Litter Layer in Broadleaf Forests

Fuel on the ground, such as leaves, twigs and decomposing matter, accumulate over time and account for a large percentage of the total fuel load in forests. In fire events, material on the ground is often referred to as a fuel bed. The air permeability of a fuel bed is a critical factor that influences fire behavior because it controls the amount of air or oxygen available for combustion within the fuel bed. The aim of this study is to provide a better understanding of the air permeability of the fuel beds in forests. The air permeability for different fuel beds were determined using experimental and theoretical methods. The pressure drop across the fuel bed samples were experimentally measured using a verified permeability testing rig. The air permeability was then calculated using Darcy's Law or the Forchheimer equation from the pressure drop measurements, depending on the Reynolds number. The particles in the fuel beds were characterized in terms of particle size and shape. Based on the particle characterization, the air permeability of the fuel beds was also calculated using the Kozeny-Carman equation. The results show that the experimental method is preferred when determining the air permeability for natural forest fuel beds due to the variability in the size and shape of the particles. The effect of Reynolds number on effective permeability was aslo investigated, and it was found that the transition from Darcian to non-Darcian flow occur at different Reynolds numbers for different fuel particles. For example, the transition occurs at 5 and 15 for gum bark and decomposing matter, respectively. The significance of this study is that it increases the ability to predict the air permeability of fuel beds in forests, which is essential for modeling wildland fire behaviors involving in porous fuel beds. All the samples were dried at 105°C to remove moisture in the samples.

Introduction

Wildfires are a recurring issue throughout summer and the drier months in many parts of the world. In addition to potential loss of life, wildfires cause tremendous economic loss. For example, the cost of the 2009 Victorian Black Saturday disaster in Australia is conservatively estimated at A$4.4 billion (Teague et al., 2010). Climate change is increasing the risk and impact of wildfires (Steffen and Hughes, 2013), hence greater economic impact can be expected without improved methods of wildfire mitigation. It is critical to develop a better understanding of wildfires, and models can be a good way to provide insights into wildfires. Rothermel's model investigates the influences of the physical fuel bed properties, such as packing ratio, fuel load, bulk density, surface area-to-volume ratio, on fire spread, and intensity (Rothermel, 1972). These physical fuel properties also affect permeability. As permeability affects combustion, fire behavior in fuel beds can be better modeled by improving the physical understanding of permeability in fuel beds.

Fuel beds account for a large percentage of fuel in forests (Biswell, 1989) and are especially important for wildfires, as it accounts for a large part of the fuel (Knapp et al., 2005). Modeling of their combustion needs to consider two different combustion regimes: smoldering and flaming (Wang et al., 2017). The combustion regime of a fuel bed can be controlled by oxygen availability (Hadden et al., 2011; Santoni et al., 2014; Huang and Rein, 2016; Wang et al., 2016, 2017), which is affected by the fuel bed's air permeability. The air permeability of a fuel bed, which can be considered a porous medium, characterizes the ease with which air can pass through it. Determining the air permeability of a fuel bed is challenging because of the diversity of the material in fuel beds. In the literature, fuel beds are often characterized based on particle size in order to simplify the analysis (Anderson, 1982; El-Sayed and Khass, 2013). Previous studies of the air permeability of biomass have been only performed on regular-shaped particles, such as pine needles and soy straw; which reveals a strong dependence of particle shape on the air permeability (Erić et al., 2011; Santoni et al., 2014; Fehrmann et al., 2017; Figueroa et al., 2019). However, to the best of the authors' knowledge, no research has been done on broadleaved forest, and therefore no such data are available in literature. Fuel moisture is a critical property that influences fire behavior and ignition probabilities (Nyman et al., 2018). Previous studies have shown that solar exposure is the driving force behind forest floor drying (Nyman et al., 2015, 2018). While, the pore sizes, and hence the permeability of fuel bed, could affect water infiltration and the propensity of the material to ignite and burn. Therefore, a better understanding of the permeability of fuel bed could help explain the heterogeneity of fuel moisture as well as propensity to burn.

The permeability of a porous medium can be determined using either Darcy's Law, or the Forchheimer equation, depending on the flow regime (Bear, 2013). The fundamental principle in determining the air permeability is based on the pressure gradient, for a particular flow velocity (Sobieski and Trykozko, 2014). The air permeability in fuel beds can also be calculated using the Kozeny-Carman equation, based on the physical properties of the porous medium. The Kozeny-Carman equation has been widely applied to flow through soils, sands, and synthetic materials (Mavis and Wilsey, 1937; Kyan et al., 1970; Chapuis and Aubertin, 2003). However, the validity of the Kozeny-Carman equation has not been demonstrated for particles in other natural forest fuel beds like twigs and leaves. Natural forest fuel beds are highly variable in shape and size, which means that rather than relying on simple correlations, experimental methods are needed to determine characteristics of fuel beds. The results may subsequently be used as an input data for models.

A considerable number of studies have focused on water and oil permeability of porous media, such as rocks and soil, which is relevant to the field of geology (Chapuis et al., 1989; Kamath et al., 1995; Chapuis and Aubertin, 2003). The testing rigs presented in the literature use water as the working fluid to determine the permeability of porous media. However, these testing rigs can only be used to determine the permeability of a porous medium which is not water-sensitive. For instance, these water permeability testing rigs are not suitable for many materials, such as biomass, coal and clay, in which the absorption of water will lead to changes in particle volume and the fuel bed structure. Therefore, the determination of permeability by gaseous fluids, such as air, is needed for these materials. However, there are only a few studies that determine the permeability of a porous medium by air, the air permeability of different materials, such as snow, soil, woven fabrics, and pine litters were determined (Corey, 1957; Shimizu, 1970; Ogulata, 2006; Santoni et al., 2014). The focus of the current study is on natural forest fuel beds, and as these materials are water-sensitive this study determines their permeability by air.

The overall aim of this study is to provide a better understanding of the air permeability of fuel beds and the interaction between flaming and smoldering in wildland fires, since the air permeability has significant effects on the fire behaviors of fuel beds. First of all, it is important to find a robust method of determining the air permeability of fuel beds. It is also necessary to examine whether the fuel bed material can be characterized in a way that is suitable for providing input data into models. The experiments described in this study were designed to investigate the air permeability of natural forest litter layer, and the effects of particle size and particle type on the air permeability. Due to the lack of data in the literature, the air permeability of natural forest fuel beds will be reported.

Methodology

Experimental Apparatus

The experimental testing rig was designed to determine the air permeability of a fuel bed by measuring the pressure drop across the fuel bed. The experimental testing rig consisted of three parts: a permeability testing rig, an air supply system and a manometer (Model 9565, TSI Inc., Shoreview, United States). The air permeability testing rig shown in Figure 1 has top and bottom sections. There is a dual air inlet and a bed of ceramic beads in the bottom section to obtain uniform flow through the fuel bed. Fuel bed samples were loaded in the top section of the air permeability testing rig.

FIGURE 1

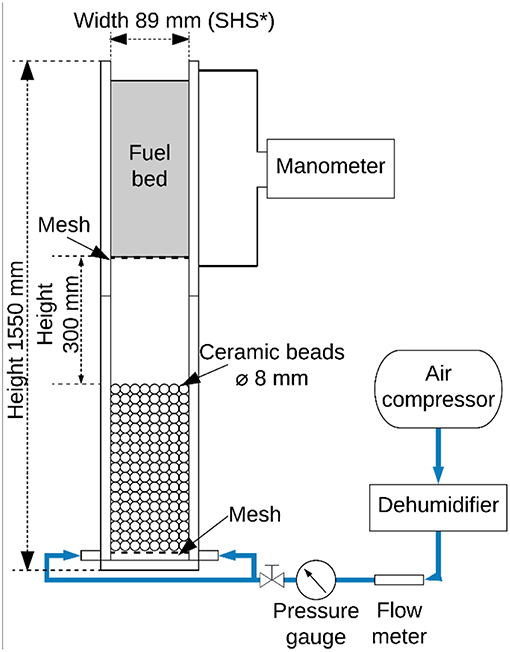
Figure 1. Schematic diagram of the experimental testing apparatus for the air permeability experiments (SHS, Square hollow section; Fuel bed depth varies from 50 to 350 mm).

The input air flow in this study was supplied by an air compressor, and the moisture in the input air flow was removed by a dehumidifier before introducing into the air permeability testing rig. By removing the moisture in the air, the accuracy of the input flowrate and the pressure drop measurements can be improved, and the uncertainties caused by the moisture in the ambient air can be minimized.

Experimental Setup and Procedure

The input air flow rate was varied from 20 to 160 L·min⁻¹ (42–337 mm·s⁻¹), with a 20 L·min⁻¹ increment. Below the lower limit (20 L·min⁻¹), the error in the pressure drop measurement significantly increases due to the range of the manometer. Above the upper limit (160 L·min⁻¹), the bed might start to fluidise. The input air flow rates (superficial velocities) in this paper were chosen to maximize the signal-to-noise ratio of the measurements; however, based on the subsequent curve-fits, these results are applicable at other flow velocities that would be encountered in a wildfire. The pressure before and after the fuel bed (Figure 1) was measured using the manometer through holes in the rig.

Prior to each experiment, fuel material was weighed and loaded into the rig. The fuel material was carefully loaded to create an unconsolidated fuel bed; this is to ensure the consistency throughout the fuel bed. The pressure drop (ΔP) across the fuel bed was based on a 60-s averaging period, with a 1 Hz sampling frequency.

Fuel Bed Samples Collection and Preparation

Three categories of fuel bed samples are used in this study: glass beads, milled biomass particles, and natural forest fuel particles. For the milled biomass particles, pulverized and dried pine chips, gum bark and gum leaves were used to represent the three common fuel types on forest floors, namely, leaves, bark, and twig. The pine chips samples are from Pinus radiata, and the bark and twig samples are from Eucalyptus camaldulensis. To reduce variability between samples, the pine chips, gum bark, and gum leaves were milled and sieved into three size ranges (1–2 mm; 2–3 mm; 3–4 mm).

All the forest fuel bed samples used in this study were collected from a forest in East Gippsland, Victoria (for more details about the collecting site, refer to Possell et al., 2015). This forest is located in one of the wildfire-prone areas of Victoria, Australia. Within the collecting site, three permanent circular plots with a radius of 5 m were established, at least 500 m apart, within similar vegetation types. The fuel samples were collected from these three plots, respectively. When collecting the fuel bed samples, especially the decomposing matter layer, attention was paid to ensure that inorganic matter, such as soils and sands, were not collected. After collecting the natural forest fuel bed, the samples were separated into three types: twig, leaf and decomposing matter. Then, the twig samples were sieved into three size ranges (>10 mm, 5–10 mm, <5 mm); and the decomposing matter samples were sieved into four size ranges (4–5 mm, 3–4 mm, 2–3 mm; 1–2 mm). To reduce uncertainty variability, and ensure experimental repeatability, the samples were dried sufficiently in an oven at 105°C for 24 h prior to experiments. Throughout the paper, the repeatability of measurements represented by ±1 standard deviation error bars.

Fuel Characterization

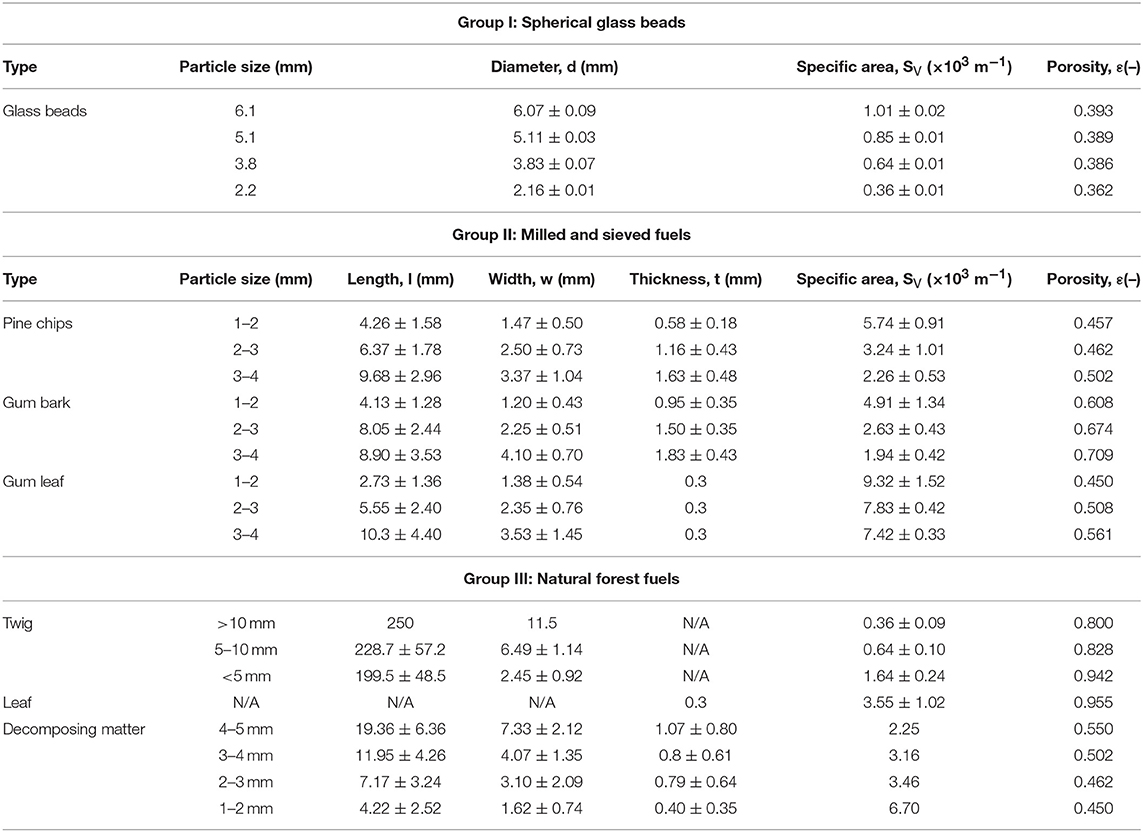
Fuel material was sieved and the fuel bed samples within each range were characterized based on physical size and projected area. The physical size of particles was measured using a micrometer and repeated for 20 samples of each fuel type. For milled biomass particles, the particle shape was assumed to be cuboid according to their apparent shapes. Hence, the length, width and thickness of particles were measured to calculate the specific area. For twigs, the samples were assumed to be cylindrical; so, the diameter and the length of twigs were measured. In the natural forest fuel particles, the projected areas of 20 randomly selected leaves were measured in order to determine the specific area, rather than assuming a regular shape. The leaf litter was not sieved due to its shape. The specific area of the decomposing matter was calculated based on the sieve aperture rather than measurements of the individual particles. The details of these measurements are listed in Table 1. The particle size grouping is based on the size of the sieve used to sort the material, apart from the glass beads which were monodisperse from the manufacturer.

TABLE 1

Table 1. Particles physical properties.

The porosities of the different fuel beds were measured. For glass beads, the porosity was measured using the fluid saturation method, in which water was used to fill the void volume of the glass beads bed. Then, the porosity was calculated through the ratio of the void volume and the total volume of the glass beads bed ($\epsilon =\frac{V_{void}}{V_{total}}$, where V_void is the void volume and V_total is the total volume of the glass beads bed). For the milled biomass and the natural forests fuel bed, the porosity was calculated based on the weight of the fuel bed and the particle density ($\epsilon =1-\frac{W_{fuelbed}}{{\rho }_p·V_{total}}$, where W_fuelbed is the weight of the fuel bed and ρ_p is the particle density), as these fuel beds are all hygroscopic. The porosity measurements are included in Table 1.

Figure 2 presents the mass distribution of the (a) twigs and (b) decomposing matter in the forest fuel bed. The results in Figure 2A imply that the thin twigs, with <5 mm particle size, contribute ~50% of the total mass in the twig litter. Similarly, the majority of the decomposing matter is smaller than 5 mm. Even though much of the forest fuel bed visually appears large, the size distribution presented in Figure 2 shows that the majority of the particles in the twigs and decomposing matter is smaller than 5 mm. From the point view of the air permeability, these small particles have significant effects on the air permeability of fuel bed.

FIGURE 2

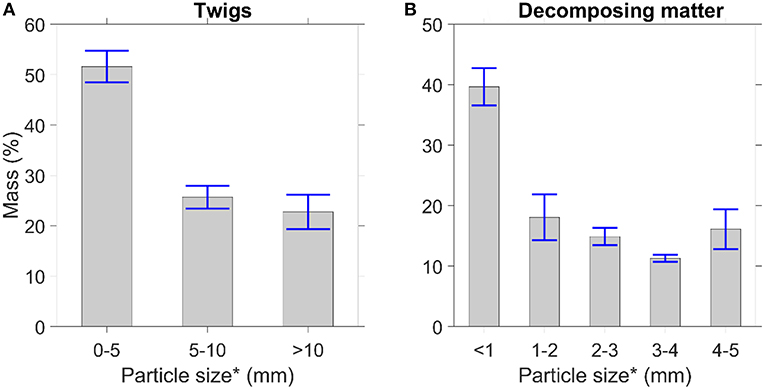
Figure 2. Mass distribution as function of particle size for natural forest fuel bed. Particle size is based on sieve aperture. (A) Twigs. (B) Decomposing matter. *Sieve opening sizes.

Based on the results of Figure 2, the focus of this study is on the air permeability of small particles (<5 mm) within the fuel bed that is an unconsolidated porous medium. To better understand the air permeability of the fuel bed, three common biomass samples, pine chips, gum bark, and gum leaf were milled and sieved. By milling and sieving the particles the results can be better controlled for repeatability, but the generality of the results still applies to the actual particles in the litter layer.

Calculation of the Fuel Bed Permeability

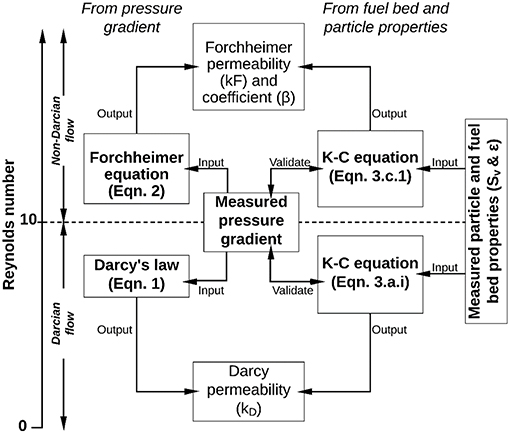
The air permeability of a porous medium particularly an unconsolidated fuel bed can be determined from pressure gradient measurements or from the fuel bed/particle properties. In this study, both methods are used to determine the air permeability of different porous media. A schematic diagram outlining how the air permeability was determined in this study is summarized in Figure 3.

FIGURE 3

Figure 3. Schematic diagram for determining the air permeability of a fuel bed.

The pressure gradient method is an empirical approach that does not need any information about the particle properties such as particle size. For the pressure gradient method, the air permeability was directly determined from the measured pressure gradient using Darcy's Law for Darcian flow regime, while the Forchheimer equation was used to determine the air permeability and the Forchheimer coefficient within the non-Darcian flow regime. It should be noted that Darcy's Law is only applicable in the Darcian flow regime, namely when the Reynolds number, Re_d < 10 (Hassanizadeh and Gray, 1987; Chapman, 2012; Sukop et al., 2013). Here, Re_d = ρ·U₀·d/μ, where U₀ is superficial velocity and d is the average particle diameter (Sobieski and Trykozko, 2014). For non-Darcian flow (Re_d > 10), the Forchheimer equation may be used.

For the fuel bed/particle properties method, the specific area of particle (S_v) and the porosity (ε) of fuel bed were measured to calculate the pressure gradient and the air permeability using the Kozeny-Carman equation. The calculated pressure gradient was compared with the measured pressure gradient to validate the Kozeny-Carman equation. Similar research has been conducted on the air permeability of pine needle fuel beds and the air permeability of fuel bed was calculated using Darcy's Law and the Kozeny-Carman equation (Santoni et al., 2014). However, both Darcy's Law and the Kozeny-Carman equation (Equation 3.a) can only be applied when Re_d < 10 (Hassanizadeh and Gray, 1987). This is because, as the air flow velocity increases, the experimental results do not agree with Darcy's law due to inertial effects (Forchheimer, 1901).

Darcy's Law

Permeability (isotropic permeability in this study) can be determined by using Darcy's Law (Equation 1) from the pressure gradient and the superficial velocity. Darcy's Law is only valid for Darcian flow, i.e., Re_D < 10, i.e., lower-velocity flow.

$\begin{array}{ll}{\nabla \text{P}}_D=\frac{\Delta P}{L}=\frac{\mu }{k_D}{U}_0& (1)\end{array}$

Equation (1) shows that the pressure drop of Darcian flows in the porous medium is proportional to the fluid dynamic viscosity and velocity. The pressure drop of Darcian flows in porous medium is mainly attributed to the skin friction of porous medium wall surface in porous voids (particle surfaces of the fuel bed in this study).

Forchheimer Equation

The air permeability of a porous medium in a non-Darcian flow (Re_d > 10) can be determined based on the Forchheimer equation (Equation 2). The difference between the Forchheimer equation (Equation 2) and Darcy's Law (Equation 1) is that the Forchheimer equation includes an additional new term to incorporate the importance of kinetic energy loss due to inertial effects in non-Darcian flows. When the flow velocity increases, the pressure drop due to inertial effects (for example the change of flow cross section area in porous pores) increases and needs to be considered when Re_d is larger than 10. As a result, the relationship between the superficial velocity and the pressure gradient is a quadratic function in non-Darcian flows. The air permeability determined through the Forchheimer equation in this paper is referred to as the Forchheimer permeability (k_F), to distinguish it from the permeability from Darcy's Law (k_D). To characterize a porous medium in non-Darcian flow, the Forchheimer permeability and the Forchheimer coefficient are required.

$\begin{array}{ll}{\nabla \text{P}}_F=\frac{\Delta P}{L}=\frac{\mu }{k_F}{U}_0+\beta ·\rho ·{U_0}^2& (2)\end{array}$

The air permeability can be determined by either Darcy's Law or the Forchheimer equation, depending on the flow regime. These methods require the experimental data of the pressure gradient and the superficial velocity, which means that a similar experiment (as stated in section Experimental Apparatus) has to be conducted before using Darcy's Law or the Forchheimer equation.

Kozeny-Carman Equation

For flows through unconsolidated beds of fuel particles, the pressure gradient can be calculated from the particle and fuel bed properties using the Kozeny-Carman (K-C) equation (Equations 3.a, b; Holdich, 2002). Equation (3.a) is for Darcian flows, while Equation (3.b) is for non-Darcian flows. In the non-Darcian flow condition, a modified Reynolds number, Re₁ (Equation 5) is required to calculate the friction factor term, $\frac{R}{\rho •U^2}$ (Equation 4). Within the Darcian flow regime, the air permeability can be calculated by rearranging the Kozeny-Carman equation, i.e., Equation (3.a.i). In the non-Darcian flow condition, the air permeability and the Forchheimer coefficient can be calculated by Equations (3.c.i, ii).

$\begin{array}{ll}{\nabla \text{P}}_{\text{KC},\text{D}}=\frac{\Delta P}{L}=\mu (\frac{K{(1-\epsilon )}^2{S_V}^2}{{\epsilon }^3})U_0& (\mathrm{3a})\end{array}$

From Equation (3.a), the air permeability can be calculated using the following equation based on Equation (1):

$\begin{array}{ll}{K}_{KC,D}=\frac{{\epsilon }^3}{K{(1-\epsilon )}^2{S_V}^2}& (\mathrm{3.a.i})\end{array}$

For non-Darcian flows, the friction factor can be represented using the Carman correlation (Equation 4) and the friction can be represented as a function of the modified Reynolds number (Carman, 1956; Holdich, 2002).

$\begin{array}{ll}\frac{R}{\rho U^2}=\frac{5}{R{e}_1}+\frac{0.4}{{R{e}_1}^{0.1}}& (4)\end{array}$

The modified Reynolds number (Reynolds number varies from 4.9 to 263 in this study) is calculated using Equation (5).

$\begin{array}{ll}R{e}_1=\frac{\rho U_0}{(1-\epsilon )S_V\mu }& (5)\end{array}$

Thus, for non-Darcian flows, the following equation can be used to calculate the pressure drop in the fuel bed.

$\begin{array}{ll}{\nabla \text{P}}_{KC,F}=\frac{\Delta P}{L}=(\frac{R}{\rho U^2})\frac{S_V(1-\epsilon )\rho {U_0}^2}{{\epsilon }^3}& (\mathrm{3.b})\end{array}$

By substituting the Carman correlation (Equation 4) into the friction factor, $\frac{R}{\rho •U^2}$ in Equation (3.b), Equation (3.c) shows Equation (3.b) in Forchheimer form:

$\begin{array}{l}{\nabla \text{P}}_{KC,F}=\frac{\Delta P}{L}=\frac{5{(1-\epsilon )}^2{S_V}^2}{{\epsilon }^3}\mu U_0\\ +[\frac{0.4{(1-\epsilon )}^{1.1}{S_V}^{1.1}{\mu }^{0.1}}{{\rho }^{0.1}{\epsilon }^3{U}_0}]\rho {U_0}^2& (\mathrm{3.c})\end{array}$

From Equation (3.c), the air permeability and the Forchheimer coefficient can be calculated using the following equations based on Equation (2):

$\begin{array}{ll}{k}_{KC,F}=\frac{{\epsilon }^3}{5{(1-\epsilon )}^2{S_V}^2}& (\mathrm{3.c.i})\end{array}$

$\begin{array}{ll}{\beta }_{KC}=\frac{0.4{(1-\epsilon )}^{1.1}{S_V}^{1.1}{\mu }^{0.1}}{{\rho }^{0.1}{\epsilon }^3{U}_0}& (\mathrm{3.c.ii})\end{array}$

To overcome the discrepancy between experimental results and Darcy's law, Forchheimer (1901) suggested adding a kinetic energy term to Darcy's Law. In this study, for the cases with Re_d >10, the air permeability was calculated using the Forchheimer equation. To calculate the air permeability of fuel bed using the Forchheimer equation, the pressure drop across fuel bed is required. The pressure drop can either be measured experimentally or calculated using the function of pressure gradient and superficial air velocity. Similarly, the Kozeny-Carman equation can be modified to account for non-Darcian flow (Equation 3.b).

Computational Fluid Dynamic Modeling

A CFD model of the testing apparatus for the air permeability has been developed and then been employed to simulate the flows in the testing apparatus with different fuel particles. For further details, please refer to Supplementary Material Part A.

Results

Spherical Glass Beads

Due to the diversity and complexity of natural forest particles, benchmarking experiments using well-controlled particles are first presented. These not only verify the reliability of the experimental testing apparatus, but can also be used as a reference for the natural forest samples. Hence, a set of experiments were conducted using the experimental testing apparatus for regular-shaped spherical glass beads.

Figure 4A shows that, for spherical glass bead particles, the pressure gradient calculated using the Kozeny-Carman equation shows good agreement with the measured pressure drop. The results in Figure 4A demonstrate that the experimental testing apparatus is reliable and gives an approximate value for the pressure gradient that may be expected for forest fuels of a similar size.

FIGURE 4

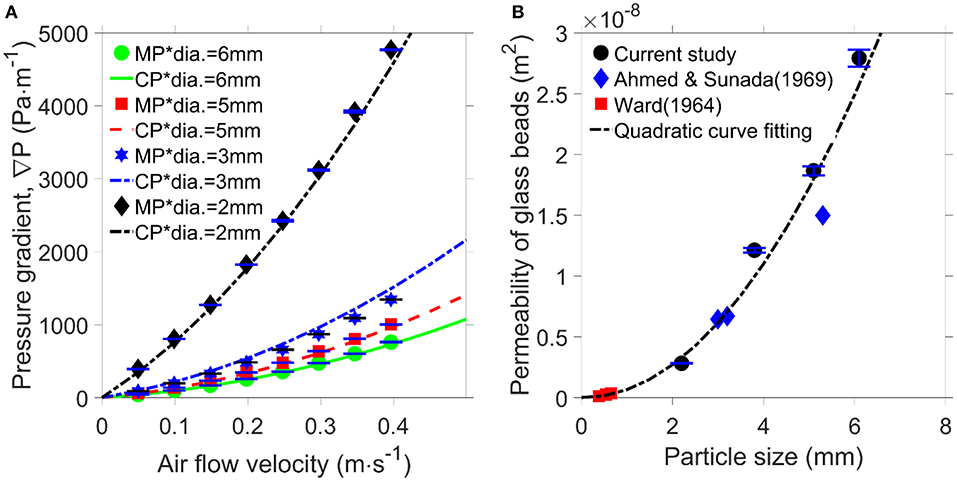
Figure 4. Spherical glass bead particle results. (A) Pressure gradient as a function of air flow velocity for various sized particles. MP* is the measured pressure gradient and CP* is the calculated pressure gradient calculated using the Kozeny-Carman equation. (B) Air permeability measurement compared with previous studies (Ward, 1964; Ahmed and Sunada, 1969).

The air permeability and the Forchheimer coefficient of glass beads were calculated using the Forchheimer equation, because at all of the measured flowrates in this study, the flow is non-Darcian (Re_d > 10). The comparison in Figure 4B between the air permeability from the current results and previous studies (Ward, 1964; Ahmed and Sunada, 1969) gives further confidence in the experimental apparatus. Worth noting is that the permeability in the current study is with air as a working fluid, whereas the previous studies used water. Permeability is a fundamental property of a porous bed and ought to be independent of the fluid (Green and Ampt, 1911), which is demonstrated in Figure 4B. The equation of the quadratic fitting is k = 7.02E⁻⁴·d² – 5.34E⁻¹¹·d, and confidence level is. 0.9616. According to Equations (3.a.i) and (3.c.i), the permeability is in inverse proportion to the square of specific surface area (Sv). For glass beads, the specific surface area is also inversely proportional to the diameter of glass beads. Therefore, the permeability of glass beads fit with particle size in a quadratic function. Note that the pore sizes of the fuel beds in the study are much larger than the mean free path of air particles so the Klinkenberg effect can be safely neglected for air flows (Tanikawa and Shimamoto, 2006).

The air permeability can be calculated using the Kozeny-Carman equation (Equations 3.a.i or 3.c.i) if the specific area is known. In the case of a sphere of diameter D, the specific area, $S_V=\frac{6}{D}$. In both Equations (3.a.i) and (3.c.i), the permeability is inversely proportional to the square of the specific area. On this basis, Figure 4B includes a quadratic curve fitting which shows a good agreement with the experimental results. Hence, this confirms that a quadratic relationship between the air permeability and particle size may be used for subsequent analysis.

The Forchheimer permeability and the Forchheimer coefficient of glass beads are listed in Table C.1. The results of the Forchheimer coefficient show that an increase in the particle size of glass beads decreases the Forchheimer coefficient. According to the Forchheimer equation, the increase in the Forchheimer coefficient implies that the kinetic energy loss of air is higher in small particles than that in large particles.

Table C.1 also includes measured air permeability of soy straw (Erić et al., 2011) and pine needles (Santoni et al., 2014), which are other fuel beds reported in the literature. Although the size of soy straw was not reported in the paper (Erić et al., 2011), the size of soy straw particles is typically smaller than 6 mm. Despite the particle size of the fuels being in the same range as the glass beads, the permeability was much higher. Hence, the results imply that particle shape has an effect on the air permeability and, therefore, needs to be determined for the irregular-shaped particles encountered within the fuel bed.

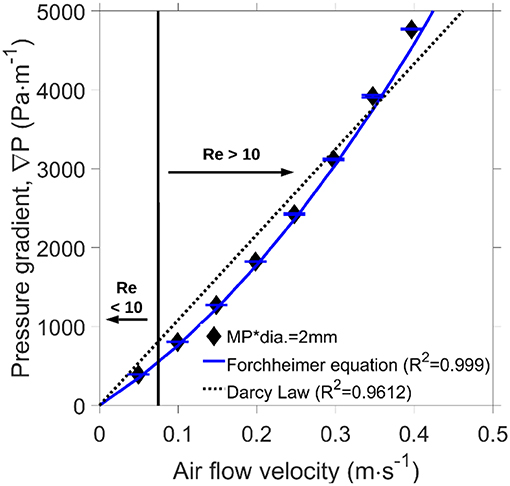
A comparison between the Darcy law and Forchheimer equation on 2 mm spherical particles is shown in Figure 5. The Forchheimer fitting (R² = 0.999) in Figure 5, shows a better agreement with the experimental data than the Darcy fitting (R² = 0.9612). This is because the Darcy law is only valid under Darcian flow (Re < 10); while most of the flows in this study are not in the Darcian flow regime. Hence, the Forchheimer equation should be used to determine the permeability of fuel beds.

FIGURE 5

Figure 5. A comparison between the Darcy law and Forchheimer equation on 2 mm spherical particles.

Milled Fuel Particles

After verifying the reliability of the experimental testing apparatus using regular-shaped particles (section Results), a set of similar experiments were conducted for milled and sieved pine chips. Compared with glass beads, the milled biomass particles are more irregular in shape, and the behavior of a porous medium made from them is expected to be more complex than that of the glass beads. In the case of spherical particles, it is accepted that the pressure gradient is independent of the bed depth. In the case of the irregular biomass fuel particles, this independence has not yet been confirmed in the literature. Hence, Figure 6 assesses the linearity of the pressure drop measurements, as a function of bed depth, for a range of different particle size milled pine chips.

FIGURE 6

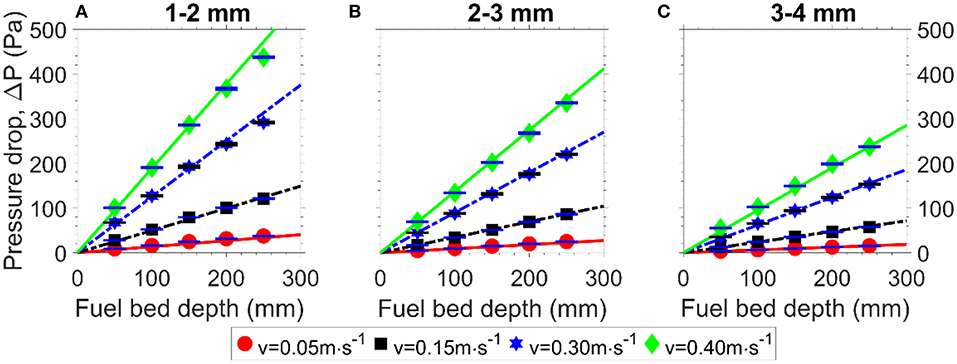
Figure 6. Measured pressure drop as a function of the fuel bed depth for (A) 1–2 mm, (B) 2–3 mm, (C) 3–4 mm milled pine chip particles across a range of air flow velocities.

Overlaid on the experimental data points in Figure 6 are lines of best fit. It is apparent that the pressure drop across fuel bed is indeed linear with the fuel bed depth, which means that the pressure gradient of fuel bed is constant with a specific superficial velocity. In other words, the pressure gradient of fuel bed is dependent of fuel type, particle size, and superficial air velocity. Hence, the pressure drop only needs to be measured at a single fuel bed depth, and can be inferred for other depths. For the remainder of the tests, only the deepest fuel bed was used, so as to maximize the pressure drop and thus minimize the uncertainty in the pressure gradient.

In Figure 7, the experimentally measured pressure drop is plotted (as per Figure 7) and overlaid with the calculated pressure drop using the Kozeny-Carman equation based on the direct measured specific area of the particles and porosity (Table 1). The error-bars on the lines are determined from the resultant variability in the specific area, i.e., one standard deviation of the mean. Even accounting for the large error-bars, the calculated pressure drop based on the Kozeny-Carman equation is consistently higher than the measured values. The discrepancy between the calculated and measured pressure drop implies that the direct measured specific area is not the actual specific area of particle. This is because the direct measured specific area assumes a regular shape, which is unlikely to be the case for the biomass fuel. The specific area and the pore structure of the actual fuel bed are different from that of the bed of regular spheres, leading to different energy losses and, therefore, different pressure drops as shown in Figure 7.

FIGURE 7

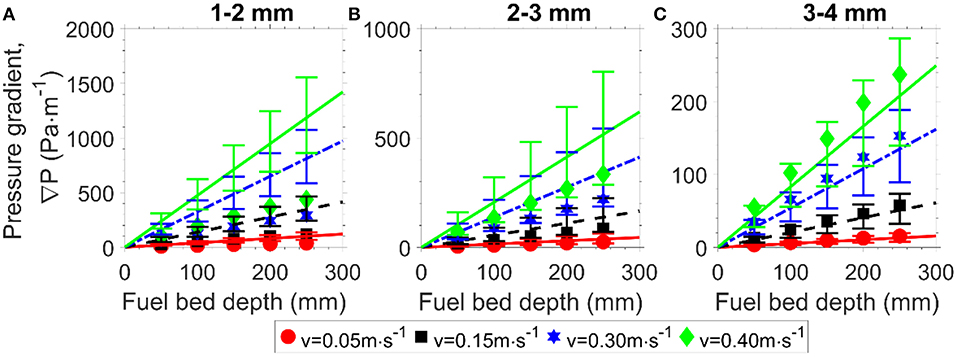
Figure 7. Pressure gradient measured directly (markers) and calculated from the direct measured specific area (lines) as a function of fuel bed depth for pine chips over a range of air flow velocities. Error bars denote the calculated pressure drop based on the measure specific area through the Kozeny-Carman equation. Particle size ranges: (A) 1–2 mm, (B) 2–3 mm, (C) 3–4 mm.

Based on the results of Figure 7, it is deduced that the Kozeny-Carman equation is not able to accurately predict the pressure drop of the actual fuel bed. This could be due to the errors in the assumptions used to determine the specific area. Instead, based on the measured pressure drop, the Kozeny-Carman equation (Equation 3.c) has been used to back-calculate the specific area. The results of this deduced specific area are compared to the direct measurements in Figure 7 for the various particle types and sizes.

Figure 8 shows the comparison between the direct measurement of the specific area and the deduced specific area, based on the Kozeny-Carman equation and pressure drop measurement, for the milled particles. The deduced measured specific area in Figure 8 is the average of the specific area calculated at the different superficial velocities. Hence, the specific area cannot accurately be determined for small particles, which are also the ones responsible for the majority of the pressure drop (Figure 4) and mass distribution (Figure 2) in a forest fuel bed. Therefore, to determine the pressure gradient using the Kozeny-Carman equation a correction of the direct measured specific area of the particles is required.

FIGURE 8

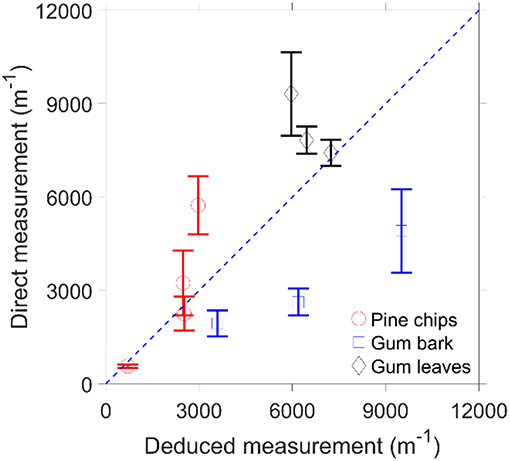
Figure 8. Comparison of the direct measurement and the measurement through pressure gradient of the specific area under the different particle size.

Figure 9 presents the measured pressure gradient (markers) and the calculated pressure gradient (lines) against the superficial velocity. The consistency between the measured and calculated pressure gradients show that the relationship between the pressure gradient and the superficial velocity is quadratic for the milled biomass fuel beds, as the pressure gradient in the Kozeny-Carman equation is a function of the square of the superficial velocity. The results in Figure 9 also show that for the same particle size and superficial air velocity, milled gum leaf particles have the highest pressure gradient and milled gum bark has the lowest pressure gradient. The difference in pressure gradient implies that fuel type has significant effects on the pressure gradient of a fuel bed, as different fuel type results in different shapes of milled particles.

FIGURE 9

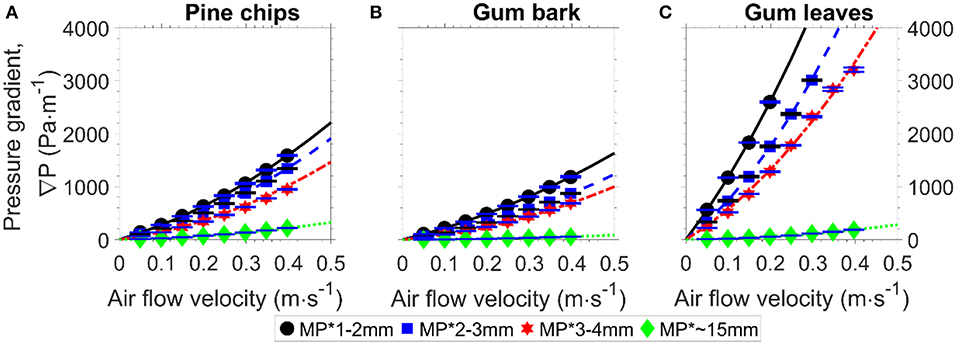
Figure 9. Pressure gradient as a function of air flow velocity for particles: (A) pine chips, (B) gum bark, (C) gum leaves (Marker, measured pressure gradient; Line, calculated pressure gradient based on deduced measured specific area).

The results in Figure 10 show that the air permeability of the fuel bed with small particles (<4 mm) is much less than that of the fuel bed with large particles (~15 mm). Furthermore, small particles contribute much more mass in natural forest fuel beds (Figure 2). Hence, small particles are expected to dominate the permeability. As discussed in section Spherical Glass Beads, the relationship between the air permeability and particle size is quadratic according to the Kozeny-Carman equation. The results shown in Figure 9 imply that the Kozeny-Carman equation is applicable for the milled biomass particles. So, theoretically, the air permeability of the milled biomass fuel beds can be presented as a function of the square of particle size. The air permeability can be calculated from either pressure gradient or the particle/fuel bed properties. However, the pressure gradient needs to be obtained by conducting the experiments because the measured specific area of particles is not robust enough for the Kozeny-Carman equation. Alternatively, the air permeability of the milled biomass fuel beds can be estimated based on the average particle size, as it is easier to measure the particle size.

FIGURE 10

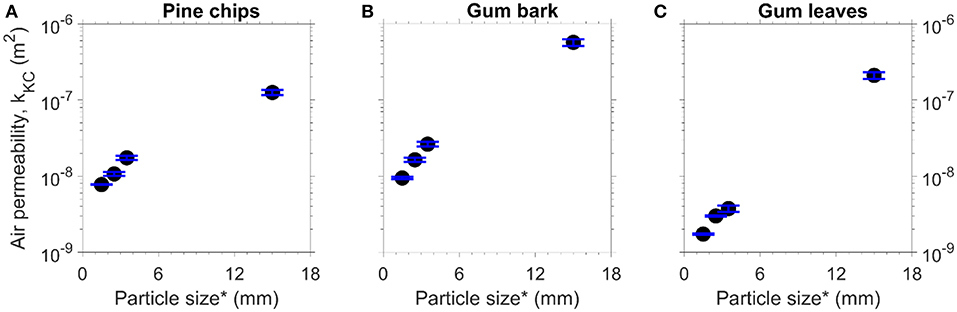
Figure 10. Permeability (k) by K-C Equation as a function of particle size for the milled particles (*average sieve opening size) (A) pine chips, (B) gum bark, (C) gum leaves.

The Forchheimer permeability and the Forchheimer coefficient of milled biomass fuel are listed in Table C.2. The results in Table C.2 show that for the same particle size, the air permeability of the pine chips beds is similar to that of the gum bark beds. The similar air permeability between the pine chips and gum bark beds is because the shape of these two fuel particles is also quite similar. The air permeability of the gum leaf beds is much lower (approximately one fifth) than those of the pine chips and gum bark beds for the same particle size. The shape of the milled leaf particle is flaky, which makes it easier for the leaf particles to create a more compact fuel bed compared to the milled pine chips and gum bark. Hence, these data imply that the particle shape has a significant effect on the air permeability, and this effect could be much higher than the effect of particle size on the air permeability.

Natural Fuel Particles

The results of the three milled biomass particles are shown in section Conclusions, where the fuel particles were broken down into small sizes using a mill. However, fuel particles in the real world are broken down through the natural decomposition processes so the shape of particles in forests may be quite different from the milled fuel particles. As discussed in section Conclusions, the particle shape has a significant effect on the air permeability. Therefore, it is important to determine the air permeability of the natural forest fuel particles.

The results in Figure 11 suggest that it is necessary to calculate the specific area for the twig particle no matter the size of the twig particle, as the deduced specific areas do not agree with the measured specific areas. The twig samples were assumed to be cylindrical when calculating their specific area; while the twig samples are so diverse that they cannot be represented by a cylindrical particle. For the decomposing matter particles (Figure 11), the deduced specific areas are in good agreement with the measured specific areas.

FIGURE 11

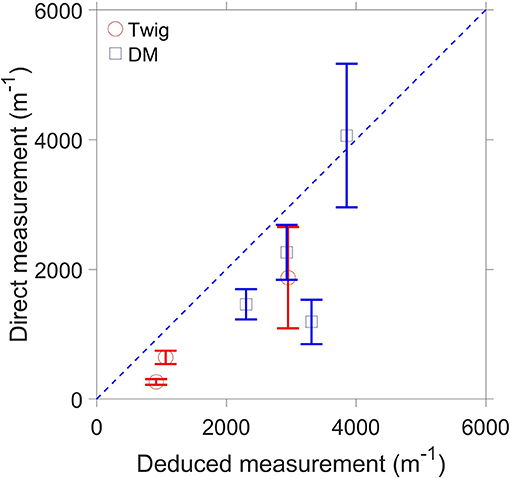
Figure 11. Comparison of the direct measurement and the measurement through pressure gradient of the specific area under the different particle size. DM, decomposing matter.

Figure 12 shows the measured pressure gradients (markers) and the calculated pressure gradients (lines) against the superficial velocity for the natural forest fuel particles. The calculated pressure gradient was calculated using the Kozeny-Carman equation (Equation 3.c) based on the deduced measured specific area. The results in Figure 12 show that the measured and calculated pressure gradients are in good agreement, and this implies that the fuel bed made of the natural forest fuel material can be represented using the Forchheimer equation and the Kozeny-Carman equation. In comparison to the milled biomass, for the same particle size, the pressure gradient vs. the superficial velocity curves of the decomposing matter beds are similar to those of the pine chips beds.

FIGURE 12

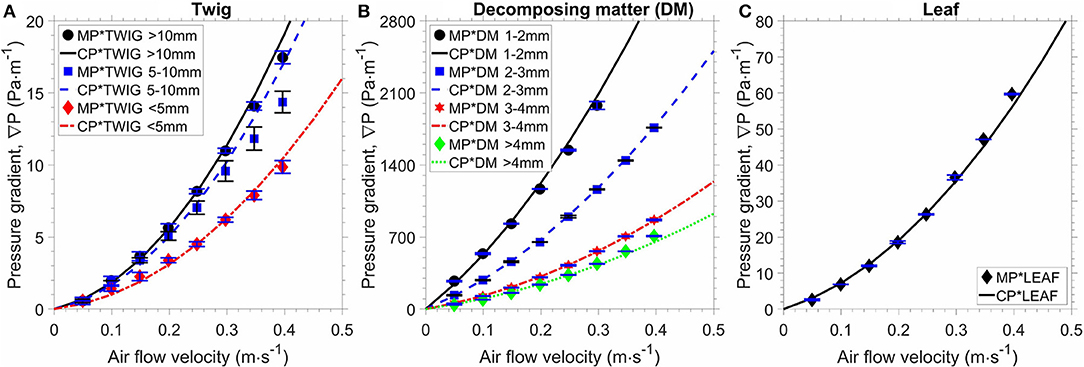
Figure 12. Pressure gradient as a function of air flow velocity for particles: (A) twig, (B) decomposing matter (DM), (C) leaf. (MP*, measured pressure gradient; CP*, calculated pressure gradient based on the deduced measured specific area).

Based on the quadratic function of the pressure gradient and the superficial air velocity, the pressure gradient for each natural forest fuel bed particle size at a given superficial air velocity can be calculated. Similarly, the Forchheimer permeability was calculated based on the Forchheimer equation and the function of the pressure gradient vs. the superficial velocity. However, similar to the milled biomass fuel particles, it is also difficult to measure the specific area of the natural forest fuel particles.

Figure 13A shows that the particle size does not have a significant effect on the air permeability for the twig particles in the range of particle sizes investigated in the current study. Figure 13B shows that decomposing matter shows a similar trend to the milled particles, i.e., a decrease in particle size decreases the air permeability. This is because the porosity of the twig fuel bed is much larger than that of the decomposing matter fuel bed. As shown in Figure 12B, the Kozeny-Carman equation is validated for the decomposing matter. Hence, the relationship between the air permeability of the decomposing matter beds and particle size is quadratic.

FIGURE 13

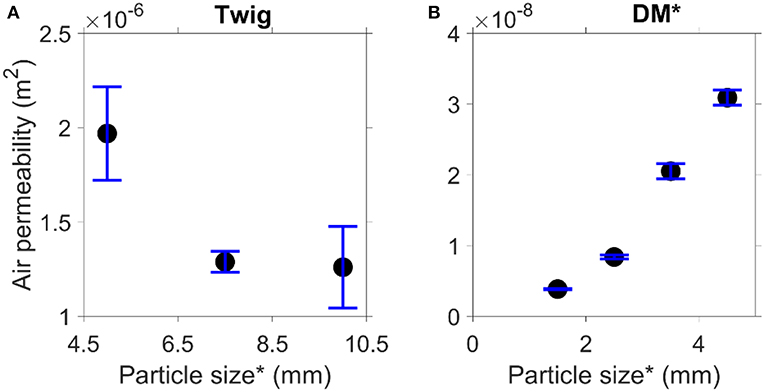
Figure 13. Permeability (k) as a function of particle size (*Average sieve opening size) (A) twig, (B) decomposing matter (DM).

The Forchheimer permeability and Forchheimer coefficient of the natural forest material are listed in Table C.3. The results in Table C.3 show that the Forchheimer permeability of the twig and leaf samples are much higher than that of decomposing matter, which are up to 512 times and 123 times higher for the twig and leaf samples, respectively. In comparison with the results of the milled biomass particles (Table C.2), it was found that for the same fuel type, the change in particle size has less effect on the air permeability than the fuel type. In the natural forest material, different fuel types have different particle shapes implying that the particle shape has a significant effect on the air permeability. Therefore, it is expected that fire behavior will be different within the different fuel beds of a natural forest due to differences in air permeability.

Discussion

Darcy's Law and the Forchheimer equation are the two basic equations used to determine the air permeability of a porous medium, depending on flow regime. The Darcy permeability is not always equal to the Forchheimer permeability. Theoretically, the Darcy permeability can only be used to characterize a porous medium in Darcian flow; while the Forchheimer permeability is to characterize a porous medium in non-Darcian flow. In Darcian flows the superficial velocity is very low, leading to a small pressure drop which is difficult to measure accurately. Furthermore, the transition from Darcian to non-Darcian flow in a porous medium is vague. The transition from Darcian to non-Darcian flow can occur over a range of Reynolds number from 1 to 10 (Hassanizadeh and Gray, 1987; Tindall et al., 1999; Chapman, 2012; Bear, 2013).

The effective permeability was calculated using Darcy's law. The effective permeability (markers) and the Darcy's permeability (lines) are presented in Figure 14. The results in Figure 14 show that the effective permeability starts to decrease when Reynolds number is over 10, which is the upper limit of Darcy's law. This is because when Reynolds number is equal to, or below 10, the effective permeability is equal to the Darcy permeability of fuel bed. For the samples with low air permeability (gum leaf and decomposing matter), the upper limit of Darcy's law is slightly higher than 10. This finding is also reported by Sobieski and Trykozko (2014). For these cases, the Darcy permeability is equal to the effective permeability within the Darcian flow regime.

FIGURE 14

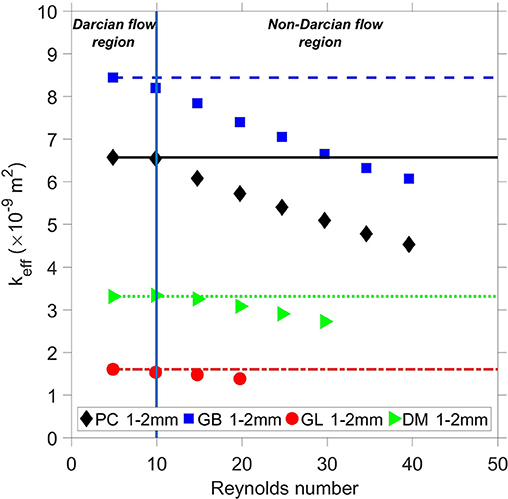
Figure 14. Effective permeability (k_eff) as a function of Reynolds number. PC, pine chips; GB, gum bark; GL, gum leaf; DM, decomposing matter.

As mentioned previously, it is difficult to measure the pressure drop across the fuel bed in Darcian flow, as the pressure drop is too low to measure. Darcy's law requires the pressure gradient to determine the Darcy permeability. Hence, a different method is needed to determine the Darcy permeability. One method is to calculate the Darcy permeability using the Kozeny-Carman equation. In this way, the Darcy permeability of a porous medium is calculated based on the specific area of particles and the porosity of the porous medium (Equation 3.c). The measured and calculated Darcy permeability for all samples is listed in Table C.3. Comparing the Darcy permeability in Table C.3 with the Forchheimer permeability in Tables C.1, C.2, and C.3, the Darcy permeability of the decomposing matter particles is close (with a maximum difference of 25% at 3–4 mm) to the Forchheimer permeability for the same size, which means that the Darcy permeability can be assumed to be the same as the Forchheimer permeability for the decomposing matter particles.

It has been reported previously that an increase in the moisture content of soy straw fuel bed significant decreased the permeability of that fuel bed (El-Sayed and Khass, 2013). As all the samples was pre-dried in this study, it is expected that the actual permeability of fuel bed in a forest will be lower than the permeability reported in this study due to higher moisture contents.

Conclusions

This paper investigated the air permeability of fuel beds in forests, from the perspective of its effect on the combustion of fuel beds. An experimental testing apparatus was designed and developed to investigate the effects of particle size and type on the air permeability. Three common biomass fuel types: pine chips, gum bark and gum leaf were milled and sieved into three sizes (1–2 mm; 2–3 mm; 3–4 mm). The air permeability of milled biomass fuel was also determined by experiment and calculation. The results show that the calculated pressure drop (Equation 3.c) is not in good agreement with the measured pressure drop. This is because it is difficult to accurately measure the specific area of particles due to their irregular shape. Hence, the air permeability of the porous medium made of the milled biomass particles can only be determined by experiment.

Natural forest fuel bed samples were separated into three categories: twig, leaf, and decomposing matter; and the twig and decomposing matter were sieved into three (0–5 mm; 5–10 mm; >10 mm) and four sizes (1–2 mm; 2–3 mm; 3–4 mm; >4 mm), respectively. The air permeability of a natural forest fuel bed was determined by experiment and calculation. Similar to the milled biomass fuel particles, the results show that the calculated pressure drop (Equation 3.c) does not match with the measured pressure drop due to the inaccuracy of the specific area estimations. The air permeability in natural forest fuel varies in different fuel types. For example, the air permeability of the twig layer is much larger (~500 times) than that of the decomposing matter layer. Particle size does not have a significant effect for twigs, and the relationship between the air permeability and particle size is quadratic for decomposing matter.

In most of the cases, it is difficult to run the experiments with a Darcian air flow because the pressure drop is too low to reliably measure. By determining the effective permeability, the results show that the upper limit of Darcy's law for the low air permeability fuel bed is slightly higher than 10. The Darcy permeability was calculated using the Kozeny-Carman equation and the results show that the Darcy permeability is similar to the Forchheimer permeability. More research is needed to better understand the relationship between the air permeability and the combustion of the forest fuel beds. The data presented in this paper is intended to be used for validation of subsequent models. The model can then be used to model the air flow in forest fuel beds.

Data Availability

The datasets for this manuscript are not publicly available. Requests to access the datasets should be directed to aG91emhpLndhbmcmI3gwMDA0MDthZGVsYWlkZS5lZHUuYXU=. The datasets for this manuscript are included in Supplementary Material Part B.

Author Contributions

HW conducted a thorough literature review and identified the research gaps of the paper. After discussion with the other co-authors, a detailed research methodology and experimental plan were decided. According to the plan, HW designed and developed an experiment testing rig. HW tested and calibrated the testing rig. The fuels used in this study were collected by one co-author, MP. HW prepared the fuel samples for the experiments. HW did preliminary experiments using the testing rig. HW discussed the preliminary experiments with the other co-authors, then, HW modified the testing rig based on feedback from the other co-authors. HW set up the experiments. HW conducted all the experiments and collected experimental data independently. HW processed, analyzed, and interpreted all the experimental data. HW performed an analysis of the experimental results, and the analysis was presented in text or figures by HW. HW interpreted data and wrote the manuscript. HW also acted as the corresponding author, responded to the reviewers', the editor's comments and recommendations. PE, PM, CB, ZT, MP, and XH provided feedback, supervised the development of work, helped in data interpretation, and manuscript evaluation.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The support of the University of Adelaide, Australian Government Research Training Program Scholarship, the Bushfire and Natural Hazards CRC, NSFC (No. 51876183), and HK PolyU (1-BE04) are gratefully acknowledged. The authors thank Mr. Marc Simpson for his assistance throughout the experimental campaign. We also thank two reviewers for their insightful comments and suggestions on the previous versions of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2019.00053/full#supplementary-material

References

Ahmed, N., and Sunada, D. K. (1969). Nonlinear flow in porous media. J. Hydraul. Div. 95, 1847–1858.

Google Scholar

Anderson, H. E. (1982). “Aids to determining fuel models for estimating fire behavior,” in Research Paper INT-122 (Ogden, UT: US Department of Agriculture, Intermountain Forest and Range Experiment Station), 22.

Google Scholar

Bear, J. (2013). Dynamics of Fluids in Porous Media. New York, NY: Courier Corporation.

Google Scholar

Biswell, H. H. (1989). Prescribed Burning in California Wildlands Vegetation Management. Berkeley, CA: University of California Press.

Google Scholar

Carman, P. C. (1956). Flow of Gases Through Porous Media. Cambridge: Academic Press.

Google Scholar

Chapman, R. E. (2012). Geology and Water: An Introduction to Fluid Mechanics for Geologists. The Hague: Springer Science & Business Media.

Google Scholar

Chapuis, R. P., and Aubertin, M. (2003). Predicting the Coefficient of Permeability of Soils Using the Kozeny-Carman Equation. Technical Report no. EPM-RT-2003-03.

Google Scholar

Chapuis, R. P., Gill, D. E., and Baass, K. (1989). Laboratory permeability tests on sand: influence of the compaction method on anisotropy. Can. Geotech. J. 26, 614–622. doi: 10.1139/t89-074

CrossRef Full Text | Google Scholar

Corey, A. T. (1957). Measurement of water and air permeability in unsaturated soil 1. Soil Sci. Soc. Am. J. 21, 7–10. doi: 10.2136/sssaj1957.03615995002100010003x

CrossRef Full Text | Google Scholar

El-Sayed, S., and Khass, T. (2013). Smoldering combustion of rice husk dusts on a hot surface. Combust. Explo. Shock Waves 49, 159–166. doi: 10.1134/S0010508213020056

CrossRef Full Text | Google Scholar

Erić, A., Dakić, D., Nemoda, S., Komatina, M., and Repić, B. (2011). Experimental method for determining Forchheimer equation coefficients related to flow of air through the bales of soy straw. Int. J. Heat Mass Transf. 54, 4300–4306. doi: 10.1016/j.ijheatmasstransfer.2011.05.015

CrossRef Full Text | Google Scholar

Fehrmann, S., Jahn, W., and de Dios Rivera, J. (2017). Permeability comparison of natural and artificial pinus radiata forest litters. Fire Technol. 53, 1291–1308. doi: 10.1007/s10694-016-0631-1

CrossRef Full Text | Google Scholar

Figueroa, S., Rivera, J. d. D., and Jahn, W. (2019). Influence of permeability on the rate of fire spread over natural and artificial pinus radiata forest litter. Fire Technol. 55, 1085–1103. doi: 10.1007/s10694-019-00824-w

CrossRef Full Text | Google Scholar

Forchheimer, P. (1901). Wasserbewegung durch boden. Zeitz. Ver. Duetch Ing. 45, 1782–1788.

Google Scholar

Green, W. H., and Ampt, G. (1911). Studies on soil phyics. J. Agric. Sci. 4, 1–24. doi: 10.1017/S0021859600001441

CrossRef Full Text | Google Scholar

Hadden, R. M., Scott, S., Lautenberger, C., and Fernandez-Pello, A. C. (2011). Ignition of combustible fuel beds by hot particles: an experimental and theoretical study. Fire Technol. 47, 341–355. doi: 10.1007/s10694-010-0181-x

CrossRef Full Text | Google Scholar

Hassanizadeh, S. M., and Gray, W. G. (1987). High velocity flow in porous media. Transp. Porous Media 2, 521–531. doi: 10.1007/BF00192152

CrossRef Full Text | Google Scholar

Holdich, R. G. (2002). Fundamentals of Particle Technology. Nottingham: Midland Information Technology and Publishing.

Google Scholar

Huang, X., and Rein, G. (2016). Interactions of Earth's atmospheric oxygen and fuel moisture in smouldering wildfires. Sci. Total Environ. 572, 1440–1446. doi: 10.1016/j.scitotenv.2016.02.201

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamath, J., de Zabala, E., and Boyer, R. (1995). Water/oil relative permeability endpoints of intermediate-wet, low-permeability rocks. SPE Format. Eval. 10, 4–10. doi: 10.2118/26092-PA

CrossRef Full Text | Google Scholar

Knapp, E. E., Keeley, J. E., Ballenger, E. A., and Brennan, T. J. (2005). Fuel reduction and coarse woody debris dynamics with early season and late season prescribed fire in a Sierra Nevada mixed conifer forest. Forest Ecol. Manage. 208, 383–397. doi: 10.1016/j.foreco.2005.01.016

CrossRef Full Text | Google Scholar

Kyan, C. P., Wasan, D., and Kintner, R. (1970). Flow of single-phase fluids through fibrous beds. Indus. Eng. Chem. Fundam. 9, 596–603. doi: 10.1021/i160036a012

CrossRef Full Text | Google Scholar

Mavis, F., and Wilsey, E. (1937). Filter sand permeability studies. Eng. News Rec. 118, 299–300.

Google Scholar

Nyman, P., Baillie, C. C., Duff, T. J., and Sheridan, G. J. (2018). Eco-hydrological controls on microclimate and surface fuel evaporation in complex terrain. Agric. Forest Meteorol. 252, 49–61. doi: 10.1016/j.agrformet.2017.12.255

CrossRef Full Text | Google Scholar

Nyman, P., Metzen, D., Noske, P. J., Lane, P. N. J., and Sheridan, G. J. (2015). Quantifying the effects of topographic aspect on water content and temperature in fine surface fuel, International Journal of Wildland Fire, 24, 1129–1142. doi: 10.1071/WF14195

CrossRef Full Text | Google Scholar

Ogulata, R. T. (2006). Air permeability of woven fabrics. J Text. Apparel Technol. Manage. 5, 1–10. Available online at: https://textiles.ncsu.edu/tatm/wp-content/uploads/sites/4/2017/11/Ogulata_Full_199-06.pdf

Google Scholar

Possell, M., Jenkins, M., Bell, T., and Adams, M. (2015). Emissions from prescribed fire in temperate forest in south-east Australia: implications for carbon accounting. Biogeoscience 12, 257–268. doi: 10.5194/bg-12-257-2015

CrossRef Full Text | Google Scholar

Rothermel, R. C. (1972). “A mathematical model for predicting fire spread in wildland fuels,” in Research Paper INT-115 (Ogden, UT: US Department of Agriculture, Intermountain Forest and Range Experiment Station), 40.

Google Scholar

Santoni, P., Bartoli, P., Simeoni, A., and Torero, J. (2014). Bulk and particle properties of pine needle fuel beds–influence on combustion. Int. J. Wildl. Fire 23, 1076–1086. doi: 10.1071/WF13079

CrossRef Full Text | Google Scholar

Shimizu, H. (1970). Air permeability of deposited snow. Contrib. Inst. Low Temperature Sci. 22, 1–32.

Google Scholar

Sobieski, W., and Trykozko, A. (2014). Darcy's and Forchheimer's Laws in Practice. Part 1. The Experiment. Technical Sciences/University of Warmia and Mazury, Olsztyn.

Google Scholar

Steffen, W., and Hughes, L. (2013). The Critical Decade 2013, Climate Change Science, Risks and Responses. Canberra: Climate Commission; Department of Industry; Innovation, Climate Change, Science, Research and Tertiary Education; Commonwealth of Australia.

Google Scholar

Sukop, M. C., Huang, H., Alvarez, P. F., Variano, E. A., and Cunningham, K. J. (2013). Evaluation of permeability and non-Darcy flow in vuggy macroporous limestone aquifer samples with lattice Boltzmann methods. Water Resour. Res. 49, 216–230. doi: 10.1029/2011WR011788

CrossRef Full Text | Google Scholar

Tanikawa, W., and Shimamoto, T. (2006). Klinkenberg effect for gas permeability and its comparison to water permeability for porous sedimentary rocks. Hydrol. Earth Syst. Sci. Discuss. 3, 1315–1338. doi: 10.5194/hessd-3-1315-2006

CrossRef Full Text | Google Scholar

Teague, B., McLeod, R., and Pascoe, S. (2010). Final Report, 2009 Victorian Bushfires Royal Commission. Parliament of Victoria, Melbourne, VIC.

Google Scholar

Tindall, J. A., Kunkel, J. R., and Dean, E. A. (1999). Unsaturated Zone Hydrology for Scientists and Engineers. Prentice Hall, Upper Saddle River, NJ.

Google Scholar

Wang, H., van Eyk, P. J., Medwell, P. R., Birzer, C. H., Tian, Z. F., and Possell, M. (2016). Identification and quantitative analysis of smoldering and flaming combustion of radiata pine. Energy Fuels 30, 7666–7677. doi: 10.1021/acs.energyfuels.6b00314

CrossRef Full Text | Google Scholar

Wang, H., van Eyk, P. J., Medwell, P. R., Birzer, C. H., Tian, Z. F., and Possell, M. (2017). Effects of oxygen concentration on radiation-aided and self-sustained smoldering combustion of radiata pine. Energy Fuels 31, 8619–8630. doi: 10.1021/acs.energyfuels.7b00646

CrossRef Full Text | Google Scholar

Wang, S., Huang, X., Chen, H., and Liu, N. (2017). Interaction between flaming and smouldering in hot-particle ignition of forest fuels and effects of moisture and wind. Int. J. Wildl. Fire 26, 71–81. doi: 10.1071/WF16096

CrossRef Full Text | Google Scholar

Ward, J. (1964). Turbulent flow in porous media. J. Hydraul. Div. 90, 1–12.

Google Scholar

Nomenclature

d Glass bead diameter [mm]

k Air permeability [m²]

K Kozeny constant (about 5) (Holdich, 2002)

l Length of the fuel particle [mm]

L Length of the fuel bed [m]

R Drag force in Equation (4) [N]

Re Modified Reynolds number in Equation (5)

S_V Specific surface area [m^–1]

t Thickness of the fuel particle [mm]

U₀ Superficial velocity [m·s^–1]

U Interstitial velocity [m·s^–1]

w Width of the fuel particle [mm]

ΔP Total pressure drop [Pa]

∇P Pressure gradient [Pa/m]

Greek symbols

β Forchheimer coefficient [m^–1]

ε Porosity of fuel bed [-]

μ Dynamic viscosity [Pa·s]

ρ density of air [kg·m^–3]

Subscripts

D Darcian flows or Darcy's Law

DM decomposing matter

F Forchheimer Law

GB gum bark

GL gum leaf

KC Kozeny-Carman equation

PC pine chips

t twig.