Effect of Structural Parameters on the Relative Contact Area for Ideal, Anisotropic, and Correlated Random Roughness

1. Introduction

The understanding of how the relative contact area a_r depends on pressure in nominally flat, linearly elastic contacts has made great progress in the past two decades (Persson, 2001; Müser et al., 2017). Many advanced simulation studies support the view that it increases linearly with pressure from non-zero but very small a_r up to a_r ≈ 0.1, at least in the limiting and much investigated case of randomly rough, self-affine surfaces (Hyun et al., 2004; Campañá and Müser, 2007; Carbone and Bottiglione, 2008; Putignano et al., 2012; Prodanov et al., 2013). The height spectrum C(q) of a self-affine surface obeys power law scaling with the magnitude of the wavevector q over several decades (Majumdar and Tien, 1990; Palasantzas, 1993; Persson, 2014; Jacobs et al., 2017), i.e., C(q) ∝ q^−2(1+H), where H is called the Hurst exponent. In the limit of ideal random roughness, the phases of Fourier transforms of the surface height are independent random numbers that are uniformally distributed on (0, 2π). In this random-phase approximation, linearity between contact area and load can be rationalized with Persson's contact mechanics theory (Persson, 2001; Persson et al., 2004), which, in addition to predicting the area-load relation reasonably well, finds a highly accurate pressure-dependence of the interfacial stiffness along with accurate distribution functions of the interfacial separation (Lorenz and Persson, 2008; Almqvist et al., 2011; Campañá et al., 2011; Dapp et al., 2012; Prodanov et al., 2013; Afferrante et al., 2018) and correct spatial stress correlations (Campañá et al., 2008; Persson, 2008), none of which bearing-area models are able to achieve.

While it is sometimes argued that there must be a rigorous linear relation between contact area and load for random surfaces (in the thermodynamic limit), there are several indications for this linearity not to be strict. When the load is so small that contact is made only in a more-or-less connected patch near the highest point, relations for randomly rough surfaces may no longer hold (Pohrt et al., 2012). This, however, can be rationalized as a finite-size effect and be accounted for in Persson theory (Pastewka et al., 2013). However, even when several asperities were in contact, deviations from linearity had been noted by Yastrebov et al. (2015). Unfortunately, their calculations were conducted at an essentially fixed ratio of system size and short-wavelength cutoff (with varying roll-off wavelengths) so that small logarithmic corrections to linear relations between contact area and load may not be particularly telling. So far, the strongest support for deviations from linearity were reported in two carefully conducted simulation studies by Nicola and coworkers (van Dokkum et al., 2018; Salehani et al., 2020). They found quite remarkable logarithmic corrections to linear laws in large, one-dimensional adhesionless contacts (van Dokkum et al., 2018) as well as clearly sublinear scaling for two-dimensional, adhesive surfaces (Salehani et al., 2020). However, the latter may have been in a regime with non-negligible adhesive hysteresis, in which case non-linearity between a_r and p is unavoidable. Thus, even these two latter works do not explicitly challenge the view that a linear dependence of contact area on load is an excellent approximation for linearly elastic, sufficiently large, two-dimensional elastic bodies squeezed against a randomly rough, non-adhesive indenter.

An unsolved question is why different Hurst exponents lead to slightly different proportionality coefficients in the equation

$\begin{array}{ll}{a}_{\text{r}}=\frac{\kappa p}{E^{*}ḡ},& (1)\end{array}$

where p is the nominal contact pressure, E^* the contact modulus, and ḡ the root-mean-square height gradient. coefficient κ correlates with the Nayak parameter (Nayak, 1971), Φ_N at fixed p^*. As we will argue in this work, Φ_N can be seen as the lowest-order unitless, scalar parameter describing a surface topography other than ḡ, however, only if the random-phase approximation (rpa) is satisfied. The Nayak parameter is mentioned in many contact-mechanics studies. However, none of them that we are aware of and that claim the proportionality coefficient κ to depend on the Nayak parameter has the numerical sophistication of Yastrebov et al.'s works (Yastrebov et al., 2015, 2017). Nonetheless, they only addressed surfaces with ideal random roughness, i.e., surfaces obeying the rpa, and, as already mentioned above, the ratio of system size and short-wavelength cutoff was kept in a relatively narrow range. Therefore, the Nayak parameter may merely have strongly correlated with other, relevant (stochastic) quantifiers, but not have causally determined the κ(H) dependence.

In fact when leaving the realm of ideally rough surfaces, it does not appear plausible that the Nayak parameter strongly affects κ. To see why consider the exact solution to a contact problem (no friction, no adhesion, small-slope approximation) between an initially smooth, linearly elastic manifold squeezed down against a rough, rigid substrate fixed in space. In a thought experiment, modify the substrate's height profile in the non-contact zones such that all moved points remain below the elastic body. Its equilibrium displacement field and contact points at this and smaller pressures will be the same as for the original substrate, however, the Nayak parameter can have changed by orders of magnitude between the original and the modified indenter. In another thought experiment, consider an indenter with blunt peaks (facing the elastic body) and steep valleys. At a given load, it will have a relatively large contact area. If the indenter's height profile is flipped around, the Nayak parameter remains the same but now the contact area is strongly diminished as the elastic body is now in contact with sharp peaks. Thus, in one thought experiment, the Nayak parameter changed its value significantly, while the contact area remained unaffected. In the other one, the situation reversed: the contact area changed while the Nayak parameter didn't. For these reasons, there can be scarcely a broadly applicable correlation between contact area and Nayak parameter, at least once the random-phase approximation has been abandoned.

The two thought experiments reveal that relevant stochastic topographic quantifiers may only depend on functions that are defined in the true contact zones. As desired, such a quantifier would remain unaffected in the first thought experiment when a_r does not change, while both would adopt new values in the second thought experiment. Dimensional analysis of the specified contact problem reveals that the root-mean-square gradient plays a central role for the contact area, even in the absence of the random-phase approximation (Prodanov et al., 2013). In fact, one of us (Müser, 2017) demonstrated that Equation (1) also holds for indenters having a harmonic height profile (asperity height decreases as a powerlaw with distance from a symmetry axis) if ḡ is averaged over the true contact area. In this case, a_r is no longer strictly linear in p since ḡ is a function of load or pressure. Similarly, line contacts between two-dimensional solids were found to obey Equation (1) but only when ḡ was averaged over the true contact (van Dokkum et al., 2018). Thus, the effective κ is a function of the bluntness of the indenting tip, where bluntness would be defined by the functional form of the indenters rather than by numerical prefactors.

In this work, we investigate what structural parameters affect the proportionality coefficient κ, or more generally, the area-pressure relation. Toward this end, we study the contact mechanics of height profiles with anisotropy and with phase correlation in the Fourier transforms of the height profiles. This correlation is realized by warping rpa height profiles such that peaks are smoothed and valleys are roughened or vice versa, whereby the rpa is destroyed. Anisotropy will also be considered. We then explore to what extent the results on relative contact area correlate with unitless scalar parameters describing the topographic features of the surfaces. These parameters include the Nayak parameter but also a variety of other parameters, which take constant values for rpa surfaces but not for surfaces with correlated (random) roughness.

The remainder of this paper is organized as follows: Model and method are introduced in section 2. The theory is introduced in section 3, which includes the systematic construction of topographic order parameters beyond the Nayak parameter. Results are presented in section 4, while conclusions are drawn in section 5.

2. Model and Method

As mentioned in the introduction, we are concerned with contacts between an initially flat, linearly elastic body in frictionless contact with a rigid, rough counterface indenting from below. Interactions between the two bodies consist of a non-overlap constraint. This model has been used extensively since Hertz.

The contact problem is solved with Green's function molecular dynamics (GFMD), which is a frequently employed and described boundary-value method (Campañá and Müser, 2006; Pastewka et al., 2012; Kajita, 2016; van Dokkum and Nicola, 2019). Here we use it in the so-called FIRE-GFMD variant (Zhou et al., 2019).

Most surfaces simulated in this work are randomly rough. The default or rather starting surfaces have the isotropic, self-affine roughness described in the introduction. In addition, it is assumed that ideal self-affine scaling only exists for wave vectors q_r ≤ q ≤ q_s, where q_r is the roll-off wave vector and q_s is the short-wavelength cutoff. Thus, the used spectra are

$\begin{array}{ll}C(q)=C(q_{\text{r}})\times \{\begin{array}{ll}\hfill f_{\text{roll}}\hfill & \text{if }q<q_{\text{r}}\\ \hfill {(q/q_{\text{r}})}^{-2(1+H)}\hfill & \text{if }{q}_{\text{r}}<q<q_{\text{s}}\\ \hfill 0\hfill & \text{else,}\end{array}& (2)\end{array}$

where f_roll is a Boolean variable, which takes the value of one if true and of zero if false. f_roll is false by default and only set to true when mentioned explicitly. Thus, by default, λ_r = 2π/q_r plays the role of a long wavelength cutoff rather than of a rolloff. In almost all cases, the linear dimension of the simulation cell ${L}$ is still chosen larger than λ_r in order to average implicitly over different random realizations, which can become relevant for large Hurst exponents at small relative contact areas.

The elastic body is discretized into elements having a linear dimension Δa, which is sufficiently small compared to π/q_s in order for the continuum limit to be reached. In fact, different discretizations are considered and results for all observables are extrapolated to the continuum limit (ε_c ≡ Δa/λ_s → 0), using a Richardson extrapolation as described in Prodanov et al. (2013). For the contact area, we find a linear dependence in ε_c of the continuum corrections rather than the previously identified ${\epsilon }_{\text{c}}^{2/3}$ dependence (Campañá and Müser, 2007; Prodanov et al., 2013). Unfortunately, we no longer posses the old configuration files so that analyzing the origin of the discrepancy cannot be clarified. While our GFMD code has been rewritten twice after the original single-authored code by Campana (version 2 by Müser, Dapp, and Prodanov while version 3 was by Müser with Zhou and Wang), we now find a linear a(ε_c) scaling even when using version 2, which was used, for example, in the contact-mechanics challenge. Although, corrections turn out differently than before, the extrapolated values between old and new results matched whenever tested.

For the so-called fractal correction, i.e., the excess contact area arising due to the ratio ε_f = λ_s/λ_r being finite, we also find different scaling than before (Prodanov et al., 2013), i.e., the exponent α_f of the correction ${\epsilon }_{\text{f}}^{{\alpha }_{\text{f}}}$ is found to vary between zero (implying approximately logarithmic corrections) and unity. Precise values are difficult to determine due to stochastic scatter. One reason for why we no longer find a unique value for α_f is that we now consider contact areas in the continuum limit before exploring the limit ε_f → 0. However, since we find α_f to be always equal or less to unity, extrapolation with α_f = 1 from finite ε_f to zero should never result in an overcorrection.

Deviations from isotropy are realized by using an effective “Peklenik” wavenumber

$\begin{array}{ll}{q}_{\text{P}}={\left(\frac{{\gamma }_P^2{q}_x^2+q_y^2/{\gamma }_P^2}{\sqrt{{\gamma }_P^4+1/{\gamma }_P^4}}\right)}^{1/2}& (3)\end{array}$

as the variable in the height spectrum rather than the true wave number q. The Peklenik parameter satisfies 0 < γ_P < ∞. Surfaces are stochastically isotropic if γ_P = 1. Anisotropy increases with increasing ${(ln{\gamma }_{\text{P}})}^2$. The such produced height profiles reveal preferred directions or “grooves” in Figure 1, which makes them somewhat more similar to scratched surfaces than topographies with isotropic random roughness.

FIGURE 1

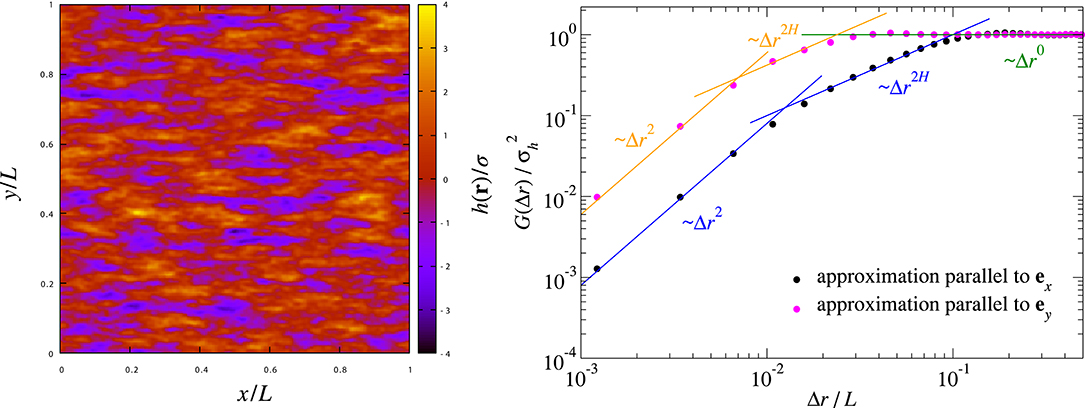
Figure 1. (Left) Topography of a surface satisfying the random-phase approximation characterized by a Peklenik number of γ_P = 4. (Right) Height-difference auto-correlation function C(r) for shown topography and r parallel to e_x (closed black circles) and e_y (closed pink circles).

Phase coherence can be destroyed through a warping transformation. A warped height is defined by

$\begin{array}{ll}{h}_w=\{\begin{array}{ll}{h}_{\text{min}}+(h-h_{\text{min}}){\left(\frac{h-h_{\text{min}}}{h_{\text{max}}-h_{\text{min}}}\right)}^w& \text{if }w\ge 0\\ h_{\text{max}}-(h_{\text{max}}-h){\left(\frac{h_{\text{max}}-h}{h_{\text{max}}-h_{\text{min}}}\right)}^{\left|w\right|}& \text{else,}\end{array}& (4)\end{array}$

where h_min ≤ Min{h(r)} and h_max ≥ Max{h(r)}. Here h indicates the height of the original (rpa) height profile at a given position r and h_w is the height at a given location of the warped surface. At w = 0, height profiles remain unchanged. For w > 0, peaks are blunted and valleys sharpened, while the opposite is achieved with w < 0, as can be seen in the cross-section of the height-profile shown in Figure 2. In the current study, h_min = 2 Min{h(r)} − Max{h(r)} and h_max = 2 Max{h(r)} − Min{h(r)} were used.

FIGURE 2

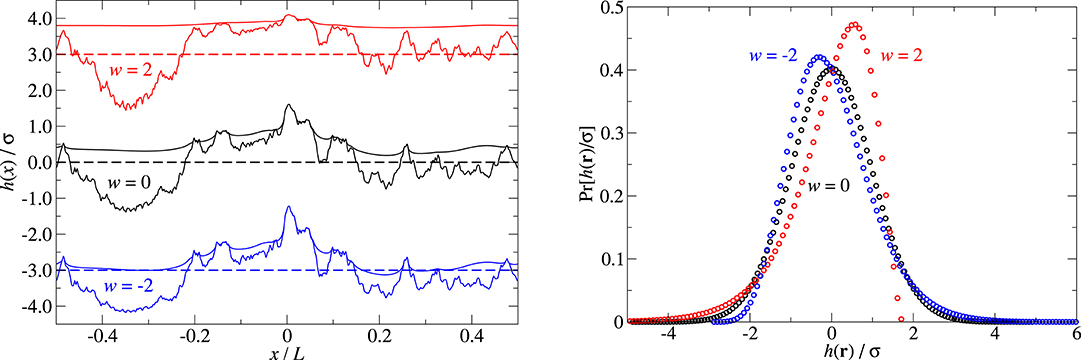
Figure 2. (Left) Contacts between an elastic body and indenters with different warpings w (top to bottom w = 2, w = 0, w = −2) at approximately 10% relative contact area. The dashed lines indicate the indenters' center-of-mass height for the shown cross section. The curves w = ±2 are shifted by a constant to improve their visualization. (Right) Height histograms for the different surfaces. The number of grid points for each warped surface is fixed to 4, 096 × 4, 096.

Phase correlation through our warping procedure is reflected by the observation that the height histograms are systematically skewed for w ≠ 0. In contrast, the height histograms of rpa surfaces are symmetric, except for finite-size effects, because each height profile has the same likelihood to occur as its mirror image in which valleys turn to peaks and vice versa. In addition, the expectation value of the root-mean-square gradient changes with height, i.e., it is much reduced in the blunted parts of the surface compared to the roughened parts. In contrast, for (sufficiently large) rpa surfaces, ḡ is independent of the height, except near the highest and lowest heights in a finite sample. In future topographic determinations of random surfaces with correlation, it would be very interesting to know to what extent the rms-height gradient changes with height. This would probably constitute an important quantity to be targeted for computer-generated surfaces. To mimic scratched surfaces realistically, it will probably be required to assume a scale or q-dependent Peklenik parameter (Candela et al., 2011) in addition to warping and to consider additional refinements. However, our impression is that the w = 2 surface already contains some features of polished surfaces, i.e., relatively deep valleys and smoothed tops.

In principle, it would have also been possible to consider phase correlation by limiting the values of the phases of $\tilde{h}(\text{q})$ to a range −φ_m ≤ φ ≤ φ_m defined by a minimum/maximum allowed phase φ_m for the phases of all $\tilde{h}(\text{q})$, while keeping the height spectra C(q) unchanged. We found this method not to be helpful, because it lead to indenters with sharp thorns. In the limit of φ_m → 0, essentially single-point indenters are obtained. Rather than investigating those, we will consider indenters with harmonic height profiles satisfying

$\begin{array}{ll}h(r)=\frac{R}{n}{\left(\frac{r}{R}\right)}^n,& (5)\end{array}$

where R is of unit length, while r is the in-plane distance of a point from the (closest) symmetry axis of an individual indenter, which we place into the center-of-mass of the simulation cell. The values of n used in this study were restricted to n = 1.5 (sharp indenter), n = 2 (Hertzian geometry), and n = 4 (blunt indenter). Analytical solution for stress and displacement fields (in the contact area and its vicinity) and thus for the dependence of contact area on load are known when the contact radii are negligibly small compared to the linear dimension of the simulation cell.

3. Theory

3.1. Phenomenological Generalization of Persson Theory

Persson theory for linear elastic contacts between ideally randomly rough surfaces predicts a relative contact area of

$\begin{array}{ll}{a}_{\text{r}}=\text{erf}\left\{\sqrt{2}{p}_0/E^{*}ḡ\right\},& (6)\end{array}$

where ḡ is the root-mean-square height gradient averaged over the entire surface, i.e,

$\begin{array}{ll}{ḡ}^2={\displaystyle \int }{d}^{2}qC(q)q^2,& (7)\end{array}$

which is the expression in the derivation of Persson theory.

One of us noticed that Equation (6) also holds for smooth indenters with harmonic height profiles if ḡ is replaced with ḡ_c, where the latter is not determined over the entire surface but only over the true contact. Thus, the range of applicability of Equation (6) appears to extend when re-expressing it through

$\begin{array}{ll}{a}_{\text{r}}=\text{erf}(\sqrt{\pi }{\kappa }_{\text{c}}{p}_{\text{c}}^{*}/2),& (8)\end{array}$

where κ_c is the proportionality coefficient between relative contact area and the reduced pressure defined by $p_{\text{c}}^{*}=p_0/(E^{*}{ḡ}_{\text{c}})$. When omitting the index “c” in κ_c, we mean to refer to the proportionality coefficient when the reduced pressure is normalized to ḡ rather than to ḡ_c.

In fact, when taking Persson theory literally, it does ask the question how the rms-height changes in a given point of contact (described using a small resolution of the surface topography) when short-wavelength roughness is added to the description of the contact problem. Using the full spectrum to estimate this increase in rms-roughness can be seen as an approximation, which might be possible to correct in future work. Some possibilities are discussed in the conclusions.

The standard Persson theory predicts a value of $\kappa =\sqrt{8/\pi }\approx 1.596$. In the formulation of the theory, it appears to us as if no distinction is made—or must be made—between κ and κ_c, at least as long as pressures lie in a range in which a_r ∝ p, that is, if p is sufficiently large for contact to spread out over clearly disconnected contact patches but still small enough so that a_r is less than, say, 0.05. Careful simulations of sufficiently large systems find a relatively weak dependence of κ on the Hurst roughness exponent, e.g., κ(H ≈ 0.8) ≲ 2 and κ(H ≈ 0.3) ≳ 2. (Hyun et al., 2004; Campañá and Müser, 2007; Hyun and Robbins, 2007; Putignano et al., 2012; Prodanov et al., 2013; Afferrante et al., 2018). Analytical results for the Hertz contact result in κ_c ≈ 1.666, see also Equation (28) and the more detailed discussion of periodically repeated, smooth indenters in section 4.5.

3.2. Dimensionless Parameters: Nayak and Beyond

Since the relative contact area is a number, it can only be a function of other unitless parameters $(p^{*},{\Phi }_1,{\Phi }_2,...)$ itself, where p^* is a reduced pressure, e.g., p/(E^*ḡ). Moreover, each variable in the set {Φ} must obey the law of dimensional analysis. Specifically, they must remain invariant under the scaling transformation r → s · r and z → t · z, since the relation $a_{\text{rel}}=a_{\text{rel}}(p/E^{*}ḡ)$ already reflects the correct dependencies on s and t (Prodanov et al., 2013). Moreover, real contact is destroyed predominantly due to roughness at small wavelengths. Thus, the Φ_i should not depend on parameters that are defined exclusively by parameters from the height-distribution also known as Abbott Feierstone curve.

Before constructing the respective unitless parameters, it is in place to discuss the square-gradient term. When determining ḡ over a periodically repeated contact, 〈(∇h)²〉 is identical to −〈δhΔh〉, as can be seen by integration in parts. However, this equality no longer holds for partial contact. Defining

$\begin{array}{ll}{({ḡ}_{\text{c}}^{\prime })}^2=-{\langle \delta h\Delta h\rangle }_{\text{c}}.& (9)\end{array}$

the dependence of a_rel on parameters depending on height profiles in the contact then becomes

$\begin{array}{ll}{a}_{\text{rel}}=a_{\text{rel}}[p/(E^{*}{ḡ}_{\text{c}}),{ḡ}_{\text{c}}/{ḡ}_{\text{c}}^{\prime },\left\{{\Phi }_{\text{c}}\right\}].& (10)\end{array}$

Ultimately, a_rel is a functional of the height topography. As such, there should exist a dependence of a_rel that does not necessitate parameters averaged over the real contact. However, those might necessitate non-local terms, or, alternatively, high-order derivatives of h(r). The latter may not be well defined when the surface profile or its (higher-order) derivatives are not well-defined, as is the case, for example, for a conical indenter. Thus, the following discussion assumes surface height profiles to be smooth and “well behaved.”

For the construction of relevant parameters, it is useful to keep in mind three symmetry relations. First, a mirror inversion (r → −r) leaves the contact area unchanged. This is why each derivative with respect to a spatial coordinate must appear an even number of times in the construction of an invariant. Second, each measure should be rotationally invariant and reduce to a scalar. This is automatically achieved when representing derivatives with the Einstein summation convention, which requires every index (enumerating an in-plane coordinate) occurring twice in a product to be summed over. To use it effectively, we use it jointly with the index notation, in which case $h_{\alpha }^2$ indicates the square-height gradient (∇h)·(∇h) and h_αα the Laplacian Δh. However, ḡ will keep indicating the rms height gradient $\sqrt{\langle h_{\alpha }^2\rangle }$. Third, the invariants may not change on a rigid, vertical translation of the surface h(r) → h(r) + h₀. This is why only δh = h − 〈h〉 can appear in the invariants. The lowest-order invariant obeying these rules that we could identify are given by

$\begin{array}{ll}{\Phi }_1=\frac{\langle \delta h{h}_{\alpha }^2\rangle }{\sqrt{\langle h_{\alpha }^2\rangle }{ḡ}^2}& (11)\end{array}$

$\begin{array}{ll}{\Phi }_2=\frac{-\langle \delta h^2{h}_{\alpha \alpha }\rangle }{2\sqrt{\langle \delta h^2\rangle }{ḡ}^2}& (12)\end{array}$

$\begin{array}{ll}{\Phi }_3=\frac{-\langle \delta h^2\rangle \langle h_{\alpha \alpha }\rangle }{2\sqrt{\langle \delta h^2\rangle }{ḡ}^2}.& (13)\end{array}$

Before constructing the next parameters, the allowed values for the parameter Φ₁ to Φ₃ will be discussed. Φ₁ and Φ₂ are identical when averaged over a periodically repeated surfaces (as can be seen again by integration in parts) but not when they are determined over partial contact, in which case the index “c” would be added. For periodically repeated surfaces, the parameter Φ₃ is automatically identical to zero but generally different from zero when averaged over partial contact. This is because the mean curvature disappears for a periodically repeated surface, while the curvature must average to a negative number for partial contact (assuming the elastic body indents the profile from above).

The values of Φ₁ and Φ₂ averaged over a single rpa surface may be finite. However, averaging these means over various disorder realization will make them disappear, as any surface realization h(r) has the same probability (density) to occur as −h(r). Thus, Φ₁ and Φ₂—as well as any other parameter, in which the symbol h appears an odd number of times as a factor—should be small when determined over a single rpa surface realization, in particular when the roll-off domain is sufficiently large.

When averaged over partial contact and/or over surfaces violating the rpa, Φ₁ and Φ₂ may and usually do take finite values. This is why we call them symmetry allowed in Table 1. For the remaining parameters, we will no longer state the rationale for why terms are symmetry allowed or forbidden, as all relevant arguments have been mentioned or can be easily derived using the relations for Gaussian random numbers summarized in section 3.3. Table 1 contains our conclusions on each parameter constructed in this work.

TABLE 1

Table 1. Values of parameters averaged over a full, periodically repeated surface (prs) if the random-phase approximation (rpa) is valid and when it is not valid (n-rpa).

Additional parameters in which numerator and denominator are second order in the derivative but higher order in h can be constructed. They will be considered up to the lowest order needed beyond the rms-height gradient, in which the parameters do not disappear in case of the random-phase approximation. This includes the parameters

$\begin{array}{ll}{\Phi }_4=\frac{\langle \delta h^2{h}_{\alpha }^2\rangle }{\langle \delta h^2\rangle {ḡ}^2}& (14)\end{array}$

$\begin{array}{ll}{\Phi }_5=\frac{-\langle \delta h^3{h}_{\alpha \alpha }\rangle }{3\langle \delta h^2\rangle {ḡ}^2}& (15)\end{array}$

For rpa-surfaces, Φ₄ is automatically equal to unity and for all periodically repeated surfaces, Φ₄ = Φ₅.

Finally, we consider parameters in which the order of the derivatives is increased from two to four while the order in the height is kept as small as possible. Three of quite a few resulting (irreducible) possibilities are

$\begin{array}{ll}{\Phi }_6=\frac{1}{{ḡ}^4}\langle \delta h^2\rangle \langle h_{\alpha \alpha }{h}_{\beta \beta }\rangle & (16)\end{array}$

$\begin{array}{ll}{\Phi }_7=\frac{2}{3{ḡ}^4}\langle \delta h^2{h}_{\alpha \alpha }{h}_{\beta \beta }\rangle & (17)\end{array}$

$\begin{array}{ll}{\Phi }_8=\frac{1}{{ḡ}^4}\left\{\langle h_{\alpha }^2{h}_{\beta }^2\rangle -3\langle h_{\alpha }^2\rangle \langle h_{\beta }^2\rangle +{\langle h_{\alpha }{h}_{\beta }\rangle }^2\right\}& (18)\end{array}$

$\begin{array}{ll}{\Phi }_9=\frac{2}{{ḡ}^4}{\langle h_{\alpha }{h}_{\beta }-h_{\gamma }^2{\delta }_{\alpha \beta }/2\rangle }^2,& (19)\end{array}$

where δ_αβ is the Kronecker-delta symbol.

The parameter Φ₆ is nothing but the Nayak parameter Φ_N, up to a multiplicative constant of 2/3. It is frequently interpreted as a measure for the spectral width. We chose the prefactor such that Φ₆ and Φ₇ are equal to unity for single-wave-vector roughness. The parameter Φ₇ is a generalization of the Nayak parameter. For randomly rough, rpa surface, its expectation value is close to but less than Φ₆. Thus, both parameters tend to infinity as the ratio ε_f = λ_s/λ_r becomes small, that is, with ${\epsilon }_{\text{f}}^{-2H}$. However, for (strongly) correlated random roughness Φ₇ takes much greater values than Φ₆, just as Φ₄ starts to substantially exceed unity, because the factorization of the various terms (see also section 3.3) no longer holds once the rpa is no longer obeyed.

The parameter Φ₈ plays the role of a generalized height gradient cumulant. It is constructed such that it takes the value of zero when the fourth-order cumulant of the surface slope s parallel to any in-plane unit vector n takes the value of zero if it is distributed normally, i.e., when $c_{4,\text{n}}=\langle s^4\rangle -3{\langle s^2\rangle }^2$ disappears for every n. This parameter is implicitly symmetrized with respect to its mirror images in the xz and yz planes so that 〈s〉 = 0 follows. Note that Φ₈ being small is a necessary but not a sufficient criterion for every c_4,n to disappear. It is only sufficient if the surfaces are stochastically isotropic.

Finally, Φ₉ is a measure for anisotropy. It takes the values of zero and one in the limits of ideal isotropic and ideal anisotropy, respectively, where, for the latter, surfaces are perfectly smooth along one spatial direction. Assuming the Peklenik number to be independent of the wavevector, Φ₉ can be easily shown to be identical to ${({\gamma }_{\text{P}}^2-1/{\gamma }_{\text{P}}^2)}^2/2$ As is the case for some other parameters too, Φ₉ is not identical to zero for an individual surface realization, but only averages to zero after taking sufficiently many surface realizations.

We conclude this section by stating that the Nayak parameter is the lowest-order scalar structural parameter that the proportionality coefficient κ can depend on if the surface is isotropic and satisfies the random-phase approximation. All other parameters of similar or smaller order in height are either identical to zero, or their expectation value is zero, or they strongly correlate with the Nayak parameter.

3.3. Evaluation of Fourth-Order Invariants

For (isotropic) randomly rough surfaces, invariants being fourth order in height and fourth order in derivatives are the leading-order, scalar structural parameters that can affect the proportionality coefficient κ. Of particular interest should be those that—unlike the Nayak parameter—cannot be reduced to products of invariants being second order in height. Yet, the evaluation of fourth-order expressions is commonly done using Wick's theorem (Wick, 1950), which, applied to the current problem, translates to

$\begin{array}{l}{C}_4({\text{q}}_1,\dots ,{\text{q}}_4)\equiv \langle \tilde{h}({\text{q}}_1)\tilde{h}({\text{q}}_2)\tilde{h}({\text{q}}_3)\tilde{h}({\text{q}}_4)\rangle \\ \approx \langle \tilde{h}({\text{q}}_1)\tilde{h}({\text{q}}_2)\rangle \langle \tilde{h}({\text{q}}_3)\tilde{h}({\text{q}}_4)\rangle \\ +\langle \tilde{h}({\text{q}}_1)\tilde{h}({\text{q}}_3)\rangle \langle \tilde{h}({\text{q}}_2)\tilde{h}({\text{q}}_4)\rangle \\ +\langle \tilde{h}({\text{q}}_1)\tilde{h}({\text{q}}_4)\rangle \langle \tilde{h}({\text{q}}_2)\tilde{h}({\text{q}}_3)\rangle ,& (20)\end{array}$

whereby expectation values of fourth-order expressions are reduced to products of height spectra, since

$\begin{array}{ll}\langle \tilde{h}({\text{q}}_m)\tilde{h}({\text{q}}_n)\rangle \propto C(|{\text{q}}_m|)\delta ({\text{q}}_m+{\text{q}}_n),& (21)\end{array}$

where C(q) is the height spectrum. Equation (20) is exact for Gaussian random variables of mean zero.

4. Results

4.1. On the Accurate Calculation of Contact Area and the Proportionality Coefficient κ

In Yastrebov et al. (2017), Yastrebov et al. claimed to ensure an unprecedented accuracy in computation of the true contact. If n_c is the number of contact points, n_cl the number of contact or rather contact-line points, which are in contact but have at least one non-contact point as nearest neighbor, then the relative contact area was estimated with

$\begin{array}{ll}{a}_{\text{r}}=\frac{n_{\text{c}}-\alpha n_{\text{cl}}}{n_{\text{tot}}},& (22)\end{array}$

where n_tot is the total number of points into which the surface is discretized and α = (π − 1 + ln 2)/24.

While we find the proposed correction to be quite useful in order to get an astoundingly accurate first estimate of the continuum correction for isotropic, rpa surfaces, we believe that it can at best be on par with a properly executed Richardson extrapolation even in that limiting case. The reason is that the numerical coefficient α ≈ 0.11811 can scarcely be universal even if the special form of writing it as (π − 1 + ln 2)/24 might convey a profound mathematical reason for its specific value. To argue why the proposed method cannot surpass a Richardson extrapolation in the asymptotic limit, let us assume that the leading order-correction were indeed proportional to the number of contact-line points within the contact. This number would ultimately scale with a/λ_s, because the fractal nature of the contact seizes to exist in this limit, so that the contact line acquires the (fractal) dimension of unity, in which case n_cl ∝ λ_s/a. This linear scaling of the leading-order corrections to the contact area would be picked up by a Richardson extrapolation and the proportionality coefficient would automatically adjust to the exact value and not only to a value, which is very good but not exact.

The proposed correction scheme can only outperform a Richardson extrapolation if higher-order corrections happened to be incorporated into it. This, in fact, might be the case, as is revealed in Figure 3 by the accurate values from the Yastrebov extrapolation at large ε_c. However, since the exact value α must depend on the specifics of a simulation (artificial geometries can be easily constructed for which α ≡ 0 at large loads), it can only be exact in isolated cases of measure zero so that it is generally asymptotically inferior to Richardson. As such, a claim of having provided data with unprecedented accuracy with this method is somewhat hazardous given that previous work used a Richardson extrapolation while employing ratios of ε_c = a/λ_s, ε_f = λ_s/λ_r, and ${\epsilon }_{\mathrm{\text{t}}}={\lambda }_{\mathrm{\text{r}}}/{L}$, which were simultaneously all greater than the data having the purportedly unprecedented accuracy.

FIGURE 3

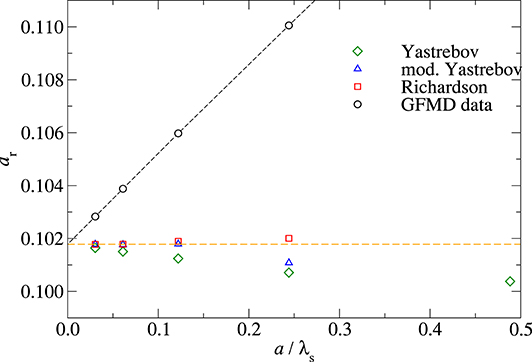
Figure 3. Comparison of different extrapolation schemes for the relative contact area a_r to the continuum limit ε_c ≡ a/λ_s → 0 for an rpa surface specified by H = 0.8, p^* = 0.05, ${\lambda }_{\text{r}}/{L}=0.5$, and ${\lambda }_{\text{s}}/{L}=0.008$. In the modified Yastrevob extrapolation, the prefactor α in Equation (22) was chosen such that the extrapolated contact area at a discretization aλ_s and at 2aλ_s gave the same estimate for the contact area. Dashed lines are drawn to guide the eye.

The ideas of Yastrebov's extrapolation can be modified by incorporating the spirit of a Richardson extrapolation into it: if the numbers of contact and contact-line points are known at two different values of a/λ_s, the parameter α could be adjusted such that the Yastrebov extrapolation gives the same estimate for both discretizations. Asymptotically, this modification leads to an improvement, as can be seen in Figure 3, however, it is usually a disimprovement for a/λ_s ≥ 1/4. To terminate our discussion on the Yastrebov extrapolation, we note that we found it to work equally well for warped surfaces as for rpa surfaces and that our final estimates for the relative contact area were always very close, say, within 0.1%, to using a rigorous extrapolation with the value that we obtained with a Yastrebov extrapolation using

$\begin{array}{ll}\alpha =0.11& (23)\end{array}$

and a discretization of a/λ_s ≲ 1/4. This value of α typically deteriorates the quality of the contact-area estimate for a = λ_s/2 but improves it overall otherwise.

Finally, given that the extrapolation used by Yastrebov and coworkers may lead to different errors at different pressures, the following question remains: What is the origin of their observed logarithmic correction of κ on pressure? Is it the lack of a rigorous extrapolation to the continuum (ε_c = a/λ_s → 0), the fractal (ε_f = λ_s/λ_r → 0), or the thermodynamic (${\epsilon }_{\mathrm{\text{t}}}={\lambda }_{\text{r}}/{L}\to 0$) limit? Or is it actually true? After all and despite our criticism of their self appraisal, we see their data to be of similar quality as that of most other cutting-edge works, which had unanimously come to the conclusion of κ acquiring a constant value at small p, but which either simply took the values at the smallest value of ε_c without further extrapolation or that made Richardson extrapolations, which we can no longer reconstruct. Moreover, one-dimensional systems show robust logarithmic corrections in κ at small p (van Dokkum et al., 2018) even for very large sizes when contact is also made far away from the highest point. (In the preparation of this manuscript, we verified those claims on 1D systems for sizes exceeding 2²⁰ grid points.)

The last limit that needs to be taken to zero is the pressure p → 0, i.e., the proportionality coefficient κ should be computed with the smallest possible errors. To do so, we compute κ as a pressure-dependent function through the equation

$\begin{array}{ll}{a}_{\text{r}}=\text{erf}(\sqrt{\pi }\kappa p^{*}/2),& (24)\end{array}$

rather than through $a_{\text{r}}/p^{*}$ or $\partial a_{\text{r}}/\partial p^{*}$, because Equation (24) accounts for some of the low-pressure non linearities, as can be appreciated in Figure 1 of Dapp et al. (2014). The zero-pressure limit can only be taken in a meaningful manner in conjunction with a proper size scaling as will be discussed next.

4.2. Isotropic rpa Surfaces

4.2.1. Does κ Have a Low-Pressure Limit?

κ cannot have a finite low-pressure limit, if it is defined or computed according to

$\begin{array}{ll}\kappa =\left({\displaystyle \prod _x}{\displaystyle \underset{{\epsilon }_x\to 0}{lim}}\right){\displaystyle \underset{p\to 0}{lim}}\kappa (p),& (25)\end{array}$

where the various limits (defined in the previous section with x taking the “values” c for continuum, f for fractal, and t for thermodynamic) are taken in arbitrary order. The reason is that for any finite system at exceedingly small pressures, only the highest (meso-scale) asperity is in contact, which (in the realm of continuum mechanics) will ultimately be Hertzian, in which case κ tends to infinity.

The interesting question is whether a_r can be proportional to p over an extended range in pressure with no or negligible logarithmic corrections to the proportionality coefficient κ if both ε_t,f are sufficiently small while ε_c is properly taken to zero at each pressure. Thus, mathematically speaking, we are interested in a limit

$\begin{array}{ll}\kappa ={\displaystyle \underset{p\to 0}{lim}}{\displaystyle \underset{{\epsilon }_{\text{t},\text{f}}\to 0}{lim}}\frac{a_{\text{r}}}{p^{*}},& (26)\end{array}$

since experimental systems, to which simulations should compare, tend to have much larger values of ε_t,f than can be realized in a computer simulation. This limit is certainly not approached if the product ε_tε_f is taken to be effectively constant while having varying discretization errors, as in Yastrebov et al. (2017). Keeping all but one ε_t,f,c constant—as done by Prodanov et al. (2013)—is only an unsatisfactory improvement, because the discretization corrections probably decrease as ε_f decreases due to the increase of the characteristic patch size. The cardinal mistake made by Prodanov et al. (2013) was to assume that leading errors to κ are sums of terms $c_x{\epsilon }_x^{{\nu }_x}$ with x ∈ (c, t, f) and 0 < ν_x, while they could also be of a more general form and involve, e.g., products of powers of different ε_x.

To explore the question raised at the beginning of the previous paragraph in a somewhat more meaningful way than before, we ran simulations in which ε_f and/or ε_t were decreased simultaneously with decreasing pressure p according to

$\begin{array}{ll}\epsilon ={\epsilon }_{\text{ref}}{(p/p_{\text{ref}})}^{\frac{1}{4}}.& (27)\end{array}$

Results are shown in Figure 4, for which we chose (arbitrarily) ε_f = 1/32 and ε_t = 1/2 at a reference pressure of p^* = 0.2. It reveals that κ increases quite noticeably with decreasing pressure for all three H = 0.3 systems, while it essentially plateaus for the two H = 0.8 systems in which ε_f is decreased as p decreases. While the H = 0.3 might also plateau at even smaller p^*, a qualitative difference between H = 0.3 and H = 0.8 would remain: The curves in which both ε_t and ε_f are decreased with decreasing p^* lead to small κ for H = 0.8 but to large κ for H = 0.3, which become even larger for fixed ε_f.

FIGURE 4

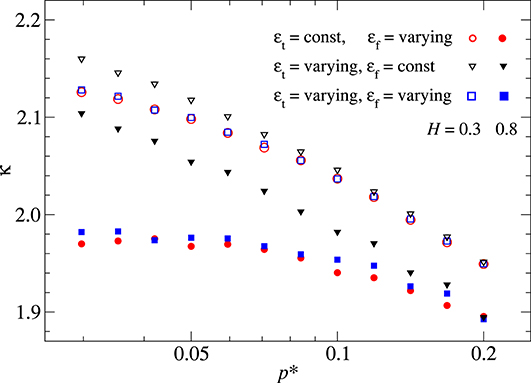
Figure 4. Proportionality coefficient κ as defined in Equation (27) for two Hurst exponents and three different choices of how ε_f,t change with pressure p. The term “const” relates to ε_t = 1/2 and ε_f = 1/32. These two values are the reference values at p^* = 0.2. The term “varying” indicates that the respective ε is scaled according to Equation (27). To give an example, the scaling makes a varying ε_f go down to 1/64 and a varying ε_t to 1.4 at p^* = 0.0125. Results were averaged over up to 100 random realizations per data point.

The reason for the different trends can be potentially linked to the distribution of contact patch areas and the characteristic contact patch size A_c, which we define to be the expected patch size that a randomly picked contact point belongs to. The three H = 0.3 cases and the H = 0.8 case with fixed ε_f, all belong to situations, in which the characteristic contact areas are rather small: A_c increases only logarithmically with ε_f for H < 0.5 (Müser and Wang, 2018) so that large patches are not possible, even when ε_f is small. Likewise, only small contact patches can arise for H = 0.8 at pressures well below the percolation threshold if ε_f is fixed to a constant value as large as ε_f = 1/32. In contrast, large contact patches can arise even at small pressures. if ε_f is small and H > 0.5. Large patches are needed for a linear a_r(p) dependence at small pressures, as can be rationalized qualitatively from bearing-area models.

In order to explore the question further, if κ can have a well-defined limit when being deduced with the meaningful limit defined in Equation (26), we compare the κ(p) relation with two sets of ε_t,f: (i) a small system with ε_t = 1 and ε_f = 1/32 and (ii) a larger systems in which both ε_t and ε_f were decreased by a factor of four to ε_t = 1/4 and ε_f = 1/128. Figure 5 reveals that the pressure sensitivity of κ reduces quite noticeably with increasing system size for H = 0.8 but not for H = 0.3, which, however, has a relatively minor logarithmic dependence of κ on p^* to begin with.

FIGURE 5

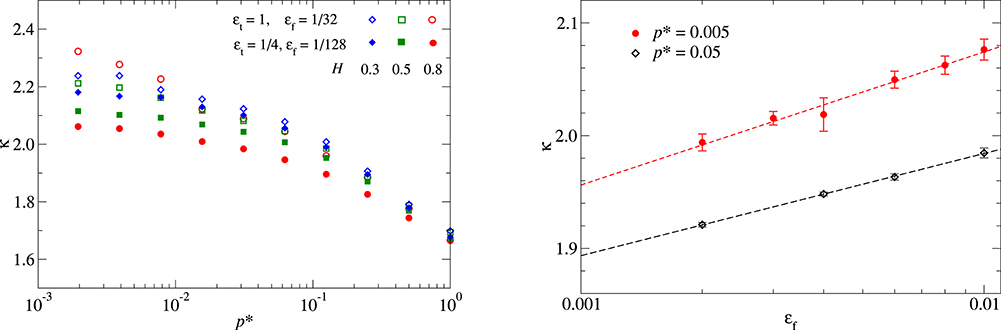
Figure 5. (Left) Proportionality coefficient κ as function of reduced pressure p^* for three Hurst parameters and two fixed ratios of ε_t,f, namely (i) ε_t = 1 and ε_f = 1/32 and (ii) ε_t = 1/4 and ε_f = 1/128. (Right) Scaling with ε_f for H = 0.8 and ε_t = 0.5. Dashed lines are linear fits to the three lowest values in ε_f. Results were averaged over up to 100 random realizations per data point.

The trends revealed in Figure 5 are consistent with those of Figure 4. Increasing system size, i.e., decreasing simultaneously ε_t and ε_f, reduces κ and its pressure sensitivity for H = 0.8 but not for H = 0.3. Our trends are also roughly consistent with the observations by Prodanov et al. (2013), who proposed the existence of a well-defined value for κ for H = 0.8 but not for H = 0.3.

While we already speculatively linked the different trends for H = 0.3 and H = 0.8 to the way how a characteristic contact patch size changes with decreasing ε_f, it remains to be explained why A_c increases only logarithmically with ε_f for H < 0.5 but algebraically for H > 0.5. One possibility could be that most of the elastic energy (in full contact) is stored in long-wavelength modes for H > 0.5 but in short-wavelength modes for H < 0.5. If this argument were true, H = 0.5 could be the dividing line for the different types of behaviors. We therefore repeated the analysis shown in Figure 5 for H = 0.5. Unfortunately, the results leave us somewhat uncertain. Significantly more work must probably be done to characterize the transition between the different scaling behaviors rigorously.

To conclude this section on the much investigated isotropic, rpa surfaces, we expect κ to have a well defined zero-pressure limit, in the sense of Equation (26), which does not depend upon how it is approached. For small Hurst exponents, i.e., for H > 0.5, it might not exist and/or it might depend on how ε_f → 0 is approached, e.g., it could take different values when reaching it with constant ε_f/ε_t than with constant ${\epsilon }_{\text{f}}/\sqrt{{\epsilon }_{\text{t}}}$. At the same time, we somewhat expect that the value of κ ≈ 2.5 predicted by the more sophisticated bearing-area models, such as that by Bush et al. (1975), might provide a (potentially rigorous) upper bound for κ when the limit ε_t → 0 is taken before ε_f → 0. In this case, the surface roughness on scales exceeding the roll-off wavelength is white noise so that the underlying mean-field model of elasticity might not be detrimental.

4.2.2. Effect of Nayak and Related Parameters on κ

Yastrebov et al. (2017) proposed the proportionality coefficient κ to decrease logarithmically with the Nayak parameter, at least for self-affine, rpa surfaces. However, two aspects of this claim and their data strike us as troublesome. First, κ is implicitly predicted to become negative for very large Nayak parameters, which is physically meaningless. Second, their data points seem to be partially inconsistent, e.g., in their Figure 10D, the points (Φ_N, κ) = (700, 1.93) and (70, 2.05) should be moved to (70, 1.93) and (700, 2.05), respectively. The Nayak parameter Φ_N would then be consistent not only with our own calculations but also with the values that Yastrebov et al. reported themselves in their Figure 1. Once these two data points are corrected, the logarithmic relation seems to be much less convincing than with improperly plotted data.

To provide an independent test of the extent with which the Nayak parameter affects the proportionality coefficient κ, we investigated a broader range of surfaces than before and contrast surfaces with cutoff to those with smooth and abrupt rolloffs. Figure 6 summarizes the results, which were averaged over up to 400 random realizations per data point.

FIGURE 6

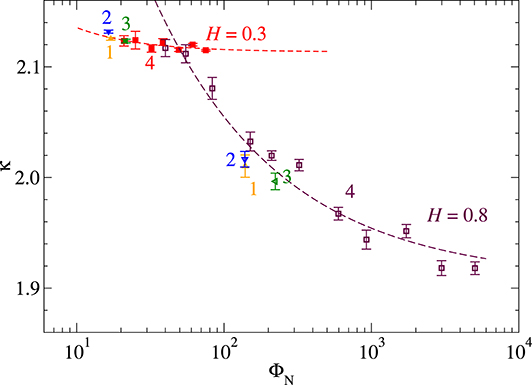
Figure 6. Proportionality coefficient κ as a function of the Nayak parameter Φ_N = 1.5Φ₆ at p^* = 0.02. Full and open symbols relate to H = 0.3 and H = 0.8, respectively. Different surface realizations were considered: (1) orange triangles up: cut-off, (2) blue triangles down: smooth roll-off, (3) green triangles left: hard roll-off. In these three cases, ε_t and ε_f were fixed: ε_t = 1/4, ε_f = 1/125, Finally, (4) squares: cut-off with 1/40 ≤ ε_f ≤ 1/1, 000. The dashed lines are fits $\kappa ={\kappa }_{\infty }+c{\Phi }_N^{-\nu }$, where ν turned out to be consistent with ν ≈ 0.5 for H = 0.8 and ν ≈ 1 for H = 0.3.

Our data appears to be consistent with a $\kappa ({\Phi }_{\mathrm{\text{N}}})=\kappa (\infty )-c_{\mathrm{\text{N}}}{\Phi }_{\mathrm{\text{N}}}^{-{\nu }_{\mathrm{\text{N}}}}$ relation rather than with a logarithmic κ(Φ_N) dependence. If the original data had been plotted without taking averages, the H = 0.3 might have scattered sufficiently much to make them appear as a continuation of the H = 0.8 data. Two markedly different dependencies of κ on Φ_N are obtained for H = 0.3 and H = 0.8. Thus, κ cannot be reduced to be a function of Φ_N (and p^*) alone.

4.3. Anisotropic rpa Surfaces

To address the question how anisotropy affects the relative contact area, we repeated the simulations presented in Figure 4 with a Peklenik number of γ_P = 4. Results are shown in Figure 7. It can be seen that anisotropy enhances the pressure dependence of κ at fixed values of ε_t,f compared to stochastically isotropic surfaces with γ_P = 1. This may not be particularly surprising in light of the observation that one-dimensional surfaces have logarithmic corrections to the κ(p) relation, even for H > 0.5. By using a Peklenik number clearly differing from unity, roughness dominates along one spatial dimension, whereby the spatial dimension can be argued to have been reduced to a certain extent.

FIGURE 7

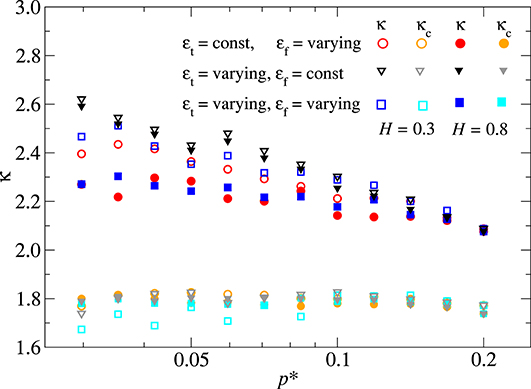
Figure 7. Same as Figure 4, however, this time for stochastically anisotropic surfaces with γ_P = 4. Symbols with faint colors represent results for κ_c rather than for κ.

Figure 7 also finds that κ(H = 0.8) is not very pressure sensitive when ε_f is decreased with pressure so that for macroscopic systems, in which ε_f is two to three orders of magnitude smaller than in simulations, the pressure sensitivity is marginally small. However, due to anisotropy, κ is noticeably increased with respect to the isotropic case. When Peklenik numbers differ very much from unity, different laws may apply as the surface's dimensionality has effectively changed from two to one. In the limit of one-dimensional surfaces, the pressure sensitivity of κ at small p^* has been convincingly established not only for small H but also for H = 0.8 (van Dokkum et al., 2018).

As a final comment on the non-isotropic rpa surfaces, we note that κ_c, whose definition of reduced pressure uses the root-mean-square height gradient ḡ averaged over contact only, has a rather weak dependence on p^*. Values are generally close to 1.8. Interestingly, the ordering of the points are essentially in reverse order compared to the analysis in which ḡ was averaged over entire surfaces.

The smallest κ_c occurs for the smallest Hurst exponent, which can be rationalized as follows: For H = 0.3, roughness exists predominantly at short wavelengths and contact patches are rather small compared to H = 0.8. The coarse-grained, or rotationally averaged height profile of an individual meso-scale asperity is therefore blunter for H = 0.8 (where many valleys are sampled over) than for H = 0.3 (containing essentially only high peaks). Neglecting the fact that contact is more and more partial in such a mesoscale asperity with distance from the highest point, Equation (28) finds that blunter tips have larger κ_c. The extreme limit at small p^* should be a Hertzian asperity, for which κ_c≈1.666. The blunter the profile, the larger κ_c.

4.4. Isotropic Height-Warped Surfaces

The assumption of the random-phase approximation is subject to the serious and legitimate criticism not only of Persson's contact mechanics theory but on a large body of simulation studies using ideal, rpa surfaces. Quite a few numerical studies use a Weierstrass profile, which has (perfect) phase correlation, while reproducing a height autocorrelation function (ACF) being similar to experimental ACFs. However, the Weierstrass profile lacks any visual similarity to experimental surfaces as demonstrated in Figure 2 of Müser (2018). We therefore believe that the warping method proposed in section 2, while probably still being far from ideal, reproduces the stochastic properties of correlated surfaces in a significantly more realistic fashion than a Weierstrass-function based height profile.

Figure 8 reveals that the increase of κ with decreasing pressure is much accentuated for a positive warping exponent w, in which case the peaks of the indenting asperities are flattened compared to the valleys. This times κ(H = 0.8) even increases with decreasing p^* when ε_f is reduced with decreasing pressure. However, for the opposite case of w < 0 leading to sharp asperities and shallow valleys, κ is found to decrease with pressure. This statement also holds in certain pressure ranges, when ε_f is not scaled according to Equation (27) but kept constant.

FIGURE 8

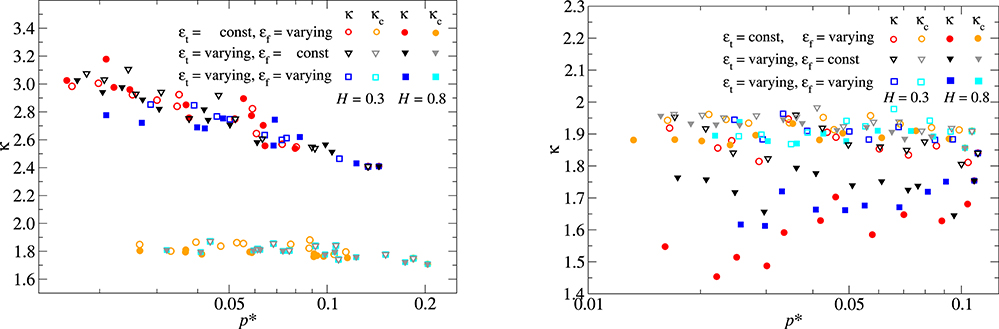
Figure 8. Same as Figure 4, however, this time for a height warped surfaces: (Left) blunt indenting peaks and steep valleys (w = 2) (Right) sharp peaks and shallow valleys (w = −2).

When defining the root-mean-square height gradient and thus the reduced pressure with respect to the true contact area, κ_c turns out yet again to be rather insensitive to the reduced pressure and to be around 1.8 for small $p_{\mathrm{\text{c}}}^{*}$. Correlating the respective values of κ_c with the structural parameters, which are symmetry-allowed and finite, has remained unsuccessful so far.

4.5. Periodically Repeated Smooth Indenters

When indenters are periodically repeated, each indenter carries the same load. If the linear contact dimension is small compared to the period, that is, at small applied external pressures p₀, a similar relation between contact area and load or pressure must be obtained as if the indenter were isolated. As already mentioned in the introduction, it has been noticed recently (Müser, 2017) that the corresponding asymptotic low-pressure relation for periodically repeated indenters with harmonic height profiles can be cast in terms of Equation (8). The prefactor κ_c can be calculated analytically, specifically

$\begin{array}{ll}{\kappa }_{\text{c}}(n)=\sqrt{\frac{\pi }{n}}\frac{\Gamma (\frac{n}{2}+\frac{3}{2})}{\Gamma (\frac{n}{2}+1)},& (28)\end{array}$

where Γ(•) represent the gamma function. The numerical data shown in Figure 9 confirms the analytical results at low pressures. Errors in the relative contact become noticeable only once a_r exceeds 0.3, but they remain below 25%. The high-pressure asymptotics can also be described reasonably well with Equation (8), however, the value for κ_c needs to be decreased. Since the approach to full contact is the quite special case of a conical dimple for the periodically repeated indenters, it will not be investigated any further in this study.

FIGURE 9

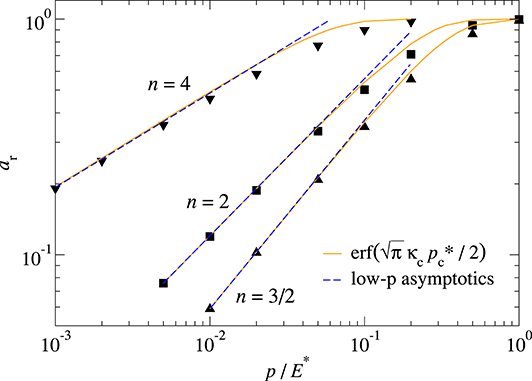
Figure 9. Relative contact area a_r as function of pressure p normalized to the contact modulus E^* for periodically repeated indenters with the height profile h(r) = R(r/R)ⁿ/n, where R defines the unit of length and with n = 4 (blunt indenter), n = 2 (Hertzian indenter), and n = 3/2 (sharp indenter).

5. Discussions and Conclusions

In this study, various structural parameters determining the relative contact area a_r in a contact between a rough surface and a linearly elastic counterbody were investigated. The focus was laid on the questions if a_r is linear in pressure p and inversely proportional to the root-mean square height gradient ḡ for small reduced pressures, defined as p^* = p/(E^*ḡ), and if yes, what structural parameters determine the proportionality coefficient κ.

One of the difficulties to determine whether or not a_r is linear in p^* at small p^* is that taking the limit p^* → 0 properly is not a simple task, because the ratios of roll-off wavelength and system size, ${\epsilon }_{\mathrm{\text{t}}}={\lambda }_{\mathrm{\text{r}}}/{L}$ (size scaling), as well as the ratio of short-wavelength cutoff and roll-off wavelength, ε_f = λ_s/λ_r (fractal scaling), have to be made systematically small. While Prodanov et al. (2013) emphasized the necessity of such a finite-size and fractal scaling, they failed to take that limit properly themselves, as they kept the ratio of linear mesh size and short-wavelength cutoff, ε_c = a/λ_s, fixed. In this study, we extrapolated results for a specific surface configuration to ε_c first and then computed contact area while taking ε_t and ε_f to zero simultaneously or by taking ε_f to zero while keeping ε_t constant.

The last type of analysis, in which effectively ε_c = 0, while ε_t is kept constant and p^* is set to a (very) small value, deserves particular attention. When doing so, only a single meso-scale asperity contact (SMAC) will ultimately remain in contact for very small ε_f and Hurst exponents H > 0.5. This is because typical contact patch sizes increase algebraically with decreasing ε_f for H > 0.5 (Müser and Wang, 2018). In an individual SMAC, which can be described as a single asperity with microscale roughness added to it, linearity between load and contact area is well satisfied (Pastewka and Robbins, 2016) and the (complementary) contact area in it can be well-determined using Persson theory (Müser, 2016). As such, linearity between load and contact area in a macroscopic system should arise automatically. However, it remains to be understood why one-dimensional (1D) interfaces behave differently from 2D interfaces, since 1D interfaces do not obey a linear $a_{\mathrm{\text{r}}}(p^{*})$ relationship at small pressures (van Dokkum et al., 2018), even for very large systems. Moreover, we are not yet certain about the small-pressure $a_{\mathrm{\text{r}}}(p^{*})$ relationship for H < 0.5, although our current analysis supports the finding (Yastrebov et al., 2015, 2017) that the relationship may have indeed non-negligible logarithmic corrections in p^*. They might be the consequence of the small, logarithmic growth of characteristic contact patch sizes with decreasing ε_f for H < 0.5. At the same time, we wonder if κ computed in the thermodynamic limit can systematically exceed predictions of the more advanced bearing-area models such as Bush, Gibson, and Thomas (BGT) (Bush et al., 1975). Thus, although we believe to have furthered the rigor with which κ is computed, we expect that the final answer to how κ has to be computed in the thermodynamic limit still needs to be found.

The discussion in the last paragraph as well as the analysis conducted in the results section of this works reveals already at the present level of rigor that the Nayak parameter Φ_N has no stringent direct correlation with the proportionality coefficient κ, which would allow the function $\kappa (p^{*},H,{\epsilon }_{\mathrm{\text{t}}},{\epsilon }_{\mathrm{\text{f}}})$ to be reduced to a smaller number of variables, such as, $\kappa =\kappa (p^{*},{\Phi }_{\mathrm{\text{N}}},{\epsilon }_{\mathrm{\text{t}}})$. This in turn emphasizes once more that a rigorous understanding of contact mechanics necessitates a spectral analysis of the height profiles. Knowledge of the Nayak parameter and even more so of simple distribution functions of asperity heights and geometries is unavailing.

While Persson theory cannot (yet) be used either to explain why different Hurst exponents lead to different κ, it does allow deviations of κ(p^*) from linearity to be rationalized for both finite systems and surfaces violating the random-phase approximation. The basic version of Persson theory assumes that the elastic body “feels” the full root-mean-square gradient (averaged over the entire surface) as soon as the elastic body hits the rough substrate. However, for any finite surface, a certain fraction must be in contact before the root-mean-square gradient and other stochastic parameters, such as the kurtosis, approach their “true” mean values. While this fraction decreases with system size, ḡ (typically) remains below its asymptotic value for finite rpa surfaces at small a_r so that (according to Persson theory and simulations presented in this work) a_r turns out larger than in the thermodynamic limit. In the case of correlated random roughness, the situation is more complex, since the rms-gradient, kurtosis, etc., can be functions of the height even when surfaces are in the thermodynamic limit. A possible correction of Persson theory for this case could be to identify the rms-gradient of the a_r × 100% top- (or bottom) most heights and use this value to determine the reduced pressure $p_{\mathrm{\text{c}}}^{*}$, which would then satisfy Equation (8) reasonably well. To some extent, this would constitute a somewhat dissatisfactory compromise between Persson theory and bearing-area models, since it is not the top- (or bottom) most, say, 20% of the peaks that are in contact at 20% relative contact area, as is implicitly assumed in bearing-area models. However, this is the simplest correction that comes to our mind at this point of time. It is certainly much less tedious to work out than the systematic corrections to Persson theory relying on a cumulant expansion of the short- but finite-range repulsive interactions between indenter and elastic body (Müser, 2008).

In full simulations, ḡ can be averaged over the true contact area and no compromise between bearing-area models and Persson theory needs to be made. In all investigated randomly-rough contacts, we find a close-to-linear relation between a_r and $p_{\mathrm{\text{c}}}^{*}$, i.e., when averaging the rms height gradient only over the true contact even if the original a_r(p) deviates clearly from linearity. In these simulations, we find κ_c to lie in the relatively narrow range satisfying κ_c ≈ 1.8 ± 0.1. This value for κ_c is only slightly larger than the value of 1.6 predicted by Persson theory but clearly below the value of 2.5 predicted by BGT (Bush et al., 1975). Thus, the range of validity of Persson theory could be substantially expanded if the approximation of using the full rms-height gradient were replaced with an accurate estimate of the mean rms-height gradient in the true contact.

It is certainly justified to consider many parts of this study to be more of a mathematical exercise rather than an attempt to model any specific real-world problem. And anyone wondering why there has to be yet another paper on κ can be assured to have our full sympathy. However, if poorly conducted studies of contact problems lead to the conclusion that a legitimate theory is brought into discredit and these studies receive many citations as evidence for the theory to be flawed, it should be in place to demonstrate that a carefully conducted analysis supports the theory.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MM designed the study and wrote the manuscript. YZ run the simulations. MM and YZ jointly analyzed the data and jointly produced the figures. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Afferrante, L., Bottiglione, F., Putignano, C., Persson, B. N. J., and Carbone, G. (2018). Elastic contact mechanics of randomly rough surfaces: an assessment of advanced asperity models and Persson's theory. Tribol. Lett. 66:75. doi: 10.1007/s11249-018-1026-x

CrossRef Full Text | Google Scholar

Almqvist, A., Campañá, C., Prodanov, N., and Persson, B. (2011). Interfacial separation between elastic solids with randomly rough surfaces: comparison between theory and numerical techniques. J. Mech. Phys. Solids 59, 2355–2369. doi: 10.1016/j.jmps.2011.08.004

CrossRef Full Text | Google Scholar

Bush, A., Gibson, R., and Thomas, T. (1975). The elastic contact of a rough surface. Wear 35, 87–111. doi: 10.1016/0043-1648(75)90145-3

CrossRef Full Text | Google Scholar

Campañá, C., and Müser, M. H. (2006). Practical green's function approach to the simulation of elastic semi-infinite solids. Phys. Rev. B 74:075420. doi: 10.1103/PhysRevB.74.075420

CrossRef Full Text | Google Scholar

Campañá, C., and Müser, M. H. (2007). Contact mechanics of real vs. randomly rough surfaces: a Green's function molecular dynamics study. Europhys. Lett. 77:38005. doi: 10.1209/0295-5075/77/38005

CrossRef Full Text | Google Scholar

Campañá, C., Müser, M. H., and Robbins, M. O. (2008). Elastic contact between self-affine surfaces: comparison of numerical stress and contact correlation functions with analytic predictions. J. Phys. 20:354013. doi: 10.1088/0953-8984/20/35/354013

CrossRef Full Text | Google Scholar

Campañá, C., Persson, B. N. J., and Müser, M. H. (2011). Transverse and normal interfacial stiffness of solids with randomly rough surfaces. J. Phys. 23:085001. doi: 10.1088/0953-8984/23/8/085001

PubMed Abstract | CrossRef Full Text | Google Scholar

Candela, T., Renard, F., Bouchon, M., Schmittbuhl, J., and Brodsky, E. E. (2011). Stress drop during earthquakes: effect of fault roughness scaling. Bull. Seismol. Soc. Am. 101, 2369–2387. doi: 10.1785/0120100298

CrossRef Full Text | Google Scholar

Carbone, G., and Bottiglione, F. (2008). Asperity contact theories: do they predict linearity between contact area and load? J. Mech. Phys. Solids 56, 2555–2572. doi: 10.1016/j.jmps.2008.03.011

CrossRef Full Text | Google Scholar

Dapp, W. B., Lücke, A., Persson, B. N. J., and Müser, M. H. (2012). Self-affine elastic contacts: percolation and leakage. Phys. Rev. Lett. 108:244301. doi: 10.1103/PhysRevLett.108.244301

PubMed Abstract | CrossRef Full Text | Google Scholar

Dapp, W. B., Prodanov, N., and Müser, M. H. (2014). Systematic analysis of Persson's contact mechanics theory of randomly rough elastic surfaces. J. Phys. 26:355002. doi: 10.1088/0953-8984/26/35/355002

PubMed Abstract | CrossRef Full Text | Google Scholar

Hyun, S., Pei, L., Molinari, J.-F., and Robbins, M. O. (2004). Finite-element analysis of contact between elastic self-affine surfaces. Phys. Rev. E 70:026117. doi: 10.1103/PhysRevE.70.026117

PubMed Abstract | CrossRef Full Text | Google Scholar

Hyun, S., and Robbins, M. O. (2007). Elastic contact between rough surfaces: effect of roughness at large and small wavelengths. Tribol. Int. 40, 1413–1422. doi: 10.1016/j.triboint.2007.02.003

CrossRef Full Text | Google Scholar

Jacobs, T. D. B., Junge, T., and Pastewka, L. (2017). Quantitative characterization of surface topography using spectral analysis. Surface Topogr. 5:013001. doi: 10.1088/2051-672X/aa51f8

CrossRef Full Text | Google Scholar

Kajita, S. (2016). Green's function nonequilibrium molecular dynamics method for solid surfaces and interfaces. Phys. Rev. E 94:033301. doi: 10.1103/PhysRevE.94.033301

PubMed Abstract | CrossRef Full Text | Google Scholar

Lorenz, B., and Persson, B. N. J. (2008). Interfacial separation between elastic solids with randomly rough surfaces: comparison of experiment with theory. J. Phys. 21:015003. doi: 10.1088/0953-8984/21/1/015003

PubMed Abstract | CrossRef Full Text | Google Scholar

Majumdar, A., and Tien, C. L. (1990). Fractal characterization and simulation of rough surfaces. Wear 136, 313–327. doi: 10.1016/0043-1648(90)90154-3

CrossRef Full Text | Google Scholar

Müser, M., and Wang, A. (2018). Contact-patch-size distribution and limits of self-affinity in contacts between randomly rough surfaces. Lubricants 6:85. doi: 10.3390/lubricants6040085

CrossRef Full Text | Google Scholar

Müser, M. H. (2008). Rigorous field-theoretical approach to the contact mechanics of rough elastic solids. Phys. Rev. Lett. 100:055504. doi: 10.1103/PhysRevLett.100.055504

PubMed Abstract | CrossRef Full Text | Google Scholar

Müser, M. H. (2016). On the contact area of nominally flat hertzian contacts. Tribol. Lett. 64:14. doi: 10.1007/s11249-016-0750-3

CrossRef Full Text | Google Scholar

Müser, M. H. (2017). On the linearity of contact area and reduced pressure. Tribol. Lett. 65:129. doi: 10.1007/s11249-017-0912-y

CrossRef Full Text | Google Scholar

Müser, M. H. (2018). Response to “comment on meeting the contact-(mechanics) challenge.” Tribol. Lett. 66:38. doi: 10.1007/s11249-018-0986-1

CrossRef Full Text | Google Scholar

Müser, M. H., Dapp, W. B., Bugnicourt, R., Sainsot, P., Lesaffre, N., Lubrecht, T. A., et al. (2017). Meeting the contact-mechanics challenge. Tribol. Lett. 65:118. doi: 10.1007/s11249-017-0900-2

CrossRef Full Text | Google Scholar

Nayak, P. R. (1971). Random process model of rough surfaces. J. Lubricat. Technol. 93, 398–407. doi: 10.1115/1.3451608

CrossRef Full Text | Google Scholar

Palasantzas, G. (1993). Roughness spectrum and surface width of self-affine fractal surfaces via the k-correlation model. Phys. Rev. B 48, 14472–14478. doi: 10.1103/PhysRevB.48.14472

PubMed Abstract | CrossRef Full Text | Google Scholar

Pastewka, L., Prodanov, N., Lorenz, B., Müser, M. H., Robbins, M. O., and Persson, B. N. J. (2013). Finite-size scaling in the interfacial stiffness of rough elastic contacts. Phys. Rev. E 87:062809. doi: 10.1103/PhysRevE.87.062809

PubMed Abstract | CrossRef Full Text | Google Scholar

Pastewka, L., and Robbins, M. O. (2016). Contact area of rough spheres: large scale simulations and simple scaling laws. Appl. Phys. Lett. 108:221601. doi: 10.1063/1.4950802

CrossRef Full Text | Google Scholar

Pastewka, L., Sharp, T. A., and Robbins, M. O. (2012). Seamless elastic boundaries for atomistic calculations. Phys. Rev. B 86:075459. doi: 10.1103/PhysRevB.86.075459

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2001). Theory of rubber friction and contact mechanics. J. Chem. Phys. 115:3840. doi: 10.1063/1.1388626

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2008). On the elastic energy and stress correlation in the contact between elastic solids with randomly rough surfaces. J. Phys. 20:312001. doi: 10.1088/0953-8984/20/31/312001

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2014). On the fractal dimension of rough surfaces. Tribol. Lett. 54, 99–106. doi: 10.1007/s11249-014-0313-4

CrossRef Full Text | Google Scholar

Persson, B. N. J., Albohr, O., Tartaglino, U., Volokitin, A. I., and Tosatti, E. (2004). On the nature of surface roughness with application to contact mechanics, sealing, rubber friction and adhesion. J. Phys. 17, R1–R62. doi: 10.1088/0953-8984/17/1/R01

PubMed Abstract | CrossRef Full Text | Google Scholar

Pohrt, R., Popov, V. L., and Filippov, A. E. (2012). Normal contact stiffness of elastic solids with fractal rough surfaces for one- and three-dimensional systems. Phys. Rev. E 86:026710. doi: 10.1103/PhysRevE.86.026710

PubMed Abstract | CrossRef Full Text | Google Scholar

Prodanov, N., Dapp, W. B., and Müser, M. H. (2013). On the contact area and mean gap of rough, elastic contacts: dimensional analysis, numerical corrections, and reference data. Tribol. Lett. 53, 433–448. doi: 10.1007/s11249-013-0282-z

CrossRef Full Text | Google Scholar

Putignano, C., Afferrante, L., Carbone, G., and Demelio, G. (2012). The influence of the statistical properties of self-affine surfaces in elastic contacts: a numerical investigation. J. Mech. Phys. Solids 60, 973–982. doi: 10.1016/j.jmps.2012.01.006

CrossRef Full Text | Google Scholar

Salehani, M. K., van Dokkum, J., Irani, N., and Nicola, L. (2020). On the load-area relation in rough adhesive contacts. Tribol. Int. 144:106099. doi: 10.1016/j.triboint.2019.106099

CrossRef Full Text | Google Scholar

van Dokkum, J. S., and Nicola, L. (2019). Green's function molecular dynamics including viscoelasticity. Modell. Simul. Mater. Sci. Eng. 27:075006. doi: 10.1088/1361-651X/ab3031

CrossRef Full Text | Google Scholar

van Dokkum, J. S., Salehani, M. K., Irani, N., and Nicola, L. (2018). On the proportionality between area and load in line contacts. Tribol. Lett. 66:115. doi: 10.1007/s11249-018-1061-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Wick, G. C. (1950). The evaluation of the collision matrix. Phys. Rev. 80, 268–272. doi: 10.1103/PhysRev.80.268

CrossRef Full Text | Google Scholar

Yastrebov, V. A., Anciaux, G., and Molinari, J.-F. (2015). From infinitesimal to full contact between rough surfaces: evolution of the contact area. Int. J. Solids Struct. 52, 83–102. doi: 10.1016/j.ijsolstr.2014.09.019

CrossRef Full Text | Google Scholar

Yastrebov, V. A., Anciaux, G., and Molinari, J.-F. (2017). The role of the roughness spectral breadth in elastic contact of rough surfaces. J. Mech. Phys. Solids 107, 469–493. doi: 10.1016/j.jmps.2017.07.016

CrossRef Full Text | Google Scholar

Zhou, Y., Moseler, M., and Müser, M. H. (2019). Solution of boundary-element problems using the fast-inertial-relaxation-engine method. Phys. Rev. B 99:114103. doi: 10.1103/PhysRevB.99.144103

CrossRef Full Text | Google Scholar