- Department of System Dynamics and Friction Physics, Technische Universität Berlin, Berlin, Germany
In the past decade, the influence of surface tension on contact properties has attracted much attention, especially in the context of contact of very soft materials (such as gels) or contacts at the nanoscale. However, in the most current studies it is assumed that the tension of the surface inside and outside the contact area is the same. In practical terms, this means that the object considered is an elastic body “coated” with a tensed membrane. In real contacts, there is no reason why the surface tensions of the “free interface” and the “contact interface” should be equal. On the contrary, especially in contacts of soft bodies with hard solid indenters, one can anticipate that they are completely different. In the present article, we consider an elastic contact taking into account different surface tensions inside and outside the contact area. However, the considered contacts are still “non-adhesive.” This means that the three surface energies in play (two surface energies of both bodies outside the contact and the interface energy in the contact region) fulfill the criterion that the work of separation vanishes. A numerical model based on the Fast Fourier transform–assisted boundary element method is implemented and is illustrated with a few examples.
Introduction
It is known that surface tension governs the contact behavior of liquids (Brown, 1974) but it is hardly seen in contacts of solid bodies at the macro- and mesoscales. It is clear that it should start to play an essential role if we consider a continuous transition from an elastic solid to a very soft body such as a gel, soft rubber, and biological tissue (Style et al., 2017). In biological studies, it is found that surface tension may determine the tissue growth and the kinetics of the regeneration of organs (Ehrig et al., 2019). Surface tension may become important even in stiff contacts if their size is very small. In particular, it may influence the function of microelectromechanical systems (MEMS) (Syms et al., 2003).
There exists a class of contact problems in which the surface energy has been considered already for almost 50 years; these are adhesive contacts. While non-adhesive contacts of isotropic elastic bodies are completely characterized by the elastic modulus E and the Poisson's ratio ν of bulk material, in adhesive contacts the surface energy plays a key role, as has been shown in the classic theory by Johnson, Kendall, and Roberts (JKR) in 1971 (Johnson et al., 1971). However, when talking about the “surface energy,” we have always to specify what surface energy is meant. At the contact boundary, three interfaces are coming together. The “surface energy” used in the JKR theory is better characterized as “specific work of separation,” which we will also call “work of adhesion,” w. This quantity was introduced already by Dupre in 1869 (Dupré, 1869); it can be expressed as
where γ1 and γ2 are specific free surface energies of two bodies and γ12 interfacial surface energy inside the contact area (Figure 1).
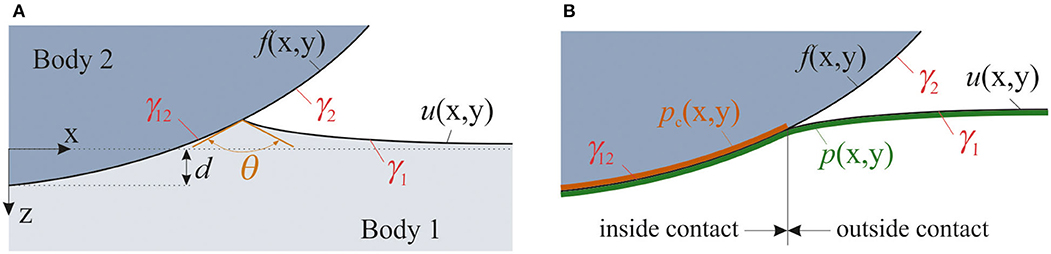
Figure 1. (A) Adhesive contact with surface tension. (B) Non-adhesive contact with surface tension. In (B), the contact angle θ = π.
From a general theoretical point of view, the JKR theory is incomplete: It makes a step by including surface energy into consideration but at the same time assumes that the surface energies of bodies outside the contact area are zero. However, there are no theoretical reasons why the surface energy of the interface should be so dominant compared to the surface energies of the surfaces outside the contact. In a general case, all three surface energies are different and may have a comparable order of magnitude.
As academic theoretical models, one can consider various relations of the three surface energies and corresponding limiting cases.
(I) If an elastic body is in contact with a rigid body and the specific surface energy of the elastic body outside the contact area can be neglected compared with the interface energy in the contact area, then we have an adhesive contact with specific work of separation w = γ2 − γ12. It is this case that is considered in the well-known work by Johnson et al. (1971). In reality, this case can be realized only in a contact of a high surface energy solid with low surface energy polymer but is hardly realizable in a contact of two materials with comparable surface energies.
(II) If the surface energy of the elastic body outside the contact area is finite, γ1 ≠ 0, but the work of adhesion is zero,
then we have a non-adhesive contact with surface tension.
(IIa) The latter case usually has been further simplified with the assumption that the surface energies inside and outside contact are equal:
which automatically leads to the conclusion that γ2 = 0. The corresponding theory was first developed for elastic foundations (Filonenko-Borodich, 1940; Kerr, 1964) and generalized to three-dimensional half-space contacts in Hajji (1978). It attracted much attention in recent years. However, this case cannot be realized physically, as there exist no substances with zero surface energy. In particular, in the cases that motivated consideration of this case—contacts of a hard indenter with a soft solid—one can assume that γ2 not only does not vanish but is also the largest of the three relevant surface energies [(Popov, 2017), Chapter 3]. This popular case can practically be realized only as a composite consisting of an elastic body coated with a tensed membrane.
(IIb) If the condition of the absence of adhesion is fulfilled, but the validity of the usual (and physical completely unrealistic) condition is not assumed, then we have a “general non-adhesive contact with surface tension,” which is characterized by two independent surface energies. It is this case that will be considered in the present article.
(III) Finally, in the general case both work of adhesion and surface tension of the free surface are finite. This leads to a general adhesive contact with surface tension. The latter attracted much interest in the past two decades in the context of indentation of soft matter (e.g., gels) (Carrillo and Dobrynin, 2012; Style et al., 2013; Cao et al., 2014).
It is interesting to note that it took almost 50 years to make the next necessary (and, as a matter of fact, obvious) step after the JKR theory. On the other hand, the appearance of the JKR theory, which is nothing but a direct implementation of the Griffith crack theory, also took 50 years (Popova and Popov, 2018). For the sake of historical truth, let us, however, mention that a solution equivalent to that of JKR was obtained by Sperling already in 1964 in his unpublished doctoral thesis (Sperling, 1964; Borodich, 2014).
In the present article, we will briefly recapitulate the studies of case IIa and then consider a more general (and more complicated) case IIb. As already stated above, case IIa can be physically realized only as an elastic body coated with a stressed membrane. The fundamental solution determining vertical displacement of the surface under the action of a concentrated force was given for this case by Hajji (1978). In this contact problem a characteristic length appears, , which is called “elastocapillary length,” determines the influence of surface tension: the surface tension effect is significant if the value of is comparable with the contact radius (Long and Chen, 2017). This leads to a “size-dependent” behavior in indentation testing (Style et al., 2013).
In the past few years, adhesive and non-adhesive contacts with surface tension have been studied intensively, for example, contact of homogeneous elastic half space including spherical contact (Long and Wang, 2013; Hui et al., 2015), conical contact (Long and Chen, 2017), and two-dimensional cylindrical contact (Liu et al., 2015), all based on the Hajji's fundamental solution, as well as complicated inhomogeneous coatings based on the semianalytical modeling of the surface effect (Zhang et al., 2018).
The present article is structured as follows: We start with a consideration and discussion of the boundary conditions in the general case of arbitrary values of specific surface energies of all three interfaces. We then recapitulate the results of the simplest “membrane model” using a Fast Fourier transform (FFT)-based boundary element method (BEM) implementation. Finally, we generalize the FFT-BEM to the case of non-adhesive contact with different surface energies inside and outside the contact and illustrate this case with a simulation example.
Boundary Conditions Taking Into Account Surface Tension
Analysis of a contact between a rigid body and an elastic half space taking into account surface tension, carried out in Karpitschka et al. (2016) and Popov (2020), shows that the Young's law determining the contact angle of liquids is also valid for solids. This leads to the following boundary conditions:
where f(x, y) is the profile of rigid indenter and u(x, y) the normal displacement of the surface of elastic half space, d is indentation depth, θ is contact angle, Δ is Laplace operator, and p(x, y) is the normal pressure at the surface immediately below the (infinitely thin) surface layer. Note that for definitions of the surface profile we used other direction of the z-axis (out of the elastic half-space) than for displacement and other quantities (into the half-space). It is also important to note that Equation (5) is written in approximation of small slopes of the surface of elastic body, which, however, is the necessary condition also for application of the superposition principle used throughout the paper. Equation (4) states that the surfaces of the indenter and the elastic half-space coincide in the contact area. Equation (5) determines the elastic stress at the surface under the tensioned surface layer. Equation (6) is the equilibrium condition of the contact boundary under the action of three surface tensions. Similarly to the contact angle in liquid contacts, θ is a thermodynamic property of the system. It does not depend on the shape of the body and deformation of the surface.
Using Equation (1) for the work of adhesion, w, Equation (6) can be rewritten as
This equation is known as Young–Dupre equation (Young, 1805; Dupré, 1869). For non-adhesive contacts with surface tension it has w = 0. From Equation (7), it follows that cosθ = −1 and
This equation means that at the boundary the slope of the surface profile is equal to the slope of the elastic half-space. Thus, in this specific case the condition (6) can be reformulated as a continuity of the surface slope at the contact boundary (Figure 1B). In this article, we focus on this non-adhesive contact with surface tension and its numerical simulation.
Numerical Simulation of Non-Adhesive Contact With Surface Tension
A numerical solution to non-adhesive contact with surface tension for the case IIa (γ1 = γ12: = γ) is based on Hajji's equation for the vertical surface displacement u at the position (x, y) caused by the pressure distribution :
with
where H0 and Y0 are Struve and Bessel functions of the second kind of zero order (Hajji, 1978). It should be stressed that the pressure pc(x, y) is the pressure acting on the surface of the upper tensed layer and is not equal to the pressure p(x, y) in Equation (5), which is the pressure under the tensed layer. Qualitatively speaking, pc(x, y) is the “external pressure” acting on the elastic body coated with membrane, while p(x, y) is the pressure in the elastic body immediately under the membrane.
For vanishing surface tension the first term approximations to (9) and (10) become the classic Boussinesq's equation
In this case, p = pc.
As already stated, according to the theory of surface elasticity (Gurtin et al., 1998), the contact with surface tension can be considered as a contact with an elastic body covered by an (infinitely) thin membrane. The equilibrium and constitutive equations in the bulk of the elastic body still follow the theory of elasticity. Therefore, we can find a solution to contact with surface tension by use of the fundamental solution for elastic half-space without surface tension. Using the definitions of pressure p(x, y) and pc(x, y), as shown in Figure 1B, the equilibrium condition of the interface in contact the contact region is
The other two boundary conditions (4) and (5) should of course also be fulfilled. The deformation u(x, y) is generated by pressure p(x, y), which can be obtained from the Boussinesq's equation.
Realization in the Boundary Element Method
The BEM was developed in the past 30 years and represents an effective numerical tool for solving various contact problems including homogeneous material and layered systems, adhesive and non-adhesive contact, rough contact, and thermal contact (Nogi and Kato, 1997; Liu et al., 2000; Campañá and Müser, 2006). Some BEM formulations are based on integral equations of the form of (9) or (11). In a discretized form they can be written as
where uij is the displacement of surface element at position (i, j) in two-dimensional discretization, is stress acting on an element located on (i′, j′), and Kiji′j′ is the influence coefficient and its value is calculated analytically or numerically depending on the form of the fundamental solution. The matrix of influence coefficients can be found, e.g., in Pohrt and Li (2014). The convolution nature of integral equations of the form (9) allows formulating and solving a contact problem using the FFT. Using this technique increases computing efficiency by replacing the integration by multiplication and therefore reducing the complexity from N4 to N2logN2 (for a system with discretization of N × N elements). For example, the algorithm of evaluating Equation (13) can be represented as
where pc is the pressure vector matrix, u is the matrix of discretized displacements, and K is the matrix of the influence coefficient. Note that for the non-periodic contact in a finite domain, the techniques of zero padding and wraparound order of matrix of pressure and influence coefficient in a doubled domain should be used to execute cyclic convolution. Thus, the pc and K should be expanded to dimension 2N × 2N when FFT is performed. The displacement u is then extracted from the obtained displacement with the same dimension 2N × 2N after the IFFT. The details of theories of the linear and cyclic convolutions and their applications to periodic and non-periodic contacts as well as numerical procedures can be found in Liu et al. (2000) and Ju and Farris (1996).
In Equation (14) the fundamental solution (given by the matrix K) should be first Fourier transformed. Alternatively, one can directly use the fundamental equation in Fourier space, which in most cases can be calculated very easily. For example, for an elastic half-space it is equal to
where . This gives the relation of the Fourier components of pressure and displacement
Displacement in the coordinate space in then calculated as
The general form of the fundamental equation in Fourier space can be written as
where the Fourier transform of the kernel of convolution, C(q), depends on a particular system. The only general prerequisite for this simple form is the lateral homogeneity of the system. In the direction perpendicular to the surface, it can be heterogeneous (e.g., a layered system or functionally graded material). C(q) is of course also a function of the effective elastic modulus in the case of a homogeneous material and coating system.
Equations (12) and (5) for non-adhesive contact with surface tension can be written in Fourier space as follows:
We first consider the simple case with equal surface energy inside and outside the contact area, γ1 = γ12 = γ. Substitution of (18) into (19) gives the relation between pressure pc and deformation u
For the displacement field in coordinate space, it follows
Thus, any available BEM program can be used for simulating this system covered with a tensed membrane just by adding the term “γq2” in the Green's function. Note that this equation connects the surface displacement with the external pressure. Therefore, the boundary condition and numerical procedure can be dealt in the same way as in all existing BEM: the pressure outside the contact is zero:
while the surface displacement inside the contact area meets the geometry condition. Of course, the zero padding and wraparound order are still needed for the non-periodic contacts as discussed in Liu et al. (2000). For an isotropic homogeneous material, Equation (22) becomes
Case Study 1: Isotropic Homogeneous Elastic Half-Space Coated With a Tensed Membrane
Let us discuss numerical simulation of a “Hertzian” contact with surface tension: a contact of a rigid parabolic indenter with elastic half-space taking into account surface tension, which we first consider equal inside and outside the contact. The result obtained using the Hajji's fundamental solution was given in Long and Wang (2013). Here we would like to compare this solution with the above-described solution based on the fundamental solution (1/C(q) + γ · q2)−1 in the Fourier space. Parameters used in the simulation are as follows: E* = 0.011 MPa; sphere radius R = 1 mm; indentation depth d = 0.01 mm; and two different specific surface energies, γ = 0.2 N/m and γ = 0.4 N/m, were considered, corresponding to the values and 0.36 of the parameter (ratio of the elastocapillary length and the Hertzian contact radius a0). Figure 2 shows numerical solution obtained with discretization 512 × 512 points, where the triangles in Figure 2A are pressure distributions calculated based on the Hajji's fundamental equation, and stars are results based on the alternative approach using the fundamental solution (1/C(q) + γ · q2)−1. The calculating time by using this fundamental solution is 12 times smaller than that with the Hajji's fundamental solution. The contact behavior found in Long and Wang (2013) practically coincides with that found with the above-described procedure. In particular, the pressure at the contact boundary has a “jump” in the case with surface tension (Figure 2A), and the surface tension leads to a reduction of contact area (Figures 2A,B).
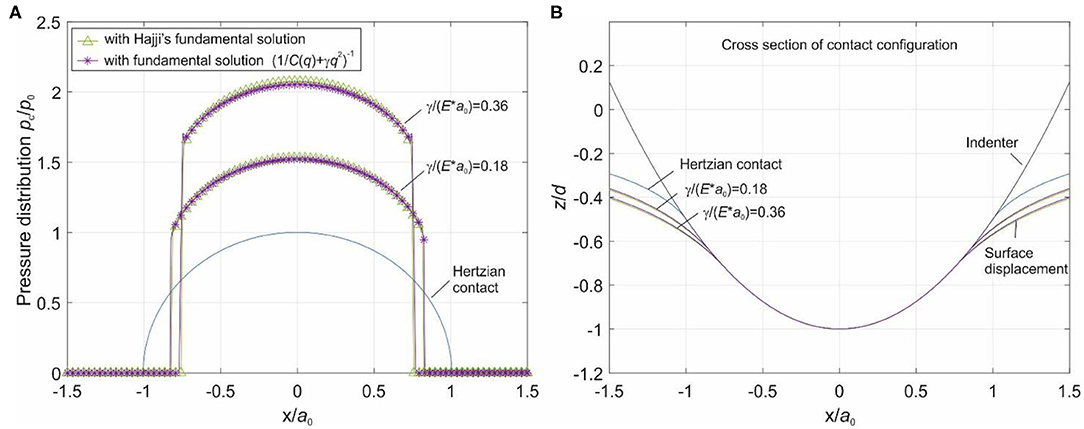
Figure 2. (A) Pressure distribution and (B) contact configuration in a contact between a rigid parabolic indenter and an elastic half-space for two different values of surface energy. The pressure is normalized by the maximum Hertzian pressure and coordinate by the Hertzian contact radius a0.
Case Study 2: Layered System
As explained above, any existing BEM formulation for a contact without surface tension can be trivially extended to include surface tension by a small change in the corresponding fundamental solution in Fourier space, according to Equation (21) or (24). Let us illustrate this with an example of an elastic layer with surface tension. We proceed from the BEM formulation without surface tension described in Li et al. (2019). Adding the term “γq2” in the fundamental solution, we include the surface tension. Here we show a case of soft layer bounded on the elastic half space. The layer had elastic modulus , specific surface energy γ = 0.2 N/m, and thickness h0 = 0.03 mm. The elastic modulus of the underlying half-space is . The profile of indenter is a sphere with radius R = 1 mm superposed with a two-dimensional waviness with wavelength λ = 0.03 mm and a small amplitude of h = 0.0005 mm. The indentation depth was d = 0.01 mm. The simulation results without and with surface tension are shown in Figure 3. The color map presents the pressure distribution in the contact region. Two cross sections of this map are selected to show the details. Under the above conditions, the contact area in the system without surface tension is compact (left figure), while “switching on” the surface tension makes it much more heterogeneous and even not simply connected (right figure). This leads to much more intensive oscillations of pressure. Note that the pressure shown in Figure 3 is the pressure immediately under the surface of the indenter. This pressure is relevant for estimating the possible damage of the indenter.
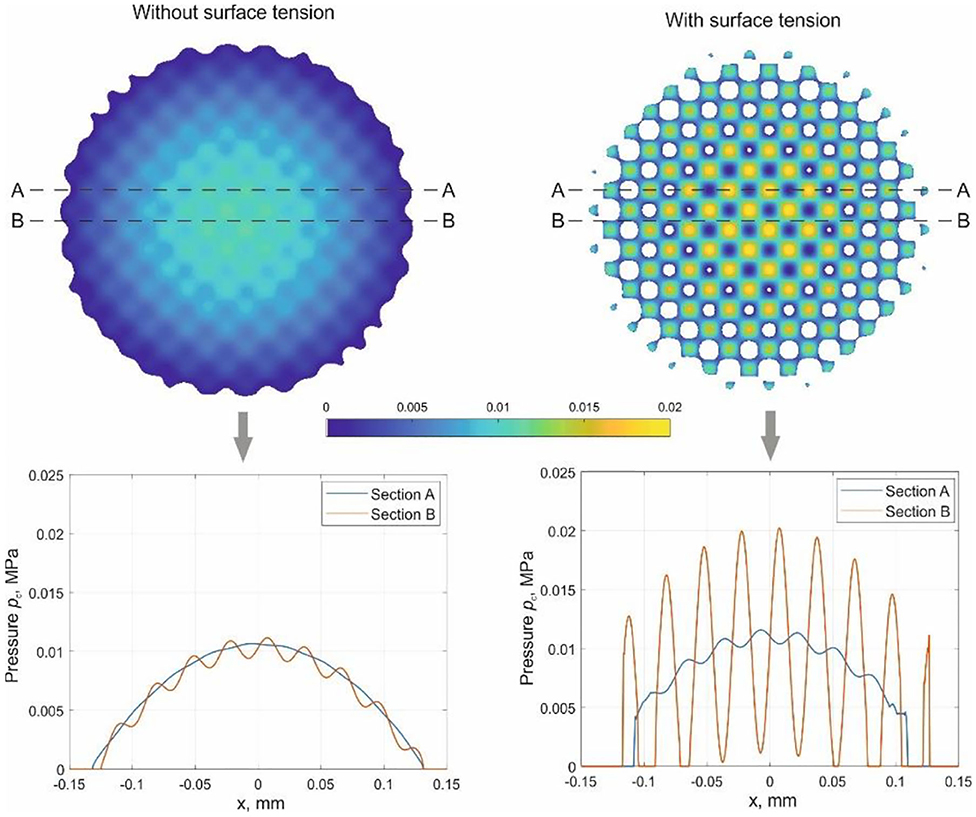
Figure 3. Pressure distribution in contact between a sphere with wavy roughness and elastic half space coated with a soft layer. The right figure is the pressure distribution in the contact region and the values at two cross sections are shown with curves below. For comparison, the case without surface tension is present on the left side.
Different Surface Energies Inside and Outside of the Contact Area
When surface energies inside and outside the contact are different, γ1 ≠ γ12, the FFT of Equations (19) and (20) cannot be directly carried out for the whole region. However, we can rewrite Equation (12) in the following form:
where p1(x, y) is an auxiliary function. In Fourier space, Equation (25) takes the form
The computation algorithm is the following. Initially we assume that the contact area is the geometrical intersection A and the displacement of the surface of the elastic half-space in this area coincides with the profile of indenter uA(x, y); the corresponding FFT(uA) is calculated. Using this FFT(uA) one can obtain the auxiliary stress function p1(q) as well as p1(x, y) appearing in (25). After that, the deformation u(x, y) can be calculated within the contact area. With p1(x, y) and u(x, y) as well as the curvature of the surface, Δu(x, y), one gets the pressure distribution p(x, y) from Equation (26). After that, the usual correction and iteration procedure starts: the elements that have negative pressure or geometrical penetration out of contact are marked as “detached” so that a new contact area, A′, is generated. With this new contact area, the above iteration is repeated until both pressure and geometry conditions for all elements in contact area are met.
Example 1 We give an example with the same parameters as studied in the case of Figure 2, with the only difference that the surface energy outside contact area, γ1, is not equal to that inside, γ12. Surface energy in the noncontact region was equal to γ1 = 0.2 N/m. Two cases were studied: one with smaller surface energy inside contact γ12 = 0.1 N/m and the other one with larger γ12 = 0.4 N/m. The obtained pressure distribution and surface displacement are shown in Figure 4. The results with equal surface energy are also shown with stars for a comparison. One can see that when the surface tension inside the contact is larger, the loading needed for generating the same indentation depth is also higher due to the surface tension effect (curve with triangles). Interestingly the contact area and the surface displacement are the same in all three cases. It is clear that the surface displacement in the contact coincides with the profile of the indenter shifted by the indentation depth. Displacement outside the contact is determined by the pressure p and surface tension γ1, where p is numerically calculated by Boussinesq's equation with the given surface deformation inside the contact. So surface displacement will be the same for unequal surface energy inside the contact if the contact area is unchanged. The difference of surface energy changes only the pressure pc with a constant value in the case of sphere contact because of the constant mean curvature.
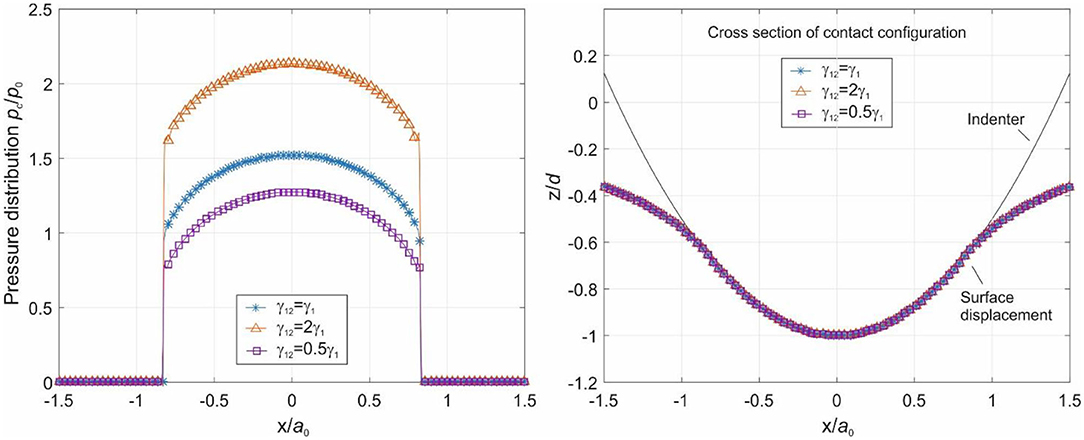
Figure 4. (A) Pressure distribution and (B) surface displacement in contact between a sphere and elastic half space. The surface energy is unequal inside and outside the contact area.
Figure 4 shows that the shape of the surface of elastic body does not depend on the surface tension inside the contact area. A posteriori, this seems to be a trivial conclusion. However, it is trivial only under the assumption of non-adhesive contact, which guarantees the unchanged condition at the boundary of the contact area, which does not depend on the interface surface energy density. The only quantity that is influenced by the specific surface energy of the contact interface is the pressure distribution. This means that the computation procedure in the case of two different surface energies can be simplified as shown in Figure 5.
1. In the first step, the contact problem is solved with a constant specific surface energy equal to the specific surface energy outside the contact area.
2. In the second step, the pressure distribution inside the contact area is corrected by the term δp(x, y) = (γ1 − γ12)Δu(x, y).
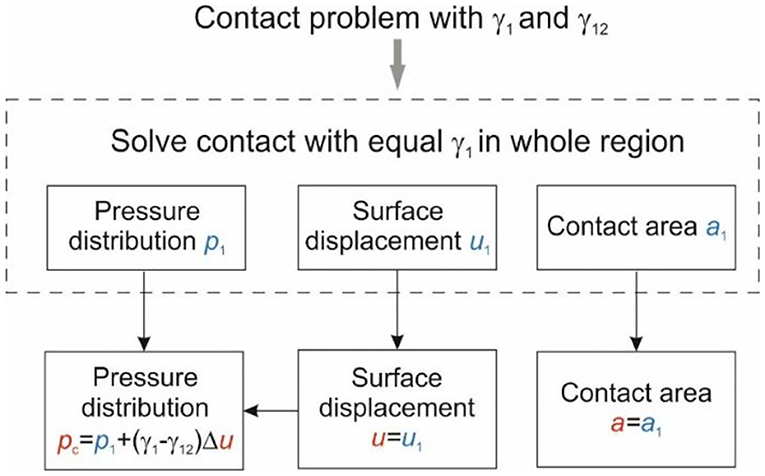
Figure 5. Solution to the contact problem with different surface energies inside and outside the contact.
Example 2 Consider a wavy surface similar to that shown in Figure 3 with the radius of curvature, R = 1 mm; wavelength, λ = 0.02 mm; and amplitude of waviness, h = 0.0001 mm. The elastic modulus of the half space is assumed and the indentation depth d = 0.012 mm. In the following two cases are considered: (1) equal specific surface energies γ1 = γ12 = 0.1 N/m and (2) two different specific surface energies, γ1 = 0.1 N/m and γ12 = 0.2 N/m, inside and outside the contact correspondingly. Numerical results are shown in Figure 6. The contact area and surface displacement are the same in both cases.
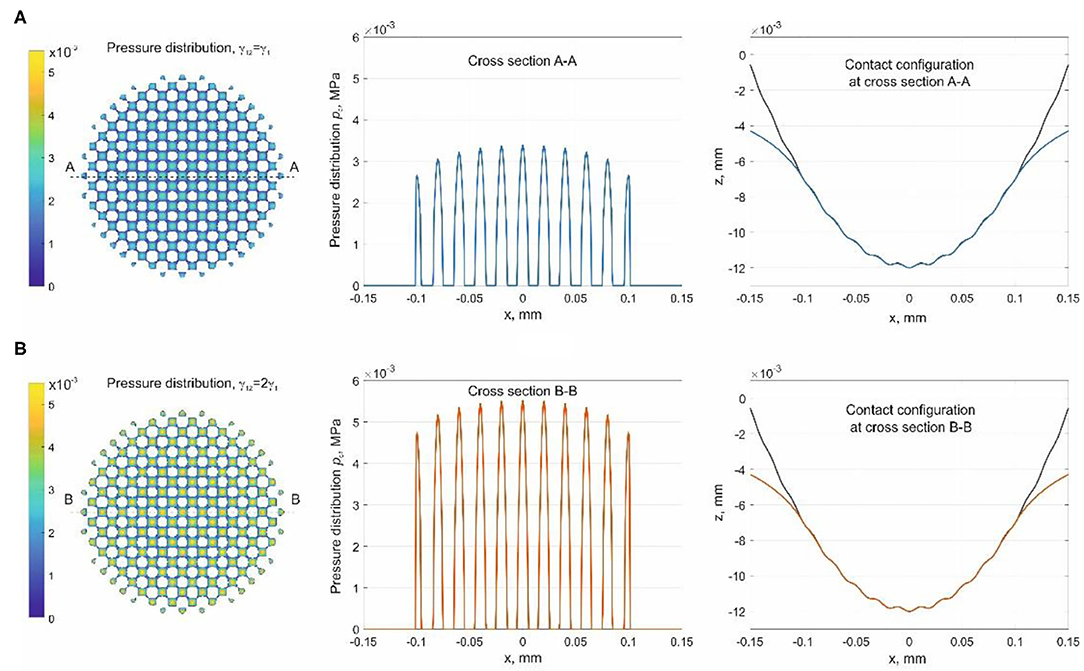
Figure 6. Colormap of pressure distribution and contact area in the case of (A) equal and (B) unequal surface energy inside and outside contact for a rough surface. The curves of pressure distribution and surface displacement at a cross section marked in the colormap are shown aside.
Conclusion
Non-adhesive contact with surface tension is usually solved using the fundamental solution of Hajji. This fundamental solution has a complicated form in the coordinate space but can be derived in an extremely simple way in the Fourier space. More than that, this derivation has a universal character and can be applied for more complicated situations, as, e.g., for layered systems or functionally graded materials. With an example of Hertzian contact this method was validated by comparison with the fundamental solution in the coordinate space, and it was then applied to the rough contact of a coated system.
We argue that the approach based on the fundamental solution can be used only in the case when the surface tension inside and outside of the contact area are equal. There are no physical reasons why it should be the case. Therefore, in the general case, the approach based on the use of the fundamental solution and superposition principle does not work. We show how this problem can be reduced to the simpler contact problem with constant surface tension inside and outside the contact area.
Of course, the case of non-adhesive contact with different surface energies inside and outside the contact is a little bit an academic exercise. In a general “dry” contact of two solids, the condition of non-adhesive contact normally will not be fulfilled. However, the contact can be made non-adhesive by introducing an intermediate liquid with dielectric constant equal to that of one of the bodies. According to the theory of van der Waals' interactions by Dzyaloshinskii et al. (1961), this leads to suppression of van der Waals force (and thus of the separation energy), while the surface tensions of both bodies remain generally non-zero.
Data Availability Statement
All datasets presented in this study are included in the article/supplementary material.
Author Contributions
VP designed the concept of the article, formulated the analytical theory, and formulated the algorithm of contact simulation in the case of different surface energies inside and outside of the contact area. QL implemented the algorithm into a BEM program and executed numerical simulations. All authors contributed equally to the analysis of simulation results as well as editing and review of the manuscript.
Funding
This work has been conducted under financial support from DFG (Grant number PO 810/55-1).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Borodich, F. M. (2014). The Hertz-Type and adhesive contact problems for depth-sensing indentation. Adv. Appl. Mech. 47, 225–366. doi: 10.1016/B978-0-12-800130-1.00003-5
Brown, R. C. (1974). The surface tension of liquids. Contemp. Phys. 15, 301–327. doi: 10.1080/00107517408210795
Campañá, C., and Müser, M. H. (2006). Practical green's function approach to the simulation of elastic semi-infinite solids. Phys. Rev. B 74, 1–15. doi: 10.1103/PhysRevB.74.075420
Cao, Z., Stevens, M. J., and Dobrynin, A. V. (2014). Elastocapillarity: adhesion and wetting in soft polymeric systems. Macromolecules 47, 6515–6521. doi: 10.1021/ma5013978
Carrillo, J.-M. Y., and Dobrynin, A. V. (2012). Contact mechanics of nanoparticles. Langmuir 28, 10881–10890. doi: 10.1021/la301657c
Dzyaloshinskii, I. E., Lifshitz, E. M., and Pitaevskii, L. P. (1961). General theory of van der Waals' forces. Sov. Phys. Usp. 4, 153–176. doi: 10.1070/PU1961v004n02ABEH003330
Ehrig, S., Schamberger, B., Bidan, C. M., West, A., Jacobi, C., Lam, K., et al. (2019). Surface tension determines tissue shape and growth kinetics. Sci. Adv. 5:eaav9394. doi: 10.1126/sciadv.aav9394
Filonenko-Borodich, M. M. (1940). Some approximate theories of the elastic foundation. Uchenye Zapiski Moskovskogo Gosudarstvennogo Universiteta. Mekhanika 46, 3–18.
Gurtin, M. E., Weissmüller, J., and Larché, F. (1998). A general theory of curved deformable interfaces in solids at equilibrium. Philos. Mag. A Phys. Condens. Matter. Struct. Defects Mech. Prop. 78, 1093–1109. doi: 10.1080/01418619808239977
Hajji, M. A. (1978). Indentation of a membrane on an elastic half space. J. Appl. Mech. Trans. ASME 45, 320–324. doi: 10.1115/1.3424295
Hui, C. Y., Liu, T., Salez, T., Raphael, E., and Jagota, A. (2015). Indentation of a rigid sphere into an elastic substrate with surface tension and adhesion. Proc. R. Soc. A Math. Phys. Eng. Sci. 471:20140727. doi: 10.1098/rspa.2014.0727
Johnson, K. L., Kendall, K., and Roberts, A. D. (1971). Surface energy and the contact of elastic solids. Proc. R. Soc. London A 324, 301–313. doi: 10.1098/rspa.1971.0141
Ju, Y., and Farris, T. N. (1996). Spectral analysis of two-dimenslonal contact problems. J. Tribol. 118, 320–328. doi: 10.1115/1.2831303
Karpitschka, S., Van Wijngaarden, L., and Snoeijer, J. H. (2016). Surface tension regularizes the crack singularity of adhesion. Soft Matter. 12, 4463–4471. doi: 10.1039/C5SM03079J
Kerr, A. D. (1964). Elastic and viscoelastic foundation models. J. Appl. Mech. 31, 491–498. doi: 10.1115/1.3629667
Li, Q., Pohrt, R., Lyashenko, I. A., and Popov, V. L. (2019). Boundary element method for nonadhesive and adhesive contacts of a coated elastic half-space. Proc. Inst.Mech. Eng. J 234, 73–83. doi: 10.1177/1350650119854250
Liu, S., Wang, Q., and Liu, G. (2000). A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 243, 101–111. doi: 10.1016/S0043-1648(00)00427-0
Liu, T., Jagota, A., and Hui, C. Y. (2015). Adhesive contact of a rigid circular cylinder to a soft elastic substrate-the role of surface tension. Soft Matter. 11, 3844–3851. doi: 10.1039/C5SM00008D
Long, J., and Chen, W. (2017). Effects of surface tension on the nanoindentation with a conical indenter. Acta Mech. 228, 3533–3542. doi: 10.1007/s00707-017-1901-9
Long, J. M., and Wang, G. F. (2013). Effects of surface tension on axisymmetric Hertzian contact problem. Mech. Mater. 56, 65–70. doi: 10.1016/j.mechmat.2012.09.003
Nogi, T., and Kato, T. (1997). Influence of a hard surface layer on the limit of elastic contact: analysis using a real surface model. Japanese J. Tribol. 42, 270–271. doi: 10.1115/1.2833525
Pohrt, R., and Li, Q. (2014). Complete boundary element formulation for normal and tangential contact problems. Phys. Mesomech. 17, 334–340. doi: 10.1134/S1029959914040109
Popov, V. L. (2017). Contact Mechanics and Friction. Physical Principles and Applications. 2nd Edn. Berlin: Springer.
Popov, V. L. (2020). Adhesive and non-adhesive contact of a rigid indenter and a thin elastic layer with surface tension. arXiv preprint arXiv:2002.01874.
Popova, E., and Popov, V. L. (2018). Note on the history of contact mechanics and friction: interplay of electrostatics, theory of gravitation and elasticity from Coulomb to Johnson-Kendall-Roberts theory of adhesion. Phys Mesomech. 21, 1–5. doi: 10.1134/S1029959918010010
Sperling, G. (1964). Eine Theorie der Haftung von Feststoffteilchen an Festen Körpern. Karlsruhe: Unpublished doctoral dissertation, Technische Hochschule Karlsruhe.
Style, R. W., Hyland, C., Boltyanskiy, R., Wettlaufer, J. S., and Dufresne, E. R. (2013). Surface tension and contact with soft elastic solids. Nat. Commun. 4, 2728–2733. doi: 10.1038/ncomms3728
Style, R. W., Jagota, A., Hui, C.-Y., and Dufresne, E. R. (2017). Elastocapillarity: surface tension and the mechanics of soft solids. Ann. Rev. Condensed Matter. Phys. 8, 99–118. doi: 10.1146/annurev-conmatphys-031016-025326
Syms, R. R. A., Yeatman, E. M., Bright, V. M., and Whitesides, G. M. (2003). Surface tension-powered self-assembly of microstructures - the state-of-the-art. J. Microelectromech. Syst. 12, 387–417. doi: 10.1109/JMEMS.2003.811724
Young, T. (1805). III. An essay on the cohesion of fluids. Philoso. Trans. R. Soc. London. 95, 65–87. doi: 10.1098/rstl.1805.0005
Keywords: boundary element method, contact angle, contact mechanics, elastocapillary length, surface tension
Citation: Li Q and Popov VL (2020) Non-adhesive Contacts With Different Surface Tension Inside and Outside the Contact Area. Front. Mech. Eng. 6:63. doi: 10.3389/fmech.2020.00063
Received: 12 June 2020; Accepted: 02 July 2020;
Published: 02 September 2020.
Edited by:
Alessandro Ruggiero, University of Salerno, ItalyReviewed by:
Qian Jane Wang, Northwestern University, United StatesAydar Akchurin, SKF, Netherlands
Feodor M. Borodich, Cardiff University, United Kingdom
Copyright © 2020 Li and Popov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qiang Li, cWlhbmcubGlAdHUtYmVybGluLmRl; Valentin L. Popov, di5wb3BvdkB0dS1iZXJsaW4uZGU=
 Qiang Li
Qiang Li Valentin L. Popov
Valentin L. Popov