- 1Department of Functional Morphology and Biomechanics, Zoological Institute, Kiel University, Kiel, Germany
- 2Institute for the Anthropic impacts and Sustainability in marine environment, CNR, Palermo, Italy
- 3Donetsk Institute of Physics and Engineering, Academy of Sciences of Ukraine, Donetsk, Ukraine
Animals and plants use adhesion to move, to anchor to a substrate, or to disperse seeds and fruits. Some plants developed a root pad as a common strategy to adhere to consolidated substrates. In the marine environment, the seagrass Posidonia oceanica attaches firmly to consolidated substrates via adhesive root hairs, forming a pad structure. We used novel morphological and ultrastructural data to develop a numerical model to study the dynamics of root hair adhesion during contact formation on rough consolidated substrates for this species. Morphological analysis, conducted using Scanning Electron Microscope, highlighted the role of root hair branching in pad formation. Transmission Electron Microscope microscopy allowed us to identify a glue-like substance at the pad/substrate interface. The numerical model highlighted the role played by the cell wall’s elasticity in pad formation and its importance in guaranteeing a firm adhesion. Furthermore, the effectiveness of these mechanisms was assessed at different simulated roughness levels. Increasing knowledge on the adhesion mechanism of seagrass to consolidated substrates could be pivotal in developing advanced seedling-based restoration protocols. The findings of this study could contribute to restoration activities planned to contrast seagrass regression. Transplanting initiatives using seedlings can now better address the search for suitable and low-impact ways to fix germinated plants to the substrate.
Introduction
Living organisms employ a great variety of attachment structures, such as hooks, suction cups, sticky pads, and glue-like substances (Scherge and Gorb, 2001), to give them the capability to climb (e.g., English Ivy), walk on smooth surfaces (e.g., geckos), be transported (e.g., zoochory), or be strongly fixed to consolidated substrates (e.g., mussels and barnacles). Plants use adhesion mainly to disperse fruits and seeds, but some species form adhesive structures to anchor to the substrate. These pad-like structures often consist of multi-layered multicellular formations that can originate from tendrils, modified leaves, or roots (Groot et al., 2003; Melzer et al., 2010; Steinbrecher et al., 2010; Steinbrecher et al., 2011; Melzer et al., 2012; Seidelmann et al., 2012; Bohn et al., 2015; Yang and Deng, 2017). The pad attachment occurs via mechanical interlocking which consists in replicating the surface of a given substrate, filling up the surface profile, and eventually becoming stiff by thickening the cell walls. Adhesion can act with or without the support of a glue. This mechanism has been shown to produce a firm attachment on a variety of surfaces in different plant species (Scherge and Gorb, 2001).
Seagrasses have thrived in the oceans for tens of millions of years (Larkum et al., 2018), but it is only in recent decades that they have begun to experience a severe regression due to human activities along coastal areas (Waycott et al., 2009; Telesca et al., 2015). Therefore, several attempts are underway to restore damaged meadows and to improve their ecological resilience (Unsworth et al., 2015). Seagrasses natural recovery usually occurs trough vegetative proliferation. In a species that lacks floating rhizomes, the recolonization of strongly damaged meadows may occur via sexual propagules. In this case, the success of seedling settlement and recruitment represents a bottleneck in the seagrass sexual reproduction strategy as its failure could impair the connectivity and genetic variability of these important habitat-forming species (Jahnke et al., 2016).
Most seagrass species have been reported to grow on soft bottoms (Green and Short, 2003; Balestri et al., 2015), but a few of them (i.e., Phyllospadix spp., Posidonia oceanica) possess specific morphological adaptations that enable them to colonize and grow on hard bottoms (Barnabas, 1994; Badalamenti et al., 2015). These species show a variety of morphological features, such as rudimental anchorage apparatuses or more sophisticated structures (e.g., adhesive root hairs) to adhere to consolidated substrates (Barnabas, 1994; Green and Short, 2003; Badalamenti et al., 2015).
The combination of knowledge on the specific morphology of the seagrass root system with the characteristics of the habitats in which each species settles and recruits is a prerequisite for developing projects aimed at advancing restoration protocols. In recent years, many transplanting projects have been planned to restore damaged meadows, and the use of sexual propagules could be pivotal in achieving restoration goals. In this context, an increase in the current knowledge on the mechanisms of root adhesion, which provide the plantlet with a strong anchorage and persistence against drag forces on the sea floor, is of fundamental importance (Badalamenti et al., 2015).
In the Mediterranean Sea, seedlings of the endemic seagrass Posidonia oceanica (L.) Delile successfully colonize hard bottoms and their settlement occurs preferentially on consolidated and firm substrates via adhesive root hairs (Badalamenti et al., 2015). Such a strategy represents a mechanism for early settlement on vegetated and unvegetated rocky shores, which favors plantlet persistence on consolidated substrates compared to unconsolidated ones (Alagna et al., 2015; Badalamenti et al., 2015). Root hairs appear soon after germination at the hypocotyl and both at the principal and adventitious roots. When not in contact with the substrate, root hair tips remain long and straight, but they quickly begin to branch after contact formation (Alagna et al., 2015; Badalamenti et al., 2015; Zenone et al., 2020). P. oceanica may thrive in habitats characterized by high hydrodynamism (Montefalcone et al., 2016) hence its anchorage system has to be highly efficient, especially in the early life stages, when seeds reach the recruitment sites and settlement occurs.
Posidonia oceanica roots form a pad starting from the branching of a single cell, the root hair, which determines the anchoring via mechanical interlocking (Zenone et al., 2020). Root hairs adapt themselves to the characteristics of the substrate on which the attachment process occurs. The pad morphology depends on the substrate micro-roughness and optimal adhesion is achieved at a micro-roughness of 3–52 µm (asperities diameter), while the maximum adhesion force occurs at a micro-roughness of 12 µm, a value similar to the average diameter of the root hair (Zenone et al., 2020).
In recent years, numerical models have been elaborated to integrate a variety of important biological and physical processes involving plant growth (Godin and Sinoquet, 2005; Dupuy et al., 2010). This approach is useful to address biological questions, as models may show hidden properties and behaviors that can be validated with experimental observations. In the present paper, we report on a numerical model that is inspired by the morphological characteristics of the P. oceanica root hairs to investigate the dynamics of P. oceanica root hair adhesion during contact formation on rough consolidated substrates.
The model was constructed to answer the following questions: 1) Does the root hair growth change vary the cell’s elastic properties when substrate micro-roughness is kept constant? 2) Does the contact formation change, varying the levels of substrate roughness, when the cell’s elastic properties are kept constant? and 3) Can attachment properties of the root hair be explained exclusively by mechanical interlocking? In this work, we hypothesize that: 1) root hair softness plays a fundamental role in the adhesion process; 2) the substrate micro-roughness at to the scale of the root hair diameter improves proper contact area formation and additionally contributes to the mechanical interlocking; and 3) a glue-like substance may be additionally involved in the adhesion mechanism, as hypothesized by Zenone et al. (2020).
Materials and Methods
Posidonia oceanica seeds were collected along the Sicilian coast (NW Sicily) between May and June 2017 and left growing (Figure 1A) for 6 months on 3 cm × 3 cm tiles of epoxy resin replicas (Spurr, 1969) of sand paper (12 µm asperities size, Starcke Ersta Abrasives, Germany). Resin replicas were created using a two-step molding method (Gorb, 2007).

FIGURE 1. The figure shows: (A) a Posidonia oceanica seedling grown experimentally in the aquarium and the detail of the roots grown in contact with the experimental tile (ES) (scale bar - 20 mm). (B) a root (RO) anchored through root hairs (RH) to the experimental tile surface (scale bar - 2 mm) with the detail of root hair pads (HP) adhering to the substrate (scale bar - 200 µm).
Different microscopy techniques were used to investigate the root hairs morphology and their principal characteristics. All the morphological features were measured on images from a set of 30 seedling samples (see Table 1 for details) by means of ImageJ software (Schneider et al., 2012).
Mean curvature and mean pad radius were calculated according to Eqs. 10–14 (see below for details) using Matlab (ver. R2019b, The Math Works, Inc., (2018) United States). For this, a batch of homogeneously distributed points (N ≥ 100) were selected along the pad perimeter. The coordinates of the points were used for calculation of the mean pad radius and the mean curvature.
Root Hair Tips Morphology (Scanning Electron Microscope)
Root hair morphology was analyzed using a Scanning Electron Microscope (SEM, Hitachi TM3000; Hitachi High-Technologies, Corp., Tokyo, Japan). Portions of resin tiles with root hairs adhered on their surfaces were dehydrated in hexamethyldisilane (HMDS/1,1,1,3,3,3-Hexamethyldisilazan, Carl Roth GmbH & Co. KG, Karlsruhe, Germany). For HMDS drying, tiles were cut into pieces of 1 mm3, fixed in a solution of 2.5% Glutardialdehyde and 2% Formaldehyde in 0.1 M cacodylate buffer overnight, and washed two times in 0.1 M cacodylate buffer, each for 20 min. They were then stained in a solution of 1% OsO4 in a 0.1 M cacodylate buffer for 1 h, then washed two times again in the 0.1 M cacodylate buffer for 20 min. Samples were then dehydrated by a graded series of ethanol (30 and 50%, 15 min each) and transferred to a 70% ethanol solution. Samples were then air-dried in a desiccator overnight. Finally, samples were mounted on SEM aluminum stubs, coated with gold palladium (10 nm thickness; Leica Bal-TEC SCD500, Leica Microsystems GmbH, Wetzlar, Germany), and immediately visualized in the SEM.
Root Hair Ultrastructure (Cryo-Scanning Electron Microscope and Transmission Electron Microscope)
Fresh portions of roots were visualized at high resolution using a cryo-SEM Hitachi S-4800 (Hitachi High-Technologies Corp., Tokyo, Japan) equipped with a Gatan ALTO2500 cryo-preparation system (Gatan, Inc., Abingdon, United Kingdom). Fresh root portions were fixed to the holder and immediately placed in the cryo-chamber (−140°C). The frozen samples were sputter-coated with gold–palladium (layer thickness 10–20 nm) and transferred to the SEM.
The root hair tips at the interface with the substrate were examined using a Transmission Electron Microscope (TEM) (Tecnai Spirit BioTWIN; FEI Company, Eindhoven, Netherlands). Samples were cut into small pieces of about 1 mm3, fixed in 2.5% glutardialdehyde and 1% OsO4, dehydrated by a graded alcohol series to 100%, and gradually transferred to Spurr resin which was then cured at 70°C for 12 h. Resin blocs were trimmed and cut into semithin (1–3 µm) and ultrathin (50–60 nm) sections with a Leica EM UC7 ultramicrotome (Leica Microsystems GmbH; Wetzlar, Germany). Ultrathin sections were post-stained with gadolinium (III) acetate tetrahydrate and lead citrate and examined in TEM.
Numerical Modelling
In order to understand interactions between individual root hairs and rigid substrates of different roughness levels, we developed a simplified two-dimensional numerical model aimed at solving the complex original 3-dimensional problem. We substituted the root hair material by its boundary with an effective “stiffness” reminiscent of the surface tension.
This approach is based on an assumption that young root hair tips, being thin-walled bladders with a fluid inside, might behave similarly to a fluid-like system in contact with a solid substrate. Further, we defined the boundary conditions as a movable and growing “elastic chain.” It allows us to naturally describe a multi-valued function of the boundary and its evolution over time. The rigidity of the chain corresponds to the surface tension of real material and allows simulating the system under consideration.
The model includes the following elements. The boundary of the root hair is modelled by an elastic fiber whose elasticity varies along its length, depends on time, and can change from initially soft to much stiffer or almost rigid (but still with some degree of flexibility). The fiber is constructed as an array of nodes connected by the segments
and
The coordinates at the beginning and end of the segment represent the two nearest neighbors
The longitudinal force,
It is important to note that the “chain” simulates a boundary of the root hair pad, so its beginning and its end must be connected. It means that the last element of the array
A further demand from the model is that the root should grow with time. To reproduce root hair elastic properties, the length of each segment must be kept more or less fixed. So, an increase of root hair length will be simulated by changing the number of the segments
Counting on the particular nature of the system, we will insert a new node
The ratio between
In general, root hairs are very soft at the growing tip. However, their hardiness increases along the shaft (Grierson et al., 2014). In the model, the elastic constant
The contact surface can be modelled in different ways depending on the particular problem. A widely accepted approach is based on the supposition of scale-invariant fractal distribution of the surface heights. In this case, one can construct the surface using Fourier transform with a large number of corresponding waves. Depending on the number of waves and on both limits, the surface will be, more or less, close to the real fractal one and include or not include irregularities with small sizes (Filippov and Popov, 2007).
Like many other natural surfaces, here, the surface was physically created by a set of deposited particles (spheres with radius
One can simplify the procedure when considering that, for our aim, the specific form of the deposed particles is not very important. In such a case, one can treat the random deposition procedure as an abstract way to construct the desired surface. One of the simplest ways to do this is to model the rough surface
The advantage of this approach is its mathematical transparency, since the simple manipulation of the position, amplitude, and width of the Gaussian functions will suffice to generate the desired kind of surface irregularity. In particular, the typical distance between the hills and valleys of the randomly generated surface
where the desired amplitude
Two basic mechanisms only will be involved in our minimalistic model: mechanical (potential) interaction with the surface and energy dissipation. These mechanisms restrict the scale of the objects which we include into the model from working in dimensionless units. The irregularities, which one can incorporate into the model, have to correspond to the size of the typical curvature, which can be described by the chain formed by the discrete segments. In this context, the surfaces with irregularities much smaller or larger than the size of the discrete segments must be treated as almost flat. That is why we will use the segment length approximately 10 times shorter than the numerically generated surface irregularities. Formal model, based on this assumption, can well explain the results of experimental studies on real surface profiles, depending on the effective “surface tension” determined by the “chain” stiffness.
In contrast to our previous studies (Filippov and Popov, 2007; Gorb and Filippov, 2014) , where the elastic curve of the connected segments represented the real fiber of an attachment pad contacting with a surface by the adhesive force of its terminal segments, now the “chain” has a meaning of the soft boundary separating internal material of the root from the external space. So, its extension, caused by the insert of the additional segments, does not mean the simple elongation of the “fiber” but rather the addition of the 2-dimentional internal area of a root hair cell enveloped by the cell wall. Further, we will return to the question and show how to implement it into the model.
In any case, expanding the boundary mechanically interacts with the relief, repulsing from its bulges and attracting to the valleys. This interaction is described by the force caused by continual potential:
Here, the derivatives are supposed to be calculated for each node at its discrete position:
Moving different segments according to the potential interactions, in principle, can result in their overlapping, what is unphysical for the boundary, containing practically incompressible material inside, with its own internal pressure. The repulsion between nodes, which could avoid overlapping between segments, should be incorporated into the of interactions. For isotropic roots, the easiest way to simulate internal pressure is to use repulsion of all the nodes from the common center. However, the form of the root boundary is very complex. It expands to the plenty of random potential valleys and produces many “local centers,” the positions of which are impossible to predict. It is preferable to use a mutual short-range repulsion between all the nodes of the chain:
This interaction should be weak and short-range, just enough to prevent the segments from overlapping. For isotropic roots, it automatically reduces to the repulsion from the common center, but for many protrusions, it causes several independent repulsions from the local centers.
Counting on the microscopic nature of the problem, we will use the so-called “over-damped” equations of motion without inertial terms. Accumulating all the forces of the problem, one can now write the equation of motion as follows:
Here, index
One can determine a mean rigidity of the root boundary from the beginning of its growth to the current time moment. To do this, one has to integrate each elastic constant
Now, the mean rigidity of the root can be found as the statistical average over the ensemble of the segments:
However, both these averaging Eqs. 8 and 9 are linear operations. Their results are proportional to the starting elastic constant
Results
Root Hair Tip Morphology (Scanning Electron Microscope)
Posidonia oceanica seedlings produced root hairs with a total length ranging between 200 and 1,000 µm and a mean width of 12.31 ± 1.94 µm (mean ± SD, Table 1). The portion of root hairs in contact with the substrate always showed a strongly branched and dactyliform pad-shaped structure (insert of Figures 1B and 2A). These branches were very thin (6.11 ± 0.74 µm), with a width equal on average to about half that of the root hair shank. The mean pad radius was 28.95 ± 4.06 µm.
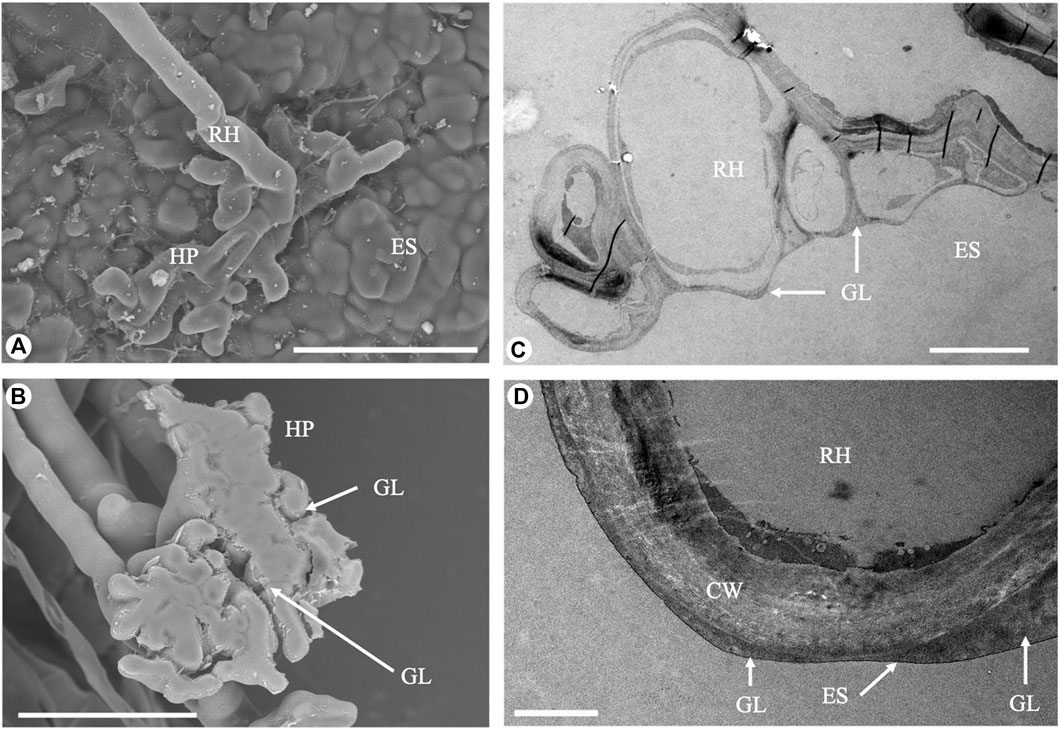
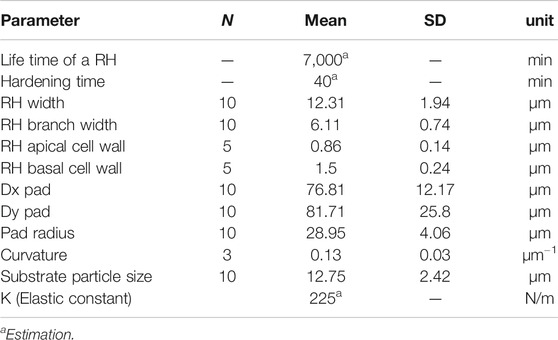
FIGURE 2. Electron microscopy images of the root hairs. (A) Branched root hair adhering to a rough surface (Scanning Electron Microscope, scale bar - 50 µm). (B) Detached root hair pad: a glue-like substance is visible at the base (Scanning Electron Microscope, scale bar - 50 µm). (C) Cross-section of a root hair adhering to a rough surface (Transmission Electron Microscope, scale bar - 10 µm). (D) Details of the interface between the root hair and the experimental substrate: a thin glue-like substance layer fills the small interstices (Transmission Electron Microscope, scale bar - 1 µm). RH, root hair; HP, root hair pad; CW, cell wall; ES, experimental substrate; GL: glue-like substance.
The contour curvature of the root hair pads attached to the substrate (resin tiles replica of a polishing paper with 12 µm particle size) was 0.1317 ± 0.0317 µm−1 (Table 1, mean ± SD).
A thin layer of a solidified substance was discovered in SEM images of the root hair pad base and of the resin tile where some of the root hairs had been detached (Figure 2B). Such an observation was confirmed by TEM analysis (Figures 2C,D).
Root Hair Ultrastructure (Cryo-Scanning Electron Microscope and Transmission Electron Microscope)
The average cell wall thickness, measured along the shaft in fractured root hairs using Cryo-SEM, was 1.50 ± 0.24 µm. In the apical region, the cell wall thickness was lower, at 0.86 ± 0.14 µm. Cross sections of root hairs adhering to the substrate were visualized in TEM, and results confirmed the presence of a glue-like substance filling the empty spaces at the root hair/substrate interface. The observed substance created a layer of different thickness in all samples tested (Figures 2C,D). The layer was thin when the root hair was in close contact with the substrate, and thicker when interstices or small gaps were present and the root hair could not penetrate into the gaps between the asperities. Moreover, TEM images allowed an estimating of the actual portion of root hair in real contact with the substrate.
Numerical Simulation
In order to model the behavior of the system with different elasticity levels, we used three representative values of the initial elastic constant: small
Typical configurations of the boundary for these three elastic constants -
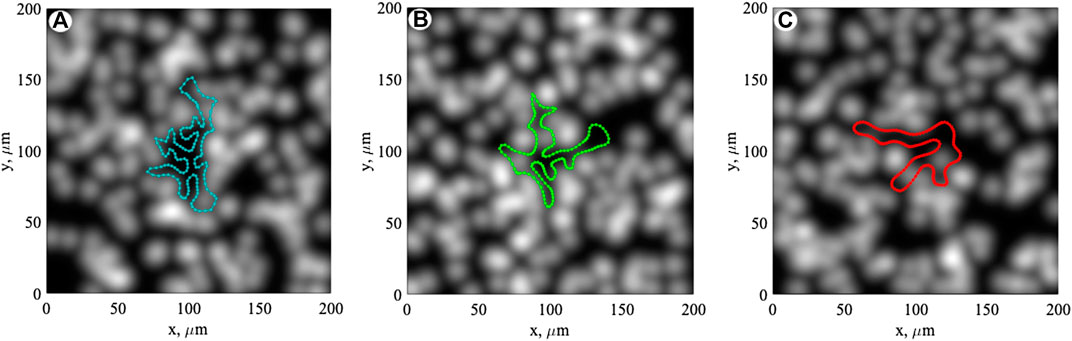
FIGURE 3. Typical configurations of the boundary for three different elastic constants,
A typical dynamic scenario of the expansion of the root boundary on the substrate is reproduced also in Supplementary Movie S1. It is directly seen how the boundary dynamically reacts on the surface structure, repulsing from the asperities and filling the valleys between them.
The visual difference between the smoothness of the boundaries plotted in the subplots (A–C) must be characterized quantitatively. For this goal one can calculate the curvature of each curve. Local curvature in arbitrary points
where derivatives are calculated along the curve:
The curvature varies with time, because the root starts to grow from a smooth circular boundary and develops into a more and more complex structure. We have performed this calculation for all three cases:
It is convenient for us to represent the value of the curvature radius as
FIGURE 4. Time dependencies of the curvature radius (A) and mean radius of the root hair (B) calculated for the same initial elastic constants:
Individual components of this radius can be calculated as follows:
And its mean value is equal to:
For the expanding root hair, this radius also depends on time
The mean radius (
As we already discussed, the elastic constants evolve independently for different segments of the boundary depending on the individual time elapsed from the moment of their appearance
However, one can use the following approach. First of all, we plot, as a set of dots, all the values
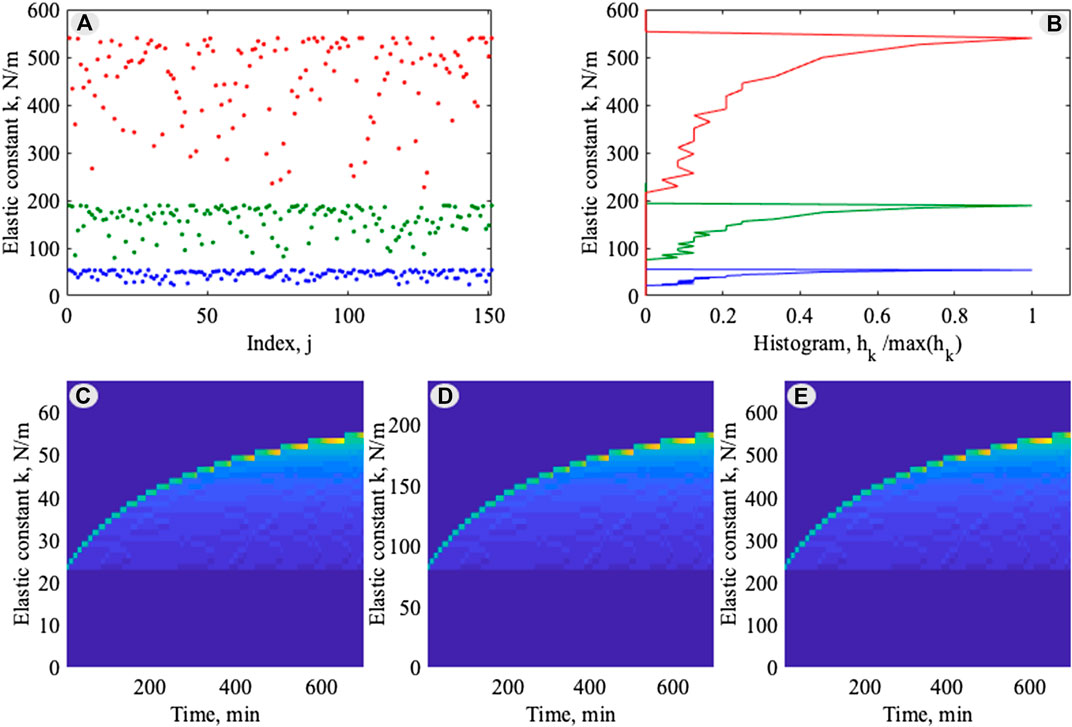
FIGURE 5. Statistically universal evolution of the individual time-dependent elastic constants: (A) instant configuration of the values
To provide a statistical description of the points distribution, one can calculate the histogram of this distribution along the vertical axis. The number of segments
What is more important here, is that all three curves have generally the same structure, which confirms the universality of the process independently on the
However, an important question remains for the validation of the model. As we stressed from the very beginning, the original problem is a complex 3-dimensional problem, and the present study is just an attempt to model it using a 2-dimensional approach. However, we still can advance the model for such a compromised approach. Let us stop the expansion of the root at some (final or intermediate) stage. Its boundary, at this moment, has a certain shape determined by a competition of all the forces involved in the problem. In particular, it is a competition between the repulsion from the surface asperities
However, the ability of the boundary to bend in
In
and find an equilibrium configuration. Here, adaptation time
We have solved this equation for three different roughness levels (6, 12, and 171 µm asperities size) using the average
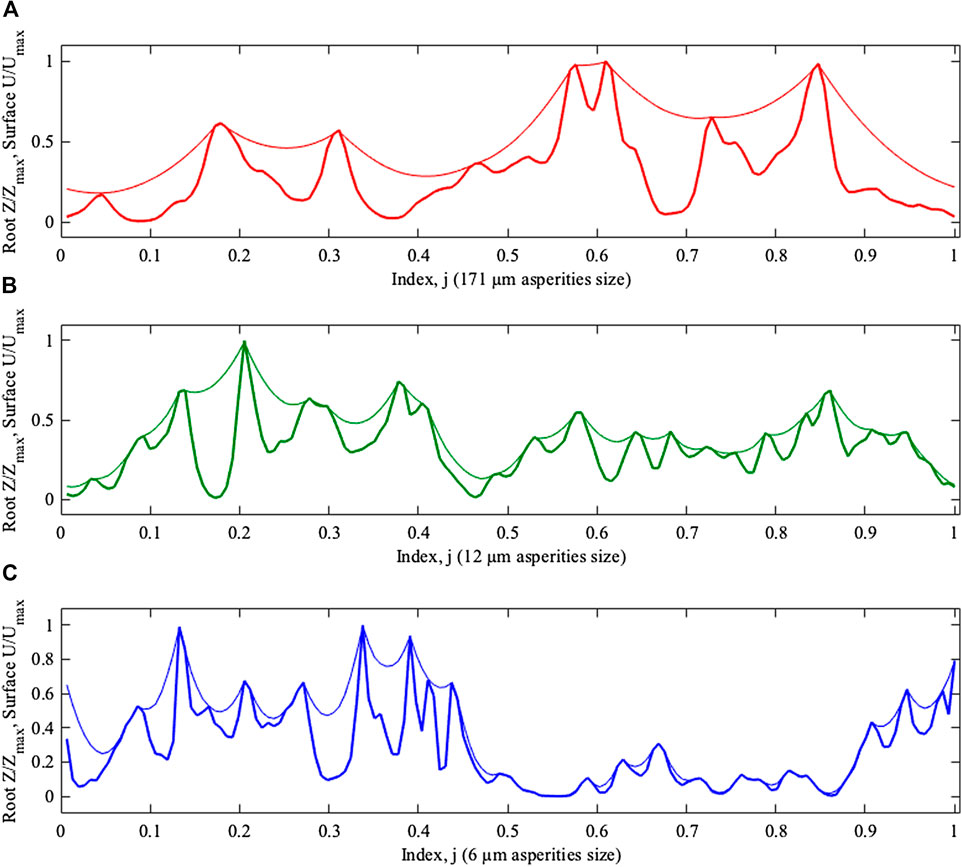
FIGURE 6. Equilibrium z-positions of the elastic boundaries plotted along closed curve as the functions of the index
In principle, the difference between the cases with different roughness levels is seen directly from Figure 6. However, it is necessary to extract this information quantitatively; it is also essential that this extraction should be done for any adaptation time
Natural formalization is to apply the following condition: if distance between the boundary and surface is less than the threshold
Using this condition, the fraction of segments in contact can be easily calculated as the following sum:
This procedure is quite efficient and it allows for performing the calculation of the fraction depending on time
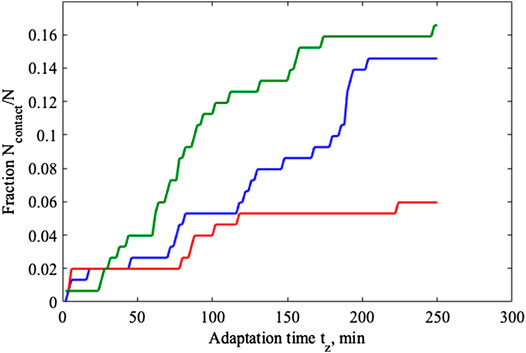
FIGURE 7. Relaxation of the fractions in contact
Discussion
Root hairs originate from trichoblasts by a highly polarized growth process that occurs at the apex of the cell, referred to as tip growth, and the concomitant repression of proximal growth along the shank (Hirano et al., 2018). Cytoarchitecture of the root hair is highly polar-organized during growth but it disappears in mature cells, when growth usually ceases (Ryan et al., 2001; Ketelaar et al., 2002; Emons and Ketelaar, 2009; Balcerowicz et al., 2015). The root hair’s cell wall is a complex network of polysaccharides. The major components are cellulose microfibrils, the polysaccharides matrix made up of hemicelluloses and pectins, and various cell wall proteins (Somssich et al., 2016). A primary cell wall, which is a thin layer that continually expands outwards, is deposited at the root hair tip, while a strong multi-layered secondary cell wall develops inside the primary cell wall, 20–30 μm from the tip, and continues along the shank (Dumais et al., 2004). Once tip growth ends, hair tips also become covered by a secondary cell wall (Galway et al., 1999).
Cellulose microfibrils are randomly distributed in the primary cell wall of root hairs, while in the nonexpanding tubular portion they present an oriented distribution (Galway, 2006). Hemicelluloses and pectins serve as cementing material and any change in their chemical nature influences the plasticity and elasticity of the cell wall. Both the microfibrils arrangement and the chemical properties of polysaccharides in the cell wall create an anisotropic gradient along the cell, which is a matter of considerable importance in the root hair adhesion process.
Our analysis of the morphology and ultrastructure of P. oceanica seedlings showed a unique pad formation process characterized by the root hair tip branching behavior and by the presence of a solidifying (filler) substance at the substrate/pad interface. These two features, reported here for the first time, together with the presented numerical model simulations allow for better understanding of the adhesion mechanism of P. oceanica described in previous works (Alagna et al., 2015; Badalamenti et al., 2015; Tomasello et al., 2018; Zenone et al., 2020). The numerical model simulated the contact formation of the P. oceanica seedling root hair on hard rough substrates, clarifying what role the physical properties of the root hairs play in pad formation and in the facilitation of the attachment process.
In contrast with most terrestrial plants, where root hairs increase the root surface area to enhance mineral and water absorption, in P. oceanica, and possibly also in other seagrass species, the main role played by root hairs is to provide anchorage to seedlings. However, similar anchorage systems have been described in some terrestrial climbing plants [eg, Ficus pumila (Groot et al., 2003), Parthenocissus tricuspidata (Scherge and Gorb, 2001; Steinbrecher et al., 2010; Steinbrecher et al., 2011), Hedera helix (Melzer et al., 2010, Melzer et al., 2012), Amphilophium crucigerum (Seidelmann et al., 2012), Passiflora discophora (Bohn et al., 2015), and Syngonium podophyllum (Yang and Deng, 2017)]. To the best of our knowledge, no similar detailed studies exist for most seagrass species, even though the morphology and ultrastructure of root hair have been described for some of them (Cooper and McRoy, 1988; Roberts, 1993; Tomasello et al., 2018).
The terrestrial species P. tricuspidata, P. discophora, and A. crucigerum, build a multi-layered and multicellular pad at the base of tendrils to increase the contact area and produce a firm adhesion to climb on a given surface. Other terrestrial species (e.g., S. podophyllum, H. helix, and F. pumila) climb by means of clusters of adventitious roots which are covered by root hairs that emerge from internodes of the plant stem and form an adhesive pad according to a multistep process (Groot et al., 2003; Melzer et al., 2010; Melzer et al., 2012; Yang and Deng, 2017). In both cases, the pad formed is a complex structure and its adhesion occurs at different spatial scales and in different moments. For these species, root/root hair adhesion occurs according to different steps. Generally, the first step starts with one of the plant adhesive structures that grows towards the substrate. In the second step, the adhesive structure establishes contact with the substrate. In this phase, adhesion is very weak. In the third step, adhesion become stronger as a consequence of mechanical interlocking, and the presence of a glue-like substance may facilitate adhesion strength in some species. The fourth and last step is the hardening of the glue, a fundamental process for bonding and strengthening the attachment. In F. pumila, S. podophyllum, and H. helix, root hairs adhere to the substrate by mechanical interlocking, swelling, or flattening the root hair tip to increase the contact area.
In P. oceanica, the pad structure is produced by the root hair tip branching. According to our results, root hair branching increases the real contact area about 50 times compared to the contact area of a single tubular root hair. The branching of P. oceanica root hairs is a pivotal mechanism for pad formation, and supports the hypothesis that adhesive root hairs may represent an adaptive trait to life in marine rocky habitats characterized by strong turbulent water movements (Badalamenti et al., 2015; Montefalcone et al., 2016). Interestingly, in terrestrial plants, root hair branching is reported to happen only under stress conditions (Yang et al., 2011; Bobrownyzky, 2015) or in mutant phenotypes (Engstrom et al., 2011).
The role played by the pad in anchoring the root hair is most likely improved by the presence of a filler substance at the interface between the pad base and the substrate. The “glue” thickness observed at the root hair/substrate interface in TEM in this study was not homogeneous. It was thinner where the root hair pad was in close contact with the substrate, and thicker where the contact was looser due to the presence of gaps or interstices. The glue can be seen as a form filler whose role is related to the improvement of root hair adhesion to the substrate by the enhancement of the gap closure at the micro-scale. On rough substrates, root hairs grow between the asperities or inside gaps and small crevices. Under these conditions, root hairs were observed filling up the empty spaces either by the branches, by the compliancy of the cell wall, or by the glue. Such a strategy improves the plant surface-replicating mechanisms. Without the glue presence, attachment would solely be based on mechanical interlocking (between the root hair pad and substrate). It can be hypothesized that the glue may facilitate the first adhesion of the root hair to the substrate and to some extent may reduce the friction of the root hair tip during growth (until the glue is solidified). A low friction environment at the root hair tip region could represent an advantage for the plant to penetrate small interstices and to follow the topography of the substrate, which we clearly see in model simulations.
The elasticity of the root hair tip has strongly affected the effectiveness of formation of the pad in our model simulations performed on a constant micro-roughness (i.e., asperities diameter of 12 µm). When the root hair tip is too soft (low value of the initial elastic constant
In the model, the medium-level elasticity (initial constant elasticity,
Compared to a smooth substrate, roughness allows root hairs to grow between the interstices, offering paths of minimum growth resistance and inducing an increase in the curvature of the pad which, in turn, contributes to generating a stronger adhesion to the substrate. In the model simulation performed under the estimated natural elasticity constant (
The shape and size of the simulated root hair pads properly reflected the real system, shedding light on the role played by pads in the attachment process of P. oceanica seedlings’ root hairs to the substrate. Root hair specific elasticity and pad formation seem to be the best combination to produce the optimal contact to a substrate with a roughness level at the scale of the root hair diameter (i.e., 12 µm). It is important to highlight that
Several restoration attempts have been made in the Mediterranean Sea to contrast the general regression caused by human impact on P. oceanica meadows, such as transplanting plugs, sods, or bare-root rhizomes collected from donor plants (Meinesz et al., 1993; Molenaar and Meinesz, 1995; Piazzi et al., 1998; Carannante, 2011; Calvo et al., 2014; Alagna et al., 2019a). These initiatives have raised concerns in relation to their environmental sustainability (Balestri et al., 2019) and also because their large-scale application has rarely achieved high success rates (van Katwijk et al., 2016). To reduce the environmental impact on donor meadows, an approach known as “nursery seagrass” has been proposed which involves the propagation of plants from seeds reared in aquaculture facilities (Balestri and Lardicci, 2012; Balestri and Lardicci, 2014; Balestri et al., 2015). Research has recently focused on finding a suitable and low-impact way to fix germinated plants to the substrate (Alagna et al., 2019b). The adhesion mechanism of P. oceanica seedlings and the model we described here may give a boost to the use of particular consolidated substrates with specific roughness levels for new restoration initiatives. Identifying the right substrate where the seedlings adhere before transplantation could represent an effective approach to avoid the limits highlighted by other experiences (Alagna et al., 2019a). The model developed in this study could be useful in identifying the best characteristics of natural substrates, where the seedlings adhere and obtain a first stable anchorage before releasing them at sea.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
AZ, SG, and FB conceived and designed the research. AZ conducted the experiments and analysis. AF and AK developed the model. SG contributed analytical tools. AZ and AK analyzed data. AZ and AF wrote the manuscript. SG, FB, and AK revised the manuscript. All authors read and approved the final manuscript.
Funding
This paper has been partially supported by the project Marine Hazard, PON03PE_00203_1, Italian Ministry of Education, University and Research (MIUR). We acknowledge financial support by DFG within the funding program Open Access Publizieren.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
AcknowledgmentsThe Authors would like to thank Esther Appel for her collaboration in laboratory work at the Functional Morphology and Biomechanics lab in Kiel and Giuseppe Di Stefano for the technical support at IAS-CNR lab in Castellammare del Golfo. This study was developed during a short-term scientific mission granted to AZ by Cost Action ENBA (CA15216).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2020.590894/full#supplementary-material
References
Alagna, A., Vega Fernández, T., D’Anna, D., Magliola, C., Mazzola, S., and Badalamenti, F. (2015). Assessing Posidonia oceanica seedling substrate preference: an experimental determination of seedling anchorage success in rocky vs. sandy substrates. PLoS One 10, e0125321. doi:10.1371/journal.pone.0125321
Alagna, A., D'Anna, G., Musco, L., Vega Fernández, T., Gresta, M., Pierozzi, N., et al. (2019a). Taking advantage of seagrass recovery potential to develop novel and effective meadow rehabilitation methods. Mar. Pollut. Bull. 149, 110578. doi:10.1016/j.marpolbul.2019.110578
Alagna, A., Zenone, A., and Badalamenti, F. (2019b). The perfect microsite: how to maximize Posidonia oceanica seedling settlement success for restoration purposes using ecological knowledge. Mar. Environ. Res. 161, 104846. doi:10.1016/j.marenvres.2019.104846
Badalamenti, F., Alagna, A., and Fici, S. (2015). Evidences of adaptive traits to rocky substrates undermine paradigm of habitat preference of the Mediterranean seagrass Posidonia oceanica. Sci. Rep. 5, 8804. doi:10.1038/srep08804
Balcerowicz, D., Schoenaers, S., and Vissenberg, K. (2015). Cell fate determination and the switch from diffuse growth to planar polarity in Arabidopsis root epidermal cells. Front. Plant Sci. 6, 1163. doi:10.3389/fpls.2015.01163
Balestri, E., De Battisti, D., Vallerini, F., and Lardicci, C. (2015). First evidence of root morphological and architectural variations in young Posidonia oceanica plants colonizing different substrate typologies. Estuar. Coast Shelf Sci. 154, 205–213. doi:10.1016/j.ecss.2015.01.002
Balestri, E., and Lardicci, C. (2012). Nursery-propagated plants from seed: a tool to improve the effectiveness and sustainability of seagrass restoration. J. Appl. Ecol. 49, 1426–1435. doi:10.1111/j.1365-2664.2012.02197.x
Balestri, E., and Lardicci, C. (2014). Effects of sediment fertilization and burial on Cymodocea nodosa transplants: implications for seagrass restoration under a changing climate. Restor. Ecol. 22, 240–247. doi:10.1111/rec.12052
Balestri, E., Vallerini, F., Seggiani, M., Cinelli, P., Menicagli, V., Vannini, C., et al. (2019). Use of bio-containers from seagrass wrack with nursery planting to improve the eco-sustainability of coastal habitat restoration. J. Environ. Manage. 251, 109604. doi:10.1016/j.jenvman.2019.109604
Barnabas, A. D. (1994). Anatomical, histochemical and ultrastructural features of the seagrass Phyllospadix scouleri hook. Aq. Bot. 49, 167–182. doi:10.1016/0304-3770(94)90036-1
Bobrownyzky, J. (2016). Production of branched root hairs under progressive drought stress in Arabidopsis thaliana. Cytol. For. Genet. 50, 324–329. doi:10.3103/S0095452716050030
Bohn, H. F., Gunther, F., Fink, S., and Speck, T. (2015). A passionate free climber: structural development and functional morphology of the adhesive tendrils in Passiflora discophora. Int. J. Plant. Sci. 176, 294–305. doi:10.1086/680231
Budhe, S., Ghumatkar, A., Birajdar, N., and Banea, M. D. (2015). Effect of surface roughness using different adherend materials on the adhesive bond strength. Appl. Adhes. Sci. 3, 20. doi:10.1186/s40563-015-0050-4
Calvo, S., Scannavino, A., Luzzu, F., Di Maida, G., Pirrotta, M., Orestano, C., et al. (2014). “Tecnica di reimpianto mediante supporto biodegradabile,” in Conservazione e gestione della naturalità negli ecosistemi marino-costieri. Il trapianto delle praterie di Posidonia oceanica. Editors Bacci, T., La Porta, B., Maggi, C., Nonnis, O., Paganelli, D., Rende, S. F., and Polifrone, M. (Roma, Italy: ISPRA), 47–51. Manuali e Linee Guida no. 106/2014.
Carannante, F. (2011). Monitoraggio a lungo termine di trapianti di Posidonia oceanica su vasta scala. PhD Thesis. Viterbo (Italy): University of Tuscia.
Cooper, L. W., and McRoy, C. P. (1988). Anatomical adaptations to rocky substrate sand surf exposure by the seagrass genus Phyllospadix. Aquat. Bot. 32, 365–381. doi:10.1016/0304-3770(88)90108-8
Dumais, J., Long, S. R., and Shaw, S. L. (2004). The mechanics of surface expansion anisotropy in Medicago truncatula root hairs. Plant. Physiol. 136, 3266–3275. doi:10.1104/pp.104.043752
Dupuy, L., Gregory, P. J., and Bengough, A. G. (2010). Root growth models: towards a new generation of continuous approaches. J. Exp. Bot. 61, 2131–2143. doi:10.1093/jxb/erp389
Emons, A. M. C., and Ketelaar, T. (2009). “Intracellular organization: a prerequisite for root hair elongation and cell wall deposition,” in Roots hairs. Editors Emons, A. M. C., and Ketelaar, T. (Berlin, Germany: Springer), 27–44. Plant Cell Monographs.
Engstrom, E., Andersen, C., Gumulak-Smith, J., Hu, J., Orlova, E., Sozzani, R., et al. (2011). Arabidopsis homologs of the Petunia HAIRY MERISTEM gene are required for maintenance of shoot and root indeterminacy. Plant Physiol. 155, 735–750. doi:10.1104/pp.110.168757
Filippov, A. E., and Popov, V. (2007). Flexible tissue with fibres interacting with an adhesive surface. J. Phys. Condens. Matter 19, 096012. doi:10.1088/0953-8984/19/9/096012
Galway, M. E. (2006) Root hair cell walls: filling in the framework. Can. J. Bot. 84, 613–621. doi:10.1139/B06-006
Galway, M. E., Lane, D. C., and Schiefelbein, J. W. (1999). Defective control of growth rate and cell diameter in tip-growing root hairs of the rhd4 mutant of Arabidopsis thaliana. Can. J. Bot. 77, 494–507. doi:10.1139/cjb-77-4-494
Godin, C., and Sinoquet, H (2005). Functional–structural plant modelling. New Phytol. 166, 705–708. doi:10.1111/j.1469-8137.2005.01445.x
Gorb, S. N., and Filippov, A. E. (2014). Fibrillar adhesion with no clusterisation: functional significance of material gradient along adhesive setae of insects. Beilstein J. Nanotechnol. 5, 837–845. doi:10.3762/bjnano.5.95
Green, E. P., and Short, F. T. (2003) World atlas of seagrasses. Prepared by the UNEP world conservation monitoring centre. Berkeley, CA: University of California Press.
Grierson, C., Nielsen, E., Ketelaarc, T., and Schiefelbe, J. (2014). Root hairs. Arabidopsis Book 12, e0172. doi:10.1199/tab.0172
Groot, E. P., Sweeney, E. J., and Rost, T. L. (2003). Development of the adhesive pad on climbing fig (Ficus pumila) stems from clusters of adventitious roots. Plant Soil 248, 85–96. doi:10.1023/A:1022342025447
Hirano, T., Konno, H., Takeda, S., Dolan, L., Kato, M., Aoyama, T., et al. (2018). PtdIns(3,5)P2 mediates root hair shank hardening in Arabidopsis. Nat. Plants 4, 888–897. doi:10.1038/s41477-018-0277-8
Jahnke, M., Christensen, A., Micu, D., Milchakova, N., Sezgin, M., Todorova, V., et al. (2016). Patterns and mechanisms of dispersal in a keystone seagrass species. Mar. Environ. Res. 117, 54–62. doi:10.1016/j.marenvres.2016.04.004
Ketelaar, T., Faivre-Moskalenko, C., Esseling, J. J., and de Ruijter, N.C. A., Grierson, C. S., Dogterom, M., et al. (2002). Positioning of nuclei in Arabidopsis root hairs: an actin-regulated process of tip growth, Plant Cell, 14, 2941–2955. doi:10.1105/tpc.005892
Larkum, A. W. D., Waycott, M., and Conran, J. G. (2018). “Evolution and biogeography of seagrasses,” in Seagrasses of Australia. Editors Larkum, A., Kendrick, G., and Ralph, P (Cham, Switzerland: Springer). doi:10.1007/978-3-319-71354-0_1
Marion, S. R., and Orth, R. J. (2010). Innovative techniques for large-scale seagrass restoration using Zostera marina (eelgrass) seeds. Restor. Ecol. 18, 514–526. doi:10.1111/j.1526-100X.2010.00692.x
Meinesz, A., Caye, G., Loques, F., and Molenaar, H. (1993). Polymorphism and development of Posidonia oceanica transplanted from different parts of the mediterranean into the national park of port-cros. Bot. Mar. 36, 209–216. doi:10.1515/botm.1993.36.3.209
Melzer, B., Seidel, R., Steinbrecher, T., and Speck, T. (2012). Structure, attachment properties, and ecological importance of the attachment system of English ivy (Hedera helix). J. Exp. Bot. 63, 191–201. doi:10.1093/jxb/err260
Melzer, B., Steinbrecher, T., Seidel, R., Kraft, O., Schwaiger, R., and Speck, T. (2010). The attachment strategy of English ivy: a complex mechanism acting on several hierarchical levels. J. R. Soc. Interface 7, 1383–1389. doi:10.1098/rsif.2010.0140
Molenaar, H., and Meinesz, A. (1995). Vegetative reproduction in Posidonia oceanica: survival and development of transplanted cuttings according to different spacings, arrangements and substratum. Bot. Mar. 38, 313–322. doi:10.1515/botm.1995.38.1-6.313
Montefalcone, M., Vacchi, M., Carbone, C., Cabella, R., Schiaffino, C. F., Elter, F. M., et al. (2016). Seagrass on the rocks: Posidonia oceanica settled on shallow-water hard substrata withstands wave stress beyond predictions. Estuar. Coast. Shelf S 180, 114–122. doi:10.1016/j.ecss.2016.06.024
Piazzi, L., Balestri, E., Magri, M., and Cinelli, F. (1998). Experimental transplanting of Posidonia oceanica (L.) delile into a disturbed habitat in the Mediterranean Sea. Bot. Mar. 41, 593–602. doi:10.1515/botm.1998.41.1-6.593
Roberts, D. G. (1993). Root hair structure and development in the seagrass Halophila ovalis (R. Br.) Hook. f. Aust. J. Mar. Freshwater Res. 44, 85–100. doi:10.1071/MF9930085
Ryan, E., Steer, M., and Dolan, L. (2001). Cell biology and genetics of root hair formation in Arabidopsis thaliana. Protoplasma 215, 140–149. doi:10.1007/BF01280310
Scherge, M., and Gorb, S. N. (2001). Biological micro-and nanotribology: nature’s solutions, New York, NY: Springer-verlag.
Schneider, C. A., Rasband, W. S., and Eliceiri, K. W. (2012). NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675. doi:10.1038/nmeth.2089
Seidelmann, K., Melzer, B., and Speck, T. (2012). The complex leaves of the monkey's comb (Amphilophium crucigerum, Bignoniaceae): a climbing strategy without glue. Am. J. Bot. 99, 1737–1744. doi:10.3732/ajb.1200288
Somssich, M., Khan, G. A., and Persson, S. (2016). Cell wall heterogeneity in root development of Arabidopsis. Front. Plant Sci. 7, 1242. doi:10.3389/fpls.2016.01242
Spurr, R. A. (1969). A low-viscosity epoxy resin embedding medium for electron microscopy. J. Ultra Mol. Struct. R. 26, 31–43. doi:10.1016/s0022-5320(69)90033-1
Steinbrecher, T., Beuchle, G., Melzer, B., Speck, T., Kraft, O., and Schwaiger, R. (2011). Structural development and morphology of the attachment system of Parthenocissus tricuspidata. Int. J. Plant Sci. 172, 1120–1129. doi:10.1086/662129
Steinbrecher, T., Danninger, E., Harder, D., Speck, T., Kraft, O., and Schwaiger, R. (2010). Quantifying the attachment strength of climbing plants: a new approach. Acta Biomater. 6, 1497–1504. doi:10.1016/j.actbio.2009.10.003
Telesca, L., Belluscio, A., Criscoli, A., Ardizzone, G., Apostolaki, E. T., Fraschetti, S., et al. (2015). Seagrass meadows (Posidonia oceanica) distribution and trajectories of change. Sci. Rep. 5, 12505. doi:10.1038/srep12505
Tomasello, A., Perrone, R., Colombo, P., Pirrotta, M., and Calvo, S. (2018). Root hair anatomy and morphology in Posidonia oceanica (L.) Delile and substratum typology: first observations of a spiral form. Aquat. Bot. 145, 45–48. doi:10.1016/j.aquabot.2017.12.001
Unsworth, R. K. F., Collier, C. J., Waycott, M., Mckenzie, L. J., and Cullen-Unsworth, L. C. (2015). A framework for the resilience of seagrass ecosystems. Mar. Pollut. Bull. 100, 34–46. doi:10.1016/j.marpolbul.2015.08.016
van Katwijk, M. M., Thorhaug, A., Marbà, N., Orth, R. J., Duarte, C. M., Kendrick, G. A., et al. (2016). Global analysis of seagrass restoration: the importance of large-scale planting. J. Appl. Ecol. 53, 567–578. doi:10.1111/1365-2664.12562
Waycott, M., Duarte, C. M., Carruthers, T. J. B., Orth, R. J., Dennison, W. C., Olyarnik, S., et al. (2009). Accelerating loss of seagrasses across the globe threatens coastal ecosystems. Proc. Natl. Acad. Sci. U. S. A 106, 12377–12381. doi:10.1073/pnas.0905620106
Yang, N., Zhu, C., Gan, L., Ng, D., and Xia, K. (2011). Ammonium-stimulated root hair branching is enhanced by methyl jasmonate and suppressed by ethylene in Arabidopsis thaliana. J. Plant Biol. 54, 92–100. doi:10.1007/s12374-011-9147-x
Yang, X., and Deng, W. (2017). Morphological and structural characterization of the attachment system in aerial roots of Syngonium podophyllum. Planta 245, 507–521. doi:10.1007/s00425-016-2621-4
Zenone, A., Alagna, A., D'Anna, G., Kovalev, A., Kreitschitz, A., Badalamenti, F., et al. (2020). Biological adhesion in seagrasses: the role of substrate roughness in Posidonia oceanica (L.) Delile seedling anchorage via adhesive root hairs. Mar. Environ. Res. 160, 105012. doi:10.1016/j.marenvres.2020.105012
Keywords: P. oceanica, root hair, adhesion, branching, transplanting initiatives
Citation: Zenone A, Filippov AE, Kovalev A, Badalamenti F and Gorb SN (2020) Root Hair Adhesion in Posidonia oceanica (L.) Delile Seedlings: A Numerical Modelling Approach. Front. Mech. Eng. 6:590894. doi: 10.3389/fmech.2020.590894
Received: 03 August 2020; Accepted: 18 September 2020;
Published: 19 November 2020.
Edited by:
Alessandro Ruggiero, University of Salerno, ItalyReviewed by:
Abhishek Srivastava, Western Digital, United StatesYoshitaka Nakanishi, Kumamoto University, Japan
Copyright © 2020 Zenone, Filippov, Kovalev, Badalamenti and Gorb. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arturo Zenone, YXJ0dXJvemVub0BnbWFpbC5jb20=
 Arturo Zenone
Arturo Zenone Alexander E. Filippov
Alexander E. Filippov Alexander Kovalev1
Alexander Kovalev1 Fabio Badalamenti
Fabio Badalamenti Stanislav N. Gorb
Stanislav N. Gorb