Boundary Reflections of Rolling Waves in Cubic Anisotropic Material

1 Introduction

Recent advances in mechanical and acoustic metamaterials have made it possible to manipulate the general intrinsic spin angular momentum (Holanda et al., 2018; Zhu et al., 2018; An et al., 2020; Burns et al., 2020; Rückriegel et al., 2020; Shi and Yang, 2020) carried by elastic waves in the bulk (Long et al., 2018; Wang et al., 2018; Shi et al., 2019; Toftul et al., 2019; Long et al., 2020). Our previous work (Zhang et al., 2020) demonstrated that, when longitudinal and transverse elastic waves propagate at the same speed, rolling waves may emerge, carrying a spin that is orthogonal to, and in general not parallel to, the wave vector. This is only possible in anisotropic materials that satisfies certain equal-wave-speed criteria (Zhang et al., 2020). As the simplest anisotropic material characterized by only three independent elastic constants, cubic materials have been investigated in many studies (Stoneley, 1955; Borcherds, 1973). Thomas (1966) analyzed the longitudinal wave velocity at different directions using orientation components, and Mielnicki (1972) studied both longitudinal and transverse waves using approximation method. The bounds of elastic wave speeds (Zuo and Hjelmstad, 1997), surface wave polarizations (Chadwick and Wilson, 1992), and supersonic surface waves (Every, 2015) have all been the topics of an active line of research. Benefited from the fast development in additive manufacturing technology, cubic symmetric metamaterials can now provide us with a broader range of possible elastic constants (Favre et al., 2018; Tancogne-Dejean and Mohr, 2018; Lohmuller et al., 2019) even to the higher-order elasticity effects, such as the compression torsion metamaterial (Frenzel et al., 2017; Wang and Liu, 2020), hyper-stress tensor with second-gradient elasticity (Weeger, 2021), and chiral-micropolar metamaterials (Chen et al., 2021).

Although the stable propagation of rolling waves with non-paraxial spins have been demonstrated (Zhang et al., 2020), effects of boundary reflections on the wave spin angular momenta have yet to be investigated. The elastic wave reflection process is often both rich in physics and useful in applications (Schoenberg, 1980; Bedford and Drumheller, 1994; Vavrycuk and Psencík, 1998; Lee et al., 2017; Chen et al., 2019). However, studies on reflections from elastically supported boundaries of cubic materials are lacking. This further motivates us to analyze the reflection of rolling waves in a cubic material incident either normally or obliquely at such boundaries. The present work fills the gap in understanding and predicting rolling reflections and offers a new technique to manipulate the spin of elastic bulk waves.

In this paper, we first review the general governing equations for plane waves in an anisotropic medium. Next, the equal-wave-speed criteria in cubic materials are derived. Furthermore, we provide a general formulation for the spin angular momentum of bulk elastic waves. Lastly, the normal and oblique incident rolling waves are analyzed with different boundary conditions, where both spin-preserving and spin-flipping phenomena may emerge.

2 Plane Waves in Anisotropic Medium

With consideration of long-wavelength limit (i.e. quasi-static limit) only, we focus on the plane wave with wavelength much larger than any micro-structure size, which implies the dispersive behavior from geometry is negligible. The general bulk elastic wave equation without body force is,

$\nabla \cdot \mathit{\sigma }=\rho \ddot{\mathit{u}},(1)$

where σ is the stress tensor and u is the displacement vector.

The general solution of plane waves is

$\mathit{u}={\mathit{u}}_0\exp [\text{i}(\mathit{k}\cdot \mathit{x}-\omega t)],(2)$

where u₀ denotes wave amplitude, and k the wave vector. We consider a plane wave propagating along an arbitrary direction specified by the unit vector,

$\hat{\mathit{k}}=l_1{\mathit{e}}_1+l_2{\mathit{e}}_2+l_3{\mathit{e}}_3,(3)$

where l₁, l₂, l₃ are direction cosines, and e₁, e₂, e₃ are the standard orthonormal basis vectors of Cartesian coordinates. Then, we have

$\mathit{k}=k\hat{\mathit{k}},(4)$

where k is the wavenumber.

The time derivative of eq. 2 gives us,

$\frac{\partial }{\partial t}\mathit{u}=-\text{i}\omega \mathit{u}.(5)$

With the definition of a matrix L,

$\mathit{L}=\left(\begin{array}{cccccc}\hfill l_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill l_3\hfill & \hfill l_2\hfill \\ \hfill 0\hfill & \hfill l_2\hfill & \hfill 0\hfill & \hfill l_3\hfill & \hfill 0\hfill & \hfill l_1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill l_3\hfill & \hfill l_2\hfill & \hfill l_1\hfill & \hfill 0\hfill \end{array}\right).(6)$

We have the spatial derivative in Voigt notation (Carcione, 2007),

$\nabla =\text{i}k\mathit{L}.(7)$

Combining the above equations, we arrive at

$k^2\mathbf{\Gamma }\cdot \mathbf{u}=\rho {\omega }^2\mathit{u},(k^2{\mathrm{\Gamma }}_{ij}{u}_j=\rho {\omega }^2{u}_i)(8)$

where

$\mathbf{\Gamma }={\mathit{L}\cdot \mathit{C}\cdot \mathit{L}}^T,({\mathrm{\Gamma }}_{ij}=L_{iI}{C}_{IJ}{L}_{Jj})(9)$

is the Kelvin-Christoffel matrix.

Here, we consider the phase velocity v and its amplitude, wave speed v given as,

$\mathit{v}=v\hat{\mathit{k}},v=\frac{\omega }{k}.(10)$

Then, we obtain the governing equation for bulk elastic wave speeds in a general anisotropic material,

$\mathbf{\Gamma }\cdot \mathbf{u}-\rho v^2\mathit{u}=(\mathbf{\Gamma }-\rho v^2\mathit{I})\cdot \mathit{u}=\mathbf{0}.(11)$

The expressions of elements in Γ are given below as,

$\begin{array}{c}{\mathrm{\Gamma }}_{11}=C_{11}{l}_1^2+C_{66}{l}_2^2+C_{55}{l}_3^2+2C_{56}{l}_2{l}_3+2C_{15}{l}_1{l}_3+2C_{16}{l}_1{l}_2,\hfill \\ {\mathrm{\Gamma }}_{22}=C_{66}{l}_1^2+C_{22}{l}_2^2+C_{44}{l}_3^2+2C_{24}{l}_2{l}_3+2C_{46}{l}_1{l}_3+2C_{26}{l}_1{l}_2,\hfill \\ {\mathrm{\Gamma }}_{33}=C_{55}{l}_1^2+C_{44}{l}_2^2+C_{33}{l}_3^2+2C_{34}{l}_2{l}_3+2C_{35}{l}_1{l}_3+2C_{45}{l}_1{l}_2,\hfill \\ {\mathrm{\Gamma }}_{12}=C_{16}{l}_1^2+C_{26}{l}_2^2+C_{45}{l}_3^2+(C_{46}+C_{25})l_2{l}_3+(C_{14}+C_{56})l_1{l}_3+(C_{12}+C_{66})l_1{l}_2,\hfill \\ {\mathrm{\Gamma }}_{13}=C_{15}{l}_1^2+C_{46}{l}_2^2+C_{35}{l}_3^2+(C_{45}+C_{36})l_2{l}_3+(C_{13}+C_{55})l_1{l}_3+(C_{14}+C_{56})l_1{l}_2,\hfill \\ {\mathrm{\Gamma }}_{23}=C_{56}{l}_1^2+C_{24}{l}_2^2+C_{34}{l}_3^2+(C_{44}+C_{23})l_2{l}_3+(C_{36}+C_{45})l_1{l}_3+(C_{25}+C_{46})l_1{l}_2,\hfill \end{array}(12)$

where C_ij are components of the stiffness matrix in Voigt notation (Carcione, 2007).

3 Constitutive Relation of Cubic Materials

Next, we focus our discussions on cubic materials characterized by the cubic crystallographic point groups. As illustrated in Figure 1, the symmetry conditions include four axes of three-fold rotational symmetry that can be identified with the body diagonals of a cubic unit cell (Bückmann et al., 2014; Dirrenberger et al., 2013; Authier, 2003). Rather counter-intuitively, this symmetry requirement does not include any axis of four-fold (90 degree) rotational symmetry (Ashcroft and Mermin, 1976, p. 121). The stiffness matrix of cubic material is given as (Authier, 2003; Norris, 2006; Zhang et al., 2020),

$\mathit{C}(\mathrm{C}\mathrm{u}\mathrm{b}\mathrm{i}\mathrm{c})=\left(\begin{array}{cccccc}\hfill C_{11}\hfill & \hfill C_{12}\hfill & \hfill C_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill C_{11}\hfill & \hfill C_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill C_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill C_{44}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \text{\hspace{0.17em}Sym}\hfill & \hfill \hfill & \hfill \hfill & \hfill C_{44}\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill C_{44}\hfill \end{array}\right),\left(3\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{s}\right)(13)$

FIGURE 1

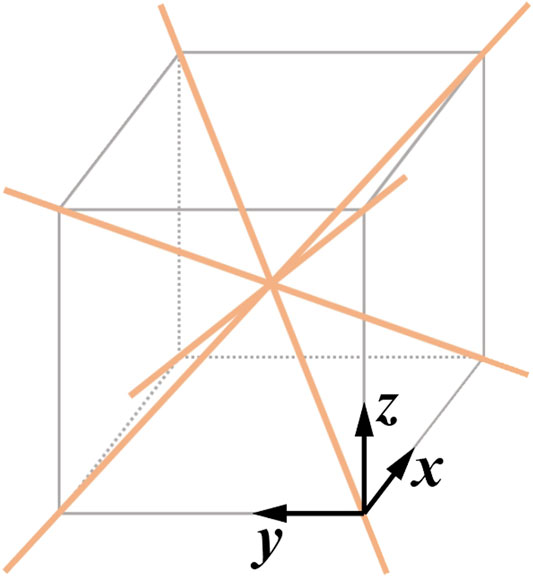
FIGURE 1. The symmetry requirement for cubic materials: Body diagonals (orange solid lines) of a cubic unit cell serve as the four axes of three-fold rotational symmetry. They are the sufficient and necessary conditions for the cubic crystallographic point groups. On the contrary to some common misconceptions, cubic materials do not need to have any four-fold rotational symmetry.

For waves propagating along the z-direction, the direction cosines are

$l_1=0,l_2=0,l_3=1.(14)$

Then, the Kelvin-Christoffel matrix components become,

${\mathrm{\Gamma }}_{11}={\mathrm{\Gamma }}_{22}=C_{44},{\mathrm{\Gamma }}_{33}=C_{11},{\mathrm{\Gamma }}_{12}={\mathrm{\Gamma }}_{13}={\mathrm{\Gamma }}_{23}=0.(15)$

Therefore, the governing eq. 11 becomes,

$\begin{array}{cc}\hfill \mathbf{0}& =(\mathbf{\Gamma }-\rho v^2\mathit{I})\cdot \mathit{u}\hfill \\ \hfill & =\left(\begin{array}{ccc}\hfill C_{44}-\rho v^2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill C_{44}-\rho v^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill C_{11}-\rho v^2\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill u_1\hfill \\ \hfill u_2\hfill \\ \hfill u_3\hfill \end{array}\right).\hfill \end{array}(16)$

We note that u₃ represents the longitudinal wave, while u₁ and u₂ represent the transverse waves. Therefore, from eq. 16, we obtain the longitudinal and transverse wave speeds as,

$v_L=\sqrt{\frac{C_{11}}{\rho }},v_T=\sqrt{\frac{C_{44}}{\rho }}.(17)$

Thus, for waves traveling in the z-direction of a cubic material, in order to have a rolling wave with non-praxial spin polarization (Zhang et al., 2020), we need the equal-speed criterion:

$C_{11}=C_{44}.(18)$

By symmetry, for the waves propagating in x− or y−direction, the equal-speed criterion is exactly the same as eq. 18.

4 Intrinsic Spin Angular Momentum of Bulk Elastic Waves

To calculate the spin density of the bulk elastic waves, we consider the displacement field of a general plane wave $\mathit{u}=\tilde{\mathit{u}}\exp [\text{i}(\mathit{k}\cdot \mathit{x}-\omega t)]$ with

$\tilde{\mathit{u}}=\left(\begin{array}{c}\hfill m\hfill \\ \hfill n\hfill \\ \hfill l\hfill \end{array}\right).(19)$

Importantly, here m, n and l are complex-valued, so that they contain the information not only about amplitudes but also about the relative phase differences among displacement components of the traveling wave. The spin angular momentum density, as a real-valued vector, can be calculated as (Berry, 2009; Long et al., 2018; Burns et al., 2020):

$\mathit{s}=\frac{\rho \omega }{2}<\tilde{u}|\hat{\mathbf{S}}|\tilde{\mathit{u}}>=\frac{\rho \omega }{2}\mathrm{I}\mathrm{m}[{\tilde{\mathit{u}}}^{*}\times \tilde{\mathit{u}}],(20)$

where (⋅)* denotes complex conjugation, and the spin-1 operator is a third-order tensor defined as

$\hat{\mathbf{S}}=\left[\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\text{i}\hfill \\ \hfill 0\hfill & \hfill \text{i}\hfill & \hfill 0\hfill \end{array}\right),\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \text{i}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\text{i}\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -\text{i}\hfill & \hfill 0\hfill \\ \hfill \text{i}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\right].(21)$

Hence, the spin density for a general traveling wave is

$\mathit{s}=\rho \omega \mathrm{I}\mathrm{m}\left(\begin{array}{c}\hfill n*l\hfill \\ \hfill l*m\hfill \\ \hfill m*n\hfill \end{array}\right).(22)$

We note that the above formulation makes physical sense only if all displacement components propagate at the same wave speed. Particularly for cubic materials, the equal-speed criterion eq. 18 needs to be true. In this case, we can have stable propagation of spins pointing at any direction by adjusting the complex amplitudes m, n and l. This can be realized by simply changing the relative phase differences. Hence, the direction of the spin vector s can be completely independent from the direction of the wave vector k.

5 Normal Incidence and Reflection

We now investigate normal reflections of a rolling wave at a general elastic boundary. This serves as an example non-paraxial spin manipulation. Considering a rolling wave along the z-direction normally incident on a flat surface, we have the instantaneous wave displacement fields at time t = 0 as ${\mathit{u}}^{\text{I}}={\tilde{\mathit{u}}}^{\text{I}}\exp (\text{i}kz)$ and ${\mathit{u}}^{\text{R}}={\tilde{\mathit{u}}}^{\text{R}}\exp (-\text{i}kz)$ with

${\tilde{\mathit{u}}}^{\text{I}}=\left(\begin{array}{c}\hfill m^{\text{I}}\hfill \\ \hfill n^{\text{I}}\hfill \\ \hfill l^{\text{I}}\hfill \end{array}\right)\text{and}{\tilde{\mathit{u}}}^{\text{R}}=\left(\begin{array}{c}\hfill m^{\text{R}}\hfill \\ \hfill n^{\text{R}}\hfill \\ \hfill l^{\text{R}}\hfill \end{array}\right),(23)$

where the superscripts, I and R, denote the incident and reflected waves, respectively.

For the displacement with small amplitude, the linear strain terms are dominant. In this case, by neglecting higher-order strain terms, the strains can be calculated from displacements by

${\epsilon }_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i}),i,j=x,y,z(24)$

where the comma “,^″ in subscripts denotes the derivative operation.

The reflection occurs at z = 0. So we have e^ikz = e^−ikz = 1, and the strain vector in Voigt notation becomes

${\mathit{\epsilon }}^{\text{I}}=\left(\begin{array}{c}\hfill {\epsilon }_{xx}^{\text{I}}\hfill \\ \hfill {\epsilon }_{yy}^{\text{I}}\hfill \\ \hfill {\epsilon }_{zz}^{\text{I}}\hfill \\ \hfill 2{\epsilon }_{yz}^{\text{I}}\hfill \\ \hfill 2{\epsilon }_{xz}^{\text{I}}\hfill \\ \hfill 2{\epsilon }_{xy}^{\text{I}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill l^{\text{I}}\text{i}k\hfill \\ \hfill n^{\text{I}}\text{i}k\hfill \\ \hfill m^{\text{I}}\text{i}k\hfill \\ \hfill 0\hfill \end{array}\right),{\mathit{\epsilon }}^{\text{R}}=\left(\begin{array}{c}\hfill {\epsilon }_{xx}^{\text{R}}\hfill \\ \hfill {\epsilon }_{yy}^{\text{R}}\hfill \\ \hfill {\epsilon }_{zz}^{\text{R}}\hfill \\ \hfill 2{\epsilon }_{yz}^{\text{R}}\hfill \\ \hfill 2{\epsilon }_{xz}^{\text{R}}\hfill \\ \hfill 2{\epsilon }_{xy}^{\text{R}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill -l^{\text{R}}\text{i}k\hfill \\ \hfill -n^{\text{R}}\text{i}k\hfill \\ \hfill -m^{\text{R}}\text{i}k\hfill \\ \hfill 0\hfill \end{array}\right).(25)$

The cubic constitutive relations are

$\left(\begin{array}{c}\hfill {\sigma }_{xx}\hfill \\ \hfill {\sigma }_{yy}\hfill \\ \hfill {\sigma }_{zz}\hfill \\ \hfill {\sigma }_{yz}\hfill \\ \hfill {\sigma }_{xz}\hfill \\ \hfill {\sigma }_{xy}\hfill \end{array}\right)=\left(\begin{array}{cccccc}\hfill C_{11}\hfill & \hfill C_{12}\hfill & \hfill C_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill C_{12}\hfill & \hfill C_{11}\hfill & \hfill C_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill C_{12}\hfill & \hfill C_{12}\hfill & \hfill C_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill C_{44}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill C_{44}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill C_{44}\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill {\epsilon }_{xx}\hfill \\ \hfill {\epsilon }_{yy}\hfill \\ \hfill {\epsilon }_{zz}\hfill \\ \hfill 2{\epsilon }_{yz}\hfill \\ \hfill 2{\epsilon }_{xz}\hfill \\ \hfill 2{\epsilon }_{xy}\hfill \end{array}\right).(26)$

It is easy to compute the stress components for incident and reflection waves, respectively:

$\left(\begin{array}{c}\hfill {\sigma }_{xx}^{\text{I}}\hfill \\ \hfill {\sigma }_{yy}^{\text{I}}\hfill \\ \hfill {\sigma }_{zz}^{\text{I}}\hfill \\ \hfill {\sigma }_{yz}^{\text{I}}\hfill \\ \hfill {\sigma }_{xz}^{\text{I}}\hfill \\ \hfill {\sigma }_{xy}^{\text{I}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill C_{12}{l}^{\text{I}}\text{i}k\hfill \\ \hfill C_{12}{l}^{\text{I}}\text{i}k\hfill \\ \hfill C_{11}{l}^{\text{I}}\text{i}k\hfill \\ \hfill C_{44}{n}^{\text{I}}\text{i}k\hfill \\ \hfill C_{44}{m}^{\text{I}}\text{i}k\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{c}\hfill {\sigma }_{xx}^{\text{R}}\hfill \\ \hfill {\sigma }_{yy}^{\text{R}}\hfill \\ \hfill {\sigma }_{zz}^{\text{R}}\hfill \\ \hfill {\sigma }_{yz}^{\text{R}}\hfill \\ \hfill {\sigma }_{xz}^{\text{R}}\hfill \\ \hfill {\sigma }_{xy}^{\text{R}}\hfill \end{array}\right)=\left(\begin{array}{c}-C_{12}{l}^{\text{R}}\text{i}k\hfill \\ -C_{12}{l}^{\text{R}}\text{i}k\hfill \\ -C_{11}{l}^{\text{R}}\text{i}k\hfill \\ -C_{44}{n}^{\text{R}}\text{i}k\hfill \\ -C_{44}{m}^{\text{R}}\text{i}k\hfill \\ \hfill 0\hfill \end{array}\right).(27)$

For a elastically supported cubic half-space, the boundary conditions are

${\sigma }_{zx}^0=K_x{u}_x^0,{\sigma }_{zy}^0=K_y{u}_y^0,{\sigma }_{zz}^0=K_z{u}_z^0.(28)$

where (K_x, K_y, K_z) are components of the distributed stiffness per unit area (Zhang et al., 2017) representing a general elastic foundation supporting the solid surface, and the total stress and displacement are

${\sigma }_{zx}^0={\sigma }_{zx}^{\text{I}}+{\sigma }_{zx}^{\text{R}},{\sigma }_{zy}^0={\sigma }_{zy}^{\text{I}}+{\sigma }_{zy}^{\text{R}},{\sigma }_{zz}^0={\sigma }_{zz}^{\text{I}}+{\sigma }_{zz}^{\text{R}}.(29)$

$u_x^0=u_x^{\text{I}}+u_x^{\text{R}},u_y^0=u_y^{\text{I}}+u_y^{\text{R}},u_z^0=u_z^{\text{I}}+u_z^{\text{R}}.(30)$

Substituting the displacement and stress components into elastic boundary conditions, we get

$C_{44}{m}^{\text{I}}\text{i}k-C_{44}{m}^{\text{R}}\text{i}k=K_x(m^{\text{I}}+m^{\text{R}}),(31)$

$C_{44}{n}^{\text{I}}\text{i}k-C_{44}{n}^{\text{R}}\text{i}k=K_y(n^{\text{I}}+n^{\text{R}}),(32)$

$C_{11}{l}^{\text{I}}\text{i}k-C_{11}{l}^{\text{R}}\text{i}k=K_z(l^{\text{I}}+l^{\text{R}}).(33)$

Solving the above system of equations, we obtain

$m^{\text{R}}=\frac{C_{44}\text{i}k-K_x}{C_{44}\text{i}k+K_x}{m}^{\text{I}},(34)$

$n^{\text{R}}=\frac{C_{44}\text{i}k-K_y}{C_{44}\text{i}k+K_y}{n}^{\text{I}},(35)$

$l^{\text{R}}=\frac{C_{11}\text{i}k-K_z}{C_{11}\text{i}k+K_z}{l}^{\text{I}}.(36)$

Because of the equal-speed requirement of rolling wave (C₁₁ = C₄₄), the amplitude of reflection wave becomes,

$m^{\text{R}}=R_x{m}^{\text{I}},n^{\text{R}}=R_y{n}^{\text{I}},l^{\text{R}}=R_z{l}^{\text{I}},(37)$

with the generalized amplitude ratio of normal reflection given as

$R_j=\frac{C_{11}\text{i}k-K_j}{C_{11}\text{i}k+K_j},j=x,y,z.(38)$

We can also write in the form of a reflection matrix (Zoeppritz, 1919; Ursin and Tjäland, 1996):

$\left(\begin{array}{c}\hfill m^{\text{R}}\hfill \\ \hfill n^{\text{R}}\hfill \\ \hfill l^{\text{R}}\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill R_x\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill R_y\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill R_z\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill m^{\text{I}}\hfill \\ \hfill n^{\text{I}}\hfill \\ \hfill l^{\text{I}}\hfill \end{array}\right).(39)$

with the reflection matrix $\hat{\mathbf{R}}=\text{diag}(R_x,R_y,R_z)$. This complex-valued non-dimensional parameter R_j is the key connection between the incident and reflected waves and deserves further analysis. We note that |R_j| = 1 is consistent with the fact that all wave energy is reflected. Hence, we have

$R_j=e^{\text{i}\varphi }\text{with}\tan \varphi =\frac{2K_j/C_{11}k}{1-{(K_j/C_{11}k)}^2}.(40)$

Here, the phase angle ϕ of R_j corresponds to the phase change during the reflection, and it dependents on the boundary-bulk stiffness ratio K_j/C₁₁ and the wave number k, as shown in Figure 2. Therefore, by adjusting the elastic stiffness at the boundary, one can manipulate the spin of the reflected waves.

FIGURE 2

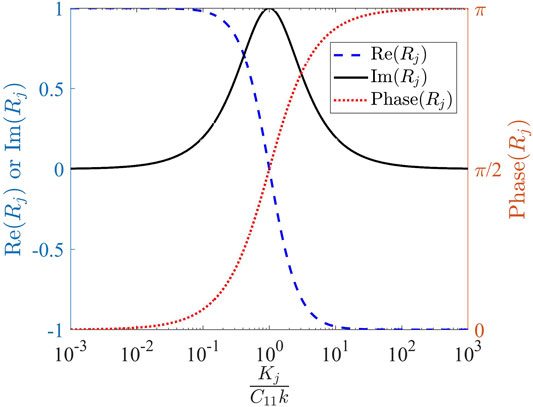
FIGURE 2. The complex-valued amplitude ratio of normal reflection, R_j, is determined by the boundary-bulk stiffness ratio, K_j/C₁₁, and wave number k.

Although all properties of both the bulk and the reflection surface are assumed to be independent of the incidence wave frequency, here the reflection phase change can be frequency-dependent, as the angular wave number k appears in the ratio. The emergence of frequency dependency can be intuitively explained by the role of wavelength during reflection. We note from eq. 25 that k first appears in the strain calculations since, for a given wave displacement amplitude, the strains in the propagation direction, ɛ_zj, are actually inversely proportional to the wavelength: Longer wavelength gives rise to a smaller strain and vice versa. Consequently, the stresses, σ_zj, and the force acting on the boundary springs are wavelength-dependent as well. If the boundary is supported by an elastic foundation with finite stiffness per area, K_j, we have the following: At the low-frequency and long-wavelength limit, the force per area acting on the boundary, |σ_zj|∝ C₁₁k → 0. So, the boundary hardly moves, and the incidence wave effectively “sees” a rigid surface; At the high-frequency and short-wavelength limit, the force per area acting on the boundary, |σ_zj|∝ C₁₁k → ∞. So, the boundary moves a lot, and the incidence wave effectively “sees” a free surface.

Next, we consider some special cases and focus on the in-xz-plane rolling waves with n^I = n^R = 0. We note that the elastic boundary condition degenerates into traction-free boundary condition (Neumann type) when the boundary stiffness K_j → 0. Then, the amplitudes of reflected wave become

$m^{\text{R}}=m^{\text{I}},l^{\text{R}}=l^{\text{I}}.(41)$

Similarly, the elastic boundary condition degenerates into the fixed rigid boundary condition (Dirichlet type) when the stiffness K_j → ∞. Then, the amplitudes of reflected wave become

$m^{\text{R}}=-m^{\text{I}},l^{\text{R}}=-l^{\text{I}}.(42)$

In both cases above, by the definition of spin given in eq. 22, we can conclude s^R = s^I, as shown in Figures 3B,C. So, the spin is unaffected by the reflection process.

FIGURE 3

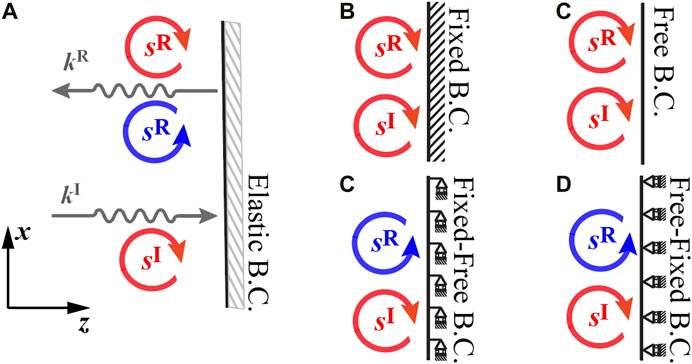
FIGURE 3. (A) Rolling wave reflections with normal incidence at a general elastic boundary. In all sub-plots, the incidence wave carries a spin angular momentum, $s_y^{\text{I}}=-1$. Here s^I and s^R indicate the spin density of incidence wave and reflection wave, respectively. They can be calculated using the eq. 22. The reflection process is (B) spin-preserving at the fixed rigid boundary, (C) spin-preserving at the free boundary, (D) spin-flipping at the fixed-free boundary, and (E) spin-flipping at the free-fixed boundary.

In addition, for the fixed-free hybrid boundary (K_x → ∞ and K_z → 0, Figure 3D), we have

$m^{\text{R}}=-m^{\text{I}},l^{\text{R}}=l^{\text{I}}\Rightarrow {\mathit{s}}^{\text{R}}=-{\mathit{s}}^{\text{I}}.(43)$

Similarly, for the free-fixed hybrid boundary (K_x → 0 and K_z → ∞, Figure 3E), we have

$m^{\text{R}}=m^{\text{I}},l^{\text{R}}=-l^{\text{I}}\Rightarrow {\mathit{s}}^{\text{R}}=-{\mathit{s}}^{\text{I}}.(44)$

Thus, both hybrid boundaries will flip the spin for any incident rolling wave.

Summarizing different cases for the normal incidence, we note that, for K_x → 0 and K_z → 0, the boundary becomes traction-free (Neumann type) and we have ${\tilde{\mathit{u}}}^{\text{R}}={\tilde{\mathit{u}}}^{\text{I}}$ with no phase change. For K_x → ∞ and K_z → ∞, the boundary becomes rigid (Dirichlet type) and we have an out-of-phase reflected wave with ${\tilde{\mathit{u}}}^{\text{R}}=-{\tilde{\mathit{u}}}^{\text{I}}$. In both cases, we have s^R = s^I, so the spin is preserved. In contrast, for hybrid boundaries (K_x → ∞, K_z → 0) and (K_x → 0, K_z → ∞), we get s^R = −s^I, so the spin is flipped due to the difference in phase change between the longitudinal and transverse displacement components during the reflection process.

Figure 3 illustrates the results using the example of an incident rolling wave carrying a non-paraxial spin of $s_y^{\text{I}}=-1$. The reflection process is spin-preserving in both rigid and free boundaries, while being spin-flipping for both hybrid free-fixed and hybrid fixed-free boundary conditions.

6 The Oblique Incidence and Reflection at 45 degree

Next we investigate the scenario in which the boundary plane is oblique to the incident rolling wave at the 45° angle. We focus on the incident rolling wave propagating towards the positive z−direction,

${\mathit{u}}^{\text{I}}=\left(\begin{array}{c}\hfill m^{\text{I}}\hfill \\ \hfill n^{\text{I}}\hfill \\ \hfill l^{\text{I}}\hfill \end{array}\right)e^{\text{i}{k}^{\text{I}}z}(45)$

As shown in Figure 4A, the incidence angle here is α^I = 45°. Importantly, we note that, due to material anisotropy, the reflection angle(s) will not necessarily be equal to the incidence angle. In fact, a single incidence wave, in general, may result in multiple reflected waves towards different directions (Achenbach, 2012; Graff, 2012). Hence, the reflection angle(s) need to be determined by a detailed analysis on boundary conditions and material properties. In this case, we can write the reflection wave as a general form in xz-plane,

${\mathit{u}}^{\text{R}}=\left(\begin{array}{c}\hfill m^{\text{R}}\hfill \\ \hfill n^{\text{R}}\hfill \\ \hfill l^{\text{R}}\hfill \end{array}\right)e^{\text{i}{k}^{\text{R}}[\cos (\theta )x+\sin (\theta )z]}(46)$

where θ is the angle of wave vector with respect to the x-axis. It follows that the reflection angle can be expressed as α^R = θ + 45°, θ ∈ (−45°, + 45°).

FIGURE 4

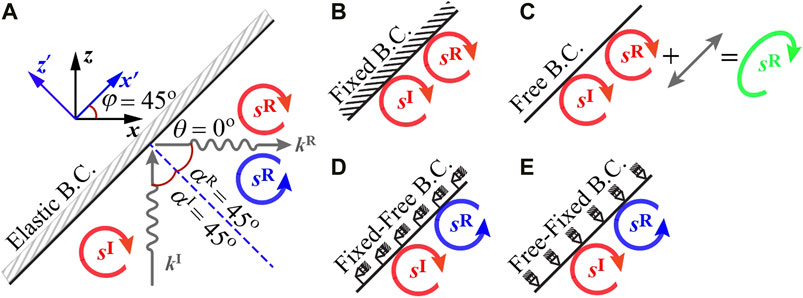
FIGURE 4. (A) Illustration of rolling wave reflections at 45° incidence. In all sub-plots, the incidence wave carries a spin angular momentum, $s_y^{\text{I}}=+1$. Here s^I and s^R indicate the spin density of incidence wave and reflection wave, respectively. They can be calculated using the eq. 22. The reflection process is (B) spin-preserving at the fixed rigid boundary, (C) spin-preserving at the free boundary, (D) spin-flipping at the fixed-free boundary, and (E) spin-flipping at the free-fixed boundary. Note that the free boundary in (C) has the specially effect of giving rise to an additional linearly polarized reflected wave. Although the spin is still exactly preserved, the overall reflected wave has an elliptical rolling polarization.

Next, we look into the general conditions for rolling waves propagating in the xz-plane. The normalized wave vector, as given in eq. 3, is now characterized by cosine directions l₂ = 0 and $l_1^2+l_3^2=1$. The element expressions of matrix Γ become,

$\begin{array}{cc}\hfill & {\mathrm{\Gamma }}_{11}=C_{11}{l}_1^2+C_{44}{l}_3^2,\hfill \\ \hfill & {\mathrm{\Gamma }}_{22}=C_{44},\hfill \\ \hfill & {\mathrm{\Gamma }}_{33}=C_{44}{l}_1^2+C_{11}{l}_3^2,\hfill \\ \hfill & {\mathrm{\Gamma }}_{12}=0,\hfill \\ \hfill & {\mathrm{\Gamma }}_{13}=(C_{12}+C_{44})l_1{l}_3,\hfill \\ \hfill & {\mathrm{\Gamma }}_{23}=0.\hfill \end{array}(47)$

Therefore, the governing eq. 11 becomes,

$\begin{array}{cc}\hfill \mathbf{0}& =(\mathbf{\Gamma }-\rho v^2\mathit{I})\cdot \mathit{u}\hfill \\ \hfill & =\left(\begin{array}{ccc}\hfill C_{11}{l}_1^2+C_{44}{l}_3^2-\rho v^2\hfill & \hfill 0\hfill & \hfill (C_{12}+C_{44})l_1{l}_3\hfill \\ \hfill 0\hfill & \hfill C_{44}-\rho v^2\hfill & \hfill 0\hfill \\ \hfill (C_{12}+C_{44})l_1{l}_3\hfill & \hfill 0\hfill & \hfill C_{44}{l}_1^2+C_{11}{l}_3^2-\rho v^2\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill u_1\hfill \\ \hfill u_2\hfill \\ \hfill u_3\hfill \end{array}\right).\hfill \end{array}(48)$

Combining with the equal speed criterion in eq. 18, i.e., C₁₁ = C₄₄, we obtain

$\begin{array}{cc}\hfill \mathbf{0}& =(\mathbf{\Gamma }-\rho v^2\mathit{I})\cdot \mathit{u}\hfill \\ \hfill & =\left(\begin{array}{ccc}\hfill C_{11}-\rho v^2\hfill & \hfill 0\hfill & \hfill (C_{12}+C_{11})l_1{l}_3\hfill \\ \hfill 0\hfill & \hfill C_{11}-\rho v^2\hfill & \hfill 0\hfill \\ \hfill (C_{12}+C_{11})l_1{l}_3\hfill & \hfill 0\hfill & \hfill C_{11}-\rho v^2\hfill \end{array}\right)\cdot \begin{array}{c}\hfill u_1\hfill \\ \hfill u_2\hfill \\ \hfill u_3\hfill \end{array}.\hfill \end{array}(49)$

This shows that the in-plane waves (u₁, u₃) are in general coupled together, and the out-of-plane wave u₂ is decoupled from the two in-plane polarizations.

For non-trivial solution to exist for in-plane wave velocities in eq. 49, the determinant must vanish. This leads to the following

${\rho }^2{v}^4-2C_{11}\rho v^2+C_{11}^2-{(C_{12}+C_{11})}^2{l}_1^2{l}_3^2=0.(50)$

This is a quadratic polynomial with respect to v². It has the discriminant as $\mathrm{\Delta }=4{\rho }^2{(C_{12}+C_{11})}^2{l}_1^2{l}_3^2\ge 0$, and the roots are

$v^2=\frac{C_{11}\pm |(C_{12}+C_{11})l_1{l}_3|}{\rho }.(51)$

For any linear material to be statically stable, it needs a positive strain energy function, and hence a positive-definite stiffness matrix (Ting, 1996), which leads to the following conditions:

$C_{11}>0\text{and}-C_{11}<C_{12}<C_{11}(52)$

Then, in order to determine the reflection angle(s) in this case, we apply Snell’s law for reflection

$\frac{{\omega }^{\text{I}}}{v^{\text{I}}}\sin ({\alpha }^{\text{I}})=\frac{{\omega }^{\text{R}}}{v^{\text{R}}}\sin ({\alpha }^{\text{R}}).(53)$

Here, the incidence angle is α^I = 45°. Combining it with ω^I = ω^R and $v^{\text{I}}=\sqrt{C_{11}/\rho }$, we arrive at

$\frac{1}{\sqrt{2C_{11}}}=\frac{\sin ({\alpha }^{\text{R}})}{\sqrt{C_{11}\pm |C_{12}+C_{11}|l_1{l}_3}}=\frac{\sin (\theta +45°)}{\sqrt{C_{11}\pm |C_{12}+C_{11}|l_1{l}_3}}(54)$

with the cosine directions,

$l_1=\cos (\theta ),l_3=\sin (\theta ).(55)$

Further simplification gives us,

$\sin (\theta )\cos (\theta )(2C_{11}\pm |C_{11}+C_{12}|)=0.(56)$

For θ ∈ (−45°, + 45°) with the positive-definite conditions of eq. 52, the only solution to above equation is

$\theta =0(57)$

which implies α^R = 45°. Therefore, there can be one reflection wave vector only, and the reflected wave will propagate along x-direction at the speed v^R = v^I. Hence, we can rewrite the reflection wave as,

${\mathit{u}}^{\text{R}}=\left(\begin{array}{c}\hfill m^{\text{R}}\hfill \\ \hfill n^{\text{R}}\hfill \\ \hfill l^{\text{R}}\hfill \end{array}\right)e^{\text{i}{k}^{\text{R}}x}\text{with}{k}^{\text{R}}=k^{\text{I}}.(58)$

For brevity, denoting the wave number as k^I = k^R = k, we obtain

${\mathit{u}}^{\text{I}}=\left(\begin{array}{c}\hfill m^{\text{I}}\hfill \\ \hfill n^{\text{I}}\hfill \\ \hfill l^{\text{I}}\hfill \end{array}\right)e^{\text{i}kz},{\mathit{u}}^{\text{R}}=\left(\begin{array}{c}\hfill m^{\text{R}}\hfill \\ \hfill n^{\text{R}}\hfill \\ \hfill l^{\text{R}}\hfill \end{array}\right)e^{\text{i}kx}.(59)$

The corresponding strain wave amplitudes are

${\mathit{\epsilon }}^{\text{I}}=\left(\begin{array}{c}\hfill {\epsilon }_{xx}^{\text{I}}\hfill \\ \hfill {\epsilon }_{yy}^{\text{I}}\hfill \\ \hfill {\epsilon }_{zz}^{\text{I}}\hfill \\ \hfill 2{\epsilon }_{yz}^{\text{I}}\hfill \\ \hfill 2{\epsilon }_{xz}^{\text{I}}\hfill \\ \hfill 2{\epsilon }_{xy}^{\text{I}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill l^{\text{I}}\text{i}k\hfill \\ \hfill n^{\text{I}}\text{i}k\hfill \\ \hfill m^{\text{I}}\text{i}k\hfill \\ \hfill 0\hfill \end{array}\right),{\mathit{\epsilon }}^{\text{R}}=\left(\begin{array}{c}\hfill {\epsilon }_{xx}^{\text{R}}\hfill \\ \hfill {\epsilon }_{yy}^{\text{R}}\hfill \\ \hfill {\epsilon }_{zz}^{\text{R}}\hfill \\ \hfill 2{\epsilon }_{yz}^{\text{R}}\hfill \\ \hfill 2{\epsilon }_{xz}^{\text{R}}\hfill \\ \hfill 2{\epsilon }_{xy}^{\text{R}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill m^{\text{R}}\text{i}k\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill l^{\text{R}}\text{i}k\hfill \\ \hfill n^{\text{R}}\text{i}k\hfill \end{array}\right).(60)$

And the stress wave amplitudes are

$\left(\begin{array}{c}\hfill {\sigma }_{xx}^{\text{I}}\hfill \\ \hfill {\sigma }_{yy}^{\text{I}}\hfill \\ \hfill {\sigma }_{zz}^{\text{I}}\hfill \\ \hfill {\sigma }_{yz}^{\text{I}}\hfill \\ \hfill {\sigma }_{xz}^{\text{I}}\hfill \\ \hfill {\sigma }_{xy}^{\text{I}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill C_{12}{l}^{\text{I}}\text{i}k\hfill \\ \hfill C_{12}{l}^{\text{I}}\text{i}k\hfill \\ \hfill C_{11}{l}^{\text{I}}\text{i}k\hfill \\ \hfill C_{11}{n}^{\text{I}}\text{i}k\hfill \\ \hfill C_{11}{m}^{\text{I}}\text{i}k\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{c}\hfill {\sigma }_{xx}^{\text{R}}\hfill \\ \hfill {\sigma }_{yy}^{\text{R}}\hfill \\ \hfill {\sigma }_{zz}^{\text{R}}\hfill \\ \hfill {\sigma }_{yz}^{\text{R}}\hfill \\ \hfill {\sigma }_{xz}^{\text{R}}\hfill \\ \hfill {\sigma }_{xy}^{\text{R}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill C_{11}{m}^{\text{R}}\text{i}k\hfill \\ \hfill C_{12}{m}^{\text{R}}\text{i}k\hfill \\ \hfill C_{12}{m}^{\text{R}}\text{i}k\hfill \\ \hfill 0\hfill \\ \hfill C_{11}{l}^{\text{R}}\text{i}k\hfill \\ \hfill C_{11}{n}^{\text{R}}\text{i}k\hfill \end{array}\right).(61)$

To analyze the normal and transverse elastic boundary condition, we introduce a local coordinate system x′ = Ψx specified by the transformation matrix,

$\mathbf{\Psi }=\left(\begin{array}{ccc}\hfill \cos (\phi )\hfill & \hfill 0\hfill & \hfill \sin (\phi )\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill -\sin (\phi )\hfill & \hfill 0\hfill & \hfill \cos (\phi )\hfill \end{array}\right)=\frac{\sqrt{2}}{2}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill \sqrt{2}\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)(62)$

where the φ = 45° as shown in Figure 4.

The general elastic boundary conditions in the local coordinate system are

${\sigma }_{z^{\prime }{x}^{\prime }}^0=K_{x^{\prime }}{u}_{x^{\prime }}^0,{\sigma }_{z^{\prime }{y}^{\prime }}^0=K_{y^{\prime }}{u}_{y^{\prime }}^0,{\sigma }_{z^{\prime }{z}^{\prime }}^0=K_{z^{\prime }}{u}_{z^{\prime }}^0.(63)$

where (K_x′, K_y′, K_z′) are components of distributed stiffness per unit area, and

${\sigma }_{z^{\prime }{x}^{\prime }}^0={\sigma }_{z^{\prime }{x}^{\prime }}^{\text{I}}+{\sigma }_{z^{\prime }{x}^{\prime }}^{\text{R}},{\sigma }_{z^{\prime }{y}^{\prime }}^0={\sigma }_{z^{\prime }{y}^{\prime }}^{\text{I}}+{\sigma }_{z^{\prime }{y}^{\prime }}^{\text{R}},{\sigma }_{z^{\prime }{z}^{\prime }}^0={\sigma }_{z^{\prime }{z}^{\prime }}^{\text{I}}+{\sigma }_{z^{\prime }{z}^{\prime }}^{\text{R}}.(64)$

$u_{x^{\prime }}^0=u_{x^{\prime }}^{\text{I}}+u_{x^{\prime }}^{\text{R}},u_{y^{\prime }}^0=u_{y^{\prime }}^{\text{I}}+u_{y^{\prime }}^{\text{R}},u_{z^{\prime }}^0=u_{z^{\prime }}^{\text{I}}+u_{z^{\prime }}^{\text{R}}.(65)$

are components of total stress and total displacement on the boundary surface.

We next perform coordinate transforms using

${\mathit{\sigma }}^{\prime }={\mathbf{\Psi }\cdot \mathbf{\sigma }\cdot \mathbf{\Psi }}^T,{\mathit{u}}^{\prime }=\mathbf{\Psi }\cdot \mathbf{u}.(66)$

In the local coordinates, x′, we obtain

${{\mathit{\sigma }}^{\prime }}^{\text{I}}=\frac{\text{i}k}{2}\left(\begin{array}{ccc}\hfill (C_{11}+C_{12})l^{\text{I}}+2C_{11}{m}^{\text{I}}\hfill & \hfill \sqrt{2}{C}_{11}{n}^{\text{I}}\hfill & \hfill (C_{11}-C_{12})l^{\text{I}}\hfill \\ \hfill \sqrt{2}{C}_{11}{n}^{\text{I}}\hfill & \hfill 2C_{12}{l}^{\text{I}}\hfill & \hfill \sqrt{2}{C}_{11}{n}^{\text{I}}\hfill \\ \hfill (C_{11}-C_{12})l^{\text{I}}\hfill & \hfill \sqrt{2}{C}_{11}{n}^{\text{I}}\hfill & \hfill (C_{11}+C_{12})l^{\text{I}}-2C_{11}{m}^{\text{I}}\hfill \end{array}\right),(67)$

${{\mathit{u}}^{\prime }}^{\text{I}}=\frac{\sqrt{2}}{2}\left(\begin{array}{c}\hfill l^{\text{I}}+m^{\text{I}}\hfill \\ \hfill \sqrt{2}{n}^{\text{I}}\hfill \\ \hfill l^{\text{I}}-m^{\text{I}}\hfill \end{array}\right).(68)$

Similarly, the local stress and displacement of reflection wave are,

${{\mathit{\sigma }}^{\prime }}^{\text{R}}=\frac{\text{i}k}{2}\left(\begin{array}{ccc}\hfill (C_{11}+C_{12})m^{\text{R}}+2C_{11}{l}^{\text{R}}\hfill & \hfill \sqrt{2}{C}_{11}{n}^{\text{R}}\hfill & \hfill (C_{12}-C_{11})m^{\text{R}}\hfill \\ \hfill \sqrt{2}{C}_{11}{n}^{\text{R}}\hfill & \hfill 2C_{12}{m}^{\text{R}}\hfill & \hfill -\sqrt{2}{C}_{11}{n}^{\text{R}}\hfill \\ \hfill (C_{12}-C_{11})m^{\text{R}}\hfill & \hfill -\sqrt{2}{C}_{11}{n}^{\text{R}}\hfill & \hfill (C_{11}+C_{12})m^{\text{R}}-2C_{11}{l}^{\text{R}}\hfill \end{array}\right),(69)$

${{\mathit{u}}^{\prime }}^{\text{R}}=\frac{\sqrt{2}}{2}\left(\begin{array}{c}\hfill l^{\text{R}}+m^{\text{R}}\hfill \\ \hfill \sqrt{2}{n}^{\text{R}}\hfill \\ \hfill l^{\text{R}}-m^{\text{R}}\hfill \end{array}\right).(70)$

Substituting the stress and displacement components eqs  67 –eqs  70 into the boundary conditions eqs  64,65, we obtain

$\frac{\text{i}k}{2}[(C_{11}-C_{12})l^{\text{I}}+(C_{12}-C_{11})m^{\text{R}}]=K_{x^{\prime }}\frac{\sqrt{2}}{2}(l^{\text{I}}+m^{\text{I}}+l^{\text{R}}+m^{\text{R}}),(71)$

$\frac{\text{i}k\sqrt{2}}{2}[C_{11}{n}^{\text{I}}-C_{11}{n}^{\text{R}}]=K_{y^{\prime }}(n^{\text{I}}+n^{\text{R}}),(72)$

$\frac{\text{i}k}{2}[(C_{11}+C_{12})l^{\text{I}}-2C_{11}{m}^{\text{I}}+(C_{11}+C_{12})m^{\text{R}}-2C_{11}{l}^{\text{R}}]=K_{z^{\prime }}\frac{\sqrt{2}}{2}(l^{\text{I}}-m^{\text{I}}+l^{\text{R}}-m^{\text{R}}).(73)$

Then, we can solve the system of eqs 71–73 for the complex-valued amplitude components of the reflected wave:

$m^{\text{R}}=-\frac{\left[K_{x^{\prime }}({\kappa }_{+}-K_{z^{\prime }})-\left(K_{z^{\prime }}+2C_{11}\frac{\text{i}k}{\sqrt{2}}\right)({\kappa }_{-}-K_{x^{\prime }})\right]l^{\text{I}}+2K_{x^{\prime }}{K}_{z^{\prime }}{m}^{\text{I}}}{K_{x^{\prime }}(K_{z^{\prime }}+{\kappa }_{+})+\left(K_{z^{\prime }}+2C_{11}\frac{\text{i}k}{\sqrt{2}}\right)({\kappa }_{-}+K_{x^{\prime }})},(74)$

$n^{\text{R}}=\frac{\frac{\text{i}k}{\sqrt{2}}{C}_{11}-K_{y^{\prime }}}{\frac{\text{i}k}{\sqrt{2}}{C}_{11}+K_{y^{\prime }}}{n}^{\text{I}},(75)$

$l^{\text{R}}=\frac{2({\kappa }_{+}{\kappa }_{-}-K_{x^{\prime }}{K}_{z^{\prime }})l^{\text{I}}+\left[\left(K_{z^{\prime }}-2C_{11}\frac{\text{i}k}{\sqrt{2}}\right)({\kappa }_{-}+K_{x^{\prime }})-K_{x^{\prime }}({\kappa }_{+}+K_{z^{\prime }})\right]m^{\text{I}}}{K_{x^{\prime }}(K_{z^{\prime }}+{\kappa }_{+})+\left(K_{z^{\prime }}+2C_{11}\frac{\text{i}k}{\sqrt{2}}\right)({\kappa }_{-}+K_{x^{\prime }})},(76)$

where

${\kappa }_{+}=\frac{\text{i}k}{\sqrt{2}}(C_{11}+C_{12}),{\kappa }_{-}=\frac{\text{i}k}{\sqrt{2}}(C_{11}-C_{12}).(77)$

We can also write in the form of a reflection matrix (Zoeppritz, 1919; Ursin and Tjäland, 1996).

$\left(\begin{array}{c}\hfill m^{\text{R}}\hfill \\ \hfill n^{\text{R}}\hfill \\ \hfill l^{\text{R}}\hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill R_{mm}\hfill & \hfill 0\hfill & \hfill R_{ml}\hfill \\ \hfill 0\hfill & \hfill R_{nn}\hfill & \hfill 0\hfill \\ \hfill R_{lm}\hfill & \hfill 0\hfill & \hfill R_{ll}\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill m^{\text{I}}\hfill \\ \hfill n^{\text{I}}\hfill \\ \hfill l^{\text{I}}\hfill \end{array}\right).(78)$

where

$\begin{array}{cc}\hfill & R_{mm}=-\frac{2K_{x^{\prime }}{K}_{z^{\prime }}}{D}\hfill \\ \hfill & R_{ml}=\frac{K_{z^{\prime }}{\kappa }_{-}-K_{x^{\prime }}{\kappa }_{+}+\sqrt{2}{C}_{11}\text{i}k({\kappa }_{-}-K_{x^{\prime }})}{D}\hfill \\ \hfill & R_{nn}=\frac{\frac{\text{i}k}{\sqrt{2}}{C}_{11}-K_{y^{\prime }}}{\frac{\text{i}k}{\sqrt{2}}{C}_{11}+K_{y^{\prime }}}\hfill \\ \hfill & R_{lm}=\frac{K_{z^{\prime }}{\kappa }_{-}-K_{x^{\prime }}{\kappa }_{+}-\sqrt{2}{C}_{11}\text{i}k({\kappa }_{-}+K_{x^{\prime }})}{D}\hfill \\ \hfill & R_{ll}=\frac{2({\kappa }_{+}{\kappa }_{-}-K_{x^{\prime }}{K}_{z^{\prime }})}{D}\hfill \end{array}(79)$

with denominator $D=K_{x^{\prime }}(K_{z^{\prime }}+{\kappa }_{+})+(K_{z^{\prime }}+2C_{11}\frac{\text{i}k}{\sqrt{2}})({\kappa }_{-}+K_{x^{\prime }})$. We note that R_ml ≠ R_lm, which means that the complex-valued reflection matrix is not Hermitian. A closer scrutiny reveals that the amplitudes of R_ml and R_lm are always the same. The two complex-valued reflective coefficients only differ in their phase angles.

We also note that the term R_nn for the out-of-xz-plane wave is independent and very similar to the normal incidence scenario, as shown in eqs 38,40 and Figure  2. All other terms in eq. 79 are illustrated in Figure  5 to show how they change with the wave number, k, and the boundary stiffness ratio, K_z′/K_x′. We observe in Figure  5B that both R_ml and R_lm shows a phase jump of 180°. This is because of two reasons: 1) The small wave number k = 0.001 leads to the fact that both R_ml and R_lm are almost purely imaginary; and 2) At the boundary stiffness ratio of K_z′/K_x′ = 3, values transition from a negative imaginary number to a positive imaginary number. This results in the 180° phase jump.

FIGURE 5

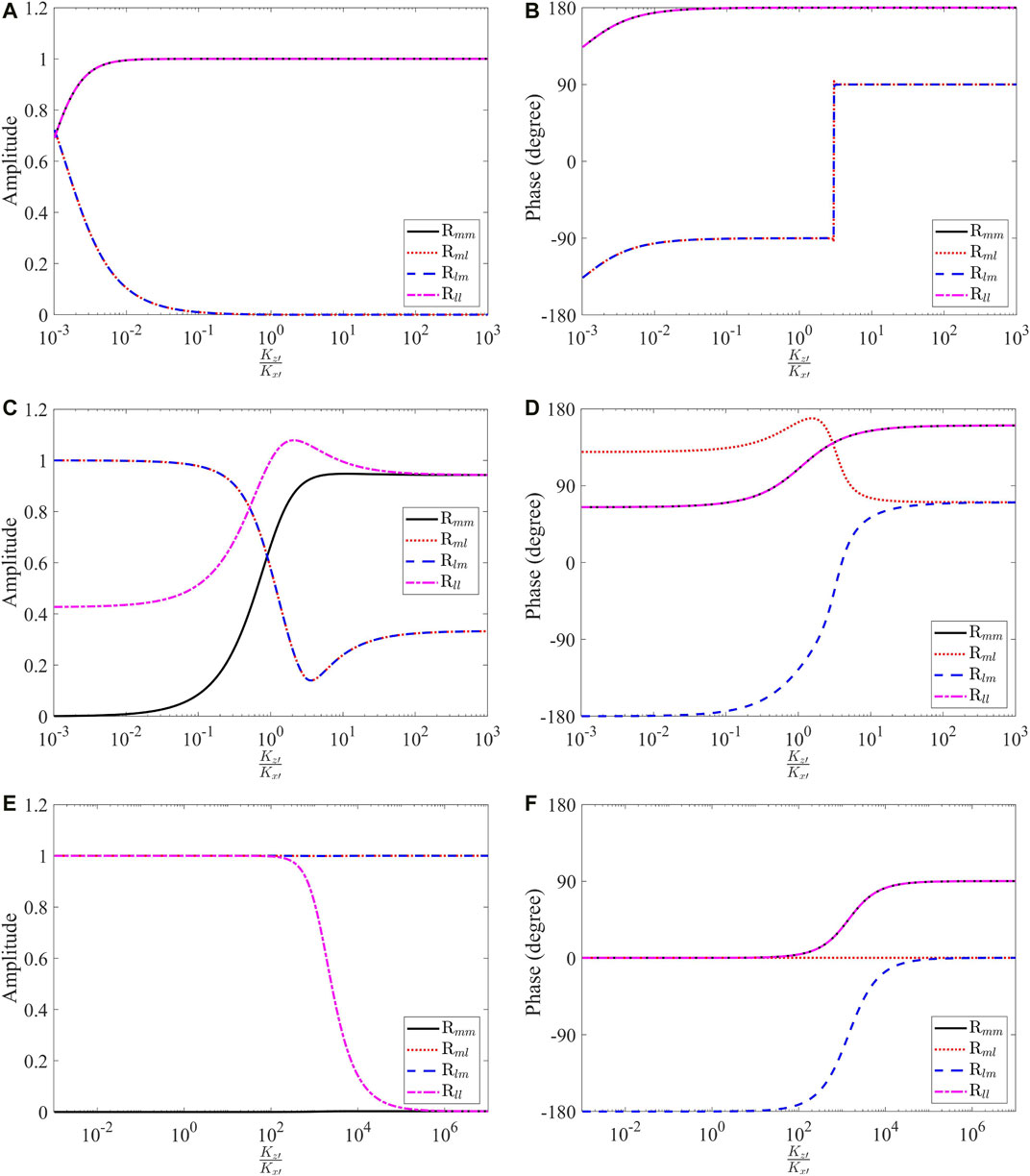
FIGURE 5. The amplitude and phase of reflection matrix elements under different wave numbers k at C_r = C₁₂/C₁₁ = 0. (A,B) Amplitude and phase at k = 0.001, (C,D) Amplitude and phase at k = 1, (E,F) Amplitude and phase at k = 1,000.

Clearly, the out-of-xz-plane wave n^R only depends on n^I:

$n^{\text{R}}=n^{\text{I}}\text{for}{K}_{y^{\prime }}=0,(80)$

$n^{\text{R}}=-n^{\text{I}}\text{for}{K}_{y^{\prime }}=\infty .(81)$

The four extreme cases for in-xz-plane wave polarizations are:

Case I (Figure 4B), K_x′ → ∞, K_z′ → ∞:

$m^{\text{R}}=-m^{\text{I}},l^{\text{R}}=-l^{\text{I}},\Rightarrow {\mathit{s}}^{\text{R}}={\mathit{s}}^{\text{I}}.(82)$

Case II (Figure 4C), K_x′ → 0, K_z′ → 0:

$m^{\text{R}}=l^{\text{I}},l^{\text{R}}=-m^{\text{I}}+\left(\frac{C_{11}+C_{12}}{C_{11}}\right)l^{\text{I}}=-m^{\text{I}}+\left(1+C_r\right)m^{\text{R}}\Rightarrow {\mathit{s}}^{\text{R}}={\mathit{s}}^{\text{I}}(83)$

with C_r = C₁₂/C₁₁. Here, the second term in l^R is associated with l^I, and m^R = l^I. So, this term does not have any contribution to the circularly rolling polarization, and it gives rise to an additional linearly polarized wave. Consequently, the spin is still exactly preserved, but the overall reflected wave has a elliptically rolling polarization.

Case III (Figure 4D), K_x′ → ∞, K_z′ → 0:

$m^{\text{R}}=-l^{\text{I}},l^{\text{R}}=-m^{\text{I}}\Rightarrow {\mathit{s}}^{\text{R}}=-{\mathit{s}}^{\text{I}}.(84)$

Case IV (Figure 4E), K_x′ → 0, K_z′ → ∞:

$m^{\text{R}}=l^{\text{I}},l^{\text{R}}=m^{\text{I}}\Rightarrow {\mathit{s}}^{\text{R}}=-{\mathit{s}}^{\text{I}}.(85)$

As illustrated in Figure  4C, the results in eq. 83 for Case II are special and remarkable. The reflected wave from the free boundary is different from all other cases. However, the reflected spin density is indeed still the same to that of the incidence wave. The reason is that the additional term in l^R does not contribute to the circularly rolling polarization. To further investigate this especially interesting case, we calculate the polarization of reflected waves with different ratios of C_r = C₁₂/C₁₁ and plot the result in Figure 6. Note that the ratios of C_r = −1 in Figure 6A and C_r = 1 in Figure 6E are actually extreme scenarios not attainable in statically stable materials due the positive definite conditions listed in eq. 52.

FIGURE 6

FIGURE 6. In the oblique reflection at 45°, elliptically rolling polarizations of the reflected waves from the free boundary may appear due to different material stiffness constants C₁₁ and C₁₂. An incident spin which is the same of that shown (A) is assumed throughout. (A) also represents the purely circularly rolling polarization for C_r = −1. (B–F) show the elliptically rolling polarizations for the cases of C_r = −0.5, C_r = 0, C_r = 0.5 and C_r = 1, respectively. Note that all polarizations are scaled for the purpose of clearly demonstrating differences in elliptical eccentricity.

7 The Oblique Incidence and Reflection at Arbitrary Angle

Next, we look into the situation with an arbitrary incidence angle. From Snell’s law eq. 53, we can obtain

$\frac{\sin ({\alpha }^{\text{I}})}{\sqrt{C_{11}}}=\frac{\sin ({\alpha }^{\text{R}})}{\sqrt{C_{11}\pm (C_{12}+C_{11})l_1{l}_3}}(86)$

where l₁ = cos(θ), l₃ = sin(θ). Noticed from Figure 4A that the incidence angle is identical to the rotation angle, i.e., α^I = φ and then the reflection angle α^R = π/2 − φ + θ. The reflection angle α^R is the solution of the transcendental equation depending on the incidence angle α^I and the material constant ratio C_r = C₁₂/C₁₁:

$\sqrt{1\pm (1+C_r)\sin ({\alpha }^{\text{R}}+{\alpha }^{\text{I}}-\pi /2)\cos ({\alpha }^{\text{R}}+{\alpha }^{\text{I}}-\pi /2)}\sin ({\alpha }^{\text{I}})=\sin ({\alpha }^{\text{R}})(87)$

where “±” gives rise to two different reflected wave modes. In general, those two modes have two different reflection angles.

Next, we numerically solve eq. 87 for the reflection angle α^R and illustrate the results in Figure 7. The points P₁ and P₂ in the plots indicate the cases of the normal incidence and the 45° incidence, respectively. Both cases have been thoroughly discussed in previous sections. The next critical point P₃ is where the reflection angle α^R → π/2 for Mode 1. Plugging α^R = π/2 into eq. 87, we obtain:

${(1+C_r)}^2{\sin }^6({\alpha }_3^{\text{I}})+{\sin }^2({\alpha }_3^{\text{I}})-1=0.(88)$

FIGURE 7

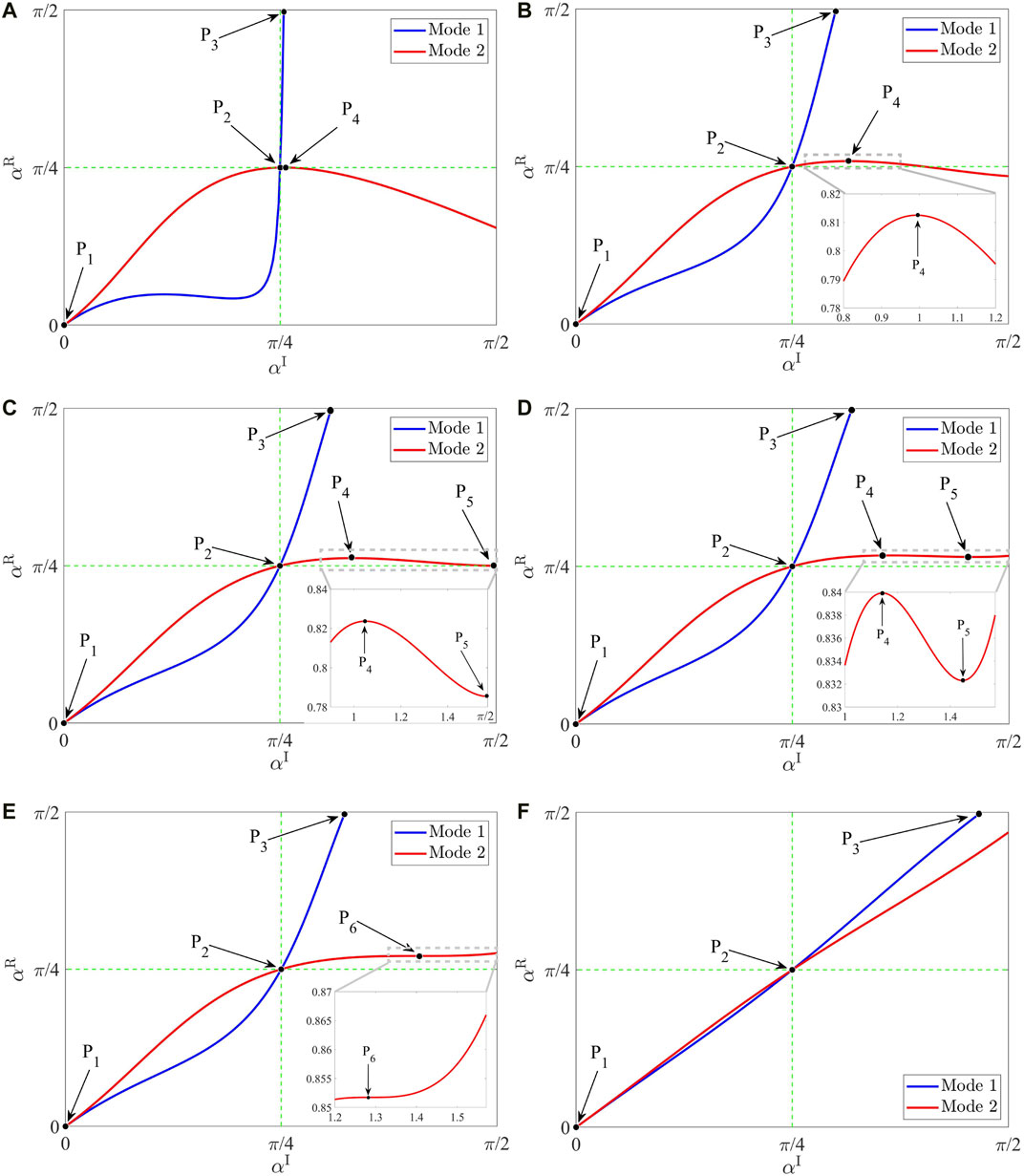
FIGURE 7. The reflection angle α^R of two modes with respect to the incidence angle α^I. (A) C_r = 0.9, (B) C_r = 0.1, (C) C_r = 0, (D) C_r = −0.1, (E) C_r = −0.149452, (F) C_r = −0.9.

Thus, we arrive at the analytical solution of the above equation,

${\alpha }_3^{\text{I}}=\arcsin \left(\sqrt{\sqrt[3]{\frac{1}{2{(1+C_r)}^2}+\sqrt{\mathrm{\Delta }}}+\sqrt[3]{\frac{1}{2{(1+C_r)}^2}-\sqrt{\mathrm{\Delta }}}}\right)(89)$

with

$\mathrm{\Delta }=\frac{1}{4{(1+C_r)}^4}+\frac{1}{27{(1+C_r)}^6}>0.(90)$

We know that, with Δ > 0, the cubic function always has one real root and two complex conjugate roots. In this case, we can only obtain one critical angle ${\alpha }_3^{\text{I}}$. Therefore, we conclude that, for incidence angle larger than the critical angle ${\alpha }_3^{\text{I}}$, the reflection wave of Mode 1 will no longer exist.

Here, from eq. 52 we have the constraint −1 < C_r = C₁₂/C₁₁ < 1. Hence, we investigate all values of C_r within this range and find the following four representative scenarios for Mode 2 of the reflected waves:

• For 0 < C_r < 1, as shown in Figures  7A,B, we have one local maximum (point P₄) and no local minimum for Mode 2. The reflection angle α^R will increase together with the incidence angle α^I until it reaches to the maximum at point P₄. Then, the anomalous trend appears, and the reflection angle α^R will decrease if we further increase the incidence angle α^I. Consequently, for Mode 2, we may have two different incidence angles with the same reflection angle.

• For −0.149 < C_r ≤ 0, as shown in Figures  7C,D, we have one local maximum (point P₄) and one local minimum (point P₅). Remarkably, as shown in the inset of Figure 7D, we may have three different incidence angles with the same reflection angle for Mode 2. Also, we note that, with the decreasing value of C_r, point P₄ and point P₅ move closer to each other.

• For C_r = −0.149, as shown in Figure 7E, we have no local maximum, no local minimum, but a saddle point (point P₆). This saddle point P₆ is the result of point P₄ and point P₅ merging together.

• For −1 < C_r < −0.149452 as shown in Figure 7F, we have a monotonic curve for Mode 2. The reflection angle α^R always increases with the increasing incidence angle α^I. And this is the normal phenomenon generally understood.

In the first two scenarios listed above, we have the anomalous trend phenomenon: The reflection angle α^R does not have a monotonic relationship with the incidence angle α^I. This may provide us with a new technique to control the direction of reflected waves.

Furthermore, we can take the derivative of both sides of eq. 87 with respect to the incidence angle α^I and obtain the changing rate of reflection angle α^R of Mode 2,

$\frac{\text{d}{\alpha }^{\text{R}}}{\text{d}{\alpha }^{\text{I}}}=\frac{\left[1-\frac{1+C_r}{2}\sin (2{\alpha }^{\text{R}}+2{\alpha }^{\text{I}})\right]\sin (2{\alpha }^{\text{I}})-(1+C_r){\sin }^2({\alpha }^{\text{I}})\cos (2{\alpha }^{\text{R}}+2{\alpha }^{\text{I}})}{\sin (2{\alpha }^{\text{R}})+(1+C_r){\sin }^2({\alpha }^{\text{I}})\cos (2{\alpha }^{\text{R}}+2{\alpha }^{\text{I}})}(91)$

We note that this derivative of α^R with respect to the α^I is the root of another transcendental equation and rarely has closed-form solution. Thus, we solve it numerically and plot the results in Figure 8. The same four represented scenarios discussed above can be easily categorized here as different number of roots of eq. 91. The results shown in Figures 7, 8 are consistent with each other.

FIGURE 8

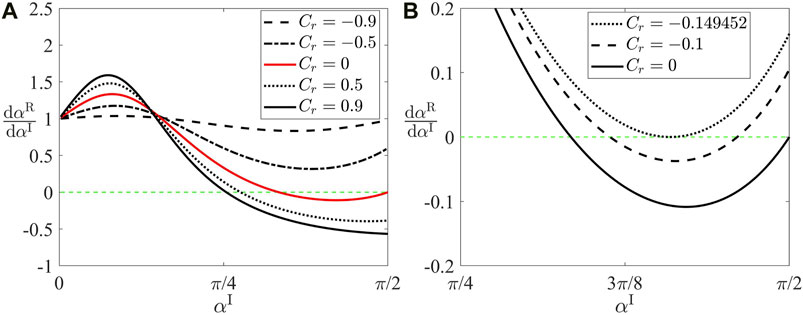
FIGURE 8. The derivative of reflection angle α^R with respect to the incidence angle α^I. (A) Whole range of C_r, (B) Zoom-in range of C_r with two zero roots.

8 Conclusion

Cubic materials are anisotropic elastic materials that satisfy the symmetry requirements illustrated in Figure 1, and their stiffness matrix is given by eq. 13. If the equal-speed criteria for longitudinal and transverse waves, as given in eq. 18, also holds in a cubic material, then we can have stable propagation of any spin angular momentum carried by bulk elastic waves. In this paper, we focus on rolling waves, which have a spin vector orthogonal to its wave vector, in cubic materials. We investigate the reflections of rolling waves incident either normally or obliquely at an elastically supported flat boundary. Behaviors of spin-preserving, spin-flipping, and general arbitrary phase shifts are shown by adjusting the boundary conditions. This work provides a new approach to manipulating bulk elastic wave spins. Several other key findings are summarized below:

1) For the normal incidence of rolling waves, the reflection is spin-preserving at both the fixed rigid boundary and the free boundary, while being spin-flipping at both the fixed-free and free-fixed boundaries. Most generally, we can even introduce the arbitrary phase shifts between reflection and incidence waves by adjusting the elastic boundary conditions.

2) For oblique incidence at 45°, we prove that, contrary to the general anisotropic case, there will be only 1 reflected wave with a unique reflection angle of 45°.

3) With the 45° incidence, the reflection is spin-preserving at a fixed rigid boundary, while being spin-flipping at both fixed-free and free-fixed boundaries. The free boundary is a uniquely special case here: While the reflection is still spin-preserving, depending on the cubic material constant ratio, C₁₂/C₁₁, it will also introduce an additional linearly polarized part. Hence, an incidence wave with circularly rolling polarization will result in a reflected wave with elliptically rolling polarization.

4) For an arbitrary incidence angle, we showed that each incidence wave will in general result in two reflected wave modes with different reflection angles. One of the mode (Mode 1 in Figure 7) exists only when the incidence angle is less than a critical value ${\alpha }_3^{\text{I}}$. Also, The other mode (Mode 2 in Figure 7) may show anomalous trend.

5) We developed a new way to manipulate the elastic wave spin. Further, the present study can be extended to more general cases, i.e., arbitrary incidence angle for reflection and refraction problem, the reflection matrix properties of arbitrary incidence angle, visco-elastically supported boundary condition, or breaking the limit of statically stable materials by using metamaterials.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

PZ is the primary contributor to this study and this manuscript. PW is the secondary contributor to this study and this manuscript.

Funding

This work was supported by start-up funds of the Dept. Mechanical Engineering at Univ. Utah.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The support and resources from the Center for High Performance Computing at Univ. Utah are gratefully acknowledged.

References

Achenbach, J. (2012). Wave Propagation in Elastic Solids. Amsterdam: Elsevier.

An, K., Litvinenko, A., Kohno, R., Fuad, A., Naletov, V., Vila, L., et al. (2020). Coherent Long-Range Transfer of Angular Momentum Between Magnon Kittel Modes by Phonons. Phys. Rev. B 101, 060407. doi:10.1103/physrevb.101.060407

CrossRef Full Text | Google Scholar

Ashcroft, N. W., and Mermin, N. D. (1976). Solid State Physics. New York London): Holt, Rinehart and Winston.

Authier, A. (2003). International Tables for Crystallography: Volume D: Physical Properties of Crystals. Wiley Online Library.

Bedford, A., and Drumheller, D. (1994). Elastic Wave Propagation. Amsterdam: John Wileg g Sons, 151–165.

Berry, M. V. (2009). Optical Currents. J. Opt. A: Pure Appl. Opt. 11, 094001. doi:10.1088/1464-4258/11/9/094001

CrossRef Full Text | Google Scholar

Borcherds, P. H. (1973). The Scattering of Light by Elastic Waves in Cubic Crystals. Optica Acta Int. J. Opt. 20, 147–159. doi:10.1080/713818743

CrossRef Full Text | Google Scholar

Bückmann, T., Schittny, R., Thiel, M., Kadic, M., Milton, G. W., and Wegener, M. (2014). On Three-Dimensional Dilational Elastic Metamaterials. New J. Phys. 16, 033032. doi:10.1088/1367-2630/16/3/033032

CrossRef Full Text | Google Scholar

Burns, L., Bliokh, K. Y., Nori, F., and Dressel, J. (2020). Acoustic versus Electromagnetic Field Theory: Scalar, Vector, Spinor Representations and the Emergence of Acoustic Spin. New J. Phys. 22, 053050. doi:10.1088/1367-2630/ab7f91

CrossRef Full Text | Google Scholar

Carcione, J. M. (2007). Wave fields in Real media: Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic media. Amsterdam: Elsevier.

Chadwick, P., and Wilson, N. (1992). The Behaviour of Elastic Surface Waves Polarized in a Plane of Material Symmetry. Iii. Orthorhombic and Cubic media. Proc. R. Soc. Lond. A. 438, 225–247. doi:10.1098/rspa.1992.0104

CrossRef Full Text | Google Scholar

Chen, Y., Kadic, M., and Wegener, M. (2021). Chiral Triclinic Metamaterial Crystals Supporting Isotropic Acoustical Activity and Isotropic Chiral Phonons. Proc. R. Soc. A. 477, 20200764. doi:10.1098/rspa.2020.0764

CrossRef Full Text | Google Scholar

Chen, Y., Li, X., Nassar, H., Norris, A. N., Daraio, C., and Huang, G. (2019). Nonreciprocal Wave Propagation in a Continuum-Based Metamaterial with Space-Time Modulated Resonators. Phys. Rev. Appl. 11, 064052. doi:10.1103/physrevapplied.11.064052

CrossRef Full Text | Google Scholar

Dirrenberger, J., Forest, S., and Jeulin, D. (2013). Effective Elastic Properties of Auxetic Microstructures: Anisotropy and Structural Applications. Int. J. Mech. Mater. Des. 9, 21–33. doi:10.1007/s10999-012-9192-8

CrossRef Full Text | Google Scholar

Every, A. G. (2015). Supersonic Surface Acoustic Waves on the 001 and 110 Surfaces of Cubic Crystals. The J. Acoust. Soc. America 138, 2937–2944. doi:10.1121/1.4934557

CrossRef Full Text | Google Scholar

Favre, J., Lohmuller, P., Piotrowski, B., Kenzari, S., Laheurte, P., and Meraghni, F. (2018). A Continuous Crystallographic Approach to Generate Cubic Lattices and its Effect on Relative Stiffness of Architectured Materials. Additive Manufacturing 21, 359–368. doi:10.1016/j.addma.2018.02.020

CrossRef Full Text | Google Scholar

Frenzel, T., Kadic, M., and Wegener, M. (2017). Three-Dimensional Mechanical Metamaterials with a Twist. Science 358, 1072–1074. doi:10.1126/science.aao4640

PubMed Abstract | CrossRef Full Text | Google Scholar

Graff, K. F. (2012). Wave Motion in Elastic Solids. Amsterdam: Courier Corporation.

Holanda, J., Maior, D. S., Azevedo, A., and Rezende, S. M. (2018). Detecting the Phonon Spin in Magnon-Phonon Conversion Experiments. Nat. Phys 14, 500–506. doi:10.1038/s41567-018-0079-y

CrossRef Full Text | Google Scholar

Lee, H. J., Lee, J. R., Moon, S. H., Je, T. J., Jeon, E. C., Kim, K., et al. (2017). Off-Centered Double-Slit Metamaterial for Elastic Wave Polarization Anomaly. Sci. Rep. 7, 1–13. doi:10.1038/s41598-017-15746-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Lohmuller, P., Favre, J., Kenzari, S., Piotrowski, B., Peltier, L., and Laheurte, P. (2019). Architectural Effect on 3d Elastic Properties and Anisotropy of Cubic Lattice Structures. Mater. Des. 182, 108059. doi:10.1016/j.matdes.2019.108059

CrossRef Full Text | Google Scholar

Long, Y., Ge, H., Zhang, D., Xu, X., Ren, J., Lu, M.-H., et al. (2020). Symmetry Selective Directionality in Near-Field Acoustics. Natl. Sci. Rev. 7, 1024–1035. doi:10.1093/nsr/nwaa040

CrossRef Full Text | Google Scholar

Long, Y., Ren, J., and Chen, H. (2018). Intrinsic Spin of Elastic Waves. Proc. Natl. Acad. Sci. USA 115, 9951–9955. doi:10.1073/pnas.1808534115

PubMed Abstract | CrossRef Full Text | Google Scholar

Mielnicki, J. (1972). Elastic Waves in {100}, {110}, and {111} Planes of Cubic Crystals. IEEE Trans. Son. Ultrason. 19, 15–17. doi:10.1109/t-su.1972.29636

CrossRef Full Text | Google Scholar

Norris, A. N. (2006). Poisson's Ratio in Cubic Materials. Proc. R. Soc. A. 462, 3385–3405. doi:10.1098/rspa.2006.1726

CrossRef Full Text | Google Scholar

Rückriegel, A., Streib, S., Bauer, G. E. W., and Duine, R. A. (2020). Angular Momentum Conservation and Phonon Spin in Magnetic Insulators. Phys. Rev. B 101, 104402. doi:10.1103/physrevb.101.104402

CrossRef Full Text | Google Scholar

Schoenberg, M. (1980). Elastic Wave Behavior Across Linear Slip Interfaces. J. Acoust. Soc. America 68, 1516–1521. doi:10.1121/1.385077

CrossRef Full Text | Google Scholar

Shi, C., Zhao, R., Long, Y., Yang, S., Wang, Y., Chen, H., et al. (2019). Observation of Acoustic Spin. Natl. Sci. Rev. 6, 707–712. doi:10.1093/nsr/nwz059

CrossRef Full Text | Google Scholar

Shi, X., and Yang, J. (2020). Spin-1 Weyl Point and Surface Arc State in a Chiral Phononic Crystal. Phys. Rev. B 101, 214309. doi:10.1103/physrevb.101.214309

CrossRef Full Text | Google Scholar

Stoneley, R. (1955). The Propagation of Surface Elastic Waves in a Cubic Crystal. Proc. R. Soc. Lond. A. 232, 447–458. doi:10.1098/rspa.1955.0230

CrossRef Full Text | Google Scholar

Tancogne-Dejean, T., and Mohr, D. (2018). Elastically-Isotropic Elementary Cubic Lattices Composed of Tailored Hollow Beams. Extreme Mech. Lett. 22, 13–18. doi:10.1016/j.eml.2018.04.005

CrossRef Full Text | Google Scholar

Thomas, T. Y. (1966). Longitudinal Waves in Cubic Crystals. Proc. Natl. Acad. Sci. 55, 1011–1014. doi:10.1073/pnas.55.5.1011

PubMed Abstract | CrossRef Full Text | Google Scholar

Ting, T. C. T. (1996). Positive Definiteness of Anisotropic Elastic Constants. Maths. Mech. Sol. 1, 301–314. doi:10.1177/108128659600100302

CrossRef Full Text | Google Scholar

Toftul, I. D., Bliokh, K. Y., Petrov, M. I., and Nori, F. (2019). Acoustic Radiation Force and Torque on Small Particles as Measures of the Canonical Momentum and Spin Densities. Phys. Rev. Lett. 123, 183901. doi:10.1103/physrevlett.123.183901

PubMed Abstract | CrossRef Full Text | Google Scholar

Ursin, B., and Tjåland, E. (1996). The Information Content of the Elastic Reflection Matrix. Geophys. J. Int. 125, 214–228. doi:10.1111/j.1365-246x.1996.tb06547.x

CrossRef Full Text | Google Scholar

Vavrycuk, V., and Psencík, I. (1998). Pp-Wave Reflection Coefficients in Weakly Anisotropic Elastic media. Geophysics 63, 2129–2141.

Google Scholar

Wang, L., and Liu, H.-T. (2020). 3D Compression-Torsion Cubic Mechanical Metamaterial with Double Inclined Rods. Extreme Mech. Lett. 37, 100706. doi:10.1016/j.eml.2020.100706

CrossRef Full Text | Google Scholar

Wang, S., Ma, G., and Chan, C. T. (2018). Topological Transport of Sound Mediated by Spin-Redirection Geometric Phase. Sci. Adv. 4, eaaq1475. doi:10.1126/sciadv.aaq1475

PubMed Abstract | CrossRef Full Text | Google Scholar

Weeger, O. (2021). Numerical Homogenization of Second Gradient, Linear Elastic Constitutive Models for Cubic 3d Beam-Lattice Metamaterials. Int. J. Sol. Structures 224, 111037. doi:10.1016/j.ijsolstr.2021.03.024

CrossRef Full Text | Google Scholar

Zhang, P., Kern, C., Sun, S., Weitz, D. A., and Wang, P. (2020). Rolling Waves with Non-Paraxial Phonon Spins. arXiv preprint arXiv:2009.13014

Google Scholar

Zhang, P., Wei, P., and Li, Y. (2017). Reflection of Longitudinal Displacement Wave at the Viscoelastically Supported Boundary of Micropolar Half-Space. Meccanica 52, 1641–1654. doi:10.1007/s11012-016-0514-z

CrossRef Full Text | Google Scholar

Zhu, H., Yi, J., Li, M.-Y., Xiao, J., Zhang, L., Yang, C.-W., et al. (2018). Observation of Chiral Phonons. Science 359, 579–582. doi:10.1126/science.aar2711

PubMed Abstract | CrossRef Full Text | Google Scholar

Zoeppritz, K. (1919). Erdbebenwellen viii b, uber reflexion and durchgang seismischer wellen durch unstetigkeisflachen. Gottinger Nachr 1, 66–84.

Google Scholar

Zuo, Q. H., and Hjelmstad, K. D. (1997). Bounds and Approximations for Elastic Wave Speeds in Cubic Crystals. J. Acoust. Soc. America 101, 3415–3420. doi:10.1121/1.418381

CrossRef Full Text | Google Scholar