An Insight on the Estimation of Wave Propagation Constants in an Orthogonal Grid of a Simple Line-Supported Periodic Plate Using a Finite Element Mathematical Model

This article describes the propagation of free waves in a two-dimensional periodic plate using the finite element (FE) method. The advantage of periodic structure analysis is that all the dynamic properties of a finite structure are derived from a single phase-frequency curve or surface. Infinite plates are considered as a combination of periodic plates on an orthogonal array of simple, evenly spaced line supports. A single periodic unit of the system is represented by a more accurate high-precision arbitrary triangular shallow shell FE model to find the plane wave frequency in terms of the propagation constants of the 2D periodic plate. Only the purely propagating waves with no attenuation are considered here. The natural frequency of the infinite plate was obtained for different propagation constants in the two directions of the plate. The results are compared with the literature data. The bounding frequency of the propagation surface is compared to the data published from single square and rectangular plates with different edge boundary conditions. In addition, the natural frequency of the plate supported by finite line support with spans N_x (x-direction) and N_y (y-direction) is compared with the frequency obtained from the propagation curve by the discretization principle. The comparison is seen to be very close. It is found that the current PS-FEM approach can be used to generate dispersion relations with reasonable accuracy.

1 Introduction

The application of the wave propagation approach to the dynamics of periodic lattices has been originated by solid state physicists (Brillouin, 1953). In particular, the consequences of periodicity at the movement of electromagnetic waves were significantly studied and that they were carried out by many optical and electromagnetic devices. The capacity of periodic configurations to create electron/photonic band gap in semiconductors and crystals is much similar to the structural/acoustic band gap of elastic media. Due to their high rigidity-to-weight ratio and good value cost, stiffened plate and shell systems are applied widely in extraordinary designing applications like bridges, ship hulls and decks, and aircraft and launch vehicle structures. Within few decades, many researchers have mentioned the overall performance of stiffened plates/shells under dynamic loading, which may motive an excellent implementation in the area of vibration and noise control. Determining the free vibration characteristics of a structural system may be a fundamental task in dynamic analysis. In aerospace structures, periodically corrugated boundaries are formed by friction-stir-welding. In civil engineering structures, railway lines have periodicity in one-dimension, and rebars used in reinforced concrete foundations, beams, and slabs have a periodic surface. Periodic structural systems are also getting used to create desired acoustic band gaps. For health monitoring of these structures, a good understanding of the elastic wave propagation through such periodic structures is necessary. The method was extended to the study of flexural wave motion in engineering periodic structures (Heckl, 1964; Mead, 1970; Mead, 1973). This approach differs from other techniques where the natural frequencies of the system are calculated by initially considering the propagation constants of a single bay of the structure. In periodic structure analysis, the whole structure is considered as number of periodic elements joined end to end or side by side to form a whole structure. The natural frequencies of a finite periodic structure can be obtained by discretizing the dispersion curve in the propagation bands (Gupta, 1970). Based on the periodic structure theory, extensive work on flexural wave motion in periodically supported beams and plates was carried out (Gupta, 1970; Mead, 1970; Mead, 1973; Orris and Petyt, 1974; Mead and Parthan, 1979; Abdel-Rahman and Petyt, 1980). In the case of propagation bands of periodically supported beams, there are alternate bands of free wave propagation and decay. The upper bounding frequency of each of the propagation bands corresponds to that of a single periodic beam element vibrating with fixed ends, and the lower bounding frequency of each of the propagation bands corresponds to that of a single periodic beam element vibrating with simply supported ends. Mead (1973) has presented a general theory for harmonic wave propagation in one-dimensional periodic systems with multiple coupling. Harmonic wave propagation has studied the infinite beam and skin rib structure by Orris and Petyt (1974) and free and forced wave propagation in the two-dimensional periodic plate by Abdel-Rahman and Petyt (1980) using a finite element (FE) method. Mead and Parthan (1979) have applied beam functions and polynomial function, combined with the periodic structure theory to two-dimensional plates. In case of a periodic plate, the lowest bounding frequency of the first propagation band corresponds to that of a single flat rectangular panel with all its four edges simply supporting and vibrating in the first axial and the first transverse modes. The highest bounding frequency in the first propagation band corresponds to that of a single rectangular panel with all its four edges fixed.

The advantage of periodic structural (Gupta, 1970; Mead, 1970; Mead, 1973; Orris and Petyt, 1974; Mead and Parthan, 1979; Abdel-Rahman and Petyt, 1980) analysis is that all dynamic properties of finite structures are derived from a single phase-frequency curve or surface. An extensive review of the existing literature on the vibration analysis of periodic structures is presented by Mead (1996). A simple smearing method has been presented for calculating the natural frequencies, mode shapes, and forced vibrations of simply supported doubly curved and cross-stiffened thin rectangular shells (Luan et al., 2011). Experimental investigation (Kundu et al., 2006) has been carried out to study the guided wave propagation through plates with periodic boundaries and compared with theoretical predictions. The experimental results clearly showed that elastic waves can propagate through the corrugated plate (waveguide) for certain frequencies called “pass bands” and find it difficult to propagate for some other frequencies called “stop bands.” Stop bands are found to increase with the degree of corrugation. Wang et al. (2012) presented an improved FE model for the periodic stiffened plate structures with any number or orientation of stiffeners. Using the model, we analyzed flexural vibration band gaps and studied the physical mechanism for their formation in these periodic structures. These band gaps primarily correspond to the frequency ranges of vibration attenuation. Jin et al. (2017) studied the vibration band gap properties of periodic rectangular plate structures with general boundary conditions and are using the spectral-dynamic stiffness method. Manconi et al. (2021) studied the free and forced wave motion in a two-dimensional plate with radial periodicity using the wave FE approach. Pany and Parthan (2002) have studied free wave propagation in an unsupported ring using the periodic structure theory. The bounding frequencies and modes are identified. The natural frequencies of multi-span curved beams forming the portion of the ring and some frequencies of the stiffened ring on any number of equi-spaced, identical, radial supports are found out from dispersion curves using the discretization scheme (Gupta, 1970). The dispersion curve does not change whether it is an open structure or a closed structure. The basic method of computing the free wave motion in any one-dimensional or quasi-one dimensional continuous periodic systems has been applied to uniform cylindrical shells. Free wave propagation has been studied in the unsupported shell (Pany et al., 1999; Pany et al., 2002), axial line simple support infinitely curved panels (Pany and Parthan, 2003a), and orthogonal line simple support curved panels (Pany et al., 2003) using the periodic structure theory with FEM (PS-FEM). In the case of a circular cylindrical shell, each periodic element is a segment of the shell between two consecutive nodal positions. The optimum periodic angle is proposed in this study, which is to be considered for the periodic shell analysis. The periodic element corresponding to the optimum angle is named the optimum periodic curved panel, which is the most logical insight to choose in periodic structure analysis of the shell structure. The frequency factor corresponding to this optimum periodic subtended angle is the lowest frequency of the curved panel dimension oscillating in the first axial and circumferential modes. Furthermore, this will be the lowest frequency of a full circular cylindrical shell. One-dimensional axial wave propagation in an infinitely long periodically supported cylindrically curved panel subjected to supersonic airflow has been presented using the PS-FEM approach (Pany and Parthan, 2003b).

Recently, Jeon et al. (2021) have presented the analytic method to envisage the wave transmission at joints linking two semi-infinite periodic stiffened plates and the response of a finite periodic structure using Fourier transform and the Floquet’s theorem to a harmonic external point force. It is told that the property of periodic structures influences the stiffened plates’ energy transmission and the vibration response as well. Muzaffaruddin and Peter (2019) presented a new finite element–based design method for the geometrical periodic beam structures to aim a particular wanted attenuation frequency band. Jin et al. (2021) have demonstrated and analyzed the difference in band structures between lattice structures (an array of straight and infinite cylinders) of 2D acoustic metamaterials (AMMs) and 3D specimen models using FEM. It is found that there are variations in the physical characteristics (energy bands) between 2D AMMs and the 3D specimen model due to the changes in the mode shapes. Maxit et al. (2020) proposed a semi-analytical method to model the vibro-acoustic dynamic behavior of the submerged cylindrical shells periodically stiffened by axisymmetric frames through the circumferential admittance approach by FEM. The impact of Bloch–Floquet’s waves and the support spacing on the noise radiation are brought out. Chenge et al. (2020) applied a symplectic wave-based approach to know the vibro-acoustic outcome of the submerged ring-stiffened cylindrical shells, considering the hydrostatic pressure and acoustic-structure reciprocity.

Assessing the structural integrity with mechanical wave is an established nondestructive method for performing structural health monitoring (SHM). In this case, knowledge of the interaction between the wave propagation and the shape of the waveguide is essential. Groth et al. (2020), for offshore oil industry applications, they have studied the propagation (dispersion curve) of mechanical waves determined by a rectangular waveguide.

Thierry et al. (2018) have presented vibrational acoustics and ultrasonic wave propagation analysis of the highly anisotropic textile composite materials on a mesoscopic scale using the wave finite element method. Band gap behavior within a particular frequency range was predicted using a mesoscale model but not observed in a macroscale model. The propagation of elastic or acoustic waves in artificial periodic composite structures, known as phononic crystals (PCs), has received a great deal of attention (Kushwaha et al., 1993; Sigalas and Economou, 1994; Liu et al., 2000; Wang et al., 2004). One of the most attractive characteristics of PCs is that the propagation of sound and other vibrations is forbidden in their elastic wave band gaps. PCs are essentially periodic structures, and they have inherent relations with the periodic structures widely used in traditional engineering. Introducing the theoretical and calculation methods of PCs into the investigation of dynamic behavior of periodic structures in engineering will provide a new technique for the control of vibration and noise.

Waveguides, like transmission lines, are structures used to guide electromagnetic waves from point to point. Electromagnetic waves in a rotationally symmetric and perfectly conducting waveguide with a periodically varying cross section are considered by Bostrom (1983). Using the T-matrix approach, the axial wave number is derived. For a waveguide where the radius varies sinusoidal with the axial coordinate, the pass band and stop band modes are numerically computed. It is reported that when the axial wave numbers of two modes differ by a multiple of the wave number of the wall corrugations, the result is a stop band in the following cases for two TE (transverse electric) modes propagating in opposite directions, for a TE and a TM (transverse magnetic) mode in the same direction and sometimes for two TM modes in opposite directions.

Earlier, the FE method in wave propagation analysis using the periodic structure (PS) theory has been applied to multispan curved panel rests on orthogonal array of the equi-spaced simple line support by Pany et al. (2003) to determine the propagation surface of circular cylindrical shells. In this method, the basic periodic unit (i.e., any of the repeating units of curved panel) is modeled by using the arbitrary triangular shallow shell FEM of Cowper et al. (1970) and Sinha et al. (1992). The periodic structure (PS) concept is then used to take into account the coupling between the adjacent units. The capabilities of the combined FEM-PS theory can, therefore, be exploited for the cost-effective prediction of dynamical properties of the system by modeling only one bay of such a system. These numerical methods enable high accuracy up to high frequencies with very little computational effort and are the recommended choice for predicting waves in one-dimensional and two-dimensional single waveguides (beams, plates and shells, and cylindrical structure).

Albeit these phenomena are well comprehended, most literature reports on the periodic engineering structures are dedicated to the development of theoretical and numerical approaches to know its wave propagation behavior and characteristics. The purpose of this work was to extend the approach (Abdel-Rahman and Petyt, 1980; Pany et al., 2003) to analyze the wave propagation characteristics (propagation surfaces) in 2D periodic (orthogonal line supported) plate structures. Here, the shallow shell FE is employed to model a periodic plate unit considering infinite radius of curvature. Only the purely propagating waves with no attenuation are considered here. Also, there is not much literature related to the current work (free vibration of multi-supported flat panels) available. The first propagation surface is plotted in a three-dimensional plot for a 2D periodic plate (rectangular and square plates) for plane wave motion. It is observed that the three-dimensional plot of the first propagation surface obtained from current PS-FEM is compared well to that of Mead and Parthan (1979). The wave propagation results are identified in the propagation surface along μ_x and μ_y, respectively. Bounding frequencies of the first propagation surface of multi-supported flat panels are compared. The frequency of a flat finite plate (part of a periodic flat plate) with any number of spans both axially and transversely is determined from the propagation surface.

2 Theory and Model Development for Free Wave Propagation in an Orthogonal Line-Supported Periodic Plate

2.1 Stiffness and Mass Matrix of a Single Curved Panel by Finite Element

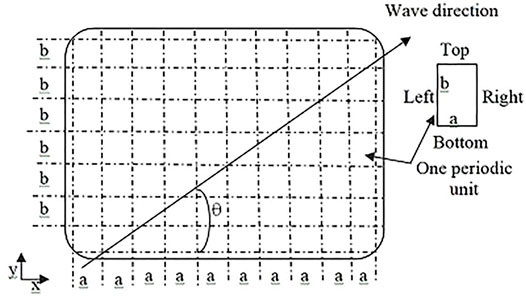
A two-dimensional infinite uniform plate system is considered resting on a grid of orthogonal simple line support composition of identical flat panels joined together in an identical manner at equal intervals, a in the x-direction and b in the y-direction (Figure 1). The “plane wave” type of motion is considered here. The problem is attempted using a numerical method based on Floquet’s PS theory and the FE discretization of a single periodic unit of the periodic structure. Only a single periodic unit of the structure is analyzed, which is approximated by using the FE method. The periodic structure (PS) concept is then used to take into account the coupling between the adjacent units. The wave characteristics of each unit are obtained by the theory of wave propagation in the periodic structure.

FIGURE 1

FIGURE 1. Two-dimensional multispan flat panels on simple orthogonal line supports.

The basic periodic unit of a two-dimensional periodic plate system (an assembly of periodic flat plates joined by on all sides and corners) is identified by the two integers n=(n₁, n₂). This represents the position of the unit within the periodic structure (Figure 2).

FIGURE 2

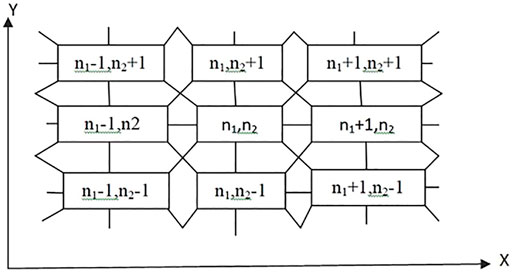
FIGURE 2. Basic particular unit is identified by the two integers n=(n₁, n₂), which represent the position of the unit within the structure ( two dimensional periodic plate) as an assembly of the periodic flat panel joined together on all sides and corners.

Using the FE method, a periodic unit can be represented by a model with the internal and boundary degrees of freedom (Pany et al., 2003). Each periodic unit is joined to its adjacent units at all sides and corners. Let {q_I}, {F_I}, {q_L}, {F_L}, { q_R}, {F_R}, {q_B}, { F_B}, {q_T}, {F_T}, {q_LB}, {F_LB}, {q_RB}, {F_RB}, {q_LT}, {F_LT}, { q_RT}, and {F_RT} be the degrees of freedom and forces at the inside, left, right, bottom, top, and corner of the cell (Figure 3).

FIGURE 3

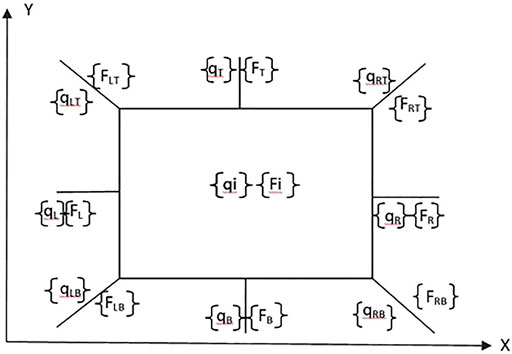
FIGURE 3. One periodic unit showing interior and boundary degrees of freedom (generalized forces and displacements of a single periodic unit).

The linear equation of motion of an undamped periodic unit or cell is given by (Mead, 1973; Orris and Petyt, 1974; Pany et al., 2003)

$\left(\left[K\right]-{\mathrm{\Omega }}^2\left[M\right]\right)\left\{q\right\}=\left\{F\right\},(1)$

where [K] and [M] are the stiffness and inertia matrices for the periodic unit, respectively. {q} and {F} are the generalized displacements and forces, respectively, of the periodic unit. Ω is the non-dimensional frequency $\left(\Omega =\frac{\omega a^2}{{\pi }^2}\sqrt{\frac{\rho }{D}}\right)$. a is the length of the periodic unit. ω is the radian frequency in Hertz. D is the bending stiffness $\left(=\frac{E{h}^3}{12\left(1-{\nu }^2\right)}\right)$, E is Young’s modulus of elasticity, $\text{ν}$ is Poisson’s ratio, and h is the thickness of the plate.

$\left\{\text{q}\right\}=\lceil {\mathrm{q}}_{\text{I}}{\text{ q}}_{\text{L}}{\text{ q}}_{\text{R}}{\text{ q}}_{\text{B}}{\text{ q}}_{\text{T}}{\text{ q}}_{\text{LB}}{\text{ q}}_{\text{RB}}{\text{ q}}_{\text{LT}}{\text{ q}}_{\text{RT}}{\rceil }^{\text{T}},(2)$

$\left\{\text{F}\right\}=\lceil {\text{F}}_{\text{I}}{\text{ F}}_{\text{L}}{\text{ F}}_{\text{R}}{\text{ F}}_{\text{B}}{\text{ F}}_{\text{T}}{\text{ F}}_{\text{LB}}{\text{ F}}_{\text{RB}}{\text{ F}}_{\text{LT}}{\text{ F}}_{\text{RT}}{\rceil }^{\text{T}}.(3)$

These can be partitioned according to the interior, left, right, bottom, top, and corner degrees of freedom (Abdel-Rahman and Petyt, 1980; Pany et al., 2003); hence,

$\left[K\right]\mathrm{=}\left[\begin{array}{l}{K}_{I,I}{K}_{I,L}{K}_{I,R}{K}_{I,B}{K}_{I,T}{K}_{I,LB}{K}_{I,RB}{K}_{I,LT}{K}_{I,RT}\\ K_{L,I}\\ K_{R,I}\\ K_{B,I}symmetric\\ K_{T,I}\\ K_{LB,I}\\ K_{RB,I}\\ K_{LT,I}\\ K_{RT,I}\end{array}\right].(4)$

A similar expression can be written for [M]. The element stiffness (Cowper et al., 1970) and mass matrices (Sinha et al., 1992; Pany et al., 2003), which are used in this work, are presented elsewhere. For brevity, it is described in Supplementary Material. The degrees of freedom at the nodes consist of out of plane displacements $w,w_{,x},w_{,y},w_{,xx},w_{,xy},w_{,yy}$ and in-plane displacements $u,u_{,x},u_{,y},v,v_{,x},v_{,y}$.The triangular FE with 12 degrees of freedom per node (Cowper et al., 1970) is shown in Figure 4.

FIGURE 4

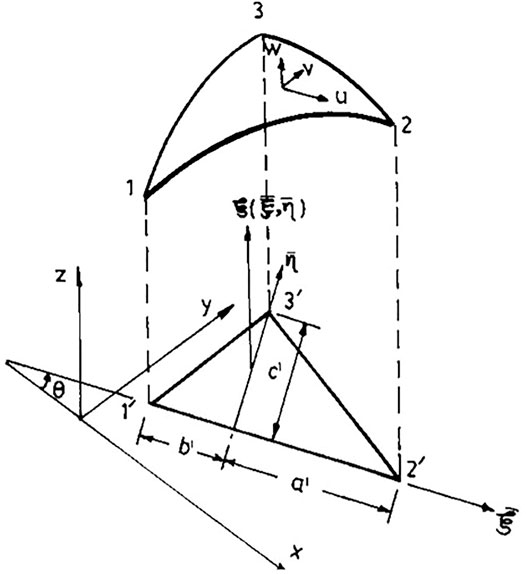
FIGURE 4. Geometry of the arbitrary triangular shallow shell element (Cowper et al., 1970)

2.2 Incorporation of Floquet’s Principle to Stiffness and Mass Matrices

The nodal forces {F} arise from all external forces acting on the system and internal forces between the periodic unit and its adjacent units. For free wave motion, {F_I} = 0. However, the force at the boundary of an element (the force of interaction between one element and its neighbors) is not zero because it transmits waves from one element to the next. This wave is characterized by associating the degrees of freedom and equivalent nodal forces of one unit (n₁, n₂) with the corresponding degrees of freedom and forces in adjacent units by relationship (Abdel-Rahman and Petyt, 1980; Pany et al., 2003) (Figures 2, 3). The propagation constant μ (μ_r + iμ_i) is generally complex. In this work, free wave propagation is considered with a purely imaginary propagation constant μ = iμ_i. This means that the current approach can predict the dispersion relation of “pure propagation band without attenuation” and does not produce “attenuation but no propagation band” or pure “attenuation but non propagating band”. This is based on the a priori assumption of the imaginary propagation constant (μ_r = 0), which is generally not true.

The propagation constants are represented by iμ_x and iμ_y in the axial direction (x direction of the plate) and transverse direction (y-direction of the plate), respectively. This condition is met when a “plane wave” of frequency ω propagates across the line reinforcement plate at an angle θ with respect to the x-axis, and each periodic unit of the plate oscillates in the same complex mode w (x, y) e^iωt, but there is a phase difference of μ_x in the x direction and μ_y in the y direction between the motion of one bay and the motion immediately next to it (Mead and Parthan, 1979; Pany et al., 2003). This phase difference is the same for all pairs of adjacent bays and is the “propagation constant” of the wave. The relation between the nodal forces can be expressed of the form

$\begin{array}{l}{\left\{F_L\right\}}_{n_1+1,n_2}=e^{-i{\mu }_x}{\left\{F_L\right\}}_{n_1,n_2};{\left\{F_B\right\}}_{n_1,n_2+1}=e^{-i{\mu }_y}{\left\{F_B\right\}}_{n_1,n_2},\\ {\left\{F_{LT}\right\}}_{n_1+1,n_2}=e^{-i{\mu }_x}{\left\{F_{LT}\right\}}_{n_1,n_2};{\left\{F_{RB}\right\}}_{n_1,n_2+1}=e^{-i{\mu }_y}{\left\{F_{RB}\right\}}_{n_1,n_2},\\ {\left\{F_{LB}\right\}}_{n_1+1,n_2+1}=e^{-i\left({\mu }_x+{\mu }_y\right)}{\left\{F_{LB}\right\}}_{n_1,n_2}.\end{array}$(5a-e)

The nodal degrees of freedom can be related as follows.

$\begin{array}{l}{\left\{q_L\right\}}_{n_1+1,n_2}=e^{-i{\mu }_x}{\left\{q_L\right\}}_{n_1,n_2};{\left\{q_B\right\}}_{n_1,n_2+1}=e^{-i{\mu }_y}{\left\{q_B\right\}}_{n_1,n_2},\\ {\left\{q_{LB}\right\}}_{n_1+1,n_2}=e^{-i{\mu }_x}{\left\{q_{LB}\right\}}_{n_1,n_2};{\left\{q_{LB}\right\}}_{n_1,n_2+1}=e^{-i{\mu }_y}{\left\{q_{LB}\right\}}_{n_1,n_2},\\ {\left\{q_{LB}\right\}}_{n_1+1,n_2+1}=e^{-i\left({\mu }_x+{\mu }_y\right)}{\left\{q_{LB}\right\}}_{n_1,n_2}. \end{array}$(6a-e)

At the common boundaries between the periodic unit or cell (n₁ and n₂) and its neighboring periodic units, displacements must be equal, with interconnecting forces being in equilibrium,

$\begin{array}{l}{\left\{F_R\right\}}_{n_1,n_2}+{\left\{F_L\right\}}_{n_1+1,n_2}=0,\\ {\left\{F_T\right\}}_{n_1,n_2}+{\left\{F_B\right\}}_{n_1,n_2+1}=0,\\ {\left\{F_{RT}\right\}}_{n_1,n_2}+{\left\{F_{LT}\right\}}_{n_1+1,n_2}+{\left\{F_{RB}\right\}}_{n_1,n_2+1}+{\left\{F_{LB}\right\}}_{n_1+1,n_2+1}=0.\end{array}$(7a-c)

The displacements can be related as follows:

$\begin{array}{l}{\left\{q_L\right\}}_{n_1+1,n_2}={\left\{q_R\right\}}_{n_1,n_2},\\ {\left\{q_B\right\}}_{n_1,n_2+1}={\left\{q_T\right\}}_{n_1,n_2},\\ {\left\{q_{LB}\right\}}_{n_1+1,n_2}={\left\{q_{RB}\right\}}_{n_1,n_2};{\left\{q_{LB}\right\}}_{n_1,n_2+1}={\left\{q_{LT}\right\}}_{n_1,n_2},\\ {\left\{q_{LB}\right\}}_{n_1+1,n_2+1}={\left\{q_{RT}\right\}}_{n_1,n_2}.\end{array}$(8a-e)

Substituting Eq. (5) into Eq. (7) gives

$\begin{array}{l}{\left\{F_R\right\}}_{n_1,n_2}+e^{-i{\mu }_x}{\left\{F_L\right\}}_{n_1,n_2}=0,\\ {\left\{F_T\right\}}_{n_1,n_2}+e^{-i{\mu }_y}{\left\{F_B\right\}}_{n_1,n_2}=0,\\ {\left\{F_{RT}\right\}}_{n_1,n_2}+e^{-i{\mu }_x}{\left\{F_{LT}\right\}}_{n_1,n_2}+e^{-i{\mu }_y}{\left\{F_{RB}\right\}}_{n_1,n_2}+e^{-i\left({\mu }_x+{\mu }_y\right)}{\left\{F_{LB}\right\}}_{n_1,n_2}=0.\end{array}$(9a-c)

Similarly using Eq. (6) into Eq. (8) gives

$\begin{array}{l}{\left\{q_R\right\}}_{n_1,n_2}=e^{-i{\mu }_x}{\left\{q_L\right\}}_{n_1,n_2};{\left\{q_T\right\}}_{n_1,n_2}=e^{-i{\mu }_y}{\left\{q_B\right\}}_{n_1,n_2},\\ {\left\{q_{RB}\right\}}_{n_1,n_2}=e^{-i{\mu }_x}{\left\{q_{LB}\right\}}_{n_1,n_2};{\left\{q_{LT}\right\}}_{n_1,n_2}=e^{-i{\mu }_y}{\left\{q_{LB}\right\}}_{n_1,n_2},\\ {\left\{q_{RT}\right\}}_{n_1,n_2}=e^{-i\left({\mu }_x+{\mu }_y\right)}{\left\{q_{LB}\right\}}_{n_1,n_2}.\end{array}$(10a-e)

One can use relationship (Eq. 10) to remove { q_B }, { q_T }, { q_RB }, { q_LT }, and { q_RT} at the boundaries of the periodic cells. Using degrees of freedom and forces (Eqs (8) and (10)) on the free vibration (Eq. 1), one can obtain the following equations:

$\left(\left[\overline{K}\left({\mu }_x,{\mu }_y\right)\right]-{\mathrm{\Omega }}^2\left[\overline{M}\left({\mu }_x,{\mu }_y\right)\right]\right)\left\{\begin{array}{l}{q}_i\\ q_L\\ q_B\\ q_{LB}\end{array}\right\}=0,(11)$

where

$\left[\overline{K}\left({\mu }_x,{\mu }_y\right)\right]=\left[W\prime \right]\left[K\right]\left[W\right],(\mathrm{12a})$

$\left[\overline{M}\left({\mu }_x,{\mu }_y\right)\right]=\left[W\prime \right]\left[M\right]\left[W\right].(\mathrm{12b})$

[W^’] = [W^∗]^T, and ^∗ denotes the complex conjugate.

$\left[\text{W}\right]\mathrm{=}\left[\begin{array}{c}I 0 0 0\\ 0 I 0 0\\ 0 e^{-i{\mu }_x} 0 0\\ 0 0 I 0\\ 0 0 e^{-i{\mu }_y} 0\\ 0 0 0 I\\ 0 0 0 e^{-i{\mu }_x}\\ 0 0 0 e^{-i{\mu }_y}\\ 0 0 0 e^{-i({\mu }_x+{\mu }_y)}\end{array}\right].(13)$

Equation (11) represents an eigenvalue problem in Ω for the given values of μ_x and μ_y.

$\left[\overline{K}\right]$ and $\left[\overline{M}\right]$ are Hermitian, i.e., ${\left[{\overline{K}}^{\ast }\right]}^T=\left[\overline{K}\right],{\left[{\overline{M}}^{\ast }\right]}^T=\left[\overline{M}\right]$.

Equation (11) can be solved for different values of real propagation constants μ _x and μ_y to find the corresponding frequencies of propagation and associated wave forms. μ _x and μ_y are varied from 0 to π (3.142).

3 Results and Discussions

3.1 Model Simulation

Current numerical (FE) codes have been developed using the arbitrary triangular high-precision shallow shell finite element method (FEM), taking into account the periodic structure (PS) theory. The code is used in the plate periodic units where the radius of curvature tends to be infinite. The FE discretization is selected based on the convergence studies to evaluate reasonably accurate results and uses a 4 × 4 mesh (Figure 5) to derive the wave characteristics (the propagation surface) of periodic square and rectangular plates. The eigenvalues of Eq. (11) were calculated from the FE mass and stiffness matrix using the Floquet’s principle (the periodic structure theory) for thin square and rectangular line simply supported periodic unit plate. The natural Ω of the flat panel is obtained for various propagation constants using the current PS-FEM code. This can significantly reduce the number of DOFs involved in the calculation and significantly reduce the calculation time (Pany et al., 2003) compared to other traditional FE approaches (Pany et al., 2001).

FIGURE 5

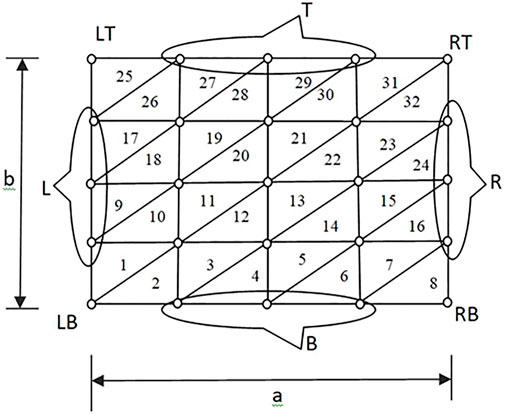
FIGURE 5. FE model (triangular mesh (4 × 4)) for one periodic unit showing nodes corresponding to left(L), left bottom (LB), bottom (B), right bottom (RB), right(R), right top (RT), top(T), and left top (LT).

3.2 Validation

3.2.1 Propagation Surface of the Periodic Square Plate

The propagation surfaces comprised nondimensional frequency Ω and propagation constants (μ_x and μ_y) for the first propagation surface of the square plate, as shown in Figure 6. The variation of nondimensional frequency versus axial (μ_x) and transverse (μ_y) propagation constants is presented in Table 1. The variation of frequencies shows a symmetric pattern for the square plate. The trend of the propagation surface generated using the present periodic FE is similar to that of Mead and Parthan, (1979), and nondimensional frequencies values are compared well. It may be noted that Mead and Parthan (1979) have used beam functions and polynomial function, combined with the periodic structure theory to find the propagation surface of two-dimensional plates.

FIGURE 6

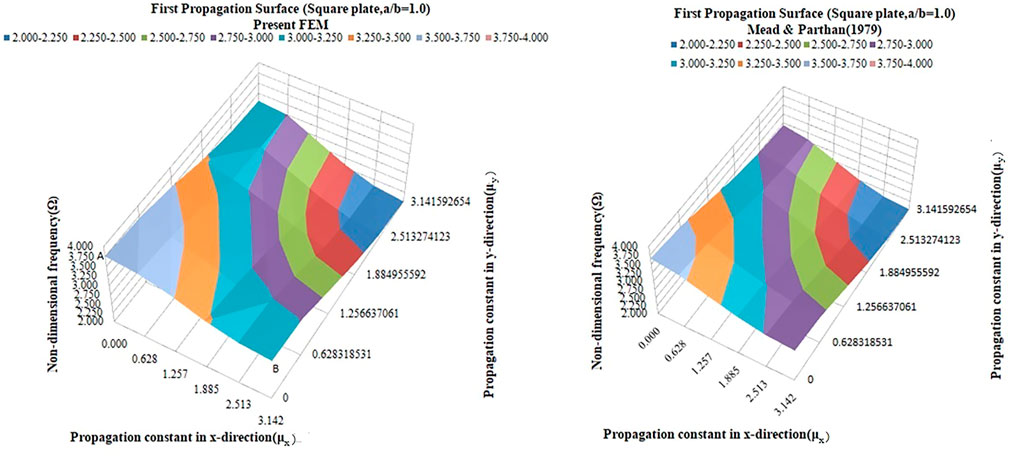
FIGURE 6. Comparison of the present propagation surface of the periodic square plate using PS-FEM with (Mead and Parthan, 1979).

TABLE 1

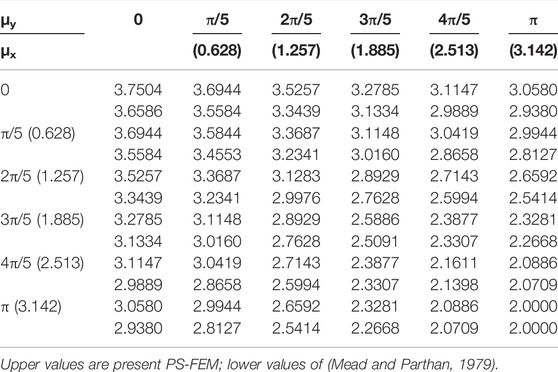
TABLE 1. Nondimensional frequencies (Ω) for a periodic plate (orthogonal line-supported) with the square element.

3.2.2 Propagation Surface of the Periodic Rectangular Plate

The propagation surface of the rectangular plate is shown in Figure 7. The variation of the nondimensional frequency versus axial (μ_x) and transverse (μ_y) propagation constant is presented in Table 2 and Figure 7. The trend of the propagation surface generated using the present PS-FEM is similar to that of Mead and Parthan, (1979), and nondimensional frequencies values are compared well.

FIGURE 7

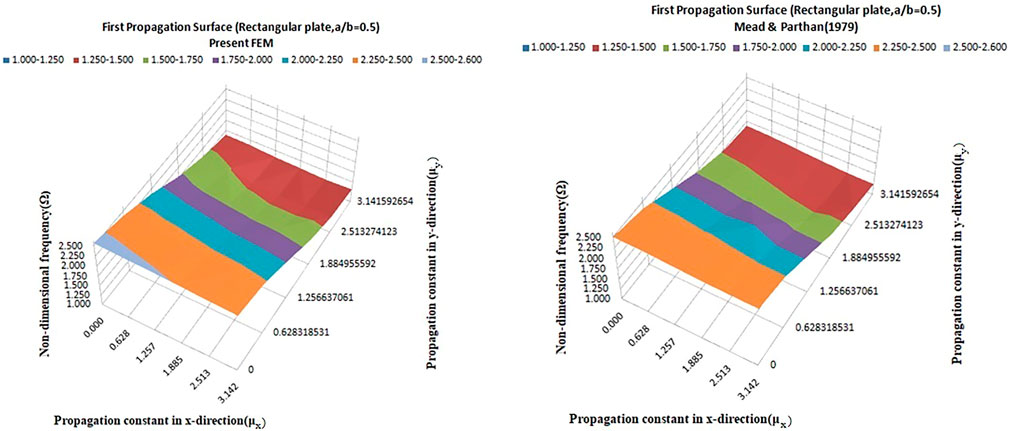
FIGURE 7. Comparison of the present propagation surface of the periodic rectangular plate using PS-FEM with (Mead and Parthan, 1979).

TABLE 2

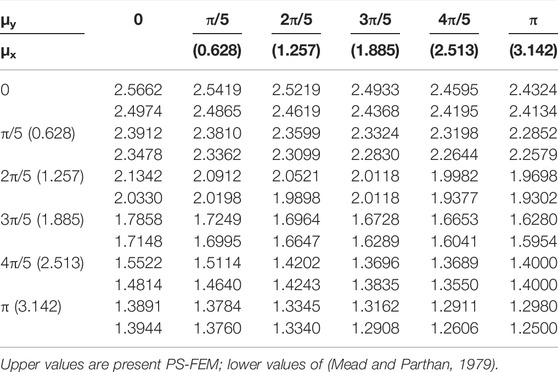
TABLE 2. Nondimensional frequencies (Ω) for a periodic plate (orthogonal line-supported) with the rectangular element.

3.3 Bounding Frequency of the Propagation Surface

The displayed frequency (Figures 6, 7; Tables 1, 2) can be identified by the natural frequency of each square or rectangular plate. The modes and boundary conditions are described as follows. The highest point in the propagation surface is μ_x = μ_y = 0. In this state, all the adjacent elements oscillate in phase with each other. The frequency (Ω) at this point is the same as the natural frequency of a single periodic element with all its edges fixed (CCCC) boundary conditions and is the upper bounding frequency of the first propagation band of the 2D periodic plate. The lowest point of the propagation surface is at μ_x = μ_y = π (3.142). In this state, the adjacent bays of the plate oscillate in antiphase to each other, the corresponding frequency (Ω) is the same as the natural frequency of a single periodic element, and all its edges are simply supported (SSSS) boundary conditions. This frequency is the lowest bounding frequency of the first propagation band of the 2D periodic plate. In the directions of μ_x = μ_y = π, the waves propagate at the lowest possible free wave frequency. Also, if the periodic plate is subjected to a plane harmonic pressure field that convicts in that direction, and at that frequency the largest possible plate response is elicited (Mead and Parthan, 1979). The boundary conditions are shown in Figure 8.

FIGURE 8

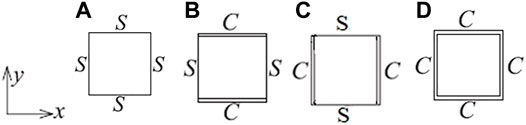
FIGURE 8. Periodic unit (square plate, a/b = 1) with different edge boundary conditions (A) simply supported (SSSS), (B) axially fixed and simply supported transverse direction (CSCS), (C) axially simply supported and fixed transverse directions (SCSC), and (D) all edges fixed (CCCC).

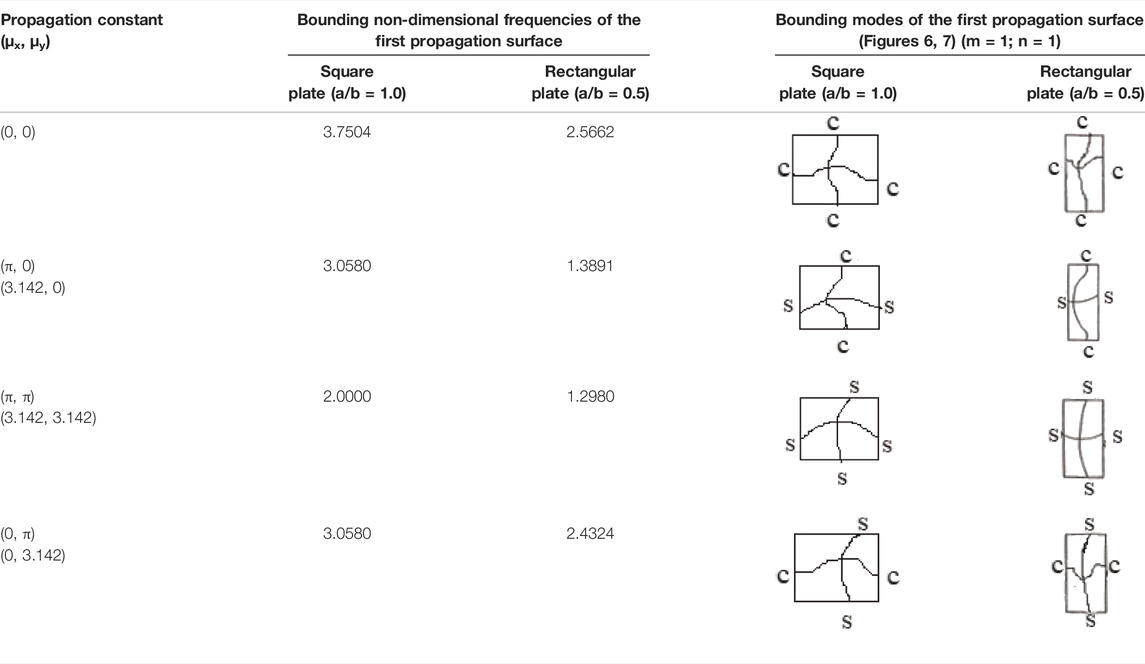
Furthermore, the other two bounding points of the propagation surface are in between the lowest (μ_x = μ_y = π) and highest (μ_x = μ_y = 0) points. The two points are corresponding to propagation constants (i) (μ_x = π, μ_y = 0) and (ii) (μ_x = 0, μ_y = π), respectively. These two points’ frequencies are corresponding to a finite square plate with (i) axially fixed and simply supported transverse direction (CSCS) and (ii) axially simply supported and fixed in a transverse direction (SCSC). The bounding frequencies and modes are tabulated and presented in Table 3.

TABLE 3

TABLE 3. Nondimensional bounding frequencies and bounding modes of the periodic plate.

3.3.1 Single Square Plate (a/b = 1)

The highest bounding point in the propagation surface is μ_x = μ_y = 0. The frequency (Ω) at this point is the same as the natural frequency of a single periodic element with all its edges fixed. The current PS-FEM analysis shows that the nondimensional frequency (Ω) is 3.75 (Table 3). The value of the nondimensional frequency of all edges fixed of a square plate is 3.6586 (Mead and Parthan, 1979) and vibrating in the first (m = 1) axial (x-direction) and first (n = 1) transverse (y-direction) modes. The similar values Ω = 3.690, Ω = 3.66, and Ω = 3.65 are reported by Kolarevic et al. (2016) using DSM based on the HSDT by KrishnaBhaskar and MeeraSaheb (2017) using couple displacement field energy formulation and by Kalita and Haldar (2018) using the 9-noded finite element, for a four edge-fixed square single plate, respectively. The vibration modes are corresponding to m = n = 1. Here, the frequency values reported by Kolarevic et al. (2016) and KrishnaBhaskar and MeeraSaheb (2017) are converted to the present nondimensional frequency form.

Similarly, the lowest bounding point of the propagation surface is at μ_x = μ_y = π. The frequency (Ω) at this point is the same as the natural frequency of a single periodic element with all its edges simply supported. The present PS-FEM analysis shows the nondimensional frequency (Ω) of 2.0 (Table 3). The value of the nondimensional frequency (Ω) of all edges simply supported square plate is 2.0 (Mead and Parthan, 1979) and vibrates in the first (m = 1) axial (x-direction) and the first (n = 1) transverse (y-direction) modes. The nondimensional frequency(Ω) values of 2.1, 1.99, and 2.00 are reported by Kolarevic et al. (2016), KrishnaBhaskar and MeeraSaheb (2017), and Kalita and Haldar (2018) for four-edge simply supported square single plates, respectively. The vibrating mode is m = n = 1.

Again, the other two bounding points of the propagation surface are in between the lowest (μ_x = μ_y = π) and highest (μ_x = μ_y = 0) points and are corresponding to propagation constants (i) (μ_x = 0, μ_y = π) and (ii) (μ_x = π, μ_y = 0), respectively. These two points’ frequencies are corresponding to a single square plate with SCSC and CSCS boundary conditions. In case of a square plate, in both conditions, the frequency will be same. The nondimensional frequency (Ω) reported by Mead and Parthan (1979) is 2.938 and vibrates in the first axial mode and first transverse mode. The nondimensional frequency values (Ω) calculated in Kolarevic et al. (2016) and Monterrubio and Ilanko (2015) are 3.025 and 2.933, respectively, in the isolated panel, which is close to the bounding frequency value (Ω = 3.058) of the current PS-FEM approach (Table 3).

It can be concluded that the propagation surface or band obtained using the combined FEM with PS approach can be used to find the frequency of the single plate for various extreme edge boundary conditions. However, when using the traditional FE approach, the HSDT and couple displacement field approach, to analyze the free vibrations of a finitely isolated single plate, requires a large amount of memory and more analysis time in the computer.

3.3.2 Single Rectangular Plate (a/b = 0.5)

The highest point inside the propagation surface is μ_x = μ_y = 0. The frequency (Ω) at this point is the same as the natural frequency of a single periodic element with all its edges absolutely fixed (Figure 9). The present PS-FEM shows that the nondimensional frequency (Ω) is 2.5662 (Table 3). The value of the nondimensional frequency (Ω) of all edges fixed to a rectangular plate is 2.497 (Mead and Parthan, 1979) and vibrates in the first (m = 1) axial (x-direction) and first (n = 1) transverse (y-direction) modes. The comparable values 2.5603 and 2.493 are reported by KrishnaBhaskar and MeeraSaheb (2017) and Kalita and Haldar (2018) for the four-edged rectangular plate and vibrates in a mode identical to that of the present approach. Here, the frequency value reported by KrishnaBhaskar and MeeraSaheb (2017) is converted to the current nondimensional frequency form.

FIGURE 9

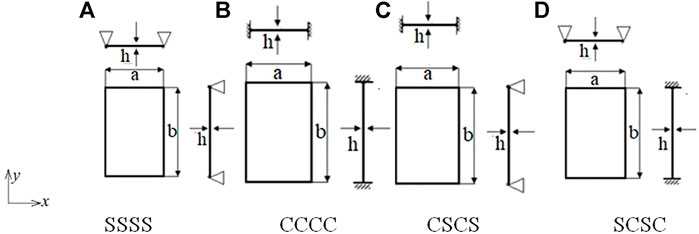
FIGURE 9. Periodic unit (rectangular plate, a/b = 0.5) with different edge boundary conditions(A) SSSS, (B) CCCC, (C) CSCS, and (D) SCSC.

Similarly, the bottom point of the propagation surface is at μ_x = μ_y = π. The frequency (Ω) at this point is the same as the natural frequency of a single periodic element or isolated plate with all its edges simply supported (Figure 9). The present FEM solution shows a value (Ω) of 1.3 (Table 3). The nondimensional frequency (Ω) value of 1.25 is reported by Mead and Parthan, (1979) with all edges simply supported for the rectangular plate and vibrating in the first (m = 1) axial (x-direction) and first (n = 1) transverse (y-direction) modes. The nondimensional frequency (Ω) values of 1.25, 1.251 are reported by KrishnaBhaskar and MeeraSaheb (2017) and Kalita and Haldar (2018) for the four-edged simply supported single rectangular plate, respectively, and vibrating in the identical mode to present analysis i.e., m,n = 1,1 and (Mead and Parthan, 1979).

The other two boundary points of the propagation surface are in between the lowest point (μ_x = μ_y = π) and the highest point (μ_x = μ_y = 0), corresponding to the propagation constant (i) (μ_x = 0, μ_y = π) and (ii) (μ_x = π, μ_y = 0). The nondimensional frequency (Ω) values for the SCSC (μ_x = 0, μ_y = π) and CSCS (μ_x = π, μ_y = 0) boundary conditions are the result of the current PS-FEM approach, 2.4324 and 1.3891, respectively (Table 3). These are well compared to Mead and Parthan, (1979).

3.4 Identification of the Lowest Frequency of the Multi-Span Flat Panel in the Propagation Surface

Xiang et al. (2002) conducted a study to determine the free vibration frequencies of multispan rectangular and square Mindlin plates in exact solutions. An isotropic plate that is simply supported by the two edges parallel to the x-axis (y = 0 and y = a) is considered. There are internal line supports (n-1) in the x direction that divide the plate into n spans. The internal line support imposes a zero lateral displacement (w) along the line support of the plate. The exact frequency parameters of a rectangular Mindlin plate with two equal spans are presented using the Levy solution method (Xiang et al., 2002), and the four equal spans are presented using the receptance method. The first mode nondimensional frequency (Ω) parameters for these cases with simply supported parallel to x-axis of plates (Xiang et al., 2002) and four edges simply supported (Azimi et al., 1984) is reported of 2.0. It corresponds exactly to the current PS-FEM solution frequency (Ω) values of 2 vibrating in the first axial and transverse modes (m = n = 1) and is simply supported by a square panel with four edges. It also shows the exact frequency parameters of the two, three, and four equi-span rectangular Mindlin plates with internal line support and simply supported by two edges parallel to the x axis (y = 0 and y = a), using the Levy solution method (Xiang and Wei, 2002). The nondimensional frequency (Ω) parameter of the first mode in these cases, where parallel to the x-axis of the plate is simply supported, does not change.

Kim and Dickinson (1987)’s free vibration frequency uses the Rayleigh–Ritz method’s considering polynomial functions for displacement, with five internal line supports and six equal-span thin rectangular plates (a/b = 6) fixed to four edges (Figure 10), for the flexural vibration. They (Kim and Dickinson, 1987) showed the first six natural frequency parameters (Table 4 of Kim and Dickinson (1987)’s study) for the six equal-span thin rectangular plates, fixed on four edges. The lowest frequency (Ω) in this case is 3.738, and the current PS-FEM value of the periodic square plate match is Ω = 3.7504 (μ_x = 0, μ_y = 0) (Tables 1, 3).

FIGURE 10

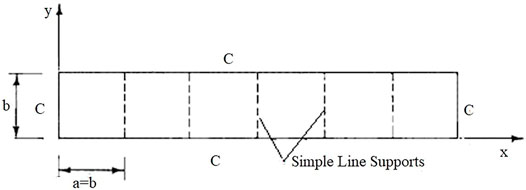
FIGURE 10. Finite (6 equal span) 2D periodic line supported rectangular plate with fixed edge boundary conditions.

TABLE 4

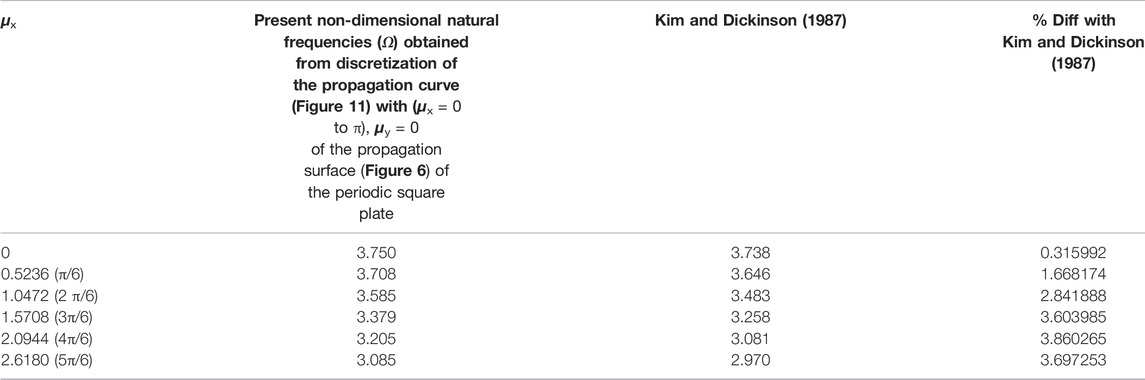
TABLE 4. Nondimensional frequencies of the 6 × 1 span finite periodic plate (fixed on four edges) obtained from the propagation surface of the square periodic plate.

Therefore, one more advantage of this approach is that the same propagation surface can be used to find the lowest frequency of multi-supported flat panels with the internal line supports.

3.5 Estimation of Natural Frequencies of 2D Finite Periodic Plates on Simple Line Supports From the Current Propagation Surface or Band

Now consider a rectangular periodic plate with N_x elements in the x-direction and N_y elements in the y-direction (Figure 10). Here, N_x is 6, N_y = 1, and a = b. The total length and width of the plate are N_xa (= 6 a) and N_yb (= a), respectively. As mentioned earlier, the plate is assumed to be on simple line supports, even if the outermost boundaries are completely fixed. If the finite plate has rigid edges that impede the movement of the edges, free vibrations can occur at the natural frequencies of μ_x = i π/N_x and μ_y = j π/N_y because there is no phase change in the reflection process. This is a direct extension of Sen Gupta’s (1970) method for finding the natural frequency of the one-dimensional periodic beams.

For a particular quadrant (Figure 6) of a propagation surface between the two bounding frequencies (propagation band A-B as shown in Figure 6 obtained using the present FEM and plotted in Figure 11), all the distinct natural frequencies of a finite plate (extreme boundary fixed, Figure 10) can be read off in this frequency range from the propagation surface corresponding to μ_x = iπ/N_x (i = 0,1,2, … , N_x -1) and μ_y = 0. The results obtained from the present PS-FEM approach using the aforementioned discretization scheme of Gupta, (1970) is shown in Table 4.

FIGURE 11

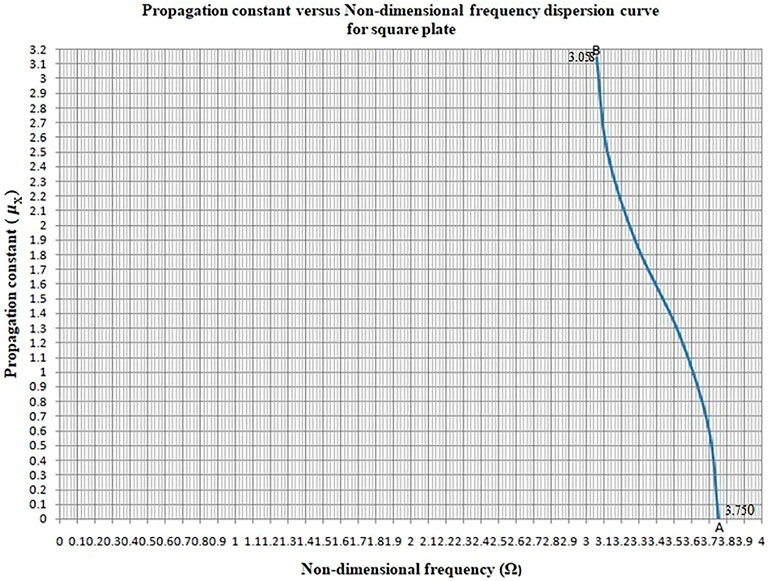
FIGURE 11. Propagation band A-B (at A, Ω = 3.750 and μ_x = 0; at B, Ω = 3.058 and μ_x = π (3.142)) of the propagation surface (Figure 6) of the periodic square plate using present PS-FEM.

4 Conclusion

The purpose of this study was to apply a numerical method combined with Floquet’s theory (periodic structure concept) to the periodic plate structure. Here, the FE discretization of a single periodic unit is performed using the arbitrary high-precision triangular element. The periodic structure (PS) concept is then used to take into account the coupling between the adjacent units. This method can predict the dispersion relation of the “pure propagation band without attenuation” and does not generate the “propagation band with attenuation”. In this study, it was shown that the propagation surface of the periodic line-supporting orthogonal plate can be obtained from the present developed PS-FEM code (combination of the conventional FE method with the periodic structure theory). The current approach provides the natural Ω of the flat periodic plate for various propagation constants. The upper and lower bounding frequencies of the propagation band can be identified by the natural frequency of the well-known normal mode type of the single plate element. The current numerical results are compared well to the available literature.

From this study, it is demonstrated that one can use the propagation surface or band obtained by the combined PS and FEM approach to find single plate frequencies for various edge boundary conditions. However, analyzing the free vibrations of a finite plate with the extreme edge boundary conditions, using the traditional FE approach without the PS theory, requires a large amount of memory and computer analysis time. Another usefulness of this approach is that one can use the propagation surface to find the natural frequencies of a finite multi-supported flat panel with internal line supports through discretization of the propagation band.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work was performed when the author was at Aerospace Engineering Department, IIT′ Kharagpur (India). The author would like to thank the faculty members of the department, especially Professor S. Parthan (Rtd.), for providing the department’s computing facility to perform this task.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2022.926559/full#supplementary-material

References

Abdel-Rahman, A. Y. A., and Petyt, M. (1980). “Free and Forced Wave Propagation in Two-Dimensional Periodic Systems Using Matrix Techniques,” in The Recent Advances in Structural Dynamics (University of Southampton, Southampton, England: ISVR Southampton), 361–373.

Google Scholar

Azimi, S., Hamilton, J. F., and Soedel, W. (1984). The Receptance Method Applied to the Free Vibration of Continuous Rectangular Plates. J. Sound Vib. 93 (1), 9–29. doi:10.1016/0022-460x(84)90348-1

CrossRef Full Text | Google Scholar

Bostrom, A. (1983). Passbands and Stopbands for an Electromagnetic Waveguide with a Periodically Varying Cross Section. IEEE Trans. Microw. Theory Techn. 31 (9), 752–756. doi:10.1109/tmtt.1983.1131585

CrossRef Full Text | Google Scholar

Brillouin, L. (1953). Wave Propagation in Periodic Structure. New York: Dover Publication.

Google Scholar

Chenge, P., Xianbo, S., and Yahui, Z. (2020). Vibro-acoustic Analysis of Submerged Ring-Stiffened Cylindrical Shells Based on a Symplectic Wave-Based Method. Thin-Walled Struct. 150, 106698. doi:10.1016/j.tws.2020.106698

CrossRef Full Text | Google Scholar

Cowper, G. R., Lindberg, G. M., and Olson, M. D. (1970). A Shallow Shell Finite Element of Triangular Shape. Int. J. Solids Struct. 6, 1133–1156. doi:10.1016/0020-7683(70)90052-1

CrossRef Full Text | Google Scholar

Groth, E. B., Clarke, T. G. R., Schumacher da Silva, G., Iturrioz, I., and Lacidogna, G. (2020). The Elastic Wave Propagation in Rectangular Waveguide Structure: Determination of Dispersion Curves and Their Application in Nondestructive Techniques. Appl. Sci. 10, 4401. doi:10.3390/app10124401

CrossRef Full Text | Google Scholar

Gupta, G. S. (1970). Natural Flexural Waves and the Normal Modes of Periodically-Supported Beams and Plates. J. Sound Vib. 13, 89–101. doi:10.1016/s0022-460x(70)80082-7

CrossRef Full Text | Google Scholar

Heckl, M. A. (1964). Investigations on the Vibrations of Grillages and Other Simple Beam Structures. J. Acoust. Soc. Am. 36, 1335–1343. doi:10.1121/1.1919206

CrossRef Full Text | Google Scholar

Jeon, J., Ih, J.-G., and Brunskog, J. (2021). Wave Transmission and Vibration Response in Periodically Stiffened Plates Using a Free Wave Approach. J. Acoust. Soc. Am. 149, 3694–3702. doi:10.1121/10.0005125

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, G., Zhang, C., Ye, T., and Zhou, J. (2017). Band Gap Property Analysis of Periodic Plate Structures under General Boundary Conditions Using Spectral-Dynamic Stiffness Method. App. Acoust. 121, 1–13. doi:10.1016/j.apacoust.2017.01.024

CrossRef Full Text | Google Scholar

Jin, W., Guo, H., Sun, P., Wang, Y., and Yuan, T. (2021). Numerical Investigation of Discrepancies between Two-Dimensional and Three-Dimensional Acoustic Metamaterials. Front. Mat. 8, 759740. doi:10.3389/fmats.2021.759740

CrossRef Full Text | Google Scholar

Kalita, K., and Haldar, S. (2018). Natural Frequencies of Rectangular Plate with- and Without-Rotary Inertia. J. Inst. Eng. India Ser. C 99 (5), 539–555. doi:10.1007/s40032-016-0327-9

CrossRef Full Text | Google Scholar

Kim, C. S., and Dickinson, S. M. (1987). The Flexural Vibration of Line Supported Rectangular Plate Systems. J. Sound Vib. 114 (1), 129–142. doi:10.1016/s0022-460x(87)80239-0

CrossRef Full Text | Google Scholar

Kolarevic, N., Marjanović, M., Nefovska-Danilovic, M., and Petronijevic, M. (2016). Free Vibration Analysis of Plate Assemblies Using the Dynamic Stiffness Method Based on the Higher Order Shear Deformation Theory. J. Sound Vib. 364, 110–132. doi:10.1016/j.jsv.2015.11.016

CrossRef Full Text | Google Scholar

KrishnaBhaskar, K., and MeeraSaheb, K. (2017). Effect of Aspect Ratio on Large Amplitude Free Vibrations of Simply Supported and Clamped Rectangular Mindlin Plates Using Coupled Displacement Field Method. J. Mech. Sci. Technol. 31 (5), 2093–2103. doi:10.1007/s12206-017-0406-8

CrossRef Full Text | Google Scholar

Kundu, T., Banerjee, S., and Jata, K. V. (2006). An Experimental Investigation of Guided Wave Propagation in Corrugated Plates Showing Stop Bands and Pass Bands. J. Acoust. Soc. Am. 120, 1217–1226. doi:10.1121/1.2221534

CrossRef Full Text | Google Scholar

Kushwaha, M. S., Halevi, P., Dobrzynski, L., and Djafari-Rouhani, B. (1993). Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 71 (13), 2022–2025. doi:10.1103/PhysRevLett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally Resonant Sonic Materials. Science 289, 1734–1736. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

Luan, Y., Ohlrich, M., and Jacobsen, F. (2011). Smearing Technique for Vibration Analysis of Simply Supported Cross-Stiffened and Doubly Curved Thin Rectangular Shells. J. Acoust. Soc. Am. 129, 707–716. doi:10.1121/1.3523305

PubMed Abstract | CrossRef Full Text | Google Scholar

Manconi, E., Sorokin, S. V., Garziera, R., and Quartaroli, M. M. (2021). Free and Forced Wave Motion in a Two-Dimensional Plate with Radial Periodicity. Appl. Sci. 11, 10948. doi:10.3390/app112210948

CrossRef Full Text | Google Scholar

Maxit, L., Guasch, O., Meyer, V., and Karimi, M. (2020). Noise Radiated from a Periodically Stiffened Cylindrical Shell Excited by a Turbulent Boundary Layer. J. Sound Vib. 466 (3), 115016. doi:10.1016/j.jsv.2019.115016

CrossRef Full Text | Google Scholar

Mead, D. J. (1973). A General Theory of Harmonic Wave Propagation in Linear Periodic Systems with Multiple Coupling. J. Sound Vib. 27, 235–260. doi:10.1016/0022-460x(73)90064-3

CrossRef Full Text | Google Scholar

Mead, D. J. (1970). Free Wave Propagation in Periodically Supported, Infinite Beams. J. Sound Vib. 11, 181–197. doi:10.1016/s0022-460x(70)80062-1

CrossRef Full Text | Google Scholar

Mead, D. J., and Parthan, S. (1979). Free Wave Propagation in Two-Dimensional Periodic Plates. J. Sound Vib. 64, 325–348. doi:10.1016/0022-460x(79)90581-9

CrossRef Full Text | Google Scholar

Mead, D. J. (1996). Wave Propagation in Continuous Periodic Structures: Research Contributions from Southampton, 1964-1995. J. Sound Vib. 190 (3), 495–524. doi:10.1006/jsvi.1996.0076

CrossRef Full Text | Google Scholar

Monterrubio, L. E., and Ilanko, S. (2015). Proof of Convergence for a Set of Admissible Functions for the Rayleigh-Ritz Analysis of Beams and Plates and Shells of Rectangular Planform. Comput. Struct. 147, 236–243. doi:10.1016/j.compstruc.2014.09.008

CrossRef Full Text | Google Scholar

Muzaffaruddin, S., and Peter, L. B. (2019). Analysis and Design of Periodic Beams for Vibration Attenuation. J. Vib. Control. 25 (1), 228–239. doi:10.1177/1077546318774436

CrossRef Full Text | Google Scholar

Orris, R. M., and Petyt, M. (1974). A Finite Element Study of Harmonic Wave Propagation in Periodic Structures. J. Sound Vib. 33 (2), 223–236. doi:10.1016/s0022-460x(74)80108-2

CrossRef Full Text | Google Scholar

Pany, C., Mukherjee, S., and Parthan, S. (1999). Study of Circumferential Wave Propagation in an Unstiffened Circular Cylindrical Shell Using Periodic Structure Theory. J. Inst. Eng. IE(I), Aerosp. Div. 80, 18–24.

Google Scholar

Pany, C., and Parthan, S. (2003a). Axial Wave Propagation in Infinitely Long Periodic Curved Panels. J. Vib. Acoust. 125 (1), 24–30. doi:10.1115/1.1526510

CrossRef Full Text | Google Scholar

Pany, C., and Parthan, S. (2003b). Flutter Analysis of Periodically Supported Curved Panels. J. Sound Vib. 267, 267–278. doi:10.1016/S0022-460X(02)01493-1

CrossRef Full Text | Google Scholar

Pany, C., and Parthan, S. (2002). Free Vibration Analysis of Multi-Span Curved Beam and Circular Ring Using Periodic Structure Concept. J. Inst. Eng. IE(I), Aerosp. Div. 83, 18–24.

Google Scholar

Pany, C., Parthan, S., and Mukherjee, S. (2002). Vibration Analysis of Multi-Supported Curved Panel Using the Periodic Structure Approach. Int. J. Mech. Sci. 44 (2), 269–285. doi:10.1016/S0020-7403(01)00099-6

CrossRef Full Text | Google Scholar

Pany, C., Parthan, S., and Mukhopadhyay, M. (2001). Free Vibration Analysis of an Orthogonally Supported Multi-Span Curved Panel. J. Sound Vib. 241 (2), 315–318. doi:10.1006/jsvi.2000.3240

CrossRef Full Text | Google Scholar

Pany, C., Parthan, S., and Mukhopadhyay, M. (2003). Wave Propagation in Orthogonally Supported Periodic Curved Panels. J. Eng. Mech. 129 (3), 342–349. doi:10.1061/(ASCE)0733-9399(2003)129:3(342)

CrossRef Full Text | Google Scholar

Sigalas, M. M., and Economou, E. N. (1994). Elastic Waves in Plates with Periodically Placed Inclusions. J. Appl. Phys. 75 (6), 2845–2850. doi:10.1063/1.356177

CrossRef Full Text | Google Scholar

Sinha, G., Sheikh, A. H., and Mukhopadhyay, M. (1992). A New Finite Element Model for the Analysis of Arbitrary Stiffened Shells. Finite Elem. Analysis Des. 12, 241–271. doi:10.1016/0168-874x(92)90036-c

CrossRef Full Text | Google Scholar

Thierry, V., Brown, L., and Chronopoulos, D. (2018). Multi-scale Wave Propagation Modelling for Two-Dimensional Periodic Textile Composites. Compos. Part B Eng. 150, 144–156. doi:10.1016/j.compositesb.2018.05.052

CrossRef Full Text | Google Scholar

Wang, G., Wen, X., Wen, J., Shao, L., and Liu, Y. (2004). Two-dimensional Locally Resonant Phononic Crystals with Binary Structures. Phys. Rev. Lett. 93 (15), 154302. doi:10.1103/PhysRevLett.93.154302

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Gang, W., Jihong, W., and Xisen, W. (2012). Flexural Vibration Band Gaps in Periodic Stiffened Plate Structures. Mechanika 18 (2), 186–191. doi:10.5755/j01.mech.18.2.1557

CrossRef Full Text | Google Scholar

Xiang, Y., and Wei, G. W. (2002). Exact Solutions for Vibration of Multi-Span Rectangular Mindlin Plates. J. Vib. Acoust. 124, 545–551. doi:10.1115/1.1501083

CrossRef Full Text | Google Scholar

Xiang, Y., Zhao, Y. B., and Wei, G. W. (2002). Levy Solutions for Vibration of Multi-Span Rectangular Plates. Int. J. Mech. Sci. 44, 1195–1218. doi:10.1016/s0020-7403(02)00027-9

CrossRef Full Text | Google Scholar