Two-dimensional irregular packing problems: A review

1 Introduction

Two-dimensional (2D) irregular packing problems are widespread in industries such as machinery manufacturing, aviation, shipbuilding, automobile manufacturing, clothing and furniture manufacturing. An efficient 2D irregular packing algorithm can effectively improve material utilization and reduce processing costs. The reduction in material consumption will also have a beneficial impact on the environment (Ke et al., 2020). Therefore, research of the packing problem is of great significance for technology and social interest.

The 2D packing problem is a type of combinatorial optimization problems to locate parts with different shapes compactly in one or more master sheet material to minimize the occupied space or maximize the utilization of the material. The 2D packing problem is currently recognized as a NP problem, which is mainly solved by heuristic algorithms. In recent years, many scholars have conducted research on 2D irregular packing problems with a verity of solutions.

There exists a number of review articles on packing and cutting problems. We have summarized the main review literature in the field of 2D packing and cutting as shown in Table 1. Brown (Brown, 1971) introduced an optimum packing and depletion problem with optimization of space and resource usage. Harvey (Salkin and De Kluyver, 1975) surveyed the application of mathematical optimization models such as linear programming to the knapsack problem. Bruce (Golden, 1976) surveyed various approaches to the cutting stock problem. Hinxman (Hinxman, 1980) surveyed the trim-loss and assortment problems, this research paid more attention to cutting and packaging problems in practical applications, and did not mention much about theoretical methods. Garey and Coffman (Garey and Johnson, 1981; Coffman et al., 1984) surveyed the approximation algorithms for bin packing problems. Israni (Israni and Sanders, 1982) reviewed the 2D cutting stock problem including almost all 2D packaging problems. The author also proposed a rectangular layout method. Sarin (Sarin, 1983) reviewed methodologies and literature to solve 2D stock cutting problems and introduced an interactive optimization procedure for a general 2D stock cutting problem. Dyckhoff (Dyckhoff et al., 1985) described a trim loss and related problems and categorized them briefly. Dudziński (Dudziński and Walukiewicz, 1987) summarized the exact methods for knapsack problems, such as linear programming. Matthias (Rode and Rosenberg, 1987) analyzed the algorithm for the trim-loss problems. Haessler (Haessler and Sweeney, 1991) reviewed the solution process of cutting stock problems, including placement algorithm and sequence optimization algorithm. Dowsland (Dowsland and Dowsland, 1992) reviewed the application of operations research methods to the packing problem and summarized some exact heuristics. Sweeney (Sweeney and Paternoster, 1992) categorized cutting and packing problems and made application-oriented research records. Cheng (Cheng et al., 1994) discussed 2D cutting stock problems and their application cases including the pallet loading problem and VLSI placement problem. With the gradual deepening of research on 2D layout problems, typology becomes a common research topic. 2D regular and irregular layout problems are clearly distinguished in practical applications and theoretical methods. Dowsland (Dowsland and Dowsland, 1995) gave a special review of the 2D irregular nesting problem for the first time. Mavridou (Mavridou and Pardalos, 1997) summarized applications of the genetic algorithm and simulated annealing algorithm in the optimization of facility layout problems. Dyckhoff (Dyckhoff, 1990) made a typology of the cutting and packing problems in detail, and Wäscher (Wäscher et al., 2007) improved the typology later. Hopper (Hopper and Turton, 1999; Hopper and Turton, 2001a; Hopper and Turton, 2001b) investigated the application of meta-heuristic and heuristic algorithms in 2D and 3D packing problems. Lodi (Lodi et al., 2002a; Lodi et al., 2002b) reviewed algorithms proposed in the 1990s of 2D packing problems. Bennell et al. (Bennell and Oliveira, 2008; Bennell and Oliveira, 2009) discussed 2D irregular packing problems and related geometric problems. Leao (Leao et al., 2020) introduced the mathematical models in the 2D irregular packing problem.

TABLE 1

TABLE 1. Review literature in the field of cutting and packing problems.

The scope of these reviews is broad, mainly for all 2D packing problems including rectangular packing and other regular packing problems. These review papers are out of date with missed innovative algorithms of 2D irregular packing. Since 2010, only Leao (Leao et al., 2020) reviewed 2D irregular packing problems. But he only introduced the mathematical models, instead of reviewing 2D irregular packing problems comprehensively. In recent years, there is not a comprehensive review paper of the 2D irregular packing problems.

The mathematical models of 2D packing problems are mature, and few disruptive technologies have emerged in recent years. Most of works are to improve original methods (Liu et al., 2021). Due to the rapid development of computer technology, many people studied heuristic algorithms and applied them to 2D irregular packing problems (Rakotonirainy and van Vuuren, 2021). In this paper, we review recent advances in the domain of 2D irregular packing problems based on a variety of research papers. We also summarize and classify new 2D irregular packing algorithms especially some very innovative ideas proposed in recent years. We hope that this review could provide guidance to researchers in the field of 2D irregular packing.

The structure of this paper is organized as follows. Section 2 introduces the packing and 2D irregular packing problems. In Section 3, we summarize the current state of research on 2D irregular packing problems, followed by conclusions in Section 4.

2 Problem description

The general trim-loss problems refer to the optimal allocation of various resources, such as time, space, capital, value, and tasks. The layout or packing optimization is mainly for the optimal allocation of spatial resources (Cook, 1971). The ultimate optimization goal of a cutting and packing problem is to maximize the utilization of the sheet material or to minimize the amount of sheet material left over.

The performance evaluation indicators of packing algorithms include material utilization (or filling rate) and time computational overhead. For strip materials, the material utilization rate is mainly reflected by the final height value after the packing has been completed. Since there is no posture constraint, a part can be placed anywhere in the master surface with any angle, and the same batch of parts can have multiple orders, the solution space for the 2D irregular packing problem is very large. The packing problem is therefore an NP-complete (NP-C) problem (Zhang et al., 2022a; Li et al., 2022); that is, there is no effective polynomial algorithm that can identify an optimal solution in polynomial time. For NP-C problems, the existing solution is to find an approximate optimal solution using a heuristic algorithm.

2.1 Packing problem classification

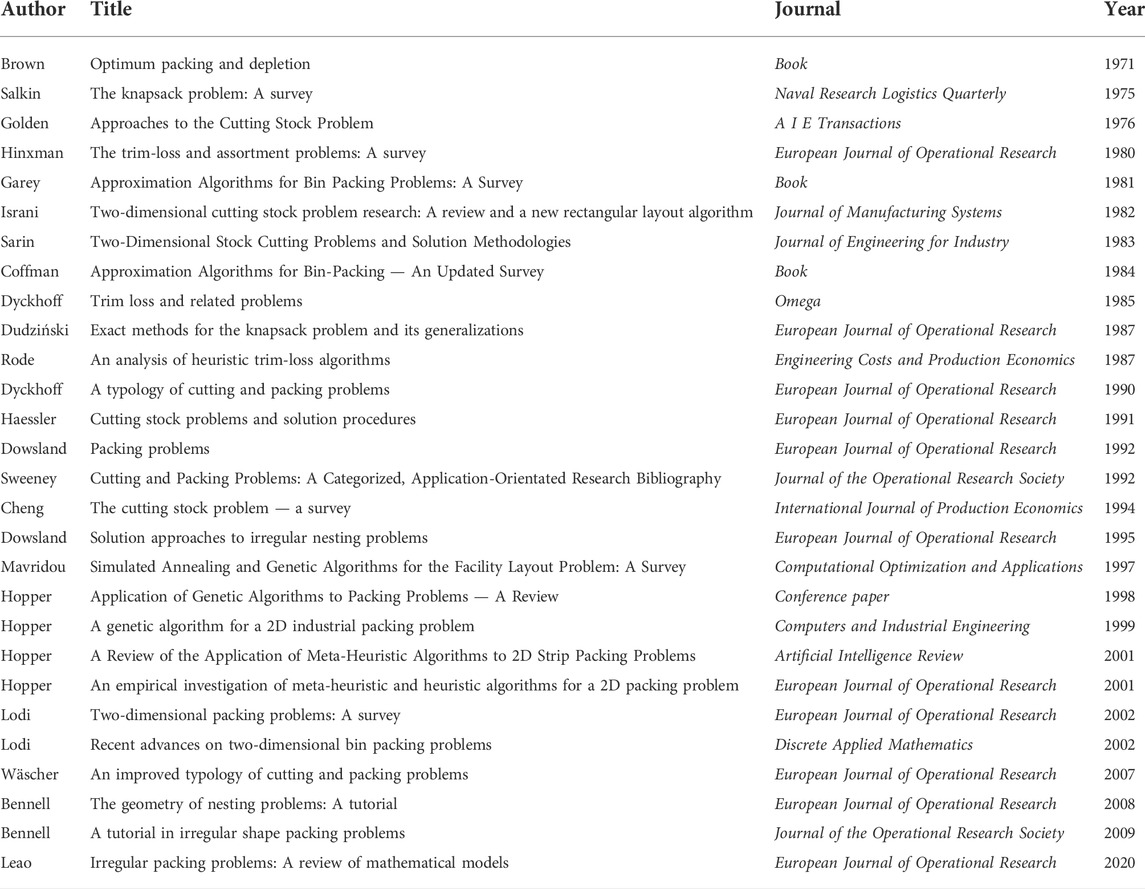
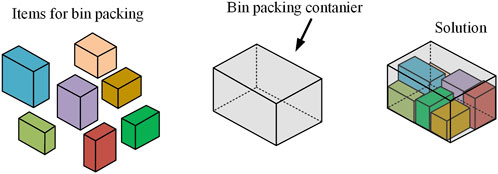
The packing problem can be divided into three categories according to spatial dimensions and application types: the one-dimensional (1D) packing problem (wire packing problem) (Loh et al., 2008; Fleszar and Charalambous, 2011; Kucukyilmaz and Kiziloz, 2018), as shown in Figure 1; the 2D packing problem (planar packing problem); and the three-dimensional (3D) packing problem (Martello et al., 2000; Allen et al., 2011; Paquay et al., 2018; Lamas-Fernandez et al., 2022; Zhao et al., 2022), as shown in Figure 2. According to the regularity of shapes of participating parts, the 2D packing problem can be further divided into 2D regular (such as Figure 3) and irregular packing problems. The 2D regular packing problem includes the layout problem of regular polygons such as rectangles (Martello and Monaci, 2015; Wu et al., 2016; Wu et al., 2017; Joós, 2018; Erzin et al., 2021) and circles (George et al., 1995; Nurmela and Östergård, 1997; Huang and Xu, 1999; Wang et al., 2002; Zhang and Deng, 2005; Liu et al., 2016; Fekete et al., 2019). The 2D irregular layout problem mainly involves the layout of irregular shapes.

FIGURE 1

FIGURE 1. 1D packing problem.

FIGURE 2

FIGURE 2. 3D bin packing problem.

FIGURE 3

FIGURE 3. 2D regular packing problem.

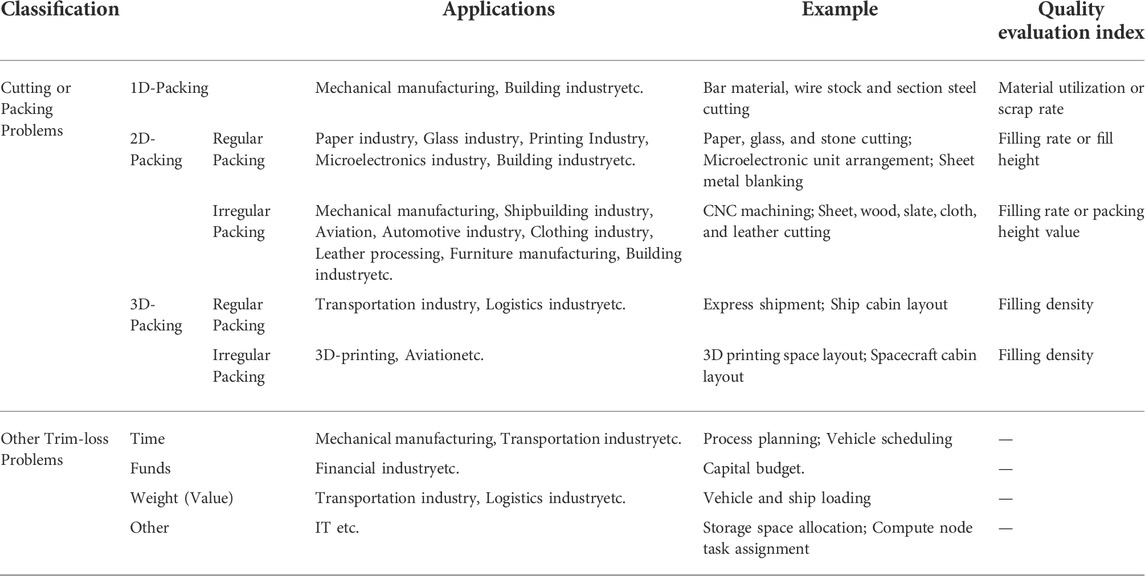
We have summarized the classification and application of some packing problems, as shown in Table 2. The problem of packing is widely experienced in production with different characteristics in different industries. The nomenclature of packing problems in different fields is also different. The literature (Dyckhoff, 1990) provides a detailed introduction to various type names, which can be divided into following five categories:

1) cutting stock and trim loss problems,

2) bin packing, dual bin packing, strip packing, and knapsack (packing) problems,

3) vehicle loading, pallet loading, container loading, and car loading problems,

4) assortment, depletion, design, dividing, layout, nesting, and partitioning problems,

5) capital budgeting, change making, line balancing, memory allocation, and multiprocessor scheduling problems.

TABLE 2

TABLE 2. Classification of packing problems and their applications.

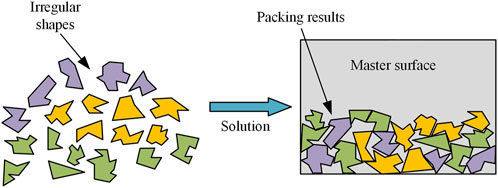
According to the literature published by a large number of scholars in the past (Hartmanis and Johnson, 1982; Hemaspaandra and Williams, 2012; Bodas et al., 2021; Fang et al., 2021; Wang et al., 2022), we define 2D irregular problems as the problem in which a set of pieces that contain at least one piece of the irregular shape must be placed in a non-overlapping configuration within a given placement area in order to optimize an objective. A piece is irregular if it requires a minimum of three parameters to identify it (Bennell and Oliveira, 2008). The placement area may include one or more regular or irregular master surface. Figure 4 describes a simple 2D irregular shape layout process.

FIGURE 4

FIGURE 4. A simple 2D irregular packing problem.

2.2 Mathematical model of 2D irregular packing problem

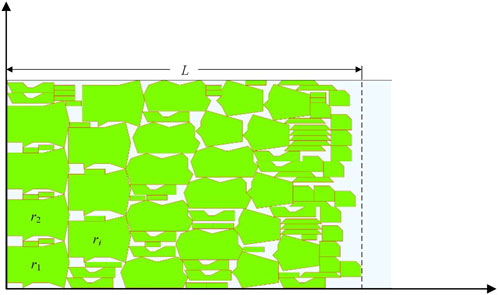
The 2D irregular packing problem is described as: some shapes are placed into a plate with a certain width and unlimited length, so that the length occupied by the shapes in the plate is the shortest (Zhang et al., 2022b; Hawa et al., 2022), as shown in Figure 5. The definition of variables is shown in Table 3.

FIGURE 5

FIGURE 5. Mathematical model of 2D irregular packing problem.

TABLE 3

TABLE 3. Variable definitions.

The mathematical model is defined as follows.

Objective function:

$\min F=\max \left\{x|\left(x,y\right)\in r_i,r_i\in R\right\}-\min \left\{x|\left(x,y\right)\in r_i,r_i\in R\right\}(1)$

Constraints:

$r_i\cap r_j=\varnothing \left(i\ne j\right)(2)$

$r\in R(3)$

$O_i\in O(4)$

$T={\displaystyle \sum _{i=1}^n{r}_i}(5)$

where, Eq. 1 indicates that the goal is to minimize the length of the area occupied by the shapes in the plate; Eq. 2 ensures that shapes do not overlap each other; Eq. 3 ensures that shapes do not exceed the plate area; Eq. 4 ensures that rotation angles of each shape are within the index range; Eq. 5 ensures that all shapes are placed on the plate.

3 Research status

Two phases are involved in solving an irregular packing problem: optimization phase and placement phase. The optimization phase searches for the packing sequence that minimizes the waste of the motherboard, and the placement phase determines the final solution of the shape. The placement optimization algorithm is used to solve the problem of mutual matching among parts, the ultimate goal is to find the best match strategy between two parts and reduce the placement gap to increase the fill rate. The ultimate goal of the sequential optimization algorithm is to find the optimal placement order for a batch of parts.

The 2D irregular packing problem generates multiple sub-problems, but the two main sub-problems are the geometric problem of the shape and the optimization of the placing sequence (Li et al., 2022). The two sub-problems are reviewed separately. In a sub-problem, we categorized the solution to 2D irregular packing problems. And some representative literatures are summarized based on the development of these algorithms.

3.1 Geometric approach

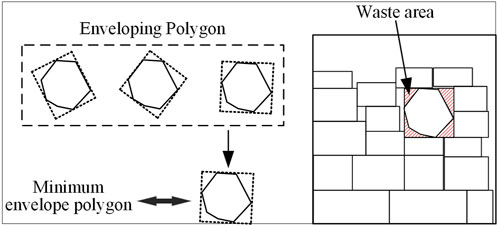
The envelope polygon is a relatively simple method for 2D irregular shape packing problems (Adamowicz and Albano, 1976; Grinde and Cavalier, 1995; Del Valle et al., 2012; Peralta et al., 2018). Its main idea for the irregular shape layout is to envelop the irregular shape with a regular polygon, and place the regular shape instead of the original irregular shape after the envelope is formed. The irregular shape can be enveloped using rectangles, circles, triangles, or other regular polygons. Although the envelope polygon can simplify the irregular shape layout problem, its packing density is very low due to the waste area generated by the envelope process, as shown in Figure 6. In addition to the enveloping polygon method, early methods for solving simple irregular packing problems included the clustering feature combination method and fitting method (Koroupi and Loftus, 1991). Elkeran (Elkeran, 2013) proposed an envelope polygon method based on pairwise clustering. Shapes were combined according to their contour features, and the envelope polygon method was then used for the layout. Stoyan et al. (Stoyan et al., 2016) proposed an improved starting point algorithm (SPA) to solve the problem of positioning a convex polygon with a minimum area. But the solution to the non-convex polygon was not good enough. The core idea of the above methods is to convert irregular parts into regular parts by specific methods, and then to packing regular parts instead of (the initial) irregular parts. However, above method does not essentially avoid the waste area. Also, for parts with a complex shape, it is difficult to solve for the smallest possible enveloping polygon.

FIGURE 6

FIGURE 6. The polygon enveloping method for 2D irregular packing.

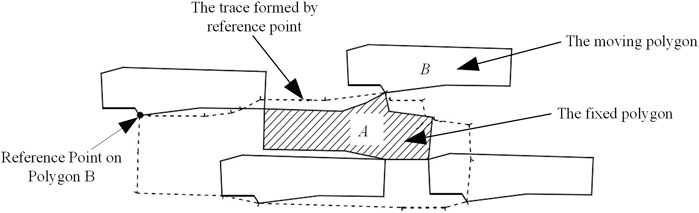
To better solve the 2D packing problem of complex shape parts, researchers in the late 1970s began to study contour features of irregular parts themselves. They explored ways to match up the contour features of items. The no-fit polygon (NFP) method was suggested at that time. NFP is an effective means of solving 2D packing problems (Oliveira et al., 2000; Bennell et al., 2001; Burke et al., 2007). A brief definition of the no fit polygon (NFP) is as follows: given two polygons, one of which is fixed, the other polygon does non-rotating rigid body motion around a fixed polygon, and slides around the fixed polygon until it returns to the starting position, in the process of motion when a point is selected as a reference point on the polygon, the trajectory formed by the reference point during the circular motion is called a no fit polygon, as shown in Figure 7. The NFP method is a popular method used to calculate an area in which no two shapes will overlap, and in which it is possible to find all possible match positions between two shapes. The NFP method obtains the best placement position by finding all relative positions of two shapes in different postures, which provides an exact solution. Although the NFP method is effective in solving 2D packing problems, it also has following two limitations: 1) The NFP method requires multiple rotations of the shape when searching an optimal placement position, which results in an increase in computation time overhead and even miss the optimal placement position. Some scholars have proposed using the NFP method combined with a free rotation for the layout (Martinez-Sykora et al., 2017; Abeysooriya et al., 2018), but it was only applied in a very simple data set, and the applicability has not been sufficiently verified. 2) It is very difficult to solve the NFP of non-convex polygons, especially with deformed contours. The NFP method also has another problem for the 2D free-form shape layout. It uses vertices of the shape to determine the relative position between shapes. For 2D free-form shapes, after the layout is completed by the NFP method, the shapes mainly rely on the point contact, which reduces the filling rate. In summary, a significant drawback of the NFP approach is the non-trivial task of developing a robust NFP generator for general nonconvex polygons. Art (Art, 1966) first used the NFP in its most basic form as the placement envelope. However, the potential of the NFP was not fully exploited until the work of Milenkovic et al. (Milenkovic et al., 1992). Other methodologies to generate NFP can be found in publications of relevant scholars (Agarwal et al., 2002; Dean et al., 2006; Huyao et al., 2007; Burke et al., 2010).

FIGURE 7

FIGURE 7. The process of solving NFP of two polygons.

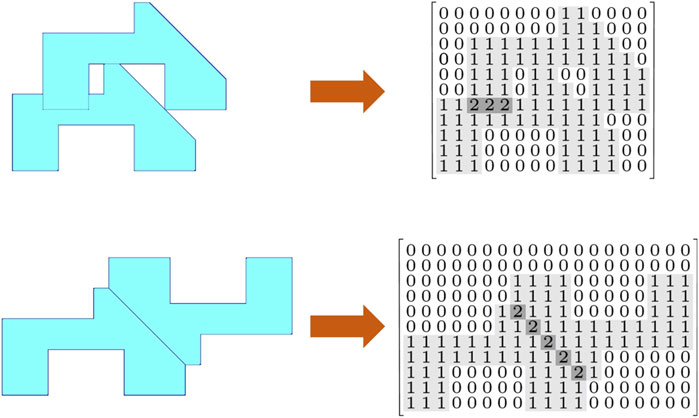
Raster methods (also called pixel methods) divide the continuous stock sheet into discrete areas, hence reducing geometric information to code data by a grid represented by a matrix. The raster method performs packing by discretizing the master surface and parts into dots or pixels. The master surface and parts are discretized into lots of grids; the pixel value of occupied areas is set to 0 or 1, and the pixel value of unoccupied areas is set to 1 or 0. It relies on the discrete pixels to complete the positioning, docking, and overlap judgment among the parts. In each case the process of eliminating overlap between pieces or identifying non-overlapping placement positions is just a matter of counting cells in the grid. A simple raster method for 2D irregular packing is shown in Figure 8. In earlier times, three scholars (Segenreich and Faria Braga, 1986; Oliveira and Ferreira, 1993; Ramesh Babu and Ramesh Babu, 2001) gave different interpretations of the raster method. In recent years, the raster method has been widely used in 2D irregular layout packing problems (Guo, Peng, Cheng, Dai; Sato et al., 2016; Mundim et al., 2017). Computer vision was also used in 2D irregular packing problems (Bouganis and Shanahan, 2007). By discriminating the part and master surface using assigned black and white pixel values, it can be determined whether there is sufficient placement space on the master surface for the part. These approaches reduce the complexity of packing problems. However, disadvantages are that these methods are memory intensive and cannot exactly represent pieces with non-orthogonal edges. In addition, the size of the final discrete point of shapes affects the placement accuracy, and the size of the discrete points is often difficult to determine.

FIGURE 8

FIGURE 8. The pixel (or raster) method.

Linear programming (LP) and mixed-integer linear programming (MIP) models are also used for 2D irregular packing problems. The LP method and MIP model were first used to deal with 1D packing problems. This method was later used for irregular packing problems with good results. The MIP and LP methods solve the problem by establishing an exact mathematical model of the packing process under constraints that do not allow overlaps between parts, and the parts must be included in the master surface. The idea of solving 2D irregular layout problems by MIP and LP methods can be referred to literature (Gomes and Oliveira, 2006; Fischetti and Luzzi, 2009; Toledo et al., 2013; Santoro and Lemos, 2015; Cherri et al., 2016; Leao et al., 2016; Rodrigues and Toledo, 2017; Cherri et al., 2018). Mixed integer programming (MIP) and other operational research methods were often combined with the NFP method for 2D layout problems (Silva et al., 2010). The method works well for most of 2D irregular shape layout problems. But if the shape vertices are numerous, the determination of constraints of the MIP model will be difficult.

3.1.1 Placement rules

During the part placement process in 2D irregular packing, the placement algorithm is a rule to evaluate the candidate position. Commonly used placement algorithms are as follows.

The BL algorithm prioritizes placing the reference point of the piece in the leftmost feasible position on the stock sheet breaking ties by selecting the bottom-most of left most positions. This rule iteratively moves each piece horizontally as far to the left as possible and then vertically until it is able to move horizontally again or touches another piece or the bottom of the stock sheet, as shown in Figure 9. This rule may equally apply to other directions such as top right. The final piece position is constrained to be inside the stock sheet and should not overlap previously placed pieces. This placement strategy was first applied to nesting problems by Chazelle (Chazelle, 1983), and the same principles were still applied in more recent solution approaches (Dowsland et al., 2002). The implementation of the BL placement heuristic depends on the geometric representation adopted for the pieces. If the raster or polygonal representations are adopted, we must use a strategy of moving the pieces in steps over the layout while checking for feasibility at each step. If overlap is detected after a movement to the left, the previous position is resumed and a movement towards the bottom is tried. If this move is feasible, the algorithm returns to movements towards the left and the algorithm continues. The piece finds its final position when it cannot move to the left or towards the bottom. This implementation of the BL strategy basically imitates the sliding of a piece over the layout. Some scholars have proposed iBL (improving bottom-left) (Liu and Teng, 1999) and BLF (bottom left fill) algorithms (Gomes and Oliveira, 2002) on the basis of the BL algorithm. As an alternative method to BL, the above placement rules are also widely used.

FIGURE 9

FIGURE 9. BL placement rules.

Three alternative placement rules to BL were proposed with the aim of keeping the layout as compact as possible while trying to avoid an increase in length as follows.

1) Maximum utilization (Burke et al., 2006): The Maximum utilization placement rule selects the position that provides the maximum area utilization in the earliest bin. The rule calculates the utilization after each iteration of the part placement, and then selects the location where the utilization is maximized.

2) Minimum length (Burke et al., 2006): The minimum length placement rule minimizes the length of the rectangular enclosure of the newly generated partial solution.

3) Lowest gravity center: This method first finds the center of gravity (geometric center) of the polygon, and then selects the position with the lowest center of gravity of the part as the final entry position of the part during the nesting process. To get a fast and effective placement principle for pieces, Liu and He (Liu and He, 2006) proposed a principle named the lowest-gravity-center principle to rapidly find the placement position on NFP. In this placement principle, the placement position on NFP is chosen where the piece has the lowest gravity center. This principle is aimed to “push” the piece to the nested pieces as closely as possible, and make a relatively flat nesting boundary for the remaining pieces to be nested in. Dowsland (Dowsland, Dowsland, Bennell) proposed the classic Jostle approach. By simulating the action of a gravitational field, this method arranges parts in the lower area of the motherboard, minimizing the overall center of gravity of all parts and thus rendering them stable.

The above placement rules were used in many of methods proposed in literature (Wang et al., 2018).

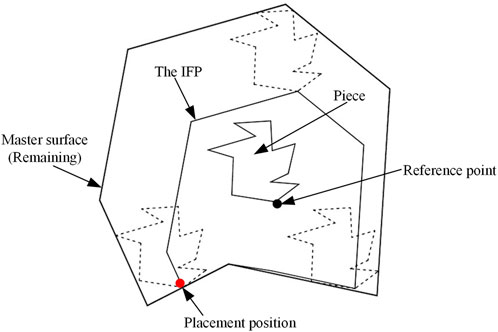
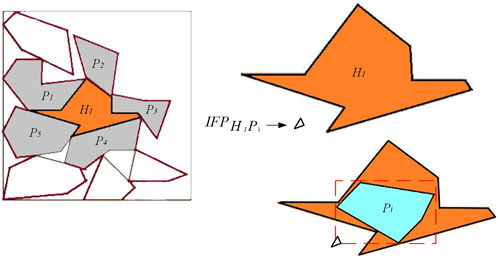
Referring to NFP, inner fit polygon (IFP) (Bennell and Song, 2008) is also an effective placement algorithm. By finding the IFP, the optimal placement position of the shape in the remaining space of the master surface can be calculated, as shown in Figure 10. One of the advantages of IFP is that it can fill holes generated by the combination of shapes during the layout process to improve the layout density. As shown in Figure 11, suppose H1 is a hole formed by shapes P1, P2, P3, P4, P5, and the hole can be filled by solving IFP. First, the IFP of hole H1 and shape Pi is obtained. According to the IFP, a feasible solution of the placement position of shape Pi in hole H1 can be obtained. Before filling the hole, we can determine whether the shape meets conditions for placing in the hole. If the area of arbitrary shape Pi is larger than the area of the hole, shape Pi cannot be placed in the hole.

FIGURE 10

FIGURE 10. Solve the IFP between the remaining space of the master surface and shape.

FIGURE 11

FIGURE 11. Use IFP to complete Hole-filling.

In addition to placement algorithms mentioned above, we have also summarized some new placement algorithms proposed in recent years. Bennell (Bennell and Song, 2010) proposed a beam search algorithm that combines placement strategies with search strategies to place instances. To overcome complex constraints of geometry (non-convex polygons and holes) and produce robust mathematical programming models, Cherri (Cherri et al., 2016) used non-overlapping constraints for direct triangulation functions. This method can solve the problem of any non-convex polygon, and be still applicable to any geometry with holes, and the method is stable in numerical stability. Guo (Guo et al., 2019) proposed a placement strategy based on curve coding and feature matching. This is a new placement strategy based on curve similarity feature matching. The above-mentioned placement algorithms have very good results for specific problems, but the reliability and applicability need to be further verified.

3.1.2 Collision algorithms

During the packing process of irregular parts, regardless of the method is used, the collision should be considered to determine the exact part placement position and avoid any overlap among the parts. In short, how exactly the shape is placed in a predetermined position during layout.

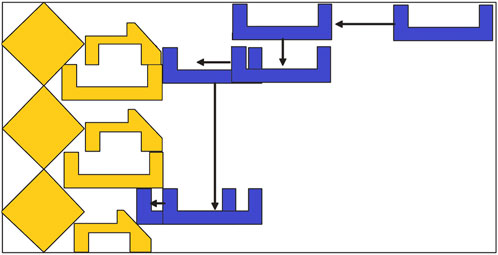
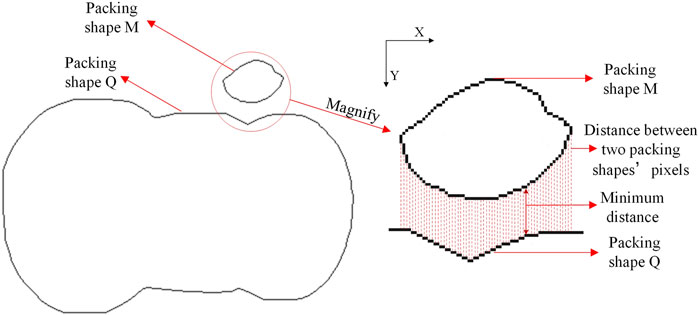
In addition to solving problems of 2D irregular packing, the pixel method is also an effective method of collision detection. Boundary pixels of the shape are usually used to determine the angle of rotation and the distance that the shape needs to be moved to place it in a predetermined position. Therefore, we can make a collision between shapes using judgment of distance. This method determines the amount of movements required for a collision to occur between parts by calculating the distance between the two parts. Generally, the shortest collision distance between parts is selected by calculating the distance between line and line, between line segment and arc, between arc and arc, etc. As shown in Figure 12, shape M is placed on the boundary of shape Q. The shortest distance is first calculated between boundary pixels of shapes M and Q, and shape M can then be accurately placed on Q’s boundary as long as it moves along the Y-axis by a shortest distance. Liu et al. (Liu et al., 2015) proposed a point-to-point interactive collision algorithm to determine the intersection and distance along the collision direction. Cherri (Cherri et al., 2018) and Peralta (Peralta et al., 2018) noticed the relationship between a point and a line, and used D-Function to calculate the distance between line and point to measure overlapping.

FIGURE 12

FIGURE 12. Make a collision using judgment of distance.

The mobile collision method is an effective method of collision. This method moves the part into a collision with another part to determine whether the two parts are overlapping. If the two parts do overlap, the parts are separated; if they do not overlap, they are moved toward each other in steps until the appropriate placement is achieved. The mobile collision method was described in literature (Riff et al., 2009) as a theoretical method. Burke et al. (Burke et al., 2007) proposed an improved moving collision method for solving all placement positions between two polygons. Stoyan (Stoyan et al., 2016) and Akang Wang (Wang et al., 2018) improved the circular fill algorithm. They relaxed problems using quadratic programming for optimality.

3.2 Sequence optimization

Another sub-problem involved in 2D irregular packing problems is the sequence optimization of parts during the packing process. Specifically, for a batch of parts, the goal of the optimization phase is to determine the order to place the parts. The order of the parts placed is critical to the final packing result. A slight change in sequence can affect the overall packing effect. Therefore, an efficient sequential optimization algorithm is critical to increase the fill rate of final nested results. Since the nesting problem is combinatorial and NP-complete, most of the core meta-heuristics have been applied to nesting problems, including Tabu Search (Glover and Marti, 1998), Simulated Annealing (van Laarhoven and Aarts, 1987), Genetic Algorithm (Cinat et al., 2020), Colony Algorithm (Dorigo et al., 1996) and other meta-heuristic or heuristic algorithms.

Genetic algorithm is a widely used intelligent algorithm. It is widely used in industrial engineering, artificial intelligence, biological engineering, automatic control and other fields to solve complex optimization problems. The genetic algorithm simulates the genetic laws of nature. A nearly optimal solution is obtained by setting the genetic code of the population and individuals, and simulating operations of selection, crossover, and mutation in the natural world to produce a better feasible solution with several generations of iterations. When using a genetic algorithm to solve the 2D irregular alignment problem, a complete shape sequence is encoded as an individual, and a new solution is then generated through operations of each genetic operator. The packing density or filling rate can be defined as the fitness function used to evaluate the quality of solutions. After multiple iterations, a better sequence will eventually be obtained. Genetic algorithms have been used as an efficient method for optimizing layout problems. Specific literature can refer to (Goodman et al., 1994; Jakobs, 1996; Tay et al., 2002; Onwubolu and Mutingi, 2003; Bortfeldt, 2006; Soke and Bingul, 2006).

The simulated annealing algorithm simulates the annealing process of solid metals, and its essence is to optimize the objective function by imitating the movement process of metal particles in the process of temperature rise and fall so that the particles finally reach the ground state and have low internal energy. For the 2D irregular packing problem, each part can be regarded as a metal particle. In the process of temperature rise or fall, all shapes will produce different permutations and combinations. When the layout shapes are most compactly, that is, when the material utilization of the master surface is the highest or the layout density is the highest, the ground state is reached, and the optimal solution of the layout problem is obtained. The simulated annealing algorithm has advantages of the strong robustness, simple and flexible operations. The simulated annealing algorithm was also used in optimizing the shape sequence of 2D layout problems, such as (Mancapa et al., 2009; Mundim et al., 2018).

The ant colony algorithm was inspired by the process of an ant colony searching for food. Unlike other meta-heuristic algorithms, the ant colony algorithm has the characteristics of distributed computing, positive information feedback, and heuristic search. It is essentially a heuristic global optimization algorithm in evolutionary algorithms. When dealing with 2D irregular layout problems, the walking path of the ant is used to represent the feasible solution of the shape sequence, and all the paths of the entire ant colony constitute the solution space of the shape sequence. Ants with shorter paths release more pheromone. As time progresses, the concentration of pheromone accumulated in shorter paths gradually increases, and the number of ants who choose this path (shape sequence) is increasing. In the end, the entire ant will focus on the best path under effect of the positive feedback. At this time, it corresponds to the solution with the highest packing density in the solution space. References on the use of ant colony algorithms to optimize 2D irregular layout can refer to (Heckmann and Lengauer, 1995; Souilah, 1995).

Particle swarm optimization and Tabu Search were also used in the optimization of 2D irregular layout problems. Unlike the previous methods, these two algorithms are more suitable for the local search. Particle swarm optimization takes the clustering behavior of organisms as a model, focusing on the collaboration and competition among individuals. Compared to the uniform search strategy of the genetic algorithm, the particle swarm optimization algorithm guides the search process in the direction of the current optimal solution. Relatively speaking, the particle swarm algorithm is simpler and faster than the genetic algorithm, but it often converges prematurely and is greatly affected by its parameters. References on the use of particle swarm optimization to optimize 2D irregular layout can refer to (Levine and Ducatelle, 2004; Mohamed and Adnan, 2009; Arnaout et al., 2020). The Tabu search algorithm is different from other heuristic algorithms, such as simulated annealing and genetic algorithms. The Tabu search algorithm prevents backtracking in multiple iterations when performing a search. References on the use of Tabu search to optimize 2D irregular layout can refer to (Bennell and Dowsland, 1999; Liu et al., 2008; Omar and Ramakrishnan, 2013; Shalaby and Kashkoush, 2013).

In addition to the above methods, some new optimization methods have been proposed in recent years. Gomes et al. (Gomes and Oliveira, 2002) proposed a 2-exchange heuristic to guide the search through the solution space consisting of sequences of pieces. Cherri et al. (Cherri et al., 2016) proposed an improved mixed-integer linear programming model which was easier to implement than previous models for problems of non-convex polygons with or without holes. Beyaz et al. (Beyaz et al., 2015) proposed a hyper-heuristic algorithm for solving the 2D irregular packing problem with the good robustness. Fernández et al. (Fernández et al., 2013) proposed a parallel multi-objective algorithm for 2D bin packing with rotations and load balancing. Mundim et al. (Mundim et al., 2017) used a biased random key genetic algorithm to solve the sequential optimization problem of 2D irregular packing. Segredo et al. (Segredo et al., 2014) combined Mimetic and hyper-heuristic algorithms for certain multi-objective optimization problems of 2D irregular packing. Hong et al. (Hong et al., 2014) proposed combining a heuristic packing algorithm with the best fit algorithm to solve the single bin problem. Elkeran et al. (Elkeran, 2013) developed an approach for sheet packing problems using a guided cuckoo search (Yang and Deb, 2014) and pairwise clustering. Gomez (Gomez and Terashima-Marín, 2018) used integer programing models to determine the association between geometries, and then applied the mixed integer programming (MIP) to locate geometries in the motherboard. Bennell (Bennell and Song, 2010) proposed a heuristic algorithm with the beam search using a search structure for nodes and branch trees that are similar to branch ingesting, but only a subset of nodes was evaluated in the search tree.

4 Conclusion

This paper reviewed literature on 2D irregular packing problems and solutions. Main algorithms for 2D irregular layout problems were summarized including the placement and sequence optimization.

For the packing process of 2D irregular parts, mature solutions mainly include the envelope polygon method, pixel method, NFP method and MIP method. Each method has its own advantages, but the current mainstream method is the NFP method. The envelope polygon method is more suitable for processing the packing problem of parts with simple shapes. However, for deformed parts, the envelope polygon method could not achieve good results. The pixel method is easier to complete collisions and determine whether two parts overlap, but the pixel method is not good at searching for the best layout position. The MIP method was an early method for solving packing problems. At present, many scholars still use the MIP method in the packing problem with good results. Although the NFP method performs well in dealing with 2D irregular packing problems, it still has its limitations. For complex free shapes, the current NFP algorithm could not find the satisfied solution. Therefore, for the problem of NFP, further research is required for a more efficient method. Heuristic and meta-heuristic algorithms are the mainly methods used in the sequential optimization of 2D irregular packing (Gardeyn and Wauters, 2022; Sato et al., 2022). Machine learning and deep learning algorithms may help the sequential optimization of packing in the future, but there is a lack of research in this area currently.

Most of the research on 2D irregular packing approaches are from two aspects. On the one hand, the problem of packing is regarded as an optimization problem from the perspective of mathematics, physics, and geometry. On the other hand, from the perspective of engineering, the packing problem is regarded as practical applications of the project. The focus and expected goals of these two perspectives are different. Research on packing problems from the perspective of mathematics, physics, and geometry focuses on to achieve placement operations and compile a reasonable description of the shape of parts. The biggest difference in solving packing problems from the engineering perspective is that the process constraints and feasibility of manufacturing must be considered. In addition to this, the efficiency of packing algorithms is an important factor. In general, the starting point of the two viewpoints is different, but the same issues are at stake for the same problems, the final problem to be solved is the same, and the ultimate goal is to improve the efficiency and quality of the packing. Currently, 2D irregular layout algorithms have been applied to industry, such as additive manufacturing (Zhang et al., 2016; Griffiths et al., 2019), factory layout (Jeong et al., 2018; Qin et al., 2018), and other manufacturing industries (M'Hallah and Bouziri, 2016; Xu, 2016; Ciulli, 2019; Hamada et al., 2019).

Although the existing research on 2D irregular layouts has achieved significant results and has been applied in practical engineering problems, some problems remain to be solved. First, the current algorithms are less versatile with significant differences in performance across different data sets. There are two reasons for this phenomenon. One is due to the diversity of the contours of parts, but we think this is not the main reason. The main reason for this phenomenon is that the current methods cannot rely on the shape characteristics of the parts to match them. Although scholars have proposed some packing algorithms based on the contour features of the part, there is no complete theoretical basis and mathematical model, and the reliability also needs to be verified. Therefore, the future research on 2D irregular packing should focus on solving this problem. Using a more accurate mathematical language to describe contour features and guide matching of parts should be the main direction of future research.

Another shortcoming of current methods is in solutions of the NP-C problem. There is currently no good way to solve the NP-C problem. However, to some extent, the reason that 2D irregular packing as an NP-C problem is mainly due to the current packing strategy. At present, all mainstream packing strategies place parts into the packing motherboard according to the optimal sequence, or they search for the best matching parts and collision locations by constantly searching. In this case, 2D irregular packing problems will undoubtedly become an NP-C problem. Although the existing search algorithms and optimization methods are able to perform the packing strategy well, the computational overhead is high. Let us envision another packing strategy: put all parts into a motherboard at the same time, regardless of the order and position, but treat each part as an individual that follows physical laws to achieve independent motion or relative motion. This method may achieve the steady state of the entire packing system by means of the free movement of parts. This concept is modeled on natural phenomena and has not been realized at present, but we believe that this is the direction of the future packing strategy development. This idea can be seen as a key to solving packaging problems in the future. In theory, this idea can ignore dimensional boundaries. Of course, to continually find the solution of NP-C problems is still a challenge for academics.

Author contributions

BG provided writing ideas and designed the structure of the paper. FW proofread the paper. JH completed the chapters 1 and 4 of the paper. JL looked up literature. QP completed language editing and proofreading. QZ guided all the work of this research. YZ completed the chapters 2 and 3 of the paper. All authors read and approved the final manuscript.

Funding

This work was supported by the Natural Science Foundation of China 52175488 and the Scientific research youth top talent project of Hebei Province BJ2021045.

Acknowledgments

The authors would like to thank the School of Mechanical Engineering of Yanshan University for providing research conditions. Funding from the the Natural Science Foundation of China (52175488) and the Scientific research youth top talent project of Hebei Province (BJ2021045) is gratefully acknowledged. The authors would like to thank the editors and the reviewers for reviewing this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abeysooriya, R. P., Bennell, J. A., and Martinez-Sykora, A. (2018). Jostle heuristics for the 2d-irregular shapes bin packing problems with free rotation. Int. J. Prod. Econ. 195, 12–26. doi:10.1016/j.ijpe.2017.09.014

CrossRef Full Text | Google Scholar

Adamowicz, M., and Albano, A. (1976). Nesting two-dimensional shapes in rectangular modules. Computer-Aided Des. 8 (1), 27–33. doi:10.1016/0010-4485(76)90006-3

CrossRef Full Text | Google Scholar

Agarwal, P. K., Flato, E., and Halperin, D. (2002). Polygon decomposition for efficient construction of minkowski sums. Comput. Geom.-Theory Appl. 21 (1), 39–61. doi:10.1016/S0925-7721(01)00041-4

CrossRef Full Text | Google Scholar

Allen, S. D., Burke, E. K., and Kendall, G. (2011). A hybrid placement strategy for the three-dimensional strip packing problem. Eur. J. Operational Res. 209 (3), 219–227. doi:10.1016/j.ejor.2010.09.023

CrossRef Full Text | Google Scholar

Arnaout, J. P., ElKhoury, C., and Karayaz, G. (2020). Solving the multiple level warehouse layout problem using ant colony optimization. Oper. Res. Int. J. 20 (1), 473–490. doi:10.1007/s12351-017-0334-5

CrossRef Full Text | Google Scholar

Art, J. R. C. (1966). An approach to the two dimensional irregular cutting stock problem. Cambridge, MA, USA: Massachusetts Institute of Technology.

Google Scholar

Bennell, J. A., and Dowsland, K. A. (1999). A tabu thresholding implementation for the irregular stock cutting problem. Int. J. Prod. Res. 37 (18), 4259–4275. doi:10.1080/002075499189763

CrossRef Full Text | Google Scholar

Bennell, J. A., Dowsland, K. A., and Dowsland, W. B. (2001). The irregular cutting-stock problem - a new procedure for deriving the no-fit polygon. Comput. Operations Res. 28 (3), 271–287. doi:10.1016/S0305-0548(00)00021-6

CrossRef Full Text | Google Scholar

Bennell, J. A., and Oliveira, J. F. (2009). A tutorial in irregular shape packing problems. J. Operational Res. Soc. 60, S93–S105. doi:10.1057/jors.2008.169

CrossRef Full Text | Google Scholar

Bennell, J. A., and Oliveira, J. F. (2008). The geometry of nesting problems: A tutorial. Eur. J. Operational Res. 184 (2), 397–415. doi:10.1016/j.ejor.2006.11.038

CrossRef Full Text | Google Scholar

Bennell, J. A., and Song, X. (2010). A beam search implementation for the irregular shape packing problem. J. Heuristics 16 (2), 167–188. doi:10.1007/s10732-008-9095-x

CrossRef Full Text | Google Scholar

Bennell, J. A., and Song, X. (2008). A comprehensive and robust procedure for obtaining the nofit polygon using minkowski sums. Comput. Operations Res. 35 (1), 267–281. doi:10.1016/j.cor.2006.02.026

CrossRef Full Text | Google Scholar

Beyaz, M., Dokeroglu, T., and Cosar, A. (2015). Robust hyper-heuristic algorithms for the offline oriented/non-oriented 2d bin packing problems. Appl. Soft Comput. 36, 236–245. doi:10.1016/j.asoc.2015.06.063

CrossRef Full Text | Google Scholar

Bodas, H., Drabkin, B., Fong, C., Jin, S., Kim, J., Li, W., et al. (2021). Consequences of the packing problem. J. Algebr. Comb. 54 (4), 1095–1117. doi:10.1007/s10801-021-01039-5

CrossRef Full Text | Google Scholar

Bortfeldt, A. (2006). A genetic algorithm for the two-dimensional strip packing problem with rectangular pieces. Eur. J. Operational Res. 172 (3), 814–837. doi:10.1016/j.ejor.2004.11.016

CrossRef Full Text | Google Scholar

Bouganis, A., and Shanahan, M. (2007). A vision-based intelligent system for packing 2-d irregular shapes. IEEE Trans. Autom. Sci. Eng. 4 (3), 382–394. doi:10.1109/TASE.2006.887158

CrossRef Full Text | Google Scholar

Brown, A. R. (1971). Optimum packing and depletion. Amsterdam: American Elsevier.

Google Scholar

Burke, E., Hellier, R., Kendall, G., and Whitwell, G. (2006). A new bottom-left-fill heuristic algorithm for the two-dimensional irregular packing problem. Operations Res. 54 (3), 587–601. doi:10.1287/opre.1060.0293

CrossRef Full Text | Google Scholar

Burke, E. K., Hellier, R. S. R., Kendall, G., and Whitwell, G. (2007). Complete and robust no-fit polygon generation for the irregular stock cutting problem. Eur. J. Operational Res. 179 (1), 27–49. doi:10.1016/j.ejor.2006.03.011

CrossRef Full Text | Google Scholar

Burke, E. K., Hellier, R. S. R., Kendall, G., and Whitwell, G. (2010). Irregular packing using the line and arc no-fit polygon. Operations Res. 58 (4), 948–970. doi:10.1287/opre.1090.0770

CrossRef Full Text | Google Scholar

Chazelle, B. (1983). The bottomn-left bin-packing heuristic: An efficient implementation. IEEE Trans. Comput. C-32 (8), 697–707. doi:10.1109/TC.1983.1676307

CrossRef Full Text | Google Scholar

Cheng, C. H., Feiring, B. R., and Cheng, T. C. E. (1994). The cutting stock problem - a survey. Int. J. Prod. Econ. 36 (3), 291–305. doi:10.1016/0925-5273(94)00045-X

CrossRef Full Text | Google Scholar

Cherri, L. H., Cherri, A. C., and Soler, E. M. (2018). Mixed integer quadratically-constrained programming model to solve the irregular strip packing problem with continuous rotations. J. Glob. Optim. 72 (1), 89–107. doi:10.1007/s10898-018-0638-x

CrossRef Full Text | Google Scholar

Cherri, L. H., Mundim, L. R., Andretta, M., Toledo, F. M. B., Oliveira, J. F., and Carravilla, M. A. (2016). Robust mixed-integer linear programming models for the irregular strip packing problem. Eur. J. Operational Res. 253 (3), 570–583. doi:10.1016/j.ejor.2016.03.009

CrossRef Full Text | Google Scholar

Cinat, P., Gnecco, G., and Paggi, M. (2020). Multi-scale surface roughness optimization through genetic algorithms. Front. Mech. Eng. 6. doi:10.3389/fmech.2020.00029

CrossRef Full Text | Google Scholar

Ciulli, E. (2019). Tribology and industry: From the origins to 4.0. Front. Mech. Eng. 5. doi:10.3389/fmech.2019.00055

CrossRef Full Text | Google Scholar

Coffman, E. G., Garey, M. R., and Johnson, D. S. (1984). “Approximation algorithms for bin-packing - an updated survey,” in Algorithm design for computer system design (Vienna: Springer Vienna), 49–106. doi:10.1007/978-3-7091-4338-4_3

CrossRef Full Text | Google Scholar

Cook, S. A. (1971). “The complexity of theorem-proving procedures,” in Proceedings of the third annual ACM symposium on Theory of computing (New York, NY: Association for Computing Machinery), 151–158. doi:10.1145/800157.805047

CrossRef Full Text | Google Scholar

Dowsland, K. A., and Dowsland, W. B. (1995). Solution approaches to irregular nesting problems. Eur. J. Operational Res. 84 (3), 506–521. doi:10.1016/0377-2217(95)00019-M

CrossRef Full Text | Google Scholar

Dean, H. T., Tu, Y., and Raffensperger, J. F. (2006). An improved method for calculating the no-fit polygon. Comput. Operations Res. 33 (6), 1521–1539. doi:10.1016/j.cor.2004.11.005

CrossRef Full Text | Google Scholar

Del Valle, A. M., de Queiroz, T. A., Miyazawa, F. K., and Xavier, E. C. (2012). Heuristics for two-dimensional knapsack and cutting stock problems with items of irregular shape. Expert Syst. Appl. 39 (16), 12589–12598. doi:10.1016/j.eswa.2012.05.025

CrossRef Full Text | Google Scholar

Dorigo, M., Maniezzo, V., and Colorni, A. (1996). Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man. Cybern. B 26 (1), 29–41. doi:10.1109/3477.484436

CrossRef Full Text | Google Scholar

Dowsland, K. A., Dowsland, W. B., and Bennell, J. A. (1998). Jostling for position: Local improvement for irregular cutting patterns. J. Oper. Res. Soc. 49 (6), 647–658. doi:10.1057/palgrave.jors.260056310.1038/sj.jors.2600563

CrossRef Full Text | Google Scholar

Dowsland, K. A., and Dowsland, W. B. (1992). Packing problems. Eur. J. Operational Res. 56 (1), 2–14. doi:10.1016/0377-2217(92)90288-K

CrossRef Full Text | Google Scholar

Dowsland, K. A., Vaid, S., and Dowsland, W. B. (2002). An algorithm for polygon placement using a bottom-left strategy. Eur. J. Operational Res. 141 (2), 371–381. doi:10.1016/S0377-2217(02)00131-5

CrossRef Full Text | Google Scholar

Dudziński, K., and Walukiewicz, S. (1987). Exact methods for the knapsack problem and its generalizations. Eur. J. Oper. Res. 28 (1), 3–21. doi:10.1016/0377-2217(87)90165-2

CrossRef Full Text | Google Scholar

Dyckhoff, H. (1990). A typology of cutting and packing problems. Eur. J. Operational Res. 44 (2), 145–159. doi:10.1016/0377-2217(90)90350-K

CrossRef Full Text | Google Scholar

Dyckhoff, H., Kruse, H. J., Abel, D., and Gal, T. (1985). Trim loss and related problems. Omega 13 (1), 59–72. doi:10.1016/0305-0483(85)90083-0

CrossRef Full Text | Google Scholar

Elkeran, A. (2013). A new approach for sheet nesting problem using guided cuckoo search and pairwise clustering. Eur. J. Operational Res. 231 (3), 757–769. doi:10.1016/j.ejor.2013.06.020

CrossRef Full Text | Google Scholar

Erzin, A., Melidi, G., Nazarenko, S., and Plotnikov, R. (2021). A 3/2-approximation for big two-bar charts packing. J. Comb. Optim. 42 (1), 71–84. doi:10.1007/s10878-021-00741-1

CrossRef Full Text | Google Scholar

Fang, J., Rao, Y. Q., Liu, P., and Zhao, X. (2021). Sequence transfer-based particle swarm optimization algorithm for irregular packing problems. IEEE Access 9, 131223–131235. doi:10.1109/ACCESS.2021.3114331

CrossRef Full Text | Google Scholar

Fekete, S. P., Morr, S., and Scheffer, C. (2019). Split packing: Algorithms for packing circles with optimal worst-case density. Discrete Comput. Geom. 61 (3), 562–594. doi:10.1007/s00454-018-0020-2

CrossRef Full Text | Google Scholar

Fernández, A., Gil, C., Baños, R., and Montoya, M. G. (2013). A parallel multi-objective algorithm for two-dimensional bin packing with rotations and load balancing. Expert Syst. Appl. 40 (13), 5169–5180. doi:10.1016/j.eswa.2013.03.015

CrossRef Full Text | Google Scholar

Fischetti, M., and Luzzi, I. (2009). Mixed-integer programming models for nesting problems. J. Heuristics. 15 (3), 201–226. doi:10.1007/s10732-008-9088-9

CrossRef Full Text | Google Scholar

Fleszar, K., and Charalambous, C. (2011). Average-weight-controlled bin-oriented heuristics for the one-dimensional bin-packing problem. Eur. J. Operational Res. 210 (2), 176–184. doi:10.1016/j.ejor.2010.11.004

CrossRef Full Text | Google Scholar

Gardeyn, J., and Wauters, T. (2022). A goal-driven ruin and recreate heuristic for the 2D variable-sized bin packing problem with guillotine constraints. Eur. J. Operational Res. 301 (2), 432–444. doi:10.1016/j.ejor.2021.11.031

CrossRef Full Text | Google Scholar

Garey, M. R., and Johnson, D. S. (1981). “Approximation algorithms for bin packing problems: A survey,” in Analysis and design of algorithms in combinatorial optimization (Vienna: Springer Vienna), 147–172. doi:10.1007/978-3-7091-2748-3_8

CrossRef Full Text | Google Scholar

George, J. A., George, J. M., and Lamar, B. W. (1995). Packing different-sized circles into a rectangular container. Eur. J. Operational Res. 84 (3), 693–712. doi:10.1016/0377-2217(95)00032-L

CrossRef Full Text | Google Scholar

Glover, F., and Marti, M. (1998). “Tabu search,” in Metaheuristic procedures for training neutral networks (Boston, MA: Springer US), 53–69. doi:10.1007/0-387-33416-5_3

CrossRef Full Text | Google Scholar

Golden, B. L. (1976). Approaches to the cutting stock problem. A I I E Trans. 8 (2), 265–274. doi:10.1080/05695557608975076

CrossRef Full Text | Google Scholar

Gomes, A. M., and Oliveira, J. F. (2002). A 2-exchange heuristic for nesting problems. Eur. J. Operational Res. 141 (2), 359–370. doi:10.1016/S0377-2217(02)00130-3

CrossRef Full Text | Google Scholar

Gomes, A. M., and Oliveira, J. F. (2006). Solving irregular strip packing problems by hybridising simulated annealing and linear programming. Eur. J. Operational Res. 171 (3), 811–829. doi:10.1016/j.ejor.2004.09.008

CrossRef Full Text | Google Scholar

Gomez, J. C., and Terashima-Marín, H. (2018). Evolutionary hyper-heuristics for tackling bi-objective 2d bin packing problems. Genet. Program Evolvable Mach. 19 (1), 151–181. doi:10.1007/s10710-017-9301-4

CrossRef Full Text | Google Scholar

Goodman, E. D., Tetelbaum, A. Y., and Kureichik, V. M. (1994). “A genetic algorithm approach to compaction, bin packing, and nesting problems,” in Case center for computer-aided engineering and manufacturing (Michigan, USA: Michigan State University), 940702.

Google Scholar

Griffiths, V., Scanlan, J. P., Eres, M. H., Martinez-Sykora, A., and Chinchapatnam, P. (2019). Cost-driven build orientation and bin packing of parts in selective laser melting (slm). Eur. J. Operational Res. 273 (1), 334–352. doi:10.1016/j.ejor.2018.07.053

CrossRef Full Text | Google Scholar

Grinde, R. B., and Cavalier, T. M. (1995). A new algorithm for the minimal-area convex enclosure problem. Eur. J. Operational Res. 84 (3), 522–538. doi:10.1016/0377-2217(95)00020-Q

CrossRef Full Text | Google Scholar

Guo, B., Ji, Y., Hu, J., Wu, F., and Peng, Q. (2019). Efficient free-form contour packing based on code matching strategy. IEEE Access 7, 57917–57926. doi:10.1109/ACCESS.2019.2914248

CrossRef Full Text | Google Scholar

Guo, B., Peng, Q., Cheng, X., and Dai, N. (2015). Free-form contour packing based on material grid approximation and lowest-gravity-center methods. Expert Syst. Appl. 42 (4), 1864–1871. doi:10.1016/j.eswa.2014.10.005

CrossRef Full Text | Google Scholar

Haessler, R. W., and Sweeney, P. E. (1991). Cutting stock problems and solution procedures. Eur. J. Operational Res. 54 (2), 141–150. doi:10.1016/0377-2217(91)90293-5

CrossRef Full Text | Google Scholar

Hamada, K., Ikeda, Y., Tokumoto, H., and Hase, S. (2019). Development of automatic nesting system for shipbuilding using the branch-and-bound method. J. Mar. Sci. Technol. 24 (2), 398–409. doi:10.1007/s00773-018-0559-x

CrossRef Full Text | Google Scholar

Hartmanis, M. R., and Johnson, D. S. (1982). Computers and intractability: A guide to the theory of NP-completeness (michael R. Garey and david S. Johnson). SIAM Rev. 24 (1), 90–91. doi:10.1137/1024022

CrossRef Full Text | Google Scholar

Hawa, A. L., Lewis, R., and Thompson, J. M. (2022). Exact and approximate methods for the score-constrained packing problem. Eur. J. Operational Res. 302 (3), 847–859. doi:10.1016/j.ejor.2022.01.028

CrossRef Full Text | Google Scholar

Heckmann, R., and Lengauer, T. (1995). A simulated annealing approach to the nesting problem in the textile manufacturing industry. Ann. Oper. Res. 57 (1), 103–133. doi:10.1007/BF02099693

CrossRef Full Text | Google Scholar

Hemaspaandra, L. A., and Williams, R. (2012). SIGACT news complexity theory column 76. SIGACT News 43 (4), 70–89. doi:10.1145/2421119.2421135

CrossRef Full Text | Google Scholar

Hinxman, A. I. (1980). The trim-loss and assortment problems: A survey. Eur. J. Operational Res. 5 (1), 8–18. doi:10.1016/0377-2217(80)90068-5

CrossRef Full Text | Google Scholar

Hong, S., Zhang, D., Lau, H. C., Zeng, X., and Si, Y.-W. (2014). A hybrid heuristic algorithm for the 2d variable-sized bin packing problem. Eur. J. Operational Res. 238 (1), 95–103. doi:10.1016/j.ejor.2014.03.049

CrossRef Full Text | Google Scholar

Hopper, E., and Turton, B. C. H. (1999). A genetic algorithm for a 2d industrial packing problem. Comput. Ind. Eng. 37 (1), 375–378. doi:10.1016/S0360-8352(99)00097-2

CrossRef Full Text | Google Scholar

Hopper, E., and Turton, B. C. H. (2001a). A review of the application of meta-heuristic algorithms to 2d strip packing problems. Artif. Intell. Rev. 16 (4), 257–300. doi:10.1023/A:1012590107280

CrossRef Full Text | Google Scholar

Hopper, E., and Turton, B. C. H. (2001b). An empirical investigation of meta-heuristic and heuristic algorithms for a 2d packing problem. Eur. J. Operational Res. 128 (1), 34–57. doi:10.1016/S0377-2217(99)00357-4

CrossRef Full Text | Google Scholar

Huang, W., and Xu, R. (1999). Two personification strategies for solving circles packing problem. Sci. China Ser. E-Technol. Sci. 42 (6), 595–602. doi:10.1007/BF02916995

CrossRef Full Text | Google Scholar

Huyao, L., Yuanjun, H., and Bennell, J. A. (2007). The irregular nesting problem: A new approach for nofit polygon calculation. J. Operational Res. Soc. 58 (9), 1235–1245. doi:10.1057/palgrave.jors.2602255

CrossRef Full Text | Google Scholar

Israni, S., and Sanders, J. (1982). Two-dimensional cutting stock problem research: A review and a new rectangular layout algorithm. J. Manuf. Syst. 1 (2), 169–182. doi:10.1016/S0278-6125(82)80027-7

CrossRef Full Text | Google Scholar

Jakobs, S. (1996). On genetic algorithms for the packing of polygons. Eur. J. Operational Res. 88 (1), 165–181. doi:10.1016/0377-2217(94)00166-9

CrossRef Full Text | Google Scholar

Jeong, Y. K., Ju, S., Shen, H., Lee, D. K., Shin, J. G., and Ryu, C. (2018). An analysis of shipyard spatial arrangement planning problems and a spatial arrangement algorithm considering free space and unplaced block. Int. J. Adv. Manuf. Technol. 95 (9), 4307–4325. doi:10.1007/s00170-017-1525-1

CrossRef Full Text | Google Scholar

Joós, A. (2018). On packing of rectangles in a rectangle. Discrete Math. 341 (9), 2544–2552. doi:10.1016/j.disc.2018.06.007

CrossRef Full Text | Google Scholar

Ke, Q., Zhang, P., Zhang, L., and Song, S. (2020). Electric vehicle battery disassembly sequence planning based on frame-subgroup structure combined with genetic algorithm. Front. Mech. Eng. 6. doi:10.3389/fmech.2020.576642

CrossRef Full Text | Google Scholar

Koroupi, F., and Loftus, M. (1991). Accommodating diverse shapes within hexagonal pavers. Int. J. Prod. Res. 29 (8), 1507–1519. doi:10.1080/00207549108948028

CrossRef Full Text | Google Scholar

Kucukyilmaz, T., and Kiziloz, H. E. (2018). Cooperative parallel grouping genetic algorithm for the one-dimensional bin packing problem. Comput. Industrial Eng. 125, 157–170. doi:10.1016/j.cie.2018.08.021

CrossRef Full Text | Google Scholar

Lamas-Fernandez, C., Bennell, J. A., and Martinez-Sykora, A. (2022). Voxel-based solution approaches to the three-dimensional irregular packing problem. Operations Res. doi:10.1287/opre.2022.2260

CrossRef Full Text | Google Scholar

Leao, AaS., Toledo, F. M. B., Oliveira, J. F., and Carravilla, M. A. (2016). A semi-continuous mip model for the irregular strip packing problem. Int. J. Prod. Res. 54 (3), 712–721. doi:10.1080/00207543.2015.1041571

CrossRef Full Text | Google Scholar

Leao, A. A. S., Toledo, F. M. B., Oliveira, J. F., Carravilla, M. A., and Alvarez-Valdés, R. (2020). Irregular packing problems: A review of mathematical models. Eur. J. Operational Res. 282 (3), 803–822. doi:10.1016/j.ejor.2019.04.045

CrossRef Full Text | Google Scholar

Levine, J., and Ducatelle, F. (2004). Ant colony optimization and local search for bin packing and cutting stock problems. J. Operational Res. Soc. 55 (7), 705–716. doi:10.1057/palgrave.jors.2601771

CrossRef Full Text | Google Scholar

Li, D., Gu, Z., Wang, Y., Ren, C., and Lau, F. C. M. (2022). One model packs thousands of items with recurrent conditional query learning. Knowledge-Based Syst. 235, 107683. doi:10.1016/j.knosys.2021.107683

CrossRef Full Text | Google Scholar

Liu, D., Tan, K. C., Huang, S., Goh, C. K., and Ho, W. K. (2008). On solving multiobjective bin packing problems using evolutionary particle swarm optimization. Eur. J. Operational Res. 190 (2), 357–382. doi:10.1016/j.ejor.2007.06.032

CrossRef Full Text | Google Scholar

Liu, D., and Teng, H. (1999). An improved BL-algorithm for genetic algorithm of the orthogonal packing of rectangles. Eur. J. Operational Res. 112 (2), 413–420. doi:10.1016/S0377-2217(97)00437-2

CrossRef Full Text | Google Scholar

Liu, H. Y., and He, Y. J. (2006). Algorithm for 2d irregular-shaped nesting problem based on the nfp algorithm and lowest-gravity-center principle. J. Zhejiang Univ. - Sci. A 7 (4), 570–576. doi:10.1631/jzus.2006.A0570

CrossRef Full Text | Google Scholar

Liu, J., Zhang, K., Yao, Y., Xue, Y., and Guan, T. (2016). A heuristic quasi-physical algorithm with coarse and fine adjustment for multi-objective weighted circles packing problem. Comput. Industrial Eng. 101, 416–426. doi:10.1016/j.cie.2016.09.029

CrossRef Full Text | Google Scholar

Liu, Q., Cheng, H. B., Tian, T., Wang, Y., Leng, J., Zhao, R., et al. (2021). Algorithms for the variable-sized bin packing problem with time windows. Comput. Industrial Eng. 155, 107175. doi:10.1016/j.cie.2021.107175

CrossRef Full Text | Google Scholar

Liu, X., Liu, J. M., Cao, A. X., and Yao, Z. L. (2015). HAPE3D-a new constructive algorithm for the 3D irregular packing problem. Front. Inf. Technol. Electron. Eng. 16 (5), 380–390. doi:10.1631/FITEE.1400421

CrossRef Full Text | Google Scholar

Lodi, A., Martello, S., and Monaci, i. M. (2002a). Two-dimensional packing problems: A survey. Eur. J. Operational Res. 141 (2), 241–252. doi:10.1016/S0377-2217(02)00123-6

CrossRef Full Text | Google Scholar

Lodi, A., Martello, S., and Vigo, D. (2002b). Recent advances on two-dimensional bin packing problems. Discret Appl. Math. 123 (1), 379–396. doi:10.1016/S0166-218X(01)00347-X

CrossRef Full Text | Google Scholar

Loh, K. H., Golden, B., and Wasil, E. (2008). Solving the one-dimensional bin packing problem with a weight annealing heuristic. Comput. Operations Res. 35 (7), 2283–2291. doi:10.1016/j.cor.2006.10.021

CrossRef Full Text | Google Scholar

M'Hallah, R., and Bouziri, A. (2016). Heuristics for the combined cut order planning two-dimensional layout problem in the apparel industry. Intl. Trans. Op. Res. 23 (1-2), 321–353. doi:10.1111/itor.12104

CrossRef Full Text | Google Scholar

Mancapa, V., Van Niekerk, T., and Hua, T. (2009). A genetic algorithm for two dimensional strip packing problems. S. Afr. J. Ind. Eng. 20 (2), 144–162. doi:10.7166/20-2-766

CrossRef Full Text | Google Scholar

Martello, S., and Monaci, M. (2015). Models and algorithms for packing rectangles into the smallest square. Comput. Operations Res. 63, 161–171. doi:10.1016/j.cor.2015.04.024

CrossRef Full Text | Google Scholar

Martello, S., Pisinger, D., and Vigo, D. (2000). The three-dimensional bin packing problem. Operations Res. 48 (2), 256–267. doi:10.1287/opre.48.2.256.12386

CrossRef Full Text | Google Scholar

Martinez-Sykora, A., Alvarez-Valdes, R., Bennell, J. A., Ruiz, R., and Tamarit, J. M. (2017). Matheuristics for the irregular bin packing problem with free rotations. Eur. J. Operational Res. 258 (2), 440–455. doi:10.1016/j.ejor.2016.09.043

CrossRef Full Text | Google Scholar

Mavridou, T. D., and Pardalos, P. M. (1997). Simulated annealing and genetic algorithms for the facility layout problem: A survey. Comput. Optim. Appl. 7 (1), 111–126. doi:10.1023/A:1008623913524

CrossRef Full Text | Google Scholar

Milenkovic, V., Daniels, K., and Li, Z. (1992). Placement and compaction of nonconvex polygons for clothing manufacture. translators, Citeseer, Fourth Canadian Conference on Computational Geometry. St. John's: Newfoundland.

Google Scholar

Mohamed, B. M. A., and Adnan, Y. (2009). Optimization by ant colony hybryde for the bin-packing problem. Proc. World Acad. Sci. Eng. Technol. 3 (1), 27–30.

Google Scholar

Mundim, L. R., Andretta, M., Carravilla, M. A., and Oliveira, J. F. (2018). A general heuristic for two-dimensional nesting problems with limited-size containers. Int. J. Prod. Res. 56 (1-2), 709–732. doi:10.1080/00207543.2017.1394598

CrossRef Full Text | Google Scholar

Mundim, L. R., Andretta, M., and de Queiroz, T. A. (2017). A biased random key genetic algorithm for open dimension nesting problems using no-fit raster. Expert Syst. Appl. 81, 358–371. doi:10.1016/j.eswa.2017.03.059

CrossRef Full Text | Google Scholar

Nurmela, K. J., and Östergård, P. R. J. (1997). Packing up to 50 equal circles in a square. Discrete Comput. Geom. 18 (1), 111–120. doi:10.1007/PL00009306

CrossRef Full Text | Google Scholar

Oliveira, J. F. C., and Ferreira, J. (1993). “Algorithms for nesting problems,” in Applied simulated annealing (Berlin, Heidelberg: Springer Berlin Heidelberg), 255–273. doi:10.1007/978-3-642-46787-5_13

CrossRef Full Text | Google Scholar

Oliveira, J. F., Gomes, A. M., and Ferreira, J. S. (2000). Topos - a new constructive algorithm for nesting problems. OR Spektrum 22 (2), 263–284. doi:10.1007/s002910050105

CrossRef Full Text | Google Scholar

Omar, M. K., and Ramakrishnan, K. (2013). Solving non-oriented two dimensional bin packing problem using evolutionary particle swarm optimisation. Int. J. Prod. Res. 51 (20), 6002–6016. doi:10.1080/00207543.2013.791754

CrossRef Full Text | Google Scholar

Onwubolu, G. C., and Mutingi, M. (2003). A genetic algorithm approach for the cutting stock problem. J. Intell. Manuf. 14 (2), 209–218. doi:10.1023/A:1022955531018

CrossRef Full Text | Google Scholar

Paquay, C., Limbourg, S., and Schyns, M. (2018). A tailored two-phase constructive heuristic for the three-dimensional multiple bin size bin packing problem with transportation constraints. Eur. J. Operational Res. 267 (1), 52–64. doi:10.1016/j.ejor.2017.11.010

CrossRef Full Text | Google Scholar

Peralta, J., Andretta, M., and Oliveira, J. F. (2018). Solving irregular strip packing problems with free rotations using separation lines. Pesqui. Oper. 38 (2), 195–214. doi:10.1590/0101-7438.2018.038.02.0195

CrossRef Full Text | Google Scholar

Qin, Y., Chan, F. T. S., Chung, S. H., Qu, T., and Niu, B. (2018). Aircraft parking stand allocation problem with safety consideration for independent hangar maintenance service providers. Comput. Operations Res. 91, 225–236. doi:10.1016/j.cor.2017.10.001

CrossRef Full Text | Google Scholar

Rakotonirainy, R. G., and van Vuuren, J. H. (2021). The effect of benchmark data characteristics during empirical strip packing heuristic performance evaluation. OR Spectr. 43 (2), 467–495. doi:10.1007/s00291-021-00619-y

CrossRef Full Text | Google Scholar

Ramesh Babu, A., and Ramesh Babu, N. (2001). A generic approach for nesting of 2-d parts in 2-d sheets using genetic and heuristic algorithms. Computer-Aided Des. 33 (12), 879–891. doi:10.1016/S0010-4485(00)00112-3

CrossRef Full Text | Google Scholar

Riff, M. C., Bonnaire, X., and Neveu, B. (2009). A revision of recent approaches for two-dimensional strip-packing problems. Eng. Appl. Artif. Intell. 22 (4), 823–827. doi:10.1016/j.engappai.2008.10.025

CrossRef Full Text | Google Scholar

Rode, M., and Rosenberg, O. (1987). An analysis of heuristic trim-loss algorithms. Eng. Costs Prod. Econ. 12 (1), 71–78. doi:10.1016/0167-188X(87)90064-4

CrossRef Full Text | Google Scholar

Rodrigues, M. O., and Toledo, F. M. B. (2017). A clique covering mip model for the irregular strip packing problem. Comput. Operations Res. 87, 221–234. doi:10.1016/j.cor.2016.11.006

CrossRef Full Text | Google Scholar

Salkin, H. M., and De Kluyver, C. A. (1975). The knapsack problem: A survey. Nav. Res. Logist. 22 (1), 127–144. doi:10.1002/nav.3800220110

CrossRef Full Text | Google Scholar

Santoro, M. C., and Lemos, F. K. (2015). Irregular packing: Milp model based on a polygonal enclosure. Ann. Oper. Res. 235 (1), 693–707. doi:10.1007/s10479-015-1971-9

CrossRef Full Text | Google Scholar

Sarin, S. C. (1983). Two-dimensional stock cutting problems and solution methodologies. J. Eng. Ind. 105 (3), 155–160. doi:10.1115/1.3185882

CrossRef Full Text | Google Scholar

Sato, A. K., Castro Martins, T. C., and Tsuzuki, M. S. G. (2022). A study on GPU acceleration applied to 2D irregular packing problems. Int. J. Comput. Integr. Manuf. 35 (4-5), 427–443. doi:10.1080/0951192X.2022.2050302

CrossRef Full Text | Google Scholar

Sato, A. K., de Sales Guerra Tsuzuki, M., de Castro Martins, T., and Gomes, A. M. (2016). Study of the grid size impact on a raster based strip packing problem solution. IFAC-PapersOnLine. 49 (31), 143–148. doi:10.1016/j.ifacol.2016.12.176

CrossRef Full Text | Google Scholar

Segenreich, S. A., and Faria Braga, L. M. P. (1986). Optimal nesting of general plane figures: A Monte Carlo heuristical approach. Comput. Graph. 10 (3), 229–237. doi:10.1016/0097-8493(86)90007-5

CrossRef Full Text | Google Scholar

Segredo, E., Segura, C., and León, C. (2014). Memetic algorithms and hyperheuristics applied to a multiobjectivised two-dimensional packing problem. J. Glob. Optim. 58 (4), 769–794. doi:10.1007/s10898-013-0088-4

CrossRef Full Text | Google Scholar

Shalaby, M. A., and Kashkoush, M. (2013). A particle swarm optimization algorithm for a 2-d irregular strip packing problem. Ajor 03 (2), 268–278. doi:10.4236/ajor.2013.32024

CrossRef Full Text | Google Scholar

Silva, E., Alvelos, F., and Valério de Carvalho, J. M. (2010). An integer programming model for two- and three-stage two-dimensional cutting stock problems. Eur. J. Operational Res. 205 (3), 699–708. doi:10.1016/j.ejor.2010.01.039

CrossRef Full Text | Google Scholar

Soke, A., and Bingul, Z. (2006). Hybrid genetic algorithm and simulated annealing for two-dimensional non-guillotine rectangular packing problems. Eng. Appl. Artif. Intell. 19 (5), 557–567. doi:10.1016/j.engappai.2005.12.003

CrossRef Full Text | Google Scholar

Souilah, A. (1995). Simulated annealing for manufacturing systems layout design. Eur. J. Operational Res. 82 (3), 592–614. doi:10.1016/0377-2217(93)E0336-V

CrossRef Full Text | Google Scholar

Stoyan, Y., Pankratov, A., and Romanova, T. (2016). Cutting and packing problems for irregular objects with continuous rotations: Mathematical modelling and non-linear optimization. J. Operational Res. Soc. 67 (5), 786–800. doi:10.1057/jors.2015.94

CrossRef Full Text | Google Scholar

Sweeney, P. E., and Paternoster, E. R. (1992). Cutting and packing problems: A categorized, application-orientated research bibliography. J. Operational Res. Soc. 43 (7), 691–706. doi:10.1057/jors.1992.101

CrossRef Full Text | Google Scholar

Tay, F. E., Chong, T., and Lee, F. (2002). Pattern nesting on irregular-shaped stock using genetic algorithms. Eng. Appl. Artif. Intell. 15 (6), 551–558. doi:10.1016/S0952-1976(03)00009-5

CrossRef Full Text | Google Scholar

Toledo, F. M. B., Carravilla, M. A., Ribeiro, C., Oliveira, J. F., and Gomes, A. M. (2013). The dotted-board model: A new mip model for nesting irregular shapes. Int. J. Prod. Econ. 145 (2), 478–487. doi:10.1016/j.ijpe.2013.04.009

CrossRef Full Text | Google Scholar

van Laarhoven, P. J. M., and Aarts, E. H. L. (1987). “Simulated annealing,” in Simulated annealing: Theory and applications (Dordrecht: Springer Netherlands), 7–15. doi:10.1007/978-94-015-7744-1_2

CrossRef Full Text | Google Scholar

Wang, A., Hanselman, C. L., and Gounaris, C. E. (2018). A customized branch-and-bound approach for irregular shape nesting. J. Glob. Optim. 71 (4), 935–955. doi:10.1007/s10898-018-0637-y

CrossRef Full Text | Google Scholar

Wang, H., Huang, W., Zhang, Q., and Xu, D. (2002). An improved algorithm for the packing of unequal circles within a larger containing circle. Eur. J. Operational Res. 141 (2), 440–453. doi:10.1016/S0377-2217(01)00241-7

CrossRef Full Text | Google Scholar

Wang, T., Hu, Q., and Lim, A. (2022). An exact algorithm for two-dimensional vector packing problem with volumetric weight and general costs. Eur. J. Operational Res. 300 (1), 20–34. doi:10.1016/j.ejor.2021.10.011

CrossRef Full Text | Google Scholar

Wäscher, G., Haußner, H., and Schumann, H. (2007). An improved typology of cutting and packing problems. Eur. J. Operational Res. 183 (3), 1109–1130. doi:10.1016/j.ejor.2005.12.047

CrossRef Full Text | Google Scholar

Wu, L., Tian, X., Zhang, J., Liu, Q., Xiao, W., and Yang, Y. (2017). An improved heuristic algorithm for 2d rectangle packing area minimization problems with central rectangles. Eng. Appl. Artif. Intell. 66, 1–16. doi:10.1016/j.engappai.2017.08.012

CrossRef Full Text | Google Scholar

Wu, L., Zhang, L., Xiao, W. S., Liu, Q., Mu, C., and Yang, Y. (2016). A novel heuristic algorithm for two-dimensional rectangle packing area minimization problem with central rectangle. Comput. Industrial Eng. 102, 208–218. doi:10.1016/j.cie.2016.10.011

CrossRef Full Text | Google Scholar

Xu, Y. X. (2016). An efficient heuristic approach for irregular cutting stock problem in ship building industry. Math. Problems Eng. 2016, e8703782. doi:10.1155/2016/8703782

CrossRef Full Text | Google Scholar

Yang, X. S., and Deb, S. (2014). Cuckoo search: Recent advances and applications. Neural Comput. Applic 24 (1), 169–174. doi:10.1007/s00521-013-1367-1

CrossRef Full Text | Google Scholar

Zhang, H., Liu, Q., Wei, L. J., Zeng, J., Leng, J., and Yan, D. (2022). An iteratively doubling local search for the two-dimensional irregular bin packing problem with limited rotations. Comput. Operations Res. 137, 105550. doi:10.1016/j.cor.2021.105550

CrossRef Full Text | Google Scholar

Zhang, D. F., and Deng, A. S. (2005). An effective hybrid algorithm for the problem of packing circles into a larger containing circle. Comput. Operations Res. 32 (8), 1941–1951. doi:10.1016/j.cor.2003.12.006

CrossRef Full Text | Google Scholar

Zhang, H., Yao, S. W., Liu, Q., Wei, L., Lin, L., and Leng, J. (2022). An exact approach for the constrained two-dimensional guillotine cutting problem with defects. Int. J. Prod. Res. 2022, 1–18. doi:10.1080/00207543.2022.2074907

CrossRef Full Text | Google Scholar

Zhang, Y. C., Gupta, R. K., and Bernard, A. (2016). Two-dimensional placement optimization for multi-parts production in additive manufacturing. Robotics Computer-Integrated Manuf. 38, 102–117. doi:10.1016/j.rcim.2015.11.003

CrossRef Full Text | Google Scholar

Zhao, H., Zhu, C. Y., Xu, X., Xu, H., and Xu, K. (2022). Learning practically feasible policies for online 3D bin packing. Sci. China Inf. Sci. 65 (1), e112105. doi:10.1007/s11432-021-3348-6

CrossRef Full Text | Google Scholar