- 1Wake Forest University School of Medicine, Department of Biomedical Engineering, Winston-Salem, NC, United States
- 2Department of Biomedical Engineering, Purdue University, West Lafayette, IN, United States
- 3Wake Forest University School of Medicine, Department of Biostatistics and Data Science, Winston-Salem, NC, United States
Introduction: Blunt cardiac trauma (BCT) is seen throughout high-velocity blunt thoracic trauma, and while it is considered to be low prevalence, it often leads to fatalities. The finite element ovine thorax model (FE-OTM) was developed to investigate high-velocity blunt trauma and the resulting injuries; however, it has a simplified cardiac geometry that does not consider cardiac muscle nor differences in chamber behavior.
Methods: This study seeks to improve upon the heart within the FE-OTM v2 through the additions of more anatomically correct mesh geometry with muscle fiber directionality and material constitutive models for each chamber that considers hyperelasticity and anisotropy. Newly added regions with improved material models included the right and left atria, the right and left ventricles, and the septum.
Results and Discussion: The ventricles and septum were made of hexahedral solid elements that included myocardial fiber directions, whereas the atria were made of quadrilateral elements due to the lack of anisotropy in literature. The final cardiac geometry included about 21k nodes, 53k elements, 13 individual parts, and 10 constitutive material models. The heart was then implemented into the existing model and re-validated based on peak forces using a subject-specific simulation matrix. A paired t-test was conducted to quantitatively validate the model, where p = 0.85, signifying that the model and experimental forces were similar. The FE-OTM v3 with the updated heart geometry and materials can be used in future work focusing on BCT risk.
Introduction
In cases of blunt thoracic trauma, there is a risk of blunt cardiac trauma (BCT) (Singh et al., 2024). BCT includes commotio cordis, cardiac contusion, arrhythmias, cardiac tamponade, cardiac rupture, and valve injuries (Schultz and Trunkey, 2004; Singh et al., 2024). While BCT is typically considered to be of low prevalence, it often has fatal consequences if no chain of survival is established (Geocadin et al., 2023). Blunt cardiac trauma (BCT) is not well understood, but studies from the early 1930s showed that there are three primary risk factors for occurrence–type of impact, impact location, and force of impact (Nesbitt et al., 2001; Schlomka, 1934).
The timing of the heart wave was found to be a risk factor for BCT (Cooper et al., 1982; Link et al., 1999). Mechanical deformation has been stated to be a risk factor for cardiac injury, yet no cardiac-specific mechanical injury thresholds have been created for injury risk. General soft tissue injury metrics have been developed using cadavers, such as the viscous criterion, however, these experiments do not take into account physiological changes such as electric pathway disruptions nor location of impact (Lau and Viano, 1986). Studies have used viscous criterion as a metric for cardiac injury, however, there have been conflicting results based on animal subject mass, impact velocities (automobile applications vs. high-velocity projectile applications), and injury definition and diagnosis (Yoganandan et al., 2024; Janda et al., 1998; Yoganandan et al., 2014). While all work regarding BCT is much needed, it requires a cardiac model that considers regional tissue mechanics, anatomy, and tissue anisotropy.
Non-penetrating blunt trauma (NPBI), which occurs when protective equipment deforms and impacts the chest, can lead to BCT (Cannon, 2001; Kunz et al., 2011). NPBI has been studied in several animal models, particularly porcine and ovine (Yoganandan et al., 2024; Caffrey et al., 2025; Kunz et al., 2011; Drobin et al., 2007; Gryth, 2007; Gryth et al., 2007; Sondén et al., 2009). In a study with porcine subjects, it was hypothesized that energy was a potential predictor of BCT risk (Kunz et al., 2011). In another study, several ovine subjects experienced blunt cardiac injury (about 20%), specifically cardiac arrest and arrhythmia post-impact to the thorax. The finite element ovine thorax model (FE-OTM) was developed to match those ovine experiments, and an improved cardiac model would allow for further analysis in silico of the injuries sustained, particularly with developing injury thresholds (Caffrey et al., 2024, Caffrey et al., 2025). The model was developed using CT scans of a 35 kg male Katahdin sheep, where the resulting model had 6.04 million elements and 1.03 million nodes (Caffrey et al., 2023; Caffrey et al., 2024).
In its original development, the heart in the FE-OTM v2 was represented with a simplified solid tetrahedral mesh (Caffrey et al., 2024). The single part approach does not account for cardiac muscle nor differentiated tissues of the heart; it only considers blood. Furthermore, it is defined using an elastic fluid material representative of blood (K = 480 MPa, ρ = 1 E−6 kg/mm3). This approach was used as the model was not originally intended for use in determining cardiac injury. In order to extend the functionality of this existing model to predict BCT, a more anatomically and biomechanically accurate model of the organ is required, as seen in existing abdominal injury risk and pelvic floor prolapse studies (Beillas and Berthet, 2017; Chen et al., 2015). Combined with an increased biofidelic geometry, more biofidelic material definitions would also improve injury risk predictions. Material characterization data from Javani et al. shows that the behavior of ovine cardiac muscle varies depending on chamber, making it essential to account for to investigate blunt cardiac injuries and their mechanisms (Javani et al., 2016).
For blunt cardiac injury thresholds to be developed, the existing heart geometry needs to be modified. The objective of this study therefore is to improve the ovine cardiac geometry within the FE-OTM, optimize the material models to match the data reported by Javani et al. to reflect the behavior of different regions of the myocardial muscle, and re-validate the model.
Methods
To update the FE-OTM with an improved cardiac geometry and cardiac materials, a more biofidelic geometry needs to be developed, and the cardiac material models from literature need to be adapted for in silico applications for use in each atrium, each ventricle, and the septum. Then, both the geometry and materials need to be implemented, and the model validated.
Adaptation of ovine cardiac material data from literature
Ventricle, atria, and septum material characterization data from literature were adapted for in silico applications (Javani et al., 2016; Nguyen-Truong et al., 2021). Since the previous version of the FE-OTM was developed and validated in LS-Dyna (ANSYS, Canonsburg, PA), all material and geometric modifications were completed for final use in LS-Dyna using solver R12.2.1.
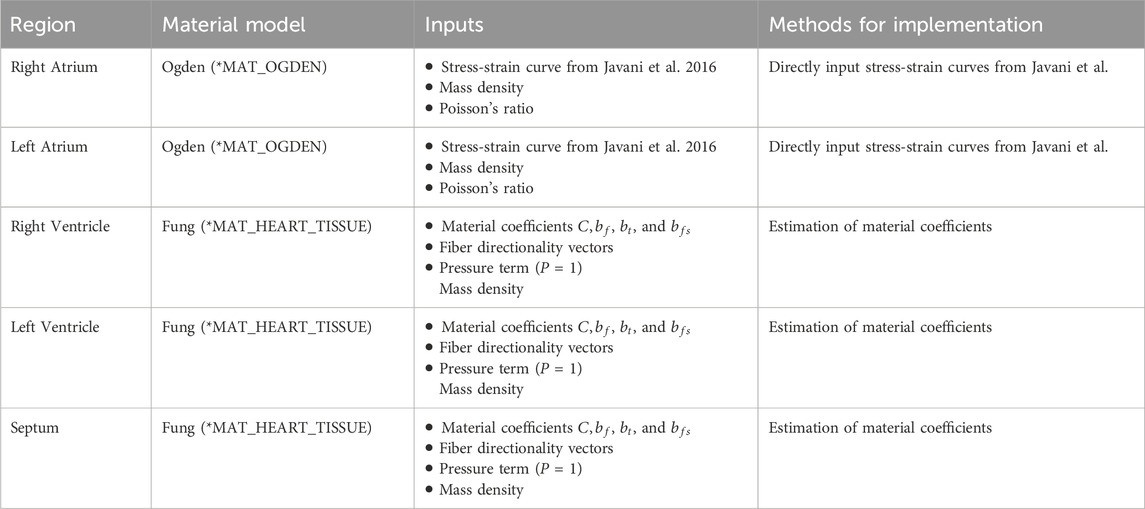
Javani et al. characterized fresh ovine cardiac tissue by chamber (N = 19). The study evaluated the right and left atria and ventricles and saw regional differences in behavior (Javani et al., 2016). Due to limited anisotropy observed in the atria tested from Javani et al., in this study, the atria did not use the same material as the ventricles. A simpler, more computationally efficient material model that did not account for anisotropy was used in the atrium for use in silico. A hyperelastic material model (*MAT_OGDEN_RUBBER) was used for the atria to account for hyperelasticity of the myocardium, where the stress-strain data from Javani et al., mass density, and Poisson’s ratio were input into the material model in LS-Dyna (LSTC, 2021), as seen in Table 1.
For the ventricles and septum, the Fung model (*MAT_HEART_TISSUE) was used to incorporate both hyperelasticity and anisotropy (Equations 1 and 2) (LSTC, 2021; Javani et al., 2016; Guccione and McCulloch, 1991). The fiber directionality is incorporated based on each element normal, where the angle is defined in the material input (LSTC, 2021). The angle of the fibers is said to vary throughout the ventricle wall, ranging from 30° to 150° from the horizontal axis seen in Figure 1 (Power et al., 1999; Nguyen-Truong et al., 2021). Javani et al. made assumptions to simplify the material model presented in their work, one of which assumed that z-direction strains were negligible, making adaptation required for use in silico as those assumptions cannot be applied in silico.
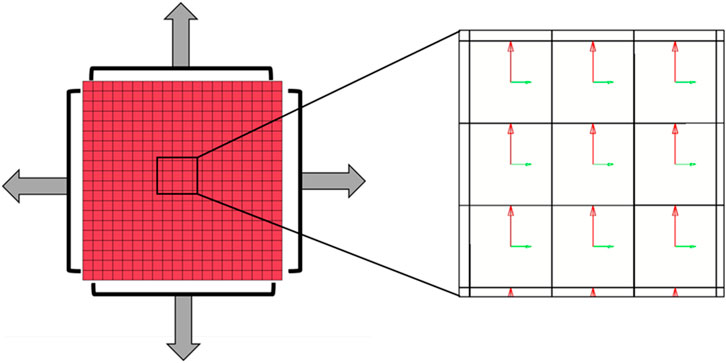
Figure 1. (Left) In silico model of biaxial cardiac test completed by Javani et al. with (Right) fiber directionality represented by the horizontal green vectors.
The variables
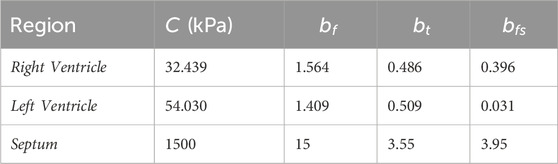
The adaptation of the data for use in silico was completed using an in silico set-up matching the bi-axial experimental set-up reported by Javani et al. The in silico set-up utilized 1600 hexahedral elements and 2205 nodes and incorporate fiber directionality within each element (Figure 1). The fiber directionality is based on local element axes, where the fiber angle is input and based on the element normal, resulting in the need for hexahedral elements over tetrahedral elements (LSTC, 2021; Guccione and McCulloch, 1991). Stress and strain of the center elements were obtained through ELOUT using a Python script for comparison to experimental data. The baseline trial used the reported mean material constant values from Javani et al. for the right and left ventricles (Table 2). The following runs each utilized ± 1 and ± 2 standard deviations, as well as magnitude and material constant ratio adjustments. Following this baseline matrix, coefficients were manually adjusted to lower error based on coefficient effects on resulting stress-strain curves. The objective of this series of simulations is to ensure the resulting material coefficients result in the same behavior as what was observed ex vivo in the experiments from Javani et al. (2016).
The resulting stress-strain curves of each run were evaluated using Equation 3, where the evaluation metric, similar to the mean squared error (MSE), was calculated at each point along the data curve for each fiber direction and then averaged. The integral of each stress-strain curve was calculated at each point due to the nonlinearity of the target stress-strain curve. A squared error was used to negate any crossing of the simulation and experimental data traces. The resulting data trace was also visually evaluated.
The integral over the duration of the simulation/experiment of the simulated stress-strain curve and the experimental stress-strain curve from Javani et al. to calculate the evaluation metric. The evaluation metric was calculated in each direction (with the fiber, with the cross fiber) and then averaged to compare between simulations for final coefficient selection. The standard MSE was also calculated for each simulation (James et al., 2013). A total of 188 simulations were run for the right ventricle and 62 were run for the left ventricle on a standard PC on 8 cores to obtain the lowest evaluation metric values for final material parameter selection.
Sensitivity analysis was completed using a subset of 50 simulations for the right ventricle to guide and fine tune further efforts. For this analysis, the stress at 10% true strain was compared to the experimental stress at 10% true strain for each simulation. To justify the use of 50 simulations and ensure adequate statistical power, a one-sample t-test power analysis was completed using the simulated values and the experimental mean. Assuming a significance level at 0.05, a two-sided test, and a sample size of 50, the analysis yielded an effect size is 0.40, corresponding to a statistical power of 0.80 (1-β). For the sensitivity analysis, the differential of the stress over the parameter value was calculated. The resulting differential for each simulation was then averaged across simulations for the final calculation of sensitivity. The results from the sensitivity analysis were used to guide further adaptation efforts, including those for the left ventricle. Parameters with low sensitivity were adjusted after the parameters with high sensitivity, as those with higher sensitivity resulted in larger changes in the material behavior. All parameters were then further manually adjusted to lower the evaluation metric.
A third set of simulations were also completed to obtain the material constants of the septum. Based on the work completed by Nguyen-Truong et al., ovine septum material behavior is different from ovine ventricle wall behavior (N = 12) (Nguyen-Truong et al., 2021). Due to the tests not being completed on fresh samples on the day of sacrifice in the study from Nguyen-Truong et al., an average ratio of the septum and right ventricle stress values was taken to adapt the stress-strain curve from Javani et al (Javani et al., 2016; Nguyen-Truong et al., 2021). The right ventricle was approximately 64% stiffer in the fiber direction based on the slope throughout the curve in Nguyen-Truong et al. Therefore, the right ventricle fiber stress-strain data was multiplied by 0.64 to estimate the fiber direction behavior of fresh tissue. The ventricle cross-fiber was 78% stiffer than the septum cross-fiber, and the cross-fiber stress-strain data was multiplied by 0.78 to estimate the cross-fiber behavior in fresh tissue. Each of these resulting data traces were used as target data for septum parameter adaptation simulation comparisons. Adaptation of the septum was completed with a total of 28 simulations using the same metrics and methodology as each of the ventricles.
Cardiac geometry development
As part of the model improvements, a more biofidelic and anatomically accurate heart was needed. Cardiac wall measurements were obtained from measurements from ovine CT scans (Caffrey et al., 2023). The ventricle wall and septum thicknesses were measured throughout the heart and averaged for wall thickness targets in updated heart structure. The atria were not measurable due to being roughly 1 mm thick according to literature, and the CT scans had 0.7 mm resolution (Javani et al., 2016; Caffrey et al., 2023). Due to the need to incorporate anisotropy, a hexahedral mesh was required for the ventricles and septum. The atria used a shell mesh due to the thin walls and lack of anisotropy.
The ventricles were initially built in TrueGrid (XYZ Applications Inc., Pleasant Hill, CA), where the geometry was built as a cone shape with three elements through the wall thickness. The atria were built separately in TrueGrid with a quarter-sphere geometry with a bottom and side plane to separate from the adjacent chambers. After the initial geometries were built, they were combined into a single file for further processing. Preliminary alignment efforts of both the atria and ventricles with the original ovine cardiac mesh were completed using TrueGrid. The resulting geometry was imported into ANSA (Cadence Design Systems, San Jose CA) for further refinement. Outer surface matching was completed using the nominal-to-real algorithm to improve surface matching with the original heart model surface. Manual adjustments of the wall thickness were done in LS-PrePost (Ansys, Canonsburg PA) as needed throughout this process to ensure proper wall thickness throughout the heart. Element quality was assessed in Hypermesh (Altair, Troy, MI) to match the parameters of the FE-OTM, as seen in Supplementary Table S6 (Caffrey et al., 2024).
After the geometry was finalized, the ventricles were split into parts. Each ventricle was split into three layers, each one element thick. This was done to allow for different fiber directions by layer, where the outermost layer was defined as 30° from the horizontal axis, the middle layer was 90°, and the innermost layer was 150° (Nakatani, 2011). A total of six parts were created for the ventricles, three on each side. The septum was its own part, where the fiber angle was input to be 9° from the horizontal axis based on measurements from literature (Nguyen-Truong et al., 2021). The material curves and/or coefficients described previously were then input into the corresponding region. Each of the four chambers were each filled with tetrahedral elements to represent blood using ANSA. The heart geometry has thirteen parts: six are ventricle walls, two are atria walls, one is the septum, and the last four are blood in each chamber. Contacts were added between the ventricles, septum, and ventricular blood as well as the atria and atrial blood. The resulting geometry and material cards were simulated with no external loads for 10 ms to ensure stability prior to implementation.
Implementation of modified heart into FE-OTM and validation
The implementation process utilized the developed geometry and region-specific materials and implemented them into the FE-OTM. The original heart solids and shell were removed before implementation, and a shell of the outermost surface was created. The resulting shell was scaled down to 80% volumetrically about its centroid to utilize the boundary prescribed final geometry algorithm within LS-Dyna. Using the algorithm, the shell was linearly grown back to full size in 250 ms with proper interactions and without penetrations or intersections with surrounding tissues using an automatic surface to surface contact. The resulting nodal coordinates of the whole model were then output.
The shell that was used in the boundary prescribed geometry simulation was then removed and the newly developed cardiac geometry was then input into the FE-OTM. The vasculature, particularly the aortic arch and inferior vasculature, was re-meshed to adjoin to the heart. The shell elements representing the walls of the vasculature were manually re-meshed to connect them to the heart, and then new solid tetrahedral elements representing blood were meshed using ANSA. An element quality check of the entire model was then completed using the same threshold that was used for the heart model development. Due to the large amount of lung tissue between the impact and the organ of interest, the lung material model within the FE-OTM was also updated to include viscoelasticity using material characterization data from Thomas et al. (2025).
The FE-OTM was then re-validated following the methods from Caffrey et al., where the experimental forces were compared to the subject-matched simulated forces (Caffrey et al., 2024). Because these methods are described in that paper, they are only briefly recapitulated here. A total of 20 scaled simulations were run, where the baseline model was scaled to match experimental subject dimensions. Each scaled subject was impacted at 40 m/s to a specific depth with an impactor representing the back face deformation of personal protective equipment. For each experimental subject, the impact force was reported and therefore used for validation of the model. A paired t-test was run to verify the validation between experimental and version 3 resulting forces (α = 0.05), where a p < 0.05 would indicate significant differences between the experimental and simulated data.
Results
Adaptation of ovine cardiac material data from literature
The sensitivity analysis showed which material constants had what effect on the resulting stress values at 10% true strain. Table 3 reports the mean sensitivity in both the fiber and cross-fiber directions for each material constant that was analyzed. Material constant
Material constant
The resulting material models for each ventricle and the septum are seen in Table 4 and in Figure 2. The parameter values for the septum are all lower than the ventricle values, as expected based on the experimental data. Both the custom metric and a standard mean squared error were calculated, with the final values in Table 4.
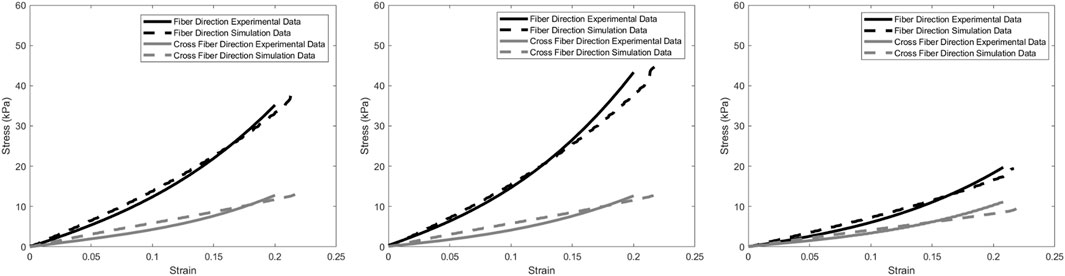
Figure 2. Resulting optimized data traces (Left) for right ventricle, (Middle) left ventricle, and (Right) septum.
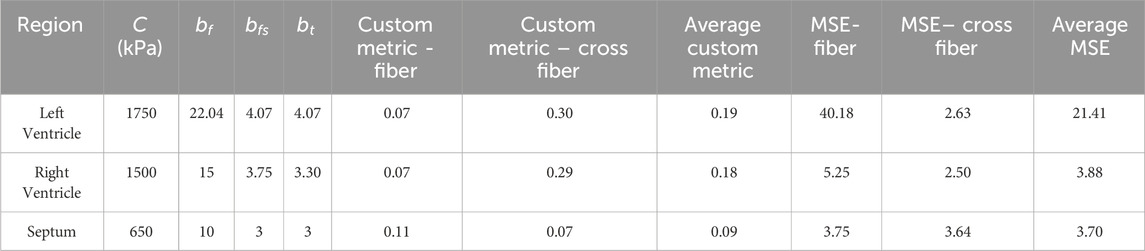
Table 4. Resulting values for each region from adaptation simulation sets. The custom metric is described with Equation 3 in the methods. MSE = mean squared error.
As seen in Figure 2 and Table 4, the cross-fiber direction matches well compared to experimental data. Visual checks were also utilized in addition to the custom metric and MSE to prevent poor-fitting data with high error.
Experimentally, the septum was less stiff than the ventricles, as seen in Figure 2. Due to the physiological function of the septum compared to each of the ventricles, the septum should be less stiff than either of the ventricles (Feher, 2017). The septum is muscle tissue like the ventricles, but is meant to prevent blood flow between the ventricles, whereas the ventricles are responsible for blood moving out of the heart.
Cardiac geometry development
The improved ovine cardiac mesh was successfully generated. Compared to the FE-OTM v2, this heart now has different material models for each chamber of the heart with more biofidelic geometries (Figure 3). The ventricle and septum walls now match the average measurements from CT scans, which can be seen in Table 5.
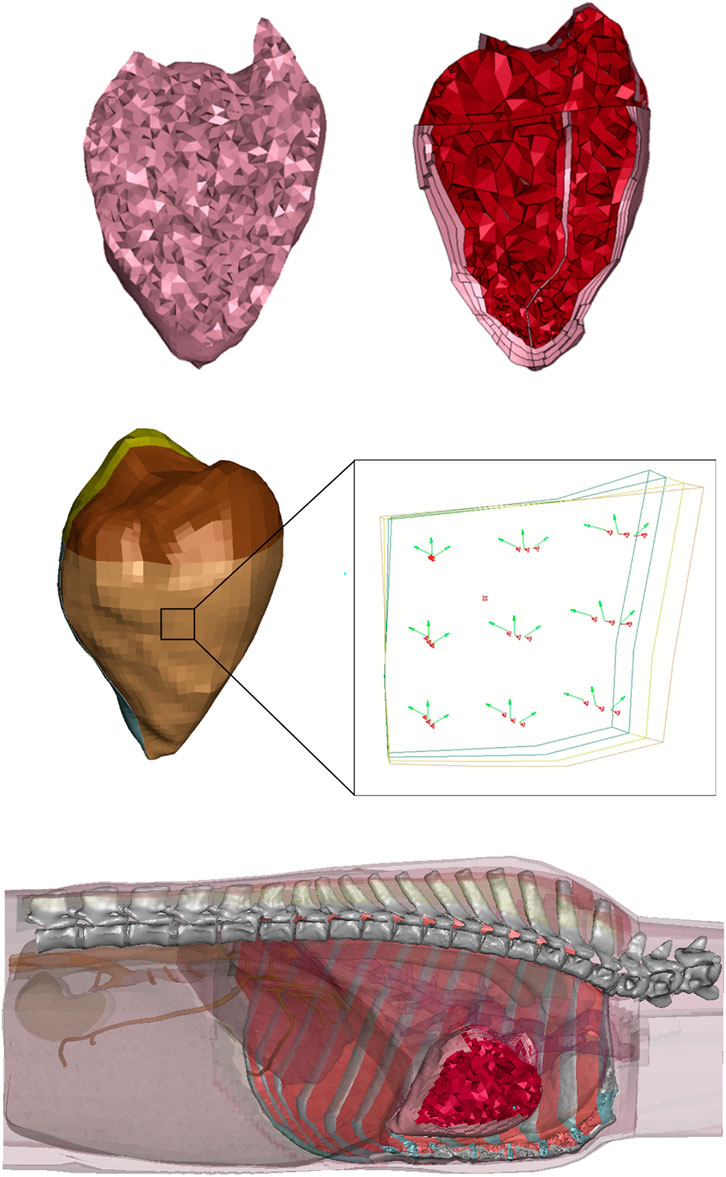
Figure 3. (Top Left) FE-OTM v2 heart cross-section (Caffrey et al., 2024), (Top Right) FE-OTM v3 heart cross-section, where the blood is red and cardiac walls are pink, (Middle) image showing element normal in red and element fiber directions in green through the thickness of the left ventricle, where the brown elements are the outermost layer and the green elements are the innermost layer, with the (Bottom) whole heart seen in the FE-OTM with surrounding organs and tissues transparent.
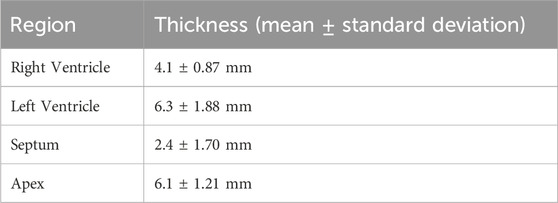
Table 5. Cardiac regional thicknesses from CT scans (Caffrey et al., 2023).
For geometry development, the thickness values were rounded to the nearest millimeter (i.e., the septum was rounded to 2 mm). The resulting geometry has 20,785 nodes and 53,167 total elements. Of the 53,167 elements, 1,595 are shell elements in the atria. All other elements were solid (51,572). The updated geometry has 13 parts and 10 different materials and can be seen on the right side of Figure 3. The four parts that represent blood share one material definition, each of the ventricle layers have their own part (6 total materials in the ventricles), the septum has a material, and each of the atria have their own materials (2 materials). There were six different material models in the ventricles to account for the changes in fiber directionality through the wall, where there were three different materials per side, where the fiber directionality is illustrated in Figure 3 (Brady et al., 2023).
Implementation of modified heart into FE-OTM and validation
After cardiac implementation and material modifications, all hard targets of element quality were met within the FE-OTM. The paired two-tail t-test run showed no statistical differences between the simulated and experimental peak force data (p = 0.85). As seen in Figure 4, the peak force observed in vivo was plotted on the x-axis, and the peak force observed in silico was plotted on the y-axis. Since the objective was to match the experimental model as best as possible, a trendline was fit, where a slope of 1 indicates perfect agreement. With a slope of 0.94, version 3 of the OTM resulting from this work slightly underestimates the observed experimental peak forces, whereas the previous iteration of the model slightly overestimated the forces (Figure 4).
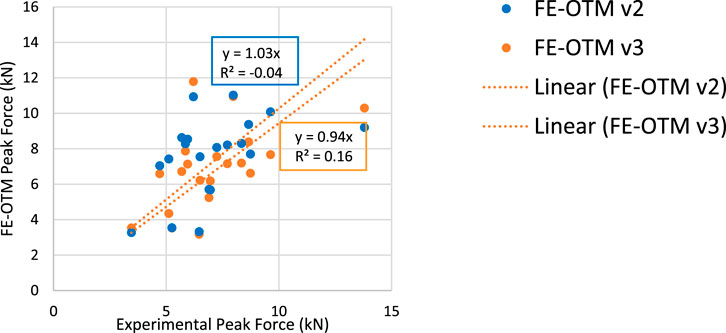
Figure 4. (Left) Peak force comparisons between experimental and FE-OTM values (Right) with the legend.
Discussion
This study successfully implemented the newly developed heart into the FE-OTM and revalidated the model. The FE-OTM v3 slightly underestimates the peak forces when compared to experiments but are still close to experimental values. New heart materials that considered hyperelasticity and anisotropy, cardiac wall mesh development for the purpose of implementing anisotropy, and updated lung materials from literature were all incorporated within the FE-OTM v3.
For material model applications in silico, there were limitations in the methodology used for material optimization. LS-OPT (ANSYS, Canonsburg, PA), a software that optimizes simulation results, was originally used for the optimization process, but due to the nonlinear nature of the target material behavior, the resulting optimized coefficients did not visually match the experimental data using the available evaluation methods within LS-OPT. As a result, a manual optimization process was used with a custom evaluation metric with success. It is worth noting that the fiber direction would match well in shape and magnitude, but the cross-fiber direction was much more linear in shape when compared to the experimental data throughout all simulations, as seen in Figure 2, due to the LS-Dyna algorithm used to calculate the directional stresses. Based on the current LS-Dyna algorithm for *MAT_HEART_TISSUE, the mean evaluation metric across the two directions was chosen to ensure the best behavior for both directions. Future iterations of LS-Dyna may include changes to the material model, so the solver version will matter when evaluating resulting stress-strain data.
The new cardiac geometry was successfully developed. While this is still a simplified geometry, it includes many important anatomical details, including region-specific thicknesses and muscle fiber direction. The fiber directionality, or anisotropy, is accounted for through the thickness of each ventricle wall and septum, further improving the heart model. Due to the number of elements through the ventricle wall, a range of muscle fiber directions were able to be defined, further improving the biofidelity of the organ. The wall thicknesses were determined using a combination of CT scan measurements and literature reported values (Caffrey et al., 2023; Javani et al., 2016). However, the thickness used did not vary over the wall surface like it would in vivo. For example, within the model, the entire right atrium was 1 mm thick, regardless of where the atrium wall was measured. While this model is not as detailed as many heart-only FE models, as it did not include electrophysiology or detailed anatomy, such as heart valves or fluid flow, it is a more detailed heart in a thorax model that did not add large amounts of computational solving time (Sugiura et al., 2022; McCulloch et al., 2020; Fritz et al., 2014). As more details are added to a model, the computational time increases, as well as the increase in the likelihood of instability. Due to the short amount of time this model would be simulating, assumptions such as lack of electrophysiology can be made. For example, every subject-specific impact was run for 10 ms. At rest in humans, different regions of the heartbeat range from 80 (QRS complex) – 120 (PR interval) ms in duration, which is longer than the time frame being investigated (Feher, 2017; Douedi and Douedi, 2023). The material chosen for the ventricles, MAT_HEART_TISSUE, in new solver versions of LS-Dyna can include physiological components such as sarcomere length, intracellular calcium concentration, and systolic material parameters, so future work may investigate these constants and the effects on material behavior (LSTC, 2021). Due to the available experimental data, minimal electrocardiogram and calcium level data, and short simulation lengths, these parameters were not utilized in this iteration of the model.
The implementation and validation of the updated FE-OTM model showed that the FE-OTM v3 still accurately predicts the resulting forces. The forces are lower than what were predicted by the second version due to the material modifications, particularly the addition of viscoelasticity to the lung tissue (LSTC, 2021). Viscoelasticity increased the fluid-like behavior of the lungs, which in turn decreased the contact forces.
Overall, the FE-OTM v3 has been successfully updated to include lung viscoelasticity, cardiac geometry, and cardiac materials. With these changes, improved injury criteria can be developed for both the lungs and heart. As the heart model now includes more biofidelic anatomy and regional differences, a detailed injury risk assessment can be completed. As the heart conduction pathway starts in the right atrium, any disruption to the pathway will likely result in arrhythmia and other heart trauma (Feher, 2017; Patel et al., 2022). The right atrium can be investigated closely as a region more sensitive to mechanical loading due to the sinoatrial node, allowing for a more detailed analysis. Each side will also be able to be separated for injury risk assessment, making the analysis more thorough based on impact location, rather than solely based on the whole organ. Future work should also include lung injury thresholds due to the added viscoelasticity and heart injury threshold development.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
PT: Writing – review and editing, Conceptualization, Investigation, Methodology, Formal Analysis, Writing – original draft, Project administration, Data curation. OR: Methodology, Writing – review and editing, Writing – original draft, Data curation, Formal Analysis. F-CH: Writing – review and editing, Methodology, Formal Analysis, Resources, Visualization. FG: Resources, Conceptualization, Project administration, Methodology, Funding acquisition, Writing – review and editing, Supervision, Writing – original draft.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. We would like to acknowledge the DEVCOM Army Research Lab for funding this project (W911NF2120034).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2025.1688242/full#supplementary-material
References
Beillas, P., and Berthet, F. (2017). An investigation of human body model morphing for the assessment of abdomen responses to impact against a population of test subjects. Traffic Inj. Prev. 18, S142–S147. doi:10.1080/15389588.2017.1307971
Brady, B., King, G., Murphy, R. T., and Walsh, D. (2023). Myocardial strain: a clinical review. Ir. J. Med. Sci. (1971-) 192, 1649–1656. doi:10.1007/s11845-022-03210-8
Caffrey, J. M., Thomas, P. K., Appt, S. E., Burkart, H. B., Weaver, C. M., Kleinberger, M., et al. (2023). Contrast enhanced computed tomography of small ruminants: Caprine and ovine. Plos One 18, e0287529. doi:10.1371/journal.pone.0287529
Caffrey, J. M., Thomas, P. K., Wade VON Kleeck, I. I. I. J. S., Davis, M., Weaver, C. M., Kleinberger, M., et al. (2024). Development of a finite element ovine thorax model for use as a pre-test prediction tool in the study of high-rate non-penetrating blunt injuries. in IRCOBI Conference 2024 Proceedings.
Caffrey, J. M., Liverett, G. K., VON Kleeck, I. I. I. B. W., Wolfson, M., and Gayzik, F. S. (2025). Validation of a finite element ovine thorax model in the high-rate non-penetrating blunt impact environment. Mil. Med. 190, 180–186. doi:10.1093/milmed/usaf139
Cannon, L. (2001). Behind armour blunt trauma-an emerging problem. BMJ Mil. Health 147, 87–96. doi:10.1136/jramc-147-01-09
Chen, Z.-W., Joli, P., Feng, Z.-Q., Rahim, M., Pirró, N., and Bellemare, M.-E. (2015). Female patient-specific finite element modeling of pelvic organ prolapse (POP). J. Biomechanics 48, 238–245. doi:10.1016/j.jbiomech.2014.11.039
Cooper, G. J., Pearce, B. P., Stainer, M. C., and Maynard, R. L. (1982). The biomechanical response of the thorax to nonpenetrating impact with particular reference to cardiac injuries. J. Trauma Acute Care Surg. 22, 994–1008. doi:10.1097/00005373-198212000-00004
Drobin, D., Gryth, D., Persson, J. K., Rocksén, D., Arborelius, U. P., Olsson, L.-G., et al. (2007). Electroencephalogram, circulation, and lung function after high-velocity behind armor blunt trauma. J. Trauma Acute Care Surg. 63, 405–413. doi:10.1097/01.ta.0000236015.68105.48
ELEMANCE (2021). Global human body models consortium user manual: M50 detailed occupant version 6.0 for LS-DYNA. Winston-Salem, NC: Elemance LLC.
Fritz, T., Wieners, C., Seemann, G., Steen, H., and Dössel, O. (2014). Simulation of the contraction of the ventricles in a human heart model including atria and pericardium: finite element analysis of a frictionless contact problem. Biomechanics Model. Mechanobiol. 13, 627–641. doi:10.1007/s10237-013-0523-y
Geocadin, R. G., Agarwal, S., Goss, A. L., Callaway, C. W., and Richie, M. (2023). Cardiac arrest and neurologic recovery: insights from the case of Mr. Damar hamlin. Ann. neurology 93, 871–876. doi:10.1002/ana.26619
Gryth, D. (2007). Hemodynamic, respiratory and neurophysiological reactions after high-velocity behind armor blunt trauma. (Sweden): Karolinska Institutet.
Gryth, D., Rocksén, D., Persson, J. K., Arborelius, U. P., Drobin, D., Bursell, J., et al. (2007). Severe lung contusion and death after high-velocity behind-armor blunt trauma: relation to protection level. Mil. Med. 172, 1110–1116. doi:10.7205/milmed.172.10.1110
Guccione, J. M., and Mcculloch, A. D. (1991). “Finite element modeling of ventricular mechanics,” in Theory of heart: biomechanics, biophysics, and nonlinear dynamics of cardiac function. Springer.
James, G., Witten, D., Hastie, T., and Tibshirani, R. (2013). An introduction to statistical learning: with applications in R. Springer.
Janda, D. H., Bir, C. A., Viano, D. C., and Cassatta, S. J. (1998). Blunt chest impacts: assessing the relative risk of fatal cardiac injury from various baseballs. J. Trauma Acute Care Surg. 44, 298–303. doi:10.1097/00005373-199802000-00011
Javani, S., Gordon, M., and Azadani, A. N. (2016). Biomechanical properties and microstructure of heart chambers: a paired comparison study in an ovine model. Ann. Biomed. Eng. 44, 3266–3283. doi:10.1007/s10439-016-1658-7
Kunz, S. N., Arborelius, U. P., Gryth, D., Sonden, A., Gustavsson, J., Wangyal, T., et al. (2011). Cardiac changes after simulated behind armor blunt trauma or impact of nonlethal kinetic projectile ammunition. J. Trauma Acute Care Surg. 71, 1134–1143. doi:10.1097/ta.0b013e318232b079
Lau, I. V., and Viano, D. C. (1986). The viscous Criterion—bases and applications of an injury severity index for soft tissues. SAE Trans., 672–691.
Link, M. S., Wang, P. J., Vanderbrink, B. A., Avelar, E., Pandian, N. G., Maron, B. J., et al. (1999). Selective activation of the K+ ATP channel is a mechanism by which sudden death is produced by low-energy chest-wall impact (commotio cordis). Circulation 100, 413–418. doi:10.1161/01.cir.100.4.413
Mcculloch, A., Guccione, J., Waldman, L., and Rogers, J. (2020). “Large-scale finite element analysis of the beating heart,” in High-performance computing in biomedical research, 27–49.
Nakatani, S. (2011). Left ventricular rotation and twist: why should we learn? J. Cardiovasc. Ultrasound 19, 1–6. doi:10.4250/jcu.2011.19.1.1
Nesbitt, A. D., Cooper, P. J., and Kohl, P. (2001). Rediscovering commotio cordis. Lancet 357, 1195–1197. doi:10.1016/s0140-6736(00)04338-5
Nguyen-Truong, M., Liu, W., Doherty, C., Lebar, K., Labus, K. M., Puttlitz, C. M., et al. (2021). The interventricular septum is biomechanically distinct from the ventricular free walls. Bioengineering 8, 216. doi:10.3390/bioengineering8120216
Patel, K. M., Kumar, N. S., Desai, R. G., Mitrev, L., Trivedi, K., and Krishnan, S. (2022). Blunt trauma to the heart: a review of pathophysiology and current management. J. Cardiothorac. Vasc. Anesth. 36, 2707–2718. doi:10.1053/j.jvca.2021.10.018
Power, J., Raman, J., Dornom, A., Farish, S., Burrell, L. M., Tonkin, A. M., et al. (1999). Passive ventricular constraint amends the course of heart failure: a study in an ovine model of dilated cardiomyopathy. Cardiovasc. Res. 44, 549–555. doi:10.1016/s0008-6363(99)00255-2
Schlomka, G. (1934). Commotio cordis und ihre Folgen.(Die Einwirkung stumpfer Brustwandtraumen auf das Herz). Ergeb. Inn. Med. Kinderheilkd. Sieben. Band, 1–91.
Schultz, J. M., and Trunkey, D. D. (2004). Blunt cardiac injury. Crit. Care Clin. 20, 57–70. doi:10.1016/s0749-0704(03)00092-7
Singh, S., Heard, M., Pester, J. M., and Angus, L. D. (2024). Blunt cardiac injury. Treasure Island, FL: StatPearls Publishing.
Sondén, A., Rocksén, D., Riddez, L., Davidsson, J., Persson, J. K., Gryth, D., et al. (2009). Trauma attenuating backing improves protection against behind armor blunt trauma. J. Trauma Acute Care Surg. 67, 1191–1199. doi:10.1097/ta.0b013e3181a5b0e1
Sugiura, S., Okada, J.-I., Washio, T., and Hisada, T. (2022). “UT-heart: a finite element model designed for the multiscale and multiphysics integration of our knowledge on the human heart,” in Computational systems biology in medicine and biotechnology: methods and protocols. (Springer).
Thomas, P. K., Ablordeppey, E., Liverett, G. K., Rutherford, O., Roy, T. J., Brown, P. J., et al. (2025). Material characterization of ovine lung parenchyma at pressures representing the breathing cycle. J. Biomechanical Eng. 147, 101001. doi:10.1115/1.4068872
Yoganandan, N., Arun, M. W., and Pintar, F. A. (2014). Normalizing and scaling of data to derive human response corridors from impact tests. J. Biomechanics 47, 1749–1756. doi:10.1016/j.jbiomech.2014.03.010
Keywords: blunt cardiac trauma, high-velocity blunt trauma, material characterization, ovine, cardiac finite element model
Citation: Thomas PK, Rutherford O, Hsu F-C and Gayzik FS (2025) Material in silico adaptation and validation of an ovine heart model for blunt cardiac trauma applications. Front. Mech. Eng. 11:1688242. doi: 10.3389/fmech.2025.1688242
Received: 18 August 2025; Accepted: 27 October 2025;
Published: 12 November 2025.
Edited by:
Bruno Rego, Louisiana State University, United StatesReviewed by:
Fethi Ali Okyar, Yeditepe University, TürkiyeFaizan Ahmad, Birmingham City University, United Kingdom
Copyright © 2025 Thomas, Rutherford, Hsu and Gayzik. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: F. Scott Gayzik, c2NvdHQuZ2F5emlrQHdmdXNtLmVkdQ==
†ORCID: Fang-Chi Hsu, orcid.org/0000-0001-6955-929X
 Patricia K. Thomas
Patricia K. Thomas Olivia Rutherford
Olivia Rutherford Fang-Chi Hsu3†
Fang-Chi Hsu3† F. Scott Gayzik
F. Scott Gayzik