- 1Laboratory of Biological Structure Mechanics, Chemistry, Materials and Chemical Engineering Department “Giulio Natta”, Politecnico di Milano, Milano, Italy
- 2Cardiac Unit, Great Ormond Street Hospital for Children, London, UK
- MOCHA Investigators: Edward Bove MD and Adam Dorfman MD (University of Michigan, USA); Andrew Taylor MD, Alessandro Giardini MD, Sachin Khambadkone MD, Jam Marek MD, Silvia Schievano PhD, and T-Y Hsia MD (Institute of Child Health, UK); G. Hamilton Baker MD and Anthony Hlavacek (Medical University of South Carolina, USA); Francesco Migliavacca PhD, Giancarlo Pennati PhD, and Gabriele Dubini PhD (Politecnico di Milano, Italy); Richard Figliola PhD and John McGregor PhD (Clemson University, USA); Alison Marsden PhD (University of California, San Diego, USA); Jeff Feinstein MD (Stanford University, USA); Irene Vignon-Clementel (National Institute of Research in Informatics and Automation, France)
Mathematical modeling is a powerful tool to investigate hemodynamics of the circulatory system. With improving imaging techniques and detailed clinical investigations, it is now possible to construct patient-specific models of reconstructive surgeries for the treatment of congenital heart diseases. These models can help clinicians to better understand the hemodynamic behavior of different surgical options for a treated patient. This review outlines recent advances in mathematical modeling in congenital heart diseases, the discoveries and limitations these models present, and future directions that are on the horizon.
Introduction
Treatment of congenital heart diseases (CHD) has evolved rapidly in recent years, requiring customized therapies due to the large inter-patient variability of anatomical and hemodynamic parameters within the vascular arrangement following a surgical repair. Virtual surgery based on computational fluid dynamics or in silico patient-specific modeling is a promising tool because it could help surgeons in the decision-making process, improving and understanding hemodynamic outcomes and reducing trial errors during complex surgeries (1–4).
The major areas of research for mathematical modeling of CHD are univentricular circulation and aortic and pulmonary malformations. The former is the focus of this article, while a detailed review on aortic coarctation has been provided recently by LaDisa et al. (5).
Univentricular Circulation Modeling
Palliations developed to treat single ventricle heart defects aim to by-pass the non-functional ventricle and establish a direct connection between the systemic venous and pulmonary arterial circulations (6). These treatments usually include three consecutive stages: (i) Norwood procedure [Blalock–Taussig shunts, central shunts, right ventricle-to-pulmonary artery conduit and the hybrid Norwood (7)], (ii) Glenn or hemi-Fontan procedures, and (iii) the complete Fontan procedure (or total cavo-pulmonary connection). The peculiar geometries resulting from these surgical procedures are associated with different fluid dynamics that may affect the univentricular circulation with different energy losses and uneven blood distribution to the lungs.
The up-to-date modeling approach to study these surgeries is based on different steps summarized in Figure 1, where a total cavo-pulmonary connection is shown as an example. First, the clinical images, generally from magnetic resonance (MR) or computed tomography (CT), are piled-up and used to extract the vessel contours. Secondly the generated curves are connected to create a three-dimensional (3D) geometry that can be eventually smoothed. The resulting geometry is then divided in small elements or volumes. This process is called mesh discretization. In the vertexes or centers of the elements or volumes, the governing fluid dynamics equations (i.e., Navier-Stokes equations) are solved, imposing proper boundary conditions and allowing the visualization of velocities, pressures fields, and the quantities that can be derived from them, e.g., the wall shear stresses. For a more detailed description on how these models work and can be constructed we refer the reader to the works by Vignon-Clementel et al. (8) and Corsini et al. (4).
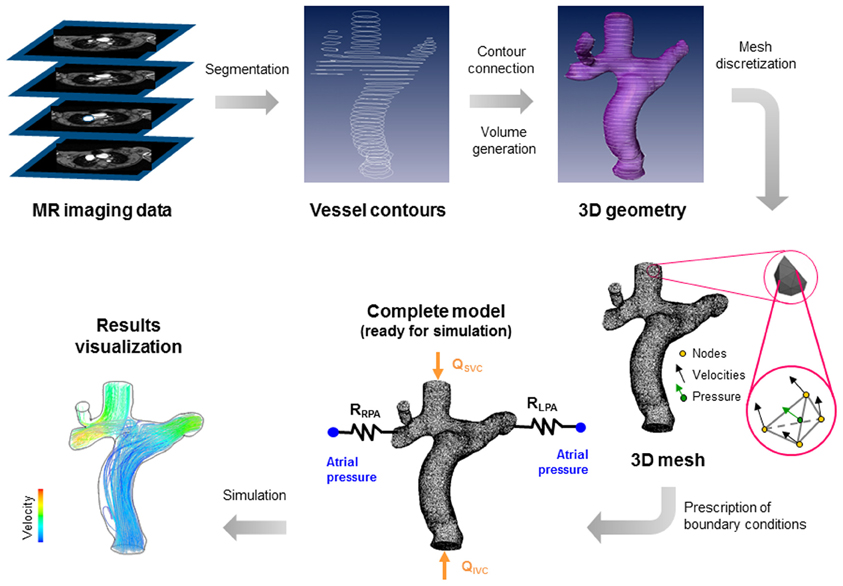
Figure 1. Steps required to build a patient-specific model of cavo-pulmonary connection. (1) Acquisition of clinical images (from magnetic resonance); (2) extraction of vessel contours; (3) generation of 3D vessel surface and volume; (4) discretization of the geometry in small elements or volumes; (5) prescription of boundary conditions (in this case the superior and inferior venae cavae flows—QSVC and QIVC—and atrial pressure); (6) simulation and visualization of results (in this case particle paths, colored by velocity, injected from superior and inferior venae cavae).
From a modeling point of view the study of fluid dynamics in systemic-to-pulmonary shunts is a more complex and challenging issue than that related to the later surgical stages, where the flows are less pulsatile and pressure fields are more uniform. In fact, fluid dynamics in stage one has rarely been investigated and modeling works represent a minority among all those related to surgical repairs for treating CHD. One reason is that the shunt and surrounding geometry after the operation varies a lot among individuals, and the shunt flow, typically the only source of pulmonary flow, is pulsatile with significant pressure gradients and velocities. An accurate mathematical description or numerical simulation of the local fluid dynamics of the shunt is thus necessary in modeling the Norwood circulation as the shunt flow is driven by the pressure difference between the systemic and pulmonary arterial circulations, and is regulated by the geometrical shunt features. Nevertheless, any hemodynamic analysis cannot be localized on the shunt region alone, since the whole circulation has to be accounted for in order to ensure proper coronary perfusion, minimize ventricular volume overload, and pulmonary hypertension. Furthermore, in infants and small babies, mathematically accurate measurements and data needed for modeling purposes are difficult to obtain. Most studies have been limited to either 3D computational models (9–14) or in vitro models (15–19) of the local fluid dynamics. Such models, although providing a very detailed description of the local hemodynamics, could not describe the mutual interactions with the remainder of the circulatory system, because boundary conditions (flows or pressures) were enforced to the model.
A first attempt to remove this limitation was made by Migliavacca and colleagues (20), who built a detailed closed-loop lumped parameter, i.e., zero-dimensional, model (LPM or 0D) accounting for the entire circulation of the patient. In particular, the complex hydraulic behavior of the shunt was modeled as a non-linear resistance varying with the shunt diameter and flow rate, whose parameter values had been previously deduced from simulations with 3D local models. Although simulation results matched clinical observations reasonably well, the lack of clinical data (except for the whole systemic and pulmonary vascular resistances) measured in peripheral regions of the circulation made parameter identification a difficult task.
Later on, in order to utilize the information obtained from both 3D models (i.e., local fluid dynamic variables and effect of changing anatomical features) and LPMs (i.e., pressures and flow distribution throughout the peripheral circulation) at the same time, a combined approach coupling the two types of models has been developed. A computational application of this methodology can be found in Laganà et al. (21), Migliavacca et al. (22), Bove et al. (23), Baretta et al. (24) and Corsini et al. (25), where the hemodynamic effects of a central shunt, a modified Blalock–Taussig shunt, a right ventricle-to-pulmonary artery shunt and the hybrid approach were analyzed in terms of pulmonary and coronary perfusion, as well as ventricular performance.
Despite the advantages brought by the combined methodology into the study of surgical procedures whose hemodynamic outcomes are still hard to predict from a clinical point of view, and given that a complete customization of the cardiovascular system is not achievable, modeling of shunts so far is limited to designs, whether 3D or 0D, which refer to clinical data averaged over groups of patients. This could be partly solved using MR scans and hemodynamic data from Doppler, MR or catheterization exams performed on a specific patient in preparation for the next surgical stage, i.e., Glenn procedure (26).
Contrary to the Norwood circulation, a number of in vitro and in silico studies evaluated the local and global fluid dynamics following the surgical creation of cavo-pulmonary anastomoses, in order to find the design that minimizes energy dissipations and optimizes the flow balance between the right and left pulmonary arteries (RPA and LPA). A review of the literature related to this topic is reported in DeGroff (27). Earlier studies reconstructed simplified geometries, representing typical anatomies of patients with cavo-pulmonary connections (28–33). More recently, the use of tomographic medical imaging techniques, such as MR and CT, has joined the well-established ultrasound and angiography imaging techniques and has allowed more realistic 3D reconstructions of a specific patient's vessels (34–39).
However, the sole geometrical accuracy does not guarantee realistic haemodynamic results. Indeed, boundary conditions required by in silico models may play a major role in determining energy dissipations and controlling flow distribution among the pulmonary branches (33, 37, 40–42).
In several in silico and in vitro studies, either volume flow rates or velocity profiles were prescribed as inlet boundary conditions together with a fixed pressure at the pulmonary outlets. As an alternative, flows were employed to set proper outlet boundary conditions (i.e., flow ratio to lungs) as well. This allows the user to define, apply or calculate different lung resistances of the model, not necessarily assuming that the right and left pulmonary vascular resistances (PVRs) are identical. In most of the recent published works, inlet and outlet flow values were assumed on the basis of averaged or time dependent clinical measurements. For example, use of MR phase contrast velocity mapping provides volume flow rates for the vessels supplying (SVC and, in case, IVC) and draining (LPA and RPA) the region of the cavo-pulmonary connection, thus allowing the simulation of patient-specific hemodynamics and power loss calculation (36, 43, 44).
In patient-specific modeling of cavo-pulmonary connections, the prescription of realistic outlet boundary conditions is necessary since they determine blood flow split into the RPA and LPA. PVR can be clinically evaluated through a catheterization exam where atrial and pulmonary arterial pressures are measured, but measurements of the individual pulmonary arterial branches (RPA and LPA) are usually absent due to the poor resolution of pressure sensors and the uncertainty of catheter tip location. Therefore, if left and right pulmonary blood flows are not available from MR data, a common assumption is to adopt equal values for left and right PVRs (29, 45, 46).
More appropriate patient-specific impedance values can be deduced on the basis of numerical simulations taking into account both pressure and flow collected data. Marsden et al. (37) used a coupled multidomain method (47) to apply resistance boundary conditions at the pulmonary outlets of 3D models of cavo-pulmonary connections reconstructed by means of MR and CT images. However, a number of important assumptions were done due to lack of clinical measurements: (i) left-right lung flow split was assumed; (ii) pulmonary resistances were chosen to obtain a pressure level in the SVC in agreement with cardiac catheterization data; (iii) left and right resistance values were assumed to be either inversely proportional to the outlet areas of the model or different fractions of the left/right pulmonary flows imposed to the pulmonary lobes.
An interesting approach for tackling the problem of outlet boundary conditions in pulmonary stenotic models was proposed by Spilker and colleagues (40) who coupled a patient-specific 3D finite element model of the proximal pulmonary arteries, with a one-dimensional linearized morphometric representation of the distal lung vasculature with diameters down to 20 μm, i.e., slightly larger than capillaries. Recently, Spilker and Taylor (42) have developed an automatic and effective method to systematically tune the LPMs used as outlet boundary conditions of 3D blood flow models (i.e., an idealized common carotid artery, an idealized iliac arterial bifurcation, and a patient-specific abdominal aorta) in order to achieve the desired features of pressure and flow waveforms. Hence, the most recent strategy suggested the use of patient-specific values not only to impose the inlet flow, but also to derive the downstream impedances coupled to patient-specific 3D anatomic models.
However, if future scenarios such as after a surgical geometry modification (35, 48) or exercise conditions (37) are simulated, actual flow rates are not available. Although usually adopted, pre-operative blood flows might be very different from those occurring in new scenarios, thus preventing an accurate virtual planning of the cardiovascular surgical repairs. Once again, combined modeling approaches which couple a 3D model of the surgical region with a LPM (22, 42, 44, 49–52) or a one-dimensional model (40) of the remainder of the cardiovascular system may solve the issue of defining reasonable boundary conditions, provided that a closed-loop coupling is performed.
The predictive role of the virtual surgery in helping surgeons choose the most effective customized procedure might be useful for the treatment of CHD, though it implies several challenges (44), and requires a considerable, interactive work among surgeons, physicians and engineers. The main limitations affecting computational modeling of CHD are: the MR imaging resolution, the wall rigidity assumption, and the absence of implementation in the LPM of short-term feed-back mechanisms (e.g., the influence of coronary perfusion on cardiac contractility) and long-term adaptive phenomena (e.g., physiologic/pathologic changes due to vessel remodeling and patient growth). Even with the state-of-the-art imaging techniques, the first limitation still impedes an accurate 3D modeling of small vessels or conduits such as the systemic-to-pulmonary shunts. The second point should be considered especially for the first stage palliation, since previous experimental (18) and computational (11) studies suggested that the shape and area of the distal anastomosis of the shunt significantly changes with the pulmonary artery pressure, thus with the PVR. Therefore, shunts with different diameters do not necessarily behave in different ways, depending on their downstream resistance. However, simulating compliant vessels with complex geometry and steeply changing wall properties (from systemic artery to Gore-Tex, to pulmonary artery) is not trivial and would require a noticeable computational effort. To overcome the last limitation implies deep knowledge of the patho-physiologic mechanisms causing the aforementioned phenomena, but enough relevant clinical data allowing realistic modeling are still not available.
Finally, a brief note should be devoted to the fluid dynamics generated by mechanical devices. In this context, blood pump specifically designed to support adolescent and adult patients with single ventricle physiology has been recently studied with the aim of providing a therapeutic option to medically stabilize patients. Rodefeld et al. (53) presented a 3D idealized computational model of the total cavo-pulmonary connection with an impeller represented as a smooth two-sided conical actuator disk with rotation in the vena caval axis. The authors demonstrated a reduction in power loss by 88%. More recently the same authors (54) investigated the hemodynamic and hemolysis performance of a catheter-based viscous impeller pump to power the Fontan circulation either with computer simulations and a mock circuit.
Aortic and Pulmonary Malformations
Mathematical modeling has also been applied with success to the studies of aortic and pulmonary malformations.
Stand-alone lumped parameters models have demonstrated a good performance in the study of pulmonary regurgitation after repair of tetralogy of Fallot (55). The authors demonstrated that amount of regurgitation, in the absence of an effective valve, depends on pulmonary arterial compliance and on the location of resistance relative to the compliance (Figure 2).
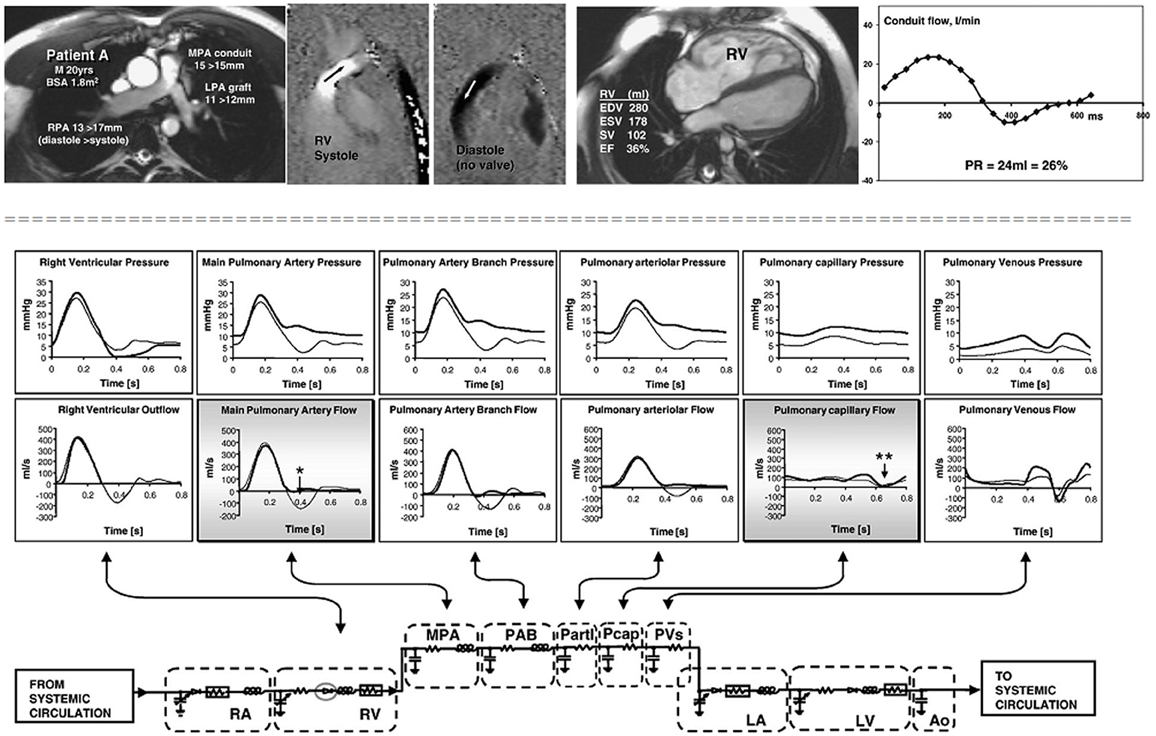
Figure 2. Cardiovascular magnetic resonance studies in a patient without an effective pulmonary valve and pulmonary regurgitation. The patient (upper panels) was a 20 year old man, born with tetralogy of Fallot, palliated with a right Blalock–Taussig shunt and repaired at 8 years with a homograft right ventricle to pulmonary artery conduit and graft augmentation of the proximal left pulmonary artery. Cine imaging (upper row, first panel) and inplane, vertically encoded velocity maps aligned with the right ventricular outflow tract (upper row, second and third panel). No effective valve action in diastole. Flow curve (upper row, fourth panel) plotted from retrospectively gated acquisitions of velocities through planes transecting the proximal MPA, giving the regurgitant volumes and fractions shown. The peak systolic velocity was 3 m/s in the conduit. Fifth panel reports the right ventricular volume measurements. Lower panel: results from a lumped parameter model describing the pulmonary circulation. The right heart and pulmonary vascular components of the numerical model represented by electrical analog symbols with plots of pressure and flow through each part of the model calculated with and without pulmonary valve function (broad and thin lines, respectively). Without the valve, there is regurgitant flow in early diastole at main pulmonary artery level (*) with late diastolic forward flow, but there is no reversal of flow at capillary level (**), which means that the regurgitant volume originates entirely from compliance of the virtual pulmonary arteries and arterioles. M, male; BSA, body surface area; MPA, main pulmonary artery; RPA, right pulmonary artery; LPA, left pulmonary artery; RV, right ventricle; PR, pulmonary regurgitation; EDV, end diastolic volume; ESV, end systolic volume; SV, stroke volume; EF, ejection fraction. RA, right atrium; RV, right ventricle; PAB, pulmonary artery branches; Partl, pulmonary arterioles; Pcap, pulmonary capillaries; PVs, pulmonary veins; LA, left atrium; LV, left ventricle; Ao, aorta. (With permission from, 55).
LaDisa et al. (5) reviewed the recent modeling literature on aortic coarctation similarly to what applied in the univentricular circulation. The results from the analysed studies provided a greater understanding of the preoperative and postoperative assessment of surgical and interventional options and an additional tool for prediction of postoperative quantities. Aortic walls are compliant and the interaction between the fluid and solid parts is more important than in the venous districts. For these reasons the most recent studies (56) included also a fluid-structure interaction (FSI) modeling.
Conclusions
In mathematical modeling of surgical corrections for univentricular hearts, pulmonary and aortic malformations, several goals have been achieved so far, namely:
- Availability of patient-specific imaging data to allow the reconstruction of customized 3D models;
- flow, velocity and pressure data acquired from the investigated patient (with MR, Doppler and catheterization exams) are used to define patient-specific boundary conditions;
- connecting a LPM to a geometrical model in a closed-loop fashion enables mutual interaction between the local (more detailed) and global descriptions of the investigated fluid dynamics, thus avoiding unrealistic assumptions on the upstream and downstream circulations;
- the modeling software currently available allows to perform various virtual surgeries on the studied anatomic models, simulating the final result of the surgical operation; such models can be used further to evaluate which is the best model in terms of hemodynamic performance;
- with the current computing power availability in computational laboratories, simulations tasks that used to require days to complete can now be solved in hours.
In the future, however, some aspects of the modeling process need to be refined:
- Both imaging (e.g., from MR) resolution and geometrical refining algorithms currently used are expected to improve, in order to reconstruct more faithfully customized complex anatomies and tiny vessels;
- virtual surgical planning needs to emphasize the importance of pre-operatively collecting as many congruent patient-specific data as possible, to predict more accurately the patient-specific hemodynamics in the new configurations;
- relevant clinical data should be collected also to explore the causes of short-term and long-term adaptive phenomena, with the final objective of their realistic implementation within the models;
- for application in a clinical environment computing power should further increase to allow simulation times to be in the order of minutes.
Information obtained from numerical models cannot substitute clinical exams and judgment, but can provide insights to guide clinical decisions. Furthermore, allowing predictions and interpretations of phenomena and mechanisms that are not well-defined, mathematical models can resolve complex, altered cardiovascular physiology, as well as evaluate clinically relevant parameters which are not routinely measured. The added value resulting from computational modeling has already been exploited in the clinical management of coronary artery disease in adults (57). This could be potentially applied to CHD, provided that proper accuracy and resolution are obtained with advancements in the measurement and imaging techniques.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Authors are partially supported by a grant from the Fondation Leducq.
References
1. Pekkan K, Whited B, Kanter K, Sharma S, de Zélicourt D, Sundareswaran K, et al. Patient-specific surgical planning and hemodynamic computational fluid dynamics optimization through free-form haptic anatomy editing tool (SURGEM). Med Biol Eng Comput. (2008) 46:1139–52.
2. Haggerty CM, de Zélicourt DA, Restrepo M, Rossignac J, Spray TL, Kanter KR, et al. Comparing pre- and post-operative Fontan hemodynamic simulations: implications for the reliability of surgical planning. Ann Biomed Eng. (2012) 40:2639–51.
3. Kung E, Baretta A, Baker C, Arbia G, Biglino G, Corsini C, et al. Predictive modeling of the virtual Hemi-Fontan operation for second stage single ventricle palliation: two patient-specific cases. J Biomech. (2013) 46:423–9.
4. Corsini C, Baker C, Kung E, Schievano S, Arbia G, Baretta A, et al. An integrated approach to patient-specific predictive modeling for single ventricle heart palliation. Comput Methods Biomech Biomed Engin. (Forthcoming 2013). doi: 10.1080/10255842.2012.758254. [Epub ahead of print].
5. LaDisa, JF Jr, Taylor CA, Feinstein JA. Aortic coarctation: recent developments in experimental and computational methods to assess treatments for this simple condition. Prog Pediatr Cardiol. (2010) 30:45–9.
7. Galantowicz M, Cheatham JP, Phillips A, Cua CL, Hoffman TM, Hill SL, et al. Hybrid approach for hypoplastic left heart syndrome: intermediate results after the learning curve. Ann Thorac Surg. (2008) 85:2063–70.
8. Vignon-Clementel IE, Marsden AL, Feinstein JA. A primer on computational simulation in congenital heart disease for the clinician. Prog Pediatr Cardiol. (2010b) 30:3–13.
9. Migliavacca F, Dubini G, Pennati G, Pietrabissa R, Fumero R, Hsia TY, et al. Computational model of the fluid dynamics in systemic-to-pulmonary shunts. J Biomech. (2000a) 33:549–57.
10. Migliavacca F, Yates R, Pennati G, Dubini G, Fumero R, de Leval MR. Calculating blood flow from Doppler measurements in the systemic-to-pulmonary artery shunt after the Norwood operation: a method based on computational fluid dynamics. Ultrasound Med Biol. (2000b) 26:209–19.
11. Migliavacca F, Pennati G, Di Martino E, Dubini G, Pietrabissa R. Pressure drops in a distensible model of end-to-side anastomosis in systemic-to-pulmonary shunts. Comput Methods Biomech Biomed Engin. (2002) 5:243–8.
12. Song MH, Sato M, Ueda Y. Three-dimensional simulation of the Blalock–Taussig shunt using computational fluid dynamics. Surg Today (2001) 31:688–94.
13. Sant'Anna JRM, Pereira DC, Kalil RAK, Prates PR, Horowitz E, Sant'Anna RT, et al. Computer dynamics to evaluate blood flow through the modified Blalock–Taussig shunt. Rev Bras Cir Cardiovasc. (2003) 18:253–60.
14. Waniewski J, Kurowska W, Mizerski JK, Trykozko A, Nowinski K, Brzezi nska-Rajszys G, et al. The effects of graft geometry on the patency of a systemic-to-pulmonary shunt: a computational fluid dynamics study. Artif Organs (2005) 29:642–50.
15. Kitagawa T, Katoh I, Fukumura Y, Yoshizumi M, Masuda Y, Hori T. Achieving optimal pulmonary blood flow in the first-stage palliation in early infancy for complex cardiac defects with hypoplastic left ventricles. Cardiol Young (1995) 5:21–7.
16. Tacy TA, Whitehead KK, Cape EG. In vitro Doppler assessment of pressure gradients across modified Blalock–Taussig shunts. Am J Cardiol. (1998) 81:1219–23.
17. DeGroff CG, Shandas R, Kwon J, Valdes-Cruz L. Accuracy of the Bernoulli equation for estimation of pressure gradient across stenotic Blalock–Taussig shunts: an in vitro and numerical study. Pediatr Cardiol. (2000) 21:439–47.
18. Pennati G, Fiore GB, Migliavacca F, Laganà, K., Fumero R, Dubini G. In vitro steady-flow analysis of systemic-to-pulmonary shunt haemodynamics. J Biomech. (2001) 34:23–30.
19. Gervaso F, Kull S, Pennati G, Migliavacca F, Dubini G, Luisi VS. The effect of the position of an additional systemic-to-pulmonary shunt on the fluid dynamics. Cardiol Young (2004) 14:38–43.
20. Migliavacca F, Pennati G, Dubini G, Fumero R, Pietrabissa R, Urcelay G, et al. Modeling of the Norwood circulation: effects of shunt size, vascular resistances, and heart rate. Am J Physiol Heart Circ Physiol. (2001) 280:H2076–86.
21. Laganà, K., Balossino R, Migliavacca F, Pennati G, Bove EL, de Leval MR, et al. Multiscale modeling of the cardiovascular system: application to the study of pulmonary and coronary perfusions in the univentricular circulation. J Biomech. (2005) 38:1129–41.
22. Migliavacca F, Balossino R, Pennati G, Dubini G, Hsia TY, de Leval MR, et al. Multiscale modelling in biofluidynamics: application to reconstructive pediatric cardiac surgery. J Biomech. (2006) 26:1010–20.
23. Bove EL, Migliavacca F, de Leval MR, Balossino R, Pennati G, Lloyd TR, et al. Use of mathematical modeling to compare and predict hemodynamic effects of the modified Blalock–Taussig and right ventricle to pulmonary artery shunts for hypoplastic left heart syndrome. J Thorac Cardiovasc Surg. (2008) 136:312.e2–20.e2.
24. Baretta A, Corsini C, Yang W, Vignon-Clementel IE, Marsden AL, Feinstein JA, et al. Virtual surgeries in patients with congenital heart disease: a multiscale modelling test case. Phil Trans R Soc A (2011) 369:4316–30.
25. Corsini C, Cosentino D, Pennati G, Dubini G, Hsia TY, Migliavacca F. Multiscale models of the hybrid palliation for hypoplastic left heart syndrome. J Biomech. (2011) 44:767–70.
26. Pennati G, Migliavacca F, Dubini G, Bove EL. Modeling of systemic-to-pulmonary shunts in newborns with a univentricular circulation: state of the art and future directions. Prog Pediat Cardiol. (2010) 30:23–9.
27. DeGroff CG. Modeling the Fontan circulation: where we are and where we need to go. Pediatr Cardiol. (2008) 29:3–12.
28. Kim YH, Walker PG, Fontaine AA, Panchal S, Ensley AE, Oshinski J, et al. Hemodynamics of the Fontan connection: an in-vitro study. J Biomech Eng. (1995) 117:423–8.
29. Dubini G, de Leval MR, Pietrabissa R, Montevecchi FM, Fumero R. A numerical fluid mechanical study of repaired congenital heart defects. Application to the total cavopulmonary connection. J Biomech. (1996) 29:111–21.
30. Sharma S, Goudy S, Walker P, Panchal S, Ensley A, Kanter K, et al. In vitro flow experiments for determination of optimal geometry of total cavopulmonary connection for surgical repair of children with functional single ventricle. J Am Coll Cardiol. (1996) 27:1264–9.
31. Lardo AC, Webber SA, Friehs I, del Nido PJ, Cape EG. Fluid dynamic comparison of intra-atrial and extracardiac total cavopulmonary connections. J Thorac Cardiovasc Surg. (1999) 117:697–704.
32. Khunatorn Y, Mahalingam S, DeGroff CG, Shandas R. Influence of connection geometry and SVC-IVC flow rate ratio on flow structures within the total cavopulmonary connection: a numerical study. J Biomech Eng. (2002) 124:364–77.
33. Bove EL, de Leval MR, Migliavacca F, Guadagni G, Dubini G. Computational fluid dynamics in the evaluation of hemodynamic performance of cavopulmonary connections after the Norwood procedure for hypoplastic left heart syndrome. J Thorac Cardiovasc Surg. (2003) 126:1040–7.
34. de Zélicourt DA, Pekkan K, Wills L, Kanter K, Forbess J, Sharma S, et al. In vitro flow analysis of a patient-specific intraatrial total cavopulmonary connection. Ann Thorac Surg. (2005) 79:2094–102.
35. Pekkan K, de Zélicourt D, Ge L, Sotiropoulos F, Frakes D, Fogel MA, et al. Physics-driven CFD modelling of complex anatomical cardiovascular flows– a TCPC case study. Ann Biomed Eng. (2005) 33:284–300.
36. Socci L, Gervaso F, Migliavacca F, Pennati G, Dubini G, Ait-Ali L, et al. Computational fluid dynamics in a model of the total cavopulmonary connection reconstructed using magnetic resonance images. Cardiol Young (2005) 15:61–7.
37. Marsden AL, Vignon-Clementel IE, Chan FP, Feinstein JA, Taylor CA. Effects of exercise and respiration on hemodynamic efficiency in CFD simulations of the total cavopulmonary connection. Ann Biomed Eng. (2007) 35:250–63.
38. Wang C, Pekkan K, de Zélicourt D, Horner M, Parihar A, Kulkarni A, et al. Progress in the CFD modeling of flow instabilities in anatomical total cavopulmonary connections. Ann Biomed Eng. (2007) 35:1840–56.
39. Sun Q, Wan D, Liu J, Hong H, Liu Y, Zhu M. Patient-specific computational fluid dynamic simulation of a bilateral bidirectional Glenn connection. Med Biol Eng Comput. (2008) 46:1153–9.
40. Spilker RL, Feinstein JA, Parker DW, Reddy VM, Taylor CA. Morphometry-based impedance boundary conditions for patient-specific modeling of blood flow in pulmonary arteries. Ann Biomed Eng. (2007) 35:546–59.
41. Vignon-Clementel IE, Figueroa CA, Jansen KE, Taylor CA. Outflow boundary conditions for 3D simulations of non-periodic blood flow and pressure fields in deformable arteries. Comput Methods Biomech Biomed Engin. (2010a) 13:625–40.
42. Spilker RL, Taylor CA. Tuning multidomain hemodynamic simulations to match physiological measurements. Ann Biomed Eng. (2010) 38:2635–48.
43. Whitehead KK, Pekkan K, Kitajima HD, Paridon SM, Yoganathan AP, Fogel MA. Nonlinear power loss during exercise in single-ventricle patients after the Fontan: insights from computational fluid dynamics. Circulation (2007) 116:I165–71.
44. Pennati G, Corsini C, Cosentino D, Hsia TY, Luisi VS, Dubini G, et al. Boundary conditions of patient-specific fluid dynamics modelling of cavopulmonary connections: possible adaptation of pulmonary resistances results in a critical issue for a virtual surgical planning. Interface Focus (2011) 1:297–307.
45. Migliavacca F, Dubini G, Bove EL, de Leval MR. Computational fluid dynamics simulations in realistic 3-D geometries of the total cavopulmonary anastomosis: the influence of the inferior caval anastomosis. J Biomech Eng. (2003) 125:805–13.
46. Dasi LP, Whitehead K, Pekkan K, de Zélicourt D, Sundareswaran K, Kanter K, et al. Pulmonary hepatic flow distribution in total cavopulmonary connections: extracardiac versus intracardiac. J Thorac Cardiovasc Surg. (2011) 141:207–14.
47. Vignon-Clementel IE, Figueroa AC, Jansen KE, Taylor CA. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Comput Methods Appl Mech Eng. (2006) 195:3776–96.
48. de Zélicourt DA, Pekkan K, Parks J, Kanter K, Fogel M, Yoganathan AP. Flow study of an extracardiac connection with persistent left superior vena cava. J Thorac Cardiovasc Surg. (2006) 131:785–91.
49. Liang F, Taniguchi H, Liu H. A multi-scale computational method applied to the quantitative evaluation of the left ventricular function. Comput Biol Med. (2007) 37:700–15.
50. Kim HJ, Vignon-Clementel IE, Figueroa CA, Jansen KE, Feinstein JA, Taylor CA. On coupling a lumped parameter heart model and a three-dimensional finite element aorta model. Ann Biomed Eng. (2009) 37:2153–69.
51. Kim HJ, Jansen KE, Taylor CA. Incorporating autoregulatory mechanisms of the cardiovascular system in three-dimensional finite element models of arterial blood flow. Ann Biomed Eng. (2010) 38:2314–30.
52. Marsden AL, Bernstein AJ, Reddy VM, Shadden SC, Spilker RL, Chan FP, et al. Evaluation of a novel Y-shaped extracardiac Fontan baffle using computational fluid dynamics. J Thorac Cardiovasc Surg. (2009) 137:394.e2–403.e2.
53. Rodefeld MD, Coats B, Fisher T, Giridharan GA, Chen J, Brown JW, et al. Cavopulmonary assist for the univentricular Fontan circulation: von Kármán viscous impeller pump. J Thorac Cardiovasc Surg. (2010) 140:529–36.
54. Giridharan GA, Koenig SC, Kennington J, Sobieski MA, Chen J, Frankel SH, et al. Performance evaluation of a pediatric viscous impeller pump for Fontan cavopulmonary assist. J Thorac Cardiovasc Surg. (2013) 145:249–57.
55. Kilner PJ, Balossino R, Dubini G, Babu-Narayan SV, Taylor AM, Pennati G, et al. Pulmonary regurgitation: the effects of varying pulmonary artery compliance, and of increased resistance proximal or distal to the compliance. Int J Cardiol. (2009) 133:157–66.
Keywords: mathematical model, fluid dynamics, patient-specific, medical images
Citation: Pennati G, Corsini C, Hsia T-Y and Migliavacca F (2013) Computational fluid dynamics models and congenital heart diseases. Front. Pediatr. 1:4. doi: 10.3389/fped.2013.00004
Received: 22 November 2012; Accepted: 01 February 2013;
Published online: 26 February 2013.
Edited by:
Piergiorgio Tozzi, Centre Hospitalier Universitaire Vaudois, SwitzerlandReviewed by:
Yves Durandy, ICPS, FrancePiergiorgio Tozzi, Centre Hospitalier Universitaire Vaudois, Switzerland
Copyright © 2013 Pennati, Corsini, Hsia and Migliavacca. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and subject to any copyright notices concerning any third-party graphics etc.
*Correspondence: Francesco Migliavacca, Laboratory of Biological Structure Mechanics, Chemistry, Materials and Chemical Engineering Department “Giulio Natta”, Politecnico di Milano, Piazza Leonardo da Vinci, 32, 20133 Milano, Italy. e-mail:ZnJhbmNlc2NvLm1pZ2xpYXZhY2NhQHBvbGltaS5pdA==


 and
and