- 1 Computational Neuroscience Section, Department of Psychiatry and Neurobehavioral Sciences, University of Virginia Health System, Charlottesville, VA, USA
- 2 Department of Psychiatry and Neurobehavioral Sciences, University of Virginia, Charlottesville, VA, USA
In this paper we view alcohol dependence and the response to treatment as a recurrent bio-behavioral process developing in time and propose formal models of this process combining behavior and biology in silico. The behavioral components of alcohol dependence and treatment are formally described by a stochastic process of human behavior, which serves as an event generator challenging the metabolic system. The biological component is driven by the biochemistry of alcohol intoxication described by deterministic models of ethanol pharmacodynamics and pharmacokinetics to enable simulation of drinking addiction in humans. Derived from the known physiology of ethanol and the literature of both ethanol intoxication and ethanol absorption, the different models are distilled into a minimal model (as simple as the complexity of the data allows) that can represent any specific patient. We use these modeling and simulation techniques to explain responses to placebo and ondansetron treatment observed in clinical studies. Specifically, the response to placebo was explained by a reduction of the probability of environmental reinforcement, while the effect of ondansetron was explained by a gradual decline in the degree of ethanol-induced neuromodulation. Further, we use in silico experiments to study critical transitions in blood alcohol levels after specific average number of drinks per day, and propose the existence of two critical thresholds in the human – one at 5 and another at 11 drinks/day – at which the system shifts from stable to critical and to super critical state indicating a state of alcohol addiction. The advantages of such a model-based investigation are that (1) the process of instigation of alcohol dependence and its treatment can be deconstructed into meaningful steps, which allow for individualized treatment tailoring, and (2) physiology and behavior can be quantified in different (animal or human) studies and then the results can be integrated in silico.
Introduction
In the past two decades, computer simulation and computer-aided design have made dramatic progress in all areas of development of complex engineering systems. There is an enormous body of literature on computer simulation methods applicable to physics, engineering, economics, biology, metabolism, aerospace, meteorology and climatology, warfare, and just about any other subject of investigation that can be approximately described by a mathematical model. The review of this literature is beyond the scope of this paper; here we will only mention a few biomedical modeling and simulation projects that are relevant to the topic at hand – in silico modeling of the effects of alcohol intoxication and alcohol dependence treatment. For example, accurate prediction of the outcome of clinical trials has been achieved using the Archimedes diabetes model (Eddy and Schlessinger, 2003a,b). Entelos, Inc., specializes in predictive biosimulation, introducing in its Physiolab suite in silico models for various physiological systems: cardiovascular, metabolic (diabetes), and others (Michelson, 2006). I diabetes, a recently developed simulator of the human metabolic system became the first tool accepted by the US Food and Drug Administration as a substitute to animal trials in the preclinical testing of control strategies in artificial pancreas studies (Kovatchev et al., 2009). These in silico models are typically based on mathematical models of the studied physiological system, which are developed from extensive data collection examining underlying physiology in sufficient detail to allow for formal modeling. The models are then used to develop algorithms and software that power up simulation experiments. According to Winsberg (2002), simulation experiments are typically classified with respect to the type of algorithm that they employ: “Discretization” techniques transform continuous differential equations into step-by-step algebraic expressions. “Monte Carlo” methods use random sampling algorithms even when there is no underlying indeterminism in the system. “Cellular automata” assign a discrete state to each node of a network of elements, and assign rules of evolution for each node based on its local environment in the network. The field of alcohol addiction is of particular interest for such applications: it is both very developed (e.g., in modeling the dynamics of ethanol in blood or the diffusion from blood to brain tissues) and in its infancy, with only three simulation studies in the past 20 years (Duffy and Alanko, 1992; Derr, 1993; Breton, 2010). It also requires modeling of behavioral system and medication effects that are not yet mainstream (Kovatchev, 2010). In this paper, we review several models of ethanol blood distribution, leading to simulation studies linking system-level characteristics to clinical outcomes (Breton, 2010). Further, we utilize both discretization and Monte Carlo (or generally stochastic) methods to describe human behaviors related to the instigation and treatment of alcohol dependence (Kovatchev, 2010). However, we first discuss three types of mathematical models of biosystems, classified according to the purpose of modeling: models to measure, to simulate, or to control the biosystem under consideration – a classification proposed by Cobelli et al. (2009) in the context of diabetes.
Models to Measure
The models to measure are generally simpler, allowing hidden relationships to be evaluated by estimating underlying parameters. Most of these models are compartmental; e.g., they represent the human body as a set of homogeneous compartments of specific concentrations and volumes linked by diffusion or rate-limited pathways. Classic examples include the Widmark Model of Ethanol Pharmacokinetics Assuming, which offers a straightforward interpretation with a constant ethanol clearance rate and the human body modeled as one compartment (Widmark, 1932), and the more complex Minimal Model of Glucose Kinetics suggested by Bergman et al. (1979) almost 30 years ago to measure insulin resistance in health and diabetes. More recently, with the advent of the digital biology paradigm, various models to measure have been developed addressing pharmacokinetics, physiology, and human behavior. Deeper understanding of the processes involved and the development of novel measuring tools have allowed for more precise measurement of ethanol pharmacokinetics and the development of more complex non-linear models (Mumenthaler et al., 2000; Norberg et al., 2000, 2003; Umulis et al., 2005). The study of ethanol kinetics in vivo has led to a better representation of the ethanol–aldehyde–acetate process via the Michaelis–Menten rate of alcohol clearance introduced by Norberg et al. (2000). It is now widely accepted that alcohol clearance is a Michaelis–Menten controlled reaction – i.e., an enzyme-enhanced chemical reaction with limited supply (Umulis et al., 2005). These and other pharmacokinetic models are discussed in detail in (Breton, 2010).
Models to Simulate
The models to simulate are maximal multi-parameter models describing the complexity of the system as comprehensively as possible (Dalla Man et al., 2007a,b; Cobelli et al., 2009). For example, the recently published meal model of glucose-insulin dynamics is a descendant of the Minimal Model, which encompasses several metabolic subsystems including the gastrointestinal tract, renal function, hepatic glucose production, and others (Dalla Man et al., 2007a,b). When a maximal model is built, the computer simulation of the observed biosystem becomes possible, leading to in silico trials involving virtual “subjects” rather than real people (Kovatchev et al., 2009). Such in silico trials can serve as precursors guiding expensive and time-consuming clinical investigations by outruling ineffective treatment approaches. Therefore, realistic computer simulation is capable of providing valuable information about the effectiveness, safety, and limits of various treatments. Computer simulation allows experiments with extreme situations and testing of extreme failure modes that are unrealistic in animals and clinically impossible in humans. Besides extreme experiments, various treatment scenarios can be efficiently tested and either rejected or accepted for inclusion in future clinical experiments, which allows for rapid, comprehensive, and cost–effective clinical trial design (Kovatchev et al., 2009). We need to emphasize, however, that good in silico performance of a treatment does not guarantee in vivo performance. Computer simulation should only be used to reject inefficient treatments; it cannot confirm the efficacy of an intervention.
Models to Control
External control of a complex technical or living system is generally achieved by control algorithms that are based on a certain mathematical representation of the system – a model to control – combined with the ability to observe the system in real time and make immediate decisions for correction of the system state. The models to control are typically simplified (frequently linearized) models that allow for rapid observation and computation of the corrective action. A prime example of medical devices that use adaptive control algorithms is the cardiac pacemaker, which in the past two decades has been incorporating automated control functions such as automatic capture and sensing control, self-adjusting rate response settings, sinus rhythm and atrioventricular conduction preference, and others (Saoudi et al., 1999; Wood, 2000; Khasnis and Tepper, 2003; Haddad et al., 2005). In diabetes, successful attempts at external closed-loop control have been made using various systems and algorithms, from cumbersome intravenous systems and implantable devices (Albisser et al., 1974; Santiago et al., 1979; Renard, 2002) to external subcutaneous control (Steil et al., 2006; Weinzimer et al., 2008; El-Khatib et al., 2010; Hovorka et al., 2010; Kovatchev et al., 2010). Relating control to simulation, comprehensive in silico testing of control algorithms is an efficient strategy if a model to control is tested against a much more complex model to simulate. In other words, the effectiveness of a controller can be judged if it is tested in realistic in silico conditions, which can be achieved by a comprehensive simulation model.
Methods
Recurrent Bio-Behavioral Process of Alcohol Dependence and Treatment
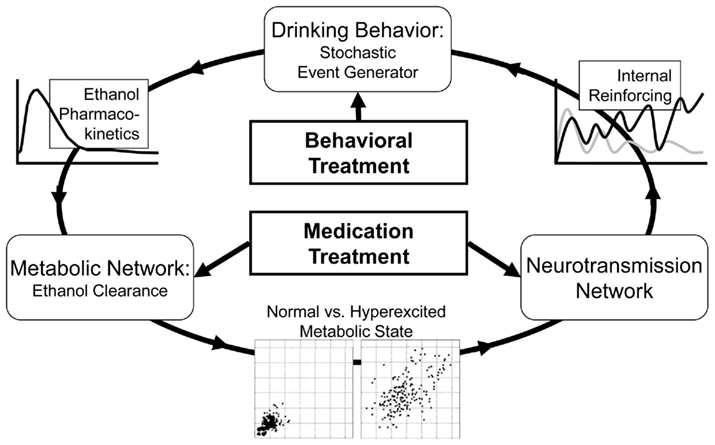
Figure 1 presents the general concept of the self-reinforcing recurrent bio-behavioral process describing the progression of alcohol dependence, its remission through medication or behavioral treatment, and potential relapse.
As presented in Figure 1, the system (person) is represented by several blocks (components) linked via a circular pattern of sequential steps. First, a behavioral event generator actuates system disturbances (e.g., drinks), which cause metabolic disturbances that can be different for each person, depending on his or her individual parameters of alcohol pharmacokinetics. Further, when the metabolic network is subjected to recurrent stress, the intensity of stress determines whether or not a phase transition to a hyperexcited metabolic state would occur (Breton, 2010). A chronic hyperexcited metabolic state would influence the neurotransmission network, potentially leading to alcohol dependence. This in turn would result in a high degree of internal reinforcing (craving), which accelerates the behavioral event generator by triggering excessive drinking. Medication treatment would typically target the neurotransmission or the metabolic component of this recurrent process, while behavioral treatment would attempt to reduce the frequency of firing of the behavioral event generator. With this formal understanding, we shall now proceed to a mathematical description of the general components of the alcohol dependence process that would be used for its in silico representation and treatment evaluation: (1) a stochastic model of behavioral and social conditioning; (2) a mathematical model of the human metabolic system specifically targeting ethanol kinetics; and (3) a comprehensive population of in silico “subjects” spanning the observed in vivo inter-individual metabolic and behavioral differences.
Formal Description of Human Behavior and Social Conditioning
In order to built comprehensive in silico models of alcohol dependence and treatment, a formal mathematical description of human behavior and environmental conditioning is needed. However, the behavioral and social modeling field is still quite limited. Whilst several theoretical models based on internal somatic perception have been proposed (Baumann et al., 1989; Leventhal and Diefenbach, 1991; Leventhal et al., 1992), their heuristic approach has not permitted their development in sufficient mathematical detail to guide data analysis. For example, the stages of change described by the Transtheoretical Model of DiClemente and Prochaska (1998) refer to a stochastic sequence – of readiness to change, stage of change status, temptation, and confidence – that has consistently shown predictive and explanatory ability for clinical outcome in alcohol dependence treatment studies. However, this sequence has not been identified as stochastic and has not been formalized to the extent that would permit computerized assessment and simulation. Another example can be provided in the context of non-specific treatment effects, such as the Hawthorne effect, which describes the tendency of an individual to change his or her behavior as a consequence of being observed or studied (Mayo, 1933; Roethlisberger et al., 1939). While this effect provides evidence for the importance of environmental conditioning and external reinforcement for all stages of the progression of alcohol dependence – from acquisition of alcohol dependence, through treatment, to potential relapse – there is no formal description of environmental conditioning that would allow its inclusion in an integrated in silico model encompassing physiology, behavior, and social conditioning. Therefore, to advance the field, we have proposed a formal stochastic bio-behavioral model of the sequence leading to self-regulation decision, in which the first three steps of the process were described by continuous variables while the decisions at Step 4 were binary (Kovatchev, 2010). The general concept is that decisions concerning self-regulation behaviors are often based on perception and appraisal of the body’s internal state. Thus, the sequence preceding a certain action includes at least four sequential steps: internal condition → perception → environmental conditioning → self-regulation decision. We have applied this general framework to evaluate the relationship between self-treatment behavior and the development of hypoglycemia in diabetics (Gonder-Frederick et al., 1997; Kovatchev et al., 1998; Clarke et al., 1999), as well as the psycho-physiological factors associated with the attention impairment experienced by those with attention deficit hyperactivity disorder (Robeva et al., 2004; Kovatchev et al., 2005; Penberthy et al., 2005).
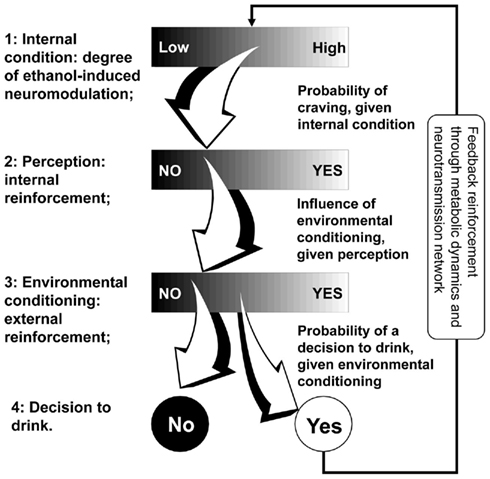
Figure 2 presents the four steps of the alcohol intake self-regulation sequence introduced above: internal condition → perception → environmental conditioning → self-regulation decision.
The basic idea behind the model of Figure 2 is that its steps are linked by a continuum of possible pathways: i.e., there are a variety of possible perceptions of internal alcohol-induced neuromodulation (Step 1 to Step 2); there is no single environment corresponding to a perception (Step 2 to Step 3); and there is no uniquely predetermined decision arising from a specific environment (Step 3 to Step 4). We, therefore, proposed a formal mathematical model in which the first three steps of this sequence are described by continuous variables, while the decisions at Step 4 are binary. The transition probabilities between the first three steps are modeled as conditional probabilities of a continuous outcome, given a continuous condition. The transition probabilities at Step 4 are conditional probabilities of a binary outcome, given a continuous condition. This reflects the clinical reality: the level of alcohol dependence, its perception, and environmental reinforcement are, by nature, continuous factors while the final decision to have or not to have another drink is binary – Yes/No. This model serves as a stochastic behavioral generator of events, each event being a drink that is supplied as an input to the recurrent process of Figure 2. In other words, the in silico preclinical experiments use behavioral and social parameters that serve as generators of metabolic disturbances to the system (person), which are then processed through the metabolic model, thereby allowing the formal reconstruction of the patterns of drinking behavior and their modulation by placebo or medication treatment. To be able to conduct in silico experiments, we need to describe our stochastic bio-behavioral model in algorithmic terms. We use a discrete-time stochastic process ξ that goes through sequential steps. The basic building block of such a process is the stochastic transition from one step to the next, which is described by the following scheme: suppose that at its Step n (n = 1, 2, 3, 4), the process ξ(n) is described by a univariate or multivariate random variable xn, having its values in some set Xn. Let S be a subset of Xn (we write S ⊂ Xn). A structure Sn of all subsets of Xn that satisfies certain conditions is called σ-algebra on Xn. A stochastic transition of the process ξ from Xn to its next stage Xn + 1 is defined by the conditional probabilities P[ξ(n + 1) = xn + 1 | ξ(n) ∈ S] for any xn + 1 ∈ Xn + 1 and S ∈ Sn. The introduction of the structure Sn is a necessary mathematical complication, which makes the model capable of incorporating continuous as well as binary variables at each step.
In silico Models of Ethanol Metabolism
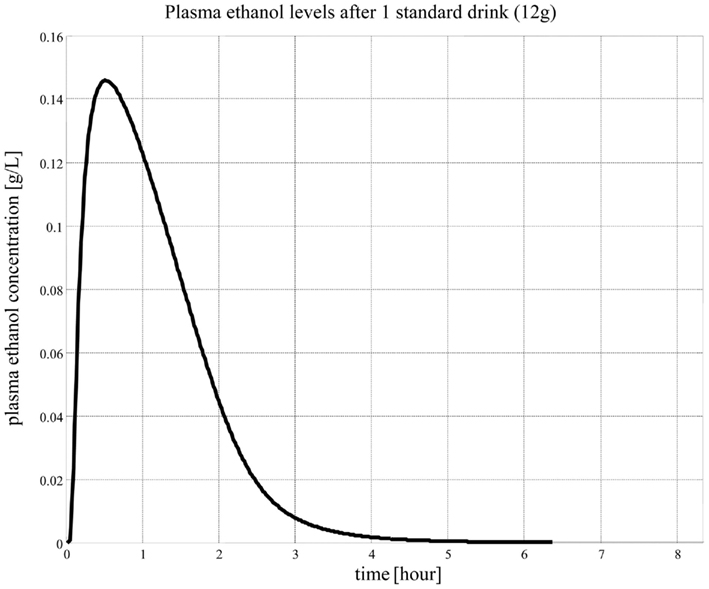
When we consume alcohol, the majority of it is absorbed from the small intestine (approximately 80%) and the stomach (approximately 20%). Generally, drinking more alcohol within a certain period of time will result in increased blood alcohol concentrations due to more alcohol being available for absorption into the bloodstream. More than 90% of the alcohol that enters the body is completely metabolized in the liver. The remaining 10% is not metabolized and is excreted in the sweat, urine, and breath. There are several routes of metabolism of alcohol in the body. The major pathways involve the liver and, in particular, the oxidation of alcohol by alcohol dehydrogenase to produce acetaldehyde, a highly toxic substance. The second step is catalyzed by acetaldehyde dehydrogenase. This enzyme converts acetaldehyde to acetic acid, a non-toxic metabolite. Acetic acid is eventually metabolized to carbon dioxide and water. The rate of alcohol metabolism depends, in part, on the amount of metabolizing enzymes in the liver, which varies among individuals and appears to have some genetic determinants (Fraser et al., 1995; Norberg et al., 2000, 2003; Matsumoto and Fukui, 2002; Ward and Coutelle, 2003). After the consumption of one standard drink1, the amount of alcohol in the drinker’s blood usually peaks within 30–45 min. The concentration of alcohol in the entire body, including the brain, is always less than that in the blood; human tissues contain a much lower percentage of water compared with the blood. However, organs having a rich blood supply, such as the brain, will quickly reach alcohol diffusion equilibrium with arterial blood. This explains why most people experience intoxication quickly after drinks and then sober up rapidly, while other bodily tissues with less blood supply, such as the muscle, are still absorbing alcohol from the bloodstream.
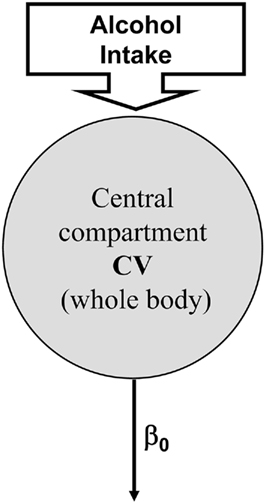
As presented in the Introduction, several models of ethanol metabolism exist (Widmark, 1932; Mumenthaler et al., 2000; Norberg et al., 2000, 2003). In these models, ethanol elimination has been assumed to exhibit a zero-order metabolism, which means that constant amount of alcohol is eliminated per unit of time regardless of blood levels. However, a number of studies have identified that elimination of ethanol follows different clearance models including first-order kinetic and a combination of zero- and first-order kinetics. Historically, the modeling of alcohol kinetics begins with the Widmark zero-order model (Widmark, 1932) presented in Figure 3, which assumes a constant clearance rate β0 and models the human body as one compartment with concentration equal to blood alcohol level, BAL(t) and constant volume V. If D(t) is the dose of ethanol received, the Widmark model is given by:

This zero-order model is still commonly used in forensic sciences for its ease of use and the relative simplicity of its structure (very few parameters, easily identifiable).
However, this oversimplification of the ethanol clearing process precludes description of inter-individual variability that is adequate for simulation purposes. A deeper understanding of the processes involved and novel measuring tools have allowed more precise measurement and understanding of ethanol pharmacokinetics and the development of more complex non-linear multi-compartment models (Oneta et al., 1998; Norberg et al., 2000, 2003; Umulis et al., 2005). Most of these models are compartmental – e.g., they represent the human body as a set of homogeneous compartments with constant ethanol concentration and volume linked by diffusion or rate-limited pathways. The study of ethanol kinetics in vivo has led to a better representation of the ethanol–aldehyde–acetate process, leading to Norberg’s model of alcohol dynamics (Norberg et al., 2000; Figure 4), which introduces a Michaelis–Menten rate of alcohol clearance – a common enzyme-catalyzed, rate-limited clearance model presented by Eq. 2:
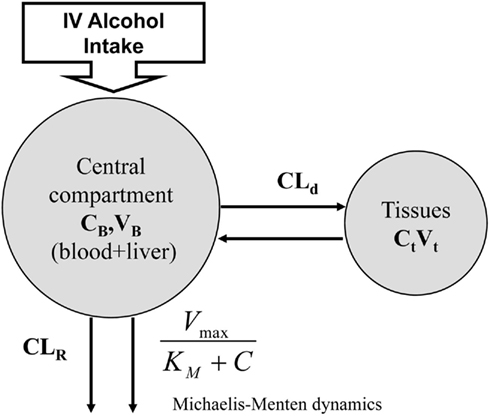
Figure 4. Norberg’s alcohol clearance model featuring Michaelis–Menten dynamics. Suitable for description of intravenous (IV) ethanol injection.
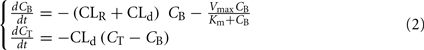
where CB stands for blood ethanol concentration, CT is the tissue concentration, CLR is the renal clearance, and CLd is the diffusion constant.
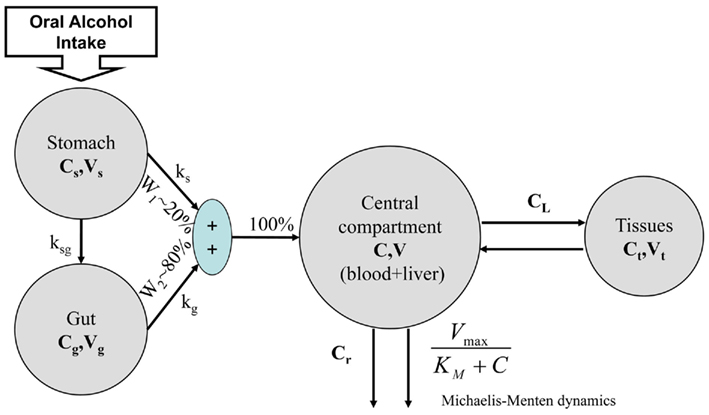
While this model describes ethanol kinetics reasonably well, one limitation is that the model relies strictly on intravenous ethanol infusion. The dynamics of orally ingested alcohol presented in Figure 5 has not been well quantified. The compartmental model in Figure 4 cannot reproduce well the dynamics of blood alcohol level of Figure 5, particularly the rate of blood alcohol level increase after alcohol ingestion. This is partly due to the slow diffusion of ethanol from the gastrointestinal tract to blood; whereas with intravenous injection the total dose of ethanol is immediately present in blood and its concentration is at equilibrium after a couple of minutes, orally ingested ethanol can take much longer to percolate fully from the digestive system to blood, therefore allowing for clearance even before the full dose has transferred to the blood. Modeling this process is difficult as ethanol diffuses to the blood from both the stomach and the intestines and at different rates; the speed of gastric emptying (and, therefore, the content and amount of what is ingested with alcohol) also plays a critical role in the dynamics of absorption.
To advance the field, we have proposed the Minimal Model of Ethanol Dynamics (Breton, 2010). To properly represent oral alcohol intake, the model includes two previously unexplored compartments of the gastrointestinal tract – the stomach and gut (Figure 6). Following the classic minimal model approach (Bergman et al., 1979), we determined that we did not need to add more compartments. Further, the processes linking these compartments include one-way diffusions from the stomach and gut into the bloodstream (ethanol in the blood cannot diffuse back to the gastrointestinal tract). The assumptions of the model include gastric emptying following an exponential decay with a certain half-life (rate constants ks and kg) and the proportion of gastric diffusion from the stomach, Ws, vs. diffusion from the gut, Wg (e.g., Ws = 20 vs. Wg = 80%; Norberg et al., 2003).
The alcohol clearance is represented by a Michaelis–Menten controlled reaction, e.g., an enzyme-enhanced chemical reaction with limited supply (Matsumoto and Fukui, 2002; Umulis et al., 2005), which has individual parameters (rate constant Cr) for each person. The differential equations governing the processes depicted in Figure 6 are as follows:
1. Ethanol is transported from the stomach to the gut with a rate constant ksg and diffuses from the stomach into the bloodstream with a rate constant kg.
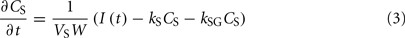
2. Ethanol diffuses from the gut into the bloodstream with a rate constant kg.
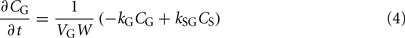
3. The total ethanol diffusion into the bloodstream is then given by the combination of diffusions from the stomach and the gut.

4. Michaelis–Menten clearance of ethanol from the bloodstream occurs.
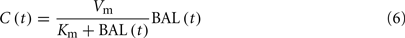
5. Two-way diffusion of ethanol between the bloodstream and tissues/liver occurs, including ethanol transport to the brain.
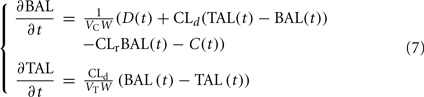
Population average values for the parameters of the models described above can be derived from the literature. For example, parameters common to Norberg’s two-compartment model can be found in Norberg et al. (2003). Tuning of the gastric model is somewhat more complex, but can be adjusted to reflect the generally admitted equilibrium between the stomach and gut of 20 vs. 80% and the 50-min half-life of gastric emptying. The Parameters given in Table 1 below were used in the analysis and represent an average “subject.”
However, while population averages are sufficient to simulate average ethanol dynamics and to extract general characteristics of the addiction process, they do not reflect the inter-person variability observed in vivo and, therefore, do not allow in silico experiments at an individual level (Kovatchev et al., 2009). To future studies aiming in silico description of individual alcohol kinetics, we suggest a clinical data collection based on the 20-point sampling protocol presented in Figure 7.
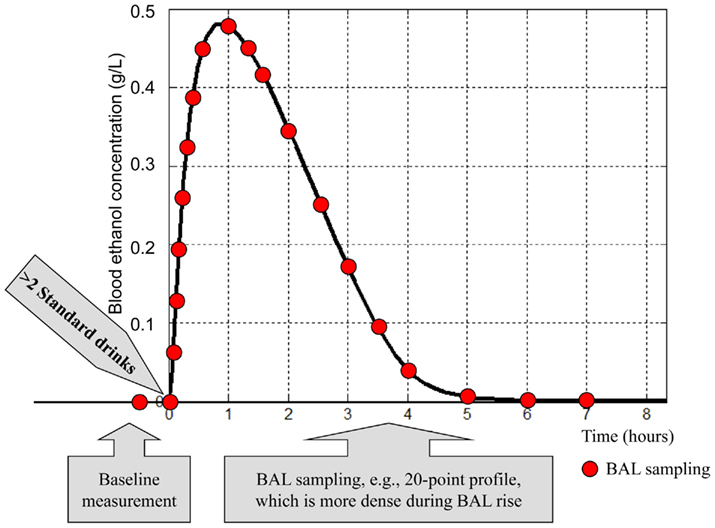
Figure 7. Common features of a clinical testing protocol collecting data for an individual ethanol dynamics profile. The blood alcohol level (BAL) sampling can be done directly through blood samples, or using a breath analyzer.
This protocol is similar to the standard profile used for determination of insulin resistance (Welch et al., 1990) and is modified to account for the specifics of ethanol dynamics. Under this protocol, plasma blood alcohol level samples are collected at times (t) = −30, 0, 5, 10, 15, 20, 30, 40, 50, 60, 75, 90, 120, 150, 180, 210, 240, 300, 360, and 420 min. Time 0 is the time of initiation of oral alcohol intake. The total amount of ingested alcohol is equivalent to three standard drinks (45 ml of ethanol). The blood alcohol level measurement prior to initiation of alcohol intake provides a baseline used for calibration; denser sampling is anticipated during the expected increase in blood alcohol level, and less frequent sampling is anticipated during blood alcohol level decay. A gradient search, simplex, or other non-linear optimization technique is used to minimize the distance between the predicted blood ethanol concentration course of the model and the data collected as described above. At convergence, the optimal parameters for this specific subject are fixed, and the model can be used to study the reaction of this subject to different scenarios, including some not easily reproducible in vivo (e.g., extreme/dangerous drinking).
Population of in silico “Subjects”
Given the theoretical basis established in the previous two sections, we can identify each in silico subject by two vectors: behavioral = (p1, p2, …) and metabolic = (ks, kg, Cr, …). In other words, each in silico “subject” is uniquely identified by a set of specific parameters that include transition probabilities (p1, p2, …) between the sequential steps of the model of Figure 2 and metabolic rate constants (ks, kg, Cr, …). The limits of the space occupied by these parameters can be identified from literature and study data. The in silico “population” can then be derived by estimating the across-subject variance of these parameters and generating a number of parameter sets to span the metabolic diversity observed in vivo. When established, this population can be used for in silico experiments (Kovatchev et al., 2009). When established, such an approach would ensure unified numerical representation of physiological, behavioral, and social interactions, and would enable the two-stage simulation procedure illustrated below.
Stage 1 – behavior
Computer-simulated idiosyncratic drinking patterns using the behavioral/social span of the set of vectors {(p1, p2, …)1, (p1, p2, …)2, …, (p1, p2, …)N}. Each of these patterns would result in a decision to drink or not to drink for each in silico subject. These decisions serve as behavioral event generators, and the generated events (i.e., drinks) are supplied to initialize the metabolic simulation model. In other words, the Stochastic Model of Behavioral and Social Conditioning creates the basic building block for in silico evaluation of treatment effect – the probability of a subject having a drink at any given point in time.
Stage 2 – metabolism
Computer-simulated idiosyncratic alcohol intoxication patterns using the span of the set of metabolic vectors {(ks, kg, Cr, …)1, (ks, kg, Cr, …)2, …, (ks, kg, Cr, …)N}. This is done as follows: at each simulated drink for each in silico subject, this subject’s metabolic model produces a specific trace in time of alcohol intoxication. The next simulated drink will come somewhere in this trace and, depending on this “individual’s” specific metabolic and drinking behavior, will hit at different stages of alcohol clearance. If the simulated drinks are sufficiently infrequent so that this “individual” can fully metabolize the ingested alcohol, the system (subject) will remain in a subcritical drinking pattern; conversely, if the drinks are too frequent, the system (subject) will transit to a super critical pattern (Breton, 2010). This simulation procedure was programmed in MATLAB®, a high-level programming language widely adopted for engineering computing.
Illustrative Results
Stage 1 – Behavior
To illustrate the methods presented in this paper we use data derived from the database of a large clinical trial of ondansetron conducted at the University of Texas – Houston Health Science Center. This study had three clearly differentiated phases: (1) a 7-day baseline period, (2) a 7-day placebo treatment, and (3) several weeks of active ondansetron treatment. This sequential design made the collected data very suitable for interpretation via the sequential stochastic model of behavioral and social conditioning that is conceptualized here.
Subjects
Subjects were 321 DSM-III-R (American Psychiatric Association, 1987) – diagnosed alcohol-dependent individuals, who had: a mean age of 41.50 ± 1.34 years; a gender distribution of 73.81% male and 26.19% female; an ethnic distribution of 76.05% White, 22.10% Black, and 1.85% Hispanic and other; a social class (Hollingshead and Redlich, 1958) distribution of 39.25% I–III, 49.05% IV–VI, and 11.70% VII–IX, and a mean drinking level of 8.04 ± 5.80 drinks/day in the past 90 days prior to enrollment.
Procedure
This study received ethics approval from the Committee for the Protection of Human Subjects at the University of Texas – Houston Health Science Center. Subjects were recruited by newspaper or radio advertisement in the Houston area. Following recruitment, subjects were scheduled to return to the clinic to commence 1 week of placebo treatment with an inert pill to be taken twice per day for 7 days. After a study calendar week (7–10 days), subjects returned to the clinic to obtain their randomized double-blind medication (ondansetron) in doses of 1, 4, or 16 μg/kg twice daily or matching placebo for a further period of 11 weeks. For the purposes of this reanalysis, we selected the homogeneous subgroup of 87 subjects who were randomized to the 4-μg/kg twice daily ondansetron condition, and concentrated on their initial placebo period and 6 weeks of ondansetron treatment data.
Empirical data
The average number of drinks per day during the baseline period for the selected subgroup of 87 subjects was 8.01 (SD = 5.28). Thus, the selected subgroup was representative of the entire study cohort, which reported an average of 8.04 (SD = 5.80) drinks/day for the 90-days prior to recruitment. At baseline, 54 subjects (62%) in the illustrative subgroup were classified as heavy drinkers, consuming ≥5 and ≥4 drinks/day for men and women, respectively. During the placebo treatment period, the alcohol consumption in the selected subgroup was reduced to 5.03 (SD = 4.64) drinks/day, followed by a further gradual reduction to 1.88 (SD = 2.21) drinks/day after 6 weeks of active ondansetron treatment (F = 56.1, p < 0.0001) using repeated-measures analysis of variance. The number of drinks per day in heavy drinkers changed from 10.70 (SD = 5.02) at baseline to 6.06 (SD = 5.31) at the end of the placebo period; in non-heavy drinkers, there was no change: 3.61 (SD = 1.06) drinks/day at baseline vs. 3.65 (SD = 2.94) drinks/day at the end of the placebo period, F = 20.1, p < 0.0001. The difference between heavy and non-heavy drinkers became negligible during the first week of active ondansetron treatment and remained negligible throughout the rest of the observation period. The complete results from this clinical trial have been published elsewhere (Johnson et al., 2000).
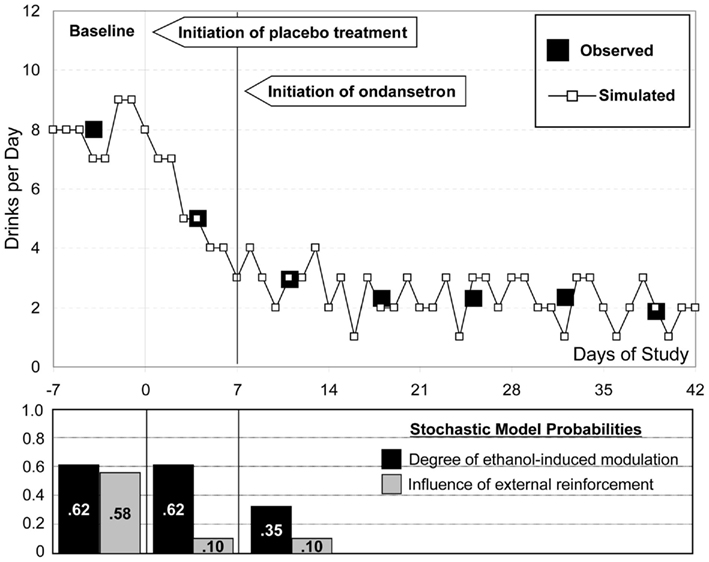
To evaluate the closeness of in silico prediction to observed clinical outcome, we compared the computer-simulated and clinically observed patterns of treatment response. Throughout the simulation, we kept the metabolic parameters of the simulated “subjects” constant and used the stochastic model of Figure 2 to deconstruct the observed drinking patterns into two sections explained by different model steps related to passive and active reduction in drinking: first, the response to initial placebo treatment was attributed to the influence of study enrollment, which was modeled as a reduction of the probability for environmental conditioning (Step 3 in Figure 2) from its baseline value of 0.58–0.10. Because this effect occurs relatively quickly (within a week) and no active medication was provided, no other system changes were anticipated, such as feedback down-regulation through modulation of the neurotransmission system. Second, the response to ondansetron was attributed to neurotransmission changes influenced by the degree of ethanol-induced neuromodulation. This was modeled via reduction of the probability of Step 1 from its baseline value of 0.62–0.35.
Figure 8 compares the results of this in silico treatment experiment to the clinically observed treatment effects. Black squares represent the empirical pattern of baseline drinking (Days −7 to 0) and the pattern of drinking reduction due to placebo (Days 1–7) and ondansetron treatment (Days 8–42). The in silico-generated pattern (black line) follows closely these empirical observations, confirming that in silico experiments could provide realistic representation of treatment effect. The lower panel of the Figure includes the change in environmental reinforcement probability, which is responsible for the “placebo” effect, and the reduction in the degree of ethanol-induced modulation describing the effect of ondansetron.
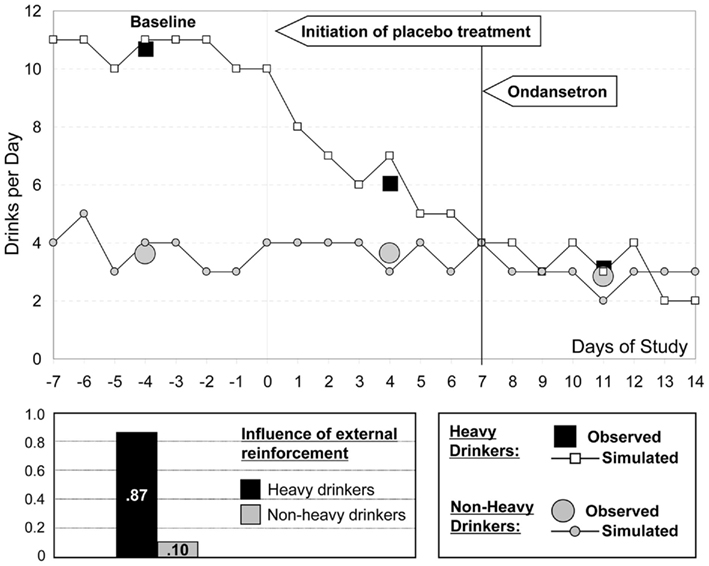
Further, the empirical results from the study (Johnson et al., 2000) suggest highly significant differences between heavy and non-heavy drinkers in their responses to placebo treatment, followed by a regression into a common pattern of response to ondansetron. Figure 9 focuses on the first 3 weeks of observation, where these idiosyncratic differences were most evident (Penberthy et al., 2007). Following the assumption that the placebo effect is primarily due to reduced environmental reinforcement, we model the difference between these two groups of subjects via different probabilities at Step 3.
Indeed, environmental reinforcement probabilities of 0.87 and 0.10 for heavy and non-heavy drinkers allow for excellent simulated approximation of the observed empirical patterns of placebo response. (Note that the overall baseline probability of environmental reinforcement, 0.58, is the weighted sum of the probabilities in the two subject subpopulations.) As is empirically established and evident from Figure 9, non-heavy drinkers (gray circles) were non-responsive to the effect of study enrollment. In contrast, heavy drinkers (black squares) appeared to be vulnerable to environmental conditioning effects, and, therefore, their response to placebo treatment was highly significant. Further, these two subject subpopulations were approximately equally responsive to the effect of medication, which explains the similarities in their patterns during the period of active ondansetron treatment. The environmental probabilities used for simulation are included in the bar graph in the lower section of Figure 9.
Stage 2 – Metabolism
The behavioral event generator described formally in the previous section challenges the metabolic system as presented in Figure 1. In silico, these challenges are absorbed following the Minimal Model of Ethanol Dynamics presented in Figure 6. Initial model parameter values were adopted from the literature: Cmax = 0.1614 g/L, tmax = 47 min, and AUC = 0.23 g × h/L (area under the curve; Fraser et al., 1995; Oneta et al., 1998; Norberg et al., 2003). Then, the model was applied to study the behavior of the system (person) during simulated drinking patterns of 1 through >10 standard drinks similar to those observed empirically. The computer reproduced the system behavior over 72 drinking days. For example with 4 drinks/day, the computer generated a 72-day sequence of drinking days with any number of drinks dispersed throughout the day, amounting to 4 drinks/day on average. To approximate empirical drinking patterns we also limited the drinks to be between 7 AM and 11 PM – i.e., what we considered a standard daytime. Each drink was standardized and the time course of blood alcohol level was recorded for each 72-day run. Two outcome measures were analyzed: the minimum of blood ethanol concentration over daytime and over 24 h. Each measure was calculated for days 10 and 72, avoiding the initiation period of 9 days to allow the system to become stationary; the mean blood alcohol level was computed as well.
Figure 10 presents the minimum blood alcohol level during daytime as a function of the average number of drinks per day. The line represents whether or not the blood alcohol level would ever go down to zero during the day. The computer simulation shows that with up to 5 drinks/day on average, the minimum blood alcohol level during daytime is zero, indicating that the system reaches its steady (sober) state at least for a while during the day. Between 5 and 11 drinks/day, there is a linear increase of the minimum blood alcohol level (slope = 0.0235, R2 = 0.99). After 11 drinks/day, the slope of the linear relationship increases sharply to 1.71 (R2 > 0.99). Thus, the computer simulation indicates that there are two well-defined threshold points defining abrupt system changes: 5 and 11 drinks/day on average. The first threshold at 5 drinks/day indicates the transition of zero vs. non-zero daily (7 AM–11 PM) blood alcohol level minimum, meaning that with 4 drinks/day or less, the system is still capable of metabolizing fully the ingested alcohol, whereas at five or more drinks per day, there is always a certain residual amount. From a system biology point of view, this first critical point indicates a phase transition from stable to unstable system dynamics, which is well visualized by the Poincaré plots in Figure 11.
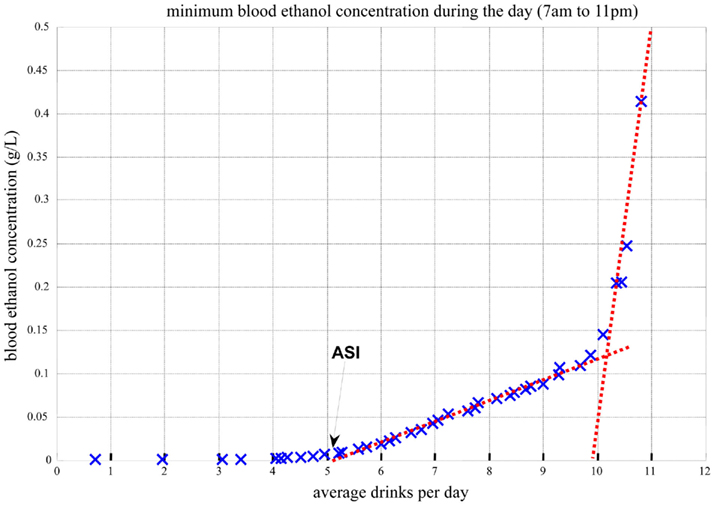
Figure 10. Minimum blood alcohol level during daytime (7 AM–11 PM) as a function of average number of drinks per day.
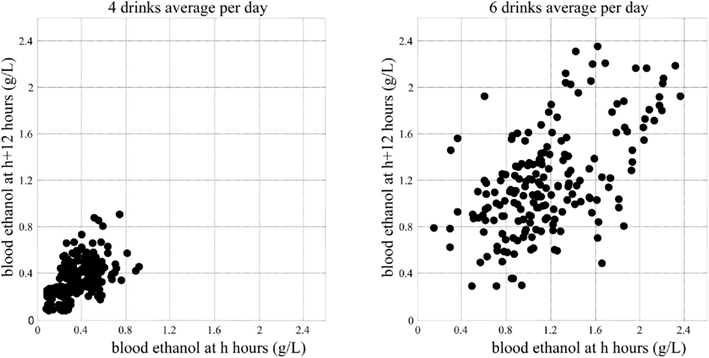
Figure 11. System phase transition from stable to unstable dynamics indicated by Poincaré plots of the system attractor.
As seen in Figure 11, five or more drinks per day would cause metabolic perturbations, never allowing the system to come to rest: the left panel represents a sustainable system dynamics, while the right panel represents a system that is out of control. This computer simulation result is consistent with – and to some degree explains at a system biology level – the generally accepted understanding of heavy drinking defined as five or more drinks per day. It appears that this critical value is not only an empirically established threshold but also an indication of an abrupt metabolic phase transition.
Further, as presented in Figure 12, the minimum blood alcohol level during the night (11 PM–7 AM, which was simulated as free of drinking) reaches zero for up to 11 drinks consumed during the day (7 AM–11 PM). When the number of drinks per day exceeds 11, the system cannot metabolize the amount of consumed alcohol even during the nighttime hours, which are free of drinking. Thus, 11 or more standard drinks per day results in a transition of the system dynamics to a higher blood ethanol value, which never goes down to zero. Because every morning there is still residual ethanol in the bloodstream, there is a very steep rise of blood alcohol level. This explains the abrupt change in the slope of the dependence of blood alcohol level on average number of drinks per day depicted in Figure 12.
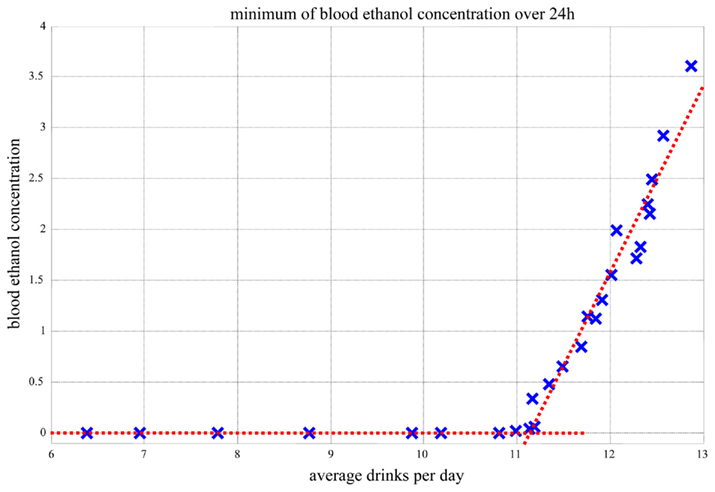
Figure 12. Minimum blood alcohol level during the night (11 PM–7 AM) as a function of average number of drinks during the day (7 AM–11 PM).
Conclusion
The basic premise of in silico modeling of alcohol dependence is that alcohol dependence and the outcome of its treatment result from the action of a stochastic self-reinforcing bio-behavioral process developing in time. In other words, the interplay between biology and behavior, which develops in a certain time frame, would trigger (with a certain probability) metabolic and neurobiological changes that in turn would reinforce uncontrolled or poorly controlled drinking behavior. Treatment would, therefore, be expected to modulate, attenuate, or reverse these changes with a certain level of probability. Such an approach captures the dynamics of sequential changes occurring during acquisition of alcohol dependence, successful treatment, or relapse. We provide a rigid mathematical framework describing formally these processes. To do so, we first introduce a stochastic model of behavioral and social conditioning describing the frequently random effects of human behavior and social reinforcement (Kovatchev, 2010). We then merge this stochastic model with the deterministic Minimal Model of Ethanol Dynamics (Breton, 2010). In combination, these two models provide the background for in silico interpretation of behavior and biology in their relationship to treatment effect. To represent formally behavioral and social conditioning, we identify several sequential steps. Each step is represented by a probability distribution, and the set of these distributions across all steps regulates the feed-forward relationships of the process from internal condition to self-regulation decision. Each person is represented by an individual treatment effect profile, defined as the set of transition probabilities between the sequential steps of the model specific to that person. This model serves as a stochastic behavioral generator of events, each event being a drink, which is supplied as an input to an individualized model of alcohol metabolism. In other words, the in silico experiments with alcohol dependence treatment use behavioral and social parameters that serve as generators of metabolic disturbances to the system (person), which are then processed through an individualized metabolic model, thereby allowing the formal decomposition and reconstruction of the patterns of drinking behavior and their modulation by placebo or medication treatment. We illustrate our proposed approach by re-analyzing data from a study of ondansetron for the treatment of alcohol dependence (Johnson et al., 2000) and include in the model the non-specific placebo effects that occurred before the active treatment phase of the study (Penberthy et al., 2007), with a special emphasis on the highly significant differences between heavy and non-heavy drinkers observed during the study. Such a quantitative approach has several potential advantages.
First, models allow the measurement of latent factors that cannot be observed directly but that frequently predetermine the behavior of a biosystem. A classical example is the Minimal Model of Glucose Kinetics suggested by Bergman et al. (1979) almost 30 years ago to measure insulin resistance in health and diabetes. In the case of alcohol addiction, the Minimal Model of Ethanol Kinetics was capable of reproducing – and to some degree explaining – the well-known empirical definition of heavy drinking, i.e., five or more standard drinks per day for men. The model also suggested other extreme situations, such as those that would occur with more than 11 drinks/day, may result in cognitive impairment due to continuous alcohol intoxication.
Second, models allow for computer simulation and in silico studies involving virtual “subjects” rather than real people. Such in silico trials can serve as cost–effective precursors, guiding expensive and time-consuming in vivo investigations by ruling out ineffective treatment approaches (Kovatchev et al., 2009). In our illustrative results, the overall treatment effect observed in a study of placebo vs. ondansetron was deconstructed into meaningful steps, with each step serving as a target for a specific treatment: Step 1 (internal condition) reflected pharmacological treatment, while Step 3 (environmental conditioning) reflected the placebo effect of study enrollment, or any type of socio-behavioral intervention. Such a deconstruction of the treatment effect allows for better understanding of the time course of treatment and the relationships among the various treatment components, as well as for individualized treatment tailoring. For example, it appears that in heavy drinkers, environmental conditioning is a significant predictor of treatment response, while in non-heavy drinkers the effect of the environment is minimal.
Third, when a system (person) is adequately modeled, its control via engineering means becomes possible. Examples include cardiac pacemakers and, more recently, the artificial pancreas emerging as a means for control of blood glucose levels in diabetes (Cobelli et al., 2009). At the level of control, the in silico models presented here are less developed than the metabolic models adopted in cardiology or diabetes. Nevertheless, this text represents an initial step to introduce the concept of in silico analysis to the area of alcohol dependence research.
Because the first results appear promising and explanatory for observed phenomena, we think that with the accumulation of data (both existing and from future clinical studies), in silico analysis would find its place in the arsenal of tools to help decipher the mechanisms that govern treatment response among alcohol-dependent individuals. A critical step in this development will be the accumulation of an in silico population spanning the large observed variability in ethanol absorption and clearance, and in alcohol-related behaviors. This step has been done in other settings using extensive metabolic data collection (Kovatchev et al., 2009) and is therefore feasible in the field of alcohol dependence. As explained elsewhere (Cobelli et al., 2009), extensive kinetic parameter sensitivity analysis and analysis of outliers will be needed to finalize this modeling effort. With this final step, it will become possible to run preclinical testing of varied treatment strategies, bypassing long-term animal studies and greatly accelerating the transition from medication development to human testing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnote
- ^In the US a standard drink is defined as 12 ounces (360 ml) of beer, 5 ounces (150 ml) of wine, or 1.5 ounces (45 ml) of 80-proof distilled spirits, all of which contain approximately the same amount of alcohol.
References
Albisser, A. M., Leibel, B. S., Ewart, T. G., Davidovac, Z., Botz, C. K., and Zingg, W. (1974). An artificial endocrine pancreas. Diabetes 23, 389–396.
American Psychiatric Association. (1987). Diagnostic and Statistical Manual of Mental Disorders, 3rd Edn. Washington, DC: American Psychiatric Press.
Baumann, L. J., Cameron, L. D., Zimmerman, R. S., and Leventhal, H. (1989). Illness representations and matching labels with symptoms. Health Psychol. 8, 449–469.
Bergman, R. N., Ider, Y. Z., Bowden, C. R., and Cobelli, C. (1979). Quantitative estimation of insulin sensitivity. Am. J. Physiol. 236, E667–E677.
Breton, M. D. (2010). In silico models of alcohol kinetics: deterministic approach,” in Addiction Medicine: Science and Practice, ed. B. Johnson (New York: Springer), 1265–1276.
Clarke, W. L., Cox, D. J., Gonder-Frederick, L., Julian, D., Kovatchev, B., and Young-Hyman, D. (1999). Biopsychobehavioral model of severe hypoglycemia. Self-management behaviors. Diabetes Care 22, 580–584.
Cobelli, C., Dalla Man, C., Sparacino, G., Magni, L., Nicolao, G., and Kovatchev, B. P. (2009). Diabetes: models, signals, and control. IEEE Rev. Biomed. Eng. 2, 54–96.
Dalla Man, C., Raimondo, D. M., Rizza, R. A., and Cobelli, C. (2007a). GIM, simulation software of meal glucose-insulin model. J. Diabetes Sci. Technol. 1, 323–330.
Dalla Man, C., Rizza, R. A., and Cobelli, C. (2007b). Meal simulation model of the glucose-insulin system. IEEE Trans. Biomed. Eng. 54, 1740–1749.
Derr, R. F. (1993). Simulation studies on ethanol metabolism in different human populations with physiological pharmacokinetic model. J. Pharm. Sci. 82, 677–682.
DiClemente, C. C., and Prochaska, J. O. (1998). “Treating addictive behaviors,” in Applied Clinical Psychology, 2nd Edn, ed. W. R. Miller (New York: Plenum Press), 3–24.
Duffy, J. C., and Alanko, T. (1992). Self-reported consumption measures in sample surveys: a simulation study of alcohol consumption. J. Off. Stat. 8, 327–350.
Eddy, D. M., and Schlessinger, L. (2003a). Archimedes: a trial-validated model of diabetes. Diabetes Care 26, 3093–3101.
Eddy, D. M., and Schlessinger, L. (2003b). Validation of the Archimedes diabetes model. Diabetes Care 26, 3102–3110.
El-Khatib, F. H., Russell, S. J., Nathan, D. M., Sutherlin, R. G., and Damiano, E. R. (2010). A bihormonal closed-loop artificial pancreas for type 1 diabetes. Sci. Transl. Med. 2, 27ra27.
Fraser, A. G., Rosalki, S. B., Gamble, G. D., and Pounder, R. E. (1995). Inter-individual and intra-individual variability of ethanol concentration-time profiles: comparison of ethanol ingestion before or after an evening meal. Br. J. Clin. Pharmacol. 40, 387–392.
Gonder-Frederick, L., Cox, D., Kovatchev, B., Schlundt, D., and Clarke, W. (1997). A biopsychobehavioral model of risk of severe hypoglycemia. Diabetes Care 20:661–669.
Haddad, S. A. P., Houben, R., and Serdijn, W. A. (2005). “The evolution of pacemakers: an electronics perspective, from the hand crank to advanced wavelet analysis,” in Proceedings of the 3rd DISENS Symposium on Biomedical Sensors, Delft.
Hollingshead, A. B., and Redlich, F. C. (1958). Social Class and Mental Illness: A Community Study. New York: Wiley.
Hovorka, R., Allen, J. M., Elleri, D., Chassin, L. J., Harris, J., Xing, D., Kollman, C., Hovorka, T., Larsen, A. M., Nodale, M., De Palma, A., Wilinska, M. E., Acerini, C. L., and Dunger, D. B. (2010). Manual closed-loop insulin delivery in children and adolescents with type 1 diabetes: a phase 2 randomised crossover trial. Lancet 375, 743–751.
Johnson, B. A., Roache, J. D., Javors, M. A., DiClemente, C. C., Cloninger, C. R., Prihoda, T. J., Bordnick, P. S., Ait-Daoud, N., and Hensler, J. (2000). Ondansetron for reduction of drinking among biologically predisposed alcoholic patients: a randomized controlled trial. JAMA 284, 963–971.
Khasnis, A., and Tepper, D. (2003). A new pacemaker algorithm for the treatment of atrial fibrillation: results of the Atrial Dynamic Overdrive Pacing Trial (ADOPT). Cardiovasc. Rev. Rep. 24, 532–533.
Kovatchev, B., Cox, D., Gonder-Frederick, L., Schlundt, D., and Clarke, W. (1998). Stochastic model of self-regulation decision making exemplified by decisions concerning hypoglycemia. Health Psychol. 17, 277–284.
Kovatchev, B. P. (2010). “In silico models of alcohol dependence treatment: stochastic approach,” in Addiction Medicine: Science and Practice, ed. B. Johnson (New York: Springer), 1277–1290.
Kovatchev, B. P., Breton, M. D., Dalla Man, C., and Cobelli, C. (2009). In silico preclinical trials: a proof of concept in closed-loop control of type 1 diabetes. J. Diabetes Sci. Technol. 3, 44–55.
Kovatchev, B. P., Cobelli, C., Renard, E., Anderson, S., Breton, M., Patek, S., Clarke, W., Bruttomesso, D., Maran, A., Costa, S., Avogaro, A., Dalla Man, C., Facchinetti, A., Magni, L., De Nicolao, G., Place, J., and Farret, A. (2010). Multi-national study of subcutaneous model-predictive closed-loop control in type 1 diabetes: summary of the results. J. Diabetes Sci. Technol. 4, 1374–1381.
Kovatchev, B. P., Penberthy, J. K., Robeva, R. S., Breton, M., and Cox, D. J. (2005). “Computational strategies in the evaluation of attention deficit/hyperactivity disorder,” in Attention Deficit/Hyperactivity Disorder (ADHD) Research, ed. M. Larimer (New York: Nova Science Publishers), 155–187.
Leventhal, H., and Diefenbach, M. (1991). “The active side of illness cognition,” in Mental Representation in Health and Illness, eds J. A. Skelton and R. T. Croyle (New York: Springer-Verlag), 247–272.
Leventhal, H., Diefenbach, M., and Leventhal, E. A. (1992). Illness cognition: using common sense to understand treatment adherence and affect cognition interactions. Cognit. Ther. Res. 16, 143–163.
Matsumoto, H., and Fukui, Y. (2002). Pharmacokinetics of ethanol: a review of the methodology. Addict. Biol. 7, 5–14.
Michelson, S. (2006). The impact of systems biology and biosimulation on drug discovery and development. Mol. Biosyst. 2, 288–291.
Mumenthaler, M. S., Taylor, J. L., and Yesavage, J. A. (2000). Ethanol pharmacokinetics in white women: nonlinear model fitting versus zero-order elimination analyses. Alcohol. Clin. Exp. Res. 24, 1353–1362.
Norberg, A., Gabrielsson, J., Jones, A. W., and Hahn, R. G. (2000). Within- and between-subject variations in pharmacokinetic parameters of ethanol by analysis of breath, venous blood and urine. Br. J. Clin. Pharmacol. 49, 399–408.
Norberg, A., Jones, A. W., Hahn, R. G., and Gabrielsson, J. L. (2003). Role of variability in explaining ethanol pharmacokinetics: research and forensic applications. Clin. Pharmacokinet. 42, 1–31.
Oneta, C. M., Simanowski, U. A., Martinez, M., Allali-Hassani, A., Parés, X., Homann, N., Conradt, C., Waldherr, R., Fiehn, W., Coutelle, C., and Seitz, H. K. (1998). First pass metabolism of ethanol is strikingly influenced by the speed of gastric emptying. Gut 43, 612–619.
Penberthy, J. K., Ait-Daoud, N., Breton, M., Kovatchev, B., DiClemente, C. C., and Johnson, B. A. (2007). Evaluating readiness and treatment seeking effects in a pharmacotherapy trial for alcohol dependence. Alcohol. Clin. Exp. Res. 31, 1538–1544.
Penberthy, J. K., Cox, D., Breton, M., Robeva, R., Kalbfleisch, M. L., Loboschefski, T., and Kovatchev, B. P. (2005). Calibration of ADHD assessments across studies: a meta-analysis tool. Appl. Psychophysiol. Biofeedback 30, 31–51.
Renard, E. (2002). Implantable closed-loop glucose-sensing and insulin delivery: the future for insulin pump therapy. Curr. Opin. Pharmacol. 2, 708–716.
Robeva, R., Penberthy, J. K., Loboschefski, T., Cox, D., and Kovatchev, B. (2004). Combined psychophysiological assessment of ADHD: a pilot study of Bayesian probability approach illustrated by appraisal of ADHD in female college students. Appl. Psychophysiol. Biofeedback 29, 1–18.
Roethlisberger, F. J., Dickson, W. J., and Wright, H. A. (1939). Management and the Worker; an Account of a Research Program Conducted by the Western Electric Company. Chicago: Hawthorne Works; Cambridge, MA: Harvard University Press.
Santiago, J. V., Clemens, A. H., Clarke, W. L., and Kipnis, D. M. (1979). Closed-loop and open-loop devices for blood glucose control in normal and diabetic subjects. Diabetes 28, 71–84.
Saoudi, N., Appl, U., Anselme, F., Voglimacci, M., and Cribier, A. (1999). How smart should pacemakers be? Am. J. Cardiol. 83, 180D–186D.
Steil, G. M., Rebrin, K., Darwin, C., Hariri, F., and Saad, M. F. (2006). Feasibility of automating insulin delivery for the treatment of type 1 diabetes. Diabetes 55, 3344–3350.
Umulis, D. M., Gürmen, N. M., Singh, P., and Fogler, H. S. (2005). A physiologically based model for ethanol and acetaldehyde metabolism in human beings. Alcohol 35, 3–12.
Ward, R. J., and Coutelle, C. H. (2003). Women and alcohol susceptibility: could differences in alcohol metabolism predispose women to alcohol-related diseases? Arch. Womens Ment. Health 6, 231–238.
Weinzimer, S. A., Steil, G. M., Swan, K. L., Dziura, J., Kurtz, N., and Tamborlane, W. V. (2008). Fully automated closed-loop insulin delivery versus semi-automated hybrid control in pediatric patients with type 1 diabetes using an artificial pancreas. Diabetes Care 31, 934–939.
Welch, S., Gebhart, S. S., Bergman, R. N., and Phillips, L. S. (1990). Minimal model analysis of intravenous glucose tolerance test-derived insulin sensitivity in diabetic subjects. J. Clin. Endocrinol. Metab. 71, 1508–1518.
Widmark, E. M. P. (1932). Die theoretischen Grundlagen und die praktische Verwendbarkeit der gerichtlich-medizinischen Alkoholbestimmung. Berlin: Urban and Schwarzenberg.
Winsberg, E. (2002). Simulated experiments: methodology for a virtual world. Philos. Sci. 70, 105–125.
Keywords: alcohol dependence, computer simulation, metabolic modeling, stochastic process
Citation: Kovatchev B, Breton M and Johnson B (2012) In silico models of alcohol dependence and treatment. Front. Psychiatry 3:4. doi: 10.3389/fpsyt.2012.00004
Received: 05 September 2011;
Paper pending published: 31 October 2011;
Accepted: 15 January 2012;
Published online: 03 February 2012.
Edited by:
Josselin Noirel, University of Sheffield, UKReviewed by:
Ying Xu, West Virginia University, USAGuillaume Launay, Université Claude Bernard de Lyon, France
Copyright: © 2012 Kovatchev, Breton and Johnson. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Boris Kovatchev, Department of Psychiatry and Neurobehavioral Sciences, University of Virginia School of Medicine, P.O. Box 40888, Charlottesville, VA 22908, USA. e-mail:Ym9yaXNAdmlyZ2luaWEuZWR1

 Marc Breton1
Marc Breton1