- Department of Psychiatry, Psychotherapy, and Psychosomatics, University Hospital of Psychiatry, University of Zurich, Zurich, Switzerland
Background: Recent meta-analyses reported placebo response rate in antidepressant trials to be stable since the 1970s. These meta-analyses however were limited in considering only linear time trends, assessed trial-level covariates based on single-model hypothesis testing only, and did not adjust for small-study effects (SSE), a well-known but not yet formally assessed bias in antidepressant trials.
Methods: This secondary meta-analysis extends previous work by modeling nonlinear time trends, assessing the relative importance of trial-level covariates using a multimodel approach, and rigorously adjusting for SSE. Outcomes were placebo efficacy (continuous), based on the Hamilton Depression Scale, and placebo response rate.
Results: Results suggested that any nonlinear time trends in both placebo efficacy (continuous) and response rate were best explained by SSE. Adjusting for SSE revealed a significant gradual increase in placebo efficacy (continuous) from 1979 to 2014. A similar observation was made for placebo response rate, but did not reach significance due higher susceptibility to SSE. By contrast, trial-level covariates alone were found to be insufficient in explaining time trends.
Conclusion: The present findings contribute to the ongoing debate on antidepressant placebo outcomes and highlight the need to adjust for bias introduced by SSE. The results are of clinical relevance because SSE may affect the evaluation of success or failure in antidepressant trials.
Highlights
● Placebo time trends in antidepressant trials were examined between 1979 and 2014.
● Placebo efficacy (continuous) was found to gradually linearly increase across decades.
● Placebo response rate did not reach significance due to large small-study effects.
● Small-study effects explained large proportions of heterogeneity.
● Trial-level covariates did not sufficiently explain heterogeneity.
● Small-study effects may be considered when evaluating success or failure in antidepressant trials.
Introduction
The term placebo effect is commonly used to designate symptom relief due to a non-pharmacological intervention that cannot be attributed to drug properties, and is therefore thought to reflect patient expectations regarding that intervention (1). While it is well-known that individuals receiving placebo in antidepressant trials in major depressive disorder (MDD) can show substantial improvement (2), there has been an ongoing debate whether this placebo effect has been raising since the 1970s (3–10). This debate is of clinical relevance because placebo effects have been suspected to contribute to a decline in antidepressant treatment effects, resulting in so-called failed antidepressant trials (3, 5, 6, 11–13).
Two recent meta-analyses conducted by Furukawa et al. (14, 15) disproved this hypothesis. The authors, who meta-analytically examined N = 252 trials conducted between 1979 and 2016, reported that placebo response rate in antidepressant trials have remained stable from 1979 to 2016. Any selective improvement in placebo response was suggested to result from trials conducted before 1991, at which year a structural break was found, after which placebo response rate was reported to be (14). The same conclusion was made by the authors based on a smaller dataset comprising N = 98 trials conducted between 1985 and 2012 (15). To assess the effects of study year, Furukawa et al. (14, 15) splitted the data and computed linear regressions separately before and after the observed structural break at 1991. Splitting data for regression is however not advisable to account for the likely nonlinearity underlying the structural break. The present analysis therefore aimed to model the nonlinear time trend to regress across the entire time span from 1979 to 2016. For this purpose, the present analysis implemented restricted cubic splines (RCS) (16), which are a powerful technique for modeling nonlinear relationships using linear regression models.
Furukawa et al. (14, 15) further suggested that any potential increase in placebo response rate before 1991 may be explained by smaller mostly older studies showing larger treatment effects than bigger studies. This phenomenon, known as small-study effect (SSE) (17, 18) describes the association between sample size and effect size in meta-analyses. To account for SSE, Furukawa et al. (14, 15) adjusted the regression for sample size (defined as the number of patients randomized). When adjusting for SSE, however, there is actually a choice between a function of sample size (or its inverse version) or a function of study precision (variance, standard error, or their inverse versions), depending on which one is more closely related to the sources of SSE. One may argue that a function of sample size is the better covariate because it does not experience measurement error or structural correlation. However, as extensively studied by Moreno (19) a function of precision is preferable since the sources of SSE have increasingly been attributed to reasons such as publication bias, outcome reporting bias, or clinical heterogeneity (20–22). A function of study precision is therefore thought to be more informative (23). The present analysis therefore aimed to account for possible SSE by allowing placebo outcomes to depend on the standard error (24, 25).
Moreover, Furukawa et al. (14, 15) suggested that the potential increase in placebo response rate may also be explained by changes in study designs across decades. The authors therefore adjusted for the trial-level covariates study center, study dosing schedule, and study length, which were found to be significant. In particular, increasing placebo response rate were suggested to be associated with shorter, single-centered trials using flexible dose regimes before 1991 compared to longer, multi-centered trails using fixed dose regimens mostly conducted after 1991. The interpretation of these assumptions however remained unclear; for example, it remained unclear why multi- versus single-centered trials or fixed versus flexible dose regimes would increase placebo effect sizes. The present analysis therefore hypothesized that these trial-level covariate effects are mediated effects (26) arising from insufficient adjustment for SSE across decades. To assess the relative importance of trial-level covariates effects before and after adjustment for SSE, multimodel inference was conducted (27). Multimodel inference is an information theoretic approach proposed as an alternative to traditional single-model hypothesis testing as applied by Furukawa et al. (14, 15). Multimodel inference examines several competing hypotheses (models) simultaneously to identify the best set of models via information criteria such as the Akaike’s information criterion (28), and is thus thought to provide more robust covariate estimates (27).
Last, Furukawa et al. (14, 15) estimated placebo response rate (defined as ≥50% reduction on the HAMD) based on the proportion of responders within placebo groups. In the second meta-analysis (15) the authors additionally assessed the original continuous outcome, i.e., symptom reduction (29) based on the Hamilton Depression Scale (HAMD) (30), from which the binary outcome (response rate) is derived through dichotomization. The continuous outcome was estimated based on the drug-placebo difference between drug and placebo groups. The authors did, however, not consider symptom reduction within placebo groups, which would be the logical equivalent to placebo response rate. The present analysis therefore aimed to extend previous work by examining symptom reduction within placebo groups estimated based on the pre-post change on the HAMD within placebo groups, hereinafter referred to as efficacy (continuous).
Together, the methodological approach presented here aimed to support the ongoing debate on placebo outcomes across decades by considering nonlinear time trends, adjusting for SSE, assessing the relative importance of trial-level covariates, and comparing the binary with the original continuous placebo outcome. The results are expected to inform clinical decision making whether time trends may require consideration when evaluating success or failure in antidepressant trials in MDD.
Materials and Methods
Data Sources
A total of 308 randomized placebo-controlled trials (240 published studies, 68 unpublished studies) were identified conducted between 1979 and 2016. Three hundred four trials constituted all the placebo-controlled trials provided in the GRISELDA dataset by Cipriani et al. (31) and four additional trials were provided by Furukawa et al. (14). For all studies, information on the year of completion was extracted from the literature, if available. For 30 studies, missing covariate values were extracted from the literature. A PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) flow-chart detailing the study selection process is given in the supplementary appendix (Supplementary S1).
Covariate study year was defined as study year of completion, study year of publication, or year of drug approval from the FDA (US Food and Drug Administration), where available in this order; preference was given to study year of completion, because unpublished trials, by definition, have no year of publication (14). The resulting study year range was 1979–2014. Other trial-level covariates were study center (multi- versus single-center), study dosing schedule (flexible versus fixed dose), study length (range 4–12 weeks), and study size (sample size, number of patients randomized) (14).
Primary continuous outcome was efficacy (continuous) (pre-post change on the HAMD, i.e., endpoint HAMD or, if not reported, change from baseline HAMD, as provided in the GRISELDA dataset (31), N = 259 trials) within placebo groups, estimated as log-transformed change score. Primary binary outcome was response rate (≥50% reduction on the HAMD, N = 277 trials), estimated as log-transformed proportions of responders within placebo groups. Remission rate was not assessed because different cut-offs (<7 or <8 total reduction on the HAMD) were used for aggregation, which can be problematic when analyzing only within groups.
Structural Break Analysis
To assess potential breaks across study year, a structural break analysis was conducted using the breakpoints command in the strucchange package (32) in R (33). To capture potential structural breaks in the meta-regression, the covariate study year was modeled using RCS (16) by use of the command rcs in the rms package (34). RCS were constructed using three knots with the middle knots set at the break date, and the first and third knots set at the 10th and 90th percentile of study year, i.e., (1986, break date, 2010).
Adjustment for Small-Study Effects
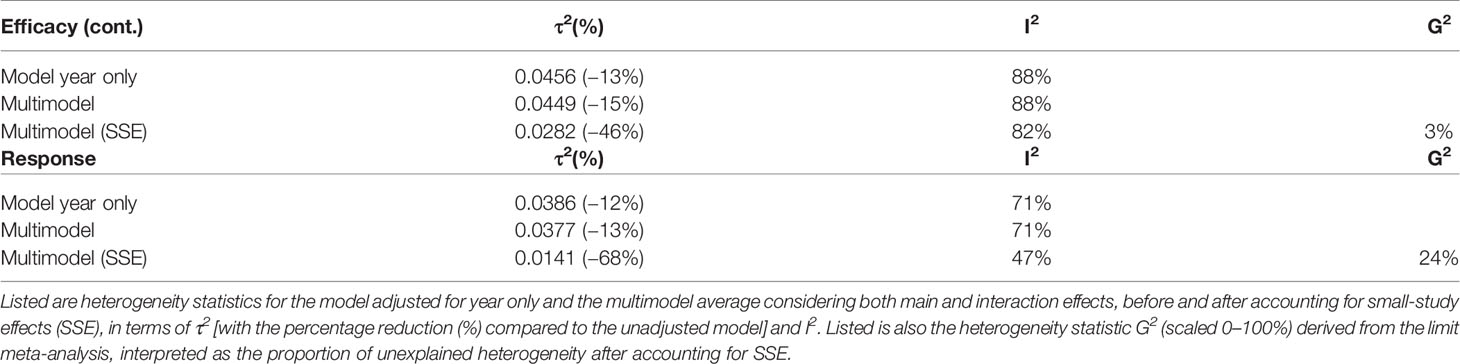
To adjust for SSE, limit meta-analysis was conducted using the metasens package (35) (Supplementary S4). Limit meta-analysis is a regression approach based on an extended random-effects model that takes account of possible SSE by allowing trial estimates to depend on the standard error (24, 25, 36). The resulting adjusted (“shrunken”) trial estimates obtained from the limit meta-analysis were then used for further analysis. Heterogeneity that remains after SSE are accounted for can be quantified by the heterogeneity statistic G2 (24, 25).
To graphically visualize potential SSE, the power of individual studies was computed based on its standard errors using a two-sided Wald test, together with a test assessing potential excess of formally significant trials in relation to the power (37) as implemented in the metaviz package (38). The test itself does not consider SSE but can have similar sources.
Multimodel Inference
Multimodel inference was conducted using the glmulti package (39) that provides the necessary functionality for multimodel averaging using an information-theoretic approach. An extensive model comparison was conducted considering all possible covariate combinations. Multimodel inference was performed both before and after adjustment for SSE based on the limit meta-analysis. The only constraint was that the nonlinear component of study year was only included in the presence of the linear component, since the former alone is uninterpretable. Together this resulted in N = 47 models. Model weighting was based on the corrected Akaike information criterion (AICc), with each model being weighted based on relative AICc evidence (39). Multimodel averaged covariate estimates were computed across the top model sets for each outcome, defined as the top-ranked models summing up to 95% AICc evidence weight (27, 40). Models were fitted using the rma function in the metafor package (41). Heterogeneity was estimated based on the method of moment (42) and reported in terms of τ2 and I2.
Results
Structural Break Analysis
Structural break analysis revealed no break date for placebo efficacy (continuous) (F = 3·09, p = 0·139), suggesting a gradual increasing trend from 1979 to 2014. By contrast, a break date was found at 1990 for placebo response (F = 11·45, p < 0·001), suggesting a steep nonlinear increase around 1990; in line with Furukawa et al. (14) (see Supplementary S2 for illustration of the structural break analysis). To assess the potential nonlinear trend across decades, the break date at 1990 was used to construct the nonlinear component of the covariate study year used in the multimodel inference (see Supplementary S3 for sensitivity analysis on the nonlinear component).
Multimodel Averaged Covariate Effects
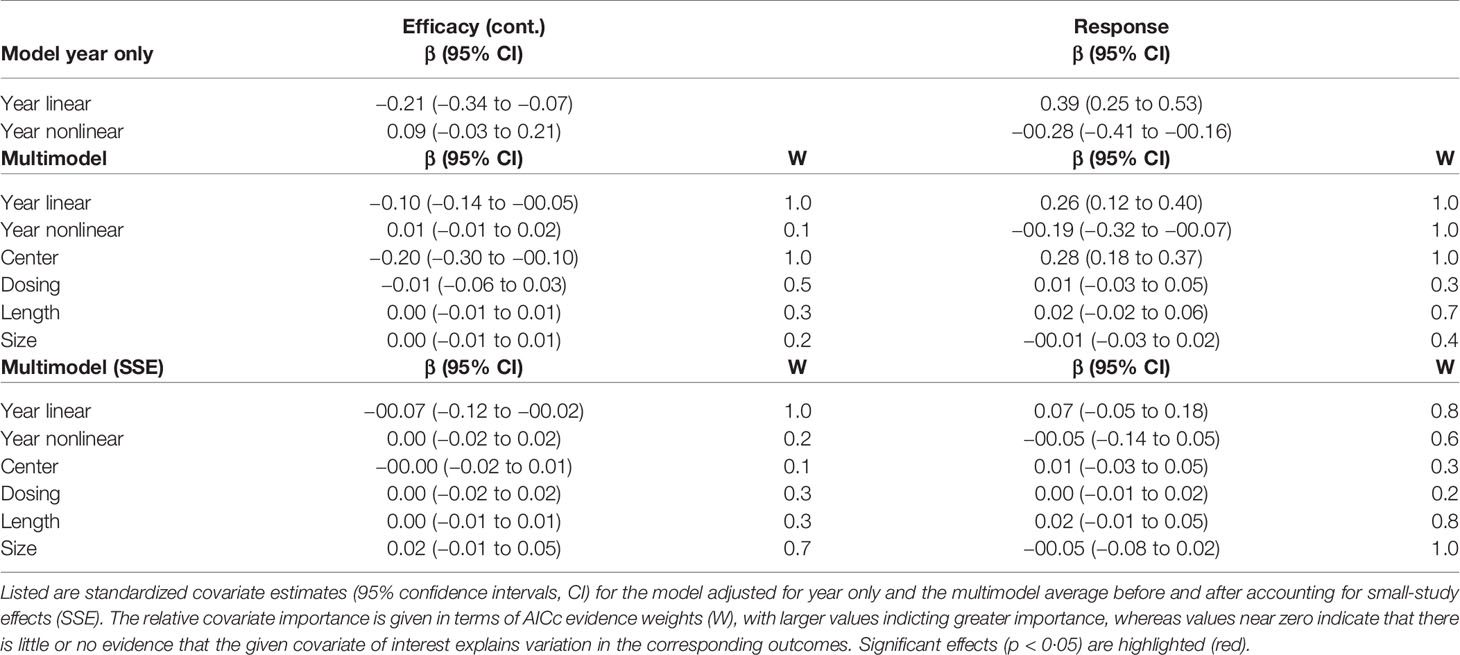
Overall, results suggested both placebo efficacy (continuous) and response rate to be affected by SSE. Adjustment for SSE weakened the effect of study year in both outcomes. However, the linear effect of study year indicated by the structural break analysis remained significant for efficacy (continuous) [linear β = −0·07 (−0·12 to −0·02) 95% CI; nonlinear β = 0·00 (−0·02 to 0·02) 95% CI] (Table 1, Figure 1). This supported a gradual increase in placebo efficacy (continuous) across decades from 1979 to 2014, that is not explained by SSE. By contrast, both linear and nonlinear components of study year became insignificant for placebo response due to wide CIs [linear β = 0·07 (−0·05 to 0·18) 95% CI; nonlinear β = −0·05 (−0·14 to 0·05) 95% CI] (Table 1, Figure 2). Together, this suggested that the binary outcome was more affected by SSE, with lower study precision observed in older and smaller studies before 1991 compared to studies conducted after 1990. Among the other trial-level covariates only study center revealed significant effects in both outcomes. However, supporting our hypothesis of possible mediated effects, any effects of study center became nearly zero after adjusting for SSE (Table 2). None of the remaining trial-level covariates were found to have significant effects (see Supplementary S5 for details on relative covariate importance). Together, this suggested that trial-level covariates alone were insufficient in explaining placebo outcomes.
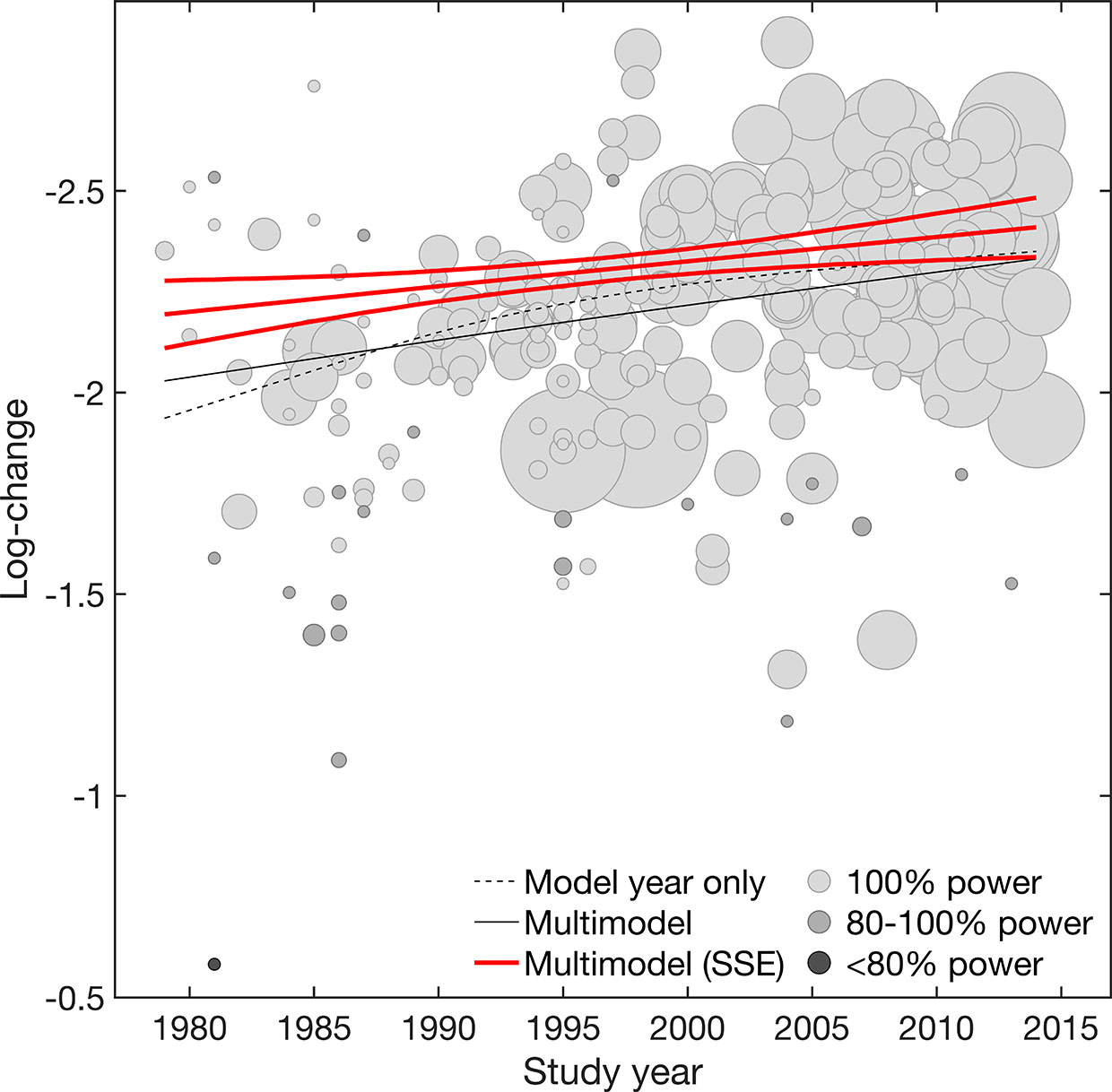
Figure 1 Efficacy (continuous). Meta-regression plot illustrating the effect of study year on placebo efficacy (continuous) for the model adjusted for year only and the multimodel average considering both main and interaction effects, before and after accounting for small-study effects (SSE). Values larger on the log-transformed change score scale indicate increase in efficacy (continuous). Circle size is proportional to study size. Circle color is proportional to the power of individual studies (100% high power [white], 100-80% adequate power [light gray], <80% low power [dark gray]). Slopes are illustrated at the means of all covariates.
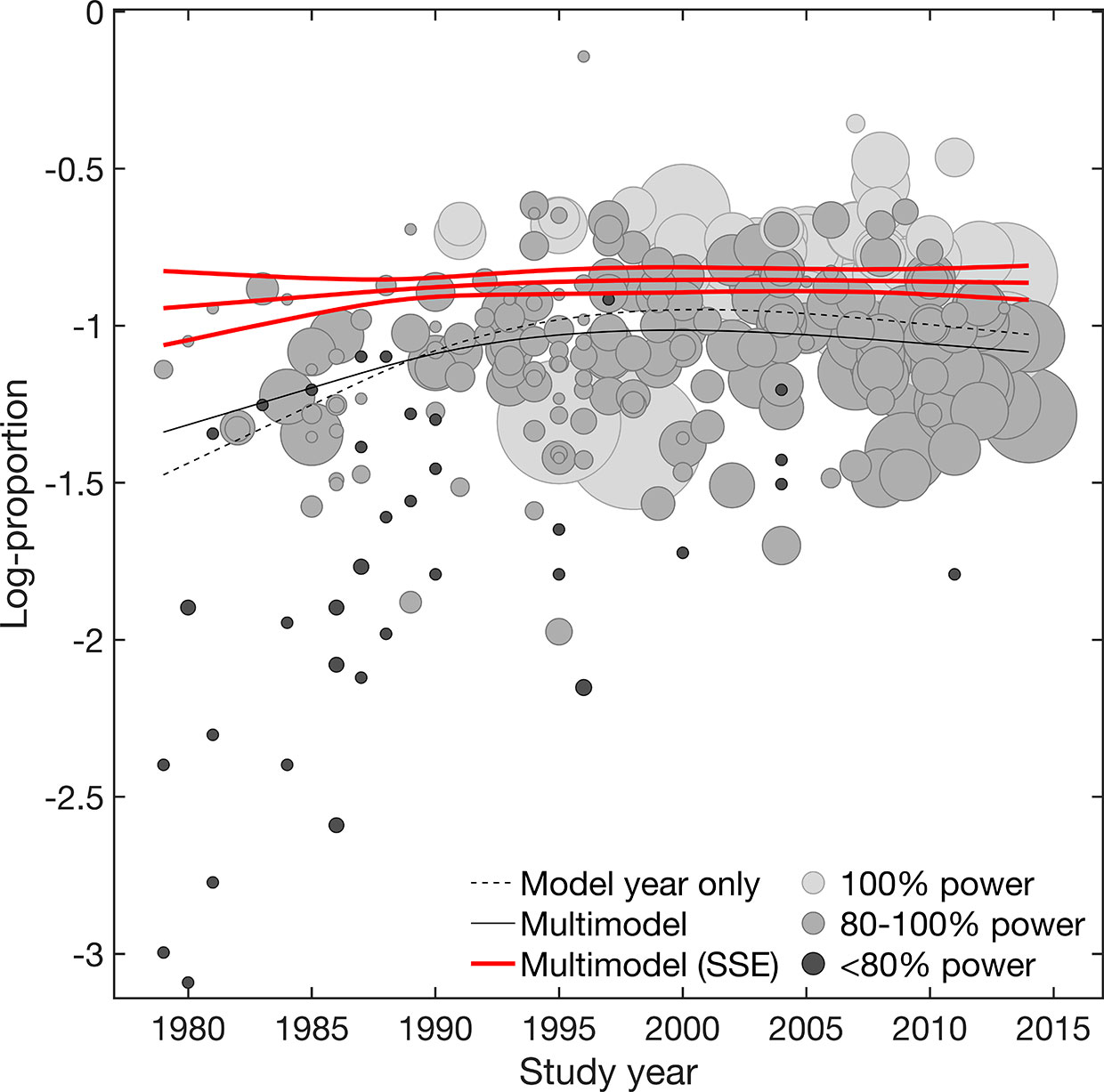
Figure 2 Response rate. Meta-regression plot illustrating the effect of study year on placebo response rate. Shown are the model adjusted for year only and the multimodel average considering both main and interaction effects, before and after accounting for small-study effects (SSE). Values smaller on the log-transformed proportion scale indicate increase in response rate. Circle size is proportional to study size. Circle color is proportional to the power of individual studies (100% high power [white], 100-80% adequate power [light gray], <80% low power [dark gray]). Slopes are illustrated at the means of all covariates.
To graphically visualize the suggested SSE, the power of individual studies was illustrated in Figures 1 and 2. The power distributions show that most of the trials estimates for efficacy (continuous) were high-powered (0·4% low power, 8% adequate power, 91% high power) with no excess of significant trials (p = 0·236), whereas placebo response rate was underpowered (13% low power, 70% adequate power, 17% high power) with an excess of significant trials (p = 0·001) (see Supplementary S4 for funnel. plots derived from limit meta-analysis compared to power-enhanced funnel plots). Together, this supported the assumption that placebo response rate was more affected by SSE than placebo efficacy (continuous).
Multimodel Averaged Heterogeneity
Since, it is well-known that I2 has undue reliance due to its dependence on precision (43, 44), it is an improper measure when comparing continuous and binary outcomes because the former result in systematically higher I2 (45). τ2, rather than I2, is therefore suggested the appropriate measure for this purpose as it is insensitive to study precision (43) (Table 2). Comparing between outcomes suggested an overall equal reduction in heterogeneity (efficacy (continuous) = −13%, response rate = −12%) when SSE were not accounted for. However, when accounting for SSE, a much larger reduction in heterogeneity was observed for response rate (−70%) compared to efficacy (continuous) (−37%). Again, this supported the assumption of larger SSE in the binary compared to the continuous outcome.
Heterogeneity was also assessed in terms of G2 derived from the limit meta-analysis. G2 represents heterogeneity that remains after SSE are accounted for. Likewise I2, G2 is determined on a percentage scale, but not dependent on study precision and thus appropriate for comparison between outcomes (25, 43). Whereas G2 was almost zero for placebo efficacy (continuous) (G2 = 2%), it was G2 = 24% for placebo response rate. This indicated that efficacy (continuous) approximated the case of G2 = 0 while > 0, that is, there is not much other heterogeneity apart from that due to SSE (to which is sensitive but not G2) (25) (Table 2, see Supplementary S4 for details on the limi meta-analysis). Together, this suggested that efficacy (continuous) was almost fully explained by SSE, whereas placebo response rate remained with some unexplained heterogeneity even after adjustment for SSE.
Discussion
Selective improvements in placebo effects can significantly affect the success or failure of antidepressant trials. Declining antidepressant efficacy across decades has been previously suggested due to increasing placebo efficacy, resulting in so-called failed antidepressant trials (3, 5, 6, 11–13). Study year has been suggested to be the second greatest effect modifier in antidepressant efficacy as reported by Cipriani et al. (31), but this itself does not inform about why outcomes are heterogeneous across years. It is therefore of clinical relevance to explore the reasons of potentially increasing placebo effects across decades.
Furukawa et al. (14, 15) suggested that any potential secular changes in placebo outcomes may be explained by changes in study designs corresponding to differences in study centers, study dosing schedule, study length, or study size. The present findings rather suggest that small-study effects drive most of the changes in placebo outcomes across decades, due to older mostly smaller antidepressant trials being greatly underpowered. This assumption is in line with previous work, suggesting fundamental flaws in antidepressant trials due to underpowered effects sizes and a lack of precision in depression outcome measurements for the past 40 years (46).
The present findings show that adjusting for these small-study bias largely reduces heterogeneity and removes any nonlinear effects of study year. Still, a remaining linear trend is suggested for efficacy (continuous) gradually increasing from 1979 to 2014, that is not explained by small-study effects. This increasing trend does not seem to follow a structural break as suggested by Furukawa et al. (14, 15), again disproving any underlying nonlinearity. Considering the low heterogeneity that remained after small-study effects were accounted for (G2 = 3%), suggests that further bias adjustments may not essentially change these findings.
By contrast, trial-level covariates alone were found to be insufficient in explaining placebo time trends and may even led to misleading conclusions by Furukawa et al. (14, 15). The present work rather suggests that at least part of the trial-level covariate effects may be mediated by small-study effects without having own effects. An example is the effect of study center that was found to be insignificant after adjusting for small-study effects. This is likely a result of the close relation between secular changes from single-centered trials with small sample size (and thus low study precision) in older trials, versus more multi-centered trials with larger sample sizes (and thus higher study precision) in more recent trials. This illustrates the importance of adjusting for small-study effects in order to derive reliable trial-level covariate effects in antidepressant trials.
The observed differences between the continuous and binary outcomes are likely a result of the dichotomization of the original HAMD scale. In clinical practice, dichotomization is sometimes justified to label groups of individuals with diagnostic or therapeutic attributes (47, 48). However, methodologists have advised against the use of dichotomization because it reduces statistical power and inflates effect sizes (49–52). To derive binary constructs, the quantitative HAMD scale is dichotomized along arbitrary cut-off scores (49, 51, 53, 54). This can create artificial boundaries, were patients just below and above the cut-off fall into different binary (49). For example, a responder, who drops 50% from 40 to 20 on the HAMD can still be quite depressed, while someone who drops from 20 to 10 is almost in remission. Compared with efficacy (continuous), response rates are thus less precise since most of the information distinguishing patients on the original scale is lost (52).
These aspects are even more problematic considering small sample sizes, because the reduction in statistical power consequently requires larger sample sizes in binary outcomes to be adequately powered (55). Although, there are no clear sample size requirements for meta-analyses, previous work showed that small trials (e.g., fewer than 50 patients) can produce 10–48% larger binary estimates than larger trials (56). Most trials completed before 1990 had on average less than 50 patients. As a consequence, the power of the binary outcome was reduced before 1990. This is because the precision of the binary outcome is statistically dependent on its effect estimate. This dependence induces a well-known asymmetry in funnel plots, a sort of mathematical artifact (57, 58), which also explains the steep nonlinear trend suggested by the break analysis. As a consequence, placebo response rate showed (59). The present findings thus provide another example that response rate in antidepressant trials may generally be avoided due to low statistical power and spuriously inflated effect sizes. The continuous outcome may be preferred when available, which is viewed as a more favorable endpoint as it is less susceptible to small-study effects.
Limiting the present analysis is the fact that the described phenomena of underpowered effect sizes and small-study effects can cause similar results besides having different reasons. Interpretation should therefore be cautious, given that it is not possible to separate the different mechanisms of bias (37, 60). Another possible and probably the most well-known reason for small-study effects is publication bias, which occurs when the chance of smaller studies being published is increased when having significant positive results, compared to larger studies which may be accepted and published regardless. Notably, publication bias can also arise from time-lag effects, resulting from the variability in the time it takes to complete and publish a study (61). Weak or negative results have been shown to take approximately two to three more years to be published compared to stronger and positive results (62, 63). To reduce the implications of potential time-lag effects (and to allow for the inclusion of non-published studies), the present analysis therefore synthesized results across completion years, if available. Other well-known causes of small-study effects are outcome selection bias, where only favorable outcomes are selectively reported (20, 64, 65), and clinical heterogeneity, e.g., patients in smaller studies may have been selected so that a favorable outcome is to be expected (59), both of which are not addressed in the present analysis.
Another limitation of the present analysis is that it did not separately address risk of bias (RoB) and how this relates to SSE, because it is difficult to relate RoB only to placebo outcomes without consideration of the drug-related RoB. The funnel plots and Egger’s test as detailed in the supplementary appendix (Supplementary S4), however, give at least some quantification of RoB related to the presence of possible publication bias. For a detailed assessment of RoB of the included studies it is referred to Cipriani et al. cipriani (31).
Further research may be required to explain the reasons for the observed increase in placebo efficacy (continuous) across decades. Earlier meta-analyses considered several other trial-level or patient characteristics, such as the use of placebo run-in, probability of being allocated to placebo, number of trial arms, publication status, co-medication, country region, primary versus secondary care, inpatient versus outpatient settings, age, sex, and baseline depression severity (3, 5, 7, 9, 14, 66–70); none of which consistently explained placebo outcomes. Based on the extensive previous work, it therefore seems unlikely that other trial-level or patient characteristics can fully explain the present observations. One might therefore also consider factors other than measurable covariates. For example, it has been suggested that marketing has led to an increased public perception that antidepressants are effective. This may increase the consumer demand for the thus advertised antidepressants, and may create conditioned responses and expectations that can produce a placebo effect similar to that when the medication is taken (71, 72). Others have argued that inter-rater and intra-rater variabilities contributed to this phenomenon (73–75). Again, others suggested that the issue of unblinded outcome-assessors in double-blind trials has led to worse placebo outcomes in older compared to more recent trials due to the older drugs’ marked side effects compared to newer generation antidepressants (76). All these aspects may also be related to overall higher standards in trial conductance by pharmaceutical companies in more recent trials, which not only significantly increased sample sizes, but may have also increased expectations in placebo receiving individuals (46).
In conclusion, there has been an ongoing debate how placebo outcomes in antidepressant trials can be explained across decades. The present analysis aimed to contribute to the debate suggesting that secular changes in placebo outcomes are best explained by small-study effects, rather than by trial-level covariates. Further research may be required to adjust the corresponding antidepressant treatment effects for small-study effects, to account for increase in placebo efficacy (continuous). This is of clinical relevance to evaluate success or failure in antidepressant trials.
Data Availability Statement
All datasets presented in this study are included in the article/Supplementary Material.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was funded by the Swiss National Science Foundation (SNSF).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyt.2020.00633/full#supplementary-material
References
1. Hróbjartsson A, Gøtzsche PC. Is the Placebo Powerless? New Engl J Med (2001) 344:1594–602. doi: 10.1056/NEJM200105243442106
2. Curkovic M, Kosec A, Savic A. Re-evaluation of Significance and the Implications of Placebo Effect in Antidepressant Therapy. Front Psychiatry (2019) 10:143. doi: 10.3389/fpsyt.2019.00143
3. Walsh BT, Seidman SN, Sysko R, Gould M. Placebo Response in Studies of Major DepressionVariable, Substantial, and Growing. JAMA (2002) 287:1840–7. doi: 10.1001/jama.287.14.1840
4. Stahl SM, Greenberg GD. Placebo response rate is ruining drug development in psychiatry: Why is this happening and what can we do about it? Acta Psychiatr Scand (2019) 139:105–7. doi: 10.1111/acps.13000
5. Khan A, Bhat A, Kolts R, Thase ME, Brown W. Why has the antidepressant-placebo difference in antidepressant clinical trials diminished over the past three decades? CNS Neurosci Ther (2010) 16:217–26. doi: 10.1111/j.1755-5949.2010.00151.x
6. Khin N, Chen YF, Yang Y, Yang P, Laughren T. Exploratory Analyses of Efficacy Data From Major Depressive Disorder Trials Submitted to the US Food and Drug Administration in Support of New Drug Applications. J Clin Psychiatry (2011) 72:464–72. doi: 10.4088/JCP.10m06191
7. Bridge JA, Birmaher B, Iyengar S, Barbe RP, Brent DA. Placebo Response in Randomized Controlled Trials of Antidepressants for Pediatric Major Depressive Disorder. Am J Psychiatry (2009) 166:42–9. doi: 10.1176/appi.ajp.2008.08020247
8. Fountoulakis KN, Möller HJ. Efficacy of antidepressants: A re-analysis and re-interpretation of the Kirsch data. Int J Neuropsychopharmacol (2011) 14:405–12. doi: 10.1017/S1461145710000957
9. Rief W, Nestoriuc Y, Weiss S, Welzel E, Barsky AJ, Hofmann SG. Meta-analysis of the placebo response in antidepressant trials. J Affect Disord (2009) 118:1–8. doi: 10.1016/j.jad.2009.01.029
10. Kirsch I. Placebo Effect in the Treatment of Depression and Anxiety. Front Psychiatry (2019) 10:407:407. doi: 10.3389/fpsyt.2019.00407
11. Schalkwijk S, Undurraga J, Tondo L, Baldessarini RJ. Declining efficacy in controlled trials of antidepressants: Effects of placebo dropout. Int J Neuropsychopharmacol (2014) 17:1343–52. doi: 10.1017/S1461145714000224
12. Rutherford BR, Roose SP. A Model of Placebo Response in Antidepressant Clinical Trials. Am J Psychiatry (2013) 170:723–33. doi: 10.1176/appi.ajp.2012.12040474
13. Montgomery S. The failure of placebo-controlled studies1Chair: S.A. Montgomery.Participants: M. Ackenheil, O. Benkert, J.-C. Bisserbe, M. Bourin, M. Briley, A. Cameron, D. Durette, P. de Koning, J.-D. Guelfi, R. Judge, S. Kasper, Y. Lecrubier, M. Malbezin, R. Nil, W. Potter, A. Saint Raymond, C. Sampaio, J.G. Storosum, S. Eisen, F. Unden, J.M. Van Ree, B.J. Van Zwieten-Boot.Rapporteur: D.B. Montgomery.1. Eur Neuropsychopharmacol (1999) 9:271–6. doi: 10.1016/S0924-977X(98)00050-9
14. Furukawa TA, Cipriani A, Atkinson LZ, Leucht S, Ogawa Y, Takeshima N, et al. Placebo response rates in antidepressant trials: A systematic review of published and unpublished double-blind randomised controlled studies. Lancet Psychiatry (2016) 3(11):1059–66. doi: 10.1016/S2215-0366(16)30307-8
15. Furukawa TA, Cipriani A, Leucht S, Atkinson LZ, Ogawa Y, Takeshima N, et al. Is placebo response in antidepressant trials rising or not? A reanalysis of datasets to conclude this long-lasting controversy. Evid Based Ment Health (2018) 21:1. doi: 10.1136/eb-2017-102827
16. Orsini N, Greenland S. A procedure to tabulate and plot results after flexible modeling of a quantitative covariate. Stata J (2011) 11:1–29. doi: 10.1177/1536867X1101100101
17. Sterne JA, Gavaghan D, Egger M. Publication and related bias in meta-analysis: Power of statistical tests and prevalence in the literature. J Clin Epidemiol (2000) 53:1119–29. doi: 10.1016/S0895-4356(00)00242-0
18. Rothstein H, Sutton A, Borenstein M. Publication Bias in Meta Analysis: Prevention, Assessment and Adjustments. Chichester, UK: Wiley (2005).
19. Moreno SG. (2012). Methods for Adjusting for Publication Bias and Other Small-Study Effects in Evidence Synthesis. Ph.D. thesis.
20. Williamson P, Gamble C. Identification and impact of outcome selection bias. Stat Med (2005) 24:1547–61. doi: 10.1002/sim.2025
21. Moreno SG, Sutton AJ, Turner EH, Abrams KR, Cooper NJ, Palmer TM, et al. Novel methods to deal with publication biases: Secondary analysis of antidepressant trials in the FDA trial registry database and related journal publications. BMJ (2009) 339:b2981–1. doi: 10.1136/bmj.b2981
22. Ioannidis J. Interpretation of tests of heterogeneity and bias in meta-analysis. J Eval Clin Pract (2008) 14:951–7. doi: 10.1111/j.1365-2753.2008.00986.x
23. Sterne JA, Egger M. Funnel plots for detecting bias in meta-analysis: Guidelines on choice of axis. J Clin Epidemiol (2001) 54(10):1046–55. doi: 10.1016/S0895-4356(01)00377-8
24. Rücker G, Carpenter JR, Schwarzer G. Detecting and adjusting for small-study effects in meta-analysis. Biometr J (2011) 53:351–68. doi: 10.1002/bimj.201000151
25. Rücker G, Schwarzer G, Carpenter JR, Binder H, Schumacher M. Treatment-effect estimates adjusted for small-study effects via a limit meta-analysis. Biostatistics (2010) 12:122–42. doi: 10.1093/biostatistics/kxq046
26. Viechtbauer W. Best Practices in Quantitative Methods. Thousand Oaks, California: SAGE Publications, Inc (2008). doi: 10.4135/9781412995627
27. Burnham K, Anderson D. Model Selection and Multimodel Inference:A Practical Information-Theoretic Approach. New York: Springer New York (2002).
29. Khan A, Fahl Mar K, Faucett J, Khan Schilling S, Brown WA. Has the rising placebo response impacted antidepressant clinical trial outcome? Data from the US Food and Drug Administration 1987-2013. World Psychiatry (2017) 16:181–92. doi: 10.1002/wps.20421
30. Hamilton M. A rating scale for depression. J Neurol Neurosurg Psychiatry (1960) 23:56–62. doi: 10.1136/jnnp.23.1.56
31. Cipriani A, Furukawa TA, Salanti G, Chaimani A, Atkinson LZ, Ogawa Y, et al. Comparative efficacy and acceptability of 21 antidepressant drugs for the acute treatment of adults with major depressive disorder: A systematic review and network meta-analysis. Lancet (2018) 391:1357–66. doi: 10.1016/S0140-6736(17)32802-7
33. Team RDC. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing (2008).
36. Moreno SG, Sutton AJ, Ades A, Stanley TD, Abrams KR, Peters JL, et al. Assessment of regression-based methods to adjust for publication bias through a comprehensive simulation study. BMC Med Res Method (2009b) 9:2. doi: 10.1186/1471-2288-9-2
37. Ioannidis JP, Trikalinos TA. An exploratory test for an excess of significant findings. Clin Trials (2007) 4:245–53. doi: 10.1177/1740774507079441
40. Grueber CE, Nakagawa S, Laws RJ, Jamieson IG. Multimodel inference in ecology and evolution: Challenges and solutions. J Evolution Biol (2011) 24:699–711. doi: 10.1111/j.1420-9101.2010.02210.x
41. Viechtbauer W. Conducting Meta-Analyses in R with the metafor Package. J Stat Softw (2010) 36:1–48. doi: 10.18637/jss.v036.i03
42. DerSimonian R, Laird N. Meta-analysis in clinical trials. Controlled Clin Trials (1986) 7:177–88. doi: 10.1016/0197-2456(86)90046-2
43. Rücker G, Schwarzer G, Carpenter JR, Schumacher M. Undue reliance on I(2) in assessing heterogeneity may mislead. BMC Med Res Method (2008) 8:79–9. doi: 10.1186/1471-2288-8-79
44. Thorlund K, Imberger G, Johnston BC, Walsh M, Awad T, Thabane L, et al. Evolution of heterogeneity (I2) estimates and their 95% confidence intervals in large meta-analyses. PloS One (2012) 7:e39471–1. doi: 10.1371/journal.pone.0039471
45. Alba AC, Alexander PE, Chang J, MacIsaac J, DeFry S, Guyatt GH. High statistical heterogeneity is more frequent in meta-analysis of continuous than binary outcomes. J Clin Epidemiol (2016) 70:129–35. doi: 10.1016/j.jclinepi.2015.09.005
46. Khan A, Mar KF, Brown WA. The conundrum of depression clinical trials: One size does not fit all. Int Clin Psychopharmacol (2018) 33:239–48. doi: 10.1097/YIC.0000000000000229
47. Royston P, Altman D, Sauerbrei W. Dichotomizing continuous predictors in multiple regression: A bad idea. Stat Med (2006) 25:127–41. doi: 10.1002/sim.2331
48. Shentu Y, Xie M. A note on dichotomization of continuous response variable in the presence of contamination and model misspecification. Stat Med (2010) 29:2200–14. doi: 10.1002/sim.3966
49. Moncrieff J, Kirsch I. Efficacy of antidepressants in adults. BMJ (Clin Res ed) (2005) 331:155–7. doi: 10.1136/bmj.331.7509.155
50. Altman DG, Royston P. The cost of dichotomising continuous variables. BMJ (Clin Res ed) (2006) 332:1080–0. doi: 10.1136/bmj.332.7549.1080
51. Hengartner MP. Methodological Flaws, Conflicts of Interest, and Scientific Fallacies: Implications for the Evaluation of Antidepressants’ Efficacy and Harm. Front Psychiatry (2017) 8:275. doi: 10.3389/fpsyt.2017.00275
52. MacCallum RC, Zhang S, Preacher KJ, Rucker DD. On the practice of dichotomization of quantitative variables. Psychol Methods (2002) 7:19–40. doi: 10.1037/1082-989X.7.1.19
53. National Institute for Clinical Excellence. Depression in adults: Recognition and management. Clinical guideline [CG90]. National Institute for Clinical Excellence (2014).
54. Kirsch I, Moncrieff J. Clinical trials and the response rate illusion. Contemp Clin Trials (2007) 28:348–51. doi: 10.1016/j.cct.2006.10.012
55. Turner RM, Bird SM, Higgins JPT. The impact of study size on meta-analyses: Examination of underpowered studies in Cochrane reviews. PloS One (2013) 8:e59202–2. doi: 10.1371/journal.pone.0059202
56. Dechartres A, Trinquart L, Boutron I, Ravaud P. Influence of trial sample size on treatment effect estimates: Meta-epidemiological study. BMJ Br Med J (2013) 346:f2304. doi: 10.1136/bmj.f2304
57. Macaskill P, Walter SD, Irwig L. A comparison of methods to detect publication bias in meta-analysis. Stat Med (2001) 20:641–54. doi: 10.1002/sim.698
58. Schwarzer G, Antes G, Schumacher M. Inflation of Type I error rate in two statistical tests for the detection of publication bias in meta-analysis with binary outcomes. Stat Med (2002) 21:2465–77. doi: 10.1002/sim.1224
59. Schwarzer G, Carpenter JR, Rücker G. Small-Study Effects in Meta-Analysis. In: Schwarzer G, Carpenter JR, Rücker G, editors. Meta-Analysis with R. Cham: Springer International Publishing (2015). p. 107–41. doi: 10.1007/978-3-319-21416-0_5
60. Higgins JPT, Green S. Cochrane Handbook for Systematic Reviews of Interventions. Wiley-Blackwell (2011).
61. Ioannidis JPA. Effect of the Statistical Significance of Results on the Time to Completion and Publication of Randomized Efficacy Trials. JAMA (1998) 279:281–6. doi: 10.1001/jama.279.4.281
62. Song F, Parekh S, Hooper L, Loke YK, Ryder J, Sutton AJ, et al. Dissemination and publication of research findings: An updated review of related biases. Health Technol Assess (Winchester England) (2010) 14:iii, ix–xi, 1. doi: 10.3310/hta14080
63. Hopewell S, Clarke M, Stewart L, Tierney J. Time to publication for results of clinical trials. Cochrane Database Systemat Rev (2007) (2). doi: 10.1002/14651858.MR000011.pub2
64. Chan AW, Hróbjartsson A, Haahr MT, Gøtzsche PC, Altman DG. Empirical Evidence for Selective Reporting of Outcomes in Randomized TrialsComparison of Protocols to Published Articles. JAMA (2004) 291:2457–65. doi: 10.1001/jama.291.20.2457
65. Chan AW, Krleža-Jerić K, Schmid I, Altman DG. Outcome reporting bias in randomized trials funded by the Canadian Institutes of Health Research. Can Med Assoc J (2004b) 171:735. doi: 10.1503/cmaj.1041086
66. Sinyor M, Levitt A, Cheung A, Schaffer A, Kiss A, Dowlati Y, et al. Does Inclusion of a Placebo Arm Influence Response to Active Antidepressant Treatment in Randomized Controlled Trials? Results From Pooled and Meta-Analyses. J Clin Psychiatry (2010) 71:270–9. doi: 10.4088/JCP.08r04516blu
67. Papakostas GI, Fava M. Does the probability of receiving placebo influence clinical trial outcome? A meta-regression of double-blind, randomized clinical trials in MDD. Eur Neuropsychopharmacol (2009) 19:34–40. doi: 10.1016/j.euroneuro.2008.08.009
68. Khan A, Khan SR, Walens G, Kolts R, Giller EL. Frequency of Positive Studies Among Fixed and Flexible Dose Antidepressant Clinical Trials: An Analysis of the Food and Drug Administraton Summary Basis of Approval Reports. Neuropsychopharmacology (2003) 28:552–7. doi: 10.1038/sj.npp.1300059
69. Landin R, DeBrota DJ, DeVries TA, Potter WZ, Demitrack MA. The Impact of Restrictive Entry Criterion During the Placebo Lead-in Period. Biometrics (2000) 56:271–8. doi: 10.1111/j.0006-341X.2000.00271.x
70. Rutherford BR, Cooper TM, Persaud A, Brown PJ, Sneed JR, Roose SP. Less is more in antidepressant clinical trials: A meta-analysis of the effect of visit frequency on treatment response and dropout. J Clin Psychiatry (2013) 74:703–15. doi: 10.4088/JCP.12r08267
71. Kirsch I. Clinical trial methodology and drug-placebo differences. World Psychiatry (2015) 14:301–2. doi: 10.1002/wps.20242
72. Almasi EA, Stafford RS, Kravitz RL, Mansfield PR. What are the public health effects of direct-to-consumer drug advertising? PloS Med (2006) 3:e145–5. doi: 10.1371/journal.pmed.0030145
73. Demitrack MA, Faries MP, Herrera JM, Potter WZ. The problem of measurement error in multisite clinical trials. Psychopharmacol Bull (1998) 34:19–24.
74. Kobak KA, Feiger AD, Lipsitz JD. Interview quality and signal detection in clinical trials. Am J Psychiatry (2005) 162:628.
75. Kobak K, Thase ME. Why do clinical trials fail?: The problem of measurement error in clinical trials: Time to test new paradigms? J Clin Psychopharmacol (2007) 27:1–5.
Keywords: placebo, antidepressants, small-study effects, time trend, meta-analysis
Citation: Holper L (2020) Raising Placebo Efficacy in Antidepressant Trials Across Decades Explained by Small-Study Effects: A Meta-Reanalysis. Front. Psychiatry 11:633. doi: 10.3389/fpsyt.2020.00633
Received: 29 April 2020; Accepted: 17 June 2020;
Published: 28 July 2020.
Edited by:
Michele Fornaro, New York State Psychiatric Institute (NYSPI), United StatesReviewed by:
Irving Kirsch, Harvard Medical School, United StatesPim Cuijpers, Vrije Universiteit Amsterdam, Netherlands
Copyright © 2020 Holper. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lisa Holper, bGlzYS5ob2xwZXJAYmxpLnV6aC5jaA==
 Lisa Holper
Lisa Holper