- Graduate School of Information Science, Nagoya University, Nagoya, Japan
Novelty search is an evolutionary search algorithm based on the superficially contradictory idea that abandoning goal-focused fitness function altogether can lead to the discovery of higher fitness solutions. In the course of our work, we have created a biologically inspired artificial development system with the purpose of automatically designing complex morphologies and controllers of multicellular, soft-bodied robots. Our goal is to harness the creative potential of in silico evolution, so that it can provide us with novel and efficient designs that are free of any preconceived notions a human designer would have. In order to do so, we strive to allow for the evolution of arbitrary morphologies. Using a fitness-driven search algorithm, the system has been shown to be capable of evolving complex multicellular solutions consisting of hundreds of cells that can walk, run, and swim; yet, the large space of possible designs makes the search expensive and prone to getting stuck in local minima. In this work, we investigate how a developmental approach to the evolution of robotic designs benefits from abandoning objective fitness function. We discover that novelty search produced significantly better performing solutions. We then discuss the key factors of the success in terms of the phenotypic representation for the novelty search, the deceptive landscape for co-designing morphology/brain, and the complex development-based phenotypic encoding.
1. Introduction
The potential to automatically design whole robots with their morphology and control system specialized for a particular task has been one of the most exciting promises of evolutionary robotics, ever since Karl Sims presented his seminal work (Sims, 1994). Over the years, a variety of approaches have been proposed to achieve this goal, often becoming staples of the field. Just like Sim’s work, most of them assumed some kind of indirect phenotypic encoding, based on a high level abstraction of development, such as the grammatical approaches [used by Komosinski and Ulatowski (1999), Lipson and Pollack (2000), and Pilat et al. (2012)] or abstractions, such as the CPPN (Stanley, 2007) used by Cheney et al. (2013) and Auerbach and Bongard (2012). Less commonly, and that includes our approach, morphologies and controllers were evolved using a more direct abstraction of biological development, where bodies progressively build themselves through subsequent cellular divisions, deaths, and realignments (Bongard and Pfeifer, 2003; Kowaliw et al., 2004; Meng et al., 2011; Schramm et al., 2011; Joachimczak et al., 2013).
While the two decades of evolutionary robotics have advanced the field to the level where evolutionary approaches excel at designing controllers for robot gaits [see, e.g., Boddhu and Gallagher (2010) and Lee et al. (2013)] or whole complex behaviors [see, e.g., Lessin et al. (2014)], co-evolving bodies and brains de novo, even despite famous physical implementations (Lipson and Pollack, 2000) remains largely at the proof-of-concept stage. This should be hardly surprising, given the exploded search space that covers possible pairs of morphologies and controllers and its potentially highly deceptive structure coming from continuous interactions between the two. Naturally, limiting the search space to the area of interest (such as by assuming that bodies consist of sticks or boxes) is essential to solve any problem through evolutionary optimization and means that a knowledge about the expected types of solutions is incorporated into the search algorithm. There is a trade-off, however, evolution, just like a human brain, can be creative and the more we limit the search space, the less likely an evolutionary search algorithm is to come up with a novel and unexpected solution. Thus, by carefully restricting the amount of knowledge about the problem domain that is transferred to the search algorithm, we give the evolutionary process a chance to offer new insights and inspire us with original ways to solve the problem [see, e.g., Hornby et al. (2010) for a classic example]. In particular, in our work, we strive to avoid restrictions put on morphologies and gaits that can evolve, and instead of assembling bodies from primitives, we allow them to grow cell-by-cell and form arbitrary shapes made from hundreds of cells.
One of the research areas where we think it would be beneficial to allow for a possibly unconstrained evolution of morphologies and gaits is soft-robotics. Soft-bodied robotics is a very recent and quickly developing branch of robotics that abandons the idea of robots made of rigid parts. Instead, robots are assumed to be made of elastic material and can deform itself in order to produce gaits or to dynamically adapt to an environment (e.g., crawl through a small opening). This makes them much more similar to animals and, in particular, invertebrates, such as cephalopods. While the field is still in its early stage, there were already multiple successful demonstrations of physical implementations of such entities. Some most prominent examples include robots relying on fluid or air-filled cavities (Steltz et al., 2009; Shepherd et al., 2011), materials that differentially respond to external pressures (Hiller and Lipson, 2012) or actual, 3-D printed biological tissue (Chan et al., 2012).
Following the inspiration from nature and, in particular, the increasing understanding of the role of development in evolution [see, e.g., Carroll et al. (2004)] and how their interactions produce what Darwin called “endless forms most beautiful,” we have proposed a biologically inspired, artificial development system that allows to evolve morphologies and controllers for 2-D, soft-bodied animats (Joachimczak et al., 2014). In our approach, animats grow from a single cell through subsequent divisions with each cell controlled by a copy of the same gene regulatory network (GRN) encoded in individual’s genotype. Other than being the way nature produces animal forms, developmental systems are well known for having higher evolvability and scalability than direct encodings [see a direct comparison in, e.g., Komosinski and Rotaru-Varga (2002) and Cheney et al. (2013)]. They also display useful properties, such as robustness, to damage during development or ability to self-repair (Andersen et al., 2009; Joachimczak and Wróbel, 2012b). We use morphologies that emerged through development as a template for a physical model of an animat, which is evaluated in a virtual environment for its performance on a given task. Movement is achieved by contracting and expanding regions of the body, with each body region (originally a cell) making independent decisions about its behavior (though potentially in communication with neighboring areas). In that way, gaits emerge as a product of a distributed control mechanism, being a continuation of the distributed self-assembly process that creates the multicellular morphology.
Using fitness-driven evolutionary search, we were successful in producing complex morphologies that consist of hundreds of cells, walk, run, and swim (Joachimczak et al., 2014) or even reshape their bodies when changing environments through the process of metamorphosis (Joachimczak et al., 2015). Importantly, we were able to show how such a fine-grained approach development leads to the emergence of higher level structural features, such as simple appendages that function as legs, fins, or tails. As a method of fitness-driven search, we have employed the NEAT algorithm [Stanley and Miikkulainen (2002), see Section 2.7.1], one of the most successful method of evolving neural networks (Mouret and Doncieux, 2011). Despite promising results, simulating multicellular growth (with hundreds of cells interacting) is very computationally expensive. Furthermore, the large search space and a complex, highly indirect relation between genotype and phenotype makes evolutionary search prone to getting stuck in local minima.
In this work, we show and analyze how a fine-grained developmental system evolving morphologies and behaviors of robots can be improved by the use of novelty search algorithm (Lehman and Stanley, 2011a; Stanley and Lehman, 2015). This seems superficially counterintuitive as the algorithm entirely abandons the use of an objective fitness function. However, it is found to improve quality of solutions as well as diversity of candidate morphologies that are evaluated during the evolutionary process. The former is needed for the approach to be useful, whereas the latter is essential given our overall aim of harnessing the creative potential of the evolutionary process.
Novelty search is an evolutionary search algorithm based on the radical idea that abandoning objective, goal-focused fitness function altogether can actually lead to a discovery of higher fitness solutions. To do so, novelty search replaces the concept of objective fitness function with the concept of novelty, a scalar value corresponding to how much a given phenotype differs from phenotypes in the current population as well as from phenotypes that have been found to be novel in previous generations, stored in a dedicated archive. This causes the evolutionary search to pursue phenotypes that are different from the already discovered ones instead of phenotypes that have higher fitnesses. While methods that increase genetic diversity have long been demonstrated to be useful in evolutionary algorithms [see, e.g., Mahfoud (1995) and Sareni and Krahenbuhl (1998)], novelty search differs from them by focusing entirely on increasing the phenotypic, not genotypic diversity.
Novelty search had been suggested to improve evolvability in problems that are deceptive in nature, i.e., where greedily focusing the search on improving fitness will likely lead population into local minima in the fitness landscape that are difficult to escape from. It is suggested that the pressure to produce novel phenotypes will instead lead to the discovery of progressively more and more complex solutions and, among them, the evolutionary stepping stones that open access to new regions of higher fitness in the solution space (Lehman and Stanley, 2011a). Importantly, it is argued that most problems of interest for evolutionary algorithms are deceptive in nature, as non-deceptive problems are simply easy to solve. To what extent different problem domains benefit from the use of novelty search is continuously being explored, with a particular focus on the evolution of robotic controllers. It has been shown to improve evolvability in Lehman and Stanley (2011b), Krčah (2012), Gomes et al. (2013), Lehman et al. (2013), and Urbano and Georgiou (2013). It has, however, been shown to decrease evolvability in problems with very large solution spaces (Cuccu and Gomez, 2011), to which co-evolution of morphologies and control likely belongs to.
In the next section, we provide a concise description of the developmental model that we used. However, we refer the reader to the original paper (Joachimczak et al., 2014) for more details and an overview of what kinds of structures it can evolve. In this work, we focus on investigating how and why novelty search contributes to evolvability in this problem domain.
2. Developmental Approach
Following the biological inspiration, we have attempted to design a possibly simple model of the developmental process, in which arbitrary morphologies could self-assemble through multicellular growth. The underlying assumptions of the approach are
• a genome encodes a control network that commands each cell’s behavior,
• self-assembly starts from a single cell, proceeds through subsequent cellular divisions and deaths, and
• all cells share the same control network and respond to local signals.
The fitness evaluation is a two-step process (Figure 1). First, an animat undergoes the developmental stage during which its morphology and controller forms. Next, the resultant morphology is used as a template for a soft-bodied model that is simulated in a physical environment for a fixed number of time steps, where it undergoes only elastic changes. We discuss each of these steps in more detail next.
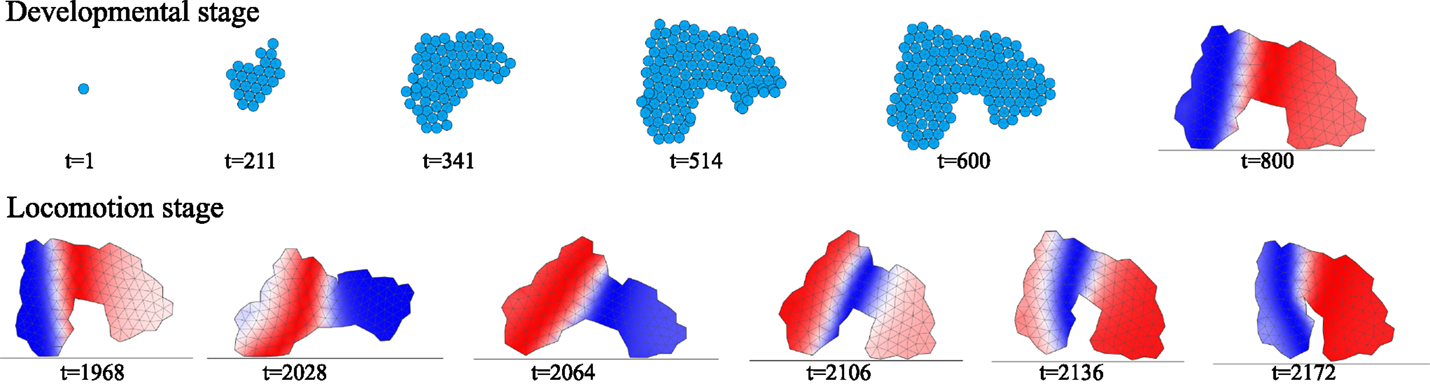
Figure 1. Example life cycle (evaluation process) of an evolved animat. The upper row shows developmental stage and the transition from multicellular representation of an embryo to the physical model of an animat that occurs at the beginning of the locomotion stage. The bottom row shows snapshots of the animat in motion, during the locomotion stage. The animat moves right. Colors indicate temporal contraction of a body region (blue) or expansion (red). Videos for each stage can be found at: http://youtu.be/K06FSr0hInI and http://youtu.be/JRgnPs8e-5c.
2.1. Growth Stage
Cells are controlled by a simple abstraction of gene regulatory network (GRN) in the form of a neural network where nodes are meant to represent genes and their state rather than neurons. To update state of each node, we used a sigmoidal transfer function (tanh) with output values within [−1, 1] applied to the weighted sum of incoming nodes outputs, as implemented by the MultiNEAT library (Chervenski and Ryan, 2014). The network determines each cell behavior during growth as well as during the locomotion stage, where cells act as “muscles.” Ultimately, the behavior of each cell depends on its internal state and the external signals received by the network, such as positional information.
Development takes place in a continuous 2-D space, where cells are represented as disks and undergo elastic collisions simulated with springs that connect them (Figure 2B). While there is nothing that would in principle prevent implementing the presented approach in 3-D [in fact, we have implemented an earlier version of the system in 3-D, see, e.g., Joachimczak and Wróbel (2011, 2012c)], a 2-D model is much less computationally demanding. As the body length generally scales with the cube root of the number of cells in 3-D and a square root in 2-D, a fine-grained 2-D development allows to produce structures of higher apparent complexity with lower numbers of cells.

Figure 2. Basics assumptions of the developmental and soft-body system. (A) Each cell is controlled by a copy of the regulatory network encoded in the genome. The output configuration shown was used in the basic, oscillator-driven actuation experiments (see Section 2.6.1). In the GRN experiments (Section 2.6.1), outputs 5 and 6 were replaced with a single output that actively determines spring deviation. (B) Physical interactions between cells during developmental stage. Cells are represented as point masses connected with springs of a fixed resting length equal to 2 cell radii, simulating adhesive force (d > 2r) or repulsion (d < 2r). Springs are removed if cells find themselves at a distance larger than 3 radii. (C) Soft-body representation of an animat during the locomotion stage. Cells are connected by springs of different rest lengths, determined by cell distances at the end of developmental stage. In analogous way, each triangular region has an equilibrium area Si associated with it. Compression of a region results in an outward forces acting on the nodes, expansion results in inward forces. To produce animat movement, each cell synchronously shortens or expands the resting lengths of all the springs attached to it, within a fixed range [gray boxes, see equations (1) and (3)].
A cell physical state is defined by its position, its velocity, and orientation vector, which determines the direction of division. Springs connect only the nearest neighbors and are determined dynamically, as the embryo grows. We use Delaunay triangulation to determine the connectivity between cells and then remove links longer than 150% of cell diameter (to allow for non-convex shapes). The resting length of a spring is equal to the sum of attached cells radii. As this simple approach can, however, produce a disjoint structure (e.g., after cells in a central part of an elongated embryo die out), a spring between a pair of nodes is removed only when some other path between these two nodes can be found. Generally, the physics of development was made to resemble soft interactions between cells suspended in a fluid environment.
To reduce computational time, the neighborhood relation was recalculated every 10 steps of physics simulation. The use of Delaunay triangulation as the way to determine neighborhood in the growing embryo is likely not essential for producing current system dynamics and other neighborhood definitions (such as distance based) can be expected to produce similar results. Delaunay was chosen for the conceptual simplicity of spring-based handling of cell adhesion and repulsion, its quasi-linear complexity of determining neighborhood for all cells, and the fact that it allowed us to use the same definition of neighborhood we later used for the locomotion stage. Additionally, the developmental physics was updated at a higher update rate than the state of control networks. More precisely, we allowed for 600 developmental steps and updated networks every 30 steps.
2.2. Network Inputs
Morphogen gradients have long been known to play a fundamental role in development and, in particular, in establishing the basic body plan of animals (Carroll et al., 2004). Thus, to facilitate differentiation of cellular fates, we provided cells with positional information, both direct and indirect (Figure 2A). The direct one was in the form of X and Y coordinate directly fed as input to a network. The indirect information would come in the form of four virtual maternal morphogens at prespecified positions in the environment. Additionally, as a simple mechanism that substitutes for morphogens produced by cells, the control network had one “morphogen” output and an associated morphogen input. For any given cell, the activation of the latter was set to the average activation of corresponding morphogen outputs of its neighbors. Finally, all cells were provided with two global signals: a bias input (set to 1 in every cell) and a time signal (with a value increasing linearly from 0 to 1 throughout development).
2.3. Cell Division and Death
All cells were bound to divide with each subsequent update of the control network unless the output interpreted as the inhibitor of division had activation above 0. Furthermore, division was allowed to occur if and only if space in the direction of the division was not entirely occupied already by other cells [see Joachimczak et al. (2014) for the rationale of this approach].
As long as some space was available, the newly created cell was placed next to the original cell in the direction determined by the network output representing the division angle. The angle was determined at the moment of division and was relative to the mean orientation angle of the cell nearest neighbors. Unless the state was different from zero, all cells would simply divide in the same direction.
Apoptosis (cellular death) occurred whenever activation of the associated network output in a cell was found to be above zero. Such cell was immediately removed from the embryo.
2.4. Termination of Development
To prevent a trivial scenario in which cells divide in an uncontrolled manner until the hard limit of embryo size is reached, we required development never to reach the limit of 256 cells. Individuals who would not fulfill this criterion (even if temporarily) would have their fitnesses set to 0. Moreover, we added a limit on the total number of cells that could be created during the development of an embryo to be no larger than 1024. Such individuals were penalized by having their fitness multiplied by 0.1. We did so in order to limit the occurrence of rather unrealistic solutions in which cells would be continuously created and destroyed (see Section 2.7.1 for a complete list of penalties applied).
2.5. Locomotion Stage
The morphology of an embryo in the final developmental step was used as a template for a soft-bodied animat that was then evaluated for its capability to produce gaits (see an example of such transformation in Figure 1). The animat was represented in the physics engine as a 2-D spring-mass system, with point masses located at cell centers and springs forming a triangular mesh.
The resting length of springs was assigned based on the distances between cell centers at the end of the developmental stage (Figure 2C). Additionally, each triangular region had its equilibrium pressure (determined based on its surface area at the end of development) providing animat with a hydrostatic skeleton and preventing excessive compression or stretching of body regions.
Springs were governed by the Hooke’s law with damping. For simplicity, all springs shared the same Hooke’s constant value k but could have different resting lengths.
To avoid self-penetration of animat bodies, masses representing cells would undergo elastic collisions with springs. Movement during locomotion stage was simulated using a custom soft-body engine that we have built on top of the rigid-body physics part of the Bullet Physics Library 2.81 (2013).1
The terrestrial environment was constructed by placing animats on top of a flat surface and introducing gravity and friction between animat’s nodes and the surface. To prevent sudden changes in resting length for cells with a non-zero phase shift at the start of a simulation, the amplitude was progressively increased during the initial 200 steps of the locomotion stage. Furthermore, to prevent evolution from exploiting any initial motion that would come from relaxation of the animat body at the beginning of the locomotion stage (when gravity, not present during development, was enabled), before actuation would start, we first waited for the structure to stabilize. This was implemented by making sure that the speeds of the nodes are sustained under a preset threshold for 800 time steps.
For an aquatic environment, gravity was disabled and fluid drag was introduced. We used the fluid drag model based on the work by Sfakiotakis and Tsakiris (2006), which assumes that fluid is stationary and that the force acting on a single edge on the outline of the body is a sum of tangential and normal drag components for the motion of this edge against the fluid [see also Joachimczak and Wróbel (2012a) for details].
Actuation meant modifying resting length of springs attached to a given cell. This resulted in the body region contracting or expanding. The total change of resting length of a spring would depend on both cells it connects. The maximum possible range of change was from −40 to +40% in the aquatic environment and from −30 to +30% in terrestrial (the maximum was reached assuming both cells acted in accord). However, due to the hydrostatic pressures and other forces, the change of resting length of springs would not result in the change of spring length of the same magnitude.
How the resting length of springs was modified to produce gaits depend on which of the two investigated control approaches were used, discussed next.
2.6. Two Approaches to Actuation
In the course of our earlier work, we have developed two different approaches to gait control for the presented model, one being simple and inspired by SodaPlay approach (Burton, 2007) and a more complex one, employing networks to actively control the state of actuators.
2.6.1. Oscillator-Driven Actuation
The simple one assumed that all “muscular” activity during locomotion stage is determined by sinusoidal patterns of contraction and expansion of body regions surrounding cells, with each cell having its own oscillation period and phase assigned. Both period and phase shift would evolve and be determined by the control network; we realized this by setting the parameters for each cell oscillations based on the state of two corresponding outputs in the given cell network at the final step of development. The state of control networks would then no longer be updated during the locomotion stage. More precisely, during the locomotion stage the default resting length L0 of a given spring was modified according to the oscillation parameters of the two cells it connects:
where t was simulation time, A was the predefined amplitude, T1, T2 were periods of oscillation (scaled to span a predefined range), and ϕ1, ϕ2 were phase shifts (scaled to −π to π) determined by the activation of corresponding network outputs at the end of development.
2.6.2. GRN-Driven Actuation
The second approach allowed for a more fine-grained control over actuation, such as using different oscillation patterns for each cell or making only a subset of cells take part in gait generation. Instead of two outputs determining the period and phase shift of muscular contractions at the end of development, we used one output which determined whether a cell contracts or expands its springs at a given point in time (and therefore the area that surrounds it), represented as an output value between −1 and 1 (0 meaning neutral). Importantly, this meant that the control networks in the cells would continue to be updated during the locomotion stage. The state of the corresponding output was, however, used indirectly. First, to limit the maximum possible frequency of changes in the spring resting lengths, the state of control networks was updated every 50 time steps of the physics simulation (which lasted for 4000 time steps in total). Second, in order to avoid strong forces that are generated if the resting lengths change in a stepwise manner after a network update, the resting length of springs was changed progressively. More precisely, in between network updates, the state of rest-length changing actuation signal ai,t in a cell i at the time t was a linear interpolation of the network’s spring output si at the time of a previous network update (tu − 50) and the new desired state determined by the most recent output at a time tu:
Just like in the previous approach [equation (1)], the amount of change applied to resting length of a spring was limited by a globally set amplitude A, and a spring’s resting length would be set according to the actuation signals a1, t, a2, t coming from both cells connected by the spring:
Previously, we have observed that the oscillator-driven method has lower computational cost and tends to evolve gaits faster. We think it is because the search space is considerably smaller: some type of a cyclic gait was guaranteed to emerge and the evolutionary search only had to optimize the periods and phase shifts of each body region. The second method allows for more fine-grained control, but it was up to evolution to discover that repetitive actuation patterns are the way to produce gaits. It is thus suitable for more complex tasks that require either some degree of irregularity or reactiveness (such as maze navigation, obstacles avoidance, and chemotaxis), but comes at the cost of a more complex and more deceptive fitness landscape. An example of such deceptiveness is structures that collapse after a single pulse of contractions: they score high on the distance measure initially but are local minima that hinder the discovery of cyclic motion patterns. This minimum does not exist in the oscillator-driven variant, as each cell will actuate periodically by default.
Finally, seeing the two approaches as a simpler and a more complex variant of control network evolution, we introduced one more change between them. Namely, in the simple oscillator-driven scenario, we only allowed for feed-forward control networks. This meant that during development, the networks were stateless and all cellular actions would depend entirely on the external signals provided for each cell. With each update of the network, the state of the inputs was set and the signals were propagated the number of steps equal to the precalculated depth of the network. In the GRN-driven variant, we allowed for recurrent connections and, therefore, the networks were no longer stateless during development and locomotion. Here, however, as the network graph would potentially contain cycles, with every network update, we propagated the signals in the network only by a distance of 1.
2.7. Evolution
Networks controlling development and determining gaits were encoded as a list of nodes with their respective types (input, output, and normal gene) and a list of connections. As our goal was to compare directly evolvability of a fitness-driven search with that of novelty search, we have performed repeated evolutionary runs using each of the two following algorithms.
2.7.1. NEAT Evolutionary Algorithm
As a method of fitness-driven search, we have employed the NEAT algorithm [neuroevolution of augmenting topologies (Stanley and Miikkulainen, 2002)], which is often considered the most successful method of evolving artificial neural networks (Mouret and Doncieux, 2011). It starts from simple topologies and grows them over evolutionary time through complexification. To do so efficiently, it relies on two mechanisms. First, it keeps tracks of new genes (new connections and new neurons) and uses history markers to perform a meaningful crossover between genomes, aware of which genes correspond to which in the two parents. Second, it uses speciation, with crossover occurring only within species (as it would likely be destructive otherwise). Speciation is based on the similarity between genomes, calculated by taking into account the number of disjoint and excess neurons and the difference between corresponding connection weights that both networks have. Finally, as means of promoting genetic diversity, it uses fitness sharing (the larger the species, the lower fitness score its members receive). While the NEAT approach turned out to be extremely fruitful and led to the development of multiple related [e.g., CPPN (Stanley, 2007), HyperNEAT (Stanley et al., 2009)] and hybrid approaches [e.g., Mouret and Clune (2012)] shown to improve over it in various domains, we used here the original version of the NEAT method. Given that it is simple, well understood and available out-of-the-box in various evolutionary optimization libraries, we think it establishes a sensible baseline for the performance of a fitness-driven search.
As a fitness function, we used the displacement of an animat’s center of mass between the time the body was found to be at rest after the simulation was started (to avoid profiting from relaxation under gravity, see also Section 2.5) and the final step of simulation:
where (xf, yf) represents the position of the animat’s center of mass at the end of locomotion stage, (xs, ys) represent its position when it came to rest after initial relaxation under gravity. The actuation bonus term ba was used only in the GRN-driven actuation experiments and was equal to:
where ucnt was the total number of network updates during the locomotion stage, ccnt was the number of cells in the embryo, and si,u was the state of the network output that modifies the resting lengths of springs attached to cell i at the time of update u. It represents a small bonus to the fitness for having some change occur at the actuators with subsequent network updates, and it was used to promote discovery of individuals that actuate. It had a maximum possible value of 1 in the case when each cell switched from maximum contraction to maximum expansion (or vice versa) with each subsequent update of network’s output during the locomotion stage.
Finally, p represents applied fitness penalties, where:
We used the MultiNEAT implementation of the NEAT algorithm (Chervenski and Ryan, 2014). The configuration file specifying the parameters of the library is linked within the reference.
2.7.2. Novelty Search
Lehman and Stanley (2011a) define novelty of a phenotype m as proportional to how sparsely the phenotype space surrounding m has been explored so far:
where μi is the i-th nearest individual to m out of k according to the distance metric d.
Introducing the novelty search algorithm into an existing, NEAT-based system required only replacing the fitness function computation with calculation of the novelty value, disabling the fitness sharing, introduction of the novelty archive that stores past novel individuals and the algorithm for dynamic updating of the novelty threshold value (the novelty value at which an individual is added to the archive). We chose to increase the threshold by 10% if more than eight individuals were added to the archive one after another and to decrease it by 10% if no individuals were added within 50 generations. We used the final coordinates of an animat’s center of mass P at the end of locomotion stage as its phenotypic representation, where P ∈ R2. We then used Euclidean metric as a measure of distance d between two phenotypes, with k = 15 [see equation (7)]. Therefore, the novelty of an individual was highest if it finished its movement in a location in which other individuals did not finish yet. Note that while the aquatic environment allowed to easily vary the phenotypic representation vector along both X and Y coordinate, in the terrestrial gait problem the variation could almost solely come from the X coordinate, as the horizontal movement of the body would be many times larger than the vertical, and we did not normalize each dimension in the phenotype characterization vector. Thus, novelty search algorithm was forced to introduce variation almost entirely by modifying the X coordinate.
Since novelty search required only the change of how the fitness function is calculated (by replacing it with a measure of novelty), we could keep the remaining properties and settings of both algorithms identical (including speciation for the meaningful crossover). Naturally, the fitness adjustments normally performed by NEAT (fitness sharing based on genetic similarity) were not applied in the case of novelty search as it would imply changing its core behavior. We used a population size of 300 individuals, and evolutionary runs lasted for 2000 generations. The initial population was created as a fully connected network with inputs directly connected to outputs and random weights.
3. Results
We compared the performance of the novelty search algorithm to the fitness-driven search (represented by the NEAT algorithm), using four different scenarios: we combined two separate tasks: evolution of aquatic and terrestrial gaits with two approaches to actuation. We used the same method of evaluating performance both in aquatic and terrestrial environments, that is, for NEAT-search experiments, fitness represented the displacement of the center of mass during locomotion stage and, in novelty search experiments, phenotype was characterized by the final location of an animat.
To allow for meaningful comparisons between the two approaches, for each of the four experimental settings, we repeated evolution using a given search algorithm 20 times, using different random seed values. To provide the reader with an overview of what kinds of designs emerge in our system, we first present examples of evolved solutions. We then compare the performance of each algorithm. Finally, we analyze how each of the algorithms explores the phenotypic space in order to understand the reason behind their different behavior and performance in this problem domain.
3.1. Evolved Morphologies
With only two exceptions, all evolutionary runs resulted in individuals capable of producing repetitive gaits in their target environments. The two exceptions were a result of fitness-driven search attempting to evolve GRN-controlled gaits and occurred both in the swimming and walking tasks. The terrestrial individual was vertically elongated and would fall after expanding its muscle to its side at the beginning of the simulation. A swimming individual would rapidly contract its body once and rely on the momentum produced by this single contraction. Thus, none of these individuals evolved a cyclic motion pattern. As this was only possible in the case of GRN-controlled actuation, this type of local minima would not be an issue in the experiments relying on oscillator-driven actuation.
In the case of oscillator-driven actuation and aquatic gait evolution, morphologies produced by each type of evolutionary search were found to be visually very similar: best evolutionary runs resulted in individuals who had elongated, snake-like morphologies, and moved with undulatory gaits. Wider, more fish-like morphologies also emerged, yet the runs that produced them reached lower fitnesses. Comparing morphologies obtained using fitness driven (Figure 3A) with individuals obtained using novelty search (Figure 3B), there was no obvious visual difference, though the top five best-performing individuals of the two experiments were obtained with novelty search (three of which are shown in Figure 3B). Similarly, in the case of ground-based locomotion (Figure 4), all evolutionary experiments converged to similar morphologies, in that case supporting themselves on two (occasionally more) appendages. Here, again, no immediately obvious visual difference was observed between novelty- and fitness-driven searches, although one more time, the top three individuals came from the novelty search experiment.
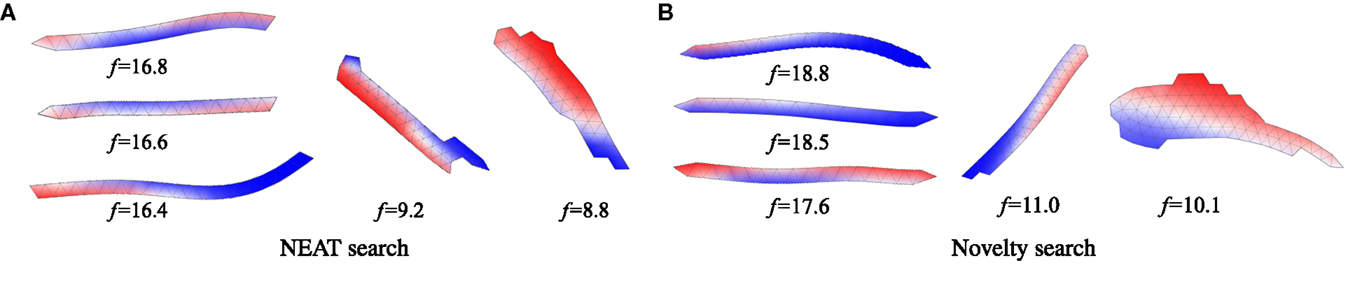
Figure 3. Morphologies of swimming individuals relying on oscillator-driven actuation evolved using NEAT (A) and novelty search (B) and their corresponding fitnesses. Best three individuals and two worst individuals obtained using each search method are shown. Colors indicate evolved phase shifts of muscular contractions, blue corresponds to −π, white to 0 and red to π. Example motion video can be accessed online: http://youtu.be/Gb-H_qy8kVQ.
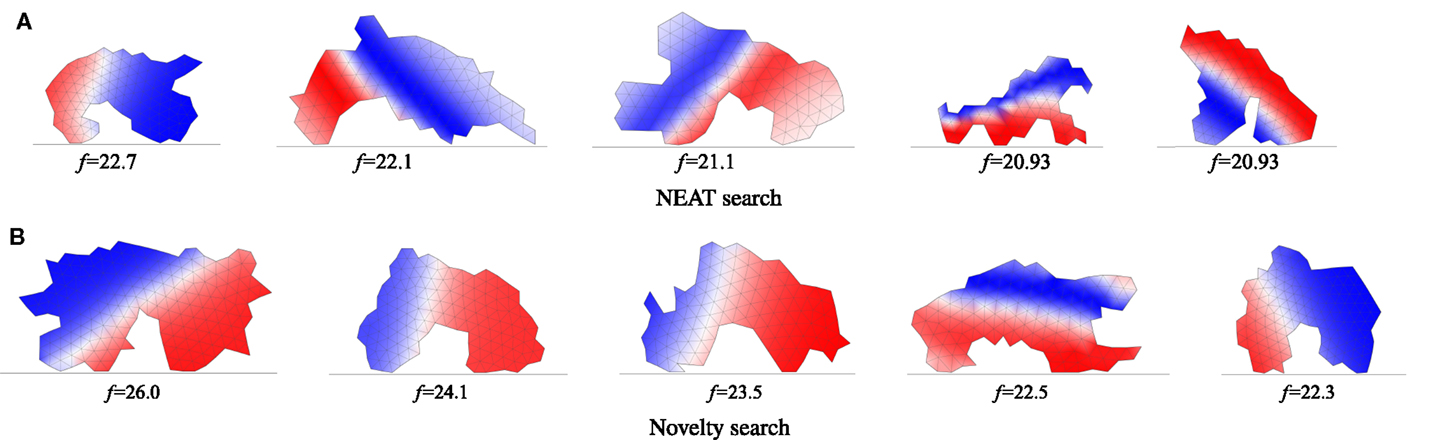
Figure 4. Morphologies of terrestrial individuals relying on oscillator-driven actuation evolved using NEAT (A) and novelty search (B) and their corresponding fitnesses. The five best individuals obtained using each search method are shown. Colors indicate evolved phase shifts of muscular contractions (blue) or expansions (red). Example motion video is linked in the caption of Figure 2.
Similarly, in the experiments with GRN-controlled terrestrial gaits, the results obtained using each search method were visually similar (cf. Figures 5A,B), with individuals running on two “legs” and highly convergent morphologies. The shapes were, however, visually quite different from those obtained with the oscillation-driven actuation approach. Likewise, in the case of individuals evolved for swimming, both search algorithms produced similar morphologies (Figures 5C,D), though this time a wider and more fish-like type of morphology dominated. Two exceptions displaying snake-like morphologies, however, emerged in the fitness-driven search experiments. They were also the two most successful swimmers obtained in both GRN-driven actuation experiments. While the investigation of how different types of genetic control over development and behavior lead to different shapes is beyond the scope of this paper, we note that a likely significant factor were different time constants determining how quickly muscular contractions could occur in each of the two types of actuation mechanisms. In any case, differences in evolutionary trajectories that emerge depending on the type of genetic control employed were the very reason we were interested in testing if novelty search behaves consistently in different setups.
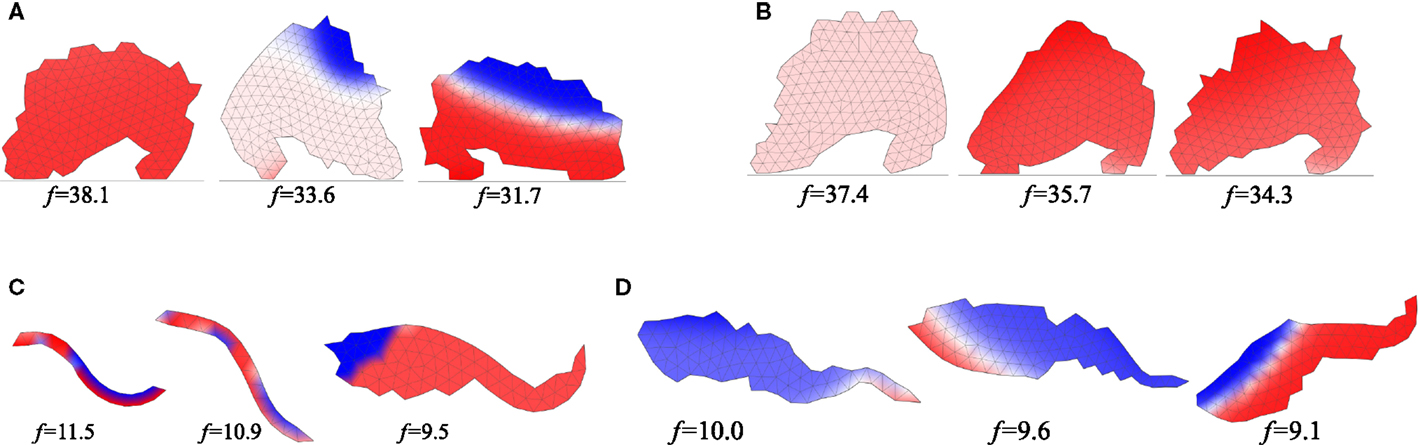
Figure 5. Morphologies of three best swimming (top) and walking individuals (bottom) evolved with GRN-driven gait control and the two search algorithms. Three best individuals for each type of experiment are shown. Colors indicate temporal contraction of a body region (blue) or expansion (red). (A) NEAT search, (B) novelty search, (C) NEAT search, (D) novelty search.
3.2. Performance: Oscillator-Driven Actuation
Figure 6A compares the performance of the two investigated search algorithms on the problem of evolving aquatic animats using the simpler approach to control. We found that novelty search clearly outperformed the NEAT algorithm (median of expected achieved distance was different, Wilcoxon two-tailed rank-sum test, p = 0.01). On average, novelty search not only produced better individuals given 2000 generations but would also do so regardless on the number of generations.
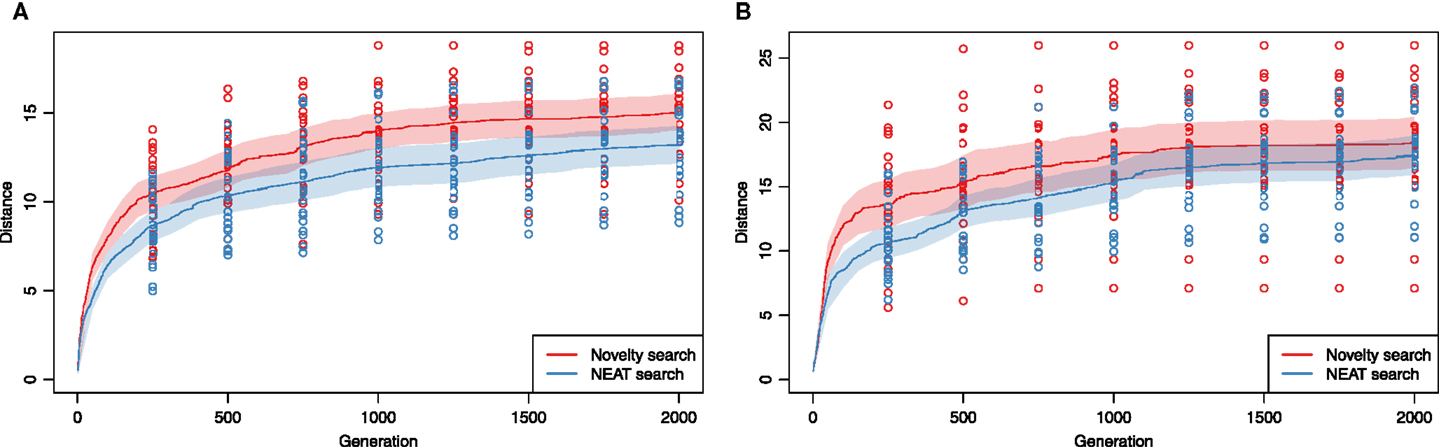
Figure 6. Oscillator-driven actuation: performance of novelty search compared to the NEAT algorithm on the problem of co-evolving morphology and controller of soft-bodied, swimming (A) and walking (B) animats. Solid lines show mean best fitness in a given generation from 20 evolutionary runs of each type of experiment. Dashed lines show 95%, bootstrapped confidence intervals for the means. (A) Aquatic environment, (B) terrestrial environment.
To investigate whether the advantage of novelty search extended to another problem, we next compared evolvability of terrestrial gaits. As novelty search could now only act on the first dimension of the phenotypic representation vector (i.e., the X coordinate of the final position), we expected novelty search advantage to diminish as the measure of novelty becomes largely synonymous with the objective fitness. Indeed, after 2000 generations (Figure 6B), novelty search seemed to hold only a small advantage over NEAT and, in fact, the median of expected achieved distance in generation 2000 was no longer significantly different (Wilcoxon two-tailed rank-sum test, p = 0.30). On average, novelty search did, however, produce higher fitness individuals regardless of the number of generations and was much faster at finding good swimmers early on (e.g., the expected median fitness of best individuals at generation 400 is significantly better, p = 0.02).
Overall, we found these results surprising since the NEAT method is by itself a state of the art evolutionary algorithm specifically tuned to evolve network topologies and employs various techniques that prevent premature convergence. Also, while developing the model, we tuned the parameters of the system while optimizing its performance under the NEAT algorithm [see, e.g., fitness function tweaks, equations (5) and (6)], which was likely to introduce a bias in favor of this search method. Nonetheless, a direct and trivial replacement of NEAT with novelty search resulted with a clear improvement, even though novelty search did not even attempt to explicitly optimize for distances.
3.3. Performance: GRN-Driven Actuation
To see if the above results hold for a more complex, but more powerful version of the model, we performed an analogous pair of experiments, this time with development controlled by a recurrent network and motion patterns generated by continuous activity of the gene regulatory network. Here, a cyclic pattern of locomotion was no longer a default and evolution had to discover that repetitive patterns of actuation are the way to produce sustained gaits. Other than increasing the search space considerably, we suspected this scenario to be less suited for novelty search, as new final positions could now be easily generated by producing movement patterns that sustain themselves only through part of the total evaluation time. To our surprise, the average performance of novelty search was one more time higher in both aquatic (Figure 7A) and terrestrial environment (Figure 7B). In the case of the former, the advantage of novelty search was significant during the first few hundreds of generations (difference in medians at generation 800, p = 0.008), but decreased over evolutionary time (the medians were no longer significantly different at generation 2000).
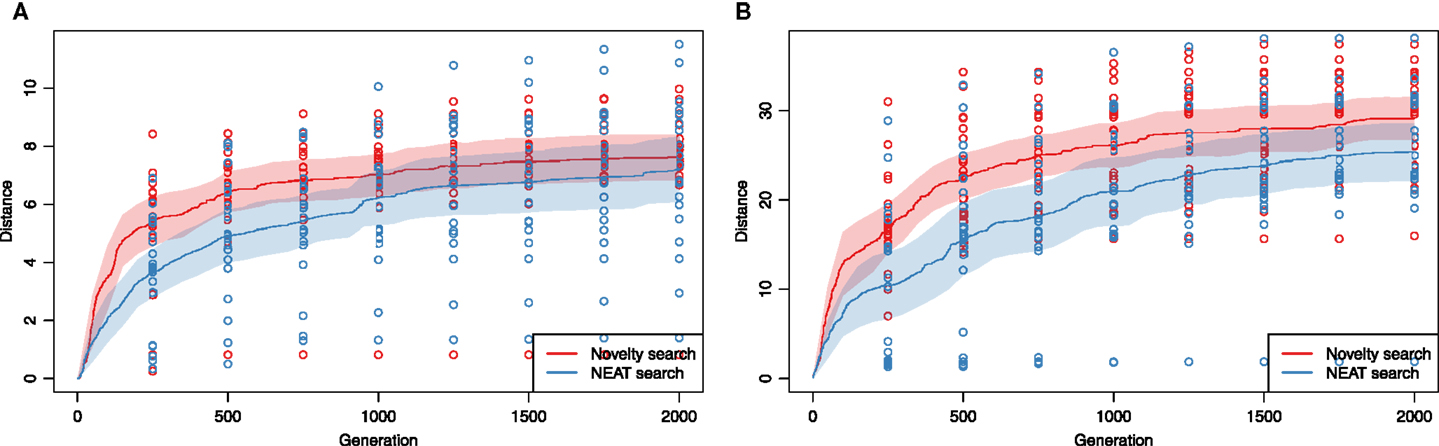
Figure 7. GRN-driven actuation: performance of novelty search compared to the NEAT algorithm on the problem of co-evolving morphology and controller of soft-bodied, swimming (A) and walking (B) animats. Solid lines show mean best fitness in a given generation from 20 evolutionary runs of each type of experiment. Dashed lines show 95%, bootstrapped confidence intervals for the means. (A) Aquatic environment, (B) terrestrial environment.
The final experiment in which GRN-controlled terrestrial animats were evolved produced similar results: novelty search converged faster and produced higher average fitnesses. The medians were clearly different at generation 800 (p = 0.01), but again, not significantly so at generation 2000 (p = 0.10).
Overall, seeing how novelty search found good individuals much faster than NEAT search and sustained average advantage throughout the full length of evolutionary runs, we consider these results consistent with superiority of novelty search method in this problem domain.
3.4. Exploration of the Phenotypic Space
To understand how novelty search improves over NEAT in our problem domain, we visualized how the phenotypic space is being explored by each of the algorithms in the case of evolving swimming animats using oscillator-driven actuation. Although a direct visualization of complex phenotypic space would be impossible, we chose to visualize each phenotype by using the same representation that was employed to compute phenotypic distances in novelty search, i.e., as points in R2 corresponding to the final locations of individuals. This allowed us to plot the final positions of all individuals who existed during a given evolutionary run on a surface. To reduce visual clutter, we have plotted only 1% of (randomly sampled) individuals. We selected two runs from each type of experiment for visualization: a run that led to the best individual obtained in a given type of experiment and a median quality individual (the best individual having fitness below the median). Inspection of the remaining runs confirmed that the patterns observed in the selected examples are representative for the experiments as a whole. The comparative results for each search algorithm are shown in Figure 8. It can be immediately seen that the way each algorithm has explored the space of possible phenotypes is qualitatively different. While the novelty search progressively discovers solutions that swim in every possible direction, the NEAT algorithm shows a clear focus toward exploring only a subregion of the phenotypic space, with individuals moving in a similar direction. This exploitation of a single direction is most likely explained by population becoming dominated by descendants of a particular good design that happened to be successful early on. This then leads to subregions being overexplored through the creation of large numbers of individuals who differ only slightly in their final position. On the other hand, novelty search algorithm clearly explores the phenotypic space in a much more even manner, without particular motion directionality and mostly avoiding overexploration of phenotypic subregions. This interpretation is further reinforced by the overlaid visualization of the trajectory of the best (in terms of objective fitness) individual in every generation (solid line in Figures 8A,B). While in the fitness-driven runs, subsequent best individuals are close neighbors in the phenotypic space, novelty search is capable of exploring different scenarios at the same time, visible as long “jumps” through the phenotypic space between generations. We note, however, that these jumps are unlikely to imply that mutations caused large phenotypic changes, rather, parallel exploration of diverse designs allows new best individuals to emerge in any of the regions of the phenotypic space that are being explored.
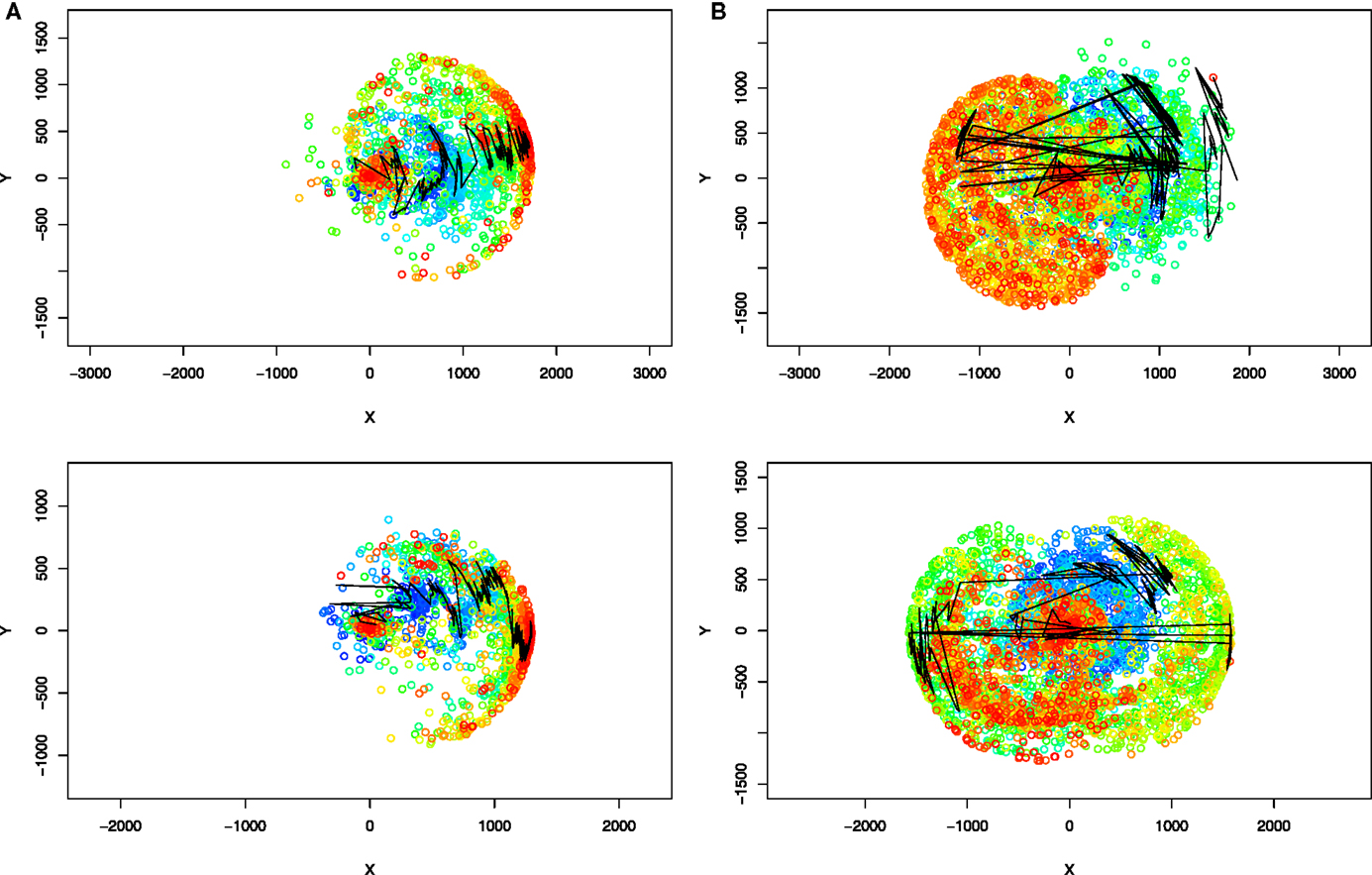
Figure 8. Evolution of aquatic animats: comparison of phenotype space coverage over evolutionary time when evolving with two search algorithms in the experiments with oscillation-driven actuation (see Figure 6A for corresponding fitness plots). The top row corresponds to the best run in each type of experiment, and the bottom row corresponds to the run that resulted in the median quality individual. Each point in a plot represents the final location of an individual who was evaluated during a given evolutionary run (a randomly chosen 1% individuals is shown). The color of a circle represents generation at which an individual was created: blue correspond to the beginning of a run, red to the end, and green to the middle. The line connects points corresponding to the best individual (in terms of objective fitness value) in every generation. (A) NEAT search, (B) novelty search.
Next, we attempted to visualize how each search algorithm behaved on the problem of evolving terrestrial animats. Due to the 1-dimensional characterization of phenotypes, we were able to more easily visualize the progression of the populations over evolutionary times (Figure 9). Here, fitness-driven search focused almost entirely on either left or right direction of motion, determined at the beginning of an evolutionary run. Also, most of the individuals being created seem to be minor modifications to the winning design, visible as a high-density region (dark blue) overlapping with the red line representing best solution found so far. On the other hand, novelty search seems to explore scenarios in which individuals move either left or right evenly, and it was not uncommon to observe how a winning left-running solution is replaced by right-running one (or vice versa), often multiple times during a single evolutionary run.
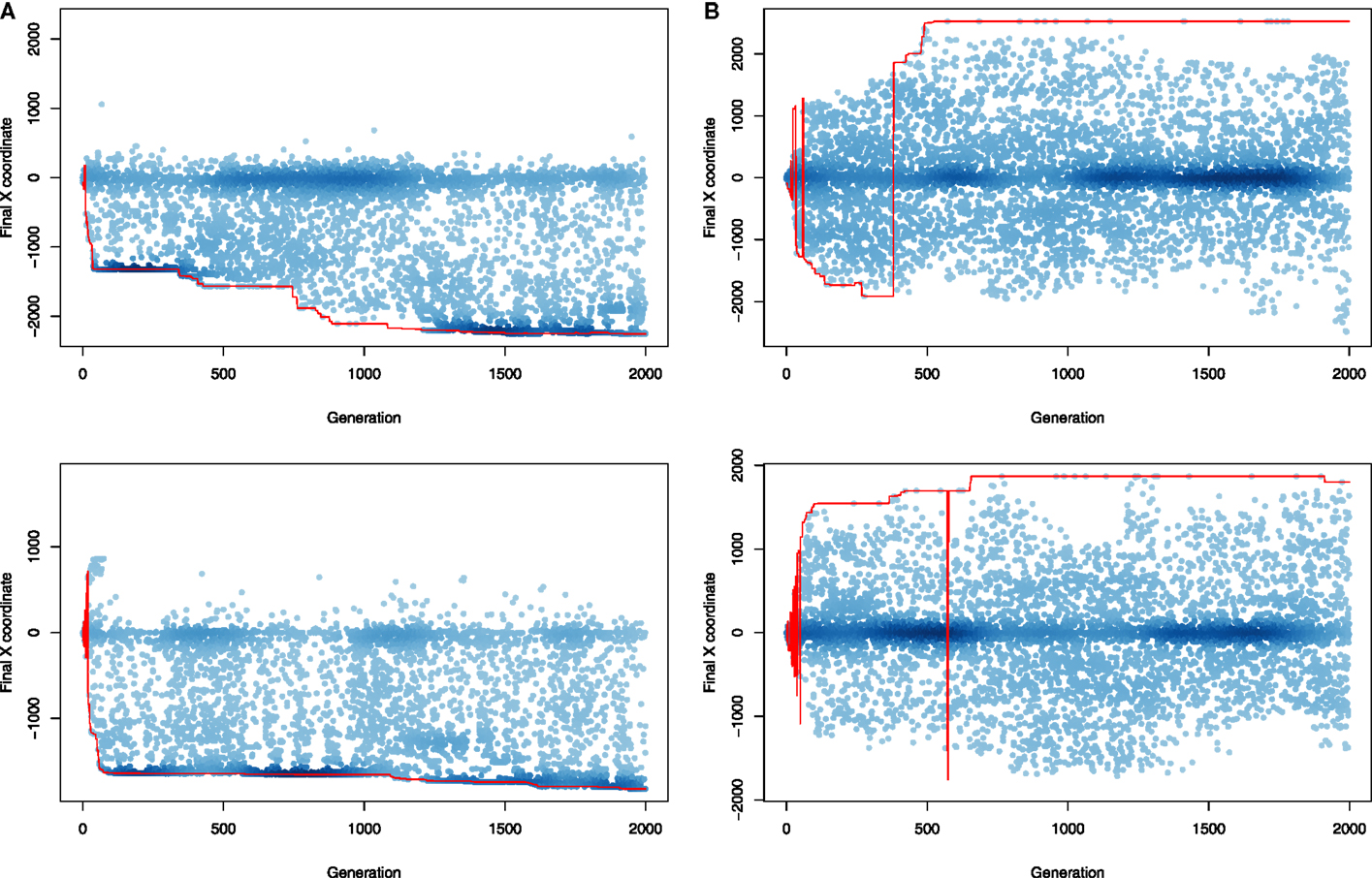
Figure 9. Evolution of terrestrial animats: comparison of phenotype space coverage over evolutionary time when evolving with two search algorithms in experiments with oscillation-driven actuation (see Figure 6B for corresponding fitness plots). The top row corresponds to the best run in each type of experiment, and the bottom row corresponds to the run that resulted in the median quality individual. Each point in a plot represents the final position of an individual who was evaluated during a given evolutionary run (a randomly chosen 1% individuals is shown). Color intensity corresponds to points density. The line connects points corresponding to the best individual (in terms of objective fitness value) in every generation. (A) NEAT search, (B) novelty search.
The observation above is further supported by inspection of the contents of the novelty search archives in novelty-driven runs (consisting of individuals who were found to be novel at the time they were created, Figure 10). It can be seen how, in the case of swimming individuals, novelty search discovers new concentric “layers” of solution space, rather than focusing on exploitation of a particular subregion of the search space (which, in that case, would manifest as discovering subsequent solutions that move roughly in the same direction). In the case of walking individuals, during the first few hundred generations, subsequent novel individuals tend to have higher objective fitnesses and are found both among left-running and right-running individuals, without any clear preference. After “low-hanging fruit” solutions are found, novelty archive is slowly populated with individuals ending at almost any possible location in the region between current best left-running and right-running solution. Ultimately, this also leads to discovering improvements to the best individuals as well.
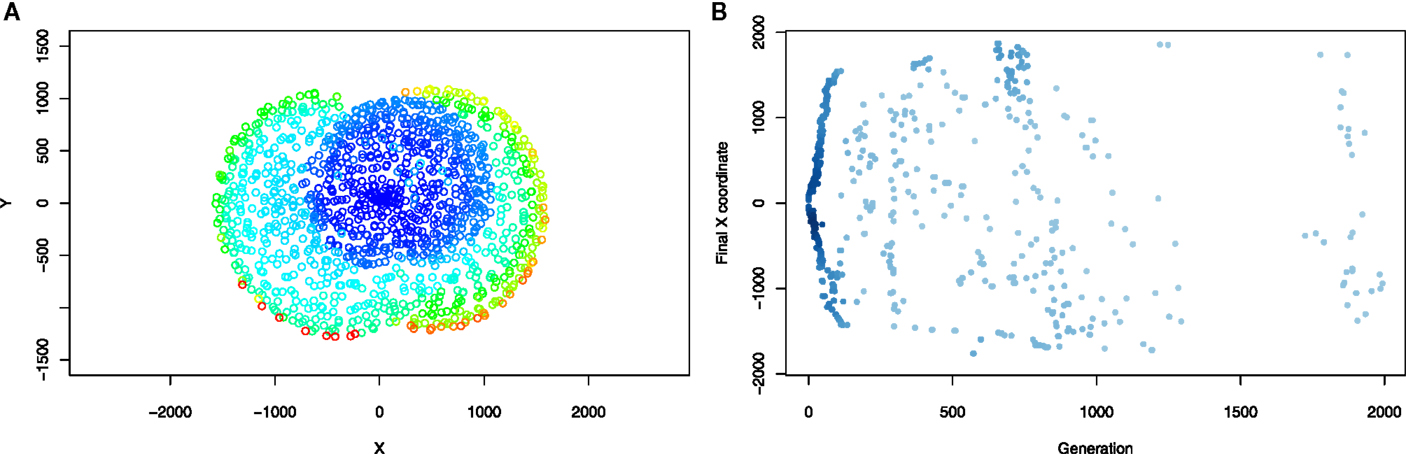
Figure 10. The contents of novelty archives in runs shown in Figures 8 and 9 (bottom rows) after 2000 generations. Points represent individuals in the same manner as in the Figures 8 and 9. (A) Aquatic environment, (B) terrestrial environment.
Finally, we have inspected evolutionary runs that relied on the more complex, GRN-driven actuation and found out that they displayed qualitatively similar properties (not shown).
3.5. Phenotypic Diversity in Populations
Phenotypic diversity is a necessary condition of an evolutionary process and hence sustaining it is of primary importance to many evolutionary algorithms. The NEAT algorithm attempts to sustain diversity at the genetic level by using speciation and fitness sharing, in which genotypes grouped into species receive lower fitnesses as the species size increases, consequently promoting novel genotypes. Grouping into species is based on the genetic distance between individuals. The genetic distance, however, does not necessarily reflect phenotypic distance (in the extreme case, neutral mutations lead to two different genomes with identical phenotypes). To understand what kind of population structure emerges during evolution, we investigated fitness distributions in the final generations and observed radical differences between the two search algorithms. Populations evolved using NEAT would progressively lose fitness diversity over evolutionary time, as the populations were slowly more and more dominated by an elite individual and its variations that differ only slightly in fitness. This pattern was universally observed in all types of experiments, as confirmed by averaging normalized fitness distributions in the final generation from independent evolutionary runs (Figure 11). The difference behavior of these algorithms can be understood if we consider that novelty search, by its very definition, attempts to diversify phenotypes. At the same time, developmental systems are known to evolve toward both environmental and mutational robustness, a process known as genetic canalization [see, e.g., Federici and Ziemke (2006), Basanta et al. (2008), Andersen et al. (2009), and Joachimczak and Wróbel (2012b)], which likely drives the phenotypic diversity down.
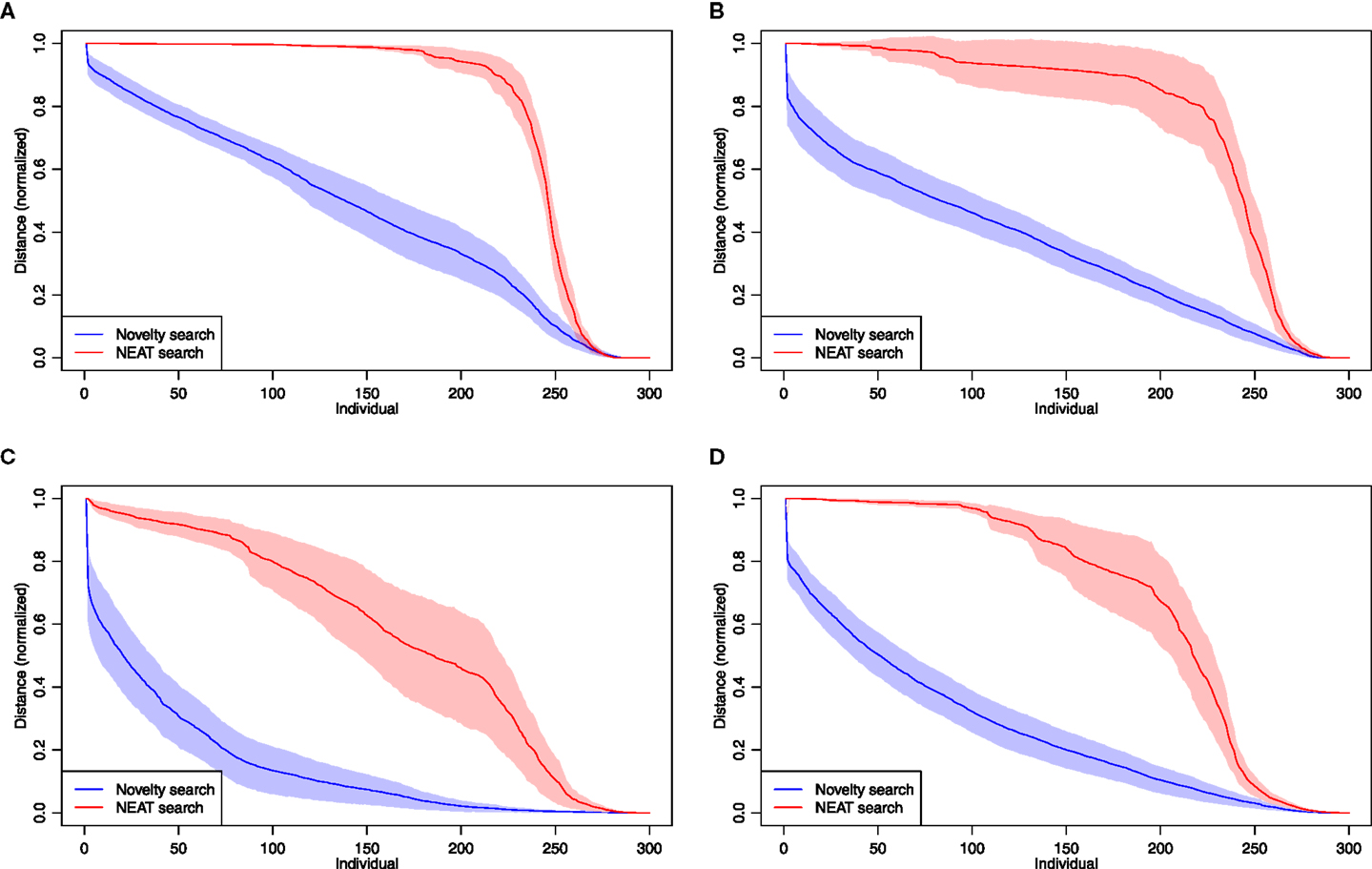
Figure 11. Normalized fitness distributions in populations at generation 2000 collected from 20 independent evolutionary runs of each of the four experiment types. (A) Aquatic environment (oscillator-driven actuation), (B) aquatic environment (GRN-driven actuation), (C) terrestrial environment (oscillator-driven actuation), (D) terrestrial environment (GRN-driven actuation).
3.6. Morphological Diversity
While the results discussed in the Section 3.4 clearly show that novelty search explores the space of possible solutions in a more even and thorough manner than the fitness-driven search, our assessment of phenotypic diversity was based solely on the final position of an animat being evaluated. Although the quality of solutions obtained with novelty search was also higher on average, we were interested whether its success can be attributed to actually having explored a greater range of potential morphologies. After all, a larger diversity of final positions does not automatically imply a larger diversity of morphologies. In particular, larger diversity of final positions could simply be a result of mutations that only influence behavior control (e.g., resulting in a change of swimmer’s angle), providing evolution with a cheap and endless source of phenotypic variation. This would, however, be strongly against our goal of creating a system that discovers innovative morphologies and controllers without any prior knowledge of desired solutions, as being able to explore a large range of morphologies is essential to its creativeness.
Measuring the diversity of arbitrary morphologies requires a way to quantify dissimilarities between them. This is generally a non-trivial problem that can be approached in multiple ways, taking things like scale or rotation invariance into consideration [e.g., through the use of shape histograms (Ankerst et al., 1999)]. Since our goal here was mainly to make sure that the higher phenotypic diversity of the novelty search scenario is not just a result of evolution tweaking the controllers, we decided to rely on a much simpler approach. We calculated diversity of individuals’ sizes (represented by their body cell count) during an evolutionary run. While a very crude approach: a potentially extremely large numbers of morphologies can be made of the same number of cells, body sizes are sometimes used in biological [e.g., Imroze and Prasad (2011)] and artificial embryogeny [e.g., Matos et al. (2009)] experiments as a way to estimate phenotypic diversity. Here, we expected that if morphologies tend to repeat more often in some experiments, we should also observe more frequent repetitions of identical cell counts in the populations. Thus, as a simple proxy of morphological diversity, we decided to apply one of the measures commonly employed to calculate ecological diversities, namely the Shannon entropy, to a set of body sizes that occur throughout an evolutionary run. For each run, we calculated Shannon entropy of body sizes over the whole evolutionary history:
where was the set of sizes (numbers of cells in the body) of all animats that existed during a given evolutionary run and were considered viable (i.e., their fitness was not zero). We calculated morphological diversity for all evolutionary runs and all types of experiments that we performed and present summary results in Figure 12. Regardless of whether we used the oscillator-driven actuation or the more complex, GRN scenario, novelty search produced much higher morphological diversity, with the difference being even more pronounced in the latter case. This result strongly suggests that novelty search indeed manages to produce significantly higher morphological diversity and increased variation of animat final positions was associated with an actually higher diversity of morphologies explored.
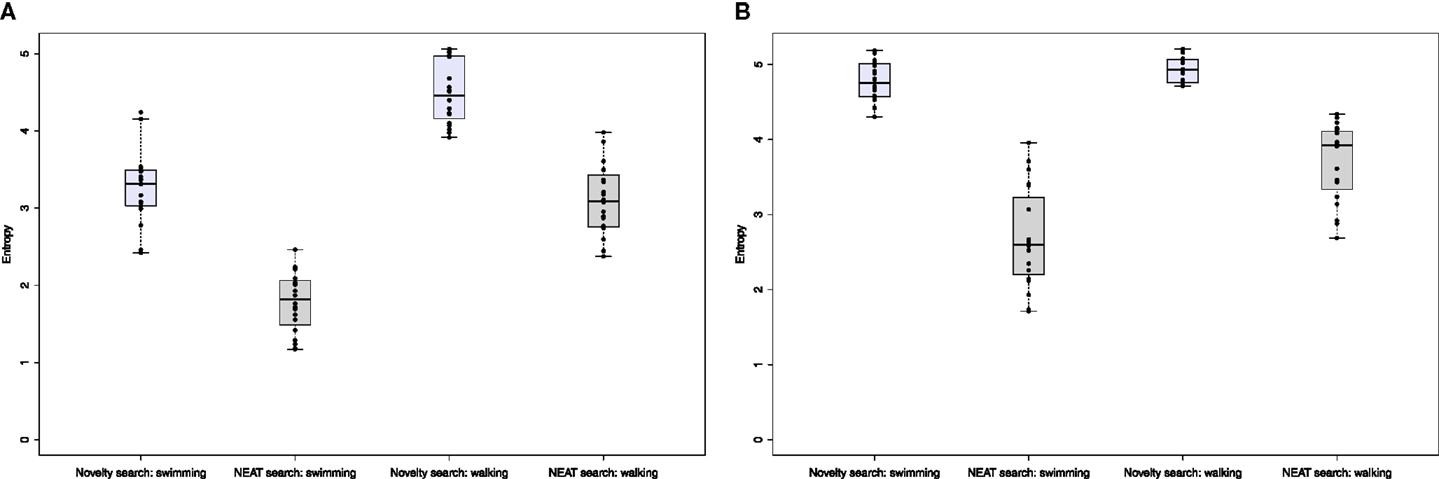
Figure 12. Measuring morphological diversity: the entropy of body sizes of all viable individuals who existed over evolutionary time. The box plots show the median and quartiles for entropies calculated for 20 independent evolutionary runs of each type of experiment. Whiskers extend to the most extreme data point that is not more than 1.5 IQR from the box. Points corresponding to each experiment are overlaid. (A) Oscillator-driven actuation, (B) GRN-driven actuation.
4. Discussion and Future Work
Throughout our work, we aim to harness the creative power of the evolutionary process in order to either inspire or to fully replace a human designer. While we were able to reach very promising results using the classical, fitness-driven evolutionary search algorithm, the large and complex search space stemming from the weakly constrained range of possible morphologies, and complex interactions between morphologies and controllers made evolutionary runs expensive and prone to being stuck in local minima. After introducing a very low cost change to the search method, a one that abandons optimization for the fitness altogether, we were surprised to see it immediately improve over the fitness-driven search, even though the novelty search method was not explicitly optimizing for gait performance.
A more extensive analysis revealed that the result was robust in respect to two types of tasks and two versions of control mechanism that we used; in all investigated scenarios, novelty search produced on average higher fitness individuals. The advantage of novelty search was especially visible within the first few hundreds of generations and given limited time for an evolutionary run, it was clearly superior at finding gaits. Performing longer evolutionary experiments (2000 generations) allowed the fitness-driven search to get closer to the results obtained with novelty, though it remained, on average, inferior. The reduced difference in performance of each algorithm given longer search can be explained by the fact that each algorithm ultimately attempts to converge on similar designs; indeed, the best solutions obtained using each search method had similar morphologies.
Importantly, our analysis revealed how both algorithms explore the space of possible solutions very differently: novelty search was far better at maintaining population diversity and explored the space of possible solutions in a much more even manner. Fitness-driven search, on the other hand, despite the use of mechanisms that promote genotypic diversity would heavily focus on subregions of the phenotypic space. Furthermore, our analysis suggests that novelty search, despite simply searching for novel end positions of locomoting animats, actually evaluated a more diverse set of morphological designs.
As novelty search is believed to show its strengths in deceptive fitness landscapes, this also suggests that the problem we are working on, i.e., evolution of morphologies and controllers based on artificial development exhibits a highly deceptive fitness landscape. Indeed, one potential source of such a deceptiveness could be constant interactions between the controller and morphology being simultaneously optimized. More precisely, when a controller becomes fine-tuned to a given morphology over evolutionary time, many potentially useful modifications of this morphology will likely turn out to be detrimental, as they will lead to a mismatch between the new morphology and a controller. Thus, only after fine-tuning of the latter, the performance of a modified morphology can be ascertained: a new hill of increased fitness landscape can only be accessed by crossing a lower fitness valley, a telltale of a deceptive fitness landscape.
Another reason we suspect novelty search turned out to be highly successful on this problem may be the difficulty of sustaining phenotypic diversity when using development-based encodings. Developmental systems are known to evolve toward being robust to perturbations, both environmental and mutational [see, e.g., Federici and Ziemke (2006), Basanta et al. (2008), Andersen et al. (2009), and Joachimczak and Wróbel (2012b)], and this robustness is one of the very reasons behind the interest in them. However, the propensity to sustain phenotype despite genetic perturbations should also mean that such systems are partially robust to methods that attempt to boost genetic diversity (e.g., through fitness sharing, as in this work), weakening their effect. Since novelty search promotes only the phenotypic novelty, it is immune to this effect, rewarding only increase in phenotypic diversity. This suggests that either novelty search or methods of promoting phenotypic diversity should be, in general, a more meaningful way to increase evolvability of developmental systems and we hope to investigate this more in depth in our future work. Furthermore, recent evidence from the domain of evolving robot behaviors (without morphological evolution) suggests that promoting phenotypic diversity also improves search performance (Gomez, 2009; Mouret and Doncieux, 2011; Trujillo et al., 2011; Lehman et al., 2013). As the presented system deals both with the evolution of development and evolution of behavior, it suggests that phenotypic diversity maintenance may have contributed at both levels.
Lacking a predefined objective, pure novelty search is unlikely to succeed at higher complexity tasks and the reason it performs so well at gait evolution is likely related to the coupling between novelty measure and the distance measure: exploring further areas of the phenotypic space means finding solutions of higher objective fitness. It has, however, already been shown that the performance of novelty search can be improved on certain problems if a novelty measure is combined with an objective fitness function through the use of multi-criteria optimization (Mouret and Doncieux, 2011; Lehman et al., 2013). Hence, as a straightforward extension of the current work, we plan to incorporate an objective fitness function into the search algorithm, through the use of a Pareto-based multi-objective approach. We hope that this will allow us to evolve robots capable of performing more complex and multi-step behaviors, such as reshaping to crawl through an opening or grabbing objects with an elastic appendage. Furthermore, a fitness component would enable evolution of behaviors that optimize energy used to perform a task or the amount of active and passive material in a design [e.g., as in Cheney et al. (2013)]. Finally, having observed the extreme importance of sustaining phenotypic diversity in an artificial embryogeny model, we are interested in finding better ways of generating the initial population. After all, the morphological diversity of multicellular life did not emerge out of random gene regulatory networks but was preceded by an extremely long period of complexification of unicellular forms. Thus, one way we hope we can further improve evolvability is to first discover promising regions of genotypic space by pre-evolving initial population toward general morphological diversity, and only later attempting to co-evolve the form and behavior. This would require developing a much less simplistic measure of morphological diversity than the proxy used in Section 3.6 but would also enable us to perform direct comparisons of morphological diversities produced by different search algorithms.
With the low-effort modifications needed to adapt an objective fitness-driven genetic algorithm into novelty search and limited number of parameters that need to be set up (novelty search being able to adjust most of its parameters dynamically), we believe novelty search is likely to be of high utility for encodings based on artificial development in general. The results presented in this work also show the overall importance of focusing on maintaining phenotypic diversity in systems with highly indirect genotype–phenotype mappings, novelty search being only one of the easiest methods to achieve it.
Author Contributions
Concept and design of experiments: MJ, RS, and TA. Implementation, running experiments, and analysis: MJ. Writing paper: MJ, RS, and TA.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the Japan Society for the Promotion of Science (JSPS) through the JSPS Fellowship for Foreign Researchers and JSPS KAKENHI Grant Number 26-04349. High-performance computing resources were provided by the Interdisciplinary Center for Molecular and Mathematical Modeling (ICM, University of Warsaw) and the Tri-city Academic Computer Center (TASK). CGAL library (CGAL, 2015) was used.
Footnote
References
Andersen, T., Newman, R., and Otter, T. (2009). Shape homeostasis in virtual embryos. Artif. Life 15, 161–183. doi: 10.1162/artl.2009.15.2.15201
Ankerst, M., Kastenmüller, G., Kriegel, H.-P., and Seidl, T. (1999). “3D shape histograms for similarity search and classification in spatial databases,” in Advances in Spatial Databases, Volume 1651 of LNCS, eds R. H. Güting, D. Papadias, and F. Lochovsky (Berlin: Springer), 207–226. doi:10.1007/3-540-48482-5_14
Auerbach, J. E., and Bongard, J. C. (2012). “On the relationship between environmental and mechanical complexity in evolved robots,” in Artificial Life 13, eds C. Adami, D. M. Bryson, C. Ofria, and R. T. Pennock (Cambridge, MA: MIT Press), 309–316. doi:10.7551/978-0-262-31050-5-ch041
Basanta, D., Miodownik, M., and Baum, B. (2008). The evolution of robust development and homeostasis in artificial organisms. PLoS Comput. Biol. 4:e1000030. doi:10.1371/journal.pcbi.1000030
Boddhu, S. K., and Gallagher, J. C. (2010). Evolving neuromorphic flight control for a flapping-wing mechanical insect. Int. J. Intell. Comput. Cybern. 3, 94–116. doi:10.1108/17563781011028569
Bongard, J. C., and Pfeifer, R. (2003). “Evolving complete agents using artificial ontogeny,” in Morpho-Functional Machines: The New Species, eds F. Hara and R. Pfeifer (Tokyo: Springer-Verlag), 237–258. doi:10.1007/978-4-431-67869-4_12
Burton, E. (2007). Soda Constructor. Available at: http://www.sodaplay.org
Carroll, S., Grenier, J., and Weatherbee, S. (2004). From DNA to Diversity: Molecular Genetics and the Evolution of Animal Design, 2nd Edn. Malden, MA: Wiley-Blackwell.
CGAL. (2015). Computational Geometry Algorithms Library. Available at: http://www.cgal.org
Chan, V., Park, K., Collens, M. B., Kong, H., Saif, T. A., and Bashir, R. (2012). Development of miniaturized walking biological machines. Sci. Rep. 2, 857. doi:10.1038/srep00857
Cheney, N., MacCurdy, R., Clune, J., and Lipson, H. (2013). “Unshackling evolution: evolving soft robots with multiple materials and a powerful generative encoding,” in Proc. of the 15th Annual Conference on Genetic and Evolutionary Computation, GECCO ‘13 (New York, NY: ACM), 167–174. doi:10.1145/2463372.2463404
Chervenski, P., and Ryan, S. (2014). MultiNEAT. Available at: http://multineat.com configuration file: http://pastebin.com/ZPNTa6kQ
Cuccu, G., and Gomez, F. (2011). “When novelty is not enough,” in Applications of Evolutionary Computation, Volume 6624 of LNCS, eds C. Di Chio, S. Cagnoni, C. Cotta, M. Ebner, A. Ekárt, A. I. Esparcia-Alcázar et al. (Berlin: Springer), 234–243. doi:10.1007/978-3-642-20525-5_24
Federici, D., and Ziemke, T. (2006). “Why are evolved developing organisms also fault-tolerant?,” in From Animals to Animats 9: Proc. of the 9th International Conference on Simulation of Adaptive Behaviour (SAB 2006), Volume 4095 of LNCS (Berlin: Springer), 449–460.
Gomes, J., Urbano, P., and Christensen, A. (2013). Evolution of swarm robotics systems with novelty search. Swarm Intell. 7, 115–144. doi:10.1007/s11721-013-0081-z
Gomez, F. J. (2009). “Sustaining diversity using behavioral information distance,” in Proc. of the 11th Annual Conference on Genetic and Evolutionary Computation, GECCO ‘09 (New York, NY: ACM), 113–120.
Hiller, J., and Lipson, H. (2012). Automatic design and manufacture of soft robots. IEEE Trans. Robot. 28, 457–466. doi:10.1109/TRO.2011.2172702
Hornby, G., Lohn, J. D., and Linden, D. S. (2010). Computer-automated evolution of an X-band antenna for NASA’s space technology 5 mission. Evol. Comput. 19, 1–23. doi:10.1162/EVCO_a_00005
Imroze, K., and Prasad, N. G. (2011). Mating with large males decreases the immune defence of females in drosophila melanogaster. J. Genet. 90, 427–434. doi:10.1007/s12041-011-0105-7
Joachimczak, M., Kowaliw, T., Doursat, R., and Wróbel, B. (2013). Evolutionary design of soft-bodied animats with decentralized control. Artif. Life Robot. 18, 152–160. doi:10.1007/s10015-013-0121-1
Joachimczak, M., Suzuki, R., and Arita, T. (2014). “Fine grained artificial development for body-controller coevolution of soft-bodied animats,” in Artificial Life 14: Proc. of the 14th International Conference on the Synthesis and Simulation of Living Systems (Cambridge, MA: The MIT Press), 239–246. doi:10.7551/978-0-262-32621-6-ch040
Joachimczak, M., Suzuki, R., and Arita, T. (2015). “From tadpole to frog: artificial metamorphosis as a method of evolving self-reconfiguring robots,” in Proc. of the 13th European Conference on the Synthesis and Simulation of Living Systems (ECAL 2015), eds P. Andrews, L. Caves, R. Doursat, S. Hickinbotham, F. Polack, S. Stepney, et al. (Cambridge, MA: The MIT Press), 51–58. doi:10.7551/978-0-262-33027-5-ch012
Joachimczak, M., and Wróbel, B. (2011). “Evolution of the morphology and patterning of artificial embryos: scaling the tricolour problem to the third dimension,” in Advances in Artificial Life. Darwin Meets Von Neumann: Proc. of the 10th European Conference on Artificial Life (ECAL 2009), Volume 5777 of LNCS (Berlin: Springer), 35–43.
Joachimczak, M., and Wróbel, B. (2012a). “Co-evolution of morphology and control of soft-bodied multicellular animats,” in Proc. of the 14th International Conference on Genetic and Evolutionary Computation, GECCO ‘12 (New York, NY: ACM), 561–568. doi:10.1145/2330163.2330243
Joachimczak, M., and Wróbel, B. (2012b). Evolution of robustness to damage in artificial 3-dimensional development. BioSystems 109, 498–505. doi:10.1016/j.biosystems.2012.05.014
Joachimczak, M., and Wróbel, B. (2012c). “Open ended evolution of 3d multicellular development controlled by gene regulatory networks,” in Artificial Life XIII: Proc. of the 13th International Conference on the Simulation and Synthesis of Living Systems (Cambridge, MA: MIT Press), 67–74. doi:10.7551/978-0-262-31050-5-ch010
Komosinski, M., and Rotaru-Varga, A. (2002). Comparison of different genotype encodings for simulated three-dimensional agents. Artif. Life 7, 395–418. doi:10.1162/106454601317297022
Komosinski, M., and Ulatowski, S. (1999). “Framsticks: towards a simulation of a nature-like world, creatures and evolution,” in Proc. of Fifth European Conference on Artificial Life (ECAL 1999), Volume 1674 of LNAI (Berlin: Springer-Verlag), 261–265. doi:10.1007/3-540-48304-7_33
Kowaliw, T., Grogono, P., and Kharma, N. (2004). “Bluenome: a novel developmental model of artificial morphogenesis,” in Genetic and Evolutionary Computation GECCO ‘04 eds T. Kanade, J. Kittler, J. M. Kleinberg, F. Mattern, J. C. Mitchell, M. Naor, et al. (Berlin: Springer), 93–104. doi:10.1007/978-3-540-24854-5_9
Krčah, P. (2012). “Solving deceptive tasks in robot body-brain co-evolution by searching for behavioral novelty,” in Advances in Robotics and Virtual Reality, Volume 26 of Intelligent Systems Reference Library eds T. Gulrez and A. E. Hassanien (Berlin: Springer), 167–186. doi:10.1007/978-3-642-23363-0_7
Lee, S., Yosinski, J., Glette, K., Lipson, H., and Clune, J. (2013). “Evolving gaits for physical robots with the hyperneat generative encoding: the benefits of simulation,” in Applications of Evolutionary Computation, Volume 7835 of LNCS ed. A. Esparcia-Alcázar (Berlin: Springer), 540–549. doi:10.1007/978-3-642-37192-9_54
Lehman, J., and Stanley, K. O. (2011a). Abandoning objectives: evolution through the search for novelty alone. Evol. Comput. 19, 189–223. doi:10.1162/EVCO_a_00025
Lehman, J., and Stanley, K. O. (2011b). “Evolving a diversity of virtual creatures through novelty search and local competition,” in Proc. of the 13th annual conference on Genetic and evolutionary computation, GECCO ‘11 (New York, NY: ACM), 211–218. doi:10.1145/2001576.2001606
Lehman, J., Stanley, K. O., and Miikkulainen, R. (2013). “Effective diversity maintenance in deceptive domains,” in Proc. of the 15th Annual Conference on Genetic and Evolutionary Computation, GECCO ‘13 (New York, NY: ACM), 215–222. doi:10.1145/2463372.2463393
Lessin, D., Fussell, D., and Miikkulainen, R. (2014). “Adopting morphology to multiple tasks in evolved virtual creatures,” in Artificial Life 14: Proc. of the 14th International Conference on the Synthesis and Simulation of Living Systems (Cambridge, MA: The MIT Press), 247–254. doi:10.7551/978-0-262-32621-6-ch041
Lipson, H., and Pollack, J. B. (2000). Automatic design and manufacture of robotic lifeforms. Nature 406, 974–978. doi:10.1038/35023115
Mahfoud, S. W. (1995). Niching Methods for Genetic Algorithms. Ph.D. thesis, University of Illinois at Urbana-Champaign, Champaign, IL.
Matos, A., Suzuki, R., and Arita, T. (2009). Heterochrony and artificial embryogeny: a method for analyzing artificial embryogenies based on developmental dynamics. Artif. Life 15, 131–160. doi:10.1162/artl.2009.15.2.15200
Meng, Y., Zhang, Y., and Jin, Y. (2011). Autonomous self-reconfiguration of modular robots by evolving a hierarchical mechanochemical model. IEEE Comput. Intell. Mag. 6, 43–54. doi:10.1109/MCI.2010.939579
Mouret, J.-B., and Clune, J. (2012). “An algorithm to create phenotype-fitness maps,” in Proceedings of the Thirteenth International Conference on the Simulation and Synthesis of Living Systems (ALIFE 13) eds C. Adami, D. M. Bryson, C. Ofria, and R. T. Pennock (Cambridge, MA: MIT Press), 593–594.
Mouret, J. B., and Doncieux, S. (2011). Encouraging behavioral diversity in evolutionary robotics: an empirical study. Evol. Comput. 20, 91–133. doi:10.1162/EVCO_a_00048
Pilat, M. L., Ito, T., Suzuki, R., and Arita, T. (2012). “Evolution of virtual creature foraging in a physical environment,” in Artificial Life XIII: Proc. of the 13th International Conference on the Simulation and Synthesis of Living Systems (Cambridge, MA: MIT Press), 423–430. doi:10.7551/978-0-262-31050-5-ch056
Sareni, B., and Krahenbuhl, L. (1998). Fitness sharing and niching methods revisited. IEEE Trans. Evol. Comput. 2, 97–106. doi:10.1109/4235.735432
Schramm, L., Jin, Y., and Sendhoff, B. (2011). “Emerged coupling of motor control and morphological development in evolution of multi-cellular animats,” in Advances in Artificial Life. Darwin Meets Von Neumann: Proc. of the 10th European Conference on Artificial Life (ECAL 2009), Volume 5777 of LNCS (Berlin: Springer), 27–34.
Sfakiotakis, M., and Tsakiris, D. (2006). SIMUUN: a simulation environment for undulatory locomotion. Int. J. Model. Simul. 26, 350–358. doi:10.2316/Journal.205.2006.4.205-4430
Shepherd, R. F., Ilievski, F., Choi, W., Morin, S. A., Stokes, A. A., Mazzeo, A. D., et al. (2011). Multigait soft robot. Proc. Natl. Acad. Sci. U.S.A. 108, 20400–20403. doi:10.1073/pnas.1116564108
Sims, K. (1994). “Evolving virtual creatures,” in Proc. of the 21st Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ‘94 (New York, NY: ACM Press), 15–22. doi:10.1145/192161.192167
Stanley, K. (2007). Compositional pattern producing networks: a novel abstraction of development. Genet. Program. Evol. Mach. 8, 131–162. doi:10.1007/s10710-007-9028-8
Stanley, K. O., D’Ambrosio, D. B., and Gauci, J. (2009). A hypercube-based encoding for evolving large-scale neural networks. Artif. Life 15, 185–212. doi:10.1162/artl.2009.15.2.15202
Stanley, K. O., and Lehman, J. (2015). Why Greatness Cannot be Planned: The Myth of the Objective. Springer Cham, Heidelberg, New York, Dordrecht, London: Springer International Publishing. doi:10.1007/978-3-319-15524-1
Stanley, K. O., and Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies. Evol. Comput. 10, 99–127. doi:10.1162/106365602320169811
Steltz, E., Mozeika, A., Rodenberg, N., Brown, E., and Jaeger, H. M. (2009). “JSEL: jamming skin enabled locomotion,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2009) (Piscataway, NJ: IEEE), 5672–5677. doi:10.1109/iros.2009.5354790
Trujillo, L., Olague, G., Lutton, E., Fernández de Vega, F., Dozal, L., and Clemente, E. (2011). Speciation in behavioral space for evolutionary robotics. J. Intell. Robot. Syst. 64, 323–351. doi:10.1007/s10846-011-9542-z
Keywords: novelty search, artificial development, soft-robotics, body–brain co-evolution, evolutionary algorithm, artificial life
Citation: Joachimczak M, Suzuki R and Arita T (2015) Improving Evolvability of Morphologies and Controllers of Developmental Soft-Bodied Robots with Novelty Search. Front. Robot. AI 2:33. doi: 10.3389/frobt.2015.00033
Received: 30 June 2015; Accepted: 23 November 2015;
Published: 17 December 2015
Edited by:
Zdzislaw Kowalczuk, Gdansk University of Technology, PolandReviewed by:
Dimitrije Markovic, Dresden University of Technology, GermanyLuís Correia, University of Lisbon, Portugal
Copyright: © 2015 Joachimczak, Suzuki and Arita. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michał Joachimczak, bWpvYWNoQGdtYWlsLmNvbQ==
 Michał Joachimczak
Michał Joachimczak Reiji Suzuki
Reiji Suzuki Takaya Arita
Takaya Arita