- Cognitive Modeling, Department of Computer Science, University of Tübingen, Tübingen, Germany
Theories on embodied cognition emphasize that our mind develops by processing and inferring structures given the encountered bodily experiences. Here, we propose a distributed neural network architecture that learns a stochastic generative model from experiencing bodily actions. Our modular system learns from various manifolds of action perceptions in the form of (i) relative positional motion of the individual body parts, (ii) angular motion of joints, and (iii) relatively stable top-down action identities. By Hebbian learning, this information is spatially segmented in separate neural modules that provide embodied state codes and temporal predictions of the state progression inside and across the modules. The network is generative in space and time, thus being able to predict both, missing sensory information and next sensory information. We link the developing encodings to visuomotor and multimodal representations that appear to be involved in action observation. Our results show that the system learns to infer action types and motor codes from partial sensory information by emulating observed actions with the own developing body model. We further evaluate the generative capabilities by showing that the system is able to generate internal imaginations of the learned types of actions without sensory stimulation, including visual images of the actions. The model highlights the important roles of motor cognition and embodied simulation for bootstrapping action understanding capabilities. We conclude that stochastic generative models appear very suitable for both, generating goal-directed actions and predicting observed visuomotor trajectories and action goals.
1. Introduction
It appears that humans are particularly good at learning by imitation, gaze following, social referencing, and gestural communication from very early on (Tomasello, 1999). Inherently, the observation of others is involved in all of these forms of social learning. Learning by imitation, for instance, is assumed to develop from pure mimicking of bodily movements toward the inference and emulation of the intended goals of others from about 1 year of age onward (Carpenter et al., 1998; Want and Harris, 2002; Elsner, 2007). Yet how are goals and intentions inferred from visual observations, and how does this facilitate the activation of the respective motor commands for imitation? The intercommunication between specific brain regions, which are often referred to as mirror neuron system or action observation network, has been suggested to enable this inference of others’ intentions and imitation of their behavior (Buccino et al., 2004; Rizzolatti and Craighero, 2004, 2005; Iacoboni, 2005, 2009; Iacoboni and Dapretto, 2006; Kilner et al., 2007). While a genetic predisposition may supply the foundation to develop such a system (Rizzolatti and Craighero, 2004; Ferrari et al., 2006; Lepage and Théoret, 2007; Bonini and Ferrari, 2011; Casile et al., 2011), its development – per se – seems to be strongly determined by social interaction (Meltzoff, 2007; Heyes, 2010; Nagai et al., 2011; Froese et al., 2012; Saby et al., 2012), sensorimotor experience, motor cognition, and embodiment (Gallese and Goldman, 1998; Catmur et al., 2007; Gallese, 2007a; Gallese et al., 2009). Due to observations such as the foregoing, cognitive science has recently undergone a pragmatic turn, focusing on the enactive roots of cognition (Engel et al., 2013).
Embodied cognitive states, according to Barsalous simulation hypothesis (Barsalou, 1999, 2008), are situated simulations that temporarily activate – or re-enact – particular events by means of a set of embodied modal codes. However, if mental states are grounded in own-bodily experiences and self-observations, how does the brain establish the correspondence to the observation of others in the first place? We have recently shown that this so-called correspondence problem [cf. Heyes (2001) and Dautenhahn and Nehaniv (2002)] can be solved by an embodied neural network model that is adapting to the individual perspectives of others (Schrodt et al., 2015). This model clustered sensorimotor contingencies and learned about their progress in a single competitive layer composed of cells with multimodal tuning, enabling it to infer proprioceptive equivalents to visual observations while taking an actors perspective.
In this paper, we propose a stochastic variant of the clustering algorithm, which we introduced in our previous work, that is generative in multiple, distributed domains. The system can be considered to develop several hidden Markov models from scratch and incorporates them by integrating conditional state transition probabilities statistically. It thereby learns an embodied action model that is able to simulate forward in time consistent visual-proprioceptive self-perceptions. This bodily grounded simulation is primed when observing biological motion patterns, leading to the ability to re-enact the observed behavior using the own embodied codes. Hence, our model supports the view that mental states are embodied simulations [cf. Gallese (2007b)] and provides an explanation to how the perception of others’ actions can be consistently incorporated with the own action experiences when encoded at distributed neural sites.
Our model can be compared to an action observation network, in that it models the processing of (i) visual motion signals, believed to be processed in the superior temporal sulcus; (ii) spatiotemporal motor codes, which can be related to neural activities in the posterior parietal lobule and the premotor cortex, and (iii) compressed, intentional action codes, which have been associated with neural activities in the inferior frontal gyrus [see, e.g., Iacoboni (2005), Kilner (2011), and Turella et al. (2013)]. Accordingly, we train and evaluate a tripartite network structure, interpreting and referring to (i) relative positional body motion as visual biological motion stimuli, (ii) joint angular motion as motor codes, and (iii) action identities as intentions or goals in our experiments. In doing so, we focus on bodily movements, including walking, running, and playing basketball, where the stimuli originate from motion captures of human subjects. Despite the simplicity of these stimuli, our results show that it is possible to identify compressed intention codes from observing biological motion patterns and to concurrently infer consistent motor emulations of observed actions using distributed, bodily grounded encodings. Analogously, actions can be simulated in visual and motor modalities when only an intention prior is provided, offering a possible explanation to how simulation processes may drive forth goal-directed and imitative behavior, and link it to social learning.
In the following, we refer to related work in Section 2 and specify the model architecture, including its modularized structure as well as the probabilistic learning and information processing mechanisms in Section 3. We then describe the motion capture stimuli, the bottom-up processing, and clarify the connection of the resulting perceptions to encodings involved in action understanding in Section 4. The model is evaluated on motion tracking data, showing action inference, completion, and imagination capabilities in Section 5. Finally, we discuss current challenges and future application options in Section 6.
2. Related Work
Lallee and Dominey (2013) implemented a model that integrates low-level sensory data of an iCub robot, encoding multimodal contingencies in a single, 3D, and self-organizing competitive map. When driven by a single modal stimulus, this multimodal integration enables mental imagery of corresponding perceptions in other modalities. In accordance with findings from neuroscience, the modeled self-organizing map is topographic with respect to its discrete multimodal cell tunings. The states generated by our model can also be embedded in metric spaces. In contrast, however, our model encodes modal prototype vectors separately and activates them stochastically. This allows to encode multimodal perceptions without redundancies. Moreover, it enables the resolution of ambiguities over time by predictive interactions between the encoded modalities. Our results show that cells can be activated by multimodal perceptions without necessarily encoding multimodal stimuli locally, while moreover being able to encode specific actions by means of distributed temporal statistics.
Taylor et al. (2006) implemented a stochastic generative neural network model based on conditional restricted Boltzmann machines (RBMs). When trained on motion captures similar to those used in our evaluations, the model is able to reproduce walking and running movements as well as transitions between them in terms of sequences of angular postures. Although the encoding capacity of RBMs is theoretically superior in comparison to Markov state-based models because they encode multidimensional state variables, the experiments show the typical tradeoff of requiring considerably more training trials and randomized sampling. Our model is able to expand its encoding capacity on-demand and thus avoids both a sampling and frequency bias. Our model, nevertheless, accounts for scalability and encoding capacity since states are distributed over several Markov models. This enables to learn modal state transition densities locally and to reconcile them with sensory signals and cross-modal predictions as required.
Comparable to the realization by Baker et al. (2009) of a qualitative cognitive model suggested by Gergely et al. (1995), intention inferences in our model are based on Bayesian statistics given visually observed action sequences. In contrast, our model learns the sensorimotor contingencies that facilitate this inference without relying on specific behavioral rationality assumptions. Comparably, the intention priors in our model are statistically determined by assessing the own behavioral biases during an embodied training phase. Thereby, our experiments are based on the assumption that an observer expects an actor to behave in the same way they would behave – that is, by inferring cross-modal observation equivalences based on the own-bodily experiences – and thus essentially models the development of social cognition [cf. Meltzoff (2007)].
Similar to Friston et al. (2011), our neural network models action understanding by inferring higher level, compact action codes, given lower level sensory motion signals. However, in contrast to Friston et al. (2011), no motion primitives are provided, but they are learned in the form of intention clusters, which integrate sensory–motor information over space and time.
3. Neural Network Architecture
The stochastic generative neural model consists of several stochastic neural layers or modules, which process information in identical fashion. The layers can be arranged hierarchically and connected selectively. Each layer calculates a normalized, discrete probability density estimate for the determination of a state in a specific state space. Each neuron corresponds to a possible state, and the binary activation of a single cell corresponds to the determination of that state. The neurons are activated by developing and incorporating prototype tunings and temporal state predictions. Each neuron sends intramodular state transition predictions to the other neurons in the layer and cross-modular predictions to associated layers, such that the distributed states are able to develop self-preserving, generative temporal dynamics. The development of these predictions can be compared to predictive coding (Rao and Ballard, 1999) and results in a Hebbian learning rule similar to Oja’s rule (Oja, 1989) as described in Section 3.3.
Figure 1 shows the particular network architecture developed here. Referring to the human action observation network, three layers of this kind interact with each other in a hierarchy of two levels: at the bottom level, a vision layer processes bottom-up visual motion cues and predicts the continuation of this visual motion over time as well as corresponding action intentions and motor codes. Further, a motor layer processes bottom-up proprioceptions of joint angular motion and predicts the continuation of these signals over time as well as corresponding action intentions and visual motion. Finally, at the top level, an intention layer encodes the individual actions for which the system is trained on, predicts possible action transitions over time, and top-down the corresponding vision and motor layer states that may be active during a particular action. Hence, at the bottom level, top-down and generative activities are fused with bottom-up sensory signals, in common with the intramodular and cross-modular predictions generated by the bottom layers themselves. In a context where each bottom module represents a specific modality, the intramodular predictions can be considered to represent the expected state progression in the respective modality, while cross-modular predictions implement cross-modal inferences. The cross-modular predictions enable the inference of motor and intention codes from visual observations during action observation, where only visual motion cues are available.
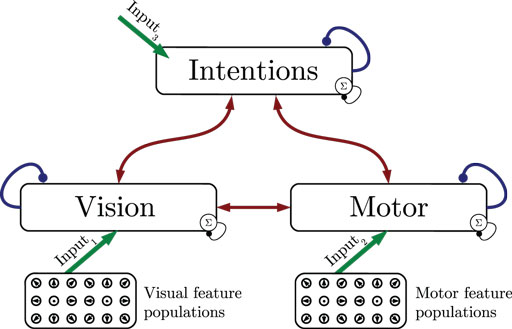
Figure 1. Architecture overview in the context of action inference and simulation. The model consists of three stochastic layers: a vision layer, a motor layer, and an intention layer. All layers predict the next state in other layers (red arrows) and the next state in the same layer (blue arrows). The vision and motor layers can be driven by sensory, bottom-up signals (green arrows 1 and 2), while the top layer can be driven by top-down signal input (green arrow 3). Normalization of a layer input is indicated by the circled Σ.
The streams of sensory information are assumed to be provided by populations of locally receptive cells with tuning to specific stimuli, which is in accordance with findings in neuroscience (Pouget et al., 2000). These populations essentially forward the information by means of a full connection to the bottom stochastic layer that reflects the corresponding modality. Section 4 elaborates further on how the respective perceptions and stimuli are encoded and how they can be related to an action observation network. This encoding has been published recently as part of a perspective-inference model given dynamic motion patterns (Schrodt et al., 2015). The following sections thus focus on the stochastic neural layers on top of the populations.
3.1. Stochastic Neural Layers
Each stochastic neural layer learns a discrete, prototypic representation of the provided sensory input information. To do so, the layer grows a set of cells on demand with distinct sensory tunings. The recruitment of cells and adaptation of prototypes is accomplished by unsupervised mechanisms as explained in Section 3.2. Each cell in a layer learns predictions of the temporal progress of these prototypic state estimates in the layer. Furthermore, each cell learns to predict the cell activations that may be observed in other, associated layers, which is explained in Section 3.3. An exemplary stochastic neural layer connected to another layer in this way, together with the neural populations that forward sensory signals is shown in Figure 2. In the following, the determination of states and incorporation of predictions is formalized.
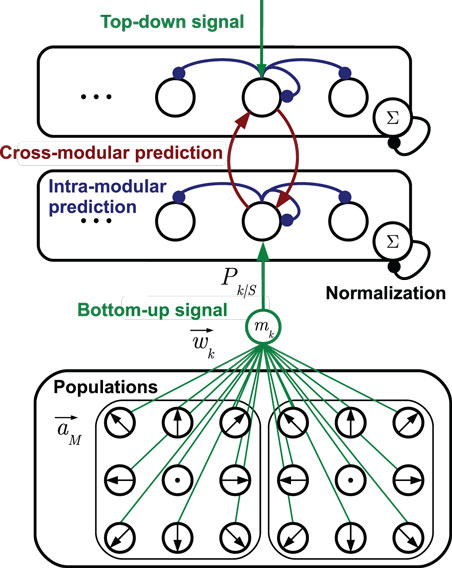
Figure 2. Two stochastic state layers in hierarchical compound. The bottom-up sensory state recognition signal is provided by multiple populations of tuned cells. The signals Pk| S provided by the match mk between cell prototypes and the current stimulus are indicated by the green connection diagram. Analogously, top-down recognition signals can be defined. Lateral recurrences in blue represent state transition probabilities, including the self-recurrence to preserve a state. Red lines denote cross-modular predictions of states. Arrow head lines indicate signals that are summed up by a cell, while bullet head lines indicate modulations of cell inputs [cf. equation (2)].
The layers in our model simplify competitive neural processes such that only a single cell in each layer is activated at the same time. Cell activations are binary and represent the event that a specific state in the corresponding state space is determined. This is comparable to a winner-takes-all approach [cf. Grossberg (1973), for evaluations]. However, the determination of the state in each layer depends on a fusion of predictive intramodular and cross-modular probabilities and sensory state recognition probabilities. By stochastic sampling, a single cell is selected as competition winner in each time step, where the winning probability is determined by the fused inputs to each cell. In the process, the input vector to a layer depicts a discrete probability density for the stochastic event of observing a particular state. For this reason, each layer uses a specific normalization of incoming signals that ensures that the all signals sum up to 1.
We denote cells inside a layer by an index set M and cells outside by an index set N. The binary output xk(t) of a state cell indexed k ∈ M is determined by the normalized probability term
where Xk(t) denotes the winning event probability, and xk(t) ∈ {0,1} denotes the realization of this probability or abstract, binary cell activation calculated by stochastic sampling at time step t. The input netk(t) to the cell k is provided by the probability fusion
where Pk| S(t) is a sensory (S) recognition signal depicting the probability that the state k is considered the current observation given sensory inputs, Pk| I(t) is the intramodular (I) prediction of the successor state, and Pk| C(t) is the cross-modular (C) prediction of the succession, defined by
Taken together, equation (2) firstly fuses probabilistic sensory recognition signals with probabilistic cross-modular predictions coming in from the last winner cells of other layers. Then, it restricts the activation of cells to probabilistic intramodular predictions propagated from the last winner cell in the layer to all potential successors (including the last winner itself), as indicated in Figure 2.
The sensory recognition probability Pk| S(t) is also responsible for clustering the sensory streams into discrete, prototypic states. In the following, we explain the segmentation by unsupervised Hebbian learning.
3.2. Segmentation and Recognition of Population-Encoded Activations
For generating the above binary stochastic cells, we use an instar algorithm that is capable of unsupervised segmentation of normalized vector spaces similar to Grossberg’s Adaptive Resonance Theory (Grossberg, 1976a,b,c). In contrast, our approach provides state recognition probabilities and can thus be applied to implement non-deterministic learning and recognition. Another difference to common implementations is that cell prototypes are created on demand and initialized with zero vectors.
We define the sensory recognition probability Pk| S(t) of a state k ∈ M as a function of the congruence or match mk(t) between a state cell’s prototype vector and the current activation vector (t) jointly provided by all population cells. The concatenated population activation dedicated to a state layer is assumed to be normalized to length 1. Since the model is designed for a separate learning and testing phase, we provide separate recognition functions, assuming full sensory confidence during training, and some sensory uncertainty during testing, which generally means observing previously unseen data. During training, this assumption inevitably results in the sensory recognition of the best matching state via
as well as a sensory recognition that is distributed over all states during testing, which we define by
where κ denotes an uncertainty measure for sensory data, and β denotes the maximum sensor confidence. The prototype match to the current stimulus is described by
where ⊙ denotes the scalar product, such that the match function is based on the angular match between the normalized prototype vector encoded in cell k and the current normalized stimulus (t). Each layer expands its capacity on demand, comparable to Growing Neural Gas by Fritzke (1995). When a cell has fired a sensory recognition signal [Pk| S(t) = 1] once during training, it is converted from a free cell to a recruited cell in the sense that its prototype vector is adapted from zero to the current stimulus [following the learning rule in equation (8)]. The match of a free cell is fixed to θ, such that when no cell match is greater than θ, the free pattern is recruited and another free cell is created with zero vector prototype. Thus, we call θ the recruitment threshold in the following. Assuming a small learning rate, we can ensure that each training input is encoded in the network with a tolerance mismatch of θ, irrespective of the amount of data, the presentation order, or frequency. Further, it was suggested previously that adding noise to the match function introduces a specific degree of noise robustness to this segmentation algorithm during training (Schrodt et al., 2015).
Prototype vectors of cells are trained to represent the current population activation using the Hebbian inspired instar learning rule:
where ηs denotes the spatial learning rate. Since learning is gated by the binary cell realization xk(t), only the prototype of the winner cell is adapted.
During testing, the sensory recognition function [equation (6)] ensures the distribution of sensory state recognition probabilities over all stochastic cells rather than a single one to account for sensory uncertainty. Perfectly matching cells are recognized with probability β (before normalization), whereas the probability to recognize states not perfectly in the center of the stimulus decreases in dependency on κ and the mismatch. This means also that when no learned prototype matches sufficiently well during testing, the sensory recognition distribution becomes nearly uniform, such that intramodular and cross-modular predictions gain a relatively strong influence on the determination of the current state [cf. equation (2)]. Therefore, the network is able to dynamically switch from a bottom-up driven state recognition to a forward simulation of the state progression when sensory information is unknown or uncertain. In the following, we detail how intramodular and cross-modular predictions can be learned by a Hebbian learning rule that is equivalent to Bayesian inference.
3.3. Learning Intramodular and Cross-Modular Predictions
Upon winning, a cell learns to predict which observations will be made next in the same and in other layers. This is realized by asymmetric bidirectional recurrences between cells in a layer, representing the intramodular predictions Pk| I(t), and between cells of two layers, representing the cross-modular predictions Pk| C(t). Intramodular recurrences propagate the state transition probability from the last winner to all cells in the same layer and thus implement a discrete-time Markov chain, where Markov states are learned from scratch during the training procedure. Cross-modular connections bias the state transition probability density in other layers, given the current sensory observation, by means of temporal Bayesian inference.
Taken together, in a fully connected architecture, intramodular and cross-modular state predictions are represented by a full connection between all state cells in the network (including self-recurrences). These connections generally encode conditional probabilities for the subsequent observation of specific states. They can be learned by Bayesian statistics, which would result in asymmetric weights.
To derive a neurally more plausible learning rule to train a weight from cell i to cell j, we transpose the derivative of this formula with respect to time:
With the predictive learning rate ηp set constant, this is a temporal variant of Oja’s associative learning rule (Oja, 1989), also referred to as outstar learning rule. Thus, this form of Hebbian learning is equivalent to Bayesian inference under the assumption of a learning rate that decays inversely proportional to the number of activations of the preceding cell i. In this case, each cell calculates the average of all observed (temporally) conditional probability densities in the same and other layers. However, since the states are adapted simultaneously with the learning of state conditionals, it is advantageous to implement a form of forgetting. Hence, we define the learning rate by , where α < 1 implements forgetting. All state predicting weights wij are initialized equally to represent multiple uniform distributions, and adapt in accordance with learning rule 11.
The capability of simulating distributed state progressions, also without sensory stimulation, follows from the stochastic selection of cell activations based on the learned, conditional state predictions. As a result of the bidirectional connections, the model becomes able to infer momentarily or permanently unobservable states and to mutually synchronize, or keep consistent, activations in the respective layers. By pre-activating a subset of cells in a layer, also a subset of learned state sequences can unfold. In the context of actions, this leads to the ability to synchronously simulate the state progression that corresponds to one of multiple encoded bodily movements in the vision and motor layers when biased top-down by a constant intention signal. The probability fusion in equation (2) accounts for an approximation of the respective, multi-conditional state probabilities. In the following section, we describe in further detail the application of this model to action understanding and the respective stimuli used in our evaluations.
4. Modeling Action Observation
The focus of this paper lies on the learning of an embodied, distributed, and multimodal model of action understanding, which involves bottom-up as well as top-down and generative processes. It consists of three stochastic layers, each modeling codes and processes that are believed to be involved in action observation, the inference of goals, and respective motor commands that facilitate the emulation of observed actions. The first layer comprises visual biological motion patterns. The second layer encodes the corresponding joint angular motor perceptions. Accordingly, the model includes two groups of modal input populations, which encode visual and proprioceptive stimuli. Moreover, we include an amodal or multimodal intrinsic representation of action intentions. These codes are believed to be represented at distributed neural sites. It is typically assumed that action goals and intentions are encoded inferior frontally, motor codes and plans posterior parietally, and biological, mainly visually driven motion patterns in the superior temporal sulcus [cf. Iacoboni (2005), Kilner (2011), and Turella et al. (2013)]. Inferences and synchronization processes between these neural sites are modeled by cross-modular state predictions between the layers in the network, while the intramodular predictions restrict the state progression to the experienced, own-bodily contingencies. Figure 1 shows an overview of the implemented learning architecture in this context.
In the following, we describe the bottom-up processing chain of our model referring to psychological and neuroscientific evidence. We start with the simulation environment and the motion capture data format that provides the respective stimuli for our evaluations. Subsequently, we focus on important key aspects for the recognition of biological motion, their implications, and implementation in the model. Finally, we describe how the resulting perceptions are interpreted in the context of different modalities involved in action perception, inference, and emulation.
4.1. Motion Captures and Data Representation
We evaluate our model making use of the CMU Graphics Lab Motion Capture Database (http://mocap.cs.cmu.edu/). Recordings from subjects performing three different cyclic movements (walking, running, and basketball dribbling) in three trials each were utilized, as shown in Figure 3. For each movement, we chose a short, cyclic segment of the first trial as the training set and the other two, full trials as the testing set. In this way, the training set was rather idealized, while the testing set contained more information which, although inside the same action classes, strongly differed to the training data. The motion tracking data were recorded with 12 high-resolution infra-red cameras at 120 Hz using 41 tracking markers attached to the subjects. The resulting 3D positions were then matched to separate skeleton templates for learning and testing to obtain series of joint angular postures and coherent relative joint positions.
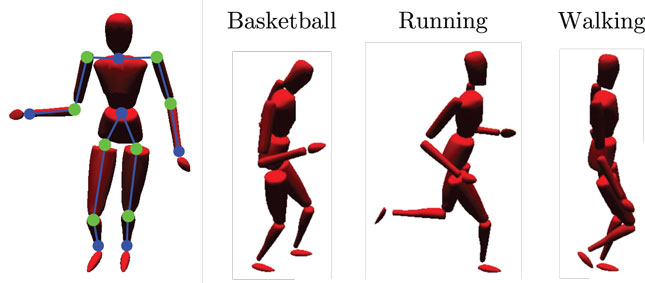
Figure 3. Simulated body driven by motion capture data. The left-sided image shows the limbs (blue lines between dots) and joints (green dots) that provide relative visual and joint angular input to the model. Moreover, three snapshots of the utilized motion tracking trials are shown: basketball dribbling, running, and walking.
In the experiments, we chose the time series of 12 of the calculated relative joint positions as input to the visual processing pathway of the model. We selected the start and end points of the left and right upper arm, forearm, upper and lower leg, shoulder, and hip joints relative to the waist, as shown in Figure 3. Each was encoded by a three-dimensional Cartesian coordinate. As input to the motor pathway, we chose the calculated joint angles of 8 joints, each encoded by a one- to three-dimensional radian vector, depending on the degrees of freedom of the respective joint. We selected the left and right hip joints, knee joint, shoulder joints, and the elbow joints, resulting in 16 DOF overall. A map of the inputs at a single, exemplary time step is shown in Figure 3. The visual and motor pathways are neural substructures of the here proposed model and preprocess the raw data as described in the following.
4.2. Aspects of Biological Motion and Preprocessing
Giese and Poggio (2003) summarize critical properties of the recognition of biological motion from visual observations, such as selectivity for temporal order, generality, robustness, and view dependence. First, scrambling the temporal order in which biological motion patterns are displayed typically impairs the recognition of the respective action. This temporal selectivity is realized in our model by learning temporally directed state predictions. Second, biological motion recognition is highly robust against spatiotemporal variances (such as position, scale, and speed), body morphology and exact posture control, incomplete representations (such as point-light displays), or variances in illumination. We model these generalization capabilities by means of (i) the usage of simplified forms of representation of biological motion stimuli as described above, (ii) the extraction of invariant and valuable information in a neural preprocessing stage, and (iii) the simulation of observed motion with the own embodied encodings. Third, the recognition performance decreases with the amount of rotation an action is perceived from with respect to common perspectives. The prototypic cells in our network also respond to specific, learned views of observed movements. However, the preprocessing of our model is able to also infer and adapt to observed perspectives to a certain degree.
This neurally deployed preprocessing is a part of the model that is not detailed in this paper. To summarize, the extraction of relevant information results in fundamental spatiotemporal invariances of the visual perception to scale, translation, movement speed, and body morphology. This is achieved by (i) exponential smoothing to account for noise in the data, (ii) calculation of the velocity, and (iii) normalization of the data to obtain the relative motion direction of each relative feature processed [see Schrodt and Butz (2014) and Schrodt et al. (2014a,b, 2015) for details]. For reasons of consistency, both the visual and motor perceptions are preprocessed in this manner. As to visual perception, the preprocessing stage is able to account also for invariance to orientation by means of active inference of the perspective an observed biological motion is perceived from. Compensating for the perspective upon observation solves the correspondence problem, which can be considered a premise for the ability to infer intrinsic action representations of others using the own, embodied encodings, as detailed in our previous work. As a matter of focus, however, we neglect the influence of orientation in the following experiments, meaning that the orientation of the learned and observed motions was identical.
Visual stimuli preprocessed in this manner are represented by a number of neural populations, each encoding the spatially relative motion direction of a specific bodily feature. Consequently, each cell in a population is tuned to a specific motion direction of a limb. Following this, the visual state layer accomplishes a segmentation of the concatenation of all visual population activations into whole-body, directional motion patterns. Analogously, the directions of changes in the joint angles are represented by populations and segmented into whole-body motor codes. In the following, we draw a comparison of this visuomotor perspective and our representation of intention codes to findings in neuroscience and psychology.
4.3. Visuomotor Perspective and Intentions
The superior temporal sulcus is particularly well known for encoding (also whole-body) biological motion patterns (Bruce et al., 1981; Perrett et al., 1985; Oram and Perrett, 1994) and has been considered to provide important visual input for the development of attributes linked with the mirror neuron system (Grossman et al., 2000; Gallese, 2001; Puce and Perrett, 2003; Ulloa and Pineda, 2007; Pavlova, 2012; Cook et al., 2014). Visual motion cues are necessary and most critical for the recognition of actions (Garcia and Grossman, 2008; Thurman and Grossman, 2008). As initially shown by Johansson (1973), the perception of point-like bodily landmarks in relative motion is sufficient in this process. Thus, we assume that the above relative directional motion information can be perceived visually and is sufficient for action recognition. In contrast, joint angular motion cannot be perceived directly from such minimal visual information, which particularly applies to inner rotations of limbs. Thus, we assume that the directional angular limb motion is perceived proprioceptively. In the context of actions, we consider a prototype of such whole-body joint angular motion a motor code. Similar motor codes are assumed to be activated during the observation of learned movements (Calvo-Merino et al., 2005) and may be found in posterior parietal areas and related premotor areas (Iacoboni, 2005; Friston et al., 2011; Turella et al., 2013).
Further, in the context of the mirror neuron system, intentional structures can be assumed to be encoded in the inferior frontal gyrus (Iacoboni, 2005; Kilner, 2011; Turella et al., 2013). We simplify these intention codes by top-down, symbolic representations of specific actions. For the following experiments, we define three binary intentions in line with the motion tracking recordings explained before (basketball, running, and walking). Due to this symbol-like nature, the resulting intention layer cells can also be considered action classes or labels, while the derivation of intentions can be considered an online classification of observed bodily motion given visual cues. Since intentions are provided during training, the intention state cells and their predictions can be considered to develop by supervised training of action labels. However, all state variables are segmented using the unsupervised algorithm as described in Section 3.2.
During the observation of others, neither information about their proprioceptions nor their intentions are directly accessible. According to the embodied simulation hypothesis, the developing embodied states can nevertheless be inferred when observing others (Barsalou, 1999, 2008; Calvo-Merino et al., 2005). Hence, in the following experiments, we evaluate the inference and embodied simulation capabilities of our model.
5. Evaluations
In the following experiments, we evaluate (a) the embodied learning of modal prototypes and predictions by means of the segmentation of different streams of information into prototypic state cells, (b) the resulting ability to infer intentions and motor states upon the observation of others’ actions, and (c) the model’s capability to simulate movements without sensory stimulation, keeping visual and motor states consistently. For all of the experiments, we chose the parameterization ηs = 0.01, α = 0.9, β = 0.5, κ = 16, and θ = 0.85 unless stated otherwise.
5.1. Experiment 1: Learning a Sensorimotor Model Mediated by Intentions
In the first experiment, we show how state cells develop from scratch given streams of relative visual and motor motion input. As shown in Figure 4, all layers are driven by data, assuming maximum sensory confidence and thus disabling the influence of predictions. Training consisted of learning perfectly cyclic motion tracking snippets: first, a 115 time steps or 0.96-s basketball trial where a single dribble and 2 footsteps were performed was shown 11 times in succession, resulting in 1265 time steps of training. Then, a 91 time steps or 0.75-s running trial performing 2 footsteps was shown 14 times, resulting in 1274 frames. Finally, a 260 time steps or 2.17-s walking trial performing 2 steps was shown 5 times repeatedly, resulting in 1300 frames. The training data thus consisted of 3.88 s of unique data samples. The whole cyclic repetition of these trials was streamed into the model five times, while recruiting states, learning state prototypes and the resulting intra- and cross-modular predictions.
Figure 4. Experiment 1: state segmentation and learning. Dashed lines indicate the learning of prototype states and temporal predictions. During learning, all information is assumed to be available, sensory signals are fully trusted.
Figure 5 shows the recruitment of five visual and three motor state cells from scratch and the respective match to the driving stimuli in the example of a recruitment threshold θ = 0.1. Because of the cyclic nature of the trained movements, the activations of those states form cyclic time series. The recruitment threshold θ basically defines the discretization of the state spaces. Hence, the higher the recruitment threshold θ, the more states develop, as concluded in Table 1. Note that learning was deterministic in these settings, which means that (a) adapted weights were not initialized randomly, but with a zero vector and (b) we assumed full sensor confidence such that the probability to recognize a state is a binary function. In consequence, there was no variance in the developing states.
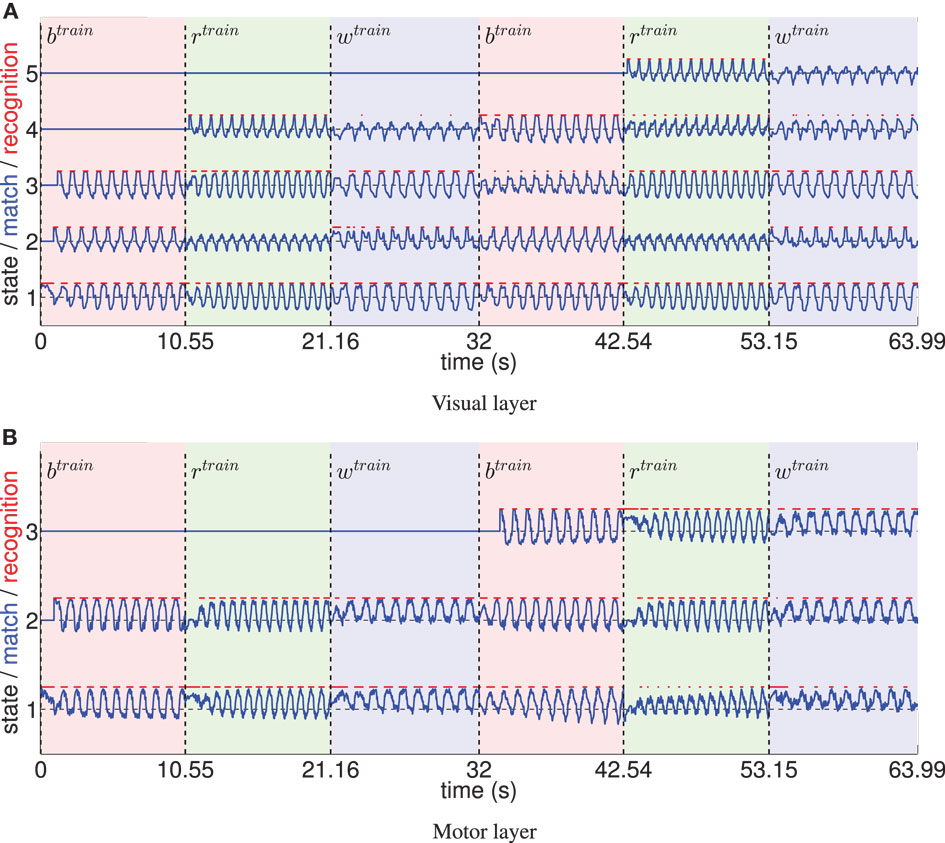
Figure 5. (A) The systematic time series of prototype matches and resulting recognition signals of five visual states, developing during training with θ = 0.1. Three different, cyclic motion tracking trials were learned repeatedly during this procedure (the first two repetitions are shown). Light red patches tagged with indicate the time intervals the basketball training trial was shown, the light green patches indicate the intervals of the running trial, and the light blue patches tagged indicate training on the walking trial. It can be seen that the time series of prototype matches (blue lines) are comparable when re-enacting the presentation of a motion tracking trial, since cells learn to encode specific parts of the data. Because the movements were cyclic, also the determined visual states (red lines) formed cyclic time series. Initially, some state prototypes were recoded when another movement was shown. (B) Equivalent evaluation of the state cell development in the motor layer.
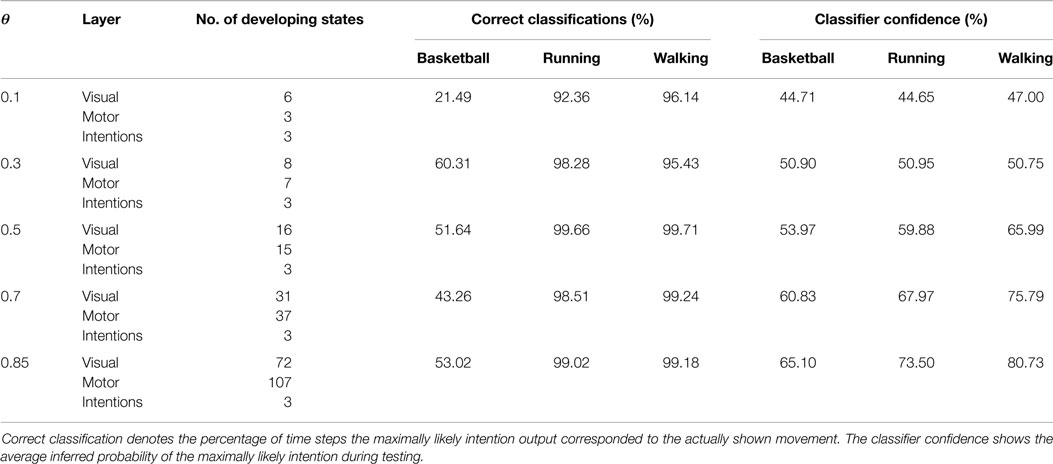
Table 1. Overview of the number of developing states during learning in dependency on θ and the resulting classification performances during observation of movements not seen during training.
Figure 5 also indicates that non-disjunct state encodings develop for the three different movements: only one of the states is recognized exclusively during the perception of a specific movement. Thus, classifications of movements are barely possible using Bayesian statistics with such a low recruitment threshold. Hence, in the following section, we examine the influence of increasing the visual and motor state granularity on the model’s ability to infer movement classes.
5.2. Experiment 2a: Inference of Intentions upon Observation
For the classification of movements, or in this context, for the inference of intentions, the distinctness of the state structures with respect to the movements developing during training plays a major role. Since the information the state cells are encoding in their prototype vector is hard to visualize, we calculated the average pixel snapshot of the simulation display for each state while it was recognized [using an averaging formula analogously to equation (11)]. Basketball movements were displayed in red, running movements in green, and walking movements in blue. Consequently, if only a single state was created to represent all of the training data, the resulting state snapshot would show a mixture of all postures included in all of the movements, while overlapping postures would be black and non-overlapping postures would be colored. On the contrary, a state cell that was recognized only at a single time step during training would result in a snapshot showing only the corresponding posture in the respective color of the movement. Hence, the color of the snapshots can be considered a qualitative measure for the distinctness of states with respect to the three movements. Also, each snapshot shows the segments of the movements a state cell responds to and thus the model’s “imagination” of the movement when modalities are inferred or simulated. Figure 6 shows exemplar snapshots of cells created during the training phases using different recruitment thresholds θ. As expected, higher thresholds lead to the creation of movement-exclusive states.
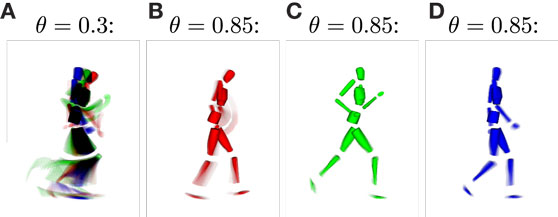
Figure 6. Average simulation display while specific sensory states were observed. (A) Displays an example snapshot of a state created with learning threshold θ = 0.3. It shows that the state was recognized non-exclusively, that is, for each of the learned movements. The disjunction of patterns improves when increasing the threshold, such that for θ = 0.85, movements and specific parts of the movements are clearly identifiable by observing specific states [snapshots (B–D)].
To evaluate the influence of the multimodal state segmentation on the model’s ability to infer intentions and to test for generalization at the same time, we measured the influence of θ on the correctness of the inferred values and the model’s confidence, when different movements were presented after training. As indicated above, the testing set did not contain the motion tracking trials trained on. Rather, it contained two other basketball trials of 4.39 and 3.2 s, two other running trials of 3.56 s each, and two other running trials of 1.15 and 1.27 s. The testing data thus consisted of 17.13 s of unique data samples. Some trials included motion segments very different from the learned movements. Particularly, the basketball testing trials contained segments where the subject stood still and was lifting the ball or segments where the dribbling was incongruent with the footstep cycle, whereas the model was only trained on a single, congruent basketball dribbling snippet. Also, as indicated in Figure 7, only the visual modality was fed into the network during testing trials, which accounts for the fact that intentions and also motor commands are not directly observable during observation of actions. Note that the model did not obtain information about the time step when a new movement was shown during testing.
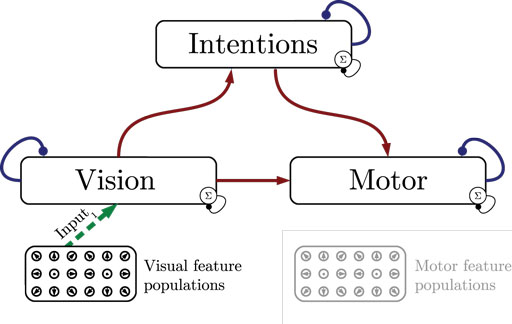
Figure 7. Experiment 2a/b: inference of intentions and motor commands from visually observed movements. Solid lines indicate the propagation of sensory signals (green), cross-modular predictive signals (red), and intramodular predictions (blue). During testing, only the visual sensor is available and fused with the emerging predictions, assuming some uncertainty in sensory information. Intentions are inferred visually, while corresponding motor commands are inferred from vision and the derived intention.
Classification results for four different θ averaged over 6 independent testing trials are shown in Figure 8. Despite the missing motor modality and the deviations in the observed posture control, the model was able to identify the character of the running and walking movements throughout, as concluded in Table 1. In doing so, accurately recognized visual state cells were enough to push the visual, motor, and intention state determination into temporal attractor sequences that consisted of the cyclic emulation of the respective movement using the embodied encodings. Following inputs then either maintained this emulation when close enough to the encodings or forced the convergence to another attractor sequence, that is, a shift in the perception. This effect can be seen clearly in the basketball trials, were episodes similar enough to the training data existed. However, as explained above, the basketball training trials were short and idealized, and they did not contain incongruent dribbling. The model then partly inferred a similarity with the trained walking movement in these segments, resulting in a bistable perception as shown in the graphs. This effect shows how the model is limited to the learned, embodied encodings when inferring intentions. It can be avoided by adding further training data.
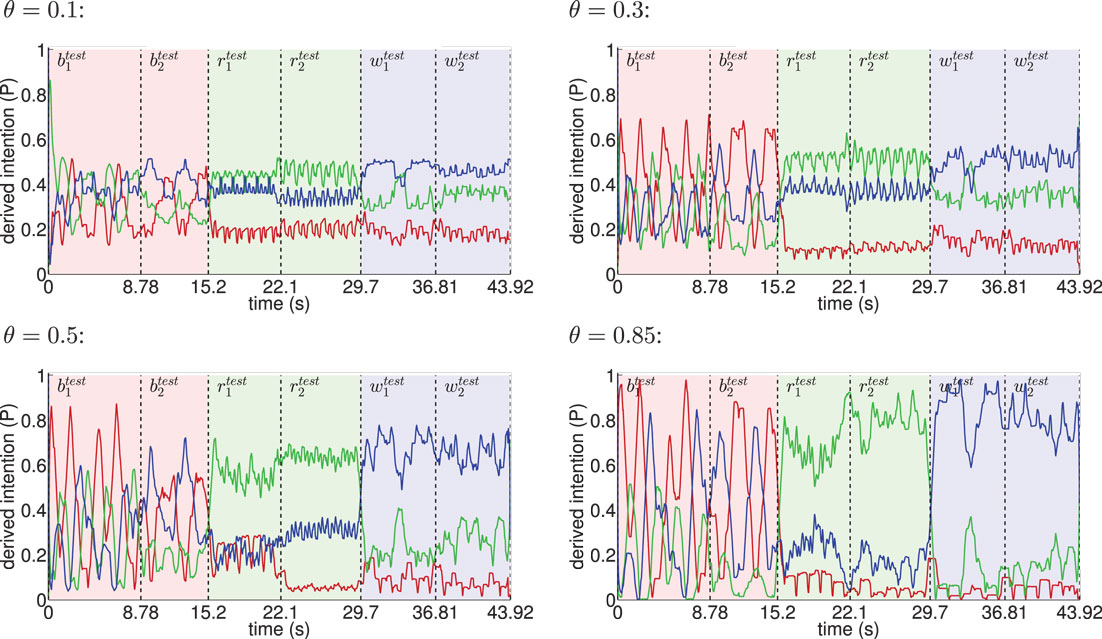
Figure 8. Inference of intentions from visually observed movements shown for different θ. The red line indicates the moving average (one-second time window) of the derived basketball state probability in the intention layer, while light red background shows the interval in time the testing trials and were actually presented. Analogously, green indicates running and blue indicates walking. The classifier confidence improves with θ as a result of learning more disjunct sets of states per movement.
When the learned movements were represented by a higher number of mainly disjunct states with respect to the movements, the model’s ability to infer the intentions slightly improved. As a result of the more disjunct patterns, however, the confidence in classification improved consistently with θ from about 45 to 73% on average. As explained in the following, the classifier confidence has an influence on the inference of motor states.
5.3. Experiment 2b: Inference of Motor Commands upon Observation
Analogously to the preceding experiment, where we could show that intentions could be classified purely from visually observed motion patterns, we now evaluate if also the corresponding motor commands can be inferred using the same mechanisms. Potentially, this task is more difficult, since the set of available motor commands consists of a larger number of states in the motor layer when compared with the intention layer, and since the motor state transitions typically underlie faster dynamics. Seeing that the observed movements differed severely from the learned movements, we evaluate if the inferred motor state snapshots correspond to the visual state snapshots at the same time steps and if the sequence in which they occur during the observation is plausible.
Figure 9 shows the coincidence of state snapshots of the recognized visual states and inferred motor states when observing the testing trials. When similar state snapshots are activated in both the visual and the motor domains, the two modalities can be considered to be synchronized in the emulation of the observed movement. In this process, both the cross-modular prediction from the vision to motor layer and the motor states predicted by the currently inferred intention bias the activation of motor states as indicated in Figure 7. The classifier confidence depicts the probability that a cell in the intention layer is selected as winner. Thus, increasing the classifier confidence will also increase the probability that movement-specific motor states are determined. Thus, since the classifier confidence increases with θ, the ability to imagine a sequence of motor codes corresponding to the currently observed visual motion, and the interpreted intention improves with the discretization of the state spaces.

Figure 9. Example clips of the state sequences recognized in the visual layer and inferred in the motor layer when observing three different movements (basketball, running, and walking testing trials). Each row shows the sequence of states by means of the representing snapshots over time (FLTR) for the respective modality and motion capture trial. Snapshots at the same position show the same time step in the sequence of visual and motor states and mostly show very similar parts of the movements. Because the inference is a stochastic process and because visual and motor states are not segmented in identical fashion as a result of the different information coding in the modalities, slight misalignments can occur. However, strong incongruence is avoided because of the visuomotor coupling. Moreover, although ambiguous patterns are included in the sequence, the network maintains the activation cycle of the movement-specific states because pattern transition probabilities are biased by top-down propagated intention signals.
5.4. Experiment 3: Simulation of Actions
Learning a tripartite model of visual motion states, corresponding motor codes, and intentions enables the inference of various bits of missing information. Seeing that information is encoded in normalized probability densities and information transfer is realized stochastically, activities in the network are self-sustaining even when sensory input is completely suppressed. When only provided with a top-down activation of a particular motion intention in the intention layer (cf. Figure 10), the model simulates likely sequences of modal visual and motor state sequences according to the learned temporal statistics.
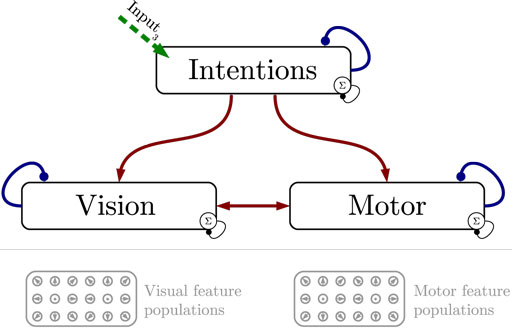
Figure 10. Experiment 3: movement simulation with visuomotor coupling. No sensory signal is provided. While the stochastically emerging visual and motor states are biased by the top-down predictions induced by a constant intention signal, the coupling between vision and motor codes ensures the synchronization of the simulated pattern sequences.
In this experiment, we recorded the coinciding visual and motor state sequences generated by the model when a top-down intention-like action code is kept active in the intention layer. The results in Figure 11 show that the learned sequences can be replicated accurately both in the visual and in the motor domains. Although multiple ambiguous states were learned, as can be seen in the visual imaginations that are multi-colored, the simulated state sequence remains in the correct sequence and movement class. This is because the transition probabilities in the respective modalities are biased by the top-down intention signal.

Figure 11. Example clips of the state sequences simulated synchronously in the visual and motor modalities when three different intention priors (basketball, running, and walking) are provided. Each row shows the respective modality and intention prior. As during motor inference, snapshots at the same position mostly show very similar parts of the movements, while misalignments are mostly avoided. Again, the network maintains the activation cycle of the movement-specific states because pattern transition probabilities are biased by the provided top-down-propagated intention signals.
The results also show that motor and visual state estimates remain approximately synchronized, seeing that the simulated states represent similar visual and motor imaginations at similar time steps. This indicates that the sensorimotor coupling is capable of synchronizing different modalities for periods of time. The reason for this synchronization lies in the lateral predictive connections between vision and motor layers: upon a transition from one visual state to another, the conditional probabilities for motor states given the new visual state change in an according fashion, such that the current motor state is more likely to transit to the most likely successor, which is not only determined by the top-down intention layer signal but also by the intramodular motor state transition probabilities and by the cross-modular activation predictions from the vision layer. Vice versa, the motor states bias the transition in the visual modality, leading to the observable mutual synchronization.
6. Summary and Conclusion
Our work shows that stochastic generative neural networks can be used to model action inference, mental imagery, and action simulation capabilities. Referring to Barsalou’s simulation hypothesis, it suggests that simulation processes in the brain may help to recognize, generalize, and maintain action perceptions and inferences using the own embodied encodings. In our model, these embodied simulations enable a consistent, multimodal interpretation of observed actions in abstract domains. In particular, we have shown that action observation models may rely on encodings that represent actions in a distributed and predictive manner: although some cells were encoding motion components that were active during the observation of various actions, cross-modular predictions enabled the consistent simulation of specific action sequences. Due to the predictive visuomotor coupling, temporal synchronicity of the activated states was ensured. Thus, the predictive, stochastic, and generative encodings resulted in the maintenance of overall consistent, multimodal motion imaginations. In combination with the previously published substructure of the model that resolves spatiotemporal variances by preprocessing of stimuli and inference of the perspective (Schrodt et al., 2015), a neural network architecture can be generated that infers the type of observed actions and possibly underlying motor commands, irrespective of the vantage point and despite variations of the movements. The model is thus able to establish the correspondence between self-perceptions and the perception of others, which can be considered an essential challenge in modeling action understanding.
Despite these successes, the model is currently based on several assumptions. For one, we assume that raw visual and motor perceptions and intentions can be simplified by compressed codes without losing model relevance, and that the respective motion features can be identified reliably. Although it is particularly unclear how to incorporate realistic motor and intention codes in computational models, future model versions can be enhanced toward the processing of raw video streams of actions: the simulation snapshots in the experiments (see Figures 9 and 11) were calculated analogously to the conditional state predictions [equation (12)]. This shows that the states developed by the system can be suitably mapped onto lower level visual modalities. Thus, further developed models may hierarchically process lower level visual information similar to Jung et al. (2015), however, based on top-down predicted, higher level, and bodily grounded motion estimates.
Further, without sensory stimuli, the system’s simulation of action states is a discrete time stochastic process. While the sequence of simulated states was mostly correct, the temporal duration of the activation was characterized by relatively high variance. Adding further modal state layers could diminish this variance. Particularly, the current model incorporates motion signals only and no static or postural information is processed. Exemplarily, the model implemented by Layher et al. (2014) triggers a reinforcement learning signal upon the encounter of low motion energy, which was used to foster the generation of posture snapshots in extreme poses. Comparably to the variance of simulated states, also the mean durations of state activations were partially distorted because of the approximate fusion of predicted state probability densities during testing. Integrating the systems predictions also during learning to a certain extent may improve the fusion of probabilities. It may also improve noise robustness and the establishment of disjunct modal state sequences. As shown in the experiments, disjunct states and state transitions are advantageous for the correct classification and emulation of actions. Techniques are available that can prevent the system to fall into an illusionary loop, when overly trusting the own predictions (Kneissler et al., 2014, 2015).
Moreover, the system currently simplifies a cell activation competition such that only one cell in each layer is adapted at each iteration. Using Mexican hat or softmax functions for the adaptation of learned states may speed up learning. Along similar lines, learning may be further improved when allowing a differential weighting of the provided input features. Currently, each input feature has the same influence in determining the creation of a new state. The recruitment of new prototypic states may be made dependent on the predictive value of all currently available states, including their specificity and accuracy, as is, for example, done in the XCSF learning classifier system architecture (Stalph et al., 2012; Kneissler et al., 2014). Another current challenge to the system is to infer limb identities purely from visual information. The observed limb positions are fed into the dedicated neural network inputs. An adaptive confusion matrix could wire respective limb information appropriately, possibly by back-propagating mismatch signals. Additionally, lower level Gestalt constraints may be learned and used to adapt such a matrix.
Finally, despite the challenges remaining, also in its current form, the system may be evaluated as a cognitive model, and it may be used in robotics applications. Main predictions of the cognitive model come in the form of how visual motion will be segmented into individual motion clusters and how predictive encodings of the modalities modeled in the system will influence each other. Also, false information or distracting information from one module is expected to impair action recognition and simulation capabilities in the connected modules. On the robotics side, related techniques were applied using virtual visual servoing for object tracking (Comport et al., 2006) and for improving the pose estimates of a robot (Gratal et al., 2011). Our model offers both generative, visual servoing options and temporal motion predictions and inference-based, action recognition capabilities. In future work, this offers the opportunity to develop a cognitive system that is able to identify and subsequently emulate specific intention- or goal-oriented actions, striving for the same goal but adapting the motor commands to the own-bodily experiences and capabilities.
Author Contributions
FS is the main author of the contribution and was responsible for model conception, implementation, and evaluation. MB made substantial contributions to the proposed work by supervising the work, providing intellectual content, and co-authoring the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge support by Deutsche Forschungsgemeinschaft and Open Access Publishing Fund of University of Tübingen. FS has been supported by postgraduate funding of the state of Baden-Württemberg (Landesgraduiertenförderung Baden-Württemberg). The motion tracking data used in this project was obtained from Carnegie Mellon University (http://mocap.cs.cmu.edu/). The database was created with funding from NSF EIA-0196217. The simulation framework used to read and display the data (AMC-Viewer) was written by James L. McCann.
References
Baker, C. L., Saxe, R., and Tenenbaum, J. B. (2009). Action understanding as inverse planning. Cognition 113, 329–349. doi: 10.1016/j.cognition.2009.07.005
Barsalou, L. W. (1999). Perceptual symbol systems. Behav. Brain Sci. 22, 577–600. doi:10.1017/S0140525X99532147
Barsalou, L. W. (2008). Grounded cognition. Annu. Rev. Psychol. 59, 617–645. doi:10.1146/annurev.psych.59.103006.093639
Bonini, L., and Ferrari, P. F. (2011). Evolution of mirror systems: a simple mechanism for complex cognitive functions. Ann. N. Y. Acad. Sci. 1225, 166–175. doi:10.1111/j.1749-6632.2011.06002.x
Bruce, C., Desimone, R., and Gross, C. G. (1981). Visual properties of neurons in a polysensory area in superior temporal sulcus of the macaque. J. Neurophysiol. 46, 369–384.
Buccino, G., Vogt, S., Ritzl, A., Fink, G. R., Zilles, K., Freund, H.-J., et al. (2004). Neural circuits underlying imitation learning of hand actions: an event-related fMRI study. Neuron 42, 323–334. doi:10.1016/S0896-6273(04)00181-3
Calvo-Merino, B., Glaser, D. E., Grèzes, J., Passingham, R. E., and Haggard, P. (2005). Action observation and acquired motor skills: an fMRI study with expert dancers. Cereb. Cortex 15, 1243–1249. doi:10.1093/cercor/bhi007
Carpenter, M., Nagell, K., Tomasello, M., Butterworth, G., and Moore, C. (1998). Social cognition, joint attention, and communicative competence from 9 to 15 months of age. Monogr. Soc. Res. Child Dev. 63, i–vi, 1–143. doi:10.2307/1166214
Casile, A., Caggiano, V., and Ferrari, P. F. (2011). The mirror neuron system: a fresh view. Neuroscientist 17, 524–538. doi:10.1177/1073858410392239
Catmur, C., Walsh, V., and Heyes, C. (2007). Sensorimotor learning configures the human mirror system. Curr. Biol. 17, 1527–1531. doi:10.1016/j.cub.2007.08.006
Comport, A., Marchand, E., Pressigout, M., and Chaumette, F. (2006). Real-time markerless tracking for augmented reality: the virtual visual servoing framework. IEEE Trans. Vis. Comput. Graph. 12, 615–628. doi:10.1109/TVCG.2006.78
Cook, R., Bird, G., Catmur, C., Press, C., and Heyes, C. (2014). Mirror neurons: from origin to function. Behav. Brain Sci. 37, 177–192. doi:10.1017/S0140525X13000903
Elsner, B. (2007). Infants’ imitation of goal-directed actions: the role of movements and action effects. Acta Psychol. 124, 44–59. doi:10.1016/j.actpsy.2006.09.006
Engel, A. K., Maye, A., Kurthen, M., and König, P. (2013). Where’s the action? The pragmatic turn in cognitive science. Trends Cogn. Sci. 17, 202–209. doi:10.1016/j.tics.2013.03.006
Ferrari, P. F., Visalberghi, E., Paukner, A., Fogassi, L., Ruggiero, A., and Suomi, S. J. (2006). Neonatal imitation in rhesus macaques. PLoS Biol. 4:e302. doi:10.1371/journal.pbio.0040302
Friston, K., Mattout, J., and Kilner, J. (2011). Action understanding and active inference. Biol. Cybern. 104, 137–160. doi:10.1007/s00422-011-0424-z
Fritzke, B. (1995). A growing neural gas network learns topologies. Adv. Neural Inf. Process Syst. 7, 625–632.
Froese, T., Lenay, C., and Ikegami, T. (2012). Imitation by social interaction? Analysis of a minimal agent-based model of the correspondence problem. Front. Hum. Neurosci. 6:202. doi:10.3389/fnhum.2012.00202
Gallese, V. (2001). The ‘shared manifold’ hypothesis. From mirror neurons to empathy. J. Conscious. Stud. 8, 33–50.
Gallese, V. (2007a). Before and below ‘theory of mind’: embodied simulation and the neural correlates of social cognition. Philos. Trans. R. Soc. Lond. B Biol. Sci. 362, 659–669. doi:10.1098/rstb.2006.2002
Gallese, V. (2007b). Embodied simulation: from mirror neuron systems to interpersonal relations. Novartis Found. Symp. 278, 3–12. doi:10.1002/9780470030585.ch2
Gallese, V., and Goldman, A. (1998). Mirror neurons and the simulation theory of mind-reading. Trends Cogn. Sci. 2, 493–501. doi:10.1016/S1364-6613(98)01262-5
Gallese, V., Rochat, M., Cossu, G., and Sinigaglia, C. (2009). Motor cognition and its role in the phylogeny and ontogeny of action understanding. Dev. Psychol. 45, 103. doi:10.1037/a0014436
Garcia, J. O., and Grossman, E. D. (2008). Necessary but not sufficient: motion perception is required for perceiving biological motion. Vision Res. 48, 1144–1149. doi:10.1016/j.visres.2008.01.027
Gergely, G., Nádasdy, Z., Csibra, G., and Biro, S. (1995). Taking the intentional stance at 12 months of age. Cognition 56, 165–193. doi:10.1016/0010-0277(95)00661-H
Giese, M. A., and Poggio, T. (2003). Neural mechanisms for the recognition of biological movements. Nat. Rev. Neurosci. 4, 179–192. doi:10.1038/nrn1057
Gratal, X., Romero, J., and Kragic, D. (2011). “Virtual visual servoing for real-time robot pose estimation,” in World Congress, Vol. 18, eds S. Bittanti, A. Cenedese and S. Zampieri (Milano: International Federation of Automatic Control), 9017–9022.
Grossberg, S. (1973). Contour enhancement, short-term memory, and constancies in reverberating neural networks. Stud. Appl. Math. 52, 213–257. doi:10.1002/sapm1973523213
Grossberg, S. (1976a). On the development of feature detectors in the visual cortex with applications to learning and reaction-diffusion systems. Biol. Cybern. 21, 145–159. doi:10.1007/BF00337422
Grossberg, S. (1976b). Adaptive pattern classification and universal recoding: I. Parallel development and coding of neural feature detectors. Biol. Cybern. 23, 121–134. doi:10.1007/BF00344744
Grossberg, S. (1976c). Adaptive pattern classification and universal recoding: II. Feedback, expectation, olfaction, illusions. Biol. Cybern. 23, 187–202.
Grossman, E., Donnelly, M., Price, R., Pickens, D., Morgan, V., Neighbor, G., et al. (2000). Brain areas involved in perception of biological motion. J. Cogn. Neurosci. 12, 711–720. doi:10.1162/089892900562417
Heyes, C. (2001). Causes and consequences of imitation. Trends Cogn. Sci. 5, 253–261. doi:10.1016/S1364-6613(00)01661-2
Heyes, C. (2010). Where do mirror neurons come from? Neurosci. Biobehav. Rev. 34, 575–583. doi:10.1016/j.neubiorev.2009.11.007
Iacoboni, M. (2005). Neural mechanisms of imitation. Curr. Opin. Neurobiol. 15, 632–637. doi:10.1016/j.conb.2005.10.010
Iacoboni, M. (2009). Imitation, empathy, and mirror neurons. Annu. Rev. Psychol. 60, 653–670. doi:10.1146/annurev.psych.60.110707.163604
Iacoboni, M., and Dapretto, M. (2006). The mirror neuron system and the consequences of its dysfunction. Nat. Rev. Neurosci. 7, 942–951. doi:10.1038/nrn2024
Johansson, G. (1973). Visual perception of biological motion and a model for its analysis. Percept. Psychophys. 14, 201–211. doi:10.3758/BF03212378
Jung, M., Hwang, J., and Tani, J. (2015). Self-organization of spatio-temporal hierarchy via learning of dynamic visual image patterns on action sequences. PLoS ONE 10:e0131214. doi:10.1371/journal.pone.0131214
Kilner, J. M. (2011). More than one pathway to action understanding. Trends Cogn. Sci. 15, 352–357. doi:10.1016/j.tics.2011.06.005
Kilner, J. M., Friston, K. J., and Frith, C. D. (2007). Predictive coding: an account of the mirror neuron system. Cogn. Process. 8, 159–166. doi:10.1007/s10339-007-0170-2
Kneissler, J., Drugowitsch, J., Friston, K., and Butz, M. V. (2015). Simultaneous learning and filtering without delusions: a bayes-optimal combination of predictive inference and adaptive filtering. Front. Comput. Neurosci. 9:47. doi:10.3389/fncom.2015.00047
Kneissler, J., Stalph, P. O., Drugowitsch, J., and Butz, M. V. (2014). Filtering sensory information with XCSF: improving learning robustness and robot arm control performance. Evol. Comput. 22, 139–158. doi:10.1162/EVCO_a_00108
Lallee, S., and Dominey, P. F. (2013). Multi-modal convergence maps: from body schema and self-representation to mental imagery. Adapt. Behav. 21, 274–285. doi:10.1177/1059712313488423
Layher, G., Giese, M. A., and Neumann, H. (2014). Learning representations of animated motion sequences – A neural model. Top. Cogn. Sci. 6, 170–182. doi:10.1111/tops.12075
Lepage, J.-F., and Théoret, H. (2007). The mirror neuron system: grasping others’ actions from birth? Dev. Sci. 10, 513–523. doi:10.1111/j.1467-7687.2007.00631.x
Meltzoff, A. N. (2007). ‘Like me’: a foundation for social cognition. Dev. Sci. 10, 126–134. doi:10.1111/j.1467-7687.2007.00574.x
Nagai, Y., Kawai, Y., and Asada, M. (2011). “Emergence of mirror neuron system: immature vision leads to self-other correspondence,” in 2011 IEEE International Conference on Development and Learning (ICDL), Vol. 2 (Frankfurt am Main: IEEE), 1–6.
Oja, E. (1989). Neural networks, principal components, and subspaces. Int. J. Neural Syst. 1, 61–68. doi:10.1142/S0129065789000475
Oram, M., and Perrett, D. I. (1994). Responses of anterior superior temporal polysensory (STPa) neurons to “biological motion” stimuli. J. Cogn. Neurosci. 6, 99–116. doi:10.1162/jocn.1994.6.2.99
Pavlova, M. A. (2012). Biological motion processing as a hallmark of social cognition. Cereb. Cortex 22, 981–995. doi:10.1093/cercor/bhr156
Perrett, D., Smith, P., Mistlin, A., Chitty, A., Head, A., Potter, D., et al. (1985). Visual analysis of body movements by neurons in the temporal cortex of the macaque monkey: a preliminary report. Behav. Brain Res. 16, 153–170. doi:10.1016/0166-4328(85)90089-0
Pouget, A., Dayan, P., and Zemel, R. (2000). Information processing with population codes. Nat. Rev. Neurosci. 1, 125–132. doi:10.1038/35039062
Puce, A., and Perrett, D. (2003). Electrophysiology and brain imaging of biological motion. Philos. Trans. R. Soc. Lond. B Biol. Sci. 358, 435–445. doi:10.1098/rstb.2002.1221
Rao, R. P., and Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 2, 79–87. doi:10.1038/4580
Rizzolatti, G., and Craighero, L. (2004). The mirror-neuron system. Annu. Rev. Neurosci. 27, 169–192. doi:10.1146/annurev.neuro.27.070203.144230
Rizzolatti, G., and Craighero, L. (2005). “Mirror neuron: a neurological approach to empathy,” in Neurobiology of Human Values, eds J.-P. Changeux, A. R. Damasio, W. Singer and Y. Christen (Heidelberg: Springer), 107–123.
Saby, J. N., Marshall, P. J., and Meltzoff, A. N. (2012). Neural correlates of being imitated: an eeg study in preverbal infants. Soc. Neurosci. 7, 650–661. doi:10.1080/17470919.2012.691429
Schrodt, F., and Butz, M. V. (2014). “Modeling perspective-taking by forecasting 3D biological motion sequences,” in Cognitive Processing, Suppl. KogWis 2014, Vol. 15, eds M. O. Belardinelli, A. Belardinelli and M. V. Butz (Tübingen: Springer), 137–139.
Schrodt, F., Layher, G., Neumann, H., and Butz, M. V. (2014a). “Modeling perspective-taking by correlating visual and proprioceptive dynamics,” in Proceedings of the 36th Annual Conference of the Cognitive Science Society (Quebec City), 1383–1388.
Schrodt, F., Layher, G., Neumann, H., and Butz, M. V. (2014b). “Modeling perspective-taking upon observation of 3D biological motion,” in Proceedings of the 4th International Conference on Development and Learning and on Epigenetic Robotics (Genoa), 328–333.
Schrodt, F., Layher, G., Neumann, H., and Butz, M. V. (2015). Embodied learning of a generative neural model for biological motion perception and inference. Front. Comput. Neurosci. 9:79. doi:10.3389/fncom.2015.00079
Stalph, P. O., Llorá, X., Goldberg, D. E., and Butz, M. V. (2012). Resource management and scalability of the xcsf learning classifier system. Theor. Comp. Sci. 425, 126–141. doi:10.1016/j.tcs.2010.07.007
Taylor, G. W., Hinton, G. E., and Roweis, S. T. (2006). “Modeling human motion using binary latent variables,” in Advances in Neural Information Processing Systems 19, eds S. Bernhard, P. John and H. Thomas (MIT Press), 1345–1352.
Thurman, S. M., and Grossman, E. D. (2008). Temporal ‘bubbles’ reveal key features for point-light biological motion perception. J. Vis. 8, 1–11. doi:10.1167/8.3.28
Tomasello, M. (1999). The human adaptation for culture. Annu. Rev. Anthropol. 28, 509–529. doi:10.1146/annurev.anthro.28.1.509
Turella, L., Wurm, M. F., Tucciarelli, R., and Lingnau, A. (2013). Expertise in action observation: recent neuroimaging findings and future perspectives. Front. Hum. Neurosci. 7:637. doi:10.3389/fnhum.2013.00637
Ulloa, E. R., and Pineda, J. A. (2007). Recognition of point-light biological motion: mu rhythms and mirror neuron activity. Behav. Brain Res. 183, 188–194. doi:10.1016/j.bbr.2007.06.007
Keywords: artificial neural networks, mental imagery, embodied simulation, sensorimotor learning, generative model, action understanding, action emulation, Bayesian inference
Citation: Schrodt F and Butz MV (2016) Just Imagine! Learning to Emulate and Infer Actions with a Stochastic Generative Architecture. Front. Robot. AI 3:5. doi: 10.3389/frobt.2016.00005
Received: 08 October 2015; Accepted: 09 February 2016;
Published: 04 March 2016
Edited by:
Guido Schillaci, Humboldt University of Berlin, GermanyReviewed by:
Lorenzo Jamone, Instituto Superior Tecnico, PortugalUgo Pattacini, Istituto Italiano di Tecnologia, Italy
Felix Reinhart, Bielefeld University, Germany
Copyright: © 2016 Schrodt and Butz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fabian Schrodt, dG9iaWFzLWZhYmlhbi5zY2hyb2R0QHVuaS10dWViaW5nZW4uZGU=
 Fabian Schrodt
Fabian Schrodt Martin V. Butz
Martin V. Butz