Behavioral Specialization in Embodied Evolutionary Robotics: Why So Difficult?

Embodied evolutionary robotics is an on-line distributed learning method used in collective robotics where robots are facing open environments. This paper focuses on learning behavioral specialization, as defined by robots being able to demonstrate different kind of behaviors at the same time (e.g., division of labor). Using a foraging task with two resources available in limited quantities, we show that behavioral specialization is unlikely to evolve in the general case, unless very specific conditions are met regarding interactions between robots (a very sparse communication network is required) and the expected outcome of specialization (specialization into groups of similar sizes is easier to achieve). We also show that the population size (the larger the better) as well as the selection scheme used (favoring exploration over exploitation) both play important – though not always mandatory – roles. This research sheds light on why existing embodied evolution algorithms are limited with respect to learning efficient division of labor in the general case, i.e., where it is not possible to guess before deployment if behavioral specialization is required or not, and gives directions to overcome current limitations.

1. Introduction

Embodied evolutionary robotics (EER) is defined as the design of on-line distributed evolutionary algorithms to be implemented in a population of robots with limited computation and local communication capabilities (Watson et al., 2002; Eiben et al., 2010). These algorithms can be deployed in a priori unknown and open environments, and aim at optimizing on-the-fly the individual’s and (ideally) the group’s performance with respect to a pre-defined objective. EER takes its root in Evolutionary Robotics (Nolfi and Floreano, 2000; Doncieux et al., 2015), but is also related to evolutionary swarm robotics (Trianni et al., 2008), as it is sometimes (though not always) concerned with the automated design of control architecture for large, swarm-like, population of robots.

In recent years, the on-line nature of such algorithms was shown to be very robust when conducting experiments with real robots (Watson et al., 2002; Prieto et al., 2010; Bredeche et al., 2012; Trueba et al., 2013): compared with more classic evolutionary robotics setup, the emphasis in EER is on the design of robust algorithms (i.e., design while already deployed) rather than on producing robust solutions (i.e., design then deploy) (Doncieux et al., 2015; Silva et al., 2016). However, the complexity of the tasks to be achieved has been quite limited so far, either resulting with each individual maximizing its own benefit [e.g., phototaxis (Watson et al., 2002), foraging, exploration, etc.] or in a limited level of cooperation among individuals who all display the same typical behavior [e.g., energy sharing (Montanier and Bredeche, 2011)].

To go further, evolving more complex organizations such as division of labor is clearly part of the research agenda. However, in the context of embodied evolution, the amount few works have tackled the evolution of populations where individuals can split in two (or more) sub-groups with specific roles. In this paper, we are interested in the evolution of specialized behaviors as a key milestone toward tackling more complex problems in collective robotics.

Classic (as in off-line) evolutionary robotics has already been used as a tool to explore important issues such as the nature of self-organized regulation mechanisms (Waibel et al., 2006; Duarte et al., 2011, 2012a,b; Lichocki et al., 2012; Ferrante et al., 2015), the benefits of communication (Trianni et al., 2007; Goldsby et al., 2010), the importance of coordination (Bernard et al., 2016b), and the trade-off between evolving polymorphic and monomorphic populations (Waibel et al., 2009; Bernard et al., 2015, 2016a; Tuci and Rabérin, 2015). However, embodied evolutionary robotics poses a problem on its own as mating and reproduction are performed in situ, meaning that how and where interactions between individuals are performed actually influence the course of evolution.

So far, the embodied evolution of specialized behaviors has been studied in two contexts: whether sub-tasks are geographically separated or not. First, some works considered the evolution of specialized behaviors in structured environments, where separate regions call for specific skills [e.g., cleaning tasks requiring two different methods (Prieto et al., 2010), increasing reproductive success with either phototaxis or photophobis behaviors (Bredeche et al., 2012; Bredeche, 2014)]. In this context, geographical separation plays an important role as sub-populations can evolve without interacting with one another due to the limitation in terms of communication range, therefore favoring the acquisition and conservation of different skills.

Second, other works have considered whether specialized behaviors could be acquired without geographical separation. It has been shown that specialized foraging behaviors can co-exist in a population of individuals (Haasdijk et al., 2014): faced with two resources available in limited quantity, the population evolves into two sub-groups, each specialized to forage one particular type of resource. However, this work showed that balancing between the two resources is challenging and could only be achieved by introducing a market mechanism explicitly favoring the smallest sub-group.

Possibly the most advanced work on this topic is presented by Trueba et al. (2013). The authors conducted an in-depth empirical study of behavioral specialization within the same geographic location. The authors showed that very specific values for the frequency of replacement and a carefully tuned recombination operator (with low rate) could be used to enforce behavioral specialization in a population of foraging individuals. However, validation in a realistic robotic setup remains to be done as the problem used in this study was greatly simplified: each robot’s genome contains a single-gene that can take only three possible values, each value accounting for predefined behaviors.

In light of the limited results obtained so far, we address the following question in this paper: in the absence of geographical separation, what challenges are posed by the evolution of behavioral specialization in embodied evolutionary robotics? Specifically, we aim at identifying the limiting constraints in the evolution of behavioral specialization, including a more general formulation of the limiting factors with respect to both setups studied so far that is with or without geographical separation.

Indeed, the challenge of evolving specialization without geographical separation in embodied robotics echoes with concerns in biological speciation, where the lack of reproductive isolation is known to be a major obstacle with respect to genotypic divergence (Coyne and Orr, 1998; Gavrilets, 2003; Nosil, 2012). In this paper, we explore how reproductive isolation (whether by geographical separation or any other means) can favor the emergence of specialization, and what are the other relevant mechanisms at play. In particular, we also explore how selection and population size may impact the evolution of specialized behavior.

In the following, we perform an experimental study using different flavors of embodied evolutionary algorithms in two variations of a task with autonomous virtual robots: a foraging task with and without geographical separation. Furthermore, an abstract model is presented and used to identify the conditions required for behavioral specialization to occur in the general case, i.e., without referring to any specific evolutionary mechanisms to artificially enforce specialization, such as dedicated evolutionary operators or environment-induced phenotypic plasticity.

2. Method

2.1. A Foraging Task with Mutually Exclusive Resources

In order to study the evolution of behavioral specialization, we devised two experimental setups where foraging resources are required to survive. In both cases, two resources are available, and located in a particular location. These locations may change through time, requiring the agents to move accordingly. In order to successfully get energy from a particular resource, one agent must be on top of the resource location and must be able to synthesize this particular resource into energy, which requires a particular genetic trait.

Both experimental setups are defined as a circular arena without obstacles. Resources R₀ and R₁ are set at a specific location, which initial locations may differ with respect to the environment considered (cf. Figure 1), and which regularly moves from one location to another through a total of 8 possible locations. In the first environment (termed collocateEnv), the two resources are located in the same area and will move to a similar new area on a regular basis. In the second environment (termed seperateEnv), the two resources are located on the opposite side to one another, and will also move on a regular basis, always remaining far from one another. In both environments, resource’s locations will move counter-clockwise.

FIGURE 1

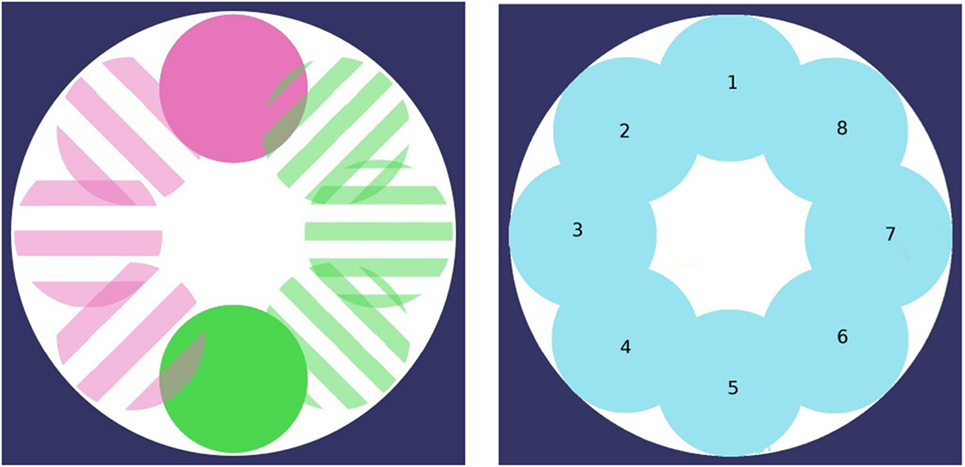
Figure 1. The two foraging areas are changing locations through time (8 possible locations, moving counter-clockwise). Foraging areas may or may not share the same position. Left: both regions simultaneously move to the same position (collocateEnv setup); right: both regions simultaneously move, always on the opposite side from one another (seperateEnv setup).

The ability for an agent to synthesize energy from one resource is defined by one specific gene, termed g_skill. It is defined in (−1.0, +1.0), and conditions the amount energy that can be automatically extracted from one resource when located in its area. The energy synthesis function, F_synth, is shown in Figure 2. It illustrates that the function is designed so that an agent can get energy from one resource only (in addition to being located in the right area).

FIGURE 2

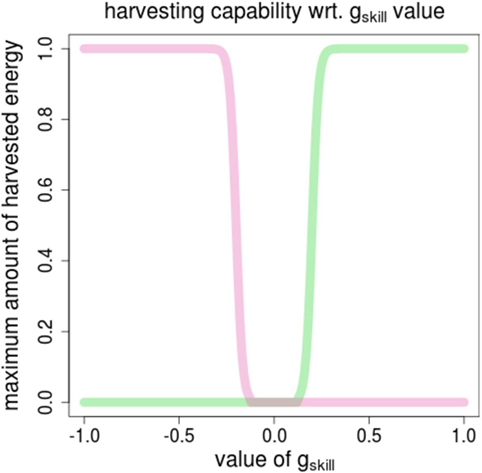
Figure 2. The energy synthesis function, F_synth for computing the amount of foraged energy depending on the value of the g_skill gene. Pink (vs. green) curve shows the amount of energy of R₀ (vs. R₁) wrt. the value of g_skill [defined in (−1.0, +1.0)].

In order to account for the evolution of specialization, we introduce an additional constraint regarding the carrying capacity of the resources. Each resource area provides a limited amount of energy available at each time step, which is set so that only half the population can feed from a particular resource. Access to a resource is set according to a first-come, first-served basis: if an agent gets access to a resource, it may extract from it until it leaves the area (or until the resource area is relocated). As a result, the optimal survival strategy for the population of agents is to specialize half the agents on one resource (both in terms of tracking and synthesizing capability) and the other half on the other resource.

The fitness function for robot x at time t is defined as $fitness(x,t)={\displaystyle {\sum }_{i=t}^{t-w}}{f}_i(x)$ where f_i(.) is computed at time step i depending on the energy synthesis function F_synth with the value of g_skill as parameter and the availability of resources at this particular location. A sliding window of size w is used in order to get a reliable estimation of the agent performance throughout its lifetime, and no genome (nor fitness value) is broadcasted during the first w iterations. Whether the value of g_skill is negative or positive conditions the resource to be harvested (g_skill <0 vs. g_skill >1, means that resource R_o vs. R₁, will be harvested), and, if the target resource is available at this location, the exact value of g_skill determines the amount of energy to be harvested thanks to the F_synth function.

In this setup, resource availability is true if the robot is located close enough to the resource and if the resource has not yet reached its carrying capacity.

2.2. Algorithms

The control function for all agents is a perceptron without hidden layer and an hyperbolic tangent activation function, which maps sensory inputs (12 proximity sensors, ground detectors, energy level, angle and distance to energy sources, and a bias node) to motor outputs (left and right motor speed). All sensory and motor values are normalized in (−1, +1). This results in a total of 38 weights to evolve. The control architecture is illustrated in Supplementary Material 1.

For the sake of simplicity, we devised a simple implementation of embodied evolution, which we term vanillaEE. As with other embodied evolution algorithm, it is assumed that each agent is able to receive genomes and current fitness values from agents within a pre-defined range, as well as to send its own genome and current fitness value to these nearby agents. After a pre-defined duration, which corresponds to the time allowed for evaluation, one of the genomes received previously is selected, and mutated, to produce a new genome, which will be used to provide the parameters for the control function in the next evaluation period.

The pseudo-code for this algorithm is described as Algorithm 1. It starts with a randomly initialized genome, whose parameters are used to set up the neural network controller. At each time step, the agent moves according to its controller outputs and broadcasts its current genome (and possibly its current fitness). Reciprocally, it may receive incoming genome from other neighboring agents [lines 13–16 of the algorithm – the ListeningQueue is filled by a subroutine (not shown here) and getListeningQueueContent(.) (line 13) is a non-blocking call]. At the end of the evaluation time, the current genome is deleted and replaced, if available, by a genome build from the list of genomes previously received [the select(.) and applyVariation(.) functions]. Once this new genome’s parameters are used to set up the new controller, the list of genomes is emptied. Being a template algorithm, the vanillaEE algorithm may yield many variations depending on the particular implementations of the functions used (see below).

ALGORITHM 1

ALGORITHM 1. The VanillaEE algorithm.

It is important to note that selection pressure in embodied evolution acts at two levels: first, pure performance with relation to a task can be evaluated by a fitness function and used to select a particular genome; second, an agent can also boost the chance for survival of its own genome by spreading more copies of this genome than other agents do, especially if a stochastic selection operator is used.

In the following, we use two different variations over the canonical vanillaEE algorithm, instantiating a particular selection scheme for each:

• vanillaEE-elitist: the best genome out of the genomes available (i.e., received from other agents during the last evaluation session) is selected (cf. line 20 of Algorithm 1). This is a pure exploitation strategy.

• mEDEA (or vanillaEE-noFitness): selection is performed by choosing a random genome among the genomes available. Therefore, no selection pressure wrt. fitness value is applied, but selection pressure wrt. ability to spread one’s own genome is still at work. The mEDEA algorithm has been extensively studied in previous works (Bredeche and Montanier, 2010; Bredeche et al., 2012; Bredeche, 2014) and provides a good baseline for embodied evolution. Efficient genomes are able to spread themselves and perform the necessary actions for survival, such as foraging, without requiring a fitness function to do so. However, the lack of selection pressure toward performance (as opposed to selection pressure toward survival only) can also lead to mitigate results with respect to foraging (i.e., no more than what is required to survive is foraged). Moreover, in some cases, the lack of selection pressure at the individual level can also ease up survival. With respect to Algorithm 1, the mEDEA algorithm does not implement the select operator (cf. line 20) nor the computeFitness() function call (cf. line 10), and does not broadcast a fitness value (cf. line 11) nor receives fitness values with incoming genomes (cf. line 13).

For both algorithms, genome initialization is performed by randomly picking weight values in (−1.0, +1.0), and the variation operator is defined as a gaussian mutation with σ = 0.1. Evaluation time (or lifetime) for one genome is set to 600 iterations.

3. Results

We devised a total of four setups testing all possible combinations of algorithms (mEDEA, VanillaEE-elitist) and environments (collocateEnv, separateEnv). For each setup, 50 independent runs are performed, each using the parameters described in Table 1. Experiments are implemented in the Roborobo 2D simulation tool (Bredeche et al., 2013) with 200 robotic agents.¹

TABLE 1

Table 1. Parameters used.

3.1. Evolution of Specialization

For each environment, two algorithms are tested: mEDEA (with random selection) and VanillaEE-elitist (with elitist selection). For each setup combining an algorithm and an environment, we classify each of the 50 independent runs depending on their outcomes: (1) all individuals display a similar harvesting pattern wrt. the resource harvested (“one group”), (2) two patterns are observed (“two groups”), and (3) individuals fail to harvest any resources as the population is extinct (“extinct”). For the first two outcomes, classification is made possible by looking at the values of g_skill in the population, i.e., whether there is one or two clusters of values. As an example, Figure 3 shows all g_skill values in the population for two typical runs over time.

FIGURE 3

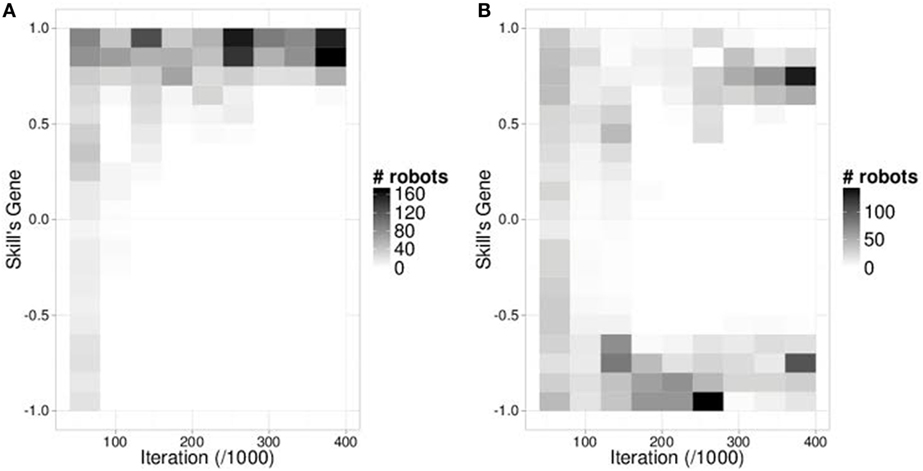
Figure 3. Skill’s gene heatmap representative of two situations. (A) heatmap of a run with one group. (B) heatmap of a run with two groups. The number of iteration is shown on the x-axis and the values of g_skill are shown on the y-axis. Darker cells’ values correspond to more robots using a g_skill value. A run receives the label one group if it relies on either positive values [such as in (A)] or only negative values. If two groups are observed in one run (one using positive g_skill values and the other using negative g_skill values), it is tagged with the two groups label [such as in (B)].

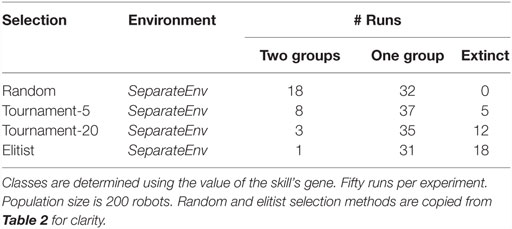
Results are shown in Table 2. For both algorithms, specialization fails to evolve in the collocateEnv environment, with the elitist algorithm also failing partly to even evolve any viable behaviors (two-third of the runs go extinct). The outcome is different in the seperateEnv environment as the mEDEA algorithm is actually able to evolve specialization in half of the runs, a result that is not observed with the VanillaEE-elitist algorithm. A statistical test (Pearson’s χ²-squared) confirms the obvious: strategies used in each environment with the random selection scheme produce significantly different results (p-value <0.01).

TABLE 2

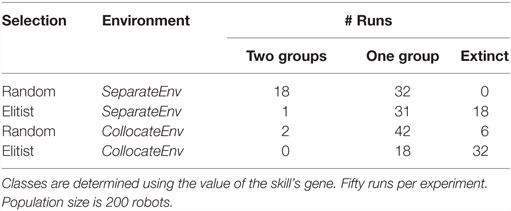
Table 2. Classification of the outcome of runs using random selection (i.e., the mEDEA algorithm) and elitist selection.

Figures 4A,B compare the outcome of runs using mEDEA algorithm in the seperateEnv environment. As expected, runs where two sub-groups evolve also display the highest survival rate, as specialization is the only way for the whole population to survive due to limited available amount of each resource. Results are identical with the VanillaEE-elitist algorithm.

FIGURE 4

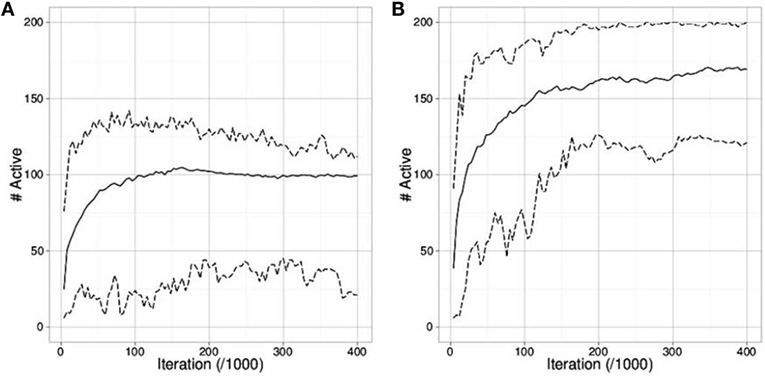
Figure 4. Number of active robots (mean, min and max from the 50 runs) in the separateEnv where (A) only one group is evolved (i.e., one cluster of values for the g_skill gene) and (B) two groups are evolved (i.e., two clusters of values). The maximum number of active robots is 200.

Results show that adding a fitness function (VanillaEE-elitist) not only hinders the survival rate but also almost completely shuts down the possibility to evolve specialization. This sheds a negative light on the use of an explicit selection pressure defined through a fitness function over simply considering environmental selection pressure, as with the mEDEA algorithm. However, we can hypothesize that performing selection solely based on task-dependant fitness values does not leave much room for exploration of survival strategies.

3.2. Investigating the Trade-off between Exploration and Exploitation

In order to explore the impact of using a fitness function, we posit that there is a trade-off between exploration, which in this case balance toward environmental selection pressure, and exploitation, i.e., selection pressure provided by using a fitness function. We introduce the VanillaEE-tournament-k algorithm, similar to what has been proposed by Fernandez Pérez et al. (2015): this algorithm uses a tournament selection of size k to regulate the trade-off between the exploitation of a fitness function and the exploration of solutions allowing the survival of robots. Tournament selection selects the best genome out of k randomly picked genomes among those received during the last evaluation session. Tournament sizes used are k = 5 and k = 20. Large tournament sizes tends to converge toward elitism selection (favoring exploitation) while small tournament sizes tends to favor exploration. It should be noted that the mEDEA algorithm is identical to a VanillaEE-tournament algorithm with k = 1, as using such a value implies random selection.

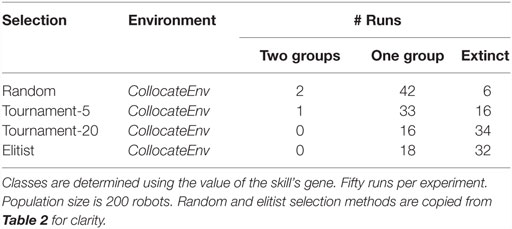
We design 4 new setups, testing all possibilities between the two tournament sizes and the two environments (collocateEnv, separateEnv). For each setup 50 independent runs are performed and classified as before. Results shown in Tables 3 and 4 reveal that as the pressure toward exploitation increases, (a) the number of runs with extinctions also increases (in both setups) and (b) the number of runs where two specialized groups evolve decreases, at least when resources are seperated. A χ² statistical test is used for significance.

TABLE 3

Table 3. Classification of the outcome of runs where resources are separated.

TABLE 4

Table 4. Classification of the outcome of runs where resources are collocated.

The smaller the tournament’s size, the closer the results are to the results obtained with random selection. Reciprocally, larger size of tournament size produce results close to results obtained with the elitist selection scheme. We conclude that increasing the pressure toward the exploitation of genomes with higher fitnesses leads to sub-optimal solutions. While this mechanism allows us to mitigate the pressure from task-driven fitness function, the pressure from the environment keeps a strong influence, and the question remains open as to why specialization is (nearly) impossible when resources are not spatially separated.

3.3. Discussion

As expected from Trueba et al. (2013), we show that when resources are collocated, it is very difficult to evolve specialization. While Trueba et al. (2013) was successful at finding a very precise set of parameter values to achieve specialization, this was done under very specific conditions: either an abstract model or a toy problem (a genome with one parameter that can take one among three possible values). Our results confirm that in the general case, evolving specialization is challenging at the least, and unlikely if resources are collocated.

Similarly, and in accordance with Prieto et al. (2010), Bredeche et al. (2012), and Bredeche (2014), we show that geographical separation promotes the evolution of specialization. However, specialization is not always evolved here (at best 36% of the runs for the best setting), while it was always the case in previously cited works. This is actually not a surprise as we face a more challenging set-up: we consider extinction, that is, the possibly to engage in evolutionary dead-ends. As a consequence, not only it is risky for the population to switch from one equilibrium (e.g., foraging without specialization) to another (e.g., foraging the two resources) but also historical contingencies can lead to early extinction, if foraging is not evolved in the very first generations.

From the results we obtained so far, we now question the current claim stating that one needs either geographical separation and/or very specific evolutionary operators as a necessary condition. In fact, bipolar crossover (Prieto et al., 2010), high replacement frequency (Trueba et al., 2013), low recombination rate (Trueba et al., 2013), market mechanism (Haasdijk et al., 2014), and geographical separation (Bredeche et al., 2012; Bredeche, 2014) can all be seen as coming from the same origin: a mean to achieve reproductive isolation.

Therefore, we posit this new hypothesis: reproductive isolation is a key factor in the evolution of specialization, whether the population is geographically dispersed or not. In order to investigate this assumption, we explore in the next Section an abstract model to study the impact of reproductive isolation independently from how it is implemented in practical, i.e., through geographical separation or any other means, and reveal the critical conditions for evolving specialization.

4. Analysis

In order to identify the necessary conditions required to evolve specialization, we introduce an abstract model to perform computationally intensive experiments. In this model, each agent is located on a node within a graph, and each node hosts one agent only. Edges between two nodes indicate that genetic material is exchanged by the agents. Each agent lives for four iterations, has a battery that consumes one unit per iteration, and forage from resources R₀ or R₁ depending on the value of its g_skill gene (as before, a value close to zero means no foraging), just as in the setup used in the previous Section (except that a genome contains now a single g_skill gene). As before, each resource enables the survival of one half of the population, meaning that specialization into two groups is mandatory for the whole population to survive. We do not consider extinction: an agent, which runs short of energy is deactivated for 4–14 iterations (random), then listen to its neighbors during 4 iterations, and is finally reactivated using one of the received (and mutated) genome.

For each run, we randomly generate graphs, fixing only the number of nodes and the average number of edges for each node. The number of edges acts as a proxy for the study of reproductive isolation. In order to do so, we have devised a method, which generates random connex graphs with a desired density of edges between nodes. The minimal density is $\frac{2}{n}$ (i.e., a ring), with n the number of agents and the maximal density is 1.0 (i.e., a complete graph). Supplementary Material 2 provides a formal definition of density, and Supplementary Material 3 provides the pseudo-code for the graph generation algorithm.

This simplified model corresponds to the collocateEnv environment used earlier, where all agents may access any of the two resources at all time, but with interactions between agents being determined by the selected density. In this Section, we first explore what are the critical parameters and parameter values that makes specialization possible (Subsection 4.1). Then, we investigate whether the non-homogeneous availability of resources impacts (or not) the possibility to evolve specialization (Subsection 4.2).

4.1. Interaction between Reproductive Isolation, Population Size, and Selection Pressure

We identify three candidate hypotheses that, if true, may lead to the evolution of specialization:

1. increasing reproductive isolation may act as a protection for groups with different skills to co-exist. This will be tested by varying the graphs’ density, i.e., the mating opportunities for each agent;

2. increasing population size may reduce the stochastic effect known to occur in small populations, which could otherwise hinder the fixation of beneficial mutations. Two different population sizes will be tested, using graphs with 100 and 500 nodes.

3. increasing exploration (over exploitation) may help to escape local minima, defined here as the convergence for the whole population to one efficient, yet sub-optimal, behavior (e.g., foraging only one resource). Tournament selection with various tournament sizes (k) will be tested, from k = 1 (i.e., mEDEA, emphasizing exploration) to k = 50 (i.e., selection largely favoring exploitation).

Figure 5 shows the results obtained with different tournament sizes (k = 1, 2, 3, 5, 10, 50), population size (100 and 500) and densities (starting from the minimal density wrt. population size). For each parameter sets, 160 independent runs are conducted (i.e., a total of 5760 runs). Results are compiled from the data of the last generation for each run and shown as violin plots to capture the details of possibly non-uniform distributions (i.e., full histograms, rather than box-plots).

FIGURE 5

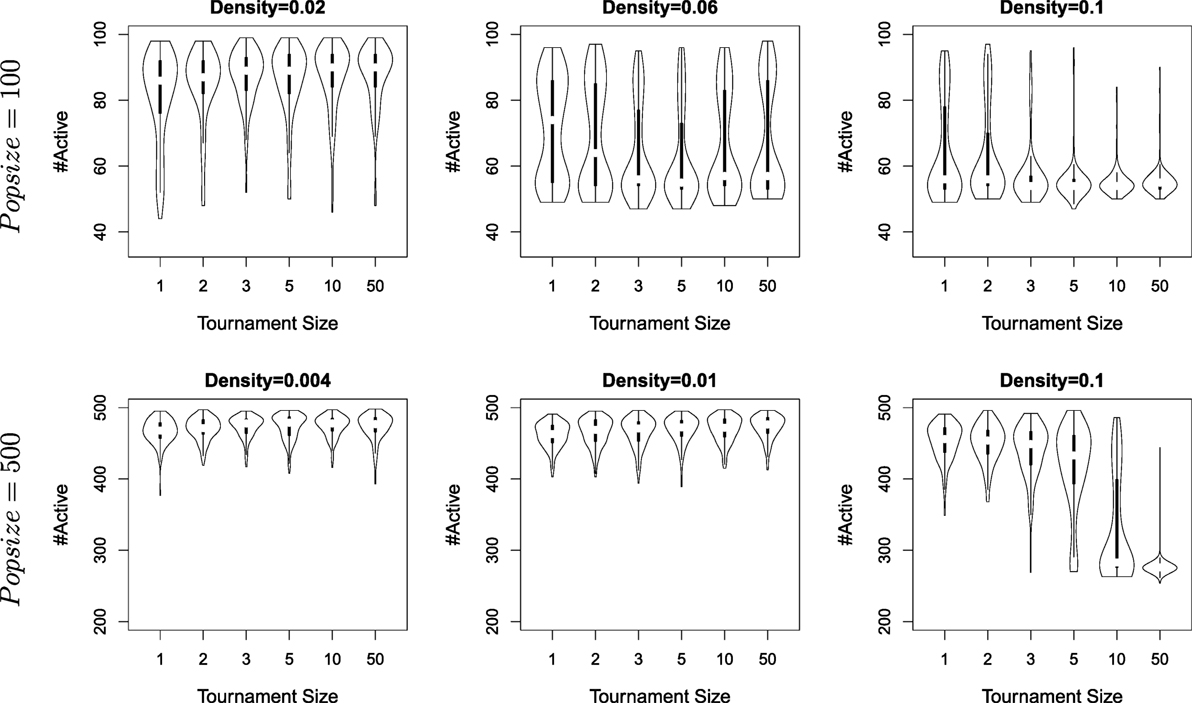
Figure 5. The number of agents alive at the end of a simulation for different densities, different tournament sizes (from 1 to 50), and population sizes (100 and 500). Each violon plots is built from the result of 160 independent runs.

All three hypotheses are validated, though their importance varies. Lower densities always lead to specialization, whatever the population size or the selection pressure. A large population size favors specialization, and selection favoring exploitation (i.e., larger tournament sizes) turns to be detrimental as density increases. Actually, the lack of detrimental effect of large tournament sizes when density is low can be explained that for the lowest densities considered, tournament sizes is quickly far superior to the actual number of neighbors (e.g., for the lowest densities, the number of neighbors for one node is 2) – in other words, tournament sizes with k > 2 do not impact further the outcome of selection for such low densities.

As a conclusion to our original question, reproductive isolation is a key factor for evolving specialization, with a larger population size and a selection scheme favoring exploration rather than exploitation as secondary factors. Results from this Section also shed light on the negative results obtained in Section 3: the failure of all algorithms to achieve specialization in the collocateEnv environment is explained by the lack of restrictions on mating opportunities (all individuals are mixed together).

4.2. Deleterious Effects of Non-Homogeneous Resources Availability

So far, we have considered situations where both resources provide the same quantity of energy. We now depart from our initial question to consider the possible impact of resources being available in different amounts. We use the same setup as in the previous Subsection, with only k = 1 as tournament size (i.e., the mEDEA algorithm), and consider two environments [termed S(75,25) and S(90,10)] with different resource distributions: one where R₀ (vs. R₁) provides 75% (vs. 25%) of the amount of energy required to sustain the whole population, and another where R₀ (vs. R₁) provides 90% (vs. 10%) of the amount of energy.

Results are shown in Figure 6, compiled from 160 runs for each set of parameters (i.e., a total of 3200 runs). Specialization can be observed whenever a run displays more active agents that can be sustained with one resource only (cf. the red lines in the graphs, which mark the maximum level of sustainability by foraging only the largest resource). When the distribution of resources follows a 75/25 distribution, more than half of the runs with a population of 100 ends up with specialization, as well as all runs with a population of 500. Specialization is confirmed by looking at the middle column of Figure 7, which displays the same results as the previous, but over-emphasizes on the (possibly different) values of g_skill rather than the number of runs. The distribution of the g_skill gene values show that all runs that display a survival success to be high above the threshold (the red lines in the graphs) are explained by the occurrence of two groups of individuals, one specialized to forage R₀ and the other to forage R₁.

FIGURE 6

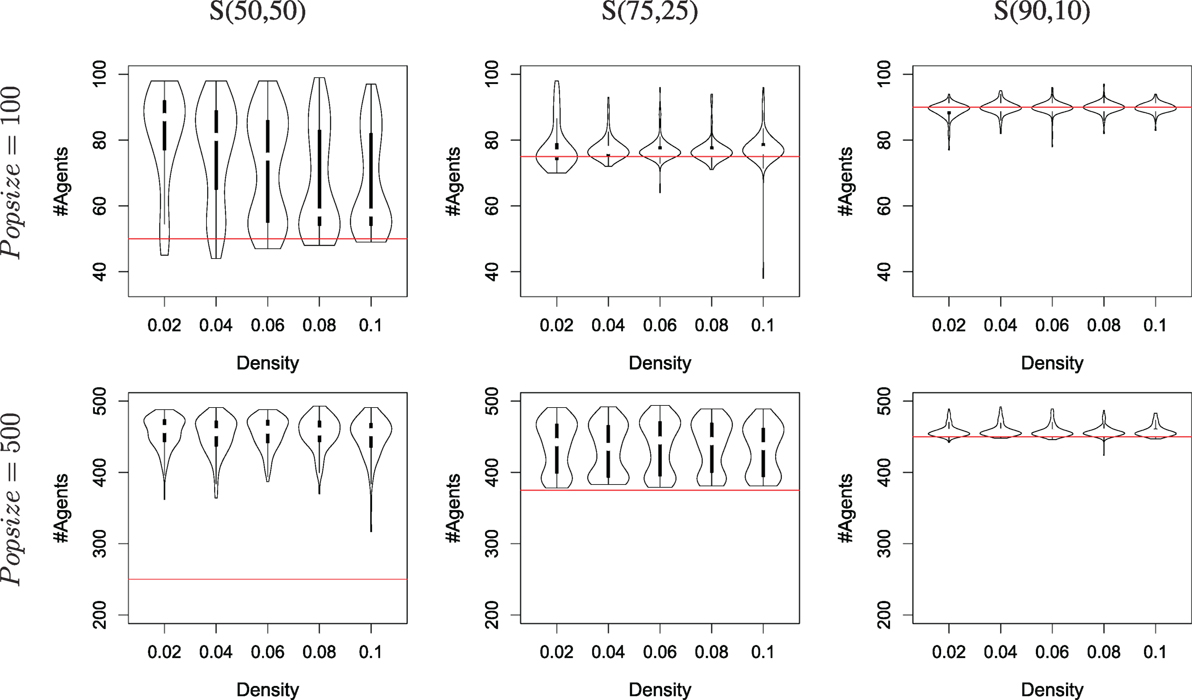
Figure 6. The number of agents alive at the end of a simulation depending on the distribution of resources available for different densities and population sizes (100 and 500), using the mEDEA algorithm. Each violon plots is built from the result of 160 independent runs. The column marked S(50,50) is a recap from Figure 5 for ease of comparison. The column marked S(75,25) show results in an environment where resource R₀ (vs. R₁) provides 75% (vs. 25%) of the amount of energy required for the whole population to survive. The column marked S(90,10) does the same for a 90/10 balance between the two resources. The horizontal line, drawn in red, shows the theoretical upper limit in terms of number of agents alive if only one resource is foraged.

FIGURE 7

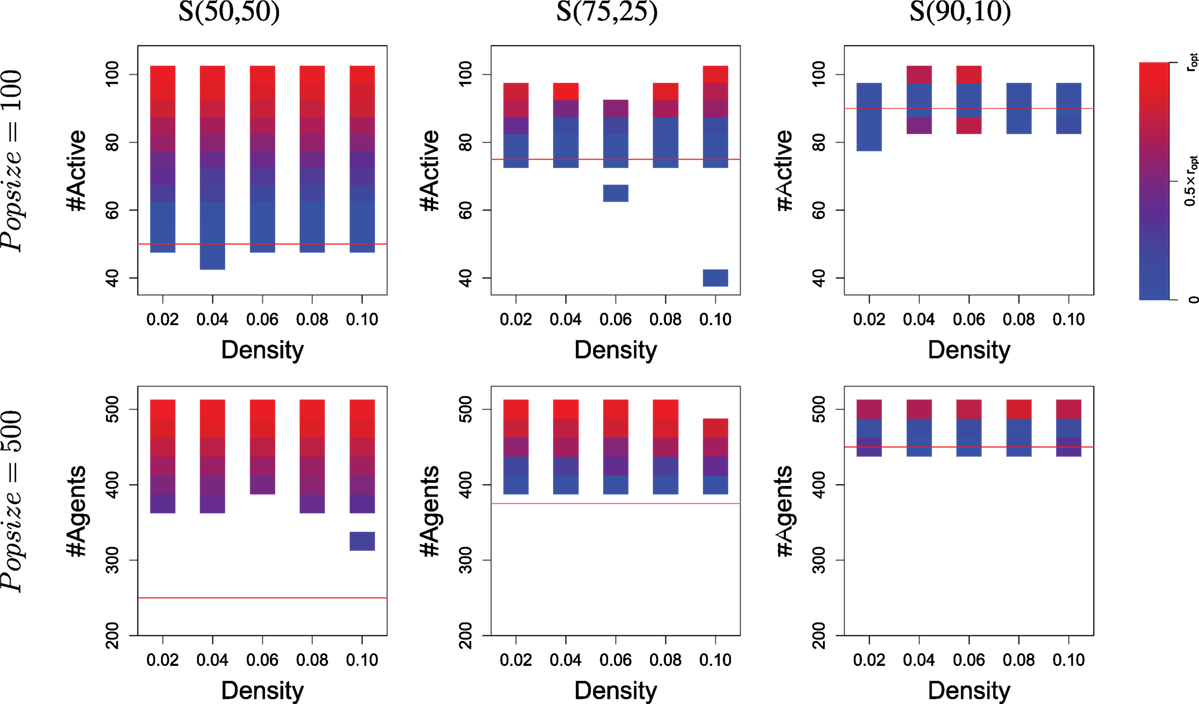
Figure 7. The level of specialization (at the end of evolution) within populations depending on the number of active agents. Results are similar to Figure 6 but display the average specialization level observed in runs, rather than the number of runs. For each cell (i.e., rectangle covering a small interval in the number of active agents), the level of specialization is calculated as the distance between the ideal distribution over the two resources and the observed distribution (averaged over all runs considered in this cell). Blue means no specialization (i.e., only one resource foraged); red means specialization (i.e., population is split in two groups, each with an optimal size wrt. resources availability). A detailed explanation of how specialization is computed can be found in Supplementary Material 4. Note that the two cells colored red which are below the threshold line in the upper-left graph are due to successful specialization but only within a sub-part of the population (i.e., some agents carry a g_skill value around zero). It is important to keep in mind that cells may correspond to very different number of runs: this Figure provides complementary information to what is shown in Figure 6.

Results are different when resources follow a 90/10 distribution, as Figure 6 displays a survival rate around the threshold for runs with a population size of 100 and slightly above for most runs with a population size of 500. A Wilcoxon rank-sum test confirms that using a population of 500 yields significantly better results than a population of 100. Again, Figure 7 provides a more precise analysis. Runs with a population of 100 almost never display specialization while runs with a population of 500 and a high survival rate are always displaying specialization (the top red boxes in the bottom-right graph).

Heterogeneous distributions of resources do have a negative effect on the ability to evolve specialization, though it can be mitigated – to a limited extent – by increasing the population size. This poses yet another challenge about ensuring the evolution of specialization even with a small population and unbalanced distribution of resources availability.

5. Conclusion and Perspectives

In this paper, we explored why evolving behavior specialization remains an important challenge in embodied evolutionary robotics. We defined a foraging task where two resources are available in limited quantity to identify the critical parameters at work in the evolution of specialization. We implemented this task in both a pseudo-realistic robotic simulation and an abstract graph-based model.

The take-home messages from this work are threefold. First, reproductive isolation is mandatory for the evolution of specialization, whether such isolation is due to geographic constraints or particular mating strategies. This may open ways toward defining new mechanisms and/or operators to reduce the amount of mating interactions between individuals, such as preferential choice.

Second, larger population sizes also help, leading toward an important remark: a significant amount of works in embodied evolutionary robotics are concerned with small populations (approximately 10 robots), and face problems that are possibly unique to such population sizes. To some extent, embodied evolution with either small or large populations may well be to two different classes of problems, each with their own issues, and we ought to be cautious not to generalize conclusions obtained with larger populations to smaller populations, and reciprocally.

Third, a selection method should leave room to exploration, to be understood as performing a trade-off between environment-driven selection versus task-driven fitness function selection. The benefit of such a trade-off has already been explored elsewhere (Haasdijk et al., 2014), but mechanisms favoring exploration explicitly could also be explored [e.g., applying novelty measures for evolutionary swarm robotics (Gomes et al., 2013)]. Here lies an important aspect of embodied evolution: mating is evolved as a strategy, and is not given for free as an algorithmic feature as would be the case with a more classic evolutionary algorithm.

As for future works, a natural extension of this work is to consider the evolution of specialization into more than two subgroups, as well as to consider behaviors that are substantially different. So far, we have considered specialization as being the product of few skills (ability to forage one resource, and possibly to track its location), which may imply a limited distance in the genotypic space between the two genetic codes. Things may be very different if two (or more) behaviors exist in very different locations of the search space: except for very specific historical contingencies or dedicated operators it might be very difficult to co-evolve both behaviors simultaneously.

Another extension of this work is to consider setups where both generalists and specialists can evolve. Even if a population of generalists may provide a suboptimal solution, it is not clear that specialists could still evolve, even when the conditions discussed throughout this paper are met. Finally, it is also not clear what would be the respective advantages and drawbacks to achieving behavioral specialization through evolutionary adaptation (as explored here) versus lifetime adaptation (e.g., learning or memory mechanisms).

Author Contributions

Conceived and designed the experiments: J-MM, SC, and NB. Analysed the data: J-MM, SC, and NB. Performed the experiments: J-MM and SC. Coordinated the writing: NB.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work is supported by the European Unions Horizon 2020 research and innovation programme under grant agreement No 640891, and the ERC Advanced Grant EPNet (340828). Part of the experiments presented in this paper were carried out using the Grid’5000 experimental testbed, being developed under the INRIA ALADDIN development action with support from CNRS, RENATER, and several Universities as well as other funding bodies (see https://www.grid5000.fr). The other parts of the simulations have been done in the supercomputer MareNostrum at Barcelona Supercomputing Center – Centro Nacional de Supercomputacion (The Spanish National Supercomputing Center).

Supplementary Material

The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/frobt.2016.00038

Footnote

1. ^Code for all experiments in this Section and the next: http://pages.isir.upmc.fr/~bredeche/Experiments/Frontiers2016/

References

Bernard, A., André, J.-B., and Bredeche, N. (2015). “Evolution of cooperation in evolutionary robotics: the tradeoff between evolvability and efficiency,” in European Conference on Artificial Life (ECAL 2015) (Cambridge, MA: MIT press), 495–502.

Google Scholar

Bernard, A., André, J.-B., and Bredeche, N. (2016a). “Evolving specialisation in a population of heterogeneous robots: the challenge of bootstrapping and maintaining genotypic polymorphism,” in Artificial Life 15: Proceedings of the Fifteenth International Conference on the Synthesis and Simulation of Living Systems, 1–8.

Google Scholar

Bernard, A., André, J.-B., and Bredeche, N. (2016b). To cooperate or not to cooperate: why behavioural mechanisms matter. PLoS Comput. Biol. 12:e1004886. doi:10.1371/journal.pcbi.1004886

CrossRef Full Text | Google Scholar

Bredeche, N. (2014). “Embodied evolutionary robotics with large number of robots,” in Artificial Life 14: Proceedings of the Fourteenth International Conference on the Synthesis and Simulation of Living Systems, Vol. 1 (New York: The MIT Press), 272–273.

Google Scholar

Bredeche, N., and Montanier, J.-M. (2010). “Environment-driven embodied evolution in a population of autonomous agents,” in Parallel Problem Solving from Nature (PPSN) (Berlin; Heidelberg: Springer), 290–299.

Google Scholar

Bredeche, N., Montanier, J.-M., Liu, W., and Winfield, A. F. T. (2012). Environment-driven distributed evolutionary adaptation in a population of autonomous robotic agents. Math. Comput. Model. Dyn. Syst. 18, 101–129. doi:10.1080/1387395YYxxxxxxxx

CrossRef Full Text | Google Scholar

Bredeche, N., Montanier, J.-M., Weel, B., and Haasdijk, E. (2013). Roborobo! a fast robot simulator for swarm and collective robotics. CoRR 2, 2.

Google Scholar

Coyne, J. A., and Orr, H. A. (1998). The evolutionary genetics of speciation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 353, 287–305. doi:10.1098/rstb.1998.0210

CrossRef Full Text | Google Scholar

Doncieux, S., Bredeche, N., Mouret, J.-B., and Eiben, A. E. (2015). Evolutionary robotics: what, why, and where to. Front. Robot. AI 2:4. doi:10.3389/frobt.2015.00004

CrossRef Full Text | Google Scholar

Duarte, A., Pen, I., Keller, L., and Weissing, F. J. (2012a). Evolution of self-organized division of labor in a response threshold model. Behav. Ecol. Sociobiol. 66, 947–957. doi:10.1007/s00265-012-1343-2

CrossRef Full Text | Google Scholar

Duarte, A., Scholtens, E., and Weissing, F. J. (2012b). Implications of behavioral architecture for the evolution of self-organized division of labor. PLoS Comput. Biol. 8:e1002430. doi:10.1371/journal.pcbi.1002430

CrossRef Full Text | Google Scholar

Duarte, A., Weissing, F. J., Pen, I., and Keller, L. (2011). An evolutionary perspective on self-organized division of labor in social insects. Ann. Rev. Ecol. Evol. Syst. 42, 91–110. doi:10.1146/annurev-ecolsys-102710-145017

CrossRef Full Text | Google Scholar

Eiben, A. E., Haasdijk, E., and Bredeche, N. (2010). “Chapter 5.2: embodied, on-line, on-board evolution for autonomous robotics,” in Symbiotic Multi-Robot Organisms: Reliability, Adaptability, Evolution, eds P. Levi and S. Kernbach (Berlin; Heidelberg: Springer), 361–382.

Google Scholar

Fernandez Pérez, I., Boumaza, A., and Charpillet, F. (2015). “Decentralized innovation marking for neural controllers in embodied evolution,” in Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation (New York: ACM), 161–168.

Google Scholar

Ferrante, E., Turgut, A. E., Duéñez-Guzman, E., Dorigo, M., and Wenseleers, T. (2015). Evolution of self-organized task specialization in robot swarms. PLoS Comput. Biol. 11:e1004273. doi:10.1371/journal.pcbi.1004273

PubMed Abstract | CrossRef Full Text | Google Scholar

Gavrilets, S. (2003). Perspective: models of speciation: what have we learned in 40 years? Evolution 57, 2197–2215. doi:10.1111/j.0014-3820.2003.tb00233.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Goldsby, H. J., Knoester, D. B., and Ofria, C. (2010). “Evolution of division of labor in genetically homogenous groups,” in GECCO 2010 – Proceedings of the 2010 Genetic and Evolutionary Computation Conference, 135–142.

Google Scholar

Gomes, J., Urbano, P., and Christensen, A. (2013). Evolution of swarm robotics systems with novelty search. Swarm Intell. 7, 115–144. doi:10.1007/s11721-013-0081-z

CrossRef Full Text | Google Scholar

Haasdijk, E., Bredeche, N., and Eiben, A. E. (2014). Combining environment-driven adaptation and task-driven optimisation in evolutionary robotics. PLoS ONE 9:e98466. doi:10.1371/journal.pone.0098466

PubMed Abstract | CrossRef Full Text | Google Scholar

Lichocki, P., Tarapore, D., Keller, L., and Floreano, D. (2012). Neural networks as mechanisms to regulate division of labor. Am. Nat. 179, 391–400. doi:10.1086/664079

PubMed Abstract | CrossRef Full Text | Google Scholar

Montanier, J.-M., and Bredeche, N. (2011). “Surviving the tragedy of commons: emergence of altruism in a population of evolving autonomous agents,” in European Conference on Artificial Life (Cambridge, MA: MIT press), 550–557.

Google Scholar

Nolfi, S., and Floreano, D. (2000). Evolutionary Robotics: The Biology, Intelligence, and Technology. Cambridge, MA: MIT Press.

Google Scholar

Nosil, P. (2012). Ecological Speciation. Oxford: Oxford University Press.

Google Scholar

Prieto, A., Becerra, J., Bellas, F., and Duro, R. (2010). Open-ended evolution as a means to self-organize heterogeneous multi-robot systems in real time. Rob. Auton. Syst. 58, 1282–1291. doi:10.1016/j.robot.2010.08.004

CrossRef Full Text | Google Scholar

Silva, F., Duarte, M., Correia, L., Oliveira, S. M., and Christensen, A. L. (2016). Open issues in evolutionary robotics. Evol. Comput. 24, 205–236. doi:10.1162/EVCO_a_00172

PubMed Abstract | CrossRef Full Text | Google Scholar

Trianni, V., Ampatzis, C., Christensen, A. L., Tuci, E., Dorigo, M., and Nolfi, S. (2007). “From solitary to collective behaviours: decision making and cooperation,” in Advances in Artificial Life, ECAL 2007 (Berlin; Heidelberg: Springer), 575–584.

Google Scholar

Trianni, V., Nolfi, S., and Dorigo, M. (2008). “Evolution, self-organisation and swarm robotics,” in Swarm Intelligence (Berlin; Heidelberg: Springer), 163–191.

Google Scholar

Trueba, P., Prieto, A., Bellas, F., Caamaño, P., and Duro, R. (2013). Specialization analysis of embodied evolution for robotic collective tasks. Rob. Auton. Syst. 61, 682–693. doi:10.1016/j.robot.2012.08.005

CrossRef Full Text | Google Scholar

Tuci, E., and Rabérin, A. (2015). On the design of generalist strategies for swarms of simulated robots engaged in a task-allocation scenario. Swarm Intell. 9, 267–290. doi:10.1007/s11721-015-0113-y

CrossRef Full Text | Google Scholar

Waibel, M., Floreano, D., Magnenat, S., and Keller, L. (2006). Division of labour and colony efficiency in social insects: effects of interactions between genetic architecture, colony kin structure and rate of perturbations. Proc. Biol. Sci. 273, 1815–1823. doi:10.1098/rspb.2006.3513

PubMed Abstract | CrossRef Full Text | Google Scholar

Waibel, M., Keller, L., and Floreano, D. (2009). Genetic team composition and level of selection in the evolution of cooperation. IEEE Trans. Evol. Comput. 13, 648–660. doi:10.1109/TEVC.2008.2011741

CrossRef Full Text | Google Scholar

Watson, R. A., Ficici, S. G., and Pollack, J. B. (2002). Embodied evolution: distributing an evolutionary algorithm in a population of robots. Rob. Auton. Syst. 39, 1–18. doi:10.1016/S0921-8890(02)00170-7

CrossRef Full Text | Google Scholar