- Evolutionary Complexity Research Group, Department of Computer Science, University of Central Florida, Orlando, FL, USA
While evolutionary computation and evolutionary robotics take inspiration from nature, they have long focused mainly on problems of performance optimization. Yet, evolution in nature can be interpreted as more nuanced than a process of simple optimization. In particular, natural evolution is a divergent search that optimizes locally within each niche as it simultaneously diversifies. This tendency to discover both quality and diversity at the same time differs from many of the conventional algorithms of machine learning, and also thereby suggests a different foundation for inferring the approach of greatest potential for evolutionary algorithms. In fact, several recent evolutionary algorithms called quality diversity (QD) algorithms (e.g., novelty search with local competition and MAP-Elites) have drawn inspiration from this more nuanced view, aiming to fill a space of possibilities with the best possible example of each type of achievable behavior. The result is a new class of algorithms that return an archive of diverse, high-quality behaviors in a single run. The aim in this paper is to study the application of QD algorithms in challenging environments (in particular complex mazes) to establish their best practices for ambitious domains in the future. In addition to providing insight into cases when QD succeeds and fails, a new approach is investigated that hybridizes multiple views of behaviors (called behavior characterizations) in the same run, which succeeds in overcoming some of the challenges associated with searching for QD with respect to a behavior characterization that is not necessarily sufficient for generating both quality and diversity at the same time.
1. Introduction
The products of nature have long served as inspiration for the investigation and practice of evolutionary algorithms and evolutionary robotics (Cliff et al., 1993; Nolfi and Floreano, 2000; Stanley, 2011). Yet the ability of such algorithms to match the complexity and sophistication of nature has frustratingly lagged, as researchers in the fields often observe (Stanley and Miikkulainen, 2003; Doncieux et al., 2015). This observation then often becomes the motivation for developing more sophisticated algorithms and encodings. Yet, even more fundamental than the question of how to abstract the most brilliant achievements of nature into an algorithm of commensurate power is a question less often explicitly asked: for what practical purpose is evolution actually suited anyway?
Until recently, throughout a large swath of the field, the implicit yet resounding answer to this question has been objective optimization (Mitchell, 1997; De Jong, 2002; Bishop, 2006). Various early pioneers in evolutionary computation independently inferred from their observations of nature that evolution can serve when abstracted artificially as a powerful optimization algorithm (Fogel et al., 1966; Holland, 1975; Goldberg and Richardson, 1987; Goldberg, 1989; Schwefel, 1993). The discoveries of evolution in nature, such as the flight of birds or the intelligence of the human brain, suggested to these pioneers that if fitness pressure is calibrated to push selection toward an ambitious objective then evolution can become a tool of directed design and creation.
The casting of evolution as an algorithm for optimization naturally pitted evolutionary computation against the many subfields of machine learning invested in optimization, leading to conflicts and critiques, sometimes portraying evolutionary computation as ad hoc, unprincipled, less effective than other more theoretically based optimization methods, or even outdated (and therefore often given less room in modern texts on machine learning) (Bäck et al., 1997; Bishop, 2006). While sometimes overly harsh or uninformed, even if such critiques are accepted, the perplexing question still hangs in the background of how it is possible that evolution in nature has managed to produce artifacts far beyond the capacity of any subfield of machine learning or optimization. If evolution is apparently so unmatched in power in nature, then why is there even a debate about its ability to compete with other approaches to optimization?
While one possible answer is that we have yet to uncover the deepest principles that unlock its true potential as an objective optimizer, a more intriguing possibility is that the real virtue of evolution is not in the end optimization at all. This suggestion goes beyond Herb Simon’s assertion that evolution is a satisficer rather than an optimizer (Simon, 1957), which casts evolution almost as a poor man’s optimizer. Rather, the hypothesis is that evolution is indeed phenomenally virtuosic at something, but that something is simply not optimization. This perspective can help to explain how it could be possible for evolution to produce sensational results in nature yet frustratingly modest ones in computation: we may be using it wrong. Perhaps the analogy with optimization was a mistake.
Indeed, it is difficult to imagine that evolution in nature is structured in the same way as a conventional optimization algorithm: there is no obvious unifying objective and organisms are often rewarded for being different in addition to being better. For example, organisms that are sufficiently different from their predecessors may establish a new niche in which they enjoy greatly reduced competition and thus are more likely to survive (Kirschner and Gerhart, 1998; Lehman and Stanley, 2013). Contrary to the tendency of optimization algorithms to converge over time to a single “best” solution, natural evolution instead exhibits a remarkable tendency toward divergence – continually accumulating myriad different ways of being. This observation is the crux of an alternative perspective in evolutionary computation (EC) that has been gaining momentum in recent years: evolution as a machine for diversification rather than optimization.
Inspired by this alternate view of natural evolution’s apparent strength as a diversifier, a new evolutionary algorithm called novelty search (NS) (Lehman and Stanley, 2008, 2011a) was introduced, which searches only for behavioral diversity without any underlying objective pressure. Surprisingly, in some domains (particularly those that are deceptive), NS quickly finds the global optimum even when objective-based approaches consistently fail. The counterintuitive result that NS can sometimes find the best solutions without explicitly searching for them has since sparked considerable research interest in applying NS and methods like it to solving problems that were previously considered to be too difficult (Lehman and Stanley, 2008, 2010, 2011a,b; Kistemaker and Whiteson, 2011; Mouret, 2011; Risi et al., 2011; Mouret and Doncieux, 2012; Cully and Mouret, 2013; Gomes and Christensen, 2013; Gomes et al., 2013; Liapis et al., 2013b; Martinez et al., 2013; Naredo and Trujillo, 2013). Novelty search has effectively demonstrated that evolution’s talent for diversification can itself be harnessed as a powerful tool for seeking a near-optimum, instead of the conventional notion of “survival of the fittest.” However, this view ignores the intrinsic value of diversity itself, treating it merely as a “means to an end” of finding the global optimum as usual.
In a true departure from conventional optimization, which seeks only the single best-performing solution, a new search paradigm has begun to emerge within EC where the effort focuses instead on finding various viable solutions, similar to how evolution in nature has discovered over billions of years a vast assortment of unique species, each of which are capable of orchestrating the complex system of biological processes necessary to sustain life. More precisely, the goal of this new type of search, called quality diversity (QD), is to find a maximally diverse collection of individuals (with respect to a space of possible behaviors) in which each member is as high performing as possible. In service of this goal, QD algorithms, such as novelty search, with local competition (NSLC) (Lehman and Stanley, 2011b) and MAP-Elites (Mouret and Clune, 2015) carefully balance a drive toward increasing diversity with localized searches for quality in an analogy with nature where species face the strongest competition from within their own niche. In this way, search can move toward different behaviors, while simultaneously improving behaviors that have already been discovered.
An important aspect of QD that differentiates it from other approaches designed to return multiple results is that in QD, diversity between individuals is measured with respect to their behavior (the actions and features of an individual over the course of its lifetime). The experimenter selects some subset of behavioral features of interest to form a behavior characterization (BC), thus defining a space of possible behaviors. The assumption in QD is that all parts of the behavior space are considered equally important. This assumption contrasts with non-QD approaches that assign priority to higher-performing regions, which draw inspiration from the idea of returning multiple local optima (Mahfoud, 1995; Trujillo et al., 2008, 2011). Instead, the goal of QD is to sample all regions of the behavior space (at some granularity), returning the best possible performance within each region. In other words, diversity takes priority over quality1 and therefore QD algorithms must be careful to avoid driving search away from lower-performing regions. More formally, the behavior space must be divided into t niches {N1, …, Nt} that together cover the entire space. That is, every point in the behavior space belongs to some niche Ni. Then, the task of QD is to maximize a quality measure Q within every niche.2
Although QD algorithms can be applied to traditional optimization-oriented tasks where they may even perform well due to their ability to overcome the problem of deception, the deeper promise of QD is to push beyond what is possible through simple optimization. In particular, QD has potential applications in the areas of computational creativity (Boden, 2006) and open-ended evolution (Standish, 2003; Bedau, 2008), where the hope is to automatically generate an endless procession of uniquely interesting artifacts. In more restricted search spaces, QD algorithms have also been called “illumination algorithms” because they effectively reveal the best possible performance achievable in each region of the phenotype space (Mouret and Clune, 2015). The types of problems inspired by QD (many of which are discussed in the next section) favor approaches that explore many promising directions at the same time and thus represent an opportunity for evolutionary algorithms to establish a more unique profile within the broader machine learning community where focused single-solution approaches such as backpropagation (Rumelhart et al., 1986) and support vector machines (Cortes and Vapnik, 1995) have historically dominated.
To help accelerate research in this emerging area, the aim of this paper is to establish a standard framework for understanding and comparing different approaches to searching for QD. [This paper is in effect a major expansion on the theme of our earlier conference paper that first introduced the term quality diversity (Pugh et al., 2015).] The hope is to unify early works in this emerging field and to promote the design of better QD algorithms in the future. To that end, this paper introduces a benchmark domain in the form of a series of maze-navigation tasks of varying difficulty that are paired with a quantifiable measure of the performance of QD algorithms called the QD-score. Experimental results in these mazes comparing current state-of-the-art approaches as well as several novel variants thereof reveal important insights into the application of QD algorithms that extend beyond individual methods.
One such insight concerns the importance of considering how diversity is characterized when applying QD algorithms. Specifically, some choices of characterization can make finding QD more difficult, which on sufficiently deceptive problems can translate into an inability to find the best solutions altogether. This apparent weakness presents a problem for researchers interested in finding QD with respect to a non-optimal characterization (i.e., one which inhibits finding the best-performing individuals) because standard practice suggests driving search with the same notion of diversity that you are ultimately interested in discovering (Trujillo et al., 2008, 2011; Lehman and Stanley, 2011b; Cully and Mouret, 2013; Szerlip and Stanley, 2013; Mouret and Clune, 2015). A solution to this problem is presented and then empirically validated in the form of new QD algorithms that drive search with multiple characterizations simultaneously. These new multi-characterization approaches, together with an increased understanding of the types of characterizations that are ideal for driving search effectively, enable the application of QD algorithms to various more difficult domains in the future.
Nature has discovered organisms both diverse and highly optimized within their own niches. This kind of divergent creative phenomenon differs from the typical convergent objective-driven process seen in search algorithms across machine learning, evolutionary computation (EC), and evolutionary robotics. By bringing QD now to the forefront of EC and providing a framework for understanding and comparing its available algorithms, the hope is that the field can progress more confidently from this initial foundation. In some cases (as later results will show), QD may even produce results beyond what an objective-driven process can accomplish, but it more broadly offers the chance to uncover a large swath of uniquely intriguing possibilities within a vast space and during just a single run.
2. Background
This section begins with a review of historical precedent for the study of QD, followed by highlights of recent works in the area and the questions they raise.
2.1. Before QD
Early work in multi-modal function optimization [MMFO; Mahfoud (1995)] foreshadowed the later arrival of QD. The aim of MMFO is to discover multiple local optima within a search space, which naturally yields a diversity of solutions. However, its main difference from QD is that MMFO traditionally focuses on genetic diversity and tends to apply only to simple phenotypes, such as mathematical functions, where the genotype and phenotype are in effect the same (Mahfoud, 1995); QD reflects a later shift in interest toward behavioral diversity and is often applied in domains such as evolutionary robotics where the relationship between genome and behavior is complex. The main limitation of genetic diversity is that it is susceptible to genetic aliasing, which means that genomes that are different may nevertheless behave similarly. Such aliasing, which is amplified especially in the presence of indirect genotype to phenotype mappings (Hornby and Pollack, 2001, 2002; Bongard, 2002; Stanley and Miikkulainen, 2003; Stanley, 2007), is thus counterproductive to find various behaviors, as shown empirically by Trujillo et al. (2011).
Another subject of research related to QD is multi-objective optimization (MOO) (Deb et al., 2002). In MOO, the search algorithm aims to uncover the key trade-offs (called the Pareto front) among two or more objectives set by the user. Similar to QD, MOO returns a set of top candidates rather than a single winner, but MOO is still ultimately driven toward specific objectives (though more than one) and therefore intrinsically convergent. By contrast, QD is a genuine divergent form of search driven explicitly to move away in the search space from where it has visited before. The unique effect is thus to reveal a sampling of the spectrum of possible behaviors latent in a search space.
2.2. Early Divergent Search Algorithms
Interest in divergence in evolutionary algorithms was sparked initially by the surprising observation that some problems are solved more reliably by searching for novel behaviors than by searching for their objective (Lehman and Stanley, 2008, 2011a). This approach, called novelty search, revealed just how pervasive and costly deception can be in otherwise unremarkable domains. It also showed that searching divergently instead of convergently can sometimes sidestep deception to uncover desirable parts of the search space. The benefits of divergent search were further confirmed through similar experiments by Mouret and Doncieux (2009) and Mouret and Doncieux (2012), who use the synonymous term behavioral diversity.
These initial studies were followed by a wave of interest in divergent search algorithms as researchers explored their potential for discovery and open-endedness (Risi et al., 2009, 2011; Soltoggio and Jones, 2009; Doucette and Heywood, 2010; Goldsby and Cheng, 2010; Graening et al., 2010; Krcah, 2010; Kistemaker and Whiteson, 2011; Woolley and Stanley, 2011; Gomes and Christensen, 2013; Gomes et al., 2013; Liapis et al., 2013a,b; Martinez et al., 2013; Morse et al., 2013; Naredo and Trujillo, 2013; Risi and Stanley, 2013). However, a clear missing ingredient from pure novelty or behavioral diversity techniques is a complementary notion of objective quality. The radical shift away from objectives toward divergence discards with it the ability to specify up front what is good and what is bad, and to have that notion influence the search. The loss of this convenient notion set the stage for its reemergence in QD algorithms.
2.3. Quality Diversity (QD) Algorithms
Early works on behavioral diversity (Mouret and Doncieux, 2009, 2012) and some more recent studies of combining novelty with objectives (Gomes et al., 2015) investigate the idea of hybridizing novelty with fitness. The means of such combination is usually through a multi-objective framework (Mouret and Doncieux, 2009, 2012), though a weighted combination is also possible (Gomes et al., 2015). However, in either case the notion of fitness (i.e., quality) is global, which means in effect that the component of the search pushing toward quality focuses its effort exclusively on the part of the search space where performance is dominant over all other areas of the search space. Thus, such approaches are not generally focused on QD. In an approach closer to QD, Trujillo et al. (2008, 2011) achieve multiple functional behaviors through behavioral speciation and fitness sharing. However, while this approach finds several locally optimal behaviors, it is still governed by global fitness because it preferentially explores higher-performing niches. A preferential push toward global quality in any approach reintroduces a strong convergent force into the search. While that may help in some cases if the aim is to discover a single near-global optimum or a handful of high-performing local optima, QD algorithms aim instead to explore the entire behavior space.
In particular, the hope in QD is to uncover as many diverse behavioral niches as possible, but where each niche is represented by a candidate of the highest possible quality for that niche. That way, the result is a kind of illumination of the best of all the diverse possibilities that exist (Mouret and Clune, 2015). The original QD algorithm of this type, called novelty search with local competition (NSLC), hybridizes novelty search with local fitness competitions only among individuals with similar behaviors, yielding a broad population of numerous simultaneous local competitions in diverse behavioral niches (Lehman and Stanley, 2011b). In its first demonstration, NSLC uncovered a collection of effective virtual creature morphologies and walking strategies in a single run, thereby demonstrating the unique benefits of QD (Lehman and Stanley, 2011b).
The potential to uncover a diverse collection of high-quality alternatives in a single run inspired further investigations and algorithms. For example, Szerlip and Stanley (2013) evolve diverse ambulating two-dimensional creatures made of sticks, also in a single run. Cully and Mouret (2013) evolve a collection of walking behaviors for hexapod robots that functions as a repertoire of skills for a robot. In a hint at the wide applicability of QD, Szerlip et al. (2015) evolve diverse low-level feature detectors for neural networks that are later aggregated into a combined classifier network. Revealing that QD encompasses more than a single algorithm, Mouret and Clune (2015) and Cully et al. (2015) introduce an alternate QD algorithm called multi-dimensional archive of phenotypic elites (MAP-Elites) that collects elite versions of diverse behavior within individual bins in a behavioral map. In yet another QD application, MAP-Elites collects diverse walking strategies for a robot that can be adapted in response to different kinds of damage (Cully et al., 2015). Other applications of MAP-Elites include generating sets of images for fooling deep networks (Nguyen et al., 2015a), and for exposing the space of concepts encoded inside a deep network as two-dimensional images (Nguyen et al., 2015b) and as three-dimensional models (Lehman et al., 2016).
The quickly expanding set of applications of QD motivates the need for a systematic study of its best practices, which is the aim in this paper. For that purpose, a key concept in any QD algorithm is the behavior characterization (BC). The BC is usually a vector that describes the chronology of actions taken by an individual during its evaluation but can also describe other salient aspects of an individual’s behavior or phenotype. This vector is then used to compute its novelty compared with other individuals (or its location in the behavior map in MAP-Elites), thereby driving the diversity component of QD. An important property of the BC is its alignment with the notion of quality, which refers to the degree to which finding novelty tends also to lead to higher fitness. For example, in a maze, if the BC is based on the final position reached, then it is highly aligned because eventually an agent that continues to find new final positions will find the endpoint of the maze. While BC alignment can be difficult to measure a priori (just as the shape of fitness landscapes are not known a priori for any challenging problems of interest), a BC’s degree of alignment can be anticipated by considering two key properties of highly aligned BCs: (1) each behavior is associated with only a narrow range of fitness values (e.g., a robot’s final position in a maze is associated with exactly one fitness value) and (2) the maximum possible fitness in adjacent regions of behavior space correlates (e.g., nearby positions in a maze generally have similar fitness).
By contrast, interestingly, most published QD applications involve finding diversity with respect to an unaligned BC because usually the notion of diversity that we find interesting is not intrinsically aligned with quality (Lehman and Stanley, 2011b; Cully and Mouret, 2013; Szerlip and Stanley, 2013; Mouret and Clune, 2015). For example, seeking creatures of different morphologies or with different numbers of legs does not naturally lead to higher-quality walking, yet we are nevertheless interested in finding such creatures. So far, QD has succeeded even despite a lack of such alignment, leaning heavily on the quality component of the algorithm to push otherwise unaligned notions of diversity toward good performance. For example, a previous study of QD that is precedent for the present paper finds that unaligned BCs often lead to a slower discovery of passable solutions (Pugh et al., 2015).
The key question raised by this previous study is whether QD algorithms with unaligned BCs ultimately stop working entirely when the domain is sufficiently hard. The maze used to test unaligned BCs in Pugh et al. (2015) is relatively simple and easy to solve; what would happen with much more complex mazes? This paper takes this next step with mazes of a scale beyond mazes in previous studies of QD and examines the effect on finding QD with respect to unaligned BCs in these new mazes. Not only does this study reveal how QD holds up in more complex domains but it also surveys new strategies for mitigating the effects of BC misalignment (which is usually the most desirable and intuitive way to setup QD). Such insight is not only critical to the future of QD as a nascent field but also important for the general progress of machine learning outside of conventional convergent closed problems, where the potential might be open-ended and the aim to collect broad possibilities rather than to converge to a final answer.
3. Domains
In the experiments described in this paper, simulated wheeled robots navigate mazes of varying complexity. To aid in their navigation, they are equipped with six rangefinder sensors (five of which are evenly distributed across the front half of the robot, and one pointing backwards) and four pie-slice sensors that indicate both the relative direction and distance to the goal. These sensors serve as inputs to an evolved neural controller with only a single continuous output that controls the degree to which the robot turns left or right (the robot always moves forward at a constant speed). The task is to evolve neural controllers that successfully guide the robot to a goal at the end of the maze.
Successfully navigating a maze can be challenging because it requires learning a complex mapping between sensors and effectors. In part, because sources of deception (and thus difficulty) are often visually apparent (e.g., dead ends), maze navigation has become a canonical domain for evolutionary robotics experiments [e.g., Lehman and Stanley (2011a) and Velez and Clune (2014)]. Another benefit of maze domains is that they tend to be computationally inexpensive, allowing many more evaluations than more intensive physics-based simulations. For this reason, maze domains are ideal for studying evolutionary dynamics over long timescales – an endeavor that would be impossible in a more computationally expensive domain.
In this study, three mazes of varying difficulty assess the efficacy of QD algorithms that will be described in the next section. In an important departure from mazes designed as an optimization problem [e.g., the HardMaze domain in Lehman and Stanley (2011a)], where there is often only a single “correct” path, the mazes here are intentionally designed with multiple viable paths to reach the goal. This unusual maze design makes it possible to investigate evolution’s potential for finding QD. Thus, the task in this study is not simply to find an agent that reaches the goal, but to find all of the different ways of driving through the maze (including those who do not necessarily reach the goal at all).
An important feature of all three mazes is the deceptive trap – areas of the maze that appear to be close to the goal (in terms of Euclidean distance) but, because of the presence of obstructions, do not actually offer a short drivable path to the goal. These traps, often in the form of an easily accessible corridor that terminates at a dead end before reaching the goal, represent local optima in the search space, and serve to deceive algorithms that simply follow a gradient of increasing fitness (Lehman and Stanley, 2011a). Thus, mazes containing such traps serve as a metaphor for complex domains in general, where successfully finding solutions requires a clever search algorithm aimed at innovation rather than straightforward optimization.
The first maze, introduced by Pugh et al. (2015) as the “QD-maze” but called the small maze (Figure 1) in this article, provides an initial example of this multi-path maze design. In this maze, individuals must escape from a single deceptive trap surrounding the start point after which the maze opens up, allowing various possible strategies for reaching the goal. Importantly, agents are given a considerable amount of time to allow for the expression of complicated and roundabout strategies (such as crossing back and forth across the map several times before driving to the goal). The ideal QD algorithm would eventually find all strategies for driving around the maze, including those that do not end up reaching the goal.
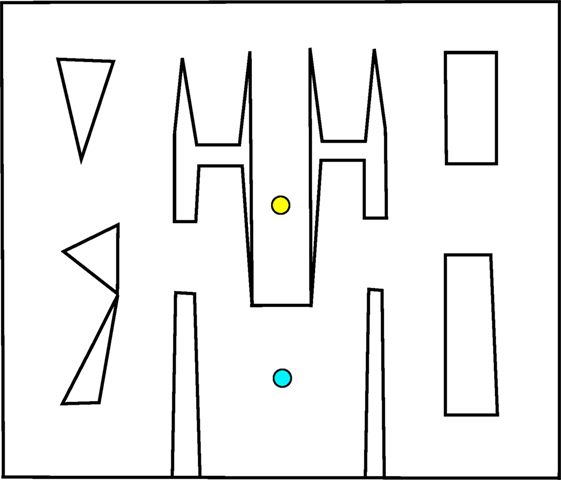
Figure 1. Small maze. Individuals start at the yellow circle (top) and must navigate to the goal point, marked with a blue circle (bottom). The relative openness and lenient time constraint allow a range of different techniques for reaching the goal.
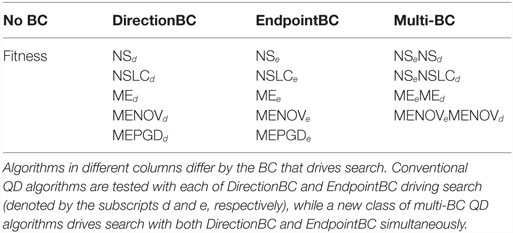
Of course, the most interesting real-world problems are often complex and challenging, and if maze navigation domains are to serve as proxies for such problems then they too should display non-trivial complexity. For this reason, two additional gauntlet mazes are introduced. While each maintains the important design principle of multiple viable paths to the goal, these mazes are intentionally made more difficult by (1) adding several larger and more pronounced deceptive traps, (2) setting strict maximum evaluation times such that individuals cannot wander down a deceptive trap and then subsequently reach the goal point, and (3) placing the goal point at the end of a series of chained sub-mazes that are each approximately as hard as the small maze and the original HardMaze from Lehman and Stanley (2011a). Navigating to the end of the asymmetric gauntlet (Figure 2) and symmetric gauntlet (Figure 3) thus requires evolving complicated behavioral strategies and overcoming significant levels of deception. In this way, these mazes test both the ability to overcome multiple successive deceptive traps and cover the space of possible solutions in the same run. Parameter settings for each maze domain are presented in Table 1, which describes differences in maze size, time constraints, and agent sensor radius.
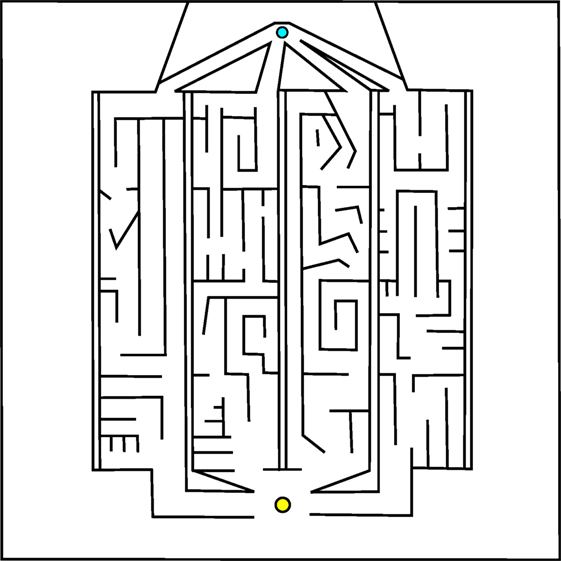
Figure 2. Asymmetric gauntlet. Individuals start at the bottom point and must navigate to the goal at the top of the maze. Because of the variation between maze legs, reaching the goal is easier by some routes than others. The presence of multiple paths through the maze increases the various potential driving strategies that can reach the goal.
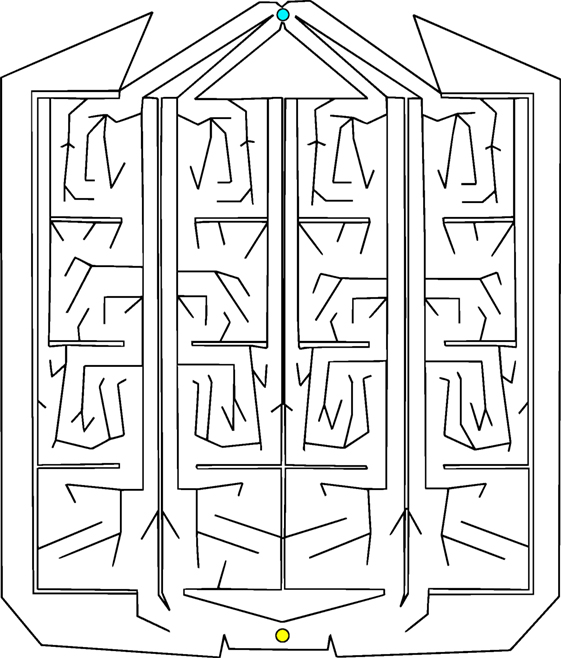
Figure 3. Symmetric gauntlet. Individuals start at the point at the bottom and must navigate to the goal at the top of the maze. Each leg of the maze is an approximate mirror image of the neighboring legs (thus, all paths through the maze are similarly difficult to achieve). The presence of multiple legs allows various different driving strategies to be successful.
4. Algorithms
This section describes each of the various algorithms considered in this study, beginning with those featured by Pugh et al. (2015). Because the pursuit of quality diversity has only recently become a subject of persistent research interest, there are only two main QD algorithms currently represented in the literature: NSLC (Lehman and Stanley, 2011b) and MAP-Elites (Cully et al., 2015; Mouret and Clune, 2015). To provide a broader perspective on the untapped algorithmic potential in this developing field, this study additionally features several novel variants of these core algorithms including some proposed improvements to MAP-Elites, which is mechanically very simple and thus particularly amenable to modification. Importantly, several other new variants specifically serve to address the problem of finding QD when the desired notion of diversity is unaligned with quality (and thus potentially incapable of finding the best solutions).
All of the following algorithm descriptions are partial in that they describe only selection and population maintenance mechanics for an underlying evolutionary algorithm. Algorithms new to this paper or otherwise not well represented in the literature are described with pseudocode in Appendix A. With the exception of Fitness (Section 4.1.1), which is implemented generationally (the entire population is replaced on every tick), all other algorithms are implemented as steady state (only a small portion of the population is replaced at a time). In particular, batches of 32 genomes are evaluated at a time to facilitate a modest amount of parallelism without substantially disrupting the composition of the population between batches.
4.1. Controls
While not themselves QD algorithms, both of the following two controls are included in the study to establish the importance of specialized approaches that simultaneously balance drives toward behavioral diversity and locally increasing quality. The controls thus, respectively, exemplify searching with quality pressure alone and with diversity pressure alone.
4.1.1. [Fitness] Neuroevolution of Augmenting Topologies
The first control, which includes only a quality component, represents a traditional objective-oriented optimization approach and is implemented as standard generational NEAT (NeuroEvolution of Augmenting Topologies) (Stanley and Miikkulainen, 2002) with a population size of 500. Agents are rewarded according to the Euclidean distance between their final position and the goal point (this heuristic also underlies the quality component of all of the QD algorithms throughout this paper). NEAT includes a sophisticated speciation and fitness-sharing mechanism for maintaining genetic diversity across the population. However, as the canonical HardMaze experiments (Lehman and Stanley, 2008, 2011a) reveal, genetic diversity is often not enough to overcome the problem of deception on difficult maze-navigation tasks, which instead favor rewarding behavioral diversity (a critical component of QD algorithms).
4.1.2. [NS] Novelty Search
The novelty search (NS) (Lehman and Stanley, 2008, 2011a) algorithm represents the other extreme: searching only for behavioral diversity with no fixed objective at all (i.e., NS has no “quality component”). Novelty search works by rewarding novelty instead of fitness, where novelty measures how different an individual’s behavior is from those who have been seen before. More formally, novelty is calculated by summing the distances to the k-nearest behaviors (in this paper, k = 20) from a set composed of the current population and an archive of past behaviors. The distance between two behaviors is simply the Euclidean distance between those behaviors when represented as a vector of numbers (which is the origin of the term behavior characterization or BC). While there exist several different strategies for managing the archive (Gomes et al., 2015), preliminary experiments indicated that an effective strategy is to add all individuals to an archive with a maximum size that is enforced by deleting those with the lowest novelty (the novelty of all archive members is recomputed before each deletion). In this study, NS has a population size of 500 and a maximum archive size of 2,500.
4.2. Quality Diversity Algorithms
Each of the following algorithms features both of the essential components of QD: pressure to discover more behavioral niches and a tendency toward increasing performance in niches that have already been discovered.
4.2.1. [NSLC] Novelty Search with Local Competition
Perhaps, the first true QD algorithm, novelty search with local competition (NSLC) (Lehman and Stanley, 2011b) combines the diversifying power of NS with a localized fitness pressure called local competition (LC), calculated as the proportion of an individual’s k-nearest (k = 20) behavior neighbors that have a lower-fitness score. LC allows a quality-based reward to be assigned within behavioral neighborhoods without asserting that some neighborhoods are better than others. In NSLC, novelty and LC are combined by Pareto ranking following the practice of the NSGA-II multi-objective optimization algorithm (Deb et al., 2002).
4.2.2. [ME] Multi-Dimensional Archive of Phenotypic Elites
An alternative approach to QD is an algorithm called Multi-dimensional Archive of Phenotypic Elites (MAP-Elites or ME) (Cully et al., 2015; Mouret and Clune, 2015). The key difference in MAP-Elites is that niches are explicitly defined rather than passively emergent from a system of local competition; the behavior space is divided into a number of discrete behavior bins (often called a “grid” and created by discretizing each dimension of the BC) where each bin remembers the single fittest individual ever mapped to that bin. The set of filled bins constitutes the active population and evolution proceeds by selecting a bin at random (with equal probability) to produce an offspring, which is then mapped to a bin corresponding to its behavior where it may be either saved or discarded depending on whether its fitness is higher or lower than the current elite occupant. Because selection is uniform, the hope is to acquire diversity passively by virtue of the observation that more bins will tend to fill over time and, once filled, they will not be forgotten.
4.2.3. [MENOV] MAP-Elites + Novelty
Unlike NS and NSLC, the original formulation of MAP-Elites does not preferentially explore under-represented behaviors, potentially causing it to lag in its discovery of new types of behaviors. Conveniently, it is easy to augment MAP-Elites with a stronger focus on diversity by simply making selection proportional to novelty. In this variant, called MAP-Elites + Novelty (MENOV), whenever offspring are generated, they are also added to an archive of past behaviors (with a maximum size of 2,500, managed in the same way as in NS) that enables calculating a novelty score for all members in the MAP-Elites grid.
4.2.4. [MEPGD] MAP-Elites + Passive Genetic Diversity
The strict elitism at each bin in the original MAP-Elites formulation may eventually cause evolution to stagnate if all stepping stones to higher fitness require first making strides through lower-fitness space. Furthermore, genetic diversity is intrinsically limited when only a single individual is saved in each bin. Addressing both of these potential pitfalls without introducing any additional overhead, a new variant called MAP-Elites + Passive Genetic Diversity (MEPGD) saves two individuals in each bin instead of one.3 Individuals with a lower fitness than the current elite still have a 30% chance of being saved in the second slot, regardless of their fitness, thus allowing MEPGD to explore the potential of some lineages that would have otherwise been discarded. Importantly, these extra slots coincide with the set of MAP-Elites bins, which guarantees that they are behaviorally diverse.
4.3. Multi-BC Quality Diversity Algorithms
As discussed in Section 2.3, BCs that are strongly aligned with quality encourage the discovery of better behaviors simply by finding different behaviors, effectively bypassing the problem of deception that causes optimization-oriented search processes to become trapped in local optima. However, no such advantage exists for unaligned BCs, which often represent the most interesting and desirable types of diversity in practice. Worryingly, Pugh et al. (2015) find that such unaligned BCs actually negatively impact the performance of QD algorithms, which on sufficiently hard problems may translate into an outright failure to find the best-performing solutions. This observation raises the important question of how QD practitioners can find unaligned diversity without losing the ability to circumvent deception offered by aligned BCs.
This section offers a promising answer in the form of driving search with multiple BCs simultaneously. To explore this idea, the following algorithms represent various options for adapting QD to support more than one BC.
4.3.1. [NS–NS] Multi-BC Novelty Search
Novelty search can be extended to support multiple BCs simultaneously by calculating a separate novelty score for each BC and then combining these scores in a multi-objective formulation [via NSGA-II of Deb et al. (2002)]. Each BC maintains its own independent archive against which individuals are evaluated to determine their novelty score for that BC. There is only a single population where the breeding potential for each member is decided by a Pareto ranking according to the various novelty scores. Although NS is not itself a QD algorithm because it lacks a mechanism for discovered behaviors to increase in quality, when extended to include multiple BCs, NS–NS can conceivably achieve some success if one BC serves to find diversity while another promotes increasing quality (e.g., an unaligned BC paired with an aligned BC). Note that even such a pairing does not quite embody the spirit of QD because any tendency toward increasing quality that emerges from an aligned BC is not explicitly local.
4.3.2. [NS–NSLC] Multi-BC Novelty Search with Local Competition
The idea of NS–NS can then be expanded to include a drive toward locally increasing quality by adding a LC objective (in the same way as NSLC) where behavioral neighbors are decided by the unaligned BC that expresses the notion of diversity that the user is ultimately interested in collecting. The resulting NS–NSLC algorithm therefore includes three distinct objectives (combined via NSGA-II): (1) a quality-aligned novelty score to facilitate overcoming deception, (2) an unaligned novelty score for discovering new behaviors of interest, and (3) an unaligned LC score to promote competition within niches of similar behaviors.
4.3.3. [ME–ME] Multi-BC MAP-Elites
In an effort to maintain its characteristic simplicity, MAP-Elites is extended to support multiple BCs by maintaining a separate grid for each BC (with similar maximum sizes). On each iteration of ME–ME, an equal amount of parents are selected from each grid, and their resulting offspring are mapped to both grids (where the decisions to save or discard them are performed independently, e.g., between two grids, a single offspring may be saved in one, both, or neither).
4.3.4. [MENOV–MENOV] Multi-BC MAP-Elites + Novelty
Finally, MENOV is extended to MENOV–MENOV similarly to ME–ME except where each grid also maintains its own novelty archive and selection within each grid is proportional to novelty.
5. Experiments
The behavior characterization (BC) determines the form of pressure that ultimately drives the diversity component of the search and thus must be selected carefully to complement the evolutionary algorithm. The experiments in this article explore two BCs that are each highly aligned or highly misaligned with the notion of quality (i.e., how close an agent is to arriving at the goal): EndpointBC, which is simply a two-dimensional vector containing the x and y coordinates of an individual’s location at the end of its trial, and DirectionBC, a five-dimensional vector with entries indicating whether the individual was most frequently facing north (0.125), east (0.375), south (0.625), or west (0.875) for each fifth of its evaluation time. On the one hand, EndpointBC is thus highly aligned with the goal of navigating to the goal point because the continual discovery of new endpoints will eventually lead to finding the goal point. On the other hand, DirectionBC is largely orthogonal to quality because the direction a robot faces at a particular time step does not fully determine whether it solves the maze (more importantly, it is possible to visit all of the behaviors in the DirectionBC space without ever reaching the goal).
Consistent with the observation that the goal of QD applications in practice is often to find diversity with respect to an unaligned BC, the assumption in this study is that the goal is to find QD with respect to DirectionBC. Therefore, exploring how different approaches to QD interact with each of EndpointBC and DirectionBC makes it possible to address several important questions:
1. How well does the approach suggested by current literature (i.e., driving search with the very notion of diversity you are interested in collecting) work? Given that preliminary experiments from Pugh et al. (2015) show that DirectionBC sometimes results in suboptimal QD-scores even in the relatively simple small maze, the hypothesis is that this conventional approach will not be optimal on complex domains such as the gauntlet mazes.
2. Can diversity with respect to DirectionBC be found without searching for it explicitly? That is, EndpointBC has been shown to be effective for driving novelty search to find solutions to deceptive mazes (Lehman and Stanley, 2008). However, it is unknown whether it is similarly effective at finding QD when diversity is measured on a separate unaligned metric. The hypothesis is that algorithms driven by EndpointBC should do well in terms of progress toward the goal, but may not necessarily result in high diversity with respect to DirectionBC.
3. Finally, can multiple BCs successfully be combined to compensate for the shortcomings of highly aligned BCs (lower diversity) and unaligned BCs (lower performance)?
Each of the algorithms from Section 4 is implemented with some combination of DirectionBC and EndpointBC for a total of fifteen treatments, enumerated in Table 2. Each treatment is run 20 times on the small maze, symmetric gauntlet, and asymmetric gauntlet for a total of 900 runs (300 per maze). Small maze runs ended after 250,000 evaluations and gauntlet runs ended after 1,000,000 evaluations (in each case, more than enough time for all algorithms to reach a performance plateau). Networks are evolved with a modified version of SharpNEAT 1.0 (Green, 2003) with mutation parameters validated by Pugh et al. (2015): 60% mutate connection, 10% add connection, and 0.5% add neuron. Networks are feedforward and restricted to asexual reproduction; other settings follow SharpNEAT 1.0 defaults. Maze-specific parameter settings are presented in Table 1.
In traditional maze navigation domains, an appropriate metric would be whether or not a robot was eventually able to navigate to the goal. However, this metric does not speak to an algorithm’s propensity for discovering diversity in a search space. For this reason, Pugh et al. (2015) introduces a new QD metric [which is also similar to the “global reliability” metric in Mouret and Clune (2015)] that reflects both the quality and diversity of individuals found by evolution (including solutions and non-solutions). Diversity in this metric, called the QD-score, is measured with respect to a BC. In the experiments reported in this article, DirectionBC always characterizes diversity for the purpose of computing the QD-score regardless of the behavior characterization driving search. This approach reflects the usual idea that the desire is to see a wide diversity of solutions at the end of a run with respect to a BC that is not necessarily directly aligned with solving the problem.
To quantify how much of the space is explored by an algorithm for the QD-score, the entire behavior space is first discretized into a collection of t bins4 {N1, …, Nt} as in the MAP-Elites algorithm described in the previous section. Each bin corresponds to a unique combination of features from the individual’s BC (in this case, DirectionBC) and represents a niche in the behavior space. Diversity is then quantified as the number of bins filled over the course of an evolutionary run. By summing the highest fitness values found in each grid bin, where Qi represents the highest fitness achieved in bin Ni, it becomes possible to simultaneously quantify both quality and diversity as
This DirectionBC-based QD-score5 is the primary metric in all mazes. Note that for the purpose of calculating QD-score, fitness is defined in a way that reflects the shortest drivable path between an agent ending location and the goal, respecting that agents cannot drive through walls. This special QD-score fitness is calculated by a breadth-first flood fill from the goal point, assigning fitness to locations in the maze that decreases linearly at each layer of the flood fill. Importantly, this fitness value, which draws a perfect non-deceptive gradient over the maze, is not available to any algorithms to drive search but merely appears during post hoc analysis to give an accurate accounting for how close each collected behavior is to solving the maze.
Due to the overwhelming historical focus on optimization and the recent realization that behavioral diversity can itself be a powerful tool for optimization (Lehman and Stanley, 2008; Mouret and Doncieux, 2009, 2012), this study includes an additional performance metric for the two gauntlets6 that captures the spirit of this more conventional search paradigm: the total maze progress metric measures how close a run is to solving all four legs of the maze. More precisely, total maze progress is the sum of four progress measures (one per leg) where progress for each leg increases linearly as endpoints are discovered further along their solution path (calculated by means of the flood fill distance to the goal point). If Ei is the set of all flood fill fitness scores associated with endpoints discovered inside leg i then total maze progress can be quantified as
A maximum score is achieved by solving all four legs. Total maze progress therefore addresses the important question of how well-suited QD algorithms are to the task of optimizing toward a series of predefined targets.7
6. Results
In all of the figures presented in this section, treatments are color coded according to which BC drives search: DirectionBC (subscript d) is drawn in blue, EndpointBC (subscript e) in yellow, multi-BC in green, and Fitness (which is not driven by any BC) in gray. For each treatment, results represent an average over 20 runs; error bars represent the SEM and can be interpreted to infer which differences are statistically significant when p values are not explicitly provided. In all reported cases, statistical significance is determined by an unpaired two-tailed Student’s t-test.8
6.1. Total Maze Progress
The total maze progress achieved by each treatment after all evaluations is depicted in Figure 4 (asymmetric gauntlet) and Figure 5 (symmetric gauntlet). A maximum possible score of 400 corresponds to solving all four legs in the same run, although such scores are not observed in practice. Unlike in the small maze, where all treatments consistently find solutions in every run, many gauntlet runs (particularly those of Fitness or DirectionBC-driven treatments) do not find solutions at all, reflecting the increased difficulty in the gauntlet mazes. Of the two gauntlet mazes surveyed by this metric, higher scores are obtained by all treatments on the asymmetric gauntlet, indicating that the asymmetric gauntlet is comparatively easier to solve, thus establishing a continuum of difficulty between the three maze domains featured in this study: small maze (easiest), asymmetric gauntlet (harder), and symmetric gauntlet (hardest).
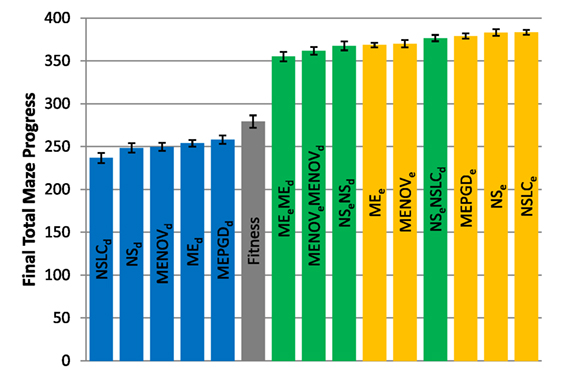
Figure 4. Total maze progress (asymmetric gauntlet). The final total maze progress achieved by each of fifteen treatments (Table 2) after 1,000,000 evaluations on the asymmetric gauntlet is shown (averaged over 20 runs). Bars are color coded according to which BC drives search (see section 6) and error bars represent SE. A maximum possible score of 400 corresponds to solving all four legs of the maze.
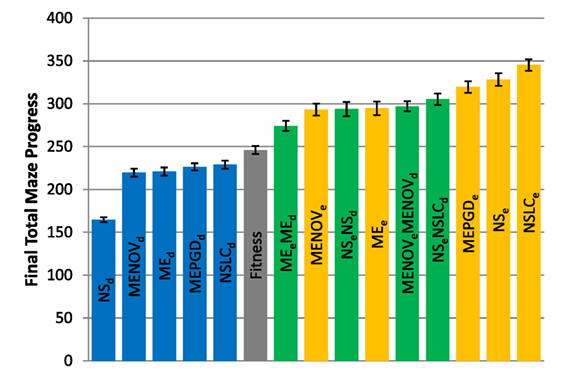
Figure 5. Total maze progress (symmetric gauntlet). The final total maze progress achieved by each of fifteen treatments (Table 2) after 1,000,000 evaluations on the symmetric gauntlet is shown (averaged over 20 runs). Bars are color coded according to which BC drives search (see section 6) and error bars represent SE. A maximum possible score of 400 corresponds to solving all four legs of the maze.
While in both gauntlets the performance of Fitness is sub-par as expected [it is known to struggle with deception in maze domains; Lehman and Stanley (2008)], a perhaps more surprising result is that all DirectionBC-driven treatments perform significantly worse than Fitness in terms of ability to find solutions (p < 0.05) to both the asymmetric gauntlet (Figure 4) and the symmetric gauntlet (Figure 5). Indeed, of these treatments on the symmetric gauntlet, only MEPGDd finds any solutions at all (two solutions found across all 20 runs).
On the other hand, all approaches that include an aligned BC (EndpointBC) always perform significantly better than Fitness (p < 0.001). Of those treatments that include EndpointBC, single-BC approaches tend to perform better (with respect to solving the maze) than multi-BC approaches that also include DirectionBC (Figures 4 and 5). This phenomenon is especially apparent on the harder symmetric gauntlet (Figure 5), where NSLCe and NSe perform significantly better than the multi-BC variants (p < 0.05). Of particular interest is that specialized QD algorithms such as NSLCe are competitive with the currently accepted method for overcoming deception on maze tasks: NSe (Lehman and Stanley, 2008, 2011a). On the symmetric gauntlet (Figure 5), there is some evidence that NSLCe may actually be better than NSe, although the evidence is not strong enough to establish statistical significance (p = 0.093).
Of the successful MAP-Elites variants (those driven by EndpointBC), MEPGDe performs significantly better than the core MEe on both gauntlets (Figures 4 and 5), while MENOVe in neither case is significantly different than MEe.
6.2. QD-Score
The final QD-score achieved by each treatment after all evaluations is depicted in Figure 6 (small maze), Figure 7 (asymmetric gauntlet), and Figure 8 (symmetric gauntlet).
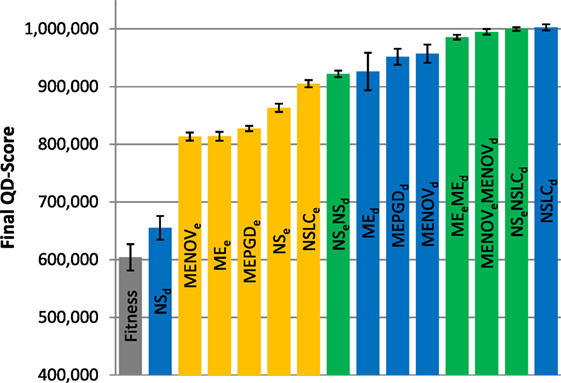
Figure 6. Final QD-score (small maze). The QD-score achieved by each of fifteen treatments (Table 2) after 250,000 evaluations on the small maze is shown (averaged over 20 runs). Bars are color coded according to which BC drives search (see section 6) and error bars represent SE. In all cases, QD-score is measured with respect to DirectionBC. The maximum possible QD-score on the small maze is 1,024,000 corresponding to a perfect solution in all 1,024 bins.
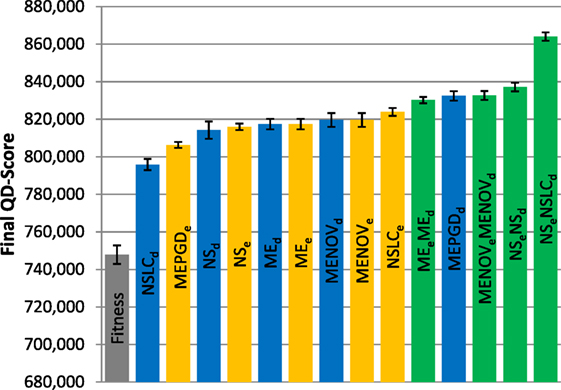
Figure 7. Final QD-score (asymmetric gauntlet). The QD-score achieved by each of fifteen treatments (Table 2) after 1,000,000 evaluations on the asymmetric gauntlet is shown (averaged over 20 runs). Bars are color coded according to which BC drives search (see section 6) and error bars represent SE. In all cases, QD-score is measured with respect to DirectionBC.
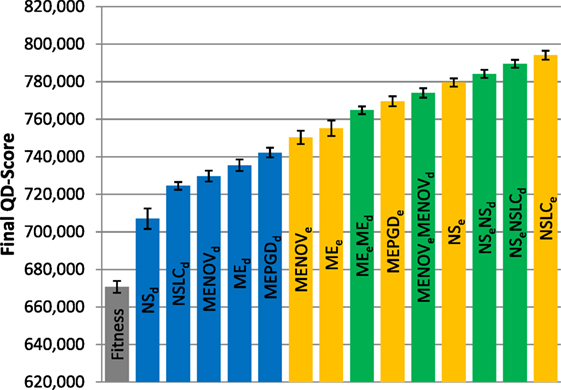
Figure 8. Final QD-score (symmetric gauntlet). The QD-score achieved by each of fifteen treatments (Table 2) after 1,000,000 evaluations on the symmetric gauntlet is shown (averaged over 20 runs). Bars are color coded according to which BC drives search (see section 6) and error bars represent SE. In all cases, QD-score is measured with respect to DirectionBC.
6.2.1. Small Maze
Reflecting its lack of challenging complexity, the best treatments on the small maze (Figure 6) consistently achieve near the maximum possible QD-score of 1,024,000, which corresponds to finding a maze solution (score = 1000) in each of the 1,024 bins. On this relatively simple task, QD-score is dominated by the multi-BC QD approaches (MEeMEd, MENOVeMENOVd, NSeNSLCd) and by NSLCd. EndpointBC-driven approaches perform poorly in comparison, though not as poorly as Fitness and NSd.
Of interest is the comparatively large variance on the MAP-Elites variants (when driven by DirectionBC) versus their NS-based counterparts (Figure 6). In particular, the most extreme such variance, on MEd, is caused by three outliers. While most runs of MEd score between 950 K and 1000 K, the outlier runs obtain scores of 791 K, 680 K, and 421 K. In each of these runs, the grid is completely filled (representing maximum diversity), but many bins contain low-quality behaviors (mostly representing agents that exclusively drive around inside the main deceptive trap). Thus, the higher variance observed by MEd here is indicative of MAP-Elites sometimes becoming stuck in local optima.
6.2.2. Gauntlet Mazes
Because of the strict time constraints on the gauntlet mazes, many types of behaviors (i.e., bins in the QD grid) can never represent full solutions even in theory; thus, the maximum possible QD-score on the gauntlet mazes is lower than on the small maze and also difficult to achieve in practice. This limitation is reflected by the comparatively lower scores observed in both the asymmetric gauntlet (Figure 7) and the symmetric gauntlet (Figure 8).
While DirectionBC-driven QD achieves the highest scores on the small maze (Figure 6), this trend is reversed as domain difficulty increases. On the asymmetric gauntlet, treatments driven by EndpointBC perform similarly to those driven by DirectionBC (Figure 7). On the comparatively more difficult symmetric gauntlet, the trend is completely reversed, with EndpointBC-driven approaches performing significantly better than those who are driven only by DirectionBC (Figure 8).
Consistently with the small maze, in each of the gauntlets, QD-score is dominated by the best multi-BC treatments. Specifically, in all three mazes, NSeNSLCd is consistently among the best-performing treatments (Figures 6–8). On the asymmetric gauntlet (Figure 7), its lead is unmatched, while on the symmetric gauntlet it is tied with NSLCe (Figure 8; the difference between NSLCe and NSeNSLCd is not statistically significant, p = 0.163).
However, it turns out that even though their final QD-scores are similar on the symmetric gauntlet, NSLCe and NSeNSLCd do exhibit different learning curves. To highlight this difference on the symmetric gauntlet, it is instructive to graph the development of QD-score over the course of evolution. Figure 9 depicts the QD-score over time for the best-performing method from each of the three classes in Table 2: EndpointBC, DirectionBC, and multi-BC. The general trend displayed by each treatment is representative of the other treatments in its respective class, e.g., DirectionBC-driven treatments tend to increase quickly and then plateau at a low score. On the other hand, NSLCe increases relatively slowly before ultimately reaching a much higher score. Combining the best of both of these options, NSeNSLCd quickly reaches high scores (Figure 9). Thus, overall the hybrid NSeNSLCd proves a competitive choice for maximizing QD-score on all the variant mazes.
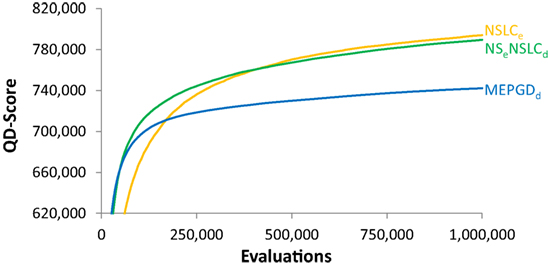
Figure 9. QD-score over time (symmetric gauntlet). The progression of the QD-score on the symmetric gauntlet for the best-performing treatment from each class (according to the BC that drives search; DirectionBC: MEPGDd, EndpointBC: NSLCe, multi-BC: NSeNSLCd) is graphed over time (averaged over 20 runs). The main result is that multi-BC treatments exhibit the best characteristics of each component BC: both increasing quickly and reaching high scores.
7. Discussion
Within the wide-ranging field of EC, two distinct types of research goals are relevant in the context of this investigation. The first and historically most dominant focus of EC is the task of optimization: harnessing the powerful natural mechanism of “survival of the fittest” to reach some predefined target (or series of targets). It is this goal that lies at the heart of the vast majority of EC literature, thereby seemingly aligning the ambitions of EC with the broader practice of machine learning, where optimization is treated as the essence of learning itself. However, having only recently begun to garner attention, the second type of research goal is less familiar, though it offers promising new opportunities for discovery and advancement uniquely accessible to EC. This goal, called quality diversity, represents a fundamental departure from optimization because instead the idea is to explore all of what is possible rather than to find only the best option. While the primary intention of this paper is to promote the theory and practice of QD, the results of this study have implications relevant to both paradigms.
The recent realization that pursuing behavioral diversity can help to overcome deception (Lehman and Stanley, 2008, 2011a; Mouret and Doncieux, 2009, 2012) has offered a source of hope to solving the problem of deception that permeates almost every optimization space of interest. However, deception does not exclusively affect optimization and not all notions of “behavioral diversity” are equally capable of thwarting it. As this study reveals, simply focusing on QD does not make evolution immune to the problem of deception because the quality-seeking component of QD algorithms can itself fall victim to it. In this study, which features maze tasks of varying difficulty, QD algorithms following the compass of an unaligned BC are incrementally less able to find QD as the level of deception increases from one maze to another (Figures 6–8). Further highlighting the problem of deception even in QD, surprisingly, as maze difficulty increases, it actually becomes more effective to drive search with an aligned BC even when you are collecting unaligned QD (Figure 8). The primary lesson is that searching for diversity with respect to an unaligned BC does not circumvent the problem of deception (doing so is mostly orthogonal to overcoming deception, similar to the shortcomings of pursuing genetic diversity). However, for QD practitioners, the magic bullet cannot be to simply drive search with some other, better-suited BC because that only leaves the diversity of interest to be collected coincidentally. Instead, this study offers the promising new idea of driving search with multiple BCs simultaneously. The so-called multi-BC algorithms (such as NS–NSLC) allow search to be driven both by the desired notion of diversity and a separate BC that is well equipped to circumvent deception, thus unlocking the best parts of the search space for discovery.
An alternative approach not tested in this study is to simply concatenate both an aligned and unaligned BC into a single BC with more dimensions. In considering this option, it is important to note that the behavior space grows exponentially with the size of the BC. Thus, such an approach generally cannot be applied with MAP-Elites because the number of bins would also grow exponentially until the grid no longer resembles a reasonably sized population. While concatenating multiple BCs into a single monolithic BC is still tractable with NS-based algorithms, the resulting vast behavior space may present an additional challenge over the multi-BC approaches tested here.
Following the lesson originally presented by Lehman and Stanley (2008), this study reconfirms that a powerful strategy for finding solutions to a difficult maze is to abandon the objective entirely and simply search for behavioral diversity (e.g., NSe in Figures 4 and 5). This conclusion itself has implications outside of maze solving that apply more generally to all of optimization. However, an important observation is that not just any type of behavioral diversity is successful. Indeed, with regard to being able to solve difficult mazes, searching for diversity with respect to an unaligned BC (such as DirectionBC) does even worse than purely objective search (Figure 5). The more general lesson is that BCs that are aligned with the notion of quality (such as EndpointBC in this study) are the key ingredient to overcoming deception on difficult problems. Furthermore, this study offers the additional insight that QD algorithms themselves offer a means for “the objective-less search for behavioral diversity” (i.e., novelty search) to be rectified with their missing objective in a way that allows search to respect the ultimate goal (e.g., solving the maze) without re-introducing the problem of deception. Specifically, NSLCe in this paper demonstrates that it can optimize in the presence of strong deception at least as well as regular novelty search (Figure 4) and, in fact, might even be better (Figure 5). This result suggests that while the ultimate goals of QD are distinct from optimization, advancements in QD can themselves directly benefit optimization.
As a relatively new approach to QD, MAP-Elites remains a largely unexplored paradigm at the time of this writing. The core MAP-Elites algorithm offers the significant appeal of a very simple algorithm (requiring in effect only a few lines of code) that powerfully distills the essence of QD. Because it is relatively new, its performance in this study serves to confirm that it is largely impacted by BCs similarly to NS-based methods (suggesting some general principles for QD across different algorithms), but of course much room remains for MAP-Elites in particular to be improved. MENOV and MEPGD in this study both suggest that the core ME algorithm can be fruitfully augmented in part to overcome any restrictive effects of its strict elitism. Some ideas not tested here include MEPGDNOV (combining genetic diversity with novelty) and MEPGD–MEPGD (ME with genetic diversity and multiple BCs). The genetic diversity component might also benefit from expansion to more than one diversity candidate per bin.
An important question raised by the results is how to decide whether a particular domain is hard (therefore likely requiring more than one BC) and in such cases whether the chosen aligned BC is sufficiently aligned to overcome the threat of deception. One way to decide whether it may be necessary to include multiple BCs is simply to run a pure fitness-based (objective-driven) search. If such a search consistently finds solutions in multiple runs then the domain can be considered sufficiently easy that multiple BCs may be unnecessary. On the other hand, if the domain proves too difficult for fitness, then it is important to make sure that the aligned BC is, in fact, sufficiently aligned to complement the unaligned BC. One way to test for alignment is to try running simple NS only with the candidate aligned BC. If the alignment is effective, such a search should at least do better than fitness-based search, which would then validate that the BC in question can complement an unaligned BC in a multi-BC hybrid.
Interestingly, while the results support that in sufficiently easy domains a more naive single-BC approach with an unaligned BC may work to collect QD, it does not appear harmful in any case to take the safer multi-BC approach even then. Thus, even though it has been customary so far in the QD-related literature to rely on a single unaligned BC (Lehman and Stanley, 2011b; Cully and Mouret, 2013; Szerlip and Stanley, 2013; Mouret and Clune, 2015), it may be possible to revisit some of the domains of the past with multiple BCs and achieve even better performance.
More broadly, the multi-BC approach and our new understanding of the implications of alignment can help us in the future to achieve significantly more impressive results with QD than seen in the past. Even domains that might have seemed inexplicably out of reach might now become accessible through the application of multiple BCs. Thus, because QD represents a promising direction exclusive to evolutionary techniques, it is in the interest not just of those working in QD, but EC and evolutionary robotics as a whole to seek out and propose such future domains. The potential for such ideas is foreshadowed by QD results already published in the diverse domains of morphology evolution (Lehman and Stanley, 2011b; Szerlip and Stanley, 2013; Mouret and Clune, 2015), robot control and adaptation (Cully and Mouret, 2013; Cully et al., 2015; Mouret and Clune, 2015), image generation (Nguyen et al., 2015a,b), and three-dimensional object evolution (Lehman et al., 2016). With increasing interest in the field, these domains may be just the beginning for QD.
8. Conclusion
In an attempt to unify and investigate the emerging field of quality diversity (QD), this paper compared various QD algorithm variants and controls in three different maze domains, two of a higher level of complexity than previously seen in such maze-based studies. By pushing the mazes to a higher level of complexity than seen in QD before, the study was able to expose conditions under which QD effectively breaks down. It turns out that driving the diversity component of QD algorithms exclusively by a BC unaligned with quality (which is heretofore common practice) performs relatively poorly under such difficult conditions. However, on a positive note, methods that hybridize more than one BC (one aligned and one unaligned) tend to perform well at the same time as finding the kind of diversity desired, suggesting a promising path forward for QD in the future as it is applied in increasingly ambitious domains.
Author Contributions
JP helped conceive the work and led experimental design, implementation, and writing. LS helped conceive the work and contributed to experimental design, implementation, and writing. KS provided vision and oversight, helped conceive the work, and contributed to experimental design and writing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
This work was supported by the National Science Foundation under grant no. IIS-1421925. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Footnotes
- ^Approaches that desire to return a handful of the best local optima (i.e., where quality takes priority over diversity) may be better served by the term diverse quality.
- ^For any niche Ni where no point has been discovered, Qi is defined as 0.
- ^The number of extra slots per bin can conceivably be expanded to any number, where all slots except the first are governed by random replacement.
- ^In this study, t = 1024 when discretizing the DirectionBC behavior space.
- ^The original small maze results from Pugh et al. (2015) instead always measure diversity with respect to the BC that drives search and thus do not explore the idea of driving search with BCs other than those which characterize the dimensions of interest.
- ^No such metric is defined for the small maze because all treatments consistently and quickly find solutions and thus it does not represent a challenging optimization problem.
- ^Total maze progress is related to the interests of multimodal optimization, where the goal is often to find all of the global optima in a fitness landscape without regard to the behaviors or phenotypes that get there.
- ^The simple Student’s t-test is chosen intentionally to avoid Type II errors, which are more likely when adjusting for multiple comparisons. As such, the results here are intended to highlight potential differences between treatments, not to establish a definitive ranking.
References
Bäck, T., Hammel, U., and Schwefel, H.-P. (1997). Evolutionary computation: comments on the history and current state. IEEE Trans. Evol. Comput. 1, 3–17. doi: 10.1109/4235.585888
Bedau, M. (2008). “The arrow of complexity hypothesis (abstract),” in Proceedings of the Eleventh International Conference on Artificial Life (Alife XI), eds S. Bullock, J. Noble, R. Watson and M. Bedau (Cambridge, MA: MIT Press), 750.
Bongard, J. C. (2002). “Evolving modular genetic regulatory networks,” in Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu (Washington, DC: IEEE).
Cliff, D., Harvey, I., and Husbands, P. (1993). Explorations in evolutionary robotics. Adapt. Behav. 2, 73–110. doi:10.1177/105971239300200104
Cortes, C., and Vapnik, V. (1995). Support-vector networks. Mach. Learn. 20, 273–297. doi:10.1007/BF00994018
Cully, A., Clune, J., Tarapore, D., and Mouret, J.-B. (2015). Robots that can adapt like animals. Nature 521, 503–507. doi:10.1038/nature14422
Cully, A., and Mouret, J.-B. (2013). “Behavioral repertoire learning in robotics,” in Proceeding of the Fifteenth Annual Conference on Genetic and Evolutionary Computation (GECCO ‘13) (New York, NY: ACM), 175–182.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6, 182–197. doi:10.1109/4235.996017
Doncieux, S., Bredeche, N., Mouret, J.-B., and Eiben, A. G. (2015). Evolutionary robotics: what, why, and where to. Front. Robot. AI 2:4. doi:10.3389/frobt.2015.00004
Doucette, J., and Heywood, M. I. (2010). “Novelty-based fitness: an evaluation under the santa fe trail,” in Proceedings of the European Conference on Genetic Programming (EuroGP-2010), Istanbul (Berlin, Heidelberg: Springer-Verlag), 50–61.
Fogel, L. J., Owens, A. J., and Walsh, M. J. (1966). Artificial Intelligence Through Simulated Evolution. New York, NY: John Wiley & Sons.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Optimization and Machine Learning. Reading, MA: Addison-Wesley.
Goldberg, D. E., and Richardson, J. (1987). ‘‘Genetic algorithms with sharing for multimodal function optimization,’’ in Genetic Algorithms and their Applications: Proceedings of the Second International Conference on Genetic Algorithms, ed. J. J. Grefenstette (Hillsdale, NJ: Lawrence Erlbaum), 41–49.
Goldsby, H. J., and Cheng, B. H. (2010). “Automatically discovering properties that specify the latent behavior of UML models,” in Model Driven Engineering Languages and Systems (Berlin, Heidelberg: Springer), 316–330.
Gomes, J., and Christensen, A. L. (2013). “Generic behaviour similarity measures for evolutionary swarm robotics,” in Proceeding of the Fifteenth Annual Conference on Genetic and Evolutionary Computation (GECCO ‘13) (New York, NY: ACM), 199–206.
Gomes, J., Mariano, P., and Christensen, A. L. (2015). “Devising effective novelty search algorithms: a comprehensive empirical study,” in Proceedings of the 17th Annual Conference on Genetic and Evolutionary Computation, Madrid (New York, NY: ACM), 943–950.
Gomes, J., Urbano, P., and Christensen, A. L. (2013). Evolution of swarm robotics systems with novelty search. Swarm Intell. 7, 115–144. doi:10.1007/s11721-013-0081-z
Graening, L., Aulig, N., and Olhofer, M. (2010). “Towards directed open-ended search by a novelty guided evolution strategy,” in Parallel Problem Solving from Nature – PPSN XI. Vol. 6239 of Lecture Notes in Computer Science, Krakow, eds R. Schaefer, C. Cotta, J. Kołodziej and G. Rudolph (Berlin, Heidelberg: Springer), 71–80.
Green, C. (2003–2006). SharpNEAT Homepage. Available at: http://sharpneat.sourceforge.net/
Holland, J. H. (1975). Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence. Ann Arbor, MI: University of Michigan Press.
Hornby, G. S., and Pollack, J. B. (2001). “The advantages of generative grammatical encodings for physical design,” in Proceedings of the 2001 Congress on Evolutionary Computation, Seoul (Washington, DC: IEEE).
Hornby, G. S., and Pollack, J. B. (2002). Creating high-level components with a generative representation for body-brain evolution. Artif. Life 8, 223–246. doi:10.1162/106454602320991837
Kirschner, M., and Gerhart, J. (1998). Evolvability. Proc. Natl. Acad. Sci. U.S.A. 95, 8420–8427. doi:10.1073/pnas.95.15.8420
Kistemaker, S., and Whiteson, S. (2011). “Critical factors in the performance of novelty search,” in Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation. GECCO ‘11, Dublin (New York, NY: ACM), 965–972.
Krcah, P. (2010). “Solving deceptive tasks in robot body-brain co-evolution by searching for behavioral novelty,” in 10th International Conference on Intelligent Systems Design and Applications (ISDA), Cairo (Washington, DC: IEEE), 284–289.
Lehman, J., Risi, S., and Clune, J. (2016). “Creative generation of 3D objects with deep learning and innovation engines,” in Proceedings of the 7th International Conference on Computational Creativity, Paris.
Lehman, J., and Stanley, K. O. (2008). “Exploiting open-endedness to solve problems through the search for novelty,” in Proceedings of the Eleventh International Conference on Artificial Life (Alife XI), Winchester, eds S. Bullock, J. Noble, R. Watson and M. Bedau (Cambridge, MA: MIT Press).
Lehman, J., and Stanley, K. O. (2010). “Revising the evolutionary computation abstraction: minimal criteria novelty search,” in Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation (GECCO ‘10) (New York, NY: ACM), 103–110.
Lehman, J., and Stanley, K. O. (2011a). Abandoning objectives: evolution through the search for novelty alone. Evol. Comput. 19, 189–223. doi:10.1162/EVCO_a_00025
Lehman, J., and Stanley, K. O. (2011b). “Evolving a diversity of virtual creatures through novelty search and local competition,” in Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation (GECCO ‘11), Dublin (New York, NY: ACM), 211–218.
Lehman, J., and Stanley, K. O. (2013). Evolvability is inevitable: increasing evolvability without the pressure to adapt. PLoS ONE 8:e62186. doi:10.1371/journal.pone.0062186
Liapis, A., Martínez, H. P., Togelius, J., and Yannakakis, G. N. (2013a). “Transforming exploratory creativity with delenox,” in Proceedings of the Fourth International Conference on Computational Creativity, Sydney (Sydney: University of Sydney).
Liapis, A., Yannakakis, G. N., and Togelius, J. (2013b). “Enhancements to constrained novelty search: two-population novelty search for generating game content,” in Proceeding of the Fifteenth Annual Conference on Genetic and Evolutionary Computation Conference, GECCO ‘13 (New York, NY: ACM), 343–350.
Mahfoud, S. W. (1995). Niching Methods for Genetic Algorithms. Ph.D. thesis, University of Illinois at Urbana-Champaign, Urbana, IL.
Martinez, Y., Naredo, E., Trujillo, L., and Galvan-Lopez, E. (2013). “Searching for novel regression functions,” in 2013 IEEE Congress on Evolutionary Computation (CEC), Cancun (Washington, DC: IEEE), 16–23.
Morse, G., Risi, S., Snyder, C. R., and Stanley, K. O. (2013). “Single-unit pattern generators for quadruped locomotion,” in Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation (GECCO ‘13), Amsterdam (New York, NY: ACM), 719–726.
Mouret, J.-B. (2011). “Novelty-based multiobjectivization,” in New Horizons in Evolutionary Robotics, eds S. Doncieux, N. Bredeche and J.-B. Mouret (Berlin, Heidelberg: Springer), 139–154.
Mouret, J.-B., and Clune, J. (2015). Illuminating search spaces by mapping elites. arXiv preprint arXiv:1504.04909.
Mouret, J.-B., and Doncieux, S. (2009). “Overcoming the bootstrap problem in evolutionary robotics using behavioral diversity,” in Proceedings of the IEEE Congress on Evolutionary Computation (CEC-2009), Trondheim (Washington, DC: IEEE), 1161–1168.
Mouret, J.-B., and Doncieux, S. (2012). Encouraging behavioral diversity in evolutionary robotics: an empirical study. Evol. Comput. 20, 91–133. doi:10.1162/EVCO_a_00048
Naredo, E., and Trujillo, L. (2013). “Searching for novel clustering programs,” in Proceeding of the fifteenth Annual Conference on Genetic and Evolutionary Computation Conference. GECCO ‘13, Amsterdam (New York, NY: ACM), 1093–1100.
Nguyen, A., Yosinski, J., and Clune, J. (2015a). “Deep neural networks are easily fooled: high confidence predictions for unrecognizable images,” in Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR ‘15), Boston (Washington, DC: IEEE).
Nguyen, A., Yosinski, J., and Clune, J. (2015b). “Innovation engines: automated creativity and improved stochastic optimization via deep learning,” in Proceedings of the 17th Annual Conference on Genetic and Evolutionary Computation (GECCO ‘15) (New York, NY: ACM).
Pugh, J. K., Soros, L. B., Szerlip, P. A., and Stanley, K. O. (2015). “Confronting the challenge of quality diversity,” in Proceedings of the 17th Annual Conference on Genetic and Evolutionary Computation (GECCO ‘15) (New York, NY: ACM).
Risi, S., Hughes, C., and Stanley, K. (2011). Evolving plastic neural networks with novelty search. Adapt. Behav. 18, 470–491. doi:10.1177/1059712310379923
Risi, S., and Stanley, K. O. (2013). “Confronting the challenge of learning a flexible neural controller for a diversity of morphologies,” in Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2013) (New York, NY: ACM).
Risi, S., Vanderbleek, S. D., Hughes, C. E., and Stanley, K. O. (2009). “How novelty search escapes the deceptive trap of learning to learn,” in Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2009) (New York, NY: ACM).
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). “Learning internal representations by error propagation,” in Parallel Distributed Processing, Vol. 1 eds J. L. McClelland and D. L. Rumelhart (Cambridge, MA: MIT Press), 318–362.
Schwefel, H.-P. P. (1993). Evolution and Optimum Seeking: The Sixth Generation. New York, NY: John Wiley & Sons, Inc.
Simon, H. A. (1957). Models of Man: Social and Rational – Mathematical Essays on Rational Human Behavior in a Social Setting. New York, NY: Wiley.
Soltoggio, A., and Jones, B. (2009). “Novelty of behaviour as a basis for the neuro-evolution of operant reward learning,” in Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation GECCO ‘09 (New York, NY: ACM), 169–176.
Standish, R. K. (2003). Open-ended artificial evolution. Int. J. Comput. Intell. Appl. 3, 167–175. doi:10.1142/S1469026803000914
Stanley, K. O. (2007). “Compositional pattern producing networks: a novel abstraction of development,” in Genetic Programming and Evolvable Machines Special Issue on Developmental Systems, Vol. 8 (Berlin, Heidelberg: Springer), 131–162.
Stanley, K. O. (2011). “Why evolutionary robotics will matter,” in New Horizons in Evolutionary Robotics, eds S. Doncieux, N. Bredeche and J.-B. Mouret (Berlin, Heidelberg: Springer), 37–41.
Stanley, K. O., and Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies. Evol. Comput. 10, 99–127. doi:10.1162/106365602320169811
Stanley, K. O., and Miikkulainen, R. (2003). A taxonomy for artificial embryogeny. Artif. Life 9, 93–130. doi:10.1162/106454603322221487
Szerlip, P., and Stanley, K. O. (2013). “Indirectly encoded sodarace for artificial life,” in Proceedings of the European Conference on Artificial Life (ECAL-2013), Taormina Vol. 12 (Cambridge, MA: MIT Press), 218–225.
Szerlip, P. A., Morse, G., Pugh, J. K., and Stanley, K. O. (2015). “Unsupervised feature learning through divergent discriminative feature accumulation,” in Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI-2015) (Menlo Park, CA: AAAI Press).
Trujillo, L., Olague, G., Lutton, E., and De Vega, F. F. (2008). “Discovering several robot behaviors through speciation,” in Applications of Evolutionary Computing (Berlin, Heidelberg: Springer), 164–174.
Trujillo, L., Olague, G., Lutton, E., De Vega, F. F., Dozal, L., and Clemente, E. (2011). Speciation in behavioral space for evolutionary robotics. J. Intell. Robot. Syst. 64, 323–351. doi:10.1007/s10846-011-9542-z
Velez, R., and Clune, J. (2014). “Novelty search creates robots with general skills for exploration,” in Proceedings of the 2014 Conference on Genetic and Evolutionary Computation, GECCO ‘14 (New York, NY: ACM), 737–744.
Woolley, B. G., and Stanley, K. O. (2011). “On the deleterious effects of a priori objectives on evolution and representation,” in GECCO ‘11: Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation (Dublin, Ireland: ACM), 957–964.
Appendix
Algorithm Descriptions
This section provides pseudocode for selected algorithms (particularly studies that were not published previously). Some algorithms represent trivial modifications to existing algorithms, in which case only the modifications are shown. In all cases, g represents an individual genome, B represents a batch of genomes (batch size: bsize), R represents the novelty archive (maximum archive size: rmax), and P represents the population or the MAP-Elites grid (population size: psize). Following NEAT (Stanley and Miikkulainen, 2002), genomes are initialized with minimal complexity; additional neurons and connections are added later through mutations.
Keywords: novelty search, non-objective search, quality diversity, behavioral diversity, evolutionary computation, neuroevolution
Citation: Pugh JK, Soros LB and Stanley KO (2016) Quality Diversity: A New Frontier for Evolutionary Computation. Front. Robot. AI 3:40. doi: 10.3389/frobt.2016.00040
Received: 31 March 2016; Accepted: 23 June 2016;
Published: 12 July 2016
Edited by:
John Howard Long, Vassar College, USAReviewed by:
Andrés Faíña Rodríguez-Vila, IT University of Copenhagen, DenmarkLeonardo Trujillo, Tijuana Institute of Technology, Mexico
Copyright: © 2016 Pugh, Soros and Stanley. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kenneth O. Stanley, a3N0YW5sZXlAY3MudWNmLmVkdQ==
 Justin K. Pugh
Justin K. Pugh Lisa B. Soros
Lisa B. Soros Kenneth O. Stanley
Kenneth O. Stanley