- 1Department of Computer Science, Vassar College, Poughkeepsie, NY, USA
- 2Interdisciplinary Robotics Research Laboratory, Vassar College, Poughkeepsie, NY, USA
Intelligent embodied robots are integrated systems: as they move continuously through their environments, executing behaviors and carrying out tasks, components for low-level and high-level intelligence are integrated in the robot’s cognitive system, and cognitive and physical processes combine to create their behavior. For a modeling framework to enable the design and analysis of such integrated intelligence, the underlying representations in the design of the robot should be dynamically sensitive, capable of reflecting both continuous motion and micro-cognitive influences, while also directly representing the necessary beliefs and intentions for goal-directed behavior. In this paper, a dynamical intention-based modeling framework is presented that satisfies these criteria, along with a hybrid dynamical cognitive agent (HDCA) framework for employing dynamical intentions in embodied agents. This dynamical intention-HDCA (DI-HDCA) modeling framework is a fusion of concepts from spreading activation networks, hybrid dynamical system models, and the BDI (belief–desire–intention) theory of goal-directed reasoning, adapted and employed unconventionally to meet entailments of environment and embodiment. The paper presents two kinds of autonomous agent learning results that demonstrate dynamical intentions and the multi-faceted integration they enable in embodied robots: with a simulated service robot in a grid-world office environment, reactive-level learning minimizes reliance on deliberative-level intelligence, enabling task sequencing and action selection to be distributed over both deliberative and reactive levels; and with a simulated game of Tag, the cognitive–physical integration of an autonomous agent enables the straightforward learning of a user-specified strategy during gameplay, without interruption to the game. In addition, the paper argues that dynamical intentions are consistent with cognitive theory underlying goal-directed behavior, and that DI-HDCA modeling may facilitate the study of emergent behaviors in embodied agents.
1. Introduction
Embodied robots can encompass everything from low-level motor control to navigation, goal-directed behavior and high-level cognition in one complex, cognitive–physical system. Accordingly, when considering modeling frameworks for the design, development, and deeper understanding of such robots and their behaviors, there are many desired criteria and required constraints for their models. This paper presents one such framework, anchored by dynamical intention modeling (Aaron and Admoni, 2010; Aaron et al., 2011) to represent cognitive elements underlying goal-directed behavior in embodied robots. With dynamical intention modeling and the accompanying hybrid dynamical cognitive agent (HDCA) framework, essential components that are often treated separately – including reactive and deliberative intelligence, and cognitive and physical behaviors – are unified in a modeling framework that supports high-level behavioral design, low-level cognitive and physical representations, and machine learning methods for integrated, autonomous learning in response to robots’ environments.
Dynamical intention modeling and the HDCA framework for integrated dynamical intelligence are influenced by several observations about models of intelligent embodied agents, biological and robotic, in dynamic environments:
• Embodied agents are integrated systems, complete autonomous agents embedded in an environment (Pfeifer and Bongard, 2006). Their high-level cognitive intelligence, low-level cognitive intelligence, and physical actions and behaviors are essential system components, and they should be modeled and analyzed together, reflecting their integration.
• Goal-directed behavior of embodied agents moving through their environments is necessarily the result of the agents’ integration across cognitive and physical components. For models to better support both production and analysis of goal-directed behavior, the relevant cognitive and physical components should be integrated in the model.
• In dynamic, unpredictable environments with arbitrary asynchrony, agents should be capable of appropriately dynamic responses and learning. If the environment cannot be known a priori, then ideally, models would not impose a priori restrictions on the granularity of possible responses in the environment. Similarly, because embodied agents are sensibly modeled as moving continuously through space and time, models should ideally support continuous space and time representations, without pre-imposed discretizations.
• Typically, models allowing only low-level representations do not effectively extend to high-level representations: for example, models that describe only kinematics of leg movement do not extend to pathfinding on large maps, and cognitive models describing only subsymbolic processes do not extend to representations of intentions guiding goal-directed planning.
• Conventional AI models of goal-directed behavior are frequently founded on high-level propositional representations, such as the goals, beliefs, and intentions of agents carrying out planning for the behavior [e.g., Georgeff and Lansky (1987)]. These representations do not readily support integration with low-level, continuous-time processes; they do not readily support cognitive–physical integration without imposing restrictions that may be ill-suited in unpredictable environments. Ideally, intelligence models would represent cognitive elements such as beliefs and intentions in a framework consistent with agents as integrated systems.
For the design and analysis of navigating, goal-directed embodied agents, a model of integrated intelligence would ideally represent and unify the cognitive and physical components – and interactions among them – underlying robust behavior in unpredictably dynamic environments. This paper presents the dynamical intention-HDCA (DI-HDCA) framework for integrated dynamical intelligence models for embodied agents, discussing its background, specifications, and foundation for extensions. Two different kinds of dynamical intention-based integration are presented, reactive–deliberative integration and cognitive–physical integration, as are required for fully integrated embodied agents. Moreover, the paper conceptually contextualizes this modeling framework in specific motivations based on the roles of embodiment and environment in agent behavior.
The DI-HDCA framework fuses ideas from cognitive modeling and general system modeling in a new synthesis, often employing them unconventionally to support the requirements of embodied intelligence. For instance, the foundation of a DI-HDCA model is a finite-state machine that combines continuous and discrete dynamics in a hybrid automaton (Alur et al., 2000): states (modes) represent continuously evolving actions or behaviors described by systems of differential equations; each mode also has conditions governing when discrete transitions to other modes occur, and what discrete changes in system state occur as part of these transitions.
The dynamical intention framework underlying cognitive models is influenced by the belief–desire–intention (BDI) theory of practical reasoning and its many implementations [e.g., Georgeff and Lansky (1987) and successors], which established the effectiveness of BDI elements (beliefs, desires, and intentions) as a foundation for goal-directed intelligence. Unlike conventional BDI agents, however, dynamical intention models link BDI elements in a continuously evolving system inspired by spreading activation networks (Collins and Loftus, 1975; Maes, 1989). Each BDI element in this dynamical intention framework is represented by an activation value indicating its salience “in mind” (e.g., intensity of a commitment to an intention, intensity of a belief). The continuous evolution of these cognitive activation values is governed by differential equations, with cognitive elements affecting the rates of change in activations of other cognitive elements, as described in sections 2.3 and 2.4. These dynamical cognitive representations can be employed for both low-level reactive intelligence and high-level deliberative planning (Aaron and Admoni, 2010), enabling integration of the two levels.
The particular physical motion of DI-HDCAs (i.e., navigation in dynamic environments) is not central to the DI-HDCA framework, as discussed in section 3.2, except that it too is governed by dynamical systems. This enables further integration: physical and cognitive components in DI-HDCAs are represented in the common language of differential equations, which is critical to the learning demonstrations in section 5.
These are the components of the general framework of dynamical intention and DI-HDCA modeling. The remainder of the paper further elaborates on these components and presents example DI-HDCAs, which illuminate general concepts and are employed in various proofs of concept.1 For example, the paper presents a simulated service robot in a grid-world office environment, for two kinds of demonstrations: how conventionally deliberative-level intelligence can be distributed over reactive-level processes in DI-HDCA models; and how new kinds of machine learning can be facilitated by dynamical intention representations. Indeed, with dynamical intention-based learning, the robot approximates deliberative rule-based performance with only reactive-level learning, minimizing reliance on deliberation and supporting dynamically responsive, adaptive behavior.
In addition, the paper presents experiments with DI-HDCAs as autonomous players in a real-time, human-interactive simulation of the child’s game Tag. In Tag, a player designated as “It” attempts to touch (“tag”) other players, who try to avoid being tagged. Safe locations called bases are in the Tag variant in this paper, as shown in Figure 1, so that players touching a base cannot be tagged. If a non-It player Pi does get tagged by It (call the It player Pj, distinct from Pi), then Pi becomes the new It, Pj is no longer It, and the game continues with players (including Pj) avoiding being tagged. This game is well suited for demonstrations of embodied intelligence: agents employ complex cognitive strategies while navigating in an unpredictably dynamic environment. Demonstrations from Tag games in this paper illustrate cognitive–physical integration in DI-HDCAs, with agents’ jointly altering cognitive and physical performance to meet new specifications for their strategies without interrupting gameplay.
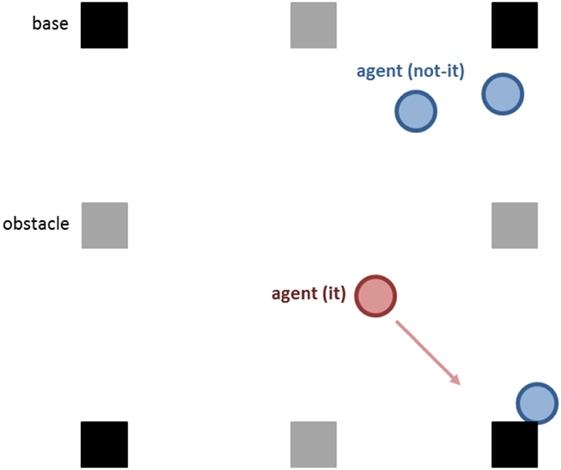
Figure 1. Diagram of a Tag game environment, containing bases (darker squares), obstacles (lighter squares), and agents (circles) playing the game. Both kinds of Tag players are represented, one It player and three non-It players.
The contributions of this paper include:
• A broad description of dynamical intention and HDCA modeling, significantly expanding upon more narrowly focused presentations in Aaron and Admoni (2010) and Aaron et al. (2011). This includes the motivation and proper contextualization of DI-HDCA modeling as a response to entailments of environment and embodiment.
• A survey of previously described DI-HDCA learning methods and experimental results in both the Tag game and office environments mentioned above (Aaron and Admoni, 2010; Aaron et al., 2011), demonstrating the role of DI-HDCA modeling in adaptive integrated intelligence.
• Several new experimental results and substantially expanded analyses, including statistical analyses of data that were previously only qualitatively described.
This paper is the first comprehensive presentation of integrated intelligence for DI-HDCAs – encompassing physical-level components for motion and navigation and cognitive-level components for reactive and deliberative intelligence – and the first casting of DI-HDCA concepts that directly exposes the elements of embodied agency underlying those concepts. In addition, section 6 briefly discusses potential extensions of the present work in new contexts, including possibilities of verifying DI-HDCA models and applying the DI-HDCA modeling framework to study emergent properties of embodied intelligence.
2. The DI-HDCA Modeling Framework
The DI-HDCA modeling framework is specifically designed for, and constrained by, the demands of embodied autonomous intelligent agents navigating in dynamic environments. It is a synthesis of three concepts – BDI theory, spreading activation networks, and hybrid system models – that are employed unconventionally to enable formally specified yet broadly expressive agent models. This section presents the background and foundational ideas on which the DI-HDCA framework is based, analyzing the roles of embodiment and environment in modeling goal-directed agents, and then discussing cognitive modeling and hybrid system modeling in that context.
2.1. Environment
In principle, goal-directed agents need not be embodied [e.g., many BDI-based planning agents (Georgeff and Lansky, 1987)], but with or without embodiment, environment constrains what factors and features may be elements of effective agent models. Some problem solving agents operate in fully known, unchanging environments, which constrains the kinds of reasoning they need; for example, pathfinding problems can be solved prior to navigation for perfect performance. Other agents might operate in stationary environments that are not fully known in advance, so problems might not be solvable ahead of time, but information once discovered would not be changed, which could simplify machine learning or other adaptation needed in this environment. Such stationary environments are not realistic for the present context, however, so this paper restricts consideration to only dynamic and unpredictable environments.
For goal-directed behavior, agents must do some kind of planning or task sequencing, potentially employing propositional reasoning-based deliberative intelligence. As an environmental constraint, however, this paper additionally considers only environments in which deliberation is not sufficient, and some kind of reactive intelligence is also necessary. This reactivity requirement is not identical to the above criterion of “dynamic and unpredictable” – one could imagine environments in which deliberation sufficed for all unpredictable changes – but it is related.
In such environments, both reactive- and deliberative-level intelligence – and their combinations – are essential for goal-directed embodied robots. DI-HDCA modeling integrates deliberative and reactive intelligence through shared representations of cognitive elements: the same elements that support reflexive, reactive responses can also be employed for task sequencing and other conventionally deliberative-level intelligence. These shared, dynamically sensitive representations allow goal-directed reasoning to be distributed over both reactive and deliberative levels; the particular agent models in section 4 exemplify this distributed approach. Thus, DI-HDCA modeling does not deny deliberation, but it can minimize reliance on deliberation for more robustly responsive and adaptive agents.
2.2. Embodiment
Section 2.1 noted that an agent’s environment could be incompletely known or unknowable, but for real-world robotics, one might potentially instead view the embodiment of the robot as the primary factor introducing such unpredictability: from dirt on a floor that affects a wheel’s traction to moving obstacles (e.g., people) in hallways navigated by service robots, embodiment seems critical to why embodied robots need to respond and adapt at unpredicted times, to unpredicted situations.
Indeed, in a real-world environment for a robot, unpredictability is general, but that may not be strictly due to embodiment. If embodiment is considered separate from real-world constraints, it is imaginable in theory that a goal-directed embodied agent and its world might be fully deterministic and known in advance. This may seem laughably implausible to anyone who has worked with real robots, but in principle, it seems that unpredictability need not follow from embodiment alone.
Similarly, it might initially seem that reasons for continuum-based modeling of time and space – to represent continuous agent motion through space, and through time – are due to attributes of and constraints from the environment. Indeed, one could assert that continuous time and space are environmental properties: once unpredictability and the need for reactive responses are part of the environment, continuous time and space representations are then needed to fully represent the environment. It is not clear, however, that the environment would actually need to be fully represented for successful goal-directed behavior by a non-embodied agent. Perhaps the needed reactivity for a non-embodied agent could be achieved with a discretized time and space model, with limited granularity of representation; the asynchrony in the environment could be arbitrary, but perhaps that complexity need not be imposed in full upon the agent model.
DI-HDCA models do represent continuous space and time, however, with embodiment rather than environment as the practical motivation. Conventionally, real-world embodied systems are modeled as moving continuously through space, often by differential equations. Because these continuous representations are well established as useful for modeling, they have been adopted for DI-HDCA models.
The effects of this design decision pervade the DI-HDCA modeling framework: because DI-HDCA models should be integrated, and continuous time and space representations are useful, added entailments arise. A navigation model sensitive to continuous time variations is needed. Reactivity should be modeled on a continuous-time scale, for integration with continuous-modeled motion. The cognitive model should thus also be modeled with real-time dynamics, for sensitivity to real-time changes in the environment. Then, as cognitive model elements are real-time dynamic parts of the environment of other cognitive elements (e.g., beliefs are parts of the cognitive environment that affects intentions), and cognitive elements are sensitive to real-time environmental variations, the cognitive model should represent micro-cognitive variations and effects throughout all cognitive components. This can be viewed as part of reactive–deliberative integration, in the context of a continuous time and space model.
For a fully integrated agent model, however, the effects cannot stop within the cognitive system. Full integration between cognitive and physical components entails that models should not restrict micro-level cognitive changes from affecting physical elements. Indeed, if a modeling framework represents arbitrary levels of detail, enabling representations of arbitrarily unpredictable environments, then integrated agent models should permit micro-cognitive effects to cause micro-physical effects (and vice versa); indeed, any cognitive element should be able to somehow affect any physical element (and vice versa). In the DI-HDCA framework, one could design models with pre-imposed constraints on the extent of cognitive–physical integration – e.g., that the agent’s heading angle for navigation has no effect on the activation of a particular desire to complete a task – but to support fully integrated models, the framework allows for models without such constraints.
The constraints from environment and embodiment therefore entail continuum-valued representations for both cognitive and physical elements of the model, and simultaneous integration across reactive and deliberative intelligence and cognitive and physical components. This is achieved in DI-HDCA models by expressing all continuously varying elements in the unifying language of differential equations, in a hybrid dynamical system model (see section 2.4). This does not entail that all model elements must be continuously varying, but critical cognitive and physical elements should vary continuously, and the agents described in sections 4 and 5 exemplify these ideas.
2.3. Cognitive Modeling and Goal-Directed Reasoning
DI-HDCAs can be viewed as having physical and cognitive system components, represented by the differential equations and variables describing behaviors conventionally considered physical or cognitive, respectively. Because DI-HDCA modeling is designed for embodied agents moving through environments, models can contain continuously time-varying representations of physical elements conventionally useful for modeling motion, such as xy-location, velocity, or heading angle; because DI-HDCA modeling is also designed for integrated, goal-directed intelligence of these navigating embodied agents, models also contain continuously time-varying representations of cognitive elements conventionally useful for modeling goal-directed behavior. These cognitive elements are derived from the BDI (belief–desire–intention) theory of practical reasoning (Bratman, 1987) and the many agent-based implementations of it [Georgeff and Lansky (1987) and many successors].
BDI theory recognizes the critical role of intentions as cognitive elements of practical reasoning, distinguishing intentions from desires. Although all three kinds of cognitive elements influence behavior selection and planning of task sequences, beliefs, desires, and intentions are distinct in their roles: in particular, desires (i.e., desired goals or conditions in the world) may conflict, whereas intentions are conduct-controlling pro-attitudes, reflecting commitment to behaviors and resisting reconsideration or conflict. A BDI-based approach provides a broader cognitive framework for goal-directed agents than conventional hybrid reactive–deliberative architectures [e.g., Arkin (1990), Gat (1998)], subsumption architectures [e.g., Brooks (1986)], or other behavioral robotics approaches that do not employ distinct desires and intentions as cognitive elements for action selection and task sequencing.
Conventional applications of BDI theory to computational agents, however, do not explicitly support all the entailments of embodiment or the multi-tiered integration described in this paper. For example, BDI implementations are not conventionally based on continuous models of time and space, and action selection and task sequencing are typically the result of deliberative processes, employing propositional representations of beliefs, desires, and intentions. Designing BDI-based agents without continuum-valued representations seems apt for some contexts – without the requirements of embodiment, continuous representations might needlessly complicate agent design and analysis – but for embodied, goal-directed mobile robots, continuous-modeled cognitive and physical representations can be beneficial, particularly to support the integration inherent in such robots. Moreover, continuum-valued cognitive representations support dynamicist perspectives of cognition (Port and van Gelder, 1995; van Gelder, 1998; Beer, 2000; Spivey, 2007), and they enable sensitivity to real-time micro-cognitive variations that can cascade into macro-level cognitive effects.
In DI-HDCA models, cognitive elements are represented by continuously varying activation values, where an activation value represents the salience “in mind” of the related cognitive element. As examples, beliefs with high activations are “strongly held,” desires with near-zero activations are not “strongly felt,” and high-active intentions indicate high priorities on the related actions. Because all cognitive elements are represented this way, and activations can vary in real time, interactions among them can be represented by an unconventional spreading activation network. Spreading activation networks are well-established models with applications in both cognitive psychology (Collins and Loftus, 1975) and agent modeling (Maes, 1989), based on neuroscience-influenced ideas that activations of cognitive elements can affect activations of other cognitive elements. Spreading activation networks are related to other connectionism-inspired approaches, including Haazebroek et al. (2011), which employs ideas from the theory of event coding to model action and cognition; similar to DI-HDCA modeling, the work in Haazebroek et al. (2011) emphasizes shared representations for integrating across levels of action and cognition, but the DI-HDCA framework is explicitly focused on dynamically sensitive representations of intentions, desires, and beliefs for goal-directed navigating agents.
Because cognitive activation values are governed by differential equations in DI-HDCA models, the spreading activation framework employed is unconventional: instead of the activation of an element directly having excitatory or inhibitory effects on activations of other elements, the activation of an element affects the rates of change in activations of other elements. That is, an activation of one element serves as part of a term in the differential equation describing the variation in another element. As a small, constrained example, consider this part of a differential equation, where BP stands for the activation on the belief of P, k > 0 is a constant, IA stands for the activation on the intention for action A, and the dotted variable stands for the rate of change in IA:
This encodes excitatory and inhibitory effects on IA: if BP > 0, will increase, for an excitatory effect on IA over time; if BP < 0, will decrease, for an inhibitory effect. The magnitude of coefficient k in that equation serves to intensify or diminish the effect of BP on IA, an observation that is exploited in mechanisms for DI-HDCA learning (see section 2.5). A system of such differential equations, in which activations of cognitive elements are parts of differential equations for other cognitive elements, thus models a spreading activation network. Although this network may be viewed as unconventional due to the layer of indirection induced by the differential equations, it might also be viewed as appropriate for continuous-time environments with arbitrary asynchrony. Activation is not passed through the model in synchronized lock step nor in pre-determined quantities, and the quantity of spread activation is time-varying and responsive to changes in the system, fitting a DI-HDCA’s environment.
The BDI-based framework of dynamical intentions presented in this paper is not the only agent model with dynamical systems-based elements that can be viewed as representing intentions. The dual dynamics framework (Hertzberg et al., 1998; Jaeger and Christaller, 1998) represents activation dynamics as different from target dynamics, analogous to intentions and navigation dynamics in DI-HDCAs. Dynamic neural field approaches (Schöner et al., 1995; Erlhagen and Bicho, 2006; Richter et al., 2012; Sandamirskaya et al., 2013), based on neuroscientific principles, also associate activations of cognitive entities with actuations of behaviors. The DI-HDCA framework shares the emphasis on dynamics with these approaches but is less tightly coupled with low-level sensorimotor systems, emphasizing cognitive dynamics of typically higher-level constructs of desires and intentions, which can directly support the high-level behavioral design and analysis desirable for many embodied robotics applications.
2.4. Hybrid Dynamical System Modeling
Continuous dynamics are essential for cognitive and physical elements in DI-HDCA models, but discrete dynamics are also important for behavioral modeling. Robots are productively designed and understood in terms of discretely delineated behaviors, with transitions between those behaviors. The idea that discrete changes between behaviors can occur when some threshold condition is met has been employed in contexts ranging from logical models (“if condition then begin action A”) to neural models (e.g., threshold for neurons firing) and beyond, including system models that combine continuous and discrete dynamics.
To support both continuous dynamics and discrete behavioral design, a DI-HDCA model can be expressed as a hybrid automaton model of a hybrid dynamical system (HDS), which explicitly represents and distinguishes continuous and discrete system dynamics (Alur et al., 2000). A hybrid automaton is a finite-state machine in which each state (mode) is a continuous behavior, specified by differential equations describing system dynamics in that mode. HDS models have been employed for many complex applications, including navigating robots or virtual agents [e.g., Egerstedt (2000) and Aaron et al. (2002)], and for the present application, the structures of a DI-HDCA model correspond naturally to elements of an HDS. For DI-HDCAs, each behavior might be specified as a mode, describing the physical and cognitive dynamics governing the robot while executing that behavior. Figure 2 illustrates a mode in a DI-HDCA model, showing cognitive elements interconnected in a dynamical system model. The physical elements (e.g., position, velocity) are also governed by differential equations in each mode, and because all physical and cognitive elements are represented as variables in a dynamical system, any one of them can be part of any differential equation in the system – i.e., for integration, any element can affect the dynamical change in any other element.
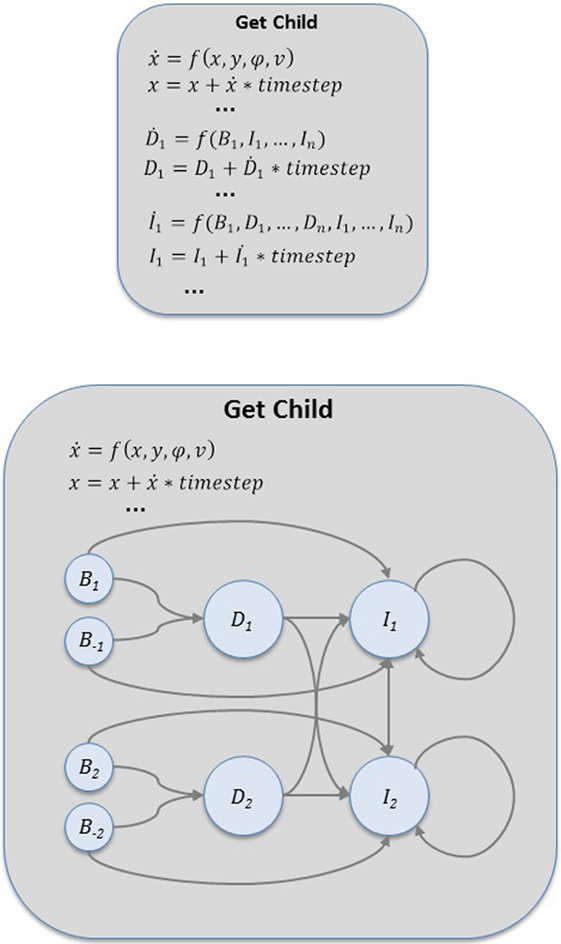
Figure 2. Visualization of cognitive elements in a behavior (a mode) in the hybrid dynamical system model of a DI-HDCA service robot (see section 4). BDI-based cognitive elements – beliefs, desires, and intentions – are interconnected with excitatory and inhibitory links, expressed by differential equations in a dynamical system, which can be viewed as an atypical spreading activation network. Because both cognitive-level and physical-level components are expressed in the shared language of dynamical systems, physical behavior components such as speed or heading angle (not visualized here) can in principle also be part of the dynamical system.
In DI-HDCA behavior, transitions between modes occur when threshold conditions (guards) are met, and transitions are represented as instantaneous changes in behavior, which may be accompanied by discrete changes in values of elements in the model. For example, when some action Ai is completed, the robot might transition to the mode for action Aj, and the activation on the intention for Ai might instantaneously drop, as the robot no longer intends to carry out Ai. Figure 3 illustrates a mode-transition system for a DI-HDCA, situating the mode from Figure 2 in a full model. The connections between modes indicate available transitions: at any given moment, an agent is in exactly one mode (call it Mi), describing its behavior at that moment; when guard conditions in mode Mi are met, the agent transitions to some other mode Mj connected to Mi in the model.
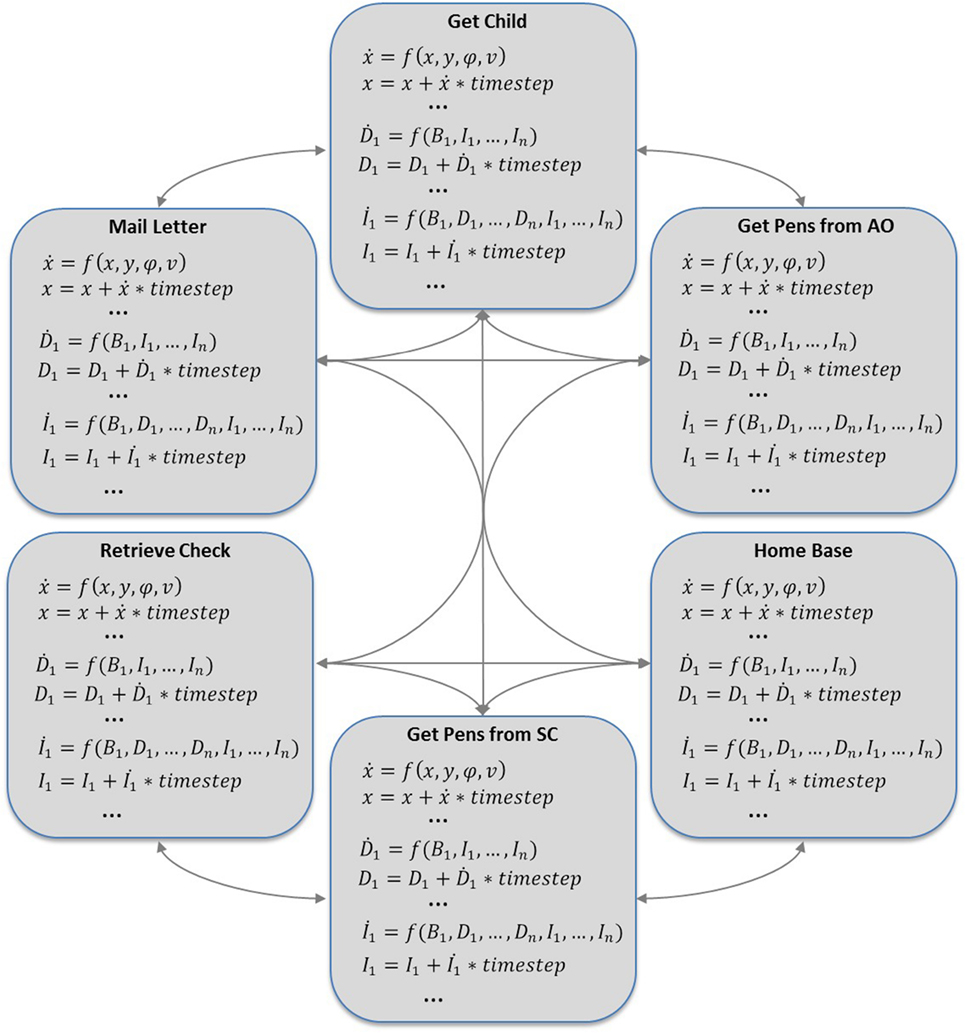
Figure 3. Visualization of a full mode-level system model of a DI-HDCA service robot (see section 4). Individual modes (see Figure 2) are in a state-transition model: at any moment, the agent is in one behavior mode; the change to a different behavior is modeled by a transition from one mode to another. It is not necessary in DI-HDCA models that every mode be connected to every other mode, but there is no restriction against a fully connected system such as the one shown here. Every cognitive and physical element in the DI-HDCA can be present in each mode, for use in that mode’s dynamical system.
2.5. DI-HDCA Learning
Because cognitive elements are represented as parts of terms in differential equations (Figure 2), they can affect each other’s activations and any behavior based on those activations. For example, with action selection or task sequencing based on which intentions have the greatest activation values, any cognitive element can influence every intention’s activation in the network, thus affecting action selection. Moreover, because physical elements (e.g., position, velocity) are also represented in that dynamical system, they can in principle also affect activation values and task sequencing. This interconnectedness is central to integration in DI-HDCA modeling.
This interconnectedness is also central to straightforward methods by which DI-HDCAs can learn from experience. As background, note that the magnitude of the effect of element Ei on element Ej in the dynamical system is expressed by the coefficient ci,j in the related term, as in this example:
Here, if coefficient ci,j became a greater positive number, the activation on Ei would have a stronger direct effect on Ej − ci,j represents the link from Ei to Ej. Thus, if an agent’s experience suggested that Ei should have a different effect on Ej, learning that new effect would only require altering that coefficient.
With this, DI-HDCA learning of new strategies for action selection or dynamic task re-sequencing – aspects of agent intelligence that are often expressed as deliberative in agent models – could require only that the appropriate coefficients change values. For example, if feedback suggests that some belief B should affect action selection, the agent can learn that connection by adjusting coefficients relating belief B to the appropriate intentions. Because intentions are the cognitive elements representing actions, this can suffice to bring about the learned adaptation; no new rules or complex mechanisms are required.
Although the relationship between beliefs and intentions is an especially important one, DI-HDCA learning is not restricted to those elements. If feedback suggested, for instance, that increased salience of a desire D is not productive during some action A, connections could be learned to lower the activation on intention IA corresponding to action A whenever the activation of D is a large value. Moreover, if faster speed of an agent is not productive when the agent is in action A (action A might require acute perception or good traction for motion), the agent could learn to calibrate the activation of IA based on speed. Because of the full interconnectedness of the cognitive–physical representations enabled by DI-HDCA models, any such relationship could be straightforwardly learned by altering the weights of links between elements.
From the perspective of an agent designer, this mechanism can effectively refine agent behavior to meet specifications, even in interactive environments (see section 5). From the perspective of a scientist modeling and analyzing behavior, this mechanism enables the study of connectionism-inspired learning – learning occurs by changing weights of links between elements – with phenomena as low-level as speed and as high-level as intention. [In context, it can also be viewed as a form of reinforcement learning; see Aaron and Admoni (2010).] The integration encoded in DI-HDCA models enables such straightforward learning approaches to be exceptionally effective in DI-HDCAs.
3. Agent Implementation
Dynamical intentions can be implemented in multiple ways to be consistent with distinguishing properties of intention in BDI theory. Similarly, the reactive navigation intelligence in DI-HDCAs can vary with different agent implementations. Nothing intrinsic to the DI-HDCA framework fully defines such options, although some constraints are imposed (e.g., navigation models are expressed as differential equations, for integration with dynamical intention). Below, this section presents general background regarding DI-HDCA implementation and simulation for the experiments in sections 4 and 5, including the navigation system and a brief summary of the factors for adherence to BDI properties.
3.1. Distinguishing Properties of BDI Intentions
As described in section 2.3, the BDI-based cognitive elements of DI-HDCAs are represented by dynamically varying activation values. For agents implemented in the demonstrations described in this paper, cognitive activations are bounded to be within [−10, 10]. Low-magnitude activation values (i.e., near 0) indicate low salience of the associated concepts, whereas greater magnitudes of activations represent more importance or intensity of the associated concepts; for example, a desire with near-zero activation would indicate relative apathy regarding the associated concept, while a belief with high activation would be strongly held and a high-active intention would indicate greater importance of and commitment to the related task or behavior. Activations with negative values indicate salience of the opposing concept – e.g., an intention with activation −2 indicates a mild commitment not to do the associated task, and a belief with activation −9 indicates that the opposite or negation of the associated concept is strongly held.
For the agents implemented in this paper, beliefs and desires can conflict with each other. For instance, if an agent model included both beliefs BamIt representing that the agent is It in a Tag game and BnotIt representing that the agent is not It, the model need not preclude them from having simultaneously high activations. DI-HDCAs could be designed to disallow conflicting beliefs, and doing so could benefit some applications, but for the explorations of computational intelligence in this paper, such conflicts were not explicitly disallowed. Similarly, it is possible for conflicting desires to have simultaneously high activations, representing an agent intensely desiring to do two things when only one at a time is possible.
The philosophical foundations of BDI agents assert that desires can conflict with each other but intentions resist conflict with each other. This is one of the distinguishing properties of intentions noted in Bratman (1987), part of explicitly establishing desires and intentions as distinct cognitive elements. For this paper, DI-HDCAs are implemented with mechanisms consistent with distinguishing properties that apply to this dynamical account of intention2:
• Intentions are conduct-controlling cognitive elements.
• When salient, intentions resist reconsideration.
• When salient, intentions resist conflict with other intentions.
It is straightforward to implement that intentions control conduct: in the state-transition system representing a DI-HDCA’s behaviors (see Figure 3), conditions for entering and exiting a mode specify that the highest-active intention determines agent state. Initially, the agent must begin in the mode corresponding to its highest-active intention, e.g., in mode Init, when intention IInit has the highest activation of any intention. Then, a transition to another mode Other occurs only when intention IOther becomes highest-active, which can happen in two ways: behavior Init becomes completed, so the activation of IInit is set to a low value (e.g., −10) and intention IOther becomes highest-active; or the cognitive activation values change over time, as governed by the dynamical system, and the activation value of IOther evolves to become greater than IInit.
For reconsideration resistance, the implemented2 mechanism [described in Aaron and Admoni (2009, 2010)] encodes that a high-active intention Ia tends to minimize other intentions’ impacts on Ia, and this effect becomes more pronounced as the activation of Ia grows. For intentions Ia and Ib (b ≠ a), the differential equation for includes the following structure:
Persistence factor PF is defined as
where i ranges over all intentions and the ϵ > 0 term prevents division by 0. Then, PF(Ia) multiplies every intention Ib in the equation for (for b ≠ a), so as Ia grows in magnitude relative to other intentions, contributions of every Ib are diminished, and when PF(Ia) = 1 (i.e., Ia = 0), such contributions are unaffected. The denominator is designed to model Ia as less reconsideration resistant when other intentions are highly active.
The implemented mechanism for conflict resistance among intentions is also in coefficients in cognitive dynamical systems. In this paper, every intention in agents’ cognitive systems is negatively interconnected with every other intention, with a non-conflict factor NCF as part of the differential equation for every intention. [Recall from equation (3) that .] The non-conflict factor function is:
This NCF component is applied similar to PF: in the differential equation for Ia, each term for an intention Ib is multiplied by NCF(Ib) (although unlike PF, it is possible that a = b). Thus, NCF decreases activation levels for conflicting intentions (and increases them for non-conflicting intentions, e.g., when a = b). The constants in equation (5) were chosen for agents in this paper by the agent designer after thought experiments and evaluation of preliminary tests; with different choices of constants, other DI-HDCAs could perform differently in the same general framework.
To test NCF effectiveness, simulations were run that isolated effects of NCF: agents did not navigate, and persistence factor PF was removed from the cognitive system; experiments compared a control group without NCF to an experimental group with NCF for results. Each group was identical in all other ways, containing ten agents (A1, …, A10) with cognitive elements designed for the office scenario in section 4. Each of the ten agents had identical cognitive activation values except for initial activations on intentions; for intentions, each agent Ai’s initial activations were i/3 times these baseline values:
The rate of change in activation on intention IML corresponding to the MailLetter behavior was then measured. On average, over the first 30 s of test runs, agents with non-conflict factor NCF in operation and the highest level of initial activation had a lower rate of decrease in activation of intention IML compared with agents in the baseline condition. The effect was reversed at medium levels of initial activation, as indicated by marginally significant (p = 0.052) interaction. For the baseline agent, mean rates of change were −0.228 when medium-active and −0.232 when high-active; for the NCF agent, −0.279 when medium-active and −0.191 when high-active, as presented in Figure 4. (All statistical analyses in the paper were conducted with SPSS, version 23.)
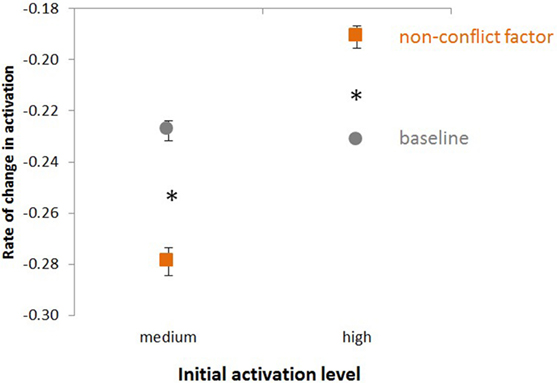
Figure 4. Intentions with high activation avoid conflict with other high-active intentions. A priori contrasts indicate significant differences (p < 0.05) between means, as shown by asterisks. The main effects of activation level and type of agent are significantly different (p < 0.05) in a 2 × 3 ANOVA, with a low activation level condition included but not shown for clarity and brevity.
Examination of distinguishing BDI properties for DI-HDCAs is not complete, but the implemented mechanisms suggest that dynamical intentions can be consistent with BDI properties, and they demonstrate the environmental sensitivity and design control capable in the DI-HDCA framework.
3.2. Navigation
Although some agent navigation for this paper is simple, straight-line motion (see section 5.1), most agent navigation in both the Tag game and the office grid-world (section 4) is instead similar to the potential-based reactive navigation of Schöner et al. (1995), Large et al. (1999), Goldenstein et al. (2001), and Aaron and Mendoza (2011). This system models environments as consisting of actors (the navigating agents), obstacles that repel actors, and targets that serve as goal locations, attracting actors. Actors, obstacles, and targets can be either moving or stationary, and actors can be treated as obstacles or targets by other actors. In the Tag game scenario for experiments in section 5, for instance, non-It players might consider It actors as obstacles, and an It player may have an actor as its target. To illustrate the system and suggest the mathematics underlying it, the dynamics of this navigation system are briefly summarized here.
Non-linear angular attractor and repeller functions represent targets and obstacles, and their weighted contributions are dynamically combined to calculate an actor’s angular velocity in real-time response to the environment. Heading angle ϕ is computed by a non-linear system of the form:
where ftar and fobs are the attractor and repeller functions for the system, and wtar and wobs are their weights in the calculation. (Noise term n helps prevent the system from becoming trapped at critical points.) The weights themselves are determined by computing fixed points of another non-linear system [see Large et al. (1999) for details]. Other parameters and details are also concealed in the terms presented above. For instance, a repeller function fobs depends on parameters that determine how much influence obstacles have on an actor. This is only a partial overview of the navigation system, but it suggests the complexity involved in modeling it and exposes the significant non-linearity in the agent models’ physical components and navigation intelligence.
Although this navigation system integrates cleanly into dynamical intention-based intelligence, it is not the only option. For example, instead of abstracting navigation to position, heading, velocity, etc., as the above system does, one might employ a more physically grounded model for motion of a wheeled robot: the robot would have volume and mass; acceleration would be critical to the model, as would friction on the wheels and drag through the air. Such a physically detailed model would also integrate cleanly with DI-HDCA intelligence, as long as the system of motion was expressed in the language of differential equations, so any element of the system could straightforwardly affect any differential equation in the system – cognitive or physical – to effect the desired integration.
3.3. Simulation
The simulations for this paper are implemented in MATLAB, although other choices could also be good for implementing DI-HDCAs. At each time step, the simulation updates the state of each agent according to the behavior mode governing the evolution of that agent. The modes themselves are implemented as functions, containing both the propositional guards for transitions to other modes and the dynamical systems describing the behavior; executing a mode function on an agent either induces a transition to another mode or updates the state of the agent. As shown in Figure 5, the simulator loops through every agent, identifying the proper mode function to execute for that agent.
Figure 6 contains a sample code skeleton for a mode. In each mode, a list of mode-transition guards is checked, and if a guard is true, the mode-transition corresponding to the first true guard is taken. This transition is effected by discrete changes in the state of the agent, including setting a new mode value for the agent; the main loop will then simulate the agent in the appropriate new mode during the next time step. If no guard is true, the agent’s state is updated according to the dynamical system in the mode. To simplify this implementation, all discrete or deliberative dynamics in the agents in sections 4 and 5 occur during these instantaneous transitions; representing deliberation during mode execution is an interesting extension of the current implementation, but it requires giving temporal dynamics to deliberation that is not typically modeled as temporally dynamic, and that complication was not engaged in the present work.
4. Reactive-Level Learning and Deliberative-Level Intelligence
Part of the integrated intelligence of DI-HDCAs is the distribution of goal-directed intelligence over both reactive and deliberative processes: task sequencing and action selection are often considered to be deliberative-level intelligence, but with dynamical intention modeling, some can be handled by reactive-level intelligence and learning. This enhancement of reactive-level intelligence reflects a fundamental motivation of dynamical intention modeling and DI-HDCA design: reactive-level intelligence can be enhanced without denying deliberative intelligence; DI-HDCAs minimize reliance on deliberative intelligence, for greater robustness in unpredictable environments.
This section discusses dynamical intention-based learning methods for DI-HDCAs and describes demonstrations of agents learning to approximate deliberative, rule-based behavior. In particular, this section emphasizes how deliberative-level intelligence is distributed over reactive-level processing and learning. Although the idea of hybrid reactive–deliberative systems is not novel to DI-HDCAs, and deliberative-level intelligence that employs the same representations as reactive systems is not extraordinary (e.g., a planner that uses the location of a robot, where location is altered by reactive navigation) in hybrid agents, DI-HDCA modeling emphasizes “the other direction” of distribution of intelligence: instead of low-level reactive representations being employed by high-level logical planners, DI-HDCAs’ dynamical intentions enable conventionally high-level intelligence such as task sequencing and action selection to be distributed down to reactive, lower-level systems.
To demonstrate this reactive–deliberative integration, experiments consider a simulated service robot carrying out tasks in a grid-world office environment, illustrated in Figure 7, requiring navigation to various locations (see section 4.1 for task descriptions). To demonstrate the effects of reactive-level learning, three agents were compared: one had straightforward deliberative rules explicitly encoded to improve efficiency, the second was a reactive agent without dynamical intention-based learning, and the third agent employed dynamical intentions and reactive-level learning to approximate the rule-based performance of the first agent without requiring explicit deliberative rules. Two kinds of DI-HDCA learning were implemented for these experiments: a Hebbian learning method that strengthens connections among cognitive elements that are concurrently salient (i.e., with concurrently high activation values); and belief–intention (BI) learning for task-specific associations of beliefs and intentions. The Hebbian and BI learning methods were originally presented and qualitatively described in Aaron and Admoni (2010); this section summarizes these learning methods and presents new analyses demonstrating their effectiveness.
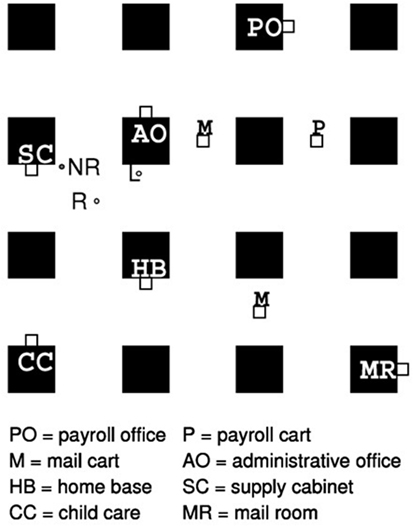
Figure 7. Simulation in progress, screenshot. A map of the office environment, top, shows offices and obstacles (black squares), targets (white squares abutting offices), and three agents (L, R, and NR). Below the grid-world map is a list of target locations corresponding to agent tasks.
4.1. The Office Grid-World: An Overview
An office environment for a simulated service robot provides a context in which navigation, action selection, and task sequencing are all essential. The particular office environment for these demonstrations (see Figure 7) is a simplified grid-world – e.g., mail carts in hallways are stationary, not moving obstacles – although future experiments in the same environment could more fully exploit DI-HDCA reactivity. In experiments, service robots can carry out six tasks, each with an associated target location: MailLetter, which requires navigating to the mail room (labeled MR in Figure 7); GetChild, with navigation to the child care center CC; RetrieveCheck, at payroll office PO; HomeBase, at home base HB; GetPensFromSC, at supply closet SC; and GetPensFromAO, at administrative office AO. Agents are therefore implemented with six behavior modes, one for each task, and cognitive elements including one intention for each behavior (e.g., IML for MailLetter, IGC for GetChild), related beliefs (e.g., BML for having a letter to mail), and related desires (e.g., DGP for the desire to get pens). These foundations enable experiments to focus on reactive and deliberative task sequencing intelligence, and this brief presentation emphasizes only the central elements for the results presented in this paper. In particular, perception and navigation intelligence are limited and not emphasized in these experiments; for additional details, see Aaron and Admoni (2010).
As introduced above, three kinds of robot agents were compared in DI-HDCA learning experiments. One agent AR (for Rules) employed two straightforwardly encoded deliberative rules: a sorting-based distance bias to prefer task sequencing that co-prioritizes tasks with proximate target locations; and the minimal-effort rule to avoid redundancy such as needlessly going to both the supply closet and the administrative office to get pens. The second agent ANRL (Non-Rules/Non-Learning) was identical to AR except it lacked the relevant deliberative rules; it employed DI-HDCA task sequencing – intention activations determined its current task – but had no DI-HDCA learning implemented. The third agent AL (Learning) employed dynamical intentions and reactive-level Hebbian and BI learning to approximate the rule-based performance of the first agent without requiring explicit deliberative rules. In the next sections below, both general expositions and specific applications to these agents are presented, for both Hebbian and BI learning, although the experimental results presented here focus primarily on BI learning.
4.2. Hebbian Learning
Inspired by observations about neuronal interconnections in Hebb (1949), Hebbian learning in these DI-HDCAs strengthens connections between co-active cognitive elements (i.e., elements that concurrently have high activation values). This broadly general dynamical intention-based Hebbian learning method could in principle apply to any elements, but for these demonstrations, it is only employed to enhance connections among intentions associated with target locations that are near each other: the closer the locations, the stronger the connection between the associated intentions.
For DI-HDCAs in this paper, the mechanism for Hebbian learning is based on a limited model of perception and additional structure in the cognitive dynamical system that allows perception to affect intention activations. Training for Hebbian learning consists of each agent simply navigating in its environment. For these demonstrations, training consists of an agent taking a pre-specified route through the office environment that passes close to all target locations for tasks (e.g., mail room, supply cabinet); training stops at the completion of that route. (Different training routines or stopping criteria could result in different learning; this choice suffices for the present demonstrations.) Each agent has a radius of perception rp roughly equal to one-quarter of the length of the grid-world, so it accurately perceives target locations within distance rp of it as it moves. During training runs for Hebbian learning, coefficients encoding interconnections between intentions have their values increased (until stopping criteria are reached) based on the proximity of target locations. In particular, for intentions Ia and Ib (corresponding to tasks a and b, where a ≠ b) and associated target locations La and Lb, if both La and Lb have been recently perceived by the agent, the following coefficients become greater in the cognitive dynamical system:
• The coefficient ka,b on intention Ib in the equation gets larger by an amount proportional to how recently Lb has been perceived.
• The coefficient kb,a on intention Ia in the equation gets larger by an amount proportional to how recently La has been perceived.
Because this occurs only when both La and Lb have been recently perceived, only proximate target locations contribute to the strengthening of connections between associated intentions, and there is greater co-activation between intentions when the target locations are perceived closer to each other during training.
Additional details are in Aaron and Admoni (2010) about how coefficients are altered during training (including a Hebbian scaling constant c1 that affects the changes in ka,b and kb,a), the mechanism by which recency of perception is implemented to result in the learning described here, and the effects of Hebbian learning without BI learning. The above description only summarizes the details necessary for the presentation of integrated Hebbian and BI learning in section 4.4 below.
4.3. Belief–Intention Learning
Intentions and beliefs have an especially important conceptual relationship regarding task completion: completion of a task T likely results in a strong belief that T has been completed; unless T needs to be repeated, the belief that T is completed would influence intention IT to have a negative value, so the agent would intend not to do task T again. Belief–intention (BI) learning, which alters cognitive connections between beliefs and intentions, is therefore especially significant for DI-HDCAs. For experiments in this paper, BI learning trains agents to relate intentions to beliefs in ways that might typically be encoded in propositional rules such as the minimal-effort rule (see section 4.1), but without any proposition-based learning. Details about BI learning, originally presented in Aaron and Admoni (2010), are summarized below.
In these experiments, the BI learning mechanism requires that coefficients relating beliefs to intentions have the form
Variables a and b (a ≠ b) refer to tasks, ranging over the six behaviors for agents; as convention, the ka,b values are designer-chosen scalars, Ia is the intention associated with task a, and Bb (, respectively) is the belief associated with task b having been completed (not completed). Coefficient IC(Ia, Bb) is then placed as the coefficient on term Bb () in the differential equation for intention Ia:
The ra,b and Ca,b values can be designer selected for specific applications. For this motivating example application – learning behavior consistent with the deliberative minimal-effort rule, avoiding redundant tasks when relevant but otherwise leaving cognition unaffected [see Aaron and Admoni (2010) for additional details] – ra,b = 1 exactly when belief Bb should affect intention Ia, otherwise ra,b = 0 (similarly for and ), i.e., ra,b = 1 exactly when a, b correspond to redundant tasks, which here are the pen-related tasks GetPensFromSC and GetPensFromAO. The Ca,b values specify how Bb affects when ra,b = 1; for this example, , so both do not effect Ia when beliefs reflect that task b has not yet been completed , but after b has been completed , the coefficient on Ia drops rapidly, preventing a redundant errand.
These ra,b and Ca,b terms are not modified due to BI learning, however. As with this Hebbian learning, this BI learning modifies coefficients ka,b during training. Training consists of an agent running errands in its office; the stopping criteria are met if that errand run ended with the agent having completed exactly one of the two pen-related tasks. If the errand run stopped but it was not the case that exactly one pen-related task had been completed, the scalar parts ka,b (for a ≠ b) in coefficients described in equation (7) are modified as follows:
(Scalars are similarly modified.) The pre-specified scalar γa,b > 1 encodes the extent of the modification. In this implementation, therefore, when tasks are not redundant, ra,b = 0 and ka,b is unchanged; when learning could lead to minimal-effort rule-like behavior, ra,b = 1 and the inhibitory link between belief Bb and Ia is strengthened. Thus, once one pen-related task is completed, activation on the intention to do the other rapidly drops.
To demonstrate the effect of BI learning (Hebbian learning is not part of these demonstrations), two agents were compared: agent ABI, which had been trained with BI learning to approximate the minimal-effort rule; and agent ANBI, identical to ABI but without training by BI learning. For these agents, the γa,b parameter values were all 1.2, and the initial activations on desires and intentions are as presented here:
Recall that agents have only one cognitive element for desires to get pens – noted as DGetPensSC in the above listing – which has the expected excitatory effect on both GetPensSC and GetPensAO behaviors; there is no separate DGetPensAO element, which is noted by the value n/a for the activation for DGetPensAO above. Agent ABI had seven training runs following the procedure described above, each starting from the same position near the supply cabinet on the left side of the office, and cognitive coefficients were adjusted during training. After training, agents ABI and ANBI were tested, with each test consisting of the agent autonomously running errands in its office; test runs began from 16 intersections in the office grid-world. Two facets of agent behavior were measured: redundancy, whether redundant tasks were completed by the agent, and speed, how long it took the agent to complete its run.
The redundancy measure was qualitatively described in Aaron and Admoni (2010): after training, agent ABI completed exactly one pen-related task on all 16 errand runs, completely avoiding redundancy and adhering to the minimal-effort rule; agent ANBI, in contrast, redundantly completed both pen-related tasks on 8 of its 16 errand runs. The speed measure, not previously statistically analyzed, is presented in Figure 8. The completion times of runs varied as expected depending on starting position: the agents’ first errand was to go to Payroll Office PO on the map (Figure 7), so runs starting farther from PO tended to take longer. Completion time data were therefore considered in four neighborhoods, each corresponding to a quadrant (lower/upper, left/right) of the map, and each containing four of the 16 starting points; a depiction of the neighborhoods is presented with the results in Figure 8. In every neighborhood, from every starting location, agent ABI completed its run faster than agent ANBI: in neighborhoods A, B, C, and D, respectively, the mean times to complete the runs are 74.885, 67.417, 73.073, and 63.375 s for ABI, and 82.198, 70.167, 80.958, and 65.573 s for ANBI.
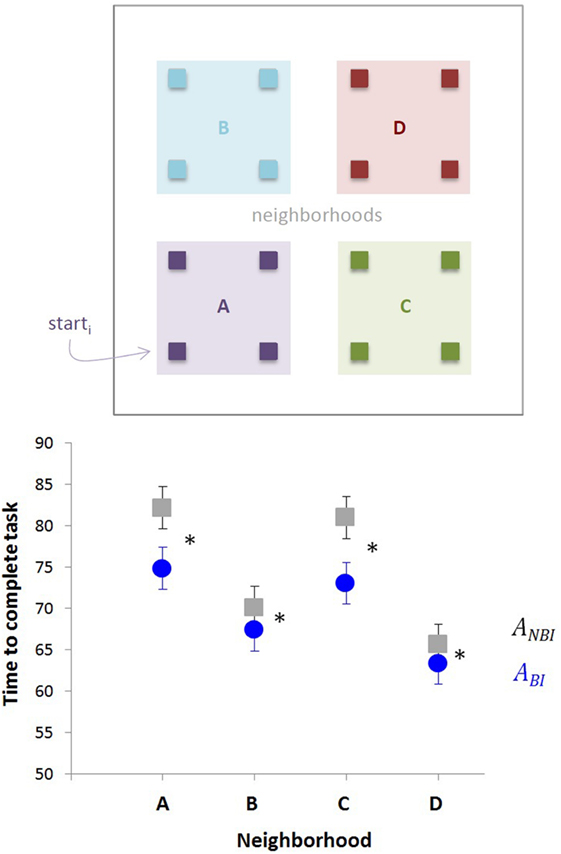
Figure 8. Belief–intention (BI) learning improves navigation. Agents started from one of 16 different positions, as indicated by the small squares on the map (top). For purposes of analysis, four neighborhoods were defined. The time for each agent to reach the target was measured (bottom). Agents that undergo BI learning navigate significantly faster to the target than agents without learning (ANOVA, significant main effects of agent type and neighborhood p < 0.05, with asterisk indicating the difference between agents). Neighborhoods are the same as in Figure 9.
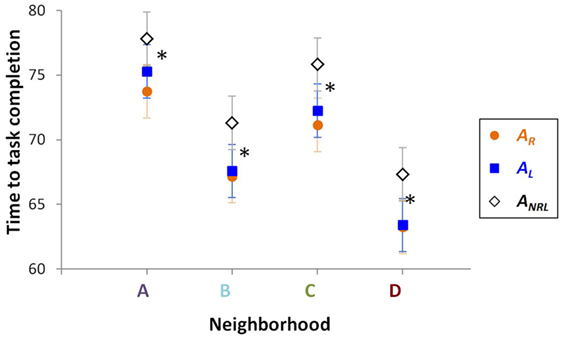
Figure 9. Hebbian–BI (HBI) learning. The three types of agent started from one of 16 different positions, grouped into the same neighborhoods as in Figure 8. The time for each agent to complete its errand run task was measured. Using a 3 × 4 fully factorial ANOVA, a significant (p < 0.05) effect of type of agent and neighborhood was detected. Post hoc t-tests determined that in all neighborhoods AR and AL were statistically indistinguishable and that both were statistically different from ANRL, as indicated by the asterisks. When the marker for AR is not visible, it is hidden behind the marker for AL.
These experiments suggest the effectiveness of BI learning for improving efficiency, enabling deliberation-level intelligence without proposition-based deliberative reasoning. Other implementations of BI learning are certainly possible for DI-HDCAs, but this simple example illustrates fundamental ideas about how learning can alter connections between beliefs and intentions to train agent behavior.
4.4. Integrating Hebbian and BI Learning
The Hebbian and BI learning methods described above can be straightforwardly integrated: because they alter disjoint sets of cognitive connections, nothing additional is needed to employ both methods together. For demonstrations of integrated Hebbian–BI (HBI) learning described in this paper, agents employ the mechanisms in sections 4.2 and 4.3 without alteration. These procedures and some results were originally in Aaron and Admoni (2010); this section summarizes the experiments run to demonstrate HBI learning and presents new and expanded statistical analyses of data from these experiments.
Training for HBI learning is consistent with procedures described above. A training run consists of an agent autonomously running errands in its office environment. Training concludes after a training run meets two conditions: the agent performs exactly one of the two pen-related tasks, suggesting learning of the minimal-effort rule; and the time taken by the errand run is not less than the time taken by the previous run, suggesting adequate learning of the distance bias. (Because DI-HDCAs in these experiments move at constant speed, time and distance are equivalent measures.) Training of agent AL (Learning) consisted of 18 training runs beginning at the same location and with the same cognitive activation values and parameters as for the BI learning in section 4.3, along with Hebbian scaling constant c1 = 4 × 104.
As described in section 1, these experiments compared agent AL to two other agents: ANRL, which is identical to the pre-learning state of agent AL; and AR, which is identical to ANRL except with propositional, deliberative encodings of the distance-bias and minimal-effort rule. For experiments, tests were run from 16 starting locations, consisting of each agent running errands as in the experiments of section 4.3. The redundancy of agents’ runs – i.e., did they execute both pen-related tasks – and the average time of completion of agents’ runs were measured and compared across the three agent types.
Considering task redundancy, the behavior of AR in these tests was dictated by its deliberative rules, as expected: it always retrieved pens from the administrative office, so it never went to the supply closet. By comparison, HBI learning agent AL also went to exactly one of those two locations on every run – indeed, on 15 of the 16 test runs, the dynamical intention-guided AL performed exactly the same task sequence as AR – but untrained agent ANRL went to both locations on every run. Because ANRL was identical to AL without the integrated HBI training, the reactive-level learning clearly reduced redundancy, bringing about the same performance as AR without additional deliberation.
Considering errand run completion times, AL finished every run faster than ANRL, but slower than AR. As with the results in Figure 8, completion time data for these agents were considered in the same four neighborhoods. Results are in Figure 9. In every neighborhood, completion times of agents AR and AL are statistically indistinguishable, indicating that HBI learning enabled the DI-HDCA agent to approximate rule-based behavior without explicit deliberative rules. Moreover, in every neighborhood, both AR and AL were statistically different from ANRL, demonstrating that learning distinguished AL from ANRL. As shown in Figure 9, the mean completion times (in seconds) to complete the errand runs in neighborhoods A, B, C, and D (respectively) are: 73.76, 67.187, 71.146, and 63.271 for AR; 75.302, 67.583, 72.25, and 63.406 for AL; and 77.822, 71.302, 75.823, and 67.333 for ANR.
4.5. Discussion
The above results demonstrate that dynamical intention-based, reactive-level learning can train agents to closely approximate deliberative-level intelligence and rule-based behavior in these experimental conditions, without reliance on deliberative structures. DI-HDCAs do not learn explicit propositional rules; agents learn reactive-level tendencies generally (though not entirely) in accord with the guiding rules. This enables deliberative-level intelligence to be distributed to reactive-level processes, for hybrid intelligence that retains the benefits of both deliberative goal-based performance and reactive responsiveness.
The generality of the tasks and this domain suggest that learned behavior can generalize beyond an agent’s training set, and that similar learning processes could generalize to other task domains. Moreover, Hebbian and BI learning alter only cognitive connections between some beliefs and intentions, but different DI-HDCA learning methods could incorporate other cognitive elements (including desires) or other connections among elements. Indeed, the underlying modeling framework of excitatory and inhibitory links among dynamically responsive cognitive elements is general enough to enable (if not encourage!) different approaches to DI-HDCA learning.
5. Cognitive–Physical Integration and Online Learning
Along with DI-HDCAs’ integration of reactive- and deliberative-level intelligence, which arises from shared cognitive representations across both levels, cognitive–physical integration arises from both cognitive and physical system components being expressed in the shared language of dynamical systems. As a demonstration domain for integrated cognitive–physical learning for DI-HDCAs, interactive simulated Tag games – i.e., requiring agent interactions with people and not just other agents – provide some especially important elements: an unpredictable environment; a requirement for navigation intelligence, including target seeking and obstacle avoidance; and the possibility of both simple and complex behaviors and strategies.
Tag has continuous, real-time play rather than turn-taking, so online learning during gameplay might be preferable to learning that interrupts play or occurs only after games. Moreover, in a user-interactive environment, agents might be asked to learn things specified by a user during gameplay – for instance, an agent might be playing too well, making the game too difficult, and the user could instruct the agent to modify some but not all of its strategy during play, for a more enjoyable game. In such a multi-faceted modification, as described in section 5.2, the agent might need to modify both its physical speed and its cognitive strategy for the desired behavior, learning during gameplay and without direct user feedback.
DI-HDCAs’ cognitive–physical integration can make it straightforward to learn this altered behavior. Because agent speed is represented by a variable in the agent’s shared cognitive–physical dynamical system, cognitive variation can directly respond to physical variation: speed can be directly employed as a parameter in learning that alters the agent’s cognitive network, so real-time micro-variations in speed can result in real-time micro-variations in cognitive-level strategy. As results in section 5.2 show, this straightforward approach can be effective for online learning in Tag-game demonstrations.
The remainder of section 5 further describes the Tag environment and related experiments. Although this is not the deepest instance of cognitive–physical integration possible in DI-HDCA models [see Aaron et al. (2011) for a brief mention of physical actions considered “involuntary” affecting cognitive elements considered “subconscious”], it illustrates the effect that cognitive–physical integration can have on adaptive agent behavior, and it illuminates the central role of dynamical intention modeling in integrated intelligence.
5.1. The Tag-World: An Overview
In the Tag game environment – called “Tag-world” here, analogous to “grid-world ” in section 4 – interactions between the user and agents are standard: each It player pursues some non-It player; each non-It agent avoids It players. To make the game more adversarial, for these demonstrations, two players at a time are It. The field of play (Figure 10) is a square with bases near the corners, obstacles between bases, and multiple players; players are penalized for touching an obstacle, requiring that they stay frozen for a specified duration, during which they are vulnerable to getting tagged by an It player. In addition, players touching base cannot become It, but they cannot stay on base too long, to prevent play from degenerating into all players staying on base and none getting tagged.
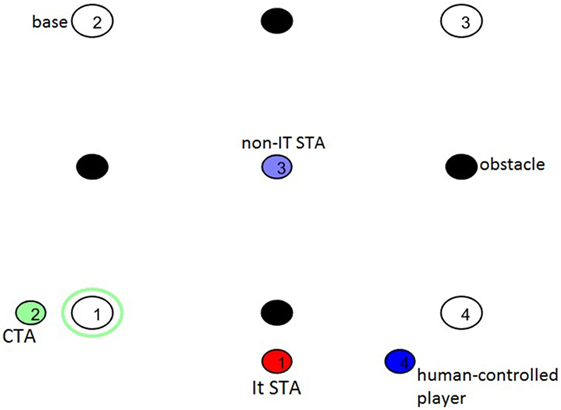
Figure 10. Simulated interactive Tag game. The screenshot (with added labels) illustrates field layout and Tag players. Elements include bases, obstacles, human-controlled players, It agents, cognitive Tag agents, and simple Tag agents. [Aaron et al. (2011) contain additional details about these Tag simulations.]
These Tag games are populated by two kinds of autonomous agents: cognitive Tag agents (CTAs), the focal agents in these experiments, with dynamical intention-based cognitive systems and relatively complex strategies; and simple Tag agents (STAs) with relatively basic strategies, serving as additional players in the game. For navigation, sometimes agents use straight-line motion that is not obstacle avoidant to move to a target location; when obstacle avoidance is needed, the navigation is the same kind as for the agents in section 4, as described in section 3.2. Tag-world and these agents were originally described in Aaron et al. (2011), which also contains details not included in the brief summary here; below, this section describes only details needed for the experiments involving CTAs, and it presents the results of online learning for CTAs, including qualitative description and new statistical analysis.
An STA, when not It, simply runs clockwise from base to base, ideally avoiding being tagged. When an STA becomes It, it chooses from two possible It-actions: it either chases the user (the person playing the game) or it chases another agent. An STA’s cognitive structure is a very simple dynamical intention-based system, straightforwardly supporting only this behavior; specifics of STA action selection are not central to results in this paper. In contrast, a CTA contains more complex intelligence and cognitive–physical integration; Figure 11 shows the mode-level architecture of CTAs in these experiments. When a CTA C is not It, it will try to execute all of the following behaviors in a game: runBases, the simple base-running strategy that STAs have; getMitten, retrieving its mitten (which, as children sometimes do, this agent drops in every game); protect, protecting a friend from being tagged; and readyToTag, actively seeking to become It, to tag an adversary. The getMitten action is implemented by selecting a time when, wherever C is, its mitten drops; soon after, C finds the mitten’s location, and cognitive activations evolve until, in general, mitten-retrieval becomes C’s highest priority. To enable protect and readyToTag, C has beliefs of affinities for each player in the game; C will protect a non-It player with maximal affinity during protect and pursue a non-It player with minimal affinity during readyToTag. When a CTA is It, it either follows through on a readyToTag action and pursues its selected adversary, or it selects between chasing the user or another agent, as STAs do. [Additional details of STAs and CTAs, not central to results in this paper, are in Aaron et al. (2011)].
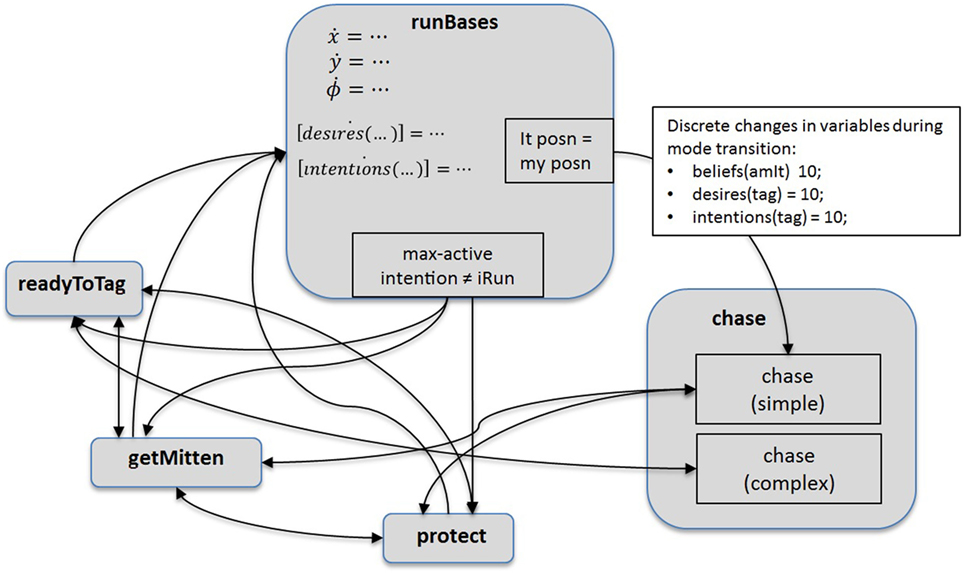
Figure 11. Behavior mode-level architecture of a cognitive Tag agent (CTA). Each mode also has a self-transition, omitted here to avoid visual clutter. [Aaron et al. (2011) contain additional details.]
The cognitive dynamical systems in these agents connect BDI cognitive elements in intuitive ways. For example, the equations governing activations of the desire to run bases, the intention to tag another player, and the intention to run bases contain the following structure:
Additional structure is also present in equations for these cognitive elements, and additional equations are present for other cognitive elements. [The specific components for distinguishing properties of BDI intentions and the experimental results in section 4, however, are not present in agents for these experiments. For additional details about these cognitive systems, see Aaron et al. (2011).] The online learning of DI-HDCAs in these examples is based on the interconnections encoded in these equations, similar to the mechanism in section 4, as further described below.
5.2. Agent Learning and Cognitive–Physical Integration
The motivation for the Tag-world learning demonstrations below was to approximate what a human game-player might want during play: a user might specify agent behavior to change, within desired bounds, to improve the gameplay experience. For example, a user might have been tagged so quickly by It agents that the game was not a fair challenge, but when agents were non-It players, their behavior was good for gameplay. Based on this idea, a CTA was tasked to learn from a simulated user request to change one aspect of gameplay without affecting another, exemplifying an arbitrary user choice, unrelated to agent design and substantively changing behavior.
As preparation, control condition behavior for CTAs was determined by letting a game play extensively (more than 8000 simulated seconds), with an automated user for replicability. In this game setup, when a CTA Cctrl became It, Cctrl would almost always tag some other player in less than 25 simulated seconds (average: 12.85 s). In addition, the value actrl of the average number of bases reached per execution of the runBases behavior, over the full game, was actrl = 4.01.
For the learning demonstrations, the CTA would learn a goal with two components: speed change, requiring speed-only learning; and base-running maintenance, requiring speed-and-bases (SB) learning.
• Speed change: after becoming It, C should optimally tag some other player between 25 and 45 s later. Speed-only training (and thus partial SB training, see below) occurs when C transitions out of chase mode. If the time C was It is outside of the desired range (25–45 s), C is trained to become slower or faster, as appropriate, by a factor depending on how far outside of the desired range C was It.
• Base-running maintenance: despite the effects of speed-only learning, C should only minimally change the value aC of the average number of bases reached during each runBases behavior. SB training occurs when C transitions out of runBases mode: aC is updated, and coefficients in cognitive differential equations are altered to train C to approach the control value of 4.01 in the future. As a partial example, if aC < 4.01, coefficients in the differential equation governing iRun are altered so that C tends to remain longer in runBases, encouraging greater aC in the future. The amounts altered depend on values such as the velocity of C when training occurs, exemplifying cognitive–physical integration: values of physical variables affect cognitive adjustments.
To focus these demonstrations, the connections modified during training were pre-selected, though the adjustments were autonomous.
Feedback for SB learning is given by the expected two measurements: how long until C tagged another player (agent or user) when C was It; and how many times C reached a base when in runBases behavior. Learning occurs when C transitions out of two behaviors:
• When C transitions out of chase, if the time t that agent C was It is less than minimum desired time tmin (here, tmin is 25 s), then C becomes slower, multiplying its speed by , where m = 0.05 controls the effect of the change. This is designed to approach 1 − m when C tags its target almost immediately, for maximal change, and approach 1 when C tags its target near the time of tmin, for minimal change. Similarly, if C takes more than some maximum desired time tmax (here, 45 s) to tag a player, then it becomes faster, multiplying its velocity by the similarly designed factor .
• When C transitions out of runBases, learning occurs under two circumstances: either when the agent transitions out because another behavior’s intention becomes highest-active and the agent has touched more or fewer bases than the desired number, or when the agent is tagged by an It player after having touched more bases than the desired number. (If the agent is tagged after having touched fewer bases than the desired number, it is not possible to know whether it would have touched fewer or more bases than the desired number, and learning does not happen in that situation.) In either of these cases, the value of the average number of bases touched by C (call it aC) each time it was in runBases is re-computed, and if that average is either more or less than the desired average, coefficients in C’s cognitive system are altered, based on agent-specific learning factor lF.
Cognitive interconnections can be altered in two ways by this learning procedure: multiplying by lF, or multiplying by . Coefficients in cognitive differential equations for which higher values would intuitively make C evolve out of runBases faster are multiplied by lF; coefficients for which high values would intuitively make C evolve out of the behavior more slowly are multiplied by . Therefore, if C were touching too many bases per runBases behavior and needed to transition out of it more quickly, lF would be increased during play, and coefficient-altering learning would be applied. Similarly, lF would be decreased if C needed to stay in runBases longer to achieve its goals.
Learning factor lF is defined as lF = s ⋅ f, the current speed s of C multiplied by a factor f, the value of which is described below. This way, an increase (decrease, respectively) in s straightforwardly results in a tendency to touch more (fewer) bases before transitioning out of runBases. Factor f is also varied during gameplay. Initially, , where sinit is the speed of C at the beginning of the game (for these demonstrations, that speed was of the size of the Tag field per simulated second). Then, the value of f can be changed when C transitions out of runBases, as part of the learning procedure. Any time the agent exits runBases, the average number of bases aC touched during the runBases behavior is computed; then, if at the time of the current transition out of runBases, aC is greater than the desired value of actrl (here, 4.01), f is multiplied by 1.2. Similarly, if aC is below 4.01 at the time of a voluntary transition, lF is multiplied by 0.8. This definition of f and its alteration during play completes the definition of lF to have the desired properties.
With this definition of lF, learning is implemented by altering cognitive coefficients as appropriate. For this paper, the coefficients intuitively presumed to increase the rate at which the system evolves out of runBases, and which were therefore multiplied by lF, are: in the equation for protect, the coefficient for Dprotect, and a positive constant term; in the equation for runBases, the coefficients for Itag, Iprotect, Imitten, and a negative constant term. Similarly, the coefficients multiplied by are: in the equation for runBases, the coefficients for DrunBases and IrunBases. This is not meant to be a comprehensive list of all coefficients that intuitively affect the speed with which C evolves out of runBases, but rather a sample sufficient to affect the behavior of C and illustrate ideas of DI-HDCA learning.
Demonstrations showed agent C successfully learning integrated cognitive–physical behavior during play: C slowed to spend more time as It before tagging another player (average: 32.62 s) while also maintaining a bases average of aC = 4.21, very close to 4.01. Additionally, speed-only learning without full SB learning resulted in aC = 2.19 in otherwise identical conditions, suggesting the importance of integrated learning for the desired goal. [see Aaron et al. (2011) for additional details.] To quantitatively analyze performance and test the hypothesis that the type of learning alters the performance of the agents, univariate ANOVA was used, with results presented in Figure 12. For the dependent measure of number of bases touched, the mean value for speed-and-bases learning was significantly higher [F(1, 18) = 15.358, p = 0.001, η2 = 0.460] than the mean for the speed-only learning (Figure 12A). For the variance in the number of bases touched, the mean value for speed-and-bases learning was significantly higher [F(1, 18) = 131.624, p < 0.000, η2 = 0.880] than the mean for the speed-only learning (Figure 12B).
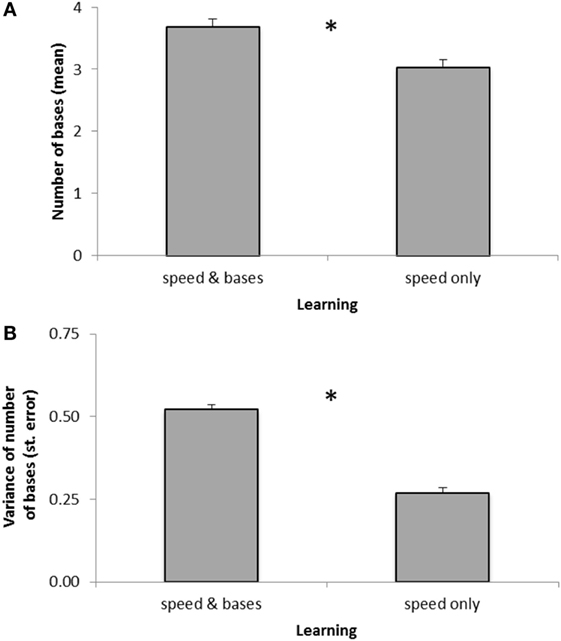
Figure 12. Learning in the Tag game. (A) Number of bases that agents touched. With learning based on speed and number of bases, agents touched significantly more bases. (B) Variance in number of bases touched. With learning based on speed and number of bases, agents had significantly greater variance.
5.3. Discussion
The above results show DI-HDCAs’ cognitive–physical integration as a substrate for online learning of multi-faceted, real-time interactive gameplay. The cognitive–physical integration makes the learning straightforward for DI-HDCAs: the extent to which speed or the agent’s cognitive network needs to be modified is not known a priori, but cognitive–physical integration enables small adjustments in one to bring about small adjustments in the other, so the integrated agent system can find the desired balance.
Other experiments presented in Aaron et al. (2011), although illustrative of cognitive–physical integration in DI-HDCAs, were not related to agent learning and hence not presented above. Specific values were varied in controlled environments, to investigate the particular effects that might result. For example, many game segments were simulated with identical CTA C; initially, C’s intentions implied task order [readyToTag, runBases, protect, getMitten]. Across simulations, two factors varied – when C dropped its mitten; and when C was tagged by the user (automated, for replicability) – to illuminate micro-level cognitive and physical effects in gameplay. As mitten-drop grew later with get-tagged held constant, for example, the time at which C moved from readyToTag into runBases was not affected, but the time at which C then entered protect tended to get earlier. In addition, for particular values of mitten-drop and get-tagged, C entered protect mode – in which movement is not obstacle-avoidant – at an inopportune moment and ran straight into an It player. This sequence of events and ensuing cascade of effects illustrates how engaging, unscripted behavior that could be considered emergent can arise in the DI-HDCA framework. Emergent behavior and the DI-HDCA framework are also briefly discussed in section 6 below.
6. Conclusion and Discussion
The DI-HDCA modeling framework is a fusion of ideas from BDI theory, spreading activation networks, and hybrid dynamical system models, each adapted and employed in new ways that are influenced by entailments of environment and embodiment. DI-HDCA modeling embraces BDI theory and spreading activation networks for cognitive modeling, adapting them to real-time varying environments, continuum-valued representations, and multi-tiered integration across a model. Representing DI-HDCA models in a formal HDS enables behavioral design, and it supports cognitive–physical integration in each behavior mode. Moreover, because all physical and cognitive elements have the real-time evolution of their activation values expressed by differential equations in the same dynamical system, any elements can affect any other in the integrated agent model.
The DI-HDCA framework’s expansive integration also supports the agent learning demonstrated in sections 4 and 5 of this paper, employing both reactive–deliberative and cognitive–physical integration for adaptive behavior of navigating, goal-directed agents. Experiments demonstrate that DI-HDCA modeling can enable the distribution of typically deliberative task sequencing intelligence onto reactive-level processes, and that cognitive–physical integration can enable straightforward online learning in interactive simulations. These experiments are not an exhaustive demonstration of the capacity of DI-HDCA models nor a full exploration of the integration and adaptation possible for DI-HDCAs – for example, they considered the reactive–deliberative and cognitive–physical dimensions independently, not jointly – but they illuminate the role of this integrated intelligence modeling and suggest the value of further exploration.
There are many possible directions in which the presently described DI-HDCA framework could be extended. In the general context of reactive and deliberative systems, extensions of dynamical intention-based reactive systems illustrated here could potentially serve as reactive adjuncts to deliberation in hybrid reactive–deliberative systems, augmenting deliberative methods with enhanced reactive intelligence; this could reduce reliance on deliberation and extend reactive benefits of responsiveness and adaptability in incompletely known environments. There is also the perhaps more ambitious potential that DI-HDCA models could extend to fully replace some deliberative systems, representing the necessary rule-based behavior in the reactive DI-HDCA framework. Neither of these approaches is currently fully explored, and it is not the intent of this paper to prescribe one of these two approaches or endorse one over the other; both seem interesting to explore.
The specific details of DI-HDCA modeling presented in this paper can also be altered in further explorations. For example, in this paper, one activation value represents both salience and cognitive intensity or commitment “in mind,” but those qualities need not be conflated: within this general modeling framework, agents could be very aware (high salience) of a mild desire (low intensity), with individual elements in the cognitive networks representing each of those qualities; the models presented in this paper could straightforwardly adopt such new elements in their cognitive dynamical systems. In addition, deliberation could be modeled differently in the DI-HDCA framework, with specific deliberation-behavior modes that represent the time during deliberation; these could be incorporated without altering reactive cognitive representations. Such extensions were not necessary, however, for the demonstrations of reactive-level learning and cognitive–physical integration in this paper.
Even within the models already developed, the capacity of dynamical intention modeling to enhance reactive-level intelligence and minimize reliance on deliberation is not confined to agent learning methods such as those presented above. Reactive task re-sequencing for DI-HDCAs, as discussed in Aaron and Admoni (2009), can enable agents with internally inconsistent cognitive elements to smoothly correct inconsistencies without deliberation: an agent with a high-active intention IML to mail a letter but also a high-active belief that it does not have a letter to mail can reactively re-order its task sequence, without propositional planning. The cognitive network enables the high activation on to have an inhibitory affect on IML until mailLetter is no longer a high-priority task for the agent; indeed, in the demonstration reported in Aaron and Admoni (2009), the activation on IML becomes negative and the mailLetter task is not completed, consistent with the belief. The agent can invoke deliberative planning when needed, but for this cognitive inconsistency, reactive activation changes governed by cognitive differential equations suffice for task re-sequencing.
Expanding the scope of planning in DI-HDCAs could involve a deeper exploration of reactive planning. At present, a plan for DI-HDCAs is represented as a sequence of activation values on intentions: at any moment, the plan is the ordering of those intentions from high priority (to be completed first) to low priority. Additional study of mechanisms for planning, and for reasoning about time in this modeling context, could yield both interesting cognitive insights and more robust, reliable robots. Relatedly, applications of DI-HDCA modeling to agents with predictive intelligence is also a potentially productive extension. Because DI-HDCA models are based on differential equations, there is inherently a predictive model in the system: at any moment, the current values of time derivatives could straightforwardly be employed to linearly extrapolate any system value to any time in the future. This capacity is not tested in the present work in this paper, but it might be employed to further enhance DI-HDCA behavior, including incorporating such predictions into agent learning methods.
The modeling of DI-HDCAs as hybrid dynamical systems is also influenced by concerns of agent reliability. There are formal logics and computational methods to analytically verify some properties of hybrid dynamical systems, and in principle, a DI-HDCA model could perhaps be analytically proved to be designed correctly according to specifications. (Indeed, some STAs in the Tag scenario had designs amenable to verification, although that analysis was not performed.) In practice, however, it is extremely difficult to analyze properties of arbitrarily complex hybrid dynamical systems; indeed, reasoning about approximations to a system may be needed in cases where exact reasoning about the desired system is computationally impossible (Alur et al., 1995, 2000). For that reason, verifiability is not presently a primary concern underlying DI-HDCA modeling, but as the verifiable correctness of complex computational agents becomes more important, it may become more beneficial to have models of intelligent robots grounded in a framework that enables verification. Moreover, there are promising HDS-related approaches to creating verifiably correct behaviors, such as synthesizing robot controllers from formal specifications [e.g., Wong et al. (2014)]; the gap between such approaches and DI-HDCA modeling is sizable, but less than the gap between such approaches and models without formal foundations.
The DI-HDCA framework may also be an apt candidate for studying emergence and mechanisms of emergence. The DI-HDCA framework enables and encourages low-level behavior design while also expressing higher-level behavioral abstractions. On a fundamental level, these are the elements needed to begin an analysis of emergent behaviors: a lower level, with respect to which behaviors can be emergent; a higher level, in which emergent behaviors can be described; and a formalized foundation in which patterns can be recognized and considered emergent. Consider, for instance, how artificial neural networks can be parts of studies involving emergence: behaviors arise that are not readily or properly described as behaviors of the network itself. Similarly, any higher-level agent behavior would not be considered emergent with respect to a system if it is already encoded in that system. With DI-HDCAs, the high-level behaviors explicitly represented as HDS modes could be a baseline against which newly recognized behaviors could be compared for determining emergence; such potentially emergent behaviors could arise from low-level cognitive and physical dynamics and interconnections, analogous to behavior arising from a neural network, without explicit high-level encoding. Moreover, because of the flexibly expressive HDS modeling, a wide variety of candidate mechanisms for generating or recognizing potentially emergent behaviors could be implemented, for a formalized approach to studying emergence.
Embodied robots are complex integrated systems, and DI-HDCA modeling represents that complexity in a structured framework that enables effective analysis and design, with new approaches to integrated intelligence and learning that can improve robot performance. Although extensions of the present work could explore narrowly construed task domains (e.g., an automated robot arm for manufacturing, designed to make only one specific weld), that is not suggested here. By design, the DI-HDCA framework is not primarily for narrowly delineated, domain-specific problems; instead, it illustrates what a modeling framework for integrated embodied intelligence might contain, which can be broadly applied to complex scenarios. For the general study and robust implementation of embodied intelligence, models expressing both broad scope and integration seem well suited, and the DI-HDCA modeling framework is designed for behaviors both low-level and high-level, both cognitive and physical, and their interactions in embodied agents.
Author Contributions
EA conceived of the theory, worked with collaborators (see Acknowledgments) to conduct experiments and analyses, and wrote the manuscript.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author gratefully acknowledges: Henny Admoni for the observation that led to the Hebbian learning approach in this paper and in Aaron and Admoni (2010); Henny Admoni and Juan Pablo Mendoza for contributions to simulations, data, and figures in papers [e.g., Aaron and Admoni (2010) and Aaron et al. (2011)] foundational to the current presentation; and John Long for statistical analyses and figures in this paper. Thanks also to all of the above, to Jim Marshall for especially inspirational conversations that helped advance this work, and to reviewers of this paper for thoughtful and helpful comments.
Funding
A Research Committee award from The Lucy Maynard Salmon Research Fund of Vassar College funded publication of this article.
Footnotes
- ^The specific agents described in this paper are far from an exhaustive demonstration of the DI-HDCA modeling framework. To distinguish the general DI-HDCA framework from specific agents, a phrase such as “in this paper” will formulaically be used to indicate specific focus.
- ^These are not the only properties of intention described or emphasized in Bratman (1987); these properties, however, can apply to reactive-level intention, not requiring, e.g., future-directedness incompatible with reactive cognition.
References
Aaron, E., and Admoni, H. (2009). “A framework for dynamical intention in hybrid navigating agents,” in Hybrid Artificial Intelligence Systems (Berlin, Heidelberg: Springer-Verlag), 18–25.
Aaron, E., and Admoni, H. (2010). Action selection and task sequence learning for hybrid dynamical cognitive agents. Rob. Auton. Syst. 58, 1049–1056. doi: 10.1016/j.robot.2010.05.006
Aaron, E., Ivančić, F., and Metaxas, D. (2002). “Hybrid system models of navigation strategies for games and animations,” in HSCC 2002, Lecture Notes in Computer Science (Berlin, Heidelberg: Springer-Verlag), 7–20.
Aaron, E., and Mendoza, J. P. (2011). “Dynamic obstacle representations for robot and virtual agent navigation,” in Proceedings of the Canadian Conference on Artificial Intelligence (Heidelberg, New York: Springer-Verlag), 1–12.
Aaron, E., Mendoza, J. P., and Admoni, H. (2011). “Integrated dynamical intelligence for interactive embodied agents,” in ICAART 2011 – Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (Setubal: SCITEPRESS), 296–301. doi:10.5220/0003188102960301
Alur, R., Courcoubetis, C., Halbwachs, N., Henzinger, T. A., Ho, P.-H., Nicollin, X., et al. (1995). The algorithmic analysis of hybrid systems. Theor. Comp. Sci. 138, 3–34. doi:10.1016/0304-3975(94)00202-T
Alur, R., Henzinger, T., Lafferriere, G., and Pappas, G. (2000). Discrete abstractions of hybrid systems. Proc. IEEE 88, 971–984. doi:10.1109/5.871304
Arkin, R. C. (1990). Integrating behavioral, perceptual, and world knowledge in reactive navigation. Rob. Auton. Syst. 6, 105–122. doi:10.1016/S0921-8890(05)80031-4
Beer, R. D. (2000). Dynamical approaches to cognitive science. Trends Cogn. Sci. 4, 91–99. doi:10.1016/S1364-6613(99)01440-0
Bratman, M. (1987). Intentions, Plans, and Practical Reason. Cambridge, MA: Harvard University Press.
Brooks, R. A. (1986). A robust layered control system for a mobile robot. IEEE J. Robot. Autom. RA-2, 14–23. doi:10.1109/JRA.1986.1087032
Collins, A. M., and Loftus, E. F. (1975). A spreading activation theory of semantic priming. Psychol. Rev. 82, 407–428. doi:10.1037/0033-295X.82.6.407
Egerstedt, M. (2000). “Behavior based robotics using hybrid automata,” in HSCC 2000 Lecture Notes in Computer Science (Berlin, Heidelberg: Springer-Verlag), 103–116.
Erlhagen, W., and Bicho, E. (2006). The dynamic neural field approach to cognitive robotics. J. Neural Eng. 3, R36–R54. doi:10.1088/1741-2560/3/3/R02
Gat, E. (1998). “On three-layer architectures,” in Artificial Intelligence and Mobile Robots, eds D. Kortenkamp, R. P. Bonnasso and R. Murphy (Menlo Park, CA: AAAI Press), 195–210.
Georgeff, M., and Lansky, A. (1987). “Reactive reasoning and planning,” in AAAI-87 (Menlo Park, CA: AAAI Press), 677–682.
Goldenstein, S., Karavelas, M., Metaxas, D., Guibas, L., Aaron, E., and Goswami, A. (2001). Scalable nonlinear dynamical systems for agent steering and crowd simulation. Comput. Graphics 25, 983–998. doi:10.1016/S0097-8493(01)00153-4
Haazebroek, P., van Dantzig, S., and Hommel, B. (2011). A computational model of perception and action for cognitive robotics. Cogn. Process. 12, 355–365. doi:10.1007/s10339-011-0408-x
Hertzberg, J., Jaeger, H., Morignot, P., and Zimmer, U. (1998). “A framework for plan execution in behavior-based robots,” in Proceedings of ISIC/ISAS (Piscataway, NJ: IEEE).
Jaeger, H., and Christaller, T. (1998). Dual dynamics: designing behavior systems for autonomous robots. Artif. Life Rob. 2, 108–112. doi:10.1007/BF02471165
Large, E., Christensen, H., and Bajcsy, R. (1999). Scaling the dynamic approach to path planning and control: competition among behavioral constraints. Int. J. Robot. Res. 18, 37–58. doi:10.1177/027836499901800103
Maes, P. (1989). “The dynamics of action selection,” in IJCAI-89 (San Mateo, CA: Morgan Kaufmann), 991–997.
Pfeifer, R., and Bongard, J. (2006). How the Body Shapes the Way We Think: A New View of Intelligence. Cambridge, MA: MIT Press.
Port, R., and van Gelder, T. J. (1995). Mind as Motion: Explorations in the Dynamics of Cognition. Cambridge, MA: MIT Press.
Richter, M., Sandamirskaya, Y., and Schöner, G. (2012). “A robotic architecture for action selection and behavioral organization inspired by human cognition,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (Piscataway, NJ: IEEE), 2457–2464.
Sandamirskaya, Y., Zibner, S. K. U., Schneegans, S., and Schöner, G. (2013). Using dynamic field theory to extend the embodiment stance toward higher cognition. New Ideas Psychol. 31, 322–339. doi:10.1016/j.newideapsych.2013.01.002
Schöner, G., Dose, M., and Engels, C. (1995). Dynamics of behavior: theory and applications for autonomous robot architectures. Robot. Auton. Syst. 16, 213–245. doi:10.1016/0921-8890(95)00049-6
van Gelder, T. (1998). The dynamical hypothesis in cognitive science. Behav. Brain Sci. 21, 615–665. doi:10.1017/S0140525X98001733
Keywords: intelligence modeling, learning, embodiment, hybrid systems, hybrid dynamical systems, machine learning, action selection, cognitive robotics
Citation: Aaron E (2016) Dynamical Intention: Integrated Intelligence Modeling for Goal-Directed Embodied Agents. Front. Robot. AI 3:66. doi: 10.3389/frobt.2016.00066
Received: 20 April 2016; Accepted: 19 October 2016;
Published: 17 November 2016
Edited by:
John Rieffel, Union College, USAReviewed by:
José Antonio Becerra Permuy, University of A Coruña, SpainMichael Spranger, Sony Computer Science Laboratories, Japan
Copyright: © 2016 Aaron. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eric Aaron, ZWFhcm9uQGNzLnZhc3Nhci5lZHU=
 Eric Aaron
Eric Aaron


