- 1Graduate School of System Design, Tokyo Metropolitan University, Tokyo, Japan
- 2Faculty of Computer Science and Information Technology, University of Malaya, Kuala Lumpur, Malaysia
In this article, we propose a new approach for mobile robot localization and hybrid map building simultaneously without using any odometry hardware system. The proposed method termed as Genetic Bayesian ARAM comprises two main components: (1) steady-state genetic algorithm (SSGA) for self-localization and occupancy grid map building and (2) Bayesian Adaptive Resonance Associative Memory (ARAM) for online topological map building. The model of the explored environment is formed as a hybrid representation, both topological and grid based, and it is incrementally constructed during the exploration process. During occupancy map building, the robot-estimated self-position is updated by SSGA. At the same time, the robot-estimated self-position is transmitted to Bayesian ARAM for topological map building and localization. The effectiveness of our proposed approach is validated by a number of standardized benchmark datasets and real experimental results carried on the mobile robot. Benchmark datasets are used to verify the proposed method capable of generating topological map in different environment conditions. Real robot experiment to verify the proposed method can be implemented in real world.
1. Introduction
An autonomous mobile robot is defined as a robot that has the ability to navigate in an environment and execute desired works with little or no human guidance. Previous work in intelligent robotics has proposed multistrategy learning that integrated several inference types and/or computational mechanisms into one learning system (Michalski and Tecuci, 1994). Examples consist of the integration of symbolic and numerical learning, hybrid computation of discrete and continuous spaces, integration of stochastic and deterministic heuristic searches, path planning and behavioral learning (Bianco and Cassinis, 1996), and reinforcement learning that uses value and policy iteration.
An efficient autonomous robot should be able to estimate its location during navigation and travel from one place to another in order to complete certain tasks. Also, the robot should be able to generate the map of the traversed environment corresponding to its position and posture (mapping) and calculate its position and posture based on the generated map (localization). These two processes are interdependent and usually termed as simultaneous localization and mapping (SLAM) (Tomono and Yuta, 2003; Thrun et al., 2005), which is considered to be an example of a multistrategy learning method.
Various conventional approaches for SLAM were developed, for instance, extended Kalman filter (EKF) SLAM, visual SLAM, and graph SLAM. These methods can handle uncertainty, high convergence, and do not require odometry hardware system. On the one hand, the EKF SLAM approach using maximum likelihood data associations for online SLAM and the resulted feature-based maps are used with point landmarks. On the other hand, graph SLAM overcomes the full SLAM problem in offline by obtaining all data gathered such as the current time, e.g., all poses and all features in the map during map building (Folkesson and Christensen, 2007; Kaess et al., 2008). However, all these conventional methods are computationally expensive.
Topological approaches map the environment as a set of nodes and edges (Benjamin and Yung-Tai, 1991). Nodes store information about the environment, while edges of the map contain robot’s odometry information gathered during navigation. Thus, a topological map represents the environment by only storing information of crucial places and connections between these places that will be used for navigation.
Hybrid approaches combine the topological and metric mapping methods in order to retain the advantages of both methods and compensate for the negative ones. Thrun (1998) proposed a method that uses the Occupancy Grid method in building a metric map of the environments, and a topological map is a posterior calculated from the metric map. However, the accuracy and consistency of the map generated by this approach are affected by accumulated odometric error present in the metric map. In Taylor and Kriegman (1998), the environment is represented as a collection of local metric maps, all of which are stored as nodes in a global topological map. The node in the topological map of this approach stores a set of landmarks observed from the boundary of each obstacle detected by the robot and uses this information for navigation between nodes in the map in the later stage. This method neglects robot pose estimation entirely.
Recently, vision-based navigation system was introduced for hybrid map building (Cristforis et al., 2015). However, this approach is based on teach-and-replay technique and requires odometry system for robot localization. Previous works such as Battesti et al. (2011) and Bazeille and Filliat (2011) used vision-based hybrid map building to create consistent topometric map and compensate odometry drift. However, these methods require robot odometry system for topometric map building.
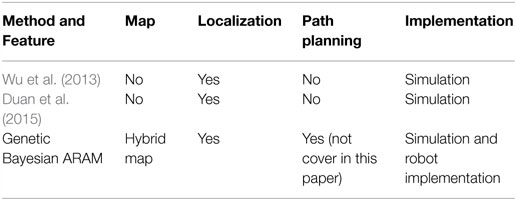
In this article, we proposed a new approach that integrated our previous work SSGA (Toda et al., 2012) and Bayesian ARAM with map maintenance for hybrid map building. The Bayesian ARAM with map maintenance is the extension of our previous work (Chin et al., 2015) that is crucial for dealing with proliferation problem of nodes. The proposed method termed as Genetic Bayesian ARAM, which constructs map, contains both a metric and a topological representation. First, SSGA allows the robot to perform self-localization and metric mapping simultaneously based on occupancy grid mapping. Then, Bayesian ARAM utilizes the localization information from the metric map and sensory information from the explored environment to construct the topological map. Topological nodes represent distinct places, while edges connect nodes and store robot’s bearing information such as orientation and direction. The metric grid map describes the explored environment outline for understanding of human operators and further operations. In addition, it also provides global position of robot for Bayesian ARAM to generate the topological map and overcome the online detection and recognition problem. With the topological map, the robot could perform localization and path planning without recalculating the entire metric grid map. In addition, previous works such as Duan et al. (2015) and Wu et al. (2013) have used genetic algorithm for SLAM purpose. Table 1 shows the difference between the previous two works and our proposed method.
Contributions of this paper are: (i) it does not require odometry system such as encoder and GPS for robot position estimation; (ii) the unsupervised online learning feature enables the robot to build the topological metric map from scratch and maintain it naturally without any human interference; and (iii) it does not require any artificial marker or adjustment and complicated cognitive intelligence for operating in a natural environment. Section 2 introduces the theoretical framework of the proposed simultaneous localization and hybrid map building approach. The experimental setup is explained in Section 3, and experimental results are discussed in Sections 4 and 5. Finally, conclusions are presented in Section 6.
2. Genetic Bayesian ARAM
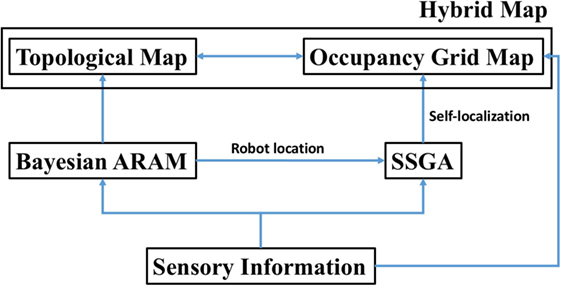
Our proposed method termed as Genetic Bayesian ARAM is the integration of our previous works (Toda et al., 2012; Chin et al., 2015). In this paper, we have further improved our proposed method with map maintenance feature, which overcomes the proliferation problem of nodes. In our proposed hybrid mapping method, the notion of map is described by both a metric and a topological feature. On the metric side, the environment is represented by a global occupancy grid map. Steady-state genetic algorithm (SSGA) simultaneously performs self-localization and metric map building based on occupancy grid mapping.
On the other hand, Bayesian ARAM obtains robot’s location from the metric mapping and sensory information to build the topological map. Bayesian ARAM continuously clusters sensory sources as nodes and creates edges to connect one another if the robot traverses between these nodes. Each of these connections contains robot’s movement information, while nodes represent important places of the explored surroundings. The proposed method continuously updates the hybrid map representations with little or no human intervention. The overall process of our proposed framework is shown in Figure 1.
2.1. Metric Map Building
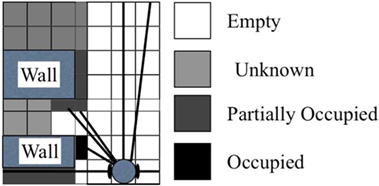
As stated in Section 1, we utilize the occupancy grid mapping (Thrun, 2003; Lee and Chung, 2009) for constructing the metric map. The theory of the occupancy grid map is shown in Figure 2.
The value of each individual cell is defined as follows:
Initially, all cell values are set as 0. The measurement value is represented as (di, θi), where i = 1, 2, …, M; i = 1, 2, …, L; di is the measurement of laser rangefinder; θi is the intersection of the measured directions; M is the sum of all measured directions; and Li = [αRes⋅di] is the value of the generated map resolution.
The updating process is shown in Algorithm 1 where (xp, yp) is the robot’s position; rp is the posture; di is the measured distance value obtained from the laser rangefinder in the ith direction; θi is the angle of the measured direction; αMAP is the scale factor for the grid mapping with respect to the real world; and f (⋅) in equation (4) is a function corresponding to IF–THEN hypothesis as stated in Table 2.
We employ SSGA for the adjustment of the position and angle. In the evolution of robotics computing, genetic algorithms (GAs) have been adequately implemented to optimize the problem-solving ability. GAs, which are capable of generating an appropriate solution, not certainly an ideal one, require less computational effort. SSGA replicates the continuous model of the generation that excludes and produces some individuals for every generation. A successor solution consists of numerical parameters or updated value of the current position (gk,x, gk,y) and rotation (gk,r).
In the learning process, only a few of current solutions are substituted by the successor candidates that are produced by the crossover and mutation processes. In this experiment, we utilize the elitist crossover and adaptive mutation. Elitist crossover irregularly chooses one candidate and produces a candidate by integrating genetic information from the chosen candidate and the best candidate to achieve suitable solutions promptly.
Then, the generated individual is updated through the following adaptive mutation as follows:
where fk is the fitness value of the kth individual; fmax and fmin are the maximum and minimum fitness values in the population; N(0, 1) shows a normal random value; and αSSGA and βSSGA are the coefficient and offset accordingly. Equation (6) is used to determine the fitness value of the kth candidate’s result.
The localization process is shown in Algorithm 2.
2.2. Topological Map Building
The MBARAM builds the topological map starting with one node (category) at the first step. Next, the map updates continuously based on the robot location generated by SSGA and sensory information gathered from robot’s sensors. The map update is shown in Algorithm 3.
2.2.1. Node Definition
Places we mentioned previously are defined as Bayesian ART categories that represent the environment where the robot is placed. Bayesian ART category is determined through categorization of sensors data. Each node contains a robot location encoded from SSGA. It has a multidimensional Gaussian component such as mean vector , covariance matrix , and prior probability . The node definition is entirely dependent on the robot’s sensing abilities and does not require human being to define the place meaning. This helps the robot to recognize places easily from sensory information.
2.2.2. Topological Map Learning and Update
The algorithm consists of three core process (Chin et al., 2016), namely, “node competition,” “node matching (vigilance test),” and “node learning.”
(1) “Node Competition”: all current nodes are competing to each other for representing a sensor reading pattern. Equation (7) shows the computation of the a posteriori probability of the jth node for describing the M-dimensional input pattern x.
where Ncat is the node quantity in the map and is the predicted prior probability of the jth node. The likelihood of wj with respect to x is predicted using all patterns that have already been correlated with the multivariate Gaussian node wj:
where and are the predicted mean and covariance matrix of the jth node.
If the algorithm receives K sensory sources for training, then the Mj for every node is:
where
and αk is the impact factor for every sensory channel; the sum of αk is always equal to 1.
The winning node J is the node that has the maximum a posteriori probability (MAP):
(2) “Node Matching (Vigilance Test)”: this process is to assure that the winner node has enough confidence for representing the particular place that the robot is currently situated. The vigilance test restrains the Jth node hypervolume SJ to the maximal hypervolume allowed for a node SMAX:
where the determinant of the Gaussian covariance matrix is the hypervolume. This hypervolume will be decreased to the product of the variances each for a dimension if it is a diagonal covariance matrix:
The learning process is started if the winner node satisfies equation (13). If the winner node failed the test, then it will be eliminated from the competition for this sensory input. Then, the algorithm continues searching for another node until one complies with equation (13). If all existing nodes failed the vigilance test, then it means that the robot is situated at a new location. Next, a new node will be added to the network, which stores the sensory pattern, an initial covariance matrix , and robot location for describing this new location. An edge will be added to link it with the previous winner node.
(3) “Node Learning”: If the chosen node satisfies equation (13), the node components will be updated as below:
where NJ is the frequency of the Jth node that chose to be winner for learning during node competition before the present input data are transmitted to the network. I is the identity matrix.
2.2.3. Topological Map Preservation
During the robot navigation, the topological map algorithm will be adding nodes continuously according to the changes in environment. This shows that the robot constantly maintains and updates the map representation for the traversed environment. This characteristic is the nature of the algorithm.
The drawback for this map preservation is that the robot will recognize all environmental changes during navigation and generate uncontrollable nodes for searching and updating. Therefore, the list of nodes must be managed for navigation and mapping in a natural environment for a long period of time. In this paper, we have implemented the Instantaneous Topological Map (ITM) technique (Jockusch and Ritter, 1999) for map maintenance. This is also an extension of our previous work in Chin et al. (2015).
Figure 3 shows the node elimination mechanism. First, the algorithm scans and deletes nodes whenever a new node is added to the topological map. If nodes are situated within the Thales sphere of the new node, then these nodes will be deleted from the map. Thales sphere is defined as radius emax, and the mathematical equation is shown in equation (19). In addition, edges that are connected to deleted nodes are either updated or removed. For instance, traverse information for the new edge can be determined from the new connection.
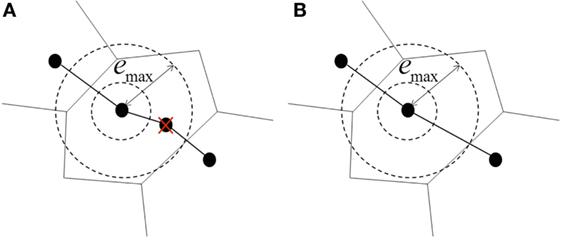
Figure 3. Topological map preservation. (A) Unwanted nodes within the given radius emax are eliminated. (B) Transitions in or out from removed nodes are relinked to maintain the connectivity of the map.
2.2.4. Self-Localization
After building the topological map, node matching and localization are accomplished by measuring sensor information at robot’s current location with destination nodes in the map. If the match value Gj is higher than vigilance parameter, the robot is localized and vice versa. However, the Genetic Bayesian ARAM has to deal with perceptual uncertainty; this method is useful when two or more nodes have similar sensory information. To differentiate these nodes, ideothetic information (robot location) has to be included. For example, assume that there are two nodes that have identical sensor data ; the equations are given as follows:
However, the ideothetic information (odometry) will not be the same for each node. Therefore, and lead to GA ≠ GB. Figure 4 illustrates the concept of the node localization.
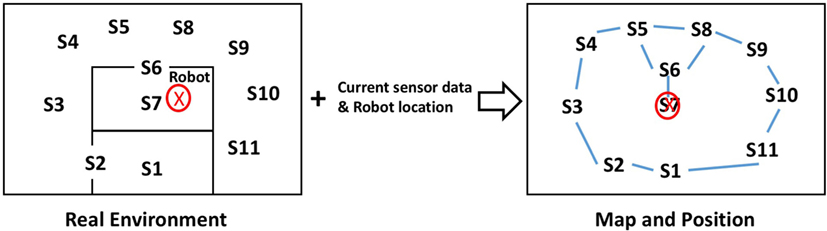
Figure 4. In the topological map, each node contains a set of sensor data and a particular robot location. The robot’s metric position can be located by recognizing the node with respect to the current sensory information.
In our experiments, we always obtain sensory (from sensors) information around the current robot location, ideothetic information (from SSGA), and destination nodes information. We then use equation (8) to determine Gdestination. If Gdestination is higher than the vigilance parameter, the robot reaches the destination point.
3. Experimental Setup
This section shows the setup of experiment, while Section 4 shows the results collected from the simulation and real robot implementation. The hybrid map is formed by the occupancy grid map and topological map. For the occupancy grid map, white color represents empty space, gray color represents unknown space, and black color represents obstacles or boundary detected, whereas the topological map represents set of nodes and links. Red color circles at the (x, y) coordinates and black color lines represent nodes and links in the map, respectively.
According to Vigdor and Lerner (2007) and Chin et al. (2016), we have mentioned the optimized range of parameters’ setting. Therefore, we follow the parameters’ setup mentioned in paper (Vigdor and Lerner, 2007; Chin et al., 2016) because the authors have determined the optimized value for the Bayesian ART parameters; therefore, we will not cover in details in this paper.
First, we set the Thales sphere radius emax as 0.3 and the initial covariance matrix to be spherical , where I is the identity matrix; hence, the parameter [equations (13) and (14)] to ensure that the is always lower than the SMAX. Then, we set the maximal category hypervolume parameter value (SMAX) as 1. Next, the value of the initial parameter was set to 0.01. Note that 682 is the laser scanner scans. Finally, we set the to 1 for generating the deterministic region instead of probabilistic region map.
As mentioned in the previous section, we have configured Genetic Bayesian ARAM to two channels for attaining laser rangefinder data and robot location in the experiment. Thus, the importance factor α for laser rangefinder channel was set to 0.8 because its data are the main dominant for map building. Last, the importance factor α was set to 0.2 for robot location channel to deal with perceptual ambiguities of sensory information but not the environment condition. For SSGA variables’ setup, we set parent candidates (μ) = 1000 and offspring candidates (λ) = 500.
4. Results
In Section 4.1, the performance of Genetic Bayesian ARAM in a hybrid map building was validated using several benchmark datasets. The benchmark datasets were produced by the University of Freiburg, Department of Computer Science, with the objective for contributing benchmarking tools to robotics community.
For the physical robot implementation, the front laser rangefinder data, rear laser rangefinder data, and robot odometry system that was installed on the robot are transmitted to Genetic Bayesian ARAM for map building and learning. Section 4.3 explains details of the setup.
4.1. Simulation Result
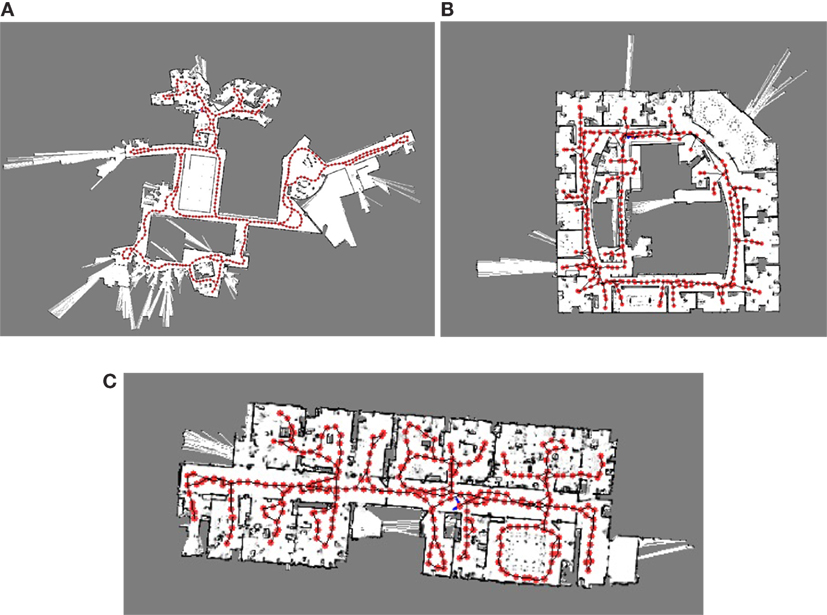
In simulation experiments, we input 3 benchmark datasets that gathered in Intel research lab, MIT CSAIL building, and Freiburg indoor building (Kümmerle et al., 2009). Figure 5 shows the exact grid map and robot navigation path for each dataset.
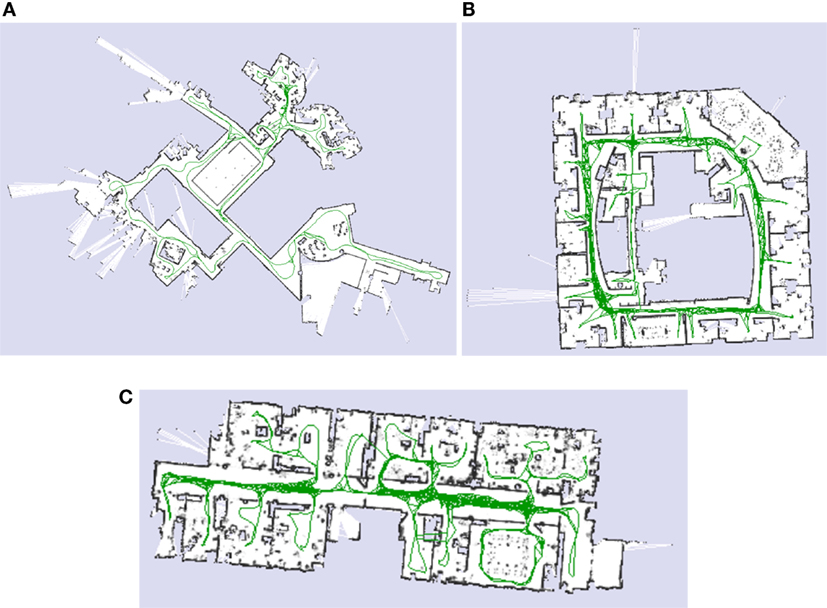
Figure 5. Simulation benchmark datasets. (A) MIT CSAIL Building. (B) Intel Research Lab. (C) Freiburg.
Figure 5 illustrates Genetic Bayesian ARAM hybrid map learning result. All the generated hybrid maps consist of grid occupancy map and topological map. As shown in Figure 6, all metric maps are almost identical to the benchmark datasets. In addition, all topological maps are almost similar to the robot traverse direction. Each node in the topological map consists of a robot metric location and a set of sensor data that represent the particular region of the environment.
4.2. Node Localization
The efficiency of the hybrid maps generated by Genetic Bayesian ARAM is validated by node localization process. For this, the laser scanner datasets are transmitted to the corresponding built map and then equation (7) is used to find out the best candidate for localization. If the best candidate’s weight and the robot’s current sensor data fulfill equation (13), it means that the best candidate node is localized.
Next, equations (22) and (23) are required to measure the Euclidean distance between the winning node and the robot current location to ensure that the robot is localized. The results of node localization are shown in Table 3; the average rate of successful node localization is 92.7%.
4.3. Physical Robot Implementation
For physical robot implementation, we used the robot with omnidirectional movement and attached with a Hokuyo UTM-30LX laser rangefinder as shown in Figure 7A. Sensors signal were sampled at 10 Hz. All processing and recording were operated on Intel Core i5 1.4-GHz processor. The mobile robot navigated locally by means of a motion control algorithm, which played the role of both wall following and obstacle avoidance. Table 4 shows the robot’s specification.
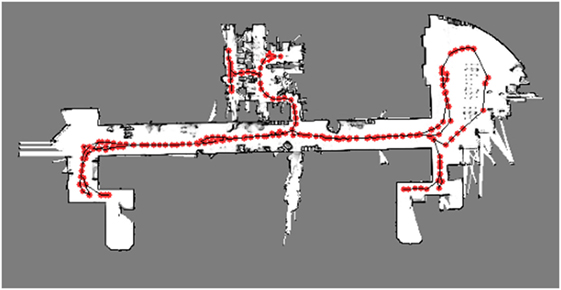
The real robot experiments were conducted in the university laboratory corridor as shown in Figure 7B. The width and length of the place are 5 m × 40 m. The environment is dynamic with pedestrian moving around, furniture and other equipment relocation, door open or close, and different lighting conditions. The experiment environment was set to be as natural as possible to verify that our proposed method is able to handle environment condition changes without any presumptions or alterations.
Then, we commanded the robot to traverse our laboratory room and corridor for two times to verify the hybrid map building. For the first exploration, the learning algorithm was without map maintenance, whereas for the second exploration, the learning algorithm was with map maintenance. Note that the two exploration paths are identical. During the navigation, the robot performed self-localization and built the grid map by using laser rangefinder measurement data. Then, robots’ position was used by Bayesian ARAM for topological map building. Figure 8 shows the resulted hybrid map built by the proposed method with map maintenance. The final hybrid map contained a grid map representing the outline of explored corridor and our laboratory room. At the same time, the topological map contained 164 nodes to represent the traversed place. For the proposed algorithm without map maintenance, the topological map contained 461 nodes. The result shows that the map maintenance feature reduces 65% of number of nodes to represent the same explored environment.
4.4. Robot Localization
After the hybrid map is generated, we commanded the robot to go to the starting point and then explore the corridor for five times to further verify the localization capability. The robot kept examining nodes in the hybrid map with respect to the current sensor data for localization. If the best candidate’s weight and robot’s current sensory information fulfilled equation (22), the localization of robot was successful and vice versa.
Table 5 shows the result of localization rate for each loop. The successful localization rate was generally 92.3%.
5. Discussion
We have shown that the Genetic Bayesian ARAM framework is capable of generating a metric–topological hybrid map incrementally using nearly unprocessed sensory information and without any feature extraction and predefined knowledge about the environment. The algorithm updates both the metric map and creates nodes incrementally to represent the explored environment as regions in real time.
In all the experiments, SSGA continuously performed localization and metric mapping without using any odometry system. Then, Bayesian ARAM uses these localization data and laser scanner data for topological map building. The localization data are important for distinguishing places that have similar sensor data, which is important to overcome the online topological nodes’ localization. After building the map, the robot can perform path planning by just comparing its current location with topological nodes without recalculating the grid map. These features help to compensate the weakness of metric map and topological map.
In addition, the experiment showed that the map maintenance algorithm greatly reduces the number of nodes that represent the explored environment. This method also reduces the amount of memory required for storing the map, especially when the area is very large.
According to the node matching and localization results, the robot failed for localization occasionally during navigation because it encountered sudden change in the environment, which caused none of topological nodes match with these sensor data. This problem can be overcome by measuring few time stamps of sensor at the same position with the topological nodes in the map. Another reason is that the robot was unable to differentiate similar sensor data at particular places. As our proposed method can take more than one sensory source, this issue can be solved by integrating camera input with certain image processing techniques to help on disambiguate similar sensory information at different locations.
6. Conclusion
In this article, we proposed a new framework for simultaneous localization and hybrid map building without any odometry hardware. The experiments presented show the feasibility of the proposed approach. The proposed framework was verified through simulation of standardized benchmark datasets and real robot application. Both metric and topological maps were generated as expected, correctly representing the environment according to our proposed method. The algorithm does not require high-level cognitive knowledge or any artificial landmark to construct the hybrid map, which makes it ready to work in a natural environment. In addition, the robot can perform self-localization automatically without any odometry system.
Future work in this subject will include an analysis of effectiveness of the value of framework parameters. Besides, we will extend our method for reinforcement learning capability for path planning. Last, we will conduct more experiments in different kinds of indoor and outdoor environment for further verification.
Author Contributions
WC is the main contributor for this research and paper writing. YT is the contributor for developing steady-state genetic algorithm and grid map building. Dr. CL and Dr. NK are the supervisors.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research is partially subsidized by “HIR grant UM.C/625/1/HIR/MOHE/FCSIT/10” from the University of Malaya.
References
Battesti, E., Bazeille, S., and Filliat, D. (2011). “Qualitative localization using vision and odometry for path following in topo-metric maps,” in European Conference on Mobile Robotics (ECMR) (Sweden: IEEE), 303–308.
Bazeille, S., and Filliat, D. (2011). “Incremental topo-metric SLAM using vision and robot odometry,” in 2011 IEEE International Conference on Robotics and Automation (ICRA) (Shanghai: IEEE), 4067–4073.
Benjamin, K., and Yung-Tai, B. (1991). A robot exploration and mapping strategy based on a semantic hierarchy of spatial representations. J. Robot. Autonomous Syst. 8, 47–63. doi: 10.1016/0921-8890(91)90014-C
Bianco, G., and Cassinis, R. (1996). “Multi-strategic approach for robot path planning,” in Proceedings of the First Euromicro Workshop on Advanced Mobile Robot, 1996 (Kaiserslautern), 108–115.
Chin, W. H., Loo, C. K., and Kubota, N. (2015). “Multi-channel Bayesian adaptive resonance associative memory for environment learning and topological map building,” in 2015 International Conference on Informatics, Electronics Vision (ICIEV) (Fukuoka), 1–5.
Chin, W. H., Loo, C. K., Seera, M., Kubota, N., and Toda, Y. (2016). Multi-channel bayesian adaptive resonance associate memory for on-line topological map building. Appl. Soft. Comput. 38, 269–280. doi:10.1016/j.asoc.2015.09.031
Cristforis, P. D., Nitsche, M., Krajnk, T., Pire, T., and Mejail, M. (2015). Hybrid vision-based navigation for mobile robots in mixed indoor/outdoor environments. Pattern Recognit. Lett. 53, 118–128. doi:10.1016/j.patrec.2014.10.010
Duan, J.-M., Liu, D., Yu, H.-X., and Shi, H. (2015). “An improved Fastslam algorithm for autonomous vehicle based on the strong tracking square root central difference Kalman filter,” in Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, ITSC’15 (IEEE Computer Society), 693–698.
Folkesson, J., and Christensen, H. (2007). Closing the loop with graphical slam. IEEE Trans. Robot. 23, 731–741. doi:10.1109/TRO.2007.900608
Jockusch, J., and Ritter, H. (1999). “An instantaneous topological mapping model for correlated stimuli,” in International Joint Conference on Neural Networks, 1999. IJCNN’99, Vol. 1, 529–534.
Kaess, M., Ranganathan, A., and Dellaert, F. (2008). iSAM: incremental smoothing and mapping. IEEE Trans. Robot. 24, 1365–1378. doi:10.1109/TRO.2008.2006706
Kümmerle, R., Steder, B., Dornhege, C., Ruhnke, M., Grisetti, G., Stachniss, C., et al. (2009). On measuring the accuracy of slam algorithms. Auton. Robots 27, 387–407. doi:10.1007/s10514-009-9155-6
Lee, K., and Chung, W. K. (2009). Effective maximum likelihood grid map with conflict evaluation filter using sonar sensors. IEEE Trans. Robot. 25, 887–901. doi:10.1109/TRO.2009.2024783
Taylor, C. J., and Kriegman, D. J. (1998). Vision-based motion planning and exploration algorithms for mobile robots. IEEE Trans. Robot. Automation 14, 417–426. doi:10.1109/70.678451
Thrun, S. (1998). Learning metric-topological maps for indoor mobile robot navigation. Artif. Intell. 99, 21–71. doi:10.1016/S0004-3702(97)00078-7
Thrun, S. (2003). Learning occupancy grid maps with forward sensor models. Auton. Robots 15, 111–127. doi:10.1023/A:1025584807625
Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic Robotics (Intelligent Robotics and Autonomous Agents). The MIT Press.
Toda, Y., Suzuki, S., and Kubota, N. (2012). “Evolutionary computation for intelligent self-localization in multiple mobile robots based on slam,” in Proceedings of the 5th International Conference on Intelligent Robotics and Applications – Volume Part I (Montreal: Springer-Verlag), 229–239.
Tomono, M., and Yuta, S. (2003). “Object-based localization and mapping using loop constraints and geometric prior knowledge,” in IEEE International Conference on Robotics and Automation, 2003. Proceedings. ICRA’03, Vol. 1 (Karlsruhe: IEEE), 862–867.
Vigdor, B., and Lerner, B. (2007). The bayesian artmap. IEEE Trans. Neural Netw. 18, 1628–1644. doi:10.1109/TNN.2007.900234
Wu, C.-H., Chen, Y.-H., Lee, Y.-Y., and Tsai, C.-H. (2013). “A fast genetic slam approach for mobile robots,” in Proceedings of the 2013 14th ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing, SNPD’13 (Honolulu: IEEE Computer Society), 563–568.
Keywords: Bayesian, genetic algorithm, SLAM, topological map, hybrid map, mobile robot, navigation
Citation: Chin WH, Loo CK, Toda Y and Kubota N (2016) An Odometry-Free Approach for Simultaneous Localization and Online Hybrid Map Building. Front. Robot. AI 3:68. doi: 10.3389/frobt.2016.00068
Received: 29 April 2016; Accepted: 24 October 2016;
Published: 14 November 2016
Edited by:
S. M. N. Arosha Senanayake, Universiti Brunei Darussalam, Brunei DarussalamReviewed by:
Shalabh Gupta, University of Connecticut, USAMuhammad Arif, Umm Alqura University, Saudi Arabia
Copyright: © 2016 Chin, Loo, Toda and Kubota. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Hong Chin, d2VpaG9uZzExODExOEBnbWFpbC5jb20=
 Wei Hong Chin
Wei Hong Chin Chu Kiong Loo2
Chu Kiong Loo2