Characteristic Model-Based Robust Model Predictive Control for Hypersonic Vehicles with Constraints

Designing robust control for hypersonic vehicles in reentry is difficult, due to the features of the vehicles including strong coupling, non-linearity, and multiple constraints. This paper proposed a characteristic model-based robust model predictive control (MPC) for hypersonic vehicles with reentry constraints. First, the hypersonic vehicle is modeled by a characteristic model composed of a linear time-varying system and a lumped disturbance. Then, the identification data are regenerated by the accumulative sum idea in the gray theory, which weakens effects of the random noises and strengthens regularity of the identification data. Based on the regenerated data, the time-varying parameters and the disturbance are online estimated according to the gray identification. At last, the mixed H₂/H_∞ robust predictive control law is proposed based on linear matrix inequalities (LMIs) and receding horizon optimization techniques. Using active tackling system constraints of MPC, the input and state constraints are satisfied in the closed-loop control system. The validity of the proposed control is verified theoretically according to Lyapunov theory and illustrated by simulation results.

Introduction

Hypersonic vehicle, a type of aircrafts with a flying speed of over 5 Mach, is a hot research topic due to its importance in national defense and military affairs. The hypersonic reentry flight usually covers a large flight envelope, during which the environmental and aerodynamic characteristics undergo huge variations (Harpold, 1979; Lu, 2014). The reentry dynamic model has fast time variability and strong coupling, is highly non-linear and is with strong disturbances and uncertainties (Wu and Meng, 2009). Thus, it is difficult to adapt the large envelope and multitasking flight movement using the traditional PID control, as the selection of the operating points and the design of the scheduling algorithm remains a time-consuming procedure for engineers. Therefore, domestic and foreign researchers study the advanced controller design to make the vehicles have stable flight characteristics and strong robustness (Zhang and Hu, 2012). Since there exist thermal and mechanical constraints in safety boundaries of reentry flight corridors, the hypersonic reentry control system must satisfy strict input and state constraints (Lu, 1999; Shen and Lu, 2003), including the constraints on aerodynamic angles, angular velocities, and control moments. If these complex physical demanding constraints are violated, the performance and stability of the control system will be deteriorated, then the safety and reliability of reentry flight can be affected seriously.

In the past decades, non-linear control methods such as adaptive backstepping control, non-linear disturbance observer, and robust control were used to improve robustness of the reentry control systems (Xu et al., 2012; Li et al., 2016; Wu and Meng, 2016). But, the system input and output constraints were not considered in Xu et al. (2012), Li et al. (2016), and Wu and Meng (2016). Well-known methods for constrained control include anti-windup control and reference governors. In Alicia and Andrea (2009), the combined reference governor and anti-windup control for hypersonic vehicles can suppress input saturation effectively. However, the compensator will be executed only when the saturation phenomenon appears, which affects the control accuracy and strong maneuverability of reentry hypersonic vehicles.

Model predictive control (MPC) has been widely accepted as an effective approach for control of constrained systems and applied in many industries, for its ability to handle hard constraints actively in receding horizon optimization (Chiristopher et al., 2013; Zhang and Sun, 2016). But high online-computation complexity brings difficulties to its applications in real-time control of hypersonic vehicles with high non-linear systems. Thus, much progress has been made to reduce computation complexity of MPC for hypersonic vehicles. In Van (2006), feedback linearization and linearized MPC were combined to design the control law for hypersonic vehicles. By transformation of the non-linear model into a linear model, it simplified the complexity of the predictive model. But, the computation was still complicated, due to the convention of original linear constraints into non-linear constraints. In Qin et al. (2016), a fuzzy predictive control strategy was designed for hypersonic vehicles with actuator constraints and input delays. Though a linearized predictive model is adopted to decrease model complexity, computational complex of the MPC is still high due to complex fuzzy rules.

Based on the above analysis, more research deserves to be done on MPC for hypersonic vehicles with permitted complexity and high robustness. Characteristic modeling, which was proposed by Wu et al. (2007), is constructed based on dynamical characteristics, environmental characteristics, and control performance, no only based on accurate system dynamics in conventional modeling (Wu et al., 2009). The main advantages of the characteristic modeling are depicting high-order linear time-varying systems and non-linear systems by low-order linear time-varying systems with a simple structure. The features including non-linear, strong coupling, and uncertainty for hypersonic flight make it hard to establish an accurate dynamic model, but the characteristic model can be well applied to this kind of complex system. Thus, such modeling method highly decreases difficulties in control design. A golden section adaptive attitude controller is presented in Gong and Wu (2010) and Xu (2012) based on the characteristic model. But the coupling in states and the coupling in controllers were not considered. The control (Gong and Wu, 2010; Xu, 2012) is difficult to be applied in the hypersonic vehicles in reentry stage since the hard constraints for the reentry vehicle were not considered.

The aim of the paper is to design characteristic model-based robust MPC for hypersonic vehicles with reentry constraints. According to input–output equivalence, dynamics of the hypersonic vehicle is described by a characteristic model composed of a linear time-varying system and a lumped disturbance. The time-varying parameters and the disturbance in the characteristic model are estimated according to the gray identification, which highly reduces effects of the measurement noises. The proposed robust MPC is obtained by solving an optimization with the characteristic model as the predictive model and a mixed H₂/H_∞ function as the cost function. In the control, the constraints are tackled by explicitly considering them in the optimization and the control robustness is improved by the use of the H₂/H_∞function. The feasibility and robustness of the proposed control are verified theoretically according to Lyapunov theory and illustrated by simulation results. The main contributions of this paper include the following:

(1) design of the characteristic model with time-varying parameters as the predictive model, which highly reduces complexity of the predictive model and approximation errors in Taylor linearization.

(2) identification of the time-varying parameters according to the gray identification, which reduces the effects of stochastic noises to identification accuracy.

(3) design of the H₂/H_∞ MPC, which satisfies reentry constraints and improves control robustness to uncertainties.

The design process of this paper is organized as follows. In Section “Model Description and Problem Formulation,” the objective of this paper is stated. In Section “Characteristic Model of the Reentry Hypersonic Vehicle,” a characteristic model composed of a linear time-varying system and a lumped disturbance are constructed for the hypersonic vehicle. In Section “Gray Identification for the Characteristic Model,” the time-varying parameters and the disturbance for characteristic model are online estimated according to the gray identification. In Section “Mixed H₂/H_∞ Robust Predictive Control,” the mixed H₂/H_∞ robust predictive control law is proposed based on linear matrix inequalities (LMIs) and receding horizon optimization techniques. Section “Simulation Analysis” presents simulation result. At last, conclusions are given in Section “Conclusion.”

Model Description and Problem Formulation

To study the attitude stability of the winged hypersonic vehicle, it is common to neglect the wind, the Earth rotation and the Earth curvature. Using linear aerodynamics hypothesis and neglecting the influences of control surface deflections on aerodynamic forces, the rigid body attitude dynamic equations are as follows (Zhang and Hu, 2012):

$\begin{array}{llll}\hfill & \dot{\mathrm{\alpha }}={\mathrm{\omega }}_y-{\mathrm{\omega }}_x\cos \mathrm{\alpha }\tan \mathrm{\beta }-{\mathrm{\omega }}_y\sin \mathrm{\alpha }\tan \mathrm{\beta }& \hfill & \\ \hfill & \dot{\mathrm{\beta }}={\mathrm{\omega }}_x\sin \mathrm{\alpha }-{\mathrm{\omega }}_z\cos \mathrm{\alpha }& \hfill & \\ \hfill & \dot{\mathrm{\phi }}={\mathrm{\omega }}_x+{\mathrm{\omega }}_y\sin \mathrm{\phi }\tan \mathrm{\theta }+{\mathrm{\omega }}_z\cos \mathrm{\phi }\tan \mathrm{\theta }\end{array}$ (1)

$\begin{array}{llll}\hfill & {\dot{\mathrm{\omega }}}_x=I_{\text{1}}{\mathrm{\omega }}_y{\mathrm{\omega }}_z+I_2{\mathrm{\omega }}_x{\mathrm{\omega }}_y+k_{\mathit{xx}}{\mathrm{\omega }}_x+k_{\mathit{xz}}{\mathrm{\omega }}_z+k_{x\mathrm{\alpha }}{\mathrm{\delta }}_a+k_r{\mathrm{\delta }}_r+M_1& \hfill & \\ \hfill & {\dot{\mathrm{\omega }}}_y=I_3{\mathrm{\omega }}_x{\mathrm{\omega }}_z+I_4\left({\mathrm{\omega }}_x^2-{\mathrm{\omega }}_z^2\right)+k_{\mathit{yy}}{\mathrm{\omega }}_y+k_{\mathit{ye}}{\mathrm{\delta }}_e+M_2& \hfill & \\ \hfill & {\dot{\mathrm{\omega }}}_x=I_5{\mathrm{\omega }}_x{\mathrm{\omega }}_y+I_6{\mathrm{\omega }}_y{\mathrm{\omega }}_z+k_{\mathit{zx}}{\mathrm{\omega }}_x+k_{\mathit{zz}}{\mathrm{\omega }}_z+k_{z\mathrm{\alpha }}{\mathrm{\delta }}_a+k_{\mathit{zr}}{\mathrm{\delta }}_r+M_3\end{array}$ (2)

and

$\begin{array}{lll}{I}_1=\frac{I_y{I}_z-I_z^2-I_{\mathit{xz}}^2}{I_x{I}_z-I_{\mathit{xz}}^2},I_2=\frac{\left(I_y-I_x-I_z\right)I_{\mathit{xz}}}{I_x{I}_z-I_{\mathit{xz}}^2},I_3=\frac{I_z-I_x}{I_y},\hfill & \hfill & \\ I_4=\frac{I_{\mathit{xz}}}{I_y},I_5=\frac{I_x^2+I_{\mathit{xz}}^2-I_x{I}_y}{I_x{I}_z-I_{\mathit{xz}}^2},I_6=\frac{\left(I_z+I_x-I_y\right)I_{\mathit{xz}}}{I_x{I}_z-I_{\mathit{xz}}^2}\hfill & \hfill & \end{array}$

where the attack angle α is the angle between the velocity vector and its longitudinal symmetry plane; the side slip angle β is the angle between the projection of the velocity vector and the vehicle vertical axis; φ and θ are the roll angle and, respectively, the pitching angle; ω_x, ω_y, ω_z are angular velocities of the flight vehicle projected to the body frame; δ_r, δ_e, δ_a are rudders deflection, elevators deflection, and left right elevator difference, respectively; k_xx, k_xz, k_xα, k_r, k_yy, k_ye, k_zx, k_zz, k_zα, k_zr are the aerodynamic moment coefficient, the detailed definition can be seen in Liu and Chen (2010); M₁, M₂, M₃ are external moment disturbances. The attack angle and the side slip angle are depicted in Figure 1. The matrix of inertia moments is given by $I=\left[\begin{array}{ccc}\hfill I_x\hfill & \hfill \text{0}\hfill & \hfill I_{\mathit{xz}}\hfill \\ \hfill 0\hfill & \hfill I_y\hfill & \hfill \text{0}\hfill \\ \hfill I_{\mathit{xz}}\hfill & \hfill \text{0}\hfill & \hfill I_z\hfill \end{array}\right]$. The task of control system is as follows:

(1) Control goal: with the constraints satisfied, track the outer guidance commands α, φ and make β keep at 0^∘ in the presence of parameter uncertainties and disturbance torques. The control errors of α and φ are within 0.5^∘.

(2) The constraints of the reentry control include

① The saturation constraints of rudder deflection

${∥{\mathrm{\delta }}_a∥}_2\le {{\mathrm{\delta }}_a}_{\max },{∥{\mathrm{\delta }}_e∥}_2\le {{\mathrm{\delta }}_e}_{\max },{∥{\mathrm{\delta }}_r∥}_2\le {{\mathrm{\delta }}_r}_{\max }$

② The state constraints

FIGURE 1

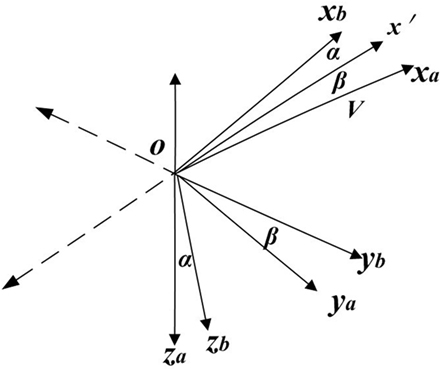
Figure 1. Relationship between the speed coordinates (Ox_ay_az_a) and the vehicle coordinates (Ox_by_bz_b).

According to the requirements of preventing heat, the following constraints should be satisfied:

${∥\mathrm{\alpha }\left(k\right)∥}_2\le {\mathrm{\alpha }}_{\max }$

According to the structural safety requirements of vehicle mechanics, the following constraints of angular velocities need to be satisfied:

${∥{\mathrm{\omega }}_x∥}_2\le {\mathrm{\omega }}_{x\max },{∥{\mathrm{\omega }}_y∥}_2\le {\mathrm{\omega }}_{y\max },{∥{\mathrm{\omega }}_z∥}_2\le {\mathrm{\omega }}_{z\max }\text{.}$

Characteristic Model of the Reentry Hypersonic Vehicle

The reentry systems (1) and (2) are strongly non-linear, time-varying, and uncertain multivariable coupling, so it is difficult to design controller directly for it. Based on the principle of input and output equivalence, we differentiate system outputs α, β, φ to second order, apply identical substitution and Taylor series approximate expansion (Wu et al., 2007). The discrete model of input–output time-varying second-order of α, β, and φ is as follows:

$\begin{array}{l}\hfill \mathrm{\alpha }\left(k+1\right)=f_{\mathrm{\alpha 1}}\left(k\right)\mathrm{\alpha }\left(k\right)+f_{\mathrm{\alpha 2}}\left(k\right)\mathrm{\alpha }\left(k-1\right)+g_1\left(k\right){\mathrm{\delta }}_{\mathrm{\alpha }}\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\alpha }}\left(k\right)\end{array}$ (3)

$\begin{array}{l}\hfill \mathrm{\beta }\left(k+1\right)=f_{\mathrm{\beta 1}}\left(k\right)\mathrm{\beta }\left(k\right)+f_{\mathrm{\beta 2}}\left(k\right)\mathrm{\beta }\left(k-1\right)+g_2\left(k\right){\mathrm{\delta }}_{\mathrm{\beta }}\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\beta }}\left(k\right)\end{array}$ (4)

$\begin{array}{l}\hfill \mathrm{\phi }\left(k+1\right)=f_{\mathrm{\phi 1}}\left(k\right)\mathrm{\phi }\left(k\right)+f_{\mathrm{\phi 2}}\left(k\right)\mathrm{\alpha }\left(k-1\right)+g_3\left(k\right){\mathrm{\delta }}_{\mathrm{\phi }}\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\phi }}\end{array}$ (5)

where characteristic model parameters f_i1, f_i2 (i = α, β, φ) and g₁, g₂, g₃ are time-varying, δ_α, δ_β, δ_φ are equivalent control input. The characteristic model for the plant (Eqs 3–5) as given in Eqs 1 and 2 possesses the following properties: the coefficients f_i1, f_i2 (i = α, β, φ) and g₁, g₂, g₃ are slowly time-varying, the ranges of these parameters can be decided a priori, in response to the same input, the output of the original model (Eqs 1 and 2) is identical to the output of the characteristic model (Eqs 3–5) at each sampling time. Sum of all the coefficients of (Eqs 3–5) equals 1 (Zhang and Hu, 2012) as follows:

$\begin{array}{llll}\hfill & f_{\mathrm{\alpha 1}}+f_{\mathrm{\alpha 2}}\approx 1{\mathrm{\delta }}_{\mathrm{\alpha }}\approx {\mathrm{\delta }}_e& \hfill & \\ \hfill & f_{\mathrm{\beta 1}}+f_{\mathrm{\beta 2}}\approx 1{\mathrm{\delta }}_{\mathrm{\beta }}\approx {\mathrm{\delta }}_r& \hfill & \\ \hfill & f_{\mathrm{\phi 1}}+f_{\mathrm{\phi 2}}\approx 1{\mathrm{\delta }}_{\mathrm{\phi }}\approx {\mathrm{\delta }}_a& \hfill & \end{array}$

Define the lumped disturbance Δ_α(k) as follows:

${\mathrm{\Delta }}_{\mathrm{\alpha }}\left(k\right)=m_{11}\mathrm{\beta }\left(k\right)+m_{12}\mathrm{\phi }\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\alpha 1}}\left(k\right)$ (6)

where m₁₁, m₁₂, and Δ_α1(k) are coupling coefficient, Δ_α(k) includes dynamic coupling information with other channels, external disturbances, and unmodeled errors. To improve robustness of the control system, Δ_α(k) is estimated online and compensated feedforwardly in control. Similarly, the lumped disturbances in the other channels are described as follows:

$\begin{array}{lll}\hfill {\mathrm{\Delta }}_{\mathrm{\beta }}=m_{21}\mathrm{\alpha }\left(k\right)+m_{22}\mathrm{\phi }\left(k\right)+{\mathrm{\Delta }}_{{\mathrm{\beta }}_1}\left(k\right)& \hfill & \\ \hfill {\mathrm{\Delta }}_{\mathrm{\phi }}=m_{31}\mathrm{\alpha }\left(k\right)+m_{32}\mathrm{\beta }\left(k\right)+{\mathrm{\Delta }}_{{\mathrm{\phi }}_1}\left(k\right)& \hfill & \end{array}$

Let δ_α ≈ δ_e, then the control constraints can be transformed into ${∥{\mathrm{\delta }}_{\mathrm{\alpha }}\left(k\right)∥}_2\le {\mathrm{\delta }}_{e\max }$ [the readers can see Zhang and Hu (2012) for detail], the output constraints are ${∥\mathrm{\alpha }\left(k\right)∥}_2\le {\mathrm{\alpha }}_{\max }$ and ${∥\dot{\mathrm{\alpha }}∥}_2\approx {∥{\mathrm{\omega }}_y∥}_2\le {\mathrm{\omega }}_{y\max }$.

Gray Identification for the Characteristic Model

To accurately identify the parameters in the characteristic model is significant for control design.

In this section, the random noise in the measured reentry dynamic state can be approximately treated as white noise. Accumulated generating operation in the gray identification is used to weaken the impact of the random noise on original data sequences efficiently (Liu and Chen, 2010) and regularize original data.

Let the original reentry state sequence be

$x^{\left(0\right)}=\left\{x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),........,x^{\left(0\right)}\left(N\right)\right\}$

where N is the total number of the identification samples. The identification data can be regenerated as follows:

$x^{\left(1\right)}\left(k\right)={\displaystyle \sum _{m=1}^k}{x}^{\left(0\right)}\left(m\right)$ (7)

where m has the number of sampling data. Operating gray accumulation generation once, we can get more regular sequence, which eliminates the impact of random noise to some extent. Then, new input data for identification are depicted as follows:

$\left\{x^1\left(1\right),x^1\left(2\right),........,x^1\left(N\right)\right\}$ (8)

In the following of this section, taking the attack-angle model (Eq. 3) as an example to illustrate identification of parameters. The identification of parameters in other models (Eqs 4 and 5) is similar and omitted. From the definition of gray data, the gray model of dynamics of the attack angle (Eq. 3) is given as follows:

$\begin{array}{l}\hfill {\mathrm{\alpha }}^1\left(k+1\right)=f_{\mathrm{\alpha 1}}\left(k\right){\mathrm{\alpha }}^1\left(k\right)+f_{\mathrm{\alpha 2}}\left(k\right){\mathrm{\alpha }}^1\left(k-1\right)+g_1\left(k\right){\mathrm{\delta }}_{\mathrm{\alpha }}^1\left(k\right)+m_{{}_{11}}{\mathrm{\beta }}^1\left(k\right)+m_{{}_{12}}{\mathrm{\phi }}^1\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\alpha 1}}^1\left(k\right)\end{array}$ (9)

During the identification time, the unmodeled error and disturbances are approximated as follows:

$\begin{array}{l}{\mathrm{\Delta }}_{\mathrm{\alpha 1}}^1\left(1\right)={\mathrm{\Delta }}_{\mathrm{\alpha 1}},{\mathrm{\Delta }}_{\mathrm{\alpha 1}}^1\left(2\right)=2{\mathrm{\Delta }}_{\mathrm{\alpha 1}}^1\left(1\right)=2{\mathrm{\Delta }}_{\mathrm{\alpha 1}},{\mathrm{\Delta }}_{\mathrm{\alpha 1}}^1\left(N-1\right)=\left(N-1\right){\mathrm{\Delta }}_{\mathrm{\alpha 1}}^1\left(1\right)=\left(N-1\right){\mathrm{\Delta }}_{\mathrm{\alpha 1}}.\hfill \end{array}$

Let

$V={\left[\stackrel{}{f_{\mathrm{\alpha 1}}}\left(k\right),\stackrel{}{f_{\mathrm{\alpha 2}}}\left(k\right),\stackrel{}{g_1}\left(k\right),{\stackrel{}{m}}_{11},{\stackrel{}{m}}_{12},{\stackrel{}{\mathrm{\Delta }}}_{\mathrm{\alpha 1}}\right]}^T$

$\begin{array}{ll}\hfill & B=\left[\begin{array}{c}{B}_2\\ B_3\\ .\\ .\\ .\\ B_{N-1}\end{array}\right]=\left[\begin{array}{cccccc}{\mathrm{\alpha }}^1\left(2\right)& {\mathrm{\alpha }}^1\left(1\right)& {\mathrm{\delta }}_{\mathrm{\alpha }}^1\left(2\right)& {\mathrm{\beta }}^1\left(2\right)& {\mathrm{\varphi }}^1\left(2\right)& 2\\ {\mathrm{\alpha }}^1\left(3\right)& {\mathrm{\alpha }}^1\left(2\right)& {\mathrm{\delta }}_{\mathrm{\alpha }}^1\left(3\right)& {\mathrm{\beta }}^1\left(3\right)& {\mathrm{\varphi }}^1\left(3\right)& 3\\ \text{.}& & & & & .\\ \text{.}& & & & & \text{.}\\ \text{.}& & & & & \text{.}\\ {\mathrm{\alpha }}^1\left(N-1\right)& {\mathrm{\alpha }}^1\left(N-2\right)& {\mathrm{\delta }}_{\mathrm{\alpha }}^1\left(N-1\right)& {\mathrm{\beta }}^1\left(N-1\right)& {\mathrm{\varphi }}^1\left(N-1\right)& N-1\end{array}\right]\end{array}$ (10)

From the gray model, we have

$D_N^{\left(1\right)}=\mathit{BV}$

where $D_N^{\left(1\right)}=\left[{\mathrm{\alpha }}^1\left(3\right){\mathrm{\alpha }}^1\left(4\right)\cdots {\mathrm{\alpha }}^1\left(N\right)\right]$. Applying the least square method, we can get

$V={\left(B^{T}B\right)}^{-1}{B}^T{D}_N^{\left(1\right)}$ (11)

To decrease effects of the lumped disturbances and improve robustness of the closed-loop control system, the feedforward input compensation is designed as follows:

$u_c\left(k\right)=-g_1^{-1}\left(k\right)\left(m_{11}\mathrm{\beta }\left(k\right)+m_{12}\mathrm{\phi }\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\alpha 1}}\left(k\right)\right)$ (12)

To accurately identify the parameters in the characteristic model is significant for control design.

Mixed H₂/H_∞ Robust Predictive Control

Let Δf _α1(k), Δf _α2(k), Δg₁(k) be the identification deviations of the actual characteristic model coefficients. Δ_T is the compensation error after the compensation of reentry channel coupling information, unmodeled dynamics and disturbances in u_c(k). It is obvious that a Δf _α1(k), Δf _α2(k), Δg₁(k), and Δ_T are bounded. Besides. Since α(k), δ_α(k) have definite region constraints, they are also bounded. As a result, the generalized disturbances d(k) are bounded and can be described as follows:

$d\left(k\right)=\mathrm{\Delta }{f}_{\mathrm{\alpha 1}}\left(k\right)\mathrm{\alpha }\left(k\right)+\mathrm{\Delta }{f}_{\mathrm{\alpha 2}}\left(k\right)\mathrm{\alpha }\left(k-1\right)+\mathrm{\Delta }{g}_1\left(k\right){\mathrm{\delta }}_{\mathrm{\alpha }}\left(k\right)+{\mathrm{\Delta }}_T$

Then characteristic model after gray identification compensation is given as follows:

$\mathrm{\alpha }\left(k+1\right)=f_{\mathrm{\alpha 1}}\mathrm{\alpha }\left(k\right)+f_{\mathrm{\alpha 2}}\mathrm{\alpha }\left(k-1\right)+g_1{\mathrm{\delta }}_{\mathrm{\alpha 1}}\left(k\right)+d\left(k\right)$

${\mathrm{\delta }}_{\mathrm{\alpha }}=u_c+{\mathrm{\delta }}_{\mathrm{\alpha 1}}$

Since ${\displaystyle \sum _{k-0}^{\infty }{d}^T(k)d(k)}\le d_{\max }$ is satisfied, d(k) is energy bounded. Since the unmodeled errors and couplings are partly compensated by estimators proposed in the last section, robust control is still needed to improve robustness of the closed-loop control system.

In this section, based on mixed H₂/H_∞ approach, a robust predictive control is proposed to have the better control performance under the premise that the general disturbance d(k) has been restrained efficiently (Patience and Orukpe, 2007).

Assume the tracking expectation is α_c = 0. To reduce the tracking errors, the integral of attack angle $e=\left[\int \left(\mathrm{\alpha }-{\mathrm{\alpha }}_c\right)\text{d}t\right]$ is considered as an extended state. Then, the augmented system is constructed as follows:

$x\left(k+1\right)=A\left(k\right)x\left(k\right)+B\left(k\right){\mathrm{\delta }}_{\mathrm{\alpha 1}}\left(k\right)+B_{d}d\left(k\right)$ (14)

$\begin{array}{l}\hfill A\left(k\right)=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& f_{\mathrm{\alpha 2}}& f_{\mathrm{\alpha 1}}\end{array}\right],B\left(k\right)=\left[\begin{array}{c}0\\ 0\\ g_1\end{array}\right],B_d=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right],x\left(k\right)=\left[\begin{array}{c}\mathit{\int }e\left(k\right)\\ \mathrm{\alpha }\left(k\right)\\ \mathrm{\alpha }\left(k+1\right)\end{array}\right]\end{array}$

In the subsequent control design, we use the characteristic model (Eq. 14) as a prediction model to simplify the complexity of predictive control. Considering the reentry thermal protection and overload safety, the constraints of the attack angle, the velocity and the input for the hypersonic vehicle control can be transformed into the following forms:

(1) constraints of the attack angle

${∥\mathrm{\alpha }\left(k\right)∥}_2={∥\left[0\text{\hspace{0.17em}\hspace{0.17em}1\hspace{0.17em}\hspace{0.17em}0}\right]x\text{(}k\text{)}∥}_2\le {\mathrm{\alpha }}_{\max }$ (15)

(2) constraints of the velocity

${∥{\mathrm{\omega }}_y∥}_2\approx {∥\dot{\mathrm{\alpha }}∥}_2\approx {∥\left[0-\text{1 1}\right]x\left(k\right)\frac{1}{T}∥}_2\le {\mathrm{\omega }}_{y\max }$ (16)

(3) the input saturation

$\begin{array}{llll}\hfill u=& {∥{\mathrm{\delta }}_{\mathrm{\alpha 1}}+u_c∥}_2\le {\mathrm{\delta }}_{e\max }\Rightarrow & \hfill & \\ \hfill & {∥{\mathrm{\delta }}_{\mathrm{\alpha 1}}∥}_2\le \min \left\{\left|{{\mathrm{\delta }}_e}_{\max }-u_c\right|,\left|-{{\mathrm{\delta }}_e}_{\max }-u_c\right|\right\}=u_{\max }\end{array}$ (17)

Define the indicator of control performance: $z\left(k\right)=\left[\begin{array}{c}\hfill Q_{1}x\left(k\right)\hfill \\ \hfill R{\mathrm{\delta }}_{\mathrm{\alpha 1}}\left(k\right)\hfill \end{array}\right]$, where Q₁ and R are weighting matrices of the state and control. Consider the following indexes (Jiang et al., 2017):

① H_∞ performance index: for any arbitrary γ > 0, the transfer function from d(k) to z(k) satisfies

${∥T_{\mathit{zd}}∥}_{\infty }\le \mathrm{\gamma }$ (18)

② H₂ performance index

${∥z∥}_2={\displaystyle \sum _{i=0}^{\infty }}{z}^T\left(k\right)z\left(k\right)\le a$ (19)

This paper is to design controller based on robust MPC and LMI, which is efficient to avoid adjusting parameters by experience, handle various reentry constraints and guarantee the robustness and stability of the time-varying characteristic system.

Theorem 1: Let x(k) be the state of the system (Eq. 14) measured at the sampling time k. Assume that there are constraints on the control input and plant output (Eqs 15–17). Then, the state feedback K in the control law δ_α1(k) = Kx(k) that minimizes the upper bound H₂ performance at sampling time k is given by the following equation:

$K=Y{Q}^{-1}$

where Q > 0 and Y are obtained from the solution (if it exists) of following linear objective minimization problem:

$\underset{Y,Q,a}{\min }a$

subject to

$\left[\begin{array}{ccc}\hfill \text{1}\hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill {\mathrm{\gamma }}^2{d}_{\max }\hfill & \hfill a{\mathrm{\gamma }}^2{d}_{\max }I\hfill & \hfill \ast \hfill \\ \hfill x\left(k\right)\hfill & \hfill 0\hfill & \hfill Q\hfill \end{array}\right]\ge 0$

and

$\left[\begin{array}{ccccc}\hfill Q\hfill & \hfill 0\hfill & \hfill \ast \hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill 0\hfill & \hfill a{\mathrm{\gamma }}^{2}I\hfill & \hfill \ast \hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill A\left(k\right)Q+B\left(k\right)Y\hfill & \hfill a{B}_d\hfill & \hfill Q\hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill Q_{1}Q\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mathit{aI}\hfill & \hfill \ast \hfill \\ \hfill \mathit{RY}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mathit{aI}\hfill \end{array}\right]>0$

$\left[\begin{array}{cc}\hfill {\mathrm{\alpha }}_{\max }^{2}I\hfill & \hfill \text{(}A\left(k\right)Q+B\left(k\right)Y{\text{)}}^T{C_1}^T\hfill \\ \hfill C_1\text{(}A\left(k\right)Q+B\left(k\right)Y\text{)}\hfill & \hfill Q\hfill \end{array}\right]\ge 0C_1=\left[\text{0 1 0}\right]$

$\left[\begin{array}{cc}\hfill {\mathrm{\omega }}_{y\max }^{2}I\hfill & \hfill {\text{(}A\left(k\right)Q+B\left(k\right)Y\text{)}}^T{C_2}^T\hfill \\ \hfill C_2\text{(}A\left(k\right)Q+B\left(k\right)Y\text{)}\hfill & \hfill Q\hfill \end{array}\right]\ge 0C_2=\frac{1}{T}\left[\text{0}-\text{1 1}\right]$

$\left[\begin{array}{cc}\hfill u_{\max }^{2}I\hfill & \hfill Y\hfill \\ \hfill Y^T\hfill & \hfill Q\hfill \end{array}\right]\ge 0$

where * represents terms readily inferred from symmetry.

Proof:

Stability constraints

Define V(x(k)) = x^T(k)P(k)x(k) and V(x(k + 1)) = x (k + 1)^TP(k)x(k + 1), where x(k + i) indicates the predictive state at k + i based on the measurement x(k) at sampling time k. δ_α1(k + i) is the ith predictive control at the sampling time k, we get the following formula:

$\begin{array}{llll}\hfill & V\left(\mathit{\text{x}}\left(k+i+1\right)\right)-V\left(\mathit{\text{x}}\left(k+i\right)\right)& \hfill & \\ \hfill & =x^T\left(k+i\right){\left(A\left(k\right)+B\left(k\right)K\right)}^{T}P\left(k+1\right)\left(A\left(k\right)+B\left(k\right)K\right)x\left(k+i\right)+d^T\left(k+i\right)B_d^{T}P\left(k\right)B_{d}d\left(k+i\right)& \hfill & \\ \hfill & +2d^T\left(k+i\right)B_d^{T}P\left(k\right)\left(A\left(k\right)+B\left(k\right)K\right)x\left(k+i\right)-x^T\left(k+i\right)P\left(k\right)x\left(k+i\right)+z^T\left(k+i\right)z\left(k+i\right)-z^T\left(k+i\right)z\left(k+i\right)& \hfill & \\ \hfill & +{\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)-{\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)& \hfill & \\ \hfill & =\left[x^T\left(k+i\right)d^T\left(k+i\right)\right]M\left(k\right){\left[x^T\left(k+i\right)d^T\left(k+i\right)\right]}^T+{\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)-z^T\left(k+i\right)z\left(k+i\right)\end{array}$ (20)

where

$M(k)=\left[\begin{array}{cc}{(A(k)+B(k)K)}^{T}P(k)(A(k)+B(k)K)-P(k)+Q_1^T{Q}_1+{(RK)}^T(RK)& {(B_{d}P(k)(A(k)+B(k)K))}^T\\ B_{d}P(k)(A(k)+B(k)K& B_d{}^{T}P(k)B_d-{\text{γ}}^{2}I\end{array}\right]$

From stability of gray identification, we can know that compensation error is close to 0. Then, if z(k + i) is also close to 0, then the system stability is obtained. If not, the following inequality is satisfied:

${\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)-z^T\left(k+i\right)z\left(k+i\right)<0$

If M(k) < 0, then V(x(k + i + 1)) − V(x(k + i)) < 0, and x(∞) = 0, V(x(∞)) = 0. Summing the both sides of Eq. (20) from i = 0 to i = ∞, we can get the following:

$\begin{array}{llll}\hfill & -x^T\text{(}k\text{)}\mathit{Px}\text{(}k\text{)}={\displaystyle \sum _{i=0}^{\infty }}\left[{\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)-z^T\left(k+i\right)z\left(k+i\right)\right]& \hfill & \\ \hfill & +{\displaystyle \sum _{i=0}^{\infty }}\left[x^T\left(k+i\right)d^T\left(k+i\right)\right]M\left(k\right){\left[x^T\left(k+i\right)d^T\left(k+i\right)\right]}^T& \hfill & \\ \hfill & {\displaystyle \sum _{i=0}^{\infty }}\left[z^T\left(k+i\right)z\left(k+i\right)\right]=x^T\left(k\right)P_{0}x\text{(}k\text{)\hspace{0.17em}}+{\displaystyle \sum _{i=0}^{\infty }}\left[{\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)\right]& \hfill & \\ \hfill & +{\displaystyle \sum _{i=0}^{\infty }}\left[x^T\left(k+i\right)d^T\left(k+i\right)\right]M\left(k\right){\left[x^T\left(k+i\right)d^T\left(k+i\right)\right]}^T\end{array}$ (21)

(I) When x(0) = 0, if M(k) < 0, ${\displaystyle \sum _{i=0}^{\infty }}\left[{\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)-z^T\left(k+i\right)z\left(k+i\right)\right]\le 0$, the H_∞ performance can be satisfied.

(II) When M(k) < 0, ${\displaystyle \sum _{i=0}^{\infty }}\left[z^T\left(k+i\right)z\left(k+i\right)\right]\le x^T\left(k\right)P_{}x\text{(}k\text{)}+{\mathrm{\gamma }}^2{d}_{\max }\le a$, the H₂ performance can be satisfied.

Therefore, the necessary and sufficient condition to realize the control target is M(k) < 0, i.e.

$\begin{array}{l}\hfill M\left(k\right)=\left[\begin{array}{cc}-P_{}\left(k\right)+Q_1^T{Q}_1+{\left(\mathit{RK}\right)}^T\left(\mathit{RK}\right)& 0\\ \text{0}& -{\mathrm{\gamma }}^{\text{2}}I\end{array}\right]+\left[\begin{array}{c}{\left(A\left(k\right)+B\left(k\right)K\right)}^T\\ B_d^T\end{array}\right]P\left(k\right)\left[\begin{array}{c}\left(A\left(k\right)+B\left(k\right)K\right)\\ B_d\end{array}\right]<0\end{array}$ (22)

Using Schur complement, the LMI (Eq. 22) is equivalent to

$\left[\begin{array}{ccccc}\hfill P_{}\left(k\right)\hfill & \hfill 0\hfill & \hfill \ast \hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill 0\hfill & \hfill {\mathrm{\gamma }}^{2}I\hfill & \hfill \ast \hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill A\text{(}k\text{)}+B\text{(}k\text{)}K\hfill & \hfill B_d\hfill & \hfill P{\left(k\right)}^{-1}\hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill Q_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill I\hfill & \hfill \ast \hfill \\ \hfill \mathit{RK}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill I\hfill \end{array}\right]>0$ (23)

Let Q = aP⁻¹, K = YQ⁻¹. Pre-multiply and post-multiply Eq. 23 by diag{a^1/2P⁻¹, a^1/2I, a^1/2I, a^1/2I, a^1/2I}, we can get

$\left[\begin{array}{ccccc}\hfill Q\hfill & \hfill 0\hfill & \hfill \ast \hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill 0\hfill & \hfill a{\mathrm{\gamma }}^{2}I\hfill & \hfill \ast \hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill A\left(k\right)Q+B\left(k\right)Y\hfill & \hfill a{B}_d\hfill & \hfill Q\hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill Q_{1}Q\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mathit{aI}\hfill & \hfill \ast \hfill \\ \hfill \mathit{RY}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mathit{aI}\hfill \end{array}\right]>0$ (24)

Performance constraints

Using Schur complement property, H₂ performance (19) is equivalent to:

$\left[\begin{array}{ccc}\hfill \text{1}\hfill & \hfill \ast \hfill & \hfill \ast \hfill \\ \hfill {\mathrm{\gamma }}^2{d}_{\max }\hfill & \hfill a{\mathrm{\gamma }}^2{d}_{\max }I\hfill & \hfill \ast \hfill \\ \hfill x\left(k\right)\hfill & \hfill 0\hfill & \hfill Q\hfill \\ \hfill \hfill \end{array}\right]\ge 0$ (25)

Output constraints

Since M(k) < 0, V(x(k + i + 1)) ≤ V(x(k + i)), and {z: z^T(k)Q⁻¹z(k) ≤ 1} is an invariant ellipsoid for the predicted states of the uncertain system (Eq. 13). Then

$\begin{array}{lll}\underset{i\ge 1}{\max }{∥y\text{(}k+i|k\text{)}∥}_2=\underset{i\ge 1}{\max }{∥C\text{(}A\text{(}k+i\text{)\hspace{0.17em}}+B\text{(}k+i\text{)}K\text{)}x\text{(}k+i|k)∥}_2\hfill & \hfill & \\ \le \underset{z^{T}z\le 1}{\max }\underset{}{{∥C\text{(}A\text{(}k+i\text{)}+B\text{(}k+i\text{)}K\text{)}{Q_{}}^{1∕2}z∥}_2}=\stackrel{-}{\mathrm{\sigma }}[C\text{(}A\text{(}k+i\text{)}+B\text{(}k+i\text{)}K\text{)}{Q_{}}^{1∕2}],i\ge 0\hfill \end{array}$ (26)

Since ${∥y\left(k+i|k\right)∥}_2\le y_{\max }$, then

$\stackrel{-}{\mathrm{\sigma }}\left[C\text{(}A\text{(}k+i\mathrm{|}k\text{)}+B\text{(}k+i\mathrm{|}k\text{)}K\text{)}{Q_{}}^{1∕2}\right]\le y_{\max }$ (27)

which is equivalent to

${Q_{}}^{1∕2}\text{(}A\text{(}k+i\text{)}+B\text{(}k+i\text{)}K\text{)}{C}^{T}C\text{(}A\text{(}k+i\text{)}+B\text{(}k+i\text{)}K\text{)}{Q_{}}^{1∕2}\le y_{\max }^{2}I$ (28)

Then, the attack-angle constraint (Eq. 15) is equivalent to

$\left[\begin{array}{cc}\hfill {\mathrm{\alpha }}_{\max }^{2}I\hfill & \hfill \text{(}A\left(k\right)Q+B\left(k\right)Y{\text{)}}^T{C_1}^T\hfill \\ \hfill C_1\text{(}A\left(k\right)Q+B\left(k\right)Y\text{)}\hfill & \hfill Q\hfill \end{array}\right]\ge 0C_1=\left[\text{\hspace{0.17em}0\hspace{0.17em}1\hspace{0.17em}0\hspace{0.17em}}\right]$ (29)

and the angular velocity constraint (Eq. 16) is equivalent to

$\left[\begin{array}{cc}\hfill {\mathrm{\omega }}_{y\max }^{2}I\hfill & \hfill {\text{(}A\left(k\right)Q+B\left(k\right)Y\text{)}}^T{C_2}^T\hfill \\ \hfill C_2\text{(}A\left(k\right)Q+B\left(k\right)Y\text{)}\hfill & \hfill Q\hfill \end{array}\right]\ge 0C_2=\frac{1}{T}\left[\text{\hspace{0.17em}0\hspace{0.17em}}-\text{1\hspace{0.17em}1\hspace{0.17em}}\right]$ (30)

Input constraint

Physical limitations inherent in process equipment invariably impose hard constraints on the manipulated variable δ_α1(k + i). The amplitude constraint can be represented as follows:

${∥{\mathrm{\delta }}_{\mathrm{\alpha 1}}\left(k+i\right)∥}_2^2\le u_{\max }^2,i\ge 0$ (31)

Setting K = YQ⁻¹, then δ_α1 = Kx = YQ⁻¹x. Then, Eq. (31) is equivalent to

$\begin{array}{l}\underset{i\ge 0}{\max }{∥{\mathrm{\delta }}_{\mathrm{\alpha 1}}\left(k+i\right)∥}_2^2=\underset{i\ge 0}{\max }{∥Y{Q}^{-1}x\left(k+i\right)∥}_2^2\le \\ \underset{z^{T}z\le 1}{\max }{∥Y{Q}^{-1}z∥}_2^2={\mathrm{\lambda }}_{\max }\left(Q^{-1∕2}{Y}^{T}Y{Q}^{-1∕2}\right)\end{array}$ (32)

Using Schur complement, Eq. (32) is equivalent to

$\left[\begin{array}{cc}\hfill u_{\max }^{2}I\hfill & \hfill Y\hfill \\ \hfill Y^T\hfill & \hfill Q\hfill \end{array}\right]\ge 0$ (33)

Theorem 2 (Feasibility): Any feasible solution of the optimization in Theorem 1 at a time k is also feasible for all times t > k. Thus, if the optimization problem in Theorem 1 is feasible at a time k, then it is feasible for all times t > k.

The proof of Theorem 2 is similar to Korhare et al. (1996) and Jiang et al. (2017), which is omitted here.

Theorem 3 (Robust stability): The feasible receding horizon state feedback control law obtained from Theorem 1 robustly asymptotically stabilizes the closed-loop system.

Proof: Choose the Lyapunov function V(x(k)) = x^T(k)P(k)x(k), then we have

$\begin{array}{llll}\hfill & V\left(x\left(k+i+1\right)\right)-V\left(x\left(k+i\right)\right)& \hfill & \\ \hfill & =\left[x^T\left(k+i\right)d^T\left(k+i\right)\right]M\left(k\right){\left[x^T\left(k+i\right)d^T\left(k+i\right)\right]}^T+{\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)-z^T\left(k+i\right)z\left(k+i\right)& \hfill & \end{array}$

From stability of gray identification, we can know that compensation error is close to 0. Then, if z(k + i) is also close to 0, then the system stability is obtained. If not, the following inequality is satisfied:

${\mathrm{\gamma }}^2{d}^T\left(k+i\right)d\left(k+i\right)-z^T\left(k+i\right)z\left(k+i\right)<0$

Since the constraint (Eq. 24) guarantees M(k) < 0 and V(x(k + i + 1)) − V(x(k + i)) < 0, V(x(k)) is a strictly decreasing Lyapunov function for the closed loop.

Algorithm realization

The process of the algorithm proposed in this paper is

① At the sampling time k, based on the real-time input and output data, identify the characteristic model parameters of attack-angle channel f _α1(k), f _α2(k), g₁(k), m₁₁(k), m₁₂(k), and Δ_α1(k) according to gray identification.

② Design compensator u_c to compensate three-channel coupling motion information, unmodeled information, and disturbance Δ_α1(k).

③ Compute robust predictive control law δ_α1 = Kx based on Theorem 1. Then, apply total control u = δ_α1 + u_c into the reentry vehicle.

④ Repeat process ①.

Control algorithms in other channels are similar to the algorithm for the attach channel and are omitted.

Simulation Analysis

According to a certain flight state of a plane-symmetry near space hypersonic vehicle, such as (α, β, φ) = (10^∘, 0^∘, 0^∘), obtain the corresponding characteristic model parameters range (Zhang and Hu, 2012). Let the flight height is 40 km, speed is 10 Ma, and the range of aerodynamic coefficient (Liu and Chen, 2010) be k_xx ∈ [−0.3585 −1.4341], k_xz ∈ [−0.0101 −0.0152], k_yy ∈ [−0.1060 −0.2945], k_zx ∈ [−0.0127 −0.0506], k_zz ∈ [−0.0253 −0.0380], k_xa ∈ [40.5909 34.3395], k_xr ∈ [3.1819 3.1729], k_ye ∈ [25.3225 22.7902], k_za ∈ [2.7196 2.2845], and k_zr ∈ [4.5363 4.1338].

Let the maximum of attitude angular velocity is ${\left|{\mathrm{\omega }}_x\right|}_{\max }={\left|{\mathrm{\omega }}_y\right|}_{\max }={\left|{\mathrm{\omega }}_z\right|}_{\max }={60}^{\circ }∕\text{s}$, the maximum of input control is 30^∘, sampling time is 0.01 s.

Angle of attack control channel

$\begin{array}{llll}\hfill & \mathrm{\alpha }\left(k+1\right)=f_{\mathrm{\alpha 1}}\mathrm{\alpha }\left(k\right)+f_{\mathrm{\alpha 2}}\mathrm{\alpha }\left(k-1\right)+g_1{\mathrm{\delta }}_{\mathrm{\alpha }}\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\alpha }}& \hfill & \\ \hfill & f_{\mathrm{\alpha 1}}\in \left[1.99682.0032\right],f_{\mathrm{\alpha 2}}\in \left[-1.0032-0.9968\right],g_1\in \left[2.27542.5363\right]\times {10}^{-3}.& \hfill & \end{array}$

Side slip angle control channel

$\begin{array}{llll}\hfill & \mathrm{\beta }\left(k+1\right)=f_{\mathrm{\beta 1}}\mathrm{\beta }\left(k\right)+f_{\mathrm{\beta 2}}\mathrm{\beta }\left(k-1\right)+g_2{\mathrm{\delta }}_{\mathrm{\beta }}\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\beta }}& \hfill & \\ \hfill & f_{\mathrm{\beta 1}}\in \left[1.99652.0035\right],f_{\mathrm{\beta 2}}\in \left[-1.0035-0.9965\right],g_2\in \left[3.37604.0577\right]\times {10}^{-4}.& \hfill & \end{array}$

Roll angle control channel

$\begin{array}{llll}\hfill & \mathrm{\phi }\left(k+1\right)=f_{\mathrm{\phi 1}}\mathrm{\phi }\left(k\right)+f_{\mathrm{\phi 2}}\mathrm{\alpha }\left(k-1\right)+g_3{\mathrm{\delta }}_{\mathrm{\phi }}\left(k\right)+{\mathrm{\Delta }}_{\mathrm{\phi }}& \hfill & \\ \hfill & f_{t1}\in \left[1.98232.0181\right],f_{t2}\in \left[-1.0181-0.9823\right],g_3\in \left[3.30554.1957\right]\times {10}^{-3}.& \hfill & \end{array}$

The requirement of the control system is to keep side slip angle around 0^∘, the tracking accuracy of attack angle <0.5^∘, simulation is taken based on the parameters above.

(1) Attack-angle tracking without coupling characteristic model disturbance

Assume the identified parameter is $A=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill \text{1.9968}\hfill & \hfill -\text{1.0032}\hfill \end{array}\right]$, the initial value is 5^∘, and the expected value of attack angle is 2^∘, the coupling characteristic model disturbance Δ_α is 0. The weighting matrices in the robust predictive control are Q₁ = diag(1,000, 1,000, 1,000) and R = 10. The simulation results are as follows: the tracking curve of attack angle is shown in Figure 2. The predictive control and gray identification guarantee the attack-angle tracking accuracy. The input and angular velocity constraints are shown in Figures 3 and 4, which meet the constraints, respectively. The results show that the prediction based on the characteristics model is feasible.

(2) Attack-angle tracking with coupling characteristic model disturbance

FIGURE 2

Figure 2. Tracking attack angle.

FIGURE 3

Figure 3. Control input.

FIGURE 4

Figure 4. Angular velocity.

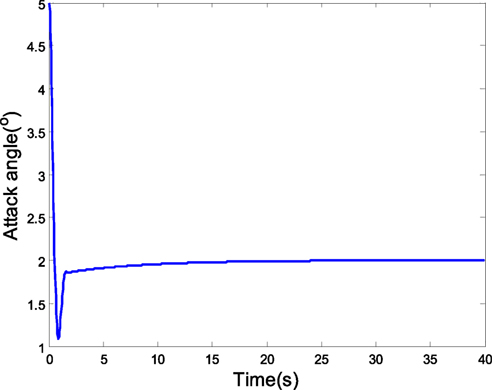
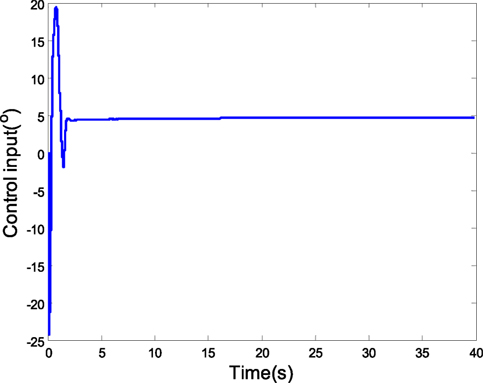
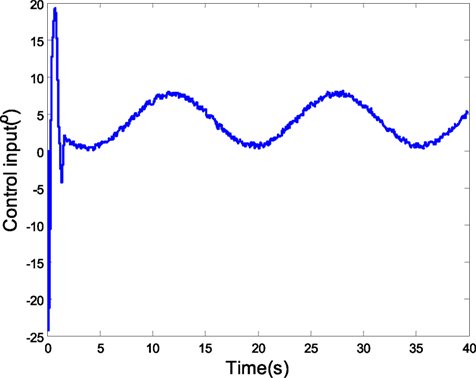
Assume the identified parameter is $A=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill \text{1.9968}\hfill & \hfill -\text{1.0032}\hfill \end{array}\right]$, the initial value is 5^∘, and the expected value of attack angle is 2^∘, the coupling characteristic model disturbance is Δ_α = m₁₁β(k) + m₁₂ϕ(k) + Δ_α1(k) is 1^∘*sin(0.2t). The weighting matrices in the robust predictive control are Q₁ = diag(1,000, 1,000, 1,000) and R = 10. The simulation results are as follows: the tracking curve of attack angle is shown in Figure 5. The predictive control and gray estimation compensation resist the disturbances of the characteristic model and model uncertainties. Figure 6 presents the input, from which we can see the constraint are satisfied.

(3) Attack-angle tracking with random noise and time-varying disturbance

FIGURE 5

Figure 5. Tracking attack angle.

FIGURE 6

Figure 6. Control input.

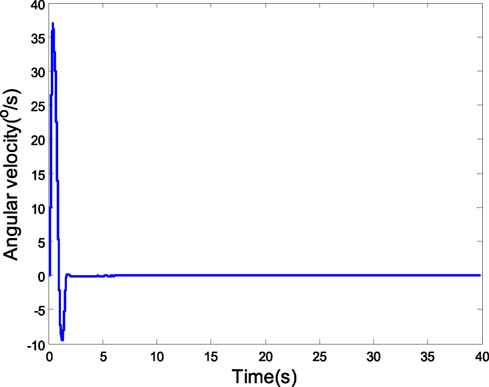
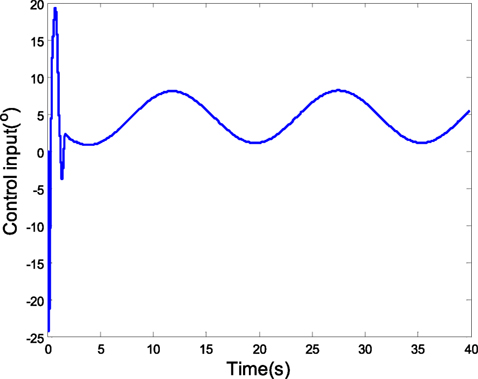
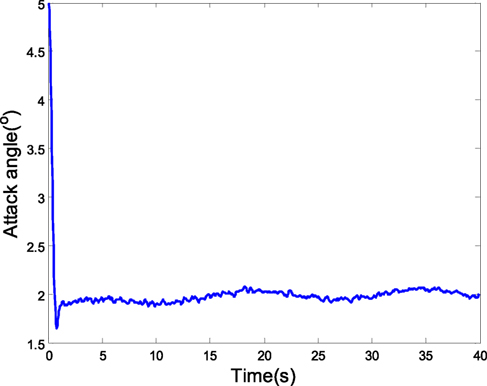
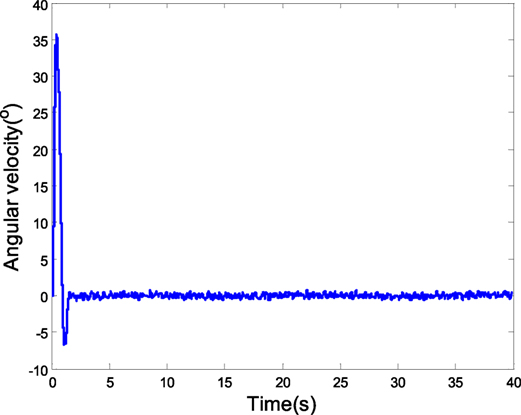
Assume the attack-angle initial value is 5^∘, and the expected value is 2^∘. The coupling characteristic model disturbance is Δ_α = m₁₁β(k) + m₂₁ϕ(k) + Δ_α1(k) is 1^∘*sin(0.2t) in the sinusoidal change form 1^∘*sin(0.2t). The attack angle is of 0 mean. In the case of the random state noise with the variance of 0.1, the characteristic model parameter of the attack angle $A=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1.89\hfill & \hfill -\text{0.976}\hfill \end{array}\right],g_1=2.367\times {10}^{-3}$ is obtained using the gray identification. Then, the robust MPC is adopted in the simulation. Figure 7 is the tracking curve of attack angle, which presents that the disturbance and model uncertainty in the characteristic model are resisted with the common effects of H₂/H_∞ predictive control and gray estimation compensation. Figures 8 and 9 are the curves of rudder input and angular velocity, respectively, showing the satisfaction of input and output constraints with LMIs (Eqs 29–31).

(4) Robustness analysis

FIGURE 7

Figure 7. Tracking attack angle.

FIGURE 8

Figure 8. Control input.

FIGURE 9

Figure 9. Angular velocity.

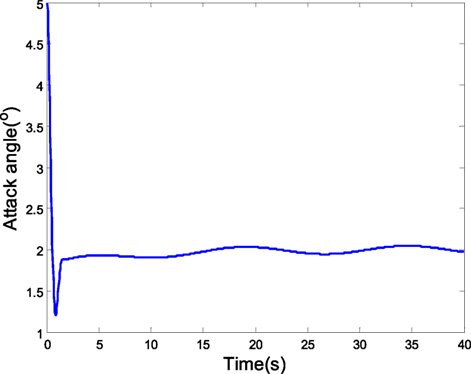
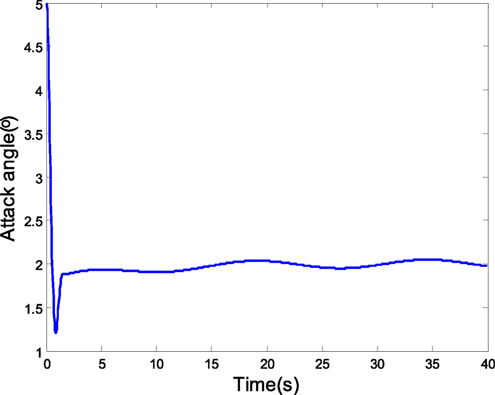
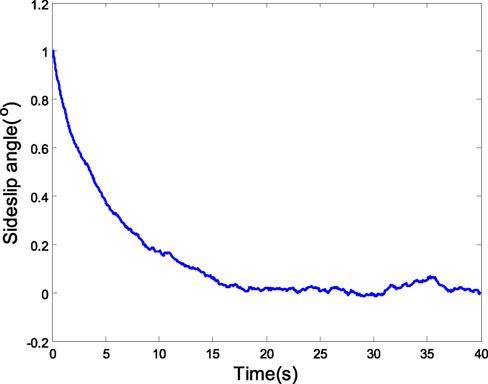
If the identified parameters model parameter is A = [0 1; 2 −1], but the actual model parameter is A = [0 1; 1.9968 −1.0032], and the coupling characteristic model disturbance is Δ_α = m₁₁β(k) + m₁₂ϕ(k) + Δ_α1(k) is 1^∘*sin(0.2t), the tracking curve of attack angle is shown in Figure 10, which can show the good tracking performance. The side slip angle keeps near the 0 according to the curve of side slip angle shown in Figure 11. The results show that the robust predictive control has the strong robust tracking ability.

FIGURE 10

Figure 10. Tracking attack angle.

FIGURE 11

Figure 11. Tacking side slip angle.

Conclusion

To design control for constrained, strong coupled, uncertain non-linear reentry hypersonic vehicles, the characteristic model is constructed and used as the predictive model in MPC. The original complicated reentry kinetics and dynamics are simplified by identification of the time-varying parameters in the characteristic model-based gray identification. The robust predictive control law is proposed based on the receding moving horizon optimization and LMI, which ensures stability of the closed-loop system and guarantees constraints satisfaction. Theoretical proof and simulation results confirm the effectiveness of the proposed algorithm.

Author Contributions

YP proposed the main idea. JZ and TS derived the controller and carried out simulations. JZ, TS, and YP wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors gratefully acknowledge the reviewers for their constructive and insightful comments for further improve the quality of this work.

Funding

This work was supported by the National Natural Science Foundation of China (No. 51379044, No. 51375210, No. 61503158, and No. 51375307).

References

Alicia, Z., and Andrea, S. (2009). “Combined reference governor and anti-windup design for constrained hypersonic vehicles models,” in AIAA (New York, NY: American Institute of Aeronautics and Astronautics), 2009–6283.

Google Scholar

Chiristopher, P., Morgan, B., and Ilya, K. (2013). “Model predictive control guidance with extended command governor inner-loop flight control for hypersonic vehicles,” in Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit (New York, NY: American Institute of Aeronautics and Astronautics), 5028–5048.

Google Scholar

Gong, Y. L., and Wu, H. X. (2010). Characteristic model-based adaptive attitude control for hypersonic vehicle. J. Astronaut. 31, 2122–2128. doi: 10.3873/j.issn.1000.1328

CrossRef Full Text | Google Scholar

Harpold, J. (1979). Shuttle entry guidance. J. Astronaut. Sci. 28, 239–268.

Google Scholar

Jiang, W., Wang, H. L., Lu, J. H., Qin, W. W., and Cai, G. B. (2017). Nonfragile robust model predictive control for uncertain constrained time-delayed system with compensations. J Franklin. Inst. 354, 2832–2855. doi:10.1016/j.jfranklin.2017.02.001

CrossRef Full Text | Google Scholar

Korhare, M. V., Balakrishnans, V., and Moraris, M. (1996). Robust constrained model predictive control using linear matrix inequalities. Auromotica 32, 1361–1379.

Google Scholar

Li, Z. Y., Zhou, W. J., and Liu, H. (2016). Nonlinear robust control of hypersonic aircrafts with interactions between flight dynamics and propulsion systems. ISA Trans. 64, 1–11. doi:10.1016/j.isatra.2016.04.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., and Chen, R. W. (2010). Modeling algorithm using accumulated generating operation and weighted product. Syst. Eng. Electron. 32, 976–979. doi:10.3969/j.issn.1001-506X

CrossRef Full Text | Google Scholar

Lu, P. (1999). Regulation about time-varying trajectories: precision entry guidance illustrated. J. Guid. Control Dyn. 22, 784–790. doi:10.2514/2.4479

CrossRef Full Text | Google Scholar

Lu, P. (2014). Entry Guidance: a unified method. J. Guid. Control Dyn. 37, 713–728. doi:10.2514/1.62605

CrossRef Full Text | Google Scholar

Patience, E., and Orukpe, I. M. (2007). “Model predictive control based on mixed H₂/H_∞control approach,” in Proc of the 2007 American Control Conf (New York, NY: IEEE Computer Society), 6147–6150.

Google Scholar

Qin, W. W., He, B., Liu, G., and Zhao, P. T. (2016). Robust model predictive tracking control of hypersonic vehicles in the presence of actuator constraints and input delays. J. Franklin Inst. 353, 4351–4367. doi:10.1016/j.jfranklin.2016.08.007

CrossRef Full Text | Google Scholar

Shen, Z. J., and Lu, P. (2003). On board generation of three-dimensional constrained entry trajectories. J. Guid. Control Dyn. 26, 111–121. doi:10.2514/2.5021

CrossRef Full Text | Google Scholar

Van, W. R. (2006). Combined feedback linearization and constrained model predictive control for entry flight. J. Guid. Control Dyn. 29, 427–434. doi:10.2514/1.14511

CrossRef Full Text | Google Scholar

Wu, G. H., and Meng, X. Y. (2016). Nonlinear disturbance observer based robust backstepping control for a flexible air-breathing hypersonic vehicle. Aerosp. Sci. Technol. 54, 174–182. doi:10.1016/j.ast.2016.04.018

CrossRef Full Text | Google Scholar

Wu, H., and Meng, B. (2009). Review of the control research of hypersonic vehicle. Adv. Mech. 39, 756–765. doi:10.3321/j.issn:1000-0992

CrossRef Full Text | Google Scholar

Wu, H. X., Hu, J., and Xie, Y. C. (2007). Characteristic model-based all-coefficient adaptive control method and its applications. IEEE Trans. Syst. Man Cybern. Syst. 37, 213–221. doi:10.1109/TSMCC.2006.887004

CrossRef Full Text | Google Scholar

Wu, H. X., Hu, J., and Xie, Y. C. (2009). Characteristic Model-Based Intelligent Adaptive Control. Beijing: China Science and Technology Publishing.

Google Scholar

Xu, B., Sun, F., Liu, H., and Ren, J. (2012). Adaptive Kriging controller design for hypersonic flight vehicle via back-stepping. IET Control Theory Appl. 4, 487–497. doi:10.1049/iet-cta.2011.0026

CrossRef Full Text | Google Scholar

Xu, L. J. (2012). Hypersonic vehicle control based on the all-channel-coupled characteristic model. Aerosp. Control Appl. 38, 12–18. doi:10.3969/j.issn.1674-1579

CrossRef Full Text | Google Scholar

Zhang, J., and Sun, T. (2016). Disturbance observer-based sliding manifold predictive control for reentry hypersonic vehicles with multi-constraint. Proc. Inst. Mech. Eng. 230, 485–495. doi:10.1177/0954410015593564

CrossRef Full Text | Google Scholar

Zhang, Z., and Hu, J. (2012). Stability analysis of a hypersonic vehicle controlled by the characteristic model based adaptive controller. Sci. China Inf. Sci. 55, 2243–2256. doi:10.1007/s11432-011-4455-9

CrossRef Full Text | Google Scholar