Evolutionary Policy Transfer and Search Methods for Boosting Behavior Quality: RoboCup Keep-Away Case Study

1. Introduction

Recent work in Evolutionary Robotics (ER) (Doncieux et al., 2015) has provided increasing empirical evidence that maintaining diversity in phenotypes (robot behaviors) improves the quality (task performance) of evolved behaviors (Mouret and Doncieux, 2012; Cully et al., 2015; Cully and Mouret, 2016; Gomes et al., 2016). Specifically, replacing objective search with the search for behavioral diversity in controller evolution (Moriguchi and Honiden, 2010; Mouret and Doncieux, 2012; Lehman et al., 2013; Gomes et al., 2015) has been demonstrated to boost the quality of evolved behaviors across a range of simulated (Lehman and Stanley, 2011a; Mouret and Doncieux, 2012; Gomes et al., 2016) and physical (Cully et al., 2015; Cully and Mouret, 2016) ER tasks.

In controller design in the field of ER, there has been an increasing research and empirical data indicating that non-objective evolutionary search, such as novelty search (Lehman and Stanley, 2011a) and other behavioral diversity maintenance approaches (Mouret and Doncieux, 2012), out-perform objective-based search in various evolutionary robotic control tasks defined by complex, high dimensional, and deceptive fitness landscapes (Cully et al., 2015; Cully and Mouret, 2016; Gomes et al., 2016). However, current empirical data indicate that for controller evolution to solve complex collective behavior tasks, then neither objective nor non-objective-based search performs well (evolves high-quality behaviors). Rather, recent research results indicate that hybridizing these two search approaches facilitates the evolution of the high-quality behaviors (Gomes and Christensen, 2013b; Gomes et al., 2013, 2015).

Furthermore, related work intersecting the fields of evolutionary controller design and policy (behavior) transfer¹ indicate that coupling evolutionary search with the transfer of behaviors between tasks of increasing complexity is an effective means to boost evolved behavior quality for a broad range of tasks (Whiteson and Stone, 2006; Taylor et al., 2010; Verbancsics and Stanley, 2010; Didi and Nitschke, 2016a). Policy transfer is a method that aims to improve learning by leveraging knowledge from learning in related but simpler tasks (Pan and Yang, 2010). Policy transfer reuses learned information across tasks, where information is shared between source and target tasks, and used as a starting point for learning new behaviors in target tasks. Transferring knowledge learned on a source task accelerates learning and increases solution quality in target tasks by exploiting relevant prior knowledge.

While the benefits of non-objective (behavioral and genotypic diversity maintenance) and hybrid (Gomes et al., 2015) evolutionary search (Mouret and Doncieux, 2012) and policy transfer (Taylor and Stone, 2009) methods have been separately demonstrated for increasing behavioral quality in various tasks, the impact (on behavior quality) of using non-objective and hybrid evolutionary search in the context of policy transfer remains unknown. Given previous work elucidating the efficacy of hybrid evolutionary search (Gomes and Christensen, 2013b; Gomes et al., 2013, 2015) and policy transfer (Taylor et al., 2006; Verbancsics and Stanley, 2010; Didi and Nitschke, 2016b) in collective behavior tasks the following hypothesis forms the research focus of this study.

Hybridized novelty and objective-based evolutionary search used in company with policy transfer across increasingly complex collective behavior tasks, results in significantly higher behavior quality compared to other evolutionary search methods.

In this study, the evolutionary search method is Hyper-Neuro-Evolution for Augmenting Topologies (HyperNEAT) (Stanley et al., 2009), the task domain is RoboCup keep-away, and five evolutionary search variants are integrated into HyperNEAT to direct its behavior evolution process. These variants are a fitness function (objective-based search), behavioral diversity maintenance (novelty search), genotypic diversity maintenance (Section 3), and both genotypic and behavioral diversity maintenance hybridized with objective-based search. RoboCup keep-away was selected as it is a well-established multiagent (robot) experimental platform (Taylor et al., 2010).

This study thus evaluates various evolutionary search methods coupled with policy transfer as a means to increase the quality of evolved collective (keep-away) behaviors. A key contribution of this research is a comprehensive empirical study demonstrating that coupling policy transfer with hybrid evolutionary search (combining novelty- and objective-based search) is the most effective method for boosting evolved solution quality across increasingly complex keep-away tasks.

Results indicate that this hybrid evolutionary search coupled with policy transfer effectively addresses the bootstrapping problem (Mouret and Doncieux, 2009a) for tested tasks, in that evolved behavior quality is significantly higher compared to other methods (without policy transfer and not using hybrid evolutionary search). Behavior quality is measured by evolved behavior effectiveness and efficiency, where effectiveness is the increase in average task performance given policy transfer and task performance is the average time for which the ball is under keeper-team control. Efficiency is the average number of generations taken by evolving transferred behaviors to reach a minimum task performance threshold given policy transfer. Results analysis indicates this to be a product of the interaction between the search space exploration capacity of novelty search and the search space exploitation capacity of objective-based search. As a further result of the hybrid method’s capacity to appropriately balance exploration versus exploitation during evolutionary search, evolved controllers were topologically simple and did not contain unnecessary complexity that hindered high-behavioral quality.

Furthermore, results indicate that as task complexity increases novelty search performs increasingly poorly compared to other evolutionary search methods. This suggests that novelty search may not be an appropriate method for behavior evolution in complex collective behavior tasks such as RoboCup keep-away.

2. Related Work

In line with this study’s research focus, this section overviews relevant literature in behavioral and genotypic diversity maintenance as a means to direct evolutionary search as well as evolutionary policy transfer, with a focus on collective behavior evolution.

2.1. Behavioral and Genotypic Diversity Maintenance

Recent work in Evolutionary Robotics (ER) (Doncieux et al., 2015) has provided increasing empirical evidence that maintaining diversity in genotypes (robot controller encodings) and phenotypes (robot behaviors) improves the quality (task performance) of evolved behaviors in a range of tasks (Mouret and Doncieux, 2012; Cully et al., 2015; Cully and Mouret, 2016; Gomes et al., 2016).

Encouraging behavioral diversity has received significant research attention in ER studies that using evolutionary controller design. Behavioral diversity maintenance has been successfully applied to direct neuroevolution processes, discover novel solutions, and increase solution performance to out-perform fitness function-based controller evolution approaches in a wide range of ER tasks (Mouret and Doncieux, 2012). Replacing objective-based search (the evolutionary algorithm’s fitness function) with the search for behavioral diversity during the controller evolution process (Moriguchi and Honiden, 2010; Mouret and Doncieux, 2012; Lehman et al., 2013; Gomes et al., 2015) has been demonstrated to boost the quality of evolved behaviors across a range of simulated (Lehman and Stanley, 2011a; Mouret and Doncieux, 2012; Gomes et al., 2016) and physical (Cully et al., 2015; Cully and Mouret, 2016) robotic tasks.

Novelty search (NS) (Lehman and Stanley, 2011a) is special case of behavioral diversity maintenance (Mouret and Doncieux, 2009a,b) and has become a popular method for directing evolutionary search and boosting solution (evolved behavior) quality in a range of applications (Lehman and Stanley, 2010a; Gomes et al., 2013; Hodjat et al., 2016). Whereas behavioral diversity maintenance selects for behavioral diversity with respect to the current population (of evolved) behaviors, NS selects for the most diverse (novel) behaviors with respect to an archive of current novel behaviors (Mouret and Doncieux, 2012; Doncieux and Mouret, 2014).

That is, NS is based on the notion of behavioral diversity maintenance where a search for novel phenotypes (behaviors) replaces the fitness function traditionally used to direct evolutionary search (Eiben and Smith, 2003). Thus, a genotype is more likely to be selected for reproduction if its encoded behavior is sufficiently different from all other behaviors produced thus far in an evolutionary run. Previous work has indicated that controllers evolved with NS function in a range of tasks of varying complexity (Velez and Clune, 2014) and such controllers consistently out-performed controllers evolved with objective-based search in a range of ER tasks (Mouret and Doncieux, 2012; Gomes et al., 2015, 2016). However, related research suggests that for complex tasks such as collective behavior tasks associated with swarm robotics (Duarte et al., 2016) (defined by high dimensional, rugged, discontinuous, and deceptive fitness landscapes (Eiben and Smith, 2003)), that evolutionary search hybridizing objectives (fitness functions) and NS tend to evolve effective high-quality solutions (behaviors) overall (Gomes and Christensen, 2013b; Gomes et al., 2013, 2015). For a comprehensive survey of behavioral diversity maintenance methods used in various ER studies, the reader is referred to the review of Doncieux and Mouret (2014).

Similarly, previous work has demonstrated the benefits of maintaining genotypic diversity as a means to boost the quality of evolved behaviors for various ER tasks (Floreano et al., 2008; Doncieux et al., 2011, 2015; Mouret and Doncieux, 2012). Genotype diversity maintenance is also a well-explored topic in more general evolutionary computation research (Brameier and Banzhaf, 2002; Ekárt and Németh, 2002; Crepinsek et al., 2013; Lehman et al., 2013; Mueller-Bady et al., 2016). For example, popular genotypic diversity maintenance methods include niching techniques such as fitness sharing and crowding (Sareni and Krahenbuhl, 2013), multi-objective optimization (Deb, 2001a), and multi-population models (Gomez and Miikkulainen, 1997). Such techniques are effective at maintaining genotypic diversity throughout an evolutionary process and at boosting solution quality on a broad range of multimodal, noisy, high-dimensional benchmark problems (Salah et al., 2016).

However, the impact of using genotypic diversity maintenance as a means to direct the evolutionary search process, i.e., selecting for novel genotypes instead of novel phenotypes, as is done for novelty search (Lehman and Stanley, 2011a), has received relatively little research attention (Didi and Nitschke, 2016a,b). It is important to note that dissimilar to previous ER studies where genotypic diversity maintenance has been used as a mechanism to encourage exploration of the search space by a fitness function (Floreano et al., 2008; Doncieux et al., 2011), this study employs a genotypic novelty search method (Section 3.5). That is, genotypic diversity maintenance drives the evolutionary search process meaning that novel genotypes are selected for, instead of novel behaviors (Lehman and Stanley, 2011a). To date, the impact of controller evolution in ER systems directed by genotypic novelty has not been studied and the genotypic diversity maintenance approach described in Section 3.5 thus constitutes one of this study’s contributions.

For an overview of genotypic diversity maintenance methods derived in evolutionary computation research (Eiben and Smith, 2003) and applied to ER studies, with insights from comparisons to behavioral diversity methods, the reader is referred to the review of Mouret and Doncieux (2012).

2.2. Evolutionary Policy Transfer

Policy (behavior) transfer, or transfer learning, is a method to speed-up and improve learning by leveraging knowledge from learning in related but simpler tasks. That is, learned information is reused and shared between a source and target tasks, where target tasks are used as a starting point for learning new behaviors (Pan and Yang, 2010). Policy transfer has been widely studied in the context of Reinforcement Learning (RL) methods (Sutton and Barto, 1998), where various studies have consistently demonstrated that transferring knowledge learned on a source task accelerates learning and increases solution quality in target tasks by exploiting relevant prior knowledge (Taylor and Stone, 2009).

Policy transfer used in company with various RL methods has been applied to boost solution quality in various single-agent tasks including pole-balancing (Ammar et al., 2012), game-playing (Ramon et al., 2007), robot navigation, as well as multiagent tasks including predator-prey (Boutsioukis et al., 2012). For such single and multiagent tasks, policy transfer is typically done within the same task domain for varying task complexity (Torrey and Shavlik, 2009) and less frequently between different task domains (Bou-Ammar et al., 2015). Recently, there has been work investigating the efficacy of using policy transfer in company with Evolutionary Algorithms (EAs) (Eiben and Smith, 2003) to boost evolved solution quality of evolved genotypes with various representations. For example, Doncieux (2014) used Neuro-Evolution (NE) (Floreano et al., 2008) to search for effective Artificial Neural Network (ANN) (Haykin, 1995) controllers in a simulated robot ball collecting task. This study investigated several methods for extracting behavioral features shared between varyingly complex versions of the task, where extracted features were used as stepping stones to shape rewards in the evolution of robot controllers transferred to more complex versions of the ball collecting task.

Moshaiov and Tal (2014) used Multi-Objective Evolutionary Algorithms (Deb, 2001b) to devise a method termed Family Bootstrapping to evolve groups of complementary ANN controllers for robot navigation tasks. These controllers were then used as an evolutionary starting point for controller evolution in navigation tasks with different objectives, where more effective navigation behaviors were evolved as a result. However, using NE to facilitate collective behavior transfer has received relatively little attention, with notable exceptions that include the following.

Verbancsics and Stanley (2010) used a variant of Hyper-Neuro-Evolution for Augmenting Topologies (HyperNEAT) (Stanley et al., 2009) called HyperNEAT Bird’s Eye View (BEV) that encoded the geometric relationships of task objects to facilitate the transfer of evolved behaviors. The authors demonstrated collective (keeper agent team) behavior transfer in a keep-away soccer (Stone et al., 2006a) task, elucidating that behaviors evolved in source tasks did not need to be adapted before being transferred to target tasks with varying agent numbers and field sizes. Furthermore, keeper-team behaviors evolved and transferred to increasingly complex keep-away tasks were found to be comparable in average task performance to keeper-team policies derived with RL methods and policy transfer (Stone et al., 2006b; Whiteson and Stone, 2006).

Verbancsics and Stanley (2010) also used HyperNEAT to demonstrate successful transfer of collective behaviors between Knight’s Joust, which is a multiagent predator-prey task variant (Taylor et al., 2010), and keep-away soccer tasks. The efficacy of this policy transfer method was supported by improved task performance on target tasks given further behavior evolution. This method was supported by prior work (Bahceci and Miikkulainen, 2008) that evolved behaviors of computer board-game playing agents, where indirectly encoded representations of evolved behaviors facilitated effective agent behavior transfer between games of increasing complexity (board size).

In related research, Taylor et al. (2006) used the Neuro-Evolution for Augmenting Topologies (NEAT) method (Stanley and Miikkulainen, 2002) to further evolve a population of ANN controllers already evolved for a source keep-away soccer task. The authors demonstrated that biasing and further evolving a fittest population of controllers for more complex versions of keep-away significantly decreased evolution time and achieved a solution quality that could not have been achieved had keep-away behaviors been evolved from scratch.

Subsequent work by Taylor et al. (2010) addressed the challenge of ensuring that a behavioral solution, derived in a source task could be meaningfully transferred to be a workable solution in a dissimilar and more complex target task. Hence, a mapping function is required so that learned behaviors are transferable between tasks with different states and state-action variables. Taylor et al. (2010) derived the inter-task mappings for policy search method to transfer populations of control policies (ANN controllers) between the keep-away soccer, knight’s joust, and server job scheduling (Whiteson and Stone, 2006) tasks. This method was successfully applied with manually coded inter-task mapping functions as well as mapping functions that were only partially available or learned before behavior transfer. Results indicated that learning time in target tasks was significantly reduced and transferred behaviors out-performed those that did not use policy transfer, that is, behaviors learned from scratch.

A common feature of these studies was the use of fitness functions (Eiben and Smith, 2003), or objective-based search to direct behavior evolution. That is, previous work has only demonstrated the efficacy of evolutionary policy transfer given objective-based search to direct controller evolution. While such studies elucidate the benefits of objective-based evolutionary search coupled with policy transfer for single-agent and relatively simple multiagent tasks, the impact of other (non-objective) evolutionary search methods such as phenotypic and genotypic diversity maintenance (Mouret and Doncieux, 2012) used in company with policy transfer remains unknown. This is especially the case for collective robotic systems that must accomplish complex collective behavior tasks.

That is, previous work has only tested single-agent tasks such as robot navigation (Moshaiov and Tal, 2014) and object collection (Doncieux, 2014) and simple multiagent tasks using few agents (Taylor et al., 2006; Verbancsics and Stanley, 2010), where non-objective evolutionary search methods were not considered. The following section thus overviews recent research in non-objective search (genotypic and phenotypic diversity maintenance) methods in the context of evolutionary controller design.

3. Methods

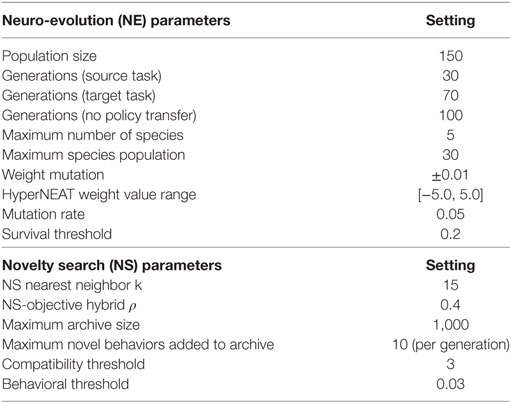
This study’s research objective was to investigate the impact of objective (Section 3.3) versus non-objective (Sections 3.4–3.5) based search to direct the NE process coupled with collective behavior transfer across increasingly complex keep-away tasks. Specifically, the evolutionary search process of HyperNEAT is driven by either objective-based search (a fitness function) (Eiben and Smith, 2003) or by non-objective-based search. The non-objective-based approaches investigated in this study are the search for behavioral (Lehman and Stanley, 2011a; Mouret and Doncieux, 2012) and genotypic (Brameier and Banzhaf, 2002; Ekárt and Németh, 2002; Lehman et al., 2013; Mueller-Bady et al., 2016; Salah et al., 2016) novelty, and hybrids of behavioral novelty search, genotypic novelty search, and objective-based search (Gomes et al., 2015). This study implements five variants of HyperNEAT, where each variant differs in terms of how neuroevolutionary search is directed. Table 1 presents the five variants of each method. These variants were selected to elucidate how policy transfer can be integrated into HyperNEAT to speed-up training and improve task performance in increasingly complex keep-away soccer tasks (Section 3.6).

TABLE 1

Table 1. HyperNEAT variants for evolving keep-away behavior in the source task.

The following sections briefly outline the heuristic taker controller, and the application of HyperNEAT to keeper-team controller evolution.

3.1. Taker-Team Heuristic Controller

Each taker agent executes the same fixed heuristic behavior for the duration of each simulation task trial. A taker agent is able to gain control of the ball by either intercepting the ball or tackling the keeper agent with the ball. In the former case, a taker moves to block the ball before it reaches it the receiving keeper. In the latter case, a taker gains control of the ball via the agent colliding with the keeper. In both cases, the simulation task trial ends and the time (as a portion of maximum task trial length) that the keepers had control of the ball is recorded for the purposes of calculating average keeper task performance at the end of the run (Table 3). Algorithm 1 formally describes the taker team controller.

ALGORITHM 1

Algorithm 1. Taker Team Heuristic Controller.

3.2. HyperNEAT: Hypercube-Based NEAT

Hypercube-based NEAT (HyperNEAT) (Stanley et al., 2009) is an indirect (generative) encoding neuroevolution method that extends NEAT (Stanley and Miikkulainen, 2002) and uses two networks, a Composite Pattern Producing Network (CPPN) (Stanley, 2007) and a substrate (ANN).

The CPPN is the generative encoding mechanism that indirectly maps evolved genotypes to ANNs and encodes pattern regularities, symmetries, and smoothness of the geometry of a given task in the form of the substrate. This mapping functions via having coordinates of each pair of nodes connected in the substrate fed to the CPPN as inputs. The CPPN outputs a value assigned as the synaptic weight of that connection and a value indicating whether that connection can be expressed or not. HyperNEAT uses the evolutionary process of NEAT to evolve the CPPN and determine ANN fitness values. The main benefit of HyperNEAT is scalability as it exploits task geometry and thus effectively represents complex solutions with minimal genotype structure (Stanley et al., 2009). This makes HyperNEAT an appropriate choice for evolving complex multiagent solutions (Verbancsics and Stanley, 2010; D’Ambrosio and Stanley, 2013).

HyperNEAT was selected as this study’s indirect encoding neuroevolution method since previous research indicated that transferring the connectivity patterns (Gauci and Stanley, 2008) of evolved behaviors is an effective way for facilitating transfer learning in multiagent tasks (Bahceci and Miikkulainen, 2008; Verbancsics and Stanley, 2010). That is, HyperNEAT evolved multiagent policies can be effectively transferred to increasingly complex tasks (Stone et al., 2006a) without further adaptation (Verbancsics and Stanley, 2010) and that transferred behaviors often yield comparable task performance to specially designed learning algorithms (Stone et al., 2006b).

HyperNEAT’s capability to evolve controllers that account for task geometry, symmetry, and regularity also makes it appropriate for deriving controllers that elicit behaviors robust to variations in state and action spaces (Risi and Stanley, 2013) and noisy, partially observable multiagent task environments (Metzen et al., 2008).

Previous work using evolutionary policy transfer in RoboCup keep-away (Verbancsics and Stanley, 2010; Didi and Nitschke, 2016a,b) demonstrated that HyperNEAT is an appropriate controller evolution method and evolves significantly higher quality behaviors compared to other NE methods such as NEAT (Stanley and Miikkulainen, 2002). Hence, HyperNEAT was selected for keep-away controller evolution in this study. Specifically, an extension to HyperNEAT called Birds Eye View HyperNEAT (HyperNEAT-BEV) (Verbancsics and Stanley, 2010) was for keep-away behavior evolution and to better facilitate behavior transfer from source to target keep-away tasks (Section 3.7).

3.2.1. HyperNEAT Keeper-Team Controller

The key feature of HyperNEAT evolved controllers is that HyperNEAT evolved a CPPN as the mapping function between each keeper agent’s sensory inputs and motor outputs. HyperNEAT evolved keeper teams were homogenous, meaning all keepers used the same ANN controller. The CPPN has five inputs, four coordinate inputs, and a bias node with a constant value of 1.0 (Figure 1B). The coordinates x1, y1, x2, and y2 are of two sampled nodes (node 1 and node 2). That is, the x, y coordinates of node 1 on the input of the substrate network and the x, y coordinates of node 2 on the output of the substrate network. The CPPN has two outputs, which are synaptic weight values assigned to the connection between node 1 and node 2, and a connection expression value, Link Expression Output (LEO) (Verbancsics and Stanley, 2011), which determines whether a connection can be created or not created.

FIGURE 1

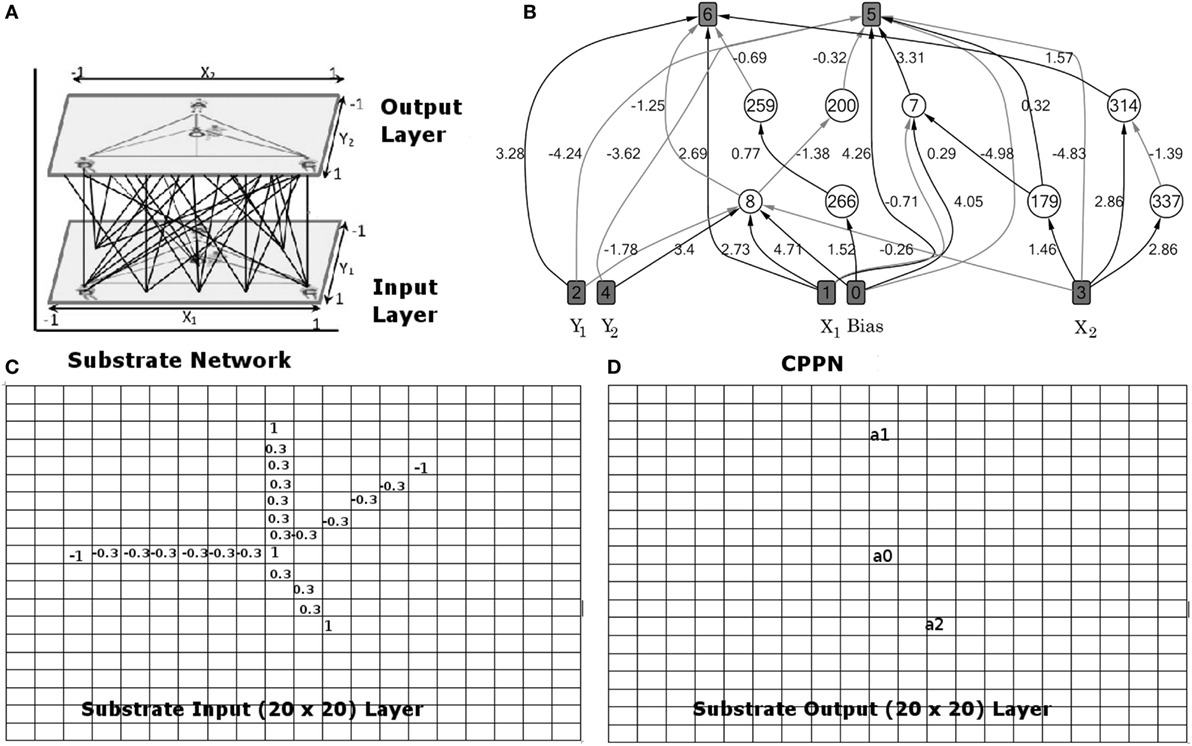
Figure 1. (A) Substrate network encoding virtual field (20 × 20 grid of inputs and outputs). (B) Connections from pairs of nodes in the substrate are sampled and the coordinates passed as inputs to the CPPN, which then outputs the synaptic weight (connecting input and output layers in the substrate). (C) Substrate input layer (20 × 20) corresponding to bottom layer in sub-figure (a). (D) Substrate output layer (20 × 20) corresponding to top layer in sub-figure (a). Note: this figure assumes 3vs2 keep-away, though any keep-away task is applicable. See text (Section 3.2.1) for explanation.

To implement HyperNEAT controller evolution, we use methods from previous work to represent the current keep-away task state, which includes the virtual field size, and the relative positions of the ball, taker, and keeper agents. Specifically, the keep-away state representation uses the Birds Eye View (BEV) extension to HyperNEAT (HyperNEAT-BEV) (Verbancsics and Stanley, 2010).

Given that HyperNEAT-BEV uses indirect encoding it can represent changes in task complexity without changing genotype representation (Verbancsics and Stanley, 2010). A 20 × 20 keep-away field was encoded on a two-dimensional substrate with 20 × 20 input layer and 20 × 20 output layer with coordinates in the x, y plane in the range of [−1.0, 1.0], where a 400 × 400 input-output vector yielded 160,000 possible connections. Each square of the field was represented by a node in the substrate network. A keeper’s position was marked with the value 1.0 and a taker with the value −1.0.

In task trial simulation, straight line paths were calculated from the keeper with the ball to all other agents. If the path intersected another keeper then this node to node connection was assigned a 0.3 value. If the path intersected a taker a −0.3 value was assigned to this node to node connection. Otherwise, a 0.0 was assigned if there was no agent in that grid square. Thus, the number of keepers was indicated by the number of squares having a 1.0 value.

Figure 1 presents an example of a HyperNEAT evolved CPPN (Figure 1B) coupled with its substrate network (Figure 1A). This substrate encodes the task environment state as a 20 × 20 grid of inputs and a grid of 20 × 20 outputs. Connections between input and output nodes had a value in the range: [−1.0, 1.0]. Connections from pairs of nodes in the substrate network are sampled and the coordinates passed as inputs to the CPPN, which then outputs the synaptic weight of each sampled connection (connections between the substrate input and output layers depicted in Figure 1A). The substrate input layer corresponds to the bottom layer in Figure 1A, where grid cells contain values: 1: Keeper, −1: Taker, −0.3: Cell between a keeper a ball and a taker, 0.3: Cell between a keeper with a ball and its teammates, or 0 (white space in grid). The substrate output layer corresponds to the top layer in Figure 1A, where a0, a1, and a2 represent activation values for three keepers. The keeper with the highest activation value receives a ball pass from the keeper with the ball. If the keeper with the ball has the highest activation value, then this keeper holds the ball. Note that Figure 1 is an example given 3vs2 keep-away, though any keep-away task is applicable. The CPPN input and output nodes used linear and bipolar functions, respectively, and the hidden layer nodes used the activation functions listed in Table 3.

3.3. Objective-Based Fitness Function

The OS variant of HyperNEAT (Table 1) uses a fitness function specifically designed to direct behavior evolution in the keep-away soccer task (Stone et al., 2006a).

3.3.1. OS Variant: Objective-Based Search

Objective-based search uses the following fitness function that computes mean episodic length using equation (1):

$fi{t}_x=\frac{1}{N}{\displaystyle \sum _{j=1}^N}{T}_j.$ (1)

The length of an episode x is denoted by T_x, and N is the number of task trials, T_j is the length of task trial j. Task trial time steps (iterations) are based on the RoboCup Soccer Server² discrete time cycles, where each iteration is 100 ms of simulation time. A task trial ends when the ball goes out of field of play or if an opponent (taker agent) gets possession of the ball (Section 3.1).

3.4. Evolutionary Search with Behavioral Diversity Maintenance

The NS and ONS variants of HyperNEAT (Table 1) incorporated behavioral diversity maintenance as a means to guide the evolutionary search processes. The NS variant uses only Novelty Search (Section 3.4.1), whereas the ONS variant uses a hybrid of NS and objective-based search (Section 3.4.2) to direct the search process.

Encouraging behavioral diversity is a well-studied concept in neuroevolution and has been used to discover novel solutions and increase solution performance to out-perform controller evolution approaches that encourage genotypic diversity in a wide range of tasks (Lehman and Stanley, 2010a; Mouret and Doncieux, 2012; Gomes and Christensen, 2013a; Urbano and Georgiou, 2013).

3.4.1. NS Variant: Novelty Search

Novelty search (NS) (Lehman and Stanley, 2011a) is based on the notion of behavioral diversity maintenance where a search for novel phenotypes (behaviors) replaces the fitness function of evolutionary search. That is, a genotype is more likely to be selected for reproduction if its encoded behavior is sufficiently different from all other behaviors produced thus far in an evolutionary run.

Previous work indicated that controllers evolved with NS functioned in a range of tasks of varying complexity (Velez and Clune, 2014) and such controllers consistently out-performed controllers evolved with objective-based search in a range of ER tasks (Mouret and Doncieux, 2012; Gomes et al., 2015, 2016).

Given this, NS was selected as the behavioral diversity mechanism to be applied as the second (NS) variant of HyperNEAT (Table 1). In this study, the function of NS is to consistently generate novel team (keep-away) behaviors. Hence, we define team behavior in terms of properties that potentially influence team behavior but are not directly used for task performance evaluation.

To measure behavioral novelty, we use the following three normalized task-specific behavioral vectors, where the addition of these vectors always sums in the range: [0, 1]:

1. Average number of passes;

2. Average dispersion of team members;

3. Average distance of the ball to the center of the field.

This team level behavioral characterization has been used previously (Gomes et al., 2014) and out-performs individual behavioral characterizations and fitness-based search. Behavioral distance is computed using the Euclidean distance (equation (2)):

${\delta }_i(x,y)=\mathrm{\parallel }{x}_i-y_{ij}\mathrm{\parallel }$ (2)

where, x_i and y_ij are normalized behavioral characterization vectors of two genotypes. The novelty is then quantified by equation (3):

$no{v}_x=\frac{1}{3k}{\displaystyle \sum _{i=1}^k}{\displaystyle \sum _{j=1}^3}{\delta }_x(x_j,y_{ij})$ (3)

where, δ_x is the behavioral distance between genotypes x and y (equation (2)), based on the behavioral characterization vector, where x_j is the jth behavior of genotype x, y_ij is the jth behavior property of the ith nearest neighbor of genotype x.

For the second variant, this novelty function (equation (3)) replaces the fitness function of HyperNEAT. The nov_x then is derived from the mean of behavioral distance of an individual with k nearest neighbors. The parameter k is specified by the experimenter to represent the number of nearest neighbors, where k = 15 has been widely used in novelty search experiments (Gomes et al., 2015). Some researchers have used k = 20 (Liapis et al., 2015) and k in the range of Bahceci and Miikkulainen (2008), Cuccu et al. (2011), and Gomes et al. (2015) though it is unclear if values were derived experimentally. Gomes et al. (2015) discovered that the choice of k value depends on the type of novelty archive used and that k = 15 yielded relatively good performance across all tested archive types. Hence, in this study, we use k = 15. As in related work (Lehman and Stanley, 2011a), the novelty of newly generated genotypes is calculated with respect to previously novel genotypes (behaviors) stored in the novelty archive, where archived behaviors are ranked by diversity. In this study the maximum archive size is 1,000, where a maximum of 10 novel behaviors are added to the archive each generation (Table 2).

TABLE 2

Table 2. Neuro-evolution (NE) and novelty search (NS) parameters and settings.

3.4.2. ONS Variant: Novelty-Objective Search Hybrid

A hybrid function combining non-objective-based search (NS) and objective-based search (fitness function) to drive the evolutionary process was selected as the next variant (ONS) of HyperNEAT (Table 1).

To elicit further performance gains and increase solution quality across a broad range of tasks, various researches have investigated such hybrid functions. For example, using a weighted balance between a fitness function and novelty metric to direct the search process (Cuccu et al., 2011), restarting converged evolutionary runs using novelty search (Cuccu et al., 2011), a minimal criteria (for survival and reproduction of controller behaviors) novelty search (Lehman and Stanley, 2010b), a progressive minimal criteria incrementing the requirements for reproduction throughout the evolutionary process (Gomes et al., 2012) and novelty search combined with speciation techniques (Inden et al., 2013), with the result of yielding optimal and near optimal solutions in various tasks including pole-balancing, maze solving, and quadruped gait evolution tasks.

Similarly, Lehman and Stanley (2010b) found that their minimal criteria novelty search evolved solutions more consistently than objective base search. Gomes et al. (2012) found that their progressive minimal criteria novelty metric out-performed pure NS in a swarm robotics task. However, it has also been found that an objective-based search can out-perform NS on the deceptive tartarus task (Cuccu et al., 2011) as well as pole-balancing and a visual discrimination task (Inden et al., 2013).

In line with previous research on hybrid NS and fitness metrics supporting performance gains in various tasks (Cuccu et al., 2011), including multi-robot ER tasks (Gomes et al., 2012), the ONS variant uses a behavioral diversity metric that linearly combines NS with the objective-based search (fitness functions) native to HyperNEAT. Thus, we use a linear combination of fitness and novelty scores (Gomes et al., 2014), specified in equation (4):

$scor{e}_i=\rho .\overline{fi{t}_i}+(1-\rho ).\overline{no{v}_i}$ (4)

where, $\overline{fi{t}_i}$ and $\overline{no{v}_i}$ are normalized fitness and novelty metric, respectively. Then, ρ ∈ [0,1] is a parameter selected by the experimenter to control the relative contribution of each metric to the selection pressure.

Previous work demonstrated that a medium to high novelty weight 50–80% on average yielded the most desirable results (Cuccu and Gomez, 2011; Gomes et al., 2012, 2013, 2014; Gomes and Christensen, 2013a). Similarly, exploratory experiments in this study found that a novelty weight of 40% (Table 2) yielded the best results. All other novelty search parameters are the same as used for NS variant (Section 3.4.1).

3.5. Evolutionary Search with Genotypic Diversity Maintenance

Previous work has demonstrated the benefits of maintaining genotypic diversity as a means to boost the quality of evolved behaviors for various ER tasks (Floreano et al., 2008; Doncieux et al., 2011) and has been well explored across a broad range of tasks in more general evolutionary computation research (Eiben and Smith, 2003). However, the impact of using genotypic diversity maintenance as a means to direct the evolutionary search process, that is, selecting for novel genotypes instead of phenotypes, as is done for novelty search (Lehman and Stanley, 2011a) has received relatively little research attention (Didi and Nitschke, 2016a,b).

The following describes the genotypic diversity methods used to direct evolutionary search processes of HyperNEAT, genotypic novelty search (Section 3.5.1), and a hybrid of objective-based search and genotypic novelty search (Section 3.5.2). One may note that these genotypic diversity maintenance approaches work in addition to the speciation mechanism of NEAT (Stanley and Miikkulainen, 2002) (also used by HyperNEAT) that encourages diversity and increased exploration of genotype search space.

3.5.1. GNS Variant: Genotypic Novelty Search

The next variant (GNS) uses genotypic diversity maintenance to drive the evolutionary search process (Table 1). That is, the GNS variant is non-objective-based search similar to NS (Section 3.4.1) except that a genotype diversity function is used instead of behavioral diversity, meaning that the evolutionary search process of HyperNEAT selects for novel genotypes.

The genotypic distance between two genotypes is measured using linear combination of Excess (E) and Disjoint (D) genes (Stanley and Miikkulainen, 2002), and a mean weight difference of matching genes (Risi et al., 2010) ($\overline{W}$ in equation (5)). Excess genes are those non-matching genes that are derived from one parent later than all the genes of the other parent genotype, whereas disjoint genes are any other non-matching genes from either of the two parent genotypes:

${\delta }_g(a,b)=\frac{c_{1}E}{N}+\frac{c_{2}D}{N}+c_3\overline{W}$ (5)

where, N is the number of genes in the longest genotype of the population, then coefficients c₁, c₂, and c₃ are parameters used to adjust the weighting of the three factors E, D, and $\overline{W}$, respectively. The sparseness (S_g) of genotype x in population evolution is computed by equation (6):

$S_g(x)=\frac{1}{k}{\displaystyle \sum _{i=1}^k}{\delta }_g(x,y_i)$ (6)

where, y_i is the i^th nearest neighbor of x, k is the number of nearest neighbors of x and δ_g is the compatibility distance measure (equation (6)).

In these experiments, we use the above measure of sparseness (equation (6)) with and without policy transfer to ascertain if genotypic diversity influences selection pressure toward good solutions in the search space. The same nearest neighbor and archive parameters are used for this genotypic diversity maintenance function as used for novelty search (Section 3.4.1).

3.5.2. OGN Variant: Hybrid Objective-Genotypic Novelty Search

The final variant (OGN) uses a combination of objective-based search and the GNS variant (Section 3.5.1) to direct the evolutionary search process (Table 1).

The OGN variant is a hybrid function that also uses equation (4), except that $\overline{no{v}_i}$ now represents the genotype diversity metric. Similarly, ρ ∈ [0, 1] controls the relative contribution of fitness versus genotypic diversity-directed search. We also found that a genotypic diversity weight of 40% yielded favorable results for this case study (Table 2).

However, in this case, equation (6) specifying the genotype population’s mean sparseness (normalized into the range [0, 1]) replaces the normalized novelty function value $\overline{no{v}_i}$ in equation (4). All other parameters are the same as used for the genotypic diversity maintenance-directed search.

3.6. Keep-Away Task Complexity

A key goal of this research is to evaluate various behavior evolution methods across tasks of increasing complexity (Section 1); hence, it is necessary to define complexity in the keep-away domain. Previous work indicated that keep-away task complexity increases with the number of taker and keeper agents (Whiteson et al., 2005; Stone et al., 2006a; Didi and Nitschke, 2016b). Complexity refers to task difficulty and thus the level of sophistication required by evolved behaviors to solve the task. Increasing the number of takers correlates with making successful passes between keeper agents more difficult. Similarly, more agents on the keeper team necessitates increased controller complexity for each keeper to appropriately process increased sensory input, as the keeper controllers must process many more possibilities for passing the ball versus advantageous field positions. Specifically, more keepers must be accounted for and given a fixed field size, the potential for interference between keepers also increases.

Consider, at each simulation iteration of TvsK keep-away (T and K denote the number of keepers and takers, respectively, where: T ≥ 2, K ≥ 1), each keeper must process the N × N virtual field space, accounting for I −1 keeper teammates, J takers, and the ball. Equation (7) specifies the calculation of keep-away task (x) complexity:

$Complexity(x)=\frac{T}{K}\ast OBJ$ (7)

where, T and K are the total number of taker and keeper agents, respectively. The ratio of taker to keeper agents is multiplied by the total number of dynamic objects (all keepers, takers, and the ball) on the field (OBJ). This is all sensory information each keeper must process to select an action at each simulation iteration. Given the range of keep-away tasks tested in this study (Table 1), OBJ was in the range: Brameier and Banzhaf (2002) and Cuccu and Gomez (2011). Complexity values were normalized to the range: [0, 1], where the minimum and maximum taker to keeper ratios were determined by the range of keep-away tasks tested. Table 4 presents the keep-away tasks ordered from least complex (4vs3) to most complex (6vs5) and corresponding task complexity values.

As with many collective behavior tasks, we consider keep-away to be complex, with an underlying fitness landscape that increases in complexity with the number of agents on the field. That is, as the number of agents increases, the amount of sensory information that must be processed into effective motor outputs increases. This is reflected by an increase in task dimensionality and complexity (ruggedness and modality (Eiben and Smith, 2003) of the fitness landscape) that makes the discovery of effective keep-away behaviors less probable for objective-based (exploitative) evolutionary search processes.

Dissimilar to previous tasks that have tested behavioral diversity maintenance methods (Lehman and Stanley, 2011a; Gomes et al., 2015), we consider the keep-away task to be non-deceptive. To establish that keep-away is non-deceptive, consider that keeper-team fitness is equated with the total time that the ball is under keeper-team control, where fitness is rewarded at the end of a simulation task trial (Section 3.3). That is, the nature of the keeper-away task and the fitness function negated the possibility of a deceptive case. For example, there was no possibility for a task instance where a keeper executed behaviors that were deleterious to team fitness, but would be an essential stepping stone to the eventual evolution of beneficial behaviors. That is, deceptive fitness landscapes³ are characterized by low fitness regions that are necessary stepping stones for an evolutionary process to reach desired high fitness regions (Lehman and Stanley, 2011a).

3.7. Collective Behavior (Policy) Transfer

For each of the five variants of HyperNEAT (Section 3.2), we first evolved keep-away behavior in the 3vs2 task and then transferred evolved behavior as a starting point for further evolution in more complex keep-away tasks. This section describes the method used for collective behavior policy transfer in this study’s experiments (Section 4).

As in related research, the Birds Eye View (BEV) extension to HyperNEAT (Verbancsics and Stanley, 2010) was used to facilitate evolved behavior transfer across increasingly complex tasks. That is, a key advantage of HyperNEAT-BEV is that geometric relationships encoded in evolved CPPNs are extrapolated for varying task environment complexity. For example, as the number of agents changes between keep-away tasks, the task complexity also changes (Section 3.6), though connectivity patterns encoded in evolved CPPNs have been demonstrated as readily transferable across different tasks (Verbancsics, 2011).

In preliminary parameter tuning experiments done in previous research (Didi and Nitschke, 2016b), several approaches for collective behavior policy transfer were tested, though the following approach was found to be the most effective for all HyperNEAT variants and all keep-away tasks tested in this study. Specifically, the entire evolved population was transferred from the source task (at the final generation of neuroevolution) and set as the initial population for keep-away behavior evolution in the target task. This approach was selected given its similarity to incremental learning (Gomez and Miikkulainen, 1997), which has been demonstrated as beneficial for evolving effective solutions to increasingly complex tasks.

This approach is presented in algorithm 2, where collective (keep-away) policy transfer takes place between the source task (3vs2 keep-away) and target tasks of differing complexities (Table 1). That is, the final HyperNEAT evolved population of CPPNs is copied as the initial population in the given target task, where varying behavioral complexity is encoded in the CPPN but the substrate network representation remains constant (Figure 1) during policy transfer.

ALGORITHM 2

Algorithm 2. Collective Behavior Policy Transfer.

4. Experiments

This study’s experiments evaluated the effectiveness and efficiency (Section 1) of five variants of HyperNEAT for evolving keep-away behavior in a source task (3vs2 Keep-Away) and then transferring evolved behaviors to progressively more complex target tasks. That is, 4vs3, 5vs3, 5vs4, 6vs4, and 6vs5 keep-away (Table 1).

4.1. Experiment Goals

Experiments were designed to address this study’s key objective (Section 1), to ascertain the most appropriate NE method for facilitating evolved collective behavior policy transfer to boost solution quality. High-quality solutions are those evolved behaviors yielding the highest average maximum task performance. In these experiments, RoboCup keep-away (Taylor et al., 2010) is the collective behavior case study, where we measure the effectiveness and efficiency of evolved keep-away behaviors across increasing complex keep-away tasks (Section 3.6).

Effectiveness is improved average task performance after behavior transfer between source and target tasks, where transferred keep-away behaviors are further evolved. Average task performance is measured as the total time for which the ball is under control of the keeper team, calculated as the maximum taken at the end of each run and averaged over all runs. Efficiency is the average number of generations taken by transferred behaviors to reach a task performance threshold. The task performance threshold for collective behavior policy transfer is the average maximum task performance (over 20 runs) of behaviors evolved in a given task without policy transfer (Table 3).

TABLE 3

Table 3. HyperNEAT CPPN functions, keep-away simulation parameters and settings.

TABLE 4

Table 4. Normalized task complexity calculated for each keep-away task.

4.2. Experiment Types

Non-policy transfer experiments were those in which keep-away behaviors were evolved in each of the target keep-away tasks for 100 generations using the five variants (Table 1) of HyperNEAT (Figure 2). That is, this is the case where no policy transfer took place and keep-away behaviors were evolved from scratch in all tasks. Policy transfer experiments were those where keep-away behaviors were first evolved in the source task for three keepers versus two takers (3vs2) on the 20 × 20 simulated keep-away field for 30 generations. Evolved behaviors were then transferred and further evolved in each target task (Table 1) for another 70 generations, where 70 generations was selected for consistency (number of generations in total) in the comparison between experiments with policy transfer and without policy transfer.

FIGURE 2

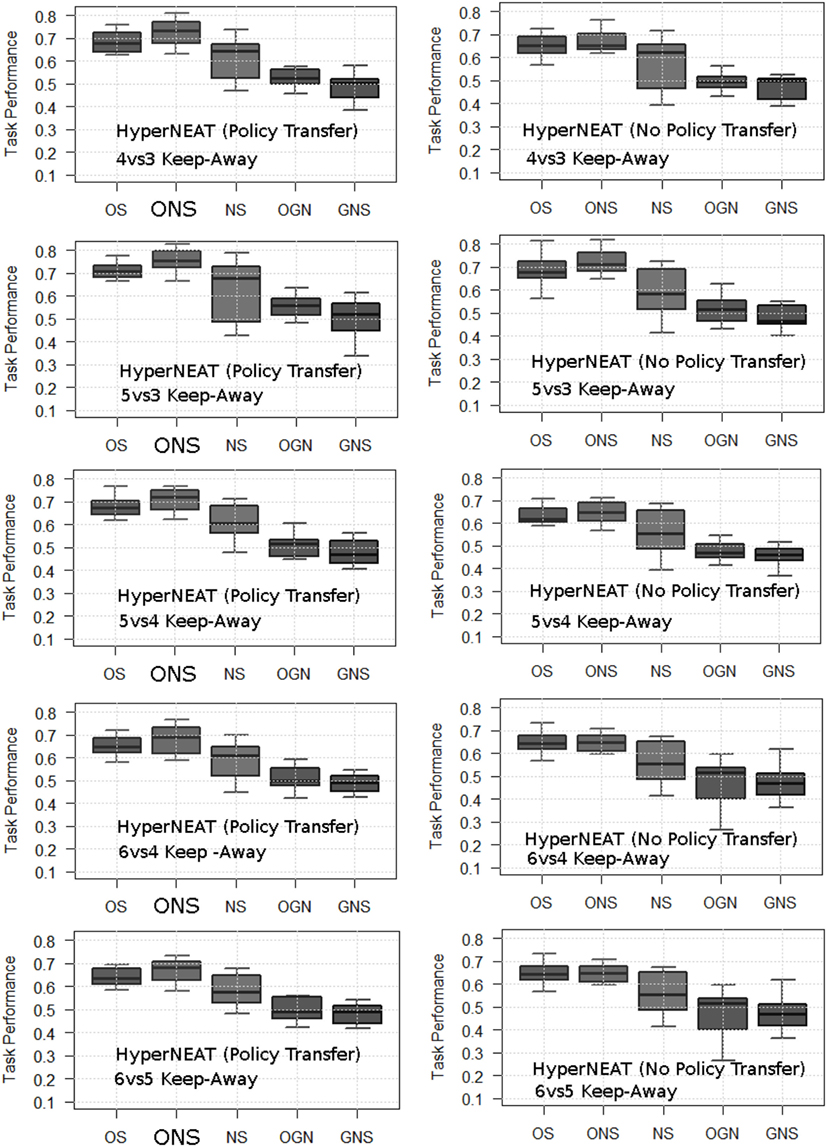
Figure 2. Average normalized maximum task performance for HyperNEAT variants with (left column) and without (right column) policy transfer in each target task. OS, objective-based; NS, Novelty Search; ONS, Objective-Novelty hybrid; GNS, Genotypic novelty search; OGN, Objective-GNS hybrid. Averages are over 20 runs. Bold ONS indicates that the ONS variant yields a higher average task performance (with statistical significance, Mann–Whitney U test, p < 0.05) for all tasks (given policy transfer). This significant difference holds for ONS over other variants (with policy transfer) and between ONS (with policy transfer) and all variants (without policy transfer).

4.3. Collective (Keep-Away) Behavior Evaluation

For both policy transfer and non-policy transfer experiments, average fitness per genotype (keep-away team) was calculated over 30 task trials per generation, where the maximum fitness was selected after 100 generations and an average maximum was calculated over 20 runs. Each task trial tested different (random) agent positions and the ball always started in the possession of a randomly selected keeper agent.

Figure 2 presents the average maximum task performance of each HyperNEAT variant, respectively, in each target task. To highlight the benefits of using HyperNEAT to facilitate (keep-away behavior) policy transfer, average task performance results of non-policy transfer experiments are included for each task.

Table 5 presents the average method efficiency of each HyperNEAT variant in each target task. Task performance efficiency results from experiments that do not use policy transfer are included to further highlight the benefits of using HyperNEAT to facilitate policy transfer.

TABLE 5

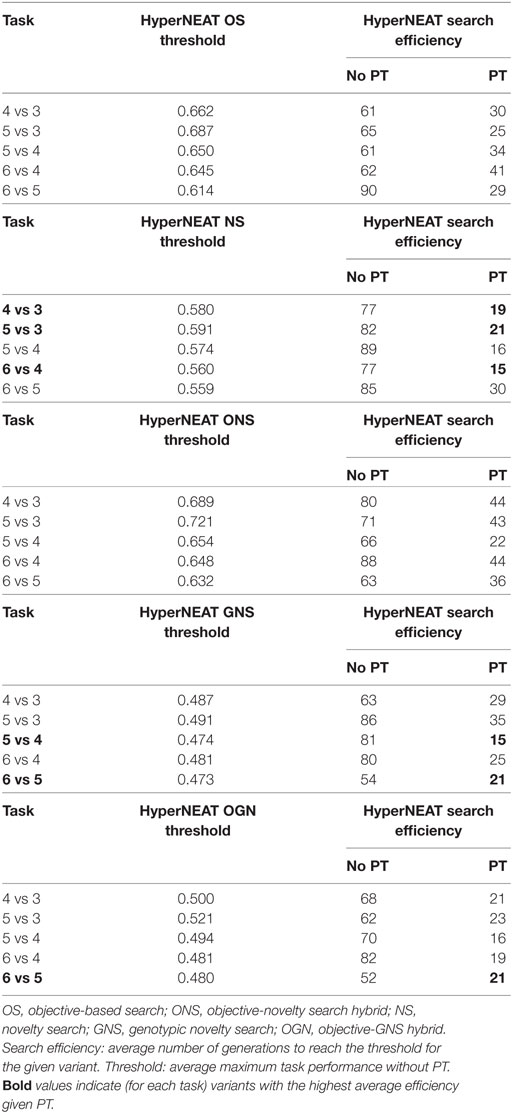
Table 5. HyperNEAT variant efficiency comparison with policy transfer (PT) and no policy transfer (No PT).

5. Results

To address this study’s research objective (Section 1) and investigate the impact of objective (Section 3.3) versus non-objective (Sections 3.4–3.5) based search on the evolution of collective behaviors transferred to increasingly complex keep-away tasks, we present results demonstrating comparative method effectiveness and efficiency.

Effectiveness was improved average task performance after behavior transfer between source and target tasks, where transferred keep-away behaviors are further evolved for 100 generations (Table 2). In this case study, task performance was a measure of a keep-away team’s capability to control the ball and keep it from taker agents. That is, task performance was calculated as the total time for which the keeper team had the ball in their possession, normalized into the range: [0, 1] and averaged over all runs. Normalization was done with respect to the average maximum episode length (Table 3), calculated for all methods applied to each task.

Efficiency was the average number of generations taken by transferred behaviors to reach a task performance threshold. The task performance threshold for collective behavior policy transfer⁴ is the average maximum task performance (over 20 runs) of behaviors evolved in a given task without policy transfer (Table 3).

5.1. Average Task Performance Comparison

Figure 2 presents the average maximum task performance (normalized to the range: [0.0, 1.0]) for the HyperNEAT variants (Table 1), respectively. Comparative box-plots are presented for all keep-away tasks with policy transfer (Figure 2, left column) and without policy transfer (Figure 2, right column).

Results data were found to be non-parametric using the Kolmogorov–Smirnov normality test with Lilliefors correction (Ghasemi and Zahediasl, 2012). Mann–Whitney U statistical tests (p < 0.05) (Flannery et al., 1986) were then applied in pair-wise comparisons between average task performance results yielded by the HyperNEAT variants in each keep-away task (Table 1). Statistical tests were applied in pair-wise comparisons, with Effect Size (Cohen, 1988) treatment, between average task performance results in the following cases, where complete overview of all statistical tests is in Appendix A in Supplementary Material.

First, comparisons between average task performance results yielded by all method variants with and without policy transfer. That is, for each task, the average task performance of each variant of HyperNEAT given policy transfer was compared with each variant without policy transfer. Section 5.1.1 outlines all such comparisons and the results of statistical tests. Second, average task performance comparisons between all method variants in each keep-away task where only results given policy transfer were considered. Section 5.1.2 outlines all such comparisons and the results of statistical tests.

5.1.1. Task Performance Comparison: Policy versus No Policy Transfer

Statistical tests were applied in pair-wise comparisons between average task performances yielded by each HyperNEAT variant with policy transfer and without policy transfer, indicating that, for all keep-away tasks, variants with policy transfer yielded a significantly⁵ higher average task performance. Exceptions where there was no significant difference between the average task performance of method variants are outlined in Appendix A in Supplementary Material.

5.1.2. Task Performance Comparison: Given Policy Transfer

To evaluate the efficacy of HyperNEAT variants in each target task given policy transfer, pair-wise statistical comparisons were applied between all method variants for each task. That is, where keep-away behavior had been further evolved by a given HyperNEAT variant after policy transfer. Comparisons of average task performance results for all variants given policy transfer, indicated that for all tasks, the ONS variant, given policy transfer yielded a significantly higher average task performance compared to the other HyperNEAT variants. Exceptions that resulted in no statistically significant difference in average task performance between pairs of HyperNEAT variants are outlined in Appendix A in Supplementary Material.

5.2. Average Method Efficiency Comparison

The next set of statistical comparisons was between all method variants with respect to method efficiency (Table 5). Specifically, statistical tests were applied in pair-wise comparisons between average method efficiency results in the following cases.

First, we compared average efficiency results of all method variants with and without policy transfer in each task (PT and No PT in Table 5, respectively). That is, for each task, the average HyperNEAT efficiency for each variant with policy transfer was compared to each variant without policy transfer. Section 5.2.1 describes these comparisons and statistical test results. Second, we compared average efficiency results between all method variants given policy transfer in each task. Section 5.2.2 presents these comparisons and the results of statistical tests.

Method efficiency was measured as the number of generations taken by HyperNEAT variants to attain a given task performance threshold in each target task. This threshold was the average maximum task performance (calculated over 20 runs) without policy transfer for a given method and task. When comparing average efficiency between methods with and without policy transfer, for method variants without policy transfer we simply used the task performance threshold itself for the comparison. That is, the average number of generations taken to reach the average maximum task performance, for a given method in a given task, without policy transfer, was compared to the average number of generations taken to reach the same threshold for a method using policy transfer in the same task.

5.2.1. Efficiency Comparison: Policy Transfer versus No Policy Transfer

Statistical tests indicated that for all tasks, a significantly higher efficiency was observed for all HyperNEAT variants, given policy transfer compared to the same method variants without policy transfer. Exceptions where there was no significant difference are outlined in Appendix A in Supplementary Material.

5.2.2. Efficiency Comparison: Given Policy Transfer

As with task performance comparisons (Sections 5.1.1 and 5.1.2), statistical tests indicated that given policy transfer, on average for all tasks, the OGN variant of HyperNEAT yielded a significantly higher average efficiency over the other variants. Comparisons that resulted in no statistically significant difference in method efficiency are outlined in Appendix A in Supplementary Material.

6. Discussion

This section discusses the capacity of each HyperNEAT variant (OS, NS, ONS, GNS, and OGN) to balance exploitation versus exploration during evolutionary search for facilitating efficient evolution of high-quality keep-away behaviors. Exploitation is the average maximum task performance of evolved behaviors and exploration is the fitness diversity of the fittest evolved behavior populations. Efficiency was measured as the number of generations (genotype evaluations) for a given method to attain task performance thresholds. For a given method variant and task, this threshold was calculated as the average maximum fitness attained without policy transfer (Section 5.2).

Since previous work (Verbancsics and Stanley, 2010; Didi and Nitschke, 2016a,b) and additional experimental results (Section 5) have already demonstrated the benefits of HyperNEAT behavior evolution coupled with policy transfer, this discussion focuses on evolved behavior analysis for policy transfer results only. That is, this study’s policy transfer results already demonstrate the same benefits as previous policy-transfer work. For example, jump-start: average task performance was improved in the target task after behavior transfer from a source task, asymptotic performance: final average maximum task performance was significantly higher, and time to threshold: the evolutionary time taken to evolve the fittest behaviors was reduced given policy transfer (Taylor and Stone, 2009; Taylor et al., 2010).

This section first discusses relationships between the fittest behaviors evolved by each HyperNEAT variant and the complexity of the evolved CPPNs corresponding to these behaviors (Section 6.1). The analysis tests a hypothesis that behavioral diversity evolves relatively high quality yet simple controllers, unhindered by unnecessary redundancy and complexity (Lehman and Stanley, 2011a; Gomes et al., 2013).

6.1. Network Complexity of Evolved Behaviors

Previous work has examined network complexity of NEAT evolved controllers given objective-based and novelty search (Lehman and Stanley, 2011a; Gomes et al., 2013), suggesting that novelty search evolves high-quality behaviors defined by structurally simple controllers. However, there has been little work investigating the complexity of HyperNEAT evolved controllers given evolutionary search driven by behavioral diversity maintenance versus objective-based search (Morse et al., 2013). Related research has suggested that as task complexity increases, simpler HyperNEAT evolved networks (CPPNs), resulting from specially placed neurons and limited connectivity, potentially results in higher quality behaviors (Risi and Stanley, 2011; Berg and Whiteson, 2013).

With the exception of preliminary work (Morse et al., 2013), the impact of behavioral diversity maintenance versus objective-based search on the complexity of evolved HyperNEAT networks as task complexity increases, remains unclear. In this study, network complexity is the number of connections and neurons (Abu-Mostafa, 1989) of the CPPN corresponding to the fittest evolved behavior in each run (equation (8)):

$E_x=\frac{1}{N}{\displaystyle \sum _{i=1}^N}(n_c+n_n)$ (8)

where, N is the number of runs, n_c, n_n, is the number of network connections and hidden nodes, respectively. For clarity, network x complexity (E) is normalized to the range: [0.0, 1.0]. A 1.0 value indicates maximum network complexity as observed for behaviors evolved with each HyperNEAT variant.

Table 6 presents, for each keep-away task, an overview of average network complexity corresponding to the fittest behaviors evolved by each HyperNEAT variant (at generation 100, Table 2). For each variant, evolved network complexity is presented together with SDs, where complexity values for each variant are averages calculated over the 20 fittest evolved networks taken at the end each run. Table 6 indicates the fittest ONS and NS evolved behaviors correspond to CPPNs with comparable network complexity (supported by statistical comparisons). However, the OS, OGN, and GNS variants all evolved significantly higher average network complexity for all tasks, where the GNS variant evolved the highest overall network complexity.

TABLE 6

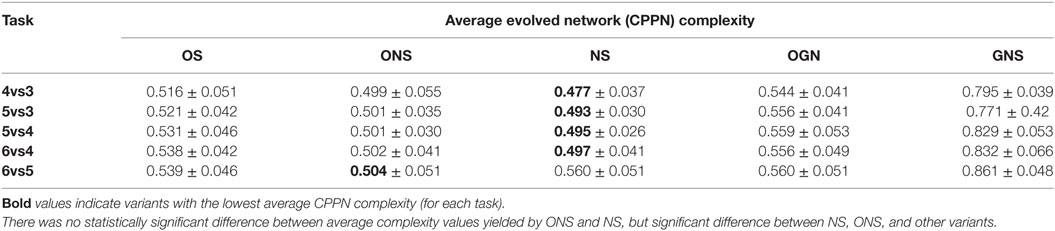
Table 6. Average normalized complexity of CPPNs corresponding to fittest evolved behaviors, for each HyperNEAT variant and each keep-away task, given behavior transfer.

That is, pair-wise statistical comparisons (Mann–Whitney U, p < 0.05) between average network complexity results, indicated that the fittest behaviors evolved by NS and ONS, for all tasks, corresponded to significantly simpler networks.⁶ These results lend support to the hypothesis that behavioral diversity maintenance search variants (NS, ONS) evolve simple CPPNs that encode high-quality behaviors, compared to objective-based (OS) and genotypic diversity maintenance search variants (OGN, GNS).

For a more detailed view, Table 7 presents network complexity and efficiency values corresponding to the fittest behaviors evolved by each variant in each keep-away task. As an indication of how evolved network complexity relates to task performance, the left-most column of Table 7 presents the average task performance range (in successive five percentile groups) that the fittest networks fall into. Also, to indicate how efficient each variant was at evolving simple or complex networks, the generations column presents the average number of generations taken to evolve the given networks.

TABLE 7

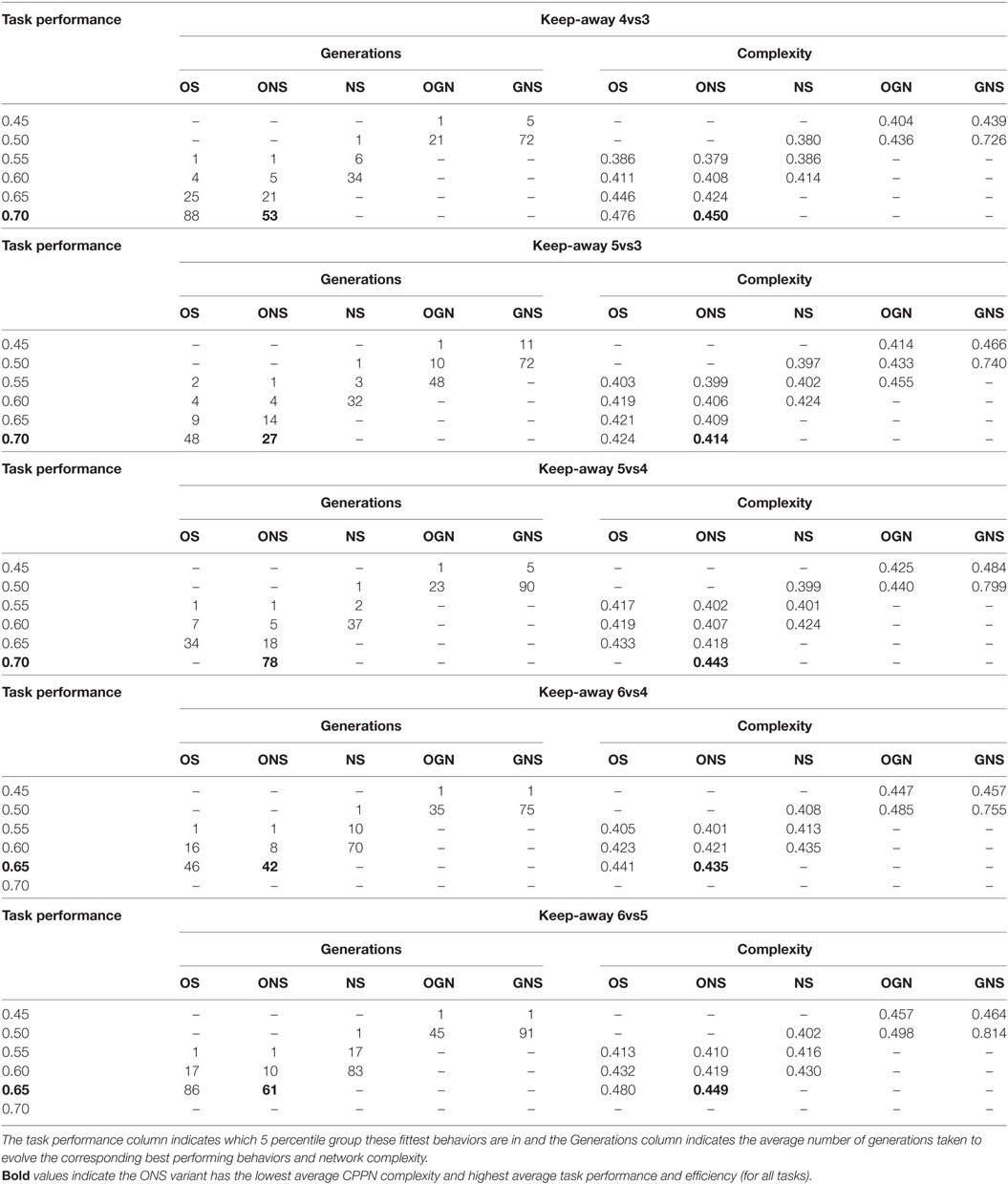
Table 7. Average normalized CPPN complexity (neurons and connections, over 20 runs) for the fittest behaviors evolved by each HyperNEAT variant for each keep-away task.

Table 7 further supports the hypothesis that behavior diversity maintenance methods evolve simple and high-quality controllers, as for all keep-away tasks, the ONS variant evolved minimal average network complexity and the highest average task performance. In some tasks, a significantly lower network complexity was evolved by the NS variant, but in these tasks NS evolved also yielded a lower average task performance. For example, in 6vs5 keep-away (the most complex task, Section 3.6), the fittest ONS evolved behaviors corresponded to average network complexity: 0.449 and task performance range: [0.65, 0.7), where the fittest NS evolved behaviors corresponded to average network complexity: 0.430 and performance range: [0.60, 0.65).

Similar results were observed in the 6vs4, 5vs4, and 5vs3 keep-away tasks. For the simplest task (4vs3 keep-away), average network complexity of the fittest ONS evolved behaviors were significantly higher than the fittest NS evolved behaviors, though task performance of ONS evolved behaviors was significantly higher. However, in the task performance range: [0.6, 0.65), ONS evolved behaviors yielded a significantly lower average network complexity of 0.408, versus 0.414 for NS evolved behaviors.

These results narrow the focus of the hypothesis about the benefits of behavior based search, via indicating that ONS yields further benefits in terms of evolving highly fit yet topologically simple controllers. In particular, these results support the notion that ONS, compared to NS, is the preferred evolutionary search method for discovering high-quality behaviors encoded by relatively simple controllers, devoid of unnecessary topological complexity and redundancy.

The suitability of ONS for evolving high-quality (effective) behaviors encoded by simple controllers (networks) is further evidenced by the efficiency (generations) values in Table 7. For each task, the ONS variant takes fewer generations, compared to the other search variants, to evolve its fittest behaviors, where such behaviors are encoded by relatively simple controllers. For example, in 6vs5 keep-away, NS takes an average of 83 generations to evolve networks with an average complexity of 0.430 in the task performance range: [0.6, 0.65), whereas ONS took 10 generations to evolve networks with an average complexity of 0.419 in the same performance range. Similar results were observed for all variant comparisons in all keep-away tasks. Comparatively, NS and GNS required longer search periods to discover their fittest behaviors. This results from NS and GNS search mechanisms optimizing for the exploration of novel behaviors and genotypes, meaning an overall broader exploration and discovery of diverse network topologies (Lehman and Stanley, 2011a; Gomes et al., 2013).

Table 7 further supports previous results demonstrating that behavioral diversity maintenance enables simple controller and high-quality behavior evolution (Lehman and Stanley, 2011a; Gomes et al., 2013). That is, OS, OGN, and GNS variants all yield significantly higher average network complexities for the fittest behaviors evolved in each task, where the GNS variant evolved the most complex networks overall.

Observing Table 7, for all tasks, when the average network complexity of OS and NS evolved behaviors is compared in the same performance category, both OS and NS yielded comparably complex networks, and in some tasks OS evolved networks were slightly less complex. Also, for all tasks, OS was significantly more efficient (generations taken) to evolve these comparable networks, and overall, OS evolved behaviors were significantly fitter. This supports the benefits of purely exploitative evolutionary search for boosting solution quality in the keep-away task. However, overall, the combination of novelty and objective-based search (ONS) yielded the most benefits, demonstrated by the efficient evolution of high-quality behaviors encoding significantly simple networks (Tables 6 and 7). Also, ONS, OS, and NS explored comparable ranges of network topologies; however, the range and complexity of ONS topologies corresponded to significantly higher task performance behaviors with few exceptions (Section 5) for all keep-away tasks.

These results contribute to this study’s main hypothesis that the ONS variant is most appropriate for balancing exploration versus exploitation during evolutionary search to efficiently evolve effective (high-quality) behavioral solutions to complex tasks (Section 1). Furthermore, these results lend support to the notion that behavioral diversity maintenance methods such as NS (Lehman and Stanley, 2011a) are suitable for evolving high-quality behaviors in complex tasks encoded by relatively simple controllers. Though, these results indicate that the hybrid search approach adopted by ONS elicits certain benefits over NS. For example, a more efficient search process, less complex controllers, and evolved behaviors with significantly higher task performance in most tasks (with few exceptions, Section 5). The following Section 6.2 continues the results analysis, elucidating the exploration versus exploitation capacity of each search variant with behavior space visualizations.

6.2. Behavioral Space Analysis

To elucidate each HyperNEAT search variant’s capacity to explore behavior spaces defining each keep-away task and thus the efficiency and effectiveness of each variant’s behavioral evolution, we applied dimensionality reduction to the final generation of behaviors evolved by each variant to visualize the contribution of various behavioral components to the fittest behaviors types and the diversity of behavior types discovered.

Since the keep-away tasks are defined by high dimensional behavior spaces (Section 3.6), we used Self-Organizing Maps (SOMs) (Kohonen, 1990) to reduce final generation behavior spaces (for each variant) to 10 × 10 maps visualizing behavior types.⁷ SOMs were selected as previous work (Gomes et al., 2013) indicated their suitability for mapping high dimensional behavior spaces into low dimensional visualizations preserving the salient topological relations between behavioral features.

For all keep-away tasks, the final generation behavior population evolved by each variant was used to create compact two-dimensional SOM representations of discrete behavior types (Figure 4).⁸ These SOMs were trained with behavior vectors characterizing keep-away behaviors, where such vectors were constituted by three components: average number of passes, dispersion of team members, and distance of the ball to the center of the field (Section 3.4). For added clarity in the SOM behavior type visualizations, we also included average keeper team ball control time (episode length in Figure 4) as a behavioral task performance indicator.

For succinctness of discussion, we only visualized behavior types for search variants in the most complex task, 6vs5 keep-away (Figure 4). This task was selected as we want to evaluate the capacity of each search variant to discover effective behavior types in high-dimensional behavior spaces (as typified by 6vs5 keep-away). Also, similar patterns of behavior type exploration and behavioral diversity were observed for given variants applied in each task. Furthermore, we do not present or discuss behavior maps for behavior types evolved at the final generation of OGN and GNS variants, since these variants yielded significantly lower average task performances, compared to ONS, NS, and OS, for all tasks (Section 5). For reference, Appendix C in Supplementary Material presents behavior type visualizations for all search variants applied in all tasks.

Figure 4 presents behavior type visualizations for 20 behavior populations produced by each variant at the final generation in 6vs5 keep-away. Figure 4 (left) depicts 10 × 10 behavior types visualized as circles composed of four slices. Each slice corresponds to a behavioral component: number of passes, dispersion of team members, distance of the ball to the field’s center, and episode length, where component slice size corresponds to its average value. Thus, varying combinations of behavioral component values define varying behavior types, where behavior types are arranged on the map according to relative behavioral component values. For example, the right hand side of the OS behavior type map in Figure 4 (left) depicts behavior types with relatively high values for distance to field’s center, whereas the left hand side depicts behavior types with relatively low values for each component. Behavior types containing larger values for episode length are progressively presented toward the bottom row.

To complement behavior type visualizations, Figure 4 (right) presents unified distance matrices (u-matrices) visualizing behavior type clusters at each variant’s final generation in 6vs5 keep-away. Vector quantization (Gersho and Gray, 1992) was applied between SOM nodes (Figure 4, left) to gauge behavioral distances (normalized Euclidean distance) between behavior types.⁹

The u-matrix in Figure 4 (right) visualizes the behavioral distance between each node in the behavior type map. Darker colors denote closer behavioral distances and lighter colors denote larger differences between two behavior types. Darker areas are equated with clusters of similar behavior types and lighter areas are tantamount to cluster separators (Ultsch and Siemon, 2001). Any two u-matrix nodes can be compared to ascertain their behavioral distance, where a given coordinate in the u-matrix (Figure 4, right) corresponds to the same coordinate in the behavior type map (Figure 4, left).

Observing the ONS behavior type map in Figure 4 (left), the fittest behavior types are characterized by the following components. First, a predisposition to maximizing keeper distance from the field’s center, with relatively few passes and little keeper-team dispersion (ONS behavior type map coordinates: 9, 10). Second, a high number of passes with little team dispersion and distance to the field’s center (ONS behavior type map coordinates: 4, 10). Comparatively, the fittest OS evolved behavior type had a similarly large episode length (OS behavior type map coordinates: 10, 10), though overall the OS behavior type map indicates lower episode lengths (fitness) associated with each behavior type in the map (Figure 4, left). This difference between ONS and OS behavior type maps is supported by the significantly lower average task performance of OS (compared to ONS) evolved behaviors in 6vs5 keep-away (Section 5). Similar to a fittest ONS evolved behavior type (ONS behavior map coordinates: 9, 10), the fittest OS evolved behavior type had a predisposition for keepers to maximize their distance from the field’s center while the team stayed relatively compact (little dispersion) and making relatively few passes. This behavioral bias toward keepers maximizing distance to the field’s center was found to be common to all the fittest OS and ONS evolved behavior types across all keep-away tasks (Appendix C in Supplementary Material).

Observing the NS behavior type map (Figure 4, left), it is notable that similar to the other fittest ONS evolved behavior type (ONS behavior type map coordinates: 4, 10), the fittest NS evolved behavior type maximized the number of passes, while keepers maintained relatively little dispersion and distance from the field’s center (NS behavior coordinates: 10, 10). Thus, the same prevalent behavioral component was present in the fittest NS and ONS evolved behavior types. However, as with comparisons between the ONS and OS behavior maps, the fitness of NS evolved behavior types, overall, was observed to be lower than that of OS evolved behavior types (Figure 4, left).

A key difference between the fittest ONS, OS, and NS evolved behavior types was the multitude of comparably fitter ONS evolved behavior types, as evident in the ONS behavior map (Figure 4, left). That is, the fittest ONS behavior types comprised specific combinations of behavioral component values that resulted in high task performance, whereas OS and NS evolved behavior types, despite having biases to some of the same prevalent behavior components, failed to discover such particular weightings of the behavioral components and thus failed to achieve comparable fitness values. This is supported by the significantly lower average task performance of the fittest OS and NS evolved behaviors compared to the fittest ONS evolved behaviors (Section 5). The capacity of ONS to evolve multiple highly fit behavior types and OS and NS to evolve relatively few is elucidated by visualizing the diversity between behavior types in the behavior space at the final generation of each variant.

The following describes u-matrices as complementary behavior space visualization tools to further explain differences between ONS, OS, and NS evolved behavior types. Consider the u-matrices corresponding to the OS, NS, and ONS behavior type maps (Figure 4, right). Each u-matrix illustrates a representation of how the final generation of behaviors evolved by each variant are topologically related to each other in the behavior space. This provides an indication of the diversity of evolved behavior types and thus the relative ease or difficulty for different search variants to discover highly fit behavior types. Comparing the OS, NS, and ONS u-matrices (Figure 4, right), it is notable that the ONS u-matrix depicts overall greater behavior distances (lighter shading), between clusters of highly fit behavioral types and relatively small behavioral distances (darker shading) within clusters of similar behavior types.

For example, consider a fittest ONS behavioral type (behavior map and u-matrix coordinates: 4, 10). This behavior type is relatively close in the behavioral space to another highly fit behavior type (behavior map and u-matrix coordinates: 9, 10), given comparable cell coloration in the u-matrix and thus negligible behavioral distance between these two behavior types. Furthermore, for both these behavior types, the adjacent (surrounding) u-matrix cells depicts minor differences in cell coloration (especially for cells on the left) indicating relatively close behavioral distances to these other behavior types. These behavior type clusters share some behavioral component biases. For example, the behavior type at coordinates: (9, 10), shares a bias toward maximizing keeper distance to the field’s center, with its neighboring behavior types, thus forming a cluster of similar behavior types. Similarly, the behavior type at behavior map coordinates: (4, 10) shares a bias to maximize the number of keeper passes, with its neighboring behavior types, thus forming a second cluster of similar behavior types. A third highly fit behavior type cluster can be observed in the top right of the ONS behavior type map and u-matrix (Figure 4). That is, there is little coloration difference between u-matrix cell coordinates: (1, 4), its neighboring cells, and the behavior type clusters defined by cell coordinates: (4, 10), (9, 10), and their surrounding cells.

Also, the overall cell coloration of the ONS u-matrix is relatively light with few dark patches, indicating an overall broad spread in behavioral distances between the behavior types evolved at the final generation of the ONS variant. This equates to the ONS variant operating in a large but highly fit behavior space region, with little behavioral distance between the fittest clusters. Discovery of the absolute fittest behavior types was enabled by the ONS objective function exploiting fitness gradients between these highly fit behavior type clusters and the overall diversity of the behavior space covered by all final generation behavior types is indicative of ONS behavioral diversity maintenance.

Comparing NS and ONS u-matrices, the overall light coloring of the NS u-matrix (Figure 4, right), indicates slightly more pronounced behavior type diversity at the final generation of NS. However, a cluster of closely related behavior types is evidenced by a series of dark patches stretching from the bottom left to the top right corner of the NS u-matrix (Figure 4, right). On both sides of this cluster (top left and bottom right hand corner, Figure 4) is a broad spread of relatively dissimilar behavior types, indicating a correspondingly broad behavior space exploration. This diversity of NS evolved behaviors is supported by related behavior space visualizations (Section 6.3). A key difference between NS and ONS evolved behavior types is evident from observing the corresponding NS and ONS behavior type maps (Figure 4, left). Overall, fitness associated with NS evolved behavior types was relatively low, as observed by the spread of dissimilar behaviors observed in the top-left hand corner of the NS u-matrix (Figure 4, left). Comparatively low fitness values were not observed for most ONS behavior types, even though a comparable diversity in behavior types was observed (Figure 4, left). This is supported by the significantly lower average task performance yielded by NS evolved behaviors, compared to ONS evolved behaviors (results 5).

Thus, ONS evolved the most diverse behavior types, where such behavior types were defined by specific compositions of the behavioral components: number of passes, dispersion of team members, distance of the ball to the field’s center, and episode length as an indication of associated behavior fitness. This diversity of behavior types was indicative of an expansive search of highly fit regions in the behavior space at the final generation of ONS, where multiple comparably highly fit behavior types were discovered in this behavior space region. This pattern of effective exploration (diversity of behavior types) balanced with exploitation (high average task performance) was observed when ONS was applied in all other tasks (Appendix C in Supplementary Material).

The NS variant evolved similarly diverse behavior types; however, this diversity did not equate with comparably fit final generation behaviors. The significantly lower average task performance of NS versus ONS evolved behaviors held true for all tasks tested (Section 5). This indicates that while the behavioral diversity maintenance mechanism of NS enabled an expansive behavior space search and discovery of diverse behavior types, the lack of an exploitative objective-based search mechanism was deleterious across all tested keep-away tasks. The following Section 6.3 provides further support of this results analysis with a discussion of genotype space visualizations that further elucidate the effectiveness and efficiency of each search variant applied across increasingly complex keep-away tasks.

6.3. Evolutionary Search Variant Efficiency and Effectiveness

To ascertain the effectiveness of each variant we visualized the spread of genotypes evolved at each variant’s final generation, where such visualizations present the portion of genotypes in different task performance regions (Figure 3). To ascertain each variant’s efficiency, we measured the average number of generations taken to evolve behaviors surpassing a task performance threshold (Section 5.2) for each task (Table 5). This section only discusses the ONS, OS, and NS variants as the other variants were found to consistently evolve significantly less effective behaviors (Figure 2) with lower efficiency (Table 5). Search efficacy is discussed with respect to exploration versus exploitation of the genotype space and hence the capacity to efficiently evolve high-quality behaviors.

FIGURE 3

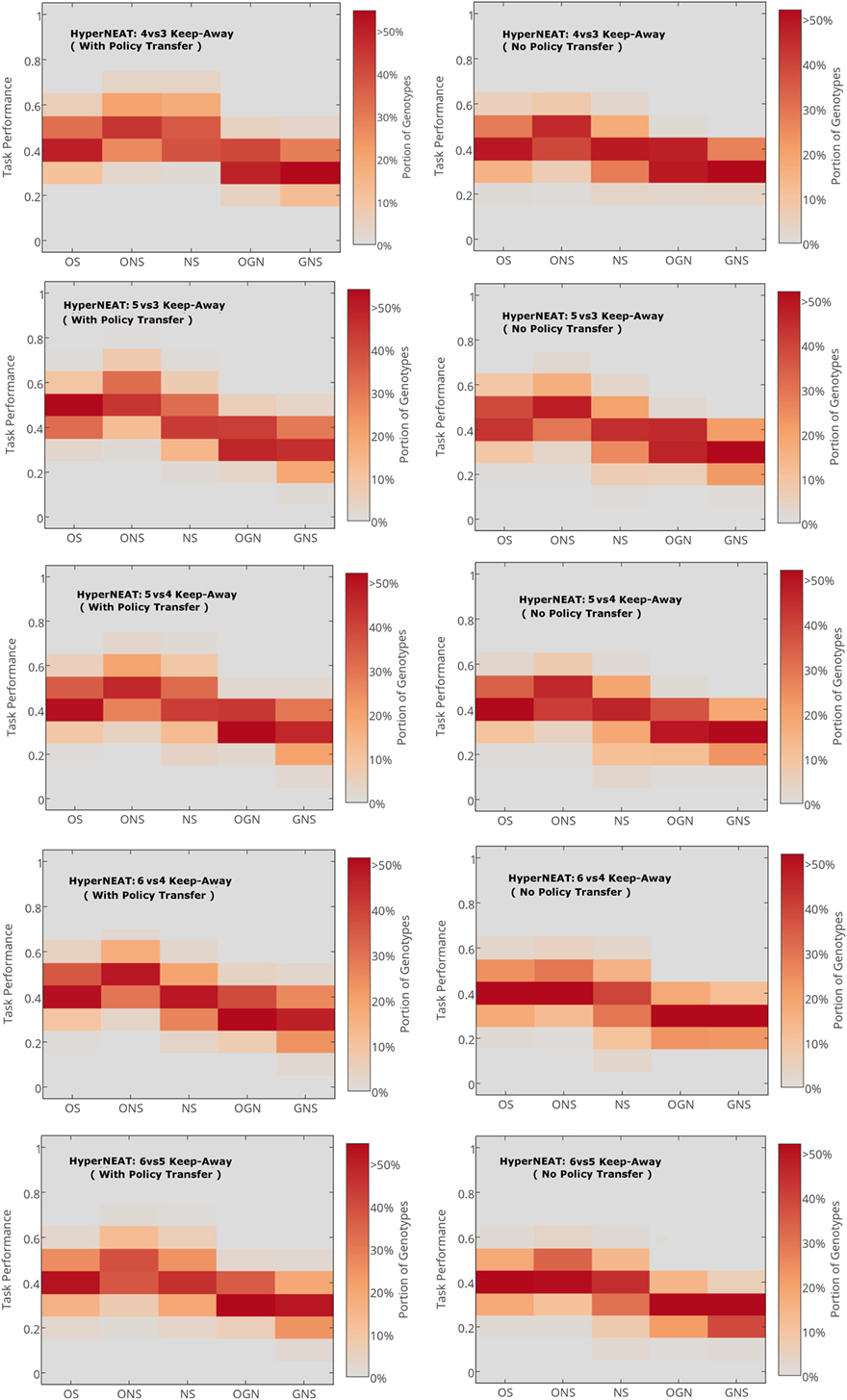
Figure 3. Heat-maps showing portions of (final generation) genotypes evolved by HyperNEAT variants with (left column) and without (right column) policy transfer. OS, objective-based; NS, novelty search; ONS, objective-novelty hybrid; GNS, genotypic novelty search; OGN, objective-GNS hybrid. Darker shading indicates a higher portion of genotypes in a given 0.2 interval of normalized task performance [0.0, 1.0].

FIGURE 4

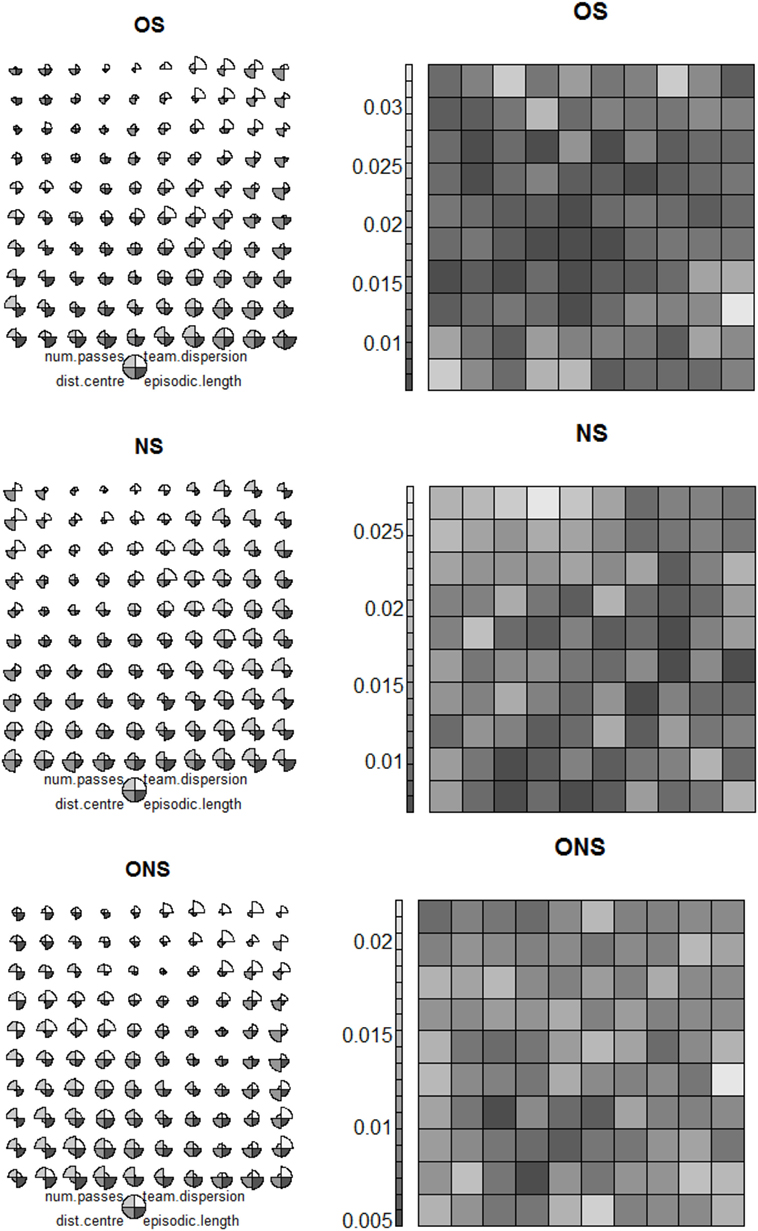
Figure 4. Left: Self-organizing map (SOM) visualizing behavior space exploration at the final generation of OS, NS, and ONS search variant in 6vs5 keep-away. Each circle represents a behavior type (four colored slices). Each slice represents one component of the behavior characterization vector (Section 3.4.1), where slice size equates to the given component’s value. Right: U-matrix visualizing the clustering of behavior types (nodes in the SOM, left) in the behavior space at the final generation of OS, NS, and ONS. The darker the color between two adjacent nodes the closer the distance between the two behavior types in the behavior space. Note the differing u-matrix Y-axis values indicating normalized behavioral distances.

6.3.1. ONS Variant

Consider that, for all keep-away tasks (with few exceptions, Section 5), ONS evolved behaviors yielded significantly higher average task performances compared to the fittest behaviors evolved by other variants (Figure 2). Higher average task performance of the fittest ONS evolved behaviors is supported by the capacity of ONS to effectively explore the behavior space during evolutionary search. This is evidenced by large portions of the fittest ONS evolved genotype populations occupying the highest 40% task performance range in behavior space regions for each task (Figure 3, left). Also, compared to other variants, relatively few genotypes of the fittest ONS evolved populations were in the lowest 60% of the keep-away task performance range (Figure 3, left).

However, average ONS efficiency was observed to be significantly worse or comparable for most keep-away tasks (Table 5). This low average efficiency of ONS search was indicative of the expansive behavior space exploration and number of generations needed for such broad behavior space exploration. The low efficiency of ONS search was, however, offset by the variants capacity to discover behaviors yielding significantly higher task performances for all tasks (Section 5). Consider the progression of average task performance presented in Figure 5. Figure 5 indicates that ONS consistently achieved the highest task performance, though average maximum task performance was attained at later generations compared to other variants. Hence, the trade-off for higher quality of ONS evolved behaviors was longer evolution times and the number of genotype evaluations taken significantly increased with task complexity (Section 5.2).

FIGURE 5

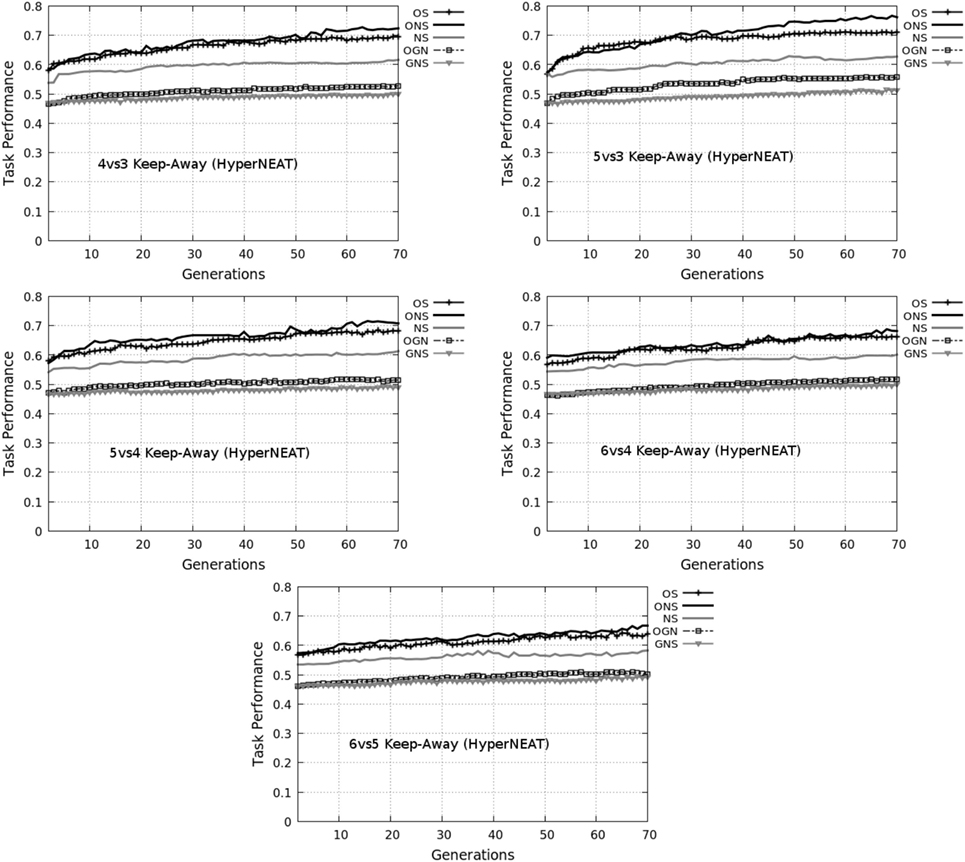
Figure 5. Average maximum task performance progression (given policy transfer), over 20 runs in each task, for each HyperNEAT. OS, objective-based search; NS, novelty search; ONS, objective-novelty search; GNS, genotypic novelty search; OGN, objective-genotypic novelty search. Note: ONS variant consistently evolves behaviors with the highest maximum task performance (observable at each final generation), and progression is over 70 generations for consistency with non-policy transfer experiments.

The success of the ONS variant was thus consequent of beneficial interactions between its behavioral diversity maintenance and objective-based search mechanisms. That is, behavioral diversity maintenance first covered expansive regions of the solution space encapsulating a diverse range of behaviors. Within such diverse behavior regions objective-based search acted as a fine tuning mechanism, following fitness gradients to propagate the evolution of increasingly fit solutions resulting in the discovery of the highest task performance behaviors overall. This notion is supported by NS and OS variant results, where neither of these methods had the benefit of complementing objective-based search or behavioral diversity maintenance mechanisms (respectively), and as a result significantly poorer quality solutions were evolved for all tasks.

This demonstrated capacity for the ONS variant to effectively balance exploration versus exploitation during evolutionary search thus boosting evolved behavioral quality is supported by related work that similarly highlighted the benefits of evolutionary search methods that hybridize objective-based search and behavioral diversity maintenance (Cuccu and Gomez, 2011; Gomes et al., 2013, 2015; Shorten and Nitschke, 2015; Didi and Nitschke, 2016a,b).

6.3.2. OS and NS Variants

For all keep-away tasks (with the exception of 5vs4 keep-away, where there was no significant difference between the fittest ONS, OS and NS evolved behaviors), the fittest NS evolved behaviors performed significantly worse than the fittest ONS and OS evolved behaviors (Section 5). Consider Figure 5, which illustrates the task performance progression of NS evolved behaviors, for all tasks, as being consistently third highest after ONS and OS evolved behaviors. Thus, while NS evolved behaviors significantly out-performed GNS and OGN for all tasks, NS evolved keep-away behaviors at best yielded average task performances comparable to OS evolved behaviors and were significantly poorer quality compared to ONS evolved behaviors (Figure 2).

Also, for all tasks, the fittest NS and ONS evolved populations yielded comparable exploration of the solution space (Figure 3). However, compared to ONS, relatively small portions of the fittest OS evolved genotypes were in the highest task performance region of the solution space range: [0.6, 1.0] (Figure 3). Though for all tasks comparable portions of OS and NS evolved genotypes were calculated as being in this task performance region of the solution space: [0.6, 1.0] (Figure 3). This comparable exploration capacity of the OS and NS variants in across all tasks is also evidenced by average task performance progression over the evolutionary process of each variant (Figure 5). Observing Figure 5, it is notable that for all tasks NS and OS evolved behaviors attain their respective average maximum task performances at approximately the same number of generations. This indicates that the NS and OS search processes were on average equally effective in that both discovered local optima in the behavior space after comparable durations of exploration.

Furthermore, these results indicate that even though the NS variant maintains the capacity for expansive exploration of the solution space for all tasks (Figure 3) and evolves diverse behavior types at the final generation of the evolutionary process (Section 6.2), the objective-based search of the OS variant was demonstrated as significantly more effective at evolving high-quality behaviors for the keep-away tasks.

The significantly higher task performance of ONS and OS evolved behaviors further supports the notion that the keep-away task is amenable to objective-based search but only to a certain degree of task complexity. Section 6.2 highlighted that specific combinations of behavioral component values are required to achieve high-quality behaviors, where the fitness function used by the OS variant (Section 3.3) was suitable for efficiently evolving such behaviors (Table 5). The NS variant was also found to be efficient, for all tasks, at evolving its fittest behaviors (Table 5), and had the capacity to explore broad regions of the behavior space (Figure 3). Though, in keep-away, the search for novel behaviors by the NS variant (Section 3.4) worked ineffectively, in that novel behaviors discovered were on average significantly less effective than those evolved by the OS and ONS variants. This indicates that despite the NS variant effectively exploring broad regions of the search space, the lack of objective-based search as an exploitative mechanism for following fitness gradients to increasingly fit behaviors, was found to significantly limit the performance of the NS variant.

This result is supported by related work demonstrating that NS is less effective in complex tasks defined by high-dimensional solution spaces (Cuccu and Gomez, 2011; Gomes et al., 2013), and that high-quality solutions attained via including objective-based search to allow exploitation of broadly explored behavior space regions.

6.4. Discussion Summary

This study’s core results indicated that the ONS variant of HyperNEAT (hybridizing behavioral diversity maintenance and objective-based search) consistently evolved behaviors with significantly higher task performance, compared to other search variants. To elucidate the mechanisms responsible for the efficiency and effectiveness of ONS evolved behaviors, we presented an analysis of the fittest behavior populations evolved by each variant.

Section 6.1 examined the impact of the objective-based versus non-objective and hybrid evolutionary search variants on the network complexity of the CPPNs corresponding to the fittest evolved behaviors. This results analysis indicated that ONS yielded benefits over the other search variants given that it enabled the evolution of significantly fitter yet topologically simple controllers. Specifically, the capacity of ONS to suitably balance exploration versus exploitation of the behavior space resulted in the evolution of high-quality behaviors encoded by relatively simple controllers, free of unnecessary topological complexity and redundancy.

Section 6.2 applied dimensionality reduction to final generation evolved behaviors to visualize the behavior types evolved by each variant. SOMs were used to represent the salient behavioral features comprising the fittest behavior types and behavior maps were used to visualize the average behavioral distance between such features. An analysis of these behavior visualizations indicated that the fittest ONS evolved behavior types comprised specific combinations of behavioral features that resulted in high-quality behaviors, whereas other variants failed to evolve such behavioral feature combinations and thus evolve behaviors of comparable quality. This analysis indicated that the ONS variant operated in large, highly fit behavior space regions. Discovery of the fittest behavior types was enabled by the ONS objective function exploiting fitness gradients between highly fit behavior types in a diverse behavior space, where the exploration of such behaviors was enabled by ONS behavioral diversity maintenance.

Section 6.3 presented genotype space visualizations indicating portions of genotypes evolved in various task performance regions. These visualizations further elucidated the capacity of the ONS variant to suitably balance exploration versus exploitation during evolutionary search. This genotype space analysis indicated that the fittest genotype populations (occupying the highest 40% task performance range in the behavior space) were consistently evolved by ONS, whereas most of the fittest populations evolved by other search variants were consistently in the lowest 60% of the task performance range. This analysis thus further supported ONS as effectively exploring the behavior space to exploit (discover) high-quality behaviors during evolutionary search.

7. Conclusion

This study’s research goal was twofold. First, to elucidate that a hybrid evolutionary search approach combining objective (fitness function) and non-objective-based (behavioral diversity maintenance) search is most suitable for efficiently evolving effective behavioral solutions to increasingly complex collective behavior tasks. The collective behavior case study in this research was RoboCup keep-away soccer. Second, to support a hypothesis that policy (behavior) transfer coupled with evolutionary search is a consistently suitable method for boosting the effectiveness and efficiency of evolved solution quality across increasingly complex tasks.

The first insight from experimental results was that evolutionary search driven by hybridized behavioral diversity maintenance and objective-based search was best suited for efficiently evolving effective behaviors across increasingly complex keep-away tasks. The second insight was that policy transfer significantly increased the average quality (task performance) and the efficiency (genotype evaluations taken) with which such behaviors were evolved. However, policy transfer had the most benefits for keep-away behaviors evolved by the hybrid evolutionary search. That is, all hybrid evolved behaviors were significantly more effective (and efficiently evolved) compared to those evolved by other evolutionary search variants. This result was supported by related work that similarly demonstrated the benefits of combining behavioral diversity maintenance and objective-based evolutionary search (Gomes et al., 2013; Shorten and Nitschke, 2015; Didi and Nitschke, 2016b) to mitigate the bootstrap problem (Gomez and Miikkulainen, 1997) for complex tasks and enable the evolution of high-quality solutions. The third insight was that the high-quality behaviors evolved by the hybrid evolutionary search method encoded relatively simple neural controllers. This was a result of this hybrid method’s capacity to appropriately balance exploration versus exploitation during evolutionary search, such that evolved controllers did not contain unnecessary complexity that hindered high-task performance.

Thus, this study contributes to increasing empirical evidence indicating the effectiveness of hybrid objective-behavioral diversity search methods in complex tasks defined by very large behavior spaces (Mouret and Doncieux, 2009b, 2012; Lehman and Stanley, 2011b; Gomes et al., 2012, 2015; Inden et al., 2013; Shorten and Nitschke, 2015). Ongoing research is investigating the impact and interaction of various behavior representations, behavior evolution and policy transfers methods, on facilitating the effective transfer of evolving behaviors across various tasks. Hence, future research aims to further elucidate the necessary methodological features for facilitating behavior evolution across increasingly complex and dissimilar tasks. The end goal is to design new methods capable of evolving controllers that elicit general problem solving behavior.

Author Contributions

GN wrote the paper and formulated the research questions, experimental design and performed analysis. SD implemented methods, ran experiments and statistical tests.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at http://www.frontiersin.org/article/10.3389/frobt.2017.00062/full#supplementary-material.

Footnotes

1. ^Also referred to as transfer learning in reinforcement learning research (Taylor and Stone, 2009).
2. ^Experiments used RoboCup Keep-Away version 6 (Taylor et al., 2010). Source code and executables can be found at: http://sourceforge.net/projects/sserver/
3. ^It is important to note that there is currently no quantitative, testable, definition of deception, that allows experimenters to quantify the degree of deception of a given task.
4. ^Collective behavior transfer, behavior transfer and policy transfer are used interchangeably.
5. ^Significant refers to a statistically significant difference in pair-wise comparison of two data-sets.
6. ^Appendix B in Supplementary Material presents an overview of average complexity yielded for all evolved controllers and statistical test results between average controller complexities for all variants.
7. ^A 10 x 10 map size was selected as this is the half the ANN sensory input layer size (Section 3.2.1).
8. ^All SOM visualizations for all variants and tasks are presented in Appendix C in Supplementary Material.
9. ^All SOM visualizations for all search variants applied in each task are presented in Appendix C in Supplementary Material.

References

Abu-Mostafa, Y. (1989). “Information theory, complexity, and neural networks,” in IEEE Communications Magazine (Piscataway: IEEE Press), 25–29.

Google Scholar

Ammar, H., Tuyls, K., Taylor, M., Driessens, K., and Weiss, G. (2012). “Reinforcement learning transfer via sparse coding,” in Proceedings of the Eleventh International Conference on Autonomous Agents and Multiagent Systems (Valencia, Spain: AAAI), 4–8.

Google Scholar

Bahceci, E., and Miikkulainen, R. (2008). “Transfer of evolved pattern-based heuristics in games,” in Proceedings of the IEEE Symposium on Computational Intelligence and Games (Perth, Australia: Morgan Kaufmann), 220–227.

Google Scholar

Berg, T. V., and Whiteson, S. (2013). “Critical factors in the performance of hyperneat,” in Proceedings of the Genetic and Evolutionary Computation Conference (Amsterdam, The Netherlands: ACM), 759–766.

Google Scholar

Bou-Ammar, H., Eaton, E., Ruvolo, P., and Taylor, M. (2015). “Unsupervised cross-domain transfer in policy gradient reinforcement learning via manifold alignment,” in Proceedings of the AAAI Conference on Artificial Intelligence (Austin: AAAI Press), 2504–2510.

Google Scholar

Boutsioukis, G., Partalas, I., and Vlahavas, I. (2012). “Transfer learning in multi-agent reinforcement learning domains,” in Recent Advances in Reinforcement Learning (Berlin, Germany: Springer), 249–260.

Google Scholar

Brameier, M., and Banzhaf, W. (2002). “Explicit control of diversity and effective variation distance in linear genetic programming,” in Proceedings of the 5th European Conference on Genetic Programming (Kinsale, Ireland: Springer-Verlag), 37–49.

Google Scholar

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. USA: Routledge.

Google Scholar

Crepinsek, M., Liu, S., and Mernik, M. (2013). Exploration and exploitation in evolutionary algorithms. ACM Comput. Surv. 45, 1–33. doi: 10.1145/2480741.2480752

CrossRef Full Text | Google Scholar

Cuccu, G., and Gomez, F. (2011). “When novelty is not enough,” in Proceedings of the European Conference on the Applications of Evolutionary Computation (Berlin: Springer), 234–243.

Google Scholar

Cuccu, G., Gomez, F., and Glasmachers, T. (2011). “Novelty-based restarts for evolution strategies,” in Proceedings of the Congress on Evolutionary Computation (New Orleans, USA: IEEE Press), 158–163.

Google Scholar

Cully, A., Clune, J., Tarapore, D., and Mouret, J. (2015). Robots that can adapt like animals. Nature 521, 503–507. doi:10.1038/nature14422

PubMed Abstract | CrossRef Full Text | Google Scholar

Cully, A., and Mouret, J. (2016). Evolving a behavioral repertoire for a walking robot. Evol. Comput. 24, 1–33. doi:10.1162/EVCO_a_00143

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Ambrosio, D., and Stanley, K. (2013). Scalable multiagent learning through indirect encoding of policy geometry. Evol. Intell. J. 6, 1–26. doi:10.1007/s12065-012-0086-3

CrossRef Full Text | Google Scholar

Deb, K. (2001a). Multi-Objective Optimization Using Evolutionary Algorithms. New York, USA: John Wiley and Sons.

Google Scholar

Deb, K. (2001b). Pareto Based Multi-Objectives Optimization Using Evolutionary Algorithms. New York, USA: John Wiley and Sons.

Google Scholar

Didi, S., and Nitschke, G. (2016a). “Hybridizing novelty search for transfer learning,” in Proceedings of the IEEE Symposium Series on Computational Intelligence (Athens, Greece: IEEE Press), 10–18.

Google Scholar

Didi, S., and Nitschke, G. (2016b). “Multi-agent behavior-based policy transfer,” in Proceedings of the European Conference on the Applications of Evolutionary Computation (Porto, Portugal: Springer), 181–197.

Google Scholar

Doncieux, S. (2014). “Knowledge extraction from learning traces in continuous domains,” in AAAI 2014 Fall Symposium on Knowledge, Skill, and Behavior Transfer in Autonomous Robots (Arlington, USA: AAAI Press), 1–8.

Google Scholar

Doncieux, S., Bredeche, N., Mouret, J.-B., and Eiben, A. (2015). Evolutionary robotics: what, why, and where to. Front. Robot. AI 2:1–18. doi:10.3389/frobt.2015.00004

CrossRef Full Text | Google Scholar

Doncieux, S., and Mouret, J. (2014). Beyond black-box optimization: a review of selective pressures for evolutionary robotics. Evol. Intell. 7, 71–93. doi:10.1007/s12065-014-0110-x

CrossRef Full Text | Google Scholar

Doncieux, S., Mouret, J.-B., Bredeche, N., and Padois, V. (2011). “Evolutionary robotics: exploring new horizons,” in New Horizons in Evolutionary Robotics (Berlin, Germany: Springer), 3–25.

Google Scholar

Duarte, M., Costa, V., Gomes, J., Rodrigues, T., Silva, F., Oliveira, S., et al. (2016). Evolution of collective behaviors for a real swarm of aquatic surface robots. PLoS ONE 11:e0151834. doi:10.1371/journal.pone.0151834

PubMed Abstract | CrossRef Full Text | Google Scholar

Eiben, A., and Smith, J. (2003). Introduction to Evolutionary Computing. Berlin, Germany: Springer-Verlag.

Google Scholar

Ekárt, A., and Németh, S. (2002). “Maintaining the diversity of genetic programs,” in Proceedings of the 5th European Conference on Genetic Programming (EuroGP 2002) (Kinsale, Ireland: Springer-Verlag), 162–171.

Google Scholar

Flannery, B., Teukolsky, S., and Vetterling, W. (1986). Numerical Recipes. Cambridge, UK: Cambridge University Press.

Google Scholar

Floreano, D., Dürr, P., and Mattiussi, C. (2008). Neuroevolution: from architectures to learning. Evol. Intell. 1, 47–62. doi:10.1007/s12065-007-0002-4

CrossRef Full Text | Google Scholar

Gauci, J., and Stanley, K. (2008). “A case study on the critical role of geometric regularity in machine learning,” in Proceedings of the AAAI Conference on Artificial Intelligence (Menlo Park, USA: AAAI Press), 628–633.

Google Scholar

Gersho, A., and Gray, R. (1992). Vector Quantization and Signal Compression. New York, USA: Springer Science+Business Media.

Google Scholar

Ghasemi, A., and Zahediasl, S. (2012). Normality tests for statistical analysis: a guide for non-statisticians. Int. J. Endocrinol. Metab. 10, 486–489. doi:10.5812/ijem.3505

PubMed Abstract | CrossRef Full Text | Google Scholar

Gomes, J., and Christensen, A. (2013a). “Generic behavior similarity measures for evolutionary swarm robotics,” in Proceedings of the Genetic and Evolutionary Computation Conference (Amsterdam, The Netherlands: ACM Press), 199–206.

Google Scholar

Gomes, J., and Christensen, A. (2013b). “Generic behaviour similarity measures for evolutionary swarm robotics,” in Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation (Amsterdam, The Netherlands: ACM), 199–206.

Google Scholar

Gomes, J., Mariano, P., and Christensen, A. (2014). “Avoiding convergence in cooperative coevolution with novelty search,” in Proceedings of the International Conference on Autonomous Agents and Multi-Agent Systems (Paris, France: ACM), 1149–1156.

Google Scholar

Gomes, J., Mariano, P., and Christensen, A. (2015). “Devising effective novelty search algorithms: a comprehensive empirical study,” in Proceedings of the Genetic Evolutionary Computation Conference (Madrid, Spain: ACM), 943–950.

Google Scholar

Gomes, J., Mariano, P., and Christensen, A. (2016). Novelty-driven cooperative coevolution. Evol. Comput. 25, 275–307. doi:10.1162/EVCO_a_00173

CrossRef Full Text | Google Scholar

Gomes, J., Urbano, P., and Christensen, A. (2012). “Progressive minimal criteria novelty search,” in Advances in Artificial Intelligence, eds J. Pavon, N. Duque-Mendez, and R. Fernandez (Berlin, Germany: Springer), 281–290.

Google Scholar

Gomes, J., Urbano, P., and Christensen, A. (2013). Evolution of swarm robotics systems with novelty search. Swarm Intell. 7, 115–144. doi:10.1007/s11721-013-0081-z

CrossRef Full Text | Google Scholar

Gomez, F., and Miikkulainen, R. (1997). Incremental evolution of complex general behavior. Adapt. Behav. 5, 317–342. doi:10.1177/105971239700500305

CrossRef Full Text | Google Scholar

Haykin, S. (1995). Neural Networks: A Comprehensive Foundation. Ontario, Canada: Prentice Hall.

Google Scholar

Hodjat, B., Shahrzad, H., and Miikkulainen, R. (2016). “Distributed age-layered novelty search,” in Proceedings of the Fifteenth International Conference on the Synthesis and Simulation of Living Systems (Cancun, Mexico: MIT Press).

Google Scholar

Inden, B., Jin, Y., Haschke, R., Ritter, H., and Sendhoff, B. (2013). An examination of different fitness and novelty based selection methods for the evolution of neural networks. Soft Comput. 5, 753–767. doi:10.1007/s00500-012-0960-z

CrossRef Full Text | Google Scholar

Kohonen, T. (1990). The self-organizing map. Proc. IEEE 78, 1464–1480. doi:10.1109/5.58325

CrossRef Full Text | Google Scholar

Lehman, J., and Stanley, K. (2010a). “Efficiently evolving programs through the search for novelty,” in Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation (Portland, USA: ACM), 837–844.

Google Scholar

Lehman, J., and Stanley, K. (2010b). “Revising the evolutionary computation abstraction: minimal criteria novelty search,” in Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation (Philadelphia, USA: ACM), 103–110.

Google Scholar

Lehman, J., and Stanley, K. (2011a). Abandoning objectives: evolution through the search for novelty alone. Evol. Comput. 19, 189–223. doi:10.1162/EVCO_a_00025

CrossRef Full Text | Google Scholar

Lehman, J., and Stanley, K. (2011b). “Novelty search and the problem with objectives,” in Genetic Programming in Theory and Practice IX (Berlin, Germany: Springer), 37–56.

Google Scholar

Lehman, J., Stanley, K., and Miikkulainen, R. (2013). “Effective diversity maintenance in deceptive domains,” in Proceedings of the Genetic and Evolutionary Computation Conference (New York: ACM Press), 215–222.

Google Scholar

Liapis, A., Yannakakis, G., and Togelius, J. (2015). Constrained novelty search: a study on game content generation. Evol. Comput. 23, 101–129. doi:10.1162/EVCO_a_00123

PubMed Abstract | CrossRef Full Text | Google Scholar

Metzen, J. H., Edgington, M., and Kassahun, Y. (2008). Analysis of an evolutionary reinforcement learning method in a multi-agent domain. Auton. Agents Multi Agent Syst. 7, 291–298.

Google Scholar

Moriguchi, H., and Honiden, S. (2010). “Sustaining behavioral diversity in neat,” in Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation (Portland, USA: ACM), 611–618.

Google Scholar

Morse, G., Risi, S., Snyder, C., and Stanley, K. (2013). “Single-unit pattern generators for quadruped locomotion,” in Proceedings of the Genetic and Evolutionary Computation Conference (Amsterdam, The Netherlands: ACM), 719–726.

Google Scholar

Moshaiov, A., and Tal, A. (2014). “Family bootstrapping: a genetic transfer learning approach for onsetting the evolution for a set of realated robotic tasks,” in Proceedings of the Congress on Evolutionary Computation (Beijing: IEEE Press), 2801–2808.

Google Scholar

Mouret, J., and Doncieux, S. (2009a). “Overcoming the bootstrap problem in evolutionary robotics using behavioral diversity,” in Proceedings of the 11th IEEE Congress on Evolutionary Computation (Trondheim, Norway: IEEE Press), 1161–1168.

Google Scholar

Mouret, J., and Doncieux, S. (2009b). “Using behavioral exploration objectives to solve deceptive problems in neuro-evolution,” in Proceedings of the Genetic and Evolutionary Computation Conference (Montreal, Canada: ACM Press), 627–634.

Google Scholar

Mouret, J., and Doncieux, S. (2012). Encouraging behavioral diversity in evolutionary robotics: an empirical study. Evol. Comput. 20, 91–133. doi:10.1162/EVCO_a_00048

PubMed Abstract | CrossRef Full Text | Google Scholar

Mueller-Bady, R., Kappes, M., Medina-Bulo, I., and Palomo-Lozano, F. (2016). “Maintaining genetic diversity in multimodal evolutionary algorithms using population injection,” in Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2016) (Denver, USA: ACM), 95–96.

Google Scholar

Pan, S., and Yang, Q. (2010). A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 22, 1345–1359. doi:10.1109/TKDE.2009.191

CrossRef Full Text | Google Scholar

Ramon, J., Driessens, K., and Croonenborghs, T. (2007). “Transfer learning in reinforcement learning problems through partial recycling,” in Proceedings of the 18th European Conference on Machine Learning (Warsaw, Poland: Springer), 699–707.

Google Scholar

Risi, S., Hughes, C., and Stanley, K. (2010). Evolving plastic neural networks with novelty search. Adapt. Behav. 18, 470–491. doi:10.1177/1059712310379923

CrossRef Full Text | Google Scholar

Risi, S., and Stanley, K. (2011). “Enhancing es-hyperneat to evolve more complex regular neural networks,” in Proceedings of the Genetic and Evolutionary Computation Conference (Dublin, Ireland: ACM Press), 1539–1546.

Google Scholar

Risi, S., and Stanley, K. (2013). “Confronting the challenge of learning a flexible neural controller for a diversity of morphologies,” in Proceedings of the Genetic and Evolutionary Computation Conference (Amsterdam, The Netherlands: ACM), 255–261.

Google Scholar

Salah, A., Hart, E., and Sim, K. (2016). “Validating the grid diversity operator: an infusion technique for diversity maintenance in population-based optimisation algorithms,” in Proceedings of the European Conference on the Applications of Evolutionary Computation (Evostar 2016) (Porto, Portugal: Springer), 11–26.

Google Scholar

Sareni, B., and Krahenbuhl, L. (2013). Fitness sharing and niching methods revisited. IEEE Trans. Evol. Comput. 2, 97–106. doi:10.1109/4235.735432

CrossRef Full Text | Google Scholar

Shorten, D., and Nitschke, G. (2015). “Evolving generalised maze solvers,” in Proceedings of the 18th European Conference on the Applications of Evolutionary Computation (Copenhagen, Denmark: Springer), 783–794.

Google Scholar

Stanley, K. (2007). Compositional pattern producing networks: a novel abstraction of development. Genet. Program. Evol. Mach. 8, 131–162. doi:10.1007/s10710-007-9028-8

CrossRef Full Text | Google Scholar

Stanley, K., D’Ambrosio, D., and Gauci, J. (2009). A hypercube-based indirect encoding for evolving large-scale neural networks. Artif. Life 15, 185–212. doi:10.1162/artl.2009.15.2.15202

CrossRef Full Text | Google Scholar

Stanley, K., and Miikkulainen, R. (2002). Evolving neural networks through augmenting topologies. Evol. Comput. 10, 99–127. doi:10.1162/106365602320169811

PubMed Abstract | CrossRef Full Text | Google Scholar

Stone, P., Kuhlmann, G., Taylor, M., and Liu, Y. (2006a). “Keepaway soccer: from machine learning testbed to benchmark,” in Proceedings of RoboCup-2005: Robot Soccer World Cup IX (Berlin, Germany: Springer), 93–105.

Google Scholar

Stone, P., Sutton, R., and Kuhlmann, G. (2006b). Reinforcement learning for robocup-soccer keepaway. Adapt. Behav. 13, 165–188. doi:10.1177/105971230501300301

CrossRef Full Text | Google Scholar

Sutton, R., and Barto, A. (1998). An Introduction to Reinforcement Learning. Cambridge, USA: John Wiley and Sons.

Google Scholar

Taylor, M. E., and Stone, P. (2009). Transfer learning for reinforcement learning domains: a survey. J. Mach. Learn. Res. 10, 1633–1685. doi:10.1007/978-3-642-29946-9_25

CrossRef Full Text | Google Scholar

Taylor, M., Stone, P., and Liu, Y. (2010). Transfer learning via inter-task mappings for temporal difference learning. J. Mach. Learn. 8, 2125–2167. doi:10.1007/978-3-642-29946-9_23

CrossRef Full Text | Google Scholar

Taylor, M., Whiteson, S., and Stone, P. (2006). “Transfer learning for policy search methods,” in ICML 2006: Proceedings of the Twenty-Third International Conference on Machine Learning Transfer Learning Workshop (Pittsburgh, USA: ACM), 1–4.

Google Scholar

Torrey, L., and Shavlik, J. (2009). “Transfer learning,” in Handbook of Research on Machine Learning Applications (Hershey, USA: IGI Global), 17–23.

Google Scholar

Ultsch, A., and Siemon, H. (2001). “Kohonen’s self organizing feature maps for exploratory data analysis,” in Proceedings of the International Neural Network Conference (Dordrecht, The Netherlands: Kluwer), 305–308.

Google Scholar

Urbano, P., and Georgiou, L. (2013). “Improving grammatical evolution in santa fe trail using novelty search,” in Proceedings of the 12th European Conference on Artificial Life (Taormina, Italy: MIT Press), 917–924.

Google Scholar

Velez, R., and Clune, J. (2014). “Novelty search creates robots with general skills for exploration,” in Proceedings of the Genetic and Evolutionary Computation Conference (Vancouver, Canada: ACM), 737–744.

Google Scholar

Verbancsics, P. (2011). Effective Task Transfer through Indirect Encoding. Ph.D. Thesis, Department of Electrical Engineering and Computer Science, University of Central Florida, Orlando, USA.

Google Scholar

Verbancsics, P., and Stanley, K. (2010). Evolving static representations for task transfer. J. Mach. Learn. Res. 11, 1737–1763.

Google Scholar

Verbancsics, P., and Stanley, K. (2011). “Constraining connectivity to encourage modularity in hyperneat,” in Proceedings of the Genetic and Evolutionary Computation Conference (Dublin, Ireland: ACM), 1483–1490.

Google Scholar

Whiteson, S., Kohl, N., Miikkulainen, R., and Stone, P. (2005). Evolving soccer keepaway players through task decomposition. Mach. Learn. 59, 5–30. doi:10.1007/s10994-005-0460-9

CrossRef Full Text | Google Scholar

Whiteson, S., and Stone, P. (2006). Evolutionary function approximation for reinforcement learning. J. Mach. Learn. Res. 7, 877–917.

Google Scholar