- 1Artificial Intelligence Research Center, National Institute of Advanced Industrial Science and Technology, Koto-ku, Japan
- 2Department of Informatics, University of Electro-Communications, Chofu, Japan
- 3Dwango Artificial Intelligence Laboratory, DWANGO Co., Ltd., Bunkyo-ku, Japan
- 4The Whole Brain Architecture Initiative, Tokyo, Japan
Equivalence structure (ES) extraction focuses on multidimensional temporal patterns that appear in a multidimensional sequence and in a different multidimensional sequence. The input of the task is a set of sequences and the output is a set of ESs. An ES is a set of K-tuples comprising elements of K IDs to specify K sequences, and it shows which K-dimensional sequences composed of K sequences specified by its K-tuples are considered equivalent. The standard for determining whether K-dimensional sequences are equivalent is based on the subsequences of the K-dimensional sequences. ES extraction can be used for multidimensional temporal feature extraction, as well as preprocessing for transfer learning or imitation learning. A method called ES incremental search (ESIS) was recently proposed, which is much faster than brute-force search, but the proofs necessary to derive it had not been sufficient. Therefore, it has been unclear why ESIS worked and can be reliable. This paper presents proofs to validate ESIS, as well as a property of the solution of ESIS that could be useful for developing a faster method.
1. Introduction
Equivalence structure (ES) extraction is conducted for focusing on multidimensional temporal patterns in a multidimensional sequence that is similar to those in a different multidimensional sequence (Satoh and Yamakawa, 2017). The extraction is a task, where the input is a set of sequences and the output is a set of ESs. A K-dimensional ES is a set of K-tuples with elements that are K IDs for K sequences, and each of the K-tuples specifies a K-dimensional sequence specified by the IDs of its K-tuple. The K-tuples of an ES indicate which K-dimensional sequences are considered equivalent. The standard for determining whether K-dimensional sequences are equivalent is based on the subsequences of the K-dimensional sequences. If we consider a tuple of an ES to represent a relation among sequences specified by its IDs, then an ES can be seen as an analogous relation of such relations. In this sense, ES extraction can be considered metarelation mining.
ES extraction can be used for multidimensional temporal feature extraction, as well as preprocessing for transfer learning and imitation learning. For examples of imitation learning, in experiments conducted by Katz et al. (2016) and Delhaisse et al. (2017), the correspondence relation between a teacher and student must be known, or it is necessary to tell key poses to a student before conducting imitation learning. However, there can be some situations, where these conditions are impossible. In such situations, ES extraction can be used to find correspondence relations between a student and teacher.
Motif discovery techniques (Lonardi and Patel, 2002; Tanaka et al., 2005; Minnen et al., 2007; Ghoneim et al., 2008; Vahdatpour et al., 2009; Mueen and Keogh, 2010; Liu et al., 2012) can be considered similar to ES extraction. The techniques allow for obtaining multidimensional temporal repeated patterns. However, the patterns must be repeated in the same multidimensional sequence. In other words, the techniques do not reveal multidimensional temporal patterns that appear in a multidimensional sequence and in a different multidimensional sequence, whereas ES extraction focuses on such patterns.
There are two methods to extract ESs (Satoh and Yamakawa, 2017). One is brute-force search (BFS), where all possible K-tuples are considered. BFS is usually infeasible, since a serious combinatorial explosion occurs in the process. The other method is the recently proposed ES incremental search (ESIS) (Satoh and Yamakawa, 2017). In the process of ESIS, K-dimensional ESs are obtained from candidates generated from (K − 1)-dimensional ESs, and ESIS obtained ESs much faster than BFS in experiments. However, it has been unclear why ESIS worked and can be reliable, because the proofs necessary to derive ESIS have not been sufficiently obtained.
This paper presents proofs to validate ESIS, as well as a property of the solution of ESIS that could be useful for developing a faster method. We investigated the property by conducting an experiment using motion capture datasets. ESIS can be derived by making an assumption, and a previous study experimentally confirmed that the assumption was satisfied using only noise-free artificial data (Satoh and Yamakawa, 2017). Therefore, in this study, we conducted another experiment to confirm that the assumption is satisfied when using real datasets with noise.
2. Equivalence Structures and Their Search Methods
2.1. Equivalence Structures
Figure 1 illustrates ES extraction. Given N sequences, we want to find sets of tuples that show which multidimensional sequences are equivalent. A K-tuple specifies a K-dimensional sequence, as shown in the figure. Such sets of tuples are called ESs. We assign an ID to each sequence and describe the IDs with a number #. For example, when the input is a set of seven sequences, their IDs are #1, …, #7. In the figure, the two three-dimensional sequences specified by tuples ⟨#1, #2, #3⟩ and ⟨#7, #6, #4⟩ are considered equivalent. We only consider tuples with elements that are not duplicated, so the number of all possible K-tuples is N PK. As a standard to determine whether K-dimensional sequences are equivalent, we use a dissimilarity function where each of the subsequences of one sequence is compared to all the subsequences of the other. We describe the details in Section 5.1.
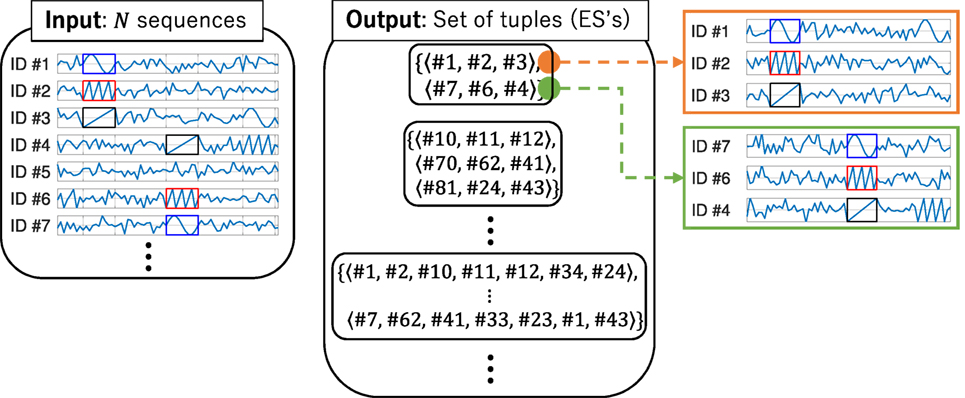
Figure 1. An illustration of the input and output of equivalence structure (ES) extraction. The left figure shows the input, and the center figure shows the output. The right figure shows an example of an ES where the elements are tuples ⟨#1, #2, #3⟩ and ⟨#7, #6, #4⟩. A subsequence of a three-dimensional sequence specified by one of the tuples closely resembles that by the other tuple.
One difficulty in the ES extraction is that we cannot easily make use of dissimilarities between one-dimensional sequences in order to calculate the dissimilarity between higher-dimensional sequences. This is because it is not always true that higher-dimensional sequences are considered equivalent if all their possible lower-dimensional sequences are considered equivalent. Figure 2 shows an example of this difficulty. Another difficulty is that BFS is usually not feasible, since the number of all possible K-tuples is N PK.
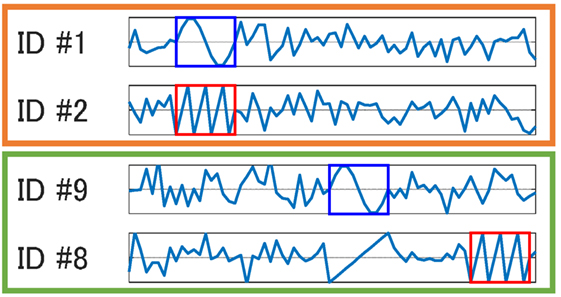
Figure 2. An illustration of one type of difficulty in equivalence structure extraction. There is a pattern for ID #1 that is similar to a pattern for ID #9, as well as a pattern for ID #2 that is similar to a pattern for ID #8. However, when we see them as two-dimensional sequences, there are no similar patterns.
2.1.1. Properties of a Dissimilarity Function
We use a dissimilarity function as a standard for equivalence between two K-dimensional sequences specified by two K-tuples, and . It is considered that a dissimilarity function usually has the following symmetries:
where
We define P(K) as the set of all K-permutations of [K], which in turn is defined as {1, …, K}. This means that if , then the number of other dissimilarities that are equal to is 2K! − 1; otherwise, the number is K! − 1. The dissimilarity function used in this paper has the symmetries.
2.2. Search Methods
There are two methods for ES extraction (Satoh and Yamakawa, 2017). One is BFS, where all possible K-dimensional sequences specified by K-tuples are compared to find K-dimensional ESs. The other is ESIS, which uses (K − 1)-dimensional ESs to find K-dimensional ESs. Previously, two experiments showed that ESIS can obtain ESs much faster than BFS (Satoh and Yamakawa, 2017).
2.2.1. Brute-Force Search
The procedure of BFS is very simple, as shown in Algorithm 1. One option for the stopping condition is one where there are no K-dimensional ESs. However, it is not guaranteed that there are no (K + 1)-dimensional ESs if there are no K-dimensional ESs. We refer to a K-dimensional ES obtained by BFS as a complete K-dimensional ES .
2.2.1.1. Number of Comparisons
If we use a method that simply compares all possible K sequences in order to obtain K-dimensional ESs, the number of comparisons is . However, considering the property of dissimilarity in Equation (1), the number can be reduced to:
because
We use the property in Equation (1) to reduce the number of the comparisons in the procedure of BFS. However, a combinatorial explosion still occurs.
2.2.1.2. A Property of Complete ESs
We consider two complete K-dimensional ESs and . If
then we call permutation-equivalent to , and vice versa. For example, if the set {⟨#1, #2, #3⟩, ⟨#4, #5, #6⟩} is a complete ES, then sets {⟨#1, #3, #2, ⟩, ⟨#4, #6, #5⟩} and {⟨#2, #1, #3, ⟩, ⟨#5, #4, #6⟩} are also complete ESs and permutation-equivalent to each other. The number of ESs that are permutation-equivalent to a complete K-dimensional ES is less than or equal to K! − 1. It is not necessary to keep ESs that are permutation-equivalent to existing ESs, since they can be generated from the corresponding ESs. For the experiments of this study, we discuss ESs after removing ESs that are permutation-equivalent to one of the other ESs.
2.2.2. ES Incremental Search
ESIS was proposed since BFS is usually not feasible (Satoh and Yamakawa, 2017). ESIS uses of (K − 1)-dimensional ESs to generate candidates for K-dimensional ESs. A candidate for a K-dimensional ES from a (K − 1)-dimensional ES is generated by the following function:
where . This function can be derived from Theorem 1, which we prove in Section 3.
Algorithm 2 shows the procedure of ESIS.
A candidate can be permutation-equivalent to other candidates. Since we do not need ESs that are permutation-equivalent to existing ESs. Step 9 of Algorithm 2 is not implemented if is permutation-equivalent to existing candidates. Furthermore, all complete two-dimensional ESs must be stored for the function g in Step 8 of Algorithm 2.
3. Validity and a Property of ESIS
This section clarifies the theorem and proof to verify ESIS. To begin with, we define the following function:
which drops the kth elements of all the K-tuples of a set U (K). The following assumption is necessary to derive ESIS (Satoh and Yamakawa, 2017).
Assumption 1:
where are complete K-dimensional ESs, and are complete (K − 1)-dimensional ESs.
For example, if {⟨#1, #2, #3⟩, ⟨#7, #6, #4⟩}, then sets {⟨#2, #3⟩, ⟨#6, #4⟩}, {⟨#1, #3⟩, ⟨#7, #4⟩}, and {⟨#1, #2⟩, ⟨#7, #6⟩} are all subsets of (K − 1)-dimensional ESs. Figure 3 shows an illustration of the example. How much this assumption holds depends on conditions such as the standard for the dissimilarity between multidimensional sequences and its parameters, but it is considered that the assumption holds to a certain extent.
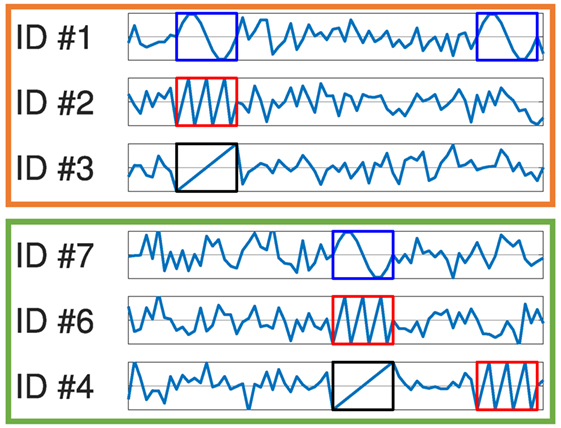
Figure 3. An illustration of Assumption 1. There is a three-dimensional equivalence structure (ES) that has tuples ⟨#1, #2, #3⟩ and ⟨ #7, #6, #4⟩ and a two-dimensional ES that has tuples ⟨#1, #2⟩, ⟨#7, #6⟩, and ⟨ #1, #4⟩. In the two-dimensional sequences, there is a subsequence that is shown by blue and red boxes.
The following corollary obviously holds under Assumption 1.
Corollary 1:
where
PROOF. Under Assumption 1, the following is clear:
From the definition of K-tuples to specify K-dimensional sequences, and .
Hence, Equation (13) holds. □
The summation of the cardinalities of all candidates for K-dimensional ESs satisfies the following inequality:
where the equality holds if and only if:
This means that every possible (K − 1)-tuple belongs to one of (K − 1)-dimensional ESs, which is unlikely to occur. Therefore, using Corollary 1, we can usually reduce the number of tuples to search.
Moreover, we can derive the following lemma under Assumption 1.
Lemma 1:
For example, if there is a complete four-dimensional ES {⟨#1, #2, #3, #4⟩, ⟨#5, #6, #7, #8⟩}, then , , and are sets {⟨#1, #2⟩, ⟨#5, #6⟩}, {⟨#1, #3⟩, ⟨#5, #7⟩}, and {⟨#3, #4⟩, ⟨#7, #8⟩}, respectively, and they are all subsets of two-dimensional ESs.
PROOF. We use mathematical induction to prove Lemma 1. Under Assumption 1, we see that
where ⟨p1, …, pK⟩ is a K-permutation of [K], 3 < K, and
Consider a particular complete K-dimensional ES and a particular complete (K − 1)-dimensional ES that satisfies . If we additionally drop the pK–first elements of all the tuples of , we have
From Equation (20), the right-hand side can be rewritten and we have
Since the left-hand side is a superset of the right-hand side, the left-hand side is still the superset even after removing the set from the right-hand side. Thus, we obtain:
Next, we assume:
where . Under this assumption, it is clear that
where
Consider a particular complete K-dimensional ES and a particular complete (K–k–1)-dimensional ES that satisfy . If we also drop the th elements of all the tuples of , we have
From Equation (26), the right-hand side can be rewritten and we have
Since the left-hand side is a superset of the right-hand side, the left-hand side is still the superset even after removing the set from the right-hand side. Thus, we obtain:
From Equations (24) and (30), we obtain:
Hence, we see that
□
Lemma 1 tells us that the sets of tuples composed of the ith and jth IDs of the tuples of a K-dimensional ES are subsets of a two-dimensional ES. Considering Lemma 1, we can derive the following theorem.
Theorem 1:
where
and and are a particular complete K-dimensional ES and a particular complete (K − 1)-dimensional ES that satisfy Equation (35), respectively.
PROOF. From Equation (35), it is clear that
From Lemma 1, we see that
Let be a ck that satisfies
We then see that
From this equation, we find that
Therefore, we have
□
The number of possible IDs for each in Equation (41) is less than or equal to . It follows that
where ,
The equality holds if and only if the number of possible values for u in Equation (33) is (N − K + 1). This is unlikely to occur. Therefore, we can usually reduce the number of tuples to search more than just by using Corollary 1. From Equations (17) and (43),
4. A Property of the Solution Obtained by ESIS
In this section, we consider ESs obtained by ESIS (simply referred to as ESs in this section). We denote a K-dimensional ES by and let be the number of the dimensions of the highest-dimensional ES. Since ESIS was derived under Assumption 1, if , there are (K–k)-tuples in (K–k) -dimensional ESs that can be expressed in the following form:
where ⟨p1, …, pk⟩ is a k-permutation of [K], 2 ≤ K–k, , and 1 ≤ k. We call such a K-tuple a derivative tuple.
The number of derivative tuples that can be derived from a K-dimensional ES is
The existence of derivative tuples may cause a substantial increase in the processing time of ESIS when is large. Therefore, solving this problem may lead to the development of a faster ES search method.
5. Experiments
Experiments were previously conducted using a noise-free artificial dataset and two motion capture datasets (Satoh and Yamakawa, 2017). The former experiment confirmed that ESIS can obtain the same ESs as those obtained by BFS, which is possible if Assumption 1 holds. The latter experiment confirmed that ESIS can obtain ESs that are considered plausible as a correspondence relation between two motion capture datasets, but BFS was stopped because the processing time exceeded one day when K was only three. However, no previous investigation has examined whether ESIS can obtain the same ESs as BFS while using real datasets with noise.
This section describes two experiments conducted using the same motion capture datasets used in a previous study (Satoh and Yamakawa, 2017). The main aim in the first experiment is to investigate derivative tuples described in Section 4. The main aim in the second experiment is to investigate whether or not ESIS can obtain the same ESs as those obtained by BFS while using real datasets. Section 5.1 first describes the dissimilarity function used as a standard for equivalence between multidimensional sequences.
5.1. Dissimilarity Function
We used the same dissimilarity as in a previous study (Satoh and Yamakawa, 2017), which utilizes all the mean-square values (MSVs) of Euclidean distances between subsequences of each sequence. Given N sequences , we denote a subsequence by:
where t is time, k is an ID, τ is the length of the subsequence, and ctr is the transposition of a vector c.
Next, we consider the following MSV of the Euclidean distances between a subsequence of a K-dimensional sequence specified by a K-tuple u1 and that by a different K-tuple u2
where u1, k and u2, k denote the kth elements of u1 and u2, respectively. Then, we define the following quantity , which is the smallest of ,
Next, we define the following quantity, which is 1 if or 0 if :
where h is the Heaviside step function. Using these quantities, the following dissimilarity function d u1, u2 is calculated as:
where
is used as a weight for a subsequence. This means that the greater is, the more likely the two K-dimensional sequences are to be considered equivalent when . β ensures that the range of values of the dissimilarity function is in the interval [0,1].
Based on values of the dissimilarity function in Equation (52), we used hierarchical clustering in the Statistics and Machine Learning Toolbox version 10.1 in the MATLAB R2015b to obtain ESs. θhc denotes the threshold for the clustering.
5.2. Experiment 1
We used two motion capture datasets obtained from two different people who were walking. We obtained the two datasets (file names 07 01.c3d and 07 02.c3d) from mocap.cs.cmu.edu, which were the same datasets used in the previous study (Satoh and Yamakawa, 2017). We refer to the two datasets as dataset 1 and dataset 2. It can usually be determined that each sequence of a motion capture dataset corresponds to which part of the body, but we assumed that it was unknown in order to test the performance of ES extraction (Satoh and Yamakawa, 2017). The ESs to be obtained can be considered to indicate correspondence relations between the positions of the two different people in the datasets.
We set the threshold θMSV in Equation (51) to 0.06, while the threshold θhc for the hierarchical clustering is 0.2, and the length τ of a subsequence is 10. For preprocessing, we first normalized each of the sequences so that the means and standard deviations would be 0 and 1, respectively. Next, we used the simple moving average technique as a low-pass filter, which uses the mean of n points of a sequence. We set n to six, so that all of the mean squared errors between original sequences and sequences after the filtering process would be less than 0.01. Then, we down sampled the sequences by six. Since we used two motion capture datasets, we restricted the elements of a tuple to IDs corresponding to only one of the two datasets.
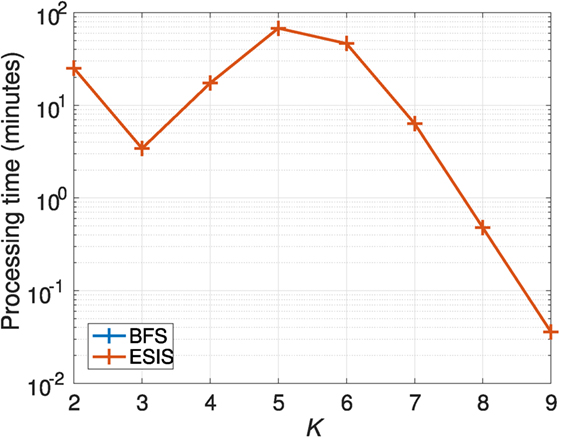
Figure 4 shows the processing time for BFS and ESIS. BFS could not obtain three-dimensional ESs within one day, but ESIS could obtain K-dimensional ESs within 68 min for K = 2, …, 8. The total processing time of ESIS was 167 min.
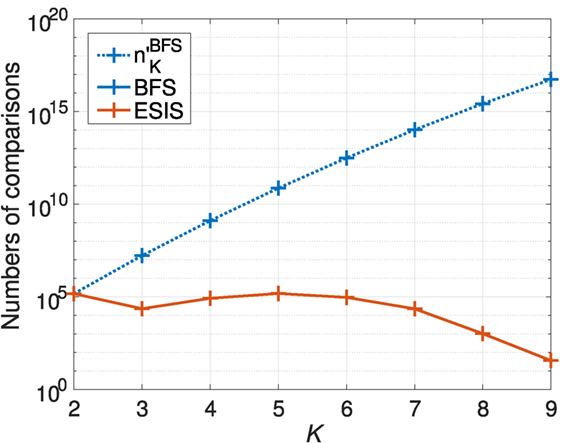
Since all possible K-tuples to specify K-dimensional sequences are considered in BFS, we can calculate the number comparisons of K-dimensional sequences for BFS in the following form obtained from Equation (4):
where N1(= 22) is the number of sequences for dataset 1 and N2(= 18) is that for dataset 2. Figure 5 shows the numbers and the numbers of comparisons for BFS and ESIS. The number of comparisons for ESIS was significantly lower than that for BFS when K = 3, …, 9.
The numbers of two- to eight-dimensional ESs obtained by ESIS were 27, 49, 72, 59, 32, 10, and 1, respectively. Figure 6 shows the sums of the cardinalities of ESs obtained by ESIS and the numbers of derivative tuples in the ESs. The number of derivative tuples was much greater than that of the other tuples for K = 2, …, 7.
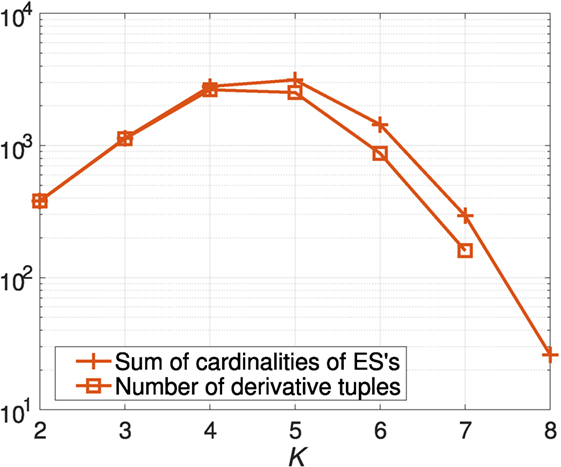
Figure 6. Sums of cardinalities of ESs obtained by ESIS and numbers of derivative tuples in the ESs for Experiment 1.
The highest ES obtained was an eight-dimensional ES with 26 tuples, as shown in Table 1. The elements in their original space are shown in Figure 7A. Figures 7B–D show three seven-dimensional ESs that do not have any derivative tuples. Although the three seven-dimensional ESs do not have the highest-dimension, the ESs appear to be useful for matching the dimensions of datasets 1 and 2.
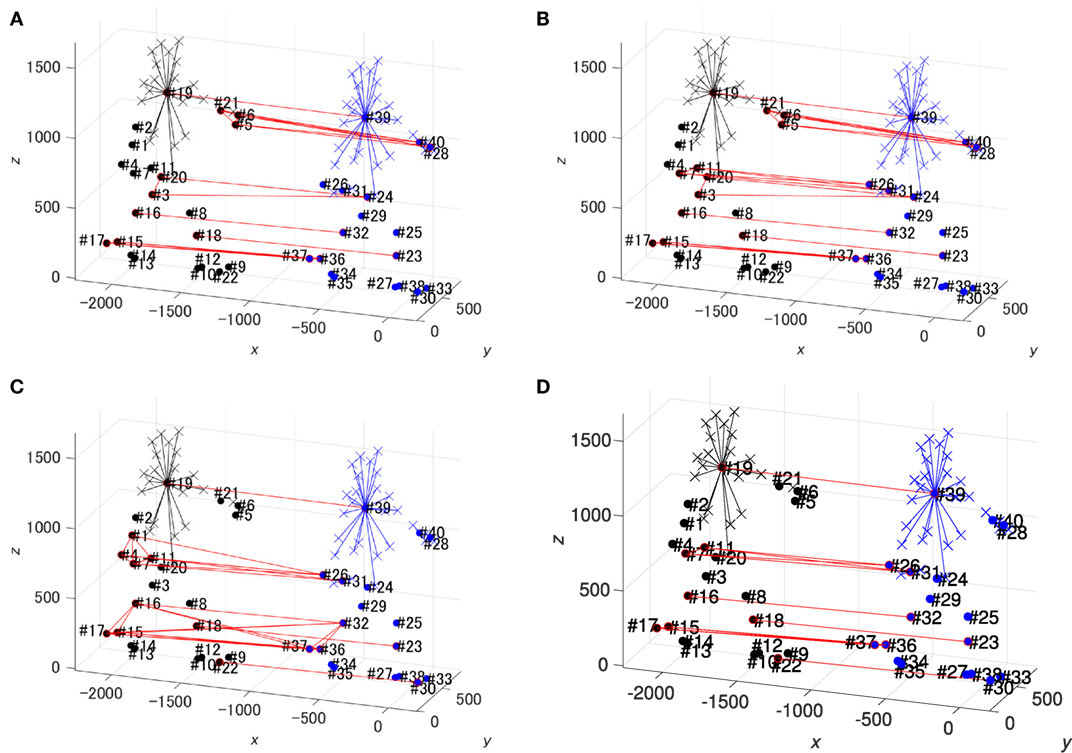
Figure 7. Equivalence structures obtained by ES incremental search: (A) eight-dimensional ES, (B) seven-dimensional ES 1, (C) seven-dimensional ES 2, and (D) seven-dimensional ES 3. Black points and cross marks represent dataset 1 at t = 1, while blue points represent dataset 2 at t = 150. Cross marks represent sequences that were merged in preprocessing. The elements at each position in the tuples are connected with red lines.
5.3. Experiment 2
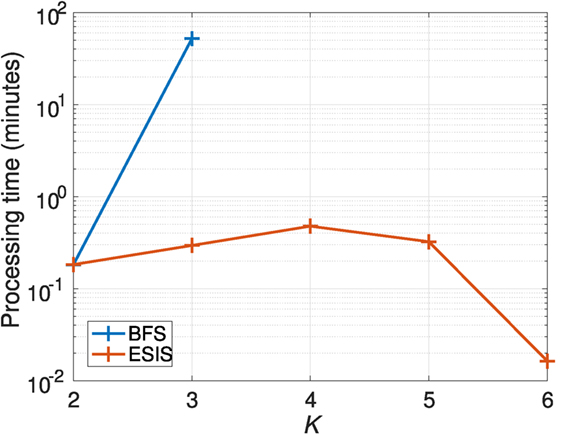
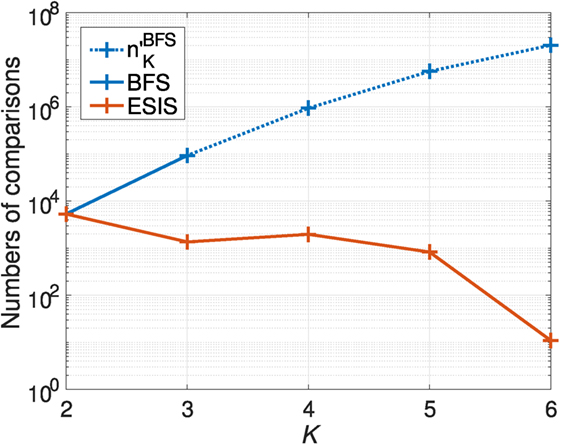
To ensure that the BFS procedure would finish within one day when K > 2 in the second experiment, we used only sequences corresponding to the IDs in the highest-dimensional ES obtained by ESIS for Experiment 1 (Table 1). The relevant sequences were #3, #5, #6, #15, #16, #17, #18, #19, #20, #21, #23, #24, #28, #32, #36, #37, #39, and #40.
Figures 8 and 9 show the processing time and the numbers of comparisons, respectively. Nine two-dimensional ESs were obtained by both BFS and ESIS. However, 14 three-dimensional ESs were obtained by BFS, whereas ESIS obtained 15. The sum of the cardinalities of the three-dimensional ESs for BFS was 257, whereas that for ESIS was 168. This means that Assumption 1 did not hold in this experiment and ESIS could not obtain the same ESs as BFS. However, we cannot say which solution was better in this case, because we do not have any measure to tell which ES was better.
6. Conclusion
This paper has presented proofs to validate ESIS and investigated derivative tuples, which are the subtuples of the tuples of an ES that can slow down the process of ES extraction. In addition, we have shown a case where ESIS did not obtain the same ESs as those obtained by BFS using real datasets.
In the future, we plan to determine whether or not it is necessary to obtain exactly the same ESs as those obtained by BFS. To do this, a measure of the usefulness of an ES will be necessary. We also plan to develop a method to obtain ESs faster than ESIS does in consideration of the findings in this paper, especially the property of ESIS for derivative tuples.
Author Contributions
All the authors contributed to the writing of the manuscript. SS proved the main theorem, designed the experiments, and prepared the manuscript as the main author. YT contributed to the validation of ESIS with helpful comments. HY supervised all the aspects of the research and provided helpful comments.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This paper is based on results obtained from a project commissioned by the New Energy and Industrial Technology Development Organization (NEDO). The motion capture data used in this paper were obtained from mocap.cs.cmu.edu. The database was created with funding from NSF EIA-0196217.
References
Delhaisse, B., Esteban, D., Rozo, L., and Caldwell, D. (2017). “Transfer learning of shared latent spaces between robots with similar kinematic structure,” in Neural Networks (IJCNN), 2017 International Joint Conference on IEEE (Anchorage: IEEE), 4142–4149.
Ghoneim, A., Abbass, H., and Barlow, M. (2008). Characterizing game dynamics in two-player strategy games using network motifs. IEEE Trans. Syst. Man Cybern. B Cybern. 38, 682–690. doi: 10.1109/TSMCB.2008.918570
Katz, G., Huang, D.-W., Gentili, R., and Reggia, J. (2016). “Imitation learning as cause-effect reasoning,” in International Conference on Artificial General Intelligence, eds B. Steunebrink, P. Wang, and B. Goertzel (New Yoke: Springer), 64–73.
Liu, J., Abbass, H. A., Green, D. G., and Zhong, W. (2012). Motif difficulty (md): a predictive measure of problem difficulty for evolutionary algorithms using network motifs. Evol. Comput. 20, 321–347. doi:10.1162/EVCO_a_00045
Lonardi, J., and Patel, P. (2002). “Finding motifs in time series,” in Proc. of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 2nd Workshop on Temporal Data Mining (Edmonton), 53–68.
Minnen, D., Isbell, C., Essa, I., and Starner, T. (2007). “Detecting subdimensional motifs: an efficient algorithm for generalized multivariate pattern discovery,” in Data Mining, 2007. ICDM 2007. Seventh IEEE International Conference on (Omaha: IEEE), 601–606.
Mueen, A., and Keogh, E. (2010). “Online discovery and maintenance of time series motifs,” in In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Washington: ACM), 1089–1098.
Satoh, S., and Yamakawa, H. (2017). “Incremental extraction of high-dimensional equivalence structures,” in Neural Networks (IJCNN), 2017 International Joint Conference on (Anchorage: IEEE), 1518–1524.
Tanaka, Y., Iwamoto, K., and Uehara, K. (2005). Discovery of time-series motif from multi-dimensional data based on mdl principle. Mach. Learn. 58, 269–300. doi:10.1007/s10994-005-5829-2
Keywords: equivalence structure, transfer learning, imitation learning, combinatorial explosion, metarelation mining
Citation: Satoh S, Takahashi Y and Yamakawa H (2017) Validation of Equivalence Structure Incremental Search. Front. Robot. AI 4:63. doi: 10.3389/frobt.2017.00063
Received: 25 July 2017; Accepted: 20 November 2017;
Published: 19 December 2017
Edited by:
Fabrizio Riguzzi, University of Ferrara, ItalyReviewed by:
Hussein Abbass, University of New South Wales, AustraliaNicola Di Mauro, Università degli studi di Bari Aldo Moro, Italy
Copyright: © 2017 Satoh, Takahashi and Yamakawa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Seiya Satoh, c2VpeWEuc2F0b2hAYWlzdC5nby5qcA==
 Seiya Satoh
Seiya Satoh Yoshinobu Takahashi
Yoshinobu Takahashi Hiroshi Yamakawa
Hiroshi Yamakawa